Non-Cooperative Behavior Management in Large-Scale Group Decision-Making Considering the Altruistic Behaviors of Experts and Its Application in Emergency Alternative Selection

1  Introduction

Over the past decades, emergencies have frequently occurred in China, causing irreversible damage. For example, the massive explosion in Tianjin, China, resulted in the death of 154 people1 ; the liquefied gas tanker explosion in Jinyu Petrochemical, resulted in the death of 10 people2. When such an emergency occurs, a high-quality emergency decision-making process can effectively reduce potentially adverse impacts [1]. Usually, emergency decision-making problems have three typical characteristics: time limitation, incomplete information, and decision pressure resulting from potentially serious effects [2,3]. Thus, solving emergency decision-making problems efficiently is definitely a great challenge for both the government and society. Because of the complexity and uncertainty of emergency events, it is necessary to invite experts from different fields and specialties to evaluate alternatives. When the number of experts exceeds 11, it can be regarded as a large-scale group decision-making (LSGDM) problem [4].

Compared with conventional group decision-making problems, LSGDM problems are more complicated, facing many challenges not only in the scale of experts but also in experts’ relationships [5]. To cope with the scale of an LSGDM problem, the dimensionality reduction which divides a large-scale expert team into several subgroups is deemed essential. Clustering analysis is known as one of the most useful dimensionality reduction methods. In this regard, traditional clustering algorithms such as the K-means clustering algorithm [6], fuzzy equivalence relation (FER) [7] and grey clustering [8] have been widely used. However, these methods cluster experts into subgroups based on the opinion similarity of experts but fail to consider the relationships among experts. With the advancement of technology and society, people can communicate and transmit information conveniently, and experts involved in decision-making problems are no more independent individuals. Social network analysis (SNA) has become a common technique for LSGDM problems. To this point, Tian et al. [9] extended the community detection method proposed by Newman et al. [10] to divide large-scale experts in a social network into different communities. Using the trust values between experts, Xu et al. [4] applied the Louvain method [11] based on the idea of modularity to classify experts into different communities in a social network. The above SNA models clustered experts according to the relationships between experts. However, the similarity of evaluation values of alternatives and the trust values between experts both play important roles in grouping experts. Du et al. [12] proposed a trust-similarity analysis (TSA)-based clustering method to manage the clustering operation in LSGDM events. Yu et al. [13] developed a trust-constrained K-means clustering algorithm in a social network large-scale decision-making model. However, in their studies, they only considered a single constraint to overcome the defect of grouping low-trust experts into the same cluster caused by traditional clustering algorithms based on preference similarity, but failed to overcome other problems, for example, high-trust experts may be assigned to different clusters. In this sense, this paper proposes a pairwise trust constrained K-means (PTC-Kmeans) clustering algorithm to cluster experts which considers the similarity of evaluation information of alternatives and the trust values between experts, simultaneously.

Besides, due to different backgrounds and interests, experts in a group may show non-cooperative behaviors in the decision-making process. How to effectively manage the non-cooperative behaviors of experts is another challenge in LSGDM problems [5]. To date, many studies [14–18] have considered the non-cooperative behaviors of experts based on the implicit assumption that the full degree of cooperation of experts is to totally accept the revisions proposed by the moderator. However, in actual situations, due to deep trust or close relationships, some individuals may incorporate the well-being of others into their own decision even at their own expense. This behavior is named altruistic behavior [19]. If an expert has a high degree of trust in another person, he/she may contribute more than a recommendation to protect that person’s interest. In other words, the existence of altruistic behavior may make up for the loss caused by the non-cooperative behaviors of experts [20]. Existing literature on non-cooperative behavior management assumes that no one would make more change than the suggested value, which essentially restricts experts with altruistic behaviors from making more contributions to the group consensus. Tang et al. [20] proposed a multi-attribute group decision-making (MAGDM) model which utilized the altruistic behaviors of experts to compensate for the adverse effects caused by the non-cooperative behaviors of other experts. However, they only focused on one type of non-cooperative behaviors in their model and did not take the whole problem into account, leading to a lack of integrity. How to incorporate altruistic behavior analysis into the process of consensus reaching and compensate for different types of non-cooperative behaviors are challenges for LSGDM.

Bear all the above analysis in mind, this paper introduces a clustering method considering the similarity of attribute values and the trust relations of experts and then develops a consensus model taking into account the altruistic behaviors of experts. A PTC-Kmeans clustering algorithm is presented to cluster experts into subgroups. After reducing the group size to small communities, we then identify three types of non-cooperative behaviors of experts: 1) experts refuse to adjust their preferences or adjust them slightly, or even change their preferences in an opposite direction; 2) hesitant experts randomly provide their preferences to avoid revealing their true intentions; 3) expert deliberately decrease/increase the evaluation value of alternatives. We propose three kinds of feedback mechanisms with respect to three types of non-cooperative behaviors, which allow experts to have altruistic behaviors to compensate for the loss caused by non-cooperative behaviors. The main contributions can be summarized as follows:

(1)   This study proposes a PTC-Kmeans clustering algorithm to cluster experts, which considers the similarity of evaluation information given by experts and the trust values between experts, simultaneously.

(2)   This study fully considers three kinds of non-cooperative behaviors of experts and distinguishes non-cooperative behaviors based on the differences between expert preferences and cluster preferences.

(3)   This paper proposes three kinds of feedback mechanisms with respect to the non-cooperative behaviors of experts, which allows experts to have altruistic behaviors to compensate for the loss caused by non-cooperative behaviors and applies weight penalty mechanisms to decrease the weights of experts with non-cooperative behaviors and increases the consensus level.

The rest of this paper is organized as follows: Section 2 performs a literature review about emergency decision-making and LSGDM methods. In Section 3, we introduce the PTC-Kmeans clustering algorithm to classify a large group of experts into subgroups. Section 4 discusses the management of non-cooperative and altruistic behaviors. We utilize an application example to illustrate the usefulness of the proposed model in Section 5. Concluding remarks are given in Section 6. To better understand this study, the mathematical symbols used in this study are presented in Table S1 in Appendix.

2  Literature Review

In this part, we present the literature review of LSGDM problems. In Section 2.1, we give a snapshot of emergency LSGDM problems. In Section 2.2, we present a short review of clustering algorithms. The review of the advance of SNA for LSGDM is shown in Section 2.3.

2.1 A Snapshot of Emergency LSGDM Problems

When emergencies occur, we often need to make effective decisions in a short period of time. Because of the complexity of emergency problems, time limitations and potential risks, it is difficult for a single expert to solve the emerging problems. Related studies have shown that in emergency decision-making, the decision made by concentrating the wisdom of a group is more reliable than that made by an individual [21,22]. Thus, it is necessary to assemble experts with different backgrounds, experiences and knowledge to make a decision with a high level of consensus. Li et al. [23] proposed an LSGDM model, which adopted fuzzy cluster analysis to integrate heterogeneous information of experts to select the best rescue plan in an emergency situation. Cao et al. [21] proposed a novel opinion formation model that considered psychological factors and relevant opinions in the emergency decision-making process. Liu et al. [24] proposed a method for GDM that introduced an expected multiplicative consistency of incomplete probabilistic linguistic preference relations to avoid the loss of evaluation information of experts and applied the method to address a forest fire rescue problem. Xu et al. [4] proposed a consensus model that considered trust relations and preference risks to manage non-cooperative behaviors in large-group emergency decision-making.

From the above analysis, we can see that current studies have considered different ways to deal with emergency decision-making problems, but seldom considered the non-cooperative behaviors of experts in emergency decision-making problems, and the existing models, which are used to manage non-cooperative behaviors of experts, do not consider the altruistic behaviors of experts. In this study, we shall introduce the altruistic behavior to compensate for the loss caused by the non-cooperative behaviors of experts.

2.2 A Short Review on Clustering Algorithms to Reduce the Dimension of a Large-Scale Group

Clustering analysis has been commonly used to reduce the dimension of many experts in LSGDM problems. A clustering process can divide a large group of experts into several subgroups so that the data in the same cluster is more similar than that from other clusters [25].

As an unsupervised machine learning algorithm, the K-means clustering algorithm is one of the most widely used clustering algorithms. It works by classifying all data objects into k clusters based on k initial clustering centroids and then iteratively refining them. Wu et al. [26] adopted the K-means clustering algorithm to classify experts with fuzzy preference relations based on the Euclidean distance. Liu et al. [27] introduced the probability K-means clustering algorithm to overcome the weakness that the K-means clustering algorithm is sensitive to the initially selected centroid points, and detected sub-groups from the preferences of all experts. In the heterogeneous LSGDM environment, Tang et al. [28] proposed the ordinal K-means clustering algorithm to classify experts into several subgroups. From the above studies, we can see that the traditional K-means clustering algorithm classifies experts mainly based on the similarity among data objects, but ignores the background knowledge from real decision scenarios.

Some experiments have proved that the prior knowledge of objects is helpful for obtaining good clustering results [29]. In this regard, Wagstaff et al. [30] proposed a semi-supervised clustering algorithm, the constrained K-means clustering algorithm, which can integrate the background knowledge into the framework of the K-means clustering algorithm. Compared with the traditional K-means clustering algorithm, the constrained K-means clustering algorithm considers two types of constraints, namely, must-link constraints and cannot-link constraints. The must-link constraints specify that two instances must be assigned into the same cluster while the cannot-link constraints indicate that two instances must be in different clusters. Considering the importance of the similarity of experts’ evaluation information and the trust values among experts in a clustering process, in this study, we propose the PTC-Kmeans clustering algorithm to cluster the experts into subgroups, which utilizes the trust relations of experts to form must-link and cannot-link constraints.

2.3 Advances of SNA for LSGDM

With the advancement of technology and information, GDM is often conducted within the context of a social network, in which individuals have trust relationships with each other. A social network is composed of a set of nodes and a set of edges, where the nodes represent experts in society and the edges represent the trust relationships among experts. In this study, the nodes are set as E={e1,e2,⋯,em} and the edge between eh and el is set as l(eh,el). A fuzzy social-matrix [8] A=(ahl)m×m on E is a relation with a membership function us:E×E→[0,1], and us(eh,el)=ahl, where ahl∈[0,1] denotes the trust degree that expert eh assigns to expert el.

In real LSGDM problems, it is probable that some experts are unable to accurately provide the trust values for other experts. Thus, some studies [31] classify the trust relationships into three types in SNA: direct, indirect and irrelevant trust. The types of trust relationships are shown in Fig. 1. In this figure, ‘direct trust’ means expert eh has a direct trust relationship toward expert el; ‘indirect trust’ means although there is no direct trust relationship between expert eh and el, expert eh can still establish an indirect trust relationship toward expert el through other experts; ‘irrelevant trust’ means that there is no direct or indirect trust relationship between expert eh and el. The existence of indirect and irrelevant trust may cause the incompletion of the sociometric. In this study, indirect trust is calculated with reference to Eqs. (1)–(6) in the article written by Liao et al. [32]. Set the trust degree to 0.01 if there is no direct or indirect relationship between two experts. The value of 0.01 indicates an irrelevant relationship between the two experts.

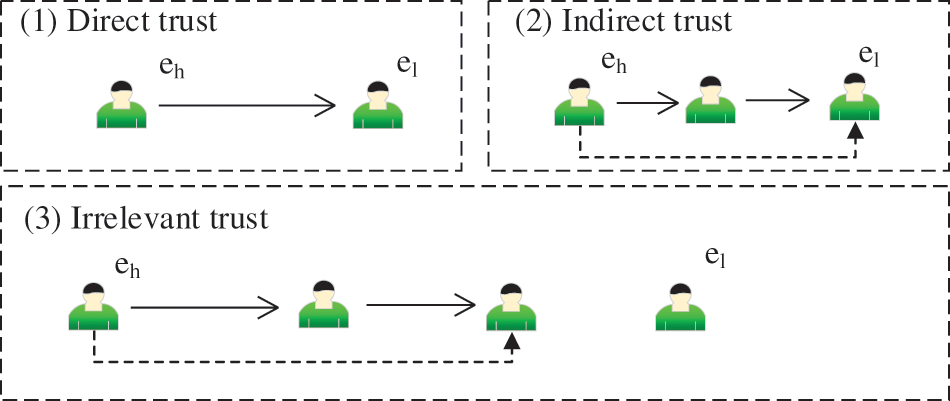
Figure 1: The types of relationship

As a new type of decision-making problem, group decision-making with SNA integrates the trust relations of experts in the process of clustering, consensus reaching and alternative selection [12]. Due to the increasing number of experts in LSGDM, it is difficult to adjust the inconsistent elements and reach a consensus. Experts who come from different fields and represent different interests are likely to display non-cooperative behaviors. The existence of non-cooperative behaviors of experts greatly affects the efficiency of decision-making. Thus, some studies proposed methods to manage non-cooperative behaviors of experts based on the social network. Zhang et al. [18] defined three types of non-cooperative behaviors: 1) dishonest behavior; 2) disobedient behavior; 3) divergent behavior, and proposed an SNA-based consensus framework to manage non-cooperative behaviors. Gao et al. [33] developed a consensus reaching algorithm with non-cooperative behavior management for personalized individual semantics-based social network GDM problem. Li et al. [34] introduced a novel framework based on the WeChat-like interaction social network to manage non-cooperative behaviors of experts. Xu et al. [4] proposed a consensus model based on interval-valued intuitionistic fuzzy numbers, which considered the trust relations of experts in a social network and the preference risks of experts to manage non-cooperative behaviors of experts.

From the above analysis we can see that: 1) the trust relationships of experts in a social network are usually used in the clustering process to cluster experts but seldom used in the CRP, 2) few studies refine the non-cooperative behaviors into different types, 3) most studies analyze non-cooperative behaviors of experts based on the assumption that the greatest degree of cooperation of experts is to totally accept the revisions proposed by the moderator. In this study, to improve the consensus level, we introduce the altruistic behaviors which allow experts to make more contributions than the recommendation proposed by the moderator to compensate for the loss caused by the experts’ different types of non-cooperative behaviors. What’s more, the trust relationship of experts in a social network serves as a condition to judge whether the experts have altruistic behaviors in the CRP.

3  Grouping Experts by a Semi-Supervised Clustering Processing

To solve an LSGDM problem, it is vital to divide the large group of experts into small communities, so as to simplify the decision process. As justified in the introduction, it is essential to consider the similarity of evaluation information of alternatives given by different experts and the trust values between experts simultaneously when grouping experts. Thus, motivated by the constrained K-means clustering algorithm [3], we introduce the PTC-Kmeans clustering algorithm to cluster experts in Section 3.1. Then, the method to determine the weights of experts and clusters is presented in Section 3.2.

3.1 Expert Clustering by the PTC-Kmeans Clustering Algorithm

In typical LSGDM problems, the degree of consistency of experts’ preferences is usually regarded as a clustering criterion [35,36]. Such a type of clustering method performs clustering based on group opinions but ignores the trust relationships between experts. In this study, we extend the trust-constrained K-means clustering algorithm [13] and utilize the trust values of experts as constraints to cluster experts. Assume that a set of experts, E={e1,e2,⋯,em}, (m≥11), are invited to conduct evaluation information on a set of emergency alternatives, X={x1,x2,x3⋯,xn}, (n≥2).

3.1.1 The Constraints

The PTC-Kmeans clustering algorithm is mainly a constraint-based K-means clustering algorithm. So, we firstly consider two types of constraints, namely must-link constraint and cannot-link constraint.

In this study, we set constraints based on the trust relationship between experts. Because the trust value provided by an expert is directional, which means the trust value between two experts may be unequal. In other words, expert eh has a high trust value to expert el, but expert el may trust expert eh to a low degree. Therefore, we divert the directed trust degree into undirected trust degree between any two experts.

Let λ=(λ1,λ2,⋯,λm)T be a weight vector such that λi∈[0,1] and ∑i=1mλi=1. The average trust degree between expert eh and expert el is calculated as:

mahl=WA(ahl,alh)=λhλl+λhahl+λlλl+λhalh(1)

where 0≤mahl≤1,mahl=malh, and min{ahl,alh}≤mahl≤max{ahl,alh}.

To simplify, we denote the aggregated social-matrix as MA=(mahl)m×m.

The trust constraints formulate that a pair of experts with a low average trust value cannot be allocated in the same cluster and a pair of experts with a high average trust value must be allocated in the same cluster.

Let the threshold of trust constraints be Con1,Con2, where Con1,Con2∈[0,1]. If the average trust value mahl between expert eh and expert el is lower than Con1, it means that they are cannot-linked. If the average trust value mahl between expert eh and expert el is higher than Con2, it means that they are must-linked.

Let Ω=(Ωhl)m×m be a cannot-linked constraint matrix, such that

Ωhl={×,mahl<Con1−,otherwise,∀h,l=1,2,⋯m;h≠l(2)

If Ωhl=×, it means that expert eh and expert el shouldn’t be classified into a same cluster.

Let Ψ=(Ψhl)m×m be a must-linked constraint matrix, such that

Ψhl={√,mahl>Con2−,otherwise,∀h,l=1,2,⋯m;h≠l(3)

If Ψhl=√, expert eh and expert el should be classified into a same cluster. In the cluster processing, their preferences will be averaged to a new individual. For example, the preferences of eh,el are: [0.5 0.80.2 0.5], [0.5 0.60.4 0.5], and Ψhl=√ between the two experts. In clustering process, the two experts will be seen as an integrated one whose preference is [0.5 0.70.3 0.5].

3.1.2 The PTC-Kmeans Clustering Algorithm

Once the constraints are defined, experts can be clustered into subgroups according to the similarity degrees of experts’ evaluation information based on the constraints.

Definition 1 [13]: Measure the similarity degree of evaluation information between expert eh and expert el. Let Peh=(pijeh)n×n and Pel=(pijel)n×n be two FPRs of expert eh and expert el. Here, we use the Euclidean distance to measure the similarity degree between two FPRs. Then, the similarity degree sdhl between the two experts can be calculated as

sdhl=1−dis(Peh,Pel)=1−(2n×(n−1)∑i=1n∑j=i+1n|pijeh−pijel|2)1/2,forh,l=1,2,⋅⋅⋅,m(4)

where sdhl=sdlh,0≤sdhl≤1. Then, the similarity matrix SD=(sdhl)m×m involving all experts can be established.

Determine the value of k according to the management experience. Denote the clustering centroid of each cluster as Qk, Qk=(qijk)n×n. For each cluster Ck, its centroid can be calculated by averaging the preference values of experts that has been assigned to it, such that

qijk=1# Ck∑eh∈Ckpijeh,∀i,j=1,2⋯,n(5)

where # Ck means the number of experts in cluster Ck.

The main steps of the PTC-Kmeans clustering algorithm are presented in Algorithm 1.

3.2 Weight Determination of Experts and Clusters

After the large-scale experts are divided into several clusters, the weights of experts and clusters should be determined. Centrality is an essential indicator to judge the influence, status and importance of an expert in a social network. We gain the weights of experts using the concept of centrality. The degree of centrality of eh∈E can be computed by averaging the trust degrees obtained by eh as below:

cen(eh)=1m−1∑l=1,l≠hmalh(6)

The weight λh of expert eh is defined as:

λh=cen(eh)∑t=1mcen(et)(7)

Clearly, 0<λh<1, and ∑h=1mλh=1.

The weight of a cluster is calculated based on the sum of the weights of the experts in the cluster. The weight μk of cluster Ck can be calculated as:

μk=∑ei∈Ckλi(8)

4  Feedback Mechanism Based on Non-Cooperative and Altruistic Behaviors

Section 4.1 presents the process of measuring the consensus degree of clusters and the whole group. In Section 4.2, we discuss the methods to identify three types of non-cooperative behaviors of experts, and altruistic behavior is introduced to reduce the degree of uncooperativeness of experts in Section 4.3. Then, a feedback mechanism is shown in Section 4.4. A punishment mechanism is used to decrease the influence of non-cooperative behaviors of experts in Section 4.5. Finally, we present the algorithm of the proposed LSGDM model in Section 4.6.

4.1 Consensus Measurement

Let PCk=(pijCk)n×n be an FPR of the cluster Ck, which can be obtained by aggregating the FPRs of the experts in the cluster Ck,

pijCk=1# Ck∑eh∈Ckpijeh(9)

where # Ck denotes the number of the experts in the cluster Ck.

Similarly, let PC=(pijC)n×n be the FPR of the global network, which can be obtained by aggregating the FPRs of the clusters,

pijC=∑t=1kμtpijCt(10)

The distance between eh and Ck is calculated as:

dis(Peh,PCk)=(2n×(n−1)∑i=1n∑j=i+1n|pijeh−pijCk|2)1/2,eh∈Ck(11)

Then, the degree of consensus of the expert eh can be computed as:

cd(eh)=1−dis(Peh,PCk)(12)

The degree of consensus of the cluster Ck is:

cd(Ck)=1# Ck∑eh∈Ckcd(eh)(13)

The degree of consensus of the whole group cg(C) has the same calculation process as the degree of consensus of the cluster, which is shown as:

cg(C)=1k∑Ck∈C(1−dis(PC,PCk))(14)

A threshold θ for cd(Ck), and a threshold δ for cg(C) should be set in advance. If cd(Ck)≥θ and cg(C)≥δ, the global group reaches the acceptable consensus level, then we can select the optimal alternative of the LSGDM problem. Otherwise, a feedback mechanism is applied to improve the consensus level. Here, we should note that a low consensus threshold may lead to controversial decisions while a high consensus threshold may result in the increasing of decision-making cost and the waste of time. The value of the threshold mainly depends on the specific problems. We should set a large value of the threshold such as 0.9 when a decision-making problem is critical; due to the time limitation, we should set a lower consensus threshold such as 0.8 in emergency decision-making problems [9]. So, in this study, we set θ,δ as 0.8.

4.2 Non-Cooperative Behaviors Identification

4.2.1 Non-Cooperative Behavior Caused by Expert Who Refuse to Follow the Revision Proposals

In the CRP, in order to achieve the ideal consensus level among experts, experts need to modify their individual preferences based on the suggestions received. However, some experts may refuse to adjust their preference information or adjust them slightly, or even change their preference information in the opposite direction. In this study, this type of behavior can be defined as the first kind of non-cooperative behavior (NCB-I).

Let P(eh,z)=(pij(eh,z))n×n be an FPR actually provided by the expert eh in consensus round z. Let SP(eh,z)=(spij(eh,z))n×n be the adjusted FPR of expert eh recommended by the moderator in round z, spij(eh,z) represents the adjusted FPR of expert eh at position (i,j) recommended by the moderator in round z, spij(eh,z)∈(min(pij(eh,z−1),pij(C,z−1)),max(pij(eh,z−1),pij(C,z−1))]. Let the size step of modification be 0.01 and determine spij(eh,z) according to the principle that the deviation between expert suggested value and actual value Δij(eh,z)≥|pij(C,z) − pij(eh,z−1)|2.

Δij(eh,z)=|spij(eh,z)−pij(eh,z−1)|,∀i,j∈1,2,…,n(15)

SAE(eh,z)=∑i=1n∑j=i+1nΔij(eh,z)(16)

where Δij(eh,z) denotes the adjusted value of expert eh at position (i,j) recommended by the moderator, and SAE(eh,z) represents the sum of the adjusted values of expert eh recommended by the moderator.

Φij(eh,z)={|spij(eh,z)−pij(eh,z)|,ifΔij(eh,z)≥|pij(eh,z)−pij(eh,z−1)|0,otherwise(17)

DAR(eh,z)=∑i=1n∑j=inΦijeh,z(18)

where Φij(h,z) represents the deviation between the actually adjusted evaluation value in position (i,j) made by expert eh and the adjusted evaluation value recommended by the moderator, and DAR(eh,z) denotes the sum of deviations between the actually adjusted evaluation value made by expert eh and the adjusted evaluation value recommended by the moderator in round z.

The non-cooperative index ONIhz of expert eh in round z can be defined as:

ONIhz=1−DAR(eh,z)SAE(eh,z)(19)

Clearly, ONIhz∈[−1,1].

(1)   −1≤ONIhz<0 means expert eh adjusts his/her preference information in an opposite direction.

(2)   ONIhz=0 means that expert eh makes no modification in round z.

(3)   0<ONIhz<1 means that expert eh changes his/her preference information by a small fraction.

(4)   ONIhz=1 means that expert eh totally accepts all the suggestions.

Let S1 (S1∈(0,1]) be a threshold, which is utilized to judge whether an expert features the NCB-I. If ONIhz≤S1, expert eh in round z has non-cooperative behavior. Because ONIhz∈[0,1] means the expert has accepted or partially accepted the revision opinion of the moderator, we use the central value as the threshold and set S1=0.5.

4.2.2 Non-Cooperative Behavior Caused by Experts Deliberately Concealing Their True Intentions

In the CRP, some hesitant experts may randomly provide their preferences to avoid revealing their true intentions, which can make experts’ adjusted opinions further away from the opinion of the subgroup. In this study, this type of behavior can be defined as the second kind of non-cooperative behavior (NCB-II).

Let P(Ck,z)=(pij(Ck,z))n×n be the collective decision matrix of cluster Ck in round z, P(eh,z)=(pij(eh,z))n×n be the individual decision matrix of expert eh in round z. Then, the distance dis(P(eh,z−1),P(Ck,z−1)) of FPRs between expert eh and cluster Ck in round z−1 and the distance dis(P(eh,z),P(Ck,z)) of FPRs between expert eh and cluster Ck in round z can be calculated using Eq. (11).

The non-cooperative index TNIhz of expert eh in round z can be defined as:

TNIhz=dis(P(eh,z−1),P(Ck,z−1))−dis(P(eh,z),P(Ck,z))(20)

Clearly, TNIhz∈[−∞,+∞].

(1)   TNIhz>0 means that after adjustment, the opinion of expert eh is closer to the opinion of cluster Ck.

(2)   TNIhz<0 means that after adjustment, the distance of opinions between expert eh and cluster Ck is larger than before.

In this study, if TNIhz∈[−∞,0], the expert eh has NCB-II.

4.2.3 Non-Cooperative Behavior Caused by Experts Who Deliberately Lower the Ranking of the Optimal Alternative Obtained in the Whole Group

In the CRP, some experts may be purposed to decrease the evaluation value of the most preferred collective alternative in the whole group and lead to a drop in the ranking of the optimal alternative in the whole group. In this study, this type of behavior can be defined as the third kind of non-cooperative behavior (NCB-III).

Let x(C,z−1) be the collective most preferred alternative of the whole group in round z−1. And let R(eh,z)=(rx1(eh,z),rx2(eh,z),rx3(eh,z),rx4(eh,z))T be the ranking vector of alternatives corresponding to expert eh in consensus round z. For example, if x1≻x2≻x3, then rx1(eh,z)=1, rx2(eh,z)=2, rx3(eh,z)=3. Then we can set the non-cooperative index FNIhz to judge whether the expert has the non-cooperative behavior III.

FNIhz=1−r(C,z−1)n(21)

Clearly, FNIhz∈[0,1]. The smaller the value of FNIhz, the lower the ranking of alternative x(C,z−1). Let S2 (S2∈(0,1]) be a parameter, which is utilized to judge whether an expert features the non-cooperative behavior III. If FNIhz<S2, we regard that expert eh exists the NCB-III. Because the measurement of FNIhz is based on the ranking of the alternatives, the determination of the threshold S2 is related to the number of alternatives. In our study, for alternatives {x1,x2,x3}, suppose that the ranking of the whole group is x1≻x2≻x3, x1 is the optimal alternative for the whole group. For expert eα, if alternative x1 is ranked in the bottom half of the total number of alternatives, such that x3≻x2≻x1 or x2≻x3≻x1, the expert eα is judged to have NCB-III. Thus, the threshold S2 is set as 0.33.

4.3 Altruistic Behavior Analysis

Because of some intimate relationships, some individuals may consider the well-being of others in the decision-making process even at their own expense [20]. In this study, we allow the expert to have altruistic behavior, which means he/she can contribute more than the recommended modification provided by the moderator. Because the consensus level of the cluster is obtained by aggregating the consensus levels of all the experts in the cluster, the altruistic behaviors of some experts can compensate for the loss caused by others’ non-cooperative behaviors in the same cluster. In other words, altruistic behavior can reduce the adverse effect of the non-cooperative behaviors of experts on decision-making results.

Suppose that expert eh in cluster Ck has non-cooperative behavior. When expert eh is judged to have non-cooperative behavior, the moderator will ask other experts in the same cluster if they are willing to show altruistic behavior towards expert eh. If expert er does, expert er intents to make more contributions than the recommended modification value provided by the moderator to make up for the loss caused by the non-cooperative behavior of expert eh. Let P¯(er,z)=(p¯ij(er,z))n×n be an adjusted FPR provided by the altruistic expert er in consensus round z. The evaluation value p¯ij(er,z) satisfies the condition that |p¯ij(er,z)−pij(er,z)|≤|pij(Ck,z−1)−pij(er,z)|.

4.4 Feedback Mechanism

If cd(Ck)≥θ,cg(C)≥δ, the consensus levels of the cluster and the whole group have reached the threshold. Otherwise, the experts whose consensus levels do not reach consensus threshold in the cluster require revising their opinions to increase the degree of consensus level of the cluster. A feedback adjustment mechanism is used to help the experts update their preferences to increase consensus level. If an expert has non-cooperative behaviors and other experts do not have altruistic behavior toward him/her or to a small degree, the expert will be subject to a weight punishment to reduce his/her negative influence on group decision-making.

4.5 The Punishment Mechanism for Non-Cooperative Behaviors

If no expert in cluster ck is willing to show altruistic behavior towards expert eh or to compensates only part of the loss caused by the non-cooperative behavior of expert eh, then a punishment mechanism will be introduced to adjust the weight of expert eh.

Let sij(eh,z) be the actual adjusted value of expert eh in position (i,j). It is calculated as:

sij(eh,z)={|pij(eh,z)−pij(eh,z−1)|,if|pij(eh,z)−pij(eh,z−1)|≤|spij(eh,z)−pij(eh,z−1)|−|pij(eh,z)−pij(eh,z−1)|,otherwise(22)

And let SEh be the actually total number of adjusted values of expert eh in the cluster Ck, it can be calculated as:

SEh=∑i=1n∑j=i+1nsij(eh,z)(23)

Suppose that the experts in the cluster Ck who agree to make more contributions to make up for the loss of eh constitute a set M, M⊂Ck. Let RAEh be the sum of adjusted values that other experts contribute to expert eh. It can be computed as:

RAEh=∑er∈M∑i=1n∑j=i+1n|p¯ij(er,z)−pij(er,z)|(24)

The altruistic index is defined as:

AIh=RAEhSAEh−SEh(25)

We determine the coefficient of the weight penalty based on the non-cooperative index and the altruistic index, with a step size of 0.2. Because AIh∈[0,1] means other experts has totally or partially compensated for the loss caused by expert eh, thus we use the central value AIh=0.5 as a demarcation value. The adjusted weight λ¯h of expert eh is denoted as:

(1)   if the expert eh has the NCB-I:

λ¯h1={λeh,if ONIh>S1or AIh=10.9×λeh,ifAIh∈[0.5,1)0.7×λeh,if ONIh∈(S12,S1],AIh∈[0,0.5)0.5×λeh,if ONIh∈(0,S12],AIh∈[0,0.5)0.3×λeh,if ONIh≤0,AIh∈[0,0.5)(26)

(2)   if the expert eh has the NCB-II:

λ¯h2={λeh,if TNIh≥0or AIh=10.9×λeh,ifAIh∈[0.5,1)0.7×λeh,if TNIh∈[−0.2,0),AIh∈[0,0.5)0.5×λeh,if TNIh∈[−0.4,−0.2),AIh∈[0,0.5)0.3×λeh,if TNIh<−0.4,AIh∈[0,0.5)(27)

(3)   if the expert eh matches the NCB-III:

λ¯h3={λeh,if FNIh>S2or AIh=10.9×λeh,ifAIh∈[0.5,1)0.7×λeh,if FNIh∈(S22,S2],AIh∈[0,0.5)0.5×λeh,if FNIh∈(0,S22],AIh∈[0,0.5)0.3×λeh,if FNIh=0,AIh∈[0,0.5)(28)

If expert eh has two or more non-cooperative behaviors, the adjusted weight is λ¯h=min(λ¯h1,λ¯h2,λ¯h3). Normalize the weights. Then the normalized weight of the expert eh can be calculated as:

λ^h=λ¯h∑t=1mλ¯t(29)

where λ^h∈[0,1].

4.6 Algorithm of the Proposed LSGDM Model

For better understanding, we provide the detailed steps of the proposed model as Algorithm 2. Fig. 2 shows the flow chart of the proposed method.

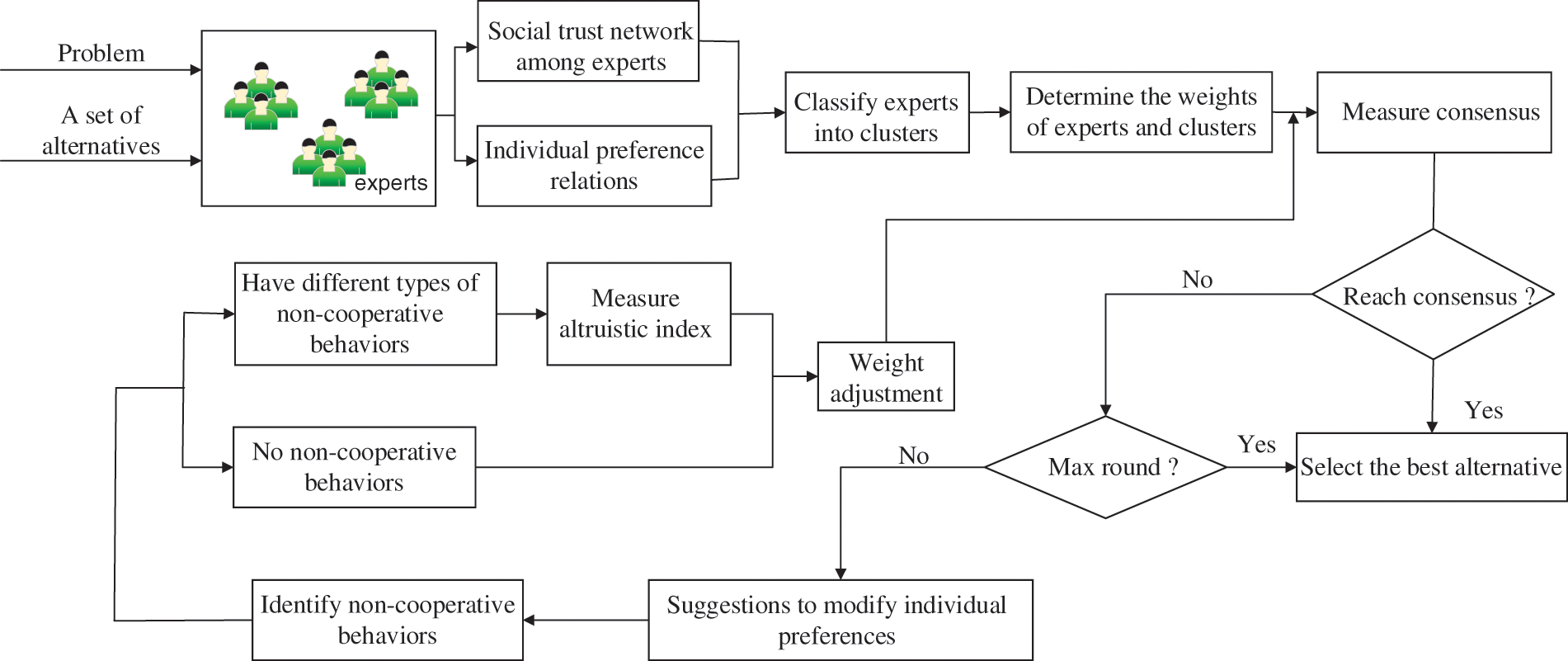
Figure 2: The flow chart of the proposed model

5  Case Study: Emergency Alternative Selection after the Flood

In this section, to demonstrate the usefulness of the proposed model, we apply the model into a case study regarding the selection of emergency alternative after the flood in Henan, China in 2021.

5.1 Case Description

From July 16 to July 2021, heavy rainfall affected 287,713 people in 140 towns and villages in 31 counties and districts in Henan, China. It caused directed economic losses of RMB 104.6047 million, resulted in 302 deaths and 50 missing3. In order to reduce the damage caused by the disaster, Henan Province Flood Control and Drought Relief Headquarters reacted quickly, made saving people a priority, and initiated the second-level response of flood control emergency plan. More than 28,000 rescue teams in Henan Province, 19 city-level commando teams for fire-fighting and flood rescue, 157 station-level attack teams which has a total of 3790 firefighters and 366 rescue boats assembled in advance, and strived to rush to the scene as soon as the disaster occurred4. An emergency headquarters composed of 15 experts was established. After analysis, three alternatives were initially identified: X={x1,x2,x3}.

x1: Set up Rescue Assault Squads to go deep into the disaster area to know about the situation as soon as possible, and guide the people in the disaster area to rescue themselves. Simultaneously, firefighters are dispatched to reinforce important locations such as major rivers, reservoirs and dams, and rescue teams are dispatched to repair communication and power facilities. After receiving information from the Rescue Assault Squads, further rescue work will be carried out.

x2: Quickly organize a certain number of firefighters and rescue boats to carry out rescue work in the disaster area and organize the transfer of the affected people. Simultaneously, firefighters are dispatched to reinforce important locations such as major rivers, reservoirs and dams, and rescue teams are dispatched to repair communication and power facilities.

x3: Let the medical rescue teams to enter the disaster area with the Rescue Squads, so as to rescue the injured person as soon as possible. Simultaneously, firefighters are dispatched to reinforce important locations such as major rivers, reservoirs and dams, and rescue teams are dispatched to repair communication and power facilities. After receiving information from the Rescue Assault Squads, further rescue work will be carried out.

5.2 Resolving Process

Step 1: Obtain the experts’ evaluation information, trust relationship and establish a complete social network.

The initial FPRs of the 15 experts are shown as follows:

P(1,0)=[0.5 0.4 0.40.6 0.5 0.90.6 0.1 0.5],P(2,0)=[0.5 0.4 0.40.6 0.5 0.30.6 0.7 0.5],P(3,0)=[0.5 0.2 0.40.8 0.5 0.40.6 0.6 0.5],P(4,0)=[0.5 0.8 0.40.2 0.5 0.70.6 0.3 0.5],P(5,0)=[0.5 0.7 0.40.3 0.5 0.30.6 0.7 0.5]

P(6,0)=[0.5 0.7 0.80.3 0.5 0.30.2 0.7 0.5],P(7,0)=[0.5 0.6 0.40.4 0.5 0.30.6 0.7 0.5],P(8,0)=[0.5 0.8 0.40.2 0.5 0.70.6 0.3 0.5],P(9,0)=[0.5 0.7 0.30.3 0.5 0.60.7 0.4 0.5],P(10,0)=[0.5 0.3 0.40.7 0.5 0.30.6 0.7 0.5]

P(11,0)=[0.5 0.4 0.20.6 0.5 0.40.8 0.6 0.5],P(12,0)=[0.5 0.4 0.90.6 0.5 0.40.1 0.6 0.5],P(13,0)=[0.5 0.9 0.40.1 0.5 0.30.6 0.7 0.5],P(14,0)=[0.5 0.2 0.90.8 0.5 0.30.1 0.7 0.5],P(15,0)=[0.5 0.4 0.20.6 0.5 0.40.8 0.6 0.5]

The direct and indirect trust relationships of experts are presented in Fig. 3.

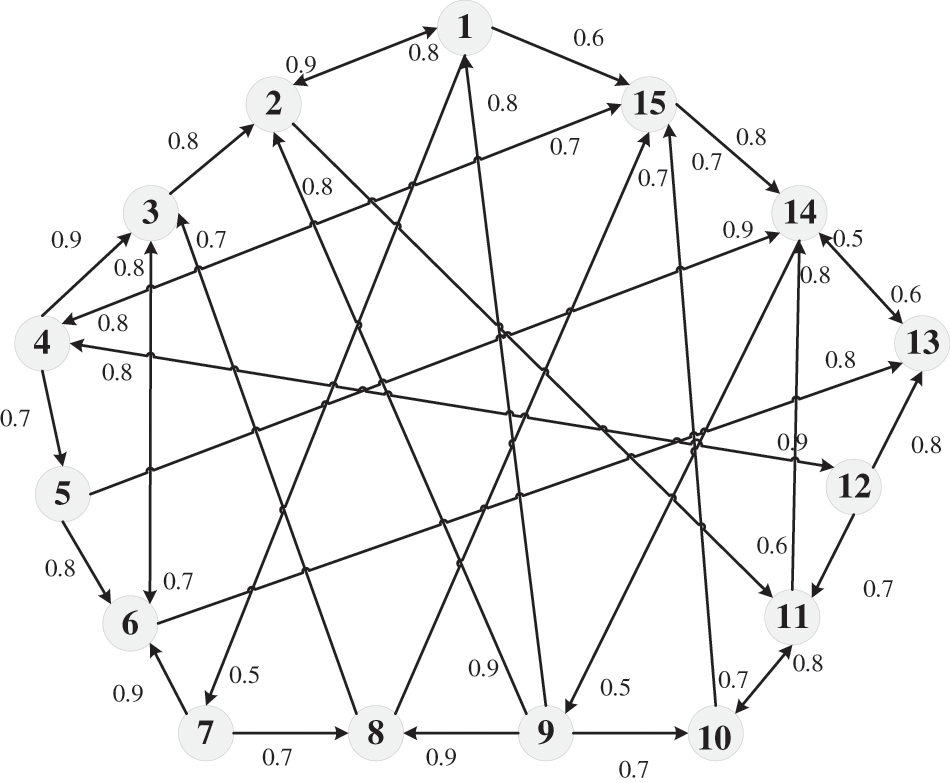
Figure 3: The social network of 15 experts

According to Eqs. (1)–(6) in the article by Liao et al. [32], we can struct a complete social network. The social-matrix among 15 experts is:

A=(–-0.900.010.180.110.110.500.390.610.210.260.220.160.400.600.80–-0.410.360.210.150.300.410.900.200.600.310.180.400.500.570.80–-0.290.170.600.230.190.370.230.110.190.150.260.410.180.260.90–-0.700.560.130.070.390.230.220.900.510.550.700.280.460.610.32–-0.800.110.170.410.240.230.270.440.900.350.330.460.800.280.16–-0.180.150.460.250.220.240.800.360.410.290.400.550.170.100.90–-0.700.350.200.200.140.330.250.200.390.530.010.520.320.310.15–-0.310.180.220.450.280.470.700.800.800.340.440.350.280.370.90–-0.700.480.130.290.340.510.180.220.240.530.320.190.060.050.21–-0.800.450.220.530.700.130.190.160.320.190.130.050.170.300.70–-0.270.200.800.450.180.310.410.800.300.250.120.110.190.220.70–-0.800.340.240.140.100.100.020.010.030.050.080.200.110.080.06–-0.500.110.360.270.260.270.040.070.140.220.500.180.230.180.60–-0.250.310.370.390.800.530.340.100.170.360.140.130.710.420.80–-)

Step 2: Classify the large group of experts into subgroups.

According to Eq. (1), we calculated the aggregated social-matrix MA=(mahl)m×m. Since MA is a symmetric matrix, we only show the upper triangular matrix.

MA=(−0.850.300.180.180.220.430.390.710.160.200.200.150.370.47−0.590.310.300.290.330.460.830.210.420.310.140.330.43−0.600.350.700.330.110.350.230.130.290.120.260.40−0.550.430.140.260.420.360.270.840.260.390.75−0.430.110.250.370.490.210.290.180.320.47−0.430.220.360.220.180.240.390.180.37−0.370.360.110.100.130.140.170.13−0.660.110.190.260.160.300.37−0.490.400.160.250.630.43−0.750.330.160.310.36−0.490.130.450.26−0.400.240.52−0.560.28−0.51−)

The PTC-Kmeans algorithm is used to cluster the experts. In this case, we assign the cannot-link constraint threshold Con1=0.15 and the must-link constraint threshold Con2=0.85. The number of clusters k=4. The clustering results are C1={e3,e14}, C2={e4,e5,e6,e13}, C3={e7,e8,e9} and C4={e1,e2,e10,e11,e12,e15}.

Step 3: Calculate the weights of experts and clusters.

According to Eq. (7), we can obtain the weights of experts and the results are shown in Table 1.

According to Eq. (8), we can obtain the weights of the clusters: μ1=0.17, μ2=0.26, μ3=0.16 and μ4=0.41.

According to Eq. (9), we can obtain the FPRs of clusters:

PC1=[0.500.200.650.800.500.350.350.650.5]PC2=[0.500.780.500.220.500.400.500.600.50]PC3=[0.500.700.370.300.500.530.630.470.50]PC4=[0.500.450.420.550.500.450.580.550.50]

According to Eq. (10), we can obtain the FPR of the whole group:

PC=[0.500.530.470.470.500.430.530.570.50]

Step 4: Consensus measurement. Eq. (13) are used to compute the degree of consensus of each cluster. The initial consensus levels are shown in Table 2. We set the clusters’ consensus threshold as θ=0.80.

From Table 2, we can see that the consensus levels of cluster C2 and C4 are lower than the threshold θ=0.80. Thus, for clusters whose consensus level is lower than the threshold, the preference information of experts within the cluster should be modified.

Step 5: Apply the feedback mechanism.

The first consensus round

Since the consensus levels of experts e4,e6 in cluster C2 and experts e1,e11,e12,e15 in cluster C4 fail to reach the threshold θ, these experts should adjust their own opinions according to the suggestions recommended by the moderator. The actual adjustment preference matrix P1, and the preference matrix SP recommended by the moderator are shown in Table 3.

Let the parameter S1=0.5 and S2=0.33, the non-cooperative indexes of the experts with non-cooperative behaviors are calculated according to Eqs. (15)–(21). The results are shown in Table 4.

It can be seen from Table 4 that ONIe121≤S1, expert e12 exists NCB-I. TNIe11<0 implies expert e1 exists NCB-II. FNI151<0.3 denotes expert e15 exists NCB-III.

After investigation by the moderator, expert e2 would like to make more contributions to make up for the loss caused by the non-cooperative behaviors of expert e1, expert e10 would like to make more contributions to make up for the loss caused by the non-cooperative behaviors of expert e15. The adjusted preference matrices of experts e2,e10 with altruistic behaviors are:

P(e2,1)=[0.50 0.47 0.400.53 0.50 0.300.60 0.70 0.50]P(e10,1)=[0.50 0.34 0.400.66 0.50 0.300.60 0.70 0.50]

According to Eq. (25), the altruistic index of experts e1,e15 is calculated as: AIe11=0.7,AIe151=0.44. Experts e1,e12,e15 suffer different weight punishment according to Eqs. (26)–(28). The weights of experts are updated as:

λ1=(0.067,0.088,0.078,0.080,0.053,0.071,0.037,0.057,0.084,0.063,0.067,0.034,0.081,0.111,0.029).

The consensus levels of clusters are: cd(C1)=0.83,cd(C2)=0.81,cd(C3)=0.85,cd(C4)=0.79.

The second consensus round

From the first consensus round, we know that the consensus level of cluster C4 is lower than the threshold θ=0.80. Thus, the preference information in cluster C4 should continue to be modified. Due to the consensus levels of expert e1,e12 in cluster C4 are lower than the threshold, the two experts should continue to adjust their preference information according to the suggestions recommended by the moderator.

The adjusted FPRs of experts e2 and e12 recommended by the moderator in round 2 are:

SP(e1,2)=[0.500.510.40.550.500.750.600.250.50]SP(e12,2)=[0.500.450.700.550.500.400.300.600.50]

The actual adjusted FPRs of experts e2 and e12 are:

P(e1,2)=[0.500.510.400.490.500.780.600.220.50]P(e12,2)=[0.500.450.820.550.500.400.180.700.50]

Then, the non-cooperative indexes are calculated. The non-cooperative indexes of the experts with non-cooperative behaviors are calculated according to Eqs. (15)–(21). The results are shown in Table 5.

Due to ONI122<S1 in Table 5, we infer that expert e12 exists NCB-I. And e15 would like to make more contributions to make up for the loss caused by the non-cooperative behavior of expert e12. The altruistic index of expert e12 is calculated as AI122=0.42. Expert e12 suffers weight punishment according to Eq. (26). The weights of experts are updated as:

λ2=(0.067,0.089,0.079,0.081,0.053,0.072,0.038,0.057,0.085,0.064,0.068,0.024,0.082,0.112,0.029).

The consensus levels of clusters are calculated as: cd(C1)=0.83, cd(C2)=0.81, cd(C3)=0.85 and cd(C4)=0.83. To show the CRP visually, we list the change of consensus level of clusters in the iterative process in Fig. 4.

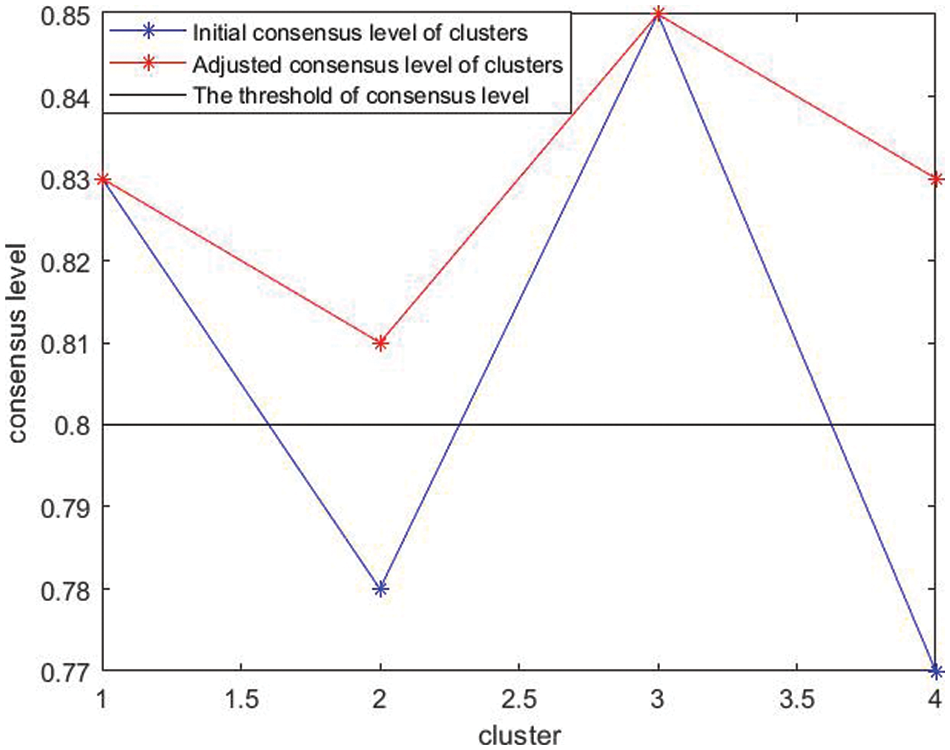
Figure 4: Changes in the consensus levels of clusters

Step 6: Calculate the consensus level of the whole group.

Set the threshold δ=0.80 in advance. Using Eq. (14), the consensus level of the whole group is calculated as: cg(C)=0.82.

Step 7: Selection of alternatives.

From Step 5 and Step 6, we can see that cd(Ck)≥θ,cg(C)≥δ. The final collective decision matrix is obtained according to Eq. (10):

PC=[0.50 0.53 0.470.47 0.50 0.420.53 0.58 0.50]

The alternatives are ranked as: x3≻x1≻x2, x3 is thus the optimal alternative.

5.3 Comparisons and Discussions

To further reflect the advantages and features of our proposed model, we conduct comparative analysis and discussion as follows:

5.3.1 Discussion on the PTC-Kmeans Clustering Algorithm

1)   Determination of k

We use the sum of the squared errors (SSE) to determine the value of k. The core idea of SSE is: as the number of clusters k increases, the division of the samples will be more refined, the aggregation degree of each cluster will gradually increase, and the value of SSE will naturally become smaller. When k is less than the optimal clustering number, since the increase of k will greatly increase the aggregation of each cluster, the decline of the value of SSE will be very large. When k reaches the optimal clustering number, the decline of the value of SSE will be slight with the increase of k. The SSE is shown as:

SSE=∑i=1k∑p∈Ci|p−mi|2(30)

where mi means the centroid of the cluster Ci.

Fig. 5 presents the relationship between SSE and the number of clusters. When the number of clusters is more than 4, the SSE decreases slightly. Thus, we set k=4 as the number of clusters.

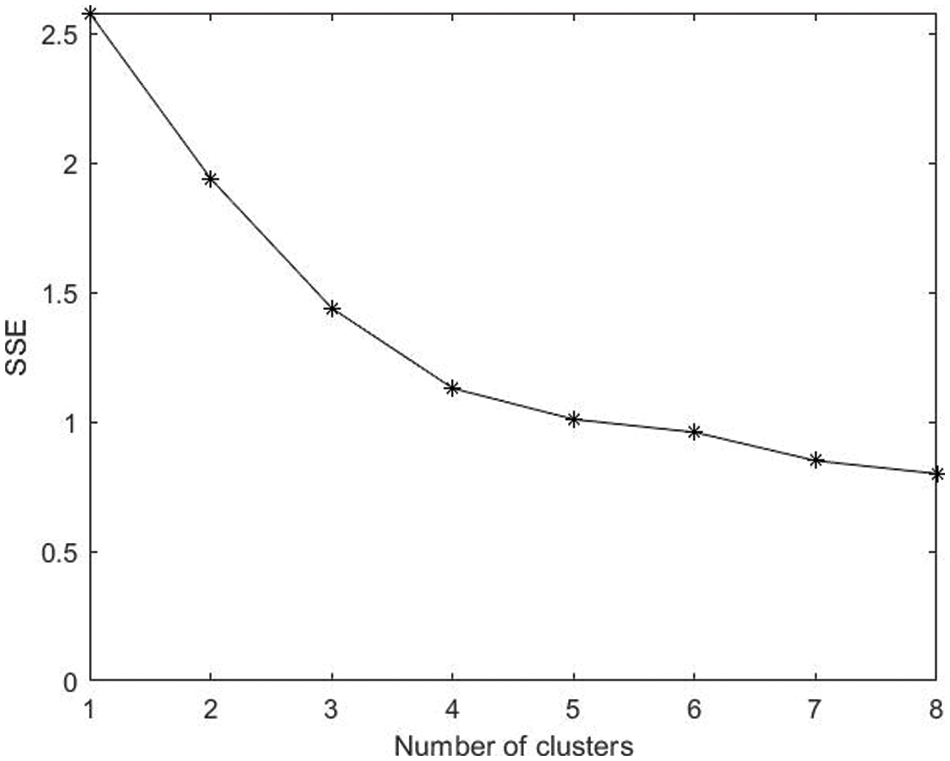
Figure 5: Relationship between SSE and the number of clusters

2)   Determination of the trust constraints thresholds Con1,Con2

The trust constraints play crucial roles in the determination of the initial clusters and the final cluster results. As shown in Fig. 6, the trust constraint threshold is positively correlated with the number of cannot-links while the threshold is negatively correlated with the number of must-links. The greater the number of cannot-links, the greater the minimum number of initial clusters, and the smaller the number of must-links, the greater the maximum number of initial clusters. For example, if there are 15 cannot-links, then it is possible that the minimum number of clusters required is 15; if there are 15 must-links, then it is possible that the maximum number of clusters is 1. In order to ensure that we can obtain 4 initial clusters, the cannot-link trust constraint link is set to con1∈[0,0.15] and the cannot-link trust constraint link is set to con2∈[0.8,1]. Specifically, we set con1=0.15, con2=0.85.

Figure 6: The relationship between the trust constraint threshold with the number of constraint links

3)   Comparison with the traditional K-means algorithm

Where our algorithm differs from traditional algorithms is the addition of trust constraints. In our algorithm, experts with low trust should not be allocated to the same cluster while those with high trust must be in the same cluster. Through directly numerical comparison with the traditional K-means clustering method, the advantages of our algorithm are highlighted. As shown in Table 6, the overall trust degree and the consensus level of the initial clusters obtained by our proposed method are both higher than the initial clusters obtained by the traditional K-means. A higher degree of consensus level means a fewer number of positions to be adjusted. The decision cost of our proposed method is lower than the traditional K-means.

5.3.2 Discussion on the GDM Models

1)   We use the data from the first consensus round in Section 5.2 to compare changes in the weight of experts when considering altruistic behavior and not considering altruistic behavior. Fig. 7 shows the difference in the weights of experts with altruistic and non-altruistic behaviors. We can see that when considering the altruistic behaviors of experts, the adjusted weight of experts is closer to the initial weight of experts than without altruistic behavior. It indicates that considering altruistic behavior not only can protect the interests of experts with non-cooperative behavior but also ensures the integrity of group opinions.

2)   The comparisons with the management of non-cooperative behaviors in GDM models are demonstrated in Table 7. Compared with Tang et al. [20], Liao et al. [37], they only considered one type of non-cooperative behaviors. It can lead to a lack of integrity as they did not consider the whole problem. In our study, we define three types of non-cooperative behaviors. Dong et al. [15] also focused on different types of non-cooperative behaviors. However, in their models, they did not cluster the experts into subgroups and they assumed the maximum degree of cooperation is to totally accept the modification suggestions. For the definition of non-cooperative behaviors, they did not consider such a behavior that hesitant experts are purposed to provide their preference randomly to avoid revealing their true intentions. In this paper, we used the PTC-Kmeans algorithm to cluster experts into different subgroups and managed the non-cooperative behaviors based on different clusters. What’s more, we allowed experts to make more contributions to make up for the loss caused by experts with the non-cooperative behaviors, it protected the interests of experts with non-cooperative behaviors and ensured the integrity of decision-making information. We set different weight punishment according to the degree of non-cooperative and the degree of altruism.

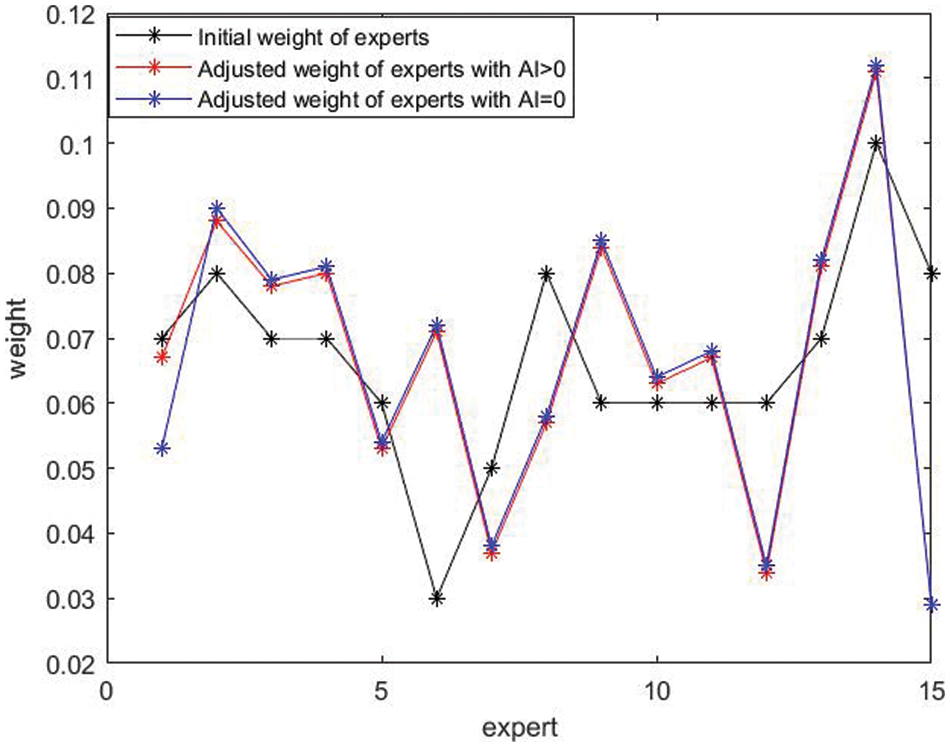
Figure 7: Changes in the weight of experts when considering altruistic behavior and not considering altruistic behavior

6  Conclusion

In this study, we proposed a consensus reaching model based on the social network which took into account different types of non-cooperative behaviors and altruistic behavior of experts in LSGDM problems. The main contributions and improvements could be summarized as follow: 1) the PTC-Kmeans algorithm was proposed to classify experts into several clusters based on the individual FPRs and trust relationships of experts. The two attributes were all regarded as important basis for classification and were seldom considered simultaneously in existing clustering methods. 2) A consensus reaching approach was proposed to improve the consensus level. Such a consensus reaching approach considered different types of non-cooperative behaviors and allowed experts with altruistic behaviors to make more contributions to compensate for the loss caused by the experts with non-cooperative behaviors. Different types of non-cooperative behaviors allowed for a more comprehensive consideration of the problem and the existence of altruistic behavior ensured the interests of experts with non-cooperative behavior. 3) The proposed LSGDM method was applied to a case study of the selection of emergency alternative after the flood in Henan, China.

There are still some limitations in this study. First, we only considered the non-cooperative behavior of experts but failed to consider the cooperative behavior. However, the cooperative behavior of experts may also affect the decision-making. Second, we did not take the cost control into consideration in the LSGDM. In the future, it is necessary to study how to merge altruistic behavior of experts into minimum cost consensus model. In addition, we assumed that all the experts used FPRs to express their preference information, in the future research, it is necessary to present the preference information of experts in more complex representations.

Funding Statement: The work was supported by the National Natural Science Foundation of China (Nos. 71771156, 71971145, 72171158).

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

1https://new.qq.com/omn/20210620/20210620A06SFS00.html.

2https://www.sohu.com/a/211253384_770379.

3http://henan.sina.com.cn/news/2021-08-02/detail-ikqciyzk9115688.shtml.

4https://www.163.com/dy/article/GFDNN7OC0514R9L4.html.

References

 1.  Xu, X. H., Zhong, X. Y., Chen, X. H., Zhou, Y. J. (2015). A dynamical consensus method based on exit-delegation mechanism for large group emergency decision making. Knowledge-Based Systems, 86, 237–249. DOI 10.1016/j.knosys.2015.06.006. [Google Scholar] [CrossRef]

 2.  Xu, X. H., Du, Z. J., Chen, X. H. (2015). Consensus model for multi-criteria large-group emergency decision making considering non-cooperative behaviors and minority opinions. Decision Support Systems, 79, 150–160. DOI 10.1016/j.dss.2015.08.009. [Google Scholar] [CrossRef]

 3.  Xu, X. H., Huang, Y. X., Chen, K. (2019). Method for large group emergency decision making with complex preferences based on emergency similarity and interval consistency. Natural Hazards, 97(1), 45–64. DOI 10.1007/s11069-019-03624-1. [Google Scholar] [CrossRef]

 4.  Xu, X. H., Zhang, Q. H., Chen, X. H. (2020). Consensus-based non-cooperative behaviors management in large-group emergency decision-making considering experts’ trust relations and preference risks. Knowledge-Based Systems, 190, 105108. DOI 10.1016/j.knosys.2019.105108. [Google Scholar] [CrossRef]

 5.  Tang, M., Liao, H. C. (2021). From conventional group decision making to large-scale group decision making: What are the challenges and how to meet them in big data era? A state-of-the-art survey. Omega, 100, 102141. DOI 10.1016/j.omega.2019.102141. [Google Scholar] [CrossRef]

 6.  Saxena, A., Prasad, M., Gupta, A., Bharill, N., Patel, O. P. et al. (2017). A review of clustering techniques and developments. Neurocomputing, 267, 664–681. DOI 10.1016/j.neucom.2017.06.053. [Google Scholar] [CrossRef]

 7.  Wu, T., Liu, X. W., Qin, J. D. (2018). A linguistic solution for double large-scale group decision-making in E-commerce. Computers & Industrial Engineering, 116, 97–112. DOI 10.1016/j.cie.2017.11.032. [Google Scholar] [CrossRef]

 8.  Dong, Y. C., Zhao, S. H., Zhang, H. J., Chiclana, F., Herrera-Viedma, E. (2018). A self-management mechanism for noncooperative behaviors in large-scale group consensus reaching processes. IEEE Transactions on Fuzzy Systems, 26(6), 3276–3288. DOI 10.1109/TFUZZ.2018.2818078. [Google Scholar] [CrossRef]

 9.  Tian, Z. P., Nie, R. X., Wang, J. Q. (2019). Social network analysis-based consensus-supporting framework for large-scale group decision-making with incomplete interval type-2 fuzzy information. Information Sciences, 502, 446–471. DOI 10.1016/j.ins.2019.06.053. [Google Scholar] [CrossRef]

10. Newman, M. E. J., Girvan, M. (2004). Finding and evaluating community structure in networks. Physical Review E, 69(2), 026113. DOI 10.1103/PhysRevE.69.026113. [Google Scholar] [CrossRef]

11. Blondel, V. D., Guillaume, J. L., Lambiotte, R., Lefebvre, E. (2008). Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment, 10. DOI 10.1088/1742-5468/2008/10/P10008. [Google Scholar] [CrossRef]

12. Du, Z. J., Luo, H. Y., Lin, X. D., Yu, S. M. (2020). A trust-similarity analysis-based clustering method for large-scale group decision-making under a social network. Information Fusion, 63, 13–29. DOI 10.1016/j.inffus.2020.05.004. [Google Scholar] [CrossRef]

13. Yu, S. M., Du, Z. J., Zhang, X. Y., Luo, H. Y., Lin, X. D. (2021). Punishment-driven consensus reaching model in social network large-scale decision-making with application to social capital selection. Applied Soft Computing, 113, 107912. DOI 10.1016/j.asoc.2021.107912. [Google Scholar] [CrossRef]

14. Cheng, D., Yuan, Y. X., Wu, Y., Hao, T. T., Cheng, F. X. (2022). Maximum satisfaction consensus with budget constraints considering individual tolerance and compromise limit behaviors. European Journal of Operational Research, 297(1), 221–238. DOI 10.1016/j.ejor.2021.04.051. [Google Scholar] [CrossRef]

15. Dong, Y. C., Zhang, H. J., Herrera-Viedma, E. (2016). Integrating experts’ weights generated dynamically into the consensus reaching process and its applications in managing non-cooperative behaviors. Decision Support Systems, 84, 1–15. DOI 10.1016/j.dss.2016.01.002. [Google Scholar] [CrossRef]

16. Mandal, P., Samanta, S., Pal, M., Ranadive, A. S. (2022). Three-way decision model under a large-scale group decision-making environment with detecting and managing non-cooperative behaviors in consensus reaching process. Artificial Intelligence Review, 55(7), 5517–5542. DOI 10.1007/s10462-021-10133-w. [Google Scholar] [CrossRef]

17. Quesada, F. J., Palomares, I., Martinez, L. (2015). Managing experts behavior in large-scale consensus reaching processes with uninorm aggregation operators. Applied Soft Computing, 35, 873–887. DOI 10.1016/j.asoc.2015.02.040. [Google Scholar] [CrossRef]

18. Zhang, H. J., Palomares, I., Dong, Y. C., Wang, W. W. (2018). Managing non-cooperative behaviors in consensus-based multiple attribute group decision making: An approach based on social network analysis. Knowledge-Based Systems, 162, 29–45. DOI 10.1016/j.knosys.2018.06.008. [Google Scholar] [CrossRef]

19. Simon, J., Saari, D., Keller, L. R. (2020). Interdependent altruistic preference models. Decision Analysis, 17(3), 189–207. DOI 10.1287/deca.2020.0411. [Google Scholar] [CrossRef]

20. Tang, M., Liao, H. C., Ding, W. P. (2022). Collective intelligence driven cross-functional group decision framework in digitalization technology selection for supply chain resilience. IEEE Transactions on Industrial Informatics. Technical Report. [Google Scholar]

21. Cao, J., Xu, X. H., Pan, B. (2022). Ambiguity-incorporated opinion formation model for multi-risk large-group emergency decision-making in social networks. Kybernetes, Ahead-of-print. DOI 10.1108/K-06-2021-0538. [Google Scholar] [CrossRef]

22. Stasser, G., Titus, W. (1985). Pooling of unshared information in group decision making: Biased information sampling during discussion. Journal of Personality and Social Psychology, 48(6), 1467–1478. DOI 10.1037/0022-3514.48.6.1467. [Google Scholar] [CrossRef]

23. Li, G. X., Kou, G., Peng, Y. (2021). Heterogeneous large-scale group decision making using fuzzy cluster analysis and its application to emergency response plan selection. IEEE Transactions on Systems, Man, and Cybernetics-Systems, 52(6), 3391–3403. [Google Scholar]

24. Liu, P. D., Wang, P., Pedrycz, W. (2020). Consistency-and consensus-based group decision-making method with incomplete probabilistic linguistic preference relations. IEEE Transactions on Fuzzy Systems, 29(9), 2565–2579. DOI 10.1109/TFUZZ.2020.3003501. [Google Scholar] [CrossRef]

25. Ding, S. F., Jia, H. J., Du, M. J., Xue, Y. (2018). A semi-supervised approximate spectral clustering algorithm based on HMRF model. Information Sciences, 429, 215–228. DOI 10.1016/j.ins.2017.11.016. [Google Scholar] [CrossRef]

26. Wu, Z. B., Xu, J. P. (2018). A consensus model for large-scale group decision making with hesitant fuzzy information and changeable clusters. Information Fusion, 41, 217–231. DOI 10.1016/j.inffus.2017.09.011. [Google Scholar] [CrossRef]