Knowledge Graph Representation Learning Based on Automatic Network Search for Link Prediction

1  Introduction

Knowledge Graphs (KGs) are graph-structured information networks. Typical KGs such as Freebase [1] and DBpedia [2], represent the knowledge in the form of the triplet (h, r, t), where the head h and tail t are entities, and the relation r refers to different types of edges between entities. Recently, KGs have been applied in many fields and achieved significant performance, such as question answering [3] and dialog system [4]. Growing efforts from both academia and industry have been made to advance the research on KGs. However, most existing KGs are incomplete and noisy, which severely limits their popularity and usefulness in practice. For example, in Freebase, more than two-thirds of person entities lack relations with the corresponding birthplace entities [5]. To tackle the missing link problem, a link prediction task has been proposed to predict the existence of links between any two entities [6], which quickly becomes a fundamental but challenging task in the KG field.

Conventional link prediction models, such as TransE [6], DistMult [7] and ComplEx [8], focus on designing shallow and scalable models by simple operations, like addition, subtraction or matrix multiplications over an embedding space. However, these simple operations can only capture the linear relationships between entities. Particularly, RotatE [9] can achieve state-of-the-art by defining relation as a rotation from the head to tail in the complex vector space to tackle the existing known datasets. Several neural models, such as ConvE [10], leverage a single convolutional layer to implicitly learn more expressive features. Despite some effectiveness of the above models, they are handcrafted by careful experimentation on several known datasets and fail to model various latent patterns of new KGs. However, in reality, it is hard to know the latent data distributions of a new KG dataset and even more difficult to mathematically model them into a single model.

Recently, many Automatic Network Search (ANS) methods [11–13] have demonstrated their superiority in automatically designing model architectures for various tasks, especially in image classification and language processing. Motivated by this, in this paper, we propose KGE-ANS, a novel approach to learning knowledge graph embedding for link prediction tasks with Automatic Network Search. As can be seen in Fig. 1, KGE-ANS is able to automatically learn the competent architecture to adapt to different datasets through automatic network search, while most existing methods are fixed no matter what dataset, and this would substantially reduce the performance of these models on the unknown dataset.

Figure 1: A demonstration of our KGE-ANS model

Specifically, for a link prediction task, we first leverage the gradient-based ANS method [13] to search for an appropriate architecture, and then further train the searched architecture on the dataset. To better adapt to different datasets, we design a general search space that is tailored for KG-related tasks, which contains five kinds of operations: convolution, pooling, self-attention, zero, and identity operations. To make different latent representations sufficiently interact with each other, our KGE-ANS introduces the self-attention operation. In this way, the self-attention operation can model the global correlation between representations while the convolution and pooling operations can model the local correlation. In this paper, our contributions can be summarized as follows:

•   We propose KGE-ANS, a novel knowledge graph embedding framework for general link prediction tasks with automatic network search. Especially, KGE-ANS can adapt to different datasets by automatically learning an appropriate neural network architecture using the automatic network search technique.

•   The general search space we designed is tailored for KG tasks. By incorporating the attention-based operation into the learning process, our KGE-ANS can model the global correlation between entity and relation.

•   We evaluate our approach on several benchmark datasets. Extensive experiments demonstrate that our approach has good generalization ability over different datasets and achieves the best Mean Reciprocal Rank compared with several state-of-the-art methods.

2  Related Work

Our work is mainly related to general embedding-based KG models and is closely connected to ANS methods. In the following parts, we present an overall review of related works in these two areas, respectively.

2.1 Embedding-Based KG Models

TransE [6] is one of the earliest translation-based models, which assumes there exists a simple mapping function that can translate the embedding of the head entity to that of the tail entity by the relation. Despite its efficiency and simplicity, TransE is ineffective in modeling 1-to-N, N-to-1, and N-to-N relations. To solve the limitations of TransE in dealing with multiple mapping relationships, TransH [14] improved TransE to learn one more mapping vector for each relationship on the basis of TransE, which is used to map entities to the hyper flat specified by the relationship. However, TranH still assumes that entities and relations are in the same semantic space, which limits the effect of TransE to a certain extent. To this end, Lin et al. proposed TransR [15], which models entity and relation representations in two distinct spaces, i.e., entity space and multiple relation spaces (relation-specific entity spaces) and performs transformations in the corresponding relation spaces. The aforementioned methods only consider simple operations like addition and matrix multiplication, which mostly results in a shallow representation of KG components that is not expressive enough for downstream tasks.

There are several approaches have been proposed to improve the above simple translation-based methods to handle more complicated relation patterns. One is to design more complicated score function in the models, such as DistMult (Bilinear Diagonal model) [7] and its extension ComplEx [8]. These models use the latent matrix factorization to model symmetric/asymmetric relations between entities. RotatE [9] model is similar to ComplEx, but with subtle difference in the definition of relation, which formulates the relation as a rotation from the head to tail in the complex vector space. Recently, several neural models have also been proposed to tackle the KGC task. ConvE [10], a convolutional neural architecture, which is defined by a single convolution layer, a projection layer and an inner product layer, has shown the effectiveness in modeling entities with high degrees. ConvKB [16] generalized transitional characteristics in transition-based models by a convolution layer. SimplE [17] employed a canonical polyadic tensor decomposition method to solve the link prediction problem, which can allow two embeddings for each entity to be learned dependently. AnyBURL [18] focused on the symbolic space to learn knowledge graph embedding using the sampling path algorithm. To better guide the sampling process, AnyBURL adopted reinforcement learning to help finding more valuable rules. However, these approaches are too shallow to model more complicated patterns and do not have good generalization ability on different datasets. Zhang et al. [19] proposed AutoSF, which first uses Automatic Machine Learning (AutoML) methods to greedily search for different optimal scoring functions to adapt to different datasets. However, these approaches are mainly designed to model a few known relation patterns in well-known datasets and do not have good generalization ability on different datasets. We hope to design a model which can automatically adapt to different datasets, and hence better model various relation patterns in the different data distributions. Compared to previous works, our proposed method can render the learned representation of KG components more expressive and comprehensive.

2.2 Automatic Network Search

Automatic Network Search (ANS) is aimed at finding an effective neural network architecture for a specific domain (dataset). It is coined by AutoML researchers and quickly applied into many fields.

State-of-the-art ANS methods can be summarized as three main categories:

Reinforcement learning-based approaches [11,12], which uses a recurrent neural network as the controller to generate child networks. These approaches use reinforcement learning to train the controller by maximizing evaluation metrics on the validation data. Although these reinforcement learning-based methods are practicable and easy to understand and implement, their optimization efficiency is low and the sampling of sub-networks can also introduce large uncertainties. Therefore, Google proposed the ENAS algorithm [12], which avoids inefficient initial training by forcing all sub-models to share weights, thereby improving the efficiency of ANS and overcoming the shortcomings of high computational cost and time-consuming of ANS.

Evolutional-based approaches [20], which simultaneously evolve along network structures and hyper-parameters to generate neural networks. These methods first randomly generate a population (N sets of solutions) and begin to cycle through the following steps: selection, crossover, mutation, until the final condition is met. In 2017, Google proposed “Large-Scale Evolution of Image Classifiers” [20], which is the first applied evolutionary algorithm to the ANS task of image classification. The method first encodes the network structure, maintains a collection (population) of structures, selects structures from the population for training and evaluation, leaves high-performance networks, and eliminates low-performance networks. Next, a new candidate is formed through a preset structural mutation operation, which is added to the population after training and evaluation. The process is iterated until the termination condition is met (for example, the maximum number of iterations is reached or the network performance after mutation no longer increases). An evolutionary algorithm is a gradient-free optimization algorithm. The advantage is that the global optimal solution may be obtained, but the disadvantage is low efficiency.

Gradient descent-based approaches. The search space of the above two methods is discrete, and ANS is regarded as a black-box optimization problem, so the efficiency is low. Therefore, scholars from CMU and Google proposed DARTS [13], based on the continuous relaxation of the representation, allowing an efficient search of architecture by using gradient descent. Specifically, DARTS represents the network space as a directed acyclic graph, where each node represents the current input and output, and the edges are various operations. The softmax function is used in the search, which turns the search space into a continuous space, and the objective function becomes a differentiable function.

Based on the comparison of the above three types of mainstream search strategies, it can be found that the method based on gradient descent can greatly improve the search efficiency through simple weight sharing, compared with reinforcement learning-based and evolutionary-based methods. Therefore, in the study of knowledge graph representation learning in this paper, a gradient descent-based method will be used to design a neural network search model.

Previous ANS researches mainly focus on vision and language fields. The search space of these methods is composed of convolution, pooling, and activation functions in most cases. Unlike existing ANS researches, our work attempts to propose a novel ANS-based method for the knowledge graph field, which mainly features the design of a new search space schema carefully tailored for the link prediction task.

3  Model and Approach

3.1 Problem Formulation

In this work, we formulate a knowledge graph G as a set of triplets {(h,r,t)}⊆E×R×E, where E is the entity set and R is the relation set. r denotes the relation between a head entity h and a tail entity t in the knowledge graph G. Following the embedding-based KG methods, we denote the entity embedding as eh,et∈RL and relation embedding as er∈RM, respectively. L and M represent embedding vector dimensions. Knowledge graph embedding models usually learn entity and relation embeddings by maximizing a score function over all triplets, which is expected to give higher scores for valid triplets than invalid ones.

3.2 Model Overview

In this section, we first give an overview of the proposed KGE-ANS framework, which is shown in Fig. 2. The goal of KGE-ANS is to search for an appropriate network architecture for different datasets on link prediction tasks through an automatic network search module. KGE-ANS first performs a row-vector look-up operation on head entity and relation embedding matrices to obtain the corresponding embedding eh and er. The two representations are then combined by a concatenation operation as em=(eh||er) and fed into the ANS module. In our ANS module, the architecture search process for a neural network is performed in a normal cell which serves as a building block for the final architecture. Each cell has the same network architecture, and the final neural network architecture consists of N same cell. Following the standard gradient-based ANS method [13], we define each cell has two inputs. As can be seen in Fig. 2a, the inputs of the first cell are both the combined representation em, called Input A and Input B. Other cells’ inputs come from the outputs of two previous cells.

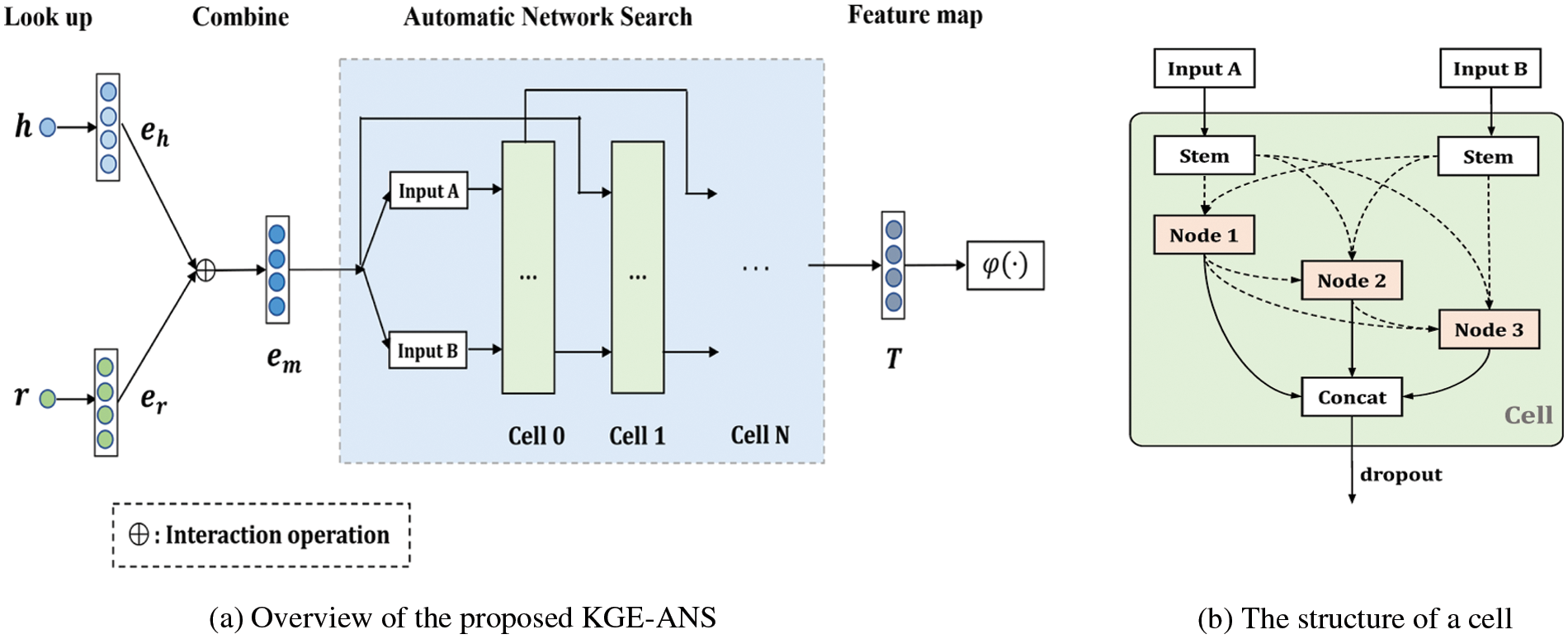
Figure 2: The proposed KGE-ANS. We first combine the entity embedding eh and relation embedding er of a triple to a new vector em. Then the combined representation em is used as the input of the ANS module. After that, the architecture search process is performed in an iterative fashion to update the architecture. Finally, the feature map generated by the ANS module is projected into entity space to predict the probability by sigmoid function φ(・). In Fig. 2b, solid lines indicate connections that are present in every architecture while dashed lines indicate optional connections that are determined by the search process

The normal cell is defined as a general Directed Acyclic Graph (DAG) which consists of n intermediate nodes. Fig. 2b illustrates the inner structure of a normal cell, with nodes marked in orange. In our scenario, we add stem (1 × 1 convolution) as pre-process operation to keep the shape of output consistent with the shape of the input. Each edge represents an atomic operation which may be the convolution, pooling, self-attention, zero, or identity atomic operation. Each node is the weighted sum of the outputs obtained from all atomic operations, which are edges connected to all previous nodes and stems. Once the search is completed, we follow the standard setting to choose two edges with the highest weight to determine the searched architecture related to a node, that is, we choose two atomic operations for a node. The output of one cell is the sum of all nodes. Note that we add Batch Normalization (BN) and ReLU activation after the convolution operation as the post-process to improve the capacity of our model.

The ANS module outputs a feature map T which incorporates the embedding of the head entity h and the relation r. Since the link prediction task can be regarded as the multiple binary classification [10], we apply the sigmoid function φ(⋅) on the inner product between T and entity embedding matrix We to score the final binary classification probability.

In the rest of this section, we first introduce the general search space schema tailored for link prediction tasks. Then, we show the search process of the network architecture in detail.

3.3 General Search Space

In ANS, network architecture search is based on a predefined search space, so designing a suitable search space is critical to find an effective network architecture. Most existing ANS researches focus on image classification and language model tasks. The search space for image classification consists of different kinds of convolution and pooling operations, while the search space for language models consists of various activation functions. Existing search spaces for the KG-related tasks are generally carefully designed, few works focus on exploring an appropriate search space. To address this issue, we explore an appropriate search space for KG-related tasks in five atomic operations: convolutional operations, pooling operations, attention operations, zero operations, and identity operations.

•   Convolutional operations. Two kinds of convolutional operations can be performed in our model: convolution 1D and convolution 2D. Specifically, we perform convolution 1D operations like TextCNN [21], which aims to extract interactions among entities and relations. As shown in Fig. 3a, the input is viewed as k × u, where k is the dimension of embeddings, u is the channel number of the current input. The filter size of convolution 1D is 3, including separable convolution and dilated separable convolution.

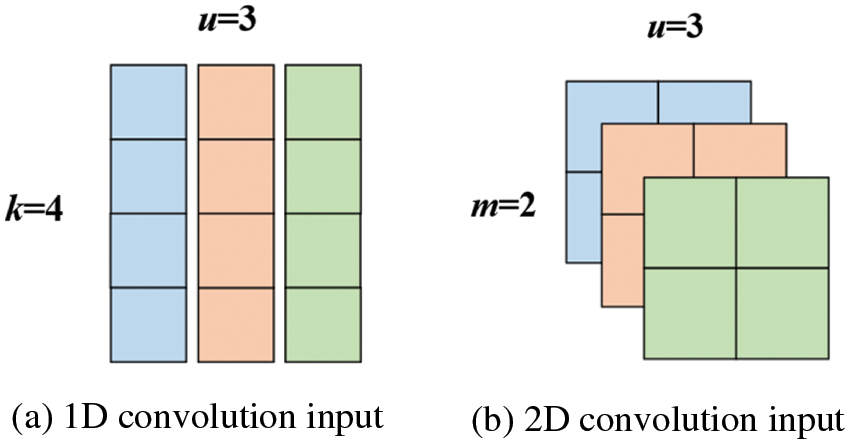
Figure 3: Illustration of 1D convolution input and 2D convolution input methods

Convolution 2D operations are the same as the 2D convolution operations in the image classification. The input is viewed as u × m × m, as shown in Fig. 3b, where m × m = k. In this way, the model has better expressiveness through additional pointwise interactions when performing 2D convolutions. The filter size of convolution 2D is 3 × 3, including separable convolution and dilated separable convolution. Take the head entity eh as the example, the embedding representation in 2D is calculated by:

ehc+1=ReLU(Conv1D(erc||etc)),ehc+1=ReLU(Conv2D(erc^||etc^))(1)

where ehc+1 refers to the head entity embedding representation in the th-(c + 1) cell of the network. || denotes concatenation operation, erc^ and etc^ represent 2D reshaping of embedding erl and etc in the th-c cell of the network.

Each convolutional operation is followed by batch normalization and dropout. Meanwhile, we set the same padding to ensure the shape of the input being maximally preserved in the output.

•   Pooling operations. Pooling operations are essential to the regularization of our model. We define two pooling operations: max pooling and average pooling with kernel size 3 × 3. The padding settings are the same as those in convolutional operations.

•   Self-attention operations. Self-attention can be seen as a major component in the Transformer [22]. In this work, we utilize multi-head self-attention operations to make different latent representations interact with each other more sufficiently. By doing so, the self-attention operation can model the global correlation between entities and relations while the convolution and pooling operations can capture their local correlation patterns. We provide two parameter settings: layer = 1&head = 1 and layer = 2&head = 4.

•   Zero operations. The zero operation refers to resetting the input of a node as 0, which is used to improve the generalization ability of the model in the searching phase.

•   Identity operations. The identity operation directly maps the input to the output without any modifications, which aims to stabilize, normalize and improve the convergence speed of our model.

3.4 Network Architecture Search Process

Gradient descent-based methods can greatly improve search efficiency compared with reinforcement learning and evolutionary algorithms through simple weight sharing. Therefore, we adopt gradient descent-based search strategy to design a neural network search model. As described previously, we perform a network architecture search in a normal cell that consists of multiple nodes. We assign a weight for each optional atomic operation and each edge between a node and its previous node or the stem. Let χi denote the currently calculated embedding in the node i that combines head entity embedding and relation embedding, which is calculated by:

χi=∑j=1i−1βj∑k=1Kωj,kϕk(χj)+λ1∑k=1Kϖ1,kϕk(χj)+λ2∑k=1Kϖ2,kϕk(χj)(2)

where K is the number of optional atomic operations described in Section 3.3. ωj,k represents the weight of the th-k atomic operation ϕk(⋅) for the edge between node i and its previous node j. ϖ1,k and ϖ2,k are the weights of the th-k atomic operation ϕk(⋅) for the edge between node i and two stems. In addition, each edge between a node i and its previous node or a stem is also assigned a weight. Node i has i − 1 previous nodes. βj is the weight of the edge between the node i and the th-j previous node. λ1 and λ2 represent the weights of the edges between node i and two stems. The output of a normal cell c is the sum of all nodes, which is formalized by:

tc=∑i=1nχi(3)

where n is the number of nodes in a normal cell.

Specially, we obtain an appropriate neural network architecture for a specific dataset related to link prediction tasks by learning the appropriate weights of different atomic operations and edges. Therefore, we define the searched network architecture A={β1,β2,…,βn,ω1,ω2,…,ωn,λ1,λ2,ϖ1,ϖ2}, where ωj=[ωj,1,ωj,2,…,ωj,K] and ϖ1=[ϖ1,1,ϖ1,2,…,ϖ1,K]. Next, we describe the details of the search process of KGE-ANS by using the gradient descent-based method. We first divide the train set Dtrain of the specific dataset D into two subsets: Dtrain={Dsearch,Darch}, and then we iteratively update the network parameters θA and the network architecture A in an inner iteration process and an architecture iteration process. Parameters θA consist of the parameters of all atomic operations. In the inner iteration process, we utilize Dsearch to update the network parameters θA with fixed A (i.e., all weights are fixed). In the architecture iteration process, we use Darch to update the architecture A with fixed parameters θA, that is, the weights of each atomic operation and the edges between nodes and nodes or stems are updated. The model parameters and weights are updated according to the following loss function:

L(θA)=−1N∑i=1N(yilog⁡(φ(⋅))+(1−yi)(1−log⁡(φ(⋅)))),(4)

φ(⋅)=σ(WeT),(5)

T=gα((eh||er);θA)(6)

where gα denotes the current searched network architecture A. eh, er, and et denote the embedding of head entity, relation and tail entity, respectively. T is the feature map outputted by A, and We is the structural embedding matrix of all entities in E. φ(⋅) is the sigmoid function that scores the probability of a triplet (h, r, t) given an input entity h or t. yi is the label whether there exists a relationship between h and t. The label yi is 1 if the triplet (h, r, t) exists and 0 otherwise. To speed up the calculation of φ(⋅), we follow ConvE [10] to take one (h, r) pair and score its probability against all entities in E simultaneously.

After the training of the inner iteration and architecture iteration process, we determine the final network architecture using the trained weighted of the atomic operations and the trained weights of the edges between the node and previous nodes (or stems). For each edge between a node and its previous node or a stem, we select the atomic operation with the highest weight as the operation of that edge. Furthermore, we split the connection of a node to its previous node or a stem to speed up the embedding learning process. Specially, we keep only the top-2 edges with the highest weights and cut off the other edges, which means that we only connect one node with the two most important elements (the previous node or stem). Finally, we use the determined final network architecture to train from scratch on the training set Dtrain to get the final result of the specific link prediction task. We summarize the searching process in Algorithm 1.

4  Experiments

4.1 Datasets

We evaluate our model on three public benchmark datasets: FB15k, FB15k-237 and WN18, which are sampled from DBpedia or Freebase. Since their relation patterns are very limited, existing methods can simply tackle these datasets by hand-coding them into the model. However, in the real data distribution, there are various intricate relation patterns that cannot be mathematically modeled into a single model. We argue that this discrepancy would prevent us from comprehensively and accurately evaluating existing methods for the KGC task. Therefore, we construct several KG datasets where intricate relation patterns exist, aiming to demonstrate KGE-ANS’s advantage in the adaptation to different datasets (domains). Table 1 describes the considered datasets in our experiments.

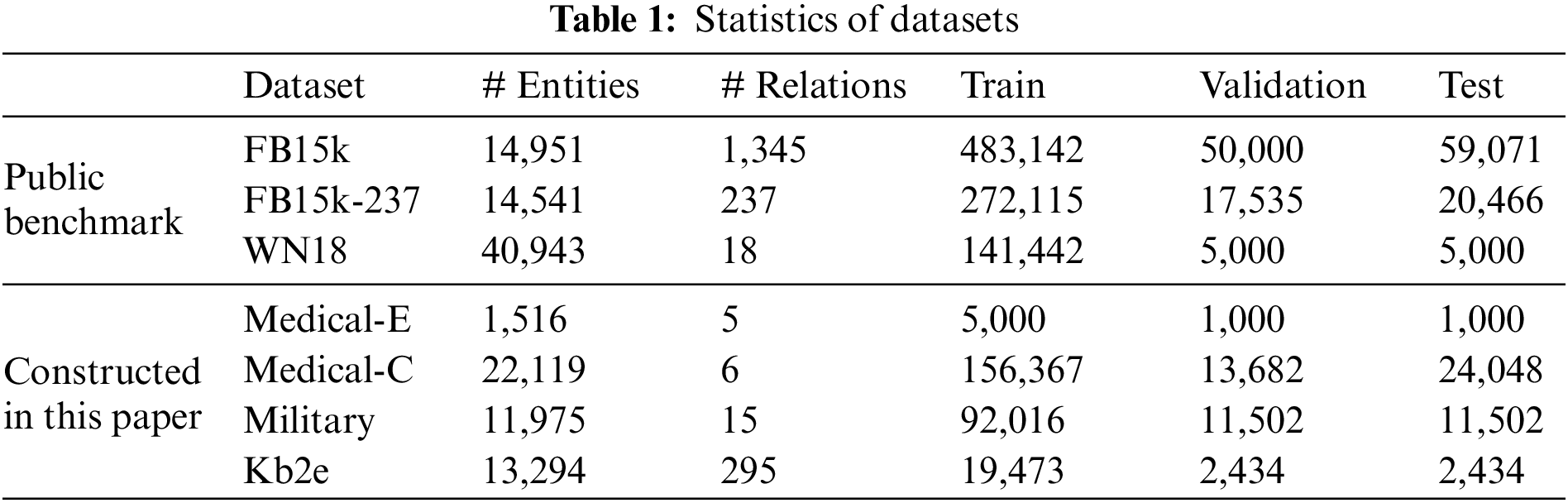
FB15k [6] is a subset of Freebase, which describes movies, actors, sports, and awards in most facts.

FB15k-237 [23] observed that most test triplets can be inferred by simply inverting the corresponding triplets in the training set. Therefore, Toutanova et al. [23] introduced FB15k-237, a subset of FB15k, in which those inverse relations were removed.

WN18 [6] is a subset of WordNet, most of which consists of lexical relations between entities.

Medical-E is a professional dataset extracted from the Freebase and most entities describe drugs and diseases. We mainly collected five relations: treatments, symptoms, risk factors, causes, and prevention factors. This dataset is randomly divided into the training set, validation set, and test set on a scale of 5:1:1. The purpose of constructing this dataset is to demonstrate that our model can achieve good performance in the medical field.

Medical-C is a disease-centered medical knowledge graph constructed based on an open-source project1. We get rid of entities that only appear at the head, not at the tail. Since there are many attribute types in this dataset, we only use six relations of them. This dataset aims to verify the expressiveness of our model in the case of very sparse entities (plenty of entities only appear once).

Military2 mainly includes the publication and citation of papers in the military field. Each entity in this dataset appears in at least 10 triples. The split ratio is 8:1:1 for the train, validation, and test set.

Kb2e is a general dataset extracted from WordNet, most of them describe relationships between people or locations. The split ratio of this dataset is the same as Military. The number of entities and relations is similar to FB15k-237, but the triplets are much less, which can show the superiority of our model when entities and relationships appear less frequently in the general field.

4.2 Experimental Setup

We implemented KGE-ANS by PyTorch [24]. Given our tailored search space for the link prediction task, we search for appropriate network architectures on different datasets. In the experiment, the grid search is used to select hyperparameters for our model. The ranges of the hyperparameters are as follows: number of cells L = {1, 2, 4, 6}, number of nodes inside one cell N = {2, 4, 6}, embedding dimension k = {200, 400}, learning rate lr = {3e-3, 3e-4, 3e-5}, dropout rate p = {0.2, 0.4, 0.6}. We find that the following combination of hyperparameters achieves the best performance on most datasets: L = 2, N = 4, k = 400, lr = 3e-4, p = 0.4. The batch size is 80 on Medical-E and 128 on other datasets. Empirically, we find that our model is unstable in the early training stage. Thus, we try two methods to apply batch normalization on convolution operations: BN-Relu-Conv and Conv-BN-Relu, and the latter is chosen due to its better performance.

After enough training epochs, a competitive architecture is obtained. For example, a normal cell that contains 4 nodes searched on FB15k-237 dataset by KGE-ANS is shown in Fig. 4. It can be seen that 1D convolution operations are more than 2D operations, the reason might be that 1D operations can better extract interactions between entities and relations. We use the searched architecture to train from scratch, and the best performance is recorded by early stopping strategy according to the metrics on the validation set. It is noteworthy that the filtering setting is used for our experiments, that is, we rank the ground truth triples against all other candidate triplets unseen in the dataset. In the experiment, the evaluation metrics contain Mean Reciprocal Rank (MRR), Hits at N (Hits@N), and running time Time/h (1 GPU Hour).

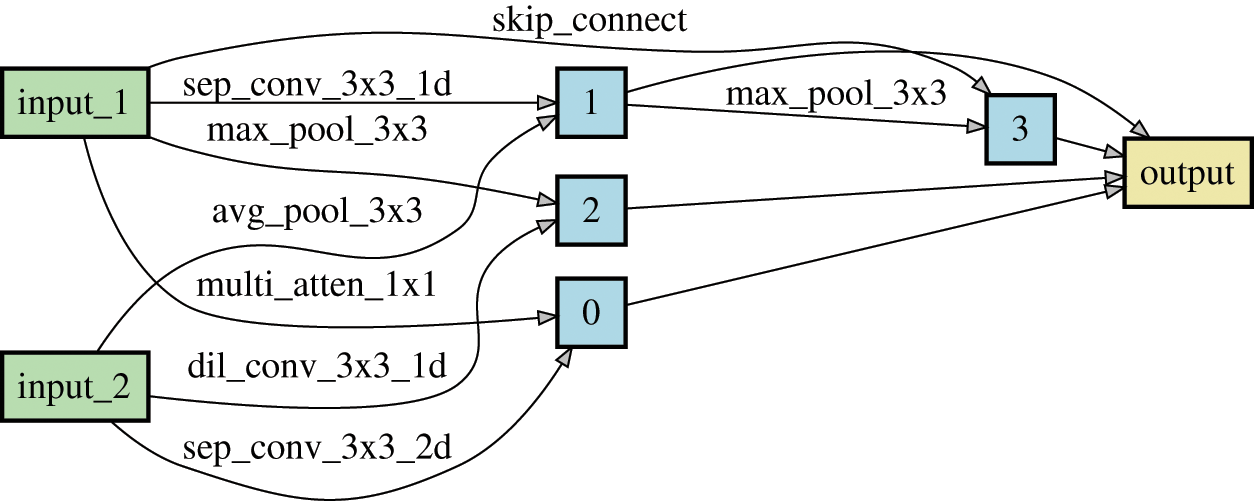
Figure 4: The normal cell searched on FB15k-237 dataset by KGE-ANS

4.3 Results

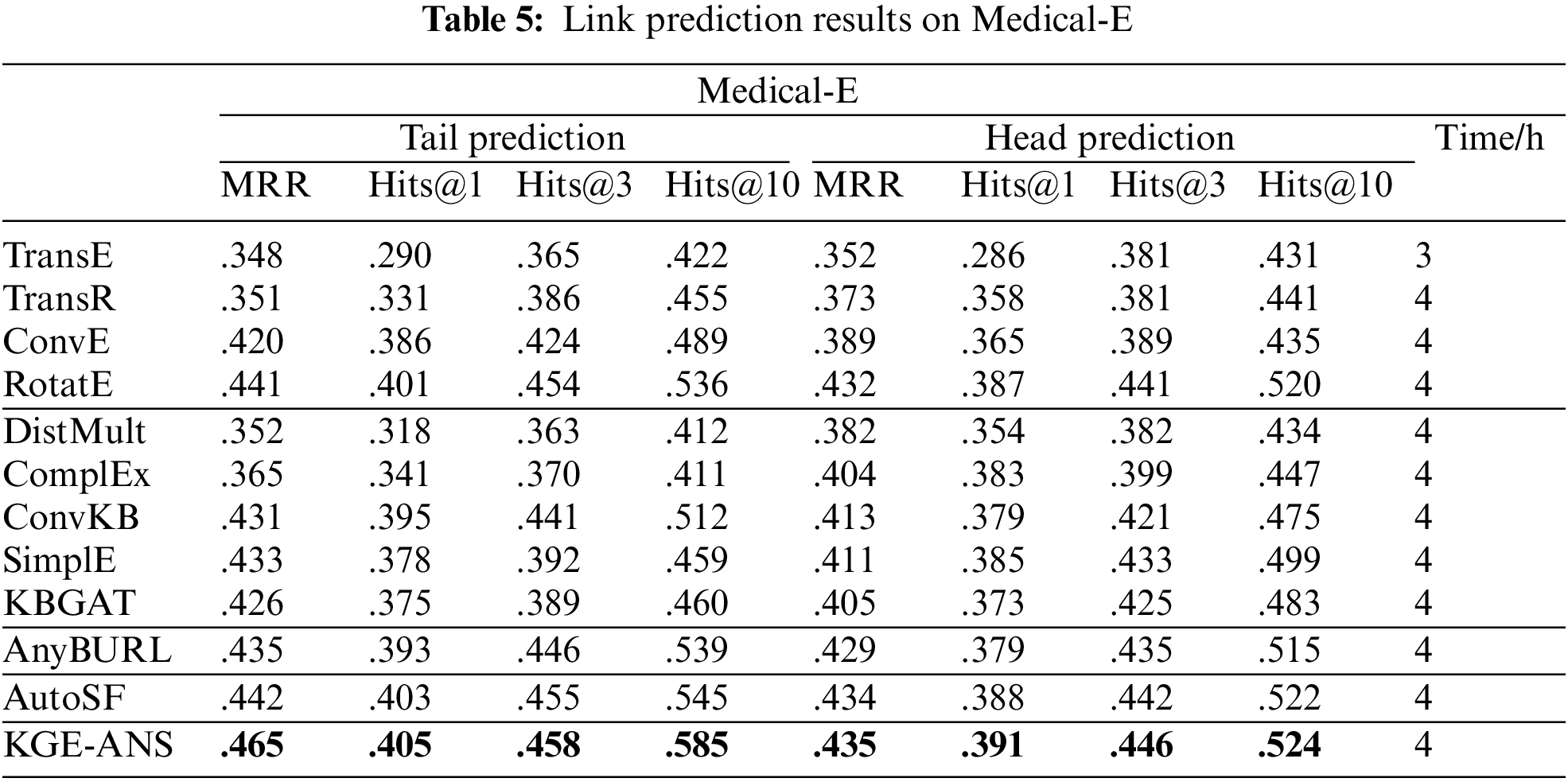
We compare our KGE-ANS with several state-of-the-art models: (1) Reconstruction-Based Models: TransE [6], TransR [15], ConvE [10] and RotatE [9]. (2) Semantic Matching Models: DistMult [7], ComplEx [8], SimplE [17] and ConvKB [16], Graph attention model KBGAT [25]. (3) Rule-based and reinforcement learning-based model AnyBURL [18]. (4) AutoML-based model AutoSF [19]. The results are summarized in Tables 2–5.

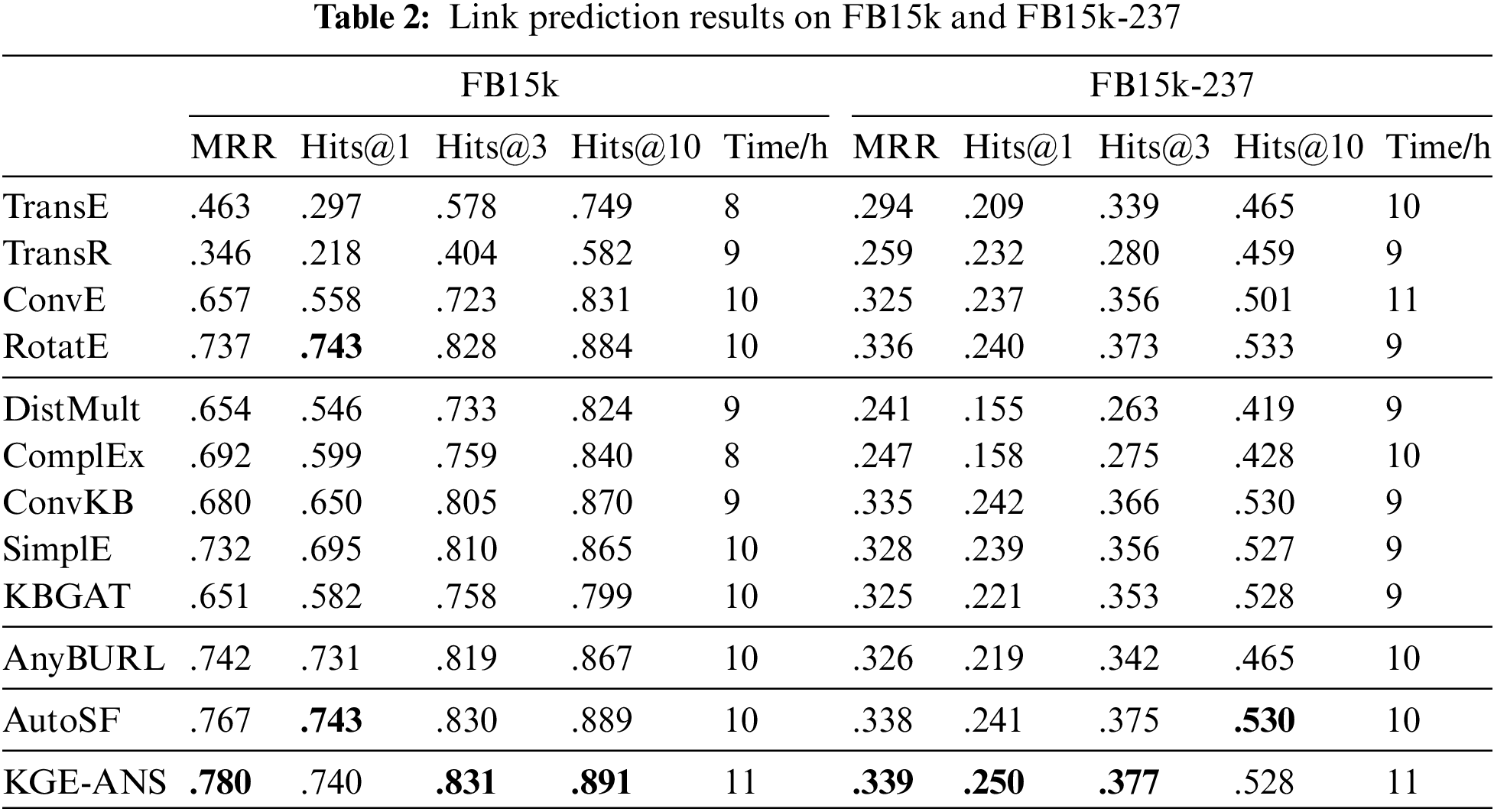
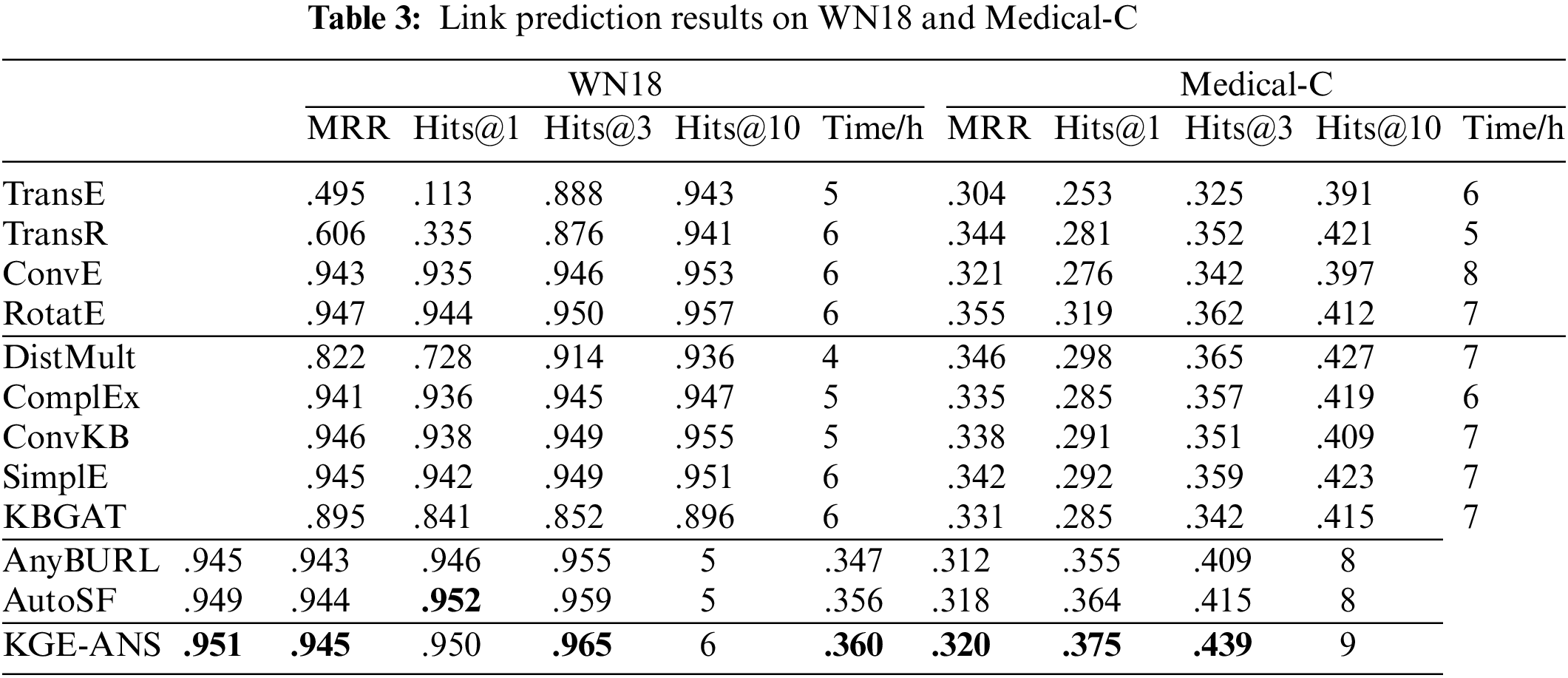
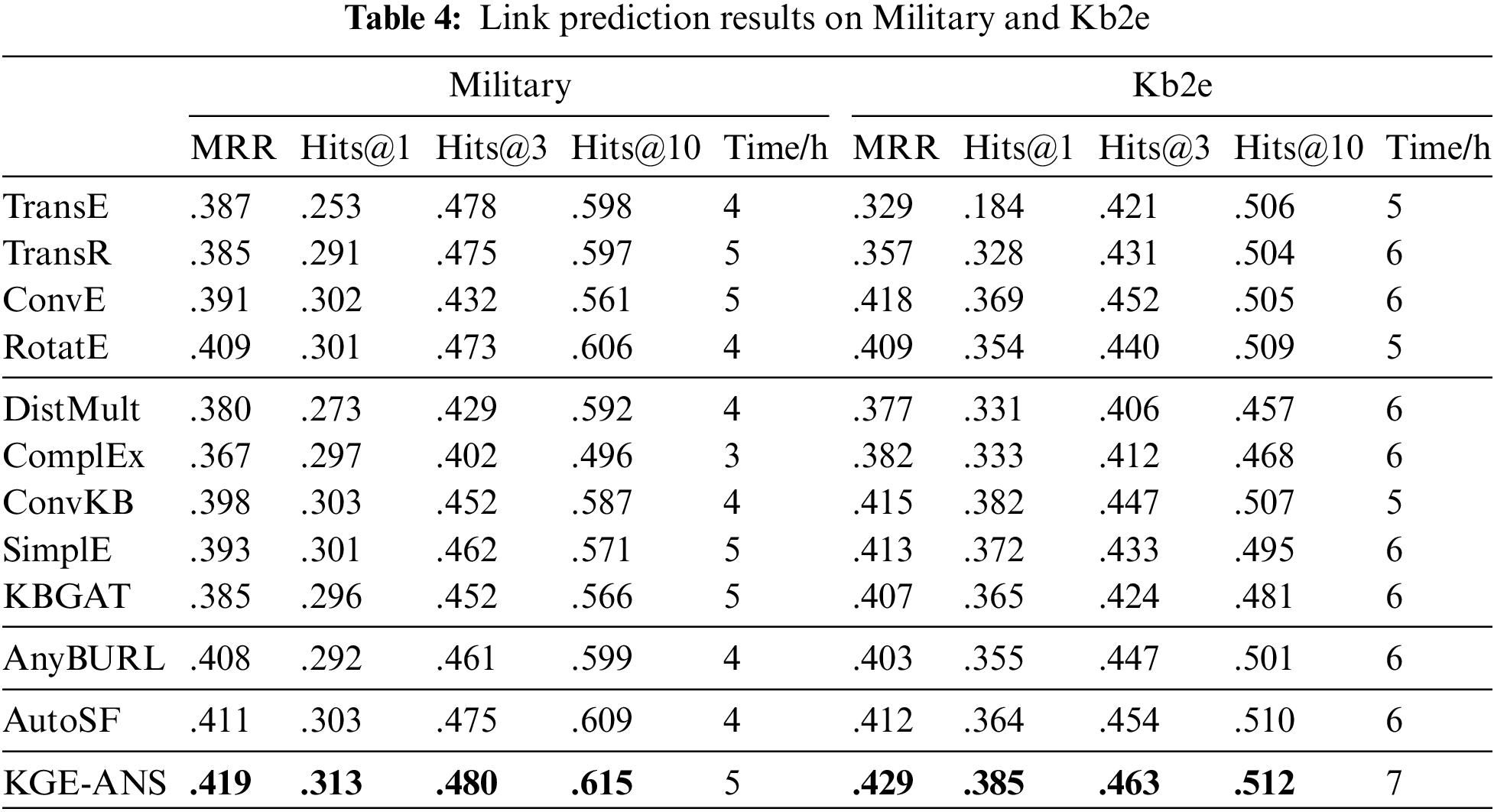
As shown in Tables 2–5, our model can achieve the best MRR in all datasets. In well-known datasets such as FB15k, FB15k-237, and WN18, KGE-ANS reaches comparable performance. Once it comes to the datasets (Medical-C, Military, Kb2e and Medical-E) within the special field that has not been studied before, our model shows superiority compared to baselines, which confirms that KGE-ANS can adapt to different datasets and thus better capture various relation patterns in different latent data distributions. TransE reveals FB15k mainly contains inversion and symmetry/antisymmetry relation patterns. As expected, ComplEx performs better than TransE on FB15k since it is designed to handle inversion and symmetry/antisymmetry relation patterns. KGE-ANS slightly underperforms RotatE on FB15k in terms of Hits@1 and on FB15k-237 in terms of Hits@10. The possible reason is that most relation patterns of this dataset are carefully designed by RotatE. On the one hand, KGE-ANS has an obvious improvement over ConvE on FB15k-237, which indicates KGE-ANS can better infer various kinds of relation patterns due to the tailored architecture searched on the dataset. KGE-ANS slightly underperforms AutoSF on WN18 in terms of Hits@3. The main reason for this phenomenon is that, as shown in Table 1, the WN18 dataset is the most sparse among the five datasets. The final architecture obtained from the AutoSF search can be viewed as a combination of multiple bilinear link prediction models, which may have better performance in this sparse case due to the ensemble property. The time consumption of KGE-ANS is comparable since we have saved a lot of time in designing the network specifically. The search process of KGE-ANS can be finished within 24 h on a single Tesla P100 GPU, and the training time is within 13 h in almost all datasets, thus the time cost is comparable to other baselines.

As for these datasets with intricate relation patterns, including Medical-C, Military, and Medical-E datasets, our KGE-ANS obviously outperforms AutoSF in all metrics. The reason is that not only does KGE-ANS have the tailored architecture search on the dataset but also can extract the intrinsic information between entities and relations during the modeling relations. Furthermore, as shown in Table 5, there is an interesting phenomenon in the experimental results. The metrics of tail prediction are always higher than those of head prediction in most of models, such as ConvE, RotaE and our KGE-ANS. By analyzing cases inside Medical-E, we find that the wrong prediction of the head entity often occurs when the frequency of the tail entity is much higher than that of the head entity in the dataset. Taking the triplet (swine_influenza, symptoms, headache) as an example, it is always easier to predict the symptom of a disease than to predict the disease of a symptom. The reason is that many diseases could cause the “headache” symptom while there are only a few symptoms caused by the “swine_influenza”. Detailed case study experiments are included in Section 5.

4.4 Analysis on KGE-ANS

Since KGE-ANS consists of stacking normal cells, we want to investigate the effect of the number of nodes N inside one cell. For the Medical-E dataset, we use KGE-ANS to search the network architecture and fix other hyperparameters (L = 2, k = 400, lr = 3e-4, p = 0.4). Fig. 5 shows the learning curves of Hits@10 on the test set. The model with fewer nodes converges faster while the model with more nodes can achieve better performance after convergence. When N = 4, continuing to increase the number of nodes does not lead to an obvious improvement. Although our model works best when N = 4, 6, 8, we choose N = 4 to train the model on the Medical-E dataset because of its faster convergence.

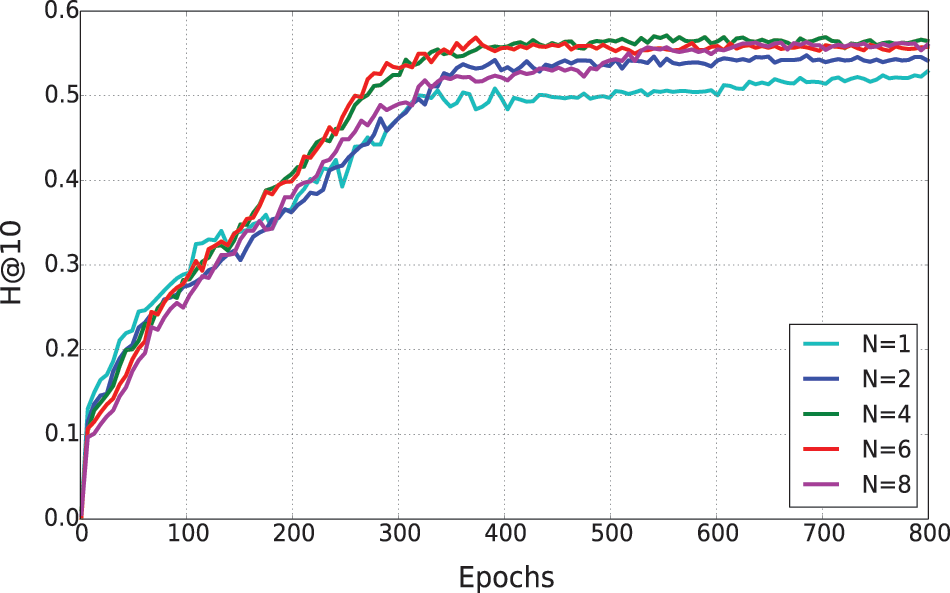
Figure 5: The learning curves on Medical-E by KGE-ANS method. The y-axis is Hits@10 calculated on the test data

4.5 ANS Comparison

To assess the feasibility of KGE-ANS, we conduct experiments to compare KGE-ANS with other state-of-the-art ANS methods, including DARTS [13], ENAS [12], ONE-SHOT [26] and RANDOM SEARCH [27] on Medical-E dataset. The baseline models3 are neither tuned hyper-parameters nor modified original search spaces, except for adapting them to the KGC task. We report the comparison results on the FB15k-237 dataset, as shown in Fig. 6. Due to the more complicated architecture, ENAS converges relatively slower than KGE-ANS and other models. Compared to DARTS, the significant improvement of KGE-ANS indicates that our designed search space is more suitable for the KGC task. Furthermore, KGE-ANS outperforms other methods with fewer GPU hours due to the simple parameter setting and appropriate search space, which is a natural advantage of our method as it is very easy and straightforward to generate effective architecture automatically.

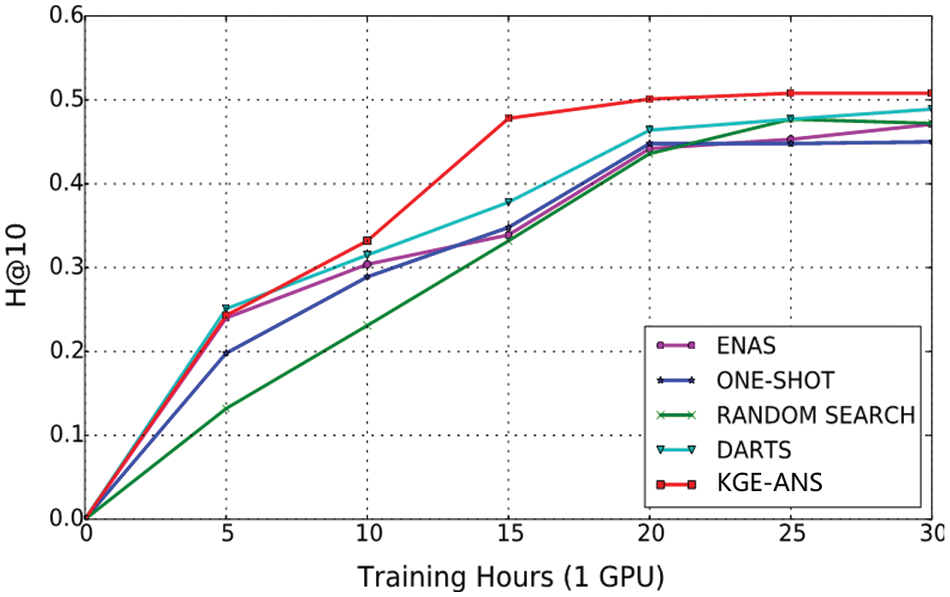
Figure 6: Search process comparison of different ANS methods on FB15k-237 dataset. For each method, we repeat experiments for 4 times with different random seeds and report the average Hits@10 performance on the test data over time

5  Case Study

In this section, we elaborate on actual link prediction results from the Medical-E dataset to highlight the strengths of our KGE-ANS. As shown in Table 6, models are provided with the head entity “hearing_loss” and the relation “risk_factors” and asked to predict the tail entity. KGE-ANS and RotatE successfully rank the correct entity within the top-2 results, while the TransE and ConvE don’t perform well enough. Since the model of TransE and ConvE are too sample to focus on the deep information, they are prone to making wrong predictions, such as more frequent entities like “fever”. RotatE method can better capture deep path information, it would result in ranking “nausea” first (the triplet “meningitis, symptoms, nausea” appears in training data). Compared to RotatE, KGE-ANS shows superiority in modeling the long-term dependency by leveraging the multi-head self-attention mechanism, thereby ranking the correct entity higher.

5.1 Ablation Study

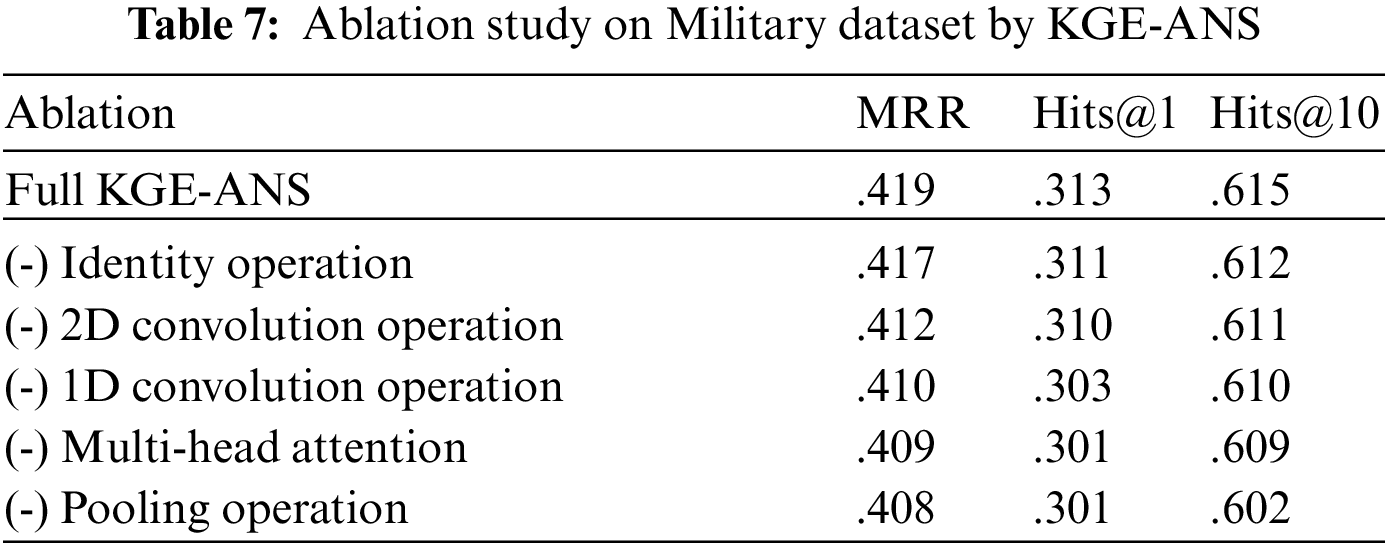
Table 7 shows the results of the ablation study on the test set of the Military. It can be seen that removing the Identity operation hardly affects the experimental results. The reason is that the Pooling operation can handle the regularization of our model during the training on this dataset. Therefore, the drop in removing the Pooling operation suggests that regularization plays an incremental role in the training procedure. Moreover, we can see that during the training on the Military dataset, 1D Convolution operation plays a more important role than 2D Convolution operation. Furthermore, the drop in removing multi-head self-attention indicates it is a crucial component in KGE-ANS, which can potentially make interactions of different latent representations more comprehensively.

6  Conclusion and Future Work

In this paper, we propose KGE-ANS, a novel knowledge graph embedding approach for link prediction, which is able to search for an appropriate neural network architecture using an automatic network search technique to model various relation patterns to adapt to different datasets. Especially, to better adapt to KG-related tasks, we design a general search space including convolution operations, pooling operations, self-attention operations, zero operations, and identity operations, for neural network architecture search. Extensive experiment results show that our KGE-ANS outperforms several state-of-the-art models on both existing benchmark datasets and constructed datasets in this paper. Furthermore, our detailed case study and exhaustive experimental analyses give more insights into our method’s superiority for different link prediction tasks. In the future work, we will explore how to use a textual description of entities to further enhance our neural network architecture search model.

Funding Statement: This work was supported in part by the Major Scientific and Technological Projects of CNPC under Grant ZD2019-183-006.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1https://github.com/liuhuanyong/QASystemOnMedicalKG.

2http://openkg.cn/dataset/techkg10.

3Come from the original open-source codes.

References

 1.  Bollacker, K., Evans, C., Paritosh, P., Sturge, T., Taylor, J. (2008). Freebase: A collaboratively created graph database for structuring human knowledge. Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, pp. 1247–1250. Canada. [Google Scholar]

 2.  Lehmann, J., Isele, R., Jakob, M., Jentzsch, A., Kontokostas, D. et al. (2015). Dbpedia–a large-scale, multilingual knowledge base extracted from wikipedia. Semantic Web, 6(2), 167–195. DOI 10.3233/SW-140134. [Google Scholar] [CrossRef]

 3.  Bordes, A., Weston, J., Usunier, N. (2014). Open question answering with weakly supervised embedding models. Joint European Conference on Machine Learning and Knowledge Discovery in Databases, pp. 165–180. Berlin, Germany. DOI 10.1007/978-3-662-44848-9_11. [Google Scholar] [CrossRef]

 4.  Moon, S., Shah, P., Kumar, A., Subba, R. (2019). Opendialkg: Explainable conversational reasoning with attention-based walks over knowledge graphs. Proceedings of the 57th Conference of the Association for Computational Linguistics, pp. 845–854. Italy. [Google Scholar]

 5.  Dong, X., Gabrilovich, E., Heitz, G., Horn, W., Lao, N. et al. (2014). Knowledge vault: A web-scale approach to probabilistic knowledge fusion. Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 601–610. New York, USA. [Google Scholar]

 6.  Bordes, A., Usunier, N., Garcia-Duran, A., Weston, J., Yakhnenko, O. (2013). Translating embeddings for modeling multi-relational data. Proceedings of the 26th International Conference on Neural Information Processing Systems, pp. 2787–2795. Australia. [Google Scholar]

 7.  Yang, B., Yih, W. T., He, X., Gao, J., Deng, L. (2014). Embedding entities and relations for learning and inference in knowledge bases. arXiv preprint arXiv:1412.6575. [Google Scholar]

 8.  Trouillon, T., Welbl, J., Riedel, S., Gaussier, É., Bouchard, G. (2016). Complex embeddings for simple link prediction. International Conference on Machine Learning, pp. 2071–2080. New York, USA. DOI 10.48550/arXiv.1606.06357. [Google Scholar] [CrossRef]

 9.  Sun, Z., Deng, Z. H., Nie, J. Y., Tang, J. (2019). Rotate: Knowledge graph embedding by relational rotation in complex space. arXiv preprint arXiv:1902.10197. [Google Scholar]

10. Dettmers, T., Minervini, P., Stenetorp, P., Riedel, S. (2018). Convolutional 2D knowledge graph embeddings. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 32, no. 1. Louisiana, USA. DOI 10.1609/aaai.v32i1.11573. [Google Scholar] [CrossRef]

11. Zoph, B., Le, Q. V. (2016). Neural architecture search with reinforcement learning. arXiv preprint arXiv:1611.01578. [Google Scholar]

12. Pham, H., Guan, M. Y., Zoph, B., Le, Q. V., Dean, J. (2018). Efficient neural architecture search via parameter sharing. arXiv preprint arXiv:1802.03268. [Google Scholar]

13. Liu, H., Simonyan, K., Yang, Y. (2018). Darts: Differentiable architecture search. arXiv preprint arXiv:1806.09055. [Google Scholar]

14. Wang, Z., Zhang, J., Feng, J., Chen, Z. (2014). Knowledge graph embedding by translating on hyperplanes. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 28, no. 1. Québec, Canada. DOI 10.1609/aaai.v28i1.8870. [Google Scholar] [CrossRef]

15. Lin, Y., Liu, Z., Sun, M., Liu, Y., Zhu, X. (2015). Learning entity and relation embeddings for knowledge graph completion. Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin Texas, USA. [Google Scholar]

16. Nguyen, D. Q., Nguyen, T. D., Nguyen, D. Q., Phung, D. (2017). A novel embedding model for knowledge base completion based on convolutional neural network. arXiv preprint arXiv:1712.02121. [Google Scholar]

17. Kazemi, S. M., Poole, D. (2018). Simple embedding for link prediction in knowledge graphs. In: Advances in neural information processing systems, pp. 4289–4300. New York, USA. [Google Scholar]

18. Meilicke, C., Chekol, M. W., Fink, M., Stuckenschmidt, H. (2020). Reinforced anytime bottom up rule learning for knowledge graph completion. arXiv preprint arXiv:2004.04412. [Google Scholar]

19. Zhang, Y., Yao, Q., Dai, W., Chen, L. (2020). AutoSF: Searching scoring functions for knowledge graph embedding. 2020 IEEE 36th International Conference on Data Engineering (ICDE), pp. 433–444. Texas, USA. [Google Scholar]

20. Fang, J., Chen, Y., Zhang, X., Zhang, Q., Huang, C. et al. (2019). EAT-NAS: Elastic architecture transfer for accelerating large-scale neural architecture search. arXiv preprint arXiv:1901.05884. [Google Scholar]

21. Kim, Y. (2014). Convolutional neural networks for sentence classification. arXiv preprint arXiv:1408.5882. [Google Scholar]

22. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L. et al. (2017). Attention is all you need. In: Advances in neural information processing systems, pp. 5998–6008. San Francisco, CA, USA: Morgan Kaufmann. [Google Scholar]

23. Toutanova, K., Chen, D. (2015). Observed versus latent features for knowledge base and text inference. Proceedings of the 3rd Workshop on Continuous Vector Space Models and their Compositionality, pp. 57–66. Peking, China. [Google Scholar]

24. Paszke, A., Gross, S., Massa, F., Lerer, A., Chintala, S. et al. (2019). Pytorch: An imperative style, high-performance deep learning library. In: Advances in neural information processing systems, vol. 32. San Francisco, CA, USA: Morgan Kaufmann. [Google Scholar]

25. Nathani, D., Chauhan, J., Sharma, C., Kaul, M. (2019). Learning attention-based embeddings for relation prediction in knowledge graphs. arXiv preprint arXiv:1906.01195. [Google Scholar]

26. Bender, G., Kindermans, P. J., Zoph, B., Vasudevan, V., Le, Q. (2018). Understanding and simplifying one-shot architecture search. International Conference on Machine Learning, pp. 549–558. Sanya, China. [Google Scholar]

27. Li, L., Talwalkar, A. (2019). Random search and reproducibility for neural architecture search. arXiv preprint arXiv:1902.07638. [Google Scholar]