Open Access

ARTICLE

On the Approximation of Fractal-Fractional Differential Equations Using Numerical Inverse Laplace Transform Methods

Kamran¹, Siraj Ahmad¹, Kamal Shah^2,3,*, Thabet Abdeljawad^2,4,*, Bahaaeldin Abdalla²

1 Department of Mathematics, Islamia College Peshawar, Khyber Pakhtoon Khwa, Peshawar, 25120, Pakistan
2 Department of Mathematics and Sciences, Prince Sultan University, P.O. Box 66833, Riyadh, 11586, Saudi Arabia
3 Department of Mathematics, University of Malakand, Chakdara Dir(L), Khyber Pakhtunkhwa, 18000, Pakistan
4 Department of Medical Research, China Medical University, Taichung, 40402, Taiwan

* Corresponding Authors: Kamal Shah. Email: ; Thabet Abdeljawad. Email:

(This article belongs to the Special Issue: Applications of Fractional Operators in Modeling Real-world Problems: Theory, Computation, and Applications)

Computer Modeling in Engineering & Sciences 2023, 135(3), 2743-2765. https://doi.org/10.32604/cmes.2023.023705

Received 10 May 2022; Accepted 14 July 2022; Issue published 23 November 2022

Abstract

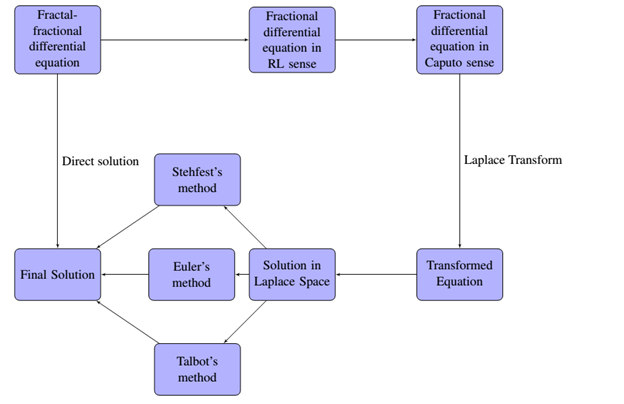
Laplace transform is one of the powerful tools for solving differential equations in engineering and other science subjects. Using the Laplace transform for solving differential equations, however, sometimes leads to solutions in the Laplace domain that are not readily invertible to the real domain by analytical means. Thus, we need numerical inversion methods to convert the obtained solution from Laplace domain to a real domain. In this paper, we propose a numerical scheme based on Laplace transform and numerical inverse Laplace transform for the approximate solution of fractal-fractional differential equations with order . Our proposed numerical scheme is based on three main steps. First, we convert the given fractal-fractional differential equation to fractional-differential equation in Riemann-Liouville sense, and then into Caputo sense. Secondly, we transform the fractional differential equation in Caputo sense to an equivalent equation in Laplace space. Then the solution of the transformed equation is obtained in Laplace domain. Finally, the solution is converted into the real domain using numerical inversion of Laplace transform. Three inversion methods are evaluated in this paper, and their convergence is also discussed. Three test problems are used to validate the inversion methods. We demonstrate our results with the help of tables and figures. The obtained results show that Euler’s and Talbot’s methods performed better than Stehfest’s method.

---

Graphic Abstract

---

Keywords

---