Vibration Diagnosis and Optimization of Industrial Robot Based on TPA and EMD Methods

1  Introduction

Industrial robot is a complex product that integrates the achievements of multi-disciplinary development. In recent years, the industrial robot has played an important role in industrial intelligence. It could be used to replace manual labor to carry out various complicated or dangerous tasks in many fields, such as medical treatment, processing, and manufacturing [1]. Because of its reliability and high efficiency, it has become indispensable equipment in the fields of assembly lines, manufacturing process, special maintenance and so on. Facing stability and reliability request of long-term operation, it is an urgent problem to improve the accuracy and durability of robots.

The research object of this paper is a six axis industrial robot of a certain brand. Its structural diagram is shown in Fig. 1. During the working movement of this robot, the arm has abnormal shaking. The vibration of the robot causes some problems such as poor accuracy, low reliability, and noise pollution. Researchers usually use two methods to study the relationship between vibration and structures [2]. The first is to simulate the vibration of industrial robots through a dynamic model [3], and the other is an experimental method. Researchers have created a series of research methods for robot vibration tests [4]. As a complex mechanical vibration system, industrial robots have many coupling components. The theoretical model is hardly matching the actual system. It is important to find the relationship between vibration problem and structure from the experimental point of view. The TPA method has brought a new approach to the experimental research methods of robots. Initially, TPA technology has been widely used in the optimization of vibration and noise in the automotive industry. Janssens proposed an improved Operational-Xtransfer Path Analysis (OPAX) method to use parametric models for identifying the operational loads. A simple model based on a small amount of measurement data is used for quick troubleshooting or increasing accuracy using a more complex model with additional measurements [5]. However, the traditional TPA analysis method has certain defects. In the process of load calculation, the ill-conditioned problem of the matrix will reduce the accuracy of the calculation result. Scholars such as Mo Chou improve the OPAX method through wavelet denoising processing and neural network algorithms [6]. Cheng et al. [7] introduced Tikhonov regularization technology in Operational Transfer Path Analysis (OTPA) to solve the ill-conditioned problems in OTPA calculation and improve the calculation accuracy of the OTPA method. TPA theory is a classic method for studying vehicle NVH problem. Aiming at insufficient accuracy in the traditional TPA method, this paper proposes an improved TPA method for robot vibration research that significantly improves the ill-conditioned problem.

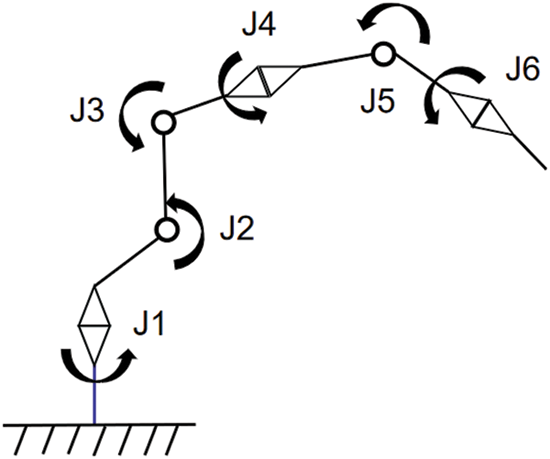
Figure 1: Robot structure model diagram

Researchers usually carried out three-dimensional model in the vibration research of RV reducer. The static performances of its main transmission components were analyzed, and the natural frequency and other performance parameters were calculated more accurately [8]; Some others established a mathematical model of the system dynamics to solve transmission error [9]; Some researchers simulated the actual operating conditions of the reducer in the vibration test [10]. The laws of RV reducer’s vibration were summarized by time and frequency domain analysis methods. However, some scholars have found that simple time-frequency analysis cannot fully explore the vibration characteristics of the reducer. Some try to introduce other methods to process the vibration signal of the reducer. Chen et al. [11] combined frequency spectrum and Kernel Principal Component Analysis (KPCA) to diagnose RV reducer faults. The signal recognition and noise reduction to vibration signals were done using wavelet transform theory and achieved good results [11,12].

As a special gearbox structure, the RV reducer has certain nonlinear and unsteady vibration characteristics. At present, the most widely used method in the field of gearbox fault diagnosis is Empirical Mode Decomposition (EMD). Its principle is to decompose the signal into several intrinsic mode functions (IMFs) and a residual. In the process of decomposition, for it can make self-adaptive adjustment according to the law of the signal, the analysis result has a high signal-to-noise ratio. This method is continuously optimized and improved to gradually expand its application range such as bearing test, rotor test, machine tool rotation fault diagnosis, mechanical torsional vibration analysis, etc. Researchers expand the application range by combining EMD with other classic methods, such as wavelet, support vector machine and other comprehensive features extraction and diagnosis methods. Immediately afterwards, Shi et al. [13] introduced the envelope method into EMD fault diagnosis. Zhang et al. [14] obtained the envelope spectrum of the EMD decomposed IMF and extracted the fault feature vector. Li et al. [15] found that the gearbox vibration had an obvious modulation phenomenon. The envelope signal in the main IMF is analyzed to identify the characteristic frequency of the fault signal [16]. Chen et al. [17] used the EMD method to analyze vibration signals, obtain intrinsic mode functions (IMFs), and calculate the weight coefficients of each IMF. Then, the quantitative value of EMD generalized energy is determined by calculating the weighted sum of IMF energy. Finally, the safety threshold of EMD generalized energy is determined to distinguish the faulty parts. Chen et al. [18] proposed a fault diagnosis method based on the combination of EMD and target feature selection (TFs). Firstly, the fault signal is analyzed by EMD, and the fault feature is extracted. Then, TFs are used to delete redundant features and optimize feature subsets. Luo et al. [19] proposed a fault diagnosis method based on empirical mode decomposition (EMD), Hilbert envelope spectrum and kurtosis criterion for the nonlinear and nonstationary characteristics of rolling bearing fault signals, which was applied to the extraction of fault information. Xie et al. [20] realized fatigue estimation and fault diagnosis to centrifugal fan blades based on the Refined Generalized Multi-Scale Entropy method and obtained perfect results. The above research rarely combines single point analysis with multi-point path recognition and hardly locates the fault from the total system to the local accurate location. The method that combined TPA and EMD with Hilbert envelope is proposed to extract the vibration characteristics of the industrial robot in this paper. Compared with the single time frequency analysis, this method can diagnose the vibration problem of the RV reducer more effectively.

2  Industrial Robot and RV Reducer Test

2.1 Robot Vibration TPA Test

The object of this experiment is an industrial robot with six axes as shown in Fig. 2. The 1–4 axis joints of the robot are RV reducers, and the 5–6 joints at the end of the robot are harmonic reducers. The rated load is 12 kg. During the movement under certain conditions, the arm shook abnormally. The vibration performances of the robot are tested to trace the source of vibration. The experimental equipment is shown in Table 1 as below. The concrete experimental steps are as follows.

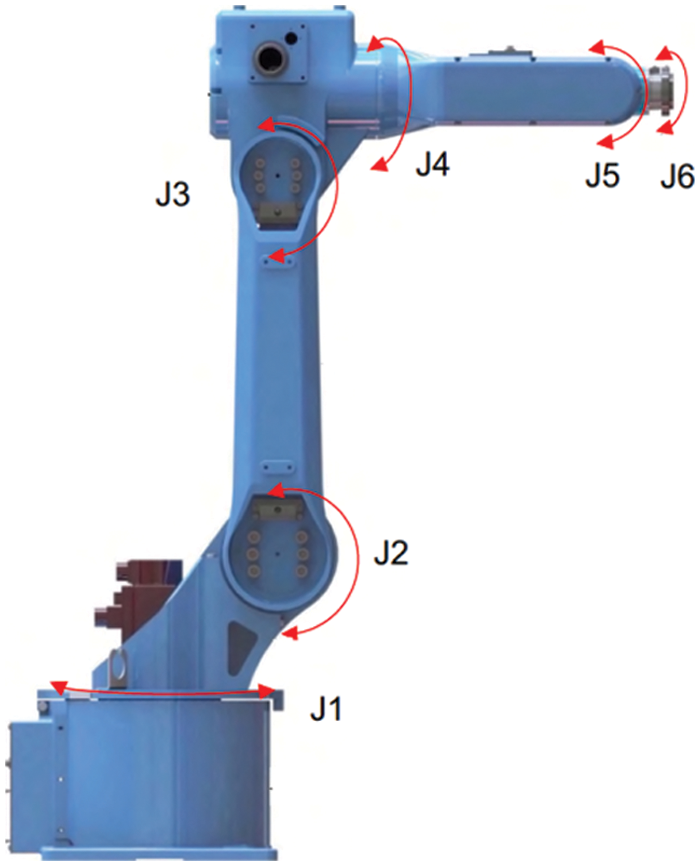
Figure 2: Schematic diagram of robot structure and layout

Firstly, the TPA analysis model is established. The excitation point is the active side of the suspension point of the permanent magnet synchronous drive motor. The transfer path is the 6 joint points of the robot arm, and each has 3 directions of X, Y, Z at load excitation point. A total of 18 transfer paths are calculated. Secondly, a test coordinate system is established. The direction of the robot arm pushing forward is the +X direction of the whole machine coordinate system. According to right-hand principle of coordinate system, the +Y direction is determined. The vertical direction vertical to the ground is +Z direction of the whole machine. Finally, the robot coordinate system, the coordinate system of three-axis acceleration sensors and the coordinate system set in the LMS Test.lab system are kept as the same. Before the test, the key position points are selected as Table 2. According to the inverse matrix method, additional reference points are usually selected near the load excitation point. In the test, a total of 6 reference points are selected. The location of the key points, corresponding points, and the location of the three-axis sensors are shown in Table 2 below.

To simulate the actual working movement of industrial robots, two typical movement postures are selected as research targets. One is the inline movement of the robot arm end (translation along the X direction of the coordinate system), and the other is the simultaneous movement of five axes of the robot. The postures are shown in Fig. 3. To compare different experimental conditions, the robot run at a specified speed under rated load. The two working postures are divided into three operating conditions: in-line slow motion conditions, five-axis linkage slow operating conditions and one-shape fast working conditions.

Figure 3: Schematic diagram of two typical robot motion conditions

After the preparation, the active sides of each joint are hit with a force hammer in a static state to measure the Frequency Response Function (FRF) of each joint. The sensor position and test system are shown in Fig. 4. Then the TPA process is done. The wide frequency band from 1 to 4960 Hz can be excited to provide a wide reference for studying the vibration transmission of the robot. At the same time, it is compared with the TPA results underthe motion excitation of the above three working conditions to ensure the accuracy of the experiment. The data of whole points are imported into the established model for TPA analysis. The TPA tests include two parts of data: (1) Data by the hammer excitation method. (2) Data on working condition: the robot was tested on normal operation. During the test, avoid the start-stop state. When the robot moves at a constant speed, data in uniform working condition is collected using the Signature Testing-Advanced module of LMS Test. lab software.

Figure 4: Sensor location and test system

2.2 TPA Analysis

The data on working condition and FRF of each path has been obtained in the test. The vibration data at the target point, the FRF data from the excitation source to the target, and the FRF data from the excitation source to the reference are imported into the TPA model. The inverse matrix and Singular value truncation method were used to solve the TPA modal. The contribution of each transmission path to the target point and sort the contribution of the 18 paths to the target point in three directions are gotten as shown in Figs. 5–7. Among them, the three histograms under each working condition correspond to the contribution of 18 paths to the target point in the X, Y, and Z directions. The abscissa JILI1 in the figure: X refers to the X direction of the robot 1 joint, and the height of the histogram is the contribution of the vibration amplitude.

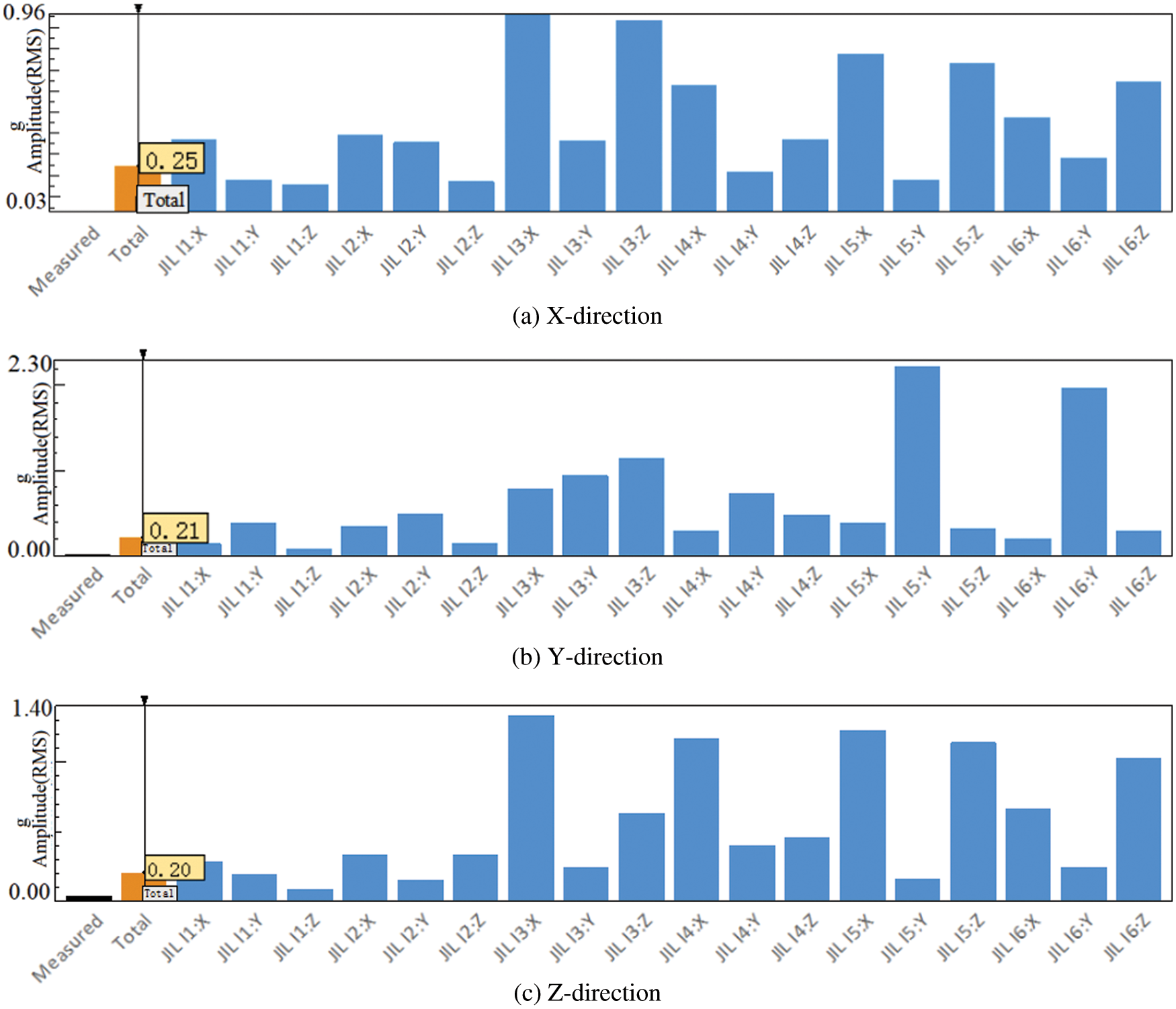
Figure 5: TPA contribution in the XYZ direction of the straight-line low working condition

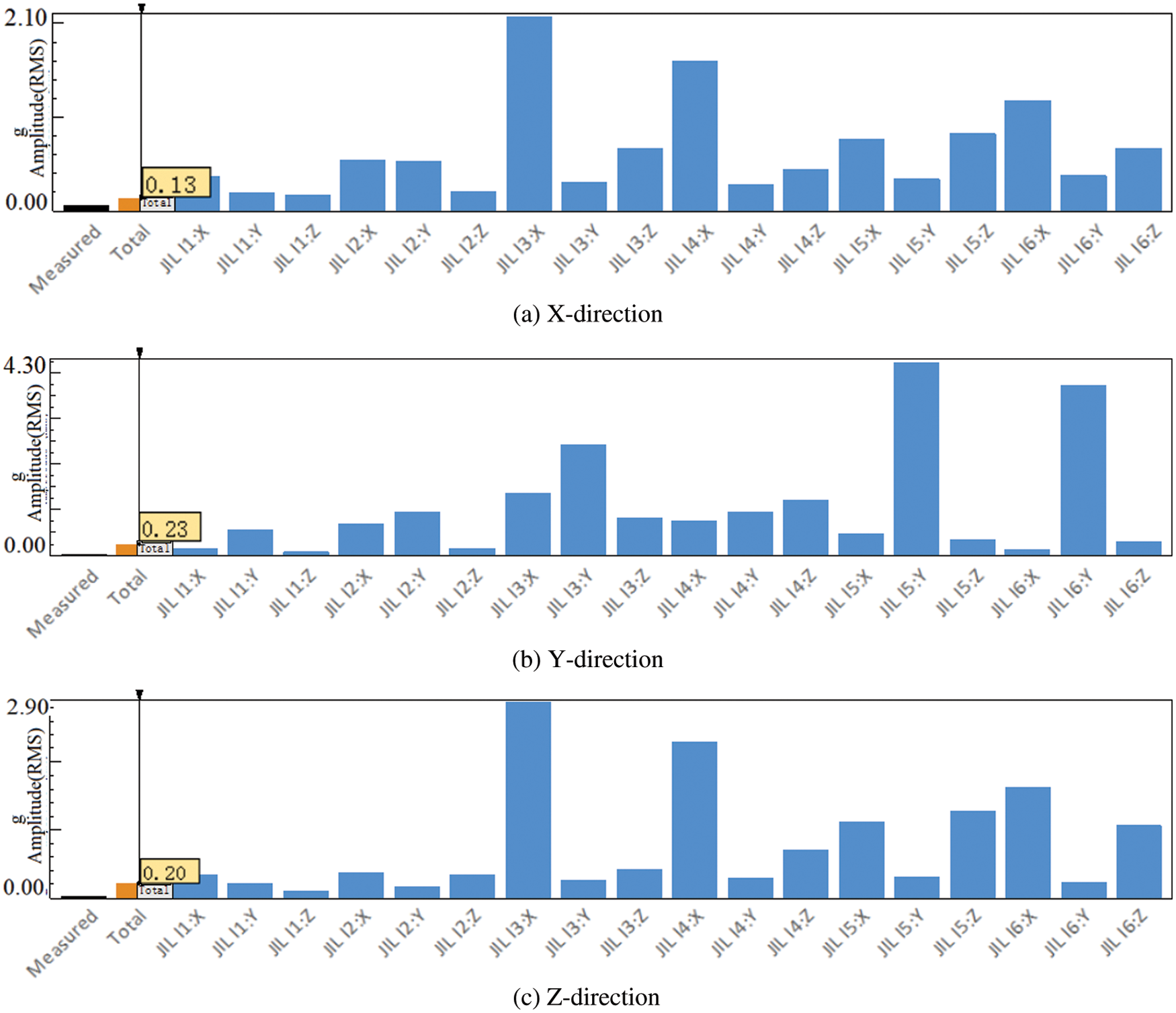
Figure 6: TPA contribution in X,Y, Z direction for five-axis linkage slow operating conditions

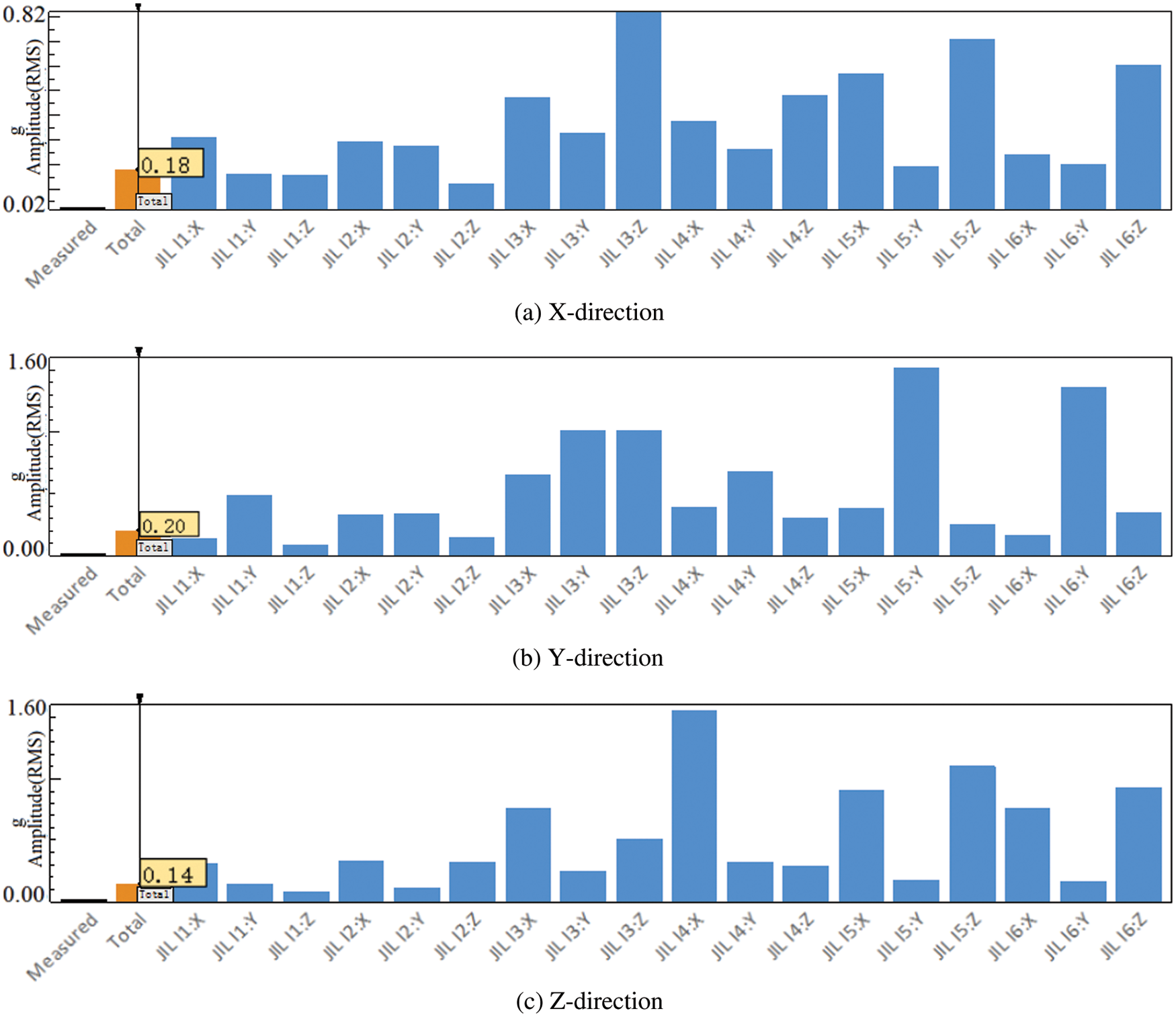
Figure 7: TPA contribution in the XYZ direction of the straight-line fast working condition

From the histogram in Figs. 5–7, it can be found that the largest contribution to the vibration of the target point is the X direction of joint #3, the Y direction of joint #5, and the X direction of joint #3 during slow motion in a straight line. In the five-axis linkage slow motion, the largest contribution to the vibration of the target point is the X direction of joint #3, the Y direction of joint #5 and the X direction of joint #3. During the in-line rapid movement, the largest contribution to the vibration of the target point is the Z direction of joint #3, the Y direction of joint #5 and the X direction of joint #4.

In summary, by analyzing the spectrogram of the target point, only the frequency of the vibration amplitude of the target point can be obtained. At the same time, since the motion situation of each joint is unknown, it is difficult to find out the cause of high amplitude in a specific frequency band. The application of the TPA method can accurately find the path point that contributes the most to the vibration of the target point. From the results of TPA, it can be concluded that the vibration of the target point in the X and Z directions under the three working conditions mainly comes from the X direction vibration of joint #3. The Y-direction vibration of the target point mainly comes from the Y-direction vibration of joint #5, and the secondary source is the Y-direction vibration of joint #3. There is a large vibration at the target point of the robot, and the vibration mainly comes from the vibration of robot joint #3.

2.3 Vibration Experiment of RV Reducer

The RV reducer is a key component of robot motion bearing alternating load. Based on the results of the TPA analysis, this paper conducts an independent vibration study on the RV reducer of the robot’s third joint.

The information on the RV reducer and instruments required for the experiment are shown in Table 3 as below. This experimental platform is driven by a variable-frequency three-phase asynchronous motor that supports speed adjustment from 0–3000 r/min. The data acquisition system is National Instruments (NI-PXI-4472) dynamic data acquisition card. The system has a maximum sampling frequency of 102.4 kHz/s, which meets the needs of multi-channel high-precision signal acquisition. At the same time, the load of the RV reducer can be adjusted according to the needs.

The essence of an RV reducer is a two-stage reduction transmission device. Their structure diagram is shown in Fig. 8. The reducer is a high-speed ratio reduction device composed of a two-stage reduction. The first stage is a planetary reduction mechanism, which consists of a sun gear located in the center and planetary gears evenly distributed around the sun gear. The second stage is a differential gear train composed of cycloid gear and needle teeth.

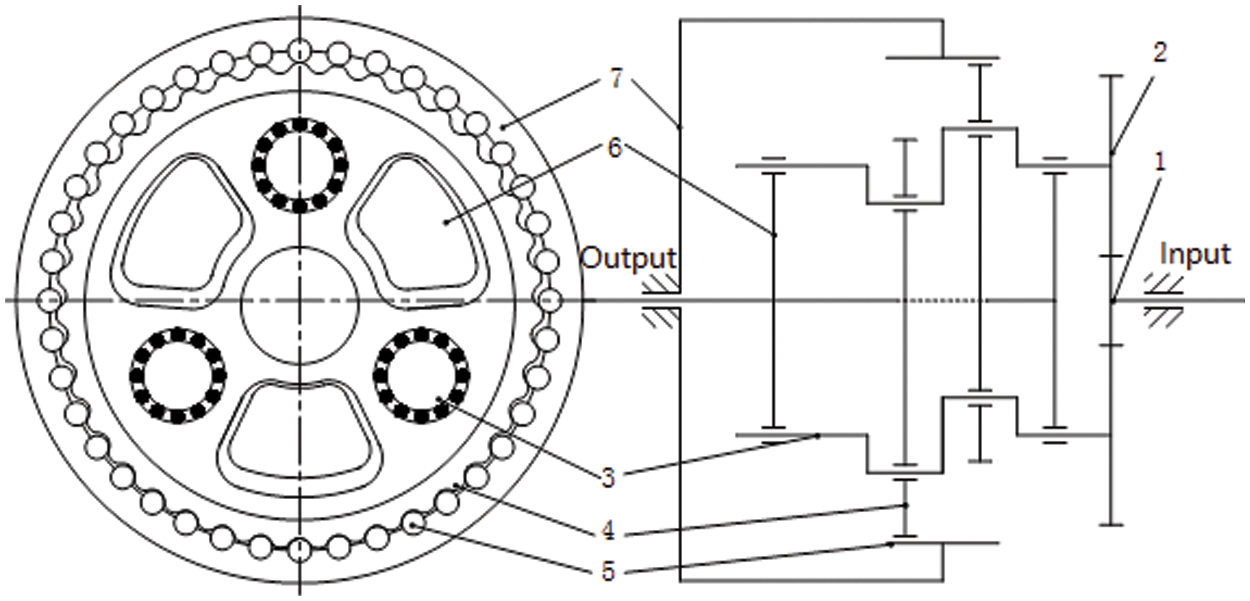
Figure 8: Schematic diagram of RV reducer structure 1-Sun gear; 2-Planet gear; 3- Camshaft; 4-Cycloid gear; 5-Pin tooth; 6-Planet carrier; 7-Pin tooth shell

The experimental bench picture is shown in Fig. 9. Firstly, the coordinate system of the reducer is set to be consistent with the coordinate system of the robot. The +X and +Z directions are the up and left radical direction of the reducer, and the Y direction is the forward axial direction of the reducer. After installing the acceleration sensors, the sensitivities are set according to the calibration value of each sensor. The acceleration sampling frequency is 4.96 kHz. Secondly, start Pre-rotation for 10 mins. Thirdly, speed of the input end is set to 605 rpm, loads of the reducer are 0%, 25%, 50%, 75%, 100%, 125%, 150% of the rated load. Maintain the stable operation of the reducer and collect test data for subsequent analysis. To compare the data of different working conditions, adjust the speed of the output shaft to 1210 and 1815 rpm. Repeat the steps three times and save all records. Finally, the collected data is sorted and analyzed.

Figure 9: Schematic diagram of reducer test system 1. Reducer test bench 2. Coupling 3. RV reducer 4. Three-axis acceleration sensor 5. Torque sensor 6. motor 7. Display screen 8. NI data collection system 9. Data acquisition card

3  Time-Domain TPA Method Using Deconvolution Filter

The linear system response is the convolution of the excitation signal and the unit impulse response function [21]. When sound and vibration are considered at the same time, the noise in the car can be expressed as:

prec(t)=∑i=1lhrec,isb∗fi(t)+∑j=1nhrec,jvb∗qj(t)(1)

where t is the time variable, prec(t) is the total sound pressure contribution of sound and vibration, fi(t) is the excitation force of the i-th path of sound, hrec,isb is the unit impulse response function of the i-th path of structured sound, and l is the total number of sound paths. qj(t) is the volume velocity of the j-th vibration source, hrec,jvb is the unit impulse response function of the j-th path of vibration, and n is the total number of vibration paths. This paper focuses on the vibration transmission path, so h(t)=hrecsb.

In actual operation, it is difficult to apply an ideal impulse input signal. Usually, the transfer function of each path is measured first, and then the inverse Fourier transform is calculated to obtain the unit impulse response function of each path. The time history of excitation force and volume velocity under working conditions are obtained by the deconvolution method.

Firstly, a certain number of acceleration sensors are arranged on both active sides and passive sides of joints. A linear and time-invariant multiple-input multiple-output system with each excitation force is built. The relationship can be expressed as:

[a(t)]l×1=[h(t)]l×m∗[f(t)]m×1(2)

where a(t) is the column vector formed by the time histories of the acceleration response of l vibration indicator points; f(t) is the column vector formed by the time histories of the excitation force of the m paths; h(t) is the l×m dimensional unit impulse response function matrix.

The process of resolving the path excitation force vector f(t) from Eq. (2) is called deconvolution processing. For this reason, the acceleration response a(t) of the indicator point is passed through the time domain deconvolution filter system s(t), and the convolution relationship can be expressed as follows:

f(t)=s(t)∗a(t)=s(t)∗h(t)∗f(t)(3)

Obviously, for deconvolution to be able to obtain f(t), the following relationship must be satisfied:

s(t)∗h(t)=diag[δ1(t),δ2(t),⋯,δm(t)](4)

Eq. (4) is the deconvolution equation. Fourier transform is performed on both sides of Eq. (4) to obtain:

S(f)⋅H(f)=E(5)

where S(f) and H(f) are the Fourier transform of s(t) and h(t), respectively, and E is the identity matrix.

From Eq. (5), we know that S(f) and H(f) are generalized inverses of each other. Therefore, the FRF matrix H(f) of the vibration acceleration response from the excitation force of each path to the indicator point is measured. Then the FRF matrix S(f) of the deconvolution filter system is obtained through generalized inverse.

Because of some nonlinear characteristics of industrial robot structure, part of the FRF vectors from different path excitation forces to different indication points of vibration acceleration are nonlinear related. The FRF matrix H(f) composed of FRF vectors is often ill-conditioned, which has negative effect on the inversion. In this paper, the singular value truncation method is used to solve the frequency domain characteristic S(f) of the deconvolution filter.

Secondly, after obtaining the frequency domain characteristics of the deconvolution filter, the frequency sampling method is used to design the deconvolution filter. The FRF matrix S(f) of the deconvolution filter system is sampled at equal intervals at the point N to obtain the amplitude response S(wk) of the ideal deconvolution filter system. wk is the sampling frequency, k=0,1,2,⋯,N−1. To make the designed deconvolution filter system have linear phase characteristics, its frequency response has the following form:

S(k)=|S(wk)|e−jτw(6)

where τ is a real number and τ=N−12. And w are the frequency values after the [0,2π] interval is equally divided into N points.

Then the discrete Fourier transform is performed on N point S(k) to uniquely determine the unit impulse response s(n) of the deconvolution filter system, namely:

s(n)=1N∑k=0N−1S(k)ej2πNkn(7)

From the interpolation formula in the frequency sampling theorem, we can also use these N frequency sampling values S(k) to obtain the frequency response S(ejw) of the deconvolution filter system:

S(ejw)=e−jN−12w∑k=0N−11NejN−1NπkS(k)sin⁡[N(w2−πkN)]sin⁡[w2−πkN](8)

Finally, after obtaining the unit impulse response s(n) of the deconvolution filter system, the deconvolution network can be written as follows:

s(n)=[s11(n)s12(n)⋯s1l(n)s21(n)s22(n)⋯s2l(n)⋮⋮⋮⋮sm1(n)sm2(n)⋯sml(n)](9)

The measured vibration acceleration signal of the indicator point is processed by the deconvolution network to obtain the time history of the excitation force. The convolution process of a(t) and s(n) can be shown in Fig. 10.

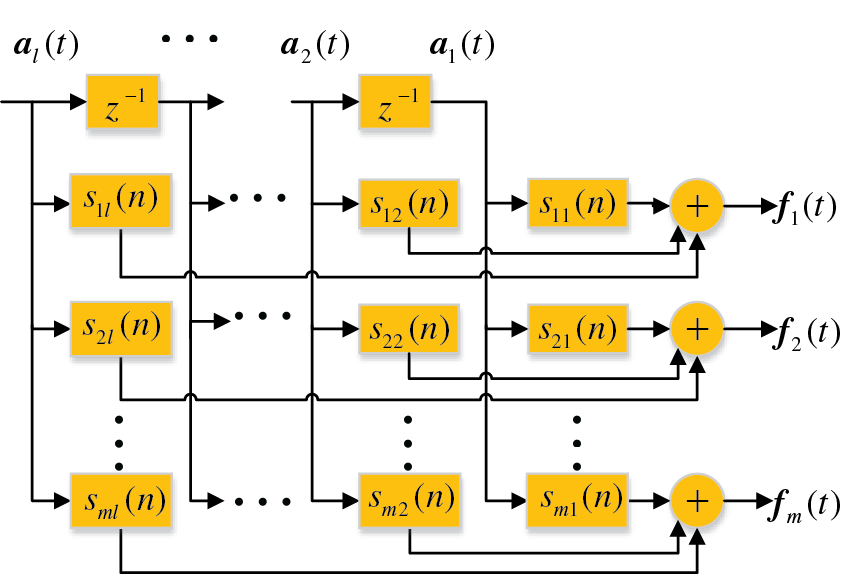
Figure 10: Time-domain deconvolution network

According to the three working conditions described in the second section, the TPA test is carried out with the test system shown in Table 1. The data sets of excitations (force), active sides (acceleration) and passive sides (acceleration) are constructed according to Table 2. h(t) can be obtained between signals of active sides and passive sides. The convolution filter system of the excitation force to the target point is also designed by the frequency sampling method. The time history of excitation and the vibration of different joints are calculated through the constructed convolution filter system. The contribution of each transmission path can be presented and provide the basis for the next step of fault diagnosis.

4  Signal Processing and Analysis

4.1 Time-Frequency Analysis of Robot Vibration Experiment

The time-frequency analysis of the vibration data at the end of the robot arm shows that the vibration acceleration amplitude has reached 0.9 g in the time domain diagram. Performing Fast Fourier Transform (FFT) on the time-domain signal to obtain the frequency spectrum as shown in Fig. 11. It can be found that the main amplitude of the robot’s arm vibration is concentrated in the low frequency special below 500 Hz. Signals in low frequency domain is the main research object. On in-line slow motion condition, frequency domain features include 100 Hz fundamental frequency and its octave frequency. The peak values appear at about 11 and 18 Hz. When the robot is moving at a slow speed with five-axis linkage, it can be found that the peak value is around 13.7 Hz. On in-line high-speed motion, the highest peak appears at about 22.3 Hz.

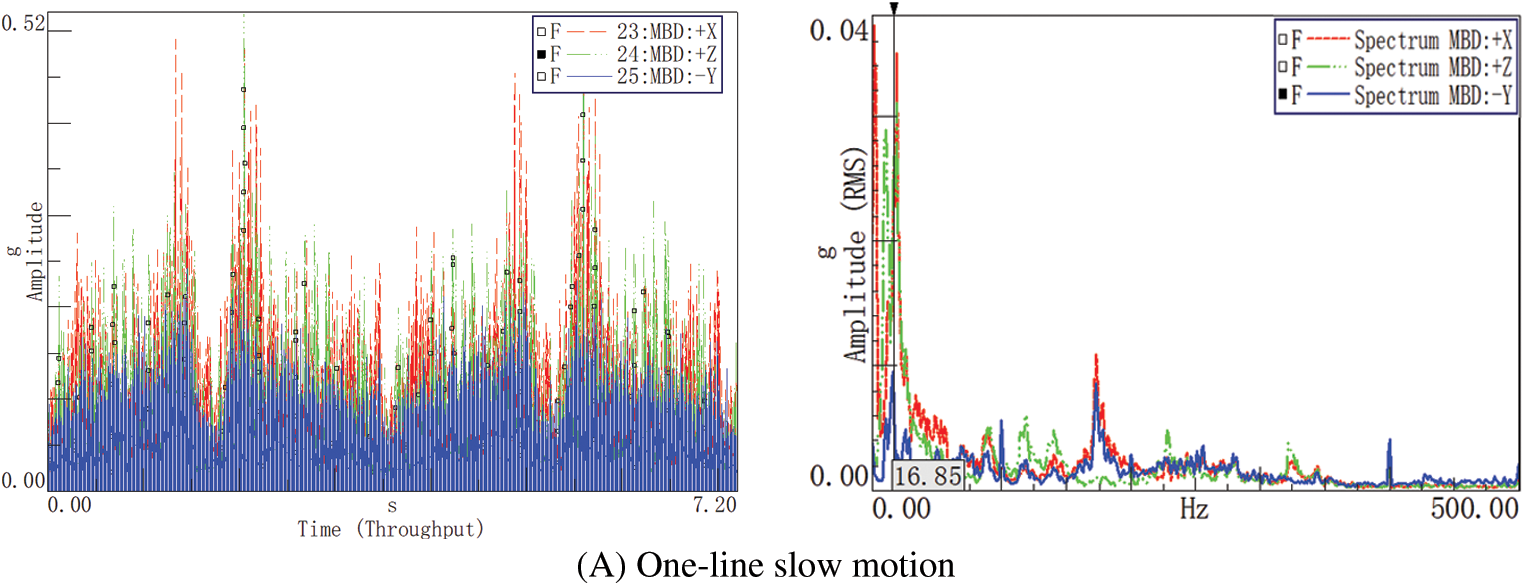
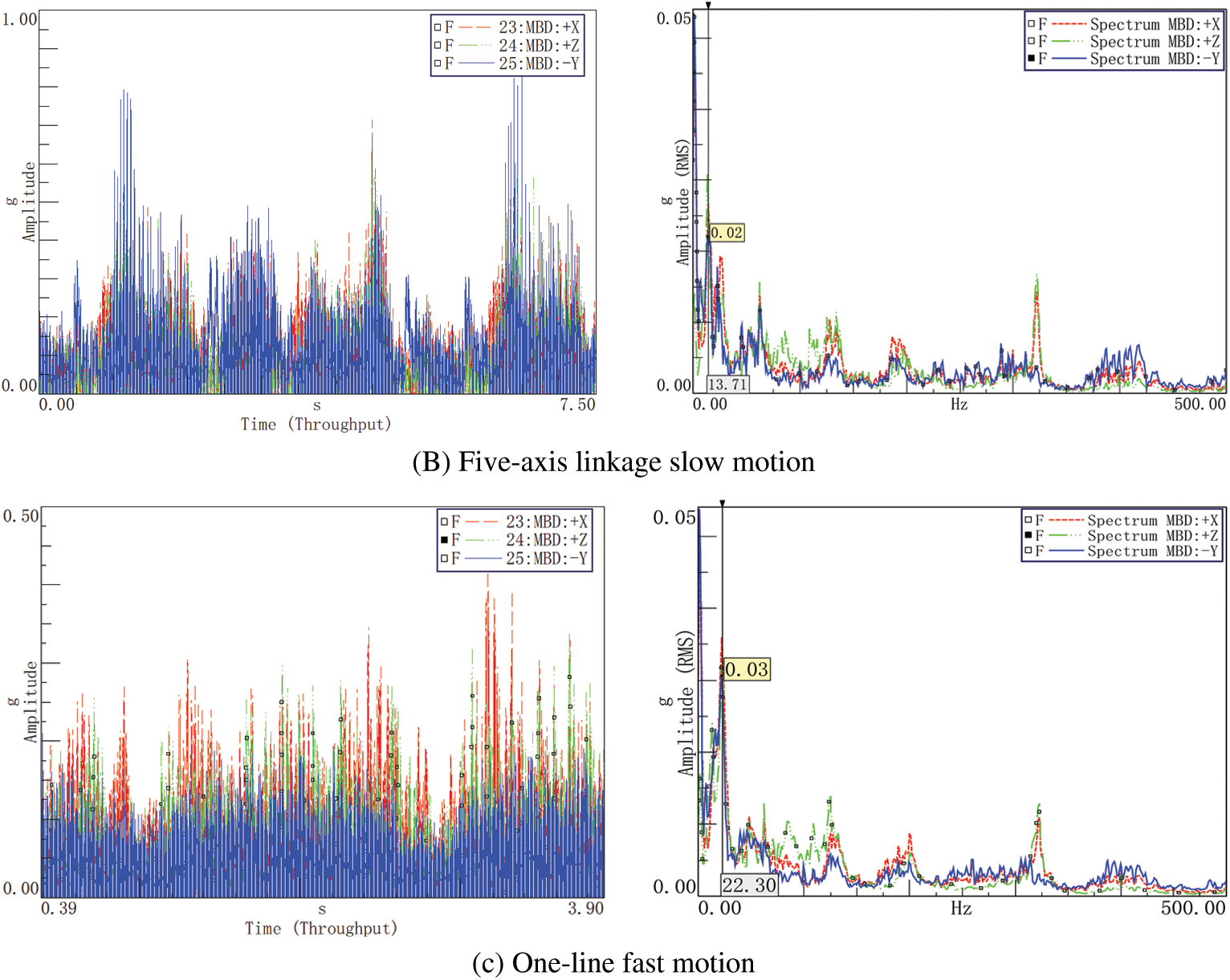
Figure 11: Time and frequency domain diagram of three working conditions

4.2 Time-Frequency Analysis of RV Reducer

According to the analysis results of TPA, a refined vibration test on the RV reducer is performed. The measurement points on the RV reducer are preliminarily screened to the representative measurement points. Then the time and frequency analysis of the vibration signal of the RV reducer is carried out. The waveforms under three representative working conditions are available as shown in Fig. 12.

Figure 12: Vibration diagram of the typical working condition of the RV reducer

It can be found that the maximum vibration amplitude has reached 2 g, and the vibration amplitude is greater than the standard value of 0.1 g for the same reducer produced by the manufacturer of Nabtesco [22]. The frequency domain diagrams show an obvious modulation phenomenon. When parts of the tested object have some defects, the low-frequency and high-frequency signal would be modulated during the operation. It can be inferred that the abnormal vibration of the reducer is related to the defects of some rotating parts inside the reducer.

4.3 Reducer Analysis Using EMD and Hilbert Envelope Method

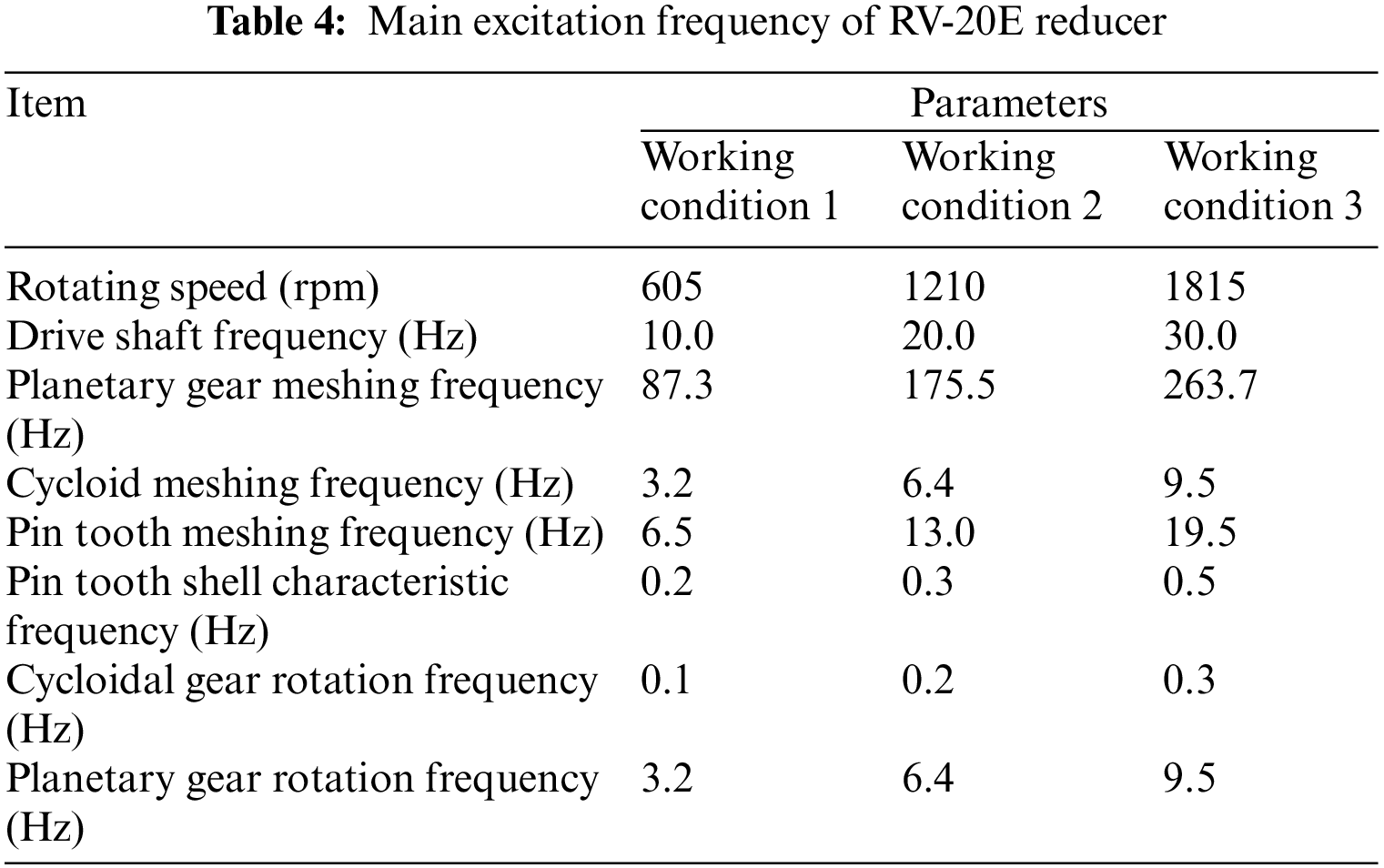
The time and frequency analysis of the vibration signal cannot accurately determine the cause of the abnormal vibration of the reducer. However, the EMD and Hilbert envelope method will make the vibration signal more refined. Combining the modulation phenomenon with the structural characteristics, the excitation sources mainly come from the non-concentric input shaft, the meshing force between the gears and the unbalanced moment of cam rotation. The meshing and rotation frequencies of the internal parts of the reducer are shown in Table 4 below.

The EMD decomposition diagram and IMF envelope spectrum of each speed under no-load conditions are obtained as shown in Figs. 13–15 through EMD and Hilbert envelope analysis. The EMD decomposition of the vibration signal of the reducer is divided into 9 layers. The correlation coefficient of each layer is shown in Table 5. The closer the correlation coefficient is to 1, the greater the correlation. It shows that the relationship between the two sequences is weaker. According to Table 5, the correlation between IMF6~IMF9 is relatively small, and the correlation coefficient between IMF1~IMF5 is larger, which is the main component and has the greatest impact on the original signal. Since the correlation of each decomposed 9th IMF is already ridiculously small, the envelope spectrum of IMF9 is omitted when drawing.

Figure 13: EMD decomposition diagram and IMF envelope spectrum diagram of 605 rpm no-load condition

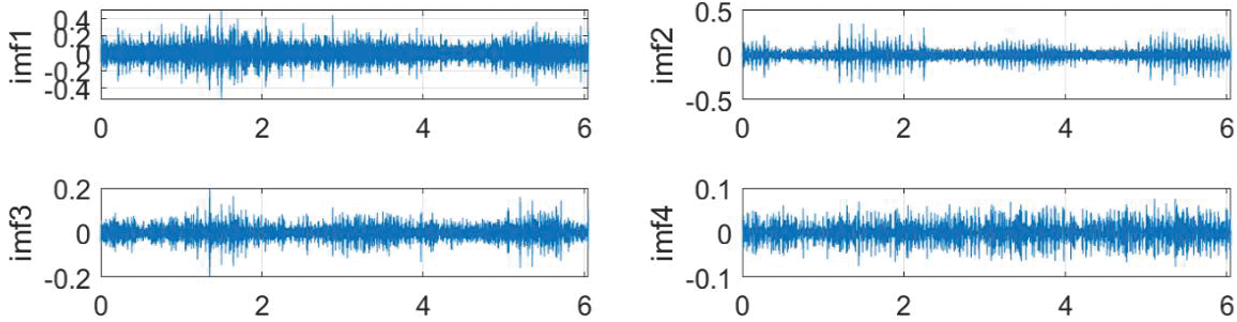
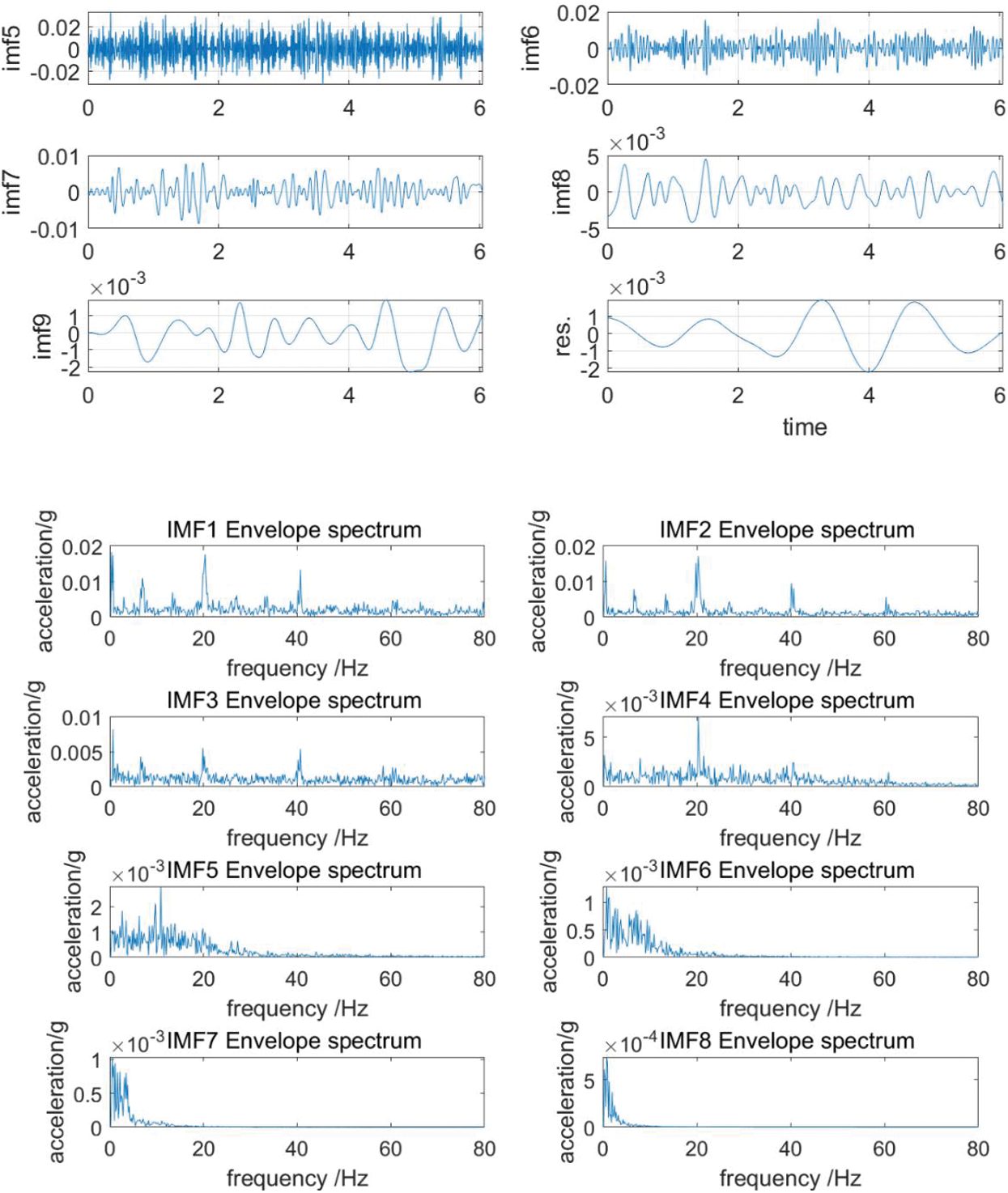
Figure 14: EMD decomposition and IMF envelope spectrum diagram of 1210 rpm no-load condition

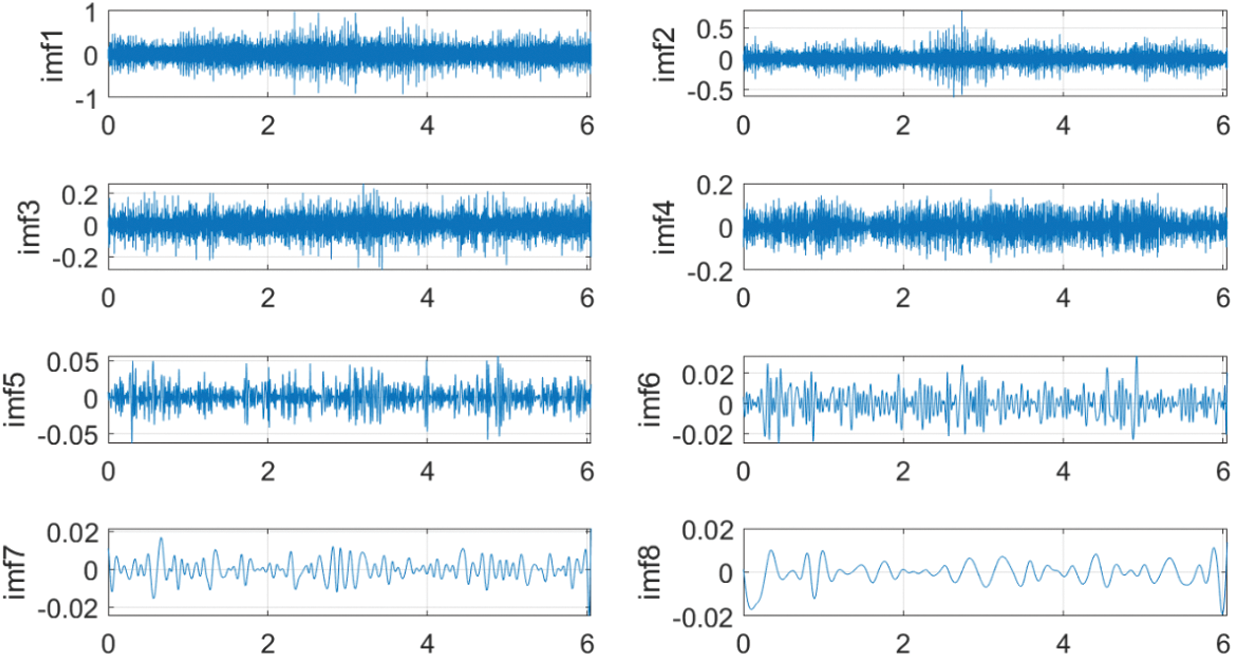
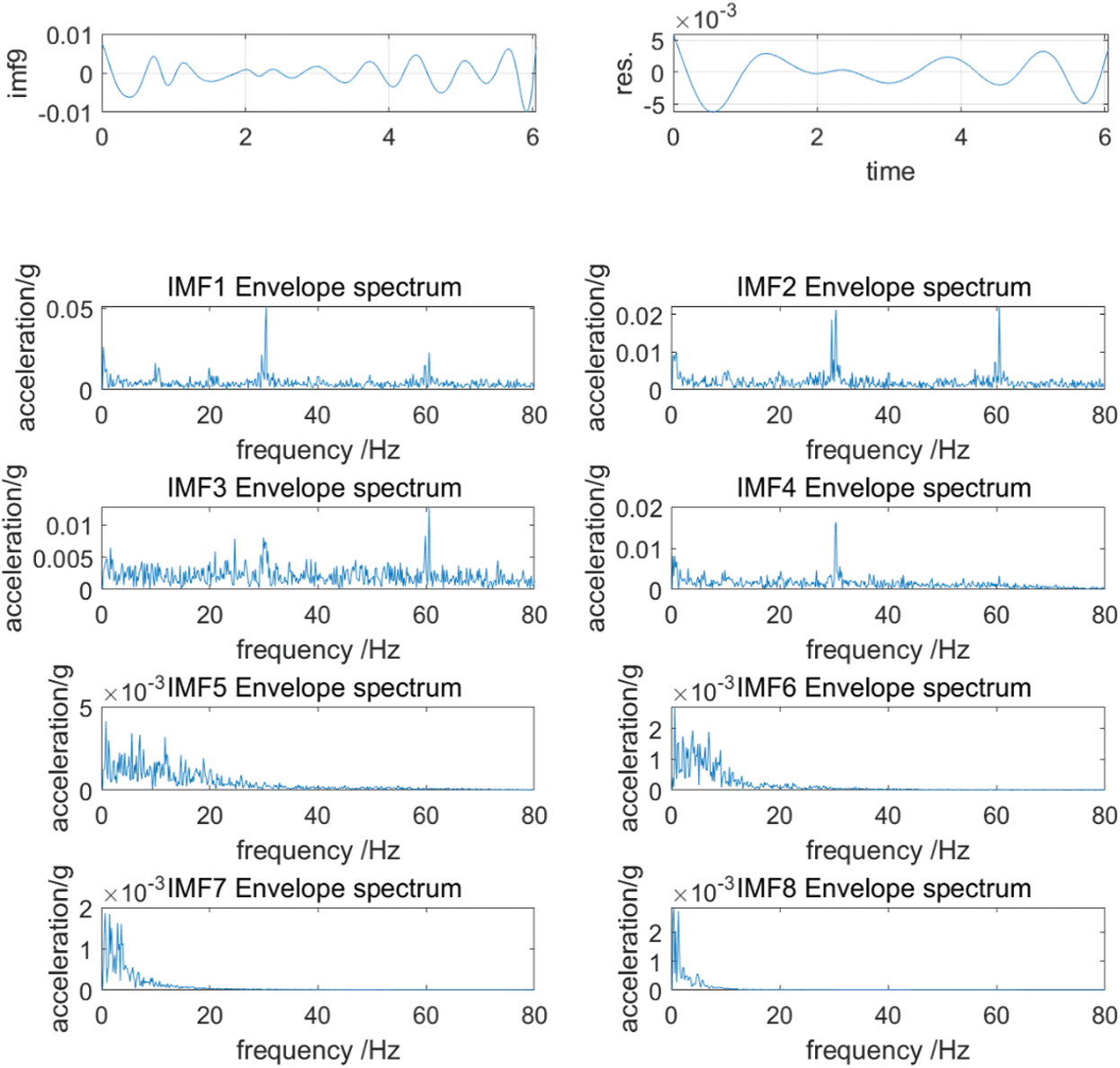
Figure 15: EMD decomposition and IMF envelope spectrum diagram of 1815 rpm no-load condition

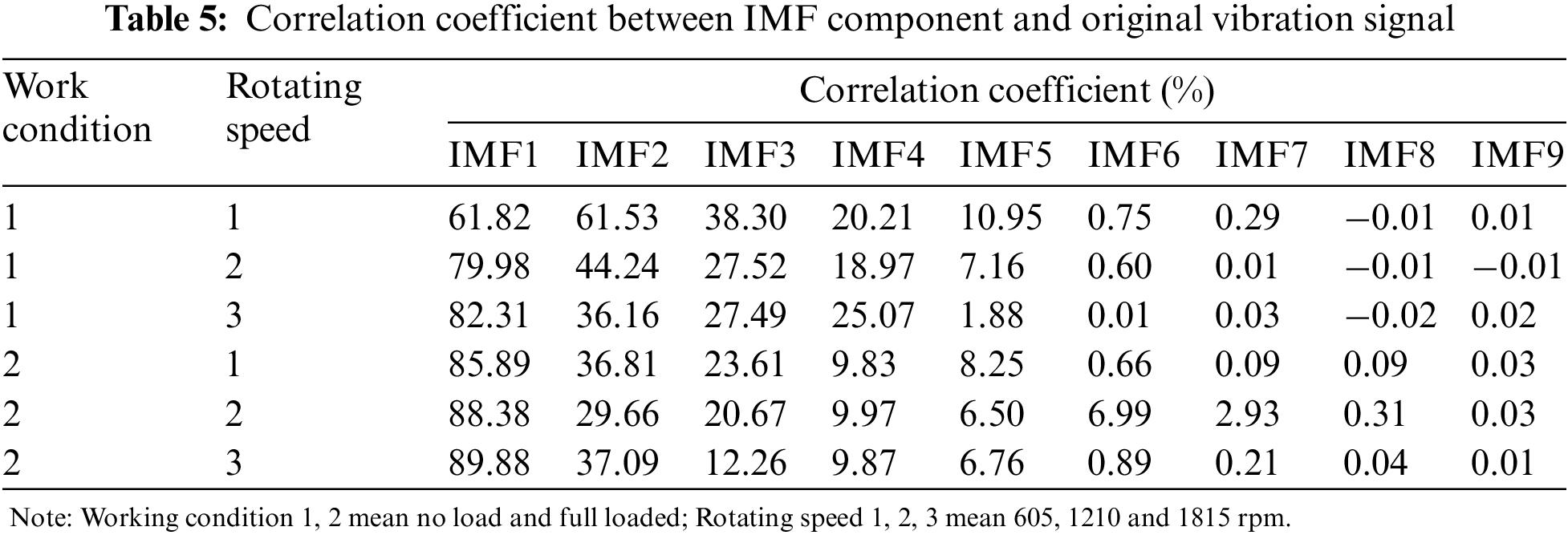
Observing Figs. 13–15, the envelope spectrums show clear vibration characteristics. When the input speed is 605 rpm with no load, the frequencies that main amplitude obtained in IMF1-IMF5 are 10 and 20 Hz. When the operating condition is 1210 rpm with no load, the frequencies that the main amplitude obtained in IMF1-IMF5 are 10 and 20 Hz, with 20 Hz as the main. When the operating condition is 1815 rpm with no load, the frequencies that the main amplitude obtained in IMF1-IMF5 are 30 and 60 Hz. Corresponding to the excitation frequency of the reducer in Table 4, it can be found that the frequencies of main amplitudes are 10 Hz at 605 rpm, 20 Hz at 1210 rpm, 30 Hz at 1815 rpm. Corresponding to the input shaft excitation frequency in Table 4, it can be judged that the input shaft of the first-stage deceleration of the reducer has vibration problems. The problems lead to a modulation effect between the high-frequency meshing noise of the reducer and the excitation frequency of the input shaft during the operation of the reducer, which causes the vibration of the reducer to increase. The vibration performance of the reducer is greatly reduced. The frequencies of a series of minor peaks in the envelope spectrum are 3.6, 7.1, and 10.3 Hz that correspond to the meshing frequencies of the cycloid in Table 4, which caused by the meshing of the reducer gears.

4.4 Comparison of Vibration Performance between Different RV Reducers

A comparative test is done to reflect the influence of the performance of the reducer on the vibration performance of the robot. The RV reducer as the same model produced by Teijin, the most famous in the field of industrial robots, is used to replace the original reducer. To ensure the accuracy of the comparison test, in addition to the replacement of the third axis reducer, keep other structures of the robot and the experimental procedures unchanged. According to the test data, the peak frequencies of the vibration of the reducer under the three conditions are as follows:

(1)   The first working condition is a linear slow-motion condition. The vibration spectrum characteristics of the target point during slow motion are shown in Fig. 16. Before the reducer is replaced, the main vibration amplitude of the target point is concentrated at about 11 Hz.

(2)   The second working condition is a five-axis linkage slow motion condition. The frequency spectrum characteristics during slow motion are shown in Fig. 17. Before the reducer is replaced, the main vibration amplitude of the target point is concentrated at about 13 Hz.

(3)   The third working condition is a straight-line fast-moving condition. The vibration spectrum characteristics of the target point during high-speed movement are shown in Fig. 18. Before the reducer is replaced, the main vibration amplitude of the target point is concentrated around 22 Hz.

The following Figs. 16–18 reflect the comparison of the target point vibration frequency domain diagram of the robot before and after the improvement of the reducer for three typical test conditions. The left picture is the original target point vibration spectrum diagram, and the right picture is after replacing the joint #3 reducer Vibration spectrogram of the target point.

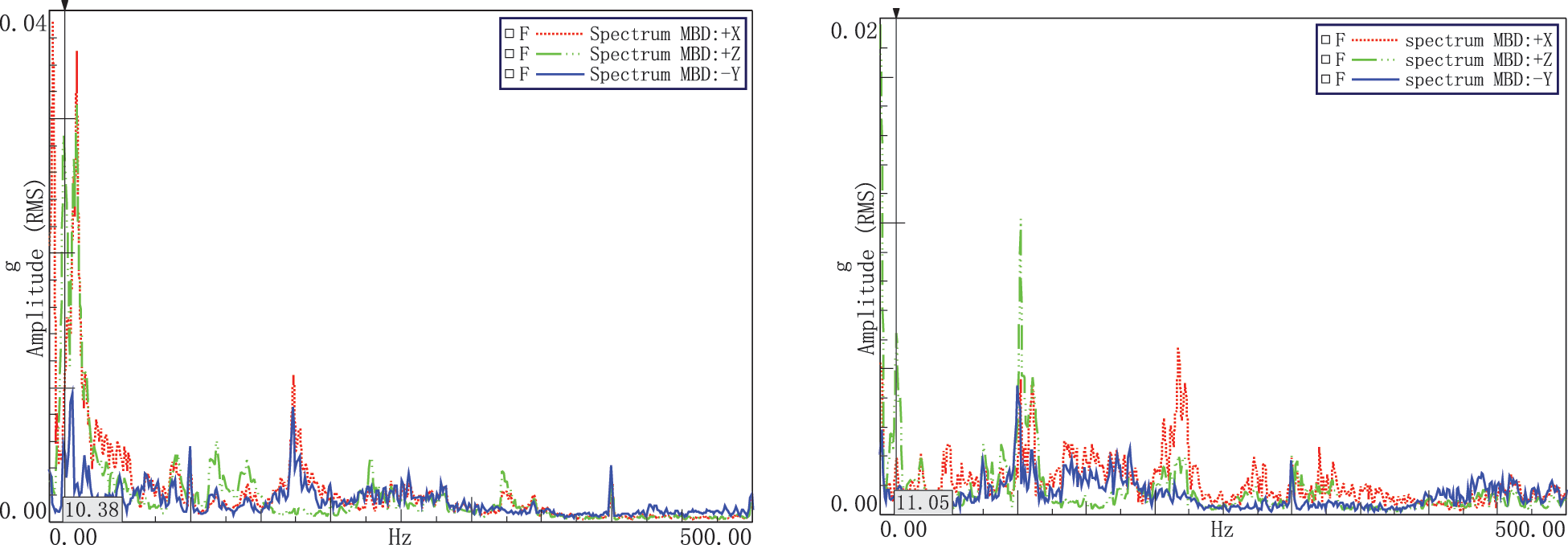
Figure 16: Comparison on the straight-line slow motion conditions

Figure 17: Comparison on five-axis linkage slow motion conditions

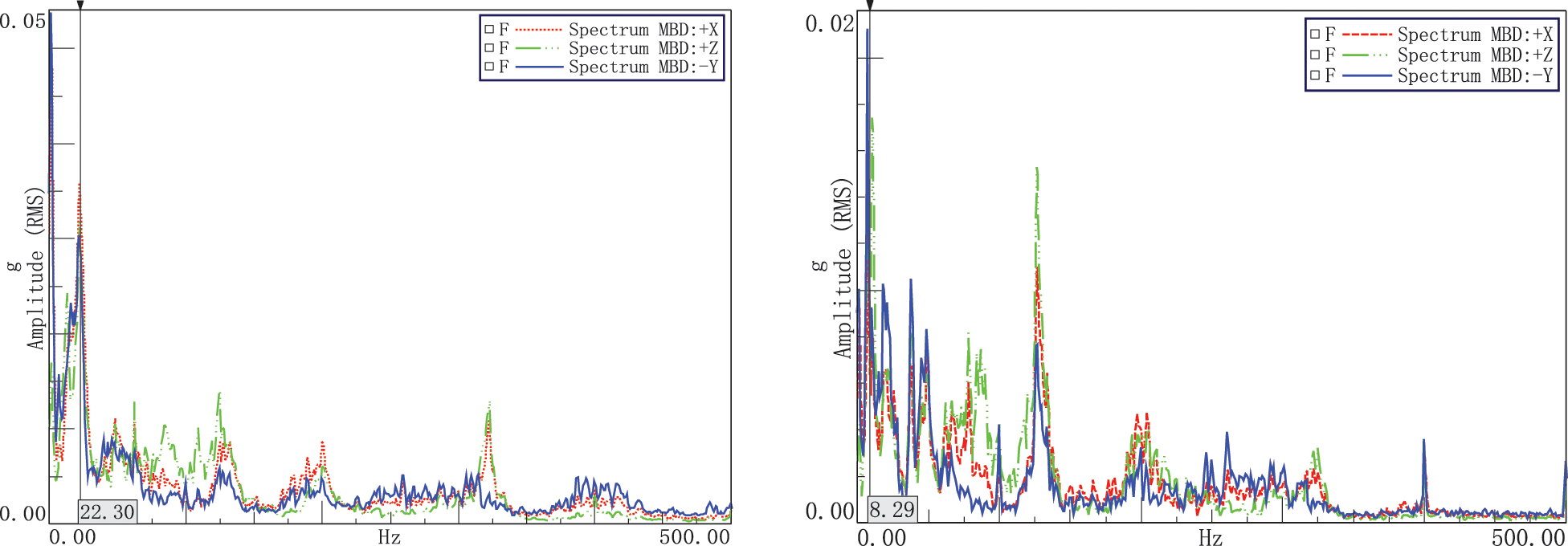
Figure 18: Comparison on straight-line fast motion conditions

Through comparison of the frequency map before and after optimization, it can be found that the vibration performance of the robot has been significantly improved after replacing the reducer. For the in-line slow motion condition, the main vibration peak of the target point is around 11 Hz before the joint #3 reducers is replaced. But after replacing the reducer, 11 Hz is no longer the main peak frequency. The robot vibration peak is concentrated in low-frequency vibration, and the overall vibration amplitude of the target point is reduced, achieving the goal of robot vibration optimization.

When the fifth axis is linked with slow motion, the 13 Hz motion noise at the target point of the robot is no longer the main peak. The peak of the robot vibration is concentrated in low-frequency vibration, but the vibration amplitude of the target point is reduced overall, achieving the robot vibration optimization.

In the fast-moving condition of the straight line and the motion state of the robot remains unchanged. After replacing the reducer of joint #3, the vibration amplitude of about 22 Hz at the target point of the robot has been significantly reduced. The value changes from 22 Hz to about 9 Hz.

There is a certain error between the measured and the theoretical value in the experiment. The error within a certain range is acceptable. In the experiment, it can be found that when the main peak reduces, the peaks at other frequencies will reduce correspondingly. This is because of some other peaks are correlated with the order and envelope of the main peak. The vibration optimization of the mechanical system is a dynamic process. The overall vibration amplitude becomes smaller, which shows the vibration performance of the robot has been improved.

5  Diagnosis and Improvement

5.1 Analysis of Vibration Problem

The reducer structure and drive shaft are shown in Fig. 19. In the gear vibration analysis, scholars have pointed out that the frequency characteristics under stationary faults also contain various meshing frequency components. The vibration response signal contains two frequency characteristics: (1) Centering on the meshing frequency and its high-order multiplier, the faulty gear rotation frequency and its multiplication frequency are the modulation sidebands of the modulation frequency; (2) The faulty gear rotation frequency and its multiplier frequency are the low-frequency components [23]. Stationary failures are mostly caused by gear tooth profile errors, uniform wear, and incorrect design and installation.

Figure 19: The physical diagram of the reducer structure and the drive shaft

Through the above analysis, it is found that the vibration problem of the reducer is a stationary failure. The vibration energy mainly comes from the frequency of the input shaft of the reducer. It is speculated that the input shaft of the reducer is abnormal. The RV reducer in this experiment is a brand-new reducer, and the input shaft and sun gear are integrated gears. After disassembling, it is found that the reducer has two problems:

(1)   The tooth profile error of the input shaft sun gear of the reducer.

(2)   The input shaft of the reducer is a cantilever beam structure. Because the rigidity of the input shaft of the reducer is insufficient, the input shaft of the reducer is misaligned during the input of fluctuating torque.

5.2 Suggestions for Improvement of RV Reducer

Through careful inspection, it is found that the input shaft of the reducer has insufficient rigidity. The fluctuating load generated by the motor caused the input shaft misaligned during operation. It will result in signal modulation in the frequency domain during the input shaft rotating and gear meshing. The vibration performance of the first-stage reduction mechanism deteriorates, which affects the vibration performance of the reducer and the robot.

In view of the above situation, the following 3 improvement suggestions are proposed for this type of reducer:

(1)   The strength of the input shaft should be appropriately increased to reduce the deformation of the shaft. Test verification should be carried out before mass production.

(2)   Properly reduce the length of the input shaft. Excessive length will reduce the stability of the input shaft and affect the vibration performance of the reducer. Test verification should also be carried out before mass production.

(3)   Adding a bearing seat and other supporting structures at the input end of the reducer or the output end of the shaft to increase the stability of the input shaft.

6  Conclusion

Through experimental research, it is found that the performance of the reducer at the robot joint will directly affect the vibration performance of the robot. The deconvolution filter time domain TPA analysis method is proposed. The main vibration source is quickly and effectively located on joint #3 of the robots. The defects of the RV reducer during the assembly and manufacturing process will be manifested in the form of vibration. The joint analysis method based on EMD decomposition and solving the Hilbert envelope spectrum can diagnose the fault of the reducer. Through the comprehensive evaluation of the modulation phenomenon and IMF component under different working conditions, it is concluded that there is a vibration problem in the input shaft of the first stage deceleration. After replacing the problematic reducer, a comparative test is performed to verify the accuracy of the above results. The RV reducer may have problems such as rotor misalignment and precision degradation during manufacturing, which will directly affect the performance of industrial robots. This paper proposes a fault diagnosis method based on TPA and EMD analysis of robot vibration problems. It is of great significance to improve the vibration performance of the robot and optimize the structure design of the robot and its parts. It also provides a reference for the subsequent online detection of robot fault and performance.

Funding Statement: This research was supported by Natural Science Foundation of Hunan Province, (Grant No. 2022JJ30147), the National Natural Science Foundation of China (Grant No. 51805155), the Foundation for Innovative Research Groups of National Natural Science Foundation of China (Grant No. 51621004).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Peng, C., Tomizuka, M., Wang, Z. N., Wang, C., Zheng, M. H. (2018). Robust iterative learning control for vitration suppression of industrial robot manipulators. Journal of Dynamic Systems Measurement and Control, 140(1), 011003. DOI 10.1115/1.4037265. [Google Scholar] [CrossRef]

 2.  Kim, Y., Park, J., Na, K., Yuan, H., Youn, B. D. et al. (2020). Phase-based time domain averaging (PTDA) for fault detection of a gearbox in an industrial robot using vibration signals. Mechanical Systems and Signal Processing, 138(10), 106544. DOI 10.1016/j.ymssp.2019.106544. [Google Scholar] [CrossRef]

 3.  Lin, Z., Yao, L. G., Zhang, J., Su, T. K., Chen, K. J. (2020). Tooth contact analysis with latent error of double circular-arc spiral bevel gears for industrial robot joint nutation drive. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 42(1), 1–12. DOI 10.1007/s40430-019-2085-0. [Google Scholar] [CrossRef]

 4.  Tang, S. M., Liu, G. X., Lin, Z. Y., Li, X. B. (2022). Multi-station test scheduling optimization method for industrial robot servo system. Journal of Ambient Intelligence and Humanized Computing, 13(3), 1321–1337. DOI 10.1007/s12652-020-02577-9. [Google Scholar] [CrossRef]

 5.  Janssens, K., Gajdatsy, P., Gielen, L., Mas, P., Britte, L. et al. (2011). OPAX: A new transfer path analysis method based on parametric load models. Mechanical Systems & Signal Processing, 25(4), 1321–1338. DOI 10.1016/j.ymssp.2010.10.014. [Google Scholar] [CrossRef]

 6.   Mo, C., Chen, J., Lan, F. (2015). Improvement of transmission path analysis method under extended working conditions. Vibration and Impact, 34(8), 129–133. [Google Scholar]

 7.  Cheng, W., Lu, Y., Zhang, Z. (2016). Tikhonov regularization-based operational transfer path analysis. Mechanical Systems and Signal Processing, 75, 494–514. DOI 10.1016/j.ymssp.2015.12.025. [Google Scholar] [CrossRef]

 8.  Huang, Z., Liang, S., Tang, Z., Tang, X., Liao, Z. (2019). Finite element analysis of RV reducer based on ANSYS software. Machinery, 57(2), 11–20. [Google Scholar]

 9.  Qiu, T., Du, Q. (2019). Study on dynamics simulation of RV reducer based on rigid-flexible coupling. Journal of Mechanical Transmission, 43(12), 93–96. [Google Scholar]

10. Wu, X., He, W. (2017). Transmission accuracy test and virtual prototype simulation of the RV reducer used in the robot. Journal of Machine Design, 34(7), 73–77. [Google Scholar]

11. Chen, L., Cao, J., Wang, X. (2020). Fault diagnosis for robot RV reducer using nonlinear frequency spectrum and kernel principal component analysis. Journal of Xi’an Jiaotong University, 54(1), 32–41. [Google Scholar]

12. Chen, L., Wang, J., Zhang, J. (2018). Vibration signal analysis of RV reducer based on wavelet theory. Journal of Mechanical Transmission, 42(5), 14–17. [Google Scholar]

13. Shi, P. M., Wang, J., Wen, J. T., Tian, G. (2016). Study on rotating machinery fault diagnosis method based on envelopes fitting algorithms EMD. Acta Metrologica Sinica, 37(1), 62–66. [Google Scholar]

14. Zhang, J., Zhang, Z., Qi, X., Liu, X. (2019). Fault diagnosis of rolling bearing based on EMD and VPMCD. Journal of Machine Design, 36(S2), 91–94. [Google Scholar]

15. Li, K., Feng, Z. (2017). Signal demodulation via the generating differential equation method for planetary gearbox fault diagnosis. Journal of Vibration and Shock, 36(8), 9–15. [Google Scholar]

16. Xu, M. (2014). Identification and control of vehicle interior low-frequency structure-borne noise based on transfer path analysisi method (Ph.D. Thesis). Tianjin University, Tianjin, China. [Google Scholar]

17. Chen, Y. J., Wang, X. L., Zhang, Y., Xing, Z. Y. (2017). Fault Diagnosis of Train Wheels Based on Empirical Mode Decomposition Generalized Energy. 3rd International Conference on Electrical Engineering and Information Technologies for Rail Transportation (EITRT), vol. 483, pp. 15–25. Changsha, China. [Google Scholar]

18. Chen, X. Y., Ge, D., Liu, X., Liu, M. C. (2019). Roller Bearing Fault Diagnosis Based on Empirical Mode Decomposition and Targeting Feature Selection. 3rd International Conference on Information Processing and Control Engineering (ICIPCE), Moscow, RUSSSIA. [Google Scholar]

19. Luo, C., Jia, M. P., Wen, Y. (2017). The Diagnosis Approach for Rolling Bearing Fault Based on Kurtosis Criterion EMD and Hilbert Envelope Spectrum. 3rd IEEE Information Technology and Mechatronics Engineering Conference (ITOEC), pp. 692–696. Chongqing, China. [Google Scholar]

20. Xie, X. P., Chen, W. D., Chen, B. G., Cheng, J. S., Tan, L. G. (2020). Comprehensive fatigue estimation and fault diagnosis based on refined generalized multi-scale entropy method of centrifugal fan blades. Measurement, 166(C), 108224. DOI 10.1016/j.measurement.2020.108224. [Google Scholar] [CrossRef]

21. Lohrmann, M., Hohenberger, T. (2008). Operational transfer path analysis: Comparison with conventional methods. Journal of the Acoustical Society of America, 123(5), 3534. DOI 10.1121/1.2934496. [Google Scholar] [CrossRef]

22. Chen, L., Wang, L., Zhang, J. (2018). Vibration test and signal analysis of RV reducer. Journal of Mechanical Transmission, 42(3), 80–84. [Google Scholar]

23. Li, Y. (2018). Vibration signal modulation mechanism of gear system and sparse decomposition method for its non-stationary signal (Ph.D. Thesis). South China University of Technology, Guangzhou, China. [Google Scholar]