 Open Access
Open Access
ARTICLE
Einstein Weighted Geometric Operator for Pythagorean Fuzzy Hypersoft with Its Application in Material Selection
1 Department of Mathematics, Zhejiang Normal University, Jinhua, China
2 Department of Mathematics, University of Management and Technology, Lahore, Pakistan
3 Department of Mathematics, College of Science and Arts, Muhayil, King Khalid University, Abha, Saudi Arabia
4 Department of Mathematics, Cankaya University, Etimesgut, Ankara, Turkey
5 Department of Mathematics, King Abdulaziz University, Jeddah, Saudi Arabia
6 Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan
7 Department of Mathematics, School of Science, University of Phayao, Mae Ka, Mueang, Phayao, Thailand
* Corresponding Author: Fahd Jarad. Email:
(This article belongs to the Special Issue: Decision making Modeling, Methods and Applications of Advanced Fuzzy Theory in Engineering and Science)
Computer Modeling in Engineering & Sciences 2023, 135(3), 2557-2583. https://doi.org/10.32604/cmes.2023.023040
Received 06 April 2022; Accepted 05 August 2022; Issue published 23 November 2022
Abstract
Hypersoft set theory is a most advanced form of soft set theory and an innovative mathematical tool for dealing with unclear complications. Pythagorean fuzzy hypersoft set (PFHSS) is the most influential and capable leeway of the hypersoft set (HSS) and Pythagorean fuzzy soft set (PFSS). It is also a general form of the intuitionistic fuzzy hypersoft set (IFHSS), which provides a better and more perfect assessment of the decision-making (DM) process. The fundamental objective of this work is to enrich the precision of decision-making. A novel mixed aggregation operator called Pythagorean fuzzy hypersoft Einstein weighted geometric (PFHSEWG) based on Einstein’s operational laws has been developed. Some necessary properties, such as idempotency, boundedness, and homogeneity, have been presented for the anticipated PFHSEWG operator. Multi-criteria decision-making (MCDM) plays an active role in dealing with the complications of manufacturing design for material selection. However, conventional methods of MCDM usually produce inconsistent results. Based on the proposed PFHSEWG operator, a robust MCDM procedure for material selection in manufacturing design is planned to address these inconveniences. The expected MCDM method for material selection (MS) of cryogenic storing vessels has been established in the real world. Significantly, the planned model for handling inaccurate data based on PFHSS is more operative and consistent.Keywords
The solution to the problems in our daily lives is based on the classification of information, data, the collection of facts, etc. The critical question in decision analysis is the absence of accurate facts. This statistical difference is bridged by taking a scientific model and applying the appropriate DM. DM’s ideas can support the manufacturing enterprise, assemble, and categorize multiple priorities from best to worst viable alternative. As a result, it is a tool to help us select, categorize, and establish our prospects and comprehensively evaluate alternatives. MS is intense in enterprise and product development. The material chosen affects the manufacturer’s success and affordability [1]. The manufacturing enterprise suffers from legislation, cost, and penetrating global goals, often inadequate content. The persistence of the manufactured equipment strategy is to select components with state-of-the-art light design standards while providing the best offer at the lowest reasonable price [2]. However, these goals and obstacles are common in conflict situations, so it is essential to address which feature is more important. Suppose the appropriate method is not ready for the design approach. The design method’s funding and resource aspects cannot be used in the restructuring or industrial agenda section [3]. Identifying the best materials is essential because design concerns are not correct. Eliminate inappropriate alternatives and manage high quality. Variables that interfere with selecting specific material engineering applications should use logical and straightforward applications [4].
MCDM has deliberated the best applicable procedure for the verdict and the best adequate alternative from all possible choices, ensuing criteria, or attributes. In real-life circumstances, most decisions are taken when the objectives and limitations are usually indefinite or ambiguous. To overcome such ambiguities and anxieties, Zadeh offered the idea of the fuzzy set (FS) [5], a prevailing tool to handle the obscurities and uncertainties in DM. Such a set allocates to all objects a membership value ranging from 0 to 1. Experts mainly consider membership and non-membership value in the DM process that FS cannot handle. Atanassov [6] introduced the generalization of the FS, the idea of the intuitionistic fuzzy set (IFS), to overcome the constraint mentioned above. In 2011, Wang et al. [7] presented numerous operations on IFS, such as Einstein product, Einstein sum, etc., and constructed two aggregation operators (AOs). They also discussed some essential properties of these operators and utilized their proposed operator to resolve multi-attribute decision making (MADM) for the IFS information.
The models mentioned above have been well-recognized by specialists. Still, the existing IFS cannot handle the inappropriate and vague data because it is deliberate to envision the linear inequality concerning the membership and non-membership grades. For example, if decision-makers choose membership and non-membership values 0.9 and 0.6, respectively, then
Peng et al. [16] introduced the division and subtraction operations for Pythagorean fuzzy numbers (PFNs), proved their basic properties, and presented a superiority and inferiority ranking approach under the considered environment. Garg [17] introduced operational laws based on Einstein norms for PFNs, proposed weighted average and ordered weighted average operators, and then utilized these operators for DM. Garg [18] presented the series of generalized geometric AOs for PFS. Garg [19] introduced logarithmic operational laws for the PFS and constructed various weighted operators based on the proposed logarithm operational laws. Gao et al. [20] developed numerous interaction AOs under the PFS environment. Wang et al. [21] offered the interactive Hamacher operations for the PFS and settled on a DM method to solve MCDM difficulties. Wang et al. [22] utilized the interval-valued PFS, presented some novel PFS operators, and offered a DM approach to resolve the MCGDM complications. Moreover, to deal with the MCDM complexities. Peng et al. [23] explored some new inequalities for AOs under PFS. They introduced some point operators under the PFS environment. They combined the Pythagorean fuzzy point operators with the generalized AOs and offered a MADM approach based on settled operators. Moreover, Arora et al. [24] presented basic operational laws and suggested several selected AOs for linguistic IFSs. Ma et al. [25] modified the existing score function and accuracy function for PFNs and defined novel AOs for PFS.
All the methods mentioned above have too many applications in many fields. But due to their inefficiency, these methods have many limitations in terms of parameterization tools. In presenting the solution to obscurity and ambiguity, Molodtsov [26] introduced the basic notions of soft sets (SS) and debated some elementary operations with their possessions. Maji et al. [27] protracted the idea of SS and defined several basic operations for SS. Maji et al. [28] combined two prevailing notions, such as FS and SS. They developed the idea of FSS, which is a more robust and reliable tool. They also presented basic operations and established and applied this concept in DM. Maji et al. [29] demonstrated the intuitionistic fuzzy soft set (IFSS) theory and offered some basic operations with their essential properties. Arora et al. [30] developed the AOs for IFSS and discussed their basic properties. Nowadays, the conception and application consequences of soft sets and the earlier-mentioned several research developments are evolving speedily. Peng et al. [31] established the concept of PFSS by merging two prevailing models, PFS and SS. Athira et al. [32] established entropy measures for the PFSS. They also offered Euclidean distance and hamming distance for the PFSS and utilized their methods for DM [33]. Naeem et al. [34] developed the TOPSIS and VIKOR methods for PFSNs and presented an approach to the stock exchange investment problem. Zulqarnain et al. [35] introduced the AOs under the PFSS environment and presented an application for green supplier chain management. Zulqarnain et al. [36,37] formed the Einstein-ordered weighted average and geometric AOs for PFSS. They also proposed the MAGDM techniques using their developed operators for sustainable supplier selection and a business to finance money.
Smarandache [38] proposed the idea of the hypersoft set (HSS), which penetrates multiple sub-attributes in the parameter function f, which is a characteristic of the cartesian product with the n attribute. Compared with SS and other existing concepts, Samarandche HSS is the most suitable theory which handles the multiple sub-attributes of the considered parameters. Rahman et al. [39] settled the DM techniques based on similarity measures for IFHSS. Zulqarnain et al. [40] prolonged the notion of IFHSS to PFHSS with fundamental operations and their properties. Zulqarnain et al. [41] expanded the AOs under the IFHSS environment and developed a DM approach based on their presented AOs. Zulqarnain et al. [42] extended the PFSS to interval-valued PFSS and developed the AOs for interval-valued PFSS. They developed the MAGDM approach to resolve DM complications. The method designated in [43] is inadequate to examine the data with a reflective intellect for higher commencement and perfect decisions. For example,
• The PFHSS competently deals the complex issues considering the multi sub-attributes of the considered parameters in the DM process. To keep this advantage in mind, we establish the AO for PFHSS.
• The Einstein operator is a well-known charming guesstimate AO. It is noticed that the prevailing Einstein AOs look unenthusiastic in marking the exact judgment through the DM procedure in some circumstances. To overwhelm these particular difficulties, these AOs need to be modified. We demonstrate advanced operational laws based on Einstein norms for Pythagorean fuzzy hypersoft numbers (PFHSNs).
• Establish the PFHSEWG operator using the above-mentioned Einstein operational laws with fundamental properties.
• A novel MCDM technique was established based on the proposed PFHSEWG to cope with DM issues under the PFHSS environment.
• MS is a significant aspect of engineering as it sees the practical standards of all constituents. MS is a time-consuming but significant step in the enterprise procedure. The industrialist’s productivity, effectiveness, and character will suffer as an outcome deprived of material selection.
• Comparative analysis of the developed MCDM technique is proposed with current approaches to deliberate the practicality and supremacy of the planned model.
This study is systematized as follows: Basic knowledge of some important notions like SS, HSS, IFHSS, PFHSS, and Einstein norms have been deliberate in Section 2. Section 3 demarcated some basic operational laws for PFHSNs based on Einstein norms and established the PFHSEWG operator. Also, the planned operator’s dynamic properties will be present in the same section. An MCDM approach is introduced using the PFHSEWG operator in Section 4. In the same section, a case study has been presented for material selection in the manufacturing industry. In Section 5, a comparison with some standing approaches is provided.
This section remembers some essential concepts such as SS, HSS, IFHSS, and PFHSS.
Definition 2.1 [26] Let X and
Also, it can be defined as follows:
Definition 2.2 [38] Let X be a universe of discourse and
It is also defined as
Definition 2.3 [38] Let X be a universe of discourse and
It is also defined as
Definition 2.4 [40] Let
It is also defined as
A Pythagorean fuzzy hypersoft number (PFHSN) can be stated as
Remark 2.1 If
For readers’ aptness, the PFHSN
But, in some cases, the above-defined score function cannot handle the scenario. For example, if we consider the two PFHSNs, such as
The consequent comparative laws will be used
1. If
2. If
• If
• If
Definition 2.5 Einstein’s sum
Under the Pythagorean fuzzy environment, Einstein sum
where
3 Einstein Weighted Geometric Aggregation Operator for Pythagorean Fuzzy Hypersoft Set
This section will introduce a novel Einstein-weighted AO such as the PFHSEWG operator for PFHSNs with essential properties.
3.1 Operational Laws for PFHSNs
Definition 3.1 [44] Let
1.
2.
3.
4.
Definition 3.2 Let
where
Theorem 3.1 Let
where
Proof: We will use mathematical induction to demonstrate the above result.
For n = 1, we get
For m = 1, we get
So, Eq. (4) true for
Assume that the equation grasps for
Now we show the Eq. (4) for
So, it is true for
Example 3.1 Let
As we know that
Theorem 3.2 Let
where
Proof: As we know that
Again
Let PFHSWG
Then, inequalities (5) and (6) can be transformed into the following forms
So,
If
If
Then,
From inequalities (7) and (8), we get
Example 3.2 Using the data given in Example 3.1
Hence, from Examples 3.1 and 3.2, it is proved that
3.2 Properties of PFHSEWA Operator
Idempotency 3.2.1 If
Proof: As we know that
Boundedness 3.2.2 Let
Proof: Let
Let
Again, let
Let
Let
If
If
If
So proved that
Homogeneity 3.2.3 Prove that
Proof: Let
So,
4 Multi-Criteria Decision Making Approach for PFHSEWG Operator
This section proposes a DM method to address the difficulties of MCDM based on the planned PFHSEWG operator with a numerical example.
Consider
Step 1: Obtain decision matrices for each alternative in the form of PFHSNs
Step 2: Convert the cost type attributes to benefit type using the normalization rule.
Step 3: Use the settled PFHSEWG operator to collective the PFHSNs
Step 4: Use Eq. (1) to calculate the scores for all alternatives.
Step 5: Pick the alternative with the highest score and check the ranking.
In this section, a practical MCDM problem comprises a decisive adequate material selection model to confirm that the conventional approach is pertinent and reasonable.
Case Study 4.2.1 According to the Diplomatic Board on Climate Variation, extreme ecological humiliation results from social accomplishments [45]. The climate variation has substantial ecological significance, containing the extermination of animal classes [46]. Lesser farming production [47]. Extra thrilling Meteorological conditions configurations [48], and humanoid movement [49]. Have Increasing momentum to moderate universal greenhouse gas discharges to alleviate climate variation corridors. For example, France recently approved a prerequisite of 40% Condense greenhouse gas discharges by 2030 paralleled 1990 [50]. Still, the routine of carbon gasses is not the solitary fabricator of greenhouse gases. The environmental protection agency released 76% of fossil fuel interpretation of all anthropogenic releases in the United States [51]. It can be realistically contingent that an extensive decrease in Greenhouse gas radiation means less usage of fossil fuels. But, this is not an informal assignment since the invention. What is formed from hydrocarbons is an energy transporter and the key energy cause. To have a substantial impression on decarbonization, it would be included in a globally friendly way. In 2017, fossil fuels accounted for extra than 85% of global energy production [52].
Consequently, energy scarcities resolve instantaneously if the world completely alters to a hydrogen budget that eradicates fossil fuel feasting. This component delivers significant tasks in verdict an appropriate power source. Though, this investigation will not insurance this issue. As mortality is impending, the ‘end of low-priced oil’ eras,” with complete compromise in science and power engineering that essential discover new energy exporters. Severe reduction procedure across nations exposed hydrogen will be the eventual optimal. Hydrogen, conceivable as complementary energy in cars, influences industrial innovations such as hydrogen fuel cells to deliver manufacturing deprived of producing any
It kinds intelligence to renovate fossil discarded energies such as natural gas is earliest transformed into hydrogen. In conclusion, while fossil fuels develop excessively and prospective unlawfully for worldwide warming, renewable, most important energy will originate into the depiction for financial or environmental causes. In expressions of power, the recently formed hydrogen fuel is dissimilar to the frequently used ones in gratified weight and volume. This hydrogen is frivolously associated with its energy capability is the top prominent feature. The energy content of hydrogen per kilogram is 120 MJ. Hydrogen has a little volumetric energy compactness related to its exceptional gravimetric density. The compactness of hydrogen is committed by its accumulation state. Unfluctuating densities up to 700 bar are not massive sufficient belongings of hydrocarbons similar to gasoline and diesel. Only fluid hydrogen can influence a reasonable amount, still less than a quarter of the amount of gasoline. So, hydrogen containers for motorized solicitations will conquer more than fluid hydrocarbons formerly used containers [53]. Cryogenic storing containers are also recognized as cryogenic holding vessels. Dewar flask is, in fact, a double-walled super-insulator container. It vehicles fluid oxygen, nitrogen, hydrogen, helium, and argon, temperatures <110 K/163°C. Fluid hydrogen has been familiar as a more significant energy cause. Since water is impartial a surplus gas, it’s unbelievably non-toxic ecological security when rehabilitated to power. Constituents used in cryogenic container enterprises are contingent on protection and budget [54]. Essentially the exertion of cryogenic vessels is security apprehensions and enterprise conditions. In perspective, short temperature embrittlement can be designated as follows:
Fracture toughness: The steaming point of melted nitrogen is around −196°C, whereas the steaming point of liquefied nitrogen is around. The temperature of hydrogen gas is approximate −253°C. The substantial cannot find ductility and converts hard. So, the considerable requirement is robust and sufficient to endure Inelastic crack. Face-centered cube metal webs are suitable since they are impervious to low temperatures. All nickel-copper compounds, aluminum, its compounds, and austenitic stainless steels contain an extra 7% nickel to construct a storing cryogenic vessel [55]. Heat transfer: heat transient over low-temperature container barriers are principally conductive. Constituents with low, warm air conductivity are chosen. Thermal stress: due to slight temperature, interior barriers contract, instigating thermal straining. So, constituents with slight thermal conductivity are suitable. Thermal diffusivity: in practice, the collective thermal isolation is ridiculous. The material must be selected in such a tactic that it can disperse heat as rapidly as conceivable.
Material assortment in any manufacturing arena is a very significant enterprise phase. Manufacturing enterprise is prepared by enactment, budget, ecological compassion objectives, And commonly inadequate by the material. The most acceptable product strategy selects the best appropriate material design criteria by providing an extreme presentation at the lowermost probable budget. Material selection is By seeing numerous contradictory DM procedures. AO shows a vital part in DM. The existing Einstein AO has originated as a DM procedure in this circumstance. These AOs must be modernized to talk about these definite concerns. We intend some novel operations and escorting AO for aggregating innumerable PFHSN. Our projected ideal outclasses other models. Conferring to the clarification stated above and DM perception, all structures can be categorized. The case study was shown in a motorized portions engineering corporation in Malaysia, and a motorized constituent, cryogenic storing, accompanied the study. As part of applying the concept of sustainability, companies must choose suitable materials for produced parts. It focuses first on cryogenic storage containers and then on other factors input of weights for gathering parameters and materials from DM. PFHSN theory and proposed AO are used to overcome complexity and indecision human judgment. MS with three remember the essential pillar of sustainability: materials must be reasonable, ecologically pleasant, and beneficial to humanity.
The most imperative aspects (parameters) to consider when selecting a substantial dashboard DM. Choose the procedure starts with an initial screening of material used for dashboards, captivating into justification structures intrinsic to the application. In the screening process, identify the fabrics that may be appropriate. It is serious about deciding the material that can be used initial MS for the instrument board process. Four materials are selected, subsequently examining the abilities:
PFHSEWG Operator 4.2.2
Step 1: According to the expert’s opinion, Pythagorean fuzzy hypersoft decision matrices for all alternatives are given in Tables 1–4.




Step 2: All parameters are of the same type. So, no need to normalize.
Step 3: Apply the proposed PFHSEWG operator to the obtained data (Tables 1–4), and obtain the expert’s estimations such as follows:
Step 4: Use Eq. (1),
Step 5: Compute the ranking of the alternatives
Since the material estimation surprises at the theoretic phase through the enactment stage of the plan, there is extra scope to area the appropriateness of the particular materials. Face-centered cube materials are used at small temperatures of −163°C. Austenitic steel
To demonstrate the efficiency of the anticipated approach, a comparison with some standing methods under the IFS, IFSS, IFHSS, PFS, PFSS, and proposed PFHSS model.
5.1 Superiority of the Proposed Method
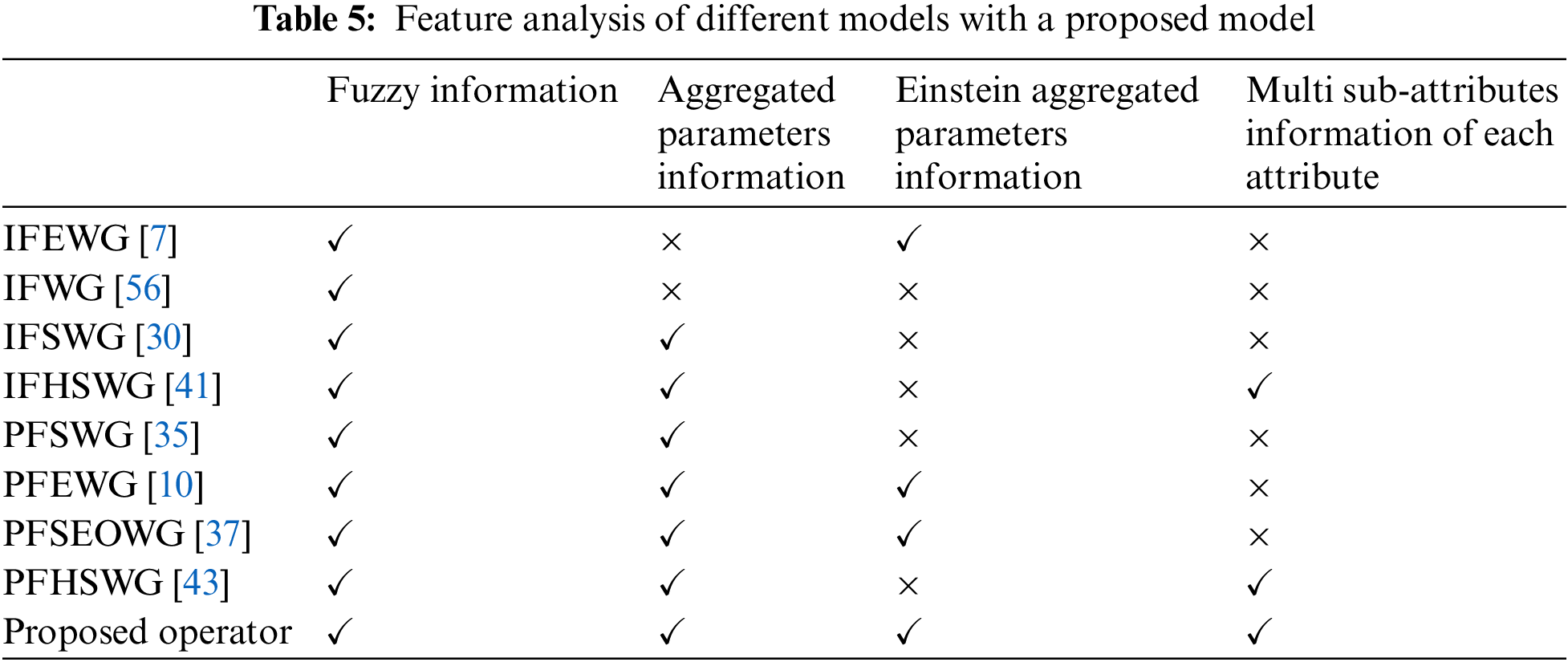
The planned methodology is competent and realistic; we have established an innovative MCDM model under the PFHSS setting over the PFHSEWG operator. Our projecting model is more talented than prevalent methods and can produce the most delicate significance in MCDM problems. The collective model is multipurpose and familiar, adapting to budding volatility, engagement, and productivity. Different models have specific ranking procedures, so there is an immediate difference between the rankings of the proposed techniques to be feasible according to their assumptions. This scientific study and evaluation conclude that results obtained from existing methods are unpredictable compared to hybrid structures. Furthermore, many hybrid FS, IFSS, IFHSS, and PFSS become uncommon in PFHSS due to some fortunate circumstances. It is easy to combine incomplete and uncertain facts in DM techniques. They were mixing inaccurate and insecure data in the DM process. Thus, our intended methodology will be more skilled, imperative, superior, and restored than various hybrid-structured FS. Table 5 below presents the feature analysis of the proposed method and some existing models.
To endorse the usefulness of the planned technique, we compare the attained outcomes with some state-of-the-arts in the PFSS setting are concise in Table 6. In this work, an innovative aggregation operator, the PFHSEWG operator, is projected to fuse suggestive information, and then a score function is utilized to assess the organization of alternatives. The PFHSS is the most generalized form of PFSS because it deals with the multi-sub attributes of the considered parameters. Wang et al. [7] presented some geometric AOs under the IFS setting, ut these AOs cannot deal with the parametrized and sub-parametrized values of the alternatives. Arora et al. [30] prolonged the Pythagorean fuzzy soft weighted geometric operation, which competently accommodated the alternatives’ parametrized values. But, it also fails to deal with the sub-parametrized values of the alternatives. Wei et al. [12] developed PFWG unable to handle the parametrized values of the alternatives. Rahman et al. [10] competently deal with the Einstein aggregation value of the alternative but cannot take the parametrization values of the alternatives. Zulqarnain et al. [35] proposed that aggregation operators based on algebraic norms cannot cope with the multi sub-attributes of the considered parameters. On the other hand, our developed model effectively deals with the alternatives’ multi- sub-attributes. Zulqarnain et al. [37,57] protracted Einstein weighted and Einstein ordered weighted geometric AOs under PFSS environment are unable to deal with the multi sub-attributes of the alternatives. Zulqarnain et al. [41] introduced the intuitionistic fuzzy hypersoft weighted geometric operator, which handles the sub-parametrized values of the alternatives. Siddique et al. [43] developed the DM technique for PFHSNs using their established laws that cannot accommodate the Einstein aggregated values of the alternatives. Meanwhile, our established approach competently deals with parametrized values of the alternatives and delivers better information than existing techniques. This work recommends innovative Einstein AO, such as PFHSEWG, to integrate the evaluation materials and then use the score function to calculate the substitute score. Therefore, it is inevitable that, based on the above facts, the plan operator in this work is more influential, consistent, and effective.
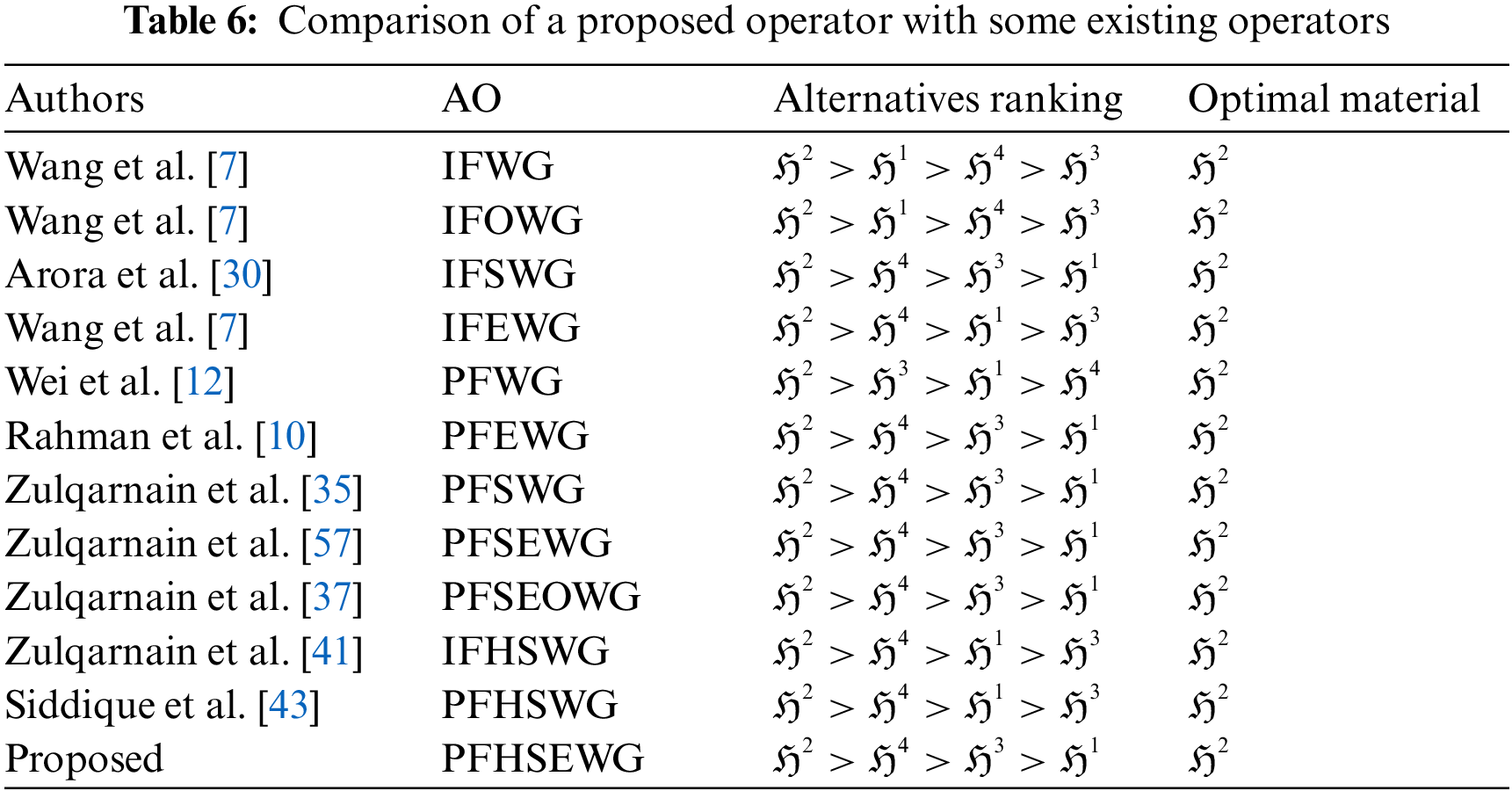
It is also an appropriate tool for dealing with contemptible inaccuracies and misrepresentation in DM plans. The advantage of expecting skill and associated dealings compared to existing methods is to avoid inspirations based on abominations. Hence, it is a proper tool for integrating erroneous and vague data in DM.
In engineering, the subtle stability of designing is impartial; authentic materials and manufacture comprise wide-ranging matters. Mathematical modeling in manufacturing enterprise establishments utilizes all capitals while combining design objectives under financial, superior, and security constraints. Questions must be defined for the most acceptable decision, conferring to judgment necessities. In actual DM, the assessment of alternative facts delivered by the expert is habitually imprecise, rough, and unpredictable; thus, PFHSNs can be used to conduct this indeterminate info. The core goal of this research is to use Einstein’s norms to develop some operational laws for PFHSS. Then, a new operator, such as PFHSEWG, developed according to the designed operational laws. Some fundamental properties have been presented using our developed PFHSEWG operator. Also, a DM approach is established to address MCDM problems based on the endorsed operator. To certify the robustness of the settled approach, we provide an inclusive mathematical illustration for MS in the manufacturing industry. A comparative analysis has been presented to ensure the practicality of the planned model. Lastly, based on the outcomes attained, it is determined that the technique projected in this study is the most practical and effective way to solve the problem of MCDM. In the future, several other hybrid AOs for PFHSS will be introduced with their decision-making techniques. Furthermore, the developed AOs can be extended to T-spherical fuzzy hypersoft, and q-rung orthopair fuzzy hypersoft settings with decision-making approaches.
Acknowledgement: The authors extend their appreciation to Deanship of Scientific Research at King Khalid University, for funding this work through General Research Project under Grant No. GRP/93/43.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Chatterjee, P., Chakraborty, S. (2012). Material selection using preferential ranking methods. Materials & Design, 35, 384–393. DOI 10.1016/j.matdes.2011.09.027. [Google Scholar] [CrossRef]
2. Thakker, A., Jarvis, J., Buggy, M., Sahed, A. (2008). A novel approach to materials selection strategy case study: Wave energy extraction impulse turbine blade. Materials & Design, 29(10), 1973–1980. DOI 10.1016/j.matdes.2008.04.022. [Google Scholar] [CrossRef]
3. Edwards, K. L. (2011). Materials influence on design: A decade of development. Materials & Design, 32(3), 1073–1080. DOI 10.1016/j.matdes.2010.10.009. [Google Scholar] [CrossRef]
4. Reddy, G. P., Gupta, N. (2010). Material selection for microelectronic heat sinks: An application of the Ashby approach. Materials & Design, 31(1), 113–117. DOI 10.1016/j.matdes.2009.07.013. [Google Scholar] [CrossRef]
5. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8, 338–353. DOI 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
6. Atanassov, K. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20, 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]
7. Wang, W., Liu, X. (2011). Intuitionistic fuzzy geometric aggregation operators based on Einstein operations. International Journal of Intelligent Systems, 26(11), 1049–1075. DOI 10.1002/int.20498. [Google Scholar] [CrossRef]
8. Yager, R. R. (2013). Pythagorean membership grades in multicriteria decision making. IEEE Transactions on Fuzzy Systems, 22(4), 958–965. DOI 10.1109/TFUZZ.2013.2278989. [Google Scholar] [CrossRef]
9. Ejegwa, P. A. (2019). Pythagorean fuzzy set and its application in career placements based on academic performance using max–min–max composition. Complex & Intelligent Systems, 5(2), 165–175. DOI 10.1007/s40747-019-0091-6. [Google Scholar] [CrossRef]
10. Rahman, K., Abdullah, S., Ahmed, R., Ullah, M. (2017). Pythagorean fuzzy Einstein weighted geometric aggregation operator and their application to multiple attribute group decision making. Journal of Intelligent & Fuzzy Systems, 33(1), 635–647. DOI 10.3233/JIFS-16797. [Google Scholar] [CrossRef]
11. Zhang, X., Xu, Z. (2014). Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. International Journal of Intelligent Systems, 29(12), 1061–1078. DOI 10.1002/int.21676. [Google Scholar] [CrossRef]
12. Wei, G., Lu, M. (2018). Pythagorean fuzzy power aggregation operators in multiple attribute decision making. International Journal of Intelligent Systems, 33(1), 169–186. DOI 10.1002/int.21946. [Google Scholar] [CrossRef]
13. Wang, L., Li, N. (2020). Pythagorean fuzzy interaction power Bonferroni mean aggregation operators in multiple attribute decision making. International Journal of Intelligent Systems, 35(1), 150–183. DOI 10.1002/int.22204. [Google Scholar] [CrossRef]
14. Ilbahar, E., Karaşan, A., Cebi, S., Kahraman, C. (2018). A novel approach to risk assessment for occupational health and safety using Pythagorean fuzzy AHP & fuzzy inference system. Safety Science, 103, 124–136. DOI 10.1016/j.ssci.2017.10.025. [Google Scholar] [CrossRef]
15. Zhang, X. (2016). A novel approach based on similarity measure for pythagorean fuzzy multiple criteria group decision making. International Journal of Intelligent Systems, 31(6), 593–611. DOI 10.1002/int.21796. [Google Scholar] [CrossRef]
16. Peng, X., Yang, Y. (2015). Some results for Pythagorean fuzzy sets. International Journal of Intelligent Systems, 30(11), 1133–1160. DOI 10.1002/int.21738. [Google Scholar] [CrossRef]
17. Garg, H. (2016). A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. International Journal of Intelligent Systems, 31(9), 886–920. DOI 10.1002/int.21809. [Google Scholar] [CrossRef]
18. Garg, H. (2017). Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision-making process. International Journal of Intelligent Systems, 32(6), 597–630. DOI 10.1002/int.21860. [Google Scholar] [CrossRef]
19. Garg, H. (2019). New logarithmic operational laws and their aggregation operators for Pythagorean fuzzy set and their applications. International Journal of Intelligent Systems, 34(1), 82–106. DOI 10.1002/int.22043. [Google Scholar] [CrossRef]
20. Gao, H., Lu, M., Wei, G., Wei, Y. (2018). Some novel Pythagorean fuzzy interaction aggregation operators in multiple attribute decision making. Fundamenta Informaticae, 159(4), 385–428. DOI 10.3233/FI-2018-1669. [Google Scholar] [CrossRef]
21. Wang, L., Garg, H., Li, N. (2021). Pythagorean fuzzy interactive Hamacher power aggregation operators for assessment of express service quality with entropy weight. Soft Computing, 25(2), 973–993. DOI 10.1007/s00500-020-05193-z. [Google Scholar] [CrossRef]
22. Wang, L., Li, N. (2019). Continuous interval-valued Pythagorean fuzzy aggregation operators for multiple attribute group decision making. Journal of Intelligent & Fuzzy Systems, 36(6), 6245–6263. DOI 10.3233/JIFS-182570. [Google Scholar] [CrossRef]
23. Peng, X., Yuan, H. (2016). Fundamental properties of Pythagorean fuzzy aggregation operators. Fundamenta Informaticae, 147(4), 415–446. DOI 10.3233/FI-2016-1415. [Google Scholar] [CrossRef]
24. Arora, R., Garg, H. (2019). Group decision-making method based on prioritized linguistic intuitionistic fuzzy aggregation operators and its fundamental properties. Computational and Applied Mathematics, 38(2), 1–32. DOI 10.1007/s40314-019-0764-1. [Google Scholar] [CrossRef]
25. Ma, Z., Xu, Z. (2016). Symmetric Pythagorean fuzzy weighted geometric/averaging operators and their application in multicriteria decision-making problems. International Journal of Intelligent Systems, 31(12), 1198–1219. DOI 10.1002/int.21823. [Google Scholar] [CrossRef]
26. Molodtsov, D. (1999). Soft set theory—First results. Computers & Mathematics with Applications, 37(4–5), 19–31. DOI 10.1016/S0898-1221(99)00056-5. [Google Scholar] [CrossRef]
27. Maji, P. K., Biswas, R., Roy, A. R. (2003). Soft set theory. Computers & Mathematics with Applications, 45(4–5), 555–562. DOI 10.1016/S0898-1221(03)00016-6. [Google Scholar] [CrossRef]
28. Maji, P. K., Biswas, R., Roy, A. R. (2001). Fuzzy soft sets. Journal of Fuzzy Mathematics, 9, 589–602. [Google Scholar]
29. Maji, P. K., Biswas, R., Roy, A. R. (2001). Intuitionistic fuzzy soft sets. Journal of Fuzzy Mathematics, 9, 677–692. [Google Scholar]
30. Arora, R., Garg, H. (2018). A robust aggregation operators for multi-criteria decision-making with intuitionistic fuzzy soft set environment. Scientia Iranica, 25(2), 931–942. [Google Scholar]
31. Peng, X. D., Yang, Y., Song, J., Jiang, Y. (2015). Pythagorean fuzzy soft set and its application. Computer Engineering, 41(7), 224–229. [Google Scholar]
32. Athira, T. M., John, S. J., Garg, H. (2020). A novel entropy measure of Pythagorean fuzzy soft sets. AIMS Mathematics, 5(2), 1050–1061. DOI 10.3934/math.2020073. [Google Scholar] [CrossRef]
33. Athira, T. M., John, S. J., Garg, H. (2019). Entropy and distance measures of Pythagorean fuzzy soft sets and their applications. Journal of Intelligent & Fuzzy Systems, 37(3), 4071–4084. DOI 10.3233/JIFS-190217. [Google Scholar] [CrossRef]
34. Naeem, K., Riaz, M., Peng, X., Afzal, D. (2019). Pythagorean fuzzy soft MCGDM methods based on TOPSIS, VIKOR and aggregation operators. Journal of Intelligent & Fuzzy Systems, 37(5), 6937–6957. DOI 10.3233/JIFS-190905. [Google Scholar] [CrossRef]
35. Zulqarnain, R. M., Xin, X. L., Garg, H., Khan, W. A. (2021). Aggregation operators of Pythagorean fuzzy soft sets with their application for green supplier chain management. Journal of Intelligent & Fuzzy Systems, 40(3), 5545–5563. DOI 10.3233/JIFS-202781. [Google Scholar] [CrossRef]
36. Zulqarnain, R. M., Siddique, I., Ahmad, S., Iampan, A., Jovanov, G. et al. (2021). Pythagorean fuzzy soft Einstein ordered weighted average operator in sustainable supplier selection problem. Mathematical Problems in Engineering, 2021. DOI 10.1155/2021/2559979. [Google Scholar] [CrossRef]
37. Zulqarnain, R. M., Siddique, I., EI-Morsy, S. (2022). Einstein-ordered weighted geometric operator for Pythagorean fuzzy soft set with its application to solve MAGDM problem. Mathematical Problems in Engineering, 2022. DOI 10.1155/2022/5199427. [Google Scholar] [CrossRef]
38. Smarandache, F. (2018). Extension of soft set to hypersoft set, and then to plithogenic hypersoft set. Neutrosophic Sets and Systems, 22(1), 168–170. [Google Scholar]
39. Rahman, A. U., Saeed, M., Khalifa, H. A. E. W., Afifi, W. A. (2022). Decision making algorithmic techniques based on aggregation operations and similarity measures of possibility intuitionistic fuzzy hypersoft sets. AIMS Math, 7(3), 3866–3895. DOI 10.3934/math.2022214. [Google Scholar] [CrossRef]
40. Zulqarnain, R. M., Xin, X. L., Saeed, M. (2021). A development of Pythagorean fuzzy hypersoft set with basic operations and decision-making approach based on the correlation coefficient. In: Theory and application of hypersoft set, neutrosophic sets and systems, vol. 40, pp. 149–168. Pons Publishing House, Brussels. [Google Scholar]
41. Zulqarnain, R. M., Siddique, I., Ali, R., Pamucar, D., Marinkovic, D. et al. (2021). Robust aggregation operators for intuitionistic fuzzy hypersoft set with their application to solve MCDM problem. Entropy, 23(6), 688. DOI 10.3390/e23060688. [Google Scholar] [CrossRef]
42. Zulqarnain, R. M., Siddique, I., Iampan, A., Baleanu, D. (2022). Aggregation operators for interval-valued Pythagorean fuzzy soft Set with their application to solve multi-attribute group decision making problem. Computer Modeling in Engineering & Sciences, 131(3), 1717–1750. DOI 10.32604/cmes.2022.019408. [Google Scholar] [CrossRef]
43. Siddique, I., Zulqarnain, R. M., Ali, R., Jarad, F., Iampan, A. (2021). Multicriteria decision-making approach for aggregation operators of pythagorean fuzzy hypersoft sets. Computational Intelligence and Neuroscience, 2021. DOI 10.1155/2021/2036506. [Google Scholar] [CrossRef]
44. Sunthrayuth, P., Jarad, F., Majdoubi, J., Zulqarnain, R. M., Iampan, A. et al. (2022). A novel multicriteria decision-making approach for einstein weighted average operator under Pythagorean fuzzy hypersoft environment. Journal of Mathematics, 2022. DOI 10.1155/2022/1951389. [Google Scholar] [CrossRef]
45. Stocker, T. (2014). Climate change 2013: The physical science basis: Working group I contribution to the fifth assessment report of the intergovernmental panel on climate change. UK: Cambridge University Press. [Google Scholar]
46. CaraDonna, P. J., Cunningham, J. L., Iler, A. M. (2018). Experimental warming in the field delays phenology and reduces body mass, fat content and survival: Implications for the persistence of a pollinator under climate change. Functional Ecology, 32(10), 2345–2356. DOI 10.1111/1365-2435.13151. [Google Scholar] [CrossRef]
47. Kontgis, C., Schneider, A., Ozdogan, M., Kucharik, C., Duc, N. H. et al. (2019). Climate change impacts on rice productivity in the Mekong River Delta. Applied Geography, 102, 71–83. DOI 10.1016/j.apgeog.2018.12.004. [Google Scholar] [CrossRef]
48. Mazdiyasni, O., AghaKouchak, A. (2015). Substantial increase in concurrent droughts and heatwaves in the United States. Proceedings of the National Academy of Sciences, 112(37), 11484–11489. DOI 10.1073/pnas.1422945112. [Google Scholar] [CrossRef]
49. Warner, K., Ehrhart, C., Sherbinin, A. D., Adamo, S., Chai-Onn, T. (2009). In search of shelter: Mapping the effects of climate change on human migration and displacement. https://www.refworld.org/docid/4ddb65eb2.html. [Google Scholar]
50. Environmental Protection Agency. United States. (2017) Inventory of US greenhouse gas emissions and sinks: 1990–2015. http://www3.epa.gov/climatechange/emissions/usinventoryreport.html. [Google Scholar]
51. Dudley, B. (2018). BP statistical review of world energy. BP statistical review, pp. 00116. London, UK. https://www.bp.com/content/dam/bp/en/corporate/pdf/energyeconomics/statistical-review/bp-stats-review-2018-full-report.Pdf. [Google Scholar]
52. Saito, S. (2010). Role of nuclear energy to a future society of shortage of energy resources and global warming. Journal of Nuclear Materials, 398(1–3), 1–9. DOI 10.1016/j.jnucmat.2009.10.002. [Google Scholar] [CrossRef]
53. Farag, M. M. (2020). Materials and process selection for engineering design. USA: CRC Press. [Google Scholar]
54. Flynn, T. M. (2005). Cryogenic engineering, 2nd edition, pp. 257–291. New York: Marcel and Dekker Publishing, Ltd. [Google Scholar]
55. Godula-Jopek, A., Jehle, W., Wellnitz, J. (2012). Hydrogen storage technologies: New materials, transport, and infrastructure. USA: John Wiley & Sons. [Google Scholar]
56. Xu, Z. (2007). Intuitionistic fuzzy aggregation operators. IEEE Transactions on Fuzzy Systems, 15(6), 1179–1187. DOI 10.1109/TFUZZ.2006.890678. [Google Scholar] [CrossRef]
57. Zulqarnain, R. M., Siddique, I., Jarad, F., Hamed, Y. S., Abualnaja, K. M. et al. (2022). Einstein aggregation operators for pythagorean fuzzy soft sets with their application in multiattribute group decision-making. Journal of Function Spaces, 2022. DOI 10.1155/2022/1358675. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools