Minimal Doubly Resolving Sets of Certain Families of Toeplitz Graph

1  Introduction and Preliminaries

To understand the abstract structure of graphs, graph invariants can be a powerful tool. Metric generators in graphs have evolved into a variety of distinct types based on their popularity or usefulness. As an example, virus propagation in complicated network difficulties can be detected using the double metric dimension (DMD).

We consider a finite, undirected, and connected graph Γ with the edge set EΓ and the vertex set VΓ. In a connected graph Γ, the distance between a pair of distinct vertices, say k and l in Γ, is the smallest path length among the lengths of all paths between them and is represented by d(k, l). For any two distinct vertices j and k in VΓ, a vertex l∈VΓ resolves the vertices j and k if the condition d(j,l)≠d(k,l) holds true. Let k be a vertex of Γ and HΓ={hμ|1≤μ≤ρ} be an ordered subset of the vertex set VΓ, then r(k,HΓ) is the representation of k with respect to HΓ which is the ρ-vector (d(k,hμ))μ=1ρ, also known as vector of metric coordinates. If each vertex of graph Γ possesses a unique vector of metric coordinates with respect to HΓ then the subset HΓ is called a resolving set for graph Γ. If the subset HΓ is the resolving set with the minimum number of elements in Γ, then its count becomes the metric dimension (MD) of Γ and can be denoted as dim⁡(Γ).

It is common in computer science, chemistry, biology, and operations research to structure graph theory models. In graph theory, the computation of the resolving sets and MD for general graphs is complex. In various disciplines, such as optimization, pattern recognition, and loran detecting devices, the MD has gained all the interest due to its applications.

Slater [1], a mathematician, was the first to discover the term MD. This notion was used to describe the study of the Loran or sonar model station. Another mathematician, Harary, independently described the concept of MD with the help of Harary et al. [2]. Additionally, this concept cleared the path for finding the unique recipient of a message on a network. Since then, several studies have been done on resolving sets, including [3,4]. Many different tasks can be accomplished with resolving sets, like network discovery and verification [5], strategies for the mastermind games [6], as well as digital geometry, pattern recognition, and processing of images [7]. The minimum order of a resolving set of Hamming graphs closely relates to the problem of weighing the coins discussed in [8,9]. Also, there are numerous applications in different fields, such as chemical structures [10], robotics [11], combinatorial optimization [12], geographic routing protocols [13] for the theoretical study of the MD.

The MD of any graph is a computationally difficult problem to solve. So, valuable bounds for different types of graphs have been found. The MD of all connected graphs, as well as the MD of certain well-known graph families, such as trees, pathways, and complete graphs, were established by Chartrand et al. [10,14]. For some families of generalized Petersen graphs, MD bounds were studied in [15]. The MD for chorded cycles and kayak paddles graphs was found to be constant by Ahmad et al. [16]. Many authors have extensively studied the MD of path-related graphs. The MD of the Kenser graph was computed by Hui et al. [17]. On the other hand, Alholi et al. [18] also contributed to this area by finding that the MD is constant. Buczkowski and others [19] presented a generic concept of k-dimensional graphs. The NP-completeness of the MD for general graphs was demonstrated by Khuller et al. [11]. The minimum order of a resolving set of Jahangir graphs has also been discussed in detail by Tomescu et al. [20].

Caceres et al. [21] developed the concept of doubly resolving sets (DRSs) of a graph Γ, demonstrating that the MD of the Cartesian product Γ◻Γ is closely linked to the minimal doubly resolving sets (MDRSs) of Γ. Consider the vertices k1,k2,l1,l2∈VΓ, then any pair of vertices k1,k2 is said to be doubly resolved by the vertices l1,l2 if the condition d(k1,l1)−d(k1,l2)≠d(k2,l1)−d(k2,l2), holds true. A subset NΓ∈VΓ is said to be a DRS, if any two distinct vertices of graph Γ are doubly resolved by some two vertices of the subset NΓ. A MDRS is a DRS having minimum order. The order of MDRS is denoted by ψ(Γ) and is termed the DMD of Γ. Note that if the vertices l1,l2 doubly resolve the vertices k1,k2 then d(k1,l1)−d(k2,l1)≠0 or d(k1,l2)−d(k2,l2)≠0. For all graphs Γ, any DRS is obviously a resolving set, with dim⁡(Γ)≤ψ(Γ). The MDRS problem has been proven to be NP-hard in the context of general graphs [22]. Furthermore, it was shown in [21] that the upper bound on the MD of the Cartesian product of Γ and Ω can be stated as; dim⁡(Γ◻Ω)≤dim⁡(Γ)+ψ(Ω)−1.

Therefore, DRSs are essential for studying the MD of Cartesian product graphs. These results have inspired us to work on finding the MDRSs. Also, MDRSs themselves have a unique combinatorial nature that can be seen in their integer programming model, which was shown in [22]. There are several families of graphs for which the problem of finding the MDRS has been examined. For example, MDRSs of prisms [23], convex polytopes [24], and Hamming graphs [25] have all been studied in the literature. The family of circulant graphs in [26] was found to have the same MD and MDRS. The MDRSs for the line graphs of prisms and sunlet graphs were found in [27]. For the first time, Chen et al. explicitly approximated the upper and lower bounds for the MDRS problem [28]. In [29], the minimal resolving sets and DMD of the line graph of chorded cycles were examined. Authors demonstrated that the DMD of L(Cnt) is exactly one greater than its MD. Ahmad et al. discussed the problem of finding the minimal resolving set and MDRS for line graphs of kayak paddles graphs [30]. The authors in [31,32] presented some families of convex polytopes with constant DMD. While solving the MDRS problem, certain families of Harary graphs, layer-sun graphs have also been investigated in [33,34], respectively. Cocktail, jellyfish and necklace graphs and their line graphs have also been studied for the MD and MDRS problems, see [35–37].

Our research is the continuation of the literature work mentioned earlier. We have investigated the DMD for some particular classes of Toeplitz graphs to contribute to our knowledge of this distance-based parameter in graphs. However, this variant is helpful in many fields, for instance, diffusion over the network, epidemics in human beings, the origin of a disease outbreak, etc. Using MDRSs, it is possible to identify the source of diffusion in complicated networks. Attempting to find the source of an infection in an extensive network might be difficult, but it is still an exciting challenge. For example, to detect the spread of the virus throughout a network, we need to know when specific nodes in the network are infected. However, maintaining observer nodes that can report their infection time may be costly. In addition, the position of a node in the network affects how much information it contains. Which nodes should we use as observers in order to increase our chances of correctly identifying the source? Because of its close relationship to another well-known DRS problem, we can reduce the number of observers required to achieve perfect detection even if the initial time at which an epidemic spreads is unknown [38,39].

Liu et al. [40] determined the MD of some families of Toeplitz graph Tn(1,t) for n ≥ t + 2 given in the following theorems:

Theorem 1.1. For n ≥ 4, the metric dimension of Toeplitz graph Tn(1,2) = 2.

Theorem 1.2. For n ≥ 6, the metric dimension of Toeplitz graph Tn(1,4) = 2.

Theorem 1.3. For n ≥ 5, the metric dimension of Toeplitz graph Tn(1,3) = 3.

•   Our discussion of Toeplitz graphs in Section 2 included the computation of MDRSs for the family of Toeplitz graphs Tn(1,2) for n ≥ 4.

•   The MDRSs for the family of Toeplitz graphs Tn(1,4), for n ≥ 6 were conjectured in Section 3.

•   The MDRSs for the family of Toeplitz graph Tn(1,3) for n ≥ 5, were discussed in Section 4.

•   In Section 5, we conclude this article by expressing an opinion.

2  Minimal Doubly Resolving Sets for the Family of Toeplitz Graph Tn(1,2)

For a graph Γ with n vertices labelled as {1, 2, …, n} its adjacency matrix A is n × n matrix whose jkth entry is 1 if the vertex j and vertex k joined by an edge and 0 otherwise. An n × n matrix B=bjk is known as Toeplitz matrix if bjk=bj+1,k+1 for each {j, k = 1, …, n − 1}. A simple undirected graph Tn is Toeplitz graph if matrix n × n which is B=bjk is the symmetric Toeplitz matrix and for all j, k = {1, …, n} satisfied the following: edge j, k is in EΓ iff bjk=bkj=1. An n × n matrix B will be labelled 0, 1, …, n − 1 which has n distinct diagonals. The main diagonal has bjj=0 for all j = 1, …, n, so Toeplitz graph has no loop. The diagonals {x1,x2,…,xq} containing ones 0<x1<x2<…<xq<n. The Toeplitz graph Tn<x1,x2,…,xq> with vertex set {1, 2, …, n} has edge j, k for 1 ≤ j ≤ k ≤ n, occurs iff k−j=xp for some p, 1 ≤ p ≤ q. Toeplitz graphs are defined as graphs formed from Toeplitz matrices. Specifically, in this part, we computed the MDRSs for the family of Toeplitz graph Tn(1,2). Fig. 1 illustrates the graph T11(1,2).

Figure 1: The Toeplitz graph T11(1,2)

It follows from Theorem 1.1 that ψ(Tn(1,2))≥2, for n ≥ 4. We will also calculate that ψ(Tn(1,2))=2, for n ≥ 4. To compute the distances between the vertices of the Toeplitz graph Tn(1,2): Define Sω(e0)={e∈Tn(1,2):d(e0,e)=ω}, which is the vertex subset in VTn(1,2) at distance ω from e0. The Table 1 shows the sets Sω(e0) for Toeplitz graph Tn(1,2), where n ≥ 4.

Due to the symmetry of Tn(1,2), where n ≥ 4: d(eω,eν)=d(e0,e|ν−ω|) if 0≤|ν−ω|≤n−1.

Due to the fact that, in order to calculate the distance between any pair of vertices in VTn(1,2), we must know the distance d(e0,e) for each e∈Tn(1,2).

Lemma 2.1. Let Tn(1,2) be the family of Toeplitz graph, then ψ(Tn(1,2))=2 for any even positive integer n ≥ 4.

Proof. Consider the case n = 2l, where l ≥ 2. We must prove that ψ(Tn(1,2))≤2 for any even positive integer n ≥ 4. So, finding a DRS of order 2 is sufficient. The Table 2 displays the metric coordinate vectors for all vertices of Tn(1,2) with respect to the set NTn(1,2)={e1,en−1}.

It turns out that the value of the first metric coordinate of the vertex e0 from Sω(e0) in Table 2 is 1. Using Table 2, we may check that there exist a pair of vertices f1,f2∈Sω(e0), for some ω∈{1,2,…,l}, such as the condition r(f1,NTn(1,2))−r(f2,NTn(1,2))≠0, holds true. Also, there exist the vertices f1∈Sω(e0) and f2∈Sν(e0) for any ω,ν∈{1,2,…,l}, such as ω≠ν, then the condition r(f1,NTn(1,2))−r(f2,NTn(1,2))≠ω−ν, holds true. Therefore, the set NTn(1,2)={e1,en−1} is the MDRS. As a result, the Lemma 2.1 holds.

Lemma 2.2. Let Tn(1,2) be the family of Toeplitz graph, then ψ(Tn(1,2))=2 for any odd positive integer n ≥ 5.

Proof. Consider the case n = 2l + 1, where l ≥ 2. We must prove that ψ(Tn(1,2))≤2 for any odd positive integer n ≥ 5. So, finding a DRS of order 2 is sufficient. The Table 3 displays the metric coordinate vectors for all vertices of Tn(1,2) with respect to the set NTn(1,2)={e0,en−1}.

It turns out that the value of the first metric coordinate of the vertex e0 from Sω(e0) in Table 3 is 0. Using Table 3, we may check that there exist a pair of vertices f1,f2∈Sω(e0), for some ω∈{1,2,…,l}, such as the condition r(f1,NTn(1,2))−r(f2,NTn(1,2))≠0, holds true. Also, there exist the vertices f1∈Sω(e0) and f2∈Sν(e0) for any ω,ν∈{1,2,…,l}, such as ω≠ν, then the condition r(f1,NTn(1,2))−r(f2,NTn(1,2))≠ω−ν, holds true. Therefore, the set NTn(1,2)={e0,en−1} is the MDRS. As a result, the Lemma 2.2 holds.

The main theorem is stated below by using Lemmas 2.1 and 2.2.

Theorem 2.1. Let Tn(1,2) be the family of Toeplitz graph. Then ψ(Tn(1,2))=2, for n ≥ 4.

Example 2.1. For the Toeplitz graph Tn(1,2), where n ≥ 4, let us consider the set NT8(1,2)={e1,e7}. Now, the vectors of metric coordinates for T8(1,2) with respect to the set NT8(1,2) are: r(e0|NT8(1,2))=(1,4), r(e1|NT8(1,2))=(0,3), r(e2|NT8(1,2))=(1,3), r(e3|NT8(1,2))=(1,2), r(e4|NT8(1,2))=(2,2), r(e5|NT8(1,2))=(2,1), r(e6|NT8(1,2))=(3,1), r(e7|NT8(1,2))=(3,0). Thus, the set NT8(1,2) is clearly a DRS, as can be observed.

3  Minimal Doubly Resolving Sets for the Family of Toeplitz Graph Tn(1,4)

Specifically, in this part, we computed the MDRSs for the family of Toeplitz graph Tn(1,4). Fig. 2 illustrates the graph T11(1,4).

Figure 2: The Toeplitz graph T11(1,4)

It follows from Theorem 1.2 that ψ(Tn(1,4))≥2, for n ≥ 6. We will also calculate that ψ(Tn(1,4))=3, for n ≥ 6. To compute the distances between the vertices of the Toeplitz graph Tn(1,4): Define Sω(e0)={e∈Tn(1,4):d(e0,e)=ω}, which is the vertex subset in VTn(1,4) at distance ω from e0. The Table 4 shows the sets Sω(e0) for Toeplitz graph Tn(1,4), where n ≥ 6.

Due to the symmetry of Tn(1,4), where n ≥ 6: d(eω,eν)=d(e0,e|ν−ω|) if 0≤|ν−ω|≤n−1. Due to the fact that, in order to calculate the distance between any pair of vertices in VTn(1,4), we must know the distance d(e0,e) for each e∈Tn(1,4).

Lemma 3.1. ψ(Tn(1,4))>2, for all n ≥ 6.

Proof. We already know that ψ(Tn(1,4))≥2, for n ≥ 6. As a result, it suffices to demonstrate that no subset NTn(1,4)⊆VTn(1,4) of order 2 is a DRS for Tn(1,4). We can assume that e0∈NTn(1,4) because of the symmetry of Tn(1,4). Table 5 lists the non-doubly resolved pair of vertices from VTn(1,4) that correspond to each of the five distinct forms of set NTn(1,4). Let us explain why the vertices en−2,en−3 cannot be doubly resolved by any two vertices of the set NTn(1,4)={e0,eω;ω=n−1}. It is clear that for ω=n−1, we have d(e0,en−2)=d(e0,e|n−2|)=l, d(e0,en−3)=d(e0,e|n−3|)=l+1, d(eω,en−2)=d(e0,e|n−2−ω|)=1 and d(eω,en−3)=d(e0,e|n−3−ω|)=2. So, d(e0,en−2)−d(e0,en−3)=d(eω,en−2)−d(eω,en−3)=−1, that is, the set NTn(1,4)={e0,eω;ω=n−1} is not a DRS of Tn(1,4). The non-doubly resolved pairs of vertices for all the other types of set NTn(1,4) listed in Table 5 can be verified in the same way.

Lemma 3.2. Let n ≡ 0(mod 4) and n ≥ 8, we have ψ(Tn(1,4))=3.

Proof. Suppose that n ≡ 0(mod 4) and n ≥ 8. We need to prove that ψ(Tn(1,4))≤3, for n ≥ 8. So, finding a DRS having order 3 is sufficient. Now, from Table 4 using the sets Sω(e0), the following Table 6 illustrates the metric coordinate vectors for all vertices of Tn(1,4) with respect to the set NTn(1,4)={e0,e2,en−3}, where n = 4l and l ≥ 2 be an integer.

It turns out that the value of the first metric coordinate of the vertex e0 from Sω(e0) in Table 6 is 0. Using Table 6, we may check that there exist a pair of vertices g1,g2∈Sω(e0), for some ω∈{1,2,…,l+1}, such as the condition r(g1,NTn(1,4))−r(g2,NTn(1,4))≠0, holds true. Also, there exist the vertices g1∈Sω(e0) and g2∈Sν(e0) for any ω,ν∈{1,2,…,l+1} such as ω≠ν, then the condition r(g1,NTn(1,4))−r(g2,NTn(1,4))≠ω−ν, holds true. Therefore, the set NTn(1,4)={e0,e2,en−3} is the MDRS. As a result, the Lemma 3.2 holds.

Lemma 3.3. Let n ≡ 1(mod 4) and n ≥ 9, we have ψ(Tn(1,4))=3.

Proof. Suppose that n ≡ 1(mod 4) and n ≥ 9. We need to prove that ψ(Tn(1,4))≤3, for n ≥ 9. So, finding a DRS having order 3 is sufficient. Now, from Table 4 using the sets Sω(e0), the following Table 7 illustrates the metric coordinate vectors for all vertices of Tn(1,4) in relation to the set NTn(1,4)={e0,e2,en−3}, where n = 4l + 1 and l ≥ 2 be an integer.

It turns out that the value of the first metric coordinate of the vertex e0 from Sω(e0) in Table 7 is 0. Using Table 7, we may check that there exist a pair of vertices g1,g2∈Sω(e0), for some ω∈{1,2,…,l+1}, such as the condition r(g1,NTn(1,4))−r(g2,NTn(1,4))≠0, holds true. Also, there exist the vertices g1∈Sω(e0) and g2∈Sν(e0) for any ω,ν∈{1,2,…,l+1} such as ω≠ν, then the condition r(g1,NTn(1,4))−r(g2,NTn(1,4))≠ω−ν, holds true. Therefore, the set NΓ={e0,e2,en−3} is the MDRS. As a result, the Lemma 3.3 holds.

Lemma 3.4. Let n ≡ 2(mod 4) and n ≥ 6, we have ψ(Tn(1,4))=3.

Proof. Suppose that n ≡ 2(mod 4) and n ≥ 6. We need to prove that ψ(Tn(1,4))≤3, for n ≥ 6. So, finding a DRS having order 3 is sufficient. Now, from Table 4 using the sets Sω(e0), the following Table 8 illustrates the metric coordinate vectors for all vertices of Tn(1,4) with respect to the set NTn(1,4)={e0,e2,en−3}, where n = 4l + 2 and l ≥ 1 be an integer.

It turns out that the value of the first metric coordinate of the vertex e0 from Sω(e0) in Table 8 is 0. Using Table 8, we may check that there exist a pair of vertices g1,g2∈Sω(e0), for some ω∈{1,2,…,l+1}, such as the condition r(g1,NTn(1,4))−r(g2,NTn(1,4))≠0, holds true. Also, there exist the vertices g1∈Sω(e0) and g2∈Sν(e0) for any ω,ν∈{1,2,…,l+1} such as ω≠ν, then the condition r(g1,NTn(1,4))−r(g2,NTn(1,4))≠ω−ν, holds true. Therefore, the set NTn(1,4)={e0,e2,en−3} is the MDRS. As a result, the Lemma 3.4 holds.

Lemma 3.5. Let n ≡ 3(mod 4) and n ≥ 7, we have ψ(Tn(1,4))=3.

Proof. Suppose that n ≡ 3(mod 4) and n ≥ 7. We need to prove that ψ(Tn(1,4))≤3, for n ≥ 7. So, finding a DRS having order 3 is sufficient. Now, from Table 4 using the sets Sω(e0), the following Table 9 illustrates the metric coordinate vectors for all vertices of Tn(1,4) with respect to the set NTn(1,4)={e0,e2,en−3}, where n = 4l + 3 and l ≥ 1 be an integer.

It turns out that the value of the first metric coordinate of the vertex e0 from Sω(e0) in Table 9 is 0. From Table 9, we may check that there exist a pair of vertices g1,g2∈Sω(e0), for some ω∈{1,2,…,l+2}, such as the condition r(g1,NTn(1,4))−r(g2,NTn(1,4))≠0, holds true. Also, there exist the vertices g1∈Sω(e0) and g2∈Sν(e0) for any ω,ν∈{1,2,…,l+2} such as ω≠ν, then the condition r(g1,NTn(1,4))−r(g2,NTn(1,4))≠ω−ν, holds true. Therefore, the set NTn(1,4)={e0,e2,en−3} is the MDRS. As a result, the Lemma 3.5 holds.

The main theorem is stated below by using Lemmas 3.2–3.5.

Theorem 3.1. Let Tn(1,4) be the family of Toeplitz graph. Then ψ(Tn(1,4))=3, for n ≥ 6.

4  Minimal Doubly Resolving Sets for the Family of Toeplitz Graph Tn(1,3)

Specifically, in this part, we computed the MDRSs for the family of Toeplitz graph Tn(1,3). Fig. 3 illustrates the graph T11(1,3).

Figure 3: The Toeplitz graph T11(1,3)

It follows from Theorem 1.3 that ψ(Tn(1,3))≥3, for n ≥ 5. We will also calculate that

 ψ(Tn(1,3))={3,for 5≤n≤7;4,for n≥8.

To compute the distances between the vertices of the Toeplitz graph Tn(1,3): Define Sω(e0)={e∈Tn(1,3):d(e0,e)=ω}, which is the vertex subset in VTn(1,3) at distance ω from e0. The Table 10 shows the sets Sω(e0) for Toeplitz graph Tn(1,3), where n ≥ 5.

Due to the symmetry of Tn(1,3), where n ≥ 5: d(eω,eν)=d(e0,e|ν−ω|) if 0≤|ν−ω|≤n−1. Due to the fact that, in order to calculate the distance between any pair of vertices in VTn(1,3), we must know the distance d(e0,e) for each e∈Tn(1,3).

Lemma 4.1. ψ(Tn(1,3))>3, for all n ≥ 5.

Proof. We already know that ψ(Tn(1,3))≥3, for n ≥ 5. As a result, it suffices to demonstrate that no subset NTn(1,3)⊆VTn(1,3) of order 3 is a DRS for Tn(1,3). We can assume that e0∈NTn(1,3) because of the symmetry of Tn(1,3). Table 11 lists the non-doubly resolved pair of vertices from VTn(1,3) that correspond to each of the seven distinct forms of set NTn(1,3). Let us explain why the vertices en−2,en−1 cannot be doubly resolved by any two vertices of the set NTn(1,3)={e0,eω,eν;ω=1,ν=n−2}. It is clear that for ω=1,ν=n−2, we have d(e0,en−2)=d(e0,e|n−2|)=l, d(e0,en−1)=d(e0,e|n−1|)=l+1, d(eω,en−2)=d(e0,e|n−2−ω|)=l−1, d(eω,en−1)=d(e0,e|n−1−ω|)=l, d(eν,en−2)=d(e0,e|n−2−ν|)=0 and d(eν,en−1)=d(e0,e|n−1−ν|)=1. So, d(e0,en−2)−d(e0,en−1)=d(eω,en−2)−d(eω,en−1)=d(eν,en−2)−d(eν,en−1)=−1, that is, the set NTn(1,3)={e0,eω,eν;ω=1,ν=n−2} is not a DRS of Tn(1,3). The non-doubly resolved pairs of vertices for all the other types of set NTn(1,3) listed in Table 11 can be verified in the same way.

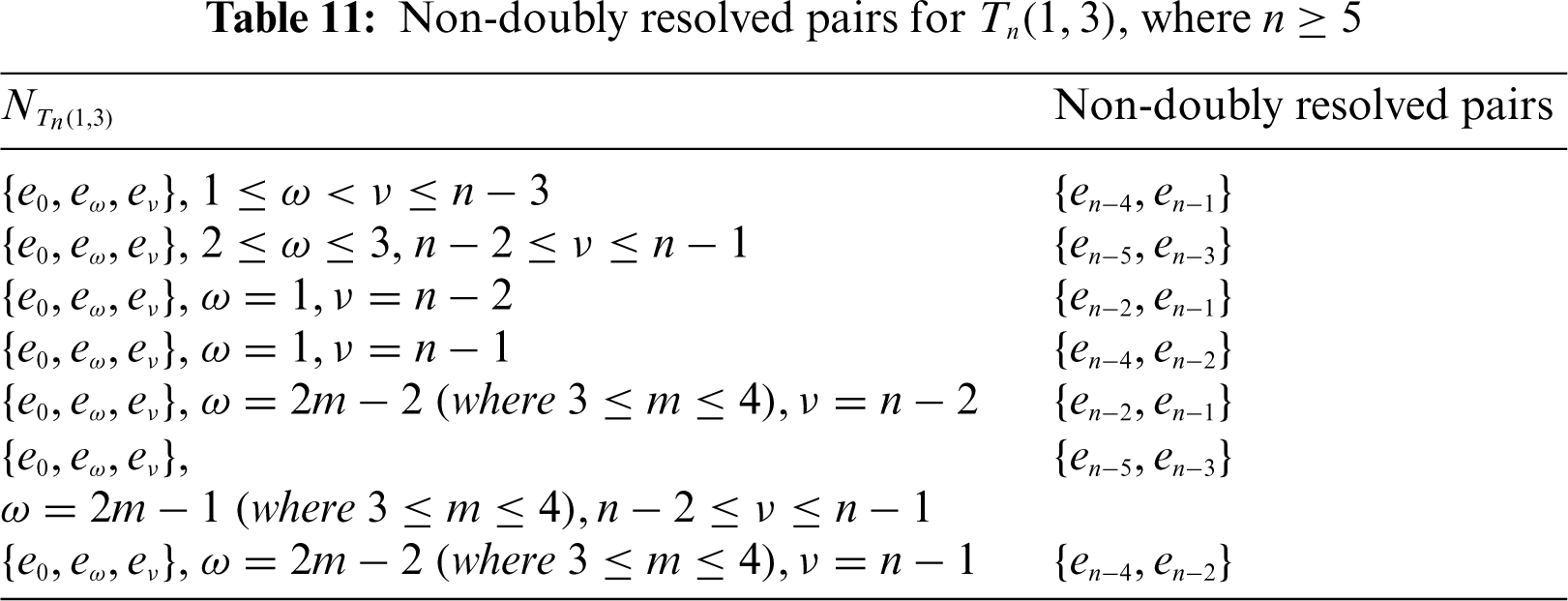
Lemma 4.2. Let n ≡ 0(mod 3) for n ≥ 6, we have  ψ(Tn(1,3))={3,for n=6;4,for n>6.

Proof. Suppose that n ≡ 0(mod 3) and n ≥ 6. Then, in the case n ≡ 0(mod 3) and n = 6, the MDRS for T6(1,3) is NTn(1,3)={e0,e1,e2}. Now, for the case n ≡ 0(mod 3) and n > 6, we need to prove that ψ(Tn(1,3))≤4. So, finding a DRS having order 4 is sufficient. From Table 10 using the sets Sω(e0), the following Table 12 illustrates the metric coordinate vectors for all vertices of Tn(1,3) with respect to the set NTn(1,3)={e0,e1,e2,en−2}, where n = 3l, and l ≥ 3 be an integer.

It turns out that the value of the first metric coordinate of the vertex e0 from Sω(e0) in Table 12 is 0. Using Table 12, we may check that there exist a pair of vertices h1,h2∈Sω(e0) for some ω∈{1,2,…,l+1} such as the condition r(h1,NTn(1,3))−r(h2,NTn(1,3))≠0, holds true. Also, there exist the vertices h1∈Sω(e0) and h2∈Sν(e0) for any ω,ν∈{1,2,…,l+1} such as ω≠ν, then the condition r(h1,NTn(1,3))−r(h2,NTn(1,3))≠ω−ν, holds true. Therefore, the set NTn(1,3)={e0,e1,e2,en−2} is the MDRS. AS a result, the Lemma 4.2 holds.

Lemma 4.3. Let n ≡ 1(mod 3) for n ≥ 7, we have

Proof. Suppose that n ≡ 1(mod 3) and n ≥ 7. Then, in the case n ≡ 1(mod 3) and n = 7, the MDRS for T7(1,3) is NTn(1,3)={e1,e2,e5}. Now, for the case n ≡ 1(mod 3) and n > 7, we need to prove that ψ(Tn(1,3))≤4. So, finding a DRS having order 4 is sufficient. From Table 10 using the sets Sω(e0), the following Table 13 illustrates the metric coordinate vectors for all vertices of Tn(1,3) with respect to the set NTn(1,3)={e0,e1,e2,en−2}, where n = 3l + 1, and l ≥ 3 be an integer.

It turns out that the value of the first metric coordinate of the vertex e0 from Sω(e0) in Table 13 is 0. Using Table 13, we may check that there exist a pair of vertices h1,h2∈Sω(e0) for some ω∈{1,2,…,l+1} such as the condition r(h1,NTn(1,3))−r(h2,NTn(1,3))≠0, holds true. Also, there exist the vertices h1∈Sω(e0) and h2∈Sν(e0) for any ω,ν∈{1,2,…,l+1} such as ω≠ν, then the condition r(h1,NTn(1,3))−r(h2,NTn(1,3))≠ω−ν, holds true. Therefore, the set NTn(1,3)={e0,e1,e2,en−2} is the MDRS. AS a result, the Lemma 4.3 holds.

Lemma 4.4. Let n ≡ 2(mod 3) for n ≥ 5, we have

Proof. Suppose that n ≡ 2(mod 3) and n ≥ 5. Then, in the case n ≡ 1(mod 3) and n = 5, the MDRS for T5(1,3) is NTn(1,3)={e1,e2,e4}. Now, for the case n ≡ 2(mod 3) and n > 5, we need to prove that ψ(Tn(1,3))≤4. So, finding a DRS having order 4 is sufficient. From Table 10 using the sets Sω(e0), the following Table 14 illustrates the metric coordinate vectors for all vertices of Tn(1,3) with respect to the set NTn(1,3)={e0,e1,e2,en−2}, where n = 3l + 2, and l ≥ 2 be an integer.

It turns out that the value of the first metric coordinate of the vertex e0 from Sω(e0) in Table 14 is 0. Using Table 14, we may check that there exist a pair of vertices h1,h2∈Sω(e0) for some ω∈{1,2,…,l+1} such as the condition r(h1,NTn(1,3))−r(h2,NTn(1,3))≠0, holds true. Also, there exist the vertices h1∈Sω(e0) and h2∈Sν(e0) for any ω,ν∈{1,2,…,l+1} such as ω≠ν, then the condition r(h1,NTn(1,3))−r(h2,NTn(1,3))≠ω−ν, holds true. Therefore, the set NTn(1,3)={e0,e1,e2,en−2} is the MDRS. As a result, the Lemma 4.4 holds.

The main theorem is stated below by using Lemmas 4.2–4.4.

Theorem 4.1. Let Tn(1,3) be the family of Toeplitz graph, then

5  Application

Recently, some applications of DRSs can be seen to localizing the epidemic source in different complex networks such as social networks, epidemics in human beings and the origin of a disease outbreak, etc. (see [38,39]). In particular, we consider a network to reduce the number of observers using the DRSs in order to achieve the perfect detection of an epidemic source.

Let us assume, a social network arranged in the form of Toeplitz network T11(1,3), where the node set VT11(1,3)={e0,e1,e2,e3,e4,e5,e6,e7,e8,e9,e10} represents the people and the edge set ET11(1,3)={e0e1,e1e2,e2e3,e3e4,e4e5,e5e6,e6e7,e7e8,e8e9,e9e10} ∪ {e0e3,e1e4,e2e5,e3e6,e4e7,e5e8,e6e9,e7e10} between the nodes represents the links between the people. If the observers are placed throughout the network, and the inter-node distances are reliable and known, a direct solution can be found. But, the entire process would be very costly and time taking.

So, what are the fewest number of observers required to account epidemic source with an unknown starting time and irregular transmission delays among the nodes? Such that each node has a unique representation depending upon minimum distances from the observer nodes. In order to reduce the number of observers, we employed the MDRS NT11(1,3)={e0,e1,e2,e9} of the Toeplitz network T11(1,3).

By using the Lemma 4.4 and Theorem 4.1, we placed the observers only on the nodes e0,e1,e2,e9. It is clear from Table 14 and Fig. 4 that each node has a unique representation and epidemic propagation will be optimal by placing observers at the nodes e0,e1,e2,e9. This scenario explains the applicability of DRSs in source localization problems.

Figure 4: DRS in T11(1,3)

6  Conclusion

This study is concerned with the concept of calculating MDRSs of graphs using an integer linear programming formulation that has been proposed earlier in the literature. In this article, we theoretically establish the MDRSs for the certain families of Toeplitz graphs Tn(1,t) for t = 2, 3, 4 and n ≥ t + 2. We observed that the MD and DMD are equal for the Toeplitz graphs Tn(1,2). Also, the DMD for the Toeplitz graphs Tn(1,4) is exactly one greater than its MD. In the case of Tn(1,3), the DMD is equal to the MD for n = 5, 6, 7 and is exactly one greater than its MD for n ≥ 8. In future work, certain classes of subdivision graphs of circulant graphs Cn(1,k) will be investigated for the MDRS problem.

This research work may lead to the following open problem.

Open Problem 6.1. Investigate the minimal doubly resolving sets for the family of the generalized Toeplitz graphs Tn(1,t) for all values of t and n ≥ t + 2.

Acknowledgement: The authors are grateful to the editor and reviewers for the careful reading to improve the manuscript.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.   Slater, P. J. (1975). Leaves of trees. Congressus Numerantium, 14(549–559), 37.

 2.   Harary, F., Melter, R. A. (1976). On the metric dimension of a graph. Ars Combinatoria, 2, 191–195.

 3.   Chartrand, G., Erwin, D., Johns, G. L., Zhang, P. (2003). Boundary vertices in graphs. Discrete Mathematics, 263(1–3), 25–34.

 4.   Chartrand, G., Zhang, P. (2003). The theory and applications of resolvability in graphs. A survey. Congress us Numerantium, 1, 47–68.

 5.   Beerliova, Z., Eberhard, F., Erlebach, T., Hall, A., Hoffmann, M. et al. (2006). Network discovery and verification. IEEE Journal on Selected Areas in Communications, 24(12), 2168–2181.

 6.   Chvatal, V. (1983). Mastermind. Combinatorica, 3(3), 325–329.

 7.   Melter, R. A., Tomescu, I. (1984). Metric bases in digital geometry. Computer Vision, Graphics, and Image Processing, 25(1), 113–121.

 8.   Erdos, P., Renyi, A. (1963). On two problems of information theory. Magyar Tudományos Akadémia Matematikai És Fizikai Osztalyanak, 8, 229–243.

 9.   Lindström, B. (1964). On a combinatory detection problem I. Magyar Tudományos Akadémia Matematikai És Fizikai Osztalyanak, 9, 195–207.

10.  Chartrand, G., Eroh, L., Johnson, M. A., Oellermann, O. R. (2000). Resolvability in graphs and the metric dimension of a graph. Discrete Applied Mathematics, 105(1--3), 99–113.

11.  Khuller, S., Raghavachari, B., Rosenfeld, A. (1996). Landmarks in graphs. Discrete Applied Mathematics, 70(3), 217–229.

12.  Sebo, A., Tannier, E. (2004). On metric generators of graphs. Mathematics of Operations Research, 29(2), 383–393.

13.  Liu, K., Abu-Ghazaleh, N. (2006). Virtual coordinates with backtracking for void traversal in geographic routing. International Conference on Ad-Hoc Networks and Wireless, pp. 46–59. Berlin, Heidelberg: Springer.

14.  Chartrand, G., Poisson, C., Zhang, P. (2000). Resolvability and the upper dimension of graphs. Computers and Mathematics with Applications, 39(12), 19–28.

15.  Shao, Z., Sheikholeslami, S. M., Wu, P., Liu, J. B. (2018). The metric dimension of some generalized petersen graphs. Discrete Dynamics in Nature and Society, 2018, 1–10.

16.  Ahmad, A., Baca, M., Sultan, S. (2020). Computing the metric dimension of kayak paddles graph and cycles with chord. Proyecciones, 39(2), 287–300.

17.  Hui, P., Xunting, W., Jing, W., Siyuan, C. (2016). The metric dimension of some kneser graphs. Journal of Computational and Theoretical Nanoscience, 13(5), 3013–3018.

18.  Alholi, M. M., Abughneim, O. A., Ezeh, H. A. (2017). Metric dimension of some path related graphs. Global Journal of Pure and Applied Mathematics, 3(2), 149–157.

19.  Buczkowski, P. S., Chartrand, G., Poisson, C., Zhang, P. (2003). On k-dimensional graphs and their bases. Periodica Mathematica Hungarica, 46(1), 9–15.

20.  Tomescu, I., Javaid, I. (2007). On the metric dimension of the jahangir graph. Bulletin Mathématiques de la Société des Sciences Mathématiques de Roumanie, 50(4), 371–376.

21.  Cáceres, J., Hernando, C., Mora, M., Pelayo, I. M., Puertas, M. L. et al. (2007). On the metric dimension of cartesian products of graphs. SIAM Journal on Discrete Mathematics, 21(2), 423–441.

22.  Kratica, J., Cangalovic, M., Kovacevic-Vujcic, V. (2009). Computing minimal doubly resolving sets of graphs. Computers and Operations Research, 36(7), 2149–2159.

23.  Cangalovic, M., Kratica, J., Kovacevic-Vujcic, V., Stojanovic, M. (2013). Minimal doubly resolving sets of prism graphs. Optimization, 62(8), 1037–1043.

24.  Kratica, J., Kovacevic-Vujcic, V., Cangalovic, M., Stojanovic, M. (2012). Minimal doubly resolving sets and the strong metric dimension of some convex polytopes. Applied Mathematics and Computation, 218(19), 9790–9801.

25.  Kratica, J., Kovacevic-Vujcic, V., Cangalovic, M., Stojanovic, M. (2012). Minimal doubly resolving sets and the strong metric dimension of hamming graphs. Applicable Analysis and Discrete Mathematics, 6(1), 63–71.

26.  Ahmad, A., Sultan, S. (2017). On minimal doubly resolving sets of circulant graphs. Acta Mechanica Slovaca, 21(1), 6–11.

27.  Ahmad, M., Zahid, Z., Zafar, S. (2018). On minimal edge version of doubly resolving sets of a graph. arXiv preprint arXiv:1807.02365.

28.  Chen, X., Hu, X., Wang, C. (2016). Approximation for the minimum cost doubly resolving set problem. Theoretical Computer Science, 609, 526–543.

29.  Ahmad, M., Zahid, Z., Rashid, T., Guirao, J. L. G. (2022). Computing edge version of resolvability and double resolvability of a graph. Journal of Chemistry, 2022, 1–11.

30.  Ahmad, M., Ameen, N., Zahid, Z., Zafar, S. (2020). Computing edge version of metric and double metric dimensions of kayak paddle graphs. Discrete Mathematics, Algorithms and Applications, 12(5), 2050070.

31.  Ahmad, M., Alrowaili, D., Zahid, Z., Siddique, I., Iampan, A. (2022). Minimal doubly resolving sets of some classes of convex polytopes. Journal of Mathematics, 2022.

32.  Pan, L., Ahmad, M., Zahid, Z., Zafar, S. (2021). Computation of the double metric dimension in convex polytopes. Journal of Mathematics, 2021, 1–11.

33.  Ahmad, A., Baca, M., Sultan, S. (2019). On the minimal doubly resolving sets of Harary graph. Acta Mathematica Universitatis Comenianae, 89(1), 123–129.

34.  Liu, J. B., Zafari, A. (2020). Computing minimal doubly resolving sets and the strong metric dimension of the layer sun graph and the line graph of the layer sun graph. Complexity, 2020, 1–8.

35.  Ahmad, A., Baca, M., Sultan, S. (2018). Minimal doubly resolving sets of necklace graph. Mathematical Reports, 2, 123–129.

36.  Liu, J. B., Zafari, A., Zarei, H. (2020). Metric dimension, minimal doubly resolving sets, and the strong metric dimension for jellyfish graph and cocktail party graph. Complexity, 2020, 1–7.

37.  Liu, J. B., Zahid, Z., Nasir, R., Nazeer, W. (2018). Edge version of metric dimension and doubly resolving sets of the necklace graph. Mathematics, 6(11), 243.

38.  Spinelli, B., Celis, L. E., Thiran, P. (2016). Observer placement for source localization: the effect of budgets and transmission variance. 2016 54th Annual Allerton Conference on Communication, Monticello, IL, USA, Control, and Computing (Allerton), pp. 743–751. IEEE. DOI 10.1109/ALLERTON.2018.8635897.

39.  Spinelli, B., Celis, L. E., Thiran, P. (2018). How many sensors to localize the source? the double metric dimension of random networks. 2018 56th Annual Allerton Conference on Communication, Control, and Computing (Allerton), pp. 1036–1043. Monticello, IL, USA. IEEE. DOI 10.1109/ALLERTON.2018.8635897.

40.  Liu, J. B., Nadeem, M. F., Siddiqui, H. M. A., Nazir, W. (2019). Computing metric dimension of certain families of toeplitz graphs. IEEE Access, 7, 126734–1267.