Observer-Based Control for a Cable-Driven Aerial Manipulator under Lumped Disturbances

Nomenclature

1  Introduction

Recently, unmanned aerial vehicles (UAVs), as a special robotic system, have been widely used in various aerial applications including aerial photography [1], mapping [2] and emergency search [3] benefiting from their high maneuverability and low cost. Unfortunately, most existing UAVs can only perform some perceptional tasks passively while being unable to interact with the environment actively. Hence, researchers have tried to develop aerial manipulators [4–7], which is composed of UAVs and multiple degrees of freedom manipulators or grippers. Thanks to the dexterous motion capacity of the aircrafts, aerial manipulators can achieve aerial-ground interaction activities such as remote scientific sampling [8], aerial grasping [9], and ground target capture [10]. However, existing robotic manipulators mounted on the flying robots are mainly classical rigid robotic arms, which in turn bring in large moving mass and low operation accuracy. To handle this problem, scholars applied the cable-drive technology to the robotic manipulator [11], so that the drive motors can be placed at the base, thereby reducing the inertia and energy consumption of the robotic arm. In contrast, since the driving cable is flexible, this will also lead to a decrease in the overall stiffness of the aerial manipulator, which in turn makes the system extremely sensitive to external disturbances and its own vibration [12]. Hence, it remains a challenging job to develop a high-performance control strategy to realize the anti-disturbance operation of the cable-driven aerial manipulators under lumped uncertainties such as joint flexibility, time-varying disturbance, and unmodeled dynamics.

To effectively solve the above issue, various robust control schemes for aerial manipulators have already been designed and investigated including sliding mode control (SMC) [13], adaptive control [14], H-infinity control [15], etc. Among these methodologies, SMC has been broadly implemented in robotic manipulators owing to its strong robustness and fast response. Although providing excellent control performance, some issues including the incapacity to converge finite-time and the chattering phenomena still reduce the applicability of the classical SMC. To guarantee convergence in finite time, terminal SMC (TSMC) [16] and its variants such as fast TSMC (FTSMC) [17], fast nonsingular TSMC (FNTSMC) [18] and fractional-order (FO) nonsingular TSMC (FONTSMC) [19] have been proposed. By combing NTSMC with FO technique, the FONTSMC can achieve fast convergence speed and high tracking accuracy, so it has been used in many applications [20,21]. Li et al. [20] proposed a FONTSMC method for space tethered satellite system that effectively avoided the singularity problem and ensured finite-time convergence, improving the deployment performance of the system. To counteract chattering effect, many techniques have been proposed that can be mentioned, such as boundary layer scheme [22], fuzzy logic control [23], and super-twisting (ST) method [24]. ST method can both avoid chattering occurrence and achieve excellent performance, so it has been a hotpot in recent literature [25–27]. Bastola et al. [25] designed a super-twisting sliding mode controller for a spherical robot, which was demonstrated through simulation to be able to track the given trajectory under complex disturbances, while the chattering was effectively suppressed. Although excellent results have been achieved with above approaches, most of them are model-based schemes that rely on accurate mathematical models.

To employ these methods easily in complex practical applications, scholars have tried to find methods that do not need precise system information as much as possible. In these methods [28–30], the lumped disturbances such as unmodelled dynamics, unknown uncertainties and disturbances are estimated by the observers. Linear extended state observer (LESO) is well-known as a simple structure observer that can estimate not only disturbances but also unmeasured states, making it easier to implement in engineering. Thanks to its model-free feature, LSEO is applied in many systems such as quadrotor [31], mobile robot [32], underwater vehicle [33] and robotics manipulator [34]. The adoption of LESO will, however, inevitably lead to estimation errors, which could result in a reduction in control performance. Hence, LESOs are usually combined with other control techniques, such as backstepping scheme [35], fuzzy logic control [36] and SMC [37], etc. Despite the good control performance achieved by these methods, to the authors’ best knowledge, the application of LESO-based anti-disturbance control strategy to cable-driven aerial manipulator has rarely been reported. So, in this article, we combine FONTMSC, adaptive ST (AST) and LESO to propose a mode-free robust control strategy, aiming to realize the accurate control for the cable-driven aerial manipulator in joint space. Firstly, a virtual prototype of the cable-driven aerial manipulator was designed according to the operational task requirements, and then the rigid-flexible coupled dynamics model of the system was obtained by the Lagrange-Euler method. In the controller, the FONTSMC is adopted to guarantee fast convergence and singularity elimination while the adaptive STA counteracts chattering problem and enhance good tracking accuracy. The LESO is used to approximate the lumped uncertainties and enhance the control performance. The convergence and stability of our controller designed in this article are then proved utilizing the Lyapunov method, and eventually its effectiveness and superiorities are validated by visualization simulations and ground experiments.

The major contributions of our research are briefly summarized as follows:

1)   A cable-driven aerial manipulator used for remote water sampling has been designed. The adoption of cable-driven technique makes drive motors installed at the base, therefore the energy consumption and the dynamics coupling effect of the system are significantly reduced.

2)   To achieve high precision trajectory tracking in joint space under lumped disturbances, an observer-based robust control strategy is proposed. Combining the LESO as basic framework and utilizing FONTSMC along with AST, the proposed strategy can achieve good control performance while being model-free.

3)   To demonstrate the validity and superiorities of our designed strategy, visualization simulations and ground test experiments are performed compared with existing other control strategies.

The rest of this article is arranged as follows: The structure of our proposed cable-driven aerial manipulator and its rigid-flexible coupled dynamics model are presented in Section 2. Section 3 describes the control design, which includes the LESO design and the AST-FONTSMC design. In Section 4, the convergence and stability of control strategy is proved. Then, various simulations and experiments are performed in Sections 5 and 6, demonstrating the effectiveness of our proposed controller. Lastly, some noteworthy conclusions and further works are presented in Section 7.

2  System Description

2.1 Structure Design

The cable-driven aerial manipulator we designed is shown in Fig. 1, it is composed mainly of a rotorcraft and a 2-DOF cable-driven manipulator. And they are held together by a pod in which the drive motors, power supply, water pump, and other devices are placed. This aerial robotic system is used to complete the task of collecting water samples at the drain mouth, which can help the scholars greatly reduce the effort and time required for sampling. In the specific task, ground personnel must first manipulate the cable-driven aerial manipulator flight to hover near the mouth of the sewage pipe, and then control the arm to make the end effector extend into the pipe for sampling by the water pump. As we can see, if the manipulator is a conventional one, the mass ratio between arm and quadrotor will increase, thus amplifying the coupling effect between the two. Then the huge dynamic coupling effect will cause greater interference with the hovering of the quadrotor and, in severe cases, may even cause it to tip over [38]. Furthermore, if the arm mass is large, it will result in a short battery life, a low load capacity, and poor pose control.

Figure 1: Virtual prototype of cable-driven aerial manipulator used for water sampling

To minimize the mass of manipulator, we employ cable drive technology (as shown in Fig. 2), which allows the two drive motors to be housed within the pod. Meanwhile, with the exception of critical components such as the joint shaft and linkages, all other components are made of 3D printed lightweight nylon, substantially lowering the arm’s mass. The designed cable-driven robot arm has a fully extended length of 515 mm and a moving part mass of 221 g, while the entire system weighs 2651 g. The mass ratio of the moving elements to the total mass of the system is only 0.083, which considerably reduces the influence of their coupling on the system's control. Additionally, it should be highlighted that this research focuses exclusively on the dynamics of the cable-driven robotic arm and the controller architecture, excluding the investigation of aircraft dynamics and control.

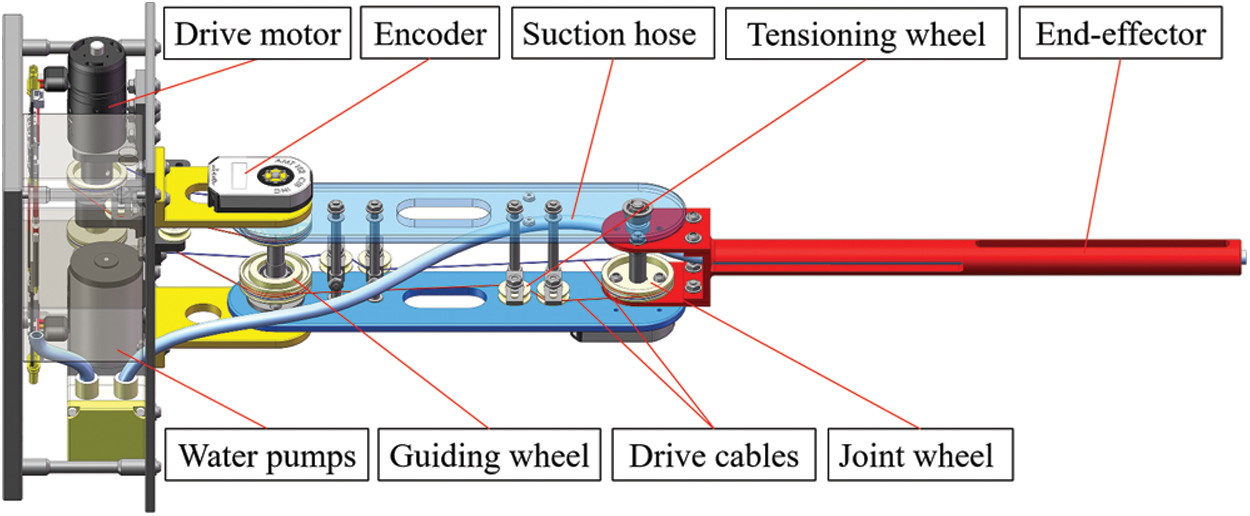
Figure 2: 3D model of the cable-driven manipulator

2.2 Dynamical Modeling

When the cable-driven manipulator is in motion, the drive motor transmits the torque to the joint axis through the flexible cable. Obviously, the flexibility of the cable is mainly concentrated at the joint. So, the joint of the cable-driven manipulator can be treated as a flexible one and furtherly simplified to a linear spring for modelling and analyzing [39], as shown in Fig. 3. Using the Lagrange-Euler method, we can derive the rigid-flexible coupling dynamics model of our designed cable-driven manipulator as follows:

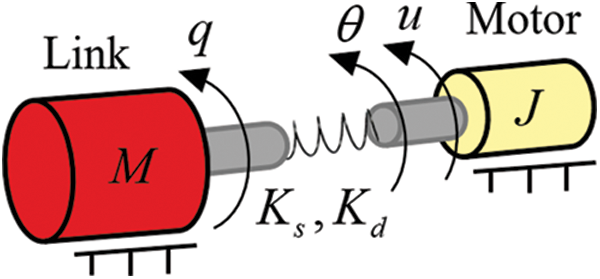
Figure 3: Simple model of flexible joint

Mq¨+Cq˙+G+τext=Ks(θ−q)+Kd(θ˙−q˙)(1)

Jθ¨+Dθ˙+Ks(θ−q)+Kd(θ˙−q˙)=u(2)

where M is the inertia matrix of links, C is Coriolis and centrifugal matrix and G is the gravitational force vector. J and D denote the inertia and damping matrix of motors individually. Ks and Kd denote the stiffness and damping matrices of joint. q and θ represent the angular position vector of links and motors, individually. τext represents the disturbance torque vector, and u is the vector of motor torque which is also the output of controller.

Combining Eqs. (1) and (2), we can get the dynamics model of cable-driven manipulator which is driven directly by motors:

Mq¨+Cq˙+G+Jθ¨+Dθ˙+τext=u(3)

Actually, exact dynamics model of cable-driven manipulator is usually difficult to obtain. So, we adopt a diagonal gain matrix M¯ to estimate the dynamic properties of system and further rewrite the Eq. (3) as

u=M¯q¨+N(4)

where N represents the lumped disturbances containing system uncertainties and external disturbances defined as

N=(M−M¯)q¨+Cq˙+G+Jθ¨+Dθ˙+τext(5)

3  Controller Design

3.1 Design of LESO

As can be seen in Eq. (4), the lumped disturbance N is so complex and nonlinear that it is difficult to obtain the accurate value using conventional methods. Hence, LESO is introduced in this section to estimate the lumped disturbance N, and the actual system can be reduced to two second-order subsystems. For simplicity, the design process of our control strategy in this article is deduced using the joint 1 subsystem as an example:

{q¨1=M¯1−1(u1−N1)y1=q1(6)

where y1 is the system output.

Rewrite the Eq. (6) into the form of state space equation:

{x˙=Ax+Bu+Efy=Cx(7)

where x=[q1,q˙1]T, u=u1, y=y1f=−M¯1−1N1 and other matrices can be defined as

A=[0100],B=[0M¯1−1],E=[01],C=[10]T

Supposing that the disturbance N1 is differentiable, it can be expanded to a new state x3. Then, rewrite Eq. (7) as follows:

{z¯˙=A¯z¯+B¯u+E¯hy=C¯z¯(8)

where z¯=[q1,q˙1,x3]T, h=f˙, x3=−M¯1−1N1 and other matrices can be defined as

A¯=[010001000],B¯=[0M¯1−10],E¯=[001],C¯=[100]T

Finally, the linear extended state observers for system (6) can be suggested as

{z¯^˙=Az¯^+Bu+L(y−y^)y^=Cz¯^(9)

where y^ is the system output, z¯^=[q^1,q˙^1,x^3]T is the estimation of z¯, q^1,q˙^1,x^3 are the estimation of system states. L=[β,β2,β3]T=[ξ1ωo,ξ2ωo,ξ3ωo]T denotes the observer gain matrix, ω0>0 is observer bandwidth. Selecting the appropriate ξi(i=1,2,3) by the pole assignment [40] allows the observer to track each state variable in the system (6).

3.2 Design of AST-FONTSM

Taking joint 1 as an example to extrapolate the design process of our control scheme. Joint position tracking error and its first order derivative are defined as e1=q1r−q^1, e˙1=q˙1r−q˙^1. For realizing high control accuracy and convergence speed in sliding phase, the following FONTSM surface is designed as

s1=e˙1+a11Db11[sig(e1)c11]+a21Db21−1[sig(e1)c21](10)

where 0<b11,b21,c11,c21<1, a11,a21 are the positive parameters to be designed. sig(x)α=|x|αsign(x), Dα(0<α<1) represents Riemann-Liouville fractional derivative and integration, it can be defined as follows:

Definition 1 [41]. The αth order Riemann-Liouville fractional derivative and integration of function f(t) with respect to t are given by

t0Dtαf(t)=dαf(t)dtα=1Γ(1−α)ddt∫t0tf(τ)(t−τ)αdτ(11)

t0Itαf(t)=1Γ(α)∫t0tf(τ)(t−τ)1−αdτ(12)

where 0<α<1, t0 is the terminal value, and Γ(α)=∫0∞e−ttα−1dt is the Euler’s Gamma function. For simplicity, Dα is used in this paper to denote t0Dtα.

Taking the derivative of Eq. (9) and combining with Eq. (5) yields

s˙1=q¨1r−M¯1−1(u1−N1)+a11Db11+1[sig(e1)c11]+a21Db21[sig(e1)c21](13)

In order to further achieve high performance and strong robustness in the reaching phase, we adopt the AST method as follows:

s˙1=−η^11sig(s1)0.5+μ1(14)

μ˙1=−η^21sgn(s1)(15)

where η^11 and η^21 are the adaptive parameter updated as

η^11={−θ11,if η^11≥η11max−θ21,if η11min<η^11<η1,|si|<Δ1θ11,if η^11≤η11min or η11min<η^11<η11max,|si|≥Δ1(16)

η^21=θ31η^11(17)

where θ11,θ21(θ21>θ11),θ31,Δ1 are constant parameters. As can be seen in (16), the adaptive law has two different speeds. The decreasing speed will increase from θ11 to θ21 once the tracking performance is reasonably satisfying and the adaptive parameter η^11 is in design range. Therefore, the control performance can be maximized while the noise effect is suppressed.

Finally, combining Eqs. (13)–(15), the control law of joint 1 can be given as

u1=M¯1φ1+N^1φ1=q¨1r+a11Db11+1[sig(e1)c11]+a21Db21[sig(e1)c21]+η^11sig(s1)0.5+η^21∫0tsgn(s1)dt(18)

Similarly, we can get the control law of joint 2 as follows:

u2=M¯2φ2+N^2φ2=q¨2r+a12Db12+1[sig(e2)c12]+a22Db22[sig(e2)c22]+η^21sig(s1)0.5+η^22∫0tsgn(s1)dt(19)

with N^1 and N^2 are defined as (9). The structure of proposed LESO-based AST-FONTSM control strategy is described in Fig. 4. As can be seen from the diagram, our control strategy only needs the reference and actual signals qd and q except some controller parameters. All other signals including angular tracking error e and e˙, FONTSM surface s and LESO output are obtained via qd and q. Obviously, our proposed scheme does not rely on any system dynamics. Hence, a model-free control scheme is ensured.

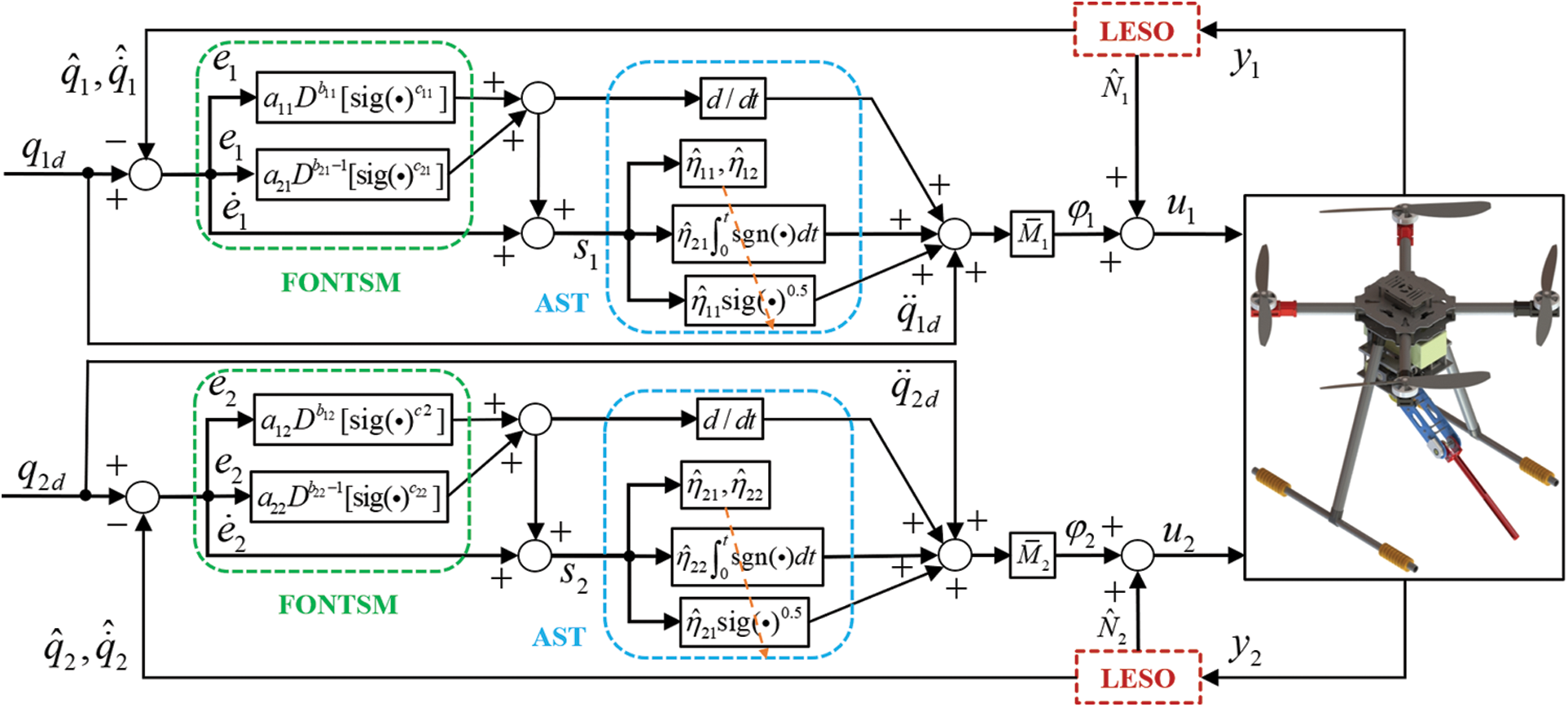
Figure 4: Structure of the proposed strategy

4  Stability and Convergence Analysis

Lemma 1 [42]. For a nonlinear system x˙=f(x,u), suppose that there is a continuous function V(x), coefficients λ>0, 0<μ<1, 0<ω<∞ such that

V˙(x)≤−λVμ(x)+ω(20)

Meanwhile, the system x˙=f(x,u) is practical finite-time stable and the states will be bounded in finite time t≤T as

T≤V1−μ(x0)λδ0(1−μ)(21)

where 0<δ0<1, V(x0) is the initial value of V(x).

Lemma 2 [43]. The fractional integration operators Ia+c and Ib−c with R(c)>0 are bounded in Lp(a,b), 1≤p≤∞:

‖Ia+cy‖p≤K‖y‖p,‖Ib−cy‖p≤K‖y‖p(H=(b−a)ℜ(c)ℜ(c)|Γ(c)|)(22)

For simplify, we also use the joint 1 to prove the convergence and stability of our designed strategy. Combining the above control law (18) with (6), the error dynamic equation can be obtained as follows:

s˙1=−η^11sig(s1)0.5−ρ21s1+μ1μ˙1=−η^21sgn(s1)+ε˙1(23)

where ε1=M¯1−1(N1−N^1)=M¯1−1N1−x^3 is estimation error of LESO.

Then, two steps are followed to demonstrate the stability.

First, the Eq. (23) is rewritten and a new vector x1=[x11,x21]T=[sig(s1)0.5μ1]Tis introduced so that the stability can be conveniently proved. And, the Eq. (23) can be given:

x˙11=12|x11|(−η^11x11+x21)x˙21=−η^21|x11|x11+ε˙1(24)

Then, the Eq. (24) can be further expressed as

[x˙11x˙21]=12|x11|[−η^111−2η^210][x11x21]+12|x11|[0002|x11|][1ε˙1](25)

Because of the first order derivative of LESO error ε˙1 is bounded as ε˙1≤ξ1, where ξ1 is a positive constant (bounded proof of ε˙1 can be found in [44]). Hence, there is a bounded function f11(e1,t) such that |f11(e1,t)|≤ξ1 holds for t≥0. Then, the LESO error ε˙1can be further expressed as

ε˙1=−f11(e,t)sgn(x11)=−f11(e,t)x11|x11|(26)

Combining (25) and (26), a compact form can be obtained

x˙1=A(x11)x1(27)

where A(x11) is defined as

A(x11)=12|x11|[−η^111−2η^21−2f11(e1,t)0](28)

Thus, we can conclude from the above analytical process that if x1 can converge in finite time, the FONTSM surface s1 will also be finite-time bounded.

Second, the stability analysis of our controller is performed. The following Lyapunov function is chosen

V(x11,x21,η^11,η^21)=V0(x1)+12η∼112+12η~212(29)

where η~11=η^11−η11,η~21=η^21−η21 and V0(x1) is given as

V0(x1)=(k1+4θ212)x112−4x11x21θ21+x212=x1TK1x1K1=[k1+4θ212−2θ21−2θ211](30)

where k1>0, η11, η21 are some coefficients. In fact, the adaptive parameters η^11 and η^21 are determined by x1. So, the Lyapunov V(x11,x21,η^11,η^21) can be rewritten as V(x1). Obviously, K1 will be positive definite with k1>0. Then, the following inequality will hold for V0(x1)

λmin{K1}‖x1‖22≤V0(x1)≤λmax{K1}‖x1‖22(31)

Remark 1. Note that the chosen Lyapunov function V1 is continuous while not locally Lipschitz because it cannot be differentiated at x1=0. As a result, it is unable to adopt the common second Lyapunov method here. Nevertheless, we can still use the Zubov’s theorem [45,46] which only requires the Lyapunov function is continuous to prove the convergence. Furthermore, where the derivative of V1 does not exist, the arguments given in [47] are used. The details on this issue can be found in [45].

Differentiating (29) and combing with (27):

V˙(x1)=V˙0(x1)+η~11η^˙11+η~21η^˙21=−12|x11|x1TP1x1+η~11η^˙11+η~21η^˙21(32)

Combing with (17), the symmetric matrix P1 can be given as

P1=[P1−11P1−12P1−21P1−22]=[2k1η^11−8θ21f112f11−k1−4θ2122f11−k1−4θ2124θ21](33)

The V˙0(x1) will be negative definite when P1>0, which can be easily fulfilled under the subsequent situation

η^11≥(k1+4θ212−2f11)8θ21k1+4θ21f11k1(34)

For V˙0(x1), the following inequality can be obtained

V˙0(x1)≤−12|x11|λmin{P1}‖x1‖22(35)

Considering |x11|=|s1|1/2≤‖x1‖2≤V01/2(x1)/λmin1/2{K1} and combing (31) and (35), we can have the following inequality:

V˙0(x1)≤−λmin1/2{K1}λmin(P1)2λmax{K1}V01/2(x1)=−λ11V01/2(x1)(36)

where λ11=λmin1/2{K1}λmin(P1)2λmax{K1}

Substituting (36) into (32) yields

V˙(x1)≤−λ11V01/2(x1)+η~11η^˙11+η~21η^˙21=−λ11V01/2(x1)−λ212|η~11|−λ312|η~21|+η~11η^˙11+η~21η^˙21+λ212|η~11|+λ312|η~21|(37)

Considering the inequality (a2+b2+c2)1/2≤|a|+|b|+|c| and the definition of V(x1), (37) can be further given as

V˙(x1)≤−λ01V1/2(x1)+η~11η^˙11+η~21η^˙21+λ212|η~11|+λ312|η~21|=−λ01V1/2(x1)+Ψ(38)

where λ01=min(λ11,λ21,λ31), Ψ=η~11η^˙11+η~21η^˙21+λ212|η~11|+λ312|η~21|.

It is obvious that η~11,η~21,η^˙11,η^˙21 are bounded considering the adaptive law (16) and (17), so the Ψ is bounded. Furthermore, it can be concluded from Lemma1 that the system state x1 is also finite-time bounded.

In fact, system state x1 is composed of FONTSM variable s1, so we can conclude that s1 will converge into |s1|≤Φ in finite time. Furthermore, the finite-time boundness of the tracking error e1 can be demonstrated as follows.

Taking (13) into consideration, we have

s1=e˙1+a11Db11[sig(e1)c11]+a21Db21−1[sig(e1)c21],|s1|≤Φ(39)

Eq. (39) can be rewritten into two forms as follows:

e˙1+a11Db11[sig(e1)c11]+(a21−s1(Db21−1[sig(e1)c21])−1)Db21−1[sig(e1)c21]=0(40)

e˙1+(a11−s1(Db11[sig(e1)c11])−1)Db11[sig(e1)c11]+a21Db21−1[sig(e1)c21](41)

Eq. (39) will remain the FONTSM form as (13) when a21−s1(Db21−1[sig(e1)c21])−1>0. Consequently, the system trajectory will converge persistently toward FONTSM (13) until |Db21−1[sig(e1)c21]|≤a21−1Φ. Based on Lemma 2 and p=∞, we have

esssup|Db21−1[sig(e1)c21]|≤H1esssup|e1|c21(42)

where esssupf(x) denotes the essential maximum values of the function f(x). For simplicity, |e1|maxc21 is used in this paper to denote esssup|e1|c21.

Combining |Db21−1[sig(e1)c21]|≤esssup|Db21−1[sig(e1)c21]| and Eq. (42), we get |Db21−1[sig(e1)c21]|≤H1|e1|maxc21. Then, a bounded time-varying variable φ≥1 in introduced so that we have

|Db21−1[sig(e1)c21]|=φ−1H1|e1|maxc21(43)

Considering |Db21−1[sig(e1)c21]|≤a21−1Φ, we have φ−1H1|e1|maxc21≤a21−1Φ. Hence, the trajectory error e1 will be finite-time bounded as

|e1|≤|e1|max≤(a21−1ΦφH1−1)1/c21(44)

Similarly, we can conclude |Db11[sig(e1)c11]|≤a11−1Φ. Then, combining (13) and |Db21−1[sig(e1)c21]|≤a21−1Φ, we have

|e˙1|≤|s1|+|a11Db11[sig(e1)c11]|+|a21Db21−1[sig(e1)c21]|=3Φ(45)

Lastly, the overall system stability is demonstrated and the tracking errors will converge as (44) and (45) in finite-time.

5  Simulation Demonstrations

5.1 Setup

To demonstrate the effectiveness of our designed controller, we molded the cable-driven aerial manipulator in MATLAB/SIMSCAPE and performed two visualization simulations. In the following simulations, the quadrotor is hovering, as shown in Fig. 5, and the cable-driven manipulator is controlled to track the given signals by different controllers. Considering the different disturbances faced by cable-driven aerial manipulator such as gust of wind, flexible deformation of cable, and mechanical vibration, various disturbances defined later are added into the simulation. Meanwhile, the conventional linear active disturbance rejection control (LADRC) [48] and the FNTSMC [49] are adopted to compare the control performance with our proposed one. The parameters of the three controllers were adjusted in SIMULINK and the final selected values are shown in Table 1.

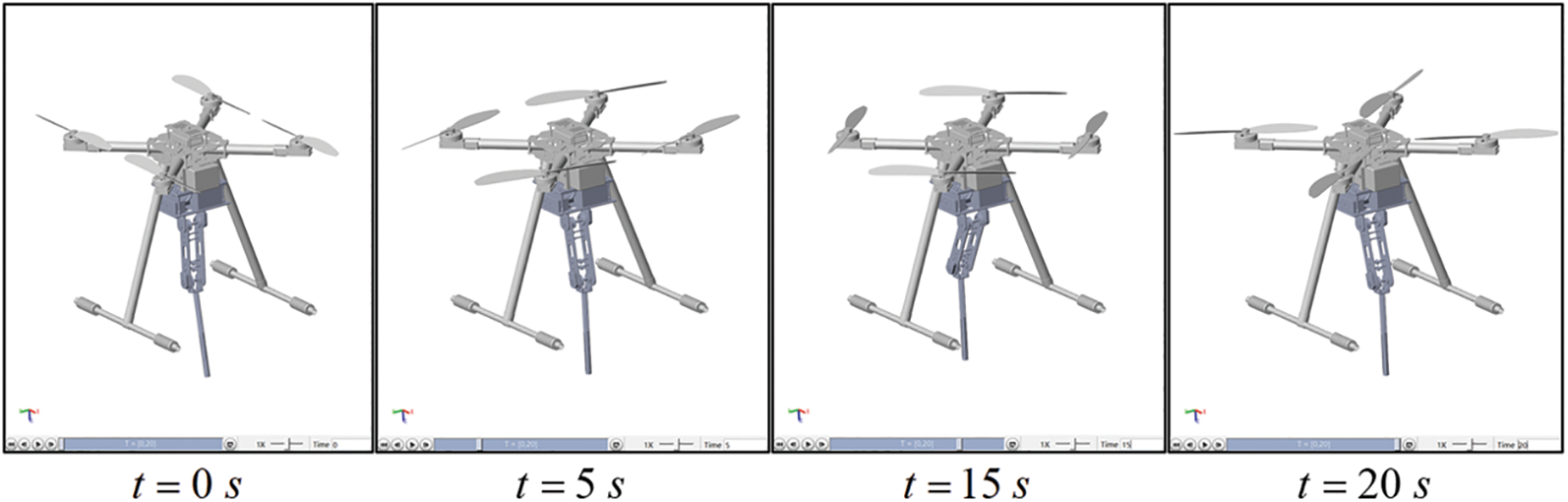
Figure 5: Visualization simulation in MATLAB/SIMSCAPE

5.2 Results

1) Simulation 1: In the first simulation case, for validating the effectiveness of our control method, the cable-driven manipulator is controlled to track sinusoidal reference trajectories without payload. And a disturbance τd=0.1sin⁡(2πt) Nm is adopted for the cable-driven manipulator. Finally, the obtained simulation outcomes are shown in Fig. 6.

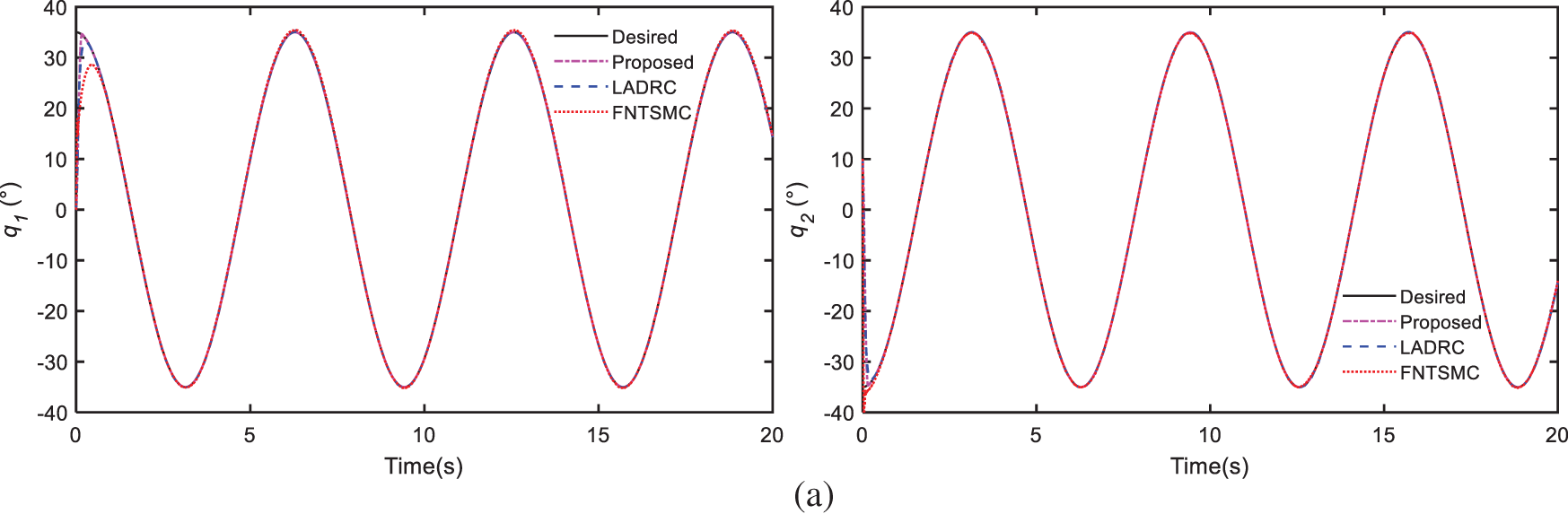
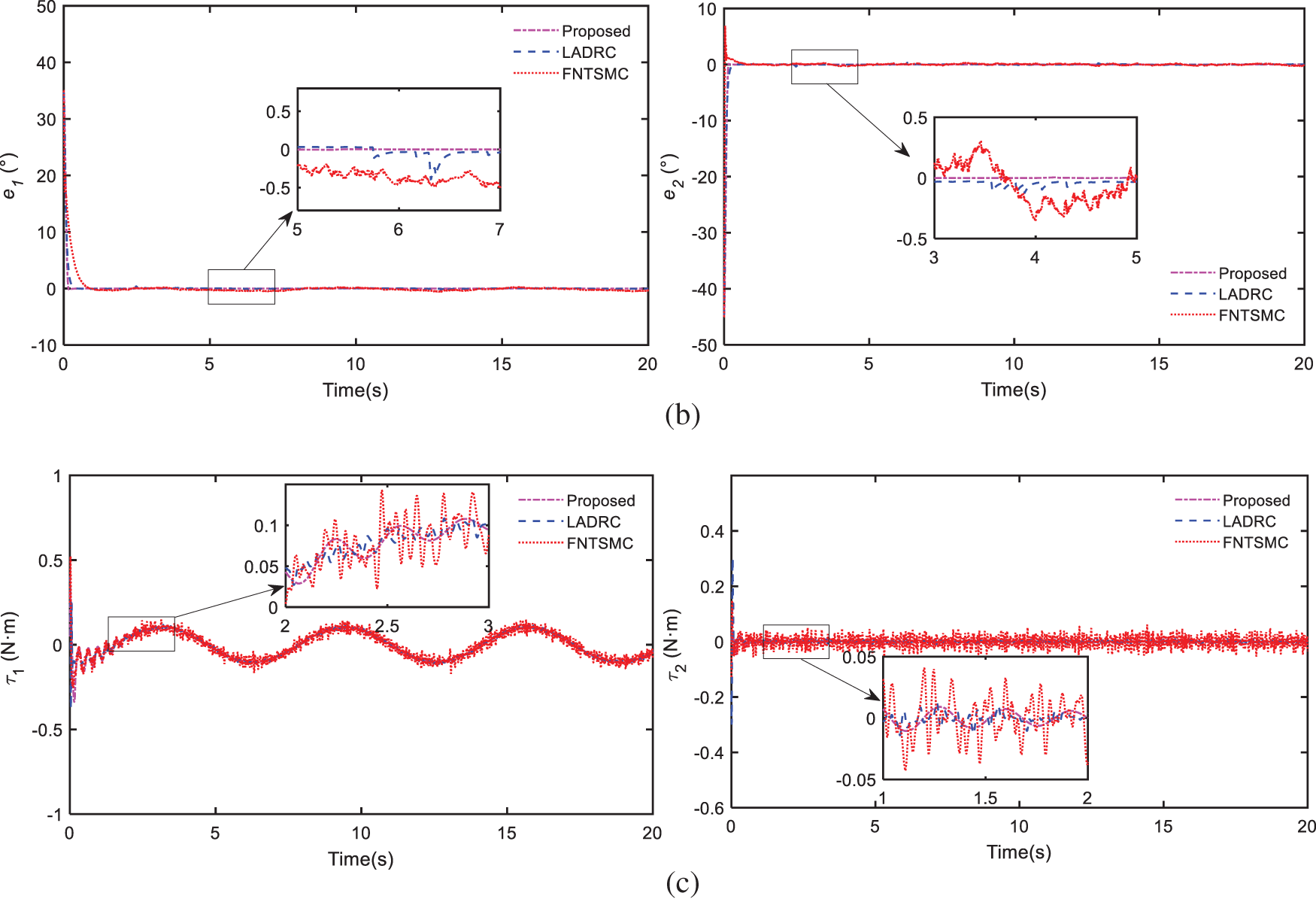
Figure 6: Compare results of simulation 1: (a) trajectory tracking of joints, (b) trajectory tracking errors, (c) control efforts

The Figs. 6a and 6b show the angular tracking of joints and the tracking errors among the three methods. As can be seen from the outcomes, all three methods can guarantee satisfied control performance under high nonlinearities and time-varying disturbances. Thanks to AST and FONTSM schemes, our proposed controller can achieve faster convergence speed and higher tracking accuracy than the other two. Fig. 6c shows the comparison of control efforts, it is obvious that the FNTSMC exists chattering phenomenon. With the LESO compensation, the designed controller can minimize chattering and ensure smooth control torques. What’s more, the designed controller is model-free and can be easily applied in the practical application by utilizing the LESO scheme.

2) Simulation 2: In the second simulation, the cable-driven manipulator is controlled to track a signal designed by Cycloidal [50]. Gaussian noise with an amplitude of 0.1 Nm is added and a 50 g payload is brought into the manipulator to test the robustness of our controller. The results are given in Fig. 7.

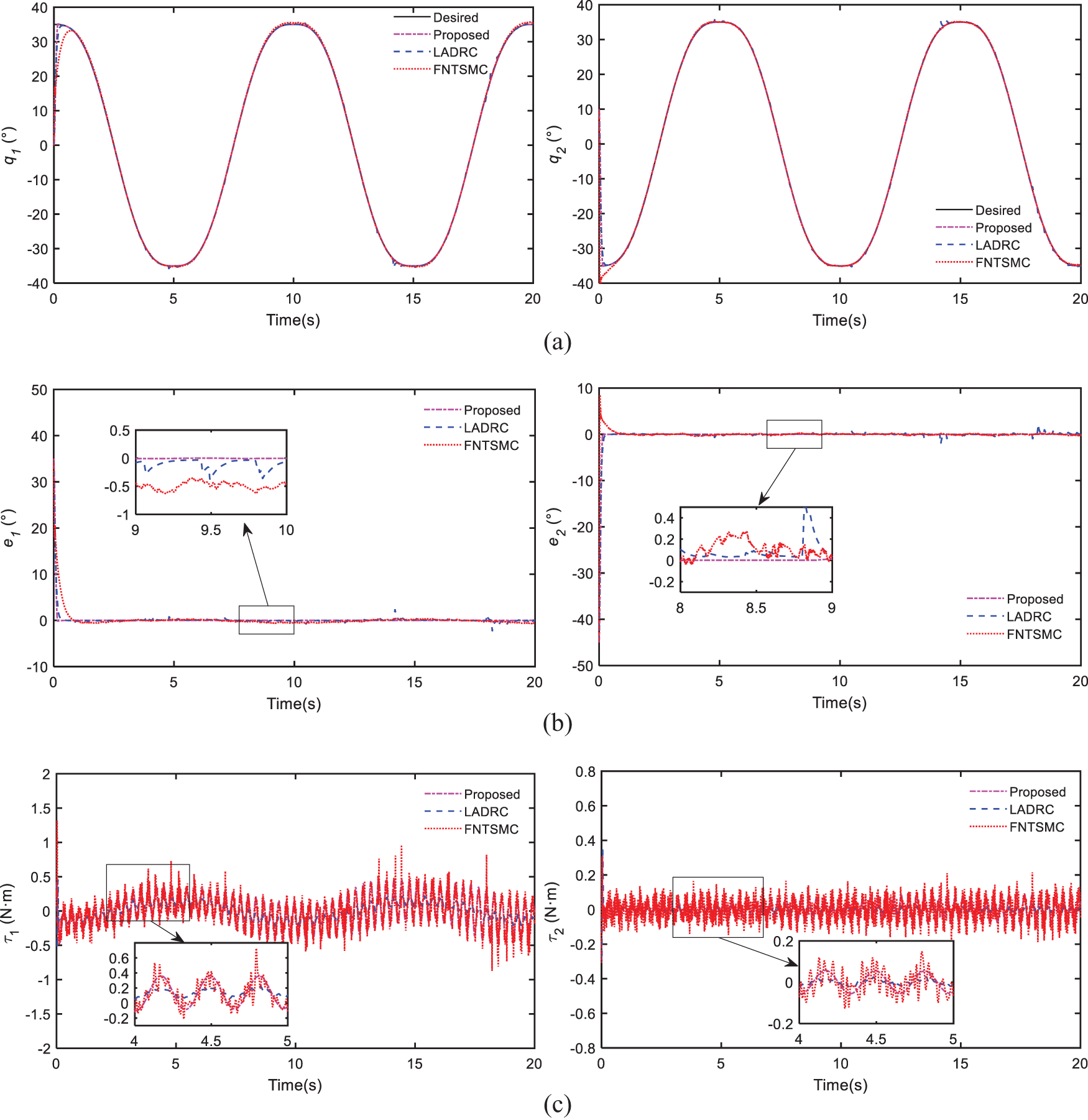
Figure 7: Compare results of simulation 2: (a) trajectory tracking of joints, (b) trajectory tracking errors, (c) control efforts

As shown in Fig. 7, all the controllers can track the desired signal under noise and 50 g payload. Nevertheless, the control performance of our scheme is still the best among the three controllers, which greatly verifies its robustness. Additionally, our controller can still achieve smooth controller efforts which is beneficial to motors.

Overall, the effectiveness and superiority of our method have clearly been proved through the above simulations. The proposed controller can converge quickly and track accurately due to AST and FONTSM schemes. Moreover, benefiting from LESO scheme, the control efforts of designed strategy are continued and nonsingular while without chattering.

6  Experimental Demonstrations

6.1 Setup

For further validating the control performance of our designed controller practically, we performed ground experiments with a platform as shown in Fig. 8. All drive motors and accompanying drivers are RoboMaster M2006 and RoboMaster C610, respectively. They are all placed in the base to minimize inertia during motion. The reduction ration, rated speed, and rated torque of the motor are 36:1, 500 rpm and 1 Nm, respectively. The encoder installed at the joint is AMT102-V, and its resolution is 0.044°. Similarly, the LADRC and FNTSMC are adopted to compare with our scheme, and they are all executed by x Pc system with a PCI6225e board. In the experiment, the reference trajectory of the two joints was set as a Cycloidal signal, and the sampling frequency was set to 1 kHz. The controller parameters are selected according to Table 1 and the experiment results are shown in Fig. 9.

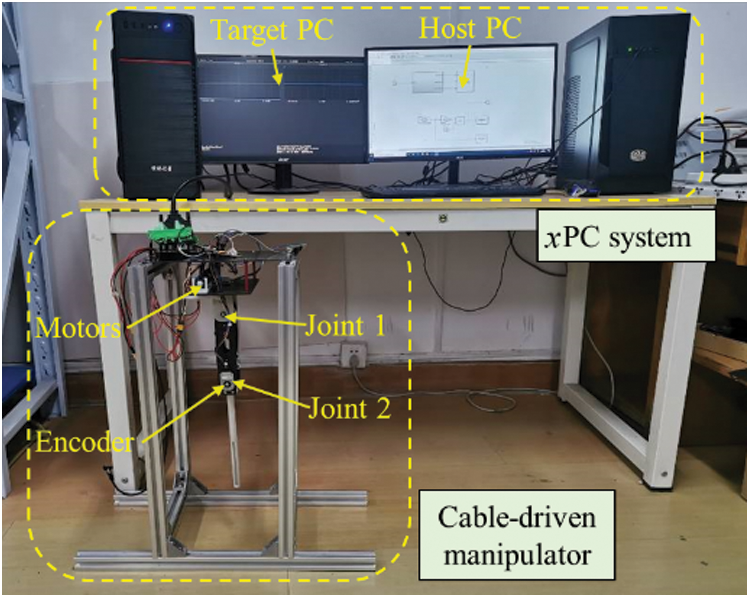
Figure 8: Ground test platform

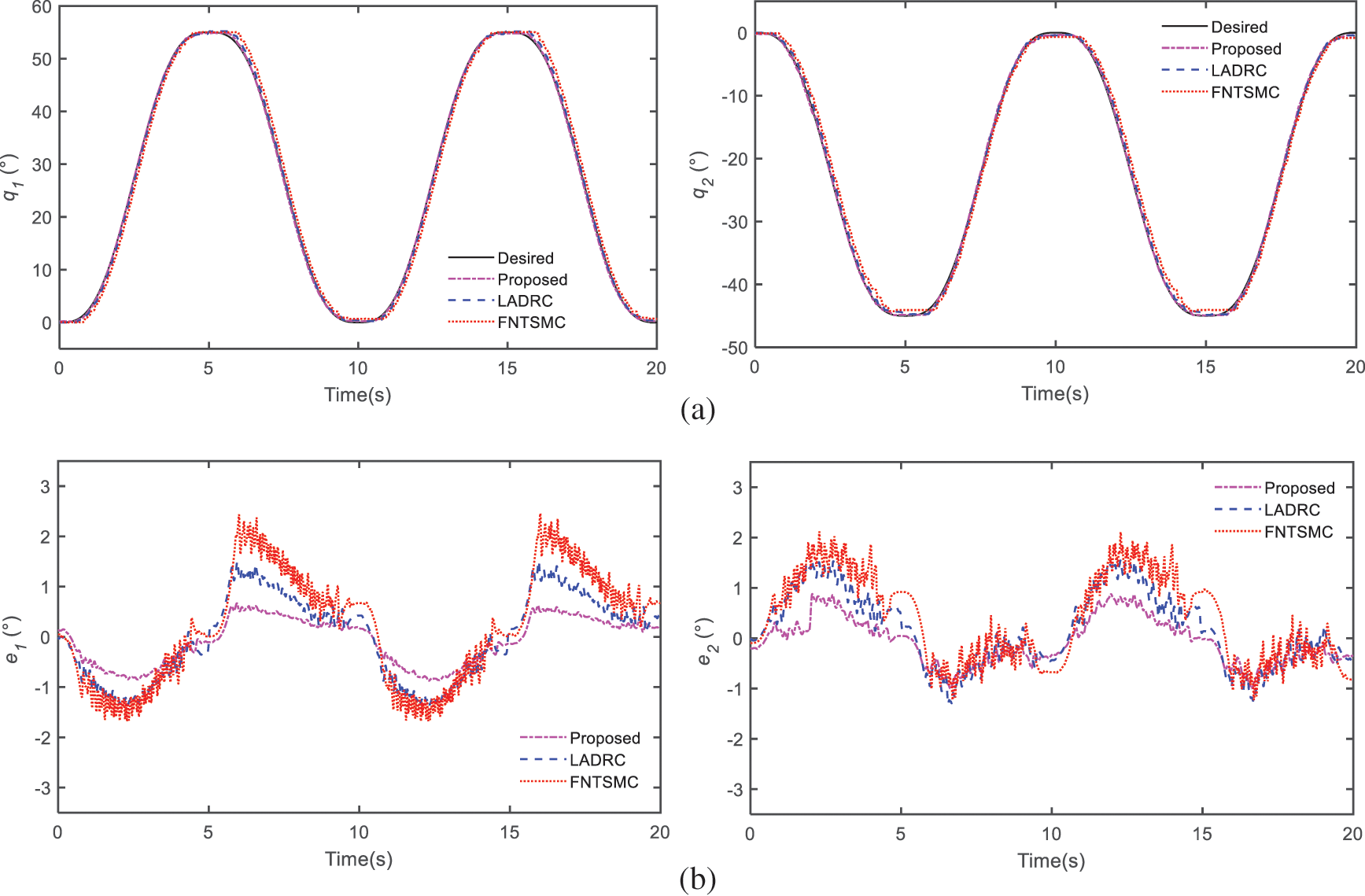
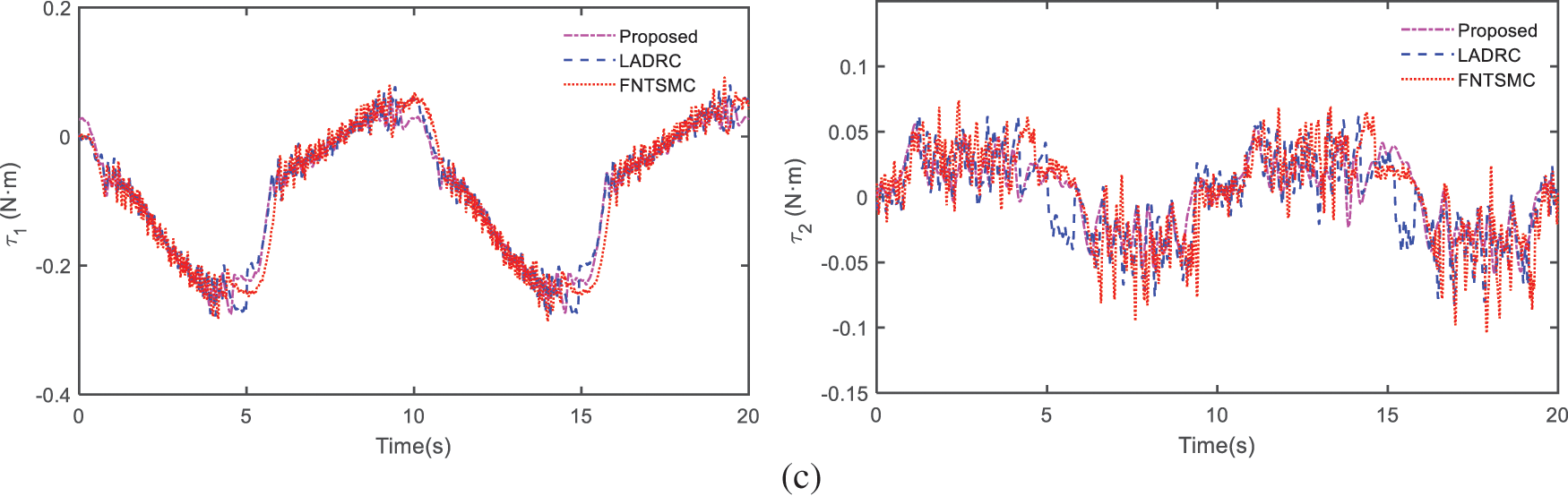
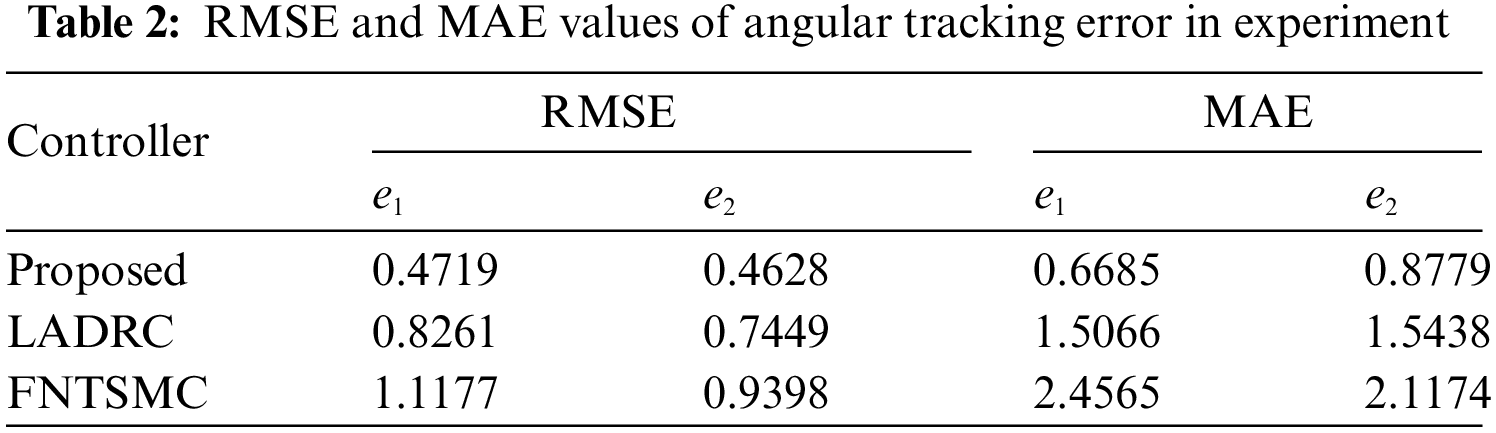
Figure 9: Compare results of experiment: (a) trajectory tracking of joints, (b) trajectory tracking errors, (c) control efforts

6.2 Results

As shown in Figs. 9a and 9b, q1 and q2 can still effectively track the desired signal with three controllers in experiment. Meanwhile, our control methodology can achieve the best tracking performance. Nevertheless, there is a large tracking error at the joint reversal, which may be caused by the loosening and tightening of the cable when the joint is reversed. Furtherly, the root-mean-square-error (RMSE) and the Maximum error (MAE) are adopted to quantify the trajectory tracking errors of the two joints, as shown in Table 2. To specific, the RMSE of joint 1 decreases 42.9% and 58.8% when compared to the LADRC and FNTSMC, while the MAE reduces 55.6% and 72.8%. The RMSE of joint 2 decreases 37.9% and 50.8% while the MAE reduces 43.1% and 58.6%.

Finally, Fig. 9c shows the control torque of the two joints. It is obvious that the torque of LADR and FNTSMC exist discontinuous control torque, which is mainly due to the existence of the flexibility of the cable. Nevertheless, LESO makes it possible to effectively estimate and compensate these disturbances, and the AST operator can also effectively suppress the chattering phenomenon. So, our proposed control manner offers smooth control effort with a significant elimination of the chattering phenomena.

Generally speaking, the experiment outcomes are highly match with the above visualization simulation, verifying the effectiveness and comprehensive control performance of the controller we proposed.

7  Conclusions

This article presents a novel robust controller for joint-space tracking control of a cable-driven aerial manipulator, which is used to realize remote sampling task at the drain mouth. Because of the adoption of the cable-driven scheme, all drive motors are installed at the manipulator base, which reduces energy consumption and dynamic coupling effect. Then, the proposed controller is developed from LESO and AST-FONTSMC. The AST-FONTSMC guarantees fast convergence and high accuracy while avoiding both singularity and chattering issues. What’s more, the utilization of LESO enhances the control performance of our designed strategy and makes it model-free. Next, the convergence and stability of our controller are proved through Lyapunov method. Lastly, the comparative simulations and experiments results between proposed controller and the other controllers, such as the LADRC and the FNTSMC, prove the superiority of the designed scheme in achieving comprehensive control performance under the lumped disturbances.

In future works, the complex coupling effect between quadrotor and cable-driven manipulator will be further investigated and a hybrid control strategy for the cable-driven aerial manipulator will be designed. Additionally, actual water sampling tests will also be performed outdoors for verifying the effectiveness of designed strategy.

Funding Statement: This work has been supported by the National Natural Science Foundation of China (52005231, 52175097) and Social Development Science and Technology Support Project of Changzhou (CE20215050).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Wang, Z. G., Yue, P. (2020). Marine island UAV aerial photography: A path-planning algorithm-based study. Journal of Coastal Research, 106(sp1), 642–645. DOI 10.2112/SI106-145.1. [Google Scholar] [CrossRef]

 2.  Liu, J. C., Xu, W., Guo, B. X., Zhou, G., Zhu, H. C. (2021). Accurate mapping method for UAV photogrammetry without ground control points in the map projection frame. IEEE Transactions on Geoscience and Remote Sensing, 59(11), 9673–9681. DOI 10.1109/TGRS.2021.3052466. [Google Scholar] [CrossRef]

 3.  Zhao, N., Lu, W., Sheng, M., Chen, Y. F., Tang, J. et al. (2019). UAV-assisted emergency networks in disasters. IEEE Wireless Communications, 26(1), 45–51. DOI 10.1109/MWC.2018.1800160. [Google Scholar] [CrossRef]

 4.  Emami, S. A., Banazadeh, A. (2021). Simultaneous trajectory tracking and aerial manipulation using a multi-stage model predictive control. Aerospace Science and Technology, 112(2), 106573. DOI 10.1016/j.ast.2021.106573. [Google Scholar] [CrossRef]

 5.  Ladig, R., Paul, H., Miyazaki, R., Shimonomura, K. (2021). Aerial manipulation using multirotor UAV: A review from the aspect of operating space and force. Journal of Robotics and Mechatronics, 33(2), 196–204. DOI 10.20965/jrm.2021.p0196. [Google Scholar] [CrossRef]

 6.  Mohiuddin, A., Tarek, T., Zweiri, Y., Gan, D. M. (2020). A survey of single and multi-UAV aerial manipulation. Unmanned Systems, 8(2), 119–147. DOI 10.1142/S2301385020500089. [Google Scholar] [CrossRef]

 7.  Ollero, A., Tognon, M., Suarez, A., Lee, D., Franchi, A. (2022). Past, present, and future of aerial robotic manipulators. IEEE Transactions on Robotics, 38(1), 626–645. DOI 10.1109/TRO.2021.3084395. [Google Scholar] [CrossRef]

 8.  Kutia, J. R., Stol, K. A., Xu, W. L. (2018). Aerial manipulator interactions with trees for canopy sampling. IEEE-ASME Transactions on Mechatronics, 23(4), 1740–1749. DOI 10.1109/TMECH.2018.2837005. [Google Scholar] [CrossRef]

 9.  Luo, B., Chen, H. Y., Quan, F. Y., Zhang, S. W., Liu, Y. H. (2020). Natural feature-based visual servoing for grasping target with an aerial manipulator. Journal of Bionic Engineering, 17(2), 215–228. DOI 10.1007/s42235-020-0017-4. [Google Scholar] [CrossRef]

10. Ali, Z. A., Li, X. D. (2020). Controlling of an under-actuated quadrotor UAV equipped with a manipulator. IEEE Access, 8, 34664–34674. DOI 10.1109/ACCESS.2020.2974581. [Google Scholar] [CrossRef]

11. Wang, Y. Y., Zhu, K. W., Yan, F., Chen, B. (2019). Adaptive super-twisting nonsingular fast terminal sliding mode control for cable-driven manipulators using time-delay estimation. Advances in Engineering Software, 128(2), 113–124. DOI 10.1016/j.advengsoft.2018.11.006. [Google Scholar] [CrossRef]

12. Wang, Y. Y., Zhang, R., Ju, F., Zhao, J. B., Chen, B. et al. (2020). A light cable-driven manipulator developed for aerial robots: Structure design and control research. International Journal of Advanced Robotic Systems, 17(3). DOI 10.1177/1729881420926425. [Google Scholar] [CrossRef]

13. Yi, S. L., Watanabe, K., Nagai, I. (2021). Anti-disturbance control of a quadrotor manipulator with tiltable rotors based on integral sliding mode control. Artificial Life and Robotics, 26(4), 513–522. DOI 10.1007/s10015-021-00700-3. [Google Scholar] [CrossRef]

14. Pierri, F., Muscio, G., Caccavale, F. (2018). An adaptive hierarchical control for aerial manipulators. Robotica, 36(10), 1527–1550. DOI 10.1017/S0263574718000553. [Google Scholar] [CrossRef]

15. Zhang, G. Y., He, Y. Q., Dai, B., Gu, F., Han, J. D. et al. (2020). Robust control of an aerial manipulator based on a variable inertia parameters model. IEEE Transactions on Industrial Electronics, 67(11), 9515–9525. DOI 10.1109/TIE.2019.2956414. [Google Scholar] [CrossRef]

16. Liang, J., Chen, Z. H., Yuan, X. H., Zhang, B. Q., Yuan, Y. B. (2020). Terminal sliding mode controllers for hydraulic turbine governing system with bifurcated penstocks under input saturation. Computer Modeling in Engineering & Sciences, 123(2), 603–629. DOI 10.32604/cmes.2020.09328. [Google Scholar] [CrossRef]

17. Truong, T. N., Vo, A. T., Kang, H. J. (2021). A backstepping global fast terminal sliding mode control for trajectory tracking control of industrial robotic manipulators. IEEE Access, 9, 31921–31931. DOI 10.1109/ACCESS.2021.3060115. [Google Scholar] [CrossRef]

18. Zhou, Z. C., Tang, G. Y., Xu, R. K., Han, L. J., Cheng, M. L. (2021). A novel continuous nonsingular finite-time control for underwater robot manipulators. Journal of Marine Science and Engineering, 9(3), 269. DOI 10.3390/jmse9030269. [Google Scholar] [CrossRef]

19. Wang, Y. Y., Chen, J. W., Yan, F., Zhu, K. W., Chen, B. (2019). Adaptive super-twisting fractional-order nonsingular terminal sliding mode control of cable-driven manipulators. ISA Transactions, 86(2), 163–180. DOI 10.1016/j.isatra.2018.11.009. [Google Scholar] [CrossRef]

20. Li, X. L., Sun, G. H., Han, S., Shao, X. Y. (2021). Fractional-order nonsingular terminal sliding mode tension control for the deployment of space tethered satellite. IEEE Transactions on Aerospace and Electronic Systems, 57(5), 2759–2770. DOI 10.1109/TAES.2021.3061815. [Google Scholar] [CrossRef]

21. Zhou, X. L., Li, X. F. (2021). Trajectory tracking control for electro-optical tracking system using ESO based fractional-order sliding mode control. IEEE Access, 9, 45891–45902. DOI 10.1109/ACCESS.2021.3067680. [Google Scholar] [CrossRef]

22. Gandikota, G., Das, D. K. (2019). Disturbance observer-based adaptive boundary layer sliding mode controller for a type of nonlinear multiple-input multiple-output system. International Journal of Robust and Nonlinear Control, 29(17), 5886–5912. DOI 10.1002/rnc.4701. [Google Scholar] [CrossRef]

23. Giap, V. N., Huang, S. C. (2020). Effectiveness of fuzzy sliding mode control boundary layer based on uncertainty and disturbance compensator on suspension active magnetic bearing system. Measurement & Control, 53(5–6), 934–942. DOI 10.1177/0020294020905044. [Google Scholar] [CrossRef]

24. Tan, L. W., Gao, J., Luo, Y. H., Zhang, L. Y. (2021). Super-twisting sliding mode control with defined boundary layer for chattering reduction of permanent magnet linear synchronous motor. Journal of Mechanical Science and Technology, 35(5), 1829–1840. DOI 10.1007/s12206-021-0403-9. [Google Scholar] [CrossRef]

25. Bastola, S., Zargarzadeh, H. (2019). Super twisting sliding mode control of spherical robot. 22nd IEEE International Symposium on Measurement and Control in Robotics (ISMCR)-Robotics for the Benefit of Humanity, University of Houston, Clear Lake, TX. [Google Scholar]

26. Fei, J. T., Feng, Z. L. (2019). Adaptive super-twisting sliding mode control for micro gyroscope using fuzzy sliding gain. 12th Asian Control Conference (ASCC), pp. 1425–1430. IEEE, Kitakyushu, Japan. [Google Scholar]

27. Lee, S. D., Phuc, B. D. H., Xu, X., You, S. S. (2020). Roll suppression of marine vessels using adaptive super-twisting sliding mode control synthesis. Ocean Engineering, 195(9), DOI 10.1016/j.oceaneng.2019.106724. [Google Scholar] [CrossRef]

28. Gao, P., Zhang, G. M., Lv, X. D. (2021). Model-free control using improved smoothing extended state observer and super-twisting nonlinear sliding mode control for PMSM drives. Energies, 14(4), 922. DOI 10.3390/en14040922. [Google Scholar] [CrossRef]

29. Saleki, A., Fateh, M. M. (2018). Model free control of electrically driven manipulator by optimized linear extended state observer, based on voltage control strategy. 6th RSI International Conference on Robotics and Mechatronics (IcRoM), pp. 548–553. Tehran, Iran. [Google Scholar]

30. Song, T. Z., Fang, L. J., Wang, H. Z. (2022). Model-free finite-time terminal sliding mode control with a novel adaptive sliding mode observer of uncertain robot systems. Asian Journal of Control, 15(3), 1437–1451. DOI 10.1002/asjc.2542. [Google Scholar] [CrossRef]

31. Liang, X. H., Li, J. T., Zhao, F. (2019). Attitude control of quadrotor UAV based on LADRC method. 31st Chinese Control and Decision Conference (CCDC), pp. 1924–1929. IEEE, Nanchang, China. [Google Scholar]

32. Fu, H. X., Xin, L., Wang, B. Y., Wang, Y. C. (2019). Trajectory tracking use linear active disturbance control of the omnidirectional mobile robot. 16th IEEE International Conference on Mechatronics and Automation (IEEE ICMA), pp. 1478–1483. IEEE, Tianjin, China. [Google Scholar]

33. Wang, H. D., Li, X. G., Liu, X., Karkoub, M., Zhou, L. Q. (2020). Fuzzy sliding mode active disturbance rejection control of an autonomous underwater vehicle-manipulator system. Journal of Ocean University of China, 19(5), 1081–1093. DOI 10.1007/s11802-020-4250-6. [Google Scholar] [CrossRef]

34. Ye, X., Hong, J. C., Dong, Z. H. (2019). Research on angle and stiffness cooperative tracking control of VSJ of space manipulator based on LESO and NSFAR control. Electronics, 8(8), 893. DOI 10.3390/electronics8080893. [Google Scholar] [CrossRef]

35. Zhang, J. Q., Gu, D. W., Deng, C., Wen, B. C. (2019). Robust and adaptive backstepping control for hexacopter UAVs. IEEE Access, 7, 163502–163514. DOI 10.1109/ACCESS.2019.2951282. [Google Scholar] [CrossRef]

36. Zhou, X. S., Cui, Y. Y., Ma, Y. J. (2021). Fuzzy linear active disturbance rejection control of injection hybrid active power filter for medium and high voltage distribution network. IEEE Access, 9, 8421–8432. DOI 10.1109/ACCESS.2021.3049832. [Google Scholar] [CrossRef]

37. Gao, P., Zhang, G. M., Lv, X. D. (2020). Model-free hybrid control with intelligent proportional integral and super-twisting sliding mode control of PMSM drives. Electronics, 9(9), 1427. DOI 10.3390/electronics9091427. [Google Scholar] [CrossRef]

38. Yang, B., He, Y., Han, J., Liu, G. (2015). Survey on aerial manipulator systems. Jiqiren/Robot, 37(5), 628–640. [Google Scholar]

39. Jin, M., Lee, J., Tsagarakis, N. G. (2017). Model-free robust adaptive control of humanoid robots with flexible joints. IEEE Transactions on Industrial Electronics, 64(2), 1706–1715. DOI 10.1109/TIE.2016.2588461. [Google Scholar] [CrossRef]

40. Ding, L., He, Q., Wang, C. J., Qi, R. Z. (2021). Disturbance rejection attitude control for a quadrotor: Theory and experiment. International Journal of Aerospace Engineering, 2021(2), 8850071. DOI 10.1155/2021/8850071. [Google Scholar] [CrossRef]

41. Coronel-Escamilla, A., Gomez-Aguilar, J. F., Torres, L., Escobar-Jimenez, R. F. (2018). A numerical solution for a variable-order reaction-diffusion model by using fractional derivatives with non-local and non-singular kernel. Physica A: Statistical Mechanics and its Applications, 491(1–2), 406–424. DOI 10.1016/j.physa.2017.09.014. [Google Scholar] [CrossRef]

42. Wang, Y. Y., Li, B. B., Yan, F., Chen, B. (2019). Practical adaptive fractional-order nonsingular terminal sliding mode control for a cable-driven manipulator. International Journal of Robust and Nonlinear Control, 29(5), 1396–1417. DOI 10.1002/rnc.4441. [Google Scholar] [CrossRef]

43. Wang, Y. Y., Gu, L. Y., Xu, Y. H., Cao, X. X. (2016). Practical tracking control of robot manipulators with continuous fractional-order nonsingular terminal sliding mode. IEEE Transactions on Industrial Electronics, 63(10), 6194–6204. DOI 10.1109/TIE.2016.2569454. [Google Scholar] [CrossRef]

44. Yoo, D. C., Yau, S. S. T., Gao, Z. Q. (2006). On convergence of the linear extended state observer. IEEE International Symposium on Intelligent Control, pp. 328–334. Munich, Germany. [Google Scholar]

45. Moreno, J. A., Osorio, M. (2012). Strict lyapunov functions for the super-twisting algorithm. IEEE Transactions on Automatic Control, 57(4), 1035–1040. DOI 10.1109/TAC.2012.2186179. [Google Scholar] [CrossRef]

46. Poznyak, A. (2008). Theorem 20.2. In: Advanced mathematical tools for automatic control engineers, vol. 2, UK: Elsevier. [Google Scholar]

47. Salgado, I., Camacho, O., Yanez, C., Chairez, I. (2014). Proportional derivative fuzzy control supplied with second order sliding mode differentiation. Engineering Applications of Artificial Intelligence, 35(69), 84–94. DOI 10.1016/j.engappai.2014.06.005. [Google Scholar] [CrossRef]

48. Huang, J. Z., Cen, Y. W. (2020). Research on variable mass control of series manipulator based on linear active disturbance rejection control. Measurement & Control, 53(7–8), 1194–1202. DOI 10.1177/0020294020922260. [Google Scholar] [CrossRef]

49. Lin, J. F., Tian, X. H., Wang, Z. C., Liu, H. T. (2020). Nonsingular fast terminal sliding mode trajectory tracking control of surface vessel with disturbances. Chinese Automation Congress (CAC), pp. 2091–2096. IEEE, Shanghai, China. [Google Scholar]

50. Qiu, Z. C., Zhang, W. Z. (2019). Trajectory planning and diagonal recurrent neural network vibration control of a flexible manipulator using structural light sensor. Mechanical Systems and Signal Processing, 132(1), 563–594. DOI 10.1016/j.ymssp.2019.07.014. [Google Scholar] [CrossRef]