Open Access

ARTICLE

Explicit Topology Optimization Design of Stiffened Plate Structures Based on the Moving Morphable Component (MMC) Method

Xudong Jiang¹, Chang Liu^1,2,*, Shaohui Zhang³, Weisheng Zhang^1,2, Zongliang Du^1,2, Xiaoyu Zhang³, Huizhong Zeng³, Xu Guo^1,2,*

1 Department of Engineering Mechanics, State Key Laboratory of Structural Analysis for Industrial Equipment, International Research Center for Computational Mechanics, Dalian University of Technology, Dalian, 116023, China
2 Ningbo Institute of Dalian University of Technology, Ningbo, 315016, China
3 Beijing Institute of Spacecraft System Engineering, Beijing, 100094, China

* Corresponding Authors: Chang Liu. Email: ; Xu Guo. Email:

(This article belongs to the Special Issue: New Trends in Structural Optimization)

Computer Modeling in Engineering & Sciences 2023, 135(2), 809-838. https://doi.org/10.32604/cmes.2023.023561

Received 02 May 2022; Accepted 21 July 2022; Issue published 27 October 2022

Abstract

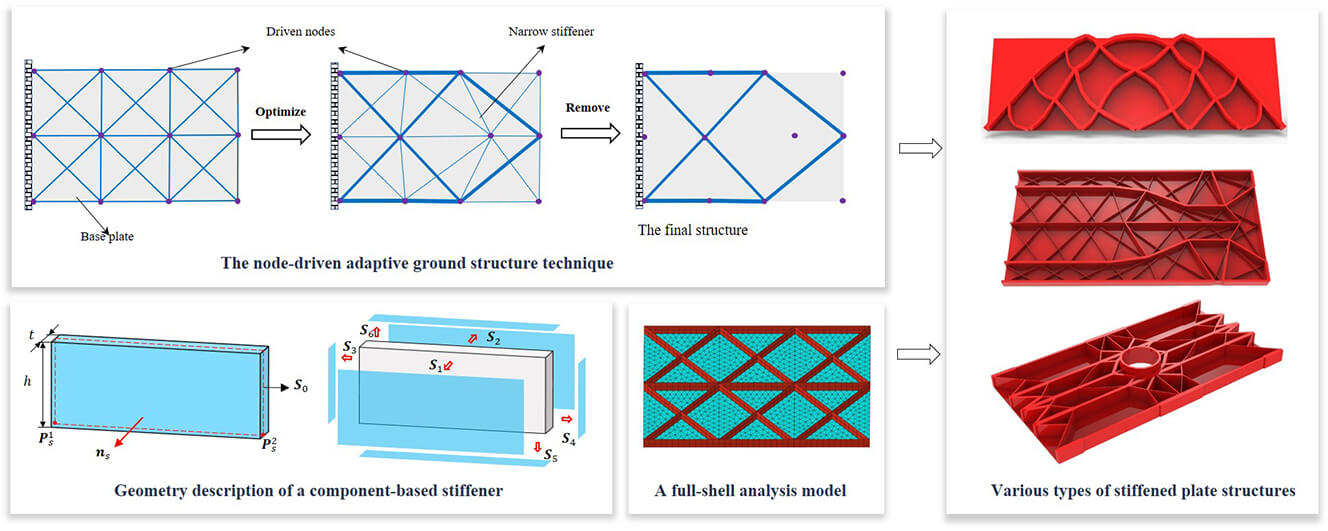
This paper proposes an explicit method for topology optimization of stiffened plate structures. The present work is devoted to simultaneously optimizing stiffeners’ shape, size and layout by seeking the optimal geometry parameters of a series of moving morphable components (MMC). The stiffeners with straight skeletons and the stiffeners with curved skeletons are considered to enhance the modeling and optimization capability of the current approach. All the stiffeners are represented under the Lagrangian-description framework in a fully explicit way, and the adaptive ground structure method, as well as dynamically updated plate/shell elements, is used to obtain optimized designs with more accurate analysis results. Compared with existing works, the proposed approach provides an explicit description of the structure. Thus, a stiffened plate structure with clear stiffener distribution and smooth geometric boundary can be obtained. Several numerical examples provided, including straight and curved stiffeners, hierarchical stiffeners, and a stiffened plate with a cutout, validate the effectiveness and applicability of the proposed approach.

---

Graphic Abstract

---

Keywords

---