Topological Aspects of Dendrimers via Connection-Based Descriptors

1  Introduction

Nanobiotechnology is a swiftly growing field of technological and analytical opportunity that applies the mechanism of nanofabrication to fabricate devices for exploring biosystems. One of the main elements of this field is a dendrimer. Dendrimers are prolonged artificially synthesized or amalgamated natural macromolecules with a sequential layer of branches enclosing a central core. Dendrimers are considered to be a primary element of nanobiotechnology. The cores, end groups and branches are the main three parts of dendrimers. Nowadays, dendrimers are getting much more consideration from the researchers due to their exceptional attributes and a large span of utilization in various areas of bioscience, involving immunology, drug delivery and the development of vaccines and antivirals, for more details see [1–3].

At present, in computational and mathematical chemistry, researchers and scientists are taking heed to characterize the molecular structures by utilizing different topological perspectives incorporating graph invariants. These topological descriptors are broadly utilized in the study of quantitative structure-activity relationships (QSAR) and quantitative structure-property relationships (QSPR) [4]. Graph invariants are essential to achieve the mathematical characterization of molecular structures successfully. The field of network theory (NT) has played an indispensable role in distinct areas of life. During the last decade, NT has found a remarkable use in the field of nanobiotechnology. Topological indices (TIs), the numerical parameters which link a number with a molecular network, are widely used in chemical network theory and mathematical chemistry to characterize the topology of a molecular network. TIs can predict many psychochemical properties of molecular structures in theocratical chemistry. TIs enable researchers to find the chemical reactivity, physical attributes and biological actions of molecular compounds. A molecular network in terms of a graph is a portrayal of structural information of a chemical compound in which the atoms are displayed by vertices while the bonds are represented by edges between the vertices. The applications of TIs in various fields of science are boundless, as one can see in [5–7]. According to the reported literature, TIs have great importance in nanotechnology and theoretical chemistry. Some important categories of TIs are degree-based, distance-based and connection-based TIs. In 1972, Wiener [8] introduced the concept of a distance-based TI, which is known as the Wiener index. By theoretical and conceptual framework, the Wiener index was the most studied TI. Moreover, in 2019, Gao et al. [9] utilized distance-based indices to study the topological aspects of dendrimers.

The idea of the first ZI (FZI) was invented by Gutman et al. [10]. The second and third ZIs were discovered by Gutman et al. [11] and Furtula et al. [12]. All of these degree-based TIs have a variety of applications in the field of cheminformatics which is a combination of three major fields, namely, chemistry, mathematics and information technology [13–15]. These TIs have been utilized to distinct wide-ranging physicochemical applications, especially to characterize the different chemical structures such as dendrimers nanostars, for details see [16–18]. Among these defined TIs, the connection-based TIs have much importance because of their utilizations in characterizing the molecular chemical compounds and their ability to predict various physical and chemical properties in a comprehensive and logical way. A number of those vertices at a distance of two from a vertex v is called CN of a vertex v. According to researchers, connection-based TIs as compared to the other classical TIs provide a better absolute value of the correlation coefficient. Ali et al. [19] initiated Zagreb connection indices (ZCIs) and used octane isomers to examine their applicability. For a detailed review of some connection-based TIs, the readers are referred to [20–22]. Haoer et al. [23] computed multiplicative ZIs of some T-thorny graphs. Moreover, Javaid et al. [24] found the topological aspects of distinct wheel graphs. Further, Liu et al. [25] found the topological properties of neural networks. Recently, Sattar et al. [26–28] worked on computing the general expression of ZIs for two types of dendrimers. For the other terminologies not discussed in this paper, the readers are referred to [29–31]. The motivation for this article is as follows:

1.    TIs, the numerical descriptors, are efficient enough to characterize the topology of molecular structures and assist in correlating their distinct psychochemical properties.

2.    Dendrimers are symmetric, versatile and well defined chemical polymers forming a tree like structure. These nanoparticles are signalized by a numerous attributes which make them advantageous for wide ranging utilizations in various fields of science.

3.    The connection-based ZIs have better applicability to predict the various psychochemical properties of distinct molecular structures in chemistry rather than the other classical ZIs present in the literature.

In this paper, first, we define the third Zagreb connection index. Further, we calculate ZCIs of two special types of dendrimer nanostars, namely, PPEtIm dendrimer and PPIO dendrimer. Moreover, we compare the results of both types of dendrimers.

This research article is structured as: in Section 1, we stated preliminaries which help the readers to understand the idea of this article. In Section 2, we computed ZCIs for PPEtIm dendrimer. In Section 3, we calculated ZCIs for the other type of dendrimer, namely, PPIO dendrimer in a comprehensive way. In Section 4, we compared the computed values of both types of dendrimers with each other. Section 5 holds the conclusions. The acronyms used in this paper are given in Table 1.

2  Preliminaries

This section gives some primary definitions which are helpful for the good understanding of this manuscript.

Definition 2.1. In [10] let ξ=(P(ξ),Q(ξ)) be a network, where P(ξ) be the vertex set and Q(ξ) be the edge set. Then, the FZI can be defined as

Z^1(ξ)=∑m∈P(ξ)(d˘ξ(m))2.

which can also be rewritten in the given form

Z^1(ξ)=∑mn∈Q(ξ)(d˘ξ(m)+d˘ξ(n)),

where d˘ξ(m) and d˘ξ(n) represent the degree of the vertex m and n, respectively.

Definition 2.2. In [11] for network ξ, the SZI can be defined as

Z^2(ξ)=∑mn∈Q(ξ)(d˘ξ(m)×d˘ξ(n)),

where d˘ξ(m) and d˘ξ(n) represent the degree of the vertex m and n, respectively.

Definition 2.3. In [12] for network ξ, the TZI can be given as

Z^3(ξ)=∑mn∈Q(ξ)(d˘ξ2(m)+d˘ξ2(n)).

Third Zagreb index is also called forgotten index.

Definition 2.4. In [19] for a network ξ, the FZCIs and SZCI can be defined as

1. Z^C1(ξ)=∑m∈P(ξ)⁡(ωξ~(m))2,

2. Z^C2(ξ)=∑mn∈Q(ξ)⁡(ωξ~(m)×ωξ~(n)),

where ωξ~(m) and ωξ~(n) indicate the CN of the vertex m and n, respectively.

Definition 2.5. In [19] for a network ξ, the modified FZCI can be defined as

Z^C1∗(ξ)=∑mn∈Q(ξ)(ωξ~(m)+ωξ~(n)).

Definition 2.6. In [20] for a network ξ, the modified SZCI and modified TZCI can be given as

1.    Z^C2∗(ξ)=∑mn∈Q(ξ)⁡[d⌣ξ(m)ωξ~(n)+d⌣ξ(n)ωξ~(m)],

2.    Z^C3∗(ξ)=∑mn∈Q(ξ)⁡[d⌣ξ(m)ωξ~(m)+d⌣ξ(n)ωξ~(n)].

Now, we rewrite the above defined ZCIs. Let A be the set of all CNs and B be the set of all degrees of the vertices in ξ. Then the above defines ZCIs can be written as

Definition 2.7. For a network ξ, the FZCI can be rewritten as

Z^1C(ξ)=∑ϕ∈A|Aϕ(ξ)|[ϕ2],(1)

where |Aϕ(ξ)| is the cardinality of those vertices of ξ which have CN ϕ.

The SZCI rewritten as

Z^2C(ξ)=∑ϕ,ψ∈A|A(ϕ,ψ)(ξ)|[ϕ×ψ],(2)

Similarly, the modified FZCI can be rewritten as

Z^C1∗(ξ)=∑ϕ,ψ∈A|A(ϕ,ψ)(ξ)|[ϕ+ψ].(3)

where |A(ϕ,ψ)(ξ)| is the cardinality of those vertices of ξ which have CNs (ϕ,ψ).

Similarly, for the modified SZCI, we have

Z^C2∗(ξ)=∑ϕ,ψ∈A,μ,ν∈B|A(μ,ν)(ϕ,ψ)(ξ)|[μψ+νϕ].(4)

The modified TZCI can be rewritten as

Z^C3∗(ξ)=∑ϕ,ψ∈A,μ,ν∈B|A(μ,ν)(ϕ,ψ)(ξ)|[μϕ+νψ].(5)

where |A(μ,ν)(ϕ,ψ)(ξ)| is the cardinality of those edges in ξ which have degrees (μ,ν) and CNs (ϕ,ψ).

3  ZCIs of Poly (propyl) Ether Imine Dendrimer

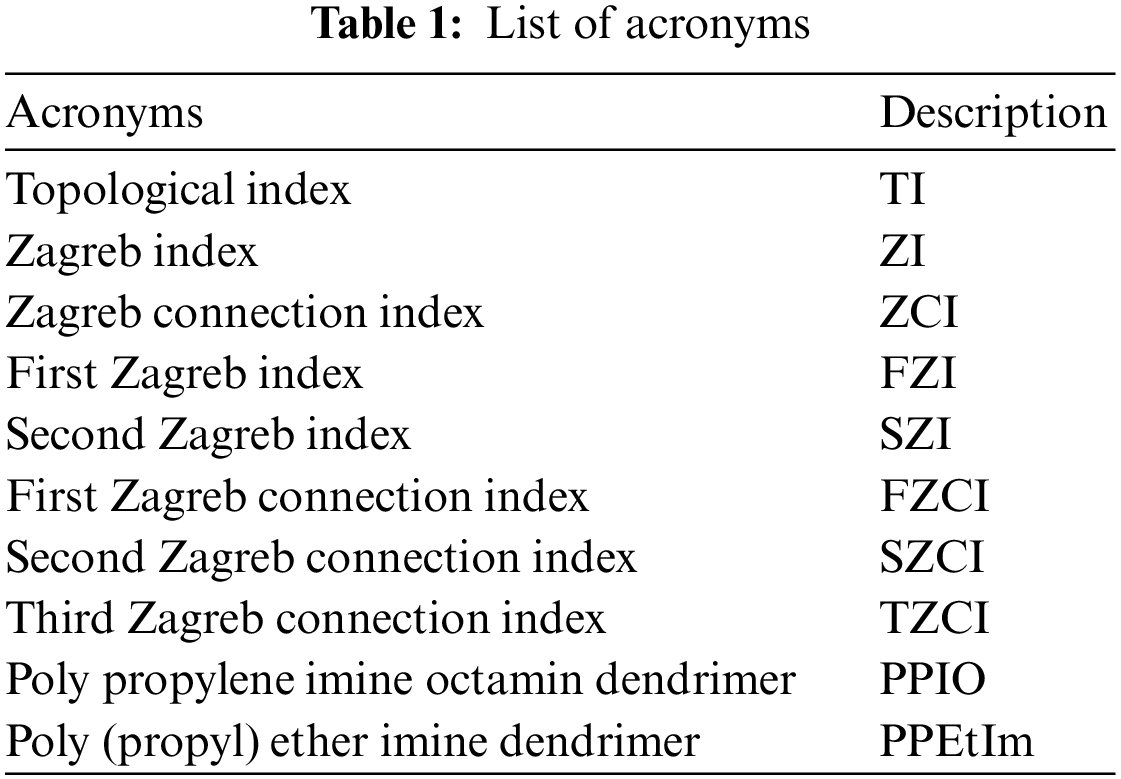
In this section, we calculate the ZCIs, namely, FZCI, SZCI, TZCI, modified FZCI, modified SZCI and modified TZCI, of PPEtIm dendrimer. PPEtIm dendrimer is a special type of dendrimer constructed by including an ether component as the linker and an imine component as the branching unit. It grows three-dimensionally in which the core is the oxygen element and tertiary nitrogen atoms are at the branches which are separated by eight bonds for each growth of dendrimer. Let ξ be a molecular network of PPEtIm dendrimer of generation Gs, where s≥1 is the growth of the dendrimer. The construction of PPEtIm dendrimer up to five generations can be depicted in Fig. 1. From Fig. 1, it can be seen that the structure of PPEtIm dendrimer is comprised of one central core having eight edges and four branches. First, we state the third Zagreb connection index in the following.

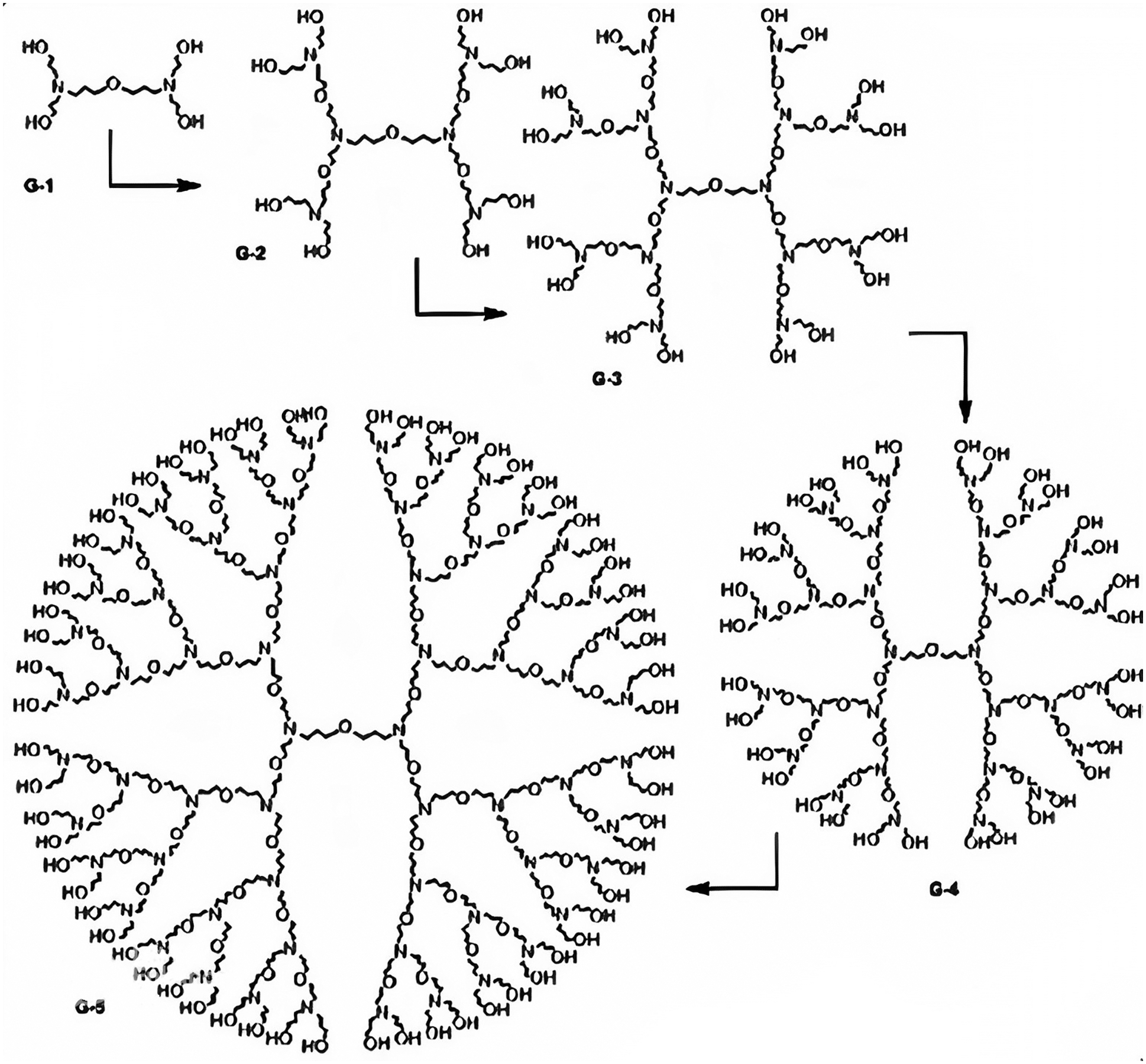
Figure 1: Chemical structural formula of PPEtIm dendrimer

Definition 3.1. Let ξ=(P(ξ),Q(ξ)) be a network, where P(ξ) be the vertex set and Q(ξ) be the edge set. Then, the third Zagreb connection index (TZCI) can be defined as

Z^C3(ξ)=∑mn∈Q(ξ)(ωξ2(m)+ωξ2(n)),

where ωξ2(m) and ωξ2(n) indicate the square of the connection number (CN) of the vertex m and n, respectively.

This can also be rewritten as

Z^C3(ξ)=∑ϕ,ψ∈A|A(ϕ,ψ)(ξ)|[ϕ2+ψ2],(6)

where |A(ϕ,ψ)(ξ)| is the cardinality of those edges of ξ which have CNs (ϕ,ψ).

Theorem 1. Let ξ be a molecular network of PPEtIm dendrimer. Then FZCI, SZCI and TZCI are given in the following:

1.    Z^C1(ξ)=124×2s−132,

2.    Z^C2(ξ)=128×2s−138,

3.    Z^C3(ξ)=264×2s−282.

Proof.

1. Firstly, we find the cardinality of vertices and edges of ξ. The total number of edges in ξ must be equal to the four times the edges in a each branch plus the number of edges in central core. One can see that central core has eight edges. Therefore,

Number of edges in each branch=(8+(2×8)+(22×8)+⋯+(2s−2×8)+(2s−1×4)),=6×2s−8.Number of edges in all branches=4×(6×2s−8),=24×2s−32.

Number of edges in ζ=8+(24×2s−32),=24×2s−24.

As ζ is a tree, so the number of vertices must be equals to 24×2s−23.

Next, we find cardinality of those vertices which have CN 1, 2 and 3 in ξ. Now, we make the partition of the number of vertices on the basis of CNs. From Fig. 2, we can see that there are three partitions of vertices given below.

A1={m∈P:ωξ~(m)=1},A2={m∈P:ωξ~(m)=2},A3={m∈P:ωξ~(m)=3}.

Figure 2: Structural formula of PPEtIm dendrimer for s=5 along with CNs

Thus, number of vertices with connection numbers 1, 2 and 3 are given as;

|A1|=4(2×2s−1),=4×2s.|A2|=4[5+(2×5)+(22×5)+(23×5)+⋯+(2s−1×1)]+5,=12×2s−15.|A3|=(24×2s−23)−(12×2s−15)−4×2s,=8×2s−8.

Now, after placing the values of |Aϕ(ξ)| in Eq. (1), we have

Z^C1(ξ)=∑ϕ∈A⁡|Aϕ(ξ)|[ϕ2]=|A1(ξ)|[12]+|A2(ξ)|[22]+|A3(ξ)|[32],=(4×2s)[1]+(12×2s−15)[22]+(8×2s−8)[32],=124×2s−132.

2. Now, we classify the edge set of ξ. From Fig. 2, we can see that there are five classes of edge set as given below

A(1,1)={e=mn∈Q:ωξ~(m)=1,ωξ~(n)=1},A(1,2)={e=mn∈Q:ωξ~(m)=1,ωξ~(n)=2},A(2,2)={e=mn∈Q:ωξ~(m)=2,ωξ~(n)=2},A(2,3)={e=mn∈Q:ωξ~(m)=2,ωξ~(n)=3},A(3,3)={e=mn∈Q:ωξ~(m)=3,ωξ~(n)=3}.

Now,

|A(1,1)|=4×2s−1=2×2s.|A(1,2)|=4×2s−1=2×2s.|A(2,2)|=4(4+(2×4)+(22×4)+(23×4)+⋯+2s−2×4)+4,=4(1+2+22+23+⋯+2s−2),=8×2s−12.|A(2,3)|=4(2+(2×2)+(22×2)+(23×2)+⋯+2s−2×2)+(2s−1×1))+2,=4×2(1+2+22+23+⋯+2s−2)+2s−1+2,=6×2s−6.|A(3,3)|=6×2s−6.

Here, we have used the following formula to find the sum of the series [32].

S=a(1−rs)1−r,

where a is the first term and r is the common difference between two terms of the series. By placing the above calculated values in Eq. (2), we have

Z^C2(ξ)=∑ϕ,ψ∈A⁡|A(ϕ,ψ)(ξ)|[ϕ×ψ],=|A(1,1)(ξ)|[1×1]+|A(1,2)(ξ)|[1×2]+|A(2,2)(ξ)|[2×2]+|A(2,3)(ξ)|[2×3]+|A(3,3)(ξ)|[3×3],=(2×2s)[1]+(2×2s)[2]+(8×2s−12)[4]+(6×2s−6)[6]+(6×2s−6)[9],=128×2s−138.

3. By placing the values of |A(ϕ,ψ)(ξ)| in the above Eq. (1), we have

Z^C3(ξ)=∑ϕ,ψ∈A⁡|A(ϕ,ψ)(ξ)|[ϕ2+ψ2],=|A(1,1)(ξ)|[12+12]+|A(1,2)(ξ)|[12+22]+|A(2,2)(ξ)|[22+22]+|A(2,3)(ξ)|[22+32]+|A(3,3)(ξ)|[32+32],=(2×2s)[2]+(2×2s)[5]+8(×2s−12)[8]+(6×2s−6)[13]+(6×2s−6)[18],=264×2s−282.

This proves the theorem.

Theorem 2. Let ξ be a molecular network of PPEtIm dendrimer. Then modified FZCI, modified SZCI and modified TZCI are given in the following

(1) Z^C1∗(ξ)=108×2s−114,

(2) Z^C2∗(ξ)=232×2s−246,

(3) Z^C3∗(ξ)=232×2s−246.

Proof.

1. For the proof, the readers are referred to see [33].

2. Now, we classify the edges on the basis of their degrees of incident vertices. It can be seen that |A(1,2)(ξ)|=2×2s,|A(2,2)(ξ)|=16×2s−18 and |A(2,3)(ξ)|=6×2s−6. In order to compute the modified SZCI and modified TZCI, we split the partitioned number of edges on degree basis with respect to the number of edges on connection bases.

Row 1 of Table 2 shows that there are total 2×2s number of edges mn∈ξ in which the vertex m with degree 1 and CN 1 is adjacent to the vertex n with degree 2 and CN 1, i.e., |A(1,2)(1,1)(ξ)|=2×2s. Similarly, the row 2 shows that there are total 2×2s number of edges mn in which the vertex m with degree 2 and CN 1 is adjacent to the vertex n with degree 2 and CN 2, i.e., |A(2,2)(1,2)(ξ)|=2×2s. Similarly for the others, we have

|A(2,2)(2,2)(ξ)|=8×2s−12,|A(2,2)(2,3)(ξ)|=6×2s−6,|A(2,3)(3,3)(ξ)|=6×2s−6.

After placing the calculated values of |A(μ,ν)(ϕ,ψ)(ξ)| in Eq. (4), we get

Z^C2∗(ξ)=∑ϕψ∈A,μ,ν∈B|A(μ,ν)(ϕ,ψ)(ξ)|[μψ+νϕ]=|A(1,2)(1,1)(ξ)|[(1)(1)+(2)(1)]+|A(2,2)(1,2)(ξ)|[(2)(2)+(2)(1)]+|A(2,2)(2,2)(ξ)|[(2)(2)+(2)(2)]+|A(2,2)(2,3)(ξ)|[(2)(3)+(2)(2)]+|A(2,3)(3,3)(ξ)|[(2)(3)+(3)(3)],=(2×2s)[3]+(2×2s)[6]+(8×2s−12)[8]+(6×2s−6)[10]+(6×2s−6)[15],=232×2s−246.

3. By placing the |A(μ,ν)(ϕ,ψ)(ξ)| in Eq. (5), we get

Z^C3∗(ξ)=∑ϕψ∈A,μ,ν∈B|A(μ,ν)(ϕ,ψ)(ξ)|[μψ+νϕ]=|A(1,2)(1,1)(ξ)|[(1)(1)+(2)(1)]+|A(2,2)(1,2)(ξ)|[(2)(1)+(2)(2)]+|A(2,2)(2,2)(ξ)|[(2)(2)+(2)(2)]+|A(2,2)(2,3)(ξ)|[(2)(2)+(2)(3)]+|A(2,3)(3,3)(ξ)|[(2)(3)+(3)(3)],=(2×2s)[3]+(2×2s)[6]+(8×2s−12)[8]+(6×2s−6)[10]+(6×2s−6)[15],=232×2s−246.

This proves the theorem.

4  ZCIs of Poly Propylene Imine Octamin Dendrimer

In this section, we find the general expressions to compute the connection-based Zagreb indices, namely, FZCI, SZCI, TZCI, modified FZCI, modified SZCI and modified TZCI of another special type of dendrimer nanostar named as, PPIO dendrimer. PPIO dendrimer grows in three dimensions and it has five bonds in the core. The structural formula of PPIO dendrimer is shown in Fig. 3 for five generations.

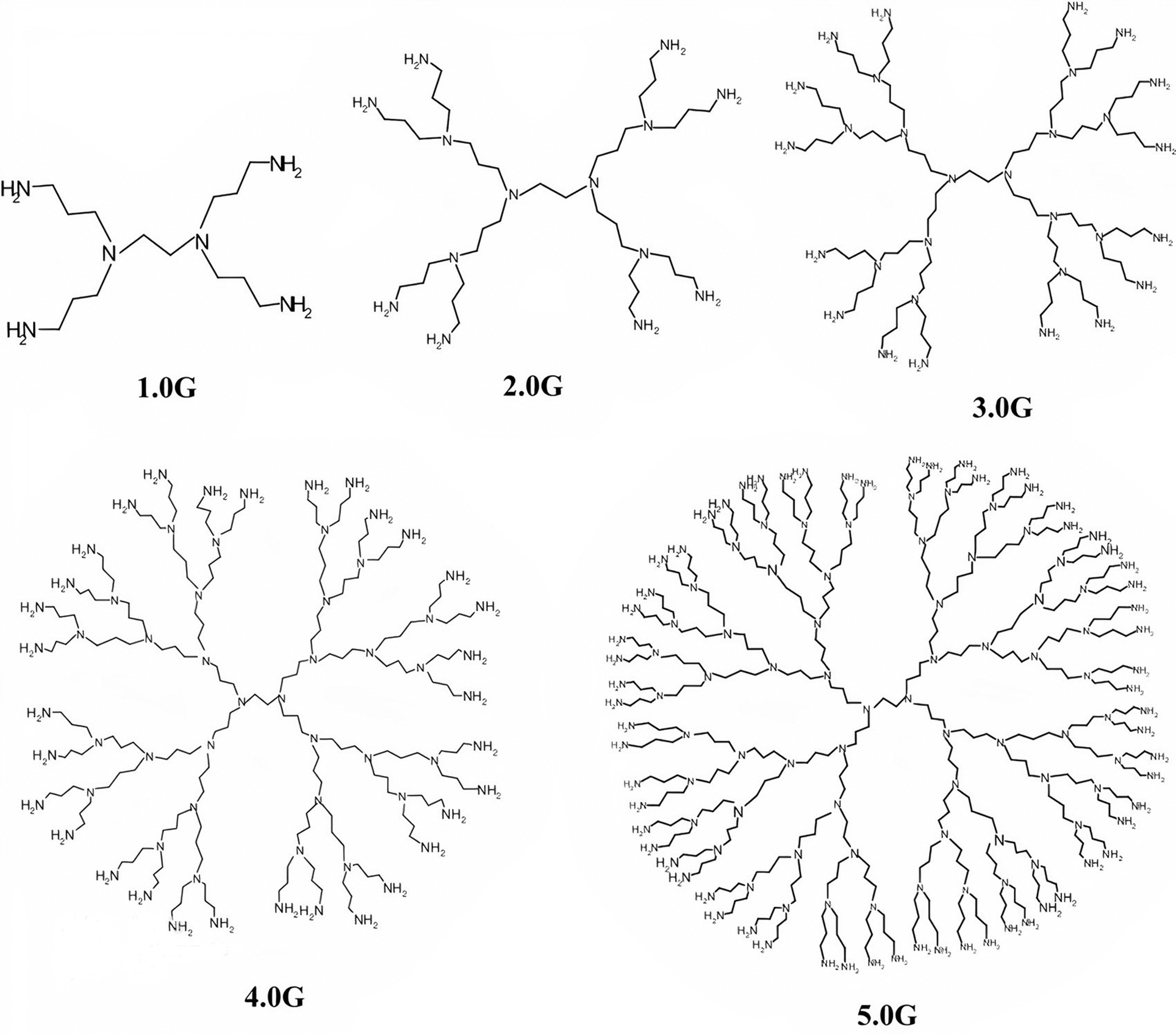
Figure 3: Structural formula of PPIO dendrimer

Theorem 3. Let ξ be a molecular network of PPIO dendrimer. Then, FZCI, SZCI and TZCI are given in the following

1.    Z^C1(ξ)=92×2s−80,

2.    Z^C2(ξ)=96×2s−86,

3.    Z^C3(ξ)=200×2s−178.

Proof.

1. Initially, we find cardinality of edges of ξ. The total number of edges in ξ must be equal to the four times of number of edges in each branch plus the number of edges in central core. It can be easily seen that central core has 5 edges. Therefore,

Number of edges in each branch=(4+(2×4)+(22×4)+⋯+(2s−1×4)),=4×2s−4.Number of edges in all branches=4×(4×2s−4),=16×2s−16.

Number of edges in ζ=5+(16×2s−16),=16×2s−11.

As ζ is a tree, so the number of vertices must be equals to 16×2s−10.

Furthermore, we find the cardinality of those vertices which have CN 1, 2 and 3 in ξ.

|A1|=4(2×2s−1),=4×2s.|A2|=4[1+(2×1)+(22×)+(23×1)+⋯(2s−1×1)]+2,=4×2s−2.|A3|=(16×2s−10)−(4×2s)−(4×2s+2),=8×2s−8.

In Fig. 4, we have labeled the vertices of PPIO dendrimer for s=5 with respect to their CNs. Now, by placing the values of |Aϕ(ξ)| in Eq. (1), we get

Z^1C(ξ)=∑ϕ∈A|Aϕ(ξ)|[ϕ2]=|A1(ξ)|[12]+|A2(ξ)|[22]+|A3(ξ)|[32],=(4×2s)[1]+(4×2s−2)[22]+(8×2s−8)[32],=92×2s−80.

Figure 4: Structural formula of PPIO dendrimer for s=5 along with CNs

2. Now, we calculate |A(ϕ,ψ)(ξ)|.

|A(1,1)|=4×2s−1=2×2s.|A(1,2)|=4×2s−1=2×2s.|A(2,2)|=1.|A(2,3)|=4[2+(2×2)+(22×2)+(23×2)+⋯+(2s−1×2)]+2=4×2[1+2+22+23+⋯+2s−1]+2=6×2s−6.|A(3,3)|=4(2+(2×2)+(22×2)+(23×2)+⋯+(2s−2×2)+(2s−1×1))+2,=4×2(1+2+22+23+⋯+2s−2)+2s−1+2,=6×2s−6.

After placing the above calculated values in Eq. (2), we have

Z^C2(ξ)=∑ϕ,ψ∈A|A(ϕ,ψ)(ξ)|[ϕ×ψ],=|A(1,1)(ξ)|[1×1]+|A(1,2)(ξ)|[1×2]+|A(2,2)(ξ)|[2×2]+|A(2,3)(ξ)|[2×3]+|A(3,3)(ξ)|[3×3],=(2×2s)[1]+(2×2s)[2]+[4](1)+(6×2s−6)[6]+(6×2s−6)[9],=96×2s−86.

3. After placing the values of |A(ϕ,ψ)(ξ)| in Eq. (6), we get

Z^C3(ξ)=∑0≤ϕ≤ψ≤3|A(ϕ,ψ)(ξ)|[ϕ2+ψ2],=|A(1,1)(ξ)|[12+12]+|A(1,2)(ξ)|[12+22]+|A(2,2)(ξ)|[22+22]+|A(2,3)(ξ)|[22+32]+|A(3,3)(ξ)|[32+32],=(2×2s)[2]+(2×2s)[5]+(1)[8]+(6×2s−6)[13]+(6×2s−6)[18],=200×2s−178.

This proves the theorem.

Theorem 4. Let ξ be a molecular network of PPIO dendrimer. Then modified FZCI, modified SZCI and modified TZCI are given in the following

1. Z^C1∗(ξ)=76×2s−62,

2. Z^C2∗(ξ)=168×2s−142,

3. Z^C3∗(ξ)=168×2s−142.

Proof.

1. For the proof, the readers are referred to see [32].

2. Now we make the partition of the edges based on their degrees of incident vertices. It can be easily seen that |A(1,2)(ξ)|=2×2s, |A(2,2)(ξ)|=8×2s−5 and |A(2,3)(ξ)|=6×2s−6. In order to compute the modified SZCI and modified TZCI, we split the number edges on degree basis with respect to the number of edges on connection bases as shown in Table 3.

Thus, we have

|A(1,2)(1,1)(ξ)|=2×2s,|A(2,2)(1,2)(ξ)|=2×2s,|A(2,2)(2,2)(ξ)|=1,|A(2,2)(2,3)(ξ)|=6×2s−6,|A(2,3)(3,3)(ξ)|=6×2s−6.

By putting the |A(μ,ν)(ϕ,ψ)(ξ)| in Eq. (4), we have

Z^C2∗(ξ)=∑ϕψ∈A,μ,ν∈B|A(μ,ν)(ϕ,ψ)(ξ)|[μψ+νϕ]=|A(1,2)(1,1)(ξ)|[(1)(1)+(2)(1)]+|A(2,2)(1,2)(ξ)|[(2)(2)+(2)(1)]+|A(2,2)(2,2)(ξ)|[(2)(2)+(2)(2)]+|A(2,2)(2,3)(ξ)|[(2)(3)+(2)(2)]+|A(2,3)(3,3)(ξ)|[(2)(3)+(3)(3)],=(2×2s)[3]+(2×2s)[6]+(1)[8]+(6×2s−6)[10]+(6×2s−6)[15],=168×2s−142.

3. By putting the |A(μ,ν)(ϕ,ψ)(ξ)| in Eq. (5), we have

Z^C3∗(ξ)=∑ϕψ∈A,μ,ν∈B|A(μ,ν)(ϕ,ψ)(ξ)|[μϕ+νψ]=|A(1,2)(1,1)(ξ)|[(1)(1)+(2)(1)]+|A(2,2)(1,2)(ξ)|[(2)(1)+(2)(2)]+|A(2,2)(2,2)(ξ)|[(2)(2)+(2)(2)]+|A(2,2)(2,3)(ξ)|[(2)(2)+(2)(3)]+|A(2,3)(3,3)(ξ)|[(2)(3)+(3)(3)],=(2×2s)[3]+(2×2s)[6]+(1)[8]+(6×2s−6)[10]+(6×2s−6)[15],=168×2s−142.

This proves the theorem.

5  Comparative Analysis and Concluding Remarks

The analysis of networks plays a remarkable role to conclude their fundamental topologies. TIs specified on chemical structures can assist the researchers to recognize the biological activity, chemical reactivity and physical features. Through TIs, researchers can easily predict the distinct psychochemical properties of the molecular structures. To check the superiority of consequences of this research article, we compare our computed values for two nanostars. Table 4 displays the comparison between the calculated results of PPEtIm and PPIO dendrimers.

From Table 4, it can be easily seen that PPEtIm dendrimer and PPIO dendrimer get the greatest value of TZCI Z^3C(ξ). The values of defined ZCIs of PPEtIm dendrimer and PPIO dendrimer for some values of s are given in Tables 5 and 6, respectively.

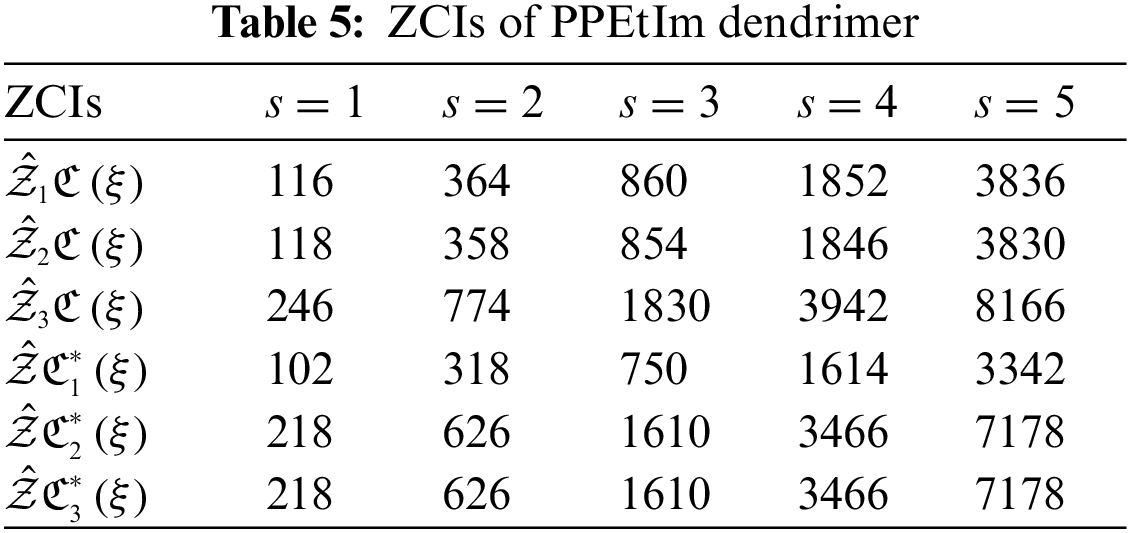
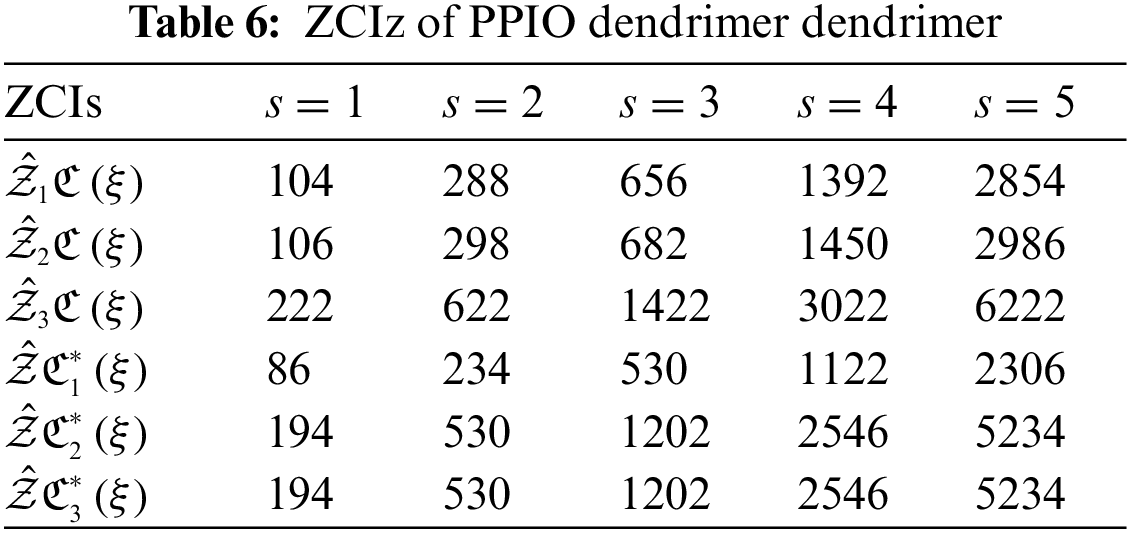
The graphical comparison of Z^3C(ξ) for both dendrimers is displayed in Fig. 5.

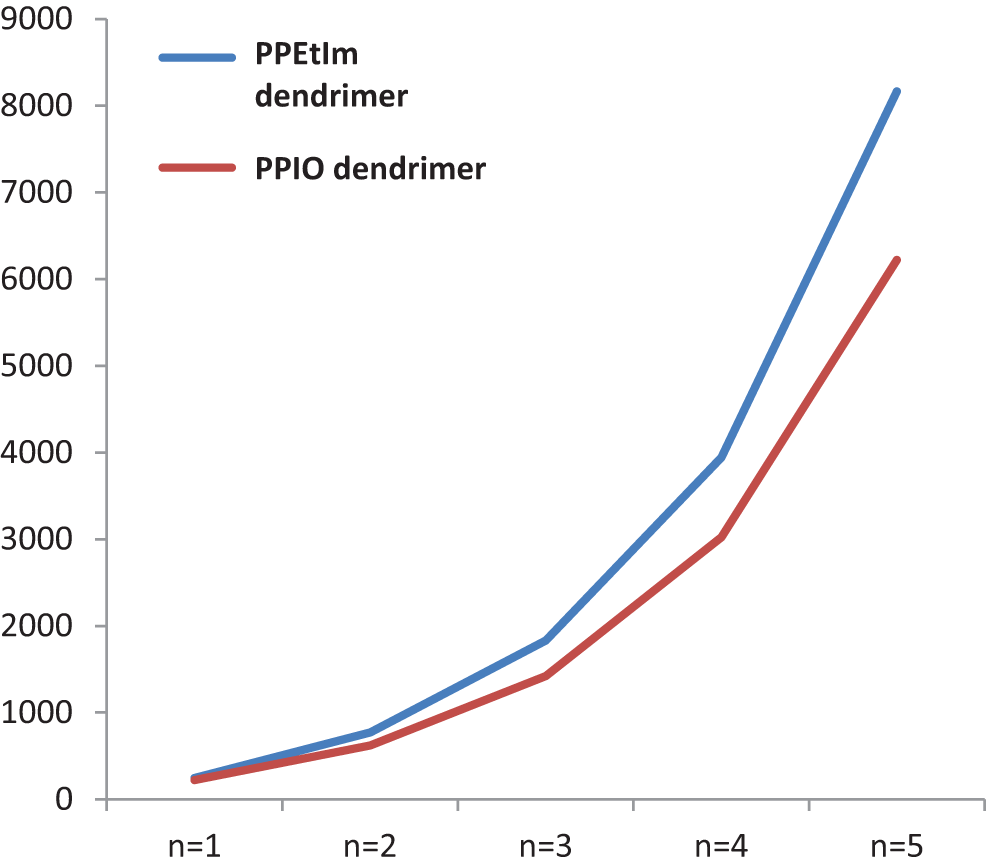
Figure 5: Graphical display of TZCI for PPEtIm and PPIO dendrimers

Now, we conclude our discussion with the following lines. In this manuscript, we have established the general results to compute ZCIs namely, FZCI, SZCI and TZCI of two special types of dendrimer nanostars, namely, PPEtIm dendrimer and PPIO dendrimer which will be helpful in computational chemistry to predict many physical and chemical attributes of the chemical substances. Moreover, we have computed modified FZCI, modified SZCI and modified TZCI for these dendrimers. The computed results just depend upon the value of s≥1. Further, we have compared the calculated results for both types of dendrimers with each other. We have found that our developed TZCI gets the greatest value for both types of dendrimers. Thus, we found that TZCI is superior in preserving the psychochemical properties of these dendrimers and PPEtIm dendrimer has greater chemical applicability than PPIO dendrimer. Now, the problem is still open to computing the Zagreb connection indices for the other types of dendrimers.

Data Availability: The data used to support the findings of this study are included within this article. However, the reader may contact the corresponding author for more details on the data.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Kesharwani, P., Gothwal, A., Iyer, A. K., Jain, K., Chourasia, M. K. et al. (2018). Dendrimer nanohybrid carrier systems: An expanding horizon for targeted drug and gene delivery. Drug Discovery Today, 23(2), 300–314. [Google Scholar]

 2.  Klajnert, B., Peng, L., Ceoa, V. (2013). Dendrimers in biomedical applications. RSC (Royal Society of ChemistryThomas Graham House, Science Park, Milton Road, Cambridge, UK. [Google Scholar]

 3.  Kurczewska, J., Ceglowski, M., Messyasz, B., Schroeder, G., (2018). Dendrimer-functionalized halloysite nanotubes for effective drug delivery. Applied Clay Science, 153, 134–143. [Google Scholar]

 4.  Todeschini, R., Consonni, V. (2009). Molecular descriptors for chemoinformatics: Volume I: Alphabetical listing/volume II: Appendices, references. 2nd edition. John Wiley and Sons, New Jersey, USA. [Google Scholar]

 5.  Afzal, H. U., Fatima, T. (2019). On topological indices of OT [m, n] octagonal tillings and TiO2 nanotubes. Acta Chimica Slovenica, 66(2), 435–442. [Google Scholar]

 6.  Gao, W., Younas, M., Farooq, A., Mahboob, A., Nazeer, W. (2018). M-polynomials and degree-based topological indices of the crystallographic structure of molecules. Biomolecules, 8(4), 107. [Google Scholar]

 7.  Imran, M., Baig, A. Q., Ali, H. (2016). On molecular topological properties of hex-derived networks. Journal of Chemometrics, 30(3), 121–129. [Google Scholar]

 8.  Wiener, H. (1947). Structural determination of paraffin boiling points. Journal of the American Chemical Society, 69(1), 17–20. [Google Scholar]

 9.  Gao, W., Iqbal, Z., Ishaq, M., Aslam, A., Sarfraz, R. (2019). Topological aspects of dendrimers via distance based descriptors. IEEE Access, 7, 35619–35630. [Google Scholar]

10. Gutman, I., Trinajstic, N. (1972). Graph theory and molecular orbitals. Total π-electron energy of alternant hydrocarbons. Chemical Physics Letters, 17(4), 535–538. [Google Scholar]

11. Gutman, I., Ruscic, B., Trinajstic, N., Wilcox Jr, C. F. (1975). Graph theory and molecular orbitals. XII. Acyclic polyenes. The Journal of Chemical Physics, 62(9), 3399–3405. DOI 10.1063/1.430994. [Google Scholar] [CrossRef]

12. Furtula, B., Gutman, I. (2015). A forgotten topological index. Journal of Mathematical Chemistry, 53(4), 1184–1190. DOI 10.1007/s10910-015-0480-z. [Google Scholar] [CrossRef]

13. Ali, A., Gutman, I., Milovanovic, E., Milovanovic, I. (2018). Sum of powers of the degrees of graphs extremal results and bounds. MATCH Communications in Mathematical and in Computer Chemistry, 80(1), 5–84. [Google Scholar]

14. Borovicanin, B., Das, K. C., Furtula, B., Gutman, I. (2017). Bounds for Zagreb indices. MATCH Communications in Mathematical and in Computer Chemistry, 78(1), 17–100. [Google Scholar]

15. Javaid, M., Ali, U., Liu, J. B. (2021). Computing analysis for first Zagreb connection index and coindex of resultant graphs. Mathematical Problems in Engineering, 2021, 1–19. [Google Scholar]

16. Bashir, Y., Aslam, A., Kamran, M., Qureshi, M. I., Jahangir, A. et al. (2017). On forgotten topological indices of some dendrimers structure. Molecules, 22(6), 867. DOI 10.3390/molecules22060867. [Google Scholar] [CrossRef]

17. Bokhary, S. A. U. H., Imran, M., Manzoor, S. (2016). On molecular topological properties of dendrimers. Canadian Journal of Chemistry, 94(2), 120–125. DOI 10.1139/cjc-2015-0466. [Google Scholar] [CrossRef]

18. Dorosti, N., Iranmanesh, A., Diudea, M. V. (2010). Computing the cluj index of the first type dendrimer nanostar. Optoelectronics and Advanced Materials-Rapid Communications, 4, 381–384. [Google Scholar]

19. Ali, A., Trinajstic, N. (2018). A novel/old modification of the first Zagreb index. Molecular Informatics, 37(6–7), 1800008. DOI 10.1002/minf.201800008. [Google Scholar] [CrossRef]

20. Ali, U., Javaid, M., Kashif, A. (2020). Modified Zagreb connection indices of the T-sum graphs. Main Group Metal Chemistry, 43(1), 43–55. DOI 10.1515/mgmc-2020-0005. [Google Scholar] [CrossRef]

21. Cao, J., Ali, U., Javaid, M., Huang, C. (2020). Zagreb connection indices of molecular graphs based on operations. Complexity, 2020, 7385682. DOI 10.1155/2020/7385682. [Google Scholar] [CrossRef]

22. Du, Z., Ali, A., Trinajstic, N. (2019). Alkanes with the first three maximal/minimal modified first Zagreb connection indices. Molecular Informatics, 38(4), 1800116. DOI 10.1002/minf.201800116. [Google Scholar] [CrossRef]

23. Haoer, R. S., Mohammed, M. A., Selvarasan, T., Chidambaram, N., Devadoss, N. (2020). Multiplicative leap Zagreb indices of T-thorny graphs. Eurasian Chemical Communications, 2(8), 841–846. [Google Scholar]

24. Javaid, M., Ali, U., Siddiqui, K. (2021). Novel connection-based Zagreb indices of several wheel-related graphs. Computational Journal of Combinatorial Mathematics, 1, 1–28. [Google Scholar]

25. Liu, J. B., Raza, Z., Javaid, M. (2020). Zagreb connection numbers for cellular neural networks. Discrete Dynamics in Nature and Society, 2020, 8038304. DOI 10.1155/2020/8038304. [Google Scholar] [CrossRef]

26. Sattar, A., Javaid, M., Bonyah, E. (2021). Connection-based multiplicative Zagreb indices of dendrimer nanostars. Journal of Mathematics, 2021, 2107623. DOI 10.1155/2021/2107623. [Google Scholar] [CrossRef]

27. Sattar, A., Javaid, M., Bonyah, E. (2022). On the studies of dendrimers via connection-based molecular descriptors. Mathematical Problems in Engineering, 2022, 1–13. DOI 10.1155/2022/1053484. [Google Scholar] [CrossRef]

28. Sattar, A., Javaid, M., Bonyah, E. (2022). Computing connection-based topological indices of dendrimers. Journal of Chemistry, 2022, 1–15. DOI 10.1155/2022/7204641. [Google Scholar] [CrossRef]

29. Julietraja, K., Venugopal, P., Prabhu, S., Liu, J. B. (2020). M-polynomial and degree-based molecular descriptors of certain classes of benzenoid systems. Polycyclic Aromatic Compounds, 1–30. DOI 10.1080/10406638.2020.1867205. [Google Scholar] [CrossRef]

30. Liu, J. B., Arockiaraj, M., Arulperumjothi, M., Prabhu, S. (2021). Distance based and bond additive topological indices of certain repurposed antiviral drug compounds tested for treating COVID-19. International Journal of Quantum Chemistry, 121(10), 26617. DOI 10.1002/qua.26617. [Google Scholar] [CrossRef]

31. Yang, Z., Arockiaraj, Z., Prabhu, S., Arulperumjothi, M., Liu, J. B. (2021). Second Zagreb and sigma indices of semi and total transformations of graphs. Complexity, 2021, 1–15. DOI 10.1155/2021/6828424. [Google Scholar] [CrossRef]

32. James, S. (2002). Calculus. Thomson brooks cole, 5th edition. Canada. [Google Scholar]

33. Noureen, S., Bhatti, A. A., Ali, A. (2020). Extremal trees for the modified first Zagreb connection index with fixed number of segments or vertices of degree 2. Journal of Taibah University for Science, 14(1), 31–37. DOI 10.1080/16583655.2019.1699227. [Google Scholar] [CrossRef]