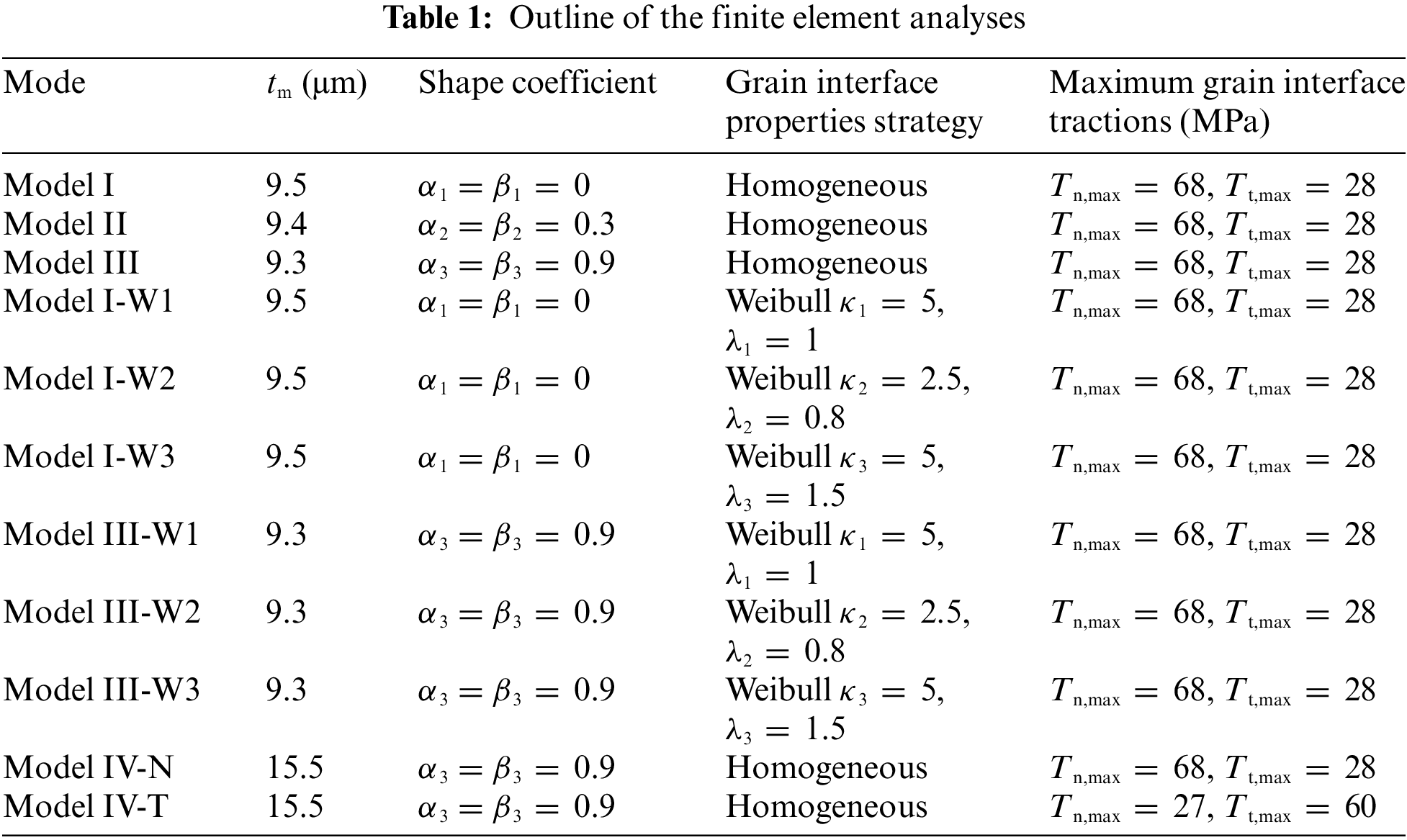
 Open Access
Open Access
ARTICLE
Computational Modeling of Intergranular Crack Propagation in an Intermetallic Compound Layer
1 Institute of Electronics Packaging Technology and Reliability, Faculty of Materials and Manufacturing, Beijing University of Technology, Beijing, 100124, China
2 Beijing Key Laboratory of Advanced Manufacturing Technology, Beijing University of Technology, Beijing, 100124, China
* Corresponding Authors: Tong An. Email: ; Fei Qin. Email:
(This article belongs to the Special Issue: Mechanical Reliability of Advanced Materials and Structures for Harsh Applications)
Computer Modeling in Engineering & Sciences 2023, 135(2), 1481-1502. https://doi.org/10.32604/cmes.2023.022475
Received 11 March 2022; Accepted 22 June 2022; Issue published 27 October 2022
Abstract
A micromechanical model is presented to study the initiation and propagation of microcracks of intermetallic compounds (IMCs) in solder joints. The effects of the grain aggregate morphology, the grain boundary defects and the sensitivity of the various cohesive zone parameters in predicting the overall mechanical response are investigated. The overall strength is predominantly determined by the weak grain interfaces; both the grain aggregate morphology and the weak grain interfaces control the crack configuration; the different normal and tangential strengths of grain interfaces result in different intergranular cracking behaviors and play a critical role in determining the macroscopic mechanical response of the system.Keywords
Nomenclature
| ai | the coordinates of the nuclei |
| A | the area of the IMC layer |
| Ael | the area of the cohesive interface element |
| bi | the coordinates of the nuclei |
| Dloc | the cohesive constitutive tangent stiffness matrix |
| E | the Young’s modulus |
| Fel | the nodal force vector of the interface element |
| Gc | the critical energy release rate |
| H | the matrix of the shape function |
| J | the Jacobian matrix |
| kn | the unloading/reloading stiffness in the normal direction |
| kt | the unloading/reloading stiffness in the tangential direction |
| Kel | the tangential stiffness of the interface element |
| KI | the stress intensity factor |
| L | the width of the IMC layer |
| N | the shape function |
| pi | a nucleus |
| P | a set of n nucleus in a plane |
| q | the coupling parameter |
| r | the coupling parameter |
| tm | the average thickness of the IMC layer |
| T | the traction vector |
| ΔTn | the increment of the normal traction |
| Tn | the normal traction component |
| Tn,max | the maximum normal traction |
| ΔTt | the increment of the tangential traction |
| Tt | the tangential traction component |
| Tt,max | the maximum tangential traction |
| Tloc | the local traction vector |
| uI | the nodal displacement vector |
| the nodal displacements of the bottom nodes | |
| the nodal displacements of the top nodes | |
| ΔuI | the relative displacements between each pair of the nodes |
| Δuloc | the local separating displacement vector |
| W | the width of the cohesive interface element |
| xi | the center points of each regular hexagon |
| XI | the initial coordinates of the nodes on the mid-line |
| the coordinates of the nodes on the mid-line after deformation | |
| yi | the center points of each regular hexagon |
| κ | the Weibull parameter |
| ν | the Poisson’s ratio |
| Θ | the transformation matrix |
| α | the contact stiffness |
| δ | the separating displacement vector |
| δcr,n | the critical normal separating displacement |
| δn | the normal separating displacement |
| Δδn | the increment of the normal separating displacement |
| δcr,t | the critical tangential separating displacement |
| δt | the tangential separating displacement |
| Δδt | the increment of the tangential separating displacement |
| the value of δn after complete shear separation | |
| δtol | the specific penetration tolerance |
| λ | the Weibull parameter |
| ϕn | the cohesive energy under the pure mode-I (opening) |
| ϕt | the cohesive energy under the pure mode-II (shearing) |
| ξ | the local element coordinate |
| IMC | intermetallic compounds |
| UEL | user subroutine to define an element in the finite element code ABAQUS |
| VCFEM | Voronoi cell finite element model |
Solder joint is a key factor affecting the electrical, thermal, and mechanical performance of electronic packages. At the solder joint-Cu pad interface, the intermetallic compound (IMC) is crucial for forming a functional metallurgical bonding. However, excessive growth of IMC layer is considered to be an initiation site for microcracks, which will degrade the mechanical strength of the solder joint [1]. To achieve improved performance, effective modeling for understanding the failure mechanism of the IMC layer in the solder joint is indispensable for the reliable design of electronic packages.
As a polycrystalline quasi-brittle material, the morphological characteristics of the IMC microstructure, such as the grain shape, size and defects, have a great influence on the failure mechanism of the IMC. However, most of the previous research [2,3] focused on the macroscopic failure behavior, not the microstructural damage evolution of the IMC. These works cannot account for the microstructure characteristics of the IMC and the grain boundary defects with random distribution in the IMC layer. As a result, finite element (FE) analysis results are not consistent with the experimental results. Therefore, a model accounting for the microstructure-based mechanism of IMC failure is important for understanding the micromechanical behavior of the IMC layer that controls the macroscopic response.
Some efforts have been made to develop an effective numerical procedure to describe material intergranular cracking in polycrystalline brittle material using the FE analysis [4,5]. With such models, the explicit discrete nature of the polycrystalline microstructure was retained, and the interface elements were applied to simulate the intergranular cracking behavior. The material failure in these models was not limited by specific fracture criteria; therefore, the initiation and propagation of microcracks were a natural outcome of the material response, the boundary constraints and the applied loading.
The three essential factors of the method are the geometric characterization of microstructure of polycrystalline materials, the description of the grain boundary defects and the numerical simulation of the grain interface behavior.
Geometric representation of grain microstructure. Typically, regular or irregular microstructures are generated in numerical modeling to reflect the geometry of polycrystalline structures on the microscopic scale. For example, Onck et al. [6] used regular hexagonal grains to study intergranular creep cracking of polycrystalline materials. In addition, a voronoi cell finite element model (VCFEM) which can be used to simulate the arbitrary microstructure of a multiphase material was proposed by Ghosh et al. [7]. Two-dimensional voronoi tessellations were applied to generate a micromechanical model for describing the brittle compressive fracture of polycrystalline ice [8,9]. Furthermore, the voronoi tessellation-based simulation was extended to three-dimensional modeling, which was employed to study the cracking process of brittle ceramics [10] and to account for the heterogeneity of polycrystalline materials [11,12]. Both regular and irregular microstructures have been extensively used in computational materials science [13–16]. In this analysis, regular hexahedral grains and irregular polygonal grains are established and applied to study the influence of the grain aggregate morphology on the crack configuration and the overall response.
Grain boundary defects. It has been realized that the existence of pre-existing flaws at grain boundaries have great influence on the mechanical properties of polycrystalline materials [17,18]. Therefore, grain boundary defects should be considered in the model [4,14]. In this analysis, the grain interface properties are described by a Weibull distribution to account for the grain boundary defects, and their influence on the crack configuration and the overall response is discussed.
Numerical modeling of grain interface behavior. The constitutive description of the grain interface should account for the relevant physical mechanisms, such as grain boundary sliding, separation, and microcracking by coalescence. The cohesive zone model has been considered a feasible tool for describing the debonding behavior of material interfaces. The concept of the cohesive zone model was originally proposed by Barenblatt [19] and Dugdale [20]. Needleman [21] used the traction-separation relationship specified by the cohesive zone law to investigate void nucleation and fracture growth at particle-matrix interfaces. In this analysis, the cohesive interface element is applied, and the behavior of the element is governed by the cohesive zone law.
The parameters of the cohesive zone law play a crucial role in determining the macroscopic mechanical response of materials. The magnitudes of the parameters vary widely, ranging from MPa to GPa for traction, J to kJ for energy, and nm to mm for separating displacement. The effect of various parameters in the cohesive zone law on the macroscopic failure of materials has been examined in the literature [22–25]. It is commonly believed that the failure behavior is dominated primarily by the energy that controls separation; thus, cohesive energy is the most important parameter. The question raised here is as follows: Can changing the maximum traction applied at the grain interfaces change the micro and macro mechanical response of a polycrystalline material, even if the cohesive energy is the same? To answer the question, we compared the predictions of the models with different maximum tractions applied in the normal and tangential directions of grain interfaces.
In this paper, a micromechanical model of an IMC layer is constructed. The polycrystalline microstructure is represented by the polygonal grains generated by voronoi tessellation. The cohesive zone elements, which are carried out by using a user-defined subroutine (UEL) in ABAQUS, are embedded along the grain interfaces to simulate the microcrack cracking process. The influence of the grain aggregate morphology, stochastically distributed grain boundary defects, and various cohesive zone parameters on the overall mechanical response and failure behavior are considered and discussed.
2 Grain-Level Micromechanical Model of the IMC Layer
Fig. 1 presents a schematic diagram of the cross-section of a solder joint. The Cu6Sn5 η-phase and Cu3Sn ε-phase are the two phases formed between the Cu substrate and the Sn-based solder during the soldering and aging process. Before aging, only a layer of Cu6Sn5 was observed, and the Cu3Sn was too thin to be observed (Fig. 2a). The solder/IMC interface showed scallop shape and was extremely rough. After isothermal aging, an IMC layer consisting of both the Cu6Sn5 and Cu3Sn layers can be observed. Both layers became thicker and the solder/IMC interface became more planar (Fig. 2b) [26]. Figs. 2c and 2d show the SEM micrographs of the Cu6Sn5 grains. Before aging, the Cu6Sn5 grains appeared to be round-like, and typical polygonal Cu6Sn5 grains can be observed after isothermal aging. According to experimental observations, delamination and cleavage of the IMC mainly occur in the layer of Cu6Sn5 grains, and the Cu3Sn grains remain mostly intact [27]. This suggests that we should pay more attention to the Cu6Sn5 layer rather than the Cu3Sn layer when modeling the solder joint.
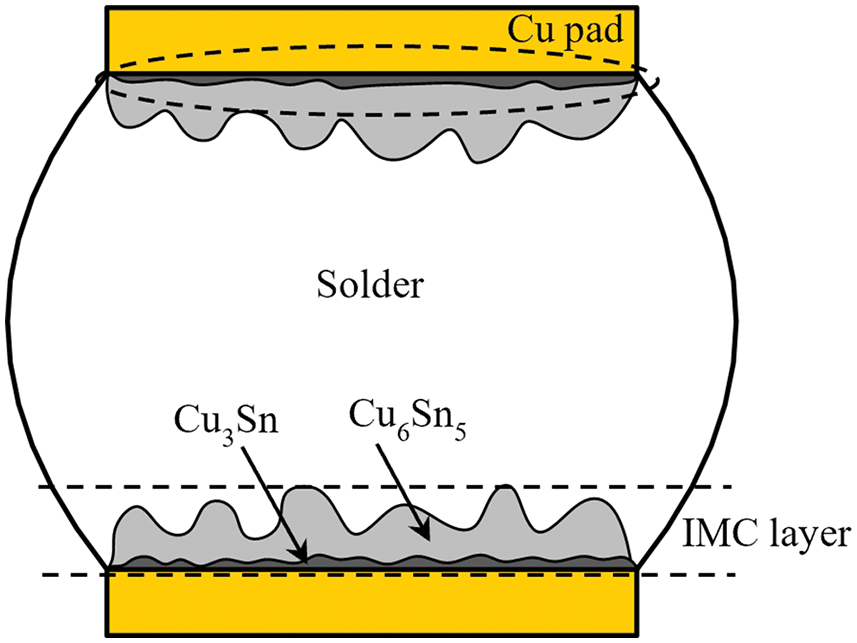
Figure 1: Schematic diagram of solder joint section

Figure 2: SEM images of the Sn3.0Ag0.5Cu/Cu interface aged at 150°C for (a) 0 h, (b) 500 h and the top views of the IMC layer aged for (c) 0 h and (d) 500 h
2.2 Geometrical Features of Grain-Level Modeling
Voronoi tessellation is widely applied to generate the geometry of the grain microstructure of polycrystalline materials [28,29]. Suppose pi is a point in a plane that can be called a nucleus, and P represents a set of n points. To divide the plane into n cells, the voronoi tessellation of P is
where q is a point lying in the cell, and d(q, pi) denotes the Euclidean distance between q and pi.
The shape and aggregate morphology of the grains are defined by the nuclei; thus, the distribution of nuclei should be predefined carefully. The center points of the regular polygon were (xi, yi). The coordinates of the nuclei (ai, bi) were chosen randomly around the center points, which were ai∈(xi − αxi, xi + αxi) and bi∈(yi − βyi, yi + βyi). The α and β were applied to control the location of the nucleus within the polygon. Here, the models of regular polygon (Fig. 3a) and irregular polygon (Fig. 3b) are established. The vertex coordinates of the cells generated by MATLAB, and the geometric model of the polycrystalline microstructure were established by Python scripting language and ABAQUS/CAE.
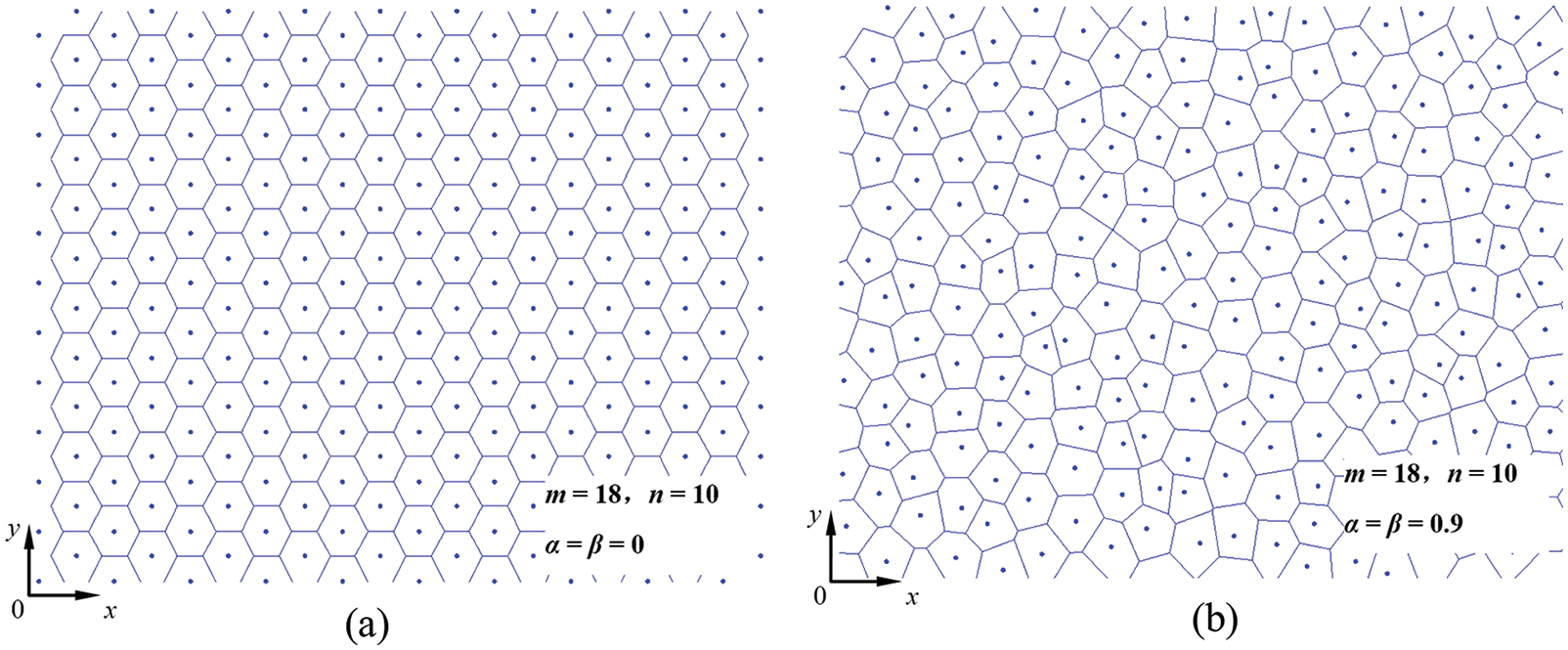
Figure 3: Voronoi tessellations with (a) Regular hexagonal grains and (b) Irregular polygonal grains
2.3 Constitutive Behavior of the Cohesive Zone Element
Cohesive zone law. A cohesive zone law is described by the relation between the traction T on the interface and the corresponding separating displacement δ [30–32]. Here, a modified exponential cohesive zone law [33] was applied, as shown in Fig. 4. The normal traction Tn and the tangential traction Tt are expressed as
where δn and δt are separating displacements in the normal and tangential directions, respectively; δcr,n and δcr,t are the critical separating displacements; Δδn and Δδt are the increments of the separating displacement; ϕn and ϕt are the cohesive energies under opening and shearing failure, respectively. The modified cohesive zone law preserves most features of the original exponential cohesive zone law proposed by Xu et al. [30] and includes a more advantageous controllable coupling effect. This modified cohesive zone law describes the mixed-mode decohesion process better and provides the possibility to account for different values for ϕn and ϕt [33].
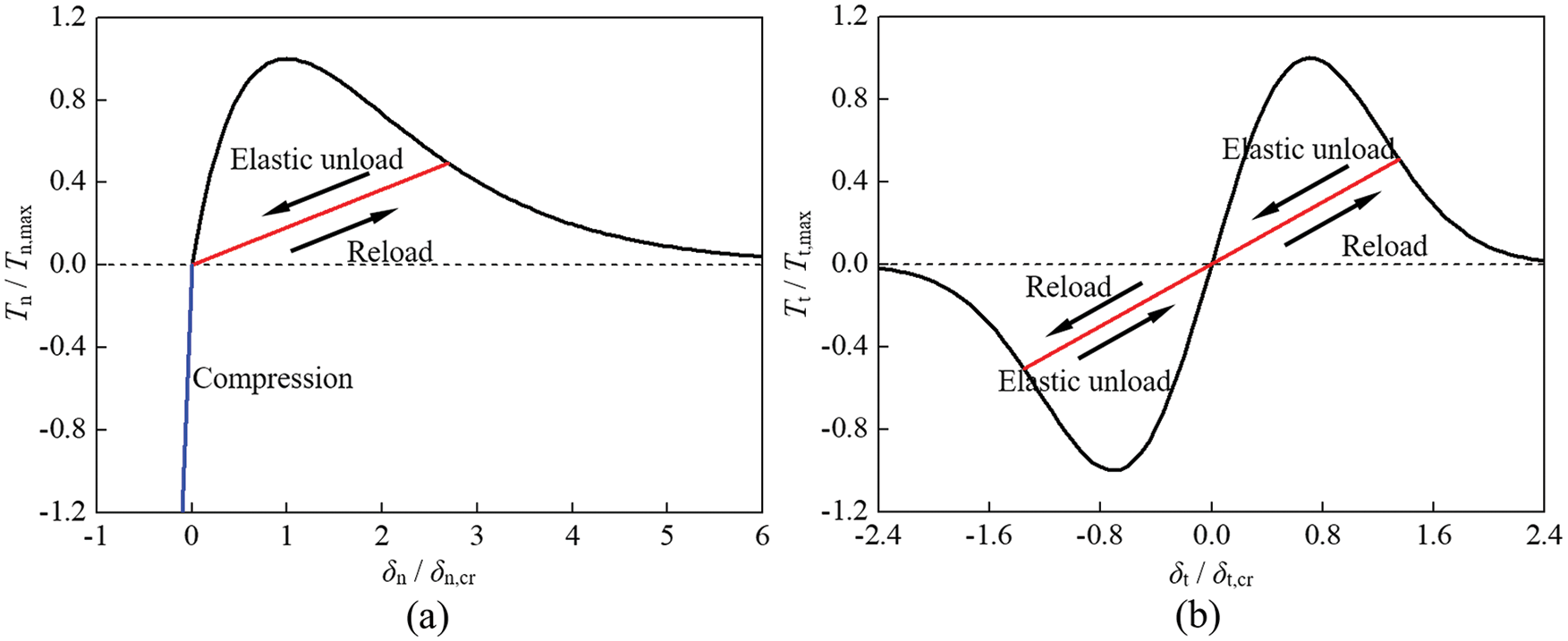
Figure 4: The cohesive zone law: (a) The normal traction-separation relationship; (b) The tangential traction-separation relationship
Unloading and reloading. In the cohesive zone element, after the maximum traction is reached, the cohesive zone element shows an irreversible response, and the traction-separation curve for unloading/reloading shows an elastic relation, as shown in Fig. 3, i.e.,
where ΔTn and ΔTt are the increments of the normal and tangential tractions, respectively, and kn and kt are the unloading/reloading stiffnesses in the normal and tangential directions, respectively.
Compression. When the cohesive zone element is under compression, the interpenetration of the two volume elements which connected by the cohesive zone elements may occur. To ensure that the interpenetration is tolerable, some efforts have been made, including applying a contact algorithm at the interfaces [34], choosing the normal stiffness value carefully [35], and modifying the constitutive equation in compression [36]. Here, when the normal displacement is negative, an extra compressive traction Tc is applied, i.e., if δn < 0,
where α is the contact stiffness and δtol is a specific interpenetration tolerance. This extra compressive traction improves the compressive capacity of the cohesive zone element, and interpenetration can be prevented.
The cohesive zone element connects the two adjacent volume elements during the fracture process. In this section, the basic formulation of the cohesive interface element used in this paper is presented [37,38].
Fig. 5 shows a two-dimensional quadrilateral cohesive zone element with two integration points, four nodes, and a local element coordinate ξ (
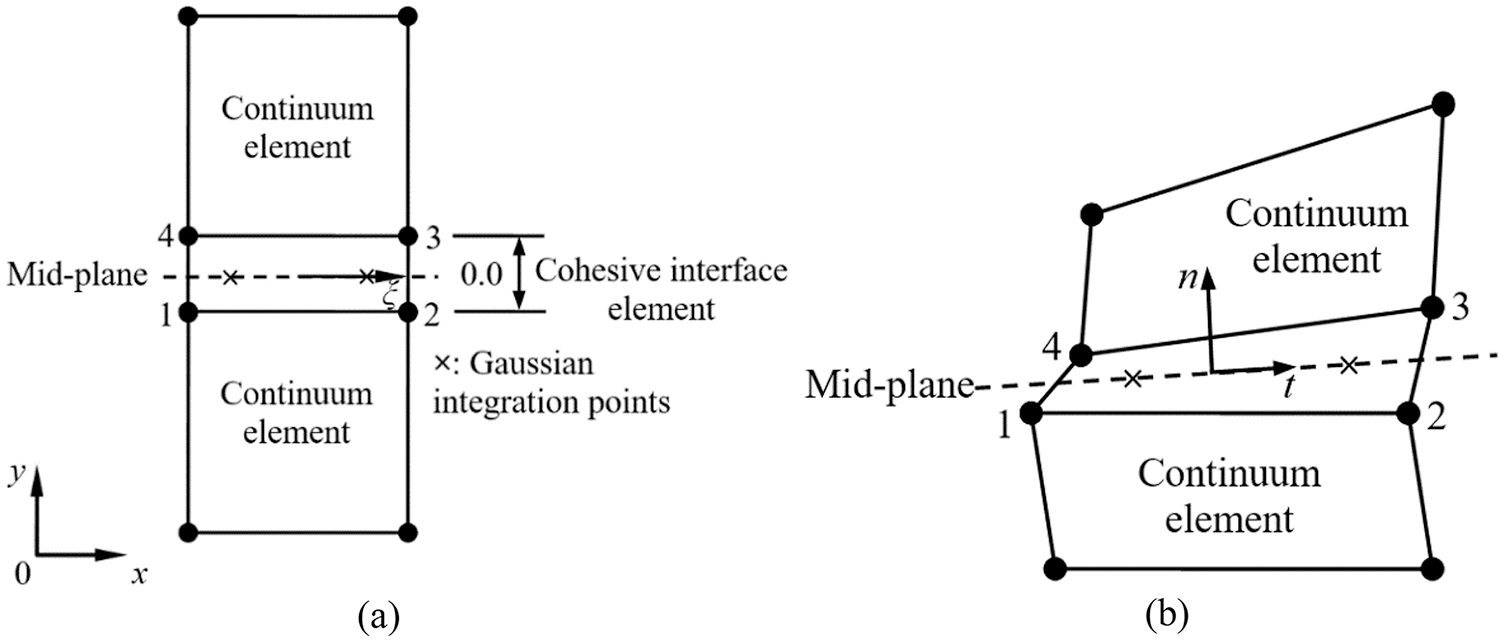
Figure 5: The cohesive interface element in (a) The initial configuration and (b) The deformed configuration
The nodal displacement vector of the four-node cohesive zone element is
The nodal displacements of the bottom and top nodes are
The separating displacement of the element is then expressed as
The continuous separating displacement field within the element is
With
where H(ξ) is a matrix of the shape function.
The nodal force vector is
where the tractions, T, are computed from the separating displacements via the cohesive zone law, which is shown in Section 2.3, and Ael is the area of the cohesive zone element. The tangential stiffness is computed by
where D is the cohesive constitutive tangent stiffness matrix derived by differentiating the traction with respect to the separation.
3.1 Effect of the Grain Aggregate Morphology on the Failure Behavior
Two-dimensional finite element models including a Cu pad, Sn3.0Ag0.5Cu solder and Cu6Sn5 grains were constructed, as presented in Fig. 5. To investigate the effect of the grain aggregate morphology, voronoi tessellations were utilized to generate three models with different shape coefficients: Model I with α1 = β1 = 0 (Fig. 6a), Model II with α2 = β2 = 0.3 (Fig. 6b), and Model III with α3 = β3 = 0.9 (Fig. 6c). An increase in the coefficients α and β indicates an increase in the irregularity of the grain aggregate morphology. The list of the related finite element models is given in Table 1. The average thickness of the IMC (Cu6Sn5) layer tm was defined by dividing the area A by its width L, i.e., tm = A/L, which were 9.5, 9.4 and 9.3 μm in the models. 48 grains and 138 grain boundaries were applied in each model.
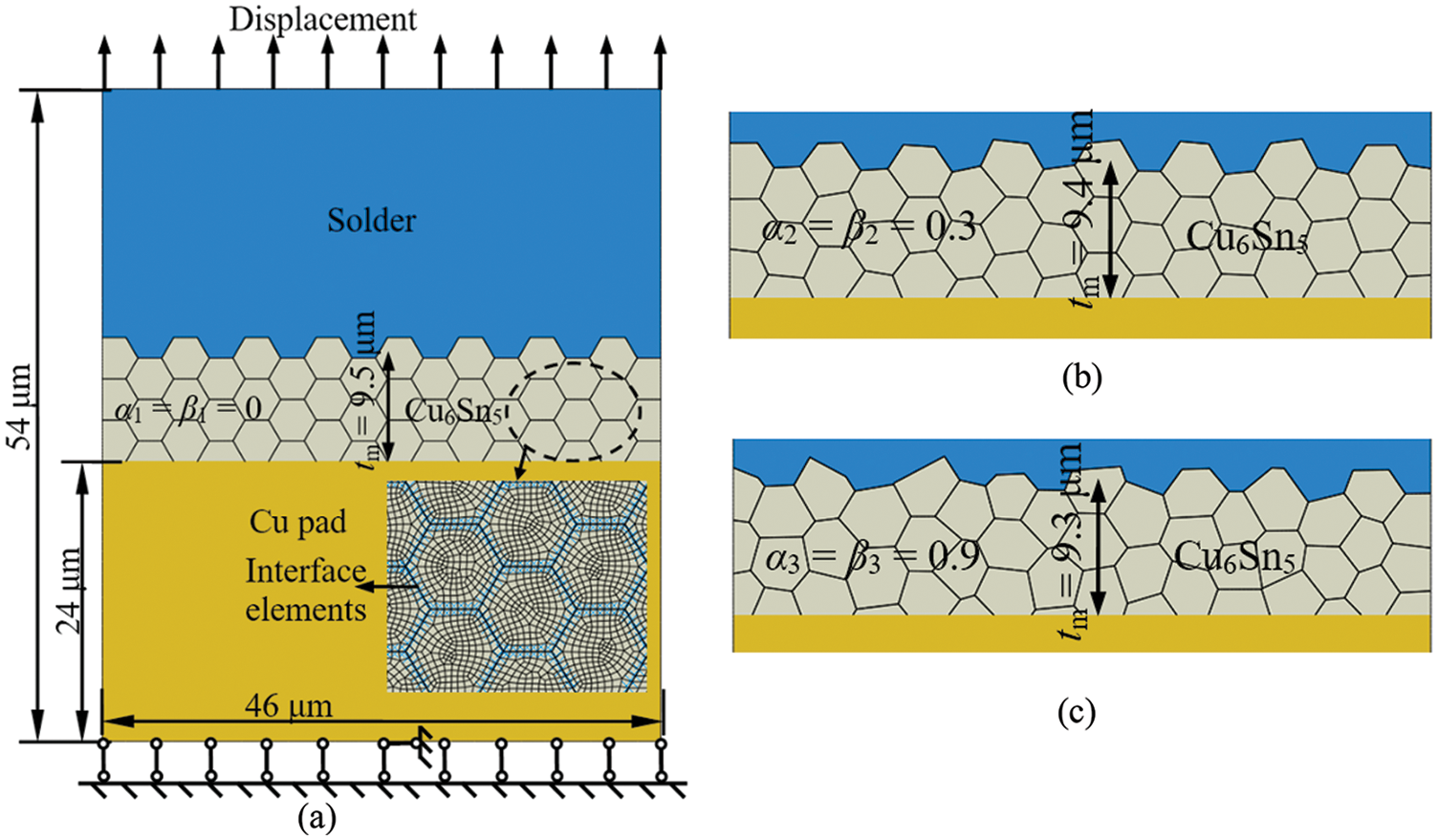
Figure 6: Models of solder/Cu6Sn5 grains/Cu pad structure with different grain aggregate morphologies: (a) Model I (α1 = β1 = 0), (b) Model II (α2 = β2 = 0.3), and (c) Model III (α3 = β3 = 0.9)
The CPE4 elements in ABAQUS were used to mesh the interior of the Cu6Sn5 grains, the solder, and the Cu pad. The cohesive zone elements described above were embedded along the grain boundaries. The boundary condition of the model is shown in Fig. 6a.
The Young’s modulus E, Poisson’s ratio ν, and the stress intensity factor KI of Cu6Sn5 are 119 GPa, 0.31, and 2.1 MPa⋅m1/2, respectively [39]. The critical energy release rate Gc of Cu6Sn5 can be calculated by
The cohesive energies are assumed to be equal to the critical energy release rate, i.e., ϕn = ϕt = Gc = 33.52 N/m. The maximum normal and tangential tractions are Tn,max = 68 MPa [40] and Tt,max = 28 MPa [41], respectively. The Young’s modulus and Poisson’s ratio of the Cu pad are 117 GPa and 0.34, respectively; The Young’s modulus and Poisson’s ratio of the Sn3.0Ag0.5Cu solder are 54 GPa and 0.36, respectively.
Fig. 7a shows the force-displacement response curves. The overall responses of the three models were almost the same, indicating that the overall response is not sensitive to the grain aggregate morphology. The results of the models with different grain aggregate morphologies show various possible crack configurations (Figs. 6c, 7b and 7d). The general direction of the three crack paths was normal to the loading axis. However, some noticeable deviations were produced by the irregular grain aggregate morphology. In Model I with α1 = β1 = 0 (Fig. 7b), the grain interfaces perpendicular to the loading direction were subjected to almost the same stress; thus, the microcracks initiated at those interfaces simultaneously. The crack configuration had a regular zigzag shape, and it remained perpendicular to the loading direction. In Model II with α2 = β2 = 0.3 (Fig. 7c), the main crack path was prone to be perpendicular to the loading direction, as in Model I, while the crack configuration was much more random due to the irregular grain aggregate morphology. Model III with α3 = β3 = 0.9 had the most random crack configuration among the three models (Fig. 7d). This indicates that the regular grain aggregate morphology can bias the propagation direction of the microcracks, and the irregular aggregate morphology results in a more random crack configuration.

Figure 7: (a) Effect of the grain aggregate morphology on the overall force-displacement response, (b) Crack configuration of Model I (α1 = β1 = 0), (c) Crack configuration of Model II (α2 = β2 = 0.3), and (d) Crack configuration of Model III (α3 = β3 = 0.9)
3.2 Effect of the Grain Boundary Defects on the Failure Behavior
To consider the grain boundary defects, a Weibull distribution [42] was applied to each of the parameters of the grain interfacial material. The four parameters of the cohesive zone law, the cohesive energies ϕn and ϕt, and the maximum tractions Tn,max and Tt,max, were all described by Weibull distributions according to the following probability density functions:
in which κ and λ are the Weibull parameters, which are measures of the variability in the material parameters.
The grain boundary defect effect for both the regular grain aggregate morphology model, Model I-W1∼W3 with α1 = β1 = 0, and the irregular grain aggregate morphology model, Model III-W1∼W3 with α3 = β3 = 0.9, was investigated. The list of the related models is given in Table 1. Models I and III, which have homogeneous grain interface properties, were used for comparison. In the models with material parameters with Weibull distributions, the grain facet was stochastically assigned a set of four parameters according to Eqs. (13a), (13b), (13c) and (13d) the four material parameters changed in a range from 0.5 to 1.5 of the values employed in Model I or III. Each grain facet had the same value of the parameters, and in this way, there were Nf different interface elements (Nf = number of facets in the microstructure). Three groups of Weibull parameters, W1 with κ1 = 5 and λ1 = 1, W2 with κ2 = 2.5 and λ2 = 0.8, and W3 with κ3 = 5 and λ3 = 1.5, were used. Fig. 8 shows the histogram for the number of grain facets with different maximum tractions.
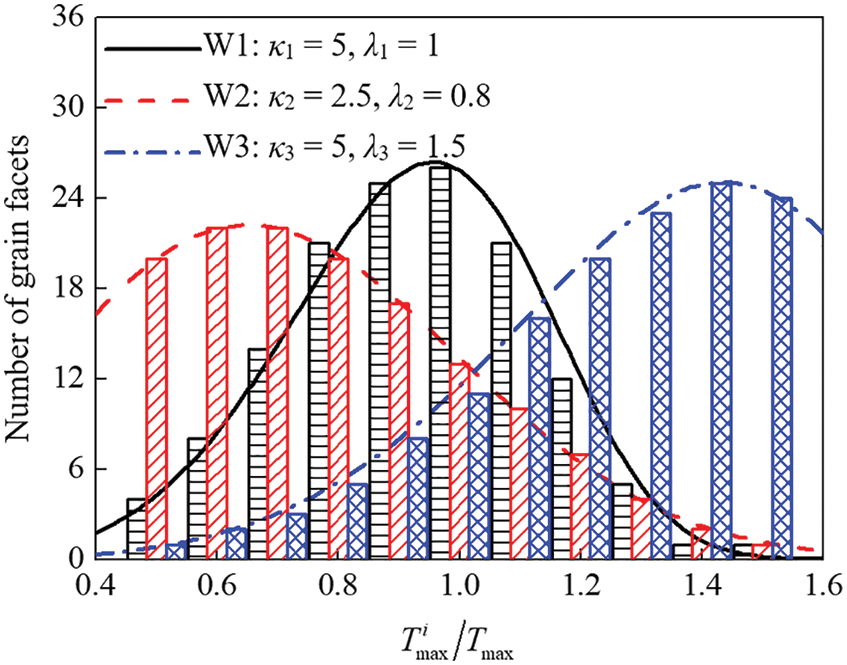
Figure 8: Weibull distribution of the grain interfacial maximum tractions
The overall force-displacement responses of the models with the interfacial material parameters with Weibull distributions are compared with that of the model with homogeneous interfacial material properties in Fig. 9. In Model I-W1 and Model III-W1 with Weibull parameters κ1 = 5 and λ1 = 1, 29% of the interface elements had higher interfacial strengths than those in Model I and Model III, and 52% of the interface elements had lower interfacial strengths. As a result, for both the regular grain aggregate morphology model (Fig. 9a) and the irregular grain aggregate morphology model (Fig. 9b), the overall strengths of Model I-W1 and Model III-W1 were approximately 14% lower than those of Model I and Model III, even though one-third of the total interfaces were stronger in Model I-W1 and Model III-W1 than in Model I and Model III. In Model I-W2 and Model III-W2 with Weibull parameters κ2 = 2.5 and λ2 = 0.8, 17% of the interface elements had higher interfacial strengths than those in Model I and Model III, and 73% of the interface elements had lower interfacial strengths. Since more weak interfaces existed in these models, the overall strengths of Model I-W2 and Model III-W2 were approximately 30% lower than those of Model I and Model III. Model I-W3 and Model III-W3 with Weibull parameters κ3 = 5 and λ3 = 1.5 had the strongest interfaces among the models, 78% of the interface elements had higher interfacial strengths than those in Model I and Model III, and only 14% of the interface elements had lower interfacial strengths. However, the overall strengths of Model I-W3 and Model III-W3 were only approximately 7% higher than those of Model I and Model III. The results indicate that the weak grain interfaces play a crucial role in the overall strength of the model.
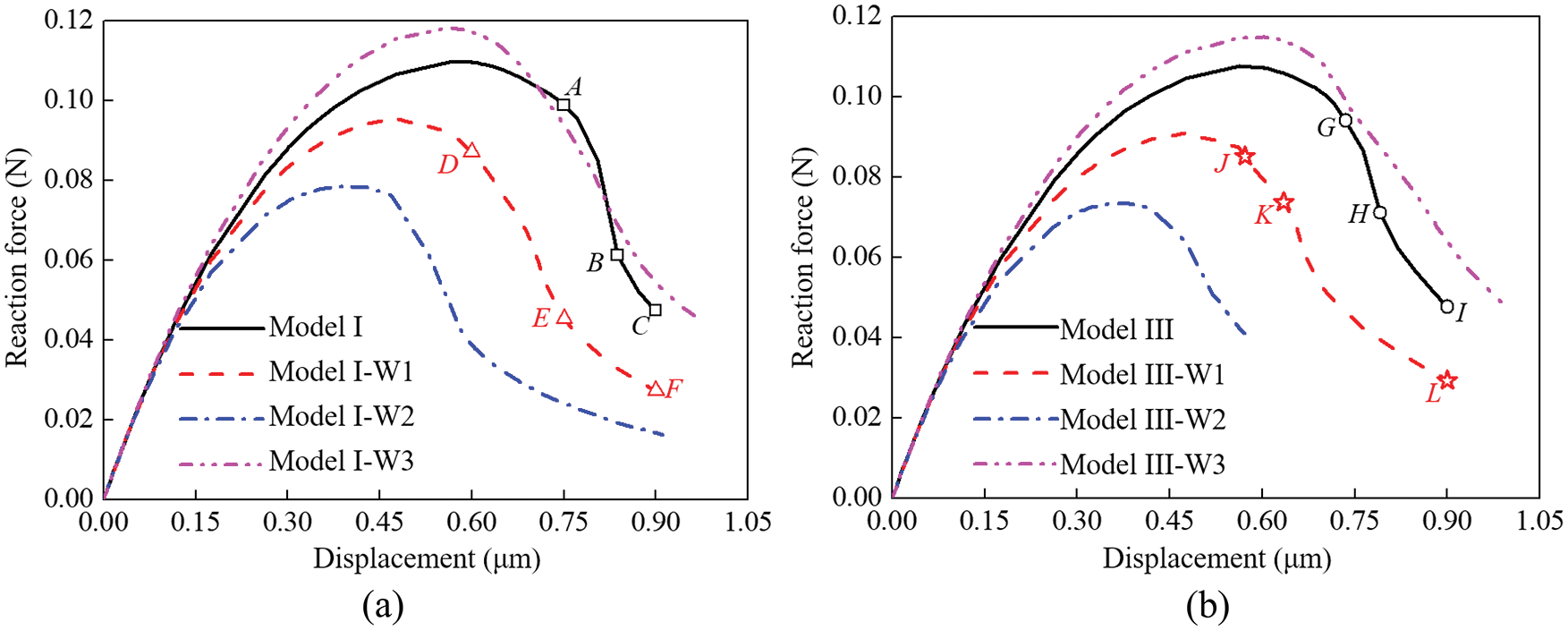
Figure 9: Effect of the grain interface property strategies on the overall force-displacement response: (a) Model with shape coefficients α1 = β1 = 0 and (b) Model with shape coefficients α3 = β3 = 0.9
To examine the difference in the crack configuration for the regular grain aggregate morphology model (shape coefficients α1 = β1 = 0) with different grain interface property strategies, three points labeled A, B and C for Model I in Fig. 9a were chose, and the corresponding crack configurations are shown in Figs. 10a–10c. Similarly, the crack configurations corresponding to points D, E and F for Model I-W1 in Fig. 9a are shown in Figs. 10d–10f.
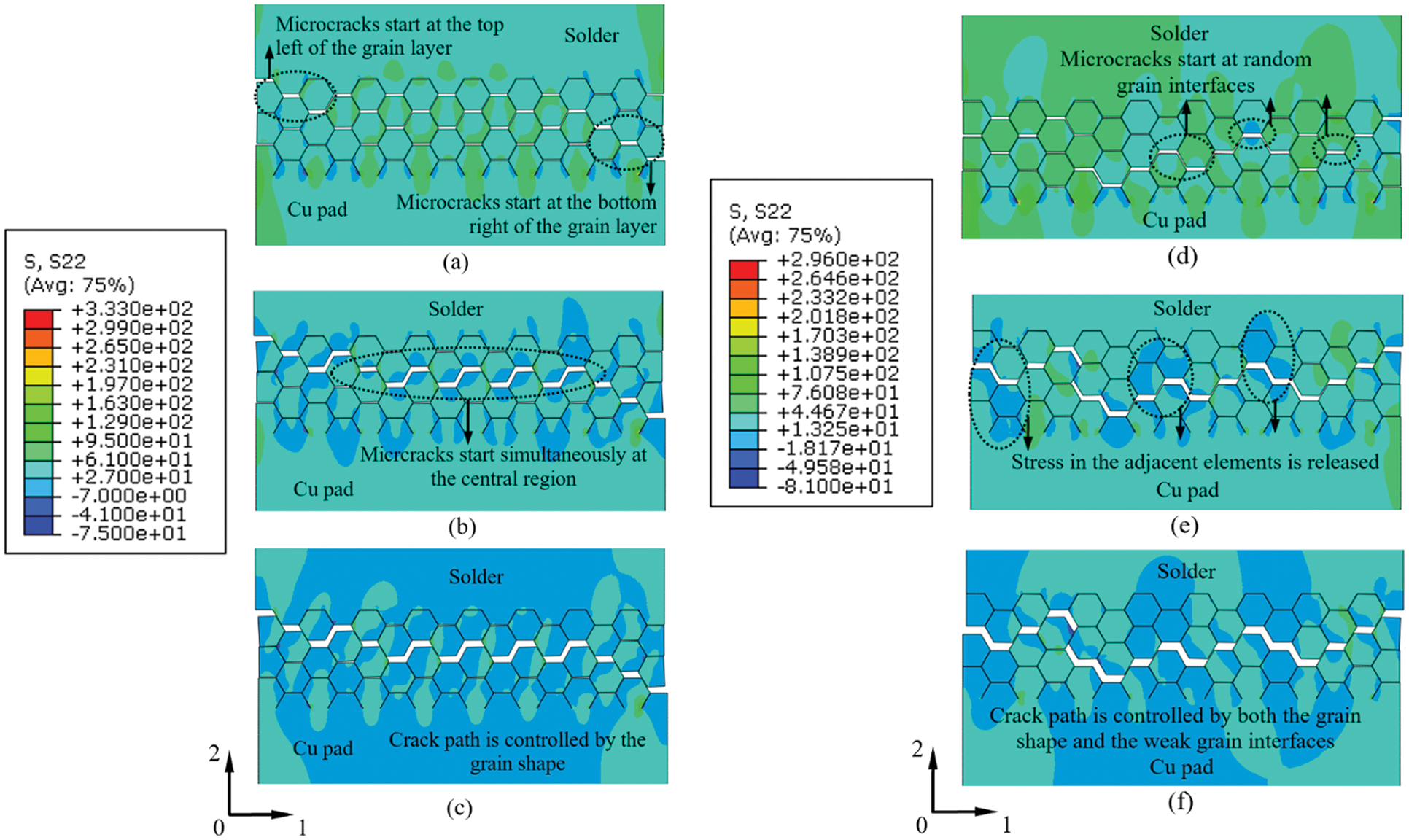
Figure 10: Crack configuration and stress σ22 of Model I at (a) Point A, (b) Point B, and (c) Point C, and Model I-W1 at (d) Point D, (e) Point E and (f) Point F in Fig. 9a
At point A, the microcracks initiated at the bottom right and top left of the grain layer (Fig. 10a). At point B, the microcracks occurred in the central region of the grain layer initiated almost simultaneously since the grain interfaces perpendicular to the loading direction were subjected to almost the same stress. The microcracks propagated and coalesced to form a main crack across the grain layer (Fig. 10b). At point C, the path of the main crack showed a regular zigzag shape, and the stress contours were generally symmetrical (Fig. 10c). In Model I, the crack configuration is determined by only the grain aggregate morphology, as all the grain interfaces have the same strength.
Figs. 10d–10f show the crack configuration and the vertical normal stress σ22 of Model I-W1. Owing to the existence of weak grain interfaces, the crack configuration of Model I-W1 was quite different from that of Model I, even though the same grain aggregate morphology was applied in the two models. At point D, the microcracks initiated at random grain interfaces (Fig. 10d). Although the grain interfaces perpendicular to the loading direction underwent a similar stress, the microcracks propagated along a random path rather than failed simultaneously, and with the development of the microcracks, the stress in the adjacent elements was released (Fig. 10e). The final crack configuration of Model I-W1 was much more irregular, and the stress contours were nonsymmetrical (Fig. 10f). In Model I-W1, the crack configuration is determined by both the grain aggregate morphology and the grain interface properties.
The effect of the grain boundary defects on the crack configuration for the irregular grain aggregate morphology model (shape coefficients α3 = β3 = 0.9) has been studied. Three points labeled G, H and I for Model III in Fig. 9b were chosen, and the corresponding crack configurations are shown in Figs. 11a–11c. Similarly, the crack configurations corresponding to points J, K and L for Model III-W1 in Fig. 9b are shown in Figs. 11d–11f.
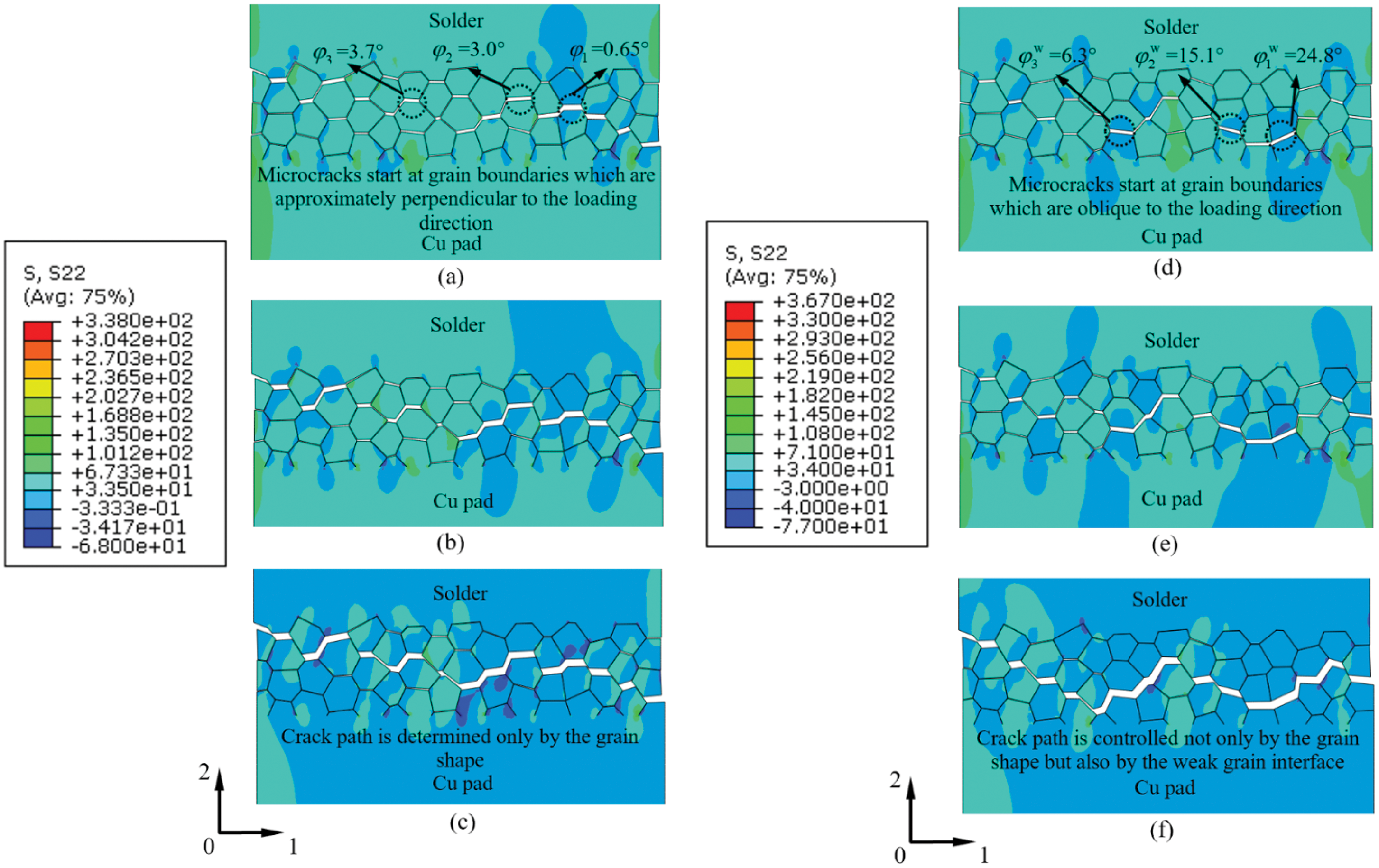
Figure 11: Crack configuration and stress σ22 of Model III at (a) Point G, (b) Point H and (c) Point I, and Model III-W1 at (a) Point J, (b) Point K and (c) Point L in Fig. 9b
Defining φ as the angle between the grain facet and the 1-axial direction, at load step G, the angles of the cracking grain interfaces were φ1 = 0.65°, φ2 = 3.0° and φ3 = 3.7°. These grain interfaces were approximately perpendicular to the loading direction (Fig. 10a). This suggests that microcracks are prone to initiate at grain interfaces whose angle φ is small. This can be explained by Fig. 12. As shown in Fig. 12a, when the displacement in the y direction is u, the normal opening separation between two grains is δn = u. When the same displacement u is applied in the grains in Fig. 11b, in which the local reference frame is not superposed with the global frame, the normal opening separation is δn = u⋅cosφ. Therefore, the normal opening separation at the grain interface decreases with increasing grain facet angle φ. This indicates that microcracks are prone to occur in the grain interfaces that are perpendicular to the loading direction, and it is more difficult for an oblique grain interface to start cracking. At point H, the microcracks propagated, and more grain interfaces opened (Fig. 11b). The microcracks coalesced to form a main crack, and the crack path was random due to the irregular grain aggregate morphology (Fig. 11c).
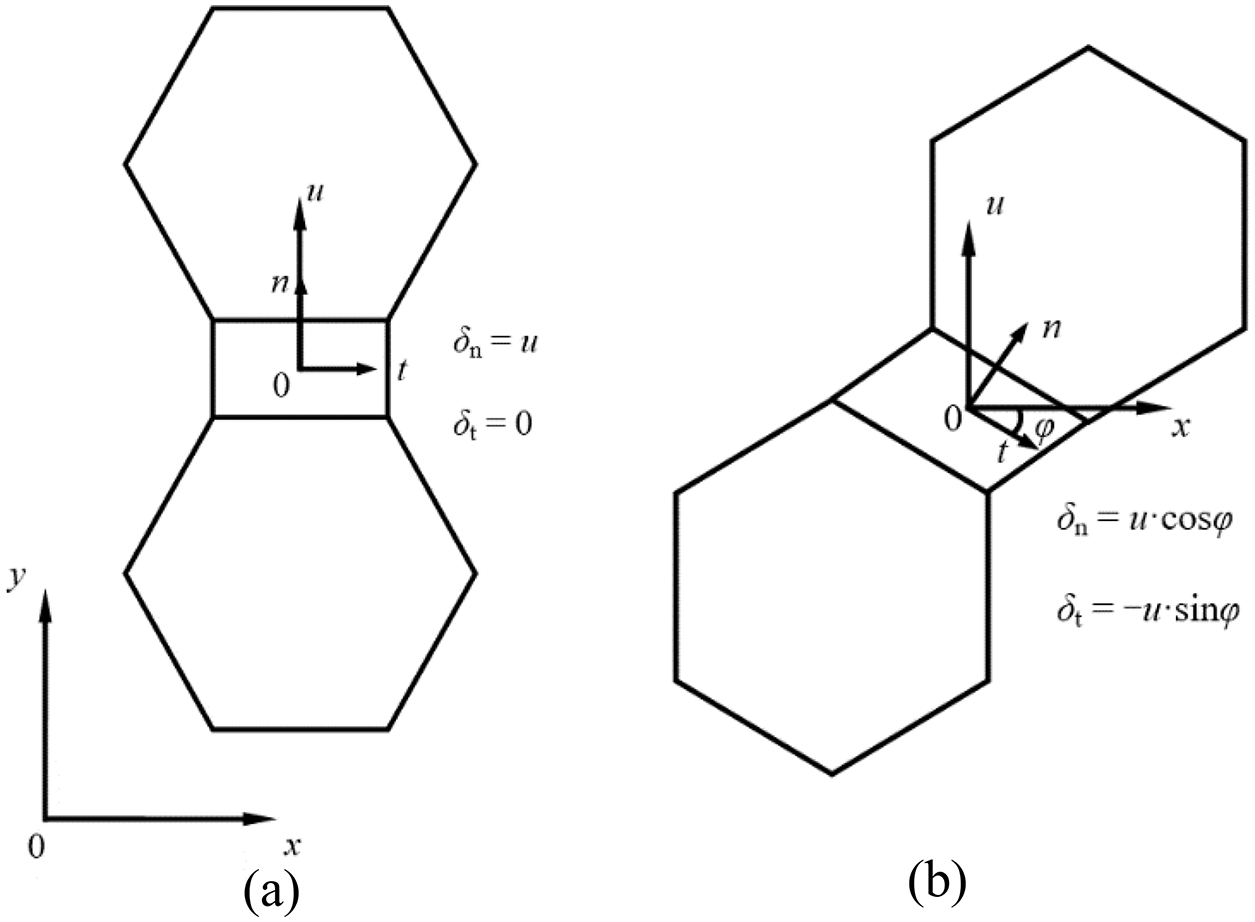
Figure 12: Effect of the grain facet angle on the separation: (a) The grain facet is perpendicular to the loading direction; (b) The grain facet is oblique to the loading direction
Figs. 11d–11f show the crack configuration and the vertical normal stress σ22 of Model III-W1. At load step J, the microcracks initiated at different locations from those in Model III. The angles of the cracking grain interfaces were
3.3 Effect of the Normal and Tangential Strengths of the Grain Interfaces on the Failure Behavior of the IMC
The normal and tangential traction-separation laws control the normal opening separation between grains and the grain boundary sliding, respectively. There are two possible grain motions, as demonstrated in Fig. 13. At one extreme, when the normal strength is low, the two grains may separate directly without any tangential sliding displacement (Fig. 13a). At the other extreme, when the tangential strength is low, the two grains may slide along their boundary without any normal opening separation (Fig. 13b). For most cases, both the normal and tangential strengths exist at grain interfaces, but their magnitudes in the two directions are different. The lowest strength always controls the mechanical behavior of the grains.
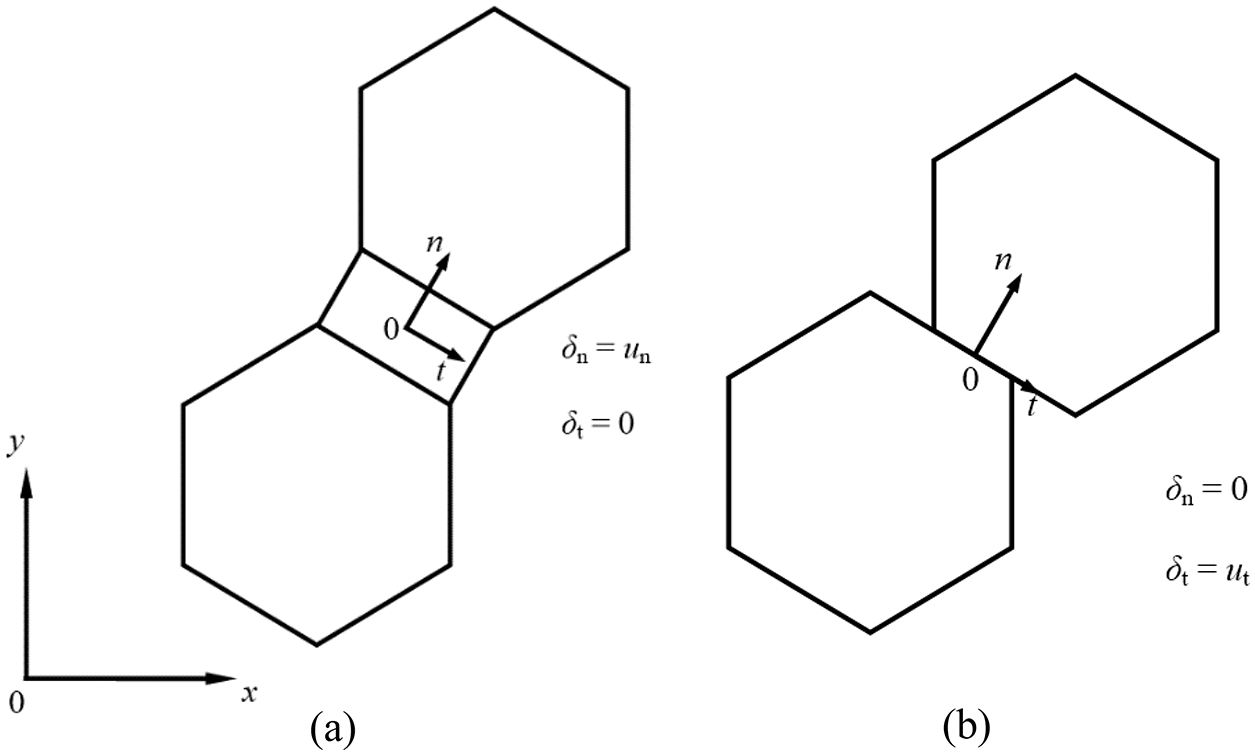
Figure 13: Deformation modes of the interface element: (a) Pure normal opening separation and (b) Pure tangential sliding separation
The thickness of IMC layer in the finite element model applied here was 15.5 μm. Model IV-N and Model IV-T were used in this study, as depicted in Fig. 14. In Model IV-N, the maximum traction in the normal direction was larger than that in the tangential direction, and the parameters of the cohesive zone law were ϕn = ϕt = 33.52 N/m, Tn,max = 68 MPa and Tt,max = 28 MPa. In contrast, in Model IV-T, the maximum traction in the tangential direction was larger than that in the normal direction, and the parameters of the cohesive zone law were ϕn = ϕt = 33.52 N/m, Tn,max = 27 MPa and Tt,max = 60 MPa [43].
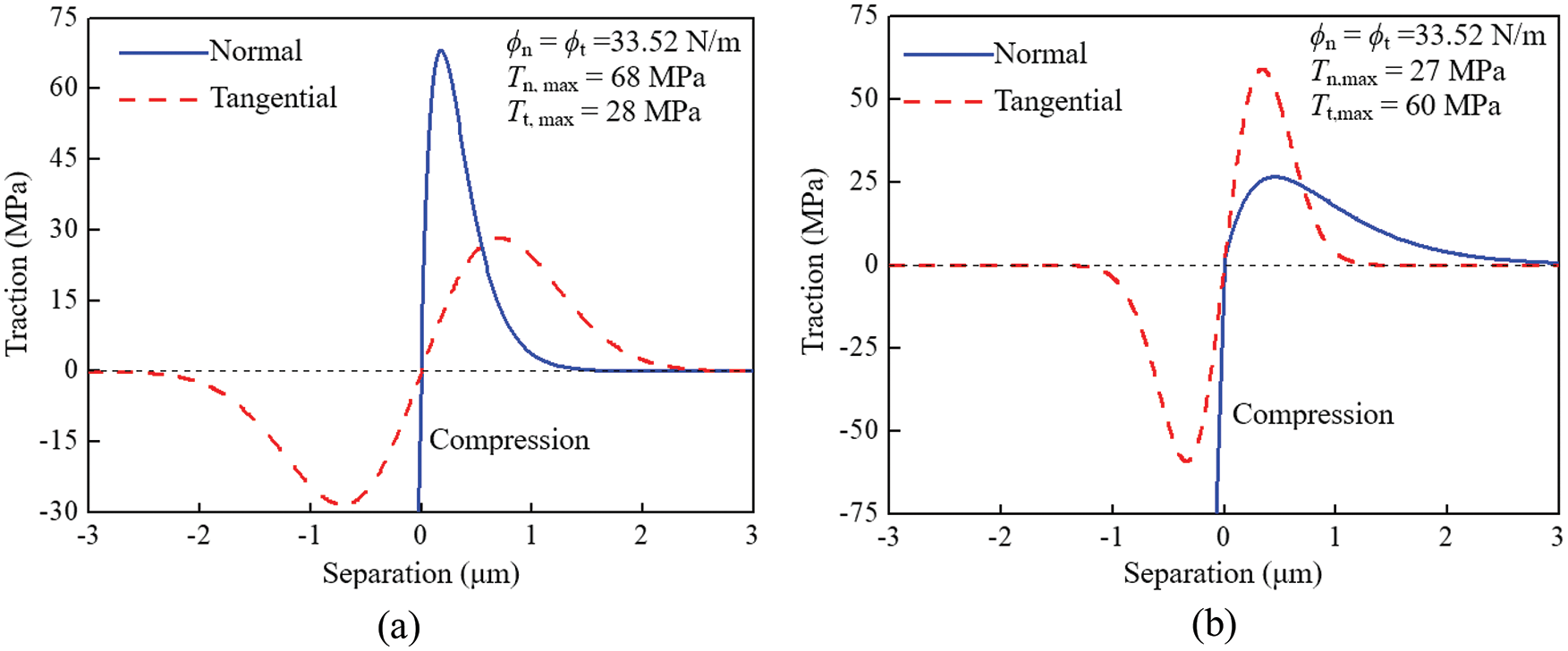
Figure 14: Normal and tangential traction-separation curves of (a) Model IV-N with ϕn = ϕt = 33.52 N/m, Tn,max = 68 MPa, and Tt,max = 28 MPa and (b) Model IV-T with ϕn = ϕt = 33.52 N/m Tn,max = 27 MPa, and Tt,max = 60 MPa
Fig. 15a gives the overall responses of the two models. The force-displacement curve of Model IV-N is very similar to a typical stress-strain curve for ductile materials, which shows a large amount of plastic deformation before failure. The force-displacement curve of Model IV-T shows features of brittle materials, which are characterized by sudden and rapid failure with little plastic deformation.
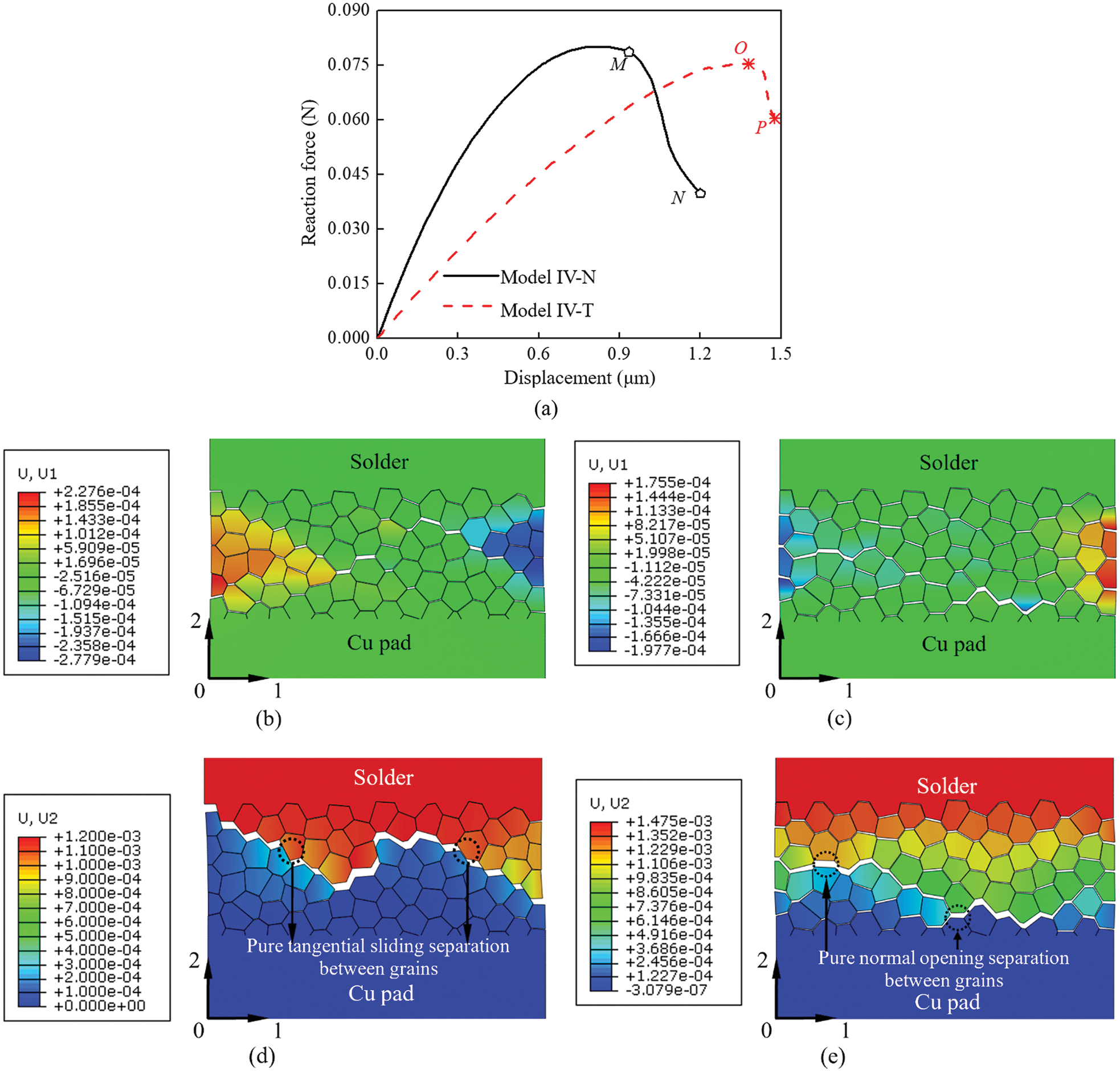
Figure 15: (a) Effect of the cohesive zone law parameters on the overall force-displacement response, crack configuration and displacement result u1 at (b) Point M in (a) for model IV-N, and (c) Point O in (a) for model IV-T, crack configuration and displacement result u2 at (d) Point N in (a) for model IV-N and (e) Point P in (a) for model IV-T
To examine the difference in the crack configuration for Model IV-N and Model IV-T, load steps labeled M and N for Model IV-N and O and P for Model IV-T in Fig. 15a were selected, and the corresponding crack configurations are shown in Figs. 15b∼15e.
Fig. 15b shows the displacement results u1 of Model IV-N at load step M. The grains were prone to slide along boundaries due to the low strength in the tangential direction of the grain interfaces; as a result, the grain region contracted, analogous to the necking phenomenon in ductile materials. Fig. 15c gives the displacement results u1 of Model IV-T at load step O. In this model, the grains were prone to separate directly from each other due to the low strength in the normal direction of the grain interfaces. The grains were extruded in this way because it was difficult for them to slide past the adjacent grains, which led to expansion of the grain region. This phenomenon is quite analogous to the dilatancy effect in rock-like materials.
Fig. 15d shows the displacement results u2 of Model IV-N at load step N. As the grains in Model IV-N were prone to slide along boundaries, the microcracks propagated along a zigzag path across the grain region. Fig. 15e shows the displacement results u2 of Model IV-T at load step P. Compared to Model IV-N, the main crack path in Model IV-T was straight and perpendicular to the loading direction. This is because the strength in the normal direction of the grain interfaces was lower in Model IV-T, and the low strength direction in the grain interfaces was the same direction as the loading direction; thus, most of these grain interfaces cracked and coalesced to form a relatively straight crack path.
The overall strains ε11 of the grain region in the two models are compared in Fig. 16. In Model IV-N, the grains were prone to slide along grain boundaries due to the low strength in the tangential direction of grain interfaces. Therefore, a contracting deformation was observed under tensile loading, and ε11 of Model IV-N was negative. In contrast, in Model IV-T, the grains were prone to separating rather than tangential sliding due to the low strength in the normal direction of the grain interfaces. The grains pushed against each other instead of sliding along the grain boundaries; as a result, the model expanded, and ε11 of Model IV-T was positive.
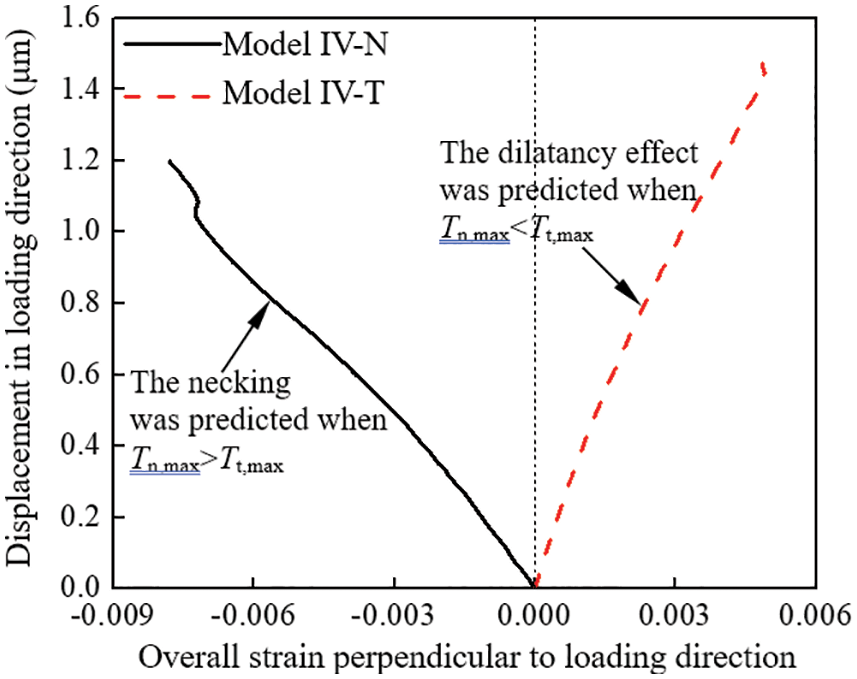
Figure 16: Effect of the cohesive zone law parameters on the overall strain of the grain region, ε11
In this paper, a micromechanical model was constructed to explicitly predict the microcrack initiation, random crack path morphology and failure mode of the IMC. The influences of the grain aggregate morphology, the grain boundary defects and the sensitivity of the various cohesive zone parameters in predicting the overall mechanical response were investigated, and the following important points were derived:
(1) The overall mechanical strength of the IMC is not sensitive to the grain aggregate morphology, but the crack configuration depends greatly on the grain aggregate morphology. In the regular grain model, the crack path is relatively regular, while in the irregular grain model, the crack path is much more random.
(2) The overall strength of the model is determined dominantly by the weak grain interfaces. In the model with material parameters described by Weibull distributions, the crack configuration is controlled by not only the grain aggregate morphology but also the weak grain interfaces.
(3) The maximum tractions in the normal and tangential directions of the grain interfaces are critical in determining the overall strength, deformation, microcrack propagation and failure mode of the model. When the maximum traction in the normal direction is larger than that in the tangential direction, the necking phenomenon occurs during model deformation. When the maximum traction in the normal direction is smaller than that in the tangential direction, the dilatancy effect can be predicted by the model.
To close, it is necessary to mention that the role of the Cu3Sn layer was neglected in this study, and the effect of the Cu3Sn layer will be considered in the future modeling work.
Funding Statement: This research was supported by the National Natural Science Foundation of China (NSFC) under Grant 11872078, and Beijing Natural Science Foundation No. 3222005.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Bang, W. H., Moon, M. W., Kim, C. U., Kang, S. H., Jung, J. P. et al. (2008). Study of fracture mechanics in testing interfacial fracture of solder joints. Journal of Electronic Materials, 37(4), 417–428. DOI 10.1007/s11664-008-0393-8. [Google Scholar] [CrossRef]
2. Jing, J. P., Gao, F., Johnson, J., Liang, F. Z., Williams, R. L. et al. (2009). Simulation of dynamic fracture along solder-pad interfaces using a cohesive zone model. Engineering Failure Analysis, 16, 1579–1586. DOI 10.1016/j.engfailanal.2008.10.019. [Google Scholar] [CrossRef]
3. Alam, M. O., Lu, H., Bailey, C., Chan, Y. C. (2009). Fracture mechanics analysis of solder joint intermetallic compounds in shear test. Computational Materials Science, 45(2), 576–583. DOI 10.1016/j.commatsci.2008.12.001. [Google Scholar] [CrossRef]
4. Zavattieri, P. D., Espinosa, H. D. (2003). A grain level model for the study of failure initiation and evolution in polycrystalline brittle materials. Part I: Theory and numerical implementation. Mechanics of Materials, 35(3–6), 333–364. DOI 10.1016/S0167-6636(02)00285-5. [Google Scholar] [CrossRef]
5. Zavattieri, P. D., Espinosa, H. D. (2003). A grain level model for the study of failure initiation and evolution in polycrystalline brittle materials. Part II: Numerical examples. Mechanics of Materials, 35(3–6), 365–394. DOI 10.1016/S0167-6636(02)00287-9. [Google Scholar] [CrossRef]
6. Onck, P., van der Giessen, E. (1998). Micromechanics of creep fracture: Simulation of intergranular crack growth. Computational Materials Science, 13(1–3), 90–102. DOI 10.1016/S0927-0256(98)00049-4. [Google Scholar] [CrossRef]
7. Ghosh, S., Liu, Y. (1995). Voronoi cell finite element model based on micropolar theory of thermoelasticity for heterogeneous materials. International Journal for Numerical Methods in Engineering, 38(8), 1361–1398. DOI 10.1002/(ISSN)1097-0207. [Google Scholar] [CrossRef]
8. Wu, M. S., Niu, J. (1995). Micromechanical prediction of the compressive failure of ice: Model development. Mechanics of Materials, 20(1), 9–32. DOI 10.1016/0167-6636(94)00047-K. [Google Scholar] [CrossRef]
9. Wu, M. S., Niu, J. (1995). Micromechanical prediction of the compressive failure of ice: Numerical simulations. Mechanics of Materials, 20(1), 33–58. [Google Scholar]
10. Toi, Y., Kiyosue, T. (1995). Damage mechanics models for brittle microcracking solids based on three-dimensional mesoscopic simulations. Engineering Fracture Mechanics, 50(1), 11–27. DOI 10.1016/0013-7944(94)00160-J. [Google Scholar] [CrossRef]
11. Barbe, F., Decker, L., Jeulin, D., Cailletaud, G. (2001). Intergranular and intragranular behavior of polycrystalline aggregates. Part 1: F.E. model. International Journal of Plasticity, 17(4), 513–536. DOI 10.1016/S0749-6419(00)00061-9. [Google Scholar] [CrossRef]
12. Barbe, F., Forest, S., Cailletaud, G. (2001). Intergranular and intragranular behavior of polycrystalline aggregates. Part 2: Results. International Journal of Plasticity, 17(4), 537–563. DOI 10.1016/S0749-6419(00)00062-0. [Google Scholar] [CrossRef]
13. Musienko, A., Cailletaud, G. (2009). Simulation of inter-and transgranular crack propagation in polycrystalline aggregates due to stress corrosion cracking. Acta Materialia, 57(13), 3840–3855. DOI 10.1016/j.actamat.2009.04.035. [Google Scholar] [CrossRef]
14. An, T., Qin, F. (2013). Intergranular cracking simulation of the intermetallic compound layer in solder joints. Computational Materials Science, 79, 1–14. DOI 10.1016/j.commatsci.2013.05.044. [Google Scholar] [CrossRef]
15. Zeng, X., Li, S. (2010). A multiscale cohesive zone model and simulations of fracture. Computer Methods in Applied Mechanics and Engineering, 199(9–12), 547–556. DOI 10.1016/j.cma.2009.10.008. [Google Scholar] [CrossRef]
16. Li, S., Zeng, X., Ren, B., Qian, J., Zhang, J. et al. (2012). An atomistic-based interphase zone model for crystalline solids. Computer Methods in Applied Mechanics and Engineering, 229, 87–109. DOI 10.1016/j.cma.2012.03.023. [Google Scholar] [CrossRef]
17. Hosford, W. (2010). Solid mechanics. New York, USA: Cambridge University Press. [Google Scholar]
18. Zavattieri, P. D. (2000). Computational modeling for bridging size scales in the failure of solids (Ph.D. Thesis). Purdue University, West Lafayette, IN, USA. [Google Scholar]
19. Barenblatt, G. I. (1962). Mathematical theory of equilibrium cracks. Advances in Applied Mechanics, 7, 56–129. [Google Scholar]
20. Dugdale, D. S. (1960). Yielding of steel sheets containing slits. Journal of the Mechanics and Physics of Solids, 8(2), 100–104. DOI 10.1016/0022-5096(60)90013-2. [Google Scholar] [CrossRef]
21. Needleman, A. (1987). A continuum model for void nucleation by inclusion debonding. Journal of Applied Mechanics, 54, 525–531. DOI 10.1115/1.3173064. [Google Scholar] [CrossRef]
22. Chandra, N., Li, H., Shet, C., Ghonem, H. (2002). Some issues in the application of cohesive zone models for metal-ceramic interfaces. International Journal of Solids and Structures, 39(10), 2827–2855. DOI 10.1016/S0020-7683(02)00149-X. [Google Scholar] [CrossRef]
23. Salih, S., Davey, K., Zhenmin, Z. (2019). A computationally efficient cohesive zone model for fatigue. Fatigue & Fracture of Engineering Materials & Structures, 42(2), 518–532. DOI 10.1111/ffe.12927. [Google Scholar] [CrossRef]
24. Li, H., Li, L., Fan, J. K., Yue, Z. F. (2021). Verification of a cohesive model-based extended finite element method for ductile crack propagation. Fatigue & Fracture of Engineering Materials & Structures, 44(3), 762–775. DOI 10.1111/ffe.13392. [Google Scholar] [CrossRef]
25. Maio, U. D., Greco, F., Leonetti, L., Luciano, R., Blasi, P. N. et al. (2019). A refined diffuse cohesive approach for the failure analysis in quasibrittle materials--part II: Application to plain and reinforced concrete structures. Fatigue & Fracture of Engineering Materials & Structures, 42(12), 2764–2781. DOI 10.1111/ffe.13115. [Google Scholar] [CrossRef]
26. Yu, D. Q., Wang, L. (2008). The growth and roughness evolution of intermetallic compounds of Sn-Ag-Cu/Cu interface during soldering reaction. Journal of Alloys and Compounds, 458(1–2), 542–547. DOI 10.1016/j.jallcom.2007.04.047. [Google Scholar] [CrossRef]
27. Yazzie, K. E., Xie, H. X., Williams, J. J., Chawla, N. (2012). On the relationship between solder-controlled and intermetallic compound (IMC)-controlled fracture in Sn-based solder joints. Scripta Materialia, 66(8), 586–589. DOI 10.1016/j.scriptamat.2012.01.009. [Google Scholar] [CrossRef]
28. Qian, J., Li, S. (2011). Application of multiscale cohesive zone model to simulate fracture in poly-crystalline solids. ASME Journal of Engineering Materials and Technology, 133(1), 011010. DOI 10.1115/1.4002647. [Google Scholar] [CrossRef]
29. Fan, H., Shi, C., Li, S. (2013). Application of multiscale process zone model to simulate fracture in polycrystalline solids. Journal of Multiscale Modeling, 5(4), 1350015. DOI 10.1142/S1756973713500157. [Google Scholar] [CrossRef]
30. Xu, X. P., Needleman, A. (1993). Void nucleation by inclusion debonding in a crystal matrix. Modelling and Simulation in Materials Science and Engineering, 1(2), 111–132. DOI 10.1088/0965-0393/1/2/001. [Google Scholar] [CrossRef]
31. Tvergaard, V., Hutchinson, J. W. (1992). The relation between crack growth resistance and fracture process parameters in elastic-plastic solids. Journal of the Mechanics and Physics of Solids, 40(6), 1377–1397. DOI 10.1016/0022-5096(92)90020-3. [Google Scholar] [CrossRef]
32. Geubelle, P. H., Baylor, J. S. (1998). Impact-induced delamination of composites: A 2D simulation. Composites Part B: Engineering, 29(5), 589–602. DOI 10.1016/S1359-8368(98)00013-4. [Google Scholar] [CrossRef]
33. van den Bosch, M. J., Schreurs, P. J. G., Geers, M. G. D. (2006). An improved description of the exponential Xu and needleman cohesive zone law for mixed-mode decohesion. Engineering Fracture Mechanics, 73(9), 1220–1234. DOI 10.1016/j.engfracmech.2005.12.006. [Google Scholar] [CrossRef]
34. Espinosa, H. D., Zavattieri, P. D., Emore, G. L. (1998). Adaptive FEM computation of geometric and material nonlinearities with application to brittle failure. Mechanics of Materials, 29(3–4), 275–305. DOI 10.1016/S0167-6636(98)00018-0. [Google Scholar] [CrossRef]
35. Luther, T., Könke, C. (2009). Polycrystal models for the analysis of intergranular crack growth in metallic materials. Engineering Fracture Mechanics, 76(15), 2332–2343. DOI 10.1016/j.engfracmech.2009.07.006. [Google Scholar] [CrossRef]
36. Van den Bosch, M. J., Schreurs, P. J. G., Geers, M. G. D. (2007). A cohesive zone model with a large displacement formulation accounting for interfacial fibrillation. European Journal of Mechanics-A/Solids, 26(1), 1–19. DOI 10.1016/j.euromechsol.2006.09.003. [Google Scholar] [CrossRef]
37. Qiu, Y., Grisfield, M. A., Alfano, G. (2001). An interface element formulation for the simulation of delamination with buckling. Engineering Fracture Mechanics, 68(16), 1755–1776. DOI 10.1016/S0013-7944(01)00052-2. [Google Scholar] [CrossRef]
38. Gao, Y. F., Bower, A. F. (2004). A simple technique for avoiding convergence problems in finite element simulations of crack nucleation and growth on cohesive interfaces. Modelling and Simulation in Materials Science and Engineering, 12(3), 453–463. DOI 10.1088/0965-0393/12/3/007. [Google Scholar] [CrossRef]
39. Ghosh, G. (2004). Elastic properties, hardness, and indentation fracture toughness of intermetallics relevant to electronic packaging. Journal of Materials Research, 19(5), 1439–1454. DOI 10.1557/JMR.2004.0193. [Google Scholar] [CrossRef]
40. Prakash, K. H., Sritharan, T. (2004). Tensile fracture of tin-lead solder joints in copper. Materials Science and Engineering: A, 379(1–2), 277–285. DOI 10.1016/j.msea.2004.02.049. [Google Scholar] [CrossRef]
41. Zhao, J., Cheng, C. Q., Qi, L., Chi, C. Y. (2009). Kinetics of intermetallic compound layers and shear strength in bi-bearing SnAgCu/Cu soldering couples. Journal of Alloys and Compounds, 473(1–2), 382–388. DOI 10.1016/j.jallcom.2008.05.082. [Google Scholar] [CrossRef]
42. Weibull, W., Sweden, S. (1951). A statistical distribution function of wide applicability. Journal of Applied Mechanics, 18, 293–297. DOI 10.1115/1.4010337. [Google Scholar] [CrossRef]
43. Lee, H. T., Chen, M. H., Jao, H. M., Liao, T. L. (2003). Influence of interfacial intermetallic compound on fracture behavior of solder joints. Materials Science and Engineering: A, 358(1–2), 134–141. DOI 10.1016/S0921-5093(03)00277-6. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools