Login
Register
Submit a Paper
Propose a Special lssue
Open Access
ARTICLE
Novel Distance Measures on Hesitant Fuzzy Sets Based on Equal-Probability Transformation and Their Application in Decision Making on Intersection Traffic Control
1 Naval Architecture and Port Engineering College, Shandong Jiaotong University, Weihai, 264209, China
2 College of Transport and Communications, Shanghai Maritime University, Shanghai, 201306, China
3 College of Automotive and Traffic Engineering, Nanjing Forestry University, Nanjing, 210037, China
4 School of Civil and Environmental Engineering, Ningbo University, Ningbo, 315211, China
5 School of Business, National University of Singapore, 118414, Singapore
6 Durham Law School, Durham University, Durham, DH1 3LE, UK
* Corresponding Author: Yi Zhao. Email:
(This article belongs to the Special Issue: Decision making Modeling, Methods and Applications of Advanced Fuzzy Theory in Engineering and Science)
Computer Modeling in Engineering & Sciences 2023, 135(2), 1589-1602. https://doi.org/10.32604/cmes.2022.022431
Received 09 March 2022; Accepted 07 June 2022; Issue published 27 October 2022
View Full Text
Download PDFAbstract
The purpose of this study is to reduce the uncertainty in the calculation process on hesitant fuzzy sets (HFSs). The innovation of this study is to unify the cardinal numbers of hesitant fuzzy elements (HFEs) in a special way. Firstly, a probability density function is assigned for any given HFE. Thereafter, equal-probability transformation is introduced to transform HFEs with different cardinal numbers on the condition into the same probability density function. The characteristic of this transformation is that the higher the consistency of the membership degrees in HFEs, the higher the credibility of the mentioned membership degrees is, then, the bigger the probability density values for them are. According to this transformation technique, a set of novel distance measures on HFSs is provided. Finally, an illustrative example of intersection traffic control is introduced to show the usefulness of the given distance measures. The example also shows that this study is a good complement to operation theories on HFSs.Keywords
As an important tool of group decision making, hesitant fuzzy set (HFS) assigns the membership degree of an element to a set with a set of possible values [0,1] ([1–5]). Distance is a fundamental feature in describing the relationship between HFSs. It is well known that when the distance of different hesitant fuzzy elements (HFEs) are calculated, their cardinalities should be unified firstly ([6–9]). How to realize it? The classical models usually extend the shorter HFE until they have the same cardinal number. Usually, the shorter HFE is extended by putting more minimum value, maximum value, or any value in it with the existing ones. Actually, many values empirically exist in the shorter HFE. Thus, it is very necessary to improve the classical distance measures on HFSs by using some novel techniques to unify the cardinal numbers of the calculated HFEs. In this study, the cardinality problem is considered in another way, where equal-probability mapping, cardinality, and impulse function are combined to define a kind of novel distance measures for HFSs. Based on the new proposed distance measures, any two HFSs with different cardinal numbers can be dealt with as the same in the case that they have the same number of elements. Such a theory is feasible from the point of probability ([10–12]), and some classical studies on the combination of probability theory and hesitation fuzzy sets please refer to Liu et al. [13], Liu et al. [14], etc. Meanwhile, since this kind of technique is of multi-source heterogeneous data, it can also be used in intuitionistic fuzzy sets (IFSs). For example, Mahmood et al. [15] divided the information on IFSs and HFSs into different grades, and proposed a novel algorithm to integrate this information. Similarly, the research results of this study can be extended to the field of IFSs too.
The characteristic of the newly proposed method is to make full use of the existing decision making information, and not to add artificial one, so as to keep the objectivity of decision making process. The technique adopted in the proposed method is equal probability transformation, which guarantees the constant probability of the theoretical truth value appearing at each point before and after the transformation. Besides, this technique is also suitable to be used in aggregation operators on HFSs. For more details on this issue, please refer to Xia et al. [16]. To describe the idea clearly, the remainder of this study is arranged as follows. Section 2 introduces some basic concepts on HFSs, and introduces a series of classical distance measures. Section 3 introduces the concept of equal-probability transformation on HFSs, gives three properties of the transformation, and proposes a series of improved distance measures. Section 4 introduces a traffic control mode decision making problem, and solves it by the proposed improved distance measures on HFSs. Finally, the main innovation points are concluded in Section 5.
In this section, some basic definitions and some classical distance measures on HFSs are reviewed. For convenience’s sake X={x1,x2,…,xn}, is denoted as the discourse set throughout this study.
Definition 1 (Torra [2]) Let X be a given set, an HFS E on X is demonstrated as a function that when applied to X returns a subset of [0,1], which can be described as E={⟨x,hE(x)⟩|x∈X}, where hE(x) is a set of values in [0,1], representing the possible membership degrees of the element x to the HFS E. For convenience, hE(x) is called an HFE. The classical definition of distance measure on HFSs was addressed by Xu et al. [4] as follows.
Definition 2 (Xu et al. [4]) Let M and N be two HFSs on X, then the distance measure on M and N is described as d(M,N), which satisfies the following three properties, i.e., (i) 0≤d(M,N)≤1, if and only if M=N; (ii) d(M,N)=d(N,M). By referring to Hamming distance and the Euclidean distance, Xu et al. (2011) defined.
Definition 3 (Xu et al. [4]) Let M and N be two HFSs on X. For any xi∈X(1≤i≤n), let l(hM(xi)) and l(hN(xi)) be the cardinal numbers of hM(xi) and hN(xi), respectively. Then, the hesitant normalized Hamming distance, Euclidean distance and generalized hesitant normalized distance are proposed as
dh(M,N)=1n∑ni=1[1lxi∑lxij=1|hσ(j)M(xi)−hσ(j)N(xi)|],(1)
de(M,N)=[1n∑ni=1(1lxi∑lxij=1|hσ(j)M(xi)−hσ(j)N(xi)|2)]1/2,(2)
dg(M,N)=[1n∑ni=1(1lxi∑lxij=1|hσ(j)M(xi)−hσ(j)N(xi)|λ)]1/λ,(3)
where lxi=max{l(hM(xi)),l(hN(xi))}, λ>0, hσ(j)M(xi) and hσ(j)N(xi) are the jth largest values in hM(xi) and hN(xi), respectively. It is noteworthy that l(hM(xi))≠l(hN(xi)) holds in most cases, to operate them correctly, one should extend the shorter one until the cardinal numbers of hM(xi) and hN(xi) are the same.
Definition 4 (Xu et al. [4]) Let M and N be two HFSs on X, if one takes the weight wi(i=1,2,…,n) of each element xi∈X into account, the generalized hesitant weighted distance is proposed as
dwg(M,N)=[∑ni=1wi(1lxi∑lxij=1|hσ(j)M(xi)−hσ(j)N(xi)|λ)]1/λ.(4)
where λ>0.
In classical calculation process on HFSs, to satisfy Eqs. (1)–(4), part of the information on HFSs has to be artificially added when the cardinality of HFEs is different. In an environment characterized by uncertainty, this process further increases the uncertainty of computing problems and weakens support for decision-makers. To reduce the uncertainty in the calculation for HFSs, for any given HFE h1 with any given cardinal number i(i∈N), the task of this study is to transfer h1 to a new HFE h2 with cardinal number j for any given j(j∈N), where h1 and h2 are the same in statistics. Generally speaking, this transformation consists of two parts. Firstly, a probability density function for HFE is proposed. Secondly, an equal-probability transformation function is given.
3.1 Probability Density Function for HFE
From the viewpoint of probability, the truth value of membership function of any given HFE can appear at any point between the smallest and the largest occurred membership degree, but the probability of occurrence is different for different values. Logically, the probability that a certain point is the true value of membership degree of HFE is related to the occurred value of membership degree near this point. When the occurred value of membership degree function is far away from the point, it is thought that the probability of the true value in this point is low; otherwise, the probability is high. Guided by this idea, a probability density function for HFE is introduced as follows.
Definition 5 Suppose that there is an HFE h={h1,h2,…,hm}, and suppose that h1≤h2≤⋯≤hm. Then, a probability density function for h is given as
p(¯h,ε)={0,¯h<h1or¯h≥hm;1(m−1)(hi+1−hi),hi≤¯h<hi+1,hi−1<hi<hi+1<hi+2;1(m−1)(hi+1−h−εi),hi+ε≤¯h<hi+1,hi−1=hi<hi+1<hi+2;1(m−1)(hi+1−h+εi),hi≤¯h<hi+1−ε,hi−1<hi<hi+1=hi+2;1(m−1)(hi+1−h−2εi),hi+ε≤¯h<hi+1−ε,hi−1=hi<hi+1=hi+2;12(m−1)ε,hi−ε≤¯h<hi+1+ε,hi=hi+1,(5)
where 0<ε<12minhi≠hi−1{|hi−hi−1|}, whereas P(hi≤¯h≤hi+1)=limε→0+∫hi+1+εhi−εp(¯h,ε)dh=1m−1.
On the probability density function for HFSs, some properties are summarized as follows.
Property 1 By Eq. (5), for any given HFE h, there is only one probability density function p(¯h) which corresponds to it.
Property 2 If any given HFE h and its probability density function p(¯h), for any interval [hi,hi+1] in the definition domain of p(¯h), the smaller is the value hi+1−hi, the bigger the value of P(hi≤¯h≤hi+1) is.
Property 3 If any given HFE h and its probability density function p(¯h), for any duplicate elements hi in h, there is an impulse function P(hi) in p(¯h). The more able is hi, the stronger the impulse function is.
3.2 Equal-Probability Function and Their Properties
For any given HFE, the occurrence interval of the true value of its membership degree can be calculated by Eq. (5). On the premise of keeping the probability density function of true value at any point in the interval unchanged, the expression form of HFE can be changed by specific skills. Specifically, the equal-probability function for HFSs is proposed in this subsection.
Definition 6 Suppose that there is an HFE h={h1,h2,…,hm}, where h1≤h2≤⋯≤hm. Suppose the probability density function for h is given as p(¯h;ε). Then, the set h′={h′1,h′2,…,h′n} is defined as the equal-probability mapping of h to h′, where h′1=h1, h′n=hm, and for any j∈{1,2,…,n−1}, it holds that
P(h′j≤¯h≤h′j+1)=limε→0+∫h′j+1+εh′j−εp(¯h;ε)d¯h=1n−1.(6)
By using Definition 6, an HFE is transferred to another new HFE under the condition that the two variables share the same probability distribution function. An important property on equal-probability function for HFSs is introduced as follows.
Property 4 Suppose that there are two HFEs h={h1,h2,…,hm} and h′={h′1,h′2,…,h′n}, where h1≤h2≤⋯≤hm, h′1≤h′2≤⋯≤h′n. Suppose that p(¯h,ε)=p(¯h′,ε). Denote E′(¯h)=1m−1m∑i=1hi, E′(¯h′)=1n−1n∑j=1h′j. Then, it holds that E′(¯h)=E′(¯h′).
Proof By Eq. (5), it gets that ∫hmh1p(¯h,ε)d¯h=m−1∑i=1hi⋅P(hi≤¯h≤hi+1). ∫h′nh′1p(¯h,ε)d¯h=n−1∑j=1h′j⋅P(h′j≤¯h≤hj+1). Since p(¯h,ε)=p(h′,ε), it gets m−1∑i=1hi⋅P(hi≤¯h≤hi+1)=n−1∑j=1h′j⋅P(h′j≤¯h≤h′j+1). For any i∈{1,2,…,m}, j∈{1,2,…,n}, by Eq. (6), it gets that P(hi≤¯h≤hi+1)=1m−1, P(h′j≤¯h≤h′j+1)=1n−1. Therefore, it gets that 1m−1m−1∑i=1hi=1nn∑j=1h′j, i.e., E(¯h)=E(¯h′).
To illustrate Definition 6 clearly, a case is given as follows.
Case 1 Suppose that there is an HFE h∗={0.25,0.35,0.35,0.45}. Please calculate the probability density function P(¯h∗), and transfer h∗ to a new HFE h∗∗ with cardinal number 6, where P(¯h∗)=P(¯h∗∗).
Firstly, the probability density function for h∗ is obtained by Eq. (5), which is denoted as
p(¯h∗,ε)={0,¯h<0.25or¯h≥0.45;103,0.25≤¯h<0.35;16ε,0.35−ε≤¯h<0.35+ε;103,0.35+ε≤¯h<0.45.
Secondly, by Eq. (6), p(¯h∗,ε) is transferred to
p(¯h∗∗,ε)={0,¯h<0.25or¯h≥0.45;103,0.25≤¯h<0.35;16ε,0.35−ε≤¯h<0.35+ε;103,0.35+ε≤¯h≤0.39;103,0.39≤¯h≤0.45.
Therefore, it gets h∗∗={0.25,0.31,0.35,0.35,0.39,0.45}. Obviously, it holds p(¯h∗,ε)=p(¯h∗∗,ε).
By further study, Def. 7 is obtained in the following.
Definition 7 Suppose that there are K HFSs h1,h2,…,hK on X={x1,x2,…,xN}, and for any xi∈X(1≤i≤N), the set of membership values of xi to hk(1≤k≤K) is defined as hk(xi)={h1k(xi),h2k(xi),…,hl(hk(xi))k(xi)}, where l(hk(xi)) is the cardinal number of hk(xi) for any k∈{1,2,…,K}. Rank the elements of hk(xi) by monotone increasing order, and denote the ranking result as h′′k(xi)=(h′′1k(xi),h′′2k(xi),…,hl(hk(xi))k(xi)). Denote N′(xi)=max{l(hk(xi))}(1<k≤K). For any h′′k(xi), if l(h′′k(xi))=N′(xi) then remain h′′k(xi) as what it should be, otherwise, note h′′k(xi) as →hk(xi), where →hk(xi)=(→hk1(xi),→hk2(xi),…,→hkl(hk(xi))(xi)). For every →hk(xi), if any →hkj1(xi) and →hkj2(xi) are equal, it is thought that there is an impulse. If more →hkj∗(xi) are equal, it is thought that the impulse is stronger. In order to distinguish them from other →hkj(xi), denote →hkj∗(xi) as →→hj∗k(xi). If any →→hj∗k(xi)=→→h(j−1)∗k(xi), for any given ε(h(xi)), it is obtained that when →→hj∗k(xi)→→→h(j−1)∗k(xi), it holds ε(→→hj∗k(xi)−→→h(j−1)∗k(xi))→0, where ∫→→hj∗k(xi)→→hk(j−1)∗(xi)[ε(h(xi))]−1=1. Moreover, by Eq. (5), it gets the probability density function of →hk(xi) as
pij(→hk(xi))={1(l(h′′k(xi))−1)(→hjk(xi)−→hj−1k(xi)),→hj−1k(xi)≤x<→hjk(xi),1(l(h′′k(xi))−1)ε(x),|x−→→hj∗k(xi)|<ε.(7)
Definition 8 Suppose that there are K HFSs h1,h2,…,hK on X∈{x1,x2,…,xN}. For any →hk(xi), divides the interval [→hk1(xi),→hkl(hk(xi))(xi)] into N′(xi)−1 sub-intervals, and denote its corresponding set of segmentation points as ^hk(xi)={→hk1(xi),→hk2(xi),…,→hkN′(xi)(xi)}, where ^hk1(xi) equals →hk1(xi), and ^hkj(xi) satisfies ∫^hkj(xi)^hkj−1(xi)pij(→hk(xi))dx=(N∗−1)−1. It is noteworthy that there is a possibility that there are some ^hkj(xi) and ^hkj−1(xi) are equal. By
¯hk(xi)={hk′′(xi),l(hk′′(xi))=N′(xi),^hk(xi),l(hk′′(xi))≠N′(xi),(8)
K new sets ¯hk(xi)(k=1,2,…,K) are constructed. For any k∈{1,2,…,K}, rank all the elements of ¯hk(xi) in monotonically increasing order, and denote the result as h∗k(xi)={h∗k(x1),h∗k(x2),…,h∗k(xN)}, where h∗k(xi)={h1∗k(xi),h2∗k(xi),…,hN′(xi)∗k(xi)}.
3.3 Improved Distance Measures on HFSs
By using equal-probability equations, a series of improved distance measures on HFSs are obtained as follows.
Definition 9 Suppose that there are K HFSs h1,h2,…,hK on X={x1,x2,…,xN}. For any k1,k2∈{1,2,…,K}, the improved hesitant normalized Hamming distance, Euclidean distance and generalized hesitant normalized distance between hk1 and hk2 on X are proposed as
dsth(hk1,hk2)=1n∑ni=1[1N′(xi)⋅∑N′(xi)j=1|hj∗k1(xi)−hj∗k2(xi)|],(9)
dste(hk1,hk2)=1n∑ni=1[1N′(xi)⋅∑N′(xi)j=1|hj∗k1(xi)−hj∗k2(xi)|2]12,(10)
and
dstg(hk1,hk2)=1n∑ni=1[1N′(xi)⋅∑N′(xi)j=1|hj∗k1(xi)−hj∗k2(xi)|λ]1λ,(11)
where λ>0, hj∗k1(xi) and hj∗k2(xi) are the jth ordinal values in hj∗k1(xi) and hj∗k2(xi), respectively.
Definition 10 When one takes the weight wi of each element xi∈X into account, a generalized hesitant weighted distance is obtained as
dstwg(hk1,hk2)={∑ni=1wi[1N′(xi)⋅∑N′(xi)j=1|hj∗k1(xi)−hj∗k1(xi)|λ]1λ}.(12)
Analogously, for any x∈X, the distance between two HFEs hk1(x) and hk2(x) is defined as
dst1(hk1(x),hk2(x))=1N′(xi)⋅∑N′(xi)j=1|hj∗k1(xi)−hj∗k2(xi)|,(13)
dst2(hk1(x),hk2(x))=(1N′(xi)⋅∑N′(xi)j=1|hj∗k1(xi)−hj∗k2(xi)|2)12,(14)
dst3(hk1(x),hk2(x))=(1N′(xi)⋅∑N′(xi)j=1|hj∗k1(xi)−hj∗k2(xi)|λ)1λ,(15)
where λ>0, hj∗k1(x) and hj∗k2(x) are the jth ordinal values in hj∗k1(x) and hj∗k2(x), respectively.
In terms of cardinality, Eqs. (9)–(15) are consistent with Eqs. (1)–(4). To illustrate the performance of the proposed distance measures, an example is given in the following section.
At present, the at-grade intersection is an important kind of complex node in urban road. In traffic engineering fields, there are three basic methods of traffic control which could be implemented at an intersection, i.e., “method 1-uncontrolled intersection”; “method 2-intersection with right assignment using Yield or Stop signs”; and “method 3-signalized intersection” [17]. For the sake of understanding, these three kinds of traffic control modes are illustrated by the picture (Figs. 1–3), respectively.
Figure 1: Method 1 traffic control
Figure 2: Method 2 traffic control
Figure 3: Method 3 traffic control
In China, the most frequently used traffic control modes at intersections are “roundabout control”, “Yield or Stop signs control”, and “traffic signal control”, where they also belong to the above three control methods, respectively [18]. For the sake of convenience, these three kinds of control models are denoted by E1,E2,E3. To select a suitable type of control mode for an intersection, traffic engineers usually consider many factors which include “the grades of the intersection”, “traffic flow volumes”, “saturation degrees (the ratio of traffic demand to traffic capacity) of the entrance lanes”, and “geographical position of the intersection in the city”. Here, the aforementioned four kinds of factors are denoted by f1,f2,f3 and f4. Suppose in Pudong District, Shanghai City, China, an intersection E0 needs to be designed and constructed. Suppose that the traffic control modes E1,E2,E3 all satisfy existing government standards (Ministry of Housing and Urban-Rural Development of the People’s Republic of China [19]; Ministry of Construction of the People’s Republic of China [20]; Ministry of Housing and Urban-Rural Development of the People’s Republic of China [21]). Then, the novel proposed decision making method is used to determine the intersection’s traffic control mode [22]. To choose the suitable control method, nine INTs in Pudong district, Shanghai city are investigated which are all in good traffic control effects and they contain all the three traffic control modes E1,E2,E3. Denote F1 as the fuzzy set “the highway grade” where the better the functions of the intersection, the larger is the membership degree F1; denote F2 as the fuzzy set “traffic flow volume”; denote F3 as the fuzzy set “saturation degree of the traffic flow”; and denote F4 as the fuzzy set “geographical position” where the nearer the distance between the related intersection and the city center is, the larger is the membership degree of the intersection to F4. Then, the membership degree of each intersection to each attribute is obtained in Table 1.
By information aggregation, E1,E2,E3 are expressed as E1={hE1(F1),hE1(F2),hE1(F3),hE1(F4)}, E2={hE2(F1),hE2(F2),hE2(F3),hE2(F4)}, E3={hE3(F1),hE3(F2),hE3(F3),hE3(F4)}, where hE1(F1)={0.75,0.78,0.82,0.79,0.81},hE2(F1)={0.81,0.86,0.81,0.78,0.76},
hE3(F1)={0.72,0.74,0.78,0.78,0.75},hE1(F2)={0.81,0.84,0.77,0.79,0.85},
hE2(F2)={0.78,0.76,0.84,0.78,0.81},hE3(F2)={0.79,0.78,0.81,0.85,0.75},
hE1(F3)={0.82,0.88,0.84,0.79,0.86,0.85,0.87},hE2(F3)={0.78,0.76,0.81,0.88,0.89,0.79,0.78},
hE3(F3)={0.88,0.82,0.89,0.85,0.87,0.87,0.86},hE1(F4)={0.76,0.79,0.78,0.81,0.82,0.84,0.85},
hE2(F4)={0.85,0.86,0.81,0.78,0.76,0.79,0.83},hE3(F4)={0.80,0.82,0.84,0.88,0.75,0.77,0.83}.
Similarly, the studied intersection could be expressed as a hesitant fuzzy set E0={⟨F1,{0.70,0.89}⟩},{⟨F2,{0.75,0.80}⟩},{⟨F3,{0.72,0.74}⟩},{⟨F4,{0.75,0.81}⟩}. Moreover, the weight vector for f1,f2,f3,f4 is known as WT=(0.30,0.25,0.25,0.20).
In this subsection, the decision making problem is solved by using the novel distance measures. Firstly, sort the elements of each h′′E1(Fj)(i=1,2,3;j=1,2,3,4) by using ascending counts, and denote the calculation results as h′′E1(F1)=(0.75,0.78,0.79,0.81,0.82), h′′E2(F1)=(0.76,0.78,0.81, 0.81,0.86), h′′E1(F2)=(0.77,0.79,0.81,0.84,0.85),h′′E2(F2)=(0.76,0.78,0.78,0.81,0.84), h′′E3(F2)=(0.75,0.78,0.79,0.81,0.85),h′′E1(F3)=(0.79,0.82,0.84,0.85,0.86,0.87,0.88),
h′′E2(F3)=(0.76,0.78,0.78,0.79,0.81,0.88,0.89),h′′E3(F3)=(0.82,0.85,0.86,0.87,0.87,0.88,0.89),
h′′E1(F4)=(0.76,0.78,0.79,0.81,0.82,0.84,0.85),h′′E2(F4)=(0.76,0.78,0.79,0.81,0.83,0.85,0.86),
h′′E3(F4)=(0.75,0.77,0.80,0.82,0.83,0.84,0.88). Next, by the definition of N∗, N∗=7. Since N1≠7, N2≠7, N3=7, N4=7, for any i=1,2,3, remain all the h′′Ei(F3) and h′′Ei(F4) as what it should be, and denote h′′Ei(F1) as →hEi(F1), and h′′Ei(F2) as →hEi(F2).
Thereafter, for every →hEi(F1) and →hEi(F2), denote their corresponding probability density function as
p11(x)={253,0.75≤x<0.78,25,0.78≤x<0.79,252,0.79≤x<0.81,25,0.81≤x≤0.82,,p21(x)={252,0.76≤x<0.78,253,0.78≤x<0.81,18ε,0.81−ε<x<0.81+ε,5,0.81<x≤0.86,,
p31(x)={252,0.72≤x<0.74,25,0.74≤x<0.75,253,0.75≤x<0.78,18ε,0.78−ε<x≤0.78+ε,,p12(x)={252,0.77≤x<0.79,252,0.79≤x<0.81,253,0.81≤x<0.84,25,0.84≤x≤0.85,,
p22(x)={252,0.76≤x<0.78,18ε,0.78−ε<x<0.78+ε,253,0.78+ε<x≤0.81,253,0.81<x≤0.84,,p32(x)={253,0.75≤x<0.78,25,0.78≤x<0.79,252,0.79≤x<0.81,254,0.81≤x≤0.85,.
Then, the intervals corresponding to →hE1(F1), →hE2(F1), →hE3(F1), →hE1(F2), →hE2(F2), →hE3(F2) are [0.75,0.82], [0.76,0.86], [0.72,0.78], [0.77,0.85], [0.76,0.84], [0.75,0.85]. Divide them by Eq. (5) in proper sequence, and the seven sets of segmentation points are obtained as
^hE1(F1)={0.750,0.770,0.783,0.790,0.803,0.813,0.820},
^hE2(F1)={0.760,0.773,0.790,0.810,0.810,0.827,0.860},
^hE3(F1)={0.720,0.733,0.743,0.750,0.770,0.780,0.780},
^hE1(F2)={0.770,0.783,0.797,0.810,0.830,0.843,0.850},
^hE2(F2)={0.760,0.773,0.780,0.780,0.800,0.820,0.840},
^hE3(F2)={0.750,0.770,0.783,0.790,0.803,0.823,0.850}.
The following, by ^hE1(F1), ^hE2(F1), ^hE3(F1), ^hE1(F2), ^hE3(F2), and h′′E1(F3), h′′E2(F3), h′′E3(F3), h′′E1(F4), h′′E2(F4), h′′E3(F4). It is obtained that ¯E1={^hE1(F1),^hE1(F2),h′′E1(F3),h′′E1(F4)}, ¯E2={^hE2(F1),^hE2(F2),h′′E2(F3),h′′E2(F4)}, ¯E3={^hE3(F1),^hE3(F2),h′′E3(F3),h′′E3(F4)}. Subsequently, for any k∈{1,2,3}, rank all the elements of ¯Ek in monotonically increasing order, and denote the result as E∗k.
Analogously, E0 is transferred to E∗0={h∗E0(F1),h∗E0(F2),h∗E0(F3),h∗E0(F4)}, where h∗E0(F1)={0.700,0.732,0.763,0.795,0.827,0.858,0.890},
h∗E0(F2)={0.750,0.758,0.767,0.775,0.783,0.792,0.800},
h∗E0(F3)={0.720,0.723,0.727,0.730,0.733,0.737,0.740},
h∗E0(F4)={0.750,0.760,0.770,0.780,0.790,0.800,0.810}.
For λ=1,2,…,10, by using Eq. (12), and taking the weights of f1, f2, f3 and f4 into account, three kinds of generalized hesitant weighted distances dstwg(E∗1,E∗0), dstwg(E∗2,E∗0), and dstwg(E∗3,E∗0) are obtained, respectively, which are shown in Fig. 4. Besides, for any given λ=1,2,…,10, the differences between dλ(E1,E0) and dλ(E2,E0) are very small. Thereafter, Fig. 5 contrasts E1 and E2.
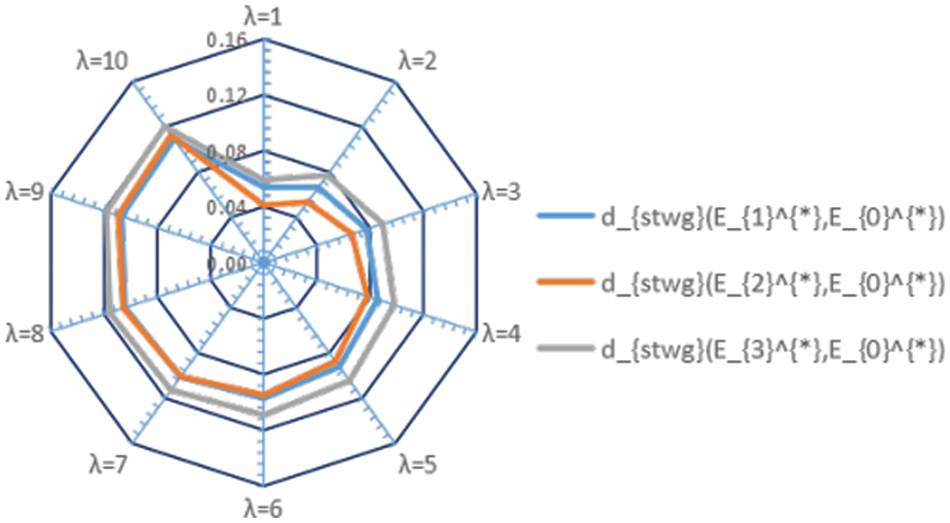
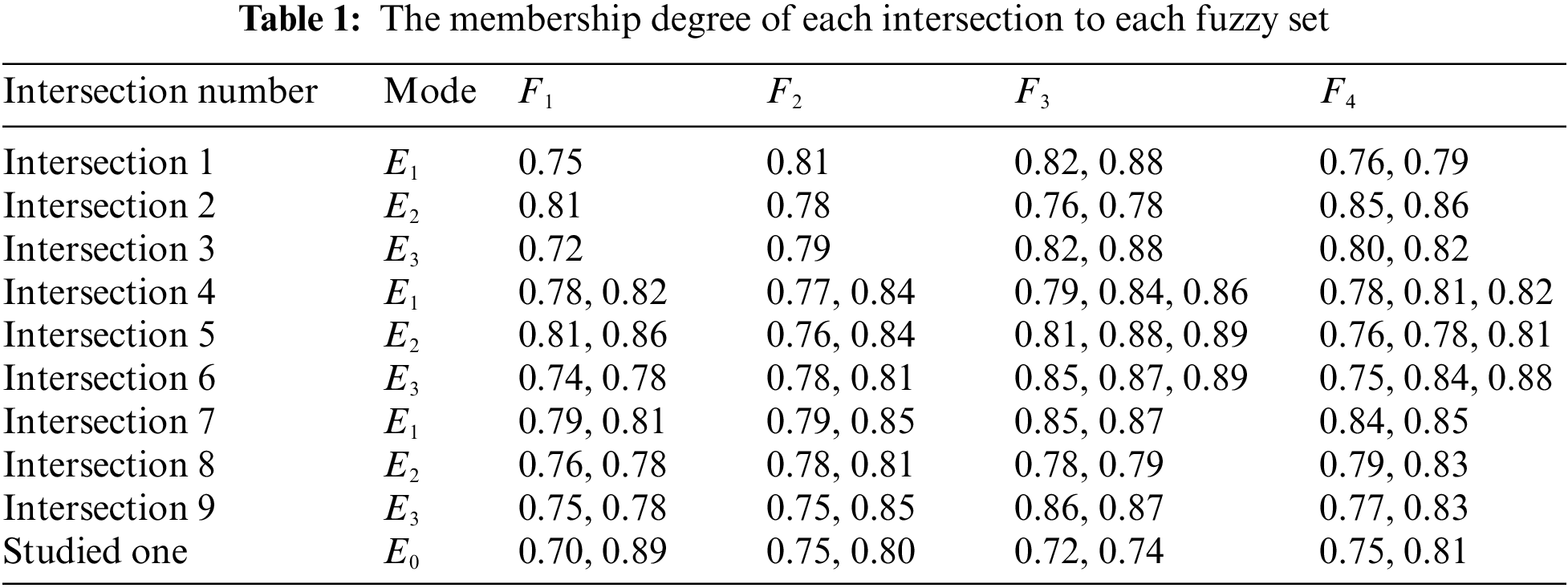
Figure 4: Distances obtained by using d__{stwg}
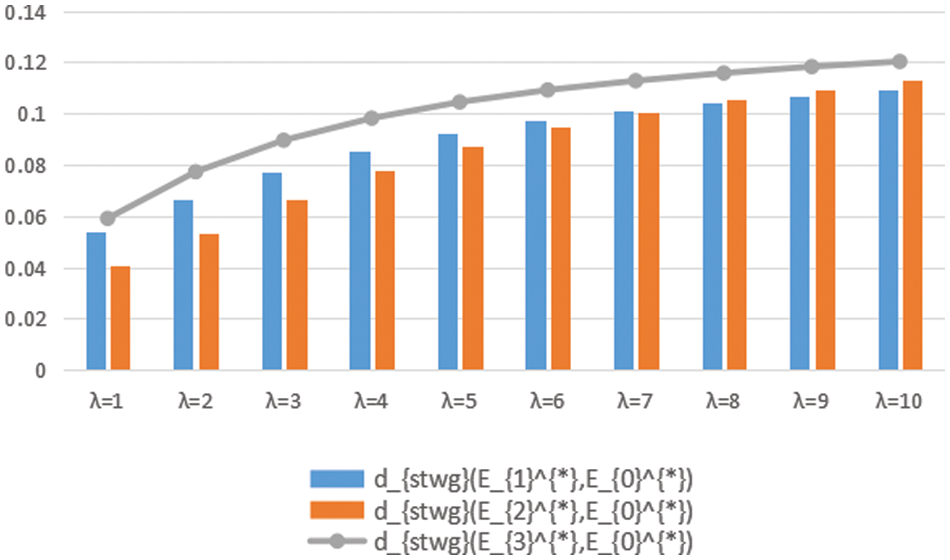
Figure 5: Contrast map of three kinds of distances
Figs. 4 and 5 illustrate that the suitable intersection Traffic Control mode varies as the parameter λ. Specifically, when λ≤7, all the suitable intersection traffic control modes are E2; when λ≥8, all the suitable intersection traffic control modes are E1. The essence of the above conclusions is that the smaller the λ is, the more appreciated the over-all evaluation information of the entire committee of experts is; meanwhile, the larger the λ is, the more appreciated the unduly large or small evaluation values of the evaluation information are. Therefore, to issue the intersection traffic control pattern decision making problem, one can firstly select a suitable parameter λ according to specific traffic control circumstances. More details on λ, please refer to Goldberg [23].
In this subsection, the given problem can is solved by using classical methods. For example, by using Definition (3) proposed by Xu et al. [4], E0 can be transferred as E′0={h′E0(F1),h′E0(F2),h′E0(F3),h′E0(F4)}, where h′E0(F1)={0.70,0.89,0.89,0.89,0.89,0.89,0.89},
h′E0(F2)={0.75,0.80,0.80,0.80,0.80,0.80,0.80},
h′E0(F3)={0.72,0.74,0.74,0.74,0.74,0.74,0.74},
h′E0(F4)={0.75,0.81,0.81,0.81,0.81,0.81,0.81}. Similarly, for any given i=1,2,3,j=1,2,3,4, hEi(Fj) can also be transferred as h′Ei(Fj). Specifically, it also gets that
^h′E1(F1)={0.75,0.78,0.79,0.81,0.82,0.82,0.82},^h′E2(F1)={0.76,0.78,0.81,0.81,0.86,0.86,0.86},
^h′E3(F1)={0.72,0.74,0.75,0.78,0.78,0.78,0.78},^h′E1(F2)={0.77,0.79,0.81,0.84,0.85,0.85,0.85},
^h′E2(F2)={0.76,0.78,0.78,0.81,0.84,0.84,0.84},^h′E3(F2)={0.75,0.78,0.79,0.81,0.85,0.85,0.85}.
Then, for λ=1,2,…,10, by using Eq. (12), and taking the weights of f1, f2, f3 and f4 into account, three kinds of generalized hesitant weighted distances dstwg(E′1,E′0), dstwg(E′2,E′0), and dstwg(E′3,E′0) are obtained, respectively, which are shown in Table 2.
Table 2 illustrates that the suitable intersection traffic control mode varies as the parameter. Specifically, when λ≤6, all the suitable intersection traffic control modes are E2; when λ≥7, all the suitable intersection traffic control modes are E1. Obviously, the results are generally consistent with those obtained by the novel method. However, there are some slight differences which mainly occur when λ=7. In essence, this is due to the added subjective data when using classical method. The differences show that the newly proposed method is more objective than classical ones in data processing.
In calculating the distance between two HFEs with different cardinal numbers, the cardinalities of them should be unified. To reduce the uncertainty in the unifying process, equal-probability transformation is used. Specially, a series of improved distance measures on HFSs are proposed. Since the essence of equal-probability transformation is a kind of dimensional transformation of the same information in the way of expression, the proposed method retains the decision information completely. By contrast, it is difficult to achieve this effect using classical methods. Moreover, the main innovations of this study are concluded as follows:
(i) The theoretical basis of this study is to deal with the membership function value of HFSs from the viewpoint of probability. Moreover, an equal-probability transformation technique is proposed to transform any given HFE into a new one with specified cardinal number.
(ii) To express the enhancement effect for the same membership function value of HFE occurring more than once, impulse function is introduced into hesitant fuzzy fields. This is consistent with people’s production experience.
(iii) This study is a multidisciplinary combination of the theories of the cardinality, equal-probability mapping, and impulse function.
In general, the innovation of this study mainly lies in the unification of multi-source heterogeneous data. This innovation can be applied not only to HFSs, but also to HFSs or NFSs, etc.
Ethical Approval: This article does not contain any studies with human participants performed by any of the authors.
Funding Statement: The Fangwei Zhang’s work is partially supported by Shanghai Pujiang Program (No. 2019PJC062), the Natural Science Foundation of Shandong Province (No. ZR2021MG003), the Research Project on Undergraduate Teaching Reform of Higher Education in Shandong Province (No. Z2021046).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zadeh, L. A. (1996). Fuzzy sets, fuzzy logic, and fuzzy systems, selected papers by Lotfi A. Zadeh. Singapore: World Scientific Publishing Company. [Google Scholar]
2. Torra, V. (2010). Hesitant fuzzy sets. International Journal of Intelligent Systems, 25(6), 529–539. DOI 10.1002/int.20418. [Google Scholar] [CrossRef]
3. Torra, V., Narukawa, Y. (2009). On hesitant fuzzy sets and decision. The 18th IEEE International Conference on Fuzzy Systems, pp. 1378–1382. Jeju Island, Korea. [Google Scholar]
4. Xu, Z. S., Xia, M. M. (2011). Distance and similarity measures for hesitant fuzzy sets. Inform Sciences, 181(11), 2128–2138. DOI 10.1016/j.ins.2011.01.028. [Google Scholar] [CrossRef]
5. Zhang, N., Wei, G. W. (2013). Extension of VIKOR method for decision making problem based on hesitant fuzzy set. Applied Mathematical Modelling, 37(7), 4938–4947. DOI 10.1016/j.apm.2012.10.002. [Google Scholar] [CrossRef]
6. Peng, D. H., Gao, C. Y., Gao, Z. F. (2013). Generalized hesitant fuzzy synergetic weighted distance measures and their application to multiple criteria decision-making. Applied Mathematical Modelling, 37(8), 5837–5850. DOI 10.1016/j.apm.2012.11.016. [Google Scholar] [CrossRef]
7. Rodríguez, R. M., Martínez, L., Torra, V., Xu, Z., Herrera, F. (2014). Hesitant fuzzy sets, state of the art and future directions. International Journal of Intelligent Systems, 29(6), 495–524. DOI 10.1002/int.21654. [Google Scholar] [CrossRef]
8. Sharp, H. (1968). Cardinality of finite topologies. Journal of Combinatorial Theory, 5(1), 82–86. DOI 10.1016/S0021-9800(68)80031-6. [Google Scholar] [CrossRef]
9. Dubois, D., Prade, H. (1985). Fuzzy cardinality and the modeling of imprecise quantification. Fuzzy Sets and Systems, 16(3), 199–230. DOI 10.1016/0165-0114(85)90025-9. [Google Scholar] [CrossRef]
10. Rosenblueth, E. (1975). Point estimates for probability moments. Proceedings of the National Academy of Sciences, 72(10), 3812–3814. DOI 10.1073/pnas.72.10.3812. [Google Scholar] [CrossRef]
11. Brownlee, K. A. (1965). Statistical theory and methodology in science and engineering. New York: Wiley. [Google Scholar]
12. Fan, C., Chen, J., Hu, K., Fan, E., Wang, X. (2022). Research on normal pythagorean neutrosophic set choquet integral operator and its application. Computer Modeling in Engineering & Sciences, 131(1), 477–491. DOI 10.32604/cmes.2022.019159. [Google Scholar] [CrossRef]
13. Liu, X. D., Wang, Z. W., Zhang, S. T., Garg, H. (2021). Novel correlation coefficient between hesitant fuzzy sets with application to medical diagnosis. Expert Systems with Applications, 2021. DOI 10.1016/j.eswa.2021.115393. [Google Scholar] [CrossRef]
14. Liu, X., Wang, Z., Zhang, S., Garg, H. (2021). An approach to probabilistic hesitant fuzzy risky multi-attribute decision making with unknown probability information. International Journal of Intelligent Systems, 36(10), 5714–5740. DOI 10.1002/int.22527. [Google Scholar] [CrossRef]
15. Mahmood, T., Ali, W., Ali, Z., Chinram, R. (2021). Power aggregation operators and similarity measures based on improved intuitionistic hesitant fuzzy sets and their applications to multiple attribute decision making. Computer Modeling in Engineering & Sciences, 126(3), 1165–1187. DOI 10.32604/cmes.2021.014393. [Google Scholar] [CrossRef]
16. Xia, M. M., Xu, Z. S., Chen, N. (2013). Some hesitant fuzzy aggregation operators with their application in group decision making. Group Decision and Negotiation, 22(2), 259–279. DOI 10.1007/s10726-011-9261-7. [Google Scholar] [CrossRef]
17. Roess, R. P., Prassas, E., McShane, W. R. (2011). Traffic engineering. 4th edition. New Jersey: Pearson Prentice Hall. [Google Scholar]
18. Wang, W., Guo, X. C. (2000). Traffic engineering. 4th edition. Nanjing, China: Southeast University Press. [Google Scholar]
19. Ministry of Housing and Urban-Rural Development of the People’s Republic of China (2010). Code for planning of intersections on urban roads. Beijing: Standards Press of China. [Google Scholar]
20. Ministry of Construction of the People’s Republic of China (1995). Code for transport planning on urban road. Beijing, China: Standards Press of China. [Google Scholar]
21. Ministry of Housing and Urban-Rural Development of the People’s Republic of China (2006). Code for design of urban road engineering. Beijing: Standards Press of China. [Google Scholar]
22. Zhang, F. W. (2016). Several kinds of uncertain multi-attribute decision-making methods and their application in transportation management. Beijing, China: People’s Communication Press. [Google Scholar]
23. Goldberg, D. (1991). What every computer scientist should know about floating-point arithmetic. ACM Computing Surveys, 23(1), 5–48. DOI 10.1145/103162.103163. [Google Scholar] [CrossRef]
Cite This Article
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Downloads
Citation Tools
