Nonlinear Algebraic Equations Solved by an Optimal Splitting-Linearizing Iterative Method

1  Introduction

Nonlinear partial differential equations (PDEs) frequently appear in many critical natural sciences and engineering technology problems. Mathematical models in physics, mechanics, and other disciplines fields can be applied to describe physical phenomena. Although some phenomena may be modeled by the linear type PDEs, the assumption of more complex conditions on the material property and geometric domain of the problem requires the use of nonlinear type PDEs. In most situations, solving nonlinear PDEs analytically and exactly is impossible. Because of the crucial role of the nonlinear problems, the researchers provided different numerical methods to obtain the solutions of nonlinear PDEs, which are properly transformed into the nonlinear algebraic equations (NAEs) by using numerically discretized methods. As mentioned in [1–4], nonlinear optimization problem, nonlinear programming, nonlinear sloshing problem, and nonlinear complementarity problem (NCP) can be recast to the issues to solve NAEs, with the help of NCP-functions, for example, the Fischer-Burmeister NCP [5]. Indeed, the numerical solution of NAEs is one of the main problems in computational mathematics. Among the many numerical methods, Newton’s method and its improvements have now been widely developed; however, if the initial guess of the solution is incorrect, these algorithms may fail. In general, it is difficult for most NAEs to choose a good initial condition. Therefore, it is necessary to develop a more effective algorithm that is less sensitive to the initial guess of the solution and converges quickly.

For the vector form of the NAEs:

F(x)=0,x:=(x1,…,xn)T∈Rn,F:=(F1,…,Fn)T∈Rn,(1)

the Newton method is given by

xk+1=xk−J−1(xk)F(xk),(2)

where J is an n×n Jacobian matrix with its ij-th component given by Jij=∂Fi/∂xj. Starting from an initial guess x0, Eq. (2) with the computed J−1(xk) at each iteration can be used to generate a sequence of xk, k=1,2,…. When xk is convergent under a specified convergence criterion, the solution of Eq. (1) is obtained.

The Newton method possesses a significant advantage in that it is quadratically convergent. However, the main drawbacks are sensitive to the initial point x0 and need to compute J−1(xk) at each iteration step. Therefore, some quasi-Newton methods have been developed to overcome these shortcomings of the Newton method. For example, in order to eliminate the requirement of finding and inverting the Jacobian matrix in Newton’s iterative algorithm, Liu et al. [5] proposed a derivative-free first-order system of nonlinear ordinary differential equations (ODE):

x˙=−vq(t)F(x),(3)

where ν is a nonzero constant and q(t) may generally be a monotonically increasing function of t. The term v/q(t) plays a vital role in stabilizing the controller in their approach. Even if the initial guess of the solution is not proper, it can help obtain a stable solution and accelerate the convergent speed. Liu et al. [2,6,7] showed that the efficiency and performance of the fictitious time integration method (FTIM) combined with the group preserving scheme [8] to integrate the resultant ODEs in Eq. (3). Atluri et al. [9] proposed an improvement of Newton’s method, which combined two methods of Newton’s method and FTIM, without the inversion of Jij. Related to the FTIM, some papers are employed to solve nonlinear problems [10,11]. To give a motivation for the present study, we begin with a system of linear algebraic equations (LAEs):

Ax=b,(4)

where A and b∈Rn are respectively a non-singular matrix and an input vector.

Let D= diag A and suppose that D is non-singular. Setting

C=D−A(A=D−C),(5)

the Jacobi iterative scheme for solving Eq. (4) is given by [12,13]

Dxk+1=Cxk+b,(6)

where xk denotes the kth step unknown variables x∈Rn. The splitting of A to A=D−C used in Eq. (6) was proposed by Jacobi to solve the linear algebraic equations (LAEs) iteratively. In general, A can be uniquely decomposed into

A=D−U−L,(7)

where U and L are a strict upper- and lower triangular matrix of A, respectively.

According to Eqs. (4) and (7), the SOR iterative method can be derived as follows [14,15]:

(D−wL)xk+1=wb+(1−w)Dxk+wUxk,(8)

where w is a nonzero relaxation factor. When w=1, it is known as the Gauss-Seidel iterative method. If Dii≠0, i=1,2,…,n, from Eq. (8), xk+1 can be easily found by the forward substitution method. The main reason is D−wL a lower triangular matrix.

Nowadays, there have different splitting techniques to decompose A as

A=M−N,(9)

where M is a non-singular matrix. Inserting Eq. (9) into Eq. (4), moving Nx to the right-hand side, taking the value of x to be xk and on the left-hand side taking the value of x to be xk+1. Then, the resulting iterative scheme expresses as follows:

Mxk+1=Nxk+b,(10)

M−1N is called an iteration matrix. The sufficient and necessary condition of the convergence for Eq. (10) is ρ(M−1N)<1, where ρ is the spectral radius, defined as the absolute value of the largest eigenvalue in the magnitude of M−1N. When ρ(M−1N) gets smaller and smaller, the convergence speed is accelerated.

For the LAE, there are many discussions about the split method to determine the best relaxation factor w in SOR [16–20]. In contrast, few results discuss the relationship between the split method and NAEs. In this paper, the split method based on the nonlinear term is applied to reduce the influence of nonlinear terms and further avoid selecting the parameters by a trail and error method. Hence, this article will propose a novel splitting-linearizing technique to iteratively solve the NAE and develop a new algorithm for determining the optimal splitting parameters.

2  A Split Linearization Method

In this paper, a new splitting idea is implemented and applied to decompose Eq. (1), and we develop an iterative method to solve it. In the general case, Eq. (1) can be expressed as follows:

Ax+B(x)x=b,(11)

where A and B are both n×n matrices and b are constant n-vector. While A is a constant matrix, B is a matrix function of x. When Ax incorporates all linear terms in the NAEs, B(x)x collects the nonlinear terms.

Then, we can decompose Eq. (11) to

Ax+(1−w)B(x)x=b−wB(x)x.(12)

The idea of the splitting technique in [21,22] has been proposed to solve a single nonlinear equation. Future, the nonlinear term B(x)x in Eq. (11) is first written as (1−w+w)B(x)x. Then, while the term (1−w)B(x)x is kept on the left-hand side, the other wB(x)x is moved to the right-hand side, as shown in Eq. (12). Above decomposition is a new splitting application, using a splitting parameter to be determined below.

We give an initial guess x0 to initialize the iteration. At the kth step of the iteration, xk is known, and Eq. (12) is linearized around xk to

Ax+(1−w)B(xk)x=b−wB(xk)xk.(13)

For x, it is a linear equations system, since the coefficients A and B(xk) are constant matrices. The right-hand side of Eq. (13) is a constant vector because B(xk)xk is available from the previous step. A new linear system can be derived and applied to determine the new xk+1 at the next step by

Ekxk+1=ek,(14)

where

Ek:=A+(1−w)B(xk),ek:=b−wB(xk)xk.(15)

The above process is a novel splitting-linearizing method for solving the NAEs.

In this study, the Gaussian elimination method solves Eq. (14) to determine xk+1 at each iterative step. However, before solving Eq. (14), an unknown parameter w is given in Eq. (15). Instead of being given a constant value w in the iterative procedure of the proposed method, which is determined through some trial and error, we can formulate a new method to determine the optimal value of wk at each step.

For a linear system

Ec=b,(16)

to minimize the merit function has been derived and proved in [23–25] as follows:

min{f0=||b||2||Ec||2[b⋅(Ec)]2},(17)

to obtain a fast descent direction c for a given residual vector b used in the iterative solution of Eq. (16).

Let

y:=Ec.(18)

The minimization in Eq. (17) is equivalent to maximize

maxy{(b⋅y)2||b||2||y||2},(19)

which is the orthogonal projection of b/||b|| onto y.

To optimize w in Eqs. (14) and (15), xk+1 on the left-hand side, are expressed as xk. Then, a linear system at each step shows as follows:

(A1k−wkA2k)xk=b1k+wkb2k,(20)

where

A1k:=A+B(xk),A2k:=−B(xk),b1k=b,b2k=−B(xk)xk.(21)

Let

a1k:=A1kxk,a2k:=A2kxk,(22)

and insert them into Eq. (17), we can derive

f0=f1(wk)f2(wk)f32(wk),(23)

f1(wk):=||a1k+wka2k||2=||a1k||2+2wka1k⋅a2k+wk2||a2k||,(24)

f2(wk):=||b1k+wkb2k||2=||b1k||2+2wkb1k⋅b2k+wk2||b2k||,(25)

f3(wk):=(a1k+wka2k)⋅(b1k+wkb2k)=a1k⋅b1k+wk(a1k⋅b2k+a2k⋅b1k)+wk2a2k⋅b2k.(26)

We can search the minimal value of wk by

minwk∈[a0,b0]{f0=f1(wk)f2(wk)f32(wk)},(27)

in a given interval [−a0,+b0] by taking wkj=a0+j(b0−a0)/Nw , j=1,2,…,Nw, for example, a0=−1, b0=+1 and Nw=10. wkj can be used to adjust the search direction. Inserting wkj into Eqs. (24)–(26), we can compute f0 in Eq. (23), and then we take the optimal value of wkj to obtain the minimization of f0. The optimal value of wk in [a0,b0] can quickly be obtained. This new algorithm with the optimal value wk is called the optimal split-linearization iterative method (OSLIM).

In the OSLIM, there is an interesting feature that by using the Cauchy-Schwarz inequality in Eq. (20),

b⋅(Ec)≤||b||||Ec||,(28)

it readily leads to

f0≥1.(29)

In general, f0>1 means that xk is not fully satisfied Eq. (11); f0=1 denotes that x satisfies Eq. (11) and gets the convergent solution simultaneously.

The procedures of the OSLIM to solve the NAEs are summarized as follows:

(i)   Give n and nonlinear equations, a0, b0 and Nw.

(ii)   Give an initial guess x0.

(iii)   For k=0,1,2,…, we repeat the follwing compuations:

A1k:=A+B(xk),

A2k:=−B(xk),

b1k=b,

b2k=−B(xk)xk,

wk from Eq. (27).

xk+1from [A+(1−wk)B(xk)]xk+1=b−wkB(xk)xk.(30)

If xk converges ||xk+1−xk||<ε, this iterative procedure stops; otherwise, go to step (iii) for the next iteration. Here, ε is a given convergence criterion and ||xk+1−xk|| named the residual norm. Also, the residual norm can be checked by

(∑i=1nFi2(xk))1/2≤ε.(31)

To further assess the performance of OSLIM, we investigate it using the convergence order. For solving a scalar equation f(x)=0, the numerically computed order of convergence (COC) is approximated by [22]

COC:=ln⁡|(xn+1−r)/(xn−r)|ln⁡|(xn−r)/(xn−1−r)|,(32)

where r is a solution of f(x)=0 and the sequence xn is generated from an iterative scheme. In the computation of COC, we store the values of xn and take n≤k0−1, where k0 is the number of iterations for the convergence.

For solving the NAEs, we can generate the sequence xk, k=0,1,…,k0 and store them in the program. We define

R(k):=||xk−xe||,(33)

COC:=ln⁡R(k0−1)/R(k0−2)ln⁡R(k0−2)/R(k0−3),(34)

where k0 is the number of iterations for satisfying the convergence criterion, xe is exact solution, and R(k) is the error in terms of Euclidean norm at the kth step. If the values of xe are unknown, we take xe=xk0.

3  Numerical Tests

3.1 Test Case 1

We first consider [26]:

F1(x1,x2)=x12+x22−2=0,

F2(x1,x2)=ex1−1+x22−2=0.(35)

Two roots are (1, 1) and (1, −1) obviously; however, there exist other roots.

As noted by Yeih et al. [26], the Newton method fails because the Jacobi matrix

J=[2x1x2ex1−1x2](36)

is singular at x2=0. Although the scalar homotopy method [26] considered the optimal hybrid search directions, the order of the residual norm only satisfies 10−4. When solving this one by the residual-norm based algorithm (RNBA) [27], the residual norm satisfies the order of 10−7. Above iteration algorithms based on the evolution of the residual vector are not satisfied the given convergence criterion, and the third solution cannot be obtained by these algorithms.

Using the OSLIM to solve this problem, a translation is applied as follows:

y1=x1+d0,y2=x2,

and choose d0 sufficiently large to render y1>0 such that we have

−2d0y1+y12+y22=2−2d02,

ey1−d0−1+y22=2.(37)

Eq. (37) can be written as

[−2d0000][y1y2]+[y1y2ey1−d0−1y1y2][y1y2]=[2−2d022],(38)

of which

A=[−2d0000],B=[y1y2ey1−d0−1y1y2].(39)

By using the OSLIM, we take d0=1, a0=−1, b0=0 and Nw=10, and starting from (1.5, 1.5) and through 34 iterations it converges under ε=10−15 as shown in Fig. 1a. The third solution is obtained as (x1,x2) = (−0.4776700623, 1.331101541), and the residuals are (|F1|,|F2|) = (4.44 × 10−16, 6.66 × 10−16). In Fig. 1b, the gradient direction is quickly found at the 5th step, and then the value of f0 quickly tend to the minimum value f0=1. The algorithm adjusts the gradient direction to approach the solution to obtain a smaller step size. As shown in Fig. 1c, the values of w change drastically after 15 steps, and the change value of w is between [a0,b0]=[−1,0]. For this example, COC = 1.2838 is obtained, which indicates that the OSLIM converges faster than the iterative scheme with linear convergence speed.

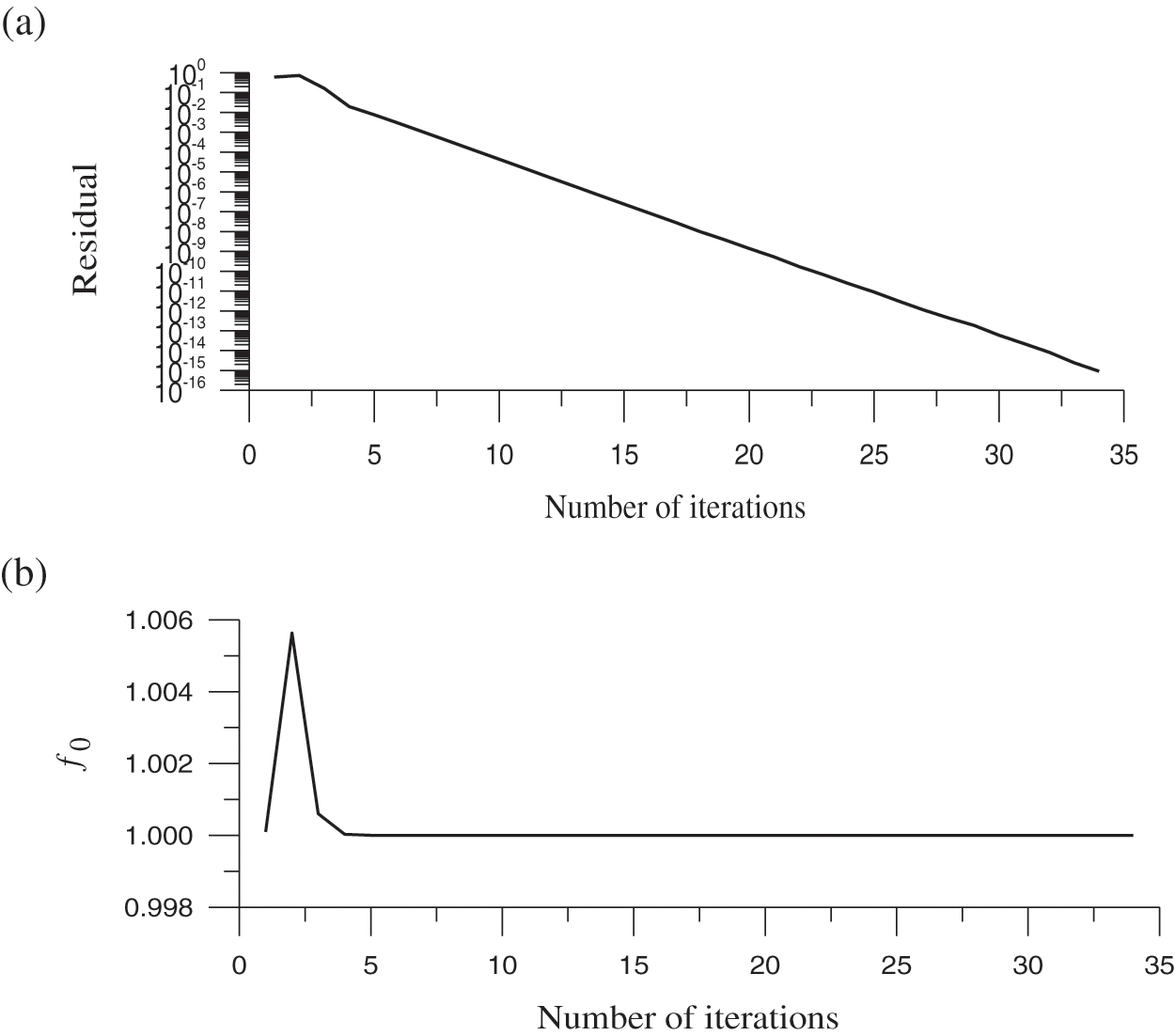
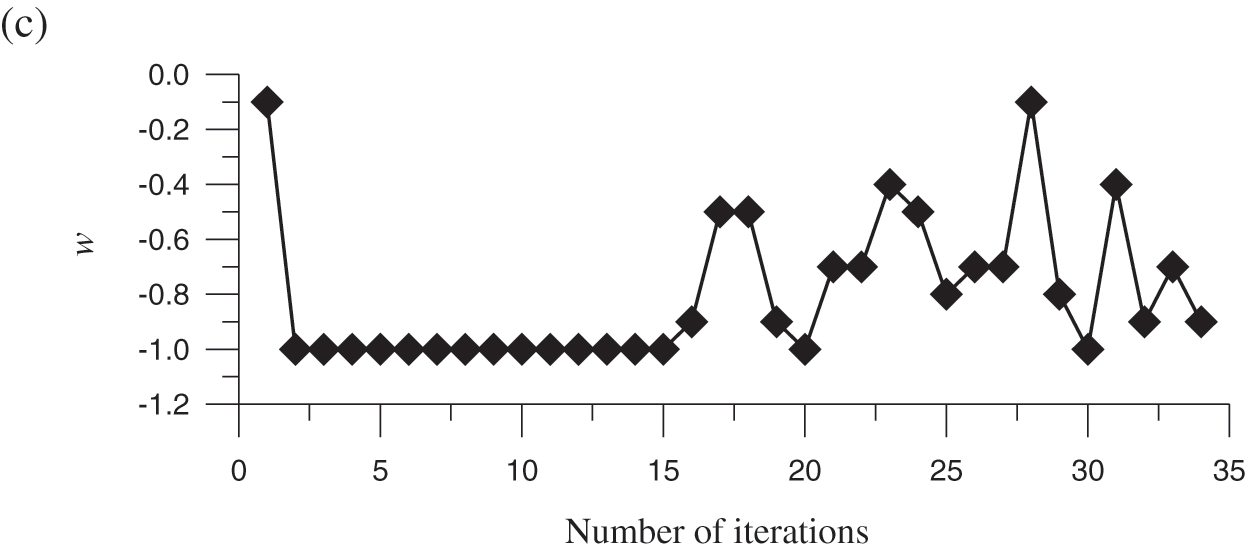
Figure 1: For test case 1, (a) display the residual plot, (b) the minimum value of the merit function, and (c) the optimized value of the splitting parameter

3.2 Test Case 2

Considering two-variable nonlinear equations [28] as follows:

F1(x,y)=x3−3xy2+a1(2x2+xy)+b1y2+c1x+a2y=0,(40)

F2(x,y)=3x2y−y3−a1(4xy−y2)+b2x2+c2=0.(41)

Hirsch et al. [28] used the continuous Newton algorithm to calculate this problem; however, the numerical results are inaccurate. Under the same situation, the FTIM [6], modified Newton method [9], and RNBA [27] have been applied and obtained three solutions from three different initial guessing values. In Liu et al. [29], this problem solved by the optimal vector drive algorithm (OVDA) can find five solutions. As stated in the literature [6], the attracting sets for several fixed points of problem are undefined. Therefore, various methods may give different solutions, even with the same initial value.

Eqs. (40) and (41) can be written as

[c1a200][xy]+[x2−3y2+2a1x+a1yb1y3xy−4a1y+b2x−y2+a1y][xy]=[0−c2],(42)

or written as

[c1a200][xy]+[x2+2a1xb1y−3xy+a1xb2x3x2−y2+a1y−4a1x][xy]=[0−c2].(43)

Eqs. (42) and (43) are of the form in Eq. (14), but with different B. For the uniqueness of B, for example, we can put the product term −3xy2 as (−3y2)x, such that −3y2 in the brace is viewed as the coefficient which is inserted into the coefficient matrix B, while x is put into the unknown vector. The principle is that the former variable x is preferred over the latter variable y placed in the unknown vector.

To compare with the result obtained by Atluri et al. [9], we take a1=25, b1=−1, c1=−2, a2=−3, b2=−4 and c2=−5. In [9], starting from (x0,y0) = (0.1, 0.1) and through 101 steps the solution (x,y) = (0.134212, 0.811128) is obtained with the residuals being (|F1|,|F2|) = (1.141 × 10−7, 8.913 × 10−7). By using the OSLIM, we take a0=−1, b0=−0.5 and Nw=10, and it converges with 35 iterations under ε=10−15 as shown in Fig. 2a. The solution (x,y) = (−0.16363472339, 0.23052874358) is obtained, and the residuals (|F1|,|F2|) = (2.22 × 10−15, 5.33 × 10−15) are much smaller than that in [9]; moreover, the OSLIM converges faster than that obtained by Atluri et al. [9]. In Fig. 2b, the gradient direction is quickly found at the 6th step, and then the value of f0 quickly tend to the minimum value f0=1. The values of w change drastically after 19 steps, and the change value of w is between [a0,b0] = [−1, −0.5] as shown in Fig. 2c. For this example, COC = 1.0895 is obtained.

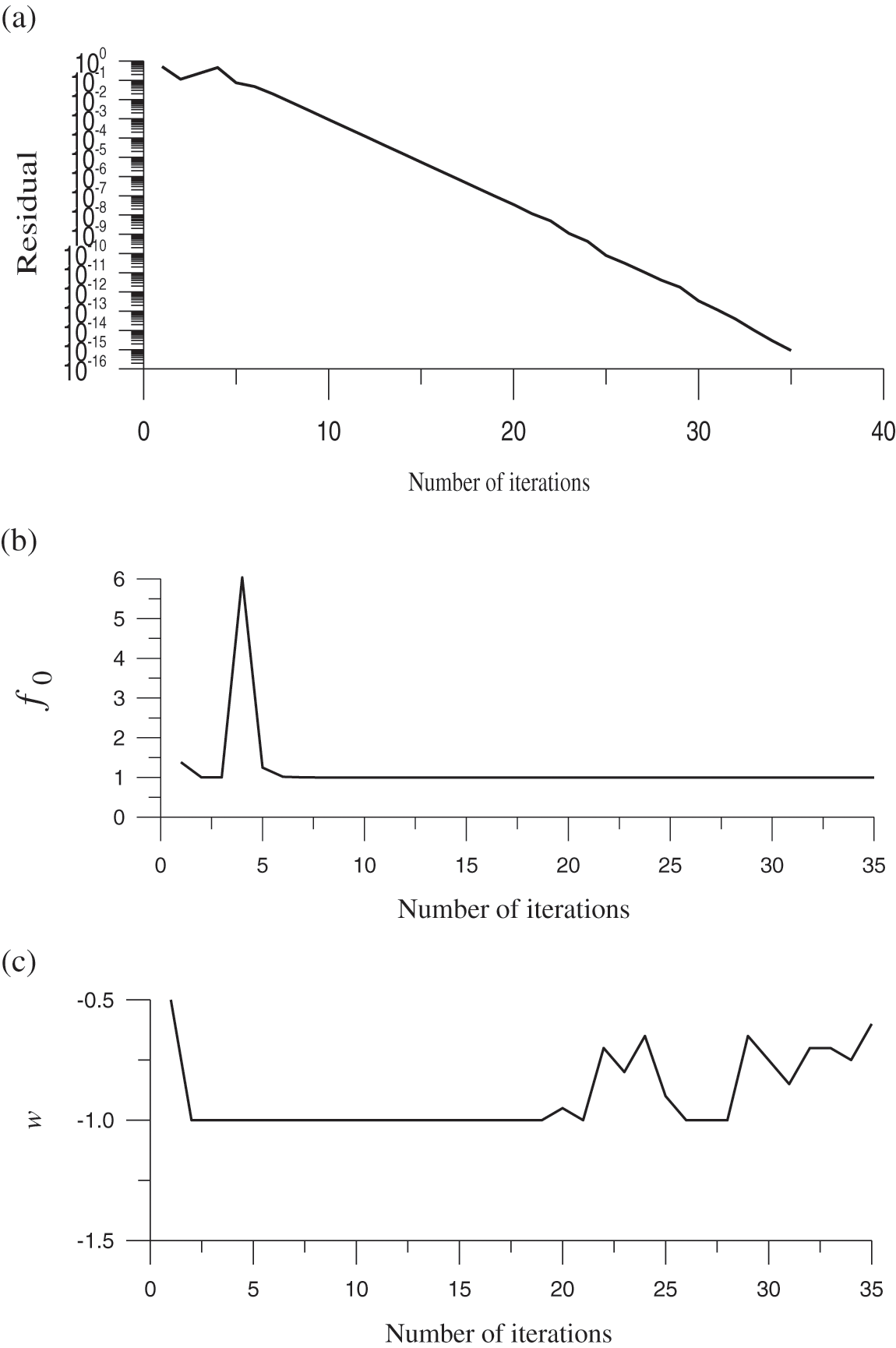
Figure 2: For test case 2, (a) display the residual plot, (b) the minimum value of the merit function, and (c) the optimized value of the splitting parameter

3.3 Test Case 3

Considering a system of three algebraic equations with three variables:

F1=x+y+z−3=0,

F2=xy+2y2+4z2−7=0,

F3=x8+y4+z9−3=0.(44)

Obviously x=y=z=1 is a solution.

By using the OSLIM, we take a0=−2, b0=−1.5 and Nw=10, and starting from (x0,y0,z0) = (0.5, 0.5, 0.6), through 33 iterations it converges under ε=10−15 as shown in Fig. 3a. The solution (x,y,z)= (0.9305422841, 1.218366932, 0.8510907842) is obtained, and the residuals are (|F1|,|F2|,|F3|) = (0, 3.553 × 10−15, 1.332 × 10−15). The OSLIM converges faster and more accurate than obtained by Atluri et al. [9], where 140 steps are required, and the residual errors are (|F1|,|F2|,|F3|) (6.046 × 10−4, 7.574 × 10−4, 3.005 × 10−6). In Fig. 3b, the gradient direction is quickly found at the 6th step, and then the value of f0 quickly tend to the minimum value f0=1. When approaching solutions, the values of w of the algorithm adjusts the iterative step size after 15 steps, and the change value of w is between [a0,b0] = [−2, −1.5] as shown in Fig. 3c. For this example, COC = 1.0429 is obtained.

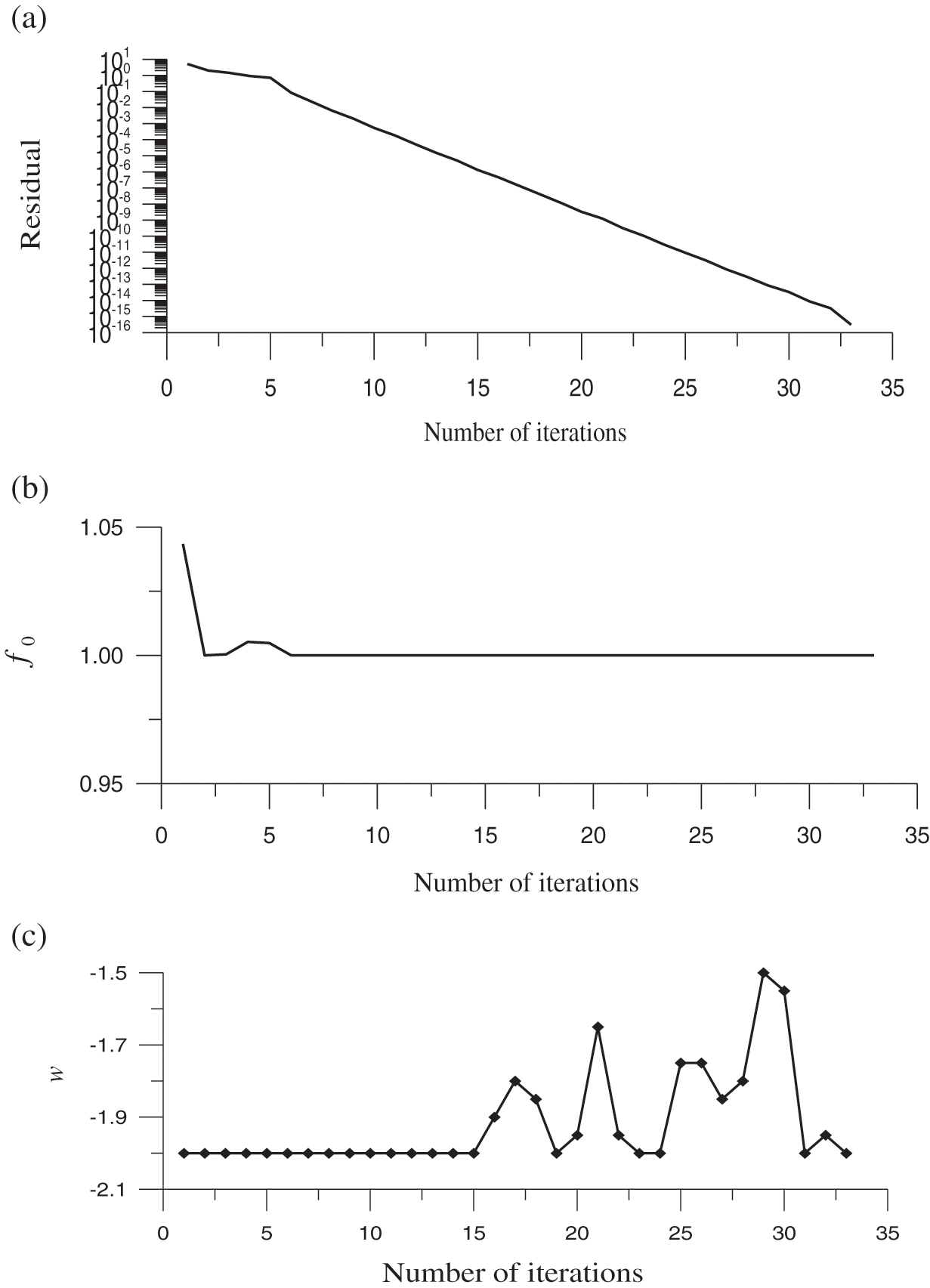
Figure 3: For test case 3, (a) display the residual plot, (b) the minimum value of the merit function, and (c) the optimized value of the splitting parameter

3.4 Test Case 4

Here, considering the following boundary value problem:

u′′=32u2,u(0)=4,u(1)=1.(45)

The exact solution is

u(x)=4(1+x)2.(46)

By using the finite difference discretisation of u at the grid points, we can obtain

Fi=1(Δx)2(ui+1−2ui+ui−1)−32ui2=0,i=1,…,n,u0=4,un+1=1,(47)

where Δx=1/(n+1) is the element length. In order to conviencely describle the coefficient matrices of B as Eq. (21), A1k, A2k, and b2k can be expressed as follows:

A1k=1(Δx)2(ui+1−2ui+ui−1)−32ui,A2k=32ui,b2k=32ui2,i=1,…,n.(48)

Setting n = 39, a0=−1, b0=1, ε = 10−10 and Nw=10, the OSLIM converges within 5 iterations as shown in Fig. 4a. In Fig. 4b, the gradient direction is quickly found at the 2nd step when the value of f0 quickly tend to the minimum value f0=1. When approaching solutions, the values of w of the algorithm adjusts the iterative step size after the 4th step, and the change value of w is between [a0,b0] = [−1, −0.25] as shown in Fig. 4c. The maximum error obtained by the OSLIM is 2.98 × 10−4, which converges faster and is more accurate than Atluri et al. [9]. In [9], the iteration number is more than 8000 steps under the convergence criterion ε = 10−4, and the errors are in the order of 10−3. COC = 1.9741 is obtained, which reveals that the OSLIM is almost quadratic convergence.

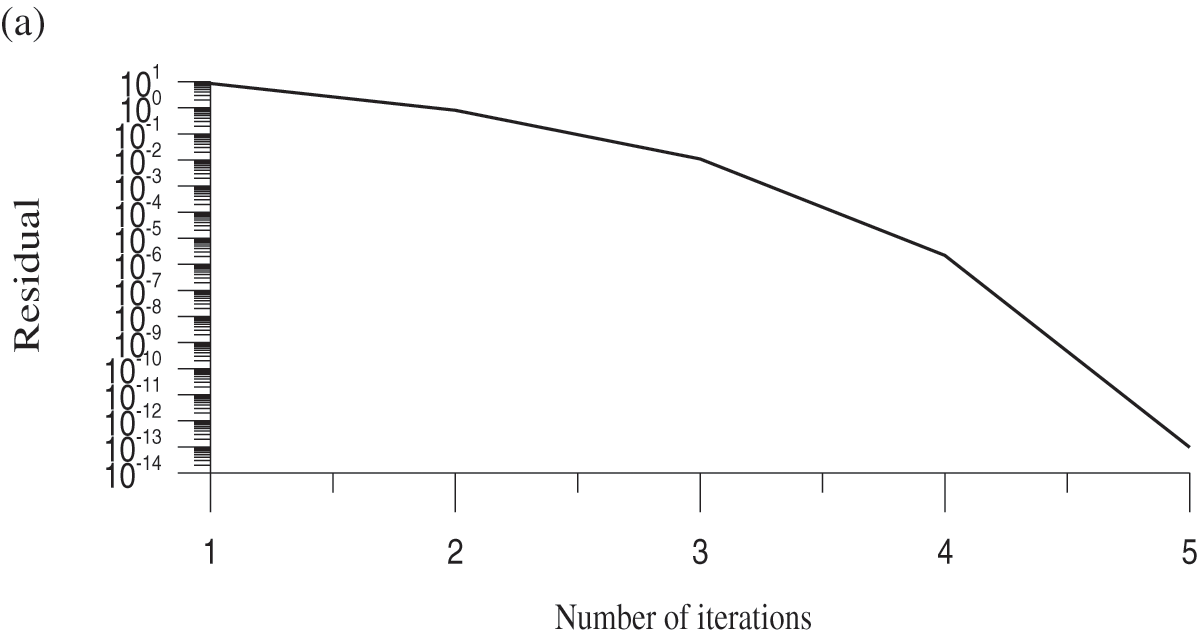
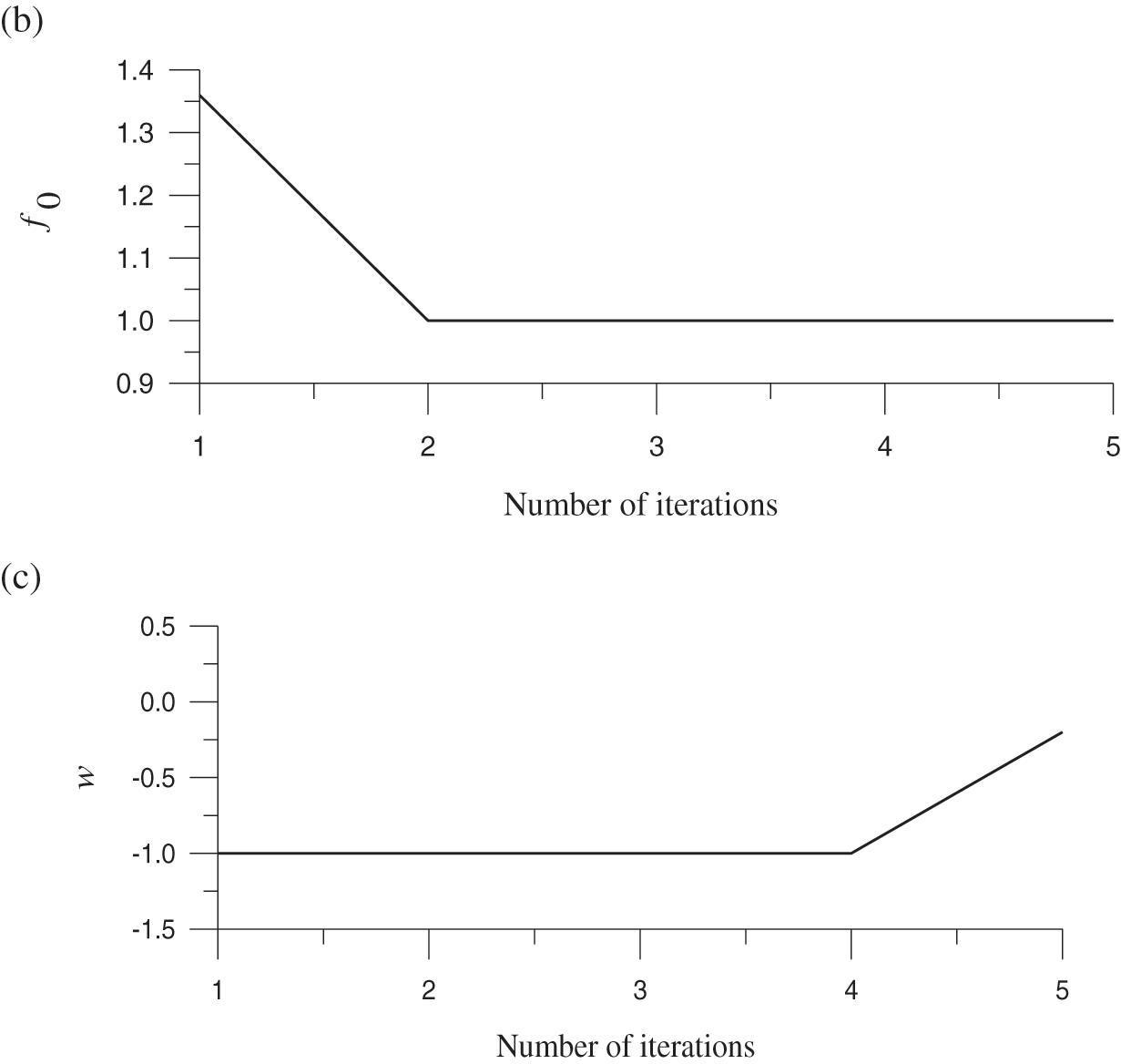
Figure 4: For test case 4, (a) display the residual plot, (b) the minimum value of the merit function, and (c) the optimized value of the splitting parameter

3.5 Test Case 5

Then, considering a test example given by Krzyworzcka [30] as follows:

F1=(3−5x1)x1+1−2x2,

Fi=(3−5xi)xi−xi−1−2xi+1,i=2,…,9,

F10=(3−5x10)x10+1−x9.(49)

To convince describe the coefficient matrices of B as Eq. (21), A1k, A2k, and b2k can be expressed as follows:

A1k=(−2xi+1+3xi−xi−1)−5xi,A2k=5xi,b2k=5xi2,i=1,…,10.(50)

Setting a0=−1, b0=1, ε = 10−10, Nw=10 and initial values xi = 1, i=1,…,10, the OSLIM converges within 10 iterations as shown in Fig. 5a. In Fig. 5b, the gradient direction is quickly found at the 5th step and then the value of f0 quickly tend to the minimum value f0=1. When approaching solutions, the values of w of the algorithm adjusts the iterative step size after the 7th steps, and the change value of w is between [a0,b0] = [−1, 0.8] as shown in Fig. 5c. The calculation results of xi, i=1,…,10, are shown in Table 1. The OSLIM converges faster than that obtained by Atluri et al. [9], where 55 steps are required to satisfy a convergence criterion ε = 10−6. COC = 1.9996 is obtained, which shows again that the OSLIM is quadratic convergence.

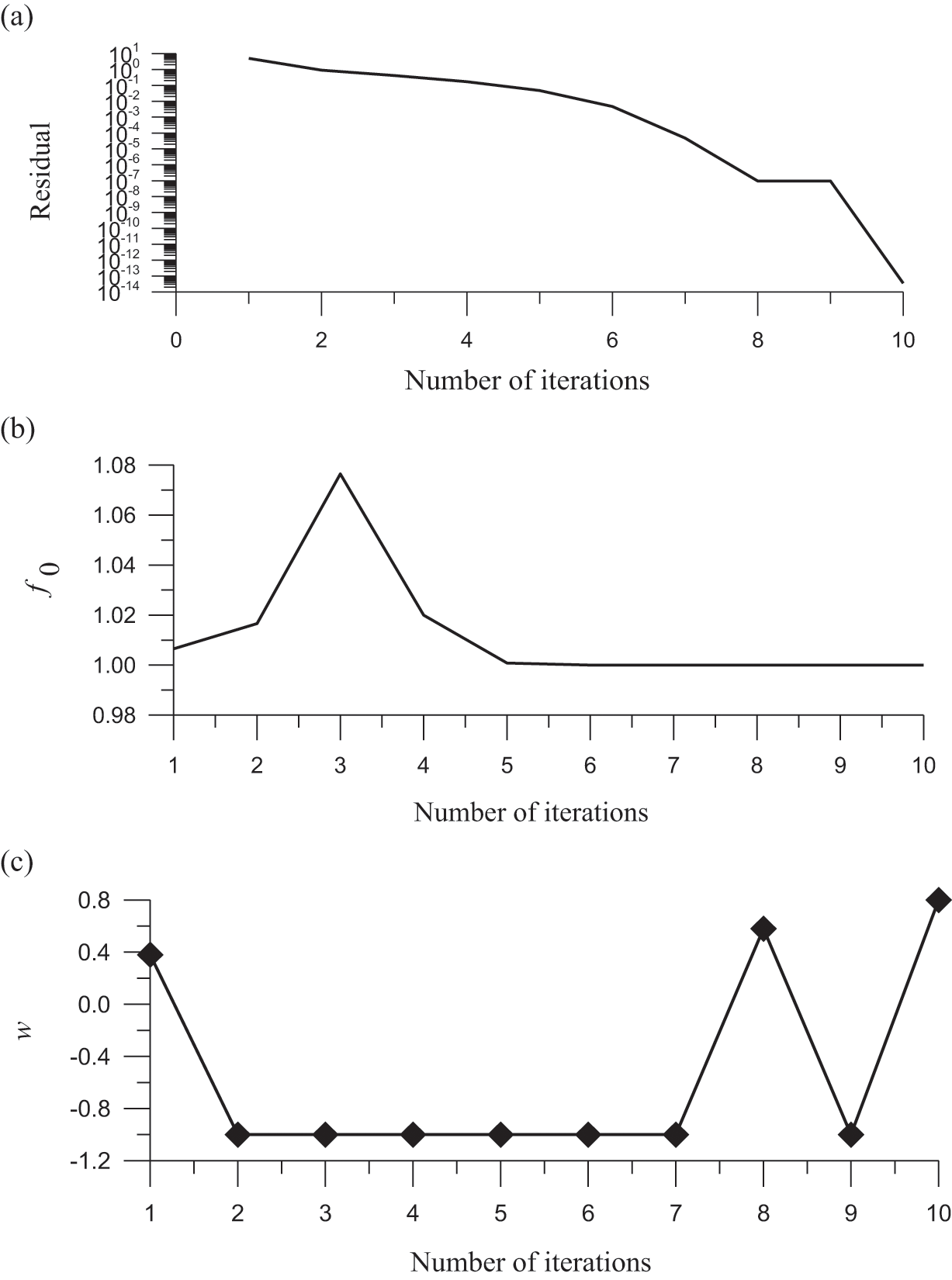
Figure 5: For test case 5, (a) display the residual plot, (b) the minimum value of the merit function, and (c) the optimized value of the splitting parameter

3.6 Test Case 6

The following example is given by Roose et al. [31]:

Fi=3xi(xi+1−2xi+xi−1)+14(xi+1−xi−1)2,i=1,…,19,u0=0,un+1=20.(51)

The OSLIM can adopt two different formulations to solve Eq. (53). The two different formulations lead to different coefficient matrices of B. First, we adopt

3(1−w)(x2k−2x1k)x1+1−w4x2kx2=−3w[x2k−2x1k]x1k−w4[x2k]2,

3(1−w)(xi+1k−2xik+xi−1k)xi+(1−w)4[xi+1kxi+1−xi−1kxi+1−xi+1kxi−1+xi−1kxi−1]=−3wxik[xi+1k−2xik+xi−1k]−w4([xi+1k]2−2xi−1kxi+1k+[xi−1k]2),i=2,…,n−1,

60xn−10xn−1+3(1−w)(xn−1k−2xnk)xn+1−w4xn−1kxn−1

=−100−3w[xn−1k−2xnk]xnk−w4[xn−1k]2,(52)

To convince desdescribee coefficient matrices of B as Eq. (21), A2k can be expressed as follows:

A2k=−3(x2k−2x1k)x1−x2k4x2,

A2k=−3(xi+1k−2xik+xi−1k)xi−14[(xi+1k−xi−1k)xi+1+(−xi+1k+xi−1k)xi−1],i=2,…,n−1,

A2k=−3(−2xnk+xn−1k)xn−xn−1k4xn−1.(53)

where the number with a superscript k denotes the kth step value, and it is inserted in the coefficient matrix when we derive the linear system. We modify the term

(xi+1k−2xik+xi−1k)xi

in the second line to

xikxi+1−2xikxi+xikxi−1,

such that we have a second formulation:

3(1−w)(x2k−2x1k)x1+1−w4x2kx2=−3w[x2k−2x1k]x1k−w4[x2k]2,

3(1−w)[xikxi+1−2xikxi+xikxi−1]+(1−w)4[xi+1kxi+1−xi−1kxi+1−xi+1kxi−1+xi−1kxi−1]=−3wxik[xi+1k−2xik+xi−1k]−w4([xi+1k]2−2xi−1kxi+1k+[xi−1k]2),i=2,…,n−1,

60xn−10xn−1+3(1−w)(xn−1k−2xnk)xn+1−w4xn−1kxn−1

=−100−3w[xn−1k−2xnk]xnk−w4[xn−1k]2.(54)

To convince describe the coefficient matrices of B as Eq. (21), A2k can be expressed as follows:

A2k=−3(x2k−2x1k)x1−x2k4x2,

A2k=6xikxi−[(xi+1k−xi−1k)4+3xik]xi+1−[(−xi+1k+xi−1k)4+3xik]xi−1,i=2,…,n−1,

A2k=−3(−2xnk+xn−1k)xn−xn−1k4xn−1.(55)

Setting n = 10, a0=−0.1, b0=0.1, ε = 10−10, Nw=10 and initial values xi = xi=2i, i=1,…,10, the first OSLIM with the first formulation converges within 14 iterations as shown in Fig. 6a. COC = 1.0651 is obtained. In Fig. 6b, the gradient direction is quickly found at the 4th step and then the value of f0 quickly tend to the minimum value f0=1. In Fig. 6c, the value of w of the algorithm adjusts the iterative step size after the 8th step, and the change value of w is between [a0,b0] = [−0.1, 0.04] as shown in Fig. 6c. The OSLIM converges faster than that obtained by Atluri et al. [9], where over 700 steps are required under ε = 10−6. The residual errors of |Fi| and the calculation results of xi, i=1,…,10, are listed in Tables 2 and 3, respectively.

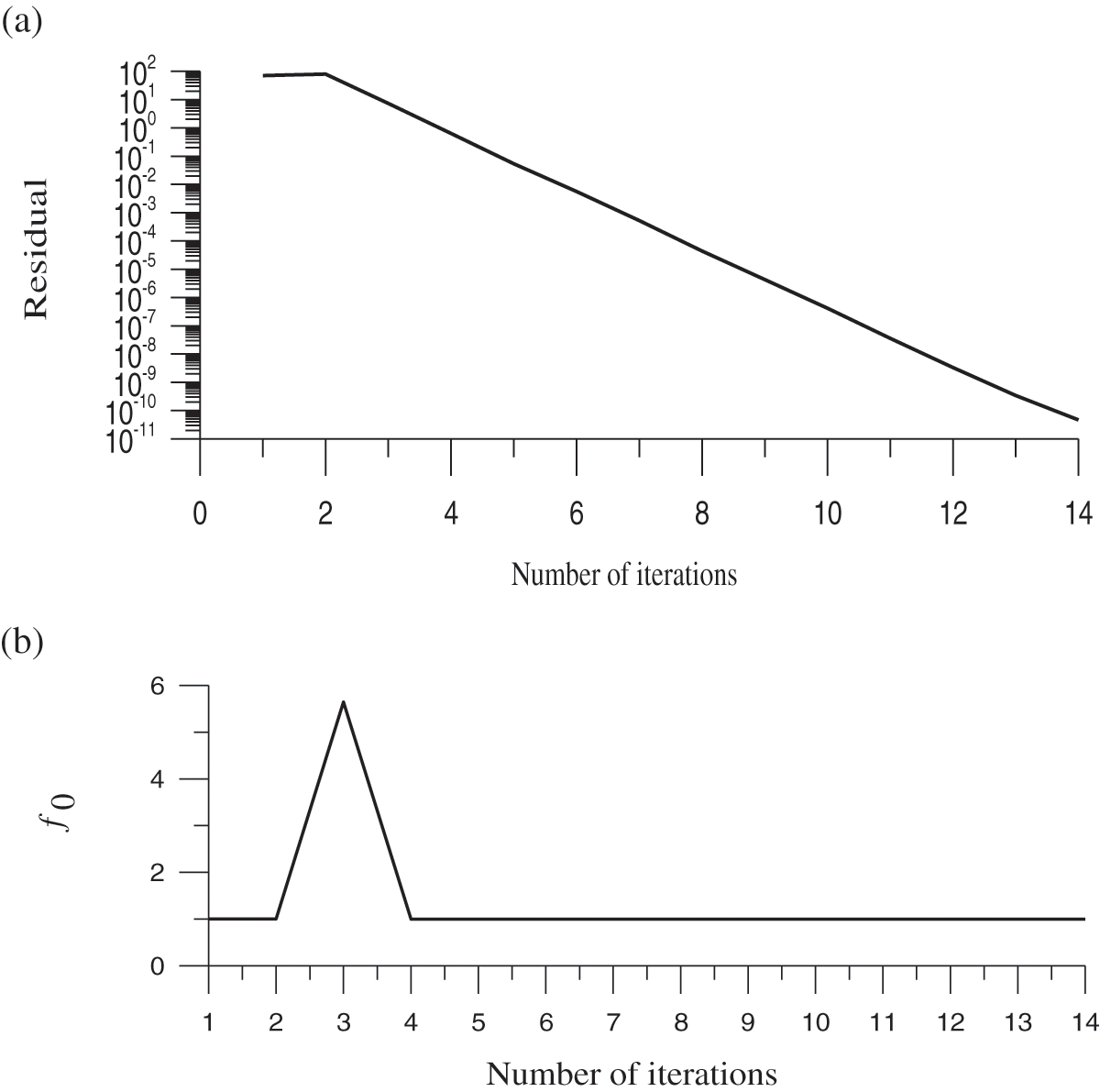
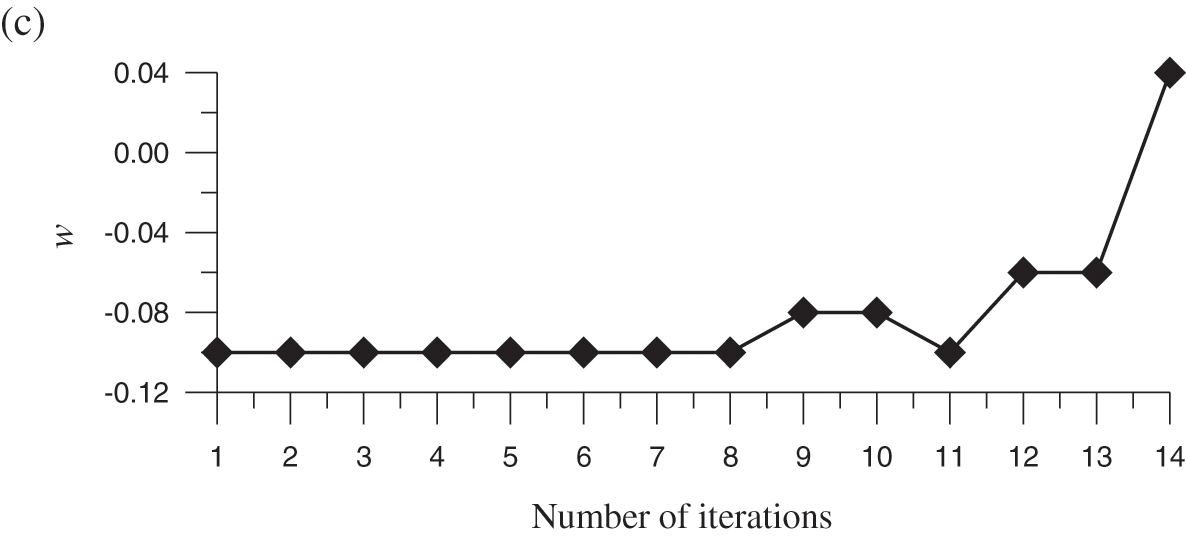
Figure 6: For test case 6, (a) display the residual plot, (b) the minimum value of the merit function, and (c) the optimized value of the splitting parameter

Setting n = 10, a0=−0.1, b0=0.1, ε = 10−10, Nw=100 and initial values xi = xi=2i, i=1,…,10, the second OSLIM with the second formulation converges within 13 iterations as shown in Fig. 7a. However, the solutions are different from those obtained from the first OSLIM with the first formulation. When n is raised to 50, both OSLIM can find solutions quickly with 12 and 15 iterations, respectively. These two solutions are compared in Fig. 7b.

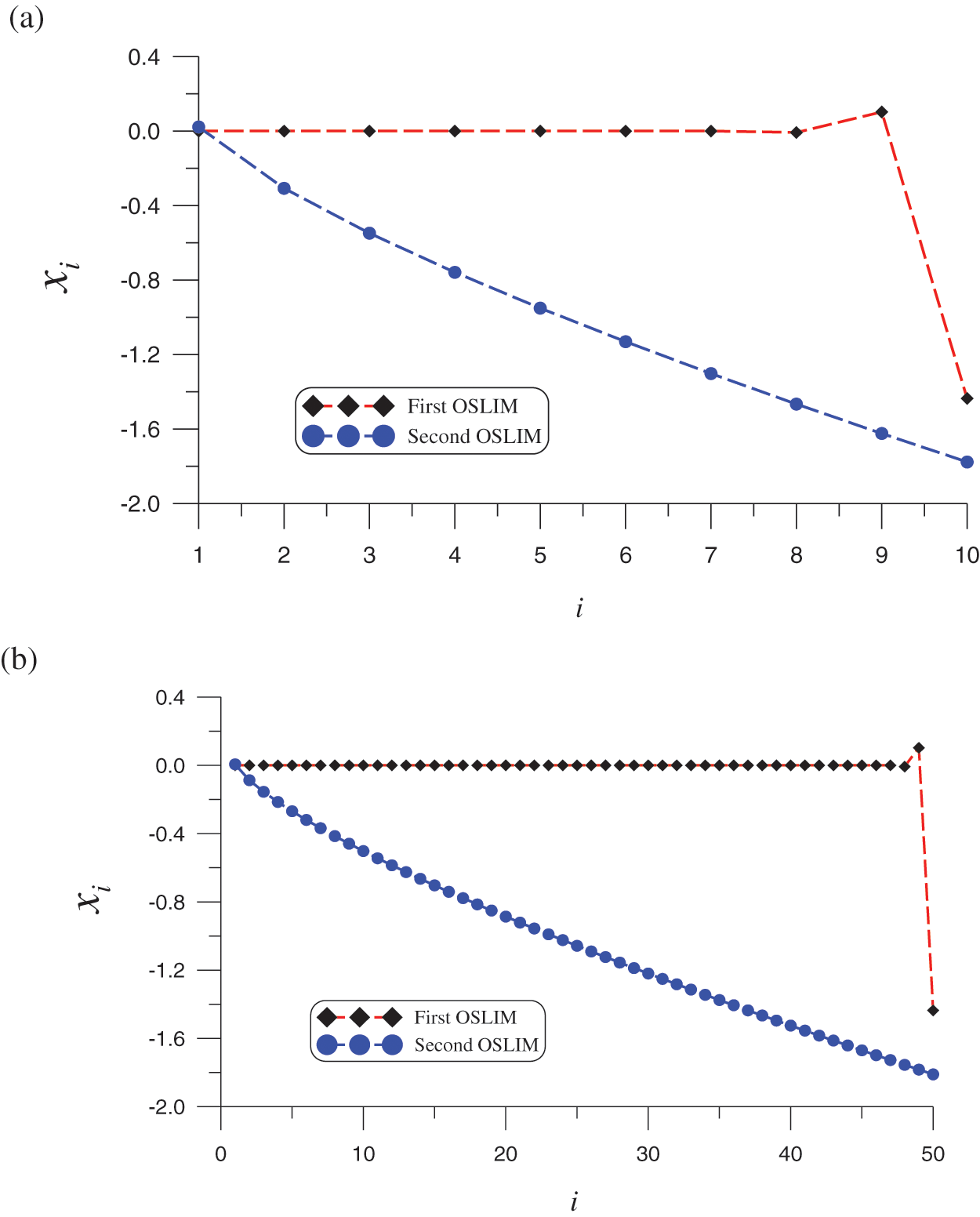
Figure 7: For test case 6, comparing two different solutions obtained by the first OSLIM and the second OSLIM: (a) n = 10, and (b) n = 50

3.7 Test Case 7

Considering the following a two-dimensional nonlinear Bratu equation:

Δu(x,y)+exp⁡u(x,y)=S(x,y),(56)

u(x,y)=ln⁡(x2+y2+2),(57)

and the domain is an ellipse with semi-axes lengths a = 1 and b = 0.5. The Dirichlet boundary condition is imposed. Due to u > 0, we decompose it to

Δu(x,y)+(1−w)exp⁡uk(x,y)uk(x,y)u(x,y)=S(x,y)−wexp⁡uk(x,y),(58)

where uk(x,y) is the value at the kth step, expanded by

uk(x,y)=∑i=0M∑j=0iaijkxi−jyj.(59)

After collocating points inside the domain and on the boundary, simultaneously, to satisfy the Eq. (56) and the boundary condition equation, we can derive NAEs to determine the n=(M+1)(M+2) coefficients aij iteratively.

By using the OSLIM, we take n=12×13/2=78, and to determine w by using the Newton method, through 24 iterations it converges under ε = 10−5 as shown in Fig. 8a. COC = 1.4926 is obtained. The gradient direction is quickly found at the 7th step, and then the value of f0 quickly tend to the minimum value f0=1 as shown in Fig. 8b. In order to satisfy f0=1, we can find that the algorithm adjusts the search direction after the 3rd step and the change value of w is between [a0,b0] = [−0.25, 1.78] as shown in Fig. 8c. The maximum error obtained by the OSLIM is 7.95 × 10−6. Interestingly, the OSLIM can be used to solve a highly nonlinear PDE with high accuracy.

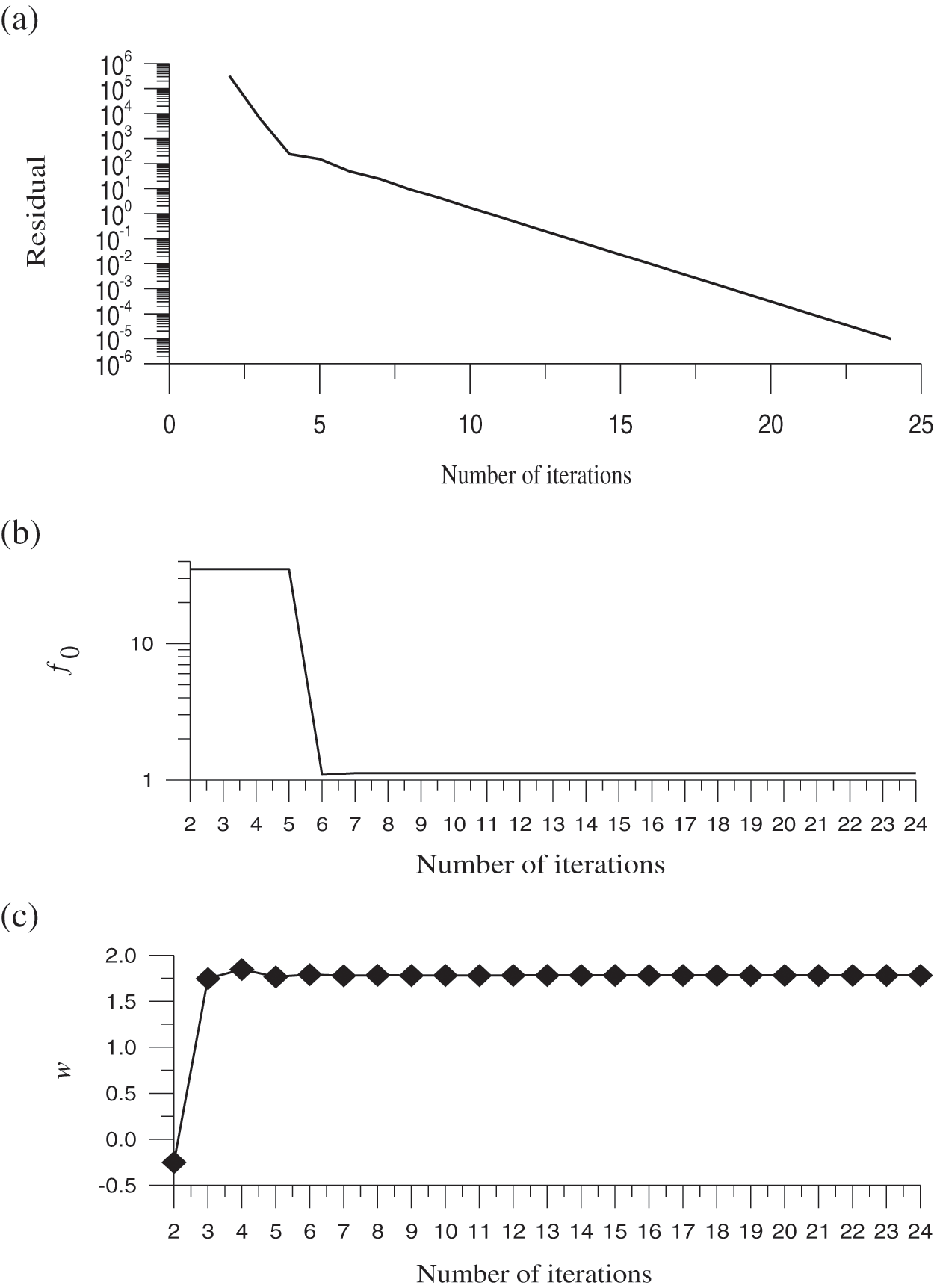
Figure 8: For test case 7, (a) display the convergence plot, (b) the minimum value of the merit function, and (c) the optimized value of the splitting parameter

4  Conclusions

When evaluating the performance of newly developed iterative solutions for solving nonlinear algebraic equations (NAE), there are two critical factors: accuracy and convergence speed. In this article, we first decomposed the nonlinear terms in the NAEs through a splitting parameter and then we linearized the NAEs around the values at the previous step and derived a system of linear algebraic equations (LAEs). Through the maximum orthogonal projection concept at each iterative step, we select the optimal value of the splitting parameter and use the Gaussian elimination method to solve the LAE. The features of the proposed method are summarized as follows: (a) The merit function is in terms of the coefficient matrix, right-side vector and the value of unknown vector at the previous step. (b) It is easy to minimize the search within a preferred interval through some operations. (c) The current OSLIM is insensitive to the initial guess and without needing the inversion of the Jacobian matrix at each iterative step, which can save much of the computational time. We have successfully applied the OSLIM to solve the NAEs resulting from the nonlinear boundary value problem in one- and two-dimensional spatial spaces. Through the numerical test, the convergence order of the OSLIM is between linear and quadratic convergence.

Funding Statement: The corresponding author appreciates the financial support provided by the Ministry of Science and Technology, Taiwan, ROC under Contract No. MOST 110-2221-E-019-044.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Liu, C. S., Atluri, S. N. (2008). A fictitious time integration method (FTIM) for solving mixed complementarity problems with applications to non-linear optimization. Computer Modeling in Engineering & Sciences, 34(2), 155–178. DOI 10.3970/cmes.2008.034.155. [Google Scholar] [CrossRef]

 2.  Kwak, B. M., Kwak, J. Y. (2021). Binary NCP: A new approach for solving nonlinear complementarity problems. Journal of Mechanical Science and Technology, 35(3), 1161–1166. DOI 10.1007/s12206-021-0229-5. [Google Scholar] [CrossRef]

 3.  Shih, C. F., Chen, Y. W., Chang, J. R., Soon, S. P. (2021). The equal-norm multiple-scale trefftz method for solving the nonlinear sloshing problem with baffles. Computer Modeling in Engineering & Sciences, 127(3), 993–1012. DOI 10.32604/cmes.2021.012702. [Google Scholar] [CrossRef]

 4.  Nurhidayat, I., Hao, Z., Hu, C. C., Chen, J. S. (2020). An ordinary differential equation approach for nonlinear programming and nonlinear complementarity problem. International Journal of Industrial Optimization, 1(1), 1–14. DOI 10.12928/ijio.v1i1.764. [Google Scholar] [CrossRef]

 5.  Fischer, A. (1992). A special newton-type optimization method. Optimization, 24(3–4), 269–284. DOI 10.1080/02331939208843795. [Google Scholar] [CrossRef]

 6.  Liu, C. S., Atluri, S. N. (2008). A novel time integration method for solving a large system of non-linear algebraic equation. Computer Modeling in Engineering & Sciences, 31(2), 71–83.15. DOI 10.3970/CMES.2008.031.071. [Google Scholar] [CrossRef]

 7.  Liu, C. S. (2009). A fictitious time integration method for a quasilinear elliptic boundary value problem, defined in an arbitrary plane domain. Computers, Materials & Continua, 11(1), 15–32. DOI 10.3970/cmc.2009.011.015. [Google Scholar] [CrossRef]

 8.  Liu, C. S. (2001). Cone of non-linear dynamical system and group preserving schemes. International Journal of Non-Linear Mechanics, 36, 1047–1068. DOI 10.1016/S0020-7462(00)00069-X. [Google Scholar] [CrossRef]

 9.  Atluri, S. N., Liu, C. S., Kuo, C. L. (2009). A modified newton method for solving non-linear algebraic equations. Journal of Marine Science and Technology, 17(3), 238–247. DOI 10.51400/2709-6998.1960. [Google Scholar] [CrossRef]

10. Jones, C., Tian, H. (2017). A time integration method of approximate fundamental solutions for nonlinear poisson-type boundary value problems. Communications in Mathematical Sciences, 15(3), 693–710. DOI 10.4310/CMS.2017.v15.n3.a6. [Google Scholar] [CrossRef]

11. Hashemi, M. S., Mustafa, I., Parto-Haghighi, M., Mustafa, B. (2019). On numerical solution of the time-fractional diffusion-wave equation with the fictitious time integration method. European Physical Journal Plus, 134, 488. DOI 10.1140/epjp/i2019-12845-1. [Google Scholar] [CrossRef]

12. Demmel, J. W. (1997). Applied numerical linear algebra. Philadelphia: SIAM. [Google Scholar]

13. Saad, Y. (2003). Iterative methods for sparse linear systems. Philadelphia: SIAM. [Google Scholar]

14. Quarteroni, A., Sacco, R., Saleri, F. (2000). Numerical mathematics. New York: Springer Science. [Google Scholar]

15. Hadjidimos, A. (2000). Successive overrelaxation (SOR) and related methods. Journal of Computational and Applied Mathematics, 123(1–2), 177–199. DOI 10.1016/S0377-0427(00)00403-9. [Google Scholar] [CrossRef]

16. Bai, Z. Z., Chi, X. B. (2003). Asymptotically optimal successive overrelaxation method for systems of linear equations. Journal of Computational Mathematics, 21(5), 603–612. [Google Scholar]

17. Wen, R. P., Meng, G. Y., Wang, C. L. (2013). Quasi-Chebyshev accelerated iteration methods based on optimization for linear systems. Computers & Mathematics with Applications, 66(6), 934–942. DOI 10.1016/j.camwa.2013.06.016. [Google Scholar] [CrossRef]

18. Meng, G. Y. (2014). A practical asymptotical optimal SOR method. Applied Mathematics and Computation, 242, 707–715. DOI 10.1016/j.amc.2014.06.034. [Google Scholar] [CrossRef]

19. Miyatake, Y., Sogabe, T., Zhang, S. L. (2020). Adaptive SOR methods based on the wolfe conditions. Numerical Algorithms, 84, 117–132. DOI 10.1007/s11075-019-00748-0. [Google Scholar] [CrossRef]

20. Yang S., G., K, M. (2009). The optimal relaxation parameter for the SOR method applied to the poisson equation in any space dimensions. Applied Mathematics Letters, 22(3), 325–331. DOI 10.1016/j.aml.2008.03.028. [Google Scholar] [CrossRef]

21. Liu, C. S. (2020). A new splitting technique for solving nonlinear equations by an iterative scheme. Journal of Mathematics Research, 12(4), 40–48. DOI 10.5539/jmr.v12n4p40. [Google Scholar] [CrossRef]

22. Liu, C. S., Hong, H. K., Lee, T. L. (2021). A splitting method to solve a single nonlinear equation with derivative-free iterative schemes. Mathematics and Computers in Simulation, 190, 837–847. DOI 10.1016/j.matcom.2021.06.019. [Google Scholar] [CrossRef]

23. Liu, C. S. (2012). A globally optimal iterative algorithm to solve an ill-posed linear system. Computer Modeling in Engineering & Sciences, 84(4), 383–403. DOI 10.3970/cmes.2012.084.383. [Google Scholar] [CrossRef]

24. Liu, C. S. (2013). An optimal tri-vector iterative algorithm for solving ill-posed linear inverse problems. Inverse Problems in Science and Engineering, 21, 650–681. DOI 10.1080/17415977.2012.717077. [Google Scholar] [CrossRef]

25. Liu, C. S. (2014). A globally optimal tri-vector method to solve an ill-posed linear system. Journal of Computational and Applied Mathematics, 260, 18–35. DOI 10.1016/j.cam.2013.09.017. [Google Scholar] [CrossRef]

26. Yeih, W. C., Ku, C. Y., Liu, C. S., Chan, I. Y. (2013). A scalar homotopy method with optimal hybrid search directions for solving nonlinear algebraic equations. Computer Modeling in Engineering & Sciences, 90(4), 255–282. DOI 10.3970/cmes.2013.090.255. [Google Scholar] [CrossRef]

27. Chen, Y. W. (2014). A residual-norm based algorithm for solving determinate/indeterminate systems of non-linear algebraic equations. Journal of Marine Science and Technology, 22(5), 583–597. DOI 10.6119/JMST-013-0912-1. [Google Scholar] [CrossRef]

28. Hirsch, M., Smale, S. (1979). On algorithms for solving f(x) = 0. Communications on Pure & Applied Mathematics, 32(3), 281–312. DOI 10.1002/cpa.3160320302. [Google Scholar] [CrossRef]

29. Liu, C. S., Atluri, S. N. (2011). An iterative algorithm for solving a system of nonlinear algebraic equations, F(x)=0, using the system of ODEs with an optimum α in x˙=λ[αF+(1−α)BTF]; Bij=∂Fi/∂xj. Computer Modeling in Engineering & Sciences, 73(4), 395–431. DOI 10.3970/cmes.2011.073.395. [Google Scholar] [CrossRef]

30. Krzyworzcka, S. (1996). Extension of the lanczos and CGS methods to systems of nonlinear equations. Journal of Computational and Applied Mathematics, 69(1), 181–190. DOI 10.1016/0377-0427(95)00032-1. [Google Scholar] [CrossRef]

31. Roose, A., Kulla, V., Lomb, M., Meressoo, T. (1990). Test examples of systems of non-linear equations. Tallin: Estonian Software and Computer Service Company. [Google Scholar]