Open Access

ARTICLE

Nonlinear Algebraic Equations Solved by an Optimal Splitting-Linearizing Iterative Method

Chein-Shan Liu¹, Essam R. El-Zahar^2,3, Yung-Wei Chen^4,*

1 Center of Excellence for Ocean Engineering, Center of Excellence for the Oceans, National Taiwan Ocean University, Keelung, 202301, Taiwan
2 Department of Mathematics, College of Sciences and Humanities in Al-Kharj, Prince Sattam bin Abdulaziz University, Alkharj, 11942, Saudi Arabia
3 Department of Basic Engineering Science, Faculty of Engineering, Menofia University, Shebin El-Kom, 32511, Egypt
4 Department of Marine Engineering, National Taiwan Ocean University, Keelung, 202301, Taiwan

* Corresponding Author: Yung-Wei Chen. Email:

Computer Modeling in Engineering & Sciences 2023, 135(2), 1111-1130. https://doi.org/10.32604/cmes.2022.021655

Received 26 January 2022; Accepted 31 May 2022; Issue published 27 October 2022

Abstract

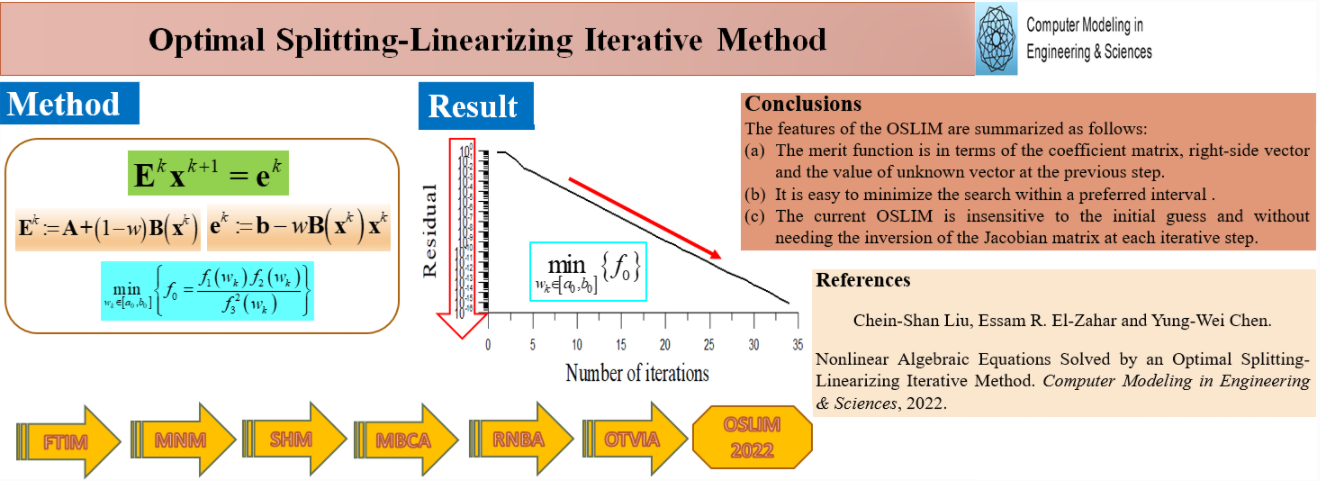
How to accelerate the convergence speed and avoid computing the inversion of a Jacobian matrix is important in the solution of nonlinear algebraic equations (NAEs). This paper develops an approach with a splitting-linearizing technique based on the nonlinear term to reduce the effect of the nonlinear terms. We decompose the nonlinear terms in the NAEs through a splitting parameter and then linearize the NAEs around the values at the previous step to a linear system. Through the maximal orthogonal projection concept, to minimize a merit function within a selected interval of splitting parameters, the optimal parameters can be quickly determined. In each step, a linear system is solved by the Gaussian elimination method, and the whole iteration procedure is convergent very fast. Several numerical tests show the high performance of the optimal split-linearization iterative method (OSLIM).

---

Graphic Abstract

---

Keywords

---