 Open Access
Open Access
ARTICLE
Covert Communication in Integrated High Altitude Platform Station Terrestrial Networks
1 School of Space Information, Space Engineering University, Beijing, 101416, China
2 College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China
* Corresponding Author: Kefeng Guo. Email:
(This article belongs to the Special Issue: Recent Advances in Backscatter and Intelligent Reflecting Surface Communications for 6G-enabled Internet of Things Networks)
Computer Modeling in Engineering & Sciences 2023, 135(1), 583-598. https://doi.org/10.32604/cmes.2022.023093
Received 09 April 2022; Accepted 16 May 2022; Issue published 29 September 2022
Abstract
In recent years, Internet of Things (IoT) technology has emerged and gradually sprung up. As the needs of large-scale IoT applications cannot be satisfied by the fifth generation (5G) network, wireless communication network needs to be developed into the sixth generation (6G) network. However, with the increasingly prominent security problems of wireless communication networks such as 6G, covert communication has been recognized as one of the most promising solutions. Covert communication can realize the transmission of hidden information between both sides of communication to a certain extent, which makes the transmission content and transmission behavior challenging to be detected by noncooperative eavesdroppers. In addition, the integrated high altitude platform station (HAPS) terrestrial network is considered a promising development direction because of its flexibility and scalability. Based on the above facts, this article investigates the covert communication in an integrated HAPS terrestrial network, where a constant power auxiliary node is utilized to send artificial noise (AN) to realize the covert communication. Specifically, the covert constraint relationship between the transmitting and auxiliary nodes is derived. Moreover, the closed-form expressions of outage probability (OP) and effective covert communication rate are obtained. Finally, numerical results are provided to verify our analysis and reveal the impacts of critical parameters on the system performance.Graphic Abstract
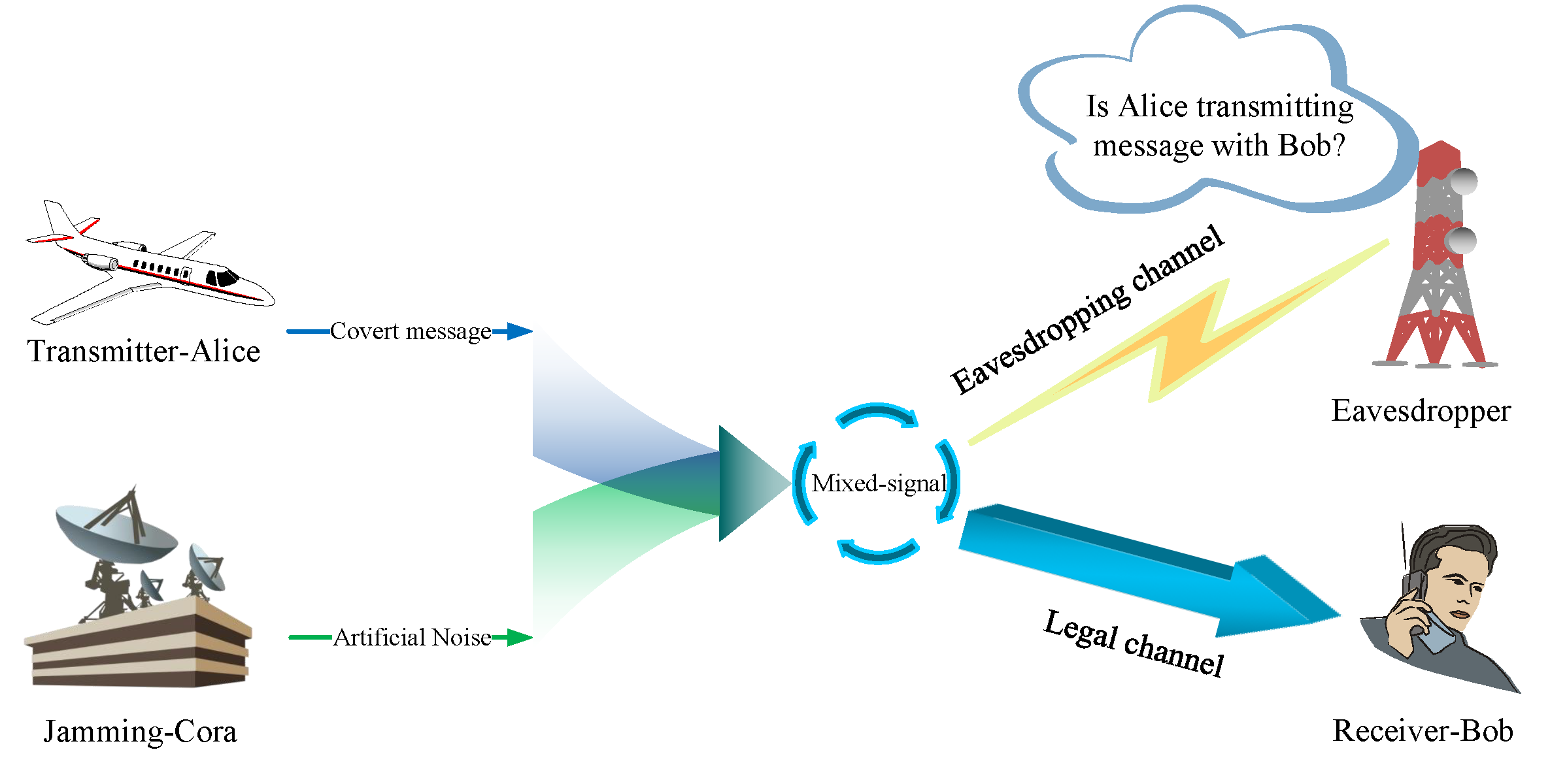
Keywords
The Internet of Things (IoT) is an information carrier based on the Internet and traditional telecommunication networks, which allows all ordinary physical objects that can be independently addressed to form an interconnected network. Nowadays, because the demand for large-scale IoT can not be satisfied by the fifth generation (5G) terrestrial mobile communication, the sixth generation (6G) terrestrial mobile communication development is becoming the general trend. Moreover, over recent years, high altitude platform station (HAPS) has been considered a critical part of the next-generation wireless communication networks for its high altitude, large capacity, flexible communication services, lower communication delay, and smaller terrestrial receiving antenna [1]. Without loss of generality, HAPS can be regarded as a “pseudo satellite,” which is viewed as a supplement or substitute for satellites in many scenes [2]. In addition, as an exemplary network architecture for future communications, the integrated HAPS terrestrial network has momentous practical significance, which can overcome obstacles and geographical constraints flexibly, compared with the integrated satellite-terrestrial network (ISTN) [3,4]. Karabulut Kurt et al. [5] provided a vision and framework for the HAPS networks of the future, including highlighting the unrealized potential of HAPS systems and elaborating on their unique ability to serve metropolitan areas. Liu et al. [6] studied the performance of non-orthogonal multiple access (NOMA)-based integrated satellite-terrestrial relay network (ISTRN) in the presence of multiple primary users (PUs) under a spectrum sharing environment. Shuai et al. [7] investigated the performance of NOMA-based integrated satellite-HAPS-terrestrial networks with transmit antenna selection (TAS) in the presence of imperfect channel state information (CSI) and successive interference cancelation (SIC). Furthermore, the performance of the NOMA-based overlay cognitive integrated satellite-terrestrial relay network with secondary network selection was investigated by Liu et al. [8]. The combined effects of channel estimation errors and hardware impairments on the secrecy performance of cognitive integrated satellite-terrestrial relay networks were researched by Guo et al. [9]. Moreover, Guo et al. [10] studied the performance of the reconfigurable intelligent surface-assisted integrated satellite-unmanned aerial vehicle (UAV)-terrestrial networks with hardware impairments and interference in the presence of an unavailable direct link. Gao et al. [11] optimized the deployment of an aerial reconfigurable intelligent surface (ARIS) to assist the HAPS down-link transmission when the direct link was blocked. Pace et al. [12] investigated optimal routing issues in a multilayered terrestrial-HAPS-satellite network. The massive access for a satellite-aerial-terrestrial network (SATN) was investigated by Huang et al. [13], where a HAPS was deployed as a relay to assist the uplink transmission from terrestrial user equipment (UE) to satellite.
However, the openness of wireless communication and the broad coverage of the HAPS beam will lead to a series of security problems, such as channel monitoring, information eavesdropping, and malicious interruption. Generally, many traditional security policies focus on preventing the extraction of information, such as coding encryption or physical layer security technology using information theory. Popovic et al. [14] analyzed and compared the security features of network architectures based on HAPS and satellites by proposing a security comparison method for network architectures that were based on airborne infrastructure. A new selective encryption and decryption framework based on the start code for high-efficiency video coding was proposed by Lee et al. [15]. On the other hand, Guo et al. [16] investigated the impacts of joint relay selection and user scheduling scheme on the physical layer security for a hybrid satellite-terrestrial relay system. Yerrapragada et al. [17] analyzed new schemes for securing applications at low latency by extending physical layer security (PLS) algorithms to beyond-5G/6G systems and designed protocols that advanced a specific form of PLS. The PLS performance of a wireless communication link through a large reflecting surface (LRS) with phase errors was analyzed by Vega Sanchez et al. [18]. Zhang et al. [19] developed a novel layered physical layer security model to secure multiple messages simultaneously.
Nevertheless, preventing transmission from being perceived is considered a more direct and effective measure. Compared with the above means, covert communication has more advantages than other security policies, which can prevent transmission content and behavior from being detected by non-cooperative eavesdroppers to solve the problem of information security fundamentally. Based on this, many scientists and engineers have focused on the research of covert communication. Covert communication was first cited in military communications by Prescott et al. [20]. Recently, the restriction theory of information transmission was being studied deeply by Bash et al. [21,22]. It was proved that to meet the demands of covert communication in the AWGN channel, the transmission power of the transmitter decreased with the increase of codeword length, resulting in a near-zero effective covert communication rate on both sides of legal communication which is meaningless [23]. Nevertheless, in the actual wireless communication environment, there are many interference signals which can be used to interfere with the eavesdropper’s communication signal [24]. Namely, widespread interference can be used to hide the transmission of information. The interference was firstly proposed to be utilized to realize a positive covert communication by Li et al. [25]. Topal et al. [26] provided a physical layer supported defense mechanism against traffic analysis attacks by exploring the covert communication capability of digital modulation schemes. Covert communication between a pair of legitimate transmitter-receiver against a watchful warden over slow fading channels was studied by Zheng et al. [27]. Yang et al. [28] considered covert communications having uncertainty about the noise variance in fading channels where an eavesdropper used a radio-meter detector to detect the legitimate signal. Furthermore, Gao et al. [29] studied the performance of covert communication under a scenario consisting of a source-destination pair, a passive warden, and multiple relays. The requirement of information freshness in covert communications was considered for the first time by Wang et al. [30]. Su et al. [31] investigated the covert communication performance in relay networks with relay selection. Zhang et al. [32] considered a covert mmWave communication system, where legitimate parties Alice and Bob adopted a beam training approach for directional link establishment. A new framework for jointly characterizing the covertness and timeliness of short-packet communications was developed by Yang et al. [33], in which a new metric named covert age of information (CAoI) was first proposed and derived. Channel uncertainty was exploited to achieve covert communication in relay networks by Wang et al. [34], in which a transmitter sent messages to the legitimate receiver with the help of a relay, and the eavesdroppers wanted to detect the existence of the transmission.
Inspired by the works mentioned above, this article considers an integrated HAPS terrestrial network with one constant power auxiliary node, a terrestrial eavesdropper, a HAPS as the transmitter, and a terrestrial user as the receiver. Moreover, all nodes are equipped with a single omnidirectional antenna and operate in half-duplex mode. Specifically, the significant contributions of this paper are summarized below:
1. Firstly, considering the single-user scenario, a novel integrated HAPS terrestrial covert communication network structure is established, and a constant power auxiliary node assists the covert communication between HAPS and the user.
2. Secondly, considering the actual situation of signal transmission, such as rainfall attenuation and free path loss, the statistical characteristics of the channel are given. In addition, the covert constraints on universal significance are derived.
3. Thirdly, based on the above, the closed expression of outage probability (OP) under this covert communication network is deduced to obtain more in-depth insights and laws. Furthermore, the index to measure the covert performance named effective covert communication rate is given.
4. Finally, the numerical simulation results are given further to analyze key parameters’ impact on system covert performance. Moreover, the observation results are analyzed in detail.
2 System Model and Problem Formulation
As shown in Fig. 1, an integrated HAPS terrestrial network is established, which consists of a HAPS
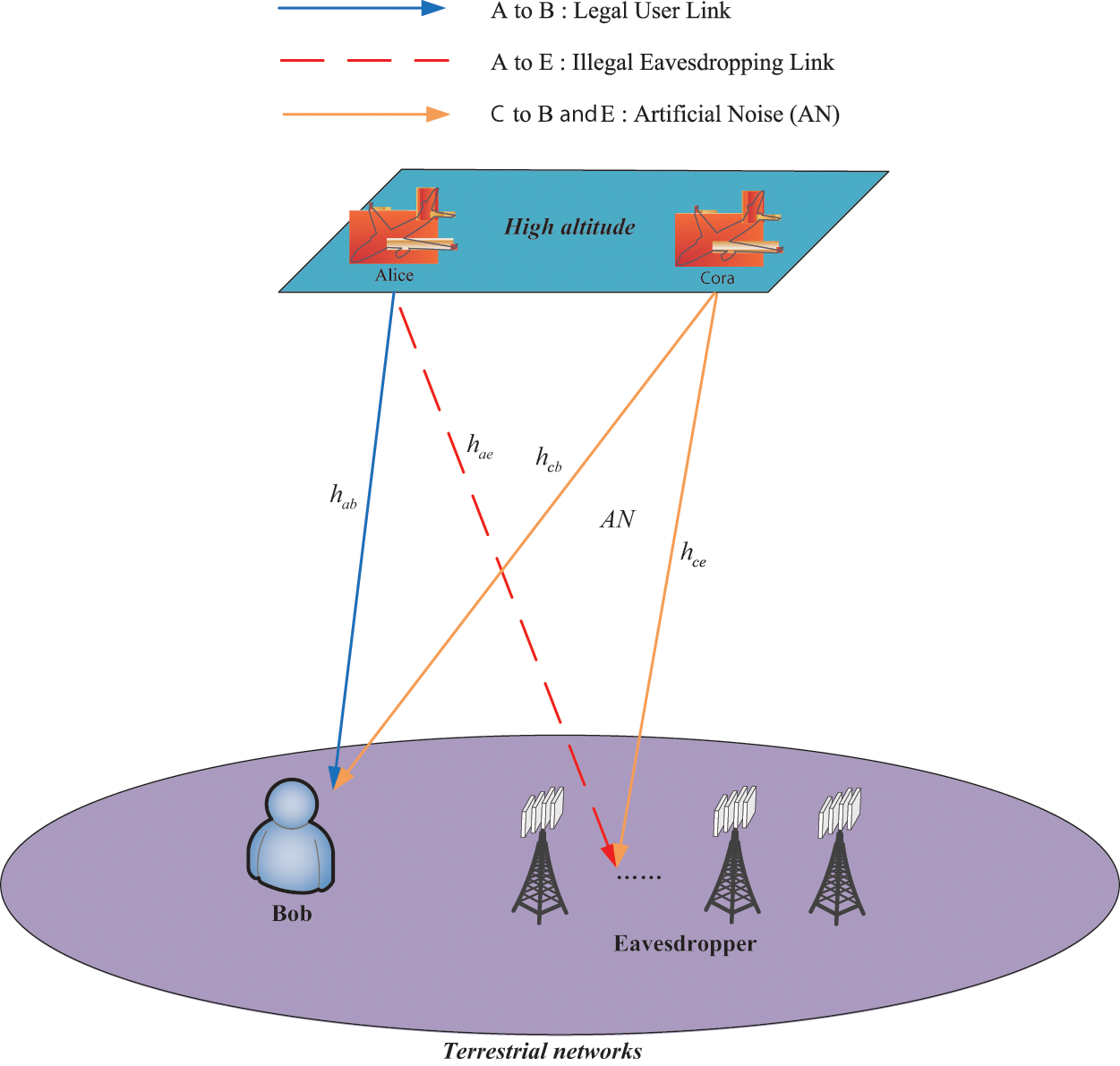
Figure 1: System model
In order to get close to realistic transmission scenarios, the impacts of rain attenuation, free space loss, and antenna gain are considered in this system. Thus, the channel coefficient between
where
In Fig. 1, all nodes are equipped with a single omnidirectional antenna and work in half-duplex mode. For specific analysis, it is assumed that there are discrete-time channels with N time slots between each node, and each time slot has n transmission symbol period or channel uses, which is expressed as the Fig. 2.

Figure 2: N time slot discrete channel
Moreover, we assume that the channels within the system experience standard SR fading, which means that the channel gain of each time slot remains unchanged but varies independently from one-time slot to another. Based on the above, it can be considered that the
Besides, following the general assumptions in covert communication theory [22], we assume that Alice and Bob share a long enough key in advance so that Bob knows the transmission strategy of Alice, but Eavesdropper knows nothing about it.
Regarding a given maximum correct detection probability
where
Similarly, the received signal of Eavesdropper can be given by
where
In our model, only a single auxiliary node is considered, and the energy detection method is adopted by Eavesdropper, which has been proved as the best method in quasi-stationary fading channel [25].
The Eavesdropper adopts the energy detection method to probe and judge whether Alice is transmitting the information. Namely, when the average power of the Eavesdropper’s received signal is larger than the preset energy detection threshold, Eavesdropper considers Alice, and Bob are transmitting signals to each other, and when the average power of the Eavesdropper’s received signal is less than the preset energy detection threshold, Eavesdropper considers that there is no information transmission between Alice and Bob, which is given by
where
Therefore, the error detection of Eavesdropper can be divided into two categories as
where
On the above foundation, the requirements of covert communication can be expressed as
Furthermore, since the probability density functions of
where
where
According to the weak law of large numbers and some mathematical steps, when
where
Proof. See Appendix A.
Similarly, when
where
By means of (9) and (10), when n is large enough, we can derive
Moreover, the sufficient conditions of (11) can be expressed as
where
With the help of (12) and in the light of the different fading conditions involved, we can obtain
Proof. See Appendix B.
Then, the following formula can be obtained as
where
Hence, the average error detection of Eavesdropper can be expressed as
In conclusion, Alice is able to meet the requirements of covert communication in (6) by controlling own transmit power, and due to the above formula (7), the covert constraint relationship between
where
In this section, the statistical properties of SR fading are provided. On this basis, the exact expression of OP for the covert communication in this integrated HAPS terrestrial network is obtained. Besides, we derive the closed-form expression of the effective covert communication rate to measure the system’s covert communication performance.
3.1 Statistical Properties of Channels
Firstly, the probability distribution function (PDF) and cumulative distribution function (CDF) of SR fading are obtained. From [35], the PDF of
where
Under the situation that
According to (18) and (19), the PDF of
From (1) and
where
OP can well evaluate the performance of the system, and in this paper we define the OP as the probability of the instantaneous capacity for any node lower than its excepted capacity. When Alice communicates with Bob legally, the SNR of the received signal at Bob can be given by
where
Assuming that the default coding rate of Alice is
where
By substituting (21) into (22), we can obtain the OP as
where
Furthermore, the final expression of OP can be derived as
where
3.3 Effective Covert Communication Rate
Effective covert communication rate is also a momentous and more intuitive index in the covert communication system, defined as the average ratio of practical transmission information to the transmission time from transmitter to the receiver under all fading conditions. Finally, the effective covert communication rate
Furthermore, the final expression of the effective covert communication rate is given by
In this section, the critical constraint relationship of average SNR between the transmitting node and the auxiliary node, and the effective covert communication rate of the considered system are proved through MC simulations. In general, we set
• Frequent heavy shadowing (FHS):
• Average shadowing (AS):
• Infrequent light shadowing (ILS):
Fig. 3 shows that
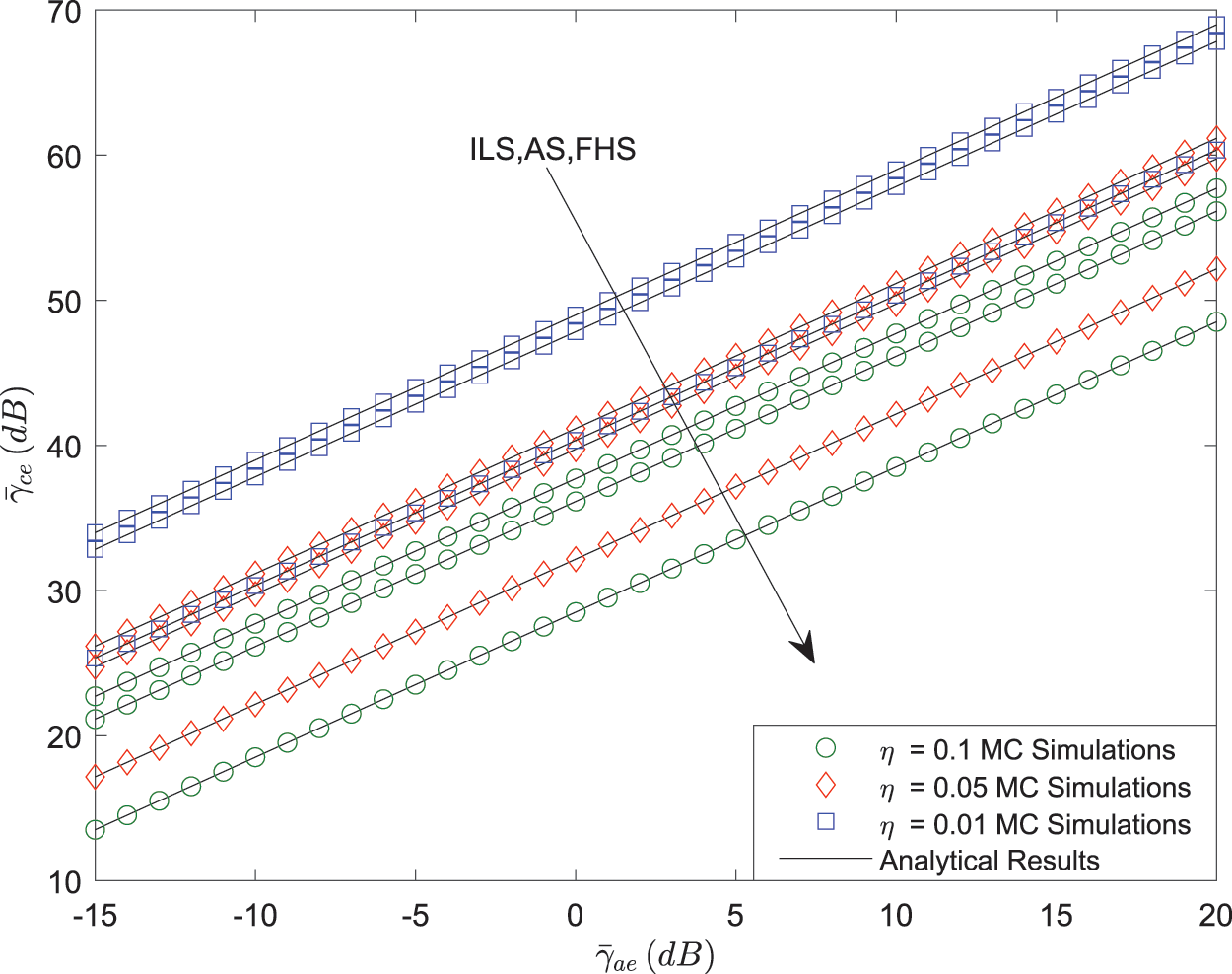
Figure 3: Covert constraint of
Fig. 4 depicts the relationship between
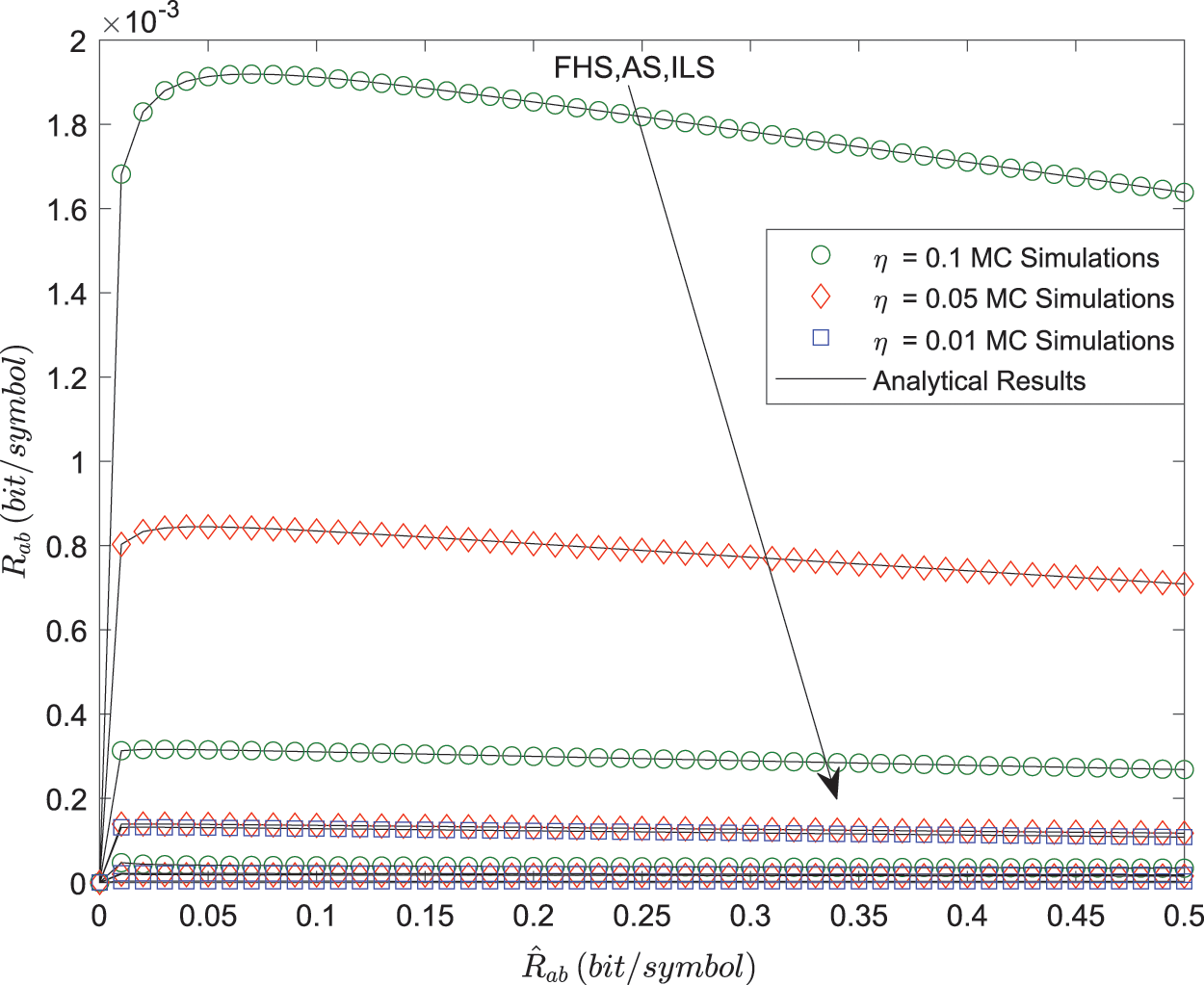
Figure 4:
Figs. 5 and 6 plot that
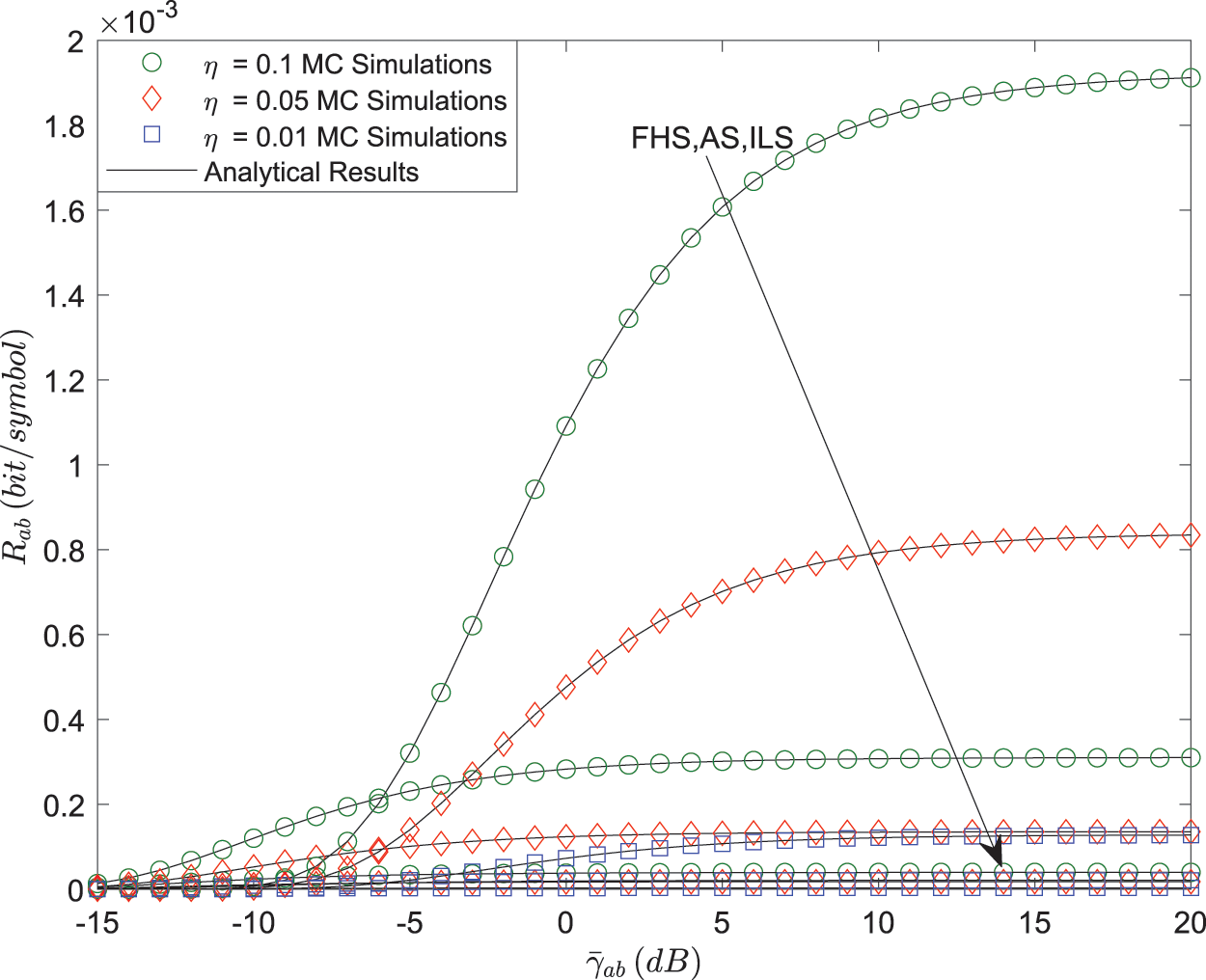
Figure 5:
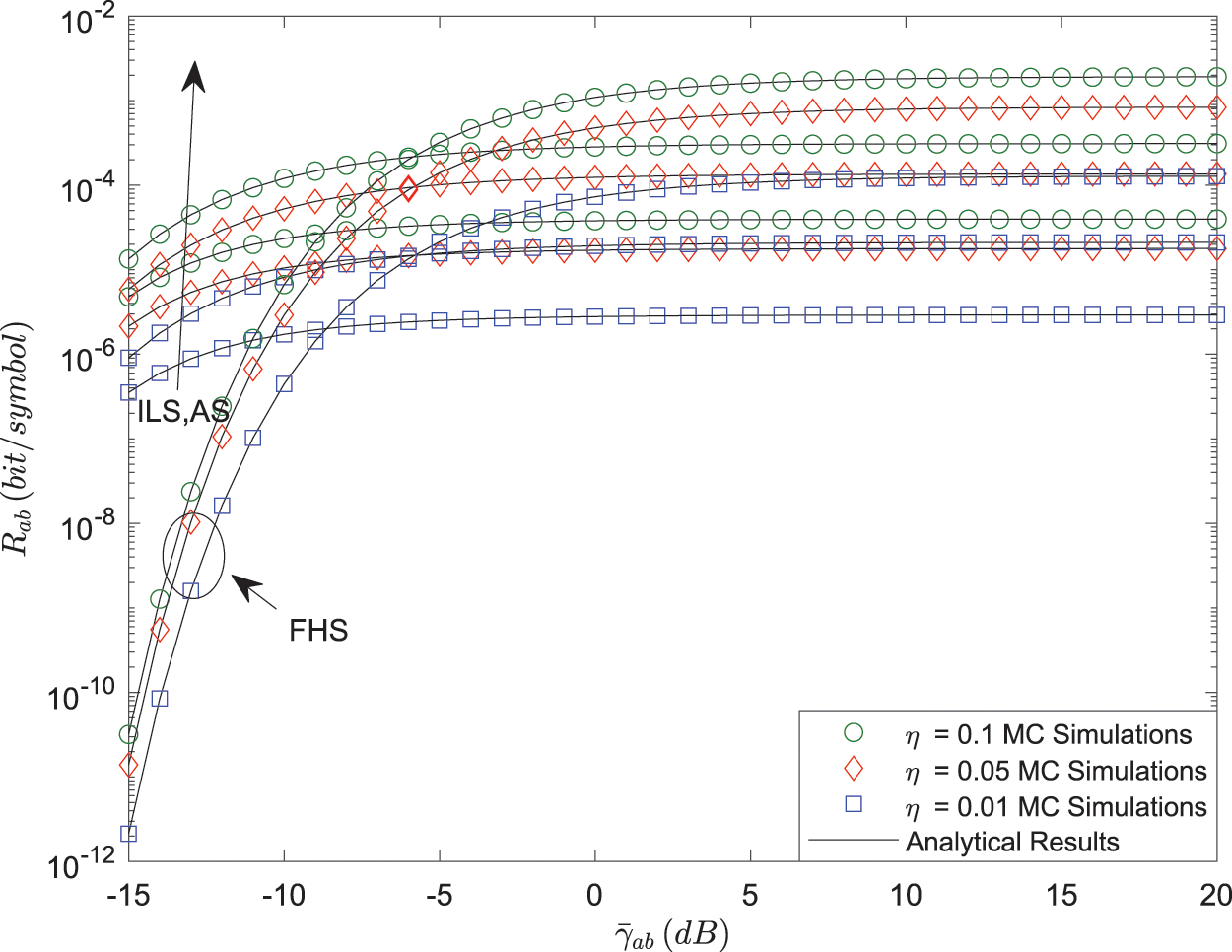
Figure 6:
This article systematically investigated the covert constraint and effective performance of covert communication in the integrated HAPS terrestrial networks, which utilized an auxiliary node with constant power. In particular, the covert constraint relationship between the transmitting node and the auxiliary node was discussed. Furthermore, the exact expressions of OP and effective covert communication rate were derived. According to numerical results, we found that the power of the transmitting node and auxiliary node under the covert constraint had a linear relationship. Secondly, the tightening of the covert constraint caused the deterioration of the achievable effective covert communication rate. Thirdly, there was an optimal preset coding rate to obtain the maximum effective covert communication rate. In addition, we knew that it was difficult for the Eavesdropper to acquire correct judgment under severe fading conditions, which means natural interference, namely, covert communication, can be realized with less interference of the auxiliary node. Similarly, it was worth noting that the worse fading condition would enhance effective performance in the high average SNR regimes.
Acknowledgement: Thanks to all the authors for their contributions to this paper. The authors would like to thank the anonymous reviewers for their insightful suggestions that helped us improve this paper’s quality.
Funding Statement: This work was supported by the National Science Foundation of China under Grant 62001517, in part by the Research Project of Space Engineering University under Grants 2020XXAQ01 and 2019XXAQ05, and in part by the Science and Technology Innovation Cultivation Fund of Space Engineering University.
Conflicts of Interest: The authors declare that they have no conflicts of interest regarding the publication of this article.
References
1. Mohammed, A., Mehmood, A., Pavlidou, F. N., Mohorcic, M. (2011). The role of high-altitude platforms in the global wireless connectivity. Proceedings of the IEEE, 99(11), 1939–1953. [Google Scholar]
2. An, K., Li, Y., Yan, X., Liang, T. (2019). On the performance of cache-enabled hybrid satellite-terrestrial relay networks. IEEE Wireless Communications Letters, 8(5), 1506–1509. DOI 10.1109/LWC.5962382. [Google Scholar] [CrossRef]
3. Zhang, X., Guo, D., An, K., Zheng, G., Chatzinotas, S. et al. (2021). Auction-based multichannel cooperative spectrum sharing in hybrid satellite-terrestrial IoT networks. IEEE Internet of Things Journal, 8(8), 7009–7023. DOI 10.1109/JIOT.2020.3037408. [Google Scholar] [CrossRef]
4. Lin, Z., Lin, M., Zhu, W. P., Wang, J. B., Cheng, J. (2021). Robust secure beamforming for wireless powered cognitive satellite-terrestrial networks. IEEE Transactions on Cognitive Communications and Networking, 7(2), 567–580. DOI 10.1109/TCCN.2020.3016096. [Google Scholar] [CrossRef]
5. Karabulut Kurt, G., Khoshkholgh, M. G., Alfattani, S., Ibrahim, A., Darwish, T. S. J. et al. (2021). A vision and framework for the high altitude platform station (HAPS) networks of the future. IEEE Transactions on Cognitive Communications and Networking, 23(2), 729–779. [Google Scholar]
6. Liu, R., Guo, K., An, K., Zhu, S., Shuai, H. (2021). Performance analysis of noma-based overlay cognitive integrated satellite-aerial-terrestrial networks. IEEE Wireless Communications Letters, 10(6), 1266–1270. DOI 10.1109/LWC.2021.3063759. [Google Scholar] [CrossRef]
7. Shuai, H., Guo, K., An, K., Huang, Y., Zhu, S. (2022). Transmit antenna selection in noma-based integrated satellite-HAP-terrestrial networks with imperfect CSI and SIC. IEEE Wireless Communications Letters, 11(8), 1565–1569. DOI 10.1109/LWC.2022.3165710. [Google Scholar] [CrossRef]
8. Liu, R., Guo, K., An, K., Zhu, S. (2022). Noma-based overlay cognitive integrated satellite-terrestrial relay networks with secondary network selection. IEEE Transactions on Vehicular Technology, 71(2), 2187–2192. DOI 10.1109/TVT.2021.3122029. [Google Scholar] [CrossRef]
9. Guo, K., Dong, C., An, K. (2022). Noma-based cognitive satellite terrestrial relay network: Secrecy performance under channel estimation errors and hardware impairments. IEEE Internet of Things Journal. DOI 10.1109/JIOT.2022.3157673. [Google Scholar] [CrossRef]
10. Guo, K., An, K. (2018). On the performance of RIS-assisted integrated satellite-UAV-terrestrial networks with hardware impairments and interference. IEEE Wireless Communications Letters, 22(6), 1240–1243. [Google Scholar]
11. Gao, N., Jin, S., Li, X., Matthaiou, M. (2022). Aerial RIS-assisted high altitude platform communications. IEEE Wireless Communications Letters, 11(1), 131–135. [Google Scholar]
12. Pace, P., Aloi, G. (2007). Effective routing algorithm for multilayered terrestrial-HAP-satellite networks. IEEE Communications Letters, 11(6), 510–512. DOI 10.1109/LCOMM.2007.070238. [Google Scholar] [CrossRef]
13. Huang, Q., Lin, M., Zhu, W. P., Cheng, J., Alouini, M. S. (2021). Uplink massive access in mixed RF/FSO satellite-aerial-terrestrial networks. IEEE Transactions on Communications, 69(4), 2413–2426. DOI 10.1109/TCOMM.2021.3049364. [Google Scholar] [CrossRef]
14. Popovic, M., Basicevic, I. (2010). On security advantages of HAPS over satellites. URSI Radio Science Bulletin, 2010(334), 19–24. [Google Scholar]
15. Lee, M. K., Jang, E. S. (2020). Start code-based encryption and decryption framework for HEVC. IEEE Access, 8, 202910–202918. DOI 10.1109/Access.6287639. [Google Scholar] [CrossRef]
16. Guo, K., An, K., Zhang, B., Huang, Y., Guo, D. (2018). Physical layer security for hybrid satellite terrestrial relay networks with joint relay selection and user scheduling. IEEE Access, 6, 55815–55827. DOI 10.1109/ACCESS.2018.2872718. [Google Scholar] [CrossRef]
17. Yerrapragada, A. K., Eisman, T., Kelley, B. (2021). Physical layer security for beyond 5G: Ultra secure low latency communications. IEEE Open Journal of the Communications Society, 2, 2232–2242. DOI 10.1109/OJCOMS.2021.3105185. [Google Scholar] [CrossRef]
18. Sanchez, V., D, J., Espinosa, R. R., Lopez-Martinez, P., J, F. (2021). Physical layer security of large reflecting surface aided communications with phase errors. IEEE Wireless Communications Letters, 10(2), 325–329. DOI 10.1109/LWC.5962382. [Google Scholar] [CrossRef]
19. Zhang, W., Chen, J., Kuo, Y., Zhou, Y. (2019). Artificial-noise-aided optimal beamforming in layered physical layer security. IEEE Communications Letters, 23(1), 72–75. DOI 10.1109/LCOMM.2018.2881182. [Google Scholar] [CrossRef]
20. Prescott, G., Gutman, L., Connolly, D., Holtzman, J. (1991). A methodology for employing modulation quality factors in the analysis of lPI waveforms. MILCOM 91-Conference Record, 2, 532–536. DOI 10.1109/MILCOM.1991.258311. [Google Scholar] [CrossRef]
21. Wang, L., Wornell, G. W., Zheng, L. (2016). Fundamental limits of communication with low probability of detection. IEEE Transactions on Information Theory, 62(6), 3493–3503. DOI 10.1109/TIT.2016.2548471. [Google Scholar] [CrossRef]
22. Bash, B. A., Goeckel, D., Towsley, D. (2013). Limits of reliable communication with low probability of detection on AWGN channels. IEEE Journal on Selected Areas in Communications, 31(9), 1921–1930. DOI 10.1109/JSAC.2013.130923. [Google Scholar] [CrossRef]
23. Bloch, M. R. (2016). Covert communication over noisy channels: A resolvability perspective. IEEE Transactions on Information Theory, 62(5), 2334–2354. DOI 10.1109/TIT.2016.2530089. [Google Scholar] [CrossRef]
24. Tse, D., Viswanath, P. (2005). Fundamentals of wireless communication. London, UK: Cambridge University Press. [Google Scholar]
25. Li, K., Sobers, T., Towsley, D., Goeckel, D. (2017). Covert communication in the presence of an uninformed jammer. IEEE Transactions on Wireless Communications, 16(9), 6193–6206. DOI 10.1109/TWC.2017.2720736. [Google Scholar] [CrossRef]
26. Topal, O. A., Kurt, G. K. (2021). A countermeasure for traffic analysis attacks: Covert communications with digital modulation. IEEE Wireless Communications Letters, 10(2), 441–445. DOI 10.1109/LWC.5962382. [Google Scholar] [CrossRef]
27. Zheng, T. X., Yang, Z., Wang, C., Li, Z., Yuan, J. et al. (2021). Wireless covert communications aided by distributed cooperative jamming over slow fading channels. IEEE Transactions on Wireless Communications, 20(11), 7026–7039. DOI 10.1109/TWC.2021.3080382. [Google Scholar] [CrossRef]
28. Yang, H., Sun, L. (2020). Power allocation for covert wireless communications in fading channels. 2020 IEEE 6th International Conference on Computer and Communications (ICCC), pp. 20–25. Chengdu, China. [Google Scholar]
29. Gao, C., Yang, B., Jiang, X., Inamura, H., Fukushi, M. (2021). Covert communication in relay-assisted IOT systems. IEEE Internet of Things Journal, 8(8), 6313–6323. DOI 10.1109/JIOT.2021.3051694. [Google Scholar] [CrossRef]
30. Wang, Y., Yan, S., Yang, W., Cai, Y. (2021). Covert communications with constrained age of information. IEEE Wireless Communications Letters, 10(2), 368–372. DOI 10.1109/LWC.5962382. [Google Scholar] [CrossRef]
31. Su, Y., Sun, H., Zhang, Z., Lian, Z., Xie, Z. et al. (2021). Covert communication with relay selection. IEEE Wireless Communications Letters, 10(2), 421–425. DOI 10.1109/LWC.5962382. [Google Scholar] [CrossRef]
32. Zhang, J., Li, M., Yan, S., Liu, C., Chen, X. et al. (2021). Joint beam training and data transmission design for covert millimeter-wave communication. IEEE Transactions on Information Forensics and Security, 16, 2232–2245. DOI 10.1109/TIFS.10206. [Google Scholar] [CrossRef]
33. Yang, W., Lu, X., Yan, S., Shu, F., Li, Z. (2021). Age of information for short-packet covert communication. IEEE Wireless Communications Letters, 10(9), 1890–1894. DOI 10.1109/LWC.2021.3085025. [Google Scholar] [CrossRef]
34. Wang, J., Tang, W., Zhu, Q., Li, X., Rao, H. et al. (2019). Covert communication with the help of relay and channel uncertainty. IEEE Wireless Communications Letters, 8(1), 317–320. DOI 10.1109/LWC.2018.2872058. [Google Scholar] [CrossRef]
35. Miridakis, N. I., Vergados, D. D., Michalas, A. (2015). Dual-hop communication over a satellite relay and shadowed rician channels. IEEE Transactions on Vehicular Technology, 64(9), 4031–4040. DOI 10.1109/TVT.2014.2361832. [Google Scholar] [CrossRef]
36. The wolfram function site. http://functions.wolfram.com. [Google Scholar]
37. Brychkov, Y. (2008). Handbook of special functions: Derivatives, integrals, series and other formulas. Florida, USA: CRC Press. [Google Scholar]
38. Abdi, A., Lau, W., Alouini, M. S., Kaveh, M. (2003). A new simple model for land mobile satellite channels: First- and second-order statistics. IEEE Transactions on Wireless Communications, 2(3), 519–528. DOI 10.1109/TWC.2003.811182. [Google Scholar] [CrossRef]
Appendix A
Recalling the transmission model, under the condition of
where
Due to the weak law of large number and
Further, for
Moreover, for
When
Therefore, at this time, for
Hence, when
where
Similarly, under the condition of
Appendix B
Based on the previous Eq. (12) in this article, we have obtained
where
Moreover, due to
we can get
Therefore, according to the scenario all we consider and the probability density distribution curve of
Namely,
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools