 Open Access
Open Access
ARTICLE
Cushioning Performance of Hilbert Fractal Sandwich Packaging Structures under Quasi-Static Compressions
1 College of Light Industry Science and Engineering, Tianjin University of Science & Technology, Tianjin, 300457, China
2 Key Laboratory of Food Packaging Materials and Technology of China Light Industry, Tianjin, 300457, China
* Corresponding Author: Haiyan Song. Email:
(This article belongs to the Special Issue: Fractal-Fractional Models for Engineering & Sciences)
Computer Modeling in Engineering & Sciences 2023, 135(1), 275-292. https://doi.org/10.32604/cmes.2022.022637
Received 18 March 2022; Accepted 19 May 2022; Issue published 29 September 2022
Abstract
The sandwich structure of cushioning packaging has an important influence on the cushioning performance. Mathematical fractal theory is an important graphic expression. Based on Hilbert fractal theory, a new sandwich structure was designed. The generation mechanism and recurrence formula of the Hilbert fractal were expressed by Lin’s language, and the second-order Hilbert sandwich structure was constructed from thermoplastic polyurethane. The constitutive model of the hyperelastic body was established by using the finite element method. With the unit mass energy absorption as the optimization goal, the fractal sandwich structure was optimized, and the best result was obtained when the order was 2.5 and the unit layer thickness was 0.75 mm. The Hilbert sandwich structure was compared with the rice-shaped sandwich structure commonly used in industry, and the Hilbert fractal structure had better energy absorption. This has practical significance for the development and application of new cushioning packaging structures.Keywords
Abbreviation List
| TPU | Thermoplastic polyurethane |
| 3D | Three-dimensional |
| EA | Total energy absorption |
| SEAm | Energy absorption per unit mass |
| SEAv | Energy absorption per unit volume |
| n | Order |
| t | Unit layer thickness |
Fractal structures, originally referred to as broken and irregular fragments, were later used to describe special geometric figures. Compared with simple geometric shapes, fractal structures have various advantages, including self-similarity, multi-scale symmetry, and compact structures. Fractal structures can fill the plane by recursion, increase the number of effective structures, realize the transfer of mechanical loads more efficiently, effectively suppress global failure, and improve the recoverability of structures [1]. In the process of constructing fractal theory, fractal calculus is very important. Fractal calculus is very simple but extremely effective in dealing with phenomena in hierarchical or porous media. The use of fractal calculus can have important application significance in microgravity space [2], mathematical iterative solution [3] and foam surface tension [4]. The traditional sandwich cushioning material is similar to a honeycomb. Because of its single structure, its energy absorption characteristics cannot be superimposed [5], which limits its application range. Therefore, designing a sandwich buffer structure based on fractal theory has become a popular research topic [6].
In 1891, the German mathematician Hilbert constructed a curve that could pass through all the points in the square lattice [7]. In Fig. 1, squares depicted by thinner lines represent squares, while curves depicted by thicker lines are Hilbert curves. Fig. 1a shows a 2 × 2 square structure corresponding to the first-order Hilbert curve, which is relatively simple. Figs. 1b and 1c show square structures with dimensions of 4 × 4 and 16 × 16, respectively, which correspond to Hilbert curves of orders 2 and 3. Careful observation shows that all square spaces are covered by Hilbert curves. A Hilbert curve has three characteristics: 1) it can be defined by a simple recursive process, and it can be simply recursive by using Lin’s language; 2) it is self-similar and can fill a limited square space as much as possible; 3) for details with any scale, order 4 can be defined arbitrarily according to its definition [8].
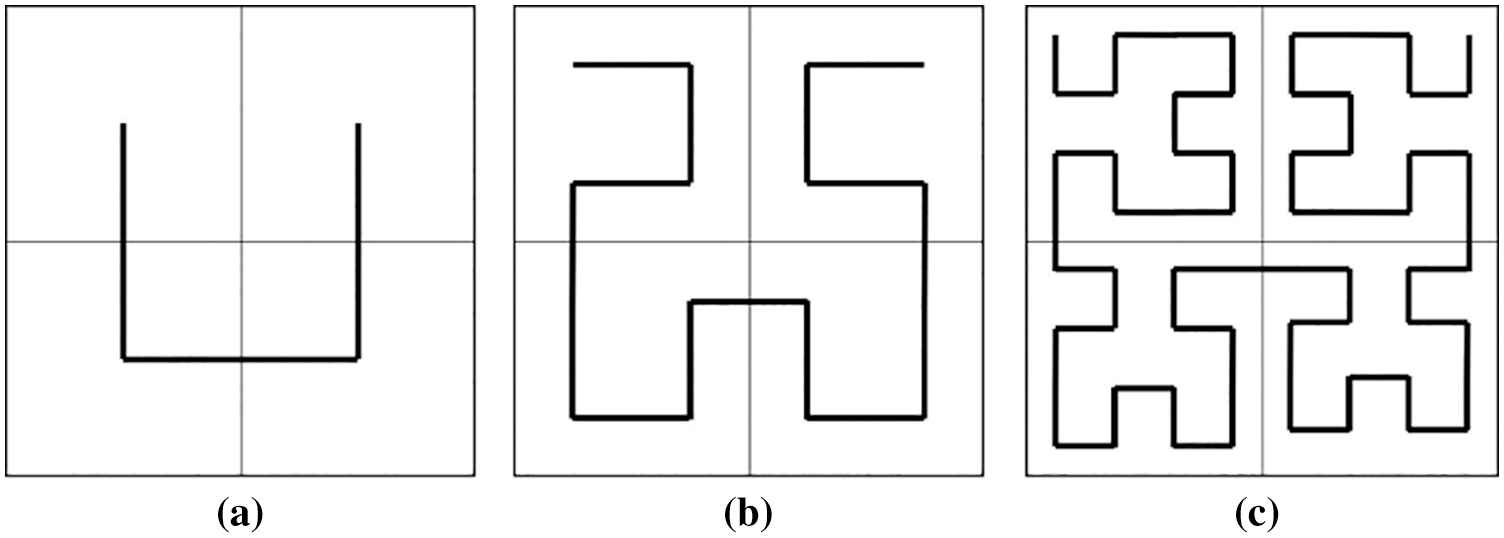
Figure 1: Fractal principle of Hilbert curve
Recently, as a powerful mathematical tool, two-scale fractal theory has appeared in the recurrence of fractal theory [9]. The two-scale fractal derivative is conformable with the traditional differential derivatives. Many scholars use two-scale fractal in the establishment of fractal theory.
Many scholars at home and abroad have made corresponding research on Hilbert fractal curve. He [10] considered Hilbert cubes starting from one-dimensional to an infinite dimensional Hilbert cube. He concluded that Hilbert cube model was the best candidate to mimic non-differentiable and discontinuous real spacetime. This paper applied the Hilbert cube model for fractal spacetime to the generation of Hilbert curve. This has a positive effect and inspiration.
Since a fractal structure has strong space filling ability and recurrence relation, it could achieve a distinct effect when it is used in a buffer structure. In the field of porous concrete, He et al. [11] established a fractal heat conduction model, which revealed the influence of concrete porosity on the internal temperature response. The theoretical results were compared with the experimental data, and the verification effect was good. In the field of composites, Zuo et al. [12] used the two-scale fractal theory, and suggested the fractal laws for the electrical conductivity of graphene, carbon nanotubes and graphene/SiC composites. In the field of fractal vibration system, He et al. [13] established a fractal-differential model and a fractal Duffing-Van der Pol oscillator with two-scale fractal derivatives and a forced term was considered as an example to reveal the basic properties of the fractal oscillator. It was revealed that the exciting external force parameter plays a destabilizing role.
Meza et al. [14] adopted a non-axial beam structure design by a recursive method. By better optimizing the layered geometry structure, it could bear 91% of the axial load and exhibited recoverability after yielding. Wang et al. [15] designed a new type of energy absorber device based on Koch fractal geometry. Through experimental tests and simulations, the collision performances of three Koch fractal designs were studied. This provided a new method for designing a new type of light energy-absorber with improved collision characteristics. Zhang et al. [16] proposed three new side fractal structures, triangle, quadrangle and hexagon, and optimized their wall thicknesses (t) and orders (n), which provided good guidance for the design of energy absorbers of protection systems. In order to further study the relationship between a Hilbert structure and a cushioning packaging, thermoplastic polyurethane (TPU) models prepared by three-dimensional (3D) printing technology can be built. Xie et al. [17] prepared a bionic sandwich structure of a TPU loofah based on 3D printing technology. Static compression experiments and finite element simulations showed that the folding angle (θ) of the panel had little effect on the cushioning performance, and the cushioning performance could be effectively improved by reducing the panel length (A). Zhang et al. [18] inspired by the unique microstructure of pomelo peel, constructed a novel layered honeycomb structure material and studied its crushing resistance and energy absorption performance. Because of its porous layered structure, it was confirmed that it had energy dissipation abilities through experiments. Cao et al. [19] designed two kinds of Weiaire–Phelan buffer structures with different cell densities and used nitrile rubber material for 3D printing. The Weaire-Phelan structure consists of two dodecahedrons and six tetrahedrons, which form a cell unit. It is found that the compression deformation process of Weiaire-Phelan structure after impact is similar to that of common porous structure. But different from the top-down folding mode of honeycomb structure. Based on fractal theory, scholars around the world have applied it to the design of cushioning structures with excellent cushioning performances. The existing research results have been an important inspiration for manufacturing new fractal cushioning materials with excellent mechanical properties.
At present, the research on the cushioning performances of fractal structures around the world is focused on automobile energy absorbers, but sandwich structures have been seldom considered. The research on Hilbert fractals is rarely used in the field of mechanics. Therefore, in this study, the main characteristic structure of Hilbert fractal is extracted, and the recursive formula is constructed by using logo language, and the three-dimensional model of sandwich panel is constructed. As shown in Fig. 2, the Hilbert fractal structure material was prepared by 3D printing, with TPU as the raw material, and its buffering performance was studied and optimized. The Hilbert fractal structure designed in this study can be applied to the cushioning packaging of some specific products, such as precision instruments, aerospace instruments and so on. Its 3D printing technology can arbitrarily change the size of the structure, and it is suitable for different contents. Moreover, TPU material can bear more static load than EPE and other materials, and has better heavy load and new energy.

Figure 2: Hilbert fractal structure diagram of order 3
2 Model Establishment and Verification
2.1 Hilbert Curve and Generating Principle
A Hilbert curve has three characteristics: ① it can fill the whole plane image, ② it is highly tortuous and continuous but non-derivable, and ③ it has self-similarity [20]. In this study, a Hilbert curve was used to represent a buffer structure to understand its features and generation mechanism. At present, the most common method is to express a Hilbert curve in Lin’s language [21].
The essence of the Lin’s system language is the string rewriting technology based on the LOGO language. The Lin’s system is a triple < V, ω, P > whose elements are defined as follows:
where ‘→’ indicates that the symbol string on the right side of the ‘→’ is used to replace the symbol on the left side when the rule is applied to the symbol, ‘+’ indicates that the current position is rotated 90° clockwise, and ‘–’ indicates that the current position is rotated 90° counterclockwise.
L, R, and F in V are all curve units to be used to draw the Hilbert curve, and the current direction is horizontal to the right. The specific definitions of L, R, and F are as shown in Fig. 3.
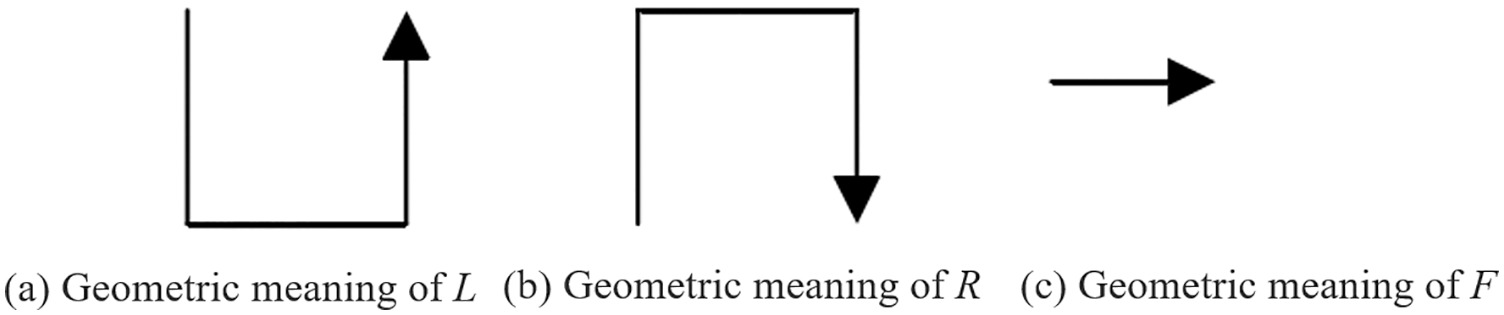
Figure 3: Basic elements of Hilbert curve
The drawing of a Hilbert curve is a process of constantly applying rules to symbols, and each order of the Hilbert curve can be expressed by L, F, and R in the L system. The details are as follows:
These three levels represent Hilbert curves of orders 1, 2, and 3, respectively, as shown in Fig. 4.
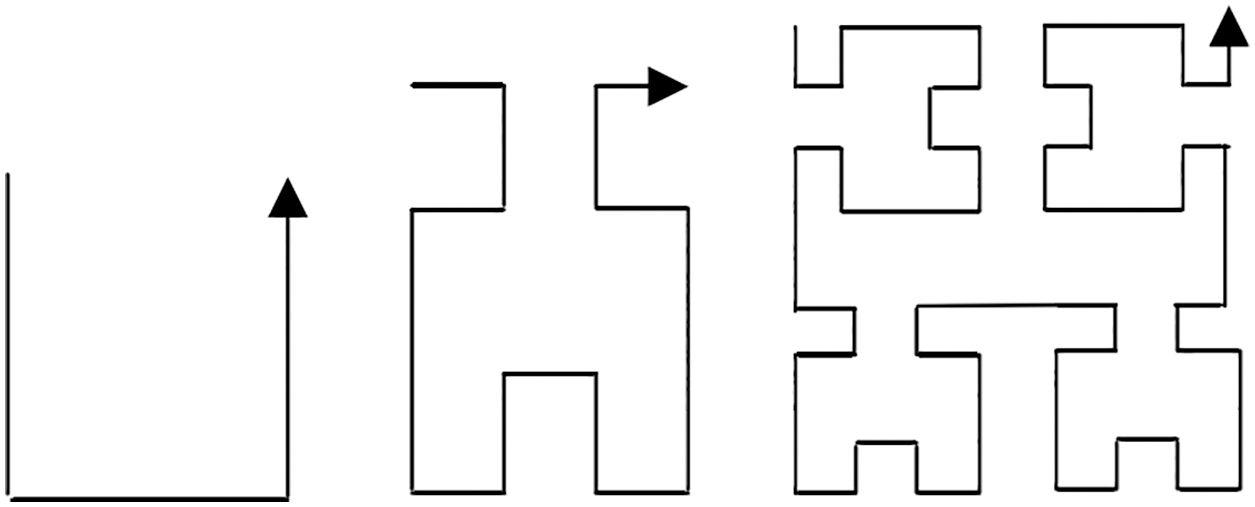
Figure 4: Hilbert curves of orders 1, 2, and 3
2.2 Test Samples and Equipment
In this study, TPU was used to prepare the fractal structure by a light-cured 3D printing method, and the room temperature and relative humidity were set to 25°C and 40%, respectively. The printing parameters of all the models are shown in Table 1.

The compression behaviors were tested using an American Instron 3369 Universal Material Testing Machine (American Instron Company, USA) with a load of 50 kN.
2.3 Establishment of Finite Element Model
ANSYS, a nonlinear finite element software, has high efficiency and accuracy in modeling nonlinear and large-deformation materials such as rubber [22]. The explicit dynamics module can simulate quasi-static compression [23]. Thus, ANSYS has become the preferred simulation software for nonlinear analysis. Through finite element analysis, the reliability of the designed bionic model was verified. If the simulation results were consistent with the tested results, it could provide guidance for the subsequent simulation design.
2.3.1 Establishment of Geometric Model
Based on the above mathematical expressions, a three-dimensional model was established. Overall, the model was 100 mm long, 100 mm wide, and 18 mm high. At the same time, in ANSYS, the explicit dynamics module was selected, and a 3D model was entered. Specifically, it consisted of a Hilbert fractal structure, mass block, and support plate, as shown in Fig. 5.

Figure 5: Hilbert fractal structure, mass block, and support plate build assembly
2.3.2 Hyperelastic Constitutive Model
Different hyperelastic models have different fitting effects on the complex deformation behaviors of rubber materials [24]. By comparing the similarity between the fitted curve and the tested data, the evaluation can directly reflect the fitting effect of the hyperelastic constitutive model on the tested data. In this study, according to the basic mechanical tested data of polyurethane rubber materials, the Yeoh second-order constitutive model was adopted.
The linear least squares method [25] was applied to fit the Yeoh second-order constitutive model with the tested data. The parameters of the constitutive model were obtained by solving the linear equations. The C10 and C01 values were substituted into the Yeoh constitutive model, and the fitted curve [26] of the corresponding model was obtained. As shown in Fig. 6, the fitting quality was good, and it was determined that C10 = 1.223 MPa, C11 = −0.0113 MPa, and D = 0.1.
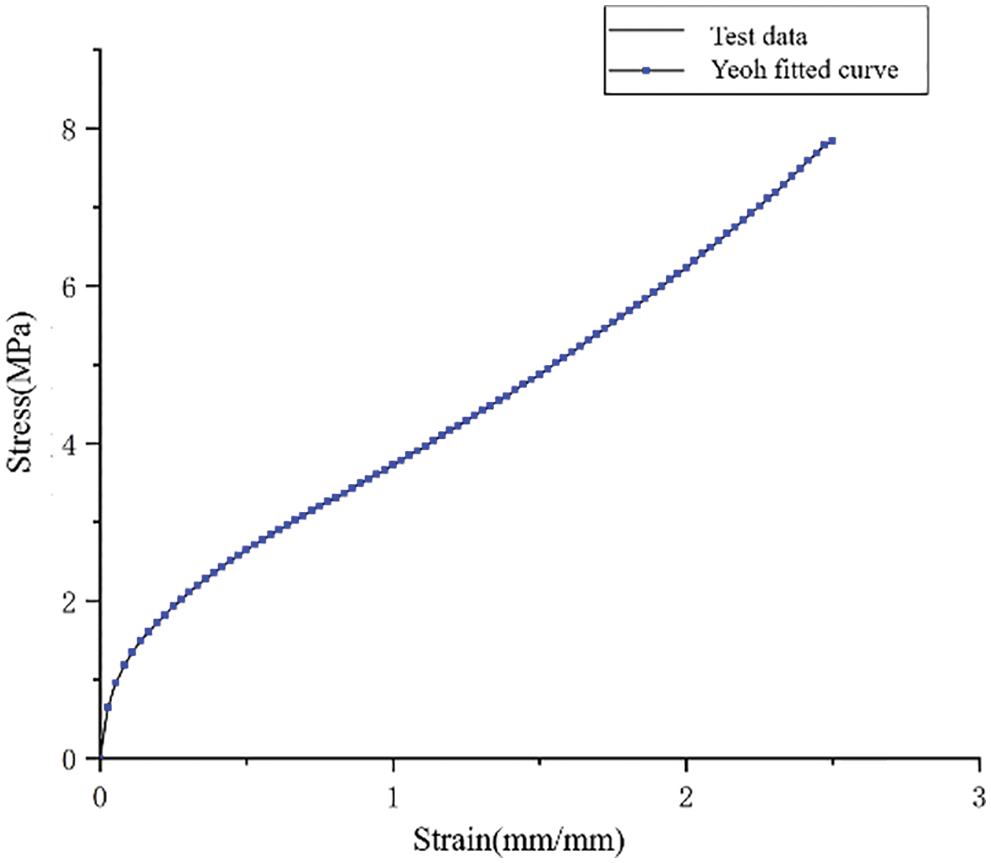
Figure 6: Data fitting of TPU material and Yeoh constitutive law
In ANSYS, the explicit dynamics module was selected. The first step was to establish a finite element model. This consisted of the Hilbert fractal structure, mass block, and support plate. The second step was to set the material properties. The Hilbert fractal structure materials used a Yeoh second-order constitutive model. Rigid blocks and rigid support plates were set according to the material properties of structural steel. The third step is to mesh the model. Firstly, the material attributes are given to the calculation model, and then the mesh is divided in an appropriate way. The entity uses hexahedral element mapping grid, the size of Hilbert fractal structure unit is 1.5 mm, and the total grid unit is 109,600, as shown in Fig. 7. The fourth step was to set the contact and loading. The analysis step length was set to 0.12 s, and face-to-face contact was set between them. The fifth step was to solve the equations. According to the quasi-static compression speed and distance, the approximate solution time was calculated. The relevant contact force and displacement data, the stress distribution, and an animation of the quasi-static compression process were obtained.

Figure 7: Grid division of Hilbert fractal structure
2.4 Finite Element Model Verification
Dumbbell specimens were designed according to the ISO527–2 standard “Testing Methods for Tensile Properties of Plastics” [27]. As shown in Fig. 8, the material mechanics data were obtained based on static tensile tests, which were input into finite element analysis software, and a Yeoh second-order hyperelastic constitutive model was used.

Figure 8: Dumbbell specimen model
According to ANSYS, the contact force between the upper late and the specimen was extracted as a reaction stress. The forward displacement of the upper discrete rigid body was extracted as the compression displacement, and the XY data were output. The XY data were imported, converted into stress–strain values by using software ‘Origin’, and the corresponding curve was drawn. The tested results showed that the finite element model could well reflect the deformation characteristics under different compression displacements, and the results were in good agreement with the compression experiments, as shown in Fig. 9.

Figure 9: Quasi-static compression of finite element model and TPU model
The stress–strain curves of the TPU were obtained by extracting the XY data from ANSYS. The stress–strain curves of the finite element model and TPU model were plotted, and the curves were in good agreement at each stage, as shown in Fig. 10.
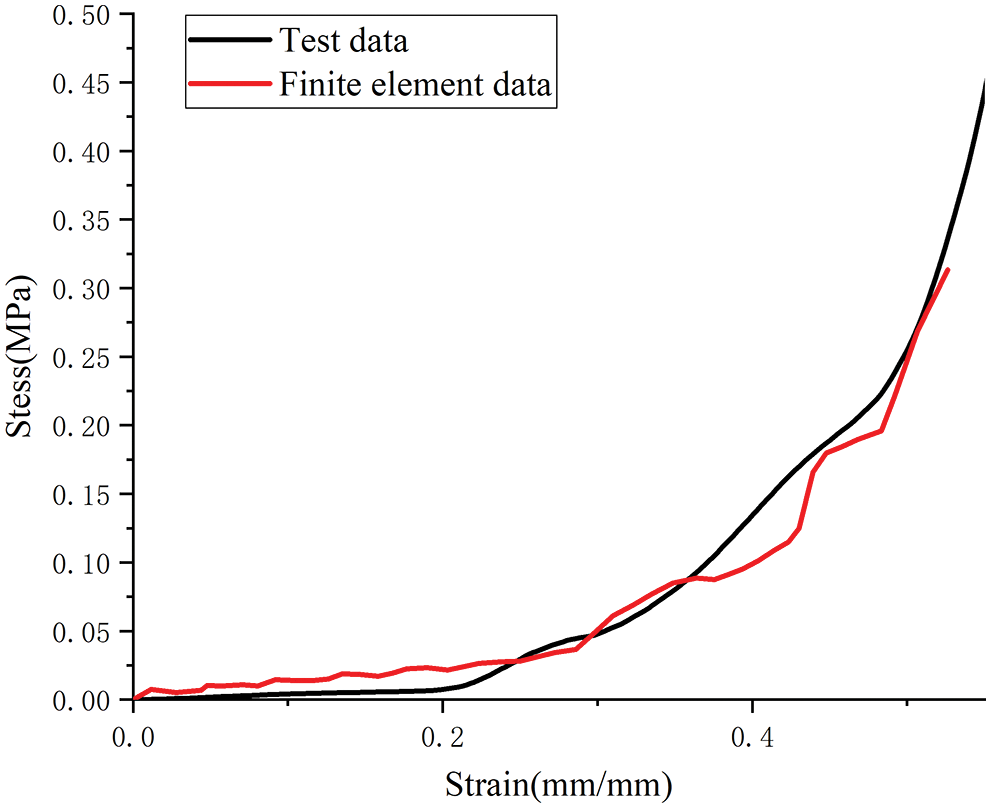
Figure 10: Comparison of stress–strain curves between finite element model and TPU model
In the plateau stress stage, the TPU model was similar to the finite element model, but due to mesh collisions, some of the finite element models showed stress reduction. However, the overall trend was similar, and the errors of key numerical points were in the range of 5%–10%. Therefore, the accuracy of the finite element model was verified, and it could be used for subsequent research.
3.1 Quasi-Static Compression Performance of Hilbert Fractal Structure
Photographs of the quasi-static compression test of the Hilbert fractal structure are shown in Fig. 11. Each fractal structural unit experienced a regular and stable collapse, which is an ideal energy absorption mode. In the process of compression, the axial deformation started from the top and gradually extended to the bottom, and the sandwich layers were squeezed and deformed.

Figure 11: Quasi-static compression test at each stage
According to the quasi-static compression tested results, the compression process of the Hilbert fractal structure could be divided into two parts: A platform area and a densification area. According to the analysis of the quasi-static compression tested data of the Hilbert fractal structure, when the maximum compressive stress of 4.17 MPa was applied, the deformation of the structure was 13.5 mm, and the compressive strain was 0.71. The energy absorption efficiency reflects the energy absorption in the densification stage. When the compressive strain was less than 0.5, the energy efficiency gradually increased, reaching 15% at the highest, and 0.5 was taken as εd (densification strain), as shown in Fig. 12. As the compression process continued, it did not enter the densification stage immediately after the compression was applied. There was a long-term plateau stress that could absorb energy, and the buffering performance was good. At the same time, the stress did not fluctuate periodically in regular intervals. This result shows that the sandwich structure always maintained a stable state during the deformation process, which was an ideal deformation state.
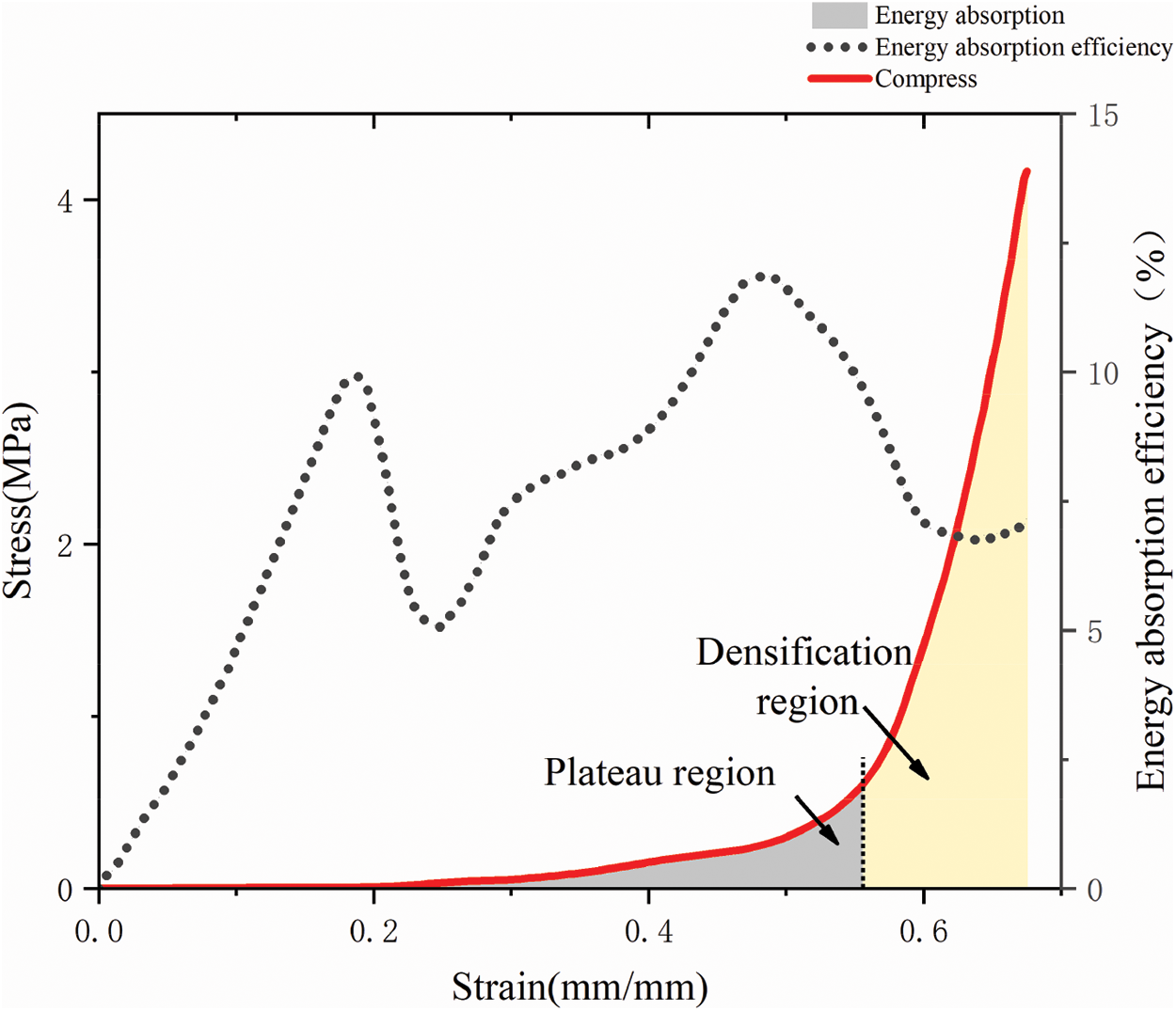
Figure 12: Energy absorption of static compressive stress and strain of Hilbert fractal structure
3.2 Influence of Order on Quasi-Static Compression Performance of Hilbert Fractal Structure
The order of the Hilbert fractal structure was varied, and its expression forms were different. In this study, the static compression performance of the Hilbert fractal structures of orders 2, 2.5, and 3 with the same layer thickness and wall thickness was mainly studied. Each structure is shown in Fig. 13.

Figure 13: Hilbert fractal structure of orders 2, 2.5, and 3
With the increase in the order, the energy-absorbing effect of the fractal structure was also greatly improved. ANSYS finite element simulations showed that the higher the order was, the greater the load under the same deformation was, as shown in Fig. 14. The third-order structure receives the largest load, followed by the second order 2.5, and finally the second order. When the deformation was less than 3 mm, the load was small.
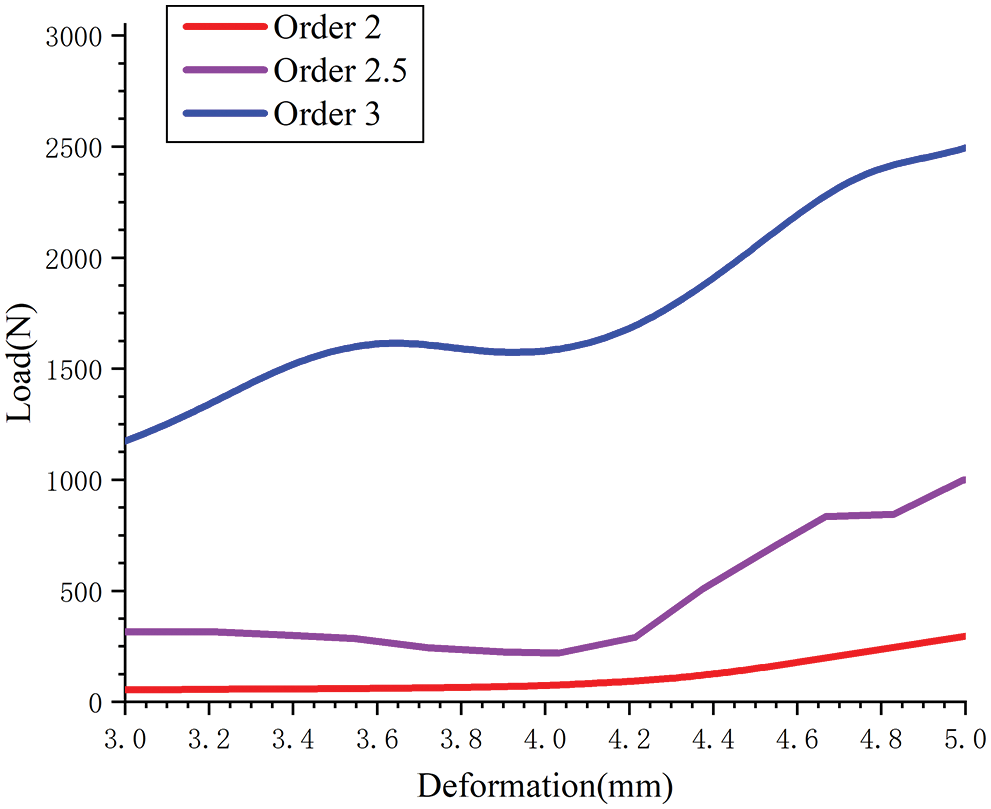
Figure 14: Deformation–load curves for different orders
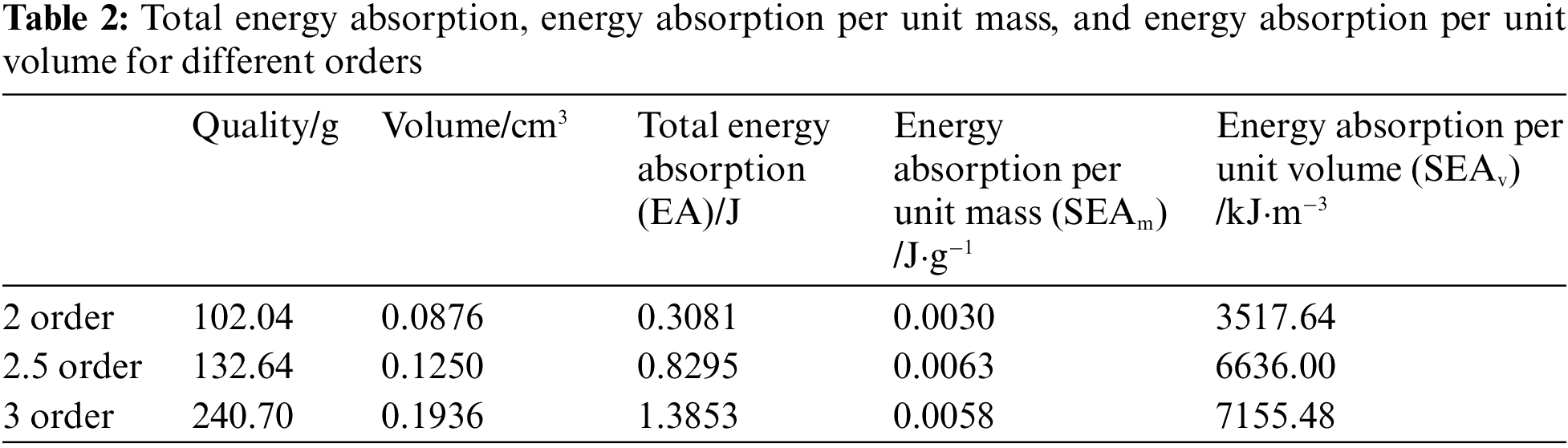
With the increase in the order, the mass and volume of the structure also increased. To obtain the best energy-absorbing structure, it is necessary to integrate factors such as the mass, volume, and energy-absorbing effect. The total energy absorption, energy absorption per unit mass, and energy absorption per unit volume of the different orders are shown in Table 2. All the selected Hilbert fractal structures are of different order with the unit layer thickness of 1 mm. The energy absorption per unit mass decreased with the increase in the order, because with the increase of order, the mass and volume increased faster. With the energy absorption per unit mass as the index, the energy absorption effect was the best at order 2.5.
3.3 Influence of Unit Layer Thickness on Quasi-Static Compression Performance of Hilbert Fractal Structure
The unit layer thickness of the Hilbert fractal structure played an extremely important role in the process of the structure bearing pressure. Through the parametric setting of the Hilbert fractal structure in SolidWorks, structures with different unit layer thicknesses were generated. The thicknesses of the upper and lower panels remained unchanged at 2 mm, and the layer thicknesses of all the units in the middle were changed to 0.5, 0.75, and 1 mm. As shown in Fig. 15, in the process of increasing the order, parametric modeling could not be realized if the layer thickness exceeded 1 mm.
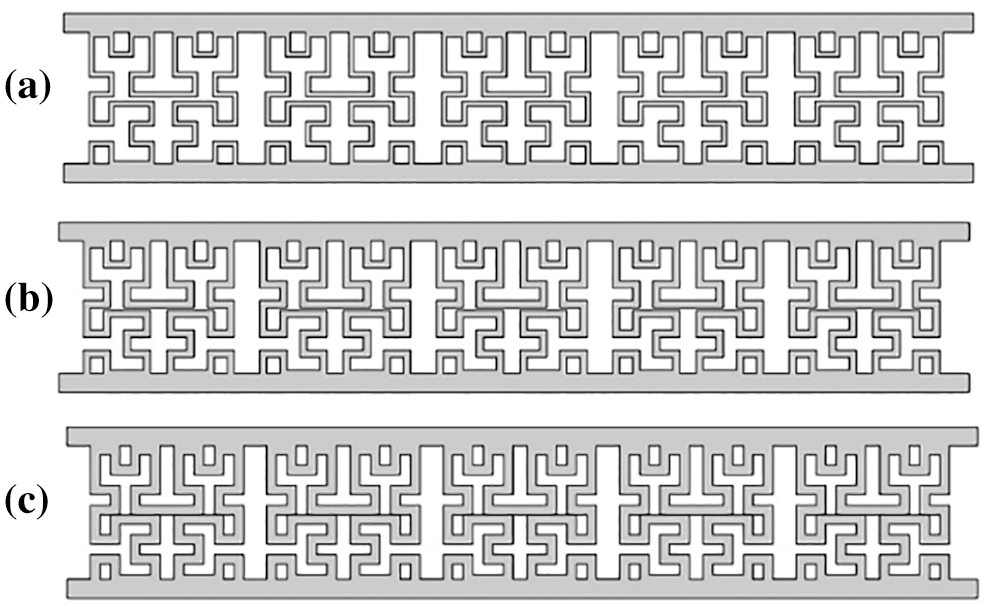
Figure 15: Hilbert fractal structures with different unit layer thicknesses: (a) 0.5-mm unit layer thickness, (b) 0.75-mm unit layer thickness, and (c) 1-mm unit layer thickness
A downward velocity load was applied to the parameterized Hilbert fractal structure with a velocity of 100 mm/min and a fixed lower surface, the displacement and equivalent effects in ANSYS were extracted, and the energy absorption per unit mass was manually calculated. The stress–strain energy efficiencies of Hilbert fractal structures with different cell wall thicknesses are shown in Fig. 16.

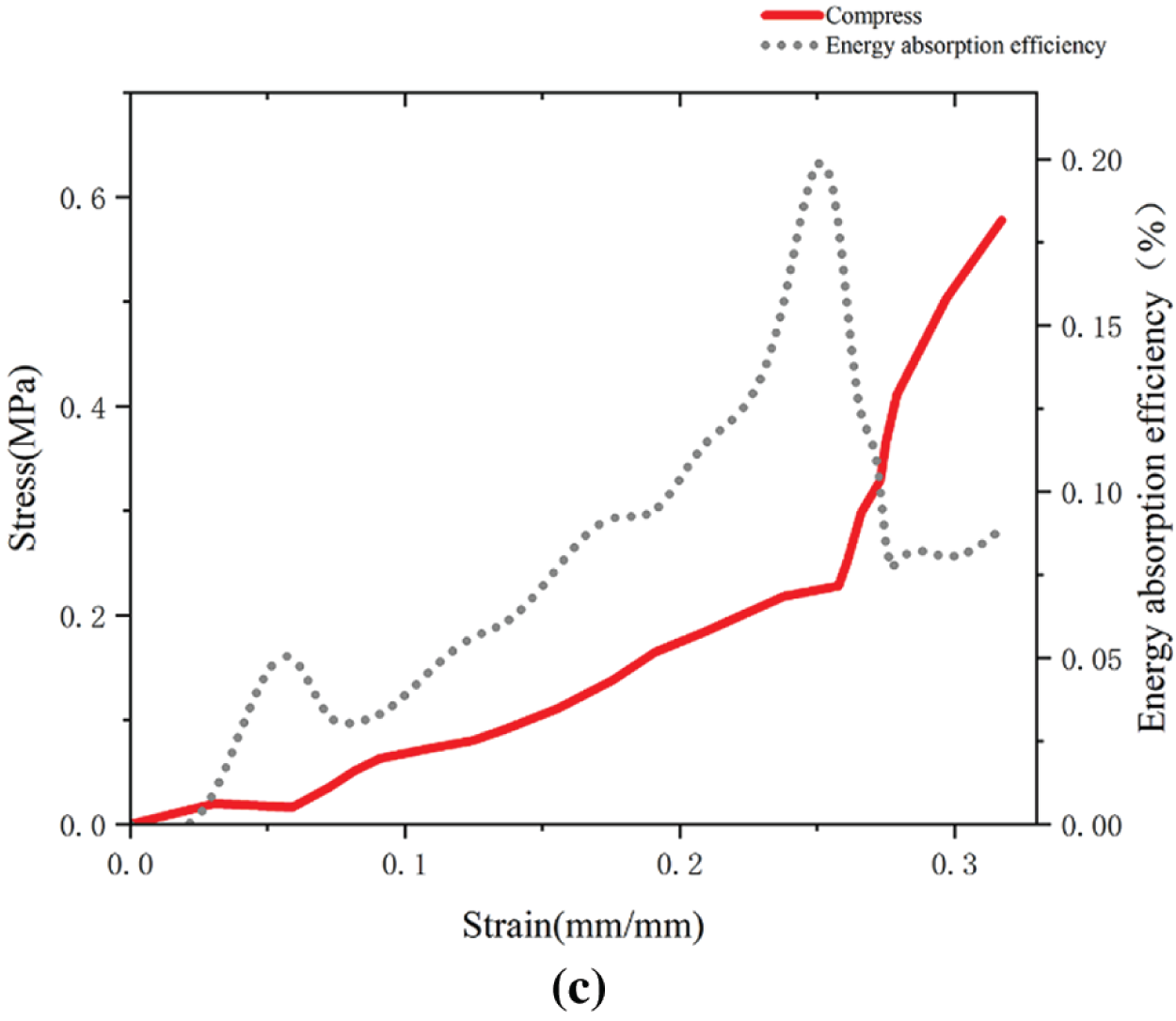
Figure 16: Stress–strain energy efficiencies of Hilbert fractal structures with different cell wall thicknesses
According to the finite element analysis, the Hilbert fractal structure with different wall thicknesses had different buffering effects, and the greater the wall thickness was, the better the buffering effect was. However, with the increase in the wall thickness, the element mass also increased. With the energy absorption per unit mass as the index, the Hilbert response surface analysis can be improved.
3.4 Hilbert Fractal Structure Optimization
The response surface optimization method can optimize multiple targets at the same time, and the best design point can be obtained from the sample points generated from the set parameter values for the optimal design [28].
In parameter response surface analysis, the response results or test values of the sample points are selected within parameter ranges, and a fitted functional relationship is established by means of regression analysis. For a Hilbert fractal structure, the order (n) and unit layer thickness (t) are taken as input parameters, and the maximum equivalent stress, strain, and mass are taken as output parameters. The results of the response surface analysis are shown in Fig. 17.
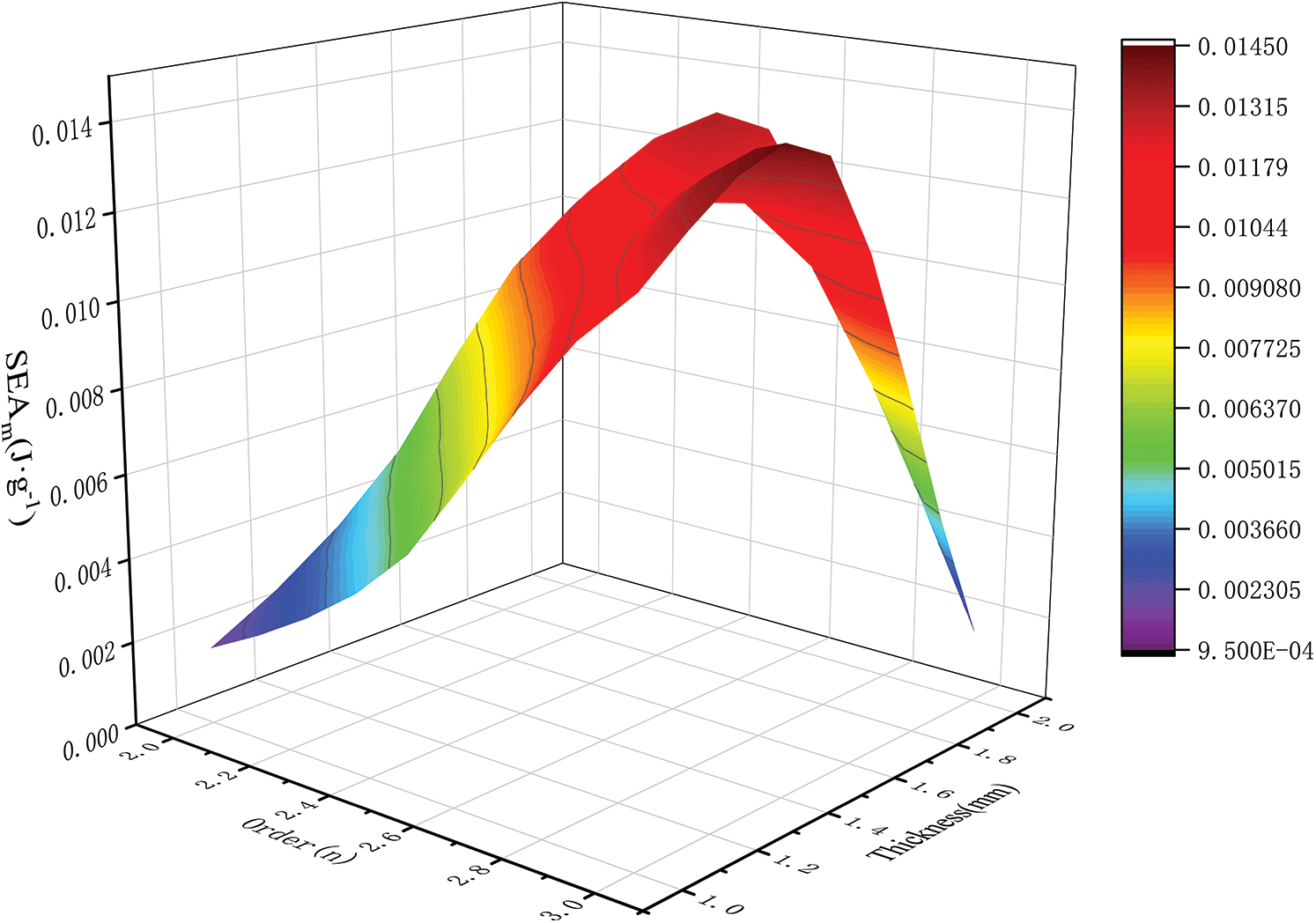
Figure 17: Response surface diagram of energy absorption per unit mass with different orders and layer thicknesses
Fig. 17 shows that the parameter order (n) and unit layer thickness (t) had a nonlinear relationship with the energy absorption per unit mass. The specific total energy absorption and energy absorption per unit mass are shown in Table 3.
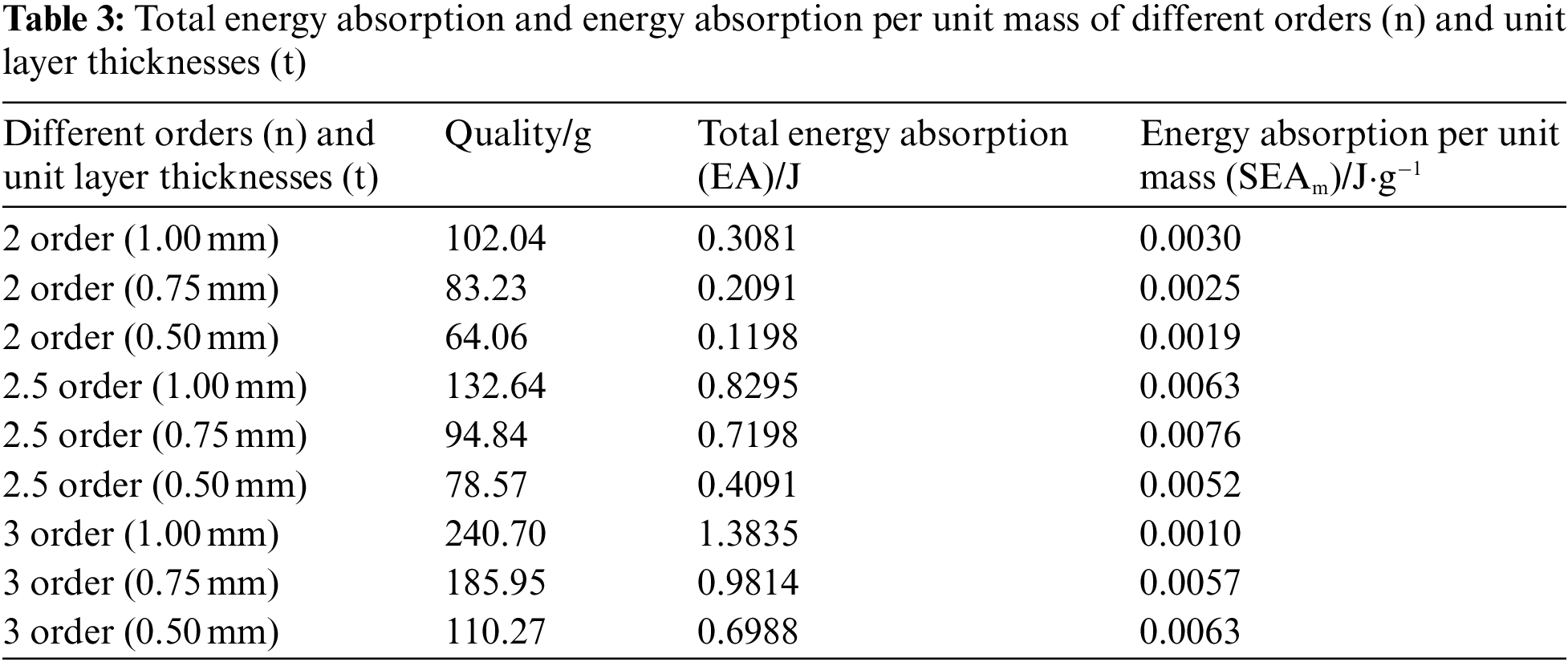
Based on the response surface analysis, the system provided the greatest advantages when the order (n) was 2.5 and the unit layer thickness (t) was 0.75 mm, as highlighted in Table 3. At this time, the energy absorption per unit mass increased from 0.0030 to 0.0076 J⋅g−1, a change of 153.3%. The force distribution of the Hilbert fractal structure remained basically unchanged, which proved that it was feasible to design the order (n) and unit layer thickness (t) to maximize the energy absorption per unit mass.
3.5 Comparison of Cushioning Performance with M-Shaped Structure
The “M-shaped” core structure is a kind of special sandwich structure in which members of “M-shaped” structures are added between adjacent vertical studs. This structure is commonly used in polypropylene sandwich panels. In this study, we also used the stereolithography 3D printing method to prepare a rice-shaped sandwich structure, with dimensions of 100 mm × 100 mm × 20 mm to ensure that the size was the same as the Hilbert fractal structure, as shown in Fig. 18.

Figure 18: Comparison of quasi-static compressive performance of M-shaped sandwich structure and Hilbert fractal structure
The GB-T 8168–2008 Static Compression Test Method for Packaging Buffer Materials 13 [29] was also used for comparison. During the compression process, the rice-shaped structure deformed and twisted after compression. There was not enough support in the longitudinal direction and no stepped platform effect. The compressive buffering performance mainly depended on the materials in the densification stage to absorb energy. The deformation process is shown in Fig. 19.

Figure 19: Quasi-static compression process of M-shaped sandwich structure
The stress–strain curves of the M-shaped and Hilbert fractal structures were examined. The total energy absorption of the Hilbert fractal structure was 120% greater, and the energy absorption per unit mass was 72% greater, as shown in Fig. 20. The Hilbert fractal structure had a significant stepped energy absorption effect, larger platform energy absorption area, and better buffer effect.
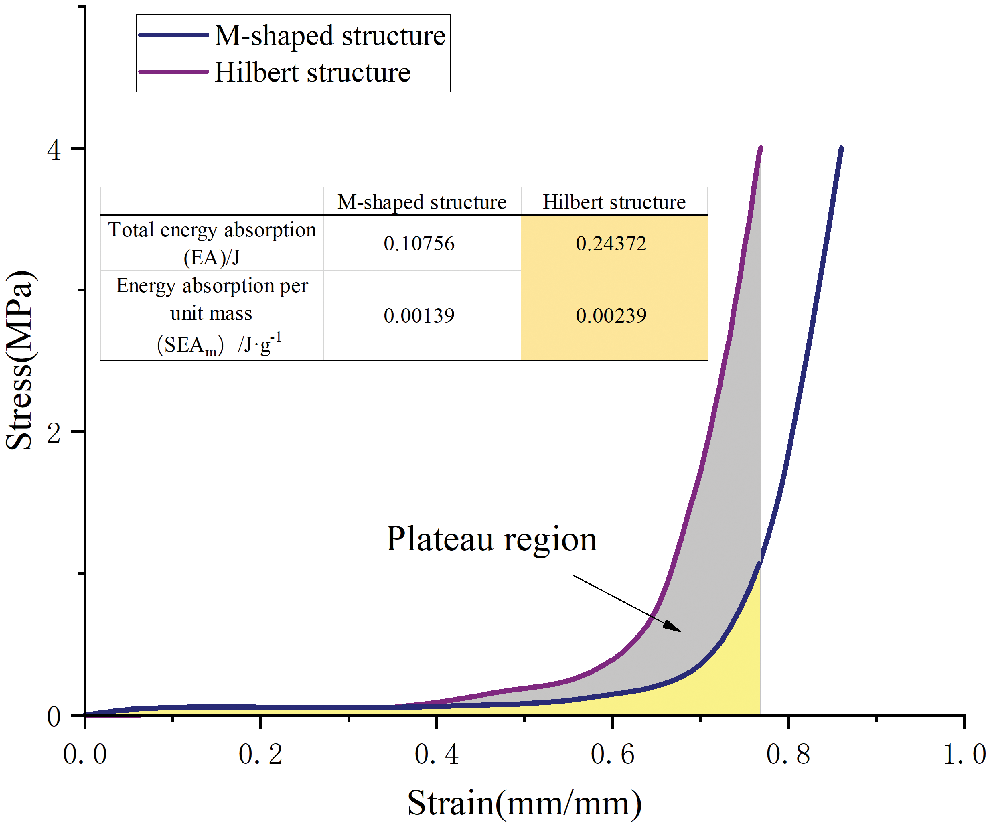
Figure 20: Comparison of stress–strain curves of Hilbert fractal structure and rice-shaped sandwich panel
(1) Through the string rewriting technology of L (Lin’s) language, the recursive formula of the Hilbert fractal structure was constructed using three variables. By using the Yoah second-order hyperelastic constitutive model, experiments and simulations of the Hilbert fractal structure were compared, and the maximum error was 8.21%. Thus, the simulations were basically considered to be reliable.
(2) With the energy absorption per unit mass as the index, the order (n) and the unit layer thickness (t) were optimized. When the order (n) was 2.5 and the unit layer thickness (t) was 0.75, the energy absorption per unit mass increased from 0.0030 to 0.0076 J⋅g−1.
(3) Compared with the commonly used rice-shaped sandwich structure, the Hilbert fractal structure was superior in terms of the total energy absorption and unit mass energy absorption, with values that were 120% and 72% greater, respectively. Thus, this structure has good market application prospects and provides new ideas for the design of sandwich structures.
Funding Statement: This work was supported by the Natural Science Foundation of Tianjin Municipality [21YDTPJC00480] and the Science and Technology Project of Tianjin [20YDTPJC00830].
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Yang, Z. W., Zhou, H. (2020). Design of metamaterial structures based on fractal geometry, a review. Materials Reports, 34(21), 21052–21060. DOI 10.11896/cldb.19080145. [Google Scholar] [CrossRef]
2. Wang, K. L. (2022). Novel approach for fractal nonlinear oscillators with discontinuities by Fourier series. Fractals, 30(1), 2250009. DOI 10.1142/S0218348X22500098. [Google Scholar] [CrossRef]
3. Wang, K. L., Wang, K. J. (2020). A new analysis for klein-gordon model with local fractional derivative. Alexandria Engineering Journal, 59(5), 3309–3313. DOI 10.1016/j.aej.2020.04.040. [Google Scholar] [CrossRef]
4. Wang, K. L. (2021). A study of the fractal foam drainage model in a microgravity space. Mathematical Methods in the Applied Sciences, 44(13), 10530–10540. DOI 10.1002/mma.7428. [Google Scholar] [CrossRef]
5. Guo, Y. F., Becker, W., Xu, W. C. (2013). Vertical static compression performance of honeycomb paperboard. International Journal of Materials Research, 104(6), 598–602. DOI 10.3139/146.110896. [Google Scholar] [CrossRef]
6. Alavi Nia, A., Sadeghi, M. Z. (2010). The effects of foam filling on compressive response of hexagonal cell aluminum honeycombs under axial loading-experimental study. Materials & Design, 31(3), 1216–1230. DOI 10.1016/j.matdes.2009.09.030. [Google Scholar] [CrossRef]
7. Alber, J., Niedermeier, R. (2000). On multidimensional curves with hilbert property. Theory of Computing Systems, 33(4), 295–312. DOI 10.1007/s002240010003. [Google Scholar] [CrossRef]
8. Falconer, K. (2003). Fractal geometry, mathematical foundations and applications. Chichester, England: John Wiley & Sons. [Google Scholar]
9. He, J. H., El-Dib, Y. O. (2021). A tutorial introduction to the two-scale fractal calculus and its application to the fractal zhiber–shabat oscillator. Fractals, 29(8), 2150268. DOI 10.1142/S0218348X21502686. [Google Scholar] [CrossRef]
10. He, J. H. (2009). Hilbert cube model for fractal spacetime. Chaos, Solitons & Fractals, 42(5), 2754–2759. DOI 10.1016/j.chaos.2009.03.182. [Google Scholar] [CrossRef]
11. He, C. H., Liu, C., He, J. H., Sedighi, H. M., Gepreel, K. A. (2021). A fractal model for the internal temperature response of a porous concrete. Applied and Computational Mathematics, 20(271–77. DOI 10.30546/1683-6154.21.1.2022.71. [Google Scholar] [CrossRef]
12. Zuo, Y. T., Liu, H. J. (2021). Fractal approach to mechanical and electrical properties of graphene/sic composites. Facta Universitatis, Series: Mechanical Engineering, 19(2), 271–284. DOI 10.22190/FUME201212003Z. [Google Scholar] [CrossRef]
13. He, J. H., Moatimid, G. M., Zekry, M. H. (2022). Forced nonlinear oscillator in a fractal space. Facta Universitatis, Series: Mechanical Engineering, 20(1), 1–20. DOI 10.22190/FUME220118004H. [Google Scholar] [CrossRef]
14. Meza, L. R., Zelhofer Alex, J., Clarke, N., Mateos, A. J., Kochmann, D. M. et al. (2015). Resilient 3D hierarchical architected metamaterials. Proceedings of the National Academy of Sciences, 112(37), 11502–11507. DOI 10.1073/pnas.1509120112. [Google Scholar] [CrossRef]
15. Wang, J., Zhang, Y., He, N., Wang, C. H. (2018). Crashworthiness behavior of koch fractal structures. Materials & Design, 144, 229–244. DOI 10.1016/j.matdes.2018.02.035. [Google Scholar] [CrossRef]
16. Zhang, Y., He, N., Song, X. Y., Chen, T. T., Chen, H. C. (2020). On impacting mechanical behaviors of side fractal structures. Thin-Walled Structures, 146, 106490. DOI 10.1016/j.tws.2019.106490. [Google Scholar] [CrossRef]
17. Xie, Y., Bai, H. L., Liu, Z. H., Chen, N. N. (2020). A novel bionic structure inspired by luffa sponge and its cushion properties. Applied Sciences, 10(7), 2584. DOI 10.3390/app10072584. [Google Scholar] [CrossRef]
18. Zhang, W., Yin, S., Yu, T. X., Xu, J. (2019). Crushing resistance and energy absorption of pomelo peel inspired hierarchical honeycomb. International Journal of Impact Engineering, 125, 163–172. DOI 10.1016/j.ijimpeng.2018.11.014. [Google Scholar] [CrossRef]
19. Cao, J., Wang, Z. W. (2020). Finite element analysis of drop impact of weaire-phelan buffer structure. Chinese Journal of Applied Mechanics, 37(4), 1607–1614 + 1863–1864. [Google Scholar]
20. Ceterchi, R., Zhang, L., Subramanian, K. G., Zhang, G. (2021). Hilbert words as arrays generated with P systems. Journal of Membrane Computing, 3(1), 1–7. DOI 10.1007/s41965-021-00078-y. [Google Scholar] [CrossRef]
21. Kamata, S. I., Eason, R. O., Bandou, Y. (1999). A new algorithm for N-dimensional hilbert scanning. IEEE Transactions on Image Processing, 8(7), 964–973. DOI 10.1109/83.772242. [Google Scholar] [CrossRef]
22. Boyce, M. C., Arruda, E. M. (2000). Constitutive models of rubber elasticity: A review. Rubber Chemistry and Technology, 73(3), 504–523. DOI 10.5254/1.3547602. [Google Scholar] [CrossRef]
23. Chen, Z. S., Qin, Q. H., Zhao, G. P. (2021). Mechanical properties and energy absorption of self-similar porous materials. Chinese Journal of Applied Mechanics, 38(5), 1846–1852. [Google Scholar]
24. Guan, G. Y., Meng, Z. W., Xie, L. X., Peng, N. L. (2021). Evaluation of fitting effectiveness of polyurethane rubber hyperelastic constitutive model. Chinese Quarterly of Mechanics, 42(3), 571–580. [Google Scholar]
25. Lv, P. F., Li, Y., Feng, G. Q., Du, Y. D., Li, J. H. et al. (2021). Study on hyper-elastic constitutive model of EPDM for laminated bearings. Rubber Science and Technology, 19(5), 219–222. [Google Scholar]
26. Poomuthu, A., Stoček, R., Chattopadhyay, S., Khastgir, D., Kaliske, M. et al. (2020). Understanding fracture of a carbon black filled rubber compound using material force theory. Theoretical and Applied Fracture Mechanics, 108, 102649. DOI 10.1016/j.tafmec.2020.102649. [Google Scholar] [CrossRef]
27. ISO 527–2–2012. (2012) Determination of tensile properties of plastics–Part 2: Test conditions for molded and extruded products. https://www.iso.org/standard/56046.html. [Google Scholar]
28. Song, X., Sun, G., Li, G., Gao, W., Li, Q. (2013). Crashworthiness optimization of foam-filled tapered thin-walled structure using multiple surrogate models. Structural and Multidisciplinary Optimization, 47(2), 221–231. DOI 10.1007/s00158-012-0820-6. [Google Scholar] [CrossRef]
29. GB/T 8168–2008 (2009) Testing method of static compression for packaging cushioning materials (in Chinese). https://www.codeofchina.com/standard/GB8168-1987.html. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools