Image Color Rendering Based on Hinge-Cross-Entropy GAN in Internet of Medical Things

1  Introduction

The Internet of Things (IoT) is getting more popular and has a high level of interest in both practitioners and academicians in the age of wireless communication due to its diverse applications. And the significant increase in the number of individuals with chronic ailments has dictated an urgent need for an innovative model for healthcare systems [1–3]. So IoT based on deep neural network model has been applied in medical treatment in recent years. The Internet of Medical Things (IoMT) based on computer-aided diagnosis is gradually developing faster and more efficiently [4–7]. Image color rendering based on deep learning can render the grayscale image into a color image to highlight the deep information and help readers to quickly understand the depth of information contained in the image [8–11]. With the rapid development of computer graphics, computer vision and related software and hardware technologies, the method of rendering existing images and enhancing details by using high-quality image data has attracted extensive research attention, and has been gradually applied to medical image processing and analysis in IoMT [12–14].

At present, the traditional color rendering method needs manual intervention and requires high reference image. The color rendering method based on deep learning uses the neural network model and the corresponding high-quality image dataset to train the model, and the image can be automatically rendered according to the model without being affected by human factors or other factors.

Image color rendering based on deep learning is generally divided into color rendering based on convolutional neural network and color rendering based on generative adversarial network [15,16]. Iizuka et al. [17] used a fusion layer in a convolutional neural network to combine low-dimensional features and global features of an image to generate the image color. Zhang et al. [18] designed an appropriate loss function to deal with multi-mode uncertainty in color rendering and maintain diversity of colors. Sangkloy et al. [19] combined a method based on graffiti with deep learning and trained images with color lines in a neural network. He et al. [20] selectively migrated reference image colors that were consistent with a target image in semantic structure and content to the target image, otherwise learn the color from large-scale data. Xiao et al. [21] proposed a depth sample-based image rendering method using a dense coded pyramid [22–25].

However, when extracting grayscale image features, the aforementioned method adopts upsampling to make the image size consistent, resulting in a loss of image information. Therefore, the network structure thus constructed cannot effectively extract and recognize complex features of the image. Hence, the rendering effect is relatively limited. Goodfellow et al. [26] proposed a generative adversarial network (GAN). GAN model based on unsupervised learning can approximate arbitrary distribution, so it has a wide range of applications in the field of image generation. But it is subject to the well-known disappearing and exploding gradient problem due to the instability of the model, resulting in a deterioration of image rendering performance. On this basis, Mirza et al. [27] proposed a conditional generative adversarial network (CGAN), which is conditional on additional information, such as class tags or data from other modes, to enter the discriminant and generator as an additional input layer for adjustment. Isola et al. [28] improved a CGAN to transform image styles, for example, from grayscale to color images, from day to night images, from lines to shaded images. The proposed pix2pix model has a powerful image conversion function, and can learn a mapping relationship between a gray and color image to achieve color rendering.

Although the GAN-based image color rendering method can automatically render images, it has certain problems such as blurred boundaries and unclear details. Moreover, unstable GAN models lead to low rendering quality [29]. Therefore, Arjovsky et al. [30] used Wasserstein distance to replace the original JS divergence to stabilize the training of GANs, whereas Gulrajani et al. [31] added penalty terms to make the training of GANs more stable. Mao et al. [32] used the least square loss function to solve the problem of gradient disappearance and enhance the stability of the model. However, the stability of these GAN models and the effectiveness of the color rendering method still need to be improved. Therefore, this paper proposes a hinge-cross-entropy GAN (HCEGAN) for automatic image rendering. First, a new hinge-cross-entropy loss function is proposed to stabilize the GAN training. Second, an improved self-attention module is added to the GAN model to improve color rendering quality more quickly and effectively. Finally, by adding a Skip Connection, a network structure based on U-Net, as a generator for the GAN model, we adopt the 70×70 PatchGAN based on image conversion as a discriminator. Experimental results show that the HCEGAN has a more significant rendering effect compared with the pix2pix model.

2  Related Works

2.1 Hinge Loss

The hinge loss allows the distance between incorrectly classified samples and correctly classified samples to be sufficiently far. Unless the difference between a threshold Δ, and an incorrect classification error is considered to be 0, a calculation error is accumulated [33]. The loss function does not simply require the highest score in the right category, but rather a certain amount. Even a calculation classified as a loss may be correct, because it is possible that a correct category score will fail to exceed a certain threshold Δ.

Suppose we classify some input xi, whose label is yi, and predict xi through a function f(xi,W). Threshold Δ generally takes a value of 1. The output is s. Then, we predict the input xi as the jth type. Therefore, the output is sj=f(xi,W)j. Let Li represent the loss of each class, the loss of a sample is the sum of the losses of all classes. Then the calculation of the loss function of the output xi is shown in Fig. 1.

Li=∑j′=yimax(0,sj−syi+Δ).(1)

Figure 1: Hinge loss

Hinge loss is often used in binary classification problems. For output y=±1, threshold Δ takes the value of 1. Then, we predict the hinge loss of y^ as

l(y)=max(0,1−y⋅y^).(2)

When y^≥1 or y^≤−1, the classification result can be determined by the classifier, the loss value l(y) at this time is 0. When the predicted value y^∈(−1,1), the classifier is uncertain as to the classification result and the loss value l(y)≠0. Obviously, the loss is greatest when y^=0.

2.2 Cross-Entropy Loss

Cross-entropy is used to measure the difference between two probability distributions in information theory. The cross-entropy loss function is not only simple and effective, but can also avoid the reduction in learning rate caused by the mean square error loss function in gradient decline using the sigmoid function [34]. Assuming that the probability of an event is p, the amount of information I is expressed as

I(p)=−log(p).(3)

Entropy represents the measurement of the uncertainty of random variables. Under the discrete condition, entropy of information can be expressed as

H(p)=Ex∼P[I(p)]=−Ex∼P[log(p)]=−∑i=1npilog(pi).(4)

In the discrete condition, if there are two probability distributions Q and P for the same random variable x, we can use KL divergence to measure the difference between these two distributions.

DKL(P∥Q)=Ex∼P[logPQ]=Ex∼P[log(p)−log(q)]=∑i=1npilog(pi)−∑i=1npilog(qi).(5)

The discrete distribution is the same, hence, the KL divergence is zero. Therefore, the cross-entropy is expressed as the sum of entropy and KL divergence.

H(P,Q)=H(P)+DKL(P∥Q)=−Ex∼P[log(p)]+Ex∼P[log(p)−log(q)]=−Ex∼P[log(q)]=−∑i=1npilog(qi).(6)

Then, in the case of binary classification, the cross-entropy loss of batch samples is

loss=−1m∑i=1n∑j=1mpijlog(qij).(7)

At present, the cross-entropy loss is mainly used to classify the problem, combined with the Sigmoid or Softmax activation function. The advantage of cross-entropy loss is that the learning speed is fast when the model effect is poor, and slow when the model effect is good. However, because the cross-entropy loss combined with the Sigmoid or Softmax activation function adopts the inter-class competition mechanism, the features learned are scattered and multiple features cannot be distinguished. Therefore, the activation function can only be continuously optimized to better strengthen the model.

3  Hinge-Cross-Entropy GAN

3.1 Hinge-Cross-Entropy Loss

The loss function in deep learning is mainly used to evaluate the degree to which the predicted sample is different from the real sample. In general, the better the loss function, the better the model performance. The original GAN model scales the output of the discriminator neural network to probability [0, 1] by the Sigmoid function, and measures the cross-entropy loss of probability. In order to minimize JS (Jensen-Shannon) difference between model distribution and target distribution, the minimax game of the GAN model is realized. Many scholars use regularizer or loss function to minimize the difference between model distribution and target distribution, and ensure the stability of the GAN model. As can be seen from the analysis of the two loss functions in Section 2, the hinge loss function is able to keep the distance between the incorrectly classified samples and the correctly classified samples sufficiently far beyond a certain threshold so that the unclassified error value remains 0. In the cross-entropy loss function, the closer the predicted output is to the real sample, the smaller the loss function is, and the closer the predicted function is to 1. In this case, the variation trend of the function is completely in line with the actual needs. Therefore, the greater the difference between the predicted output and the real sample, the greater the loss value, that is, the greater the penalty to the current model, according to a non-linear increase similar to exponential growth.

This situation is mainly determined by the log function, which influences the model to tend to make the predicted output closer to the real sample. Further, the hinge loss optimization to enforce the requirements of remaining within less than a certain distance will cease optimization, whereas the cross-entropy loss is always optimized. Hence, in general, the cross-entropy loss is better than hinge loss. However, the cross-entropy loss is good at learning information between classes. Because it adopts the inter-class competition mechanism, the model will try to learn different types of features. And only consider the accuracy of the prediction probability of the correct samples, while ignoring the differences of other wrong samples. So the learned features are scattered, and the effect generated by the generator is suboptimal. Based on the advantages and disadvantages of hinge and cross-entropy loss, we propose a hinge-cross-entropy loss function.

First, we define the loss function based on the pix2pix network model as follows:

{G∗=argminGmaxDLcGAN(G,D)+λLL1(G),LcGAN(G,D)=Ex,y(logD(x,y))+Ex(log(1−D(x,G(x)))),LL1(G)=Ex,y(∥y−G(x)1∥)(8)

where, x is the input image, y is the expected output, G is the generator, and D is the discriminator. In addition to the generating adversarial loss of CGAN model, the pix2pix model also adds a L1 regularization loss times a certain parameter to improve the training of the model. And λ is this parameter.

Meanwhile, the hinged version of adversarial loss in GAN model is defined. We set the generated image as G(z). Then, the loss functions of the generator and discriminator are, respectively:

{LD=−E(x,y)∼Pdata[min(0,−1+D(x,y))]−Ez∼Pz,y∼Pdata[min(0,−1−D(G(z),y))],LG=−Ez∼Pz,y∼PdataD(G(z),y),(9)

On this basis, the hinge-cross-entropy loss function is defined as follows:

{LD=Ex,y[log(max(0,1−D(x,y)))]+Ey,z[log(max(0,1+D(G(z),y)))],LG=Ex,y(logD(x,y))+Ex[log(1−D(x,G(x)))]+λEx,y(∥y−G(x)1∥).(10)

The loss function of the generator is the cross-entropy loss function adding L1 loss, which is the same as the loss function of the generator of the pix2pix model. The loss function of the discriminant is in the form of the cross-entropy loss function after the real or generated image is processed by the hinge loss function. In this paper, the binary cross-entropy loss (BCE Loss) function is used, which is a special case of the cross-entropy loss function used for binary classification problems. The exact definition of the function is the same. Because this is a binary classification task, there are only two possibilities, plus or minus, and the sum of probabilities is 1, so we only have to predict one probability. In practical applications, a sigmoid function should be added to the layer of BCE Loss to normalize the data first before binary cross entropy loss can be used for calculation. The hinge-cross-entropy loss function also does not need to optimize the activation function to improve its problems such as large computation and small feature discrimination due to the large number of classification datasets.

3.2 Improved Self-Attention Module

The function of the attention mechanism in computer vision is to enable a neural network model to learn to ignore irrelevant information and focus on the important information [35]. Usually, relevant features are used to learn the weight distribution. Then, the learned weight is applied to the features to extract relevant knowledge further. The weight can be applied to the original image, or to the spatial scale, channel scale, etc. The self-attention mechanism is a concept learned from natural language processing (NLP). Other tasks in the direction of computer vision have also achieved good results.

The basic structure of self-attention module is shown in Fig. 2. It can be seen that the self-attention module is divided into three branches by a 1×1 convolution:  , g and h. First, the dot product is used to calculate the similarity between f and g to get the weight. Second, a softmax function is used to normalize these weights. Finally, the weighted sum of weights and corresponding h is calculated to get the final attention value. However, this weight parameter needs to be initialized to 0, which first depends on the local original x, then gradually increases the non-local weight, and finally applies self-attention to the generator and discriminator. If the initial weight is set to 0 and the weight is gradually increased through model optimization, the generator will learn slowly, leading to slow iteration. Therefore, we need to adjust the learning method, especially the initialization matrix, to speed up the learning speed of the attention mechanism.

Figure 2: Self-attention module

In this paper, we adjust the initial weight to a diagonal matrix, and assume that the values on the diagonal of the diagonal matrix conform to the standard normal distribution with a mean of 0 and a variance of 1, such as the diagonal matrix A of size 3×3:

A=[−0.26570.00000.00000.00000.60140.00000.00000.00000.3083](11)

The calculation steps of self-attention mechanism are as follows. First, we aim to transform the feature map of the previous hidden layer x∈RC×N into the feature space f, g and calculate attention, where f(x)=Wfx, g(x)=Wgx. Each element βji in the attention map represents how much the model pays attention to the ith pixel when synthesizing the jth pixel, where sij=f(xi)Tg(xj).

βj,i=exp(sij)∑i=1Nexp(sij)(12)

Then, we use βji as the weight of attention to calculate the output o=(o1,o2,…,oj,…,oN)∈RC×N, where, oj=∑i=1Nβj,ih(xi), h(xi)=Whxi. Wf, Wg, and Wh are the weight matrices learned after a 1×1 convolution. Here, C¯=C8, Wf∈RC¯×C, Wg∈RC¯×C, Wh∈RC×C.

Finally, we multiply the output of the attention layer by a scale parameter γ and add it back to the input feature map.

yi=γoi+xi(13)

3.3 Hinge-Cross-Entropy GAN

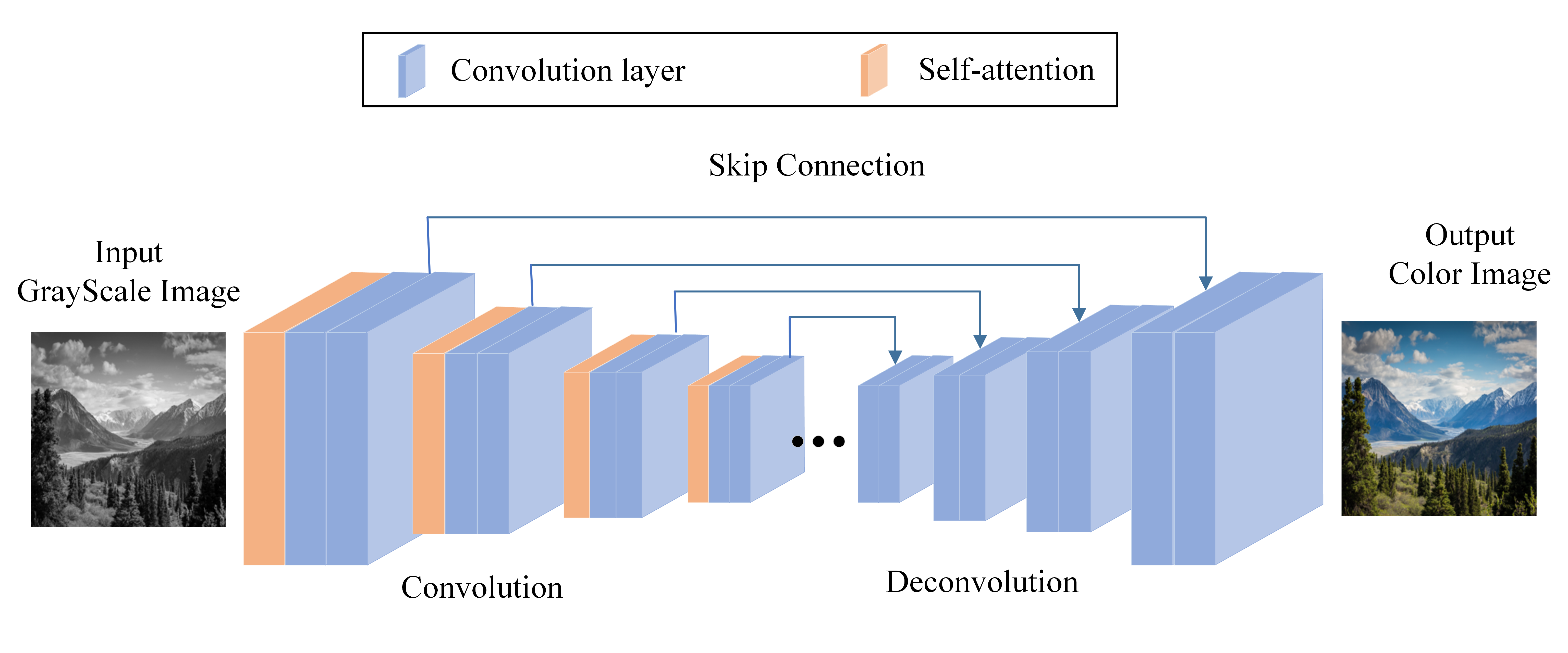
In this paper, we construct the generator of hinge-cross-entropy GAN based on U-Net structure, coding-decoding structure and Skip Connection, as shown in Fig. 3. The orange module is the improved self-attention module, and the blue module is the convolution layer, which contains 8 convolution layers and 8 deconvolution layers. Lines represent Skip Connection. The U-Net structure is a symmetric U-shaped structure of compression path and expansion path. The parameter transfer and error feedback of deep neural network can be strengthened by adding Skip Connection. In addition, in order to solve the problem of remote dependence and strengthen long-distance information, an improved self-attention module is added in the encoder, namely, in front of each convolutional layer, respectively, in order to effectively select feature information. The input of neural network is many vectors of different sizes, and there are certain relationships among them. However, the relationship between these inputs can not be fully developed in the actual training, resulting in poor results. The self-attention mechanism can establish correlations between multiple related inputs, allowing the network model to notice correlations between different parts of the entire input.

Figure 3: Proposed generator structure

The discriminator of hinge-cross-entropy GAN uses 70 × 70 PatchGAN, which contains 4 convolution layers, each of which uses the unit form of conversion-regularization-Leakyrelu activation function. Instead of measuring the whole image with a single value, PatchGAN used an N * N matrix to evaluate the whole image, so that more areas could be focused on. The input/output size is 256×256, the step size is 2, the fill pixel is 1, the activation function is LeakyReLU, and BatchNorm is used. The whole GAN model adopts minimax game, generate color image as close as possible to the expected image, deceive the discriminator. Grayscale image and generated image are input into the discriminator at the same time. The discriminator tries to distinguish the generated image and see the difference between the generated image and the expected image. During model learning and training, generator and discriminator are trained alternately. After the training is complete, the generator is used to generate the desired color image.

4  Experiments

The DIV2 K dataset covers a wide range of contexts, including people, handmade objects and cities and villages, for example based on single-image super-resolution benchmarking. The dataset participating in the NTIRE 2017 Challenge drives the state-of-the-art technology in terms of single-image super-resolution. There are 800 training sets and 100 testing sets in the DIV2 K dataset. The COCO2017 dataset is an advanced version of the Microsoft COCO dataset funded by Microsoft in 2014. Among them, the COCO competition was one of the most concerned and authoritative competitions in the field of computer vision at that time. The COCO datasets include six categories: fish, ladybug, orange, lion, dog and bird. There are 500 training sets and 100 testing sets for each category of the COCO dataset.

When DIV2 K dataset was used to verify the validity of the model, the experimental environment used was Windows 10, with a 64-bit operating system, an Intel(R) Core(TM) I7–9750H CPU @2.5 GHz on a notebook computer, as well as Python 3.7, Pytorch1.2, and CUDA 10.0. When the COCO dataset was used, the experimental environment used was Windows 10, with a 64-bit operating system, an Intel(R) Core(TM) I9–10900x CPU @3.70 GHz on a desktop computer, as well as Python 3.7, Pytorch1.7, and CUDA 10.2. In experiments, the same parameters were used for all models under the PyTorch framework, the iteration was 200, the optimizer was Adam, and the learning rate was 0.0002. In order to reflect the color rendering quality of different models, the experiment adopts PSNR and SSIM to evaluate the rendered images.

4.1 Qualitative Comparison

Effect of self-attention module To verify the effectiveness of the self-attention module, the added module was compared with the original pix2pix model, and the results on the DIV2 K dataset were shown in Figs. 4b, 4c. By comparing the rendering results of the original color image, the pix2pix model and the model with self-attention module, it can be seen that the pix2pix model has a large error in rendering due to the instability of GAN model, resulting in color pollution in the upper left corner of Fig. 4b. However, the model with self-attention module restores the real color of the image in both structure and color, and the overall tone is more harmonious. After the self-attention module is added, the self-attention mechanism can learn important features and suppress non-important features to achieve fast learning of image information. The results are shown in Table 1. After adding the self-attention module, SSIM and PSNR in the DIV2 K dataset were increased by 0.35% and 1.2 dB, respectively. In the COCO dataset, SSIM and PSNR were almost all improved. Therefore, after the self-attention module is added to the model, the module can improve the model’s attention to important information by using the inherent information of features for attention interaction, thus significantly improving the rendering quality. Therefore, adding self-attention module into the model is effective and improves the rendering effect of the model.

Figure 4: Qualitative comparison

Effect of hinge-cross-entropy loss To verify the effectiveness of the hinge-cross-entropy loss function, we added the hinge-cross-entropy loss to the pix2pix model and compared it with the original pix2pix model by adding the mean-square error (MSE) loss. The results on the DIV2 K dataset are shown in Figs. 4d, 4e. Comparing the rendering results of the original color image with the hinge-cross-entropy loss function and the mean square error loss function, it may be observed that the hinge-cross-entropy loss function has a better rendering result on the details of an image such as steps and roofs, and there is no color pollution. This is because the hinge-cross-entropy loss function inherits the advantages of the hing loss function and the cross-entropy loss function. This puts the distance between misclassified samples and correctly classified samples far beyond a certain threshold. And when the optimization of the hinge loss function is forced to keep within a certain distance, the cross-entropy loss always keeps the optimal state.

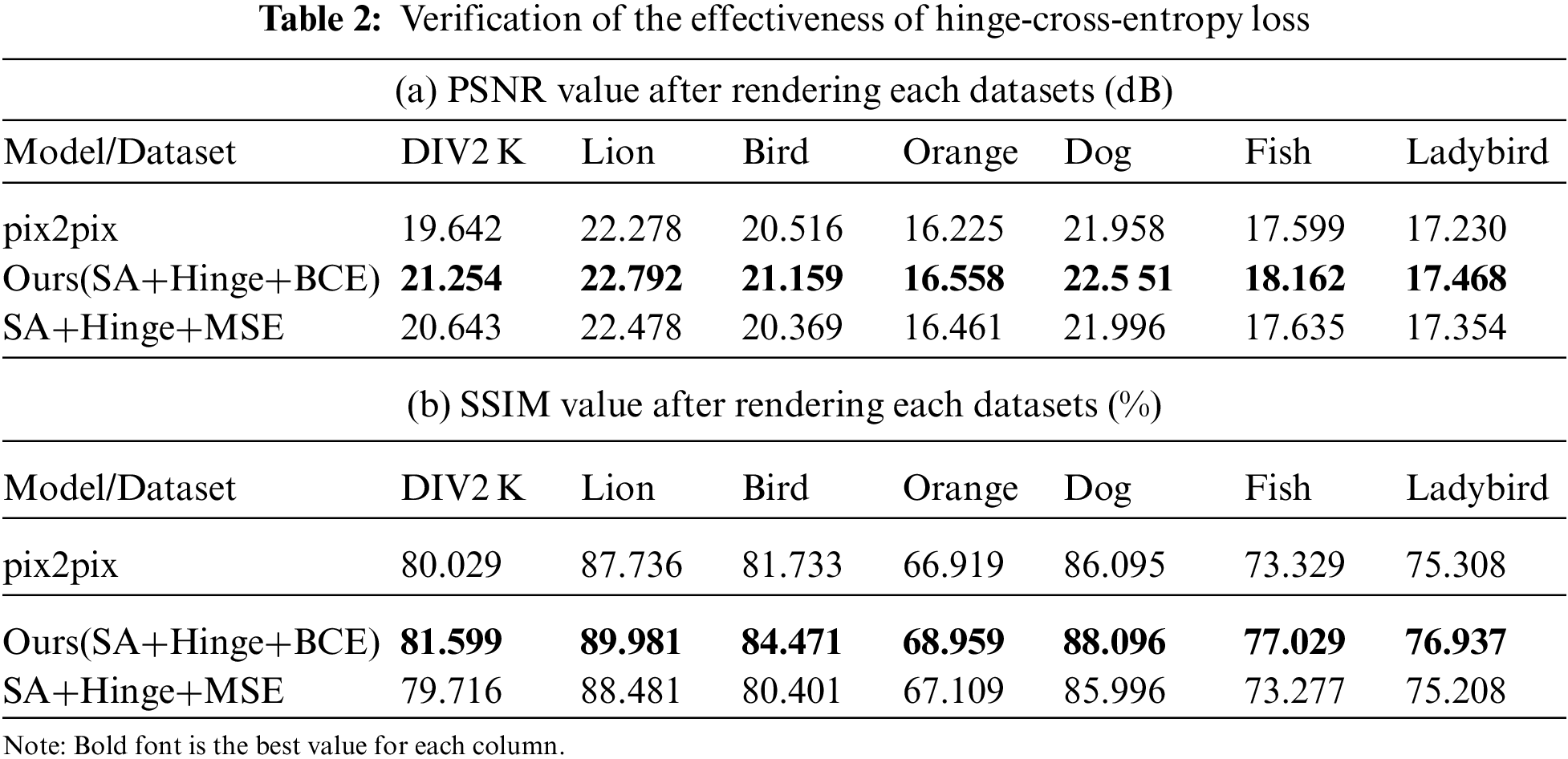
Similarly, we used PSNR and SSIM to evaluate the rendered images. The experimental results are shown in Table 2. Hinge stands for hinge loss function, BCE stands for cross-entropy loss function, and MSE stands for mean square error loss function. After adding the hinge-cross-entropy loss function, PSNR and SSIM improved by 1.61 dB and 1.57% in the DIV2 K dataset, respectively. In the six categories of the COCO dataset, PSNR increased by 0.51, 0.64, 0.33, 0.69, 0.56, 0.24 dB, and SSIM increased by 2.24%, 2.74%, 2.04%, 2.00%, 3.7%, 1.63%, respectively. This is because the partial derivative value of the MSE loss function will be very small when the output probability value is close to 0 or 1, which may cause the partial derivative value to almost disappear at the beginning of training of the model. As a result, the learning rate of the model is very slow at the beginning, and the use of cross-entropy as the loss function will not lead to such a situation. Therefore, compared to the effect without the hinged loss function and with the added the MSE loss function, the model using the hinge-cross-entropy loss function has a significant improvement in rendering quality.

4.2 Quantitative Comparison

Effect of improved self-attention module To verify the effectiveness of the improved self-attention module, we added the self-attention module and the improved module to the pix2pix model and compared it with the original pix2pix model. The experimental results are shown in Fig. 5, where SA’ is the standard normal distribution in which the diagonal line conforms to the initial weight. The mean is 0 and the variance is 1 in the diagonal matrix, and SA” is the uniform random number in the diagonal matrix where the initial weight is 0–1. By comparing the results before and after adding hinge loss, we can see that compared with other models, the rendered image obtained by adding an improved self-attention module (pix2pix+SA’ and SA’+Hinge+BCE) is closer to the original color image, with better rendering effect, clearer details and less rendering error. This is because the improved self-attention mechanism reduces the dependence on external information and uses the inherent information of features as much as possible for attentional interaction. In addition, the self-attention mechanism can effectively capture the feature dependence of long distance and extract the important information of global context. In comparison, our proposed approach SA’+Hinge+BCE has the best performance. Not only is the improved attention mechanism added, but the hinge-cross-entropy loss function makes the gap between positive and negative samples large enough to produce an image that more closely resembles the real color image.

Figure 5: Quantitative comparison

The experimental results are shown in Table 3, and we can see that the rendering effect is better when the diagonal matrix with the initial weight conforming to the standard normal distribution with a mean of 0 and a variance of 1, namely SA’, is used. Compared with the original pix2pix model, the proposed method SA’+ Hinge+BCE improved 1.82% in the DIV2 K dataset, and 1.76 dB in terms of PSNR. In the six categories of COCO dataset, SSIM increased by 2.11%, 2.47%, 2.18%, 1.54%, 3.73%, 0.43%, and PSNR increased by 0.41, 0.67, 0.27, 0.64, 0.44, 0.29 dB, respectively. Therefore, the improved self-attention module and the hinge-cross-entropy loss function can enhance the stability of the model and improve the rendering effect of the existing color rendering algorithm based on the GAN model. Therefore, the improved self-attention module and hinge-cross-entropy loss function in this paper are effective. It can enhance the stability of the model to different degrees and improve the existing image rendering algorithm based on the GAN model.

Fig. 6 shows the effect of our HCEGAN compared with the original pix2pix model on the COCO dataset. In order to improve the performance of the model, the current color rendering algorithm based on deep learning inevitably accumulates modules, which leads to the deep level and high complexity of the neural network. This paper realizes image color rendering based on GAN. Although the self-attention module is added to the model in this paper, the complexity of the system does not change much. At the same time, the addition of new loss function further strengthens the stability of the model. Therefore, the model’s lightweight and high performance are the limitations at present, and future work will also be carried out in this aspect.

Figure 6: Our results compared with other models

5  Conclusion

At present, image color rendering based on the generative adversarial network has helped the medical industry to highlight and speed up the diagnosis of many diseases in the internet of medical things. Color images are beneficial because they can better highlight deep information in an image. In order to improve the existing GAN-based color model and render grayscale images, this paper introduces a new hinge-cross-entropy loss function and an improved self-attention module, and proposes a new hinge-cross-entropy GAN. In this paper, we use the DIV2 K and COCO datasets to verify the effectiveness of the proposed method and its superiority to prior approaches. The experimental results show that our hinge-cross-entropy GAN model demonstrates a great improvement in rendering quality and effect. Moreover, the stability of the model is greatly improved. However, the current GAN model has high model complexity and difficulty in pre-training. It is difficult to realize a model lightweight on the basis of ensuring algorithm efficiency. In the future, we will focus on achieving the high performance of GAN models while reducing model complexity. At the same time, we plan to extend the method to other tasks, such as style transfer and single image super-resolution.

Acknowledgement: We extend our gratitude to the peer reviewers for their helpful comments on an earlier version of the paper.

Funding Statement: The authors received National Natural Science Foundation of China (No. 61902311) funding for this study. And the project was supported in part by the Natural Science Foundation of Shaanxi Province in China under Grants 2022JM-508, 2022JM-317 and 2019JM-162.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Islam, M., Nooruddin, S., Karray, F., Muhammad, G. (2022). Human activity recognition using tools of convolutional neural networks: A state of the art review, data sets, challenges and future prospects. arXiv preprint arXiv:2202.03274. [Google Scholar]

 2.  Islam, M., Nooruddin, S., Karray, F., Muhammad, G. (2022). Internet of things device capabilities, architectures, protocols, and smart applications in healthcare domain: A review. arXiv preprint arXiv:2204.05921. [Google Scholar]

 3.  Nasr, M., Islam, M. M., Shehata, S., Karray, F., Quintana, Y. (2021). Smart healthcare in the age of AI: Recent advances, challenges, and future prospects. IEEE Access, 9, 145248–145270. DOI 10.1109/ACCESS.2021.3118960. [Google Scholar] [CrossRef]

 4.  Gao, J., Jiang, Q., Zhou, B., Chen, D. (2019). Convolutional neural networks for computer-aided detection or diagnosis in medical image analysis: An overview. Mathematical Biosciences and Engineering, 16(6), 6536–6561. DOI 10.3934/mbe.2019326. [Google Scholar] [CrossRef]

 5.  Khan, H. A., Jue, W., Mushtaq, M., Mushtaq, M. U. (2020). Brain tumor classification in MRI image using convolutional neural network. Mathematical Biosciences and Engineering, 17(5), 6203–6216. DOI 10.3934/mbe.2020328. [Google Scholar] [CrossRef]

 6.  Zhang, Z., Wang, N., Wu, H., Tang, C., Li, R. (2021). MR-DRO: A fast and efficient task offloading algorithm in heterogeneous edge/cloud computing environments. IEEE Internet of Things Journal, 1–11. DOI 10.1109/JIOT.2021.3126101. [Google Scholar] [CrossRef]

 7.  He, L., Niu, M., Tiwari, P., Marttinen, P., Su, R. et al. (2022). Deep learning for depression recognition with audiovisual cues: A review. Information Fusion, 80, 56–86. DOI 10.1016/j.inffus.2021.10.012. [Google Scholar] [CrossRef]

 8.  Hu, S. M., Liang, D., Yang, G. Y., Yang, G. W., Zhou, W. Y. (2020). Jittor: A novel deep learning framework with meta-operators and unified graph execution. Science China (Information Sciences), 63(12), 118–138. DOI 10.1007/s11432-020-3097-4. [Google Scholar] [CrossRef]

 9.  Zhang, J., Peng, Y., Ouyang, W., Deng, B. (2019). Accelerating ADMM for efficient simulation and optimization. ACM Transactions on Graphics, 38(6), 1–21. [Google Scholar]

10. Zhou, W. Y., Yang, G. W., Hu, S. M. (2021). Jittor-GAN: A fast-training generative adversarial network model zoo based on Jittor. Computational Visual Media, 7(1), 153–157. DOI 10.1007/s41095-021-0203-2. [Google Scholar] [CrossRef]

11. Zeng, W., Li, H., Chen, L., Morvan, J. M., Gu, X. D. (2013). An automatic 3D expression recognition framework based on sparse representation of conformal images. 2013 10th IEEE International Conference and Workshops on Automatic Face and Gesture Recognition (FG), IEEE, China. [Google Scholar]

12. Zhang, T., Fu, H., Zhao, Y., Cheng, J., Guo, M. et al. (2019). SkrGAN: Sketching-rendering unconditional generative adversarial networks for medical image synthesis. International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer, Cham. [Google Scholar]

13. Mousavi, Z., Shahini, N., Sheykhivand, S., Mojtahedi, S., Arshadi, A. (2022). COVID-19 detection using chest X-ray images based on a developed deep neural network. SLAS Technology, 27(1), 63–75. DOI 10.1016/j.slast.2021.10.011. [Google Scholar] [CrossRef]

14. Li, H. A., Zhang, M., Yu, Z., Li, Z., Li, N. (2022). An improved pix2pix model based on gabor filter for robust color image rendering. Mathematical Biosciences and Engineering, 19(1), 86–101. DOI 10.3934/mbe.2022004. [Google Scholar] [CrossRef]

15. Wang, R., Yu, B., Marco, J., Hu, T., Bao, H. (2016). Real-time rendering on a power budget. ACM Transactions on Graphics, 35(4), 1–11. DOI 10.1145/2897824.2925889. [Google Scholar] [CrossRef]

16. Wang, R., Pan, M., Han, X., Chen, W., Bao, H. (2014). Parallel and adaptive visibility sampling for rendering dynamic scenes with spatially varying reflectance. Computers & Graphics, 38, 374–381. DOI 10.1016/j.cag.2013.10.036. [Google Scholar] [CrossRef]

17. Iizuka, S., Simo-Serra, E., Ishikawa, H. (2016). Let there be color!: Joint end-to-end learning of global and local image priors for automatic image colorization with simultaneous classification. ACM Transactions on Graphics, 35(4), 110.1–110.11. DOI 10.1145/2897824.2925974. [Google Scholar] [CrossRef]

18. Zhang, R., Isola, P., Efros, A. A. (2016). Colorful image colorization. European Conference on Computer Vision, pp. 649–666. Springer, Cham. [Google Scholar]

19. Sangkloy, P., Lu, J., Fang, C., Yu, F., Hays, J. (2017). Scribbler: Controlling deep image synthesis with sketch and color. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 5400–5409. [Google Scholar]

20. He, M., Chen, D., Liao, D., Sander, P., Yuan, V., L. (2018). Deep exemplar-based colorization. ACM Transactions on Graphics, 37(4), 47. DOI 10.1145/3197517.3201365. [Google Scholar] [CrossRef]

21. Xiao, C., Han, C., Zhang, Z., Qin, J., Wong, T. T. et al. (2020). Example-based colourization via dense encoding pyramids. Computer Graphics Forum, 39(1), 20–33. DOI 10.1111/cgf.13659. [Google Scholar] [CrossRef]

22. Zhang, J., Zheng, J., Wu, C., Cai, J. (2012). Variational mesh decomposition. ACM Transactions on Graphics, 31, 1–14. DOI 10.1145/2167076.2167079. [Google Scholar] [CrossRef]

23. Yang, Y. J., Zeng, W., Meng, X. X. (2016). Conformal freeform surfaces. Computer-Aided Design, 81, 48–60. DOI 10.1016/j.cad.2016.09.003. [Google Scholar] [CrossRef]

24. Zeng, W., Lui, L. M., Gu, X. (2014). Surface registration by optimization in constrained diffeomorphism space. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 4169–4176. [Google Scholar]

25. Larsson, G., Maire, M., Shakhnarovich, G. (2016). Learning representations for automatic colorization. European Conference on Computer Vision, pp. 577–593. Springer, Cham. [Google Scholar]

26. Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D. et al. (2014). Generative adversarial networks. Advances in Neural Information Processing Systems, 3, 2672–2680. [Google Scholar]

27. Mirza, M., Osindero, S. (2014). Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784. [Google Scholar]

28. Isola, P., Zhu, J. Y., Zhou, T., Efros, A. A. (2017). Image-to-image translation with conditional adversarial networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 1125–1134. [Google Scholar]

29. Qin, Y., Mitra, N., Wonka, P. (2020). How does lipschitz regularization influence gan training? European Conference on Computer Vision, pp. 310–326. Springer, Cham. [Google Scholar]

30. Arjovsky, M., Chintala, S., Bottou, L. (2017). Wasserstein generative adversarial networks. International Conference on Machine Learning, pp. 214–223. PMLR. [Google Scholar]

31. Gulrajani, I., Ahmed, F., Arjovsky, M., Dumoulin, V., Courville, A. (2017). Improved training of wasserstein gans. arXiv preprint arXiv:1704.00028. [Google Scholar]

32. Mao, X., Li, Q., Xie, H., Lau, R. Y., Wang, Z. et al. (2017). Least squares generative adversarial networks. Proceedings of the IEEE International Conference on Computer Vision, pp. 2794–2802. [Google Scholar]

33. Rosasco, L., Vito, E. D., Caponnetto, A., Piana, M., Verri, A. (2004). Are loss functions all the same? Neural Computation, 16(5), 1063–1076. DOI 10.1162/089976604773135104. [Google Scholar] [CrossRef]

34. Ma, Y. D., Liu, Q., Qian, Z. B. (2004, October). Automated image segmentation using improved PCNN model based on cross-entropy. Proceedings of 2004 International Symposium on Intelligent Multimedia, Video and Speech Processing, vol. 2004, pp. 743–746. IEEE, China. [Google Scholar]

35. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L. et al. (2017). Attention is all you need. arXiv preprint arXiv:1706.03762. [Google Scholar]