Submit

Login Login

Register Register

Home/ Journals/ CMES/ Vol.135, No.1, 2023/ 10.32604/cmes.2022.021332

Table of Content

iconOpen Access

ARTICLE

The Fractional Investigation of Fornberg-Whitham Equation Using an Efficient Technique

Hassan Khan1,2, Poom Kumam3,4,*, Asif Nawaz1, Qasim Khan1, Shahbaz Khan1

1 Department of Mathematics, Abdul Wali Khan University, Mardan, 23200, Pakistan
2 Department of Mathematics, Near East University TRNC, Mersin, 10, Turkey
3 Center of Excellence in Theoretical and Computational Science (TaCS-CoE) & KMUTTFixed Point Research Laboratory, Room SCL 802 Fixed Point Laboratory, Science Laboratory Building, Departments of Mathematics, Faculty of Science, King Mongkut's University of Technology Thonburi (KMUTT), Bangkok, 10140, Thailand
4 Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, 40402, Taiwan

* Corresponding Author: Poom Kumam. Email: email

(This article belongs to this Special Issue: Fractal-Fractional Models for Engineering & Sciences)

Computer Modeling in Engineering & Sciences 2023, 135(1), 259-273. https://doi.org/10.32604/cmes.2022.021332

Received 09 January 2022; Accepted 17 May 2022; Issue published 29 September 2022

Abstract

In the last few decades, it has become increasingly clear that fractional calculus always plays a very significant role in various branches of applied sciences. For this reason, fractional partial differential equations (FPDEs) are of more importance to model the different physical processes in nature more accurately. Therefore, the analytical or numerical solutions to these problems are taken into serious consideration and several techniques or algorithms have been developed for their solution. In the current work, the idea of fractional calculus has been used, and fractional Fornberg Whitham equation (FFWE) is represented in its fractional view analysis. A well-known method which is residual power series method (RPSM), is then implemented to solve FFWE. The RPSM results are discussed through graphs and tables which conform to the higher accuracy of the proposed technique. The solutions at different fractional orders are obtained and shown to be convergent toward an integer-order solution. Because the RPSM procedure is simple and straightforward, it can be extended to solve other FPDEs and their systems.

Keywords

1  Introduction

In mathematical physics, the Fornberg-Whitham equation is a fundamental mathematical model. The Fornberg-Whitham equation [1,2] is written as:

uξ−uℑℑξ+uℑ=uuℑℑℑ−uuℑ+3uℑuℑℑ,ξ>0.(1)

This equation was introduced to investigate how non-linear dispersive water waves break. The Fornberg-Whitham equation is shown to allow peakon solutions, as well as the occurrence of wave breaking, as a mathematical model for waves of limiting height. Fractional calculus (FC) is now widely used and accepted, owing to its well-established applications in a wide range of seemingly disparate domains of science and engineering [3–7]. Many scholars, including Gupta et al. [8], Merdan et al. [9], Singh et al. [10], have examined the fractional extension of the Fornberg-Whitham equation relevant to the Caputo fractional derivative.

FC has the potential to explain various difficult phenomena like memory and heredity. In recent years, researchers have taken a keen interest in the subject of fractional differential equations (FDEs), such as viscoelasticity, fluid mechanics, nanotechnology, electrochemistry, modelling for shape memory polymers, biological population models, optics and signal processing, modelling control theory, the damping behaviour of materials, economics and chemistry, signal processing, creeping and relaxation for viscoelastic materials and diffusion and reaction processes [11–13]. Accurate modelling of time-fractional two-mode coupled burgers equation is done with the help of fractional derivatives (FD) [14].

Analytical and numerical techniques are frequently used for the solution of FPDEs and their systems. The fractional problems that have been modelled by using FPDEs are found in various disciplines, because the mathematical modelling of real-life phenomena is usually modelled accurately by using FPDEs.

In this connection, the important fractional mathematical models are solved by using various techniques such as Chun-hui He’s algorithm [15], reproducing kernel method [16], Runge-Kutta method for time discretization and Fourier transform for spatial discretization [17], Fourier spectral method [18], He-Laplace method [19], Fractional variational iteration method [20], operational matrix of fractional Riemann-Liouville integration with Legendre basis and zeros of Chebyshev polynomials [21]. Khan et al. [22] have solved nonlinear fractional differential equations using an efficient approach. The non-linear differential equations are solved by using perturbation transform method and He’s polynomials [23]. The one-dimensional non-homogeneous partial differential equations with a variable coefficient are solved by using homotopy perturbation method and Laplace transformation [24]. Linear and non-linear differential equations arising in circuit analysis are investigated by using Maclaurin series method [25]. The analysis of Caputo fractional-order dynamics of Middle East Lungs Coronavirus (MERS-CoV) model are discussed in [26]. He’s fractional derivative and fractional complex transform are implemented for the time fractional Camassa-Holm equation [27]. The fractional complex transform is utilised to solve time-fractional Schro¨dinger equation [28]. A two-scale fractal theory is suggested for the population dynamics [29]. The idea of the two-scale fractal is utilised to model the time-fractional tsunami wave traveling on an unsmooth surface [30]. A study of projectile motion in a quadratic resistant medium via fractional differential transform method [31]. The design of a variable fractional delay (VFD) FIR filter is handled using least square method [32]. Homotopy analysis Sumudu transform method is applied to solve delay Fractional Bagley-Torvik equation (HASTM) [33]. Coupled fractional Navier-Stokes equation is computed numerically using the proposed q-homotopy analysis transform method (q-HATM) [34]. The solutions of the fifth-order dispersive equations with porous medium type non-linearity is investigated by the classical Riccati equations method [35]. The analytical solution of time-fractional Navier-Stokes equation is calculated by using Adomian decomposition method [36] and similarly the Residual power series method (RPSM) was used to analyze the solution of fractional partial differential equations [37].

Many researchers have worked hard to find the solutions to FPDEs by using RPSM and other novel techniques that have been used for the solutions of FPDEs like: Senol et al. [38] solved the time-fractional nonlinear coupled Jaulent-Miodek system with energy-dependent Schrodinger Potential using RPSM in 2019, Korpinar et al. [39] have analysed the solution of the fractional cancer model by RPSM, Kurt [40] has implemented RPSM to obtain the solution of fractional Bogoyavlensky-Konopelchenko equation, Xu et al. [41] have implemented RPSM to obtain the solution of fractional Boussinesq equations, Freihet et al. [42] have found the solution of fractional Burgers-Huxley equations in by using RPSM. Jena et al. [43] have found the solution of the fractional model of the vibration equation of large membranes using RPSM.

In the current work, the solution of FFWE is investigated by RPSM. The RPSM was found to be a very effective technique for finding the analytical solution of FFWE [44]. In the current work, we have applied the RPSM technique to solve different FPDEs and obtained the series form solutions. The closed form series solution is achieved for FFWE by using the proposed analytical technique. The accuracy of RPSM is represented by using graphs and tables. The solutions at different fractional orders are of greater interest, which show the useful information about the actual dynamics of the given problems. The graphs show the convergence of fractional solutions of the targeted problem towards integer order solution. The proposed method is also applied to other physical problems in applied sciences and engineering. The article layout is organized as follows; the fundamental concepts regarding FC are described in Section 2; the basic methodology is discussed in Section 3; the application of RPSM in the Fornberg-Whitham equation involving the Caputo fractional derivative is contained in Section 4; results and discussion are in Section 5 and the conclusion is given in Section 6.

2  Basic Definitions

In this section, we discussed some preliminaries and definitions.

2.1 Definition

The integral operator of Reimann-Liouville having order ϑ is given as [45,46]:

(Iζϑh)(ζ)={1Γ(ϑ)∫0ζh(τ)(ζ−τ)1−ϑdτ,ϑ>0,h(ζ),ϑ=0.

Its fractional derivative for ϑ≥0 is defined as:

(Dζϑh)(ζ)=(ddζ)m(Im−ϑh)(ζ),(ϑ>0,m<ϑ<m−1),

where m is an integer.

2.2 Definition

The Caputo FD operator of the fractional order σ is given as [46]:

Danσf(ξ)=Ian−σf(n)(ξ)=1Γ(n−σ)∫aℑ(ℑ−τ)n−σ−1fn(τ)dτ.n−1<σ≤n,n∈ℵ.

The operators Dσ and Iσ satisfy the following properties:

•   Daσ(af(ξ)+bg(ξ))=aDaσf(ξ)+bDaσg(ξ), a,b∈ℵ.

•   DaσIaσf(ξ)=f(ξ).

•   Daσc=0,foranyconstantc∈ℜ.

•   Iaσξϑ=Γ(ϑ+1)Γ(ϑ+1−σ)ξϑ−σ.

•   IaσDaσf(ξ)=f(ξ)−∑j=0n−1f(j)(0)ξjj!, ξ>0.

2.3 Definition

A Power Series (PS) expansion is defined as [47]:

∑n=0∞fn(ℑ)(ξ−ξo)nσ=fo(ℑ)+f1(ℑ)(ξ−ξo)σ+f2(ξ−ξo)(ℑ)2σ+f3(ℑ)(ξ−ξo)3σ+⋯,0≤n−1<σ≤n,ξ≥ξo.

Theorem

Assume that u(ℑ,ξ) has a multiple fractional PS representation at ξ=ξo of the form [48],

μ(ℑ,ξ)=∑n=0∞fn(ℑ)(ξ−ξo)nσ.0≤n−1<σ≤n,ℑ∈I,ξo≤ξ<ξo+ℜ.

If Dξnσ are continuous on I×(ξo,ξo+ℜ), n=0,1,⋯, then the coefficients of fn(ℑ) are given as:

fn(ℑ)=Dξnσu(ℑ,ξo)Γ(1+nσ),n=0,1,2,⋯.

3  RPSM Methodology

To the understand the procedure of RPSM [49–54], let consider FPDEs of the form

Dξσu(ℑ,ξ)=L(u)+N(u),ξ>0,0<σ≤1,(2)

having initial condition,

u(ℑ,0)=f(ℑ),

where Dξσ is Caputo type fractional derivative of the function u(ℑ,ξ), L(u) is linear term and N(u) is the non-linear term. Initially, RPSM is used by taking the fractional PS expansion about a fix point ξ = ξo, that is,

f(ℑ,ξ)=∑n=0∞Dξnσfn(ℑ,ξ)Γ(nσ+1)(ξ−ξo)nσ,0<σ≤1,ℑ∈[a,b],0≤ξ<ℜ,

the 0th RPSM approximate solutions of u(ℑ,ξ) is given below as:

uo(ℑ,0)=f(ℑ).

Let uk(ℑ, ξ) represent the kth term,

uk(ℑ,ξ)=∑n=0kfn(ℑ)ξnσΓ(1+nσ),(3)

exchange the kth truncated series uk(ℑ,ξ) and of Eq. (3) in Eq. (2) which is the kth residual function and is given as:

Resuk(ℑ,ξ)=Dξσu(ℑ,ξ)−L(u)−N(u),ξ>0,0<σ≤1,(4)

Also obtain Resu(ℑ,ξ)=limk→∞⁡Resuk(ℑ,ξ). It is observed that Resu(ℑ,ξ)=0,∀ values of ℑ∈[a,b]. This Res u(ℑ,ξ) is infinitely differentiable at ℑ=a and dkdℑk−1Resu(ℑ,0)=dkdℑk−1Resuk(ℑ,0) which provide the basic rule of RPSM technique, allowing it to solve a broad range FPDEs. To determine the kth RPSM solution, we review Eq. (3) and then differentiate with respect to independent variables ℑ and ξ and finally replace ξ=0, we obtain f and constant parameters. By replacing these constant parameters in uk(ℑ,ξ), we obtain the kth truncated series, which we then assign to Eq. (4) to obtain an approximate solution. This method can be repeated using RPSM solutions for other arbitrary coefficient orders of Eq. (4).

4  Solution of Time-Fractional F-W Equation

Let us consider the time fractional F-W equation,

uξσ−uℑℑξ+uℑ=uuℑℑℑ−uuℑ+3uℑuℑℑ,ξ>0,0<σ≤1,(5)

with initial condition,

u(ℑ,0)=e12ℑ.(6)

Let uk(ℑ,ξ) denote the kth truncated series of u(ℑ,ξ), we have

uk(ℑ,ξ)=∑n=0kfn(ℑ)ξnσΓ(1+nσ).(7)

We define the kth residual function of FW equation as:

Resuk(ℑ,ξ)=Dξσuk(ℑ,ξ)−(uk)ℑℑξ(ℑ,ξ)−(uk)(ℑ,ξ)(uk)ℑℑℑ(ℑ,ξ)−3(uk)ℑ(ℑ,ξ)(uk)ℑℑ(ℑ,ξ)+(uk)(ℑ,ξ)(uk)ℑ(ℑ,ξ)+(uk)ℑ(ℑ,ξ).(8)

As Resu(ℑ,ξ)=0 and Resu(ℑ,ξ)=limk→∞⁡Resuk(ℑ,ξ),∀ℑ∈I and ξ≥0, DξnσResu(ℑ,ξ)=0, the FD of a constant is 0 in the Caputo sense. Also, the FD DξnσResu(ℑ,ξ)=0 and Resuk(ℑ,ξ) and assign at ξ=0 for each n=0,1,2,3,⋯,k. We first replace uk(ℑ,ξ) into Eq. (7), and find the FD formula Dξ(k−1)αResu(ℑ,0)=0 for k=1,2,3⋯

For the first step, k=1 put in FW equation Eq. (8), in the form as:

Resu1(ℑ,ξ)=Dξσu1(ℑ,ξ)−(u1)ℑℑξ(ℑ,ξ)−(u1)(ℑ,ξ)(u1)ℑℑℑ(ℑ,ξ)−3(u1)ℑ(ℑ,ξ)(u1)ℑℑ(ℑ,ξ)+(u1)(ℑ,ξ)(u1)ℑ(ℑ,ξ)+(u1)ℑ(ℑ,ξ)(9)

Now we can write Eq. (7), for k=1, as:

u1(ℑ,ξ)=f(ℑ)+f1(ℑ)ξσΓ(1+σ).(10)

Differentiating of Eq. (10), and put Eq. (9), we have

Resu1(ℑ,ξ)=f1(ℑ)−f1′′(xξσ−1Γ(1+σ)−[(f(ℑ)+f1(ℑ)ξσΓ(1+σ))(f′′′(ℑ)+f1′′′(ℑ)ξσΓ(1+σ))]−3[(f′(ℑ)+f1′(ℑ)ξσΓ(1+σ))(f′′(ℑ)+f1′′(ℑ)ξσΓ(1+σ))]+[(f(ℑ)+f1(ℑ)ξσΓ(1+σ))(f′(ℑ)+f1′(ℑ)ξσΓ(1+σ))]+f′(ℑ)+f1′(ℑ)ξσΓ(1+σ),(11)

from Eq. (11), and ξ=0, we have

Resu1(x,0)=f1(ℑ)−f(ℑ)f′′′(ℑ)−3f′(ℑ)f′′(ℑ)+f(ℑ)f′(ℑ)+f′(ℑ),

therefore

f1(ℑ)=f(ℑ)f′′′(ℑ)+3f′(ℑ)f′′(ℑ)−f(ℑ)f′(ℑ)−f′(ℑ),(12)

then from Eq. (7), and Eq. (12), we get

u1(ℑ,ξ)=f(ℑ)+ξσΓ(1+σ)[f(ℑ)f′′′(ℑ)+3f′(ℑ)f′′(ℑ)−f(ℑ)f′(ℑ)−f′(x],(13)

using Eq. (6), put in Eq. (13), then we have

u1(ℑ,ξ)=e12ℑ−23ξσΓ(1+σ)(eℑ2).

Step 2. for k=2, put in Eq. (8), can be written as:

Resu2(ℑ,ξ)=Dξσu2(ℑ,ξ)−(u2)ℑℑξ(ℑ,ξ)−(u2)(ℑ,ξ)(u2)ℑℑℑ(ℑ,ξ)−3(u2)ℑ(ℑ,ξ)(u2)ℑℑ(ℑ,ξ)+(u2)(ℑ,ξ)(u2)ℑ(ℑ,ξ)+(u2)ℑ(ℑ,ξ).(14)

Now we can written Eq. (7), for k=2, as:

u2(ℑ,ξ)=f(ℑ)+f1(ℑ)ξσΓ(1+σ)+f2(ℑ)ξ2σΓ(1+2σ).(15)

Similarly,

Resu2(ℑ,ξ)=f1(ℑ)+f2(ℑ)ξσΓ(1+σ)−[σf1′′(ℑ)ξσ−1Γ(1+σ)+2σf2′′(ℑ)ξσ−1Γ(1+2σ)]−[(f(ℑ)+f1(ℑ)ξσΓ(1+σ)+f2(ℑ)ξ2σΓ(1+2σ))(f′′′(ℑ)+f1′′′(ℑ)ξσΓ(1+σ)+f2′′′(ℑ)ξ2σΓ(1+2σ))]−3[(f′(ℑ)+f1′(ℑ)ξσΓ(1+σ)+f2′(ℑ)ξ2σΓ(1+2σ))×((f(ℑ)′′+f1′′(ℑ)ξσΓ(1+σ)+f2′′(ℑ)ξ2σΓ(1+2σ))]+[(f(ℑ)+f1(ℑ)ξσΓ(1+σ)+f2(ℑ)ξ2σΓ(1+2σ))((f′(ℑ)+f1′(ℑ)ξσΓ(1+σ)+f2′(ℑ)ξ2σΓ(1+2σ))]×f′(ℑ)+f1′(ℑ)ξσΓ(1+σ)+f2′(ℑ)ξ2σΓ(1+2σ),(16)

applying Dξσ on both sides of Eq. (16) and then put ξ=0, yields

DξσResu2(ℑ,0)=f2(ℑ)−[f(ℑ)f1′′′(ℑ)+f1(ℑ)f′′′(ℑ)]−3[f′(ℑ)f1′′(ℑ)+f1′(ℑ)f′′(ℑ)]+f(ℑ)f1′(ℑ)+f1(ℑ)f′(ℑ)+f1′(ℑ),

f2(ℑ)=f(ℑ)f1′′′(ℑ)+f1(ℑ)f′′′(ℑ)+3f′(ℑ)f1′′(ℑ)+3f1′(ℑ)f′′(ℑ)−f(ℑ)f1′(ℑ)−f1(ℑ)f′(ℑ)−f1′(ℑ).(17)

Now using Eq. (12) and Eq. (17), in Eq. (15), we get

u2(ℑ,ξ)=f(ℑ)+ξσΓ(1+σ)[f(ℑ)f′′′(ℑ)+3f′(ℑ)f′′(ℑ)−f(ℑ)f′(ℑ)−f′(ℑ)]×ξ2σΓ(1+2σ)[f(ℑ)f1′′′(ℑ)+f1(ℑ)f′′′(ℑ)+3f′(ℑ)f1′′(ℑ)+3f1′(ℑ)f′′(ℑ)−f(ℑ)f1′(ℑ)−f1(ℑ)f′(ℑ)−f1′(ℑ)].(18)

Putting Eq. (6), and Eq. (12), in Eq. (18), we have

u2(ℑ,ξ)=e12ℑ−23ξσΓ(1+σ)(eℑ2)+13ξ2σΓ(1+2σ)(eℑ2).

For the third step, putting k=3, in FW Eq. (8), as:

Resu3(ℑ,ξ)=Dξσu3(ℑ,ξ)−(u3)ℑℑξ(ℑ,ξ)−(u3)(ℑ,ξ)(u3)ℑℑℑ(ℑ,ξ)−3(u3)ℑ(ℑ,ξ)(u3)ℑℑ(ℑ,ξ)+(u3)(ℑ,ξ)(u3)ℑ(ℑ,ξ)+(u3)ℑ(ℑ,ξ).(19)

From Eq. (7), put k=3, the truncated series as:

u3(ℑ,ξ)=f(ℑ)+f1(ℑ)ξσΓ(1+σ)+f2(ℑ)ξ2σΓ(1+2σ)+f3(ℑ)ξ3σΓ(1+3σ),(20)

same as the above procedure

Resu3(ℑ,ξ)=f1(ℑ)+f2(ℑ)ξσΓ(1+σ)+f3(ℑ)ξ2σΓ(1+2σ)−[σf1′′(ℑ)ξσ−1Γ(1+σ)+2σf2′′(ℑ)ξ2σ−1Γ(1+2σ)+3σf3′′(ℑ)ξ3σ−1Γ(1+3σ)]−[(f(ℑ)+f1(ℑ)ξσΓ(1+σ)+f2(ℑ)ξ2σΓ(1+2σ)+f3(ℑ)ξ3σΓ(1+3σ))×(f′′′(ℑ)+f1(ℑ)ξσΓ(1+σ)+f2′′′(ℑ)ξ2σΓ(1+2σ)+f3′′′(ℑ)ξ3σΓ(1+3σ))]−3[(f′(ℑ)+f1′(ℑ)ξσΓ(1+σ)+f2′(ℑ)ξ2σΓ(1+2σ)+f3′(ℑ)ξ3σΓ(1+3σ))×(f′′(ℑ)+f1′′(ℑ)ξσΓ(1+σ)+f2′′(ℑ)ξ2σΓ(1+2σ)+f3′′(ℑ)ξ3σΓ(1+3σ))]+[(f(ℑ)+f1(ℑ)ξσΓ(1+σ)+f2(ℑ)ξ2σΓ(1+2σ)+f3(ℑ)ξ3σΓ(1+3σ))×(f′(ℑ)+f1′(ℑ)ξσΓ(1+σ)+f2′(ℑ)ξ2σΓ(1+2σ)+f3′(ℑ)ξ3σΓ(1+3σ))]+f′(ℑ)+f1′(ℑ)ξσΓ(1+σ)+f2′(ℑ)ξ2σΓ(1+2σ)+f3′(ℑ)ξ3σΓ(1+3σ).(21)

Applying Dξ2σ on both sides of Eq. (21) and then put ξ=0, yields

Dξ2σResu3(ℑ,0)=f3(ℑ)−[f(ℑ)f2′′′(ℑ)+2f1(ℑ)f1′′′(ℑ)+f2(ℑ)f′′′(ℑ)]−3[f′(ℑ)f2′′(ℑ)+2f1′(ℑ)f1′′(ℑ)+f2′(ℑ)f′′(ℑ)]+f(ℑ)f2′(ℑ)+2f1(ℑ)f1′(ℑ)f2(ℑ)f1′(ℑ)+f2′(ℑ),

therefore

f3(ℑ)=f(ℑ)f2′′′(ℑ)+2f1(ℑ)f1′′′(ℑ)+f2(ℑ)f′′′(ℑ)+3f′(ℑ)f2′′(ℑ)+6f1′(ℑ)f1′′(ℑ)+3f2′(ℑ)f′′(ℑ)−f(ℑ)f2′(ℑ)−2f1(ℑ)f1′(ℑ)f2(ℑ)f1′(ℑ)−f2′(ℑ),

u3(ℑ,ξ)=f(ℑ)+ξσΓ(1+σ)[f(ℑ)f′′′(ℑ)+3f′(ℑ)f′′(ℑ)−f(ℑ)f′(ℑ)−f′(ℑ)]×ξ2σΓ(1+2σ)[f(ℑ)f1′′′(ℑ)+f1(ℑ)f′′′(ℑ)+3f′(ℑ)f1′′(ℑ)+3f1′(ℑ)f′′(ℑ)−f(ℑ)f1′(ℑ)−f1(ℑ)f′(ℑ)−f1′(ℑ)]+ξ3σΓ(1+3σ)[f(ℑ)f2′′′(ℑ)+2f1(ℑ)f1′′′(ℑ)+f2(ℑ)f′′′(ℑ)+3f′(ℑ)f2′′(ℑ)+6f1′(ℑ)f1′′(ℑ)+3f2′(ℑ)f′′(ℑ)−f(ℑ)f2′(ℑ)−2f1(ℑ)f1′(ℑ)f2(ℑ)f1′(ℑ)−f2′(ℑ)].(22)

Using Eq. (6), Eq. (12), and Eq. (18), put in Eq. (22), we have

u3(ℑ,ξ)=(eℑ2)−23ξσΓ(1+σ)(eℑ2)+13ξ2σΓ(1+2σ)(eℑ2)−16ξ3σΓ(1+3σ)(eℑ2).(23)

Equivalence of the 3rd-order approximate solution of u3(ℑ,ξ) with the exact solution is required to demonstrate the capability of the RPSM. Even when a low-order approximate solution, u3(ℑ,ξ), is used, the numerical results show that RPSM performs admirably for the FW equation. The accuracy can be improved by using a higher-order RPSM solution. Eq. (23) provides the 3rd approximate solution of the FW equation. The results are discussed through graphs and tables in the next section of the paper.

5  Results and Discussion

In Fig. 1, the exact and RPSM solutions at σ=1 are presented, respectively. The RPSM solution is calculated for k=3, that is up to the third iteration. From Fig. 1, it is very clear that the exact and RPSM solutions are very close to each other. The comparison also confirmed the greater accuracy of the present method. The domain of the given problem is −4≤ℑ≤4, while 0≤ξ≤4. Fig. 2 shows the RPSM solution up to the 3rd iteration at σ=0.9 and σ=0.8. The solution graph at the fractional order σ=0.9 is slightly different as compared to the integer order solution, which shows another useful dynamics of the given physical problem. Similarly, another solution plot of the targeted problem is discussed at σ=0.8 is slightly different as compared to the fractional order σ=0.9. The plots at σ=0.9 and σ=0.8 are vary closed to each other. In Fig. 3, the solution graphs of various mathematical models with different fractional orders of the FW equation are displayed. A very consistent relationship is observed between the solutions graphs at various fractional orders σ. The overall graphical analysis of the problem has provided the opportunity to select that mathematical model of the fractional order which has a close relationship with the actual data of the problem. It is concluded that we have upgraded the existing model with the fractional order derivative to represent the dynamics of any physical problem in a rather sophisticated manner as compared to an integer model. In Fig. 3, the 2D solution plot is presented which shows the exact solution of the FW equation. Fig. 4 shows the approximate solution of the given problem at σ=1, which is nearly equal to the exact solution. The solutions graphs obtained by exact and approximate solutions are compared with each other. The 2D plots in Figs. 3 and 4 are very close to each other in the same fractional order. Another plot in Fig. 4 shows us the combined graphs of RPSM solutions at different fractional orders σ.

images

Figure 1: Comparison plots of exact and approximate solutions at the fractional order σ = 1

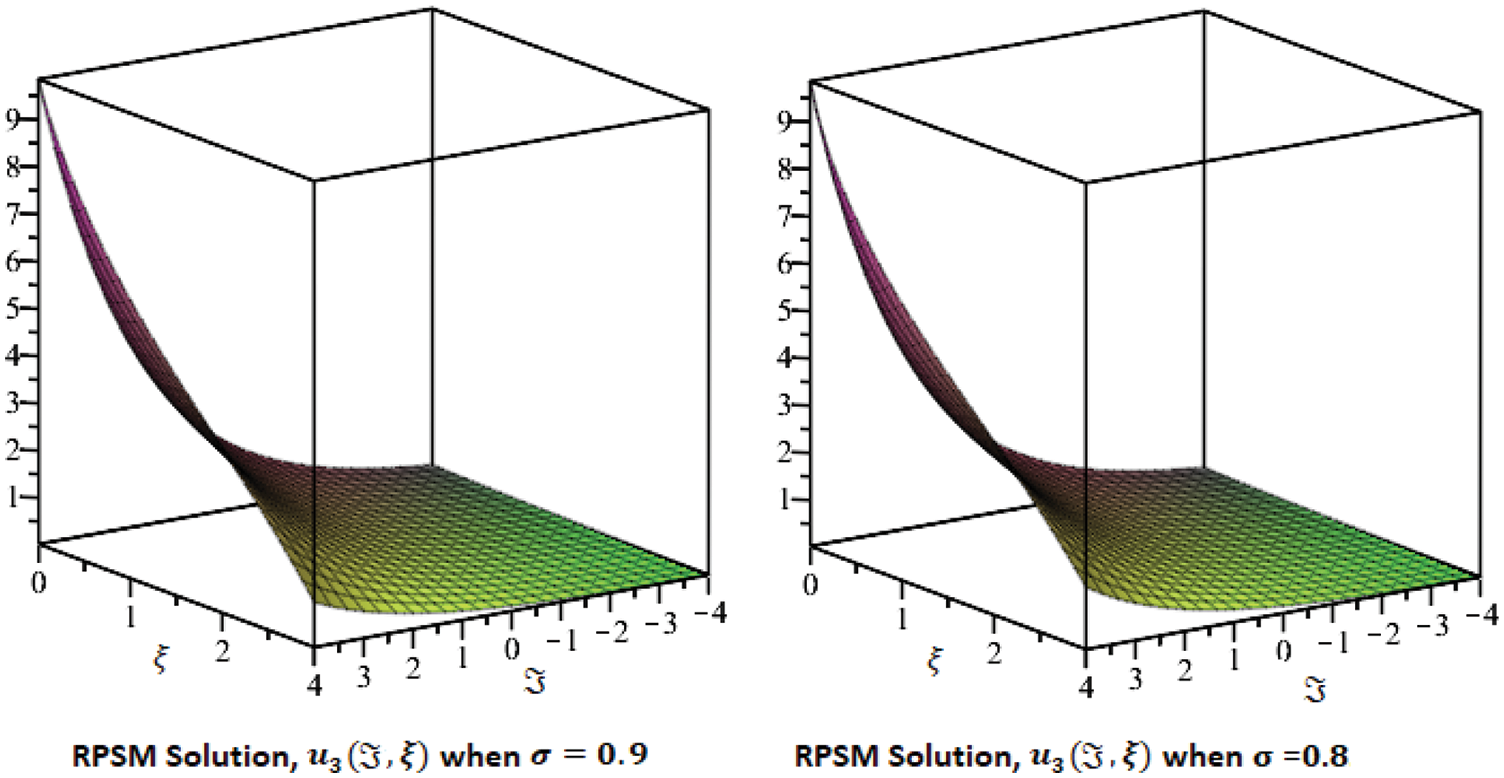
images

Figure 2: Comparison plots of approximate solutions at the fractional order σ = 0.9 and σ = 0.8

images

Figure 3: Combine 3D graphs for different fractional orders σ and exact solution of 2D plot

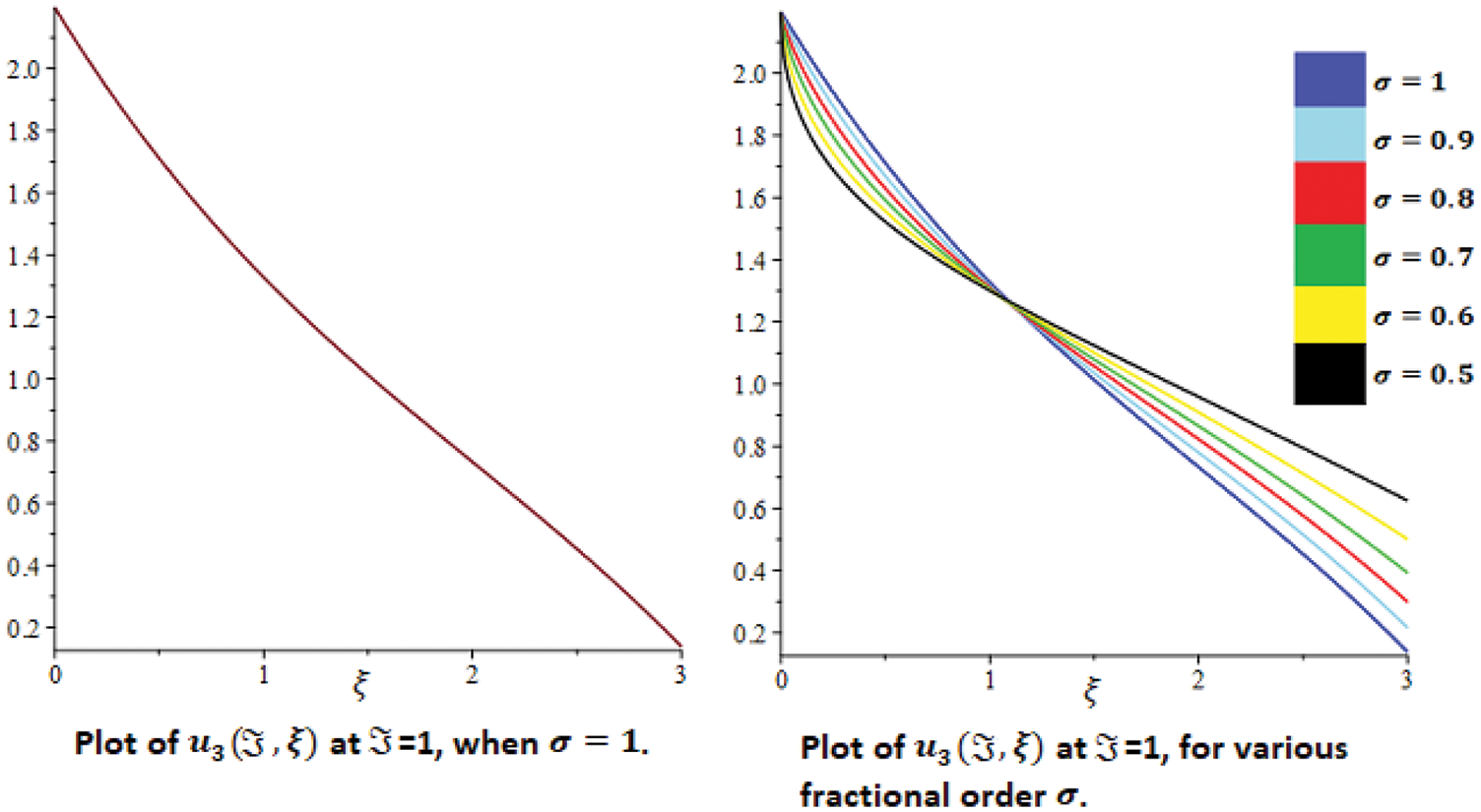
images

Figure 4: 2D plot and combine plot for various fractional order σ

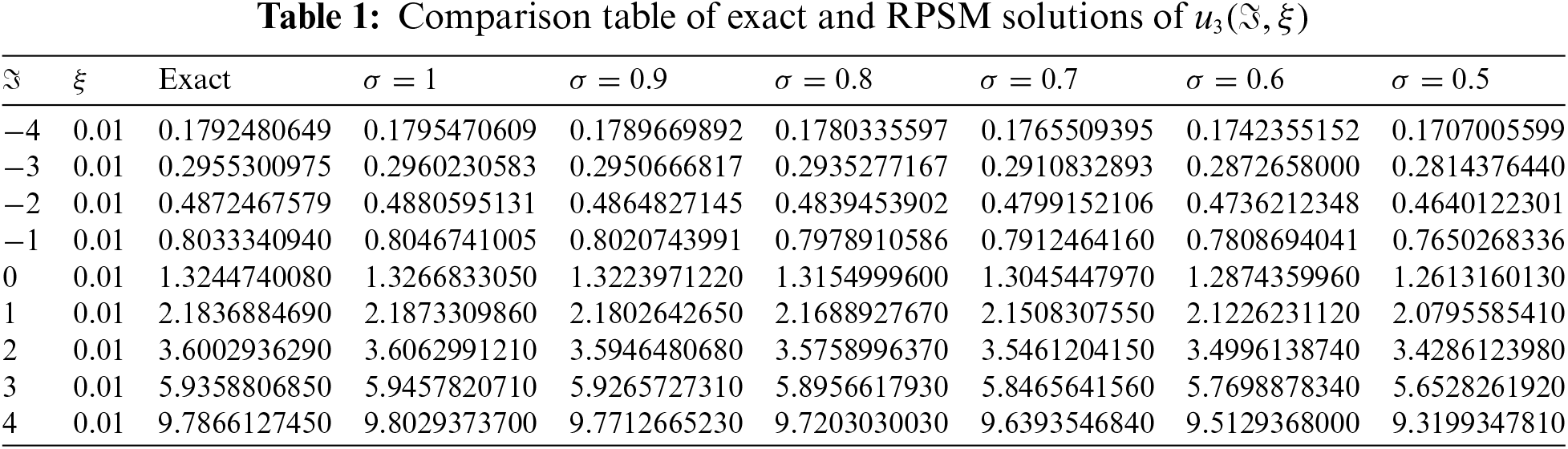
Table 1 lists the result of RPSM u3(ℑ,ξ) solution at various fractional orders σ. The numerical results have shown that RPSM works excellently to solve FPDEs, even when using low-order approximate solution. The accuracy can be improve by using higher-order approximate solutions of FFWE. The Numerical results for various particular cases of σ are presented in Figs. 1–3.

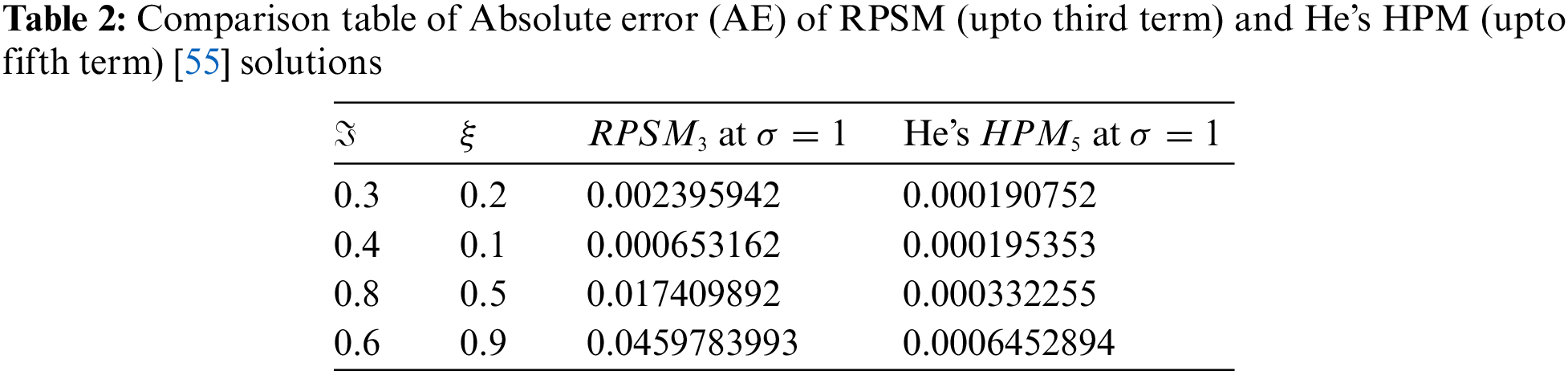
images

In Table 2, the solutions comparison of RPSM with He’s HPM is discussed. It is analyzed that the RPSM solution up to three terms is quite closed to the He’s HPM solutions which is calculated up to five terms. The tables and graphs have confirmed the higher degree of accuracy of RPSM. In Table 3, some nomenclatures are given which are frequently used in this paper.

images

images

6  Conclusion

In this work, we have implemented an efficient analytical technique, which is known as RPSM, to get an approximate series solution of FFWE with initial conditions. The suggested problems are first converted into their fractional form of the derivative and then incorporated the Caputo definition into the given problem to define FD. The general formulation for the proposed problem is discussed and then implemented for the solutions of FFWE. The proposed technique is applied to both fractional and integer orders of the suggested problem. It is observed that the procedure of the present technique is very effective and straight-forward. For verification and a better understanding of the obtained solutions, the graphical and tabular scenarios are presented. In Figs. 1–3, the exact and approximate solutions of the problem are presented, respectively. The solution graphs are presented at different fractional orders of the derivatives and show the various useful dynamics of the problem. It is investigated through numerical results and graphs that the fractional solutions are convergent to the integer-order solution. The analysis has shown the best contact between the RPSM and the exact solutions to the problem. For this purpose, the 2D graphs are discussed through Graphs 3 and 4. The 2D graphs clearly indicate that the proposed technique provides sufficient accuracy for problems with fractional orders. On the basis of the above analysis, it can be concluded that the proposed technique can be expanded easily to solve other problems in science and engineering. The values of the exact and approximate solutions of various fractional orders of the proposed method are given in Table 1, respectively. The exact and RPSM solution analyses given in Table 1 confirmed the higher accuracy.

Authors Contribution: Hassan Khan (Supervision), Poom Kumam (Funding, Draft Writing), Asif Nawaz (Methodology), Qasim Khan (Methodology, Investigation), Shahbaz Khan (Draft Writing).

Availability of Data and Material: Not applicable.

Funding Statement: The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT. This research project is supported by Thailand Science Research and Innovation (TSRI) Basic Research Fund: Fiscal year 2022 under Project No. FRB650048/0164.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

  1. Jimenez, J., & Whitham, G. B. (1976). An averaged lagrangian method for dissipative wavetrains. Proceedings of the Royal Society. A. Mathematical and Physical Sciences, 349(1658), 277-287. [Google Scholar]
  2. Fornberg, B., & Whitham, G. B. (1978). A numerical and theoretical study of certain nonlinear wave phenomena. philosophical transactions of the royal society of London. series A. Mathematical and Physical Sciences, 289(1361), 373-404. [Google Scholar]
  3. Miller, K. S., Ross, B. (1993). An Introduction to the fractional calculus and fractional differential equations. New York: Wiley.
  4. Debnath, L. (2003). Fractional integral and fractional differential equations in fluid mechanics. Fractional Calculus and Applied Analysis, 6(2), 119-155. [Google Scholar]
  5. Caputo, M. (1969). Elasticita e dissipazione. Italy: Zanichelli.
  6. Singh, J., Kumar, D., & Nieto, J. J. (2016). A reliable algorithm for a local fractional tricomi equation arising in fractal transonic flow. Entropy, 18(6), 206. [Google Scholar] [CrossRef]
  7. Srivastava, H. M., Kumar, D., & Singh, J. (2017). An efficient analytical technique for fractional model of vibration equation. Applied Mathematical Modelling, 45, 192-204. [Google Scholar] [CrossRef]
  8. Gupta, P. K., & Singh, M. (2011). Homotopy perturbation method for fractional Fornberg-Whitham equation. Computers & Mathematics with Applications, 61(2), 250-254. [Google Scholar] [CrossRef]
  9. Merdan, M., Gökdoğan, A., Yildirim, A., & Mohyud-Din, S. T. (2012). Numerical simulation of fractional Fornberg-Whitham equation by differential transformation method. Abstract and applied analysis, 2012, [Google Scholar]
  10. Singh, J., Kumar, D., & Kumar, S. (2013). New treatment of fractional Fornberg−Whitham equation via Laplace transform. Ain Shams Engineering Journal, 4(3), 557-562. [Google Scholar]
  11. Neirameh, A. (2018). New fractional calculus and application to the fractional-order of extended biological population model. Boletim da Sociedade Paranaense de Matemática, 36(3), 115-128. [Google Scholar] [CrossRef]
  12. Cao, K., & Chen, Y. (2018). Fractional order crowd dynamics. De Gruyter, 4, [Google Scholar] [CrossRef]
  13. Luchko, Y., & Yamamoto, M. (2016). General time-fractional diffusion equation: Some uniqueness and existence results for the initial-boundary-value problems. Fractional Calculus and Applied Analysis, 19(3), 676-695. [Google Scholar] [CrossRef]
  14. Shokhanda, R., Goswami, P., He, J. H., & Althobaiti, A. (2021). An approximate solution of the time-fractional two-mode coupled burgers equation. Fractal and Fractional, 5(4), 196. [Google Scholar] [CrossRef]
  15. He, C. H. (2016). An introduction to an ancient Chinese algorithm and its modification. International Journal of Numerical Methods for Heat & Fluid Flow, 26(8), 2486-2491. [Google Scholar] [CrossRef]
  16. Dai, D. D. (2021). The piecewise reproducing kernel method for the time variable fractional order advection-reaction-diffusion equations. Thermal Science, 25, 1261-1268. [Google Scholar]
  17. Han, C., Wang, Y. L., & Li, Z. Y. (2022). A high-precision numerical approach to solving space fractional gray-scott model. Applied Mathematics Letters, 125, 107759. [Google Scholar] [CrossRef]
  18. Han, C., Wang, Y. L., & Li, Z. Y. (2021). Numerical solutions of space fractional variable-coefficient KdV-modified KdV equation by Fourier spectral method. Fractals, 29(8), 2150246. [Google Scholar] [CrossRef]
  19. He, J. H., Moatimid, G. M., & Mostapha, D. R. (2021). Nonlinear instability of two streaming-superposed magnetic reiner-rivlin fluids by He-laplace method. Journal of Electroanalytical Chemistry, 895, 115388. [Google Scholar] [CrossRef]
  20. Khan, Y., Faraz, N., Yildirim, A., & Wu, Q. (2011). Fractional variational iteration method for fractional initial-boundary value problems arising in the application of nonlinear science. Computers & Mathematics with Applications, 62(5), 2273-2278. [Google Scholar] [CrossRef]
  21. Khan, Y., Ali Beik, S. P., Sayevand, K., & Shayganmanesh, A. (2015). A numerical scheme for solving differential equations with space and time-fractional coordinate derivatives. Quaestiones Mathematicae, 38(1), 41-55. [Google Scholar] [CrossRef]
  22. Khan, Y., Fardi, M., Sayevand, K., & Ghasemi, M. (2014). Solution of nonlinear fractional differential equations using an efficient approach. Neural Computing and Applications, 24(1), 187-192. [Google Scholar] [CrossRef]
  23. Khan, Y., & Wu, Q. (2011). Homotopy perturbation transform method for nonlinear equations using He’s polynomials. Computers & Mathematics with Applications, 61(8), 1963-1967. [Google Scholar] [CrossRef]
  24. Madani, M., Fathizadeh, M., & Khan, Y. (2011). On the coupling of the homotopy perturbation method and laplace transformation. Mathematical and Computer Modelling, 53(9–10), 1937-1945. [Google Scholar] [CrossRef]
  25. Khan, Y., & Faraz, N. (2021). Simple use of the maclaurin series method for linear and non-linear differential equations arising in circuit analysis. COMPEL-The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 40(3), 593-601. [Google Scholar] [CrossRef]
  26. Ain, Q. T., Anjum, N., Din, A., Zeb, A., & Djilali, S. (2022). On the analysis of caputo fractional order dynamics of Middle East lungs coronavirus (MERS-CoV) model. Alexandria Engineering Journal, 61(7), 5123-5131. [Google Scholar] [CrossRef]
  27. Anjum, N., & Ain, Q. T. (2020). Application of He’s fractional derivative and fractional complex transform for time fractional camassa-holm equation. Thermal Science, 24, 3023-3030. [Google Scholar] [CrossRef]
  28. Ain, Q. T., He, J. H., Anjum, N., & Ali, M. (2020). The fractional complex transform: A novel approach to the time-fractional Schrödinger equation. Fractals, 28(7), 2050141. [Google Scholar] [CrossRef]
  29. Anjum, N., He, C. H., & He, J. H. (2021). Two-scale fractal theory for the population dynamics. Fractals, 29(7), 2150182. [Google Scholar] [CrossRef]
  30. Anjum, N., Ain, Q. T., & Li, X. X. (2021). Two-scale mathematical model for Tsunami wave. GEM-International Journal on Geomathematics, 12(1), 1-12. [Google Scholar] [CrossRef]
  31. El-Sayed, A. M. A., Nour, H. M., Raslan, W. E., & El-Shazly, E. S. (2015). A study of projectile motion in a quadratic resistant medium via fractional differential transform method. Applied Mathematical Modelling, 39(10–11), 2829-2835. [Google Scholar] [CrossRef]
  32. Kumar, M., & Rawat, T. K. (2015). Design of a variable fractional delay filter using comprehensive least square method encompassing all delay values. Journal of Circuits, Systems and Computers, 24(8), 1550116. [Google Scholar] [CrossRef]
  33. Alomari, A. K., Syam, M. I., Anakira, N. R., & Jameel, A. F. (2020). Homotopy sumudu transform method for solving applications in physics. Results in Physics, 18, 103265. [Google Scholar] [CrossRef]
  34. Prakash, A., Veeresha, P., Prakasha, D. G., & Goyal, M. (2019). A new efficient technique for solving fractional coupled Navier-Stokes equations using Q-homotopy analysis transform method. Pramana, 93(1), 1-10. [Google Scholar] [CrossRef]
  35. Kocak, H., & Pinar, Z. (2018). On solutions of the fifth-order dispersive equations with porous medium type non-linearity. Waves in Random and Complex Media, 28(3), 516-522. [Google Scholar] [CrossRef]
  36. Momani, S., & Odibat, Z. (2006). Analytical solution of a time-fractional navier-stokes equation by adomian decomposition method. Applied Mathematics and Computation, 177(2), 488-494. [Google Scholar] [CrossRef]
  37. Bayrak, M. A., & Demir, A. (2018). A new approach for space-time fractional partial differential equations by residual power series method. Applied Mathematics and Computation, 336, 215-230. [Google Scholar] [CrossRef]
  38. Senol, M., Iyiola, O. S., Daei Kasmaei, H., & Akinyemi, L. (2019). Efficient analytical techniques for solving time-fractional nonlinear coupled Jaulent-Miodek system with energy-dependent Schrödinger potential. Advances in Difference Equations, 2019(1), 1-21. [Google Scholar]
  39. Korpinar, Z., Inc, M., Hinçal, E., & Baleanu, D. (2020). Residual power series algorithm for fractional cancer tumor models. Alexandria Engineering Journal, 59(3), 1405-1412. [Google Scholar] [CrossRef]
  40. Kurt, A. (2020). New analytical and numerical results for fractional Bogoyavlensky-Konopelchenko equation arising in fluid dynamics. Applied Mathematics–A Journal of Chinese Universities, 35(1), 101-112. [Google Scholar] [CrossRef]
  41. Xu, F., Gao, Y., Yang, X., & Zhang, H. (2016). Construction of fractional power series solutions to fractional boussinesq equations using residual power series method. Mathematical Problems in Engineering, 2016, 1-15. [Google Scholar] [CrossRef]
  42. Freihet, A. A., & Zuriqat, M. (2019). Analytical solution of fractional burgers-huxley equations via residual power series method. Lobachevskii Journal of Mathematics, 40(2), 174-182. [Google Scholar] [CrossRef]
  43. Jena, R. M., & Chakraverty, S. (2019). Residual power series method for solving time-fractional model of vibration equation of large membranes. Journal of Applied and Computational Mechanics, 5(4), 603-615. [Google Scholar]
  44. Sakar, M. G., Erdogan, F., & Yildirim, A. (2012). Variational iteration method for the time-fractional Fornberg-Whitham equation. Computers & Mathematics with Applications, 63(9), 1382-1388. [Google Scholar] [CrossRef]
  45. Podlubny, I. (1998). Fractional differential equations: An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. USA: Academic Press.
  46. Luchko, Y. F., & Srivastava, H. M. (1995). The exact solution of certain differential equations of fractional order by using operational calculus. Computers & Mathematics with Applications, 29(8), 73-85. [Google Scholar] [CrossRef]
  47. El-Ajou, A., Arqub, O. A., & Momani, S. (2015). Approximate analytical solution of the nonlinear fractional KdV-burgers equation: A new iterative algorithm. Journal of Computational Physics, 293, 81-95. [Google Scholar] [CrossRef]
  48. El-Ajou, A., Arqub, O. A., Zhour, Z. A., & Momani, S. (2013). New results on fractional power series: Theories and applications. Entropy, 15(12), 5305-5323. [Google Scholar] [CrossRef]
  49. Alquran, M. (2015). Analytical solution of time-fractional two-component evolutionary system of order 2 by residual power series method. Journal of Applied Analysis and Computation, 5(4), 589-599. [Google Scholar] [CrossRef]
  50. Alquran, M., Jaradat, H. M., & Syam, M. I. (2017). Analytical solution of the time-fractional Phi-4 equation by using modified residual power series method. Nonlinear Dynamics, 90(4), 2525-2529. [Google Scholar] [CrossRef]
  51. Freihet, A., Hasan, S., Al-Smadi, M., Gaith, M., & Momani, S. (2019). Construction of fractional power series solutions to fractional stiff system using residual functions algorithm. Advances in Difference Equations, 2019(1), 95. [Google Scholar]
  52. Hasan, S., Al-Smadi, M., Freihet, A., & Momani, S. (2019). Two computational approaches for solving a fractional obstacle system in hilbert space. Advances in Difference Equations, 2019(1), 55. [Google Scholar] [CrossRef]
  53. Prakasha, D. G., Veeresha, P., & Baskonus, H. M. (2019). Residual power series method for fractional Swift-Hohenberg equation. Fractal and Fractional, 3(1), 9. [Google Scholar] [CrossRef]
  54. Tchier, F., Inc, M., Korpinar, Z. S., & Baleanu, D. (2016). Solutions of the time fractional reaction-diffusion equations with residual power series method. Advances in Mechanical Engineering, 8(10), [Google Scholar] [CrossRef]
  55. Wang, K. L., & Liu, S. Y. (2017). He’s fractional derivative and its application for fractional Fornberg-Whitham equation. Thermal Science, 21(5), 2049-2055. [Google Scholar] [CrossRef]

Cite This Article

Khan, H., Kumam, P., Nawaz, A., Khan, Q., Khan, S. (2023). The Fractional Investigation of Fornberg-Whitham Equation Using an Efficient Technique. CMES-Computer Modeling in Engineering & Sciences, 135(1), 259–273.


cc This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

  • 794

    View

  • 660

    Download

  • 0

    Like

Related articles

Copyright© 2024 Tech Science Press
© 1997-2024 TSP (Henderson, USA) unless otherwise stated

Share Link