Scheduling an Energy-Aware Parallel Machine System with Deteriorating and Learning Effects Considering Multiple Optimization Objectives and Stochastic Processing Time

1  Introduction

Currently, the energy crisis has become one of the most prominent and urgent environmental issues [1,2]. For the last few years, excessive energy resources have been consumed, which causes both resource depletion and environmental pollution. Consequently, energy conservation attracts considerable attention from government concern and public awareness [3,4]. An official report shows that the energy demand continues to grow at a rapid rate of 56% between 2010 and 2040 (EIA 2013). The manufacturing industry consumes an amount of energy and produces a great deal of greenhouse gas, which result in seriously environmental pollution. As a result, manufacturers are encouraged to make energy-efficient decisions involving process reformation, product design and production scheduling when managing and organizing their production [5–7]. Parallel machine scheduling is an important scheduling problem in practical manufacturing systems. In the past years, vast studies have been made on this subject, such as Saricicek et al. [8], Prot et al. [9], Vallada et al. [10], Bozorgirad et al. [11], Zhong et al. [12] and Li [13]. In an actual process, it is important to take the actual environment into account when studying the parallel machine scheduling problems (PMSP). In the workplace, the parameters of scheduling problem are influenced by many existing factors [14–16]. Stec et al. [17] considered that the processing time of jobs obeys a specified normal distribution in a PMSP. Al-Khamis et al. [18] focused on the uncertain due dates when solving a PMSP. Zhang [19] used the random processing time and adjustable production rate in a PMSP.

Previous work on parallel machine scheduling tends to set the processing time as a fixed constant, which obviously deviates from the actual situation. In real-life, the processing time of jobs always changes with their start time. For example, the steel industry wants to process the job under high temperatures. However, if the processing time of the unprocessed job is very late, the temperature will drop accordingly. Therefore, due to the later start time, the processing time of this job will be prolonged, i.e., the later the job starts, the longer the corresponding processing time is. In general, it is called the deteriorating effect. Kang et al. [20] aimed at achieving maximum completion time minimization in an identical PMSP with processing deteriorating jobs. Cheng et al. [21] developed the unrelated PMSP considering the deteriorating maintenance activities. Jiang [22], Huang et al. [23], Zhao et al. [24] and Na et al. [25] proposed related PMSPs with respect to deteriorating effects. Mazdeh et al. [26] discussed the PMSP considering both machine and job deterioration effects. Except for the deteriorating effects, the learning effects usually occur as well. In the real world, production facilities (machines, workers) will continuously improve their production capacity and skills over time. Therefore, when one job is processed late, its processing time can be shortened. Mosheiov [27] summarized the classical scheduling problems with consideration of learning effects. Yeh et al. [28] concentrated on both learning effects and fuzzy processing time in a PMSP. To solve it, they used two heuristic algorithms, i.e., a simulated annealing method and a genetic approach. Hidri et al. [29] solved a PMSP with learning effects. They employed several heuristic algorithms to tackle it. Eren et al. [30] focused on the learning effects in a PMSP regarding setup and removal times. Toksari Duran et al. [31] presented a PMSP with the consideration of due dates, the deteriorating and learning effects, and sequence dependent-setups.

In practical scheduling problems, not only single objective needs to be considered, but also multi-objective needs to be solved optimally [32]. The prior research has coped with multi-objective problems under the condition of considering deteriorating and learning effects. Lu et al. [33] aimed at optimizing completion time and total load and resource cost in a multi-objective PMSP considering deteriorating and learning effects. Amini et al. [34] studied an identical PMSP where the setup and removal times of jobs are influenced by both deteriorating and learning effects. Arik et al. [35] considered a multi-objective PMSP under a fuzzy environment, in which the jobs are affected by deterioration and learning effects. Rostami et al. [36] also took the deterioration and learning effects into account in solving a multi-objective non-identical PMSP.

Through the analysis of existing studies, we find that an energy-aware PMSP with the consideration of deteriorating and learning effects and uncertainty is not be adequately considered by the existing studies. In an actual process, energy consumption optimization needs to be considered, and thus a multi-objective model should be addressed to find a balance between energy-saving and time-related criteria. Additionally, because the details of machines and jobs usually cannot be foreseen, jobs’ processing time is uncertain [37]. Besides, to depict a real-life manufacturing system, it is necessary to consider the deteriorating and learning effects. By comparing with previous studies, twofold contributions are made as follows:

1)   We propose a stochastic energy-aware parallel machine scheduling problem with deteriorating and learning effects. Its goal is to minimize the makespan and energy consumption. Furthermore, a stochastic multi-objective model is formulated to describe it mathematically.

2)   We design a multi-objective multi-verse optimization incorporating a stochastic simulation approach to solve the proposed problem. In it, a multi-objective multi-verse optimization is applied to search for favorable solutions from the entire solution domain, and the stochastic simulation approach is employed to evaluate the performance of obtained solutions. Via conducting experiments on a set of test problems and comparing the designed approach with its peers, i.e., the nondominated sorting genetic algorithm II and multi-objective evolutionary algorithm based on decomposition, we demonstrate its effectiveness in solving the considered problem.

2  Problem Description

In this paper, the investigated problem is demonstrated as: There are n jobs in a manufacturing system, and they need to choose any one out of m machines to perform production operations. The deteriorating and learning effects of jobs occur in the manufacturing process. The real processing time of jobs is calculated via using their normal processing time, start processing time, processing position and speed in a schedule. In the investigated problem, we aim at minimizing the makespan and energy consumption by determining job assignment among machines, job sequence on machines and job processing speed. We introduce the following notations:

Indices:

N set of jobs, N={0,1,2,…,n}, in which the index n indicates the number of jobs, and 0 is a virtual job.

M set of machines, M={0,1,2,…,m}, in which the index m indicates the number of machines, and 0 is a virtual machine.

D set of speeds, D={1,2,…d}, in which the index d denotes the number of processing speeds.

j job index, j∈N.

i machine index, i∈M.

k position index, k∈N.

l selected processing speed index, l∈D.

Parameters:

pij normal processing time of the job j on machine i.

βij learning rate of job j on machine i.

αij deteriorating rate of job j on machine i.

vil the l-th processing speed of machine i.

tij setup time of job j on machine i.

eijα energy consumption per unit time in the processed phase if job j is processed on machine i.

eijβ energy consumption per unit time in the setup phase if job j is processed on machine i.

Decision variables:

pijk′ actual processing time of job j at the k-th position on machine i.

sijk start processing time of job j at the k-th position on machine i.

Cmax makespan.

xijk if job j is processed at the k-th position on machine i, xijk=1; otherwise,xijk=0.

zjl if job j chooses the l-th processed speed for processing, zjl=1; otherwise, zjl=0.

A viable scheduling scheme needs to obey the following restricted conditions: 1) Only one machine is chosen for each job to perform processing operations; 2) For each machine, only one job rather than multiple jobs can be processed on it at a time; 3) No machines can be interrupted. Note that the actual processing time of jobs can be calculated as:

pijk′=(pijvi∑l∈Dzjl+αij⋅sijk)⋅kβij.(1)

According to the above notations and definitions, the considered problem can be established as follows:

minE(Cmax)(2)

minE(∑i∈M∑j∈N∑k∈N(eijα⋅pijk′⋅xijk+eijα⋅tij⋅xijk))(3)

s.t.

∑j∈N∑k∈Nxijk≤1,∀i∈M.(4)

∑i∈M∑k∈Nxijk≤1,∀j∈N.(5)

∑l∈Dzjl=1,∀j∈N.(6)

E(pijk′−(pijvi∑l∈Dzjl+αij⋅sijk)⋅kβij)=0,∀i∈M,∀j∈N,∀k∈N.(7)

E(eijα−4.0∗vil2∑l∈Dzjl)=0,∀i∈M,∀j∈N.(8)

E(sijk+1−sijk′−pijk′−tij+G(2−(xijk+xijk+1)))≥0,∀i∈M,∀j∈N,k=1,…,N−1.(9)

E(Cmax−sijk−pijk′−tij+G(1−xijk))≥0,∀i∈M,∀j∈N,∀k∈N.(10)

xijk∈{0,1},zjl∈{0,1},∀i∈M,∀j∈N,∀k∈N,∀l∈D.(11)

where the objective functions (2) and (3) are minimizing the makespan and total energy consumption, respectively. Note that E (ξ) demonstrates the expected value of the random variable ξ. Eq. (4) guarantees that at most one job can be processed at one position of a machine. Eq. (5) indicates that each job is allowed to choose only one position of a machine for processing. Eq. (6) shows that each job is processed with only one speed. Eq. (7) gives the actual processing time of jobs. Eq. (8) shows the energy consumption per unit time of jobs. Eq. (9) indicates that the start processing time of subsequent jobs on each machine should be larger than the end time of previous jobs. Eq. (10) means that the end time of each machine is smaller than the makespan. Eq. (11) represents that each decision variable equals to 0 or 1.

3  Solution Algorithm

3.1 Basic Multi-Verse Optimizer (MVO)

Recently, a global optimization algorithm named Multi-verse optimizer (MVO) is initially put forward by Hatamlou et al. [38]. It primarily contains three important cosmology notations, i.e., white hole, black hole, and wormhole. Based on them, employing three mathematical models can contribute to exploration and exploitation, respectively. More detailed descriptions about MVO can refer to [38].

Due to its advantages, such as easy implementation, powerful exploration and exploitation abilities, MVO has been successfully employed to solve many optimization problems [39–41]. Thus, it is a good choice to deal with the considered problem. Although basic MVO is initially introduced to solve continuous and single-objective optimization problems, its variants have been employed to solve various discrete and multi-objective optimization problems and shown excellent performance. Consequently, to make it suitable for handling the considered problem, a MOMVO incorporating a stochastic simulation approach is designed according to the considered problem’s characteristics. The detailed descriptions of MOMVO are shown below.

3.2 Solution Expression and Population Initialization

For solving the considered PMSP, it is necessary to make three decisions as: job assignment among machines, job sequence on machines and job processing speed. In this work, we use a double-chain structure to indicate a solution [42]. In MOMVO, a solution is expressed by an integer string S=(O,V). O=(o1,o2,…,oN) represents a job sequence where an integer is a job index, and V=(v1,v2,…,vN) indicates a speed vector where vn, vn∈D denotes the selected processing speed of its corresponding job. Taking 20 jobs and 2 machines as an example, each job has 5 available processing speeds, an individual S=(O,V) can be expressed as: O= (7, 18, 16, 20, 5, 19, 14, 1, 13, 15, 8, 4, 11, 2, 12, 3, 6, 10, 9, 17) and V= (1, 4, 2, 3, 5, 3, 5, 2, 1, 1, 3, 1, 2, 2, 3, 1, 5, 3, 3, 1). It can be seen that v1, v9, v10, v12, v16, v20 represents that the speed of processing job is 1, and their corresponding jobs are o1=7, o9=13, o10=15, o12=14, o16=3, o20=17, respectively.

The decode rules are used to transform a solution into a feasible scheme as: Each job is allocated to a machine having earliest time and its actual processing time is calculated as Eq. (1). Note that the objective function values of a solution are not directly evaluated due to the jobs’ random processing time. Hence, for estimating the solutions, we employ a well-known Monte Carlo Simulation approach.

In MOMVO, an initial population consists of 100 randomly viable solutions. Besides, to restore the obtained non-dominated solutions in the search process, an external archive is developed and a Pareto rule is employed to update it [43].

3.3 Stochastic Simulation Approach

Notice that the objective function is expressed as an expected value, and we cannot directly evaluate it. Monte Carlo simulation is one of the most effective stochastic simulation methods. It has been effectively employed to deal with various stochastic problems [44]. Therefore, it is adopted in this work to estimate the solutions. The true objective function value is calculated by taking an average of extensive replications. Each replication is regarded as a sample where the jobs’ normal processing time is generated at random from their corresponding distributions. In fact, the true objective value can be achieved if the number of replications tends to infinity. However, the computation resource is usually limited, and we need to do such work under limited resources. Thus, the number of replications is set to 10.

3.4 New Individual Generation Approach

In the proposed MOMVO, we randomly select an individual in the current population as a black hole. And a binary selection approach is regarded as wormhole, and it is employed to choose an individual as a white hole. Fig. 1 indicates Pseudo-code of selection approach, where x1 is a solution chosen from the external archive, x2 is randomly chosen from population. The two selected individuals, i.e., black hole and white hole, are regarded as parent individuals. This work uses genetic operation including crossover and mutation approaches to generate new individuals. Let S1=(O1,V1) and S2=(O2,V2) be two newly generated individuals. The crossover operation is performed as follows:

1)   Select two parent individuals by using a binary selection method, i.e., Sf=(Of,Vf) and Sm=(Om,Vm).

2)   Perform an order-based crossover approach to acquire child individuals O1 and O2. The first step is to randomly select two different points in Of. Then store the partial permutation between two points as jobs of O1 at the same positions. Then the remaining jobs need to be added as the order of their appearance in Om. Same procedure as O1 is performed to get job permutation of O2.

3)   Generate two binary strings V1 and V2 randomly. If the value in V1 of S1 is 1, the value corresponding to Vf will be inherited into V1; If the value in V1 is 0, the value corresponding to Vm will be inherited to V1. If the value in V2 of S2 is 1, the value corresponding to Vm will be inherited into V2; If the value in V2 is 0, the value corresponding to Vf will be inherited to V2. Therefore, V1 and V2 of two newly generated individuals are produced.

Figure 1: Pseudo-code of selection approach

The following mutation operations with a probability are performed on each newly generated offspring individual. Different ways of mutation operations are adopted for parts O and V of the individual S. Firstly, for part O of the individual S, (1) select two different points in the part O string randomly; (2) the genes in the two positions are exchanged. Secondly, for the part V of the individual S, (1) one point in the part V string is selected randomly; (2) the gene at this point is replaced with a random generated number, where this number is between 1 and 5.

3.5 Selection Approach

For the solution algorithm designed to tackle multi-objective problems, finding a solution set with outstanding approximation and distribution is desired. Thus, the rank and crowding distance methods [43] can availably balance the approximation and distribution. Therefore, MOMVO combines the contemporary population with new individuals, and the top 100 individuals are selected as the next population by employing aforementioned methods.

In addition, MOMVO uses the newly obtained population to update the external archive with maximum capacity constraints by employing a Pareto dominance rule [43]. The framework of the basic MOMVO is described by the pseudo-code in Fig. 2.

Figure 2: Pseudo-code of MOMVO

4  Experimental Study

To test MOMVO’s effectiveness in coping with the problem studied, we choose two classical and popular multi-objective optimization methods, i.e., Nondominated sorting genetic algorithm II (NSGA-II) [43] and Multi-objective evolutionary algorithm based on decomposition (MOEA/D) [45], as peer algorithms to perform comparison experiments.

4.1 Test Problem Generation

To validate the performance of MOMVO in solving the problem under consideration, we randomly produce 30 test problems which are the combinations of m∈{2,4,6,8,10} and n∈{20,40,60,80,100}. The normal processing time of jobs follows normal distribution. Their mean processing time is a random number from 1 to 100, and their standard deviation is calculated through multiplying their mean processing time by the coefficient γ, where γ=0.0000001. The setup time of jobs is obtained from 1 to 10. Machine processing speed at five levels, i.e., vil={1.00,1.30,1.55,1.80,2.00}. The deteriorating and learning rate of jobs on machines are randomly produced from [0,0.1] and [−0.1, 0], respectively. The energy consumption per unit time of standby machines is set to eijβ=1.0.

4.2 Parameter Setting

MOMVO, NSGA-II and MOEA/D have two identical parameters as: population size and mutation probability. For three algorithms, the population size is equal to 100. The values of mutation probability for them are equal to 0.3, 0.3 and 1.0, respectively. The maximum capacity of external archive is set as 100 and the number of fitness evaluation 100 mn is chosen as the stopping condition, in which m and n are machine number and job number, respectively.

4.3 Performance Metrics

Approximation and distribution are two key indicators for evaluating the multi-objective optimization algorithms’ performance. Therefore, this work employs C-metric by Deb et al. [43] and IGD-metric by Fu et al. [44] as performance metrics.

1)   C-metric is employed to measure a dominated percentage of two sets acquired by two optimizers. C(X,Y) represents the dominated percentage of solutions in Y dominated by at least one solution in X. C(X,Y) is calculated as:

C(X,Y)=|{y∈Y|∃x∈X:x≺y}||Y|.(12)

where |Y| denotes the number of solutions in Y. Evidently, a larger C(X,Y) value means that the X is better.

2)   IGD-metric is adopted to assess both convergence and diversity of a solution set by measuring the average distance between an optimal solution set V∗ and an approximated solution set V. It is calculated as:

IGD(V,V∗)=1|V∗|∑v∈V∗dist(v,V).(13)

where dist(v,V) denotes the Euclidean distance between a solution v in V∗ and its closest solution in V. In fact, we are unable to attain V∗ for the practical problem. Thus, all solutions acquired by MOMVO and its peers are combined, and then choose the nondominated solutions as V∗. Besides, we normalize all objective function values into [0, 1], then calculate IGD-metric. Obviously, the smaller IGD value, the better V.

4.4 Experimental Results and Analysis Discussion

In this part, MOMVO’s performance in tackling the considered problem is validated. MOMVO and its peers run 10 times for each problem, and the mean and variance values regarding C-metric and IGD-metric are calculated.

Table 1 exhibits the experiment results of C-metric, in which MOMVO, NSGA-II and MOEA/D are denoted by the indices “X”, “Y” and “Z”, respectively. It is worth mentioning that a larger mean value represents a better performance. Through looking at the results, it is clear that MOMVO shows obvious outperformance since the mean values of MOMVO is larger than those of its peers on most of test problems. In addition, the average of mean and variance values on all the test problems are calculated, we can find that the average of MOMVO, NSGA-II and MOEA/D regarding mean value are 0.6345, 0.1990, 0.7139 and 0.2082, and those of variance value are 0.1696, 0.0984, 0.1241 and 0.0813, respectively. Hence, the average of MOMVO regarding mean value performs better than its peers, while the average of MOMVO in terms of variance value shows a little worse. Through the analysis of above results, we can declare that MOMVO has obvious advantage in solving the considered problem.

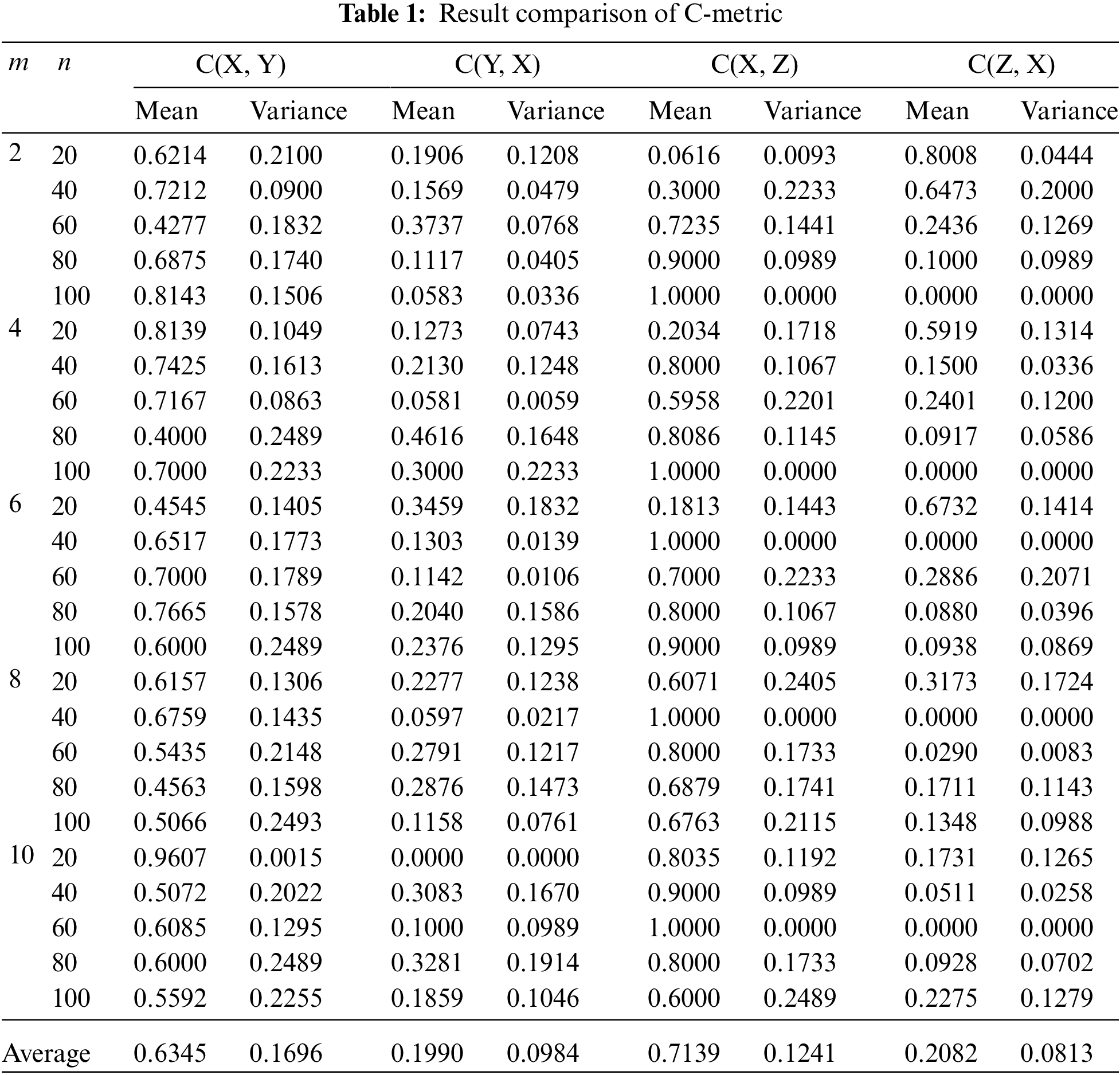
Table 2 gives the experiment results regarding IGD-metric. It is worth mentioning that a smaller mean value denotes a better approximation performance. We can observe that MOMVO has obvious advantages over its peers on most of test cases. Through calculating the average values of all instances in term of mean and variance indicators, we know that the average of MOMVO, NSGA-II and MOEA/D regarding mean values are 0.3573, 0.4800 and 0.7456, while those in terms of variance values are 0.0383, 0.0482 and 0.0683, respectively. Hence, MOMVO outperforms NSAG-II and MOEA/D regarding the average. As can be seen from the above analysis, MOMVO is superior to its peers in obtaining a better set of nondominated solutions.

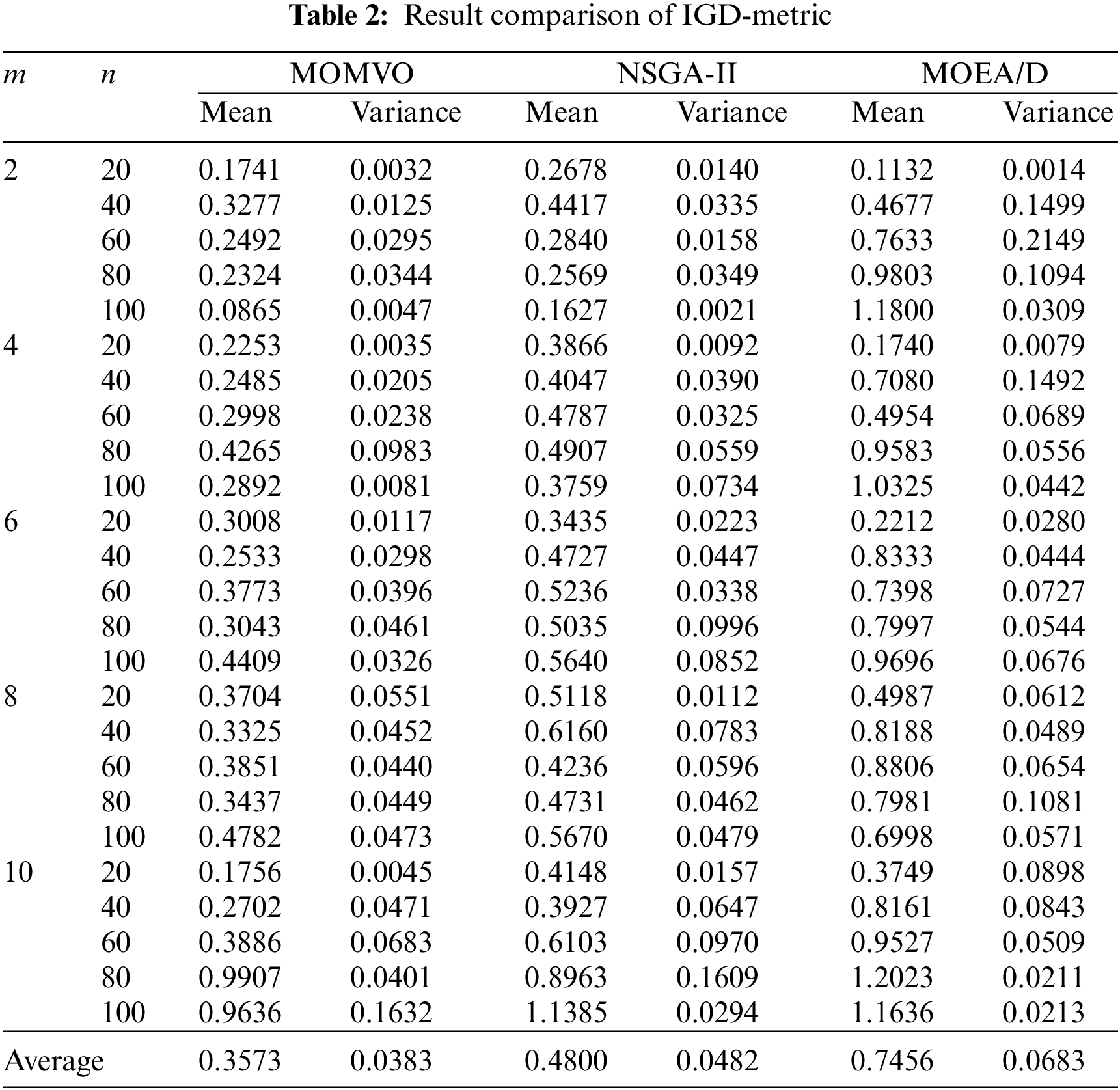
To visually analyze the experiment results, we draw the boxplot graphs of some test problems of 10 runs in Fig. 3. From them, we can find that the obtained results of MOMVO are better and more stable than its peers. Therefore, we can conclude a conclusion that MOMVO is well-converged and well-diversified in solving our considered problem.

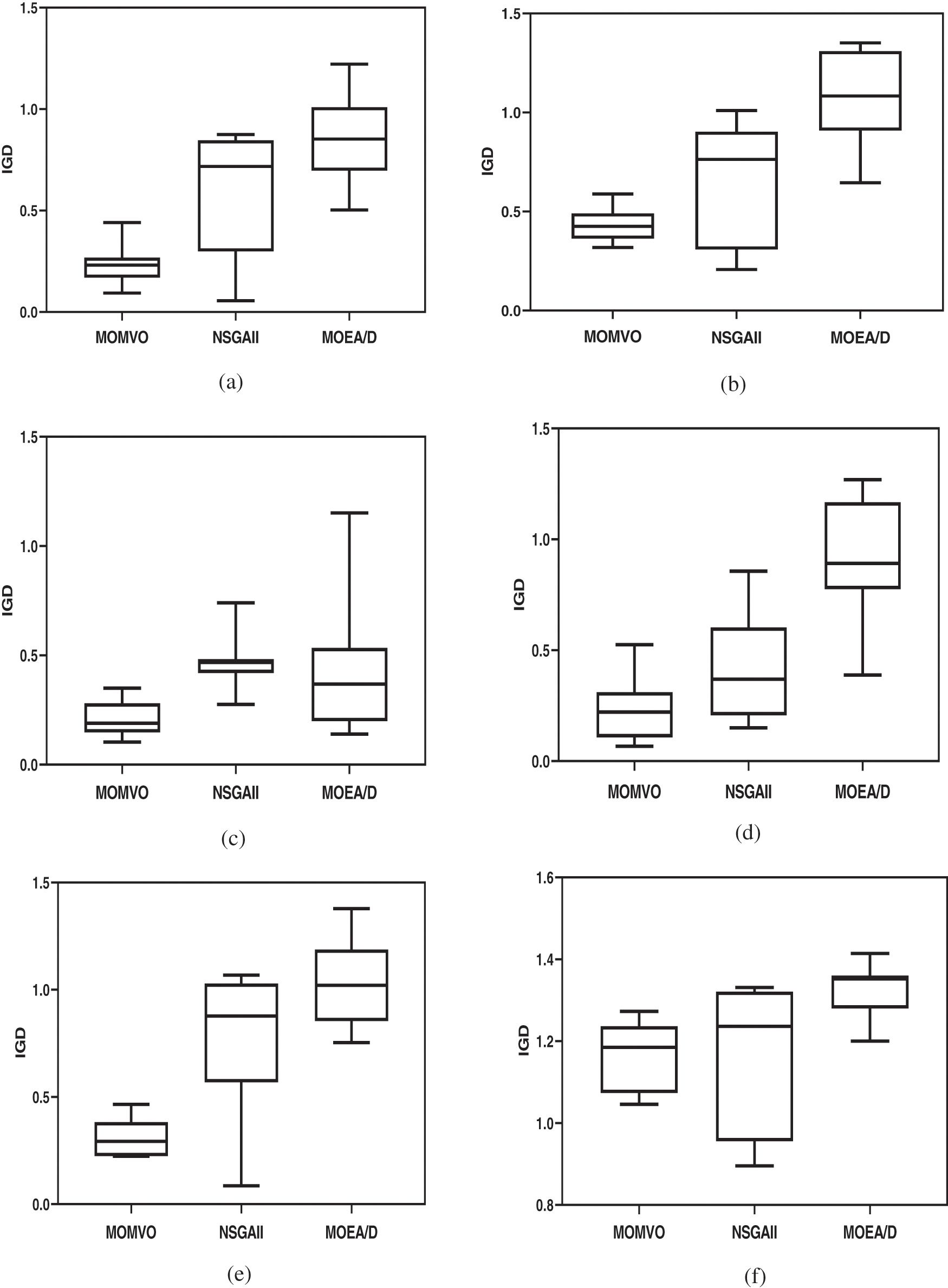
Figure 3: Boxplots of some test problems regarding IGD-metric of three approaches, (a) 6 × 80, (b) 6 × 100, (c) 10 × 20, (d) 10 × 40, (e) 10 × 60, (f) 10 × 80

5  Conclusion

This work addresses a stochastic multi-objective parallel machine scheduling problem with deteriorating and learning effects to reach makespan and energy consumption minimization. By fully considering the characteristics of the proposed problem, we design a multi-objective multi-verse optimization incorporating a stochastic simulation approach to deal with it. The experimental results show that it is an excellent optimization algorithm for solving our considered problem. The results can assist decision-makers in making effective decisions under stochastic environments when handling a parallel machine scheduling problem with multiple optimization objectives, deteriorating and learning effects. The studied problem can help the manufacturing industry improve production efficiency and decrease energy consumption, thereby protecting resources and reducing environmental pollution.

In future work, we plan: 1) To propose a rescheduling approach based on the formulated model; 2) To study an effective approach to solve parallel machine scheduling problems according to the formulated model.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Wang, Q., Su, M., Li, R. R., Ponce, P. (2019). The effects of energy prices, urbanization and economic growth on energy consumption per capita in 186 countries. Journal of Cleaner Production, 225, 1017–1032. DOI 10.1016/j.jclepro.2019.04.008. [Google Scholar] [CrossRef]

 2.  Liu, C. L., Li, Q., Wang, K. (2021). State-of-charge estimation and remaining useful life prediction of supercapacitors. Renewable and Sustainable Energy Reviews, 150, 111408. DOI 10.1016/j.rser.2021.111408. [Google Scholar] [CrossRef]

 3.  Kim, J. B., Park, K., Yang, D. R., Hong, S. (2019). A comprehensive review of energy consumption of seawater reverse osmosis desalination plants. Applied Energy, 254, 113652. DOI 10.1016/j.apenergy.2019.113652. [Google Scholar] [CrossRef]

 4.  Liu, C. L., Zhang, Y., Sun, J. R., Cui, Z. H., Wang, K. (2022). Stacked bidirectional LSTM RNN to evaluate the remaining useful life of supercapacitor. International Journal of Energy Research, 46(3), 3034–3043. DOI 10.1002/er.7360. [Google Scholar] [CrossRef]

 5.  Dey, K., Roy, S., Saha, S. (2019). The impact of strategic inventory and procurement strategies on green product design in a two-period supply chain. International Journal of Production Research, 57(7), 1915–1948. DOI 10.1080/00207543.2018.1511071. [Google Scholar] [CrossRef]

 6.  Wang, J., Wang, L. (2022). A cooperative memetic algorithm with learning-based agent for energy-aware distributed hybrid flow-shop scheduling. IEEE Transactions on Evolutionary Computation, 26(3), 461–475. DOI 10.1109/TEVC.2021.3106168. [Google Scholar] [CrossRef]

 7.  Chen, Q. D., Ding, J. L., Yang, S. X., Chai, T. Y. (2019). A novel evolutionary algorithm for dynamic constrained multiobjective optimization problems. IEEE Transactions on Evolutionary Computation, 24(4), 792–806. DOI 10.1109/TEVC.2019.2958075. [Google Scholar] [CrossRef]

 8.  Saricicek, I., Celik, C. (2011). Two meta-heuristics for parallel machine scheduling with job splitting to minimize total tardiness. Applied Mathematical Modelling, 35(8), 4117–4126. DOI 10.1016/j.apm.2011.02.035. [Google Scholar] [CrossRef]

 9.  Prot, D., Bellenguez-Morineau, O., Lahlou, C. (2013). New complexity results for parallel identical machine scheduling problems with preemption, release dates and regular criteria. European Journal of Operational Research, 231(2), 282–287. DOI 10.1016/j.ejor.2013.05.041. [Google Scholar] [CrossRef]

10. Vallada, E., Rubén, R. (2011). A genetic algorithm for the unrelated parallel machine scheduling problem with sequence dependent setup times. European Journal of Operational Research, 211(3), 612–622. DOI 10.1016/j.ejor.2011.01.011. [Google Scholar] [CrossRef]

11. Bozorgirad, M. A., Logendran, R. (2012). Sequence-dependent group scheduling problem on unrelated-parallel machines. Expert Systems with Applications, 39(10), 9021–9030. DOI 10.1016/j.eswa.2012.02.032. [Google Scholar] [CrossRef]

12. Zhong, X. L., Jiang, D. K. (2015). Parallel machine scheduling with batch delivery to two customers. Mathematical Problems in Engineering, 2015, 1–6. DOI 10.1155/2015/247356. [Google Scholar] [CrossRef]

13. Li, S. G. (2016). Parallel machine scheduling with nested processing set restrictions and job delivery times. Mathematical Problems in Engineering, 2016, 1–5. DOI 10.1155/2016/3203728. [Google Scholar] [CrossRef]

14. Hou, Y. S., Fu, Y. P., Gao, K. Z., Zhang, H., Sadollah, A. (2021). Modelling and optimization of integrated distributed flow shop scheduling and distribution problems with time windows. Expert Systems with Applications, 187, 115827. DOI 10.1016/j.eswa.2021.115827. [Google Scholar] [CrossRef]

15. Gao, K. Z., Cao, Z. G., Zhang, L., Chen, Z. H., Han, Y. Y. et al. (2019). A review on swarm intelligence and evolutionary algorithms for solving flexible job shop scheduling problems. IEEE/CAA Journal of Automatica Sinica, 6(4), 904–916. [Google Scholar]

16. Fu, Y. P., Hou, Y. S., Wang, Z. F., Wu, X. W., Gao, K. Z. et al. (2021). A review of distributed scheduling problems in intelligent manufacturing systems. Tsinghua Science and Technology, 26(5), 625–645. DOI 10.26599/TST.2021.9010009. [Google Scholar] [CrossRef]

17. Stec, R., Nova, A., Sucha, P., Hanzalek, Z. (2019). Scheduling jobs with stochastic processing time on parallel identical machines. Twenty-Eighth International Joint Conference on Artificial Intelligence, pp. 5628–5634. Macao. [Google Scholar]

18. Al-Khamis, T., M’Hallah, R. (2011). A two-stage stochastic programming model for the parallel machine scheduling problem with machine capacity. Computers & Operations Research, 38(12), 1747–1759. DOI 10.1016/j.cor.2011.01.017. [Google Scholar] [CrossRef]

19. Zhang, R. (2013). A three-stage optimization algorithm for the stochastic parallel machine scheduling problem with adjustable production rates. Discrete Dynamics in Nature and Society, 2013(1), 1–15. DOI 10.1155/DDNS.2005.1. [Google Scholar] [CrossRef]

20. Kang, L. Y., Ng, C. T. (2007). A note on a fully polynomial-time approximation scheme for parallel-machine scheduling with deteriorating jobs. International Journal of Production Economics, 109(1–2), 180–184. DOI 10.1016/j.ijpe.2006.11.014. [Google Scholar] [CrossRef]

21. Cheng, T. C. E., Hsu, C. J., Yang, D. (2011). Unrelated parallel-machine scheduling with deteriorating maintenance activities. Computers & Industrial Engineering, 60(4), 602–605. DOI 10.1016/j.cie.2010.12.017. [Google Scholar] [CrossRef]

22. Jiang, S. J. (2011). Lagrangian relaxation for parallel machine batch scheduling with deteriorating jobs. International Conference on Management of e-Commerce and e-Government, pp. 109–112. Wuhan, China. [Google Scholar]

23. Huang, X., Wang, M. Z. (2011). Parallel identical machines scheduling with deteriorating jobs and total absolute differences penalties. Applied Mathematical Modelling, 35(3), 1349–1353. DOI 10.1016/j.apm.2010.09.013. [Google Scholar] [CrossRef]

24. Zhao, C. L., Tang, H. Y. (2014). Parallel machines scheduling with deteriorating jobs and availability constraints. Japan Journal of Industrial and Applied Mathematics, 31(3), 501–512. DOI 10.1007/s13160-014-0150-8. [Google Scholar] [CrossRef]

25. Na, Y., Kang, L., Sun, T. C., Chao, Y., Wang, X. R. (2014). Unrelated parallel machines scheduling with deteriorating jobs and resource dependent processing times. Applied Mathematical Modelling, 38(19), 4747–4755. [Google Scholar]

26. Mazdeh, M. M., Zaerpour, F., Zareei, A., Hajinezhad, A. (2010). Parallel machines scheduling to minimize job tardiness and machine deteriorating cost with deteriorating jobs. Applied Mathematical Modelling, 34(6), 1498–1510. DOI 10.1016/j.apm.2009.08.023. [Google Scholar] [CrossRef]

27. Mosheiov, G. (2001). Parallel machine scheduling with a learning effect. Journal of the Operational Research Society, 52(10), 1165–1169. DOI 10.1057/palgrave.jors.2601215. [Google Scholar] [CrossRef]

28. Yeh, W. C., Lai, P. J., Lee, W. C., Chuan, M. C. (2014). Parallel-machine scheduling to minimize makespan with fuzzy processing times and learning effects. Information Sciences, 269(10), 142–158. DOI 10.1016/j.ins.2013.10.023. [Google Scholar] [CrossRef]

29. Hidri, L., Mahdi, J. (2020). Near-Optimal solutions and tight lower bounds for the parallel machines scheduling problem with learning effect. Rairo-Operations Research, 54(2), 507–527. DOI 10.1051/ro/2020009. [Google Scholar] [CrossRef]

30. Eren, T. (2009). A bicriteria parallel machine scheduling with a learning effect of setup and removal times. Applied Mathematical Modelling, 33(2), 1141–1150. DOI 10.1016/j.apm.2008.01.010. [Google Scholar] [CrossRef]

31. Toksari Duran, M., Guner, E. (2008). Minimizing the earliness/tardiness costs on parallel machine with learning effects and deteriorating jobs: A mixed nonlinear integer programming approach. The International Journal of Advanced Manufacturing Technology, 38(7), 801–808. [Google Scholar]

32. Han, Y. Y., Li, J. Q., Sang, H. Y., Liu, Y. P., Gao, K. Z. et al. (2020). Discrete evolutionary multi-objective optimization for energy-efficient blocking flow shop scheduling with setup time. Applied Soft Computing, 93, 1–16. DOI 10.1016/j.asoc.2020.106343. [Google Scholar] [CrossRef]

33. Lu, Y. Y., Jin, J., Ji, P., Wang, J. B. (2016). Resource-dependent scheduling with deteriorating jobs and learning effects on unrelated parallel machine. Neural Computing and Applications, 27(7), 1993–2000. DOI 10.1007/s00521-015-1993-x. [Google Scholar] [CrossRef]

34. Amini, A., Niakan, F., Tavakkolimoghaddam, R. (2011). A multi-objective identical parallel machine scheduling with setup and removal times with deteriorating and learning effects. 2011 IEEE International Conference on Industrial Engineering & Engineering Management, pp. 1271–1274. Singapore. [Google Scholar]

35. Arik, O. A., Toksari, M. D. (2018). Multi-objective fuzzy parallel machine scheduling problems under fuzzy job deterioration and learning effects. International Journal of Production Research, 56(7), 2488–2505. DOI 10.1080/00207543.2017.1388932. [Google Scholar] [CrossRef]

36. Rostami, M., Pilerood, A. E., Mazdeh, M. M. (2015). Multi-objective parallel machine scheduling problem with job deterioration and learning effect under fuzzy environment. Computers & Industrial Engineering, 85, 206–215. DOI 10.1016/j.cie.2015.03.022. [Google Scholar] [CrossRef]

37. Chen, J. Z., Wang, H. F., Zhong, R. Y. (2021). A supply chain disruption recovery strategy considering product change under COVID-19. Journal of Manufacturing Systems, 60, 920–927. DOI 10.1016/j.jmsy.2021.04.004. [Google Scholar] [CrossRef]

38. Hatamlou, A., Mirjalili, S., Seyedali, S. M. (2016). Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Computing and Applications, 27(2), 495–513. DOI 10.1007/s00521-015-1870-7. [Google Scholar] [CrossRef]

39. Jalali, S. M. J., Khosravi, A., Kebria, P., Hedjam, R. (2019). Autonomous robot navigation system using the evolutionary multi-verse optimizer algorithm. IEEE International Conference on Systems, Man and Cybernetics, pp. 1221–1226. Bari. DOI 10.1109/SMC.2019.8914399. [Google Scholar] [CrossRef]

40. Wang, Y., Luo, D. K., Zhao, X., Sun, Z. (2018). Estimates of energy consumption in China using a self-adaptive multi-verse optimizer-based support vector machine with rolling cross-validation. Energy, 152(1), 539–548. DOI 10.1016/j.energy.2018.03.120. [Google Scholar] [CrossRef]

41. Al-qaness, M. A. A., Elaziz, M. E. A., Ewees, A. A. E., Cui, X. H. (2019). A modified adaptive neuro-fuzzy inference system using multi-verse optimizer algorithm for oil consumption forecasting. Electronics, 8(10), 1071. DOI 10.3390/electronics8101071. [Google Scholar] [CrossRef]

42. Guo, X. W., Liu, S. X., Zhou, M. C. (2018). Dual-objective program and scatter search for the optimization of disassembly sequences subject to multi resource constraints. IEEE Transactions on Automation Science and Engineering, 15(3), 1091–1103. DOI 10.1109/TASE.2017.2731981. [Google Scholar] [CrossRef]

43. Deb, K., Pratap, A., Agarwal, S., Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182–197. DOI 10.1109/4235.996017. [Google Scholar] [CrossRef]

44. Fu, Y. P., Wang, H. F., Tian, G. D., Li, Z. W., Hu, H. S. (2019). Two-agent stochastic flow shop deteriorating scheduling via a hybrid multi-objective evolutionary algorithm. Journal of Intelligent Manufacturing, 30(5), 2257–2272. DOI 10.1007/s10845-017-1385-4. [Google Scholar] [CrossRef]

45. Zhang, Q. F., Li, H. (2007). A multi objective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 11(6), 712–731. DOI 10.1109/TEVC.2007.892759. [Google Scholar] [CrossRef]