Neutrosophic Adaptive Clustering Optimization in Genetic Algorithm and Its Application in Cubic Assignment Problem

1  Introduction

In optimization theory, heuristic algorithms are mainly used to deal with Non-deterministic Polynomial (NP) problems. The biggest characteristic of NP problems is that it is not certain whether the answer can be found in polynomial time, but it can be verified in polynomial time. In the process of solving NP problems, the control of optimization quality is the key to determining the quality of a given algorithm. Especially, with the rapid development of society, NP problems cover more and more data, and the monitoring of the optimization process is more and more important. Under the aforementioned background, to ensure the quality of the optimization model, this study introduces the neutrosophic fuzzy thought into the heuristic algorithm and achieves good results. For the convenience of introduction, this study presents a neutrosophic adaptive clustering optimization thought in a novel neutrosophic genetic algorithm (NGA).

Generally, a genetic algorithm (GA) includes four steps, i.e., coding, selection, crossover, and mutation. In the selection of individuals in each generation, the classical GA is usually mechanical to determine the proportion of crossover and variation, and cannot adjust the aforementioned proportion adaptively according to the quality of individuals in each generation. To solve this problem, this study creatively introduces the neutrosophic fuzzy thought into GA, makes an intelligent transformation of the GA, and creatively proposes a neutrosophic genetic algorithm (NGA). For convenience, some related works on neutrosophic fuzzy sets (NFSs), GA, utility function, and assignment problems are introduced in the following subsection.

1.1 Relevant Studies

In the past decade, scholars have done lots of exploratory research in the field of NFSs. Sodenkamp et al. [1] proposed a novel method to deal with independent multi-source information in the group decision-making process by using single-valued NFSs. Long et al. [2] proposed a fuzzy clustering method using a kind of neutrosophic association matrix. In the same year, Zavadskas et al. [3] proposed a hedonic shopping rent valuation model by the one-to-one neuro-marketing meth. Afterward, Rashno et al. [4] proposed a novel clustering model based on NFS theory, whose main role is to calculate the boundary points in the clustering process. Abdel-Basset et al. [5] developed an evaluation method under uncertainty of linear time-cost tradeoffs by using NFSs. In the same year, Son et al. [6] proposed a kind of novel optimal control method in a neutrosophic fuzzy environment by using granular computing. Thereafter, Xu et al. [7] proposed a novel decision-making method based on TODIM and TOPSIS with multi-valued NFSs. Rahman et al. [8] introduced a kind of parameterized NFS, and applies it to decision-making fields. These two types of research combine the NFS with the decision-making theory tightly.

As one of the most classical heuristic algorithms, GA has been a concerned by scholars and has made great improvement in the past decade. Andrade et al. [9] introduced a novel multi-parent biased random-key GA and a novel implicit path-relinking procedure. Thereafter, Wang et al. [10] analyzed the Boolean function from the viewpoint of geometric space and proposed a novel GA to construct objective space with high nonlinearity. Guijarro et al. [11] proposed a model that combined a data envelopment analysis model with a GA to handle sector restructuring problems. Su et al. [12] introduced a novel GA with a specific binary space partition tree, which showed good quality in solving eight benchmark problems, fault diagnosis problems, and hybridized with the molecular signatures’ selection problems. In the same year, Ahn et al. [13] put forward a GA for multi-objective feature selection. Koohestani [14] thought that crossover was a very important operator in a GA by which new individuals of the next generation realize time and time again. And then, it proposed a specific crossover operator to solve the problem of variable conversion in combinatorial optimization.

The latest studies regarding utility function have also been taken as foundations for this study. Greve et al. [15] proposed a utility function to calculate the exchange proportion of the monetary value of different products in a management system. Chun et al. [16] proposed a kind of product utility value based on the total performance index method. Meanwhile, a robust utility-based decision model is proposed by Hu et al. [17] to solve the fuzziness and inconsistencies in utility evaluation. Dias et al. [18] studied the generation of the utility function in the random multi-criteria acceptability analysis. This function described how rational consumers make spending decisions. Based on utility function, Niromandfam et al. [19] established the economic demand model of customer risk aversion behavior which considers the influence of incentive payment on power consumption. Mao et al. [20] proposed a comparison of regret and utility-based discrete choice modeling. Afterward, Abraham et al. [21] investigated the problem of utility calculation in wind power generation, hybridized with the main factors influencing utility calculation.

Moreover, some representative research regarding the assignment problem has also been reviewed. Due to the lack of research on the cubic assignment problem (CAP), attention has been paid to the research results on the quadratic assignment problem (QAP) for reference. Duman et al. [22] studied a kind of relative complex assignment problem in circuit board design and introduced a way to solve the given problem. Later, Xia [23] proposed a method using a continuation function to settle the QAP. Meanwhile, Zhang et al. [24] proposed two formula reduction problems for QAP, and studied the effect of constraint reduction hybridized with the effect of variable reduction in a sparse cost matrix. Hafiz et al. [25] proposed a novel probabilistic particle swarm optimization. In addition, Samanta et al. [26] introduced a novel viewpoint on QAP as double target-dependent position-oriented QAP. And then, by combining with the genetic and neighborhood search algorithm, the given problem is solved. Subsequently, Samanta et al. [27] admitted that the QAP was an NP-hard problem, and proposed a quick convergent artificial bee colony algorithm to solve it.

Based on extensive research and the aforementioned research results, this study combines the NFSs and GA organically. For convenience, the objectives and contributions of this study are introduced in the following.

1.2 Objectives and Contributions

In practice, it is hoped that the adopted algorithm is adaptively adjusted according to the specific NP problem to accelerate the optimization and avoid getting trapped into the local optimal solution. Based on the extensive investigation, this study holds that the key to solving the NP problem lies in using modern tools to deal with the multi-source uncertain information in the process of calculation. For example, classical GA includes initialization, individual evaluation, selection operation, crossover operation, mutation operation, and the judgment of termination conditions. Among them, the selection process encountered the most uncertain information, but also the most complex. To treat the encountered uncertainties in all kinds of information in the selection process scientifically, this study introduces neutrosophic thought into GA. Specifically, this study first selects the appropriate subject in the selection process. Then, around the selected subject, the uncertain information in the selection process is divided into three parts, i.e., the truth part, indeterminacy part, and falsity part. Thereafter, the utility function on NFSs is used to integrate the three types of information and calculate the selection proportion.

The main theoretical innovation of this study is to propose a novel NGA. The first characteristic of NGA is to extract the decision framework from GA and combine the optimization with decision-making theories organically. The second characteristic of this study is to calculate the selection proportion in the selection process by using a novel utility function. For convenience, some definitions of GA and NFSs are introduced below.

2  Preliminaries

Definition 1 A GA is a kind of Heuristic algorithm to solve optimization problems of both constrained and unconstrained. By referring to the natural selection process in biology, the classical GA generates a population of feasible solutions (individuals) from generation to generation. In each step, the GA selects individuals randomly from the present population and uses them as parents to generate new individuals for the next generation. Time and time again, the population gets constantly approaching the ideal solution. Through summary and induction, the aforementioned statement can be expressed as

GA=(C,E,P0,M,Φ,Γ,Ψ,N),(1)

where represents the coding methods of individuals E represents the evaluation function of the fitness value of individuals, P0 represents the initial population, M represents population size, Φ represents the operator of selection, Γ represents the operator of the crossover, Ψ represents the operator of the mutation, N represents the termination condition of GA. For the sake of convenience, a schematic diagram of GA is shown in Fig. 1.

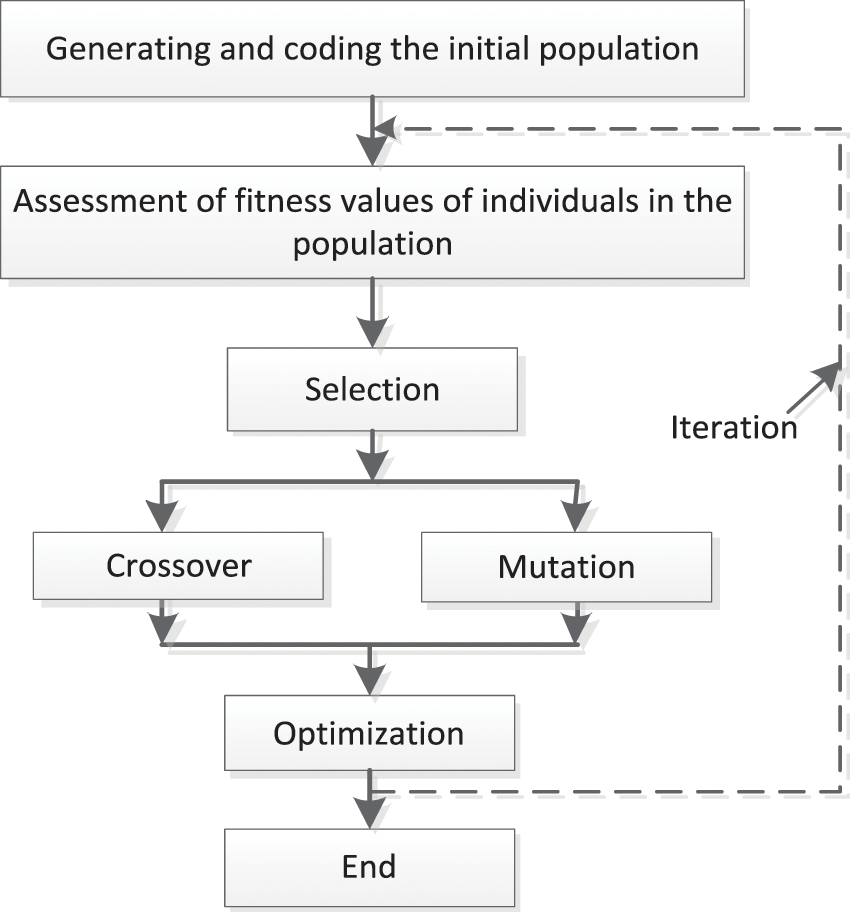
Figure 1: Classical GA process

In the following section, the concept of classical single-valued NFS is introduced. It is noteworthy that this kind of fuzzy set has been widely used in decision making, image process, and medical diagnosis.

Definition 2 Assumes the space of points with a representative element in it denoted by y. An SVNS A on Y is structured by using a truth membership function T A(y), an indeterminacy membership function and a falsity membership function FA(y), where and are all mapping functions from Y to [0,1], whereas 0≤T A(y)+I A(y)+ΓA(y)≤3. Then, an SVNS A is denoted as A(y)={⟨x,T A(y),I A(y),FA(y)⟩|y∈Y}.

For convenience, the single-valued neutrosophic element is denoted as a=⟨T A,I A,FA⟩.

In the following section, by using the proposed concepts and definitions, a novel NGA is proposed to solve the optimization problem in warehouse operation.

3  Main Results

For the sake of convenience, in this following-up subsection, a kind of generalized utility function (GUF) and a specific utility function (UF) on single-valued neutrosophic sets (SVNSs) are introduced as follows.

3.1 GUF on SVNSs

Definition 3 Suppose a single-valued neutrosophic element on Y, which is denoted as

a=⟨T A(y),I A(y),FA(y)⟩.

Then, a kind of GUF on a is denoted as

U(a)=f(T A(y)−FA(y),α2T 2A(y)+(1−α)2F2A(y)α2T A2(y)+I A2λ(y)+(1−α)2FA2(y)),(2)

where fT A′>0, fγ′>0, α∈[0,1].

It is noteworthy that U(⋅) is composed of two independent variables, where one indicates the modulus, whereas the other is

γ2=α2T 2A(y)+(1−α)2F2A(y)α2T A2(y)+I A2λ(y)+(1−α)2FA2(y),

which indicates the proportion of definite information in a.

Definition 4 Suppose a is a single-valued neutrosophic fuzzy number on Y, which is denoted as

a=⟨T A(y),I A(y),FA(y)⟩.

Then, specific UF on is denoted as

Uα(a)=1+(T A(y)−FA(y))⋅α2T 2A(y)+(1−α)2F2A(y)α2T A2(y)+I A2(y)+(1−α)2FA2(y)2,(3)

where is a positive integer which represents the characteristic of users. In industrial production, when users pay more attention to benefits, the parameter α is taken to a larger value; when the user values the cost more, the parameter α is taken to a smaller value. Theoretically, α satisfy

sig(α)={1,T A(y)−FA(y)>0;−1,T A(y)−FA(y)<0.

Especially, when T A(y)−FA(y)>0, α=1, Eq. (2) is reduced as

U1(a)=1+(T A(y)−FA(y))⋅T 2A(y)T A2(y)+I A2(y)2.

When T A(y)−FA(y)<0, α=0, Eq. (2) is reduced as

U0(a)=1+(T A(y)−FA(y))⋅F2A(y)I A2(y)+FA2(y)2.

Based on the above analysis, it gets that is suitable for the users who are benefit first and optimistic, while suitable for the users who are cost-effective and conservative. Moreover, some important properties on are introduced as follows.

Theorem 1 Suppose a=⟨T A(y),I A(y),FA(y)⟩. Then, it gets

Uα(a)=1iff⟨T A(y),I A(y),FA(y)⟩=⟨1,0,0⟩,

and

Uα(a)=0iff⟨T A(y),I A(y),FA(y)⟩=⟨0,0,1⟩.

Theorem 2 Suppose a=⟨T A(y),I A(y),FA(y)⟩. Then, when it gets Uα(a)=12. and Uα(a)=0iff⟨T A(y),I A(y),FA(y)⟩=⟨0,0,1⟩.

Theorem 3 Suppose a=⟨T A(y),I A(y),FA(y)⟩. Then, when T A(y)−FA(y)>0, α=1, it gets U1(a)>12; when T A(y)−FA(y)<0,α=0, it gets U1(a)<12.

Theorem 3 indicates that U1(a) is suitable for an optimistic environment and U0(a) is suitable for a pessimistic environment.

3.2 NGA for Warehouse Operation

Based on combining GA and NFS theories, a novel heuristic algorithm is proposed. For convenience, the benefit-oriented objective is taken as the research object, i.e., the larger the objective function value is, the better the feasible solution. In the following, the studied problem will be introduced firstly.

(i) Problem introduction

In the production activities of enterprises, there are a variety of attributes to be considered, such as risk, efficiency, cost, environmental protection, etc. Suppose that there are n objects Δi(1≤i≤n) to be assigned to n locations ∇j(1≤j≤n) which satisfy that each object is designated to exactly one location. For any given three assignments, i.e., (Δi,∇j),(Δk,∇l),(Δs,∇t), they influence each other. Under the aforementioned multiple attributes, the objective of the given problem is concluded to minimize the comprehensive target of the assignment. Denote the objective of the assignment as γ=∑i,j,k,l,s,t=1nf(xij,xkl,xst) where

xij={1iff Δiis assigned to∇j,0otherwise.

Then, the optimization problem is expressed as

{minγ=∑i,j,k,l,s,t=1nf(xij,xkl,xst),s.t.∑i=1nxij=1,∑j=1nxij=1,∑k=1nxkl=1,∑l=1nxkl=1,∑s=1nxst=1,∑t=1nxst=1,(i,j)≠(k,l),(k,l)≠(s,t),(i,j)≠(s,t),xij∈{0,1},xkl∈{0,1},xst∈{0,1}.(4)

In theories, when n is large enough, it is difficult to find accurate feasible solutions for Eq. (4) in a limited time. Then, the existing heuristics algorithms seek near-optimal solutions at a low cost, where GA is one of these heuristic algorithms.

(ii) Analysis of adaptive clustering

To solve the aforementioned problem using classical GA, one important step is to divide the newly generated offspring of each generation into two parts, where one part is to make the crossover, and the other part is to make mutation. Usually, the criterion of this division is the order of fitness function values of the individuals of the same generation. However, there is a lot of uncertain information which is related to the proportion of division. In classical GA, the proportion is often fixed, which limits the environmental applicability of the classical GA. Furthermore, when the optimization problem changes, it cannot improve the optimization by adaptive adjustment of the proportion. Based on the aforementioned analysis, this study introduces neutrosophic thought to handle the uncertain information in the selection process, and then presents a novel method to adjust the division proportion according to the optimal environment. To illustrate the neutrosophic thought better, the iterative process of individuals between different generations please see Fig. 2.

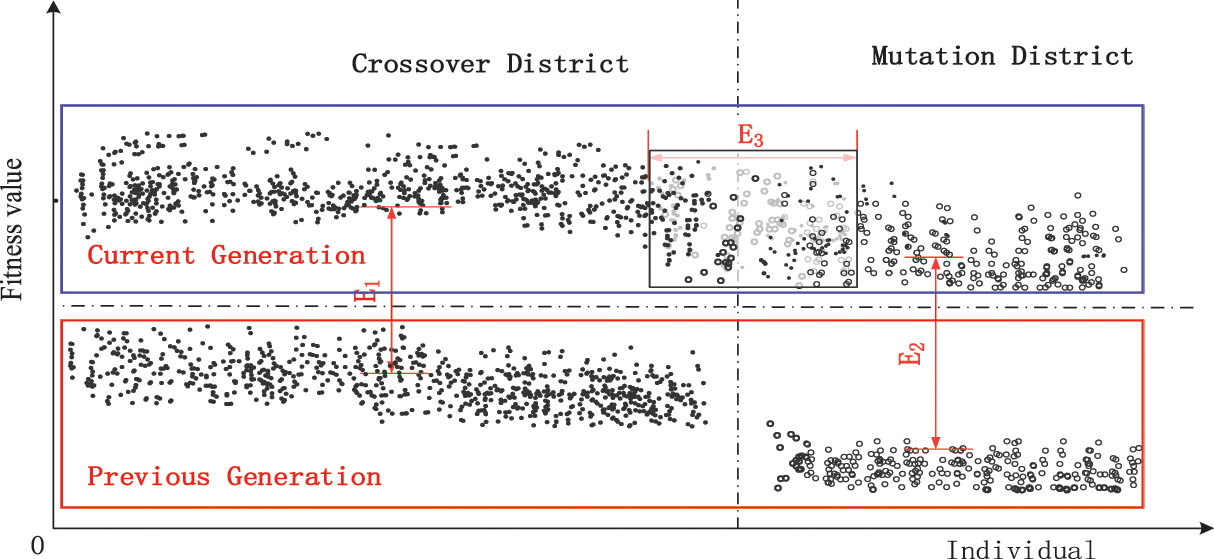
Figure 2: Iteration of individuals from the previous generation to the current generation

As illustrated in Fig. 2, the iteration effect of individuals in the crossover region and the mutation region can be evaluated by many different measurement functions. For convenience, the two aforementioned effects are denoted as E1 and E2, respectively. Meanwhile, the individuals of the previous generation are divided into two parts according to the corresponding proportion of the previous generation, where one is the crossover region, and the other is the variation region. Because the total number of crossover particles and mutation particles is certain, E1 and E2 are competitive. In other words, in the process of particle clustering, E1 and E2 are opposite. If E1 is dealt with as positive, E2 should be dealt with as negative to maintain consistency of logic.

Moreover, after one time crossover and mutation, it can be concluded by calculating the fitness function value that the next generation produced by individuals in the crossover area is not necessarily superior to the corresponding individuals in the mutation area. That is to say, some of the offspring of the individuals in the crossover zone go into the mutation zone, and some of the offspring of the individuals in the mutation zone go into the crossover zone. The penetration of the two parts of invidious into each other’s region reflects the unstructured characteristic of the region segmentation proportion. Let’s call it E3 for convenience. So far, the factors affecting the selection proportion are divided into three parts.

Next, it takes the crossover region as the subject and the variation region as the object, and analyzes the obtained three parameters E1, E2 and E3 from the perspective of neutrosophic thought. From the point of view of the crossover district, it regards the iteration effect as an NFS, which is regarded as the benefit of the NFS, E2 is regarded as the cost of the NFS, and E3 is regarded as the indeterminacy of the NFS. Further, when E1, E2 and E3 are normalized, it can get a standard NFS. Thereafter, by using the utility function, the iterative effect can be characterized by a single value, which can be handled naturally as a division proportion of the next generation of individuals.

Specifically, when E1 is large, the proportion should be a larger value, when E2 is large, the contemporary proportion should be a smaller value, and when E3 is large, the contemporary proportion should be a smaller value, which is exactly in line with the idea of NFS, exactly in line with the idea of utility. This consistency constitutes the theoretical basis of this study.

(iii) Specific steps of NGA

Based on the aforementioned analysis, and by combing NFSs and classical GA theories organically, the introduced model (Eq. (4)) is solved. Specific steps are as follows.

Step 1 Initialization. Set the number of iteration times as n, set the maximum number of iteration times as N, and randomly generate individuals as the initial population X0.

Step 2 Individual evaluations. For any given feasible solution for Eq. (4), it gets a feasible function value γ(x). Denote X0={x0,1,x0,2,⋯,x0,M}, where x0,m(1≤m≤M) represents an individual. By comparing the obtained feasible function values γ(x0,m)(1≤m≤M), the generated individuals are ordered. Denote the ordered X0 as X0′, where X0′={x01′,x02′,⋯,x0M′}. It is noteworthy that for any two x0,m1′ and x0,m2′, it gets x0,m1′≥x0,m2′ on the condition m1>m2,0≤m1,m2,≤M.

Step 3 Select operations. According to the values γ(x0m)(1≤m≤M), divide the initial population X0′ into two parts, where one part is for crossover, and the other part is for mutation. For convenience, the divided two parts are denoted as X01′ and X02′. Set the initial selection proportion as p0, then, it gets

X01′={x0,1′,x0,2′,…,x0,M1′},

X02′={x0,M1+1′,x0,M1+2′,…,x0,M′},

where M1=([p0⋅M]∨0.02)∧0.98, whereas [⋅] represents integral function.

Step 4 Crossover and mutation operations. By using certain crossover operators transferred to X11, where X11={x1,m1,x1,m2,…,x1,M1}. By using mutation operators transferred to X12, where X12={x1,M1+1,x1,M1+1,…,x1,M}.

Step 5 Fuzzification operations. The iteration effect of individuals in the crossover region and the mutation region is expressed as

E11=1M1⋅(∑q=1M1(γ(x1,mq)−γ(x0,mq′)))maxq=1M(γ(x1,mq)−γ(x0,mq′)),(5)

and

E12=1M−M1⋅(∑q=M1+1M(γ(x1,mq)−γ(x0,mq′)))maxq=1M(γ(x1,mq)−γ(x0,mq′)),(6)

respectively.

Meanwhile, denote X1={X11,X12}. by using feasible function value γ(⋅) the individuals of the offspring generation are ordered. Denote the ordered result as X∗1, where X∗1={x∗11,x∗12,…,x∗1M}.

Then, X∗1 is divided into two parts, i.e., X∗11 and X∗12 where

X∗11={x∗1,1,x∗1,2,…,x∗1,M1},X∗12={x∗1,M1+1,x∗1,M1+2,…,x∗1,M},

respectively. The aforementioned unstructured parameter is expressed as

E13=M−M1−Car(X12∩X∗12)M1,(7)

where Car(X12∩X∗12) represents the cardinality of the intersection of X12 and X∗12.

Then, a neutrosophic fuzzy number subject to the effect of crossover is obtained as

a1=⟨T E(X1),I E(X1),FE(X1)⟩=⟨E11E13,E12⟩.(8)

Step 6 Iteration of the division proportion. By referencing Eq. (2), the utility function value of a1 is obtained as

Uα,n(a)=(n+1)(E11−E12)⋅α2E112+(1−α)2E122α2E112+E132+(1−α)2E122−1−(n+1)−21−(n+1)−2.(9)

Denote the iterated selection proportion as p1=Uα,n(a). Then, X∗1 is divided into two parts, i.e., X11′ and X12′ where

X11′={x1,1′,x1,2′,…,x1,M2′},

X12′={x1,M2+1′,x1,M2+2′,…,x1,M′},

where M2=[p1⋅M]. Then, turns to Step 4 and Step 5, successively.

Step 7 Denote n=n+1, if n<N, turn to Step 3, and denote Mn+1=([pn⋅M]∨0.02)∧0.98; if else, select the final optimal solution as xn1′.

(iv) Supplement

To further explain the novel NGA model, some supplementary explanations are provided.

(1)   In Step 5, Eqs. (5) and (6) are proposed to describe the iteration effect of the individuals in crossover district and mutation district, respectively. The essence of E11 and E12 are all mean functions, comparing with the best individual of the same generation. The purpose of the proposed mean function is to improve the overall quality of individuals. Only when the overall quality is improved, can the model break through the local optimal solution more powerfully.

(2)   In Step 6, Eq. (9) is a generalized time-varying function of Eq. (2). By elementary algebra calculation, it gets Uα,1(a)∈[0,1],Uα,1(⟨1,0,0⟩)=1,Uα,1(⟨0,0,1⟩)=1, which are consistent with Eq. (2). However, when E11=E12, it gets

Uα,n(a)=(n+1)−1−(n+1)−21−(n+1)−2,

limn→∞Uα,nE11=E12(a)=limn→∞(n+1)−1−(n+1)−21−(n+1)−2=0.(10)

By Eq. (10), with the increase in time of iteration, the restriction on the crossover is tightened, and the support of mutation is strengthened, which achieves the scheduled planning.

(3)   In Step 3, the threshold function is settled in Mn. Through the threshold function, crossover and mutation can be realized generation by generation, without the sudden termination of crossover or iteration. In essence, the threshold function is a kind of protection for the adaptive adjustment of pn.

4  Illustrative Examples

4.1 Problem Introduction

In this section, a CAP in a dangerous goods warehouse is introduced to verify the proposed NGA model. Assume that there are 14 inbound points to stocking in and 14 outbound points to stocking out. For convenience, the inbound point is denoted as pi(1≤i≤14), the outbound point is denoted as qj(1≤j≤14). Assume that 3 forklifts are assigned to inbound and outbound dangerous goods. Here, inbound and outbound activities are carried out simultaneously. Specifically, the workflow of the forklift is as follows. Firstly, the operating forklift should carry the inbounding hazardous goods from the inbound container. Secondly, the forklift should discharge the goods to the inbound point. Thirdly, the empty forklift should travel to the outbound point directly, and pick up the outbound goods to the outbound container. Fourthly, the forklift should travel back to the inbound container to prepare for the next inbound activity. For convenience, the chain of the aforementioned four operations is named a closed-loop storage chain. The distance for forklifts to travel to finish a closed-loop storage chain depends on the location of the inbound point and outbound point. For any given pi and qj, there is a corresponding closed-loop storage chain whose distance is denoted as lij. Denote the distance of all pairs of (pi,qj)(1≤i,j≤14) as L=(lij)14×14 where the row in L corresponds to the inbound point, and the column in L corresponds to the outbound point. To simplify the calculation, the original distances of the closed-loop storage chains are normalized by using the function

lpik1,qjk2′=lpik1,qjk2−minS1,S2∈MlpiS1,qjS2maxS1,S2∈MlpiS1,qjS2−minS1,S2∈MlpiS1,qjS2∨0.1.

By field investigation, it gets

L′=(lij′)14×14=[0.130.180.130.240.280.280.320.340.540.510.570.540.770.770.090.180.130.210.250.250.280.310.510.470.540.510.770.730.090.180.130.180.210.210.250.280.470.430.510.470.770.730.620.590.600.800.620.190.190.190.440.410.470.410.440.410.090.180.130.180.210.210.250.280.470.430.510.470.770.730.580.550.580.770.130.150.130.190.410.380.440.380.400.380.550.520.550.740.090.120.130.190.380.340.410.340.370.340.550.520.550.740.090.120.130.190.380.340.410.340.370.340.440.410.410.440.060.060.090.030.190.190.190.220.230.200.410.380.380.410.030.030.030.010.130.150.190.190.200.170.310.280.280.310.010.010.030.010.090.120.190.150.170.130.810.780.8110.350.380.350.410.550.580.550.150.130.190.750.720.750.930.290.320.290.340.490.520.490.090.060.120.780.750.780.960.320.350.320.390.520.550.520.120.090.15].

Denote the fixed cost for operation management per hour as Cr, denote the normal speed index of the forklifts as τv, denote the time cost of the operation as Ct=Cr⋅τv−1⋅l′, denote the influence factor of variable speed on operation time as τ1, denote the influence factor of variable speed on fuel cost as τ2, and denote the normal fuel cost index for the forklift to travel as Cf. Assume that the problem is in the off-season of warehousing activities. Therefore, the cost is the only optimization goal. Of course, the cost here includes the opportunity cost caused by the storage accidents. Then, according to the field survey, the comprehensive negative-cost optimization model is obtained as

{maxγ=−(∑is=114∑jt=114xisjt⋅Cf⋅lisjt′+τ1⋅(C143)−1⋅∑is1,jt1=114∑is2,jt2=114∑is3,jt3=114(xis1jt1⋅xis2jt2⋅xis3jt3⋅r(pi1,qj1),(pi2,qj2),(pi3,qj3)′)−τ2⋅(∑is=114∑jt=114xisjt⋅(τv)−1⋅lisjt′−τ3⋅(C143)−1⋅∑is1,jt1=114∑is2,jt2=114∑is3,jt3=114(xis1jt1⋅xis2jt2⋅xis3jt3⋅r(pi1,qj1),(pi2,qj2),(pi3,qj3)′))),s.t.∑is=114xisjt=1,∑jt=114xisjt=1,∑is1=114xis1jt1=1,∑jt1=114xis1jt1=1,∑is2=114xis2jt2=1,∑jt2=114xis2jt2=1,∑is3=114xis3jt3=1,s1≠s2,s1≠s3,s2≠s3,t1≠t2,t1≠t3,t2≠t3,∑jt3=114xis3jt3=1,xisjt∈{0,1},xis1jt1∈{0,1},xis2jt2∈{0,1},xis3jt3∈{0,1}.(11)

It is noteworthy that Eq. (11) is a positive objective function, i.e., negative cost, to be consistent with the optimization environment of this study.

4.2 Optimization Process Using NGA

By using the proposed NGA model, the introduced problem is solved. First of all, a series of parameters are provided. Specifically, it values that τv=3.50, Cf=2.40; τ1=0.05, τ2=0.05, τ3=0.40. Then, by using the proposed NGA, the introduced problem is solved. Specific steps are as follows.

Step 1 Set the number of iteration times as n, set the maximum number of iteration times as N=200, and randomly generate 200 individuals as the initial population X0. For convenience, denote X0={x0,1,x0,2,⋯,x0,200}.

Step 2 For any given feasible solution x for Eq. (11), it gets a feasible function value γ(x). By comparing γ(x0,m)(1≤m≤200), the generated individuals are ordered. Denote the descending ordered X0 as X0′, where X0′={x0,1′,x0,2′,…,x0,200′}.

Step 3 Denote M1=0.80. According to γ(⋅), divide X0′ as X01′ and X02′, respectively.

Step 4 By using certain crossover operator Γ,X01′ is transferred to X11, By using mutation operator Ψ,X02 is transferred as X12.

Step 5 By using Eqs. (5) and (6), the iteration effect of individuals in the crossover region and the mutation region are obtained as E11 and E12, respectively. Denote X1={X11,X12}. Similar to Step 2, and by using γ(⋅),X1 is translated to X∗1. And then, X∗1 is divided as X∗11 and X∗12, respectively. Then, by using Eqs. (7) and (8), E13 and a1 are obtained.

Step 6 For convenience, denote α=0.5. Then, by using Eq. (9), p1 is obtained. Denote M2=[p1⋅M], then, X∗1 is divided into two parts, i.e., X11′ and X12′. Then, turns to Step 4 and Step 5, successively.

Step 7 Denote n=n+1. If n<200, turn to Step 3; if else, select the final optimal solution as x200,1′. Through random test, one optimal process is obtained as Fig. 3, the optimal fitness value is obtained as −4.9319, and the optimal solution is obtained as

x200,1′=(12345678910111213142513846711109121413).

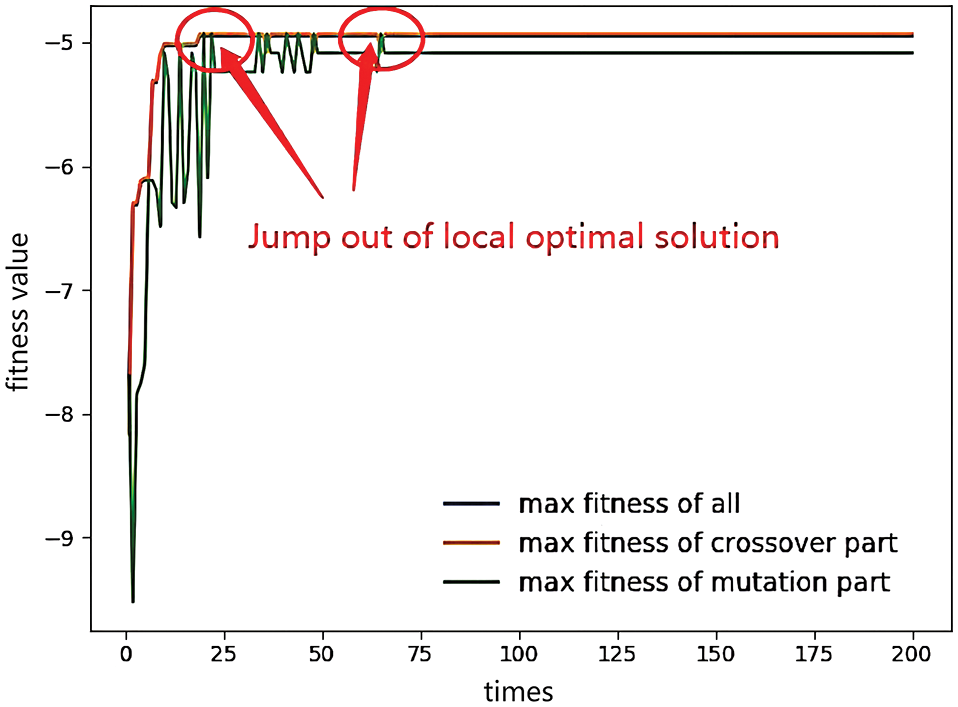
Figure 3: Optimal process

It is noteworthy that in the process of optimization, the NGA breaks through multiple locally optimal solutions by strengthening mutation. The most obvious one occurred in areas A and area B. This shows that the intelligent regulation of the proportion of crossover and mutation has achieved good results.

4.3 Comparative Analysis

In this subsection, based on example calculation, the NGA and classical GA are compared. By comparison, some peculiar characteristics of NGA are described specifically.

(1)   In NGA, the proportion of individuals in crossover and mutation districts is adjusted adaptively according to the effect of crossover and mutation. Correspondingly, in the classical GA, the proportion of crossover and mutation is fixed. Through the adaptive adjustment of the proportion of crossover and mutation, the NGA can strengthen crossover in the early stage of calculation to improve calculation efficiency, while strengthening mutation in the later stage of calculation to improve the ability to break through the local optimal solution. For more details on the change in the proportion, please see Fig. 4.

(2)   The NGA highlights the overall optimization by using the mean function E11 and E12. The calculation shows that through NGA, the overall quality of the population is guaranteed. In particular, the overall quality of the individuals of the 1st, 50th, 100th, 150th and 200th generations is shown in Fig. 5. The average fitness values of all invidious, invidious in crossover district, and invidious in mutation district in different generations are shown in Fig. 6.

(3)   The NGA focuses on the handling of the uncertain information in the optimization process, and realizes the combination of the fuzzy utility function on NFS and GA. Correspondingly, the classical algorithm pays less attention to the information from the thought of Dialectics.

(4)   By using the parameter n in Eq. (10), the NGA realizes the limited control of the optimization trend. Meanwhile, through E11 and E12 in Eq. (10), the NGA realizes the adaptive adjustment of the optimization. In contrast, classical GA is difficult to adjust the genetic strategy in the optimization process.

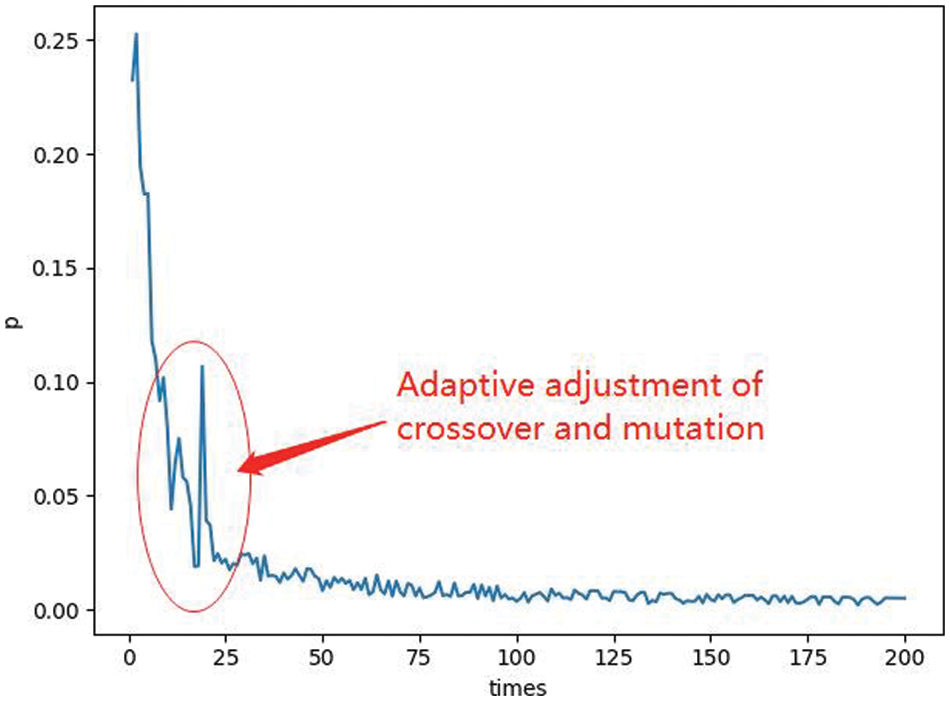
Figure 4: The proportion of crossover and mutation

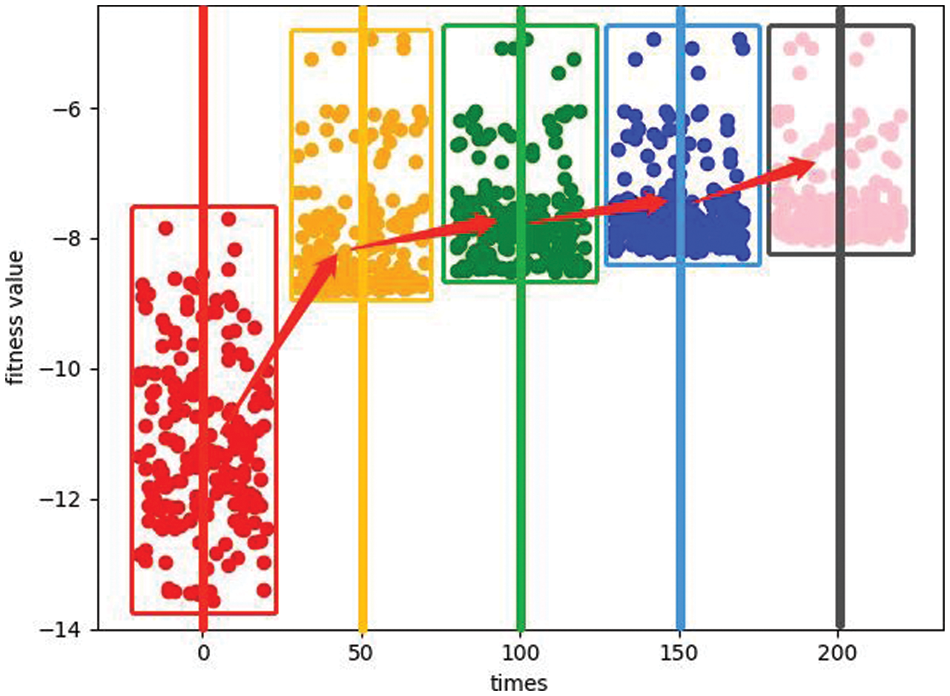
Figure 5: Quality improvement effect of invidious

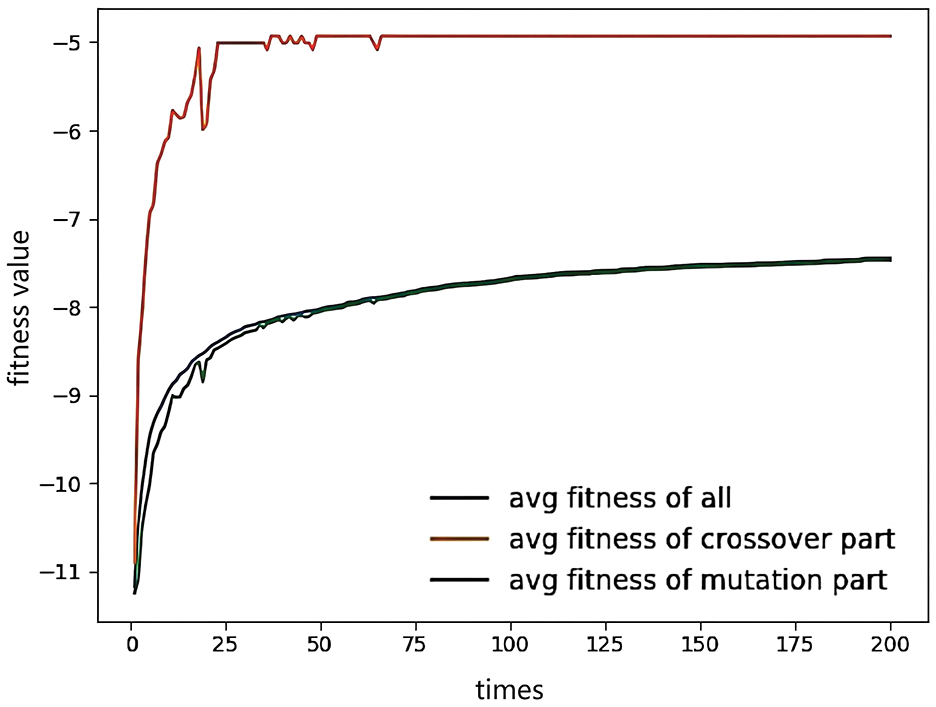
Figure 6: Average fitness function values of three kinds of invidious

In summary, the differences between the proposed NGA and classical GA are listed in Table 1.

5  Conclusions

In this study, a neutrosophic adaptive clustering optimization thought is introduced, and an NGA is also proposed. Generally, the classical GA is too mechanical to select individuals for crossover or variation adaptively. Contrastively, the proposed NGA can do this by using a novel neutrosophic adaptive clustering optimization algorithm. Furthermore, the characteristics of the proposed NGA are illustrated as follows.

Firstly, the novel NGA can adaptively adjust the proportion of crossover and mutation according to the crossover and mutation effects. By adaptively adjusting the mutation rate, the crossover can be strengthened in the early stage and the mutation can be strengthened in the later stage, which increases the ability of the proposed NGA to avoid the local optimal solution.

Secondly, in the crossover process, the crossover of the parent generation and the offspring production of the child generation uses the relative relation of position, which improves the computation speed.

Thirdly, the novel NGA treats the crossover effect as a fuzzy set, where the variation proportion is dealt with as a structural parameter, the crossover effect is dealt with as a benefit parameter and the variation effect is dealt with as a cost parameter. Thereafter, this study creatively proposes the fitness function value of the crossover effect by using utility theory on NFSs.

Fourthly, the threshold function is settled in NGA. Through the adopted threshold function, crossover and mutation can be realized generation by generation. In essence, the threshold function is a kind of protection for NGA. With the help of the proposed threshold function, the smooth operation of NGA is guaranteed.

Finally, this study takes the CAP as an example and compares it with the classical GA to verify the feasibility and effectiveness of the proposed NGA. Moreover, as revealed in this study, heuristic algorithms have the problem of dealing with uncertain information in the process of application, and there are some deficiencies in the automatic adjustment of optimization strategies. These deficiencies can be overcome by the combination of decision-making and optimization technologies. In the future, the latest decision-making technologies, such as intuitionistic fuzzy technology, hesitant fuzzy technology, and neutrosophic fuzzy technology, will be applied in optimization algorithms deeply.

Acknowledgement: The authors are thankful to the editors, and the anonymous reviewers for their constructive comments in improving this study.

Funding Statement: The work of the first author is partially supported by Shanghai Pujiang Program (2019PJC062), the Natural Science Foundation of Shandong Province (ZR2021MG003), the Research Project on Undergraduate Teaching Reform of Higher Education in Shandong Province (No. Z2021046), the National Natural Science Foundation of China (51508319), the Nature and Science Fund from Zhejiang Province Ministry of Education (Y201327642).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Sodenkamp, M. A., Tavana, M., Caprio, D. D. (2018). An aggregation method for solving group multi-criteria decision-making problems with single-valued neutrosophic sets. Applied Soft Computing, 71, 715–727. DOI 10.1016/j.asoc.2018.07.020. [Google Scholar] [CrossRef]

 2.  Long, H. V., Ali, M., Son, L. H., Khan, M., Tu, D. N. T. (2019). A novel approach for fuzzy clustering based on neutrosophic association matrix. Computers & Industrial Engineering, 127, 687–697. DOI 10.1016/j.cie.2018.11.007. [Google Scholar] [CrossRef]

 3.  Zavadskas, E. K., Bausys, R., Kaklauskas, A., Raslanas, S. (2019). Hedonic shopping rent valuation by one-to-one neuromarketing and neutrosophic PROMETHEE method. Applied Soft Computing Journal, 85, 105832. DOI 10.1016/j.asoc.2019.105832. [Google Scholar] [CrossRef]

 4.  Rashno, E., Minaei-Bidgoli, B., Guo, Y. H. (2020). An effective clustering method based on data indeterminacy in neutrosophic set domain. Engineering Applications of Artificial Intelligence, 89, 103411. DOI 10.1016/j.engappai.2019.103411. [Google Scholar] [CrossRef]

 5.  Abdel-Basset, M., Ali, M., Atef, A. (2020). Uncertainty assessments of linear time-cost tradeoffs using neutrosophic set. Computers & Industrial Engineering, 141, 106286. DOI 10.1016/j.cie.2020.106286. [Google Scholar] [CrossRef]

 6.  Son, N. T. K., Dong, N. P., Long, H. V., Son, L. H., Khastan, A. (2020). Linear quadratic regulator problem governed by granular neutrosophic fractional differential equations. ISA Transactions, 97, 296–316. DOI 10.1016/j.isatra.2019.08.006. [Google Scholar] [CrossRef]

 7.  Xu, D., Peng, L. (2021). An improved method based on TODIM and TOPSIS for multi-attribute decision-making with multi-valued neutrosophic sets. Computer Modeling in Engineering & Sciences, 129(2), 907–926. DOI 10.32604/cmes.2021.016720. [Google Scholar] [CrossRef]

 8.  Rahman, A. U., Saeed, M., Alodhaibi, S. S., Khalifa, H. A. E. (2021). Decision making algorithmic approaches based on parameterization of neutrosophic set under hypersoft set environment with fuzzy, intuitionistic fuzzy and neutrosophic settings. Computer Modeling in Engineering & Sciences, 128(2), 743–777. DOI 10.32604/cmes.2021.016736. [Google Scholar] [CrossRef]

 9.  Andrade, C. E., Toso, F. R., Gonçalves, J. F., Resende, M. G. C. (2019). The multi-parent biased random-key genetic algorithm with implicit path-relinking and its real-world applications. European Journal of Operational Research, 289(1), 17–30. DOI 10.1016/j.ejor.2019.11.037. [Google Scholar] [CrossRef]

10. Wang, Y., Zhang, Z. Q., Zhang, L. Y., Feng, J., Gao, J. et al. (2020). A genetic algorithm for constructing bijective substitution boxes with high nonlinearity. Information Sciences, 523, 152–166. DOI 10.1016/j.ins.2020.03.025. [Google Scholar] [CrossRef]

11. Guijarro, F., Martínez-Gómez, M., Visbal-Cadavid, D. (2020). A model for sector restructuring through genetic algorithm and inverse DEA. Expert Systems with Applications, 154(15), 113422. DOI 10.1016/j.eswa.2020.113422. [Google Scholar] [CrossRef]

12. Su, Y. S., Guo, N., Tian, Y., Zhang, X. Y. (2020). A non-revisiting genetic algorithm based on a novel binary space partition tree. Information Sciences, 512, 661–674. DOI 10.1016/j.ins.2019.10.016. [Google Scholar] [CrossRef]

13. Ahn, G., Hur, S. (2020). Efficient genetic algorithm for feature selection for early time series classification. Computers & Industrial Engineering, 142, 106345. DOI 10.1016/j.cie.2020.106345. [Google Scholar] [CrossRef]

14. Koohestani, B. (2020). A crossover operator for improving the efficiency of permutation-based genetic algorithms. Expert Systems with Applications, 151, 113381. DOI 10.1016/j.eswa.2020.113381. [Google Scholar] [CrossRef]

15. Greve, T., Teng, F., Pollitt, M. G., Strbac, G. (2018). A system operator’s utility function for the frequency response market. Applied Energy, 231, 562–569. DOI 10.1016/j.apenergy.2018.09.088. [Google Scholar] [CrossRef]

16. Chun, Y. Y., Lee, K. M., Lee, J. S., Lee, J. Y., Lee, M. H. et al. (2018). Identifying key components of products based on consumer-and producer-oriented ecodesign indices considering environmental impacts, costs, and utility value. Journal of Cleaner Production, 198, 1031–1043. DOI 10.1016/j.jclepro.2018.07.035. [Google Scholar] [CrossRef]

17. Hu, J., Bansal, M., Mehrotra, S. (2018). Robust decision making using a general utility set. European Journal of Operational Research, 269, 699–714. DOI 10.1016/j.ejor.2018.02.018. [Google Scholar] [CrossRef]

18. Dias, L. C., Vetschera, R. (2019). On generating utility functions in stochastic multicriteria acceptability analysis. European Journal of Operational Research, 278, 672–685. DOI 10.1016/j.ejor.2019.04.031. [Google Scholar] [CrossRef]

19. Niromandfam, A., Yazdankhah, A. S. (2020). Modeling demand response based on utility function considering wind profit maximization in the day-ahead market. Journal of Cleaner Production, 251(1), 119317. DOI 10.1016/j.jclepro.2019.119317. [Google Scholar] [CrossRef]

20. Mao, B. Q., Ao, C. L., Wang, J. X., Sun, B. S., Xu, L. S. (2020). Does regret matter in public choices for air quality improvement policies? A comparison of regret-based and utility-based discrete choice modelling. Journal of Cleaner Production, 254(1), 120052. DOI 10.1016/j.jclepro.2020.120052. [Google Scholar] [CrossRef]

21. Abraham, A., Hong, J. R. (2019). Dynamic wake modulation induced by utility-scale wind turbine operation. Applied Energy, 257(1), 114003. DOI 10.1016/j.apenergy.2019.114003. [Google Scholar] [CrossRef]

22. Duman, E., Or, I. (2007). The quadratic assignment problem in the context of the printed circuit board assembly process. Computers & Operations Research, 34, 163–179. DOI 10.1016/j.cor.2005.05.004. [Google Scholar] [CrossRef]

23. Xia, Y. (2010). An efficient continuation method for quadratic assignment problems. Computers & Operations Research, 37, 1027–1032. DOI 10.1016/j.cor.2009.09.002. [Google Scholar] [CrossRef]

24. Zhang, H. Z., Beltran-Royo, C., Constantino, M. (2010). Effective formulation reductions for the quadratic assignment problem. Computers & Operations Research, 37, 2007–2016. DOI 10.1016/j.cor.2010.02.001. [Google Scholar] [CrossRef]

25. Hafiz, F., Abdennour, A. (2016). Particle swarm algorithm variants for the quadratic assignment problems-A probabilistic learning approach. Expert Systems with Applications, 44, 413–431. DOI 10.1016/j.eswa.2015.09.032. [Google Scholar] [CrossRef]

26. Samanta, S., Philip, D., Chakraborty, S. (2018). Bi-objective dependent location quadratic assignment problem. Formulation and solution using a modified artificial bee colony algorithm. Computers & Industrial Engineering, 121, 8–26. DOI 10.1016/j.cie.2018.05.018. [Google Scholar] [CrossRef]

27. Samanta, S., Philip, D., Chakraborty, S. (2019). A quick convergent artificial bee colony algorithm for solving quadratic assignment problems. Computers & Industrial Engineering, 137, 106070. DOI 10.1016/j.cie.2019.106070. [Google Scholar] [CrossRef]