Active Kriging-Based Adaptive Importance Sampling for Reliability and Sensitivity Analyses of Stator Blade Regulator

Nomenclature

AK	Active Kriging
AIS	Adaptive Importance Sampling
AKDE	Adaptive Kernel Density Estimation
AK-IS	AK combined with Importance Sampling
AK-MCS	AK combined with MCS
AK-AIS	Active Kriging-based Adaptive Importance Sampling
C.O.V.	Coefficient of Variation
DS	Directional Simulation
FORM	First-Order Reliability Method
HCF	High Cycle Fatigue
iPDF	Instrumental PDF
IS	Important Sampling
KAIS	Kriging-based Adaptive Importance Sampling
LSF	Limit State Function
M-H	Metropolis Hastings
MCS	Monte Carlo Simulation
MPP	Most Probable Point
MCMC	Markov chain Monte Carlo
MPFRs	Most Probable Failure Region(s)
Meta-IS	Meta-model-based Importance Sampling
PDF	Probability Density Function
SORM	Second-Order Reliability Method

1  Introduction

During the air compression process of aeroengine compressor, stator blade regulator plays a key role in increasing airflow and preventing surge phenomenon [1]. As shown in Fig. 1, by driving the multiple rocker arms in regulator, the blade inlet angle can be adjusted in place quickly. Nevertheless, due to the coupling effects of complex fluid-solid loads and repeated reaction forces from stator blade, high-frequency alternating stress and high cycle fatigue (HCF) failure are inevitably induced in these rocker arms. Engineering practice shows that the HCF failure occurred in multiple rocker arms has become the main failure mode and seriously affects the structural reliability of stator blade regulator [2–9]. Moreover, on account of the multiple uncertainties of material variabilities, load variations and model randomness [10–17], large random behaviors physically emerge in these HCF lives [18–25]. Therefore, it is required to develop reasonable probabilistic analysis methods to address these multiple uncertainties, quantify the stochastic behaviors, and ensure the structural reliability of stator blade regulator.

Figure 1: Schematic diagram of stator blade regulator

For probability analysis problems involving multiple random input variables, the key point is to calculate the following multivariate integral, i.e.,

Pf=Pr{g(x)≤0}=∫g(x)≤0fX(x)dx=∫…∫RnI[g(x)≤0]fX(x)dx(1)

where x is the vector of random input variables; g(x) the limit state function, where g(x) ≤ 0 denotes the failure event; fX(x) the joint probability density function of x; I[·] the failure domain indicator function, having the value 1 if g(x) ≤ 0 and the value 0 otherwise.

To obtain the failure probability by solving Eq. (1), the first-order reliability method (FORM) [26–28], second-order reliability method (SORM) [29,30], moment method [31,32], and Monte Carlo simulation (MCS) [33,34] have been developed and widely used. Unfortunately, for small failure probability (10−3~10−7) problems, a large number of sampling times and real limit state function (LSF) calls need to be generated [35–37], which limits the MCS availability due to the unacceptable sampling efficiency. To reduce the unaffordable computing tasks of the crude MCS method, surrogate model combined with MCS strategy has been emerged [38–47]. As one impressive progress, the active learning Kriging (AK) combined with MCS (AK-MCS) is proposed, which can decrease the required LSF calls by only adding the failure samples in model updating process. Due to the advantages of fast modeling and accurate approximation, AK-MCS is widely used in reliability analysis [48–50]. However, the estimation of small failure probability remains an issue for AK-MCS, since the method still regards the MCS sample pool as the sampling candidate regions. In this case, researchers have found a wise solution to avoid such disadvantages by integrating AK-MCS with variance reduction techniques [51–53]. Wang et al. [54] incorporated multi-ring-based importance sampling into the Kriging. Tong et al. [55] introduced subset simulation importance sampling into the AK model. Zhang et al. [56] combined directional sampling with adaptive Kriging to overcome the limitations of the AK-MCS method.

In recent years, by shifting the sampling center from the origin to the most probable point (MPP), AK combined with importance sampling (AK-IS) can produce satisfactory results as long as the MPP can be well identified. Moreover, it has become hot solution paths in addressing small probability problems [57]. Nonetheless, since only single MPP can be obtained, the traditional AK-IS method can only suitable to limit state functions with one single failure region, which significantly limits its application to multiple failure regions [58,59]. In this case, to address the multiple MPPs or multiple most probable failure regions (MPFRs) in small failure probability problems, by combing AK model to obtain the samples in failure regions and kernel density estimation (KDE) to generate the importance samples, Markov chain Monte Carlo (MCMC) method based on improved Metropolis-Hastings (M-H) algorithm has been developed. Zhao et al. [60] used Markov chain Metropolis algorithm to efficiently generate samples in the failure region. Nassim et al. [61] used MCMC sampling method to explore all the failure regions. Cadini et al. [62] used MCMC and K-means clustering algorithm to identify the multiple-failure regions. Unfortunately, due to the fixed KDE function and great subjectivity in determining the initial state of MCMC [60,62], a large tail error of the kernel density function and unreasonable initial state problems can occur, inevitably decreasing the modeling accuracy.

Under such circumstances, by fitting the implicit LSF with AK model and reducing candidate sample pool with adaptive importance sampling (AIS), a novel AK-AIS method is proposed to address the high-nonlinearity, multiple failure regions, and small failure probability problems. In the proposed method, AK model is adopted to determine the initial state of Markov chain and identify the MPFRs, and the adaptive kernel density estimation (AKDE) function is constructed to generate the candidate importance samples in adaptive reduced sample pool. By sequentially importing samples to update the Kriging model, the reliability and sensitivity indices can be obtained through few real LSF calls. Compared with the current relevant methods [63–65], two computing advantages are accompanied with the AK-AIS method: (1) the AK model guided MCMC procedure can precisely determine the initial state of Markov chain and identify the MPFRs. (2) AKDE function needs fewer candidate samples and smaller candidate regions in model updating. These advantages are validated by two numerical examples and can be exploited in the reliability and sensitivity analyses of stator blade regulator.

The organization of this paper is summarized as follows: The AK-AIS method is expounded in Section 2. In Section 3, the effectiveness of the proposed method is examined by two numerical examples. In Section 4, reliability and sensitivity analyses of stator blade regulator are performed using the proposed method. Some conclusions are summarized in Section 5.

2  The Proposed AK-AIS Method

In this section, to reduce the calls of real LSF and improve the computing accuracy of complex reliability and sensitivity analysis problems, a novel AK-AIS method is presented, which includes the identification of the MPFRs, adaptive importance sampling and the corresponding procedures. The basic principle of the proposed AK-AIS method is illustrated in Fig. 2.

Figure 2: Basic principle of the proposed AK-AIS method

2.1 AK-Based MPFRs Identification

By determining the initial state of Markov chain with AK model and calibrate the boundaries by M-H algorithm, the accurate identification of the MPFRs is realized as follows.

2.1.1 MCMC Initial State Determination

To acquire the precise steady state distribution (i.e., optimal importance sampling density function) in complex reliability and sensitivity problems, the AK model instead of subjective experience [66,67] is employed to determine the initial state of Markov chain. The basic thought is introduced as follows.

(1) Initial Kriging establishment

Considering Latin hypercube sampling (LHS) technique, the initial samples x = [x1, x2, …, xs] and the corresponding responses g0(x) are extracted. Based on the initial sample set D0 = { x, g0(x)} and Kriging tool [68,69], the initial Kriging can be built as

g0(x)=f(x)Tβ+z(x)(2)

where f T(x) = [f1(x), f2(x), …, fm(x)] is the regression basis function; β = [β1, β2, …, βm] the regression coefficient; m the dimension number of regression function; z(x) the local random deviation, which follows Gaussian distribution (0, σ2).

(2) Kriging model update with active learning function

Considering the large-scale randomly generated samples (i.e., 104 samples) as candidate sampling pool, based on active learning function (i.e., U [49], expected feasibility function (EFF) [70], reliability-based expected improvement function (REIF) [71], and REIF2 [71]), the best next sample xk. can be identified and sequentially employed to update Kriging model. Regarding U function as an example, with the best next sample xk=arg⁡mini=1,2,…,N1{U(x)}, the corresponding LSF g(xk) is called and calculated. By adding the sample {xk, gk(x)} into the k-th sample set Dk, the k-th updating Kriging model gk(x) can be acquired as

gk(x)={g0(x)|D0⟶UfunctionActivelearninggk(x)|Dk}(3)

(3) Screening the samples located in failure regions

Based on the updated Kriging model, the failure region samples with g(xi) < 0 (i = 1, 2, …, N) are screened out, and selected as the initial state of Markov chain. These screened samples are denoted as {x1, x2, …, xm} (m = 1, 2, …, l, l ≥ 1). Due to the initial state obtained are determined by the failure samples, the obtained steady state distribution of MCMC would be more accurate than that of subjective experience methods.

Moreover, it should be noted that compared with the direct subjective given initial state of Markov chain, although the additional large candidate sampling pool (i.e., 104 samples) is used to update Kriging model, only few LSF calls are required during the determination of the MCMC initial state.

2.1.2 Calibration of the Multiple Failure Boundaries

During the transition of the Markov chain from one state to another, by introducing an acceptance mechanism, M-H algorithm is adopted to accept the new transition state with a certain probability. With the combination of the state transition probability and acceptance probability, the failure samples can be generated quickly in Markov chain simulation. Considering the distributions of failure samples, the multiple failure boundaries can be accurately calibrated. The main steps are introduced as follows.

(1) Stationary distribution selection

Considering the obtained initial state of Markov chain {x1, x2, …, xm}, to accurately acquire the desired samples in the failure region, and the limit stationary distribution is chosen as the optimal importance sampling density (ISD) hX(x) = IF(x)fX(x)/Pf.

(2) j-th state of Markov chain determination

Regarding the (j−1)-th state x(j-1), the j-th state x(j) can be generated by M-H algorithm. The ratio r of the conditional probability distribution of the candidate state x* to the previous state x(j−1) is defined as

r=h(x∗)h(x(j−1))=IF(x∗)fX(x∗)IF(x(j−1))fX(x(j−1))(4)

According to the improved M-H criterion [72], x* is accepted as the j-th chain state, that is x* = x(j) if r ≥ 1, and vice versa.

(3) Failure boundaries calibration

Repeat Step (2) until M Markov chain states {x(1), x(2), . . . , x(M)} are acquired. Based on Steps (1)–(3), all Markov state samples {x(1), x(2), . . . , x(M)} residing in failure regions are obtained. Regarding the distribution of failure samples, the multiple failure boundaries can be effectively calibrated, and the MPFRs can be accurately identified, which is conducive to construct the efficient probability density sampling function to enhance the sign classification precision in complex reliability and sensitivity analyses.

2.2 Adaptive Importance Sampling

To address the large tail error problem caused by the fixed KDE function and low modeling efficiency problem caused by the large candidate sampling pool in IS method, an adaptive kernel density estimation (AKDE) function is constructed based on the identified MPFRs, and an adaptive reduced sampling pool varying with the fitted Kriging model is established. By combining the AKDE to generate important samples and the adaptive reduction sample pool to reduce candidate important samples, the adaptive importance sampling (AIS) method is proposed to guarantee a small tail error and few calls of real LSF.

2.2.1 Adaptive KDE Function Construction

Considering the generated samples in identified MFPRs, by combing Gaussian kernel function with high robustness and adaptive kernel window width parameter, a width-varying KDE function (i.e., optimal important sampling density function) is built. This function can be regarded as the optimal important sampling density function, which can generate a set of important samples based on discrete random integer interpolation. Since the AKDE function fitted by the samples in identified MFPRs is closer to the optimal sampling density function, the sampling accuracy is promising to be elevated.

Based on the generated samples {x(1), x(2), . . . , x(M)} located in identified MFPRs, by modifying the window width parameter ω and local bandwidth factor λj, the probability density function of those samples can be estimated by the following AKDE function, i.e.,

hX(x)=1M∑j=1M1(ωλj)nK(x−x(j)ωλj)(5)

in which

{ω=Md−1n+4λj={[∏k=1Mf(x(k))]1M/f(x(j))}α(6)

where Md is the number of different samples, Md ≤ M; α the sensitivity factor, 0 ≤ α ≤ 1; x(j) the j-th sample in failure region, j = 1, 2, …, M; M the number of sample points; n the variable dimension; ω the window width parameter; λ the local bandwidth factor; K (·) the KDE function, the frequently-used gauss KDE function [64,72] is expressed as

K(X)=1(2π)n|C|exp⁡(−12XTC−1X)(7)

where C is the covariance matrix of the sample point set {x(1), x(2), . . . , x(M)}, which mainly describes the data dispersion of each sample point in different directions and ranges.

C=∑i=1M(x(j)−x¯)(x(j)−x¯)T(8)

where x¯ is the mean value of these samples.

Assuming that a discrete random integers u obeying uniform distribution on interval [1, M]. If u = j (j = 1, 2, …, M), the kernel density function hj(·) of the j-th component is selected to generate sample xi (i = 1, 2, …, N). hj (·) can be represented as

hj(x)=1(ωλj)nK(x−x(j)ωλj)(9)

where x(j) (j = 1, 2,…, M) are the samples generated by Markov chain. The above sampling process is repeated until N importance samples x1, x2, …, xN are obtained.

The window width parameter controls the smoothness of the AKDE function. By adaptively adjusting the kernel window width in the KDE process, the constructed AKDE function is promising to improve the smoothness degree and accelerate the convergence of the optimal sampling density function, then the desired important samples can be generated precisely.

2.2.2 Candidate Sampling Pool Reduction

Regarding the large candidate importance sampling pool will reduce the finding efficiency of the desired samples, by only selecting the importance samples close to the Kriging-fitted LSF as the candidate sample pool [73], the reduced important sampling pool is proposed. As illustrated in Fig. 3, fG(G) is the joint probability density function of the performance predictions G, the zone near the LSF G(x) = min (g1(x), g2(x)) in the input (X) space ΩxLSF and the output (G) space ΩGLSF can be defined as

Figure 3: Reduction principle of the candidate sampling pool

ΩxLSF={x|G^(x)∈ΩGLSF}(10)

ΩGLSF=ΩG^−τ∩ΩG^+τ(11)

in which

{G^(x)=min(g^1(x),g^2(x))g^i(x)=fT(x)β^+rT(x)R−1(g−Fβ^)(12)

where g indicates the real performance function; g^i the estimated value of the i-th performance function, i = 1, 2; τ the 2-elements vector whose all elements are equal to the threshold value, which can be given according to the actual situation; F the unit column vector; r=[R(x,x1),R(x,x2),…,R(x,xn)]T the correlation vector between an predicted point x and training sample points (x1, x2, …, xn); R the correlation matrix. Based on the definition of zone ΩxLSF and ΩGLSFin Eqs. (10) and (11), the whole candidate important samples pool generated by the AKDE is divided into two parts (inner zone and outer zone). By taking the importance samples inner the zone as candidate samples, the Kriging model is further updated to achieve the accuracy sign prediction of IS samples. The proposed reduction strategy of candidate sample pool has the potential to improve modeling efficiency and accuracy with few calls of real performance function.

With the reduced candidate sampling pool, the number of candidate samples is significantly reduced. Moreover, the reduced candidate sampling pool moves adaptively as the Kriging-fitted LSF updated ceaselessly, which ensures that the desired samples can be precisely found. In addition, since the Kriging update process is based on AK model described in Section 2.1.1, the best fitted LSF can be approached with fewer calls of the real LSF, which can significantly increase the modeling accuracy and efficiency. Once the best fitted LSF is acquired, the unbiased estimation P^f can be expressed as

P^f=1N∑i=1NIF[g(xi)≤0]fX(xi)hX(xi)(13)

where xi denotes the i-th sample points, N the number of candidate samples; fX(x) the joint probability density function of x; hX(x) the importance sampling probability density function; IF(·) the failure domain indicator function, having the value 1 if g(x) ≤ 0 and the value 0 otherwise.

The estimated variance V(P^f) and C.O.V. of P^f can be described as

V(P^f)=1N−1[1N∑i=1NIF[g(xi)≤0]fX2(xi)hX2(xi)−P^f2](14)

Cov(P^f)=V(P^f)P^f(15)

With the samples of input random parameters gained by massive samplings, the local sensitivity index of the failure probability Pf with respect to the distribution parameter θxi, i.e., mean μxi and standard deviation σxi in the normal distribution) of each input variable xi is estimated as

∂P^f∂θxi(k)=1N∑j=1NIF[g(xj)≤0]hX(xj)∂fX(x)∂θxi(k)|x=xj(16)

where xj is the important sampling points, j = 1, 2, …, N; θxi(k) is the k-th distribution parameter of xi; ∂P^f/∂θxi(k) the partial derivative of the k-th distribution parameter of xi.

To assess the effect of xi on the failure probability in its entire distribution ranges, a global sensitivity index is established [74,75] as

δi=E(Pf−Pf|xi)2(17)

where Pf|xi indicates the conditional failure probability, which can be rewritten as the condition expectation of the indicator function

Pf|xi=E(IF|xi)(18)

Therefore, the sensitivity index is transformed into a variance-based index of the indicator function, i.e.,

δi=E{[E(IF)−E(IF|xi)]2}=V[E(IF|xi)](19)

Based on the total variance law

V[E(IF|xi)]=E[E2(IF|xi)]−E2[E(IF|xi)]=E[E2(IF|xi)]−E2(IF)(20)

V(IF)=E(IF2)−E2(IF)=Pf−Pf2≈Pf(k)−(Pf(k))2(21)

where V(·) is the variance value function; V (IF) represents the variance of IF; E(·) the mean value function, E[E2(IF|xi)] is expressed as

{E[E2(IF|xi)]=∑k=1sPr{Xi∈Ak}E2(IF|Xi∈Ak)=∑k=1s[∫AkhXi(xi)dxi]2∫AkfXi(xi)dxi[1mk∑r=1mkIW(xr(k))]2IW(x)=IF(x)fX(x)hX(x)E2(IF)=Pf2≈(Pf(k))2(22)

The normalized version of the main effect index and total effect index are given as

Si=ViV(IF)=V[E(IF|xi)]V(IF)≈1−E[V(IF|xi)]V(IF)(23)

STi=V(IF)−V[E(IF|x−i)]V(IF)=E[V(IF|x−i)]V(IF)(24)

where Si and STi are the main effect index and total effect index of the single input variables xi, respectively.

2.3 AK-AIS Procedure

The flowchart of the proposed algorithm is depicted in Fig. 4. The basic procedure is summarized as follows:

Figure 4: The flowchart of the proposed AK-AIS method

Step 1: Transform input variables into standard normal space.

Step 2: Construct the initial Kriging model. Considering the initial samples set by LHS technique and Kriging toolbox, the initial Kriging model is constructed.

Step 3: Determine the initial state of Markov chain. The Kriging model is updated by active learning function and the initial states of Markov chain are obtained by AK model.

Step 4: Generate failure samples populating all the MPFRs. Based on the initial state of Markov chain, more samples located in the failure region are acquired through M-H algorithm, and all the MPFRs are identified. In this step, none of samples is evaluated with the real performance function.

Step 5: Perform AKDE and generate candidate important samples. A quasi-optimal iPDF for IS is constructed by AKDE, and then a large number of important samples are generated obeying the quasi-optimal iPDF hX(x).

Step 6: Determine adaptive reduced sample pool. Taking the important samples in the reduced pool as candidate samples, the Kriging model is updated again until approaching the real LSF to ensure the prediction accuracy of important sample signs. If the update stop criterion is satisfied, the active learning process stops, and the algorithm goes to Step 7. Otherwise, continue to perform Step 6 to determine the reduced sample pool and update the Kriging model. Note that the AK model in this step is to obtain a high-precision surrogate model to realize the accurate prediction of important sample signs. The AK model in Step 3 is to obtain the initial state of Markov chain. The modeling purposes of the two steps are different. Since the Kriging model has been updated in Step 3, the AK model in this step can quickly approach the real LSF with fewer real LSF calls by combing with the adaptive sample pool reduction strategy.

Step 7: Estimate failure probability, C.O.V. and sensitivity. With the final Kriging model, the failure probability, C.O.V. and sensitivity can be estimated. If the estimated C.O.V. is larger than the requested criterion (i.e., 0.05 in this paper), the procedures will go back and re-execute Step 5. Note that no information about previous true evaluations is lost in Step 7, which prevents the waste of computing resources.

Step 8: End the algorithm and output P^f. If the C.O.V. meets the requirements, the algorithm is stopped, and the final results of failure probability and sensitivity are output.

Noticeably, by precisely identifying the most probable failure regions with AK model and efficiently re-updating the Kriging-fitted LSF by adaptive importance sampling, the proposed AK-AIS method holds the potential to improve the computational efficiency and accuracy for complex reliability and sensitivity analysis problems.

3  Numerical Examples

To demonstrate the accuracy and efficiency of the proposed method, two numerical examples are selected to compare the proposed method with the existing methods. All computations are performed on an Inter(R) Core (TM) Desktop Computer (3 GHz CPU and 16 GB RAM).

3.1 Numerical Example 1 (Series with Three Branches)

The first example is taken from references [65,72]. The performance function with three failure regions is defined as

G(x1,x2)=min{3−1−x2+exp⁡(−x12/10)+(x1/5)432/2−x1⋅x2(25)

where x1 and x2 are two independent standard Gaussian random variables.

To identify the MPFRs using the proposed AK-AIS method, the real LSF functions are called 13 and 25 times to build and update the Kriging model, respectively; in the AIS process, the real LSF functions are further called 13 times to approximate the LSF curves. With 51 (i.e., 13 + 25 + 13) real LSF calls, the failure probability is achieved as 3.39 × 10−3 and the sensitivity indices are listed in Table 1. The comparisons in Fig. 5 illustrate that the MPFRs identification ability is consistent with that of the MCS method even with few real LSF calls. To investigate the effect of the active learning function on the efficacy of the AK-AIS model, several active learning functions are combined with AK-AIS model, whose sampling distributions and fitted LSF curves are depicted in Figs. 6–7, respectively. The results show that: compared with AK-AIS+REIF, AK-AIS+REIF2 and AK-AIS+EFF methods, the AK-AIS+U method can approximate the real LSF with minimal real LSF calls.

Figure 5: Comparison of MCS and the proposed method for example 1

Figure 6: Comparison of active learning function for example 1

Figure 7: Comparison of fitted LSF for example 1

To validate the computational advantages of the proposed method, MCS, FORM, Subset, Meta-IS, MetaAK-IS2, and KAIS are also performed the example. From Table 2 and Fig. 8, we observe that the AK-AIS (with U function) displays the highest accuracy and efficiency than FORM, Subset, Meta-IS, MetaAK-IS2 and KAIS, and its failure probability (3.39 × 10−3) is closest to the reference value (3.35 × 10−3) of MCS. Moreover, as shown in Fig. 8, compared to current methods, AK-AIS holds the minimum computing error of failure probability. Current small failure probability methods like MetaAK-IS2 and KAIS acquire the failure probability are 3.47 × 10−3 and 2.69 × 10−3 by calling real LSF functions with 117 and 163 times, respectively, which consumes more time and lower accuracy than that of the proposed method. Therefore, the proposed AK-AIS method is validated to achieve high computing accuracy at a smaller price than other methods with subjectively given Markov chain initial state.

Figure 8: Comparison of the reliability results for example 1

3.2 Numerical Examples 2 (Series with Four Branches)

The second example [76,77] is a LSF function with four failure regions, which is defined as

G(x1,x2)=min{3+(x1−x2)2/10−(x1+x2)/23+(x1−x2)2/10+(x1+x2)/2(x1−x2)+7/2(x2−x1)+7/2(26)

where x1 and x2 are two independent standard Gaussian random variables.

Using the proposed method, the real LSF are called 10, 19, and 23 times to build, update, and re-update the Kriging model, four failure regions are identified and the adaptive importance sampling is performed, respectively. With 52 (i.e., 10 + 19 + 23) times of real LSF calls, the failure probability is achieved as 2.22 × 10−3 and the sensitivity indices are acquired in Table 3. Compared with MCS method (Fig. 9), the proposed method can well identify four MPFRs at a lower cost. In addition, various active learning functions are combined with AK-AIS, and their sampling distributions and fitted LSF curves are compared in Figs. 10 and 11. Comparison results reveal that the AK-AIS combined with U function exhibits better LSF approximation effect than that of other combining types.

Figure 9: Comparison of MCS and the proposed method for example 2

Figure 10: Comparison of activing learning process for example 2

Figure 11: Comparison of LSF for example 2

To validate the computational advantages of the proposed method, Table 4 and Fig. 12 compare the numerical results acquired from MCS, FORM, DS, Subset, SMART, MetaAK-IS2, and the proposed method. The AK-AIS (with U function) only needs 52 Ncall to achieve the highest sign prediction and lowest coefficient of variation, which shows better computing efficacy than DS, Subset, SMART, and MetaAK-IS2. As revealed in Fig. 12, although AK-AIS has the same failure probability with that of DS, Subset, and MetaAK-IS2; AK-AIS method has lower coefficient of variation and less calls to real performance function. Moreover, for MetaAK-IS2 method with subjectively determining the initial state by engineering experience, it should call the real LSF 138 times to reach the equivalent accuracy as AK-AIS method. In summary, in four failure regions cases, the proposed method holds a strong competitive advantage on computing accuracy and efficiency.

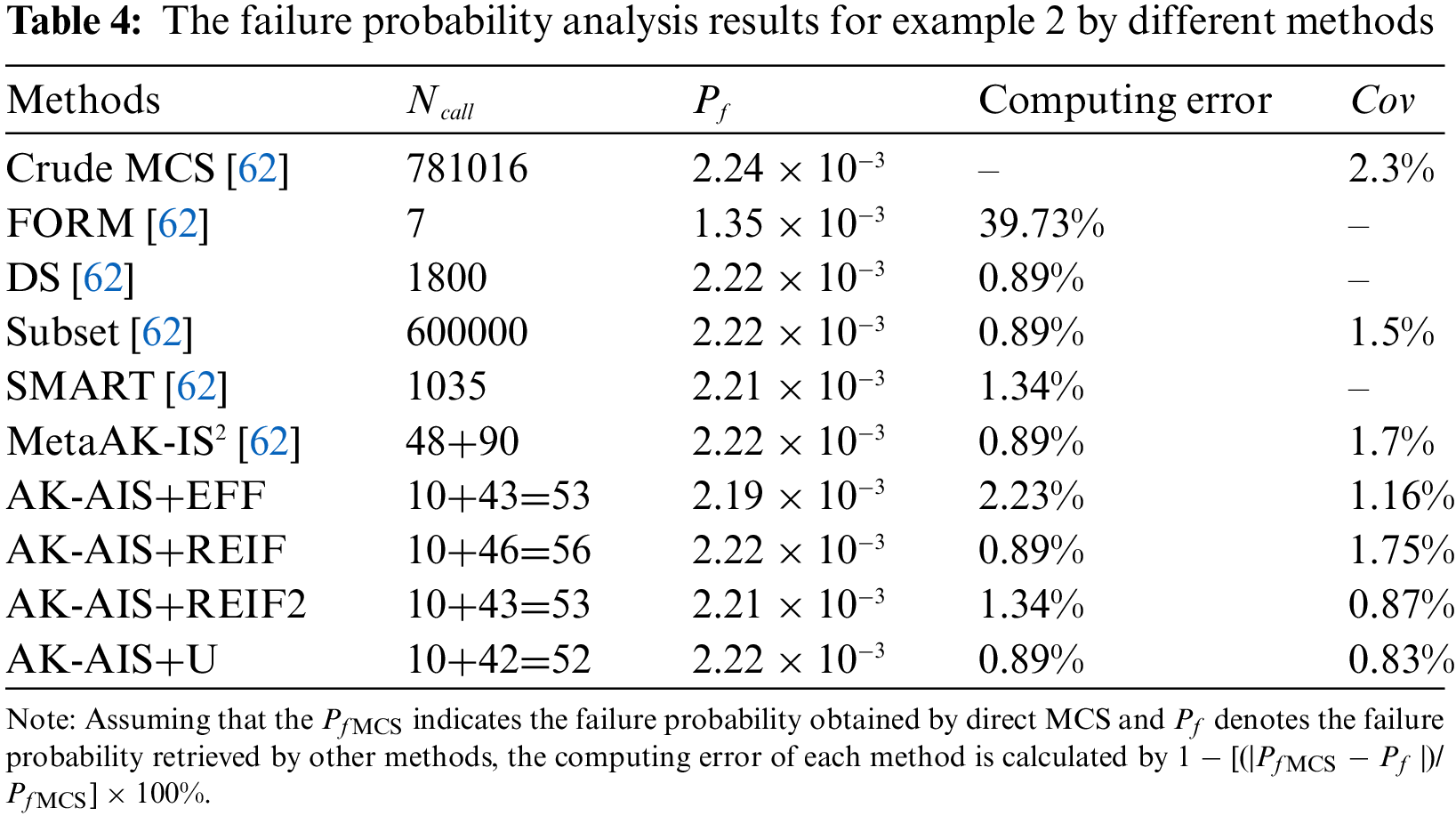
Figure 12: Comparison of the reliability results for example 2

4  Application: Reliability and Sensitivity Analyses of Stator Blade Regulator

Under the multiple uncertain parameters of flexible deformation, joint friction and multi-physics loads, the HCF life of stator blade regulator exhibits large dispersion, which seriously affects the fatigue reliability and security, and prone to HCF failure. A typical stator blade regulator with TC4 titanium alloy is illustrated in Fig. 13. To precisely quantify the dispersion of HCF life and evaluate the security performance, fatigue reliability and sensitivity analyses for the above-mentioned stator blade regulator is performed using the proposed AK-AIS method.

Figure 13: Rigid-flexible coupling schematic diagram of stator blade regulator

4.1 Material Preparations

According to the operating loads, material properties and model parameters pose important influence to the HCF life dispersion of stator blade regulator, the gas temperature T, thermal conductivity λ, expansion coefficient α, aerodynamic torque τ, elastic modulus E, material density ρ, Poisson's ratio u, friction coefficient mu, material constants γ, β, S0 are chosen as the input random variables, their mean values and standard variances are μ = [150°C, 8.02 W/(m°C), 9.15 × 10−6°C, 840 N·mm, 110 GPa, 4.44 × 10−9 t/mm−3, 0.34, 0.2, 12.23, −3.53, 120] and std = [3°C, 0.148 W/(m°C), 0.182 × 10−6°C, 16.8 N·mm, 2.2 GPa, 0.088 × 10−9 t/mm−3, 0.0068, 0.004, 0.0014, 0.0188, 28.62] [78,79], respectively. Assuming that all the selected physical random variables and model random variables obey mutually independent normal distribution. During the operation of stator blade regulator, two or more rocker arms may simultaneously undergo HCF failure. In this case, to simplify the computational complexity, HCF failure of two rocker arms are considered in this study, the series system with two failure units are given as

g(T,λ,α,τ,E,ρ,u,mu,γ,β,S0)=min{g1(T,λ,α,τ,E,ρ,u,mu,γ,β,S0),g2(T,λ,α,τ,E,ρ,u,mu,γ,β,S0)}s.t.g1(T,λ,α,τ,E,ρ,u,mu,γ,β,S0)=N−N1(X)g2(T,λ,α,τ,E,ρ,u,mu,γ,β,S0)=N−N2(X)(27)

where X = {T, λ, α, τ, E, ρ, u, mu, γ, β, S0}; N denotes the allowable life; N1 (X), N2 (X) the fatigue life of two components, which can be obtained by rigid-flexible coupling model of stator blade regulator (i.e., the real LSF) [2,5].

4.2 AK-AIS Modeling

According to Latin hypercube sampling (LHS) technique and the distributed traits of input variables, 65 groups of input variables are extracted, and the corresponding real outputs (fatigue life N1 and N2) are acquired by calling rigid-flexible coupling model. Based on the 65 groups of input variables and output responses, the initial Kriging model is established. Subsequently, with 48 and 371 times calls the complex rigid-flexible coupling model, the Kriging model is gradually updated, and re-updated to the real LSF. With the obtained Kriging-fitted LSF curves, the nephograms of the relationship between output responses and partial variables are drawn in Fig. 14. It can be found that all the nephograms appear high-nonlinearity between responses and partial parameters, which reveals that the reliability and sensitivity analysis of stator blade regulator is a highly nonlinear problem.

Figure 14: Relationship nephograms of output response with partial variables

4.3 Reliability and Sensitivity Analyses

Based on the LHS technique, 10,000 samples are generated and imported into the Kriging-fitted LSF curves instead of the complex rigid-flexible coupling model. Then, the marginal probability distributions of mean stress σm and fatigue life Nf can be acquired, as shown in Figs. 15 and 16, respectively. The relationships between HCF life and partial uncertainties are quantified utterly in Fig. 17. With the obtained Kriging-fitted LSF curves, the sensitivities and effect probability of input variables on fatigue failure are revealed. According to Fig. 18 and Table 5, we find that the material constants γ, β, aerodynamic torque τ and gas temperature T are the dominant factors affecting the HCF failure of stator blade regulator.

Figure 15: Stress probability distribution of multiple components

Figure 16: HCF life probability distribution of multiple components

Figure 17: Scatter correlation sketches of HCF life

Figure 18: Sensitivity analysis results of stator blade regulator HCF failure

4.4 Methods Comparison

To verify the advantages of the proposed AK-AIS method, we compare the failure probability analysis results with MCS, FORM and AK-MCS. As shown in Table 6, the failure probability obtained by AK-AIS is closer to the MCS reference value than that of FORM and AK-MCS. More importantly, the proposed method only calls 484 times of the real LSF. On the contrary, MCS and AK-MCS methods require 10,000 and 498 calls of the real LSF, respectively. Consequently, the proposed AK-AIS method can achieve higher failure probability by fewer calls to the real LSF, which provides a way to address the complex reliability and sensitivity analyses problems with high-nonlinearity, multiple failure regions, and small failure probability.

5  Conclusions

To address the high-nonlinearity, multi-failure regions, and small failure probability problems in reliability and sensitivity analyses of stator blade regulator, by combining the advantages of active Kriging (AK), Markov chain Monte Carlo (MCMC), adaptive kernel density estimation (AKDE) and importance sampling (IS), a novel active Kriging-based adaptive importance sampling (AK-AIS) method is developed. The proposed method is validated by two numerical examples with multiple failure regions and then is applied to a typical reliability and sensitivity analysis of aero-engine stator blade regulator. Some conclusions are summarized as follows:

(1) Numerical examples verify that the proposed AK-AIS method holds high accuracy and efficiency in MPFRs identification and the Markov chain initial state determination.

(2) Application case indicates that the proposed method can efficiently and accurately accomplish the reliability and sensitivity analysis of stator blade regulator. Moreover, it has been found that the material constant γ, β, aerodynamic torque τ and gas temperature T poses the most impact on the failure probability of stator blade regulator.

(3) The proposed method is suitable for the complex reliability and sensitivity analyses with high-nonlinearity, multiple failure regions, and small failure probability, which provides theoretical guidance for determining the initial state of Markov chain in complex engineering.

Although the study provides a feasible and efficient approach for the reliability and sensitivity analyses of stator blade regulators, limitations do exist. Most deviations from expected solution can be attributed to incomplete factors considered in this study. According to the present study and the questions raised, the following problems require to be addressed for further application of the proposed approach in future.

(1) To improve the computing quality of complex mechanism reliability analysis, more additional factors (design tolerance, performance degradation, vibration mechanics, and so forth) should be analyzed and investigated.

(2) To further improve the computational efficiency of reliability analysis with high-dimensional, small failure probability problem, a more effective method to determine the initial state of Markov chain needs to be further studied.

(3) An advanced kernel function should be adopted in high precision kernel sampling density function, such as Gaussian linear mixture kernel function, ANOVA Kernel, and Sigmoid Kernel.

Funding Statement: This work was supported by the National Natural Science Foundation of China under Grant Nos. 52105136, 51975028, China Postdoctoral Science Foundation under Grant [No. 2021M690290], the National Science and Technology Major Project under Grant No. J2019-IV-0002-0069.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Wirkowski, P. (2007). Influence of changes of axial compressor variable stator vanes setting on gas turbine engine work. Journal of Polish CIMAC, 2(2), 511-517. [Google Scholar]
2. Babich, D., Bastun, V., & Dorodnykh, T. (2019). Structural-probabilistic modeling of fatigue failure under elastic-plastic deformation. International Journal of Structural Integrity, 10(4), 484-496. [Google Scholar] [CrossRef]
3. Meng, D. B., Yang, S. Q., Zhang, Y., & Zhu, S. P. (2019). Structural reliability analysis and uncertainties-based collaborative design and optimization of turbine blades using surrogate model. Fatigue & Fracture of Engineering Materials & Structures, 42(6), 1219-1227. [Google Scholar] [CrossRef]
4. Ye, W. L., Zhu, S. P., & Niu, X. P. (2021). Fatigue life prediction of notched components under size effect using stress gradient-based approach. International Journal of Fracture, 126(6), 249–261. [Google Scholar] [CrossRef]
5. Liu, X., Zhang, Y., Xie, S., Zhang, Q., & Guo, H. (2021). Fatigue failure analysis of express freight sliding side covered wagon based on the rigid-flexibility model. International Journal of Structural Integrity, 12(1), 98-108. [Google Scholar] [CrossRef]
6. Song, L. K., Fei, C. W., Bai, G. C., & Yu, L. C. (2017). Dynamic neural network method-based improved PSO and BR algorithms for transient probabilistic analysis of flexible mechanism. Advanced Engineering Informatics, 33(7), 144-153. [Google Scholar] [CrossRef]
7. Gao, J. X., & Yuan, Y. P. (2020). Probabilistic modeling of stiffness degradation for fiber reinforced polymer under fatigue loading. Engineering Failure Analysis, 116(1), 104733. [Google Scholar] [CrossRef]
8. Zhu, S. P., Hao, Y. Z., Correia, J. A. D., & Lesiuk, G. (2019). Nonlinear fatigue damage accumulation and life prediction of metals: A comparative study. Fatigue & Fracture of Engineering Materials & Structures, 42(6), 1271-1282. [Google Scholar] [CrossRef]
9. Zhao, T. Y., Cui, Y. S., Pan, H. G., Yuan, H. Q., & Yang, J. (2021). Free vibration analysis of a functionally graded graphene nanoplatelet reinforced disk-shaft assembly with whirl motion. International Journal of Mechanical Sciences, 197, 106335. [Google Scholar] [CrossRef]
10. Liu, Y. M., Lu, Z. Z., & Xu, J. F. (2012). A simple analytical crack tip opening displacement approximation under random variable loadings. International Journal of Fracture, 173(2), 189-201. [Google Scholar] [CrossRef]
11. Meng, D. B., Hu, Z. G., Guo, J. B., Lv, Z. Y., & Xie, T. W. (2021). An uncertainty-based structural design and optimization method with interval Taylor expansion. Structures, 33(1), 4492-4500. [Google Scholar] [CrossRef]
12. Song, L. K., Bai, G. C., & Li, X. Q. (2021). A novel metamodelling approach for probabilistic LCF estimation of turbine disk. Engineering Failure Analysis, 120(10), 105074. [Google Scholar] [CrossRef]
13. Zhao, T. Y., Ma, Y., Zhang, H. Y., Pan, H. G., & Cai, Y. (2021). Free vibration analysis of a rotating graphene nanoplatelet reinforced pre-twist blade-disk assembly with a setting angle. Applied Mathematical Modelling, 93(10), 578-596. [Google Scholar] [CrossRef]
14. Zhang, W., Liu, T., Xi, A., & Wang, Y. N. (2018). Resonant responses and chaotic dynamics of composite laminated circular cylindrical shell with membranes. Journal of Sound and Vibration, 423(4), 65-99. [Google Scholar] [CrossRef]
15. Yu, S., Wang, Z. L., & Zhang, K. W. (2018). Sequential time-dependent reliability analysis for the lower extremity exoskeleton under uncertainty. Reliability Engineering and System Safety, 170(5–6), 45-52. [Google Scholar] [CrossRef]
16. Zhu, S. P., Keshtegar, B., Trung, N. T., Yaseen, Z. M., & Bui, D. T. (2021). Reliability-based structural design optimization: Hybridized conjugate mean value approach. Engineering with Computers, 37(1), 381-394. [Google Scholar] [CrossRef]
17. Zhang, Y. F., Liu, T., & Zhang, W. (2020). Nonlinear resonant responses, mode interactions, and multitime periodic and chaotic oscillations of a cantilevered pipe conveying pulsating fluid under external harmonic force. Complexity, 2020, 9840860. [Google Scholar] [CrossRef]
18. Nya, R. M., Abdullah, S., & Singh, S. S. K. (2019). Reliability-based fatigue life of vehicle spring under random loading. International Journal of Structural Integrity, 10(5), 737-748. [Google Scholar] [CrossRef]
19. Zhu, S. P., Liao, D., Liu, Q., Correia, J. A. F. O., & Jesus, A. M. P. D. (2019). Nonlinear fatigue damage accumulation: Isodamage curve-based model and life prediction aspects. International Journal of Fatigue, 128(12), 105185. [Google Scholar] [CrossRef]
20. Kebir, T., Correia, J. A. F. O., Benguediab, M., & Jesus, A. M. P. D. (2021). Numerical study of fatigue damage under random loading using rainflow cycle counting. International Journal of Structural Integrity, 12(3), 408-418. [Google Scholar] [CrossRef]
21. Wang, B. W., Tang, W. Z., Song, L. K., & Bai, G. C. (2020). PSO-LSSVR: A surrogate modeling approach for probabilistic flutter evaluation of compressor blade. Structures, 28(1), 1634-1645. [Google Scholar] [CrossRef]
22. Song, L. K., & Bai, G. C. (2020). Multi-surrogate collaboration approach for creep-fatigue reliability assessment of turbine rotor. IEEE Access, 8, 39861-39874. [Google Scholar] [CrossRef]
23. Song, L. K., Bai, G. C., & Fei, C. W. (2019). Dynamic surrogate modeling approach for probabilistic creep-fatigue life evaluation of turbine disks. Aerospace Science and Technology, 95(10), 105439. [Google Scholar] [CrossRef]
24. Li, X. Q., Song, L. K., & Bai, G. C. (2022). Deep learning regression-based stratified probabilistic combined cycle fatigue damage evaluation for turbine bladed disks. International Journal of Fatigue, 159(7), 106812. [Google Scholar] [CrossRef]
25. Gao, J. X., Yuan, Y. P., & Xu, R. X. (2021). A framework for fatigue life prediction of materials under the multi-level cyclic loading. Engineering Failure Analysis, 127(2), 105496. [Google Scholar] [CrossRef]
26. Zhu, S. P., Keshtegar, B., Seghier, M. E. A. B., Zio, E., & Taylan, O. (2022). Hybrid and enhanced PSO: Novel first order reliability method-based hybrid intelligent approaches. Computer Methods in Applied Mechanics and Engineering, 393, 114730. [Google Scholar] [CrossRef]
27. Zhu, S. P., Keshtegar, B., Chakraborty, S., & Trung, N. T. (2020). Novel probabilistic model for searching most probable point in structural reliability analysis. Computer Methods in Applied Mechanics and Engineering, 366(1), 113027. [Google Scholar] [CrossRef]
28. Zhu, S. P., Keshtegar, B., Bagheri, M., Hao, P., & Trung, N. T. (2020). Novel hybrid robust method for uncertain reliability analysis using finite conjugate map. Computer Methods in Applied Mechanics and Engineering, 371, 113309. [Google Scholar] [CrossRef]
29. Wang, B. W., Tang, W. Z., Song, L. K., & Bai, G. C. (2022). Dynamic meta-modeling method to assess stochastic flutter behavior in turbomachinery. Computer Modeling in Engineering & Sciences, 2022, [Google Scholar] [CrossRef]
30. Tawfik, M. E., Bishay, P. L., & Sadek, E. E. (2018). Neural network-based second order reliability method (NNBSORM) for laminated composite plates in free vibration. Computer Modeling in Engineering & Sciences, 115(1), 105-129. [Google Scholar] [CrossRef]
31. Zhi, P., Xu, Y., & Chen, B. (2020). Time-dependent reliability analysis of the motor hanger for EMU based on stochastic process. International Journal of Structural Integrity, 11(3), 453-469. [Google Scholar] [CrossRef]
32. Deng, K., Song, L. K., Bai, G. C., & Li, X. Q. (2022). Improved Kriging-based hierarchical collaborative approach for multi-failure dependent reliability assessment. International Journal of Fatigue, 160(8), 106842. [Google Scholar] [CrossRef]
33. Meng, D. B., Xie, T. W., Wu, P., He, C., & Hu, Z. G. (2021). An uncertainty-based design optimization strategy with random and interval variables for multidisciplinary engineering systems. Structures, 32(1), 997-1004. [Google Scholar] [CrossRef]
34. Meng, D. B., Yang, S. Y., Lin, T., Wang, J. P., & Yang, H. F. (2022). RBMDO using gaussian mixture model-based second-order mean-value saddlepoint approximation. Computer Modeling in Engineering & Sciences, 132(2), 553-568. [Google Scholar] [CrossRef]
35. Luo, C., Keshtegar, B., Zhu, S. P., Taylan, O., & Niu, X. P. (2022). Hybrid enhanced Monte Carlo simulation coupled with advanced machine learning approach for accurate and efficient structural reliability analysis. Computer Methods in Applied Mechanics and Engineering, 388(11), 114218. [Google Scholar] [CrossRef]
36. Li, X. Q., Song, L. K., Bai, G. C. (2022). Vectorial surrogate modeling approach for multi-failure correlated probabilistic evaluation of turbine rotor. Engineering with Computers. DOI 10.1007/s00366-021-01594-2. [CrossRef]
37. Li, X. Q., Song, L. K., & Bai, G. C. (2022). Recent advances in reliability analysis of aeroengine rotor system: A review. International Journal of Structural Integrity, 13(1), 1-29. [Google Scholar] [CrossRef]
38. Song, L. K., Fei, C. W., Wen, J., & Bai, G. C. (2017). Multi-objective reliability-based design optimization approach of complex structure with multi-failure modes. Aerospace Science and Technology, 64(5), 52-62. [Google Scholar] [CrossRef]
39. Song, L. K., Wen, J., Fei, C. W., & Bai, G. C. (2018). Distributed collaborative probabilistic design of multi-failure structure with fluid-structure interaction using fuzzy neural network of regression. Mechanical Systems and Signal Processing, 104(5), 72-86. [Google Scholar] [CrossRef]
40. Meng, D. B., Lv, Z. Y., Yang, S. Y., Wang, H. T., & Xie, T. W. (2021). A time-varying mechanical structure reliability analysis method based on performance degradation. Structures, 34(2), 3247-3256. [Google Scholar] [CrossRef]
41. Wang, Y. H., Zhang, C., Su, Y. Q., Shang, L. Y., & Zhang, T. (2020). Structure optimization of the frame based on response surface method. International Journal of Structural Integrity, 11(3), 411-425. [Google Scholar] [CrossRef]
42. Song, L. K., Bai, G. C., Li, X. Q., & Wen, J. (2021). A unified fatigue reliability-based design optimization framework for aircraft turbine disk. International Journal of Fatigue, 152(10), 106422. [Google Scholar] [CrossRef]
43. Zhang, D., Zhang, N., Ye, N., Fang, J., & Han, X. (2021). Hybrid learning algorithm of radial basis function networks for reliability analysis. IEEE Transactions on Reliability, 70(3), 887-900. [Google Scholar] [CrossRef]
44. Song, L. K., Bai, G. C., & Fei, C. W. (2019). Multi-failure probabilistic design for turbine bladed disks using neural network regression with distributed collaborative strategy. Aerospace Science and Technology, 92(2), 464-477. [Google Scholar] [CrossRef]
45. Song, L. K., Bai, G. C., & Fei, C. W. (2019). Probabilistic LCF life assessment for turbine discs with DC strategy-based wavelet neural network regression. International Journal of Fatigue, 119(9), 204-219. [Google Scholar] [CrossRef]
46. Meng, D. B., Li, Y., He, C., Guo, J. B., & Lv, Z. Y. (2021). Multidisciplinary design for structural integrity using a collaborative optimization method based on adaptive surrogate modelling. Materials & Design, 206(2), 109789. [Google Scholar] [CrossRef]
47. Li, X. Q., Bai, G. C., Song, L. K., & Wen, J. (2021). Fatigue reliability estimation framework for turbine rotor using multi-agent collaborative modelling. Structures, 29(10), 1967-1978. [Google Scholar] [CrossRef]
48. Soubra, A. H., Al-Bittar, T., Thajeel, J., & Ahmed, A. (2019). Probabilistic analysis of strip footings resting on spatially varying soils using kriging metamodeling and importance sampling. Computers and Geotechnics, 114(5), 103107. [Google Scholar] [CrossRef]
49. Echard, B., Gayton, N., & Lemaire, M. (2011). AK-MCS: An active learning reliability method combining Kriging and Monte Carlo simulation. Structural Safety, 33(2), 145-154. [Google Scholar] [CrossRef]
50. Su, M. J., Xue, G. F., Wang, D. Y., Zhang, Y. S., & Zhu, Y. (2020). A novel active learning reliability method combining adaptive Kriging and spherical decomposition-MCS (AK-SDMCS) for small failure probabilities. Structural and Multidisciplinary Optimization, 62(6), 3165-3187. [Google Scholar] [CrossRef]
51. Echard, B., Gayton, N., Lemaire, M., & Relun, N. (2013). A combined importance sampling and Kriging reliability method for small failure probabilities with time-demanding numerical models. Reliability Engineering and System Safety, 111(1), 232-240. [Google Scholar] [CrossRef]
52. Dubourg, V., Sudret, B., & Bourinet, J. M. (2011). Reliability-based design optimization using Kriging surrogates and subset simulation. Structural and Multidisciplinary Optimization, 44(5), 673-690. [Google Scholar] [CrossRef]
53. Depina, I., Le, T. M. H., Fenton, G., & Eiksund, G. (2016). Reliability analysis with metamodel line sampling. Structural Safety, 60(4), 1-15. [Google Scholar] [CrossRef]
54. Wang, J., Sun, Z. L., Cao, R. N., & Yan, Y. T. (2020). An efficient and robust adaptive Kriging for structural reliability analysis. Structural and Multidisciplinary Optimization, 62(6), 3189-3204. [Google Scholar] [CrossRef]
55. Tong, C., Sun, Z. L., Zhao, Q. L., Wang, Q. B., & Wang, S. (2015). A hybrid algorithm for reliability analysis combining Kriging and subset simulation importance sampling. Journal of Mechanical Science and Technology, 29(8), 3183-3193. [Google Scholar] [CrossRef]
56. Zhang, X. B., Lu, Z. Z., & Cheng, K. (2021). AK-DS: An adaptive Kriging-based directional sampling method for reliability analysis. Mechanical Systems and Signal Processing, 156(15), 107610. [Google Scholar] [CrossRef]
57. Li, X. K., Qiu, H. B., Chen, Z. Z., Gao, L., & Shao, X. Y. (2016). A local Kriging approximation method using MPP for reliability-based design optimization. Computers & Structures, 162, 102-115. [Google Scholar] [CrossRef]
58. Meng, D. B., Wang, H. T., Yang, S. Y., Lv, Z. Y., & Hu, Z. G. (2022). Fault analysis of wind power rolling bearing based on EMD feature extraction. Computer Modeling in Engineering & Sciences, 130(1), 543-558. [Google Scholar] [CrossRef]
59. Huang, X., Chen, J., & Zhu, H. (2016). Assessing small failure probabilities by AK-SS: An active learning method combining Kriging and subset simulation. Structural Safety, 59(4), 86-95. [Google Scholar] [CrossRef]
60. Zhao, H., Yue, Z., Liu, Y., Gao, Z., & Zhang, Y. (2015). An efficient reliability method combining adaptive importance sampling and Kriging metamodel. Applied Mathematical Modelling, 39(7), 1853-1866. [Google Scholar] [CrossRef]
61. Nassim, R., & Pietro, M. C. (2018). Novel algorithm using active metamodel learning and importance sampling: Application to multiple failure regions of low probability. Journal of Computational Physics, 368(32), 92-114. [Google Scholar] [CrossRef]
62. Cadini, F., Santos, F., & Zio, E. (2014). An improved adaptive Kriging-based importance technique for sampling multiple failure regions of low probability. Reliability Engineering and System Safety, 131(3), 109-117. [Google Scholar] [CrossRef]
63. Zheng, P. J., Wang, C. M., Zong, Z. H., & Wang, L. Q. (2017). A new active learning method based on the learning function U of the AK-MCS reliability analysis method. Engineering Structures, 148(5), 185-194. [Google Scholar] [CrossRef]
64. Yang, X. F., Liu, Y. S., Mi, C. Y., & Wang, X. J. (2018). Active learning Kriging model combining with kernel-density-estimation-based importance sampling method for the estimation of low failure probability. Journal of Mechanical Design, 140(5), 051402. [Google Scholar] [CrossRef]
65. Dubourg, V., Sudret, B., & Deheeger, F. (2013). Metamodel-based importance sampling for structural reliability analysis. Probabilistic Engineering Mechanics, 33(2), 47-57. [Google Scholar] [CrossRef]
66. Phuc, D. V., Anne, B., & Christophe, B. (2013). Reliability importance analysis of Markovian systems at stead state using perturbation analysis. Reliability Engineering and System Safety, 93(11), 1605-1615. [Google Scholar]
67. Mede, R. Z. Z., Flesch, J., & Peete, R. S. R. (2012). Optimal choice for finite and infinite horizons. Operations Research Letters, 40(6), 469-474. [Google Scholar] [CrossRef]
68. Zhang, D., Zhou, P., Jiang, C., Yang, M., & Han, X. (2021). A stochastic process discretization method combing active learning Kriging model for efficient time-variant reliability analysis. Computer Methods in Applied Mechanics and Engineering, 384, 113990. [Google Scholar] [CrossRef]
69. Yu, S., Wang, Z. L., & Li, Y. (2022). Time and space-variant system reliability analysis through adaptive Kriging and weighted sampling. Mechanical Systems and Signal Processing, 166(4), 108443. [Google Scholar] [CrossRef]
70. Bichon, B. J., Eldred, M. S., & Swiler, L. P. (2012). Efficient global reliability analysis for nonlinear implicit performance functions. AIAA Journal, 46(10), 2459-2468. [Google Scholar] [CrossRef]
71. Zhang, X. F., Wang, L., & Sorensen, J. D. (2019). REIF: A novel active-learning function toward adaptive Kriging surrogate models for structural reliability analysis. Reliability Engineering and System Safety, 185(3), 440-454. [Google Scholar] [CrossRef]
72. Au, S. K., & Beck, J. L. (1999). A new adaptive importance sampling scheme for reliability calculations. Structural Safety, 21(2), 135-158. [Google Scholar] [CrossRef]
73. Sadoughi, M., Li, M., & Hu, C. (2018). Multivariate system reliability analysis considering highly nonlinear and dependent safety events. Reliability Engineering and System Safety, 180(3), 189-200. [Google Scholar] [CrossRef]
74. Yuan, X. K., Gu, J., & Liu, S. L. (2021). Sensitivity of sample for simulation-based reliability analysis methods. Computer Modeling in Engineering & Sciences, 126(1), 331-357. [Google Scholar] [CrossRef]
75. Liu, Y. S., & Li, L. Y. (2020). Global reliability sensitivity analysis based on state dependent parameter method and efficient sampling techniques. Aerospace Science and Technology, 99(12), 105740. [Google Scholar] [CrossRef]
76. Bourinet, J. M., Deheeger, F., & Lemaire, M. (2011). Assessing small failure probabilities by combined subset simulation and support vector machines. Structural Safety, 33(6), 343-353. [Google Scholar] [CrossRef]
77. Katsuki, S., & Frangopol, D. M. (1994). Hyperspace division method for structural reliability. Journal of Engineering Mechanics, 120(11), 2405-2427. [Google Scholar] [CrossRef]
78. Li, X. K., Zhu, S. P., Liao, D., Correia, J. A. F. O., & Berto, F. (2022). Probabilistic fatigue modelling of metallic materials under notch and size effect using the weakest link theory. International Journal of Fatigue, 159(4), 106788. [Google Scholar] [CrossRef]
79. Nie, X. F., He, W. F., Cao, Z. Y., Song, J. D., & Li, X. (2021). Experimental study and fatigue life prediction on high cycle fatigue performance of laser-peened TC4 titanium alloy. Materials Science and Engineering A, 822(3), 141658. [Google Scholar] [CrossRef]