 Open Access
Open Access
ARTICLE
Research on Flexible Job Shop Scheduling Optimization Based on Segmented AGV
1 College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin, 150001, China
2 Carrier Platform Division, Beijing Research Institute of Special Mechanic, Beijing, 100143, China
* Corresponding Author: Nengjian Wang. Email:
(This article belongs to the Special Issue: Computer Modeling in Ocean Engineering Structure and Mechanical Equipment)
Computer Modeling in Engineering & Sciences 2023, 134(3), 2073-2091. https://doi.org/10.32604/cmes.2022.021433
Received 14 January 2022; Accepted 04 May 2022; Issue published 20 September 2022
Abstract
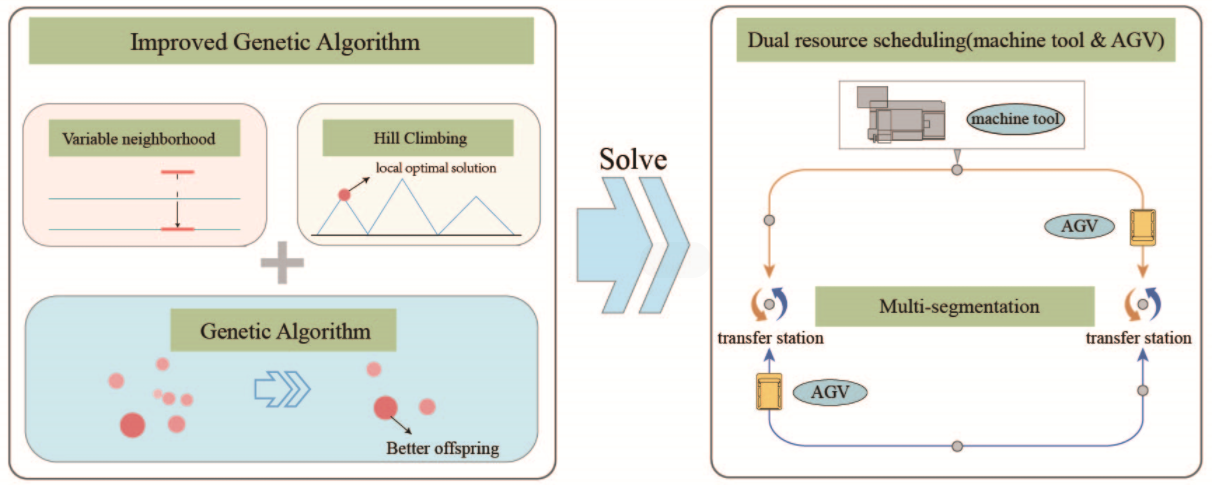
As a typical transportation tool in the intelligent manufacturing system, Automatic Guided Vehicle (AGV) plays an indispensable role in the automatic production process of the workshop. Therefore, integrating AGV resources into production scheduling has become a research hotspot. For the scheduling problem of the flexible job shop adopting segmented AGV, a dual-resource scheduling optimization mathematical model of machine tools and AGVs is established by minimizing the maximum completion time as the objective function, and an improved genetic algorithm is designed to solve the problem in this study. The algorithm designs a two-layer coding method based on process coding and machine tool coding and embeds the task allocation of AGV into the decoding process to realize the real dual resource integrated scheduling. When initializing the population, three strategies are designed to ensure the diversity of the population. In order to improve the local search ability and the quality of the solution of the genetic algorithm, three neighborhood structures are designed for variable neighborhood search. The superiority of the improved genetic algorithm and the influence of the location and number of transfer stations on scheduling results are verified in two cases.Graphic Abstract
Keywords
With the change of market demand, the current manufacturing industry presents the characteristics of multi-variety, small batch and short cycle, which puts forward higher requirements for the optimization of the production process and the formulation of the production plan. How to shorten the manufacturing cycle and improve the utilization rate of production resources has become the key to the development of the manufacturing industry under the background of intelligent manufacturing. In the traditional flexible job shop scheduling problem, the transfer time of the workpiece is not considered or assumed to be a fixed time considered within the processing time of the workpiece, which does not conform to the actual processing situation [1]. With the development of automation technology, the workpiece transfer task in the manufacturing workshop is gradually undertaken by AGV, and the production efficiency of the workshop is directly affected by the transfer efficiency of AGV. Therefore, the research on flexible job shop scheduling with AGV in this paper has more practical significance.
For the dual-resource scheduling problem of machine tools and AGVs in flexible job shops, many scholars have carried out a lot of research. Aiming at the integrated scheduling problem of machine and AGV, Philippe et al. [2] proposed a modeling framework for joint scheduling problems based on a disjunctive graph and proposed an MA algorithm to solve the problem. Then, the effectiveness of the algorithm was verified by a large number of examples. Rizvan et al. [3] proposed a multi-agent-based machine and AGV scheduling method, which works in a real-time environment and generates feasible plans using a negotiation/command mechanism between agents. Mohammad et al. [4] established a mathematical model composed of the workpiece transportation time and the collision-free path of AGV and proposed a two-stage ant colony algorithm to solve the problem. Finally, a large number of examples show that the algorithm is an effective meta-heuristic algorithm to solve the problem. Umar et al. [5] proposed a hybrid genetic algorithm-based integrated scheduling, machine job scheduling, and conflict-free path selection algorithm for job and automatic guided vehicle in the flexible manufacturing workshop environment. The algorithm can generate a complete timetable and a detailed path, while optimizing the completion time, AGV travel time, job delays caused by collision avoidance, and penalty costs caused by delays. Zacharia et al. [6] proposed an improved genetic algorithm based on fuzzy number theory to solve multiple AGV scheduling and path planning problems under the background of the uncertainty of demand and travel time. Zheng et al. [7] considered both machine scheduling and AGV scheduling, established a mixed integer linear programming (MILP) model, then used a heuristic algorithm based on tabu search to solve the problem, and introduced an improved tabu search algorithm for large-scale problems. Lyu et al. [8] established a mathematical model for simultaneous scheduling of AGV and machine, intending to minimize the maximum completion time and used a genetic algorithm to solve the problems of AGV path planning and integrated scheduling of AGV and machine. Xu et al. [9] considered the influence of behavior effect on the scheduling problem of AGV flexible workshop, proposed a whale algorithm with a hybrid local chaotic search strategy, and developed relevant experiments to verify the influence of learning effect and deterioration effect on the unit batch scheduling time. Li et al. [10] proposed a hybrid genetic whale algorithm considering the handling of AGV in flexible workshop scheduling problems. It provides a feasible method to effectively solve the fusion scheduling problem of flexible job shops considering AGV. Aiming at the integrated scheduling problem of machine and AGV, Li et al. [11] established a dual-resource scheduling model with a variable process path, and proposed an improved genetic algorithm to solve it, which improved the flexibility of the AGV scheduling process. For small-scale manufacturing systems, Lu et al. [12] established a scheduling model for a single AGV to deal with multiple tasks and designed a genetic algorithm to solve the problems studied by coding according to AGV handling priority. Aiming at the flexible job shop scheduling problem considering transportation time, Chen et al. [13] constructed a multi-objective optimization model by minimizing the maximum completion time, maximum machine load, and total machine load, and proposed a niche particle swarm optimization algorithm to solve it. In the end, the feasibility and effectiveness of the algorithm were verified by an example. The above research has achieved some results in the job shop scheduling problem integrating AGV.
However, few studies can truly integrate the traditional flexible job shop scheduling problem with the task allocation and path planning problem of AGV, owing to the complexity of the machine tool and AGV dual-resource scheduling problem. Two common strategies are used to study the dual-resource scheduling problem: one is solving the problem of machine allocation and process arrangement first, then scheduling AGV, and the dynamic programming method is mainly adopted to solve these problems. The other is scheduling the machine and AGV simultaneously under the assumption that the AGV path is known without collision, and genetic algorithm, simulated annealing algorithm, particle swarm optimization algorithm, tabu search algorithm, and other intelligent optimization algorithms are used to solve the problem [14–22]. Neither of the above two cases pays attention to the uncertainty of AGV transfer time or path planning in the actual production process, and does not realize the real dual-resource integrated scheduling.
There is no collision conflict in the transport process of the segmented AGV studied in this paper, and the configuration of the transportation system is flexible. The position and number of the transfer station can be adjusted according to the different processing tasks and the number of used machine tools, to ensure the transportation efficiency and load balance of each AGV as far as possible, and promote the production efficiency of small and medium-sized processing workshop to maximize. To realize the real integrated scheduling of segmented AGV and the machine tool, an improved genetic algorithm is designed to solve the problem. The transfer time of the workpiece and the task allocation of AGV is embedded in the decoding process, and the optimal scheduling scheme is solved by iterative optimization. The superiority of the improved genetic algorithm in this paper is verified by solving the extended case of Brandimarte scheduling example MK02, and the extended case based on MK04 verified that setting different locations and the number of transfer stations has a greater impact on scheduling results.
2 Description of Dual-Resource Scheduling Problem
There are
The assumptions are as follows:
1. Each process cannot be interrupted after it begins processing. The loading and unloading time of the machine tool is included in the processing time, and the processing time is known.
2. The material buffer area of each machine tool and the transfer station is infinite, and the transfer station allows two AGVs to be parked at the same time.
3. The AGV can be bidirectional in their respective sections, and the driving speed is not affected by no-load or load.
4. Before processing, all workpieces are in the warehouse. In the segmentation containing the warehouse, AGV is parked at the Outbound platform of the warehouse, and AGVs in other segmentations are docked at the transfer station.
5. AGV power, breakdown, and other factors are not considered. The time of AGV loading and unloading the workpiece is calculated within the transfer time.
3 Mathematical Model of Dual-Resource Scheduling
Before establishing the mathematical model of dual-resource scheduling, the introduced symbols and decision variables are defined and explained as follows:
Decision variables:
Aiming at the flexible job shop scheduling of segmented AGV, a mathematical model is established to minimize the maximum completion time
Objective function:
Constraint conditions:
Among them, Eq. (7) denotes the objective function of minimizing the maximum completion time. Eq. (8) means that the workpiece cannot be interrupted if the processing starts. Eq. (9) indicates that the starting time of the process is longer than the time when AGV is transported to the current machine tool and unloaded after the processing of the previous process is completed. Eq. (10) indicates that an AGV can only transport one workpiece once. Eq. (11) indicates that when the cross-regional transfer occurs, the AGV in the previous segmentation transfers the workpiece and unloads it to the transfer station, and when the AGV in the next segmentation reaches the transfer station, the loading and load transfer tasks in the next segmentation can be performed. Eq. (12) indicates that when the
For solving flexible job shop scheduling problems, scholars have tried to use many intelligent algorithms, such as genetic algorithm, simulated annealing algorithm, particle swarm optimization algorithm, tabu search algorithm, and so on. Among them, the simulated annealing algorithm has a simple calculation process, strong robustness, and global search capability, but the convergence speed of the algorithm is slow, and the initial value and parameter setting of the algorithm have a great influence on the performance of the algorithm [24]. Particle swarm optimization has fewer parameters and is easy to implement, but it is easy to fall into local optimal solution and the algorithm is unstable [25]. Tabu search algorithm can avoid falling into local optimum, but the algorithm has a strong dependence on the initial solution [26]. The genetic algorithm has strong parallelism and global search capability, and its random search method can better search in the solution space. The genetic information is shared in the form of genes so that the algorithm can search for the position of the global optimal solution. However, the genetic algorithm has a poor local search capability, is prone to the premature phenomenon, and the population diversity is insufficient [27].
Therefore, For the dual-resource scheduling problem of segmented AGV flexible job shop, a single intelligent optimization algorithm is difficult to solve the optimal solution. Since the genetic algorithm has been very mature in solving the flexible job shop scheduling problem, an improved genetic algorithm is designed in this paper to solve the problem. Local selection, random selection, and hill climbing algorithm are used to generate the initial population to improve the quality of the initial population [28]; the selection strategy of elite reservation and tournament method is adopted to improve the probability of good genes being inherited; three neighborhood structures are used for variable neighborhood search to enhance the local search ability of the algorithm. The details are as follows.
In this paper, the two-level coding method based on process coding and machine tool coding is adopted. Fig. 1 is a process-based coding, the number represents the workpiece number, the total number of occurrences represents the total number of processes of the workpiece, and the k-th occurrence represents the k-th process. As shown in Fig. 1, the first appearance of the number 3 indicates the first process of
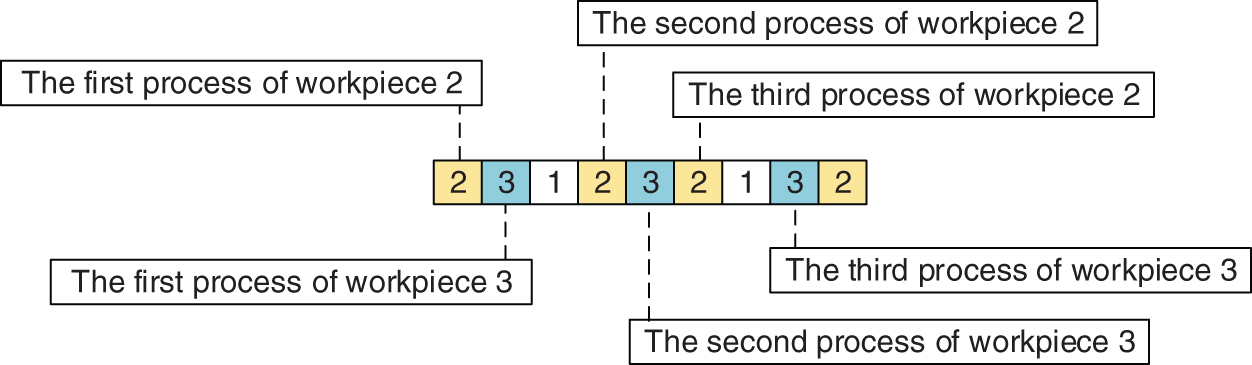
Figure 1: Chromosome representation of process-based coding

Figure 2: Chromosome representation of machine tool-based coding
When initializing the population, the process-based coding is combined with the hill climbing algorithm to improve the quality of the initial solution and the convergence speed of the algorithm. Based on machine tool coding combined with random selection and local selection strategy, random selection can promote the initial population to be distributed in the solution space evenly, maintain the diversity of the initial population, and improve the global search ability of the algorithm. And the local selection is conducive to promoting the load balance of machine tools. The details are as follows.
Starting from process 1 of workpiece 1 in the workpiece set, randomly select a machine tool from the set of optional machine tools for this process, then record the machine number and fill in the corresponding gene position, and so on, until the last process of the last workpiece has selected the processing machine.
First, the process 1 of workpiece 1 is given as the current process, and the processing time corresponding to each machine tool in the set of optional machine tools is added to the time value in the corresponding array position of the machine tool. The machine tool with the smallest sum obtains the task of processing the current process, and the machine tool number is recorded to the corresponding gene position, then the processing time of the machine tool is accumulated to the corresponding array position of the machine tool. The next process of the workpiece is selected to perform the same operation until all processes of the current workpiece are selected to process the machine tool, and the time records in the corresponding position array of the machine tool are cleared. Then select the next workpiece, and continue to perform the above operations until all processes of the workpiece are selected to complete the processing machine.
The process-based coding uses a random way for initialization first, then randomly selects some individuals to use the hill climbing algorithm. The specific steps are as follows:
Step 1: Select one of the individuals in the group that needs to be operated by hill climbing algorithm, and calculate the fitness of the individual;
Step 2: Two genes were selected randomly for exchange on the gene sequence based on process coding to obtain new individuals;
Step 3: Calculate the fitness of the new individual, if it is better than the original one, replace it, otherwise do not change;
Step 4: Repeat Step 2 and Step 3 until the number of iterations is met;
Step 5: Perform the above operations on other individuals who need to perform the mountain climbing algorithm operation, and return to the original population when all is completed.
In this paper, a mixed selection strategy of elite retention and tournament method is adopted. Firstly, an elite pool is established with 10% of the population size to determine whether there are individuals in the population that are better than those in the elite pool. If there are, the worst individuals in the elite pool will be replaced, and the elite pool will be updated. Then the individuals in the elite pool are directly copied to the cross pool. Secondly, according to the tournament method to select individuals into the next generation of population, until the selected individuals amount to the appropriate number, and then mutation operation will be taken to maintain the diversity of the population and prevent falling into local optimum.
According to the above coding characteristics, the gene sequence based on process coding adopts Improved Precedence Operation Crossover (IPOX), and the gene sequence based on machine coding adopts Maximal Preservative Crossover (MPX).
As shown in Fig. 3, the IPOX crossover operation only crosses the process sequence in the parent chromosome, and retains the machine tool selected by the process to the offspring. In the figure,
1. All workpieces are randomly divided into two sets
2. Copy
3. Copy
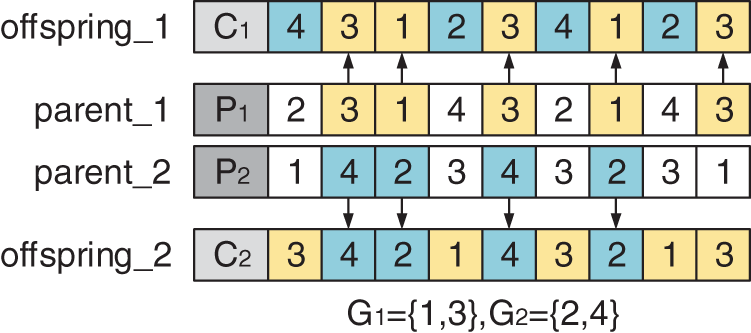
Figure 3: IPOX crossover
As shown in Fig. 4, the MPX crossover operation only crosses the machine tool sequence selected by the process in the parent chromosome, and the process sequence is directly retained to the offspring. The crossover process is as follows:
1. Randomly generate a set
2. The processes corresponding to the position of number 1 in
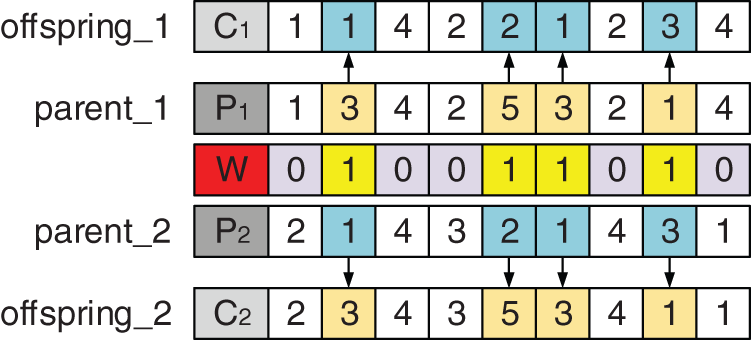
Figure 4: MPX crossover
The mutation process and schematic diagram are as follows.
1. Randomly select two genes for exchange from the gene sequence based on the process coding, as shown in Fig. 5;
2. Since there are multiple machine tool options for each process, a gene is randomly selected from the gene string based on the machine code, and its corresponding workpiece and process number are determined. Then another machine tool is randomly selected from the set of optional machines for the process to replace. The current machine tool is shown in Fig. 6.

Figure 5: Process chromosome variation
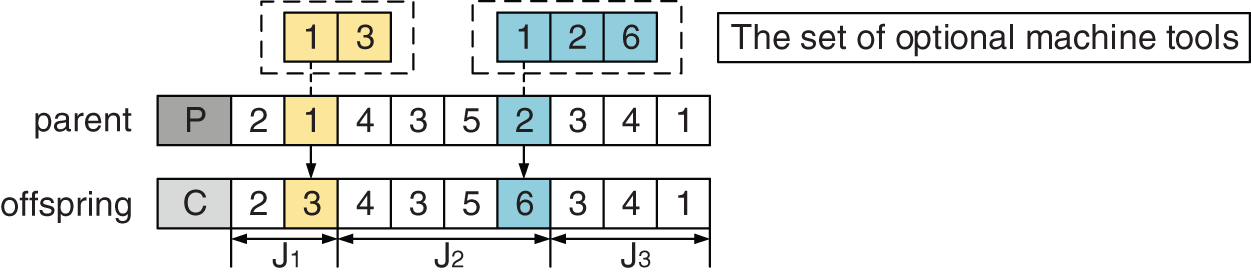
Figure 6: Machine tool chromosome variation
4.6 Variable Neighborhood Search
In order to prevent the genetic algorithm from falling into the local optimum, the following three neighborhood structures are used to design the variable neighborhood search algorithm, so as to improve the local search ability and the quality of the solution of the genetic algorithm. Variable neighborhood search algorithm steps are as follows:
Step 1: Given the initial solution
Step 2: The neighborhood structure
Step 3: If
Step 4: If
Step 5: Output the optimal solution
4.6.1 Neighborhood Structure N1
As shown in Fig. 7, two different gene loci are randomly selected from the sequence based on process coding, and then the genes on the first selected gene locus are moved behind the second selected gene locus.
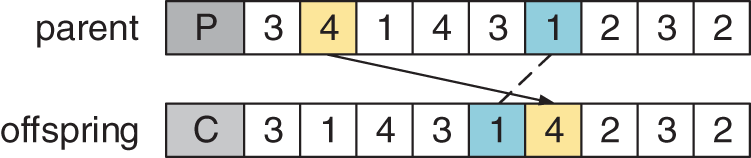
Figure 7: Neighborhood structure N1
4.6.2 Neighborhood Structure N2
As shown in Fig. 8, firstly, a process is randomly selected from the gene sequence based on process coding, and then the current machine tool number of the process and its optional machine tool set are determined. Finally, a different machine tool is randomly selected from its optional machine tool set to replace the current machine tool.
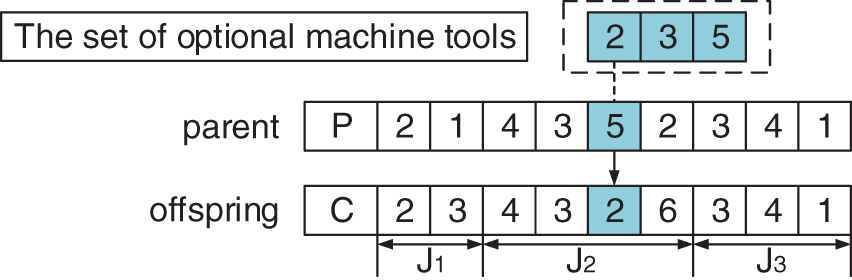
Figure 8: Neighborhood structure N2
4.6.3 Neighborhood Structure N3
As shown in Fig. 9, three gene loci are randomly selected from gene sequences based on process coding, and then an optimal neighborhood solution is found as a new solution from all their neighborhoods.
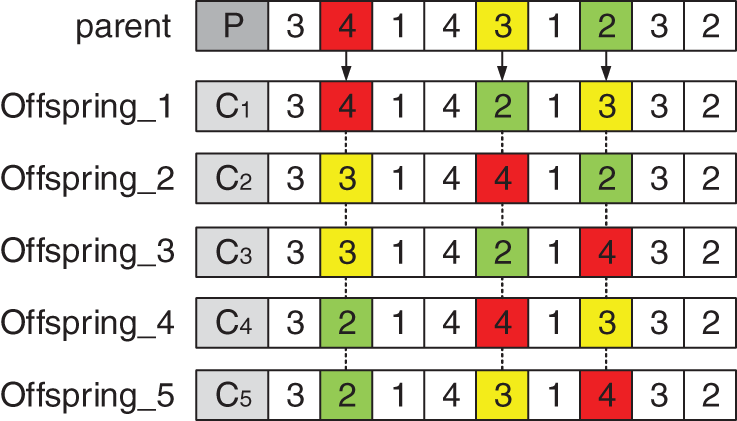
Figure 9: Neighborhood structure N3
In this paper, a decoding scheme is designed for the dual-resource scheduling model of segmented AGVs and machine tools. In the decoding process, the transfer time of the workpieces and the task allocation of AGVs are considered, and the real integrated scheduling of machine tools and AGVs is realized. The specific steps are as follows:
Step 1: Initialize the time record table of each machine tool, the processing time record table of each process, the AGV position node record table
Step 2: The gene sequence based on process coding is transformed into the corresponding process sequence; from left to right read the sequence of genes in the process, and the corresponding process
Step 3: Judge the number of AGVs required by this transfer task. If 0 AGVs are required, it means that the same machine tool is used for this process and the previous one, go to Step 13. If 1 AGV is required, it means that this process is processed in the same segmentation as the previous one, go to Step 8. If more than one AGV is required, it means that the processing is not in the same segmentation, go to Step 4;
Step 4: Read the AGV collection and the transfer station collection in turn from left to right. If the AGV is the first in the collection, go to Step 5, if it is the last one, go to Step 7, and if it is not the first or last one, go to Step 6, until the AGV collection is traversed completely;
Step 5: According to whether the transfer task is the first process, determine the position of the starting point of the AGV that performs the transfer task. If it is the first process, go to Step 9, if not, go to Step 10;
Step 6: The starting position of the AGV transfer task is at the transfer station
Step 7: The starting position of the AGV transfer task is at the transfer station
Step 8: Only one AGV is required for the transfer task. If it is the first process, the starting point is at the warehouse outbound platform, go to Step 9. If it is not the first process, the starting point is on the machine tool where the previous process is located, go to Step 11;
Step 9: AGV takes the position node
Step 10: AGV takes the position node
Step 11: AGV takes the position node
Step 12: The earliest starting processing time of the workpiece is the time node
Step 13: Judge whether the process is the last, if so, terminate; if not, go to Step 2.
The specific process of the improved genetic algorithm in this paper is shown in Fig. 10.
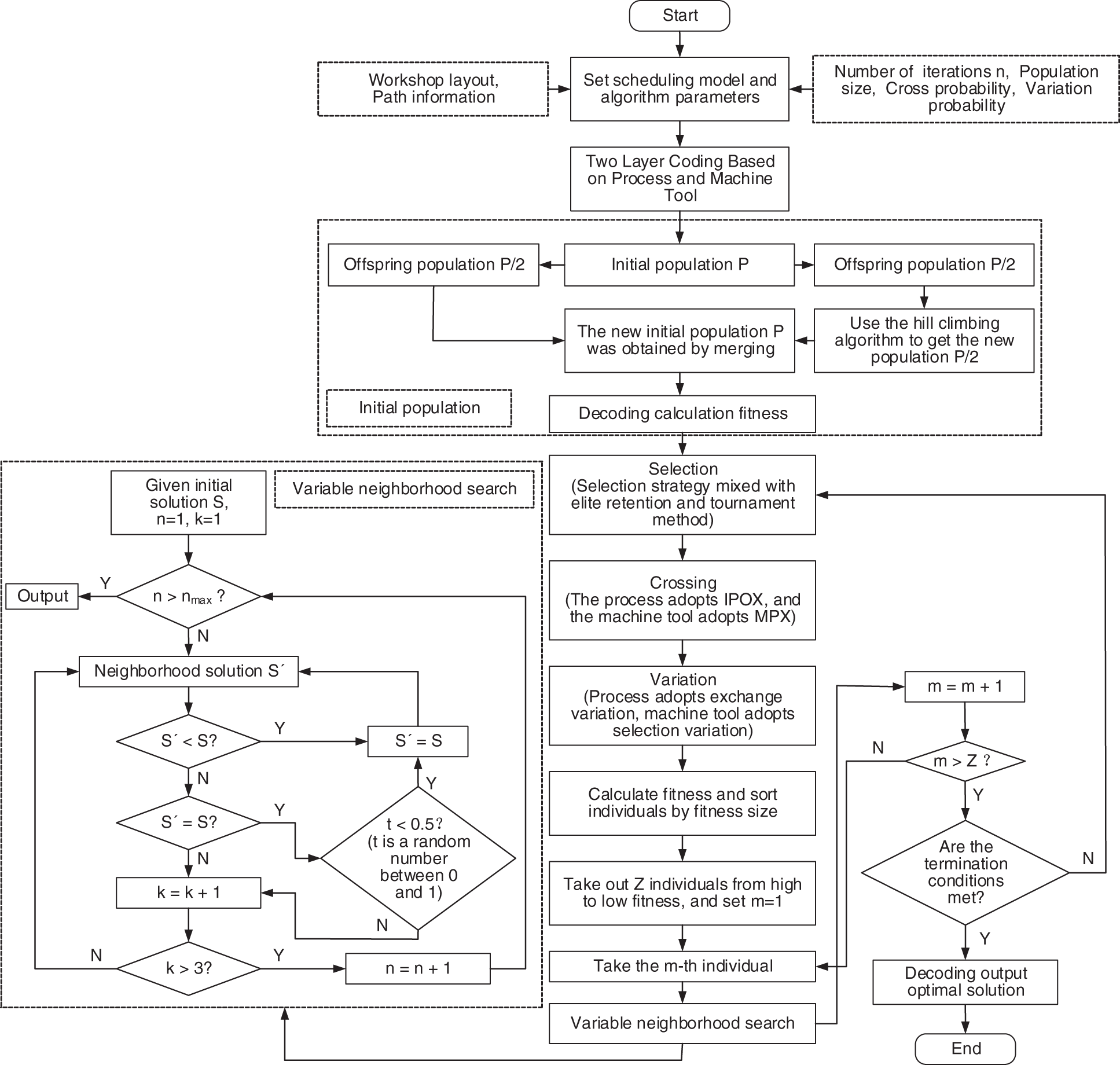
Figure 10: A flow chart of the improved genetic algorithm
In this paper, the extended case based on Brandimarte scheduling instance MK02 is used to verify the algorithm. The workshop layout is shown in Fig. 11, including 1 warehouse, 6 machine tools, 1 transfer station, 2 AGVs, 10 workpieces, and a total of 58 processes. The transfer station is located between machine tool 3 and machine tool 4. The driving speed of each AGV is 30 m/min, and the time of loading or unloading the workpiece is 0.5 min. The distance between each device is in meters.
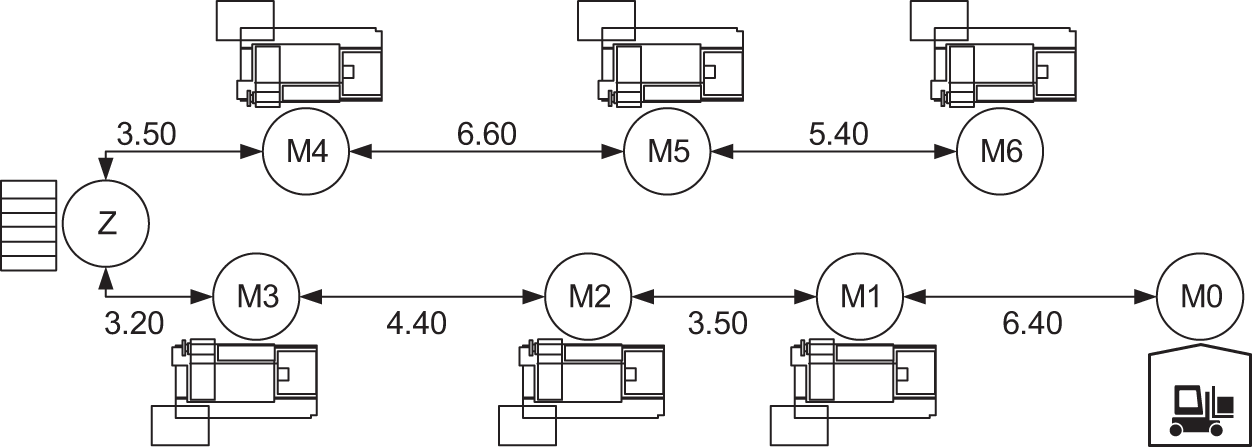
Figure 11: Layout of segmented AGV flexible job shop
Based on the job shop layout and parameter setting above, the standard genetic algorithm and the improved genetic algorithm in this paper were used for simulation verification with the optimization objective of minimizing the maximum completion time. The basic parameters of the algorithm were set as follows: initial population 100, crossover probability 0.8, mutation probability 0.1, and iteration number 200. The data of 15 runs are respectively shown in Table 1, and the comparison of statistical data is shown in Table 2. The convergence curves of optimal and average fitness for each generation and the Gantt chart of the optimized scheduling scheme are shown in Figs. 12–14. Each rectangular block in the Gantt chart represents a task. There are two numbers on the rectangular block, the upper number represents the workpiece number, and the lower number represents the process number; the white rectangular block in the row of the AGV represents the no-load driving process, and other colors represent Load driving.
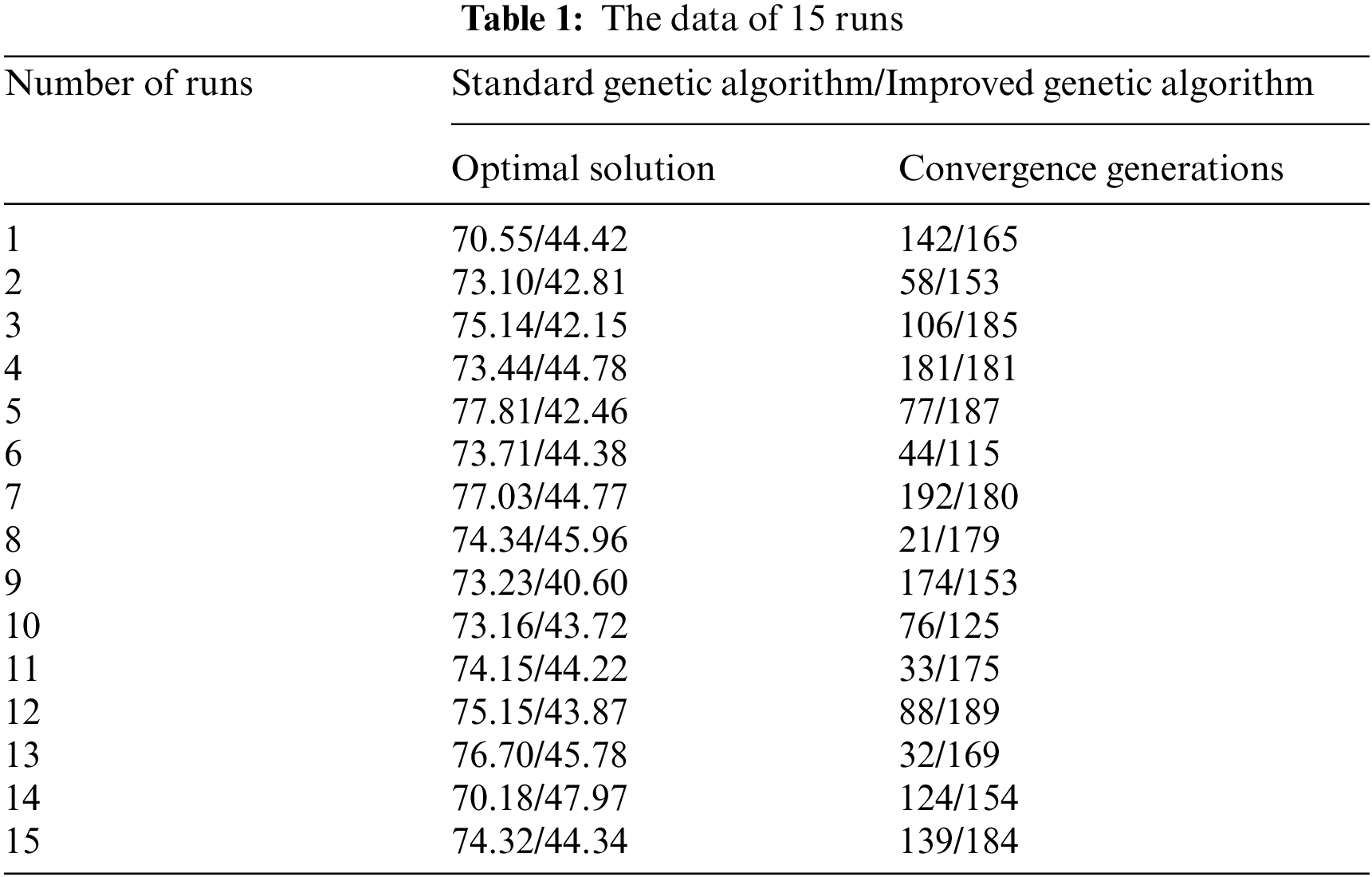
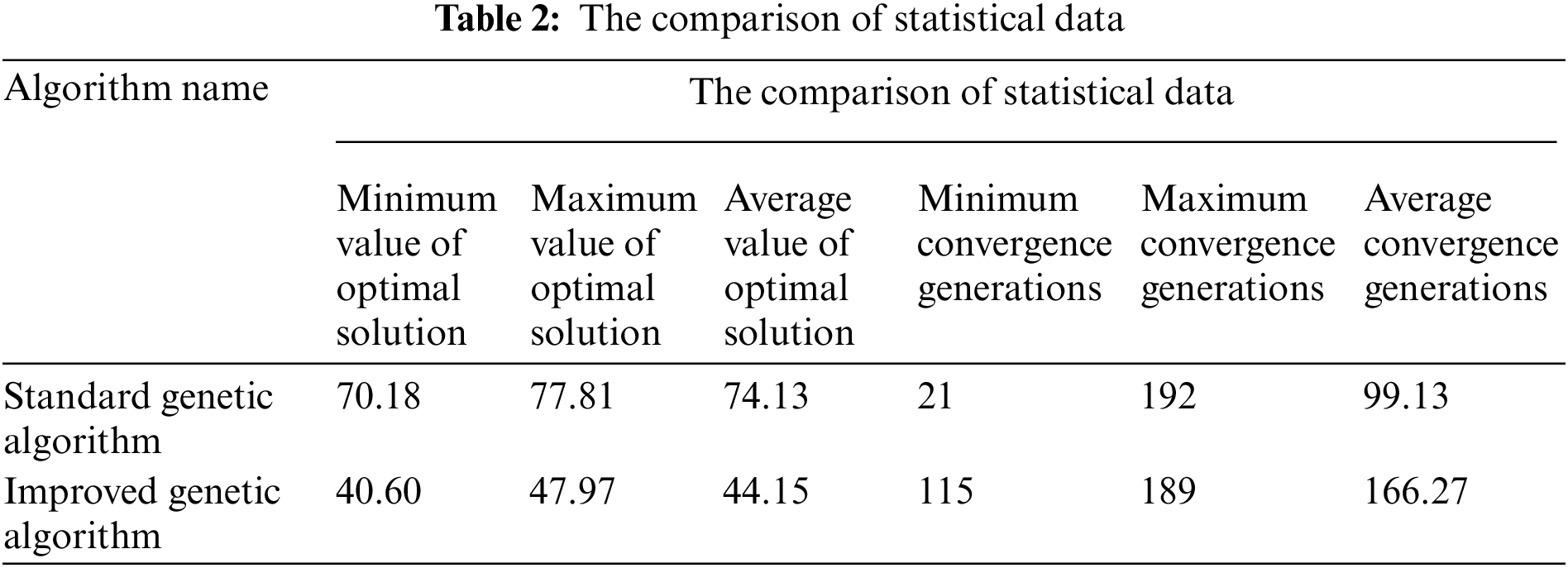
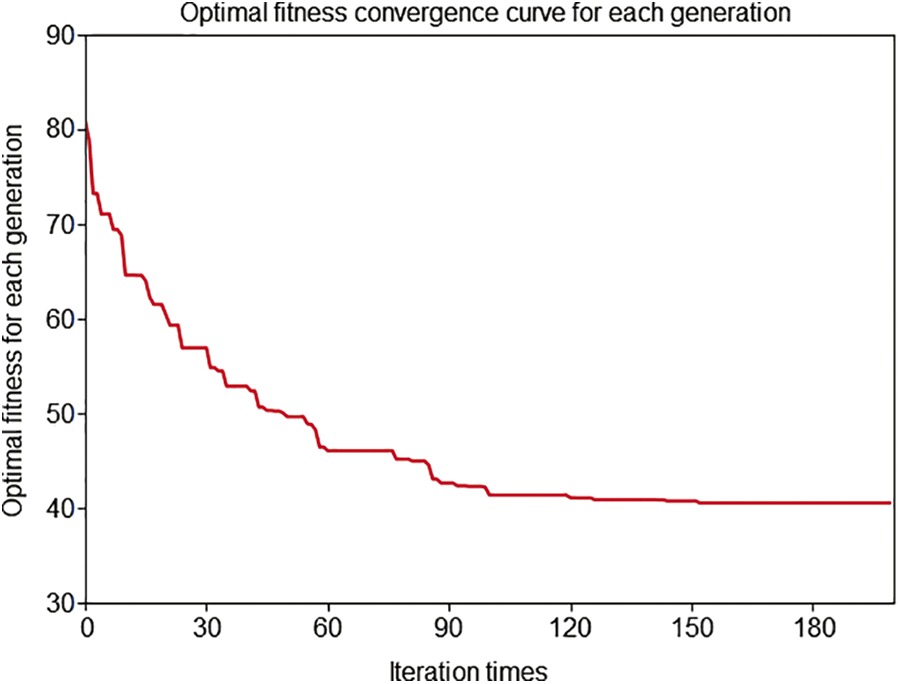
Figure 12: Optimal fitness convergence curve for each generation
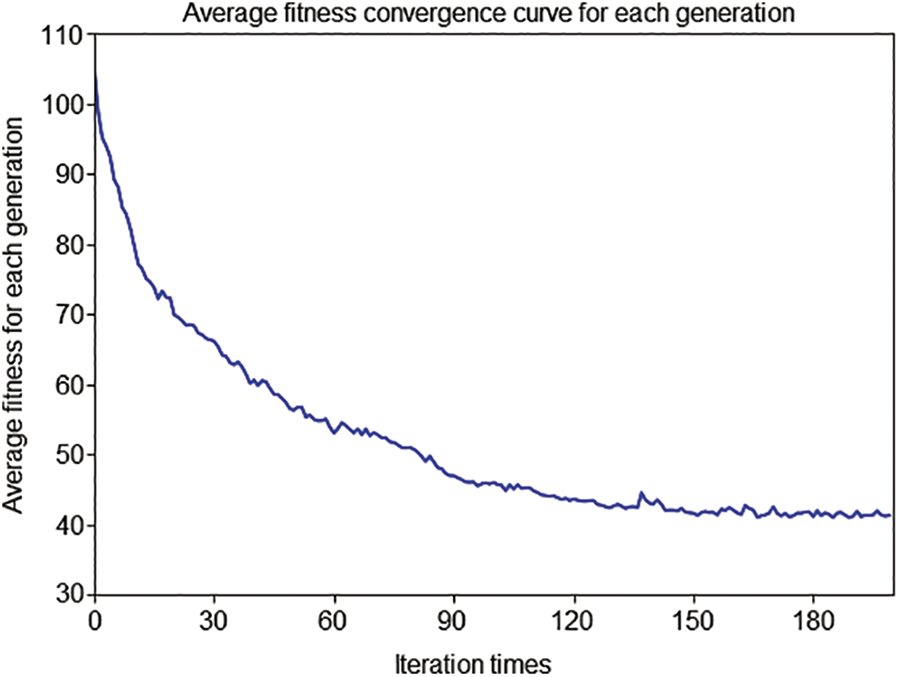
Figure 13: Average fitness convergence curve for each generation
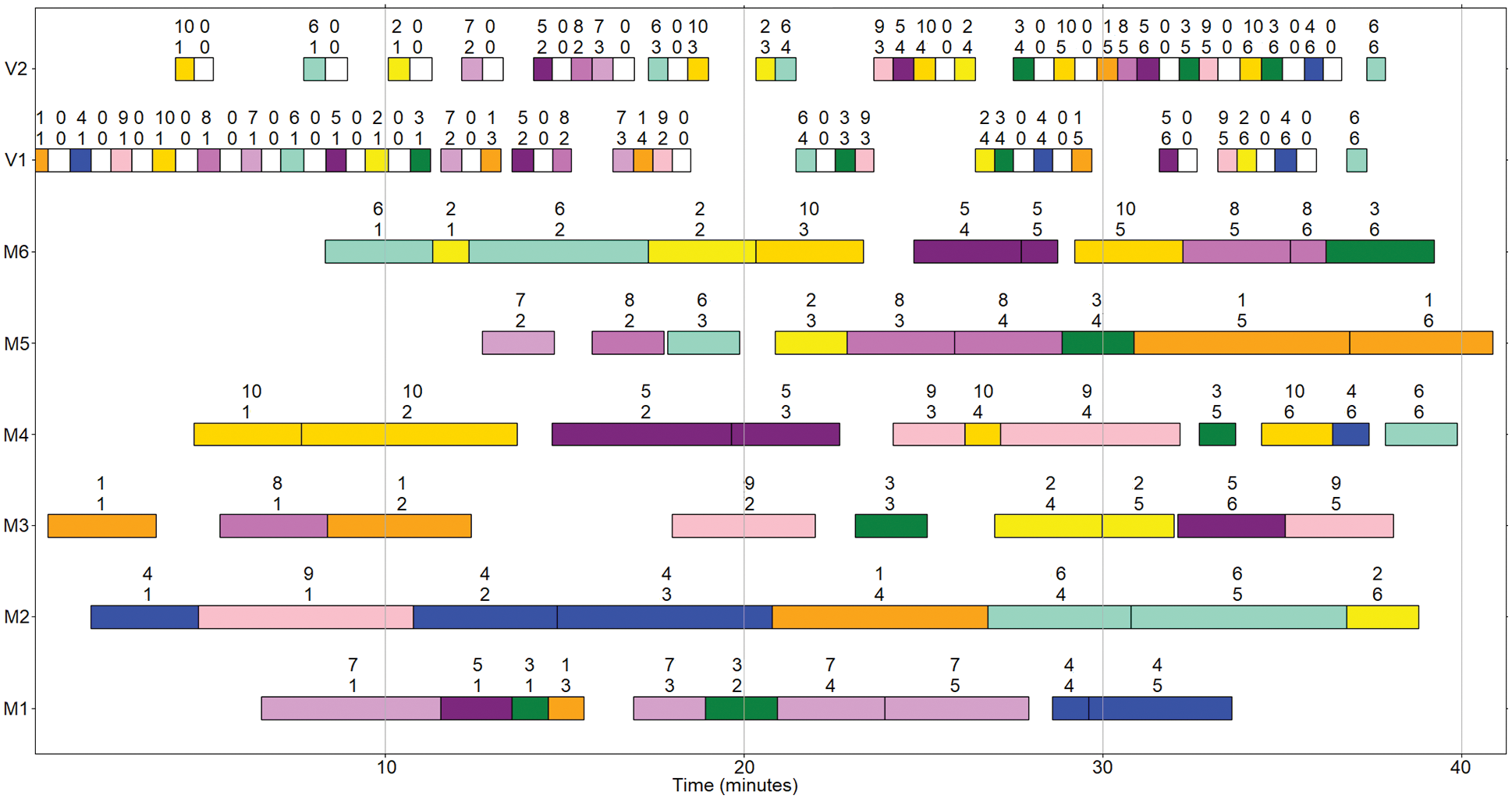
Figure 14: Gantt chart of scheduling scheme
The above results show that the improved genetic algorithm designed in this paper can avoid the premature algorithm to a large extent when the dual-resource scheduling problem of flexible job shop based on segmented AGV is solved, and the quality of the solution is significantly better than that of the standard genetic algorithm.
5.2 Research on the Location and Number of Transfer Stations
Based on the extended case of MK04, the influence of the location and number of transfer stations on the scheduling results is studied in this section. Workshop layout as shown in Fig. 15, including 1 warehouse, 8 machine tools, 15 workpieces, and a total of 90 processes. The speed of AGV is 30 meters per minute, the time of loading or unloading the workpiece is 0.5 min, and the distance between each device is in meters. The influence of different locations and quantities of transfer stations on the scheduling results is shown in Table 3, where
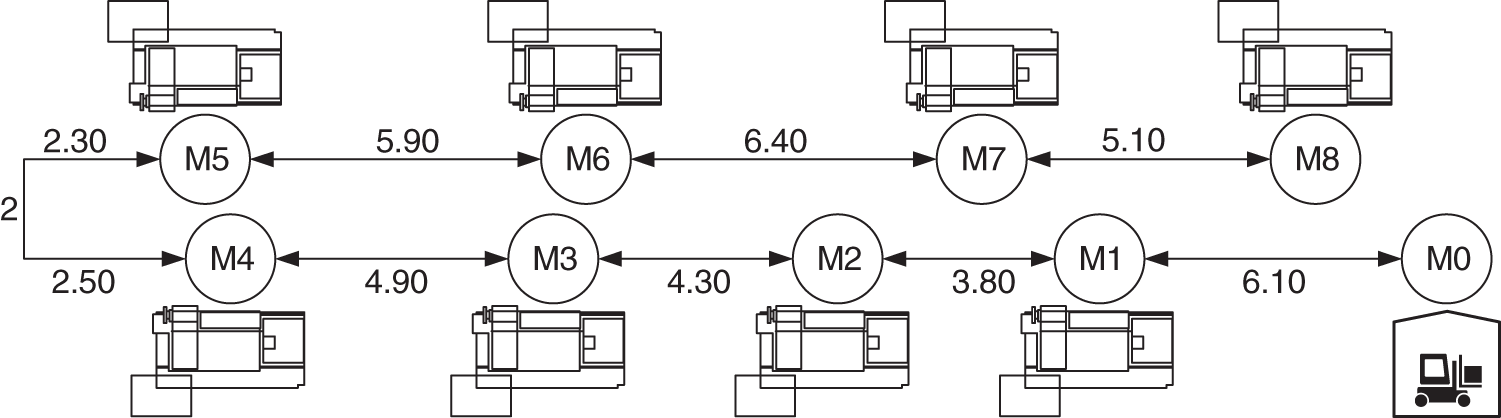
Figure 15: Workshop layout based on the extended case of MK04
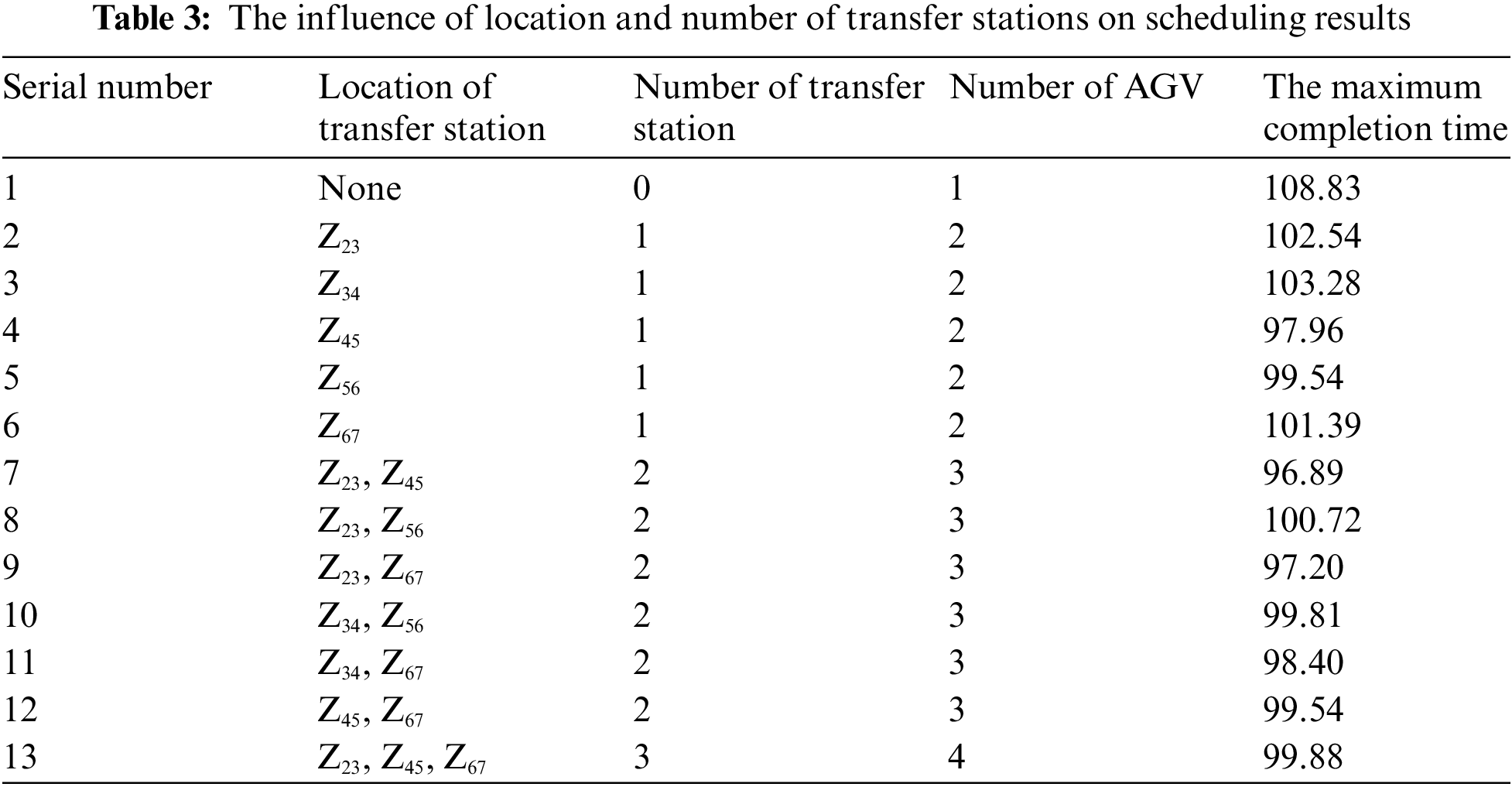
In the above cases, it can be seen from Table 3 that the maximum completion time of the optimal position with one, two, and three transfer stations is reduced by 9.99%, 10.97%, and 8.22% compared with that without transfer stations. Due to the small size of the workshop, when more than two transfer stations are set up, the number of loading and unloading of the workpiece is greatly increased, resulting in time cost is no longer reduced. Although the time cost of setting up two transfer stations is about 1% lower than that of setting up one transfer station, it increases the cost of production equipment. Therefore, the optimal configuration scheme, in this case, is to set up a transfer station between
Based on the traditional flexible job shop scheduling problem, this paper considers the workpiece transfer time and the task allocation of AGV. Aiming at the flexible job shop of segmented AGV, a mathematical model of machine tool and AGV dual resource scheduling is established to minimize the maximum completion time. An improved genetic algorithm is designed to solve the problem, and the task allocation and transfer time of AGV are taken into account when decoding. Finally, the superiority of the improved genetic algorithm in this paper is verified by solving the corresponding cases, and it is verified that the location and number of transfer stations have a greater impact on the scheduling results under the condition that the workshop layout and the processing orders remain unchanged. However, the segmented AGV transport system is mainly suitable for small and medium-sized processing workshops, which has certain limitations. Therefore, the flexible job shop scheduling problem with a more universal AGV transport system remains to be further studied.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zhang, G. H., Sun, J. H., Liu, X., Wang, G. D., Yang, Y. Y. (2019). Solving flexible job shop scheduling problems with transportation time based on improved genetic algorithm. Mathematical Biosciences and Engineering, 16(3), 1334–1347. DOI 10.3934/mbe.2019065. [Google Scholar] [CrossRef]
2. Philippe, L., Mohand, L., Nikolay, T. (2013). Job-shop based framework for simultaneous scheduling of machines and automated guided vehicles. International Journal of Production Economics, 143(1), 24–34. DOI 10.1016/j.ijpe.2010.07.012. [Google Scholar] [CrossRef]
3. Rizvan, E., Cenk, S., Adil, B., Vahit, K. (2012). A multi-agent based approach to dynamic scheduling of machines and automated guided vehicles in manufacturing systems. Applied Soft Computing Journal, 12(6), 1720–1732. DOI 10.1016/j.asoc.2012.02.001. [Google Scholar] [CrossRef]
4. Mohammad, S. M., Saeed, D. A., Farshid, E., Vahid, M. (2015). An ant colony algorithm (ACA) for solving the new integrated model of job shop scheduling and conflict-free routing of AGVs. Computers and Industrial Engineering, 86(2), 2–13. DOI 10.1016/j.cie.2015.01.003. [Google Scholar] [CrossRef]
5. Umar, U. A., Ariffin, M. K. A., Ismail, N., Tang, S. H. (2015). Hybrid multiobjective genetic algorithms for integrated dynamic scheduling and routing of jobs and automated-guided vehicle (AGV) in flexible manufacturing systems (FMS) environment. International Journal of Advanced Manufacturing Technology, 81(9), 2123–2141. DOI 10.1007/s00170-015-7329-2. [Google Scholar] [CrossRef]
6. Zacharia, P. T., Xidias, E. K. (2020). AGV routing and motion planning in a flexible manufacturing system using a fuzzy-based genetic algorithm. International Journal of Advanced Manufacturing Technology, 109(7), 1801–1813. DOI 10.1007/s00170-020-05755-3. [Google Scholar] [CrossRef]
7. Zheng, Y., Xiao, Y. J., Seo, Y. (2014). A tabu search algorithm for simultaneous machine/AGV scheduling problem. International Journal of Production Research, 52(19), 5748–5763. DOI 10.1080/00207543.2014.910628. [Google Scholar] [CrossRef]
8. Lyu, X. F., Song, Y. C., He, C. Z., Lei, Q., Guo, W. F. (2019). Approach to integrated scheduling problems considering optimal number of automated guided vehicles and conflict-free routing in flexible manufacturing systems. IEEE Access, 7, 74909–74924. DOI 10.1109/ACCESS.2019.2919109. [Google Scholar] [CrossRef]
9. Xu, Y. Q., Ye, C. M., Cao, L. (2019). Research on flexible job-shop scheduling problem with AGV constraints and behavioral effects. Application Research of Computers, 36(10), 3033–3038. [Google Scholar]
10. Li, X. X., Yang, D. M., Li, X., Wu, R. (2021). Flexible job shop AGV fusion scheduling method based on HGWOA. China Mechanical Engineering, 32(8), 938–950. [Google Scholar]
11. Li, Y., Wu, Z. M., Gan, Q. (2001). Integrated scheduling of machines and AGVs in flexible manufacturing environment. China Mechanical Engineering, 30(4), 447–450. [Google Scholar]
12. Lu, Y., Feng, K. K., Hu, Y. (2019). Study on scheduling algorithm for multiple handling requests of single automated guided vehicles. High Technology Letters, 25(2), 334–339. [Google Scholar]
13. Chen, K., Bi, L. (2021). Research on multi-objective flexible job shop scheduling considering transport time. Journal of Chinese Computer Systems, 42(5), 652–946. [Google Scholar]
14. He, C. Z., Song, Y. C., Lei, Q., Lv, X. F., Liu, Q. X. et al. (2019). Integrated scheduling of multiple AGVs and machines in flexible job shops. China Mechanical Engineering, 30(4), 438–447. [Google Scholar]
15. Kumar, N., Chandna, P., Joshi, D. (2019). Integrated scheduling of part, tool and automated guided vehicles in a flexible manufacturing system using modified genetic algorithm. International Journal of Industrial and Systems Engineering, 32(4), 443–468. DOI 10.1504/IJISE.2019.101332. [Google Scholar] [CrossRef]
16. Zhao, N., Li, K. D., Tian, Q., Du, Y. H. (2015). Fast optimization approach of flexible job shop scheduling with transport time consideration. Computer Integrated Manufacturing Systems, 21(3), 724–732. [Google Scholar]
17. Heger, J., Voß, T. (2019). Dynamic priority based dispatching of AGVs in flexible job shops. Procedia CIRP, 79(1), 445–449. DOI 10.1016/j.procir.2019.02.119. [Google Scholar] [CrossRef]
18. Wu, X. L., Xiao, X., Zhao, N. (2019). Flexible job shop dual resource scheduling problem considering loading and unloading. Control and Decision, 35(10), 2475–2485. [Google Scholar]
19. Asma, F., Hatem, H., Imed, K., Atidel, B. H. A. (2021). A hybrid genetic tabu search algorithm for minimising total completion time in a flexible job-shop scheduling problem. European Journal of Industrial Engineering, 14(6), 763–781. [Google Scholar]
20. Zhou, X., Ma, Y., Hu, Y. (2015). Mixed genetic algorithm and simulated annealing algorithm for solving job shop scheduling problem. Journal of Chinese Computer Systems, 36(2), 370–374. [Google Scholar]
21. Deroussi, L., Gourgand, M., Tchernev, N. (2001). Coupling local search methods and simulated annealing to the job shop scheduling problem with transportation. IEEE International Conference on Emerging Technologies and Factory Automation, vol. 1, pp. 659–667. DOI 10.1109/ETFA.2001.996427. [Google Scholar] [CrossRef]
22. Bekkar, A., Belalem, G., Beldjilali, B. (2019). Iterated greedy insertion approaches for the flexible job shop scheduling problem with transportation times constraint. International Journal of Manufacturing Research, 14(1), 43–66. DOI 10.1504/IJMR.2019.096746. [Google Scholar] [CrossRef]
23. Demir, Y., Kürs, A. I., leyen, S. (2013). Evaluation of mathematical models for flexible job-shop scheduling problems. Applied Mathematical Modelling, 37(3), 977–988. DOI 10.1016/j.apm.2012.03.020. [Google Scholar] [CrossRef]
24. Toader, F. A. (2015). A hybrid algorithm for job shop scheduling problem. Studies in Informatics and Control, 24(2), 171–180. DOI 10.24846/v24i2y201505. [Google Scholar] [CrossRef]
25. Zhang, R., Wu, C. (2010). A divide-and-conquer strategy with particle swarm optimization for the job shop scheduling problem. Engineering Optimization, 42(7), 641–670. DOI 10.1080/03052150903369845. [Google Scholar] [CrossRef]
26. Lin, Y. K., Chong, C. S. (2016). A tabu search algorithm to minimize total weighted tardiness for the job shop scheduling problem. Journal of Industrial and Management Optimization, 12(2), 703–717. DOI 10.3934/jimo. [Google Scholar] [CrossRef]
27. Chaudhry, I., Khan, A. M., Khan, A. A. (2013). A genetic algorithm for flexible job shop scheduling. In: Lecture notes in engineering and computer science, vol. 1, pp. 703–708. DOI 10.1080/00207540902814348. [Google Scholar] [CrossRef]
28. Bytyçi, E., Rogova, E., Beqa, E. (2021). Combination of genetic and random restart hill climbing algorithms for vehicle routing problem. In: Lecture notes on data engineering and communications technologies, vol. 76, pp. 601–612. DOI 10.1007/978-3-030-79357-9. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools