A Peridynamic Approach for the Evaluation of Metal Ablation under High Temperature

1  Introduction

The metal ablation under high temperature is ubiquitous in many engineering problems, such as the welding of the steels, the laser strengthening of the aluminum alloys, and the ablation of the reactor pressure vessels (RPVs) caused by a core melt in serious accidents, etc. Importantly, the properties of these metal materials and structures may change dramatically after the thermal ablation, which could eventually improve or reduce the levels of strength, stability, workability, safety of the materials and structures, and so on. Therefore, it is very essential to study metal ablation problems. During the past several decades, studies of metal ablation problems have been conducted by many researchers from the aspects of theories, experiments and simulations. For instance, the characteristics of the thermal ablation, such as the microtopologies, the thermal boundaries and the thermal damages, were investigated by the experimental and numerical methods [1–4]. The welding methods were studied for different metal materials, such as laser welding and friction stir welding methods [5–7]. Further, the surface and toughness hardenings of metal materials through laser ablation were researched by the theoretical, experimental and numerical methods [8–11]. In addition, Anderson et al. [12] investigated the heat transfer experimentally within the AP600 containment under postulated accident conditions. Theofanous et al. [13] and Guan et al. [14] studied the heat distributions and convective boundaries of the RPV based on a two-layer structure of core melt. Zhan et al. [15] analyzed the ablation and thermal stresses of the RPV under heating by core melt on the basis of a moving boundary scheme in the finite element framework. Although these works mentioned above have provided reliable approaches or routes for the evaluations of the metal ablation problems, novel and efficient computational methods are still of great importance for the more complex metal ablation problems, such as the coupling heat conduction, ablation and contact problems.

In the last twenty years, nonlocal peridynamics proposed by Silling [16] has attracted a lot of researchers’ interests due to its natural advantages in dealing with discontinuous and contact problems. The peridynamic method is expressed by an integral motion equation and mainly contains two kinds of forms, i.e., the bond-based peridynamics and the state-based peridynamics. Since the proposal of the peridynamic method, its basic theories have been deeply developed from several perspectives [17–26]. Meanwhile, the peridynamic method has been widely extended to many fields. For example, an improved peridynamic fracture model for the analyses of brittle fracture problems was developed by Huang et al. [27] and Hu et al. [28]. A peridynamic contact algorithm was proposed by Ye et al. [29] for the propeller-ice contact problems and Xue et al. [30] for the thermal contact problems. A peridynamic formulation for transient heat conduction was presented by Oerkus et al. [31–33] to simulate the heat conduction problems in bodies with evolving discontinuities. Wang et al. [34] developed a dual horizon peridynamic method for the thermal diffusion analysis. Further, Ouchi et al. [35–37] proposed a coupling peridynamic approach for the consolidation and dynamic analyses of saturated porous media. Silling et al. [38] and Li et al. [39] developed a peridynamic model for the nonlinear analyses of bimodular truss structures, tensegrity structures and membranes. In addition, the peridynamic theory was also used to simulate the chemical corrosion, damage and fracture problems [40–44]. As demonstrated by these successful applications of the peridynamic method to commendably deal with the heat conduction problems, contact problems and discontinuous problems, the method shows great promise for the simulation of the thermal ablation problems in metals.

This paper aims to develop a nonlocal peridynamic method for the evaluation of the metal ablation under high temperature. In the method, the peridynamic formulation for the heat conduction problem is obtained by Taylor’s expansion technique. To describe the moving boundary of the system caused by the thermal ablation, a simple and efficient moving boundary model in the peridynamic framework is proposed, in which the ablated states of the material points are represented by an additional scalar field. It is worth mentioning that due to the introduction of the scalar field, there is no need to update the computational domain and the horizon of material points during the whole computational process, which can reduce computational costs. Furthermore, a peridynamic contact algorithm is presented to determine the contact relationship between the ablated system and the heat carrier, which can be simply and conveniently achieved because of the automatic non-interpenetration properties of the peridynamic method. It is noted that during the calculation, all the material points, that is, the boundary material points (BMP), internal material points (IMP) and ablated material points (AMP), will change types due to the occurrence of the thermal ablation. In addition, the computational procedure of the present method is given out in detail and the effectiveness of the method is demonstrated by several representative numerical examples.

The remaining sections of this paper are organized as follows. Section 2 shows the peridynamic formulation for the transient heat conduction problem and the derivation of the micro-conductivity on the basis of the Taylor’s expansion technique. The moving boundary model in the peridynamics is established in Section 3 and the peridynamic contact algorithm is presented in Section 4. In Section 5, the computational implementation of the present method is described in detail. Moreover, several representative numerical examples are illustrated in Section 6 and the results verify the validity and accuracy of the present method. Finally, some concluding remarks are presented in Section 7.

2  Peridynamic Formulation for the Transient Heat Conduction Problem

On the basis of the non-local peridynamic model and the corresponding spatial uniform discretization as shown in Fig. 1, the peridynamic formulation for the transient heat conduction problem can be expressed as [33]:

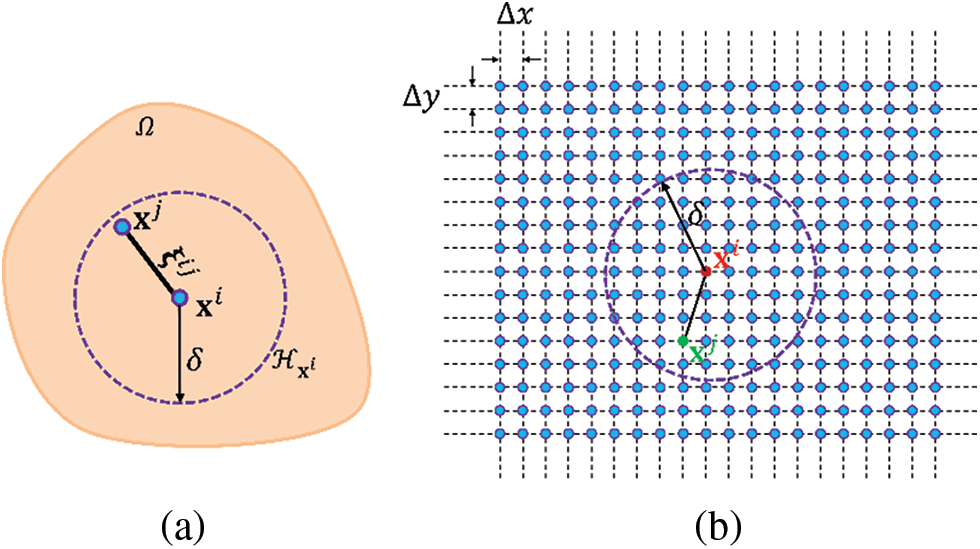
Figure 1: Schematic diagram of (a) a non-local peridynamic model and (b) a spatial discretization for evaluation

ρc∂T(xi,t)∂t=∫Hxi(J(xi,xj,t)−J(xj,xi,t)‖ξij‖)dVxj(1)

where ρ and c are the mass density and the specific thermal capacity of the material, respectively. ξij=xj−xi, in which xi and xj indicate the coordinates of the i-th and j-th material points. Vxi is the volume and Hxi is the neighborhood of the material point xi with a certain horizon δ. T(xi,t) presents the temperature of the material point xi at time t. J(xi,xj,t) is the heat flow density that the material point xj operates on the material point xi and it can be expressed as

J(xi,xj,t)={12K[δ]ω(‖ξij‖)T(xj,t)−T(xi,t)‖ξij‖,‖ξij‖≤δ0,‖ξij‖>δ(2)

where K[δ] is the micro-conductivity for the isotropic and homogeneous materials, and it can be obtained according to the local thermal conductivity k in the classical heat transfer model. It is noted that the micro-conductivity K[δ] is a variable value determined by the non-local effects of the material. ω(‖ξij‖) is the weight function that indicates the range and degree of the long-range effects of the heat diffusion between the material points xi and xj. Moreover, on the basis of the expression of J(xj,xi,t), it yields that J(xi,xj,t)=−J(xj,xi,t). Next, in order to obtain the micro-conductivity K[δ], substituting the expressions of J(xi,xj,t) and J(xj,xi,t) into Eq. (1) yields that

ρc∂T(xi,t)∂t=∫HxiK[δ]ω(‖ξij‖)T(xj,t)−T(xi,t)‖ξij‖2dVxj(3)

In addition, based on Taylor’s expansion technique, the temperature T(xi,t) can be approximately expressed as a function expanded at the material point xj, that is

T(xi,t)=T(xj,t)+(ξij⋅∇)T(xi,t)+12(ξij⋅∇)(ξij⋅∇)T(xi,t)+O(‖ξij‖2)(4)

Substituting Eq. (4) into Eq. (3) yields

ρc∂T(xi,t)∂t≅∫HxiK[δ]ω(‖ξij‖)((ξij⋅∇)+12(ξij⋅∇)(ξij⋅∇))T(xi,t)‖ξij‖2dVxj(5)

Due to the symmetric property of the integral domain, e.g., Hxi is circular for two-dimensional problems and spherical for three-dimensional problems, the odd-ordered terms in Eq. (5) can be omitted. Then we can obtain that

ρc∂T(xi,t)∂t=∫HxiK[δ]ω(‖ξij‖)(ξij⋅∇)(ξij⋅∇)T(xi,t)2‖ξij‖2dVxj

=K~:(∇(∇T(xi,t)))(6)

in which the second order tensor K~ indicates the nonlocal thermal conductivity in the peridynamics and it is given by

K~=∫Hxi12K[δ]ω(‖ξij‖)ξij⊗ξij‖ξij‖2dVxj

K~mn={∫Hxi12K[δ]ω(‖ξij‖)ξmijξnij‖ξij‖2dVxj,m=n0,m≠n(7)

where ξmij and ξnij are the components of the vector ξij. It can be seen from Eq. (7) that K~ is a diagonal matrix and it can be expressed as K~=diag(K~11,K~22) for the two-dimensional problems. Then, Eq. (6) can be rewritten as

ρc∂T(xi,t)∂t=K~mn∂2T(xi,t)∂xm∂xn

=K~11∂2T(xi,t)∂x1∂x1+K~22∂2T(xi,t)∂x2∂x2

=∇⋅(K~⋅∇T(xi,t))(8)

It is noted that Eq. (8) is similar to the governing equation of the classical heat transfer model. Therefore, it is expected from Eq. (8) that the nonlocal thermal conductivities K~11 and K~22 in the peridynamic model converge towards the local thermal conductivity k in the classical heat transfer model. Therefore, we can obtain that

k=∫Hxi12K[δ]ω(‖ξij‖)(ξmij)2‖ξij‖2dVxj(9)

Next, two kinds of weight functions are considered, i.e., ω(‖ξij‖)=1 for the constant weight function and ω(‖ξij‖)=1−‖ξij‖δ for the triangular weight function. For one-dimensional problems, we have ξmij=‖ξij‖. Moreover, according to Eq. (9), we can set ‖ξij‖=r and ξij=[rcos⁡θrsin⁡θ]T for the two-dimensional circular integral domain. Then, the corresponding expression of the micro-conductivity K[δ] can be written as [33]

K[δ]={kδ,ω(‖ξij‖)=1,1D4kπδ2,ω(‖ξij‖)=1,2D(10)

and

K[δ]={kδ,ω(‖ξij‖)=1−‖ξij‖δ,1D12kπδ2,ω(‖ξij‖)=1−‖ξij‖δ,2D(11)

Consequently, the peridynamic formulation of the one and two-dimensional transient heat conduction problems with the triangular weight function, for example, can be expressed as

ρc∂T(xi,t)∂t=∫Hxikδ(1−‖ξij‖δ)T(xj,t)−T(xi,t)‖ξij‖2dVxj,1D(12)

and

ρc∂T(xi,t)∂t=∫Hxi12kπδ2(1−‖ξij‖δ)T(xj,t)−T(xi,t)‖ξij‖2dVxj,2D(13)

In addition, both the Dirichlet (temperature) and Neumann (heat-flux) boundary conditions are considered in this paper. To impose these above boundary conditions, the fictitious material points are added outside the corresponding boundaries. For the Dirichlet boundary condition, the given temperature values are directly applied to the additional fictitious material points and remain constant all the time. For the Neumann boundary conditions, the given heat-flux values are indirectly imposed on the additional fictitious material points through the linear distributed temperatures as shown in Fig. 2. That is, after obtaining the temperatures of actual material points at every time step, the temperatures of fictitious material points are updated from the corresponding temperatures of boundary material points adding a temperature gradient related to the boundary heat-flux. In other words, for the Neumann boundary condition, the values of the temperatures of fictitious material points can be obtained by a temperature extrapolated method at every time step. The material point xi is imposed a given heat flux q, for example, the expression of the linear distributed temperatures on the fictitious material points outside the material point xi as shown in Fig. 2 can be written as

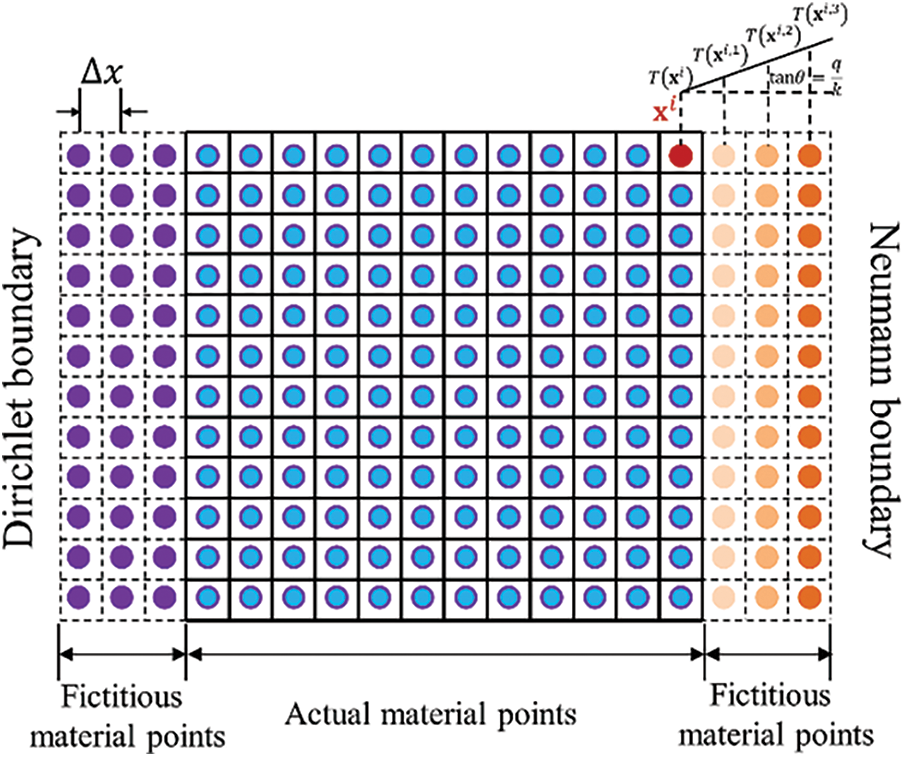
Figure 2: Schematic diagram of the fictitious material points and imposing the Dirichlet and Neumann boundary conditions

T(xi,j,t)=T(xi,t)+jΔxqk,j=1,⋯,m(14)

where T(xi,j,t) represents the temperature on the j-th fictitious material point outside the material point xi, Δx is the size of the uniform material points and m=δΔx is related to the number of material points inside the neighborhoods.

3  Moving Boundary Model

The thermal ablation is a common and direct way that may arise the serious failure for the metal structure under high temperature. The material is ablated while the temperature of the material reaches to its critical melting temperature of the material. Obviously, the geometry of the metal structure is changing along with the thermal ablation process. Therefore, to evaluate the thermal ablation process of the metal structure heated by a heat carrier with very high temperature, it is necessary to consider the moving boundaries besides the heat diffusion in the structure. For the finite element method, it is complex and uneconomical to deal with the problems with moving boundaries because the corresponding heat transfer matrix of the system needs to be reassembled when its geometry is changed during the numerical simulation. Fortunately, the peridynamics is a nonlocal method that expressed by an integral equation and the structure is discretized into many material points while a meshless method is adopted [17], which makes it convenient and prone to handle the moving boundaries. In the peridynamic moving boundary model, the whole material points are divided into three categories during the thermal ablation process of the metal structure as shown in Fig. 3. They are the internal material point (IMP), the boundary material point (BMP) and the ablated material point (AMP), respectively. During the calculation, we need to estimate whether the temperature T(xi,t) of the material point xi reaches the critical melting temperature T^ of the material. Meanwhile, during the calculation, the three kinds of material points will change types due to the occurrence of the thermal ablation. In addition, a scalar φ(xi,t) is introduced to describe the ablated state of the material point xi, that is

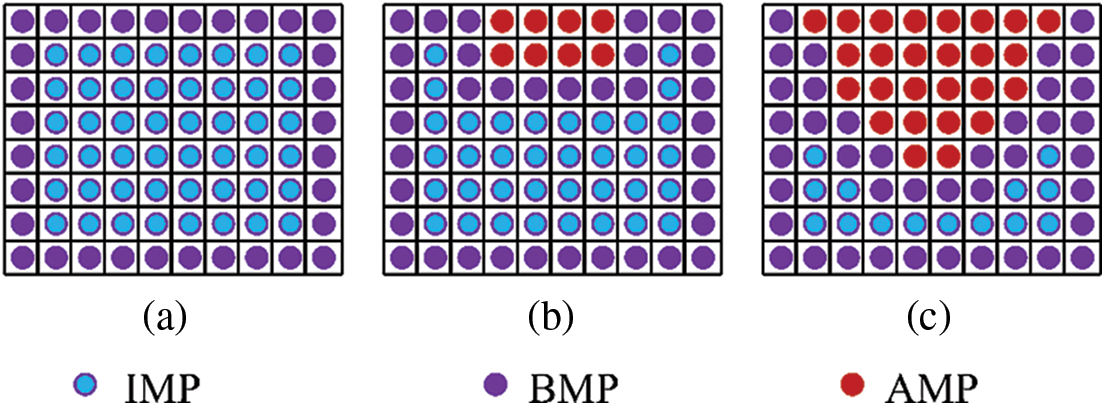
Figure 3: Moving boundary model: (a) initial boundary, (b) interim boundary and (c) final boundary, in which IMP is the internal material point, BMP is the boundary material point and AMP is the ablated material point

φ(xi,t)={1,max{T(xi,t)}<T^0,max{T(xi,t)}≥T^(15)

in which, max{T(xi,t)} presents the maximum temperature of the material point xi during the time history. It is noted that Eq. (15) can embody the irreversible features of the thermal ablation process. In addition, it can be seen from Eq. (15) that φ(xi,t)=1 presents the un-ablated state of the material point xi while φ(xi,t)=0 denotes the ablated state of the material point xi.

Taking the moving boundaries into account and substituting Eq. (15) into Eq. (3), the peridynamic formulation for the thermal ablation problem under high temperature can be expressed as

ρc∂T(xi,t)∂t=∫HxiK[δ]φ(xi,xj,t)ω(‖ξij‖)T(xj,t)−T(xi,t)‖ξij‖2dVxj(16)

in which,

φ(xi,xj,t)=min{φ(xi,t),φ(xj,t)}(17)

It is emphasized that the seeking of the neighborhood for each material point only needs to be operated once at the initial time step due to the introducing of the scalar φ(xi,t) for the moving boundary problems, which is a novel and economical technique to evaluate the thermal ablation process in metal under high temperature.

4  Contact Algorithm

In this paper, the thermal ablation process of the metal structure caused by a heat carrier with high temperature is evaluated. Except for the heat diffusion problem, the contact problem should also be considered in this simulation. Fortunately, the automatic non-interpenetration properties of the peridynamic method can naturally deal with the contact problem [45]. On the basis of the moving boundary model mentioned in Section 3, the contact algorithm for the peridynamic method is presented in this section. Fig. 4 depicts the non-contact and the contact states between the ablated metal structure and the heat carrier. For this thermal ablation problem, we consider that the contact state of the metal structure and the heat carrier should be maintained all the time. Therefore, the minimum distance d between these two bodies along the moving direction n should be calculated at every time step. In addition, the distance dH,Mi,j between the boundary material points of these two bodies along the moving direction n can be expressed as

Figure 4: Illustrations of contact model: (a) non-contact state and (b) contact state

dH,Mi,j=‖(yi−yj)⋅n‖,i∈BMPH,j∈BMPM(18)

where yi and yj present the current coordinates of the material points xi and xj, respectively. BMPM and BMPH denotes the collections of the boundary material points of the metal structure and the heat carrier, respectively.

Consequently, the displacement increment Δu of the heat carrier at the current time step can be expressed as

Δu=max{0,dH,Mi,j−d0i,j},i∈BMPH,j∈BMPM(19)

in which, d0i,j is the distance between the material points xi and xj when the representative spaces of these two material points are contact critically. In addition, it is noted that the stresses and deformations of the metal structure and the heat carrier are not considered in the present thermal ablation problem. In other words, their contact states are maintained and their contact forces are zero all the time. In our future work, the mechanical deformations of the metal structure and the heat carrier will be taken into account for the analyses of the thermal ablation problem.

5  Computational Implementations

On the basis of the discretization in spatial and temporal, the discretized peridynamic formulation for the thermal ablation problem in metal under high temperature can be expressed as

ρcT(xi,n+1)−T(xi,n)Δt=∑j=1NxiK[δ]φ(xi,xj,n)ω(‖ξij‖)T(xj,n)−T(xi,n)‖ξij‖2Vxj(20)

where n is the n-th time step and Nxi is the number of the material points in the horizon of material point xi.

In addition, the computational procedure of the proposed peridynamic method for the thermal ablation problem of the metal structures is listed in the following:

(1)  Set the control parameters (size of material points Δx, horizon of material points δ, time step Δt, total time tf, etc.), the material parameters (mass density ρ, thermal conductivity k, thermal capacity c, critical melting temperature T^, etc.) and the geometrical and boundary information.

(2)  Set the initial variables, such as the initial temperature T0(xi,t), the initial state scalar φ0(xi,t)=1, the initial coordinates x, etc.

(3)  Loop for the time step (initialize n=0).

(3.1) Set n=n+1.

(3.2) Calculate the displacement increment Δu on the basis of Eq. (19), if Δu>0, update the coordinates of the heat carrier and the new neighborhood of the material points; otherwise, go to Step (3.3).

(3.3) Calculate the current temperature field on the basis of Eq. (20).

(3.4) Update the ablated state scalar φ(xi,t) for each material point xi. if max{T(xi,t)}≥T^, φn(xi,t)=0; otherwise, φn(xi,t)=1.

(3.5) Update the classification of the material points, i.e., IMP, BMP and AMP.

(4)  If t≥tf, go to Step (5); else, go to Step (3.1).

(5)  Finish the computations and output the results.

In addition, the thermal conductivity between the metal structure and the heat carrier can be given by

k(xi,xj)=dHk(xi,t)+dMk(xj,t)‖ ξij ‖, i∈BMPH, j∈BMPM (21)

in which, dH and dM are the distances from the material points xi and xj to the contact surface, respectively. Moreover, Fig. 5 shows the definitions of the distances, the contact surface and the interaction between the material points of the metal structure and heat carrier.

Figure 5: Illustrations of the interaction between the material points of the metal structure and heat carrier

6  Numerical Examples

In this section, several representative numerical examples are considered to evaluate the validity and accuracy of the proposed method. In addition, the relative errors of the temperature fields are defined as

L2=∑i=1N(TPD,i−TR,i)2∑i=1NTR,i2(22)

where TPD is the results obtained by the present method, TR stands for the reference solutions and N is the total number of the material points of the metal structure.

6.1 Heat Conduction in a Plate

Firstly, a simple transient heat conduction in a 2D plate is considered to investigate the validity and accuracy of the present method. As shown in Fig. 6, the length and width of the plate are L=H=1.0m. For simplicity, the material properties are chosen to be unit values, i.e., k=1.0 W/(m⋅\textdegreeC) and ρc=1.0 J/(m3⋅°C).

Figure 6: Sketch and boundary conditions of the 2D transient heat conduction problem

The initial and boundary conditions are as follows:

T(x,y,0)=T0

T(0,y,t)=T(L,y,t)=T1

T(x,0,t)=T(x,H,t)=T1(23)

where T0=0°C and T1=100°C. In addition, the corresponding analytical solutions for this problem can be expressed as [46]

T(x,y,t)=T1+16(T0−T1)π2×∑i=1,3,⋯∞∑j=1,3,⋯∞exp⁡[−π2t(i2L2+j2H2)]ijsin⁡(iπxL)sin⁡(jπyH)(24)

For the numerical simulation, three kinds of horizons of material points are taken into account, i.e., δ=13L480, 13L360 and 13L240. Then, four kinds of discretization in spatial are considered, i.e., L=H=100Δx, 160Δx, 200Δx and 250Δx, in which the corresponding numbers of the material points along the radius of the neighborhood are m=δΔx≈2.71, 4.33, 5.42 and 6.77 with δ=13L480, respectively. The time step is chosen as 1.0×10−6 s.

Fig. 7 depicts the relative errors changing with the horizons and sizes of the material points. It can be seen from these curves that the horizon δ of the material points is smaller, and the relative errors are smaller when m is fixed, which reveals that it is consistent with the δ-convergence. Moreover, the relative errors are also consistent with the m-convergence, i.e., the relative errors should be smaller when the value of m is smaller. It is also noted that the minimum relative error is 0.24\%  with δ=13L480 and m=4.33 among these results obtained by different computational parameters, which is a result of the numerical error and the difference between the nonlocal theory and the local theory. Based on the convergence behavior of the results for the present method, L=H=160 Δx and δ=13L480 are selected in the following discussions. Fig. 8 shows the temperature history curves of points A, B and C obtained by the present method and from the analytical solution. The temperature distributions along the line of y=0.5m at time t=0.03s, 0.06s and 0.09s are plotted in Fig. 9, which demonstrates that the results obtained by the present method fit well with the analytical solutions. In addition, Fig. 10 shows the temperature contours at time t=0.03s, which further verifies the validity and accuracy of the present method for the heat conduction problems.

Figure 7: The relative errors changing with the horizon and size of the material point

Figure 8: Temperature history curves at different points

Figure 9: Temperature distributions along the line of y=0.5m at time t=0.03s, 0.06s and 0.09s, respectively

Figure 10: Temperature contours obtained by different methods at time t=0.03s

6.2 An Al Plate Heated by a Laser

To investigate the validity and effectiveness of the present method for the evaluation of metal ablation under high temperature, an Al plate heated with a laser is considered. As shown in Fig. 11, the dimension of the Al plate is 0.1×0.1m2. The heat source of the laser is simplified and the corresponding laser intensity follows the exponential distribution [4], i.e., S=αI(x,y)S0, where S0=2.376×107 KW/m2, α is a coefficient with initial value of 1.0. For the material properties of the aluminum, k=237.0 W/(m⋅°C), c=880 J/(kg⋅°C) and ρ=2700.0 kg/m3. The critical melting temperature T^ of the Al plate is 660°C. For the initial and boundary conditions, the initial temperature is T0=0 for the whole Al plate and all of the edges are insulated. Then, the Al plate is discretized into 160×160 uniform material points and the horizon of the material point is 13L480. The step for the time integration is 1.0×10−4s and the total time is 40.0s. Fig. 12 shows the temperature history curves of points A, B and C obtained by the present method. Fig. 13 presents the temperature distributions along the line of x=0.5m at time t=4.0s, 16.0s, 24.0s and 40.0s, in which the horizontal segments stand for the ablated maximum depths in the Al plate. In addition, three kinds of laser intensities are considered to investigate the effect of laser intensity on the speed of ablation. Fig. 14 plots the history curves of ablated depth when α=0.8, 1.0 and 1.2, respectively. It can be seen from these curves that the laser intensities are much stronger, the speeds of ablation are faster. While the speed of ablation decreases with the increase of time since the laser intensity decreases exponentially. It also reveals that the history curves of the ablated depths are smooth when the laser intensity is very strong, nevertheless, those of the ablated depths are ladder-shaped when the laser intensity is weak. Moreover, Fig. 15 shows the temperature contours and ablated shapes with α=1.0 at time t=2.0s, 4.0s, 8.0s, 12.0s, 20.0s and 40.0s, respectively, which is consistent with those in reference [4] and presents qualitatively the ablated shapes of the Al plate heated with a laser.

Figure 11: Sketch of the square plate heated with a laser source

Figure 12: Temperature history curves at different points obtained by the present method

Figure 13: Temperature distributions along the line of x=0.5m when α=1.0 at time t=4.0s, 16.0s, 24.0s and 40.0s, respectively

Figure 14: History curves of ablated depth for different laser intensities obtained by the present method

Figure 15: Temperature contours and ablated shapes when α=1.0 at time t=2.0s, 4.0s, 8.0s, 12.0s, 20.0s and 40.0s, respectively

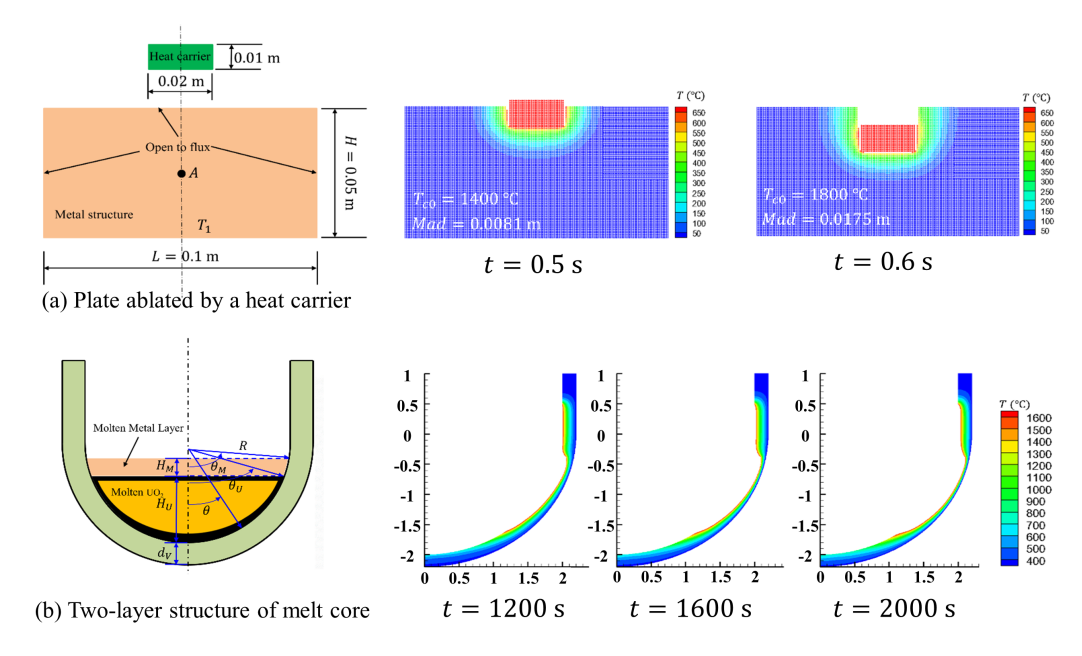
6.3 A Rectangle Al Plate Ablated by a Heat Carrier

Next, a rectangle Al plate ablated by a heat carrier is considered to examine the present contact algorithm. As shown in Fig. 16, the length and width of the Al plate are 0.1m and 0.05m. Besides, those of the heat carrier are 0.02m and 0.01m, respectively. The material parameters of the Al plate are: kAl=237.0 W/(m⋅°C), cAl=880 J/(kg⋅°C) and ρAl=2700.0  kg/m3. The material parameters of the heat carrier are: kc=300.0 W/(m⋅°C), cc=1300 J/(kg⋅°C) and ρc=8000.0 kg/m3. Further, the critical melting temperature of the Al plate is T^Al=660°C. For the initial and boundary conditions, the initial temperature is TAl0=0 for the whole Al plate. The temperature of the lower edge is fixed as TAl1=0 and the heat flux of the other edges is kept open to flow. Three kinds of temperatures of the heat carrier are taken into account, i.e., Tc0=1400°C, Tc0=1600°C and Tc0=1800°C. During the simulation, the variation of the temperature of the heat carrier is changed hypothetically to be uniform. In addition, the energy exchange between the Al plate and the heat carrier is achieved by heat conduction and the effects of the thermal radiation of the heat carrier on the Al plate are neglected. To perform numerical simulating, the Al plate is discretized into 160×80 uniform material points and the horizon of the material point is 13L480. The step for the time integration is chosen as 1.0×10−4s and the total time is 1.0s. Fig. 17 depicts the temperature history curves at point A when Tc0=1400°C, Tc0=1600°C and Tc0=1800°C, respectively. Fig. 18 plots the temperature distributions along the line of y=0.5m when Tc0=1800°C at time t=0.1s, 0.5s and 1.0s, respectively. The history curves of ablated depth for Tc0=1400°C, Tc0=1600°C and Tc0=1800°C are presented in Fig. 19, from which it can be seen that the speed of ablation is faster and the value of the final maximum ablated depth (Mad) is much larger when the initial temperature Tc0 of the heat carrier is higher. Fig. 20 demonstrates the corresponding configurations when the ablated depth achieves the maximum values for Tc0=1400°C, Tc0=1600°C and Tc0=1800°C, respectively. The maximum ablated depths for these three cases are Mad=0.0081 m when t=0.5 s, 0.0125 m when t=0.5 s and 0.0175 m when t=0.6s, respectively. In addition, Fig. 21 shows the temperature contours and ablated shapes when Tc0=1800°C at time t=0.02s, 0.1s, 0.2s and 0.4s, respectively.

Figure 16: Illustration of the rectangle plate ablated by a heat carrier

Figure 17: Temperature history curves at point A when Tc0=1400°C, 1600°C and 1800°C, respectively

Figure 18: Temperature distributions along the line of y=0.025 m when Tc0=1800°C

Figure 19: History curves of ablated depth for Tc0=1400°C, 1600°C and 1800°C, respectively

Figure 20: Temperature contours and ablated shapes when Tc0=1800°C at time t=0.02s, 0.1s, 0.2s and 0.4s, respectively

Figure 21: Temperature contours and ablated shapes with the maximum ablated depth (Mad) for Tc0=1400°C, 1600°C and 1800°C, respectively

6.4 Lower Head of RPV Ablated by a Core Melt

Finally, the ablation process of the lower head of the RPV heated by core melt, which is simplified from the nuclear engineering problems, is investigated [15]. Fig. 22a shows the two-layer structure of melt core in the lower head of the RPV, in which the radius of the inwall is R=2 m and the thickness of the wall is δV=0.2m. The thicknesses of the molten UO2 and molten metal are HU=1.325m and HM=0.270m, respectively. The material parameters of the RPV are: k=25.5 W/(m⋅K), c=740 J/(kg⋅K), ρ=6890.0 kg/m3 and the critical melting temperature is T^=1600 K. For the initial and boundary conditions, the initial temperature is T0=373K and the temperature of the outer wall is fixed by T1=373K. Moreover, a non-uniform heat flux q(θ) is imposed on the moving inwall of the RPV, in which the distribution of q(θ) is plotted in Fig. 22b. For the sake of the computational cost, only half of the symmetric RPV is utilized for the numerical simulation. Then, the RPV is discretized into many uniform material points, whose size is Δx=Δy=0.0025m. The horizon of the material point is δ=3.0Δx. The step for the time integration is chosen as 1.0×10−2s and the total time is 2000.0s. Fig. 23 shows the profile of the moving inwall of the RPV caused by the thermal ablation, from which it can be seen that the ablation occurs at the region imposed a larger heat source and the minimum thickness of the RPV becomes smaller and smaller along with the thermal ablation process. Moreover, Fig. 24 presents the temperature contours and ablated shapes of the RPV at time t=200s, 600s, 1000s, 1200s, 1600s and 2000s, respectively. The ablated shapes obtained by the present method are similar with those obtained by the finite element method [15]. Consequently, the present peridynamic method is valid and effective for the evaluation of the ablation of the RPV heating by a core melt.

Figure 22: Illustration of the RPV model: (a) Two-layer structure of melt core and (b) heat flux imposed on the inwall

Figure 23: Profile of the moving inwall of the RPV caused by the thermal ablation

Figure 24: Temperature contours and ablated shapes of the RPV at time t=200s, 600s, 1000s, 1200s, 1600s and 2000s, respectively

7  Conclusions

This paper presents a nonlocal peridynamic method for the evaluation of the thermal ablation in metal under high temperature. Firstly, the peridynamic formulation for the transient heat conduction problem is derived based on Taylor’s expansion technique. To simulate the thermal ablation problem, whose geometry is changed, a simple and efficient moving boundary model in the peridynamic framework is proposed by introducing a scalar field to describe the ablated states of material points. In addition, on the basis of the automatic non-interpenetration properties of the peridynamic method, an effective contact algorithm is suggested to determine the contact relationship between the ablated system and the additional heat carrier. Furthermore, the corresponding computational procedure is given out in detail. Finally, several representative numerical examples are taken into account. These results obtained by the present method fit well with the reference solutions, which demonstrates the validity and accuracy of the present method. Moreover, the present peridynamic method can be extended to analyze the coupling thermo-, deformation-, ablation- and fracture problems in the future.

Funding Statement: This work was supported by the National Natural Science Foundation of China (No. 12102416).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Dai, M. Q., Liu, Y. K., Fu, Z. C., Liu, J., Bi, X. L. (2019). Experimental investigation on ablation characteristics of coated and uncoated steel under 30/80 μs impulse current. Plasma Science & Technology, 21(7), 075501. DOI 10.1088/2058-6272/ab1037. [Google Scholar] [CrossRef]

 2.  Tomko, J. A., Giri, A., Donovan, B. F., Bubb, D. M., O’Malley, S. M. et al. (2017). Energy confinement and thermal boundary conductance effects on short-pulsed thermal ablation thresholds in thin films. Physical Review B, 96(1), 014108. DOI 10.1103/PhysRevB.96.014108. [Google Scholar] [CrossRef]

 3.  Ren, Y. P., Cheng, C. W., Chen, J. K., Zhang, Y. W., Tzou, D. Y. (2013). Thermal ablation of metal films by femtosecond laser bursts. International Journal of Thermal Sciences, 70, 32–40. DOI 10.1016/j.ijthermalsci.2013.03.003. [Google Scholar] [CrossRef]

 4.  Xiong, Q. L., Sha, Z. D., Pei, Q. X., Kitamura, T., Li, Z. H. (2018). Thermal damage and ablation behavior of graphene induced by ultrafast laser irradiation. Journal of Thermal Stresses, 41(9), 1153–1168. DOI 10.1080/01495739.2018.1461040. [Google Scholar] [CrossRef]

 5.  Wang, P. F., Chen, X. Z., Pan, Q. H., Madigan, B., Long, J. Q. (2016). Laser welding dissimilar materials of aluminum to steel: An overview. International Journal of Advanced Manufacturing Technology, 87(9–12), 3081–3090. DOI 10.1007/s00170-016-8725-y. [Google Scholar] [CrossRef]

 6.  Bergmann, J. P., Grӓtzel, M., Schurér, R., Regensburg, A., Weigl, M. (2016). Advances and potential in friction stir welding of aluminum alloys. Key Engineering Materials, 710, 137–142. DOI 10.4028/www.scientific.net/KEM.710.137. [Google Scholar] [CrossRef]

 7.  Kulekci, M. K., Kaluc, E., Sik, A., Basturk, O. (2010). Experimental comparison of MIG and friction stir welding processes for EN AW-6061-T6 (Al Mg Si Cu) aluminum alloy. Arabian Journal for Science and Engineering, 35, 321–330. [Google Scholar]

 8.  Nath, A. K., Gupta, A., Benny, F. (2012). Theoretical and experimental study on laser surface hardening by repetitive laser pulses. Surface and Coating Technology, 206(8–9), 2602–2615. DOI 10.1016/j.surfcoat.2011.11.019. [Google Scholar] [CrossRef]

 9.  Sarkar, S., Gopinath, M., Chakraborty, S. S., Syed, B., Nath, A. K. (2016). Analysis of temperature and surface hardening of low carbon thin steel sheets using Yb-fiber laser. Surface and Coating Technology, 302(1), 344–358. DOI 10.1016/j.surfcoat.2016.06.045. [Google Scholar] [CrossRef]

10. Kim, S., So, S., Ki, H. (2015). Controlling thermal deformation using a heat sink in laser transformation hardening of steel sheets. Journal of Materials Processing Technology, 216, 455–462. DOI 10.1016/j.jmatprotec.2014.10.014. [Google Scholar] [CrossRef]

11. Canel, T., Baglan, I., Sinmazcelik, T. (2019). Mathematical modeling of laser ablation of random oriented short glass fiber reinforced polyphenylene sulphide (PPS) polymer composite. Optics and Laser Technology, 115(7), 481–486. DOI 10.1016/j.optlastec.2019.02.049. [Google Scholar] [CrossRef]

12. Anderson, M. H., Herranz, L. E., Corradini, M. L. (1998). Experimental analysis of heat transfer within the AP600 containment under postulated accident conditions. Nuclear and Engineering Design, 185(2–3), 153–172. DOI 10.1016/S0029-5493(98)00232-5. [Google Scholar] [CrossRef]

13. Theofanous, T. G., Liu, C., Additon, S., Angelini, S., Kymalainen, O. (1997). In vessel coolability and retention of a core. Nuclear and Engineering Design, 169(1–3), 1–48. DOI 10.1016/S0029-5493(97)00009-5. [Google Scholar] [CrossRef]

14. Guan, Z. H., Yu, H. X., Jiang, G. M. (2008). Study on cooling model for debris in lower plenum and countermeasures for prevention of focusing effect. Nuclear Power Engineering, 29(5), 72–76. [Google Scholar]

15. Zhan, D. K., Liu, F. Y., Zhang, X. Y., Chen, H. D., Li, J. Y. (2018). Ablation and thermal stress analysis of RPV vessel under heating by core melt. Nuclear and Engineering Design, 330(5), 550–558. DOI 10.1016/j.nucengdes.2018.02.008. [Google Scholar] [CrossRef]

16. Silling, S. A. (2000). Reformulation of elasticity theory for discontinuities and long-range forces. Journal of the Mechanics and Physics of Solids, 48(1), 175–209. DOI 10.1016/S0022-5096(99)00029-0. [Google Scholar] [CrossRef]

17. Silling, S. A., Askari, E. (2005). A meshfree method based on the peridynamic model of solid mechanics. Computers and Structures, 83(17–18), 1526–1535. DOI 10.1016/j.compstruc.2004.11.026. [Google Scholar] [CrossRef]

18. Seleson, P., Parks, M. L., Gunzburger, M., Lehoucq, R. B. (2009). Peridynamics as an upscaling of molecular dynamics. Multiscale Modeling and Simulation, 8(1), 204–227. DOI 10.1137/09074807X. [Google Scholar] [CrossRef]

19. Silling, S. A. (2010). Linearized theory of peridynamic states. Journal of Elasticity, 99(1), 85–111. DOI 10.1007/s10659-009-9234-0. [Google Scholar] [CrossRef]

20. Silling, S. A., Lehoucq, R. B. (2010). Peridynamic theory of solid mechanics. Advaces in Applied Mechanics, 44, 73–168. DOI 10.1016/S0065-2156(10)44002-8. [Google Scholar] [CrossRef]

21. Silling, S. A., Epton, M., Wechner, O., Xu, J., Askari, E. (2007). Peridynamic states and constitutive modeling. Journal of Elasticity, 88(2), 151–184. DOI 10.1007/s10659-007-9125-1. [Google Scholar] [CrossRef]

22. Tupek, M. R., Radovitzky, R. (2014). An extended constitutive correspondence formulation of peridynamics based on nonlinear bond-strain measures. Journal of the Mechanics and Physics of Solids, 65, 82–92. DOI 10.1016/j.jmps.2013.12.012. [Google Scholar] [CrossRef]

23. Han, F., Lubineau, G., Azdoud, Y., Askari, A. (2016). A morphing approach to couple state-based peridynamics with classical continuum mechanics. Computer Methods in Applied Mechanics and Engineering, 301, 336–358. DOI 10.1016/j.cma.2015.12.024. [Google Scholar] [CrossRef]

24. Lai, X., Liu, L. S., Li, S. F., Zeleke, M., Liu, Q. et al. (2018). A non-ordinary state-based peridynamics modeling of fractures in quasi-brittle materials. International Journal of Impact Engineering, 111(1), 130–146. DOI 10.1016/j.ijimpeng.2017.08.008. [Google Scholar] [CrossRef]

25. Ren, H. L., Zhuang, X. Y., Cai, Y. C., Rabczuk, R. (2016). Dual-horizon peridynamics. International Journal for Numerical Methods in Engineering, 108(12), 1451–1476. DOI 10.1002/nme.5257. [Google Scholar] [CrossRef]

26. Ren, H. L., Zhuang, X. Y., Rabczuk, T. (2017). Dual-horizon peridynamics: A stable solution to varying horizons. Computer Methods in Applied Mechanics and Engineering, 318(4), 762–782. DOI 10.1016/j.cma.2016.12.031. [Google Scholar] [CrossRef]

27. Huang, D., Lu, G. D., Qiao, P. Z. (2015). An improved peridynamic approach for quasi-static elastic deformation and brittle fracture analysis. International Journal of Mechanical Sciences, 94(8), 111–122. DOI 10.1016/j.ijmecsci.2015.02.018. [Google Scholar] [CrossRef]

28. Hu, W., Ha, Y. D., Bobaru, F. (2012). Peridynamic model for dynamic fracture in unidirectional fiber-reinforced composites. Computer Methods in Applied Mechanics and Engineering, 217–220, 247–261. DOI 10.1016/j.cma.2012.01.016. [Google Scholar] [CrossRef]

29. Ye, L. Y., Wang, C., Chang, X., Zhang, H. Y. (2017). Propeller-ice contact modeling with peridynamics. Ocean Engineering, 139(4), 54–64. DOI 10.1016/j.oceaneng.2017.04.037. [Google Scholar] [CrossRef]

30. Xue, T., Zhang, X. B., Tamma, K. K. (2018). A two-field state-based peridynamic theory for thermal contact problems. Journal of Computational Physics, 374(1), 1180–1195. DOI 10.1016/j.jcp.2018.08.014. [Google Scholar] [CrossRef]

31. Oterkus, S., Madenci, E., Agwai, A. (2014). Peridynamic thermal diffusion. Journal of Computational Physics, 265, 71–96. DOI 10.1016/j.jcp.2014.01.027. [Google Scholar] [CrossRef]

32. Bobaru, F., Duangpanya, M. (2010). The peridynamic formulation for transient heat conduction. International Journal of Heat and Mass Transfer, 53(19–20), 4047–4059. DOI 10.1016/j.ijheatmasstransfer.2010.05.024. [Google Scholar] [CrossRef]

33. Bobaru, F., Duangpanya, M. (2012). A peridynamic formulation for transient heat conduction in bodies with evolving discontinuities. Journal of Computational Physics, 231(7), 2764–2785. DOI 10.1016/j.jcp.2011.12.017. [Google Scholar] [CrossRef]

34. Wang, B., Oterkus, S., Oterkus, E. (2020). Thermal diffusion analysis by using dual horizon peridynamics. Journal of Thermal Stresses, 44(1), 51–74. DOI 10.1080/01495739.2020.1843378. [Google Scholar] [CrossRef]

35. Ouchi, H., Katiyar, A., York, J., Foster, J. T., Sharma, M. M. (2015). A fully coupled porous flow and geomechanics model for fluid driven cracks: A peridynamic approach. Computational Mechanics, 55(3), 561–576. DOI 10.1007/s00466-015-1123-8. [Google Scholar] [CrossRef]

36. Lai, X., Ren, B., Fan, H. F., Li, S. F., Wu, C. T. et al. (2015). Peridynamics simulations of geomaterial fragmentation by impulse loads. International Journal for Numerical and Analytical Methods in Geomechanics, 39(12), 1304–1330. DOI 10.1002/nag.2356. [Google Scholar] [CrossRef]

37. Zhang, H. W., Li, H., Ye, H. F., Zheng, Y. G. (2019). A coupling peridynamic approach for the consolidation and dynamic analysis of saturated porous media. Computational Mechanics, 64(4), 1097–1113. DOI 10.1007/s00466-019-01695-2. [Google Scholar] [CrossRef]

38. Silling, S. A., Bobaru, F. (2005). Peridynamic modeling of membranes and fibers. International Journal of Non-Linear Mechanics, 40(2–3), 395–409. DOI 10.1016/j.ijnonlinmec.2004.08.004. [Google Scholar] [CrossRef]

39. Li, H., Zhang, H. W., Zheng, Y. G., Zhang, L. (2016). A peridynamic model for the nonlinear static analysis of truss and tensegrity structures. Computational Mechanics, 57(5), 843–858. DOI 10.1007/s00466-016-1264-4. [Google Scholar] [CrossRef]

40. Chen, Z. G., Bobaru, F. (2015). Peridynamic modeling of pitting corrosion damage. Journal of the Mechanics and Physics of Solids, 78, 352–391. DOI 10.1016/j.jmps.2015.02.015. [Google Scholar] [CrossRef]

41. Chen, Z. G., Zhang, G. F., Bobaru, F. (2016). The influence of passive film damage on pitting corrosion. Journal of the Electrochemical Society, 163(2), C19–C24. DOI 10.1149/2.0521602jes. [Google Scholar] [CrossRef]

42. Wang, H., Oterkus, E., Oterkus, S. (2018). Predicting fracture evolution during lithiation process using peridynamics. Engineering Fracture Mechanics, 192(9), 176–191. DOI 10.1016/j.engfracmech.2018.02.009. [Google Scholar] [CrossRef]

43. de Meo, D., Oterkus, E. (2017). Finite element implementation of a peridynamic pitting corrosion damage model. Ocean Engineering, 135(2), 76–83. DOI 10.1016/j.oceaneng.2017.03.002. [Google Scholar] [CrossRef]

44. de Meo, D., Russo, L., Oterkus, E. (2017). Modeling of the onset, propagation, and interaction of multiple cracks generated from corrosion pits by using peridynamics. Journal of Engineering Materials and Technology, 139(4), 041001. DOI 10.1115/1.4036443. [Google Scholar] [CrossRef]

45. Lu, M. K., Zhang, J. Y., Zhang, H. W., Zheng, Y. G., Chen, Z. (2018). Time-discontinuous material point method for transient problems. Computer Methods in Applied Mechanics and Engineering, 328, 663–685. DOI 10.1016/j.cma.2017.09.022. [Google Scholar] [CrossRef]

46. Tao, J., Zheng, Y. G., Chen, Z., Zhang, H. W. (2016). Generalized interpolation material point method for coupled thermos-mechanical processes. International Journal of Mechanics and Materials in Design, 12(4), 577–595. DOI 10.1007/s10999-016-9339-0. [Google Scholar] [CrossRef]