An Unambiguity and Anti-Range Eclipse Method for PD Radar Using Biphase Coded Signals

1  Introduction

Digital array radar is a kind of radar whose transmission and reception are operated digitally, which has many incomparable advantages over traditional phased array radar, such as high amplitude, phase control accuracy and beamforming flexibility, large dynamic range, strong reliability, and low loss and sidelobe [1–3]. It has played an essential role in radar field.

Pulse doppler (PD) radar is easily realized on a digital array platform and usually used to detect long-range targets. In the search stage, PD radar uses the same antenna to transmit and receive. The advantage by turning on transmission and reception alternatingly is that there will not be any transmission leakage at the receiving end.

When the delay time of target echo is greater than the repetition period of transmitted pulses, range ambiguity will occur [4–6]. In addition, when the Doppler frequency caused by target motion is greater than half of the repetition frequency of the transmitted pulse, velocity ambiguity will happen [7]. In order to solve this problem, high pulse repetition frequency (HPRF) working mode is often adopted [8,9], but it also brings range ambiguity [10–13]. The traditional method of eliminating range ambiguity is using several different pulse repetition intervals (PRIs) based on the remainder theorem [14], the one-dimensional set algorithm [15], the look-up table method [16] and so on. However, all those methods above have their own shortcomings.

The biphase coded signal is a common pulse compression radar signal. It has been widely researched and adopted for non-ultra-high-velocity targets due to its great noise-like and low probability of intercept characteristics [17]. In this paper, HPRF working mode is adopted to avoid velocity ambiguity, narrow width of transmitted pulses is applied to reduce the blind zone, and two different HPRFs are used to solve range eclipse. In addition, multiple orthogonal biphase coded signals, based on Walsh matrix and performed genetic algorithm (GA) [18,19], are transmitted within the time corresponding to the maximum range of the radar to mitigate range ambiguity. In radar receiver, data rearrangement is performed on multiple echoes of transmitted pulses, and then pulse compression and moving target detection (MTD) are performed, after which the range ambiguity can be eliminated.

The structure of this paper is as follows: The cause of pulse radar ambiguity is analyzed, and the signal model without blur and eclipse is given in Section 2. The design flow of the transmitting signals used to resolve ambiguity is given in Section 3. The radar signal processing process is presented in Section 4, and in which the data rearrangement method is changed compared with the traditional way. The flexibility of the proposed method through simulation experiments is in Section 5. The conclusion is in Section 6.

2  Signal Model and Problem Description

2.1 Distance and Velocity Ambiguity and the Solution

For pulse radar, when echo delay of a target is longer than pulse repetition interval (PRI), the target echo will not fall in the cycle, and the measured target distance is not the real distance but a distance with range ambiguity. As shown in Fig. 1, sm(t) is the mth transmitting pulse, rm(t) is the echo of the mth transmitting pulse, τ0 is the delay of the target echo, and then the transmitting pulse can be expressed as Eq. (1).

Figure 1: Echo diagram of generating range ambiguity

s1(t)=s(t)s2(t)=s(t−tPRI)s3(t)=s(t−2tPRI)⋯sm(t)=s(t−(m−1)tPRI)(1)

where s(t) is the pulse compression signal (linear frequency modulation signal or phase coded signal), and tPRI is the time corresponding to one PRI.

Pulse radar calculates the distance by measuring the delay τ0 of the echo r1(t), and τ0 is estimated by the peak position after pulse compression which is generally achieved by matched filter doing cross-correlation operation. When τ0 is greater than PRI, cross-correlation calculation is performed with the current transmitted pulse signal s2(t) using r1(t), which is as shown in Eq. (2).

C2(t)=∫−∞∞r1(τ)s2∗(t+τ)dτ=∫−∞∞s1(τ−τ0)s1∗(t−tPRI+τ)dτ(2)

The peak position is t=τ0−tPRI, and the delay reflected by the peak is different from the real echo delay τ0, so the distance ambiguity appears. However, if a group of pulse signals with low cross-correlation peak value are transmitted, the peak value will appear only when r1(t) and s1(t) are cross-correlated, which can effectively solve the distance ambiguity problem. The relative formula is as shown in Eq. (3).

C1(t)=∫−∞∞r1(τ)s1∗(t+τ)dτ=∫−∞∞s1(τ−τ0)s1∗(t+τ)dτ(3)

The peak position is t=τ0, from which the distance can be correctly calculated.

2.2 Range Eclipse and the Solution

Radar adopts the transceiver switching mode, which inevitably results in range occlusion, that is, the echo delay of the target t1=PRI. At this time, the echo of the target happens to be at the moment of pulse transmission, and the echo diagram is shown in Fig. 2.

Figure 2: Echo diagram of generating range occlusion

Traditional HPRF radar mainly realizes anti-occlusion by using varying PRFs. Therefore, three different PRFs are adopted in order to have no ambiguity and no occlusion in the traditional method. But only two different PRFs are needed to realize detection without ambiguity and occlusion if the transmitted signal with low cross-correlation peak value is adopted to solve the ambiguity.

3  Design of Transmission Signal

As can be seen from the above section, distance ambiguity can be solved by transmitting multiple signals with low cross-correlation peak values at time division. This section will take two-phase coded signals as an example to illustrate the design process of transmitting signals.

In order to obtain the obvious main lobe after pulse compression, not only the peak value of cross-correlation between signals but also the peak value of auto-correlation side lobe of each signal is reduced during signal design. For two-phase coded signal set, the ith signal can be expressed as Eq. (4).

ui(t)=1K∑k=0K−1ejϕi,jv(t−kTz)(4)

where ϕi,j is the jth element’s phase of the ith signal, and

v(t)=rect(tTz)={1,0≤t≤Tz0,else(5)

is the pulse with the width of Tz and K is the length of the encoded signal. The auto-correlation function of signals is as Eq. (6).

A(ϕl,k)={ 1N∑n=1N−kexp(j(ϕl(n)−ϕl(n+k))),0⩽k<N1N∑n=−k+1Nexp(j(ϕl(n)−ϕl(n+k))),−N<k<0                (ϕl(n)=0,π)(6)

The cross-correlation function of two signals is as Eq. (7).

C(ϕp,ϕq,k)={ 1N∑n=1N−kexp(j(ϕq(n)−ϕp(n+k))),0⩽k<N1N∑n=−k+1Nexp(j(ϕq(n)−ϕp(n+k))),−N<k<0                     (p≠q,ϕp(n)=0,π,ϕq(n)=0,π)(7)

ϕm(n) represents the nth element’s phase of the mth signal [20].

As Section 1 says, transmitting signal set is optimized by GA. The steps are as follows:

Construct the fitness function of GA as Eq. (8).

F=ω1∑l=1Mmaxk≠0|A(ϕl,k)|+ω2∑p=1M−1∑q=p+1Mmaxk|C(ϕp,ϕq,k)|(8)

The fitness function is to calculate the auto-correlation sidelobe peak and cross-correlation peak of signals. The ω1 and ω2 are weighting coefficients, satisfying ω1+ω2=1.

Generate an N×N walsh matrix and make random exchange, then take the fitness function value shown in the minimization formula as the criterion and select M waveforms from the matrix. The selected M×N matrix is as the input of GA.

Use GA to optimize the M×N matrix. The flow chart is shown in Fig. 3 and the specific steps are as follows:

a) Calculate the fitness function value of the matrix, judge whether it meets the end condition, that is, whether the number of iterations reach the upper limit, or successive differences of optimum fitness between adjacent two generations are less than the threshold. If so, stop the iteration, otherwise, carry out the next selection, crossover, mutation, and recalculate the fitness function values until the end condition is met.

b) Discard the individual with the largest fitness function value and select the remaining individuals with the smaller values in the population for later crossover and mutation.

c) Pair individuals in the population randomly and cross the biphase coded values of paired individuals randomly to recombine into new ones.

d) According to the mutation probability, the code values, also the biphase coded values, of some columns in the random mutation population get mutation from 1 to −1 or from −1 to 1.

e) Replace the individuals with the largest fitness function value in the original population with those that have the smallest fitness function value in the new population, then return to Step a for the next iteration.

Figure 3: Flow chart of genetic algorithm

4  Process of Radar Signal

4.1 Process of Transmission

In order to avoid velocity ambiguity, HPRF mode is adopted in this paper. Multiple pulses, composed of the two-phase coded signal set designed in Section 3, which have low auto-correlation sidelobe and cross-correlation peak value, are transmit within the time corresponding to the maximum detection range of radar, which can effectively solve the distance ambiguity. The design process of emission parameters is as follows:

First, the time duration of pulse τ is determined according to the radar range blind area Rb as Eq. (9).

τ=2Rbc(9)

where c is the velocity of light. Meanwhile, the maximum radar period Tmax is determined according to the farthest detection range Rmax of the radar as Eq. (10).

Tmax=2Rmaxc(10)

Then, the PRI is determined according to the maximum radial velocity vmax of the target as Eq. (11).

PRI≤12fdmax≤λ4vmax(11)

where fdmax is the maximum Doppler frequency caused by maximum radial velocity vmax. The number m of transmitted pulses in an unambiguous period Tmax is determined as Eq. (12).

m=TmaxPRI(12)

Then, select a group of signals produced by the above method to transmit in an period Tmax. As shown in Fig. 4, in one period Tmax, transmit m orthogonal signals a1,a2,…,am, which have great auto-correlation and cross-correlation performance. The radar system usually needs to accumulate to obtain a better detection on targets, so several periods Tmax form a coherent processing interval (CPI). The number of Tmax in a specific CPI can be selected according to actual scenarios.

Figure 4: Schematic diagram of transmitted signal

4.2 Process of Receiver

4.2.1 Data Reshaping

This paper focuses on transceiver switching radar system. Therefore, the receiver cannot receive signals during transmission time, so the echo data sequence R1 collected in the first period is shown as Eq. (13).

R1=[0a1ra10a2ra2⋯0amram](13)

where 0an(n=1,2,…,m) signifies that the receiver is shut off during transmitting the pulses an(n=1,2,…,m), and ran is the receive data when the radar switches to receiving mode after transmitting. All of the above received data is digital signals that have been down-converted to baseband.

The echo data matrix R is shown in Eq. (14), which is composed by rearranging the echo data of a CPI.

R=[R1R2⋮Rm⋮]=[0a1ra10a2ra2⋯ram0a2ra20a3ra3⋯ra1′⋮⋮⋮⋮⋱⋮0amram0a1ra1′⋯ra(m−1)′⋮⋮⋮⋮⋯⋮](14)

The schematic diagram of the matrix R arrangement method is shown in Fig. 5. Each row is corresponding to an unambiguous period Tmax. The beginning time of the first row is the time when the pulse signal a1 starts to be transmitted, and the second row is corresponding to the time when the pulse signal a2 starts to be transmitted, and so on for subsequent rows.

Figure 5: Data rearrangement diagram

4.2.2 Pulse Compression

Perform matched filtering on each row of the echo data matrix R to implement pulse compression processing. The first row R1 in R is performed matched filtering with A1 constructed by adding 0, that is to make A1 and R are the time series with same length, after the transmitted signal a1. Use the frequency domain pulse compression processing method as Eq. (15).

X1=IFFT{FFT{R1[n]}⋅FFT{(A1[−n])∗}}(15)

where FFT is fast Fourier transform and IFFT is inverse fast Fourier transform. A1[−n] is the reverse of the sequence A1 and []∗ is conjugate operation. The second row R is matched with R2, and then perform the same process for the remaining rows. In the end, put the processed data into corresponding rows in a new matrix X.

4.2.3 Moving Target Detection

FFT is performed on each column in the new matrix X gotten after pulse compression, that is MTD processing, to achieve coherent accumulation, and the peak value calculated finally in this new matrix reflects the range and velocity information of the target.

5  Simulation Analysis

Assuming that a certain scene requires the radar’s range blind area Rb<500 m, the maximum detectable range is Rmax=100 km, and the maximum detectable speed is vmax=2000 m/s. Then in order to meet the demand of range blind area Rb, and according to the calculation formula of transmitting parameters in radar signal process, the transmitting pulse width is at most as Eq. (16).

τ=2Rbmaxc=3.33 μs(16)

If the radar’s radio frequency is fRF=300 MHz, then the wavelength is λ=c/f=1 m, and the pulse repetition interval is met Eq. (17).

PRI⩽λ4vmax=125 μs(17)

According to Rmax the radar period Tmax is at least as Eq. (18).

Tmax=2Rmaxc=666.7 μs(18)

From the above requirements, the radar transmitting parameters are set as Eq. (19).

{τ=2.56 μsPRI=96 μsTmax=8×PRI=768 μs(19)

So Rb is as Eq. (20).

Rb=τc2=384 m(20)

The maximum unambiguity distance and velocity, according to such way in this paper, are respectively as Eq. (21).

{Rmax′=Tmax⋅c2=115.2 kmvmax′=c4⋅f⋅PRI=2604m/s(21)

By contrast, the outcome of traditional PD radar is as Eq. (22).

{Rmax′′=PRI⋅c2=14.4 kmvmax′′=c4⋅f⋅PRI=2604m/s(22)

Obviously, the traditional PD radar cannot meet the requirement of Rmax in this scenario except for increasing PRI as Eq. (23).

PRI′′=2Rmaxc=666.7 μs(23)

Then we get the values as Eq. (24).

{Rmax′′=Tmax⋅c2=115.2 kmvmax′′=c4⋅f⋅PRI′′=375m/s(24)

The requirement of vmax cannot be met at this time, so the traditional PD radar cannot complete detection in this scenario, but the method proposed in this paper can deal with this problem. The simulation results of the traditional radar and of the proposed method are given below to verify the feasibility and superiority of such way by comparison.

5.1 Simulation Analysis of Transmitting Signal Designed by GA

In the simulation of transmitting waveform design using genetic algorithm, the length of biphase code is set to 256. Moreover, at least 8 waveforms need to be designed according to Eq. (19). Therefore, 16 transmitting waveforms are designed in this paper for using (M=16, N=256). The two coefficients in the fitness function are set as ω1=0.5, ω2=0.5, the maximum genetic iteration is set as 1500 and the maximum stagnation iteration is set as 200. The convergence of the fitness value of GA is shown in Fig. 6, in which the fitness value converges to 9.564 from the 611th to 811th generation.

Figure 6: Convergence graph of fitness value

The auto-correlation function of the signal obtained at the end of iteration is shown in Fig. 7a, and the cross-correlation function is shown in Fig. 7b. It can be seen that the signal has low auto-correlation sidelobe and low cross-correlation peak value.

Figure 7: Auto-correlation and cross-correlation

5.2 Simulation Results 1

Assume that there is only one target, the distance is 20 km, and the speed is 530 m/s. Then the echo diagram is shown in Fig. 8, in which the echo delay of the target t1>PRI, that is, the target distance is beyond the maximum unambiguity range of traditional radar, but it is within the maximum of the proposed method in this paper.

Figure 8: Schematic diagram of the echoes of one target

The signal to noise ratio (SNR) is set to −20 dB in the simulation, and the transmission parameters are set as Eq. (19). The maximum unblurred distance and maximum unblurred speed of traditional PD radar are shown in Eq. (22). Traditional PD radar only adopts a two-phase coded transmitting waveform, and its moving target detection diagram (MTD diagram) is shown in Fig. 9a, in which the calculated distance is inconsistent with the set distance and it is just equal to the difference between real distance and the maximum unfuzzy range, so it is difficult for traditional radar to distinguish whether the target is within the maximum unambiguity range, generating ambiguity. But with the method in this paper with Eq. (21), and select eight signals, having low auto-correlation sidelobe and cross-correlation peak, as transmitting set from waveforms designed in Section 5.1, and the MTD figure is shown in Fig. 9b, in which range ambiguity does not exist.

Figure 9: MTD diagram comparison of single target

5.3 Simulation Results 2

Assume that there are two targets, the distance of the first is 10 km and the second is 24.4 km, and the speed of the first is 240 m/s and the second is 240 m/s too. The echo delay difference between these two targets is one PRI, which means overlap happens as shown in Fig. 10, in which the dashed red line is the echo from target 1, and the solid green line is the echo from target 2.

Figure 10: Schematic diagram of overlapping echoes of two targets

In the same way, the signal to noise ratio (SNR) is set to −20 dB, and the transmission parameters are set as Eq. (19). As shown in Fig. 11a, in which only one peak value in the figure, that is, the traditional PD radar cannot distinguish the number of the real targets, which is because the speed of the two targets is the same, and the distance difference is just equal to the maximum unblurred distance so that the peak value of the two targets in the MTD figure is at the same position. But with the method in this paper, the real targets can be found as shown in Fig. 11b, in which the two targets are detected without ambiguity.

Figure 11: MTD diagram comparison of two targets

5.4 Simulation Results 3

Assume that the target’s distance is 14.4 km and the speed is 120 m/s, and set the echo delay t1=PRI. If the radar adopts transceiver switch mode, range occlusion will be generated as shown in Fig. 12. In order to solve such problem, we can switch PRF in one Tmax like in Fig. 12, using b1,b2,b3,⋯.

Figure 12: Scheme of echoes with range eclipse

The SNR is still set to −20 dB. If there are 8 transmitting pulses in one Tmax, as shown in Fig. 13a, the target cannot be detected. But if there are 6 pulses one Tmax, as shown in Fig. 13b, the target can be found.

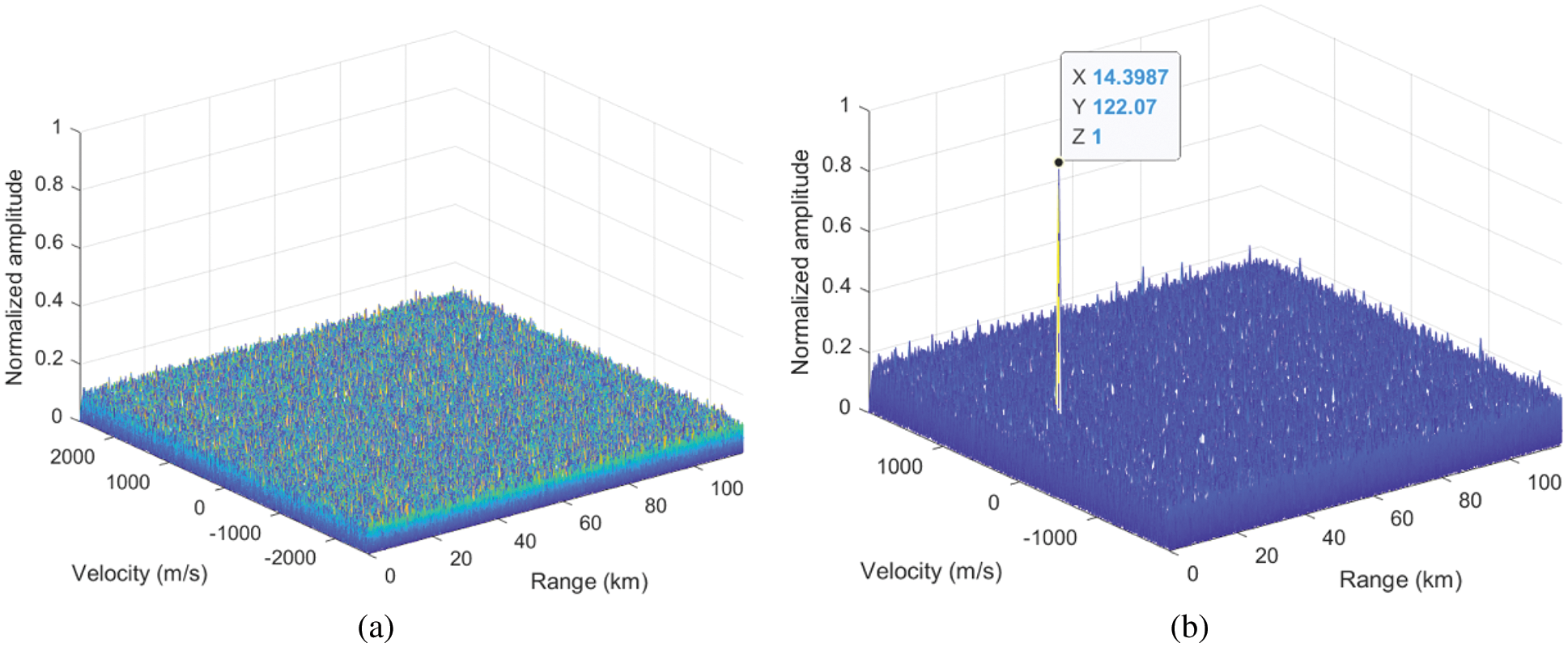
Figure 13: MTD diagram comparison with range eclipse

6  Conclusion

Range ambiguity and velocity ambiguity of traditional PD radar cannot be eliminated at the same time, which means increasing maximum unambiguous range also reduces maximum unambiguous velocity. Meanwhile, range eclipse is also a problem. The HPRF orthogonal signal transmission mode and signal processing scheme in this paper make PD Radar implement long-range unambiguous detection without velocity ambiguity and realize anti-range eclipse. Simulation results prove the feasibility of this scheme. In future work, we will consider adopting the simultaneous transceiver mode and reasonably suppressing the transmission leakage to achieve our purpose discussed in this paper more effectively.

Acknowledgement: Our deepest gratitude goes to the reviewers and editors for their careful work and thoughtful suggestions that have helped improve this paper substantially.

Funding Statement: This paper is supported by the Special Science Foundation of Quzhou (2020D007, 2021D009).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Wu, M. Q. (2004). Development and future design of digital array radar. Radar Science and Technology, 6(6), 401–405. DOI 10.3969/j.issn.1672-2337.2008.06.001. [Google Scholar] [CrossRef]

 2.  Cantrell, B. H., de Graaf, J. W., Leibowitz, L. M., Willwerth, F. G., Meurer, G. et al. (2001). Development of a digital array radar (DAR). Proceedings of the 2001 IEEE Radar Conference, pp. 157–162. Atlanta, USA. [Google Scholar]

 3.  Fulton, C., Yeary, M., Thompson, D., Lake, J., Mitchell, A. (2016). Digital phased arrays: Challenges and opportunities. Proceedings of the IEEE, 104(3), 487–503. [Google Scholar]

 4.  Lulu, A., Mobasseri, B. G. (2019). Phase matching of coincident pulses for range-doppler estimation of multiple targets. IEEE Signal Processing Letters, 26(1), 199–203. DOI 10.1109/LSP.2018.2885215. [Google Scholar] [CrossRef]

 5.  Trunk, G. V., Brockett, S. M. (1993). Range and velocity ambiguity resolution. Proceeding of the Record of the 1993 IEEE National Radar Conference, pp. 146–149. Lynnfield, USA. [Google Scholar]

 6.  Zhu, J., Li, T., Duan, C. D., Wang, W. W., Wen, C. et al. (2019). A range and velocity ambiguity resolution method based on ambiguity matrix completion and elimination with low SNR. 2019 IEEE International Conference on Signal, Information and Data Processing, pp. 1–6. Chongqing, China. [Google Scholar]

 7.  Meng, F., Xie, L. G., Li, R. H. (2009). Research on invariant imbedding method of velocity ambiguity resolution. 2009 IET International Radar Conference, pp. 1–4. Guilin, China. [Google Scholar]

 8.  Hu, J. M., Lu, D. W., Liao, Z. K., Liu, S. Q., Zhang, J. (2016). Range ambiguity resolution for high PRF radar with random frequency hopping waveforms. 2016 IEEE International Conference on Digital Signal Processing, pp. 70–73. Beijing, China. [Google Scholar]

 9.  Levanon, N. (2009). Mitigating range ambiguity in high PRF radar using inter-pulse binary coding. IEEE Transactions on Aerospace and Electronic Systems, 45(2), 687–697. DOI 10.1109/TAES.2009.5089550. [Google Scholar] [CrossRef]

10. Wang, N., Tan, S. C., Wang, G. H., Liu, Z. L. (2011). Range ambiguity resolving of HPRF radar based on IMM. Systems Engineering and Electronics, 33(9), 1970–1977. DOI 10.3969/j.issn.1001-506X.2011.09.11. [Google Scholar] [CrossRef]

11. Wang, F. X., Zhu, Y. F., Zhao, H. Z., Fu, Q. (2006). Method of resolving the range ambiguity for high PRF stepped-frequency radar. 2006 CIE International Conference on Radar, pp. 1–4. Shanghai, China. [Google Scholar]

12. Wang, W. Q. (2013). Mitigating range ambiguities in high-PRF SAR with OFDM waveform diversity. IEEE Geoscience and Remote Sensing Letters, 10(1), 101–105. DOI 10.1109/LGRS.2012.2193870. [Google Scholar] [CrossRef]

13. Axelsson, S. R. J. (2001). Suppressed ambiguity in range by phase-coded waveforms. 2001 International Geoscience and Remote Sensing Symposium, pp. 2006–2009. Sydney, Australia. [Google Scholar]

14. Huang, X. D., Wang, H. G., Huang, G. M., Luo, J. (2018). Doppler shift detection based on Chinese remainder theorem and spectrum correction. 2018 IEEE 23rd Symposiumon Digital Signal Processing, pp. 1–5. Shanghai, China. [Google Scholar]

15. Li, M. H., Li, M. (2010). A high efficiency algorithm of PD radar for range ambiguity resolution based on the one-dimension method. Electronic Information Warfare Technology, 25(5), 22–25+54. DOI 10.3969/j.issn.1674-2230.2010.05.004. [Google Scholar] [CrossRef]

16. Zhang, S. (2015). An improved method of range ambiguity resolution using look-up table. Informatization Research, 41(2), 23–26+47. [Google Scholar]

17. Wang, C., Ren, L., Li, W., Liu, Q., Mao, E. (2020). Intermediate frequency design criterion for reducing spectrum aliasing distortion in binary phase-coded radar system. IET International Radar Conference, pp. 1010–1015. IEEE. [Google Scholar]

18. Fan, G. C., Deng, W. B. (2012). MIMO radar transmit beampattern synthesis based on Genetic Algorithm. Proceeding of 2012 5th Global Symposium on Millimeter-Waves, pp. 445–448. Harbin, China. [Google Scholar]

19. Pei, B. N., Pei, T. D., Zhang, H. S. (2020). Orthogonal waveform design of MIMO radar based on niche genetic algorithm. 2020 IEEE International Conference on Signal Processing, Communications and Computing, pp. 1–6. Macau, China. [Google Scholar]

20. Zhong, W., Xia, D., Chen, Q. (2019). Radar waveform design based on phase coded signal. 2019 IEEE 4th International Conference on Image, Vision and Computing, pp. 737–741. Xiamen, China. [Google Scholar]