Optimization of Multi-Execution Modes and Multi-Resource-Constrained Offshore Equipment Project Scheduling Based on a Hybrid Genetic Algorithm

1  Introduction

Large-scale engineering projects are vulnerable to a variety of resource constraints [1] and involve numerous production activities. Offshore platform projects can be affected by many factors, such as extreme weather and sea conditions [2]. Usually, such complex operating environments often have negative effects on the construction of offshore platforms. Therefore, large-scale engineering projects are vulnerable to a variety of resource constraints [3,4], whereas they involve numerous job entries and management complexity [5]. Accordingly, recent research has focused on how best to schedule such projects under the constraints of sequence relationships, critical resources and time.

To increase production efficiency and shorten the construction period of offshore platform projects, research on the resource-constrained project scheduling problem (RCPSP) has developed rapidly, which mainly focuses on the aspects of objective functions, task activities and resource constraints.

The RCPSP is a fairly complex issue; multi-mode and multi-resource constrained project scheduling problems are far more complex than NP-hard problems. To save costs and reduce unnecessary spending during offshore platform projects, algorithms are often used. Hybrid genetic algorithms, classical genetic algorithms, and simulated annealing algorithms can be used to solve complex problems, yet their effectiveness needs to be verified and analysed numerically. Hence, an effective algorithm must be selected or designed to solve multi-resource constrained project scheduling problems.

In light of the above observations, this study established a hybrid genetic algorithm to tackle offshore equipment project scheduling problems under multi-execution modes and multi-resource constraints. The rest of this paper is organized as follows. In Section 2, related literature is reviewed. Section 3 builds a project scheduling model of multi-execution modes and multi-resource constrained offshore equipment. Section 4 describes the multi-execution modes and multi-resource constrained offshore equipment project scheduling problem and designs the algorithmic solving process. In Section 5, we use production data as an example to verify the effectiveness of the algorithm and compare it with a variety of other algorithms’ iterative results. Finally, Section 6 concludes by highlighting some advantages and limitations of our hybrid genetic algorithm and directions for future work.

2  Literature Review

This section summarizes recent relevant literature, which has two main research streams: resource-constrained project scheduling problems and hybrid genetic algorithms.

2.1 Resource-Constrained Project Scheduling Problems

Large-scale engineering projects, such as offshore platform and shipbuilding projects, are often affected by factors such as extreme weather and supplier tardiness. The complex operating environment often reduces the efficiency of offshore platform construction.

In offshore production, the resources used during manufacturing include field resources, material resources, human resources, equipment resources, technical resources and service resources. Achieving a reasonable schedule under the constraints of sequence relationships and critical resources has become a focus of current research. Multi-resource limit problems and priority rules were described by Browning et al. [6]. In recent years, most research on RCPSP has focused on adding specific constraints to make the problem more realistic. Ma et al. [7] studied a proactive project scheduling problem with flexible resource constraints. On the basis of the RCPSP problem, Cai et al. [8] considered delivery times and proposed a corresponding heuristic algorithm. Asadujjaman et al. [9] proposed a concurrent project-scheduling and material-ordering problem and proposed a hybrid immune GA solution. Ghamginzadeh et al. [10] studied a multi-objective, multi-skill, project-scheduling model.

2.2 Algorithm for RCPSP

To solve resource-constrained problems, the general exact algorithm [11,12], heuristic rules [13] and intelligent optimization algorithm can be used. The exact algorithm can only solve minor problems and remains at the theoretical stage. Heuristic rules, in addition to simple problems (such as single resources), guarantee an optimal solution but are unable to prove its optimality. Due to the large number of production operations during the execution of offshore projects, the complex logical relationship between activities, and the complex resources constraints [14], it is difficult to solve such problems with general exact algorithm and heuristic rules. Therefore, there are many studies using intelligent optimization algorithms to solve this problem.

Intelligent algorithms [15,16] have been validated as feasible solutions, and involve searching several iterations that gradually converge to the global optimal solution. The biological and evolutionary foraging swarm intelligence algorithm has been developed, which is very suitable for solving large-scale problems, especially in multi-mode and multi-resource-constrained project scheduling problems. Therefore, it has gradually become a research hotspot.

Liu et al. [13] tried to solve an RCPSP using a heuristic algorithm with the objective of minimizing activities. Hartmann [17,18], Alcaraz et al. [19], Gonçalves et al. [20], Proon et al. [21], Hindi et al. [22] and Valls et al. [23] used genetic algorithms for their approaches. Cai et al. [8] and Afshar-Nadjafi et al. [24] made improvements for certain genetic algorithms and designed a fitness function and coding rules to solve multi-mode resource-constrained project scheduling problems. Kim et al. [25] and Zhang et al. [26] proposed an adaptive hybrid genetic algorithm and particle swarm optimization for solving resource-constrained scheduling problems, obtaining very good results. Gonzalez-Pardo et al. [27] elaborated on ant colony optimization (ACO) algorithms with a novel CSP-graph-based model to solve RCPSPs. Zhao et al. [28] proposed a genetic simulated annealing algorithm based on population stability to determine the shortest construction period under the resource constraint of a single project with renewable resources. Coric et al. [29] compared the time complexity of IP formulations and genetic algorithms in solving RCPSPs and presented two different solution representations for genetic algorithms: a permutation vector and vector of floating numbers. Snauwaert et al. [30] addressed a multi-skilled extension of RCPSP (MSRCPSP) and developed a genetic algorithm to solve it. In addition to the above algorithms, the particle swarm optimization heuristic has drawn increasing attention [31,32].

2.3 Aims

Currently, there is a research foundation for multi-mode and multi-resource constrained scheduling problems. However, since marine project scheduling problems are usually large-scale, there is usually some room for optimization. This requires a higher search ability of the algorithm. To minimize the duration of a project, this article integrates a local search into a genetic algorithm and adds an elitist strategy and adaptive crossover/mutation operations to greatly reduce the computation time and ensure the quality of the search solutions. Moreover, comparisons with the classical genetic algorithm and simulated annealing algorithm are made, and the feasibility of the proposed algorithm is validated.

However, since marine project scheduling problems are usually large-scale, there are many feasible solutions during project construction.

3  Project Scheduling Model of Multi-Execution Modes and Multi-Resource Constrained Offshore Equipment

3.1 Pretreatment of Offshore Project Network Plans

In complex projects, the project execution plan is usually graded and the enterprise needs to formulate and decompose it according to contract constraints and production capacity. After making practical investigations into an offshore enterprise, we found that offshore companies usually use Oracle Primavera P6 or Microsoft Project software for project planning and task decomposition. Such software is oriented towards large-scale engineering projects, linking the plans involved in the project execution process with enterprise resources, making it easier for enterprises to manage and control their projects.

In the process of offshore engineering construction, planning and dispatching, four-stage plans are used to guide operations. Some four-level plans are able to be decomposed into a single plan, while other four-level plans cannot be decomposed. Therefore, decomposed fourth-level plans can be regarded as a complete network plan and include all operation items, the logical relationship, etc. A model of such problems requires four preprocessing schemes to form a viable network scheme, as shown in Fig. 1.

Figure 1: Decomposition of four-level network planning

In Fig. 1, S4 and E4 represent the beginning and end of the fourth-level network activities. These can be taken as two virtual activities with corresponding periods, direct costs, and resource consumptions of zero. Now, we assume that other activities added to activities outside J4 cannot continue to be broken down into fifth-level activities. Points S5 and E5 indicate the beginning and the end of the 5-stage plan, as well as two virtual activities. The earliest start times of J41 and J43 can be considered as the start times S5, J42, J43’s latest end time as the end time E5, and pretreatment is shown in Fig. 2.

Figure 2: Pretreatment of four-level network planning

3.2 Problem Description of Multi-Execution Modes and Multi-Resource-Constrained Offshore Equipment Project Scheduling

A complete offshore project can correspond to a complete network diagram, including the complete logical relationship. Engineers use professional software to decompose a complete project into a network plan of four levels to guide the actual operations. In this paper, a single-node network diagram is defined as G=(V,E). In graph G, E there is a set of directed arcs that can connect each node in set V. We define J as an activity, then j can be considered as a subset of J, where j=1,…,J. The network also contains node 0 and node J+1, which represent the beginning and end of the virtual activities, respectively. Activity J cannot start until the predecessor activities of Pj have been completed.

Each activity j may be performed under several different modes Mj={1,…,Mj}. In the execution modem∈Mj, the demand for renewable resources in activity j per unit time can be represented by rjmk, and the duration of activity j, which is under execution mode m, is expressed by djm. Assuming that once activity j starts in mode m, it cannot be allowed to change due to activity interruptions or behaviour patterns. Similarly, all of the activities must be executed continuously.

Bearing this in mind, in order to establish a multi-mode resource-constrained project scheduling optimization model, the following assumptions are made: (1) Once an activity is started, it cannot be interrupted until completion; (2) during the scheduling period considered, the resource supply capacity is evenly distributed; and (3) each operation’s resource demand per unit time must be less than the upper limit of the resource supply.

3.3 Mathematical Model

In this paper, EFTj and LFTj represent the beginning and end times of activity j, respectively, while Mj indicates a set of alternative execution modes. Furthermore, rjmk is activity j in m—the execution mode, which is required for the first k kinds of resource demands (such as personnel, cranes, plates, money, barges, and oil, in which human and oil resources are renewable and non-renewable resources, respectively). Rk indicates that k largest species of renewable resources supply. The mathematical model of the problem can be described as follows:

Minimize∑m=1Mj∑t=EFTjLFTjtxjmt(1)

∑m=1Mj∑t=EFTjLFTjxjmt=1,j=1,…,J(2)

∑m=1Mi∑t=EFTiLFTitximt≤∑m=1Mj∑t=EFTjLFTj(t−djm)txjmt,j=2,….J,i∈Pj(3)

∑j=2J−1∑m=1Mjrjmk∑τ=tt+djm−1xjmτ≤Rk,k∈R,t=1,….,T(4)

∑j=2J−1∑m=1Mjrjmk∑t=EFTjLFTjxjmt≤Rk,k∈NR(5)

xjmt∈{0,1},j=1,…,J,m=1,…,Mj,t=EFTj,…,LFTj(6)

In this model, Eq. (1) is the objective function, while Eqs. (2)–(6) describe the constraint conditions. Eq. (1) indicates the duration of the project; Eq. (2) represents that activity j can only be carried out in an execution mode; in Eq. (3), activity i is the tight predecessor activity before activity j, which only starts after its before-tight-activities event set Pj; Eq. (4) indicates the demand for renewable resources per unit time, which cannot exceed the capacity of resource supply Rk; Eq. (5) means that the demand for non-renewable resources cannot exceed its supply, and we assume that each activity’s demand per unit time is fixed; and Eq. (6) is a 0–1 decision variable, indicating whether activity j can be carried out under execution mode m at time t.

4  Solving for Multi-Execution Modes and Multi-Resource-Constrained Offshore Equipment Project Scheduling Problems

4.1 Algorithm for the Solving Strategy

Usually, offshore projects require operating items in large amounts, which results in extremely large execution modes and solution spaces. This directly leads to low efficiency and effectiveness in the general convergence speed. Genetic algorithms have a strong global cable capacity, and crossover/mutation methods protect the diversity of the population to some extent; however, the latter’s convergence results may also undermine the optimal solution that has already been searched, which is likely trapped in a local convergence optimum. Meanwhile, a local search algorithm can generate field solutions by random perturbation and accept inferior solutions of a certain probability, giving it strong local searchability. Therefore, to balance the advantages and disadvantages of these two algorithms, this paper proposes a fused hybrid genetic algorithm to solve multi-mode multi-resource-constrained project scheduling problems. The main improvements are as follows. (1) It adopts an elitist strategy to speed up convergence; (2) it uses adaptive crossover/variability to improve search quality and speed up convergence; (3) it integrates local search into the genetic algorithm and uses a maintenance population to protect the diversity of the population and come to a global optimal solution; and (4) it uses the function calibration method to accommodate the use of roulette rules.

4.2 Design of the Hybrid Genetic Algorithm

4.2.1 Encoding

This paper uses two chromosomes for encoding the hybrid genetic algorithm. One represents the sequence of activities, while the other represents the execution mode sequences. In the sequence of activities, each gene represents an activity. In the execution mode sequence, each gene represents the predecessor of its corresponding activity Fig. 3 shows a simple network diagram with the immediately preceding relations, while Fig. 4 shows an encoding example.

Figure 3: Sample of encoding rule

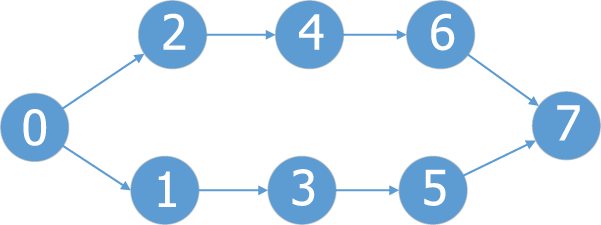
Figure 4: Simple network plan

4.2.2 Decoding

Decoding is the process of solving practical problems with information carried by chromosomes. Since this article is only related to time and resource constraints, the serial scheduling mechanism is used for decoding [30]. The decoding operation process includes h = 1,…, J steps. Each step may only be based on the earliest start time to determine the execution mode, relationships and constraints of resources after the event to select a condition immediately before the tight j∗. Meanwhile, according to a local collection PSh, an activity set is arranged at each step. Let ∼Rk(t)=Rk−∑j∈Atrjmk, as activity j supplies k classes of remaining resource capacity under execution mode m. Let Fh={fj|j∈PSh} be a selected event’s end-time collection. Use the earliest start time precedence activities ESj∗ to calculate j∗. Then, the preceding resource-constrained start-time Sj∗ activity sequence can be expressed as λ={j1,…,jh,…,jJ}. The decoding operation process details are as follows:

Step 1: Initialize h = 1, PSh={0}, Fh={0};

Step 2: If |PSh|<J, go to Step 3; else, end the period;

Step 3: Calculate the following sequence:

Fh∼Rk(t); j∗:=jh; dj∗:=dj∗m; ESj∗=maxi∈Pj∗{Fh};Sj∗=min{t|ESj∗≤t,rj∗mk≤∼Rk(τ),τ=t,…,t+dj∗−1,k=1,…,K};

Step 4: fj∗=Sj∗+dj∗;

Step 5: Fh+1:=Fh∪{fj∗}; PSh+1:=PSh∪{j∗};

Step 6: h = h + 1; go to Step 2.

4.2.3 Crossover/Mutation Operator

To change the default settings, we adjust the template as follows. Crossover and mutation are the most important parts of the genetic algorithm and must be properly designed. This paper adopts a single-point crossover method proposed by Chen et al. [33] and Hartmann [34], as shown in Fig. 5.

Figure 5: Sample of a crossover operation

In the cross-operations, q1 and q2 represent selecting location randomly, directs at a sequence of activities and implementation modality. After q1 position is selected, the sequence of activities before it crosses to the offspring; meanwhile, it excludes the activity sequence that has already been crossed from the activity sequence of the parent generation, then crosses to the progeny and offspring in order to complete the activity sequence crossover operation for now. After q2 is selected, all the execution modes before q2 are crossed to the offspring and the execution mode after q2 finds its corresponding sequence according to the activity sequence in the parent generation. Then, we join the offspring execution mode sequence.

Mutation operations are executed both on the activity sequence and execution mode sequence, but there are definite differences in the implementation of its rules. In the sequence of activities, we first select an activity randomly and then find the predecessor activities of the second-highest position, which is 0, and the successor activity of the 4th-lowest position. Then, we engender a random digit representing the active position, such as 2 from 0 and 4 activities location: 0–4 (not including 0 and 4), and move activity 2 to position 2, while the other activities do not change order and just move forward or backward as a whole. For the variation of the execution model, we generate a random digit from 1–6 in position 5 (as Fig. 6 shows) and execute the execution mode corresponding to the position mode into another option.

Figure 6: Sample of a mutation

4.2.4 Adaptive Crossover and Mutation Strategy

To accelerate convergence and increase the quality of the search solutions, an adaptive crossover operation is available. The probability of pre-crossover searching and mutation is relatively large. As the search progresses, the crossover and mutation become smaller. The crossover probability Pc and mutation probability Pm are shown by the following formula, in which fmax represents the highest fitness value in the population, f represents the current value of individual fitness and favg represents the population’s average fitness value.

Pc={k1(fmax−f)fmax−favgf≥favgk2f<favg(7)

Pm={k3(fmax−f′)fmax−favgf′≥favgk4f′<favg(8)

4.2.5 Function Calibration Method and Elitist Strategy

Under normal circumstances, the objective function can be directly used as the fitness function. However, the problem of minimizing the duration cannot be described as a fitness function directly, so the objective function must be converted to a proper fitness function. Sometimes, due to the relatively small differences between the objective functions, the probability of selecting each individual difference is small, which leads to each individual having almost the same probability choice. This might result in weak selection by the genetic algorithm. Changes are needed to fix this by using an appropriate function calibration method, such as linear calibration, dynamic linear calibration, power-law scaling or logarithmic calibration.

The difference between the values of the objective functions is quite obvious, which is the reason why we utilize a calibration method. In f‘=k/f, f‘ stands for the calibrated function, f stands for the uncalibrated function value (duration), and k is the coefficient.

We compare the individuals with the smallest fitness values among the parent and offspring individuals. If the parent is superior to the offspring, the best individual parent will replace the best offspring, or the best parent will replace the worst offspring i. This is the elitist operation, which can effectively protect the optimum solution from being destroyed and accelerate the convergence speed.

4.3 Algorithmic Process

For a higher quality solution and faster speed, in this article, a mixed genetic algorithm is used, which integrates a local search algorithm with an iterative search performed only once into the genetic algorithm for iterative search. The flow chart of the algorithm is shown in Fig. 7. The specific steps are as follows:

Step 1: Initialization. Set the maximum number of iterations G, coefficient k, initial temperature T, and largest provider of resource k values, Rk.

Step 2: Randomly generated initial solution. According to the network diagram for meeting the tight relationship between the former premise randomly generated initial solution of N, where the execution mode for each activity from Mj is randomly selected.

Step 3: Decode. Obtain the initial population of each individual period T, and use the inverse calibration method for the fitness function to convert T′.

Step 4: Select the size of N, respectively, the parent and parent on behalf of Father/Mother according to roulette rules.

Step 5: Adaptive crossover and mutation operations. Conduct crossover and mutation to produce offspring children.

Step 6: Add a local search to the solution for maintenance.

Step 6.1: Crossover and mutation to produce offspring children as its parent X;

Step 6.2: Use the mutation probability of generating a field solution Y;

Step 6.3: Sequence comparison of individuals X and Y. If the individual is superior to the corresponding Y of individual X, Y is replaced by the individual out of individual X; otherwise, keep the X in the individual unchanged.

Step 7: Carry out the elitist operation.

Step 8: Determine whether the convergence condition is satisfied, if yes, go to Step 9; otherwise, go to Step 3.

Step 9: Output the shortest duration and iterative convergence curve.

Figure 7: Algorithm flowchart

5  Case Analysis

5.1 Examples of Verification of the Test Network Diagram

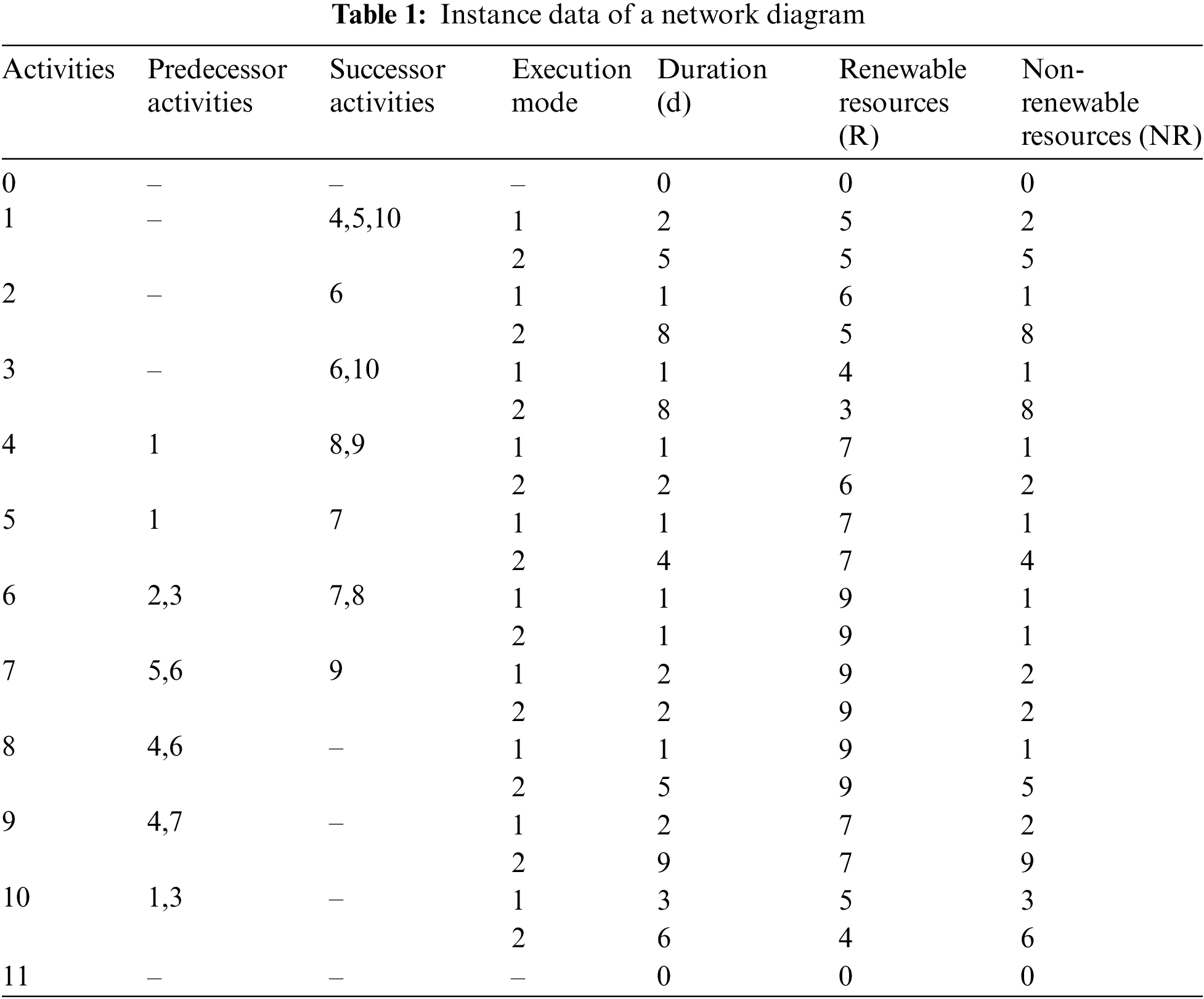
This article refers to the network in Fig. 8, a data validation instance from the literature, assuming that there is only one kind of renewable resource and one non-renewable resource. The network diagram has 12 events, in which 0 and 11 are starting and ending events, while the execution modes are mode 1 and mode 2 executive. Renewable resources are represented by R and Rk max = 12. Non-renewable resources are represented by NR. This article assumes that workers consume a certain value of non-renewable resources each day, and its total NRk is 25.

Figure 8: Network diagram of the validation instance

5.1.1 Examples of Simulation Data Acquisition

The initial size of the population genetic algorithm section is 10; the maximum number of iterations is 200; the function calibration coefficient k = 30; the cross-adaptive crossover and mutation probabilities k1 and k2 are taken as 0.7 and 0.95, respectively, while the mutation probabilities k3 and k4 are taken as 0.02 and 0.05 and the local search iteration is 1. The specific parameters are shown in Table 1.

5.1.2 Graphical Analysis

Through a comparative analysis of a traditional genetic algorithm and a simulated annealing algorithm, based on the mean value of the fitness function being the iterative convergence criterion, the article obtained the iterative convergence curve shown in Fig. 9. It shows that, compared to a classical genetic algorithm and simulated annealing algorithm, the hybrid genetic algorithm converges faster, and its trend of convergence appeared in the 10th generation. Moreover, the non-renewable resource consumption is 15, which is less than the maximum reserve 25, and it can converge the minimum 10-day duration according to the theory, which fully illustrates the improvement brought by the proposed elitist strategy, function calibration method, local search, and adaptive crossover. These strategies have a good effect on accelerating convergence/mutation.

Figure 9: Comparison of the iterative curves of three algorithms

Meanwhile, from the chart, we can see that the classical genetic algorithm’s convergence fluctuates in the later period, which fully shows that the improvement of the probability of crossover mutation proposed can achieve a more stable solution. The convergence of the simulated annealing algorithm is unstable in the later period, indicating that although it can accept an inferior solution with a certain probability, due to the initial temperature being too high and cooling slowly, it seems to result in an extremely slow rate of convergence.

5.1.3 Data Analysis

To demonstrate the feasibility of this algorithm, two indicators were used: average optimal convergence and iterations to average convergence of the three algebraic calculation algorithms after 30 runs, as shown in Table 2. Also, we list the optimal scheduling scheme of the hybrid and classical genetic algorithms, as shown in Figs. 10 and 11. We found that the hybrid genetic algorithm and simulated annealing algorithm can both find the optimal solution (10 days). The hybrid genetic algorithm can achieve optimal results but the simulated annealing algorithm did not search the optimal results at all, and fluctuations can be seen. The solution-searching quality of the hybrid genetic algorithm is significantly better than that of classical genetic algorithm 3. The fastest search algorithm is the hybrid genetic algorithm. This article shows that this can handle a multi-mode multi-resource-constrained project scheduling problem.

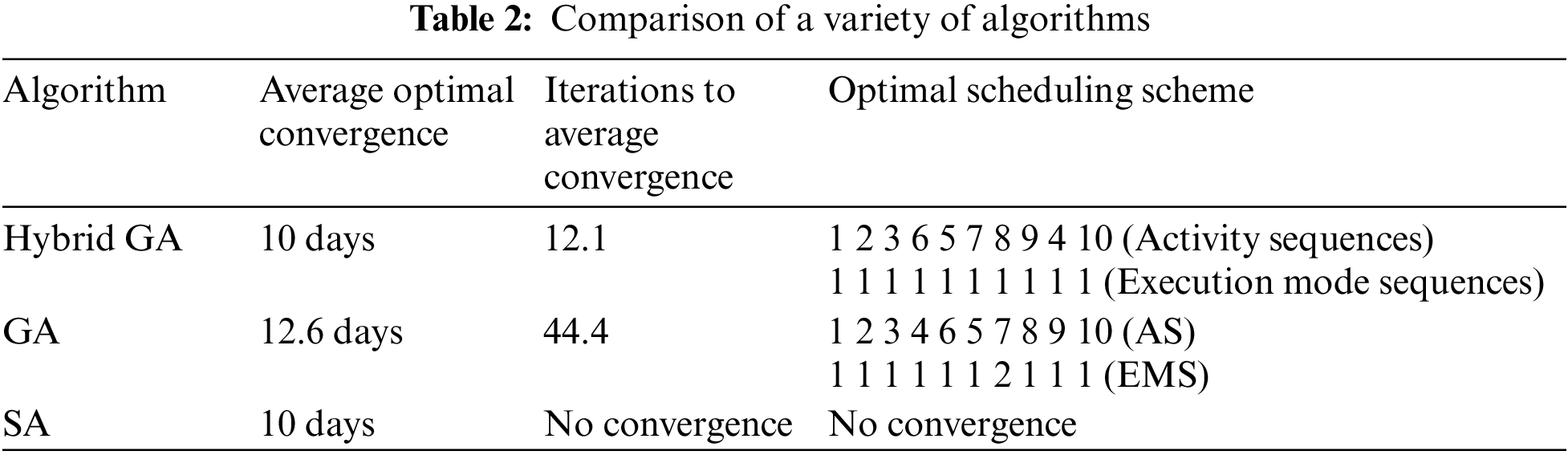
Figure 10: Hybrid genetic algorithm optimal scheduling scheme

Figure 11: Classical genetic algorithm optimal scheduling scheme

5.2 Actual Examples of Offshore Project Validation

In this example, the size of the initial population of the genetic algorithms is 20; the maximum number of iterations is 500; the renewable resources (HR) Rk limit is 40; the function calibration coefficient k is 400; the adaptive crossover and mutation probabilities k1 and k2 are 0.7 and 0.95; the mutation probabilities k3 and k4 are 0.02 and 0.05; and 1 local search iteration is used. The specific network and data are illustrated in Table 3 and Fig. 12 [35].

Figure 12: Network diagram of the onshore construction process for an offshore structure

It should be noted that renewable resources include human resources, while non-renewable resources are, by their nature, more certain in their supply. Therefore, non-renewable resources are not considered in this verification example. The basic data (onshore construction process of an offshore structure ) in the offshore project network diagram were provided by an offshore company, drawn by project2007.

By the comparative analysis of the hybrid genetic, classical genetic, and simulated annealing algorithms, we know that the classical genetic algorithm easily finds a local optimal solution because of its weakness in local search capability. The simulated annealing algorithm converges very slowly and large fluctuations still exist after 500 iterations, indicating that it does not achieve convergence. The hybrid genetic algorithm iterations have already converged after about 110 times, and the quality of the convergence solution is better than those of the other two. As a result, the optimal duration is 375 days, as shown in Fig. 13, which verifies that the hybrid genetic algorithm can solve the offshore project scheduling optimization problem.

Figure 13: Actual offshore project iteration convergence plan

6  Conclusions

This article integrated a local search algorithm into a genetic algorithm and added an elitist strategy and adaptive crossover and mutation operations. Solutions that improve the effectiveness and efficiency of a multi-mode multi-resource-constrained project scheduling problem were obtained, as follows:

(1) This paper proposed a hybrid genetic algorithm and established a multi-mode and multi-resource-constrained project scheduling optimization model. Then, this paper presented a genome sequence (based on the activity sequence and implementation modality sequence) and designed the appropriate decoding rules and crossover, mutation rules, cited an elitist strategy, and an adaptive operation. Then, local search was integrated after the crossover and mutation operation, and maintenance of the genetic algorithm’s offspring and other operations were adopted, which greatly increased the convergence speed. Improvements to the proposed algorithm were introduced to overcome the shortcomings of the large solution space, accelerate the convergence, and increase the understanding of search quality. Through the data test of the network diagram and the actual test project, it is found that the shortest period of the offshore project is 10 days and 375 days, respectively.

(2) A comparative analysis of hybrid genetic, classical genetic, and simulated annealing algorithms was made. Comparison of the resulting convergence curves and data fully shows that the proposed hybrid genetic algorithm is most suitable for solving multi-mode and multi-resource-constrained project scheduling problems.

Multi-mode and multi-resource-constrained project scheduling problems are very complex NP-hard problems. On the basis of this study, it is necessary to carry out the following research:

(1) Research is needed in multi-mode, multi-objective, single-/multi-resource-constrained project scheduling problems. Further improvements in convergence speed and the reconciliation and quality of the convergence of the algorithm are required.

(2) For large projects, especially marine research projects, it is necessary to carry out a more efficient network decomposition scheme plan, and to obtain the optimal solution in an early period of the plan.

Acknowledgement: The authors are responsible for the contents of this publication. The authors would like to thank SWS Co., Ltd. for contributing the data used in verification.

Funding Statement: This research was funded by the Ministry of Industry and Information Technology of the People’s Republic of China (Nos. [2018]473, [2019]331).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Ruan, D., Maes, D., Aït, H., Liu, J., Xu, L. et al. (2005). Cost estimations for large scale engineering projects under uncertainties. Proceedings of the Joint 4th Conference of the European Society for Fuzzy Logic and Technology and the 11th Rencontres Francophones sur la Logique Floue et ses Applications, Barcelona, Spain. [Google Scholar]

 2.  Katayama, H., Sirichan, K., Hiraki, S. (1999). Japanese offshore manufacturing in Thailand: Its difficulties and future prospects. Integrated Manufacturing Systems, 10(4), 210–220. DOI 10.1108/09576069910280459. [Google Scholar] [CrossRef]

 3.  Park, J., Lee, D., Zhu, J. (2014). An integrated approach for ship block manufacturing process performance evaluation: Case from a Korean shipbuilding company. International Journal of Production Economics, 156(6), 214–222. DOI 10.1016/j.ijpe.2014.06.012. [Google Scholar] [CrossRef]

 4.  Lee, D. K., Kim, Y., Hwang, I. H., Oh, D. K., Shin, J. G. (2014). Study on a process-centric modeling methodology for virtual manufacturing of ships and offshore structures in shipyards. The International Journal of Advanced Manufacturing Technology, 71(1), 621–633. DOI 10.1007/s00170-013-5498-4. [Google Scholar] [CrossRef]

 5.  Colledani, M., Tolio, T., Fischer, A., Iung, B., Lanza, G. et al. (2014). Design and management of manufacturing systems for production quality. Cirp Annals, 63(2), 773–796. DOI 10.1016/j.cirp.2014.05.002. [Google Scholar] [CrossRef]

 6.  Browning, T. R., Yassine, A. A. (2010). Resource-constrained multi-project scheduling: Priority rule performance revisited. International Journal of Production Economics, 126(2), 212–228. DOI 10.1016/j.ijpe.2010.03.009. [Google Scholar] [CrossRef]

 7.  Ma, Y., He, Z., Jiang, B., Wang, N. (2021). A heuristic algorithm for solving flexible resource constrained proactive project scheduling problem. Operations Research and Management Science, 30(8), 14–20+51. DOI 10.12005/orms.2021.0241. [Google Scholar] [CrossRef]

 8.  Cai, J., Peng, Z. (2019). A heuristic algorithm for solving resource constrained project scheduling problem with transfer time under resource bundle. 2019 Chinese Control Conference (CCC), pp. 2155–2160. Guangzhou, China. [Google Scholar]

 9.  Asadujjaman, M., Rahman, H. F., Chakrabortty, R. K., Ryan, M. J. (2021). Resource constrained project scheduling and material ordering problem with discounted cash flows. Computers Industrial Engineering, 158, 107427. DOI 10.1016/j.cie.2021.107427. [Google Scholar] [CrossRef]

10. Ghamginzadeh, A., Najafi, A. A., Khalilzadeh, M. (2021). Multi-objective multi-skill resource-constrained project scheduling problem under time uncertainty. International Journal of Fuzzy Systems, 23(2), 518–534. DOI 10.1007/s40815-020-00984-w. [Google Scholar] [CrossRef]

11. Dorndorf, U., Pesch, E., Phan-Huy, T. (2000). A time-oriented branch-and-bound algorithm for resource-constrained project scheduling with generalised precedence constraints. Management Science, 46(10), 1365–1384. DOI 10.1287/mnsc.46.10.1365.12272. [Google Scholar] [CrossRef]

12. Peng, W., Wang, C. (2008). A multi-mode resource-constrained DTCTP. Journal of Northeastern University: Natural Science, 29(8), 1077–1079+1095. DOI 10.3321/j.issn:1005-3026.2008.08.004. [Google Scholar] [CrossRef]

13. Liu, Z., Wang, H. (2006). Heuristic algorithm for RCPSP with the objective of minimizing activities’ cost. Journal of Systems Engineering Electronics, 17(1), 96–102. DOI 10.1016/S1004-4132(06)60018-2. [Google Scholar] [CrossRef]

14. Li, J., Hu, Z., Lv, H., Sun, M. (2013). Research on resource leveling for offshore equipment multi-project based on immune genetic algorithm. Computer Engineering and Design, 34(9), 3250–3254. DOI 10.16208/j.issn1000-7024.2013.09.014. [Google Scholar] [CrossRef]

15. Hui, W. (2012). Comparison of several intelligent algorithms for solving TSP problem in industrial engineering. Systems Engineering Procedia, 4(20), 226–235. DOI 10.1016/j.sepro.2011.11.070. [Google Scholar] [CrossRef]

16. Corchado, E., Abraham, A., de Carvalho, A. (2010). Hybrid intelligent algorithms and applications. Information Sciences, 180(14), 2633–2634. DOI 10.1016/j.ins.2010.02.019. [Google Scholar] [CrossRef]

17. Hartmann, S. (1998). A competitive genetic algorithm for resource-constrained project scheduling. Naval Research Logistics, 45(7), 733–750. DOI 10.1002/(ISSN)1520-6750. [Google Scholar] [CrossRef]

18. Hartmann, S. (2002). A self-adapting genetic algorithm for project scheduling under resource constraints. Naval Research Logistics, 49(5), 433–448. DOI 10.1002/(ISSN)1520-6750. [Google Scholar] [CrossRef]

19. Alcaraz, J., Maroto, C. (2001). A robust genetic algorithm for resource allocation in project scheduling. Annals of Operations Research, 102(1), 83–109. DOI 10.1023/A:1010949931021. [Google Scholar] [CrossRef]

20. Gonçalves, J. F., Resende, M. G., Mendes, J. J. (2011). A biased random-key genetic algorithm with forward-backward improvement for the resource constrained project scheduling problem. Journal of Heuristics, 17(5), 467–486. DOI 10.1007/s10732-010-9142-2. [Google Scholar] [CrossRef]

21. Proon, S., Jin, M. (2011). A genetic algorithm with neighborhood search for the resource-constrained project scheduling problem. Naval Research Logistics, 58(2), 73–82. DOI 10.1002/nav.20439. [Google Scholar] [CrossRef]

22. Hindi, K. S., Yang, H., Fleszar, K. (2002). An evolutionary algorithm for resource-constrained project scheduling. IEEE Transactions on Evolutionary Computation, 6(5), 512–518. DOI 10.1109/TEVC.2002.804914. [Google Scholar] [CrossRef]

23. Valls, V., Ballestin, F., Quintanilla, S. (2008). A hybrid genetic algorithm for the resource-constrained project scheduling problem. European Journal of Operational Research, 185(2), 495–508. DOI 10.1016/j.ejor.2006.12.033. [Google Scholar] [CrossRef]

24. Afshar-Nadjafi, B., Rahimi, A., Karimi, H. (2013). A genetic algorithm for mode identity and the resource constrained project scheduling problem. Scientia Iranica, 20(3), 824–831. DOI 10.1016/j.scient.2012.11.011. [Google Scholar] [CrossRef]

25. Kim, K., Yun, Y., Yoon, J., Gen, M., Yamazaki, G. (2005). Hybrid genetic algorithm with adaptive abilities for resource-constrained multiple project scheduling. Computers in Industry, 56(2), 143–160. DOI 10.1016/j.compind.2004.06.006. [Google Scholar] [CrossRef]

26. Zhang, H., Li, H., Tam, C. (2006). Particle swarm optimization for resource-constrained project scheduling. International Journal of Project Management, 24(1), 83–92. DOI 10.1016/j.ijproman.2005.06.006. [Google Scholar] [CrossRef]

27. Gonzalez-Pardo, A., Del Ser, J., Camacho, D. (2017). Comparative study of pheromone control heuristics in ACO algorithms for solving RCPSP problems. Applied Soft Computing, 60(5), 241–255. DOI 10.1016/j.asoc.2017.06.042. [Google Scholar] [CrossRef]

28. Zhao, W., Lin, S. (2018). Rcpsp study based on simulated annealing and genetic algorithm. Software Guide, 17(12), 61–64+68. DOI 10.11907/rjdk.182560. [Google Scholar] [CrossRef]

29. Čorić, R., Đumić, M., Jakobović, D. (2017). Complexity comparison of integer programming and genetic algorithms for resource constrained scheduling problems. 2017 40th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), pp. 1182–1188. Croatia. DOI 10.23919/MIPRO.2017.7973603. [Google Scholar] [CrossRef]

30. Snauwaert, J., Vanhoucke, M. (2021). A new algorithm for resource-constrained project scheduling with breadth and depth of skills. European Journal of Operational Research, 292(1), 43–59. DOI 10.1016/j.ejor.2020.10.032. [Google Scholar] [CrossRef]

31. Fahmy, A., Hassan, T. M., Bassioni, H. (2014). Improving RCPSP solutions quality with Stacking justification--Application with particle swarm optimization. Expert Systems with Applications, 41(13), 5870–5881. DOI 10.1016/j.eswa.2014.03.027. [Google Scholar] [CrossRef]

32. Jin, Q., Wang, K., Zhao, Z., Cao, L. (2014). HPSO algorithm with high speed convergent based on particle health degree. Applied Mathematics Information Sciences, 8(4), 1809–1821. DOI 10.12785/amis/080438. [Google Scholar] [CrossRef]

33. Chen, P. H., Weng, H. (2009). A two-phase GA model for resource-constrained project scheduling. Automation in Construction, 18(4), 485–498. DOI 10.1016/j.autcon.2008.11.003. [Google Scholar] [CrossRef]

34. Hartmann, S. (2001). Project scheduling with multiple modes: A genetic algorithm. Annals of Operations Research, 102(1), 111–135. DOI 10.1023/A:1010902015091. [Google Scholar] [CrossRef]

35. Ghoddousi, P., Eshtehardian, E., Jooybanpour, S., Javanmardi, A. (2013). Multi-mode resource-constrained discrete time-cost-resource optimization in project scheduling using non-dominated sorting genetic algorithm. Automation in Construction, 30(1), 216–227. DOI 10.1016/j.autcon.2012.11.014. [Google Scholar] [CrossRef]