 Open Access
Open Access
ARTICLE
Shape Effect of Nanoparticles on Nanofluid Flow Containing Gyrotactic Microorganisms
1 School of Mathematical Sciences, Jiangsu University, Zhenjiang, 212013, China
2 Department of Mathematics and Natural Sciences, Prince Mohammad Bin Fahd University, Al Khobar, 31952, Saudi Arabia
3 Department of Mathematics and Statistics, College of Science, Taif University, Taif, 21944, Saudi Arabia
* Corresponding Author: Azhar Iqbal. Email:
(This article belongs to the Special Issue: Recent Trends in Nanofluids: Modelling and Simulations)
Computer Modeling in Engineering & Sciences 2023, 134(1), 483-494. https://doi.org/10.32604/cmes.2022.020033
Received 30 October 2021; Accepted 18 March 2022; Issue published 24 August 2022
Abstract
In this paper, we discussed the effect of nanoparticles shape on bioconvection nanofluid flow over the vertical cone in a permeable medium. The nanofluid contains water, Al2O3 nanoparticles with sphere (spherical) and lamina (non-spherical) shapes and motile microorganisms. The phenomena of heat absorption/generation, Joule heating and thermal radiation with chemical reactions have been incorporated. The similarity transformations technique is used to transform a governing system of partial differential equations into ordinary differential equations. The numerical bvp4c MATLAB program is used to find the solution of ordinary differential equations. The interesting aspects of pertinent parameters on mass transfer, energy, concentration, and density of the motile microorganisms’ profiles are computed and discussed. Our analysis depicts that the performance of sphere shape nanoparticles in the form of velocity distribution, temperature distribution, skin friction, Sherwood number and Motile density number is better than lamina (non-spherical) shapes nanoparticles.Keywords
Nomenclature
| Thermal coefficient | |
| Solute expansion coefficient | |
| Magnetic field strength | |
| Thermal conductivity of the fluid (W/m.K) | |
| Thermal conductivity of the solid (W/m.K) | |
| Specific heat capacity (J/kg K) | |
| Thermal diffusivity of the nanofluid (m/s2) | |
| Density of the nanofluid (kg/m3) | |
| Cone half-angle | |
| Thermal radiation coefficient | |
| Brownian diffusion coefficient | |
| Heat generation/Absorption parameter | |
| Maximum cell swimming speed | |
| Rate of chemical reaction | |
| Reference temperature constant | |
| Concentration dimensionless constant | |
| Diffusivity of microorganisms | |
| Suction/Injection parameter | |
| Convective parameter | |
| Porous parameter | |
| Magnetic parameter | |
| bioconvection Rayleigh number | |
| Prandtl number | |
| Buoyancy ratio parameter | |
| Radiation parameter | |
| Lewis number | |
| Schmidt number | |
| Bio convection constant | |
| Chemical reaction parameter | |
| Boit number | |
| Solutal stratification | |
| Bio convection Lewis number | |
| Skin friction | |
| Nusselt number | |
| Sherwood number | |
| Motile density number | |
| m | Nanopareticles shape factor |
Nanofluid has become an essential topic of research because of its low thermal resistance and effective thermophysical. Furthermore, cooling is required to sustain the performance of a wide range of technologies and industrial items, including power electronics, laptops, computers, high-powered rays, and motor engines. Nanofluid technology is the most exciting development in recent years, with extremely high production and low cost. Nanofluid attribute to nanoparticles suspended in the base fluid. The very first-time idea of nanofluid was introduced by Aman et al. [1–3]. Also, the nanofluid in the existence of bioconvection is become the attention of researchers because of its extensive use in biomedical, bio-microsystem, and biotechnology. In several industrial processes, including enzyme biosensors, microbial enhanced crude oil recovery, and chip size microdevices for assessing nanoparticle toxicity, the interaction between convection induces motile microorganisms, and solid particles are also important [4]. Geng et al. [5] discussed the impacts of nanoparticles on the growth of bioconvection induced by plums. Uddin et al. [6] discussed the application of bioconvection and nanobiofuel with the inaction of nanoparticles. Kuznetsov [7] used the motile microorganism in nanofluid flow to increase mass transfer, microscale mixing, and the nanofluid’s expected stability. Furthermore, several studies related to the biological nanofluid and motile microorganisms are discussed [8,9].
Bio-convection is an increasing surprise of liquid mechanics determined by the swimming of microorganisms and was observed a few years ago. Bio-convection designs generally show up because of the upswimming of microorganisms with a denser density than water. The bio-convection has several applications in biotechnology and normal system. Microorganisms particles have been broadly used to make business things and mechanical such as ethanol, composts, and biofuel produced using waste. Microorganisms are also employed in water treatment facilities, biodiesel, and hydrogen gas, a promising sustainable energy source [10]. Amirsom et al. [11] presented a mathematical model for three-dimensional bio-convection nanofluid flow along with gyrotactic microorganisms from a biaxial stretching sheet involving the impact of mass slip, thermal jump, and anisotropic slip. Aziz et al. [12] studied the numerical solution of free convection nanofluid flow with gryotatcic microorganisms over a flat plate. The authors conclude that biconvection parameters have significantly impacted the motile microorganisms. Khan et al. [13] investigated a comparison of Williamson and Casson nanofluids flow containing gyrotactic microorganisms. The authors conclude that stratification is dependent on microorganism concentration.
Fluid performance has a significant role in daily life, and it is necessary to study fluid flow motion [14]. Many authors did work on nanofluid flow containing gyrotactic microorganisms. Khan et al. [15] studied the natural convection nanofluid flow around a cone that contained gyrotactic microorganisms. The authors concluded that the density number of motile microorganisms, Sherwood number, Skin friction, and Nusselt number enhance along the surface. Khan et al. [16] demonstrated the bio-convection Oldroyd-B nanofluid over a stretched sheet with Prandtl number effects. Waqas et al. [4] investigated the results of a modified second-grade nanofluid over a stretched surface using motile microorganisms. The approximate results were compared to those from previous investigations and found to be very similar. Amirsom et al. [11] analyzed magnetohydrodynamic gyrotactic bioconvection in a square cavity filled with nanofluid. Waqas et al. [17] discussed the approximate solution of micropolar nanofluid across a porous stretching sheet with microorganisms, activation energy, and Nied boundary conditions. Sampath Kumar et al. [18] discussed the bioconvection in magnetofluid containing gyrotactic microorganisms across an elongate plate with a second-order velocity slip. They found that motile microorganisms’ boundary layer flow decreased for greater bioconvection lewis and bioconvection number. Sohail et al. [19] investigated the entropy generation in Maxwell nanofluid having microorganisms in the existence of heterogeneous-homogenous reactions. For more studies related to the gyrotactic microorganisms, see [20].
According to the literature, the shape effects of Al2O3 on bioconvection nanofluid with gyrotactic microorganisms over the vertical cone in a permeable medium have not yet been reported. The current research aims to examine the shape effect of nanoparticles on bioconvection nanofluid with gyrotactic microorganisms over the vertical cone in a permeable medium. The partial differential equations are converted into ordinary differential equations to find the numerical solutions of the mathematical problem. The results are discussed with graphical illustrations.
The following is the paper’s structure. Section 1 introduces the background and importance of the effect of nanoparticles shape on nanofluid flow. The methodology used in the paper is described in Section 2. The results and discussions are presented in Section 3. The figs are plotted for several values of the parameters. Finally, the study’s conclusion is written in Section 4.
Consider the bio convection Al2O3-water nanofluid flow containing with sphere (spherical) and lamina (non-spherical) shapes nanoparticles and motile microorganisms over the vertical cone in a permeable medium. Furthermore, solutal stratification, heat generation/absorption, chemical reaction, and Joule heating are all phenomena that come with the model. The magnetic field is generated along the y-axis, while the flow is produced parallel to the x-axis, as shown in Fig. 1. The equations of the problem are the model as [21]
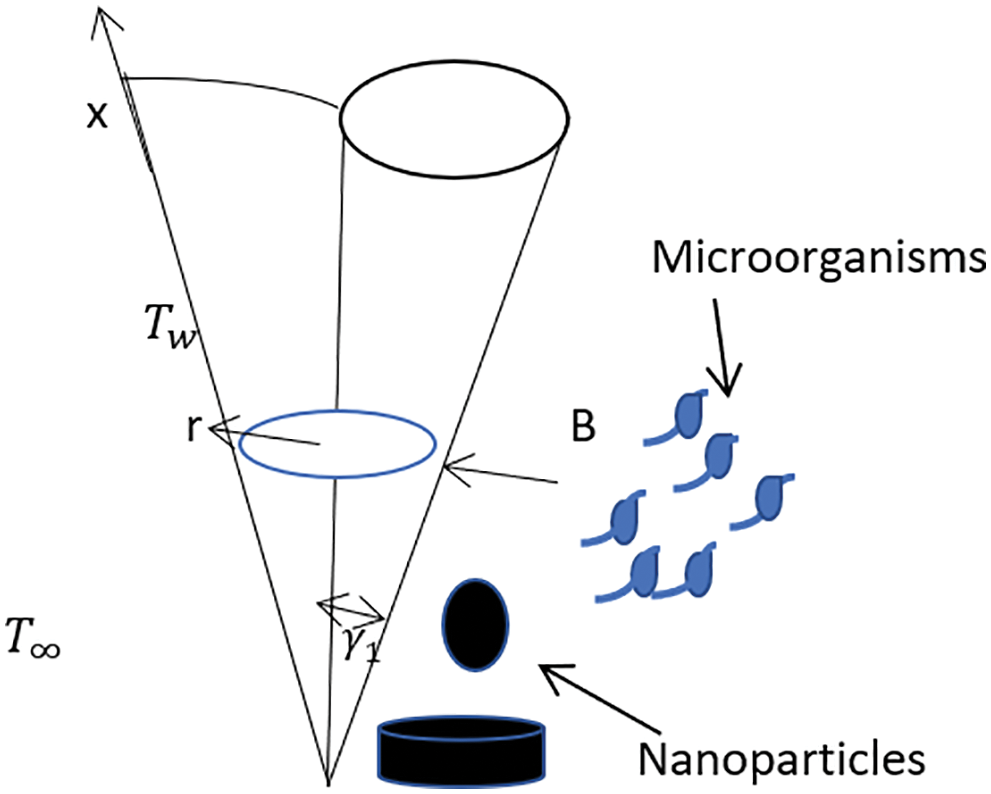
Figure 1: The geometry of the problem
The boundary conditions subjected to the problems are
Here
We introduced the similarity transformation variables to non-dimensionalize the above governing equations
Substituting Eq. (7) into (Eqs. (1)–(5)), we get the following form:
The relevant boundary conditions are described as
where
The evaluated physical quantities are
The dimensionless form of evaluated physical quantities is
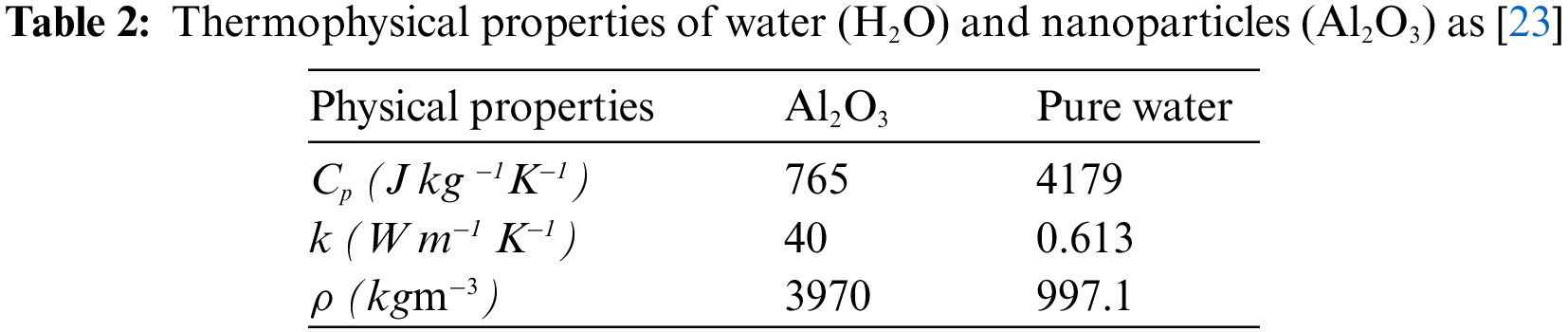
The numerical values of the nanoparticles shape factors (m) are given in Table 1, while the thermophysical properties are tabulated in Table 2.

First step of bvp4c converts the higher-order non-linear ODE’s into first order (ordinary differential equations) ODEs, the procedure of bvp4c is following as
We have introduced
The arguments of MATLAB function are as under.
solinit=bvp4c (linespace (0, infinity, 500), Zeros);
options=bvpset (stats, on, RelTol, 1e-6);
sol =bvp4c (@ex8ode, @ex8bc, solinit, options).
The shape effects of nanoparticles are graphically presented in this section. The expressions for velocity and the temperature profiles are calculated numerically by using the bvp4c program. The effects of various physical parameters values on velocity are shown in Figs. 2–3. The impact of the magnetic parameter (M) on the velocity profile is depicted in Fig. 2. Fig. 2 illustrates that the velocity of nanofluid has an inverse relation with magnetic parameter (M). It is also examined that the velocity of sphere (spherical) shape nanoparticles is greater than that of lamina (non-spherical) shape nanoparticles. Fig. 3 illustrates the expression of velocity with the effect of the porous parameter (K1). Fig. 3 expresses that the velocity of sphere (spherical) shape nanoparticles is greater in a flow system; also, it is noted from Fig. 3 that velocity decrease with intensifying the value of the porous parameter (K1). Fig. 4 demonstrates the velocity profile with the influence of bio convection Lewis number (Pe). The velocity is shown to decrease as the bio convection Lewis number (Pe) rises, and the velocity of sphere (spherical) shape nanoparticles is higher as compared to the lamina (non-spherical) shape nanoparticles.
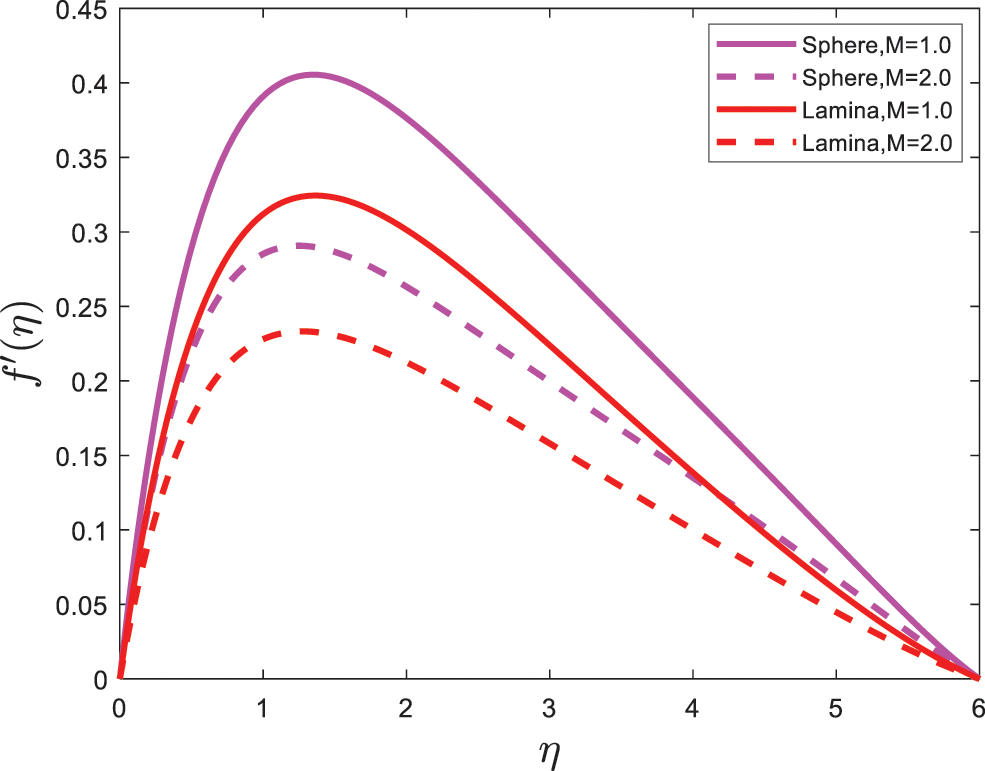
Figure 2:
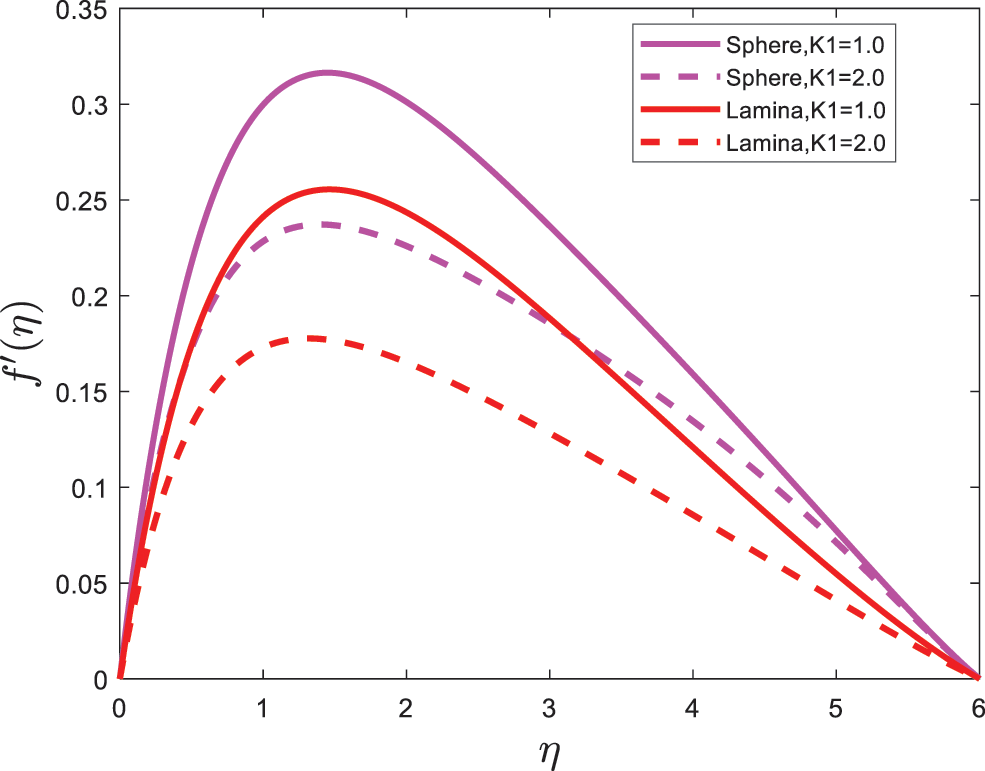
Figure 3:
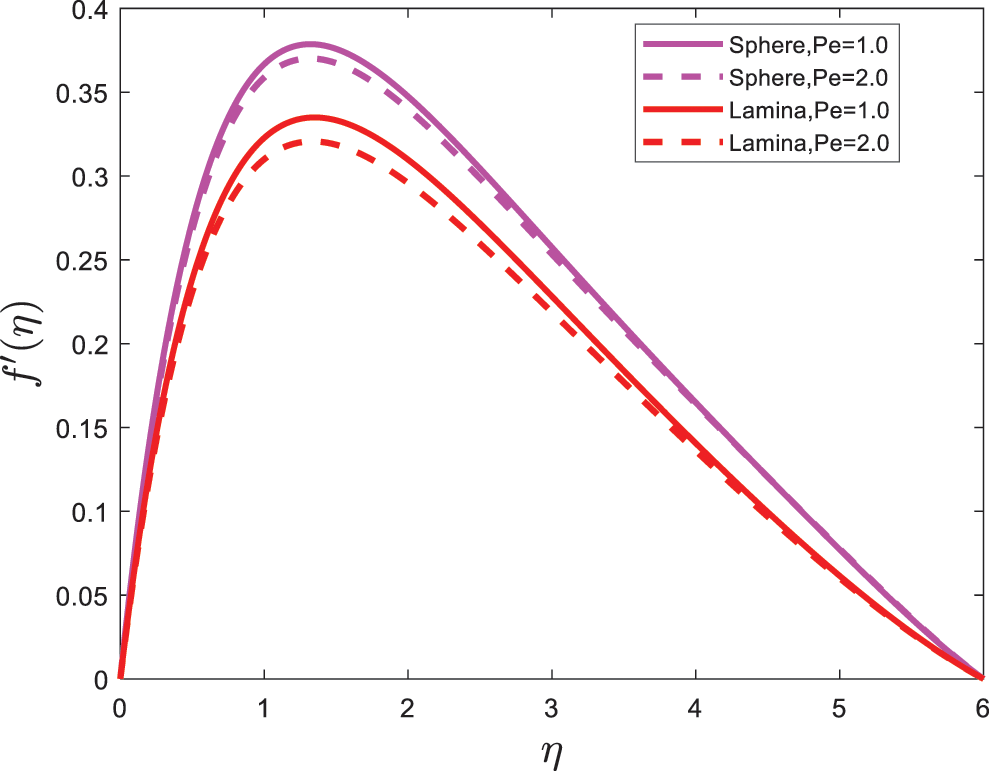
Figure 4:
The impacts of parameters on temperature profiles are plotted in Figs. 5–6. The variation on the nanofluid temperature with the influence of Boit number (
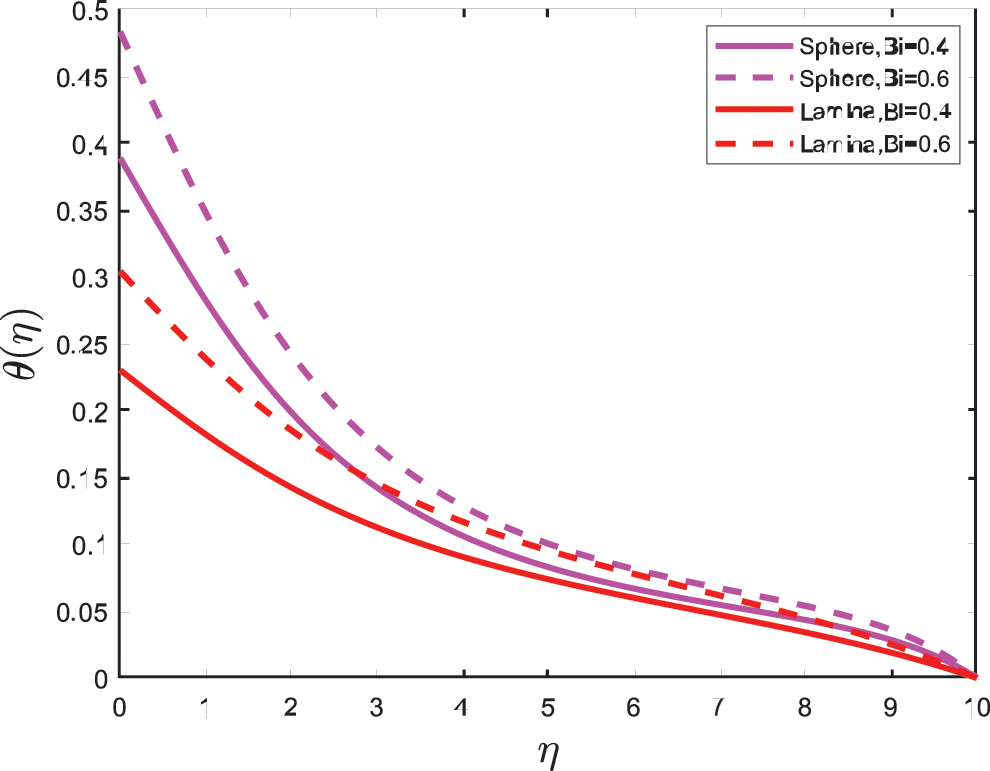
Figure 5:
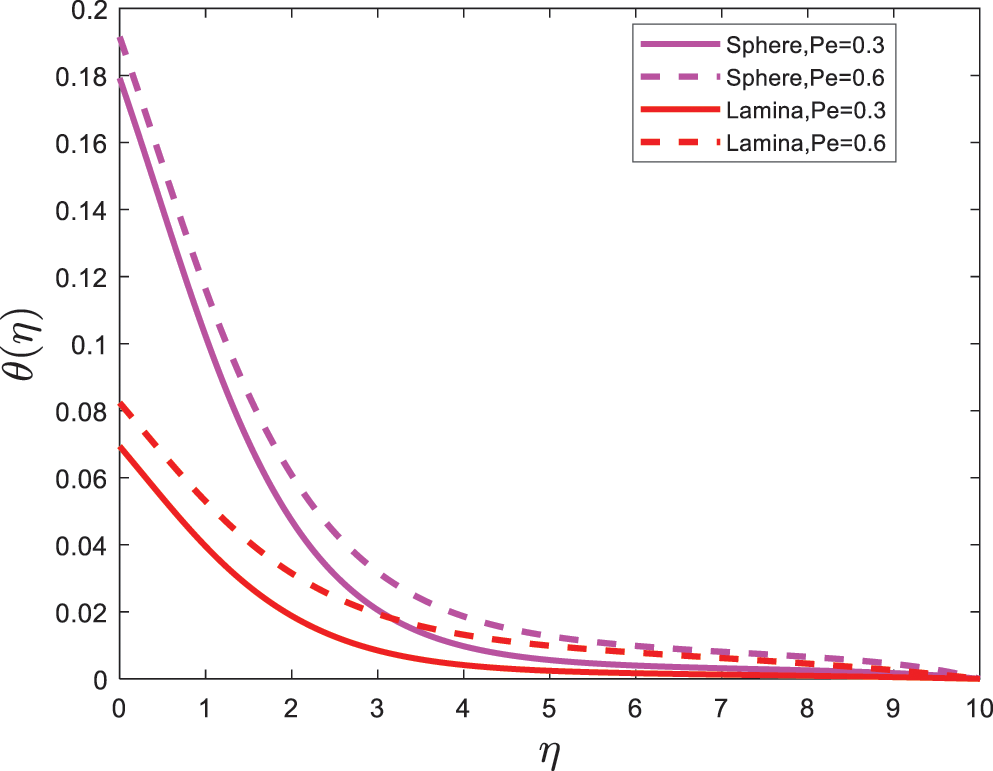
Figure 6:
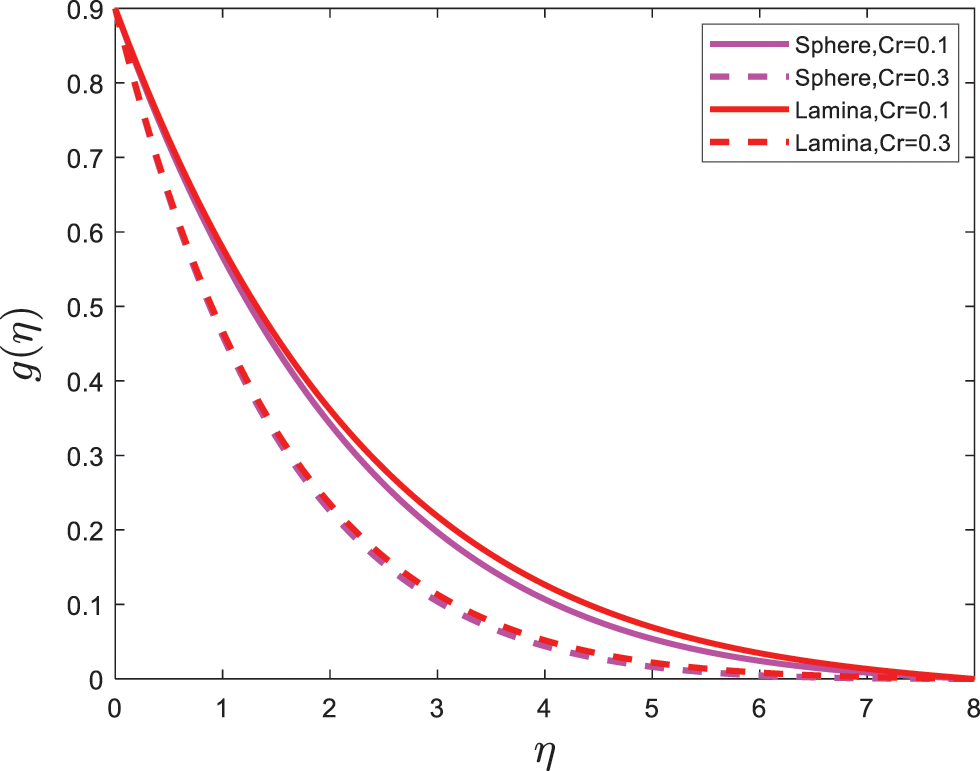
Figure 7:
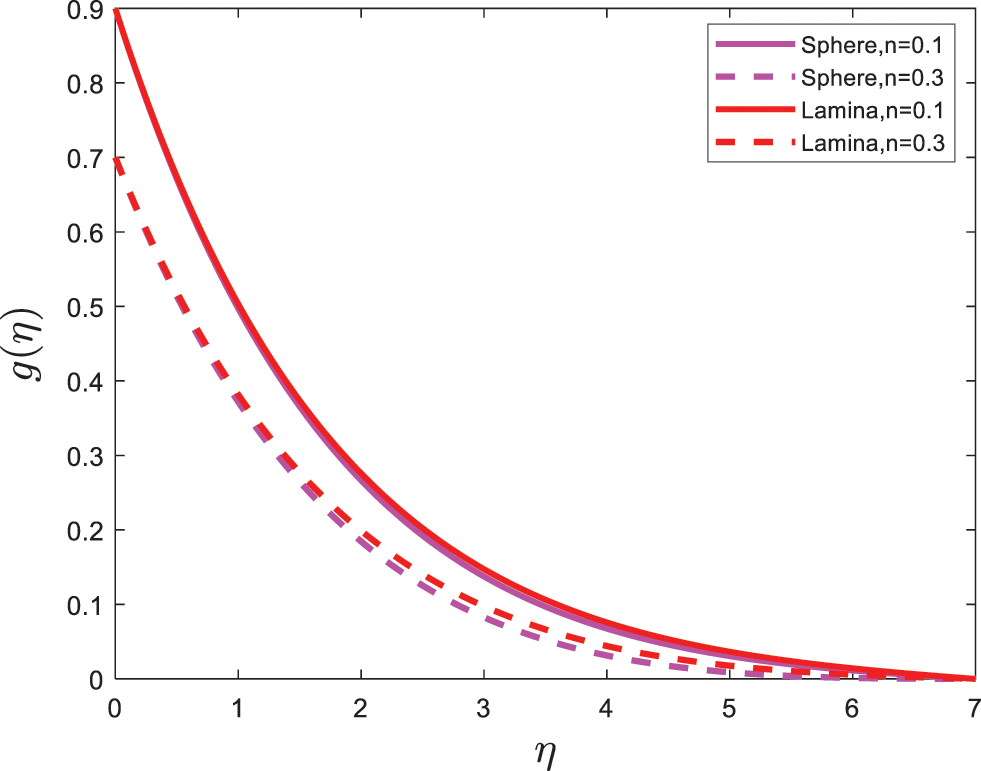
Figure 8:
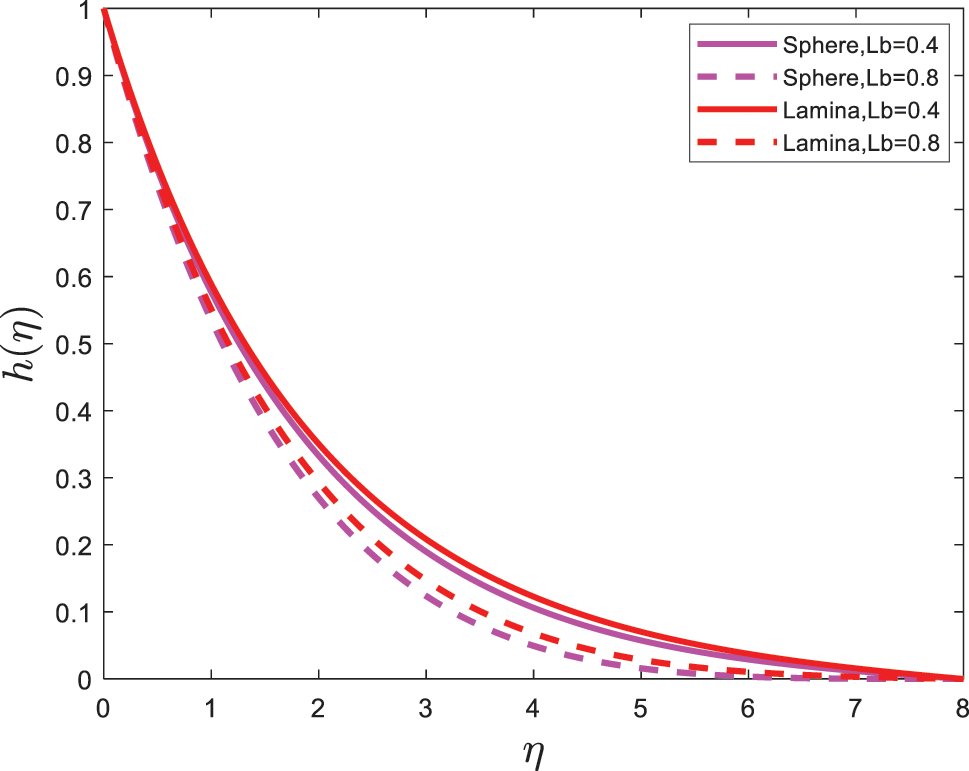
Figure 9:
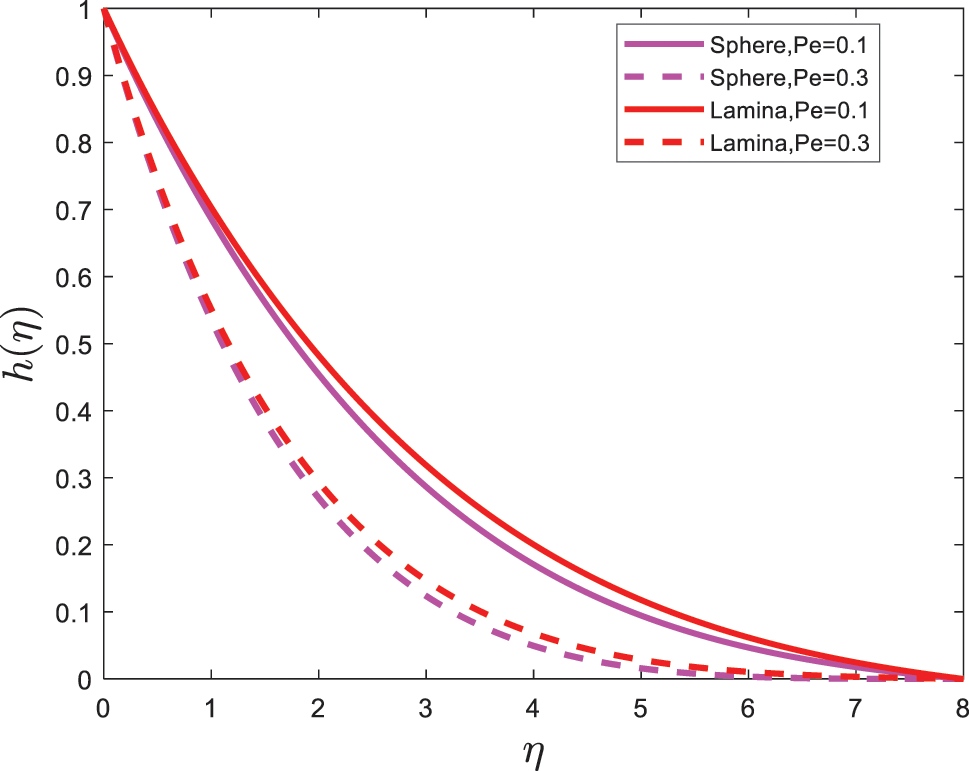
Figure 10:
Figs. 11–14 are plotted to explore the behaviors particles shape on skin friction
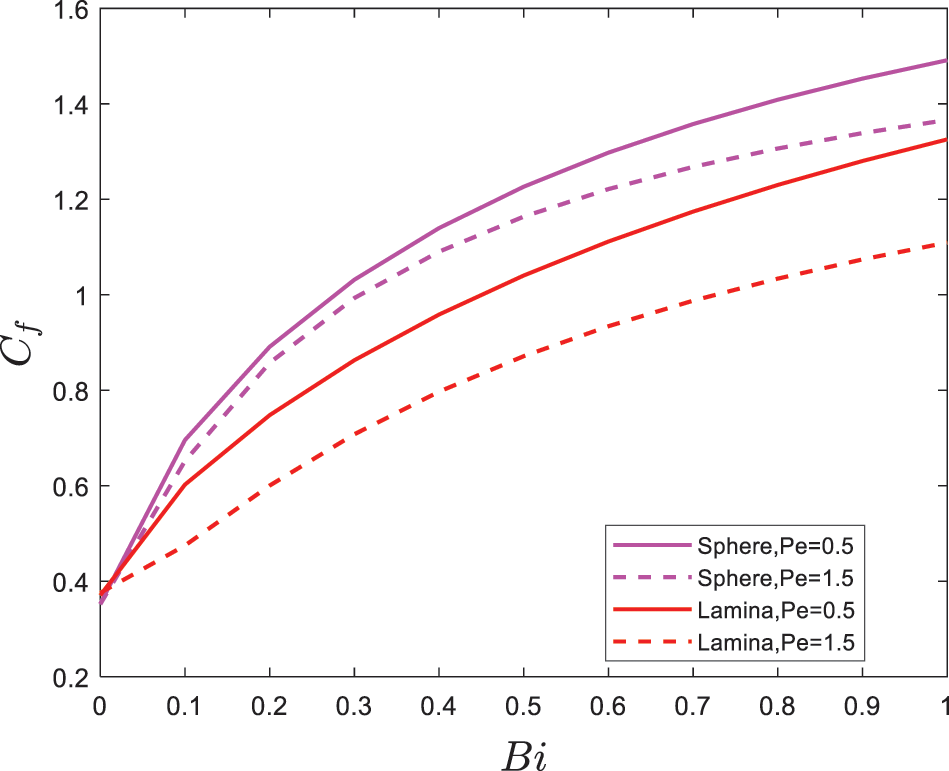
Figure 11:
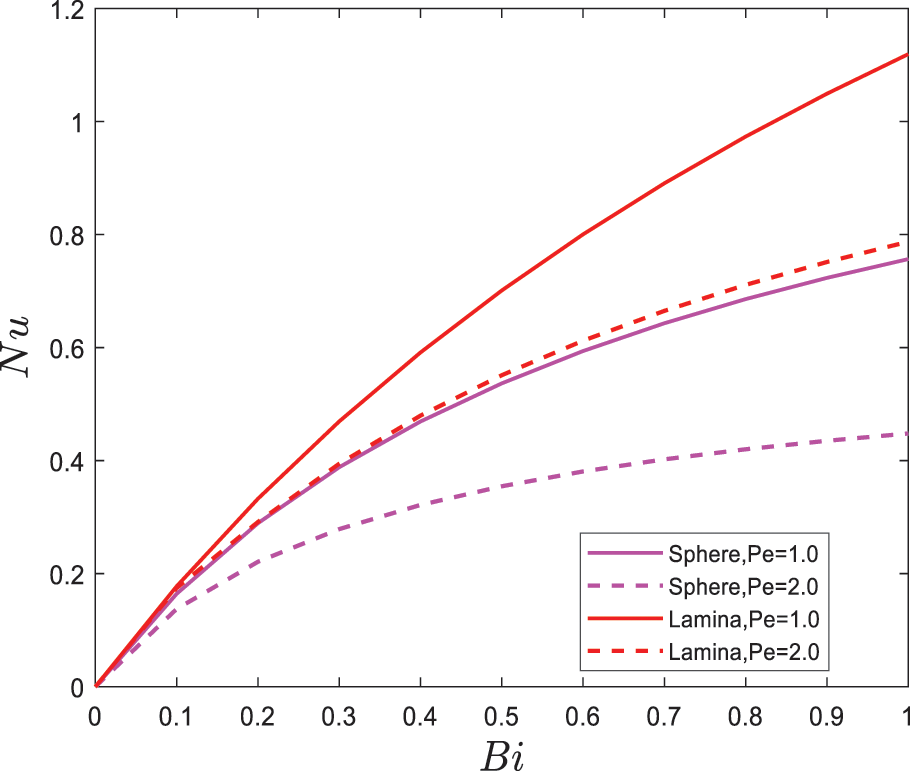
Figure 12:
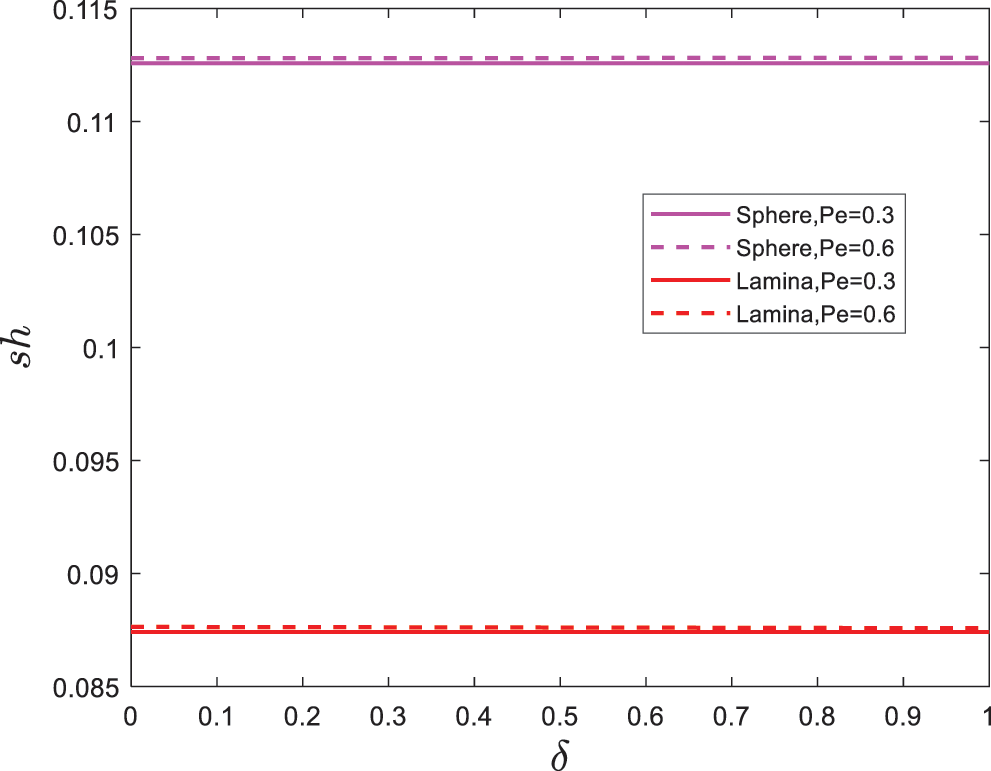
Figure 13:
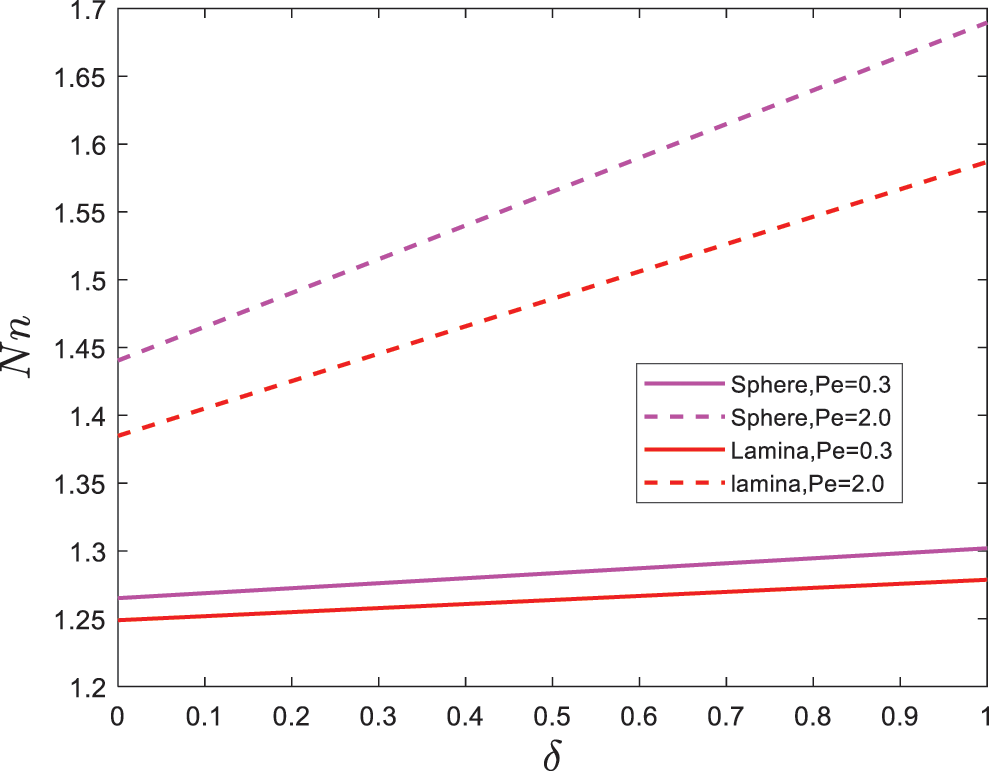
Figure 14:
This paper studies the effects of nanoparticle shape on nanofluid flow, including gyrotactic microorganisms. The impacts of various parameters on the profiles of motile microorganisms’ velocity, temperature, concentration, density, Nusselt number, concentration, Skin friction, and density number of microorganisms are investigated. The points listed below are summarized as follows:
• Velocity profiles of nanofluid decrease for both sphere (spherical) and lamina (non-spherical) shapes nanoparticles.
• Temperature profiles of nanofluid increase for both sphere (spherical) and lamina (non-spherical) shapes nanoparticles.
• Concentration profile and motile microorganisms’ profile are decreased for both sphere (spherical) and lamina (non-spherical) shapes nanoparticles.
• Skin friction and Nusselt number are decreased for both sphere (spherical) and lamina (non-spherical) shapes nanoparticles.
• Sherwood number and Motile density number are increased for both sphere (spherical) and lamina (non-spherical) shapes nanoparticles.
• Sphere (spherical) shapes nanoparticles play a dominant role in the velocity and temperature distribution.
• Lamina (non-spherical) shapes nanoparticles have poor performance in the distribution of velocity and temperature.
• Lamina (non-spherical) shapes nanoparticles play a dominant role on concentration distribution, density of motile microorganisms and Nusselt number.
• Sphere (spherical) shapes nanoparticles have poor performance on concentration distribution, density of motile microorganisms and Nusselt number.
Funding Statement: The authors would like to thank Taif University Researches Supporting Project (TURSP–2020/96), Taif University, Taif, Saudi Arabia, for their financial assistance.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Aman, S., Khan, I., Ismail, Z., Salleh, M. Z., Al-Mdallal, Q. M. (2017). Heat transfer enhancement in free convection flow of CNTs Maxwell nanofluids with four different types of molecular liquids. Scientific Reports, 7, 1–13. DOI 10.1038/s41598-017-01358-3. [Google Scholar] [CrossRef]
2. Hussanan, A., Salleh, M. Z., Khan, I., Shafie, S. (2017). Convection heat transfer in micropolar nanofluids with oxide nanoparticles in water, kerosene and engine oil. Journal of Molecular Liquids, 229, 482–488. DOI 10.1016/j.molliq.2016.12.040. [Google Scholar] [CrossRef]
3. Khan, N. S., Gul, T., Islam, S., Khan, I., Alqahtani, A. M. et al. (2017). Magnetohydrodynamic nanoliquid thin film sprayed on a stretching cylinder with heat transfer. Applied Sciences, 7(3), 271. DOI 10.3390/app7030271. [Google Scholar] [CrossRef]
4. Waqas, H., Khan, S. U., Hassan, M., Bhatti, M. M., Imran, M. (2019). Analysis on the bioconvection flow of modified second-grade nanofluid containing gyrotactic microorganisms and nanoparticles. Journal of Molecular Liquids, 291, 111231. DOI 10.1016/j.molliq.2019.111231. [Google Scholar] [CrossRef]
5. Geng, P., Kuznetsov, A. V. (2004). Effect of small solid particles on the development of bioconvection plumes. International Communications in Heat and Mass Transfer, 31(5), 629–638. DOI 10.1016/S0735-1933(04)00050-8. [Google Scholar] [CrossRef]
6. Uddin, M. J., Khan, W. A., Qureshi, S. R., Bég, O. A. (2017). Bioconvection nanofluid slip flow past a wavy surface with applications in nano-biofuel cells. Chinese Journal of Physics, 55(5), 2048–2063. DOI 10.1016/j.cjph.2017.08.005. [Google Scholar] [CrossRef]
7. Kuznetsov, A. V. (2011). Nanofluid bioconvection in water-based suspensions containing nanoparticles and oxytactic microorganisms: Oscillatory instability. Nanoscale Research Letters, 6(1), 1–13. DOI 10.1186/1556-276X-6-100. [Google Scholar] [CrossRef]
8. Munawar, S., Saleem, N. (2022). Mixed convective cilia triggered stream of magneto ternary nanofluid through elastic electroosmotic pump: A comparative entropic analysis. Journal of Molecular Liquids, 352, 118662. DOI 10.1016/j.molliq.2022.118662. [Google Scholar] [CrossRef]
9. Saleem, N., Munawar, S., Tripathi, D. (2021). Entropy analysis in ciliary transport of radiated hybrid nanofluid in presence of electromagnetohydrodynamics and activation energy. Case Studies in Thermal Engineering, 28, 101665. DOI 10.1016/j.csite.2021.101665. [Google Scholar] [CrossRef]
10. Mekheimer, K. S., Ramadan, S. F. (2020). New insight into gyrotactic microorganisms for bio-thermal convection of Prandtl nanofluid over a stretching/shrinking permeable sheet. SN Applied Sciences, 2(3), 1–11. DOI 10.1007/s42452-020-2105-9. [Google Scholar] [CrossRef]
11. Amirsom, N. A., Uddin, M. J., Basir, M. F. M., Ismail, A. I. M., Beg, O. A. et al. (2019). Three-dimensional bioconvection nanofluid flow from a bi-axial stretching sheet with anisotropic slip. Sains Malaysiana, 48(5), 1137–1149. DOI 10.17576/jsm-2019-4805-23. [Google Scholar] [CrossRef]
12. Aziz, A., Khan, W. A., Pop, I. (2012). Free convection boundary layer flow past a horizontal flat plate embedded in porous medium filled by nanofluid containing gyrotactic microorganisms. International Journal of Thermal Sciences, 56, 48–57. DOI 10.1016/j.ijthermalsci.2012.01.011. [Google Scholar] [CrossRef]
13. Khan, N. S., Gul, T., Khan, M. A., Bonyah, E., Islam, S. (2017). Mixed convection in gravity-driven thin film non-newtonian nanofluids flow with gyrotactic microorganisms. Results in Physics, 7, 4033–4049. DOI 10.1016/j.rinp.2017.10.017. [Google Scholar] [CrossRef]
14. Javaid, M., Tahir, M., Imran, M., Baleanu, D., Akgül, A. et al. (2022). Unsteady flow of fractional burgers’ fluid in a rotating annulus region with power law kernel. Alexandria Engineering Journal, 61(1), 17–27. DOI 10.1016/j.aej.2021.04.106. [Google Scholar] [CrossRef]
15. Khan, W. A., Rashad, A. M., Abdou, M. M. M., Tlili, I. (2019). Natural bioconvection flow of a nanofluid containing gyrotactic microorganisms about a truncated cone. European Journal of Mechanics-B/Fluids, 75, 133–142. DOI 10.1016/j.euromechflu.2019.01.002. [Google Scholar] [CrossRef]
16. Khan, S. U., Rauf, A., Shehzad, S. A., Abbas, Z., Javed, T. (2019). Study of bioconvection flow in Oldroyd-B nanofluid with motile organisms and effective Prandtl approach. Physica A: Statistical Mechanics and its Applications, 527, 121179. DOI 10.1016/j.physa.2019.121179. [Google Scholar] [CrossRef]
17. Waqas, H., Khan, S. U., Shehzad, S. A., Imran, M. (2019). Significance of the nonlinear radiative flow of micropolar nanoparticles over porous surface with a gyrotactic microorganism, activation energy, and nield’s condition. Heat Transfer–Asian Research, 48(7), 3230–3256. DOI 10.1002/htj.21539. [Google Scholar] [CrossRef]
18. Sampath Kumar, P. B., Gireesha, B. J., Mahanthesh, B., Chamkha, A. J. (2019). Thermal analysis of nanofluid flow containing gyrotactic microorganisms in bioconvection and second-order slip with convective condition. Journal of Thermal Analysis and Calorimetry, 136(5), 1947–1957. DOI 10.1007/s10973-018-7860-0. [Google Scholar] [CrossRef]
19. Sohail, M., Naz, R., Abdelsalam, S. I. (2020). On the onset of entropy generation for a nanofluid with thermal radiation and gyrotactic microorganisms through 3D flows. Physica Scripta, 95(4), 045206. DOI 10.1088/1402-4896/ab3c3f. [Google Scholar] [CrossRef]
20. Atif, S. M., Hussain, S., Sagheer, M. (2019). Magnetohydrodynamic stratified bioconvective flow of micropolar nanofluid due to gyrotactic microorganisms. AIP Advances, 9(2), 025208. DOI 10.1063/1.5085742. [Google Scholar] [CrossRef]
21. Ramzan, M., Mohammad, M., Howari, F. (2019). Magnetized suspended carbon nanotubes based nanofluid flow with bio-convection and entropy generation past a vertical cone. Scientific Reports, 9(1), 1–15. DOI 10.1038/s41598-019-48645-9. [Google Scholar] [CrossRef]
22. Rashid, U., Liang, H., Ahmad, H., Abbas, M., Iqbal, A. et al. (2021). Study of (Ag and TiO2)/water nanoparticles shape effect on heat transfer and hybrid nanofluid flow toward stretching shrinking horizontal cylinder. Results in Physics, 21, 103812. DOI 10.1016/j.rinp.2020.103812. [Google Scholar] [CrossRef]
23. Aman, S., Khan, I., Ismail, Z., Salleh, M. Z., Al-Mdallal, Q. M. (2017). Heat transfer enhancement in free convection flow of CNTs Maxwell nanofluids with four different types of molecular liquids. Scientific Reports, 7(1), 1–13. DOI 10.4236/anp.2020.91002. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools