 Open Access
Open Access
ARTICLE
Amassing the Security: An Enhanced Authentication and Key Agreement Protocol for Remote Surgery in Healthcare Environment
1 Shandong University of Science and Technology, Qingdao, 266400, China
2 Chaudhary Charan Singh University, Meerut, Uttar Pradesh, 250004, India
3 California State University, Fresno, 93740, USA
* Corresponding Author: Matin Pirouz. Email:
(This article belongs to the Special Issue: Internet of Things in Healthcare and Health: Security and Privacy)
Computer Modeling in Engineering & Sciences 2023, 134(1), 317-341. https://doi.org/10.32604/cmes.2022.019595
Received 30 September 2021; Accepted 09 March 2022; Issue published 24 August 2022
Abstract
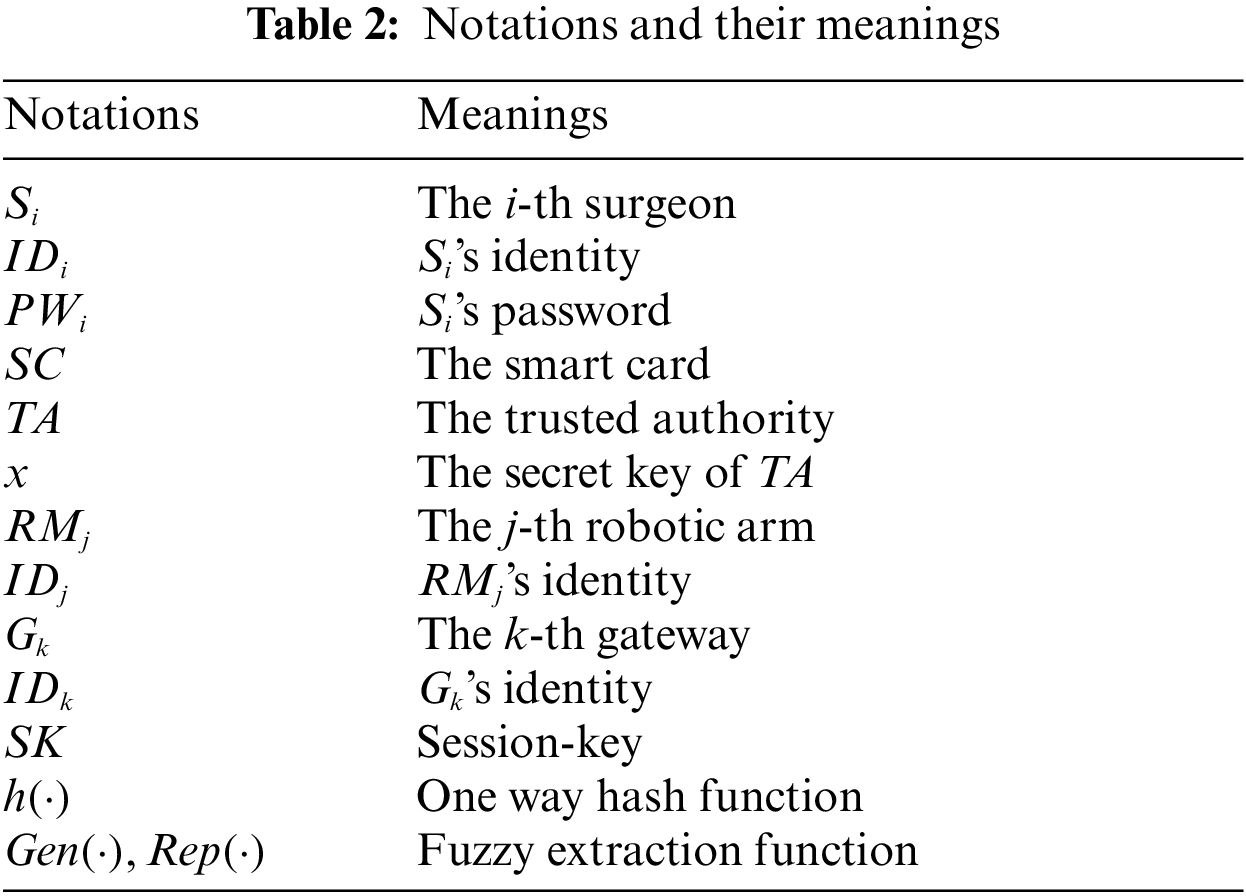
The development of the Internet of Things has facilitated the rapid development of various industries. With the improvement in people’s living standards, people’s health requirements are steadily improving. However, owing to the scarcity of medical and health care resources in some areas, the demand for remote surgery has gradually increased. In this paper, we investigate remote surgery in the healthcare environment. Surgeons can operate robotic arms to perform remote surgery for patients, which substantially facilitates successful surgeries and saves lives. Recently, Kamil et al. proposed a secure protocol for surgery in the healthcare environment. However, after cryptanalyzing their protocol, we deduced that their protocols are vulnerable to temporary value disclosure and insider attacks. Therefore, we design an improved authentication and key agreement protocol for remote surgeries in the healthcare environment. Accordingly, we adopt the real or random (ROR) model and an automatic verification tool Proverif to verify the security of our protocol. Via security analysis and performance comparison, it is confirmed that our protocol is a relatively secure protocol.Keywords
As a novel paradigm, Internet of Things (IoT) [1–5] can effectively share data, coordinate and utilize resources. Simultaneously, in addition to reducing data transmission delay, the active of the emergence of the 5G [6] technology also improves the data transmission rate, which makes it possible to exchange of large amounts of data. This technology has been widely adopted in smart agriculture, smart cities, transportation, healthcare [7,8], artificial intelligence [9–11], etc., and has become an important part of people’s life.
Healthcare is an important application of the IoT. With the improvement of living standards, the requirements for medical and health care are gradually increasing. Today, there is a substantial demand for medical and health care systems. The application of IoT in healthcare involves the use of the most advanced internet technology to realize interactions between patients and doctors and medical institutions and medical equipment, which enables the informatization. With the help of IoT technology, artificial intelligence [12] and intelligent equipment, we can build a perfect IoT medical system to solve or reduce the problems of difficult medical treatment and tense doctor-patient relationships caused by the lack of medical resources. Although healthcare can provide people with significant convenience, several security problems [13–17] exist, such as the disclosure of patients’ medical data and the tampering of patients’ medical schemes by illegal personnel of the system. Many researchers have proposed a large number of schemes [12,18–20] to address the security problems inherent in the healthcare environment. However, some existing authentication and key agreement protocols have security vulnerabilities, such as against offline guessing, impersonation and insider attacks. Therefore, it is crucial to propose an AKA protocol to address these challenges.
Wu et al. [21] proposed an authentication scheme, suitable for telemedicine information systems (TMIS). However, Debiao et al. [22] have confirmed that their scheme is vulnerable to several security problems, such as impersonation attacks and insider attacks. To address these vulnerabilities, Debiao et al. [22] proposed an improved scheme, which is also applicable to TMIS. Wei et al. [23] proposed a protocol suitable for TMIS without the pre-deployment phase; however, Zhu et al. [24] verified that the protocol proposed by Wei et al. [23] could not resist offline password guessing attacks. Xu et al. [25] proposed an elliptic curve cryptography (ECC)-based scheme. They claimed that their protocol can effectively provide authentication and user anonymity. However, Islam et al. [26] pointed out that Xu et al.’s [25] scheme are vulnerable to replay attacks and smart card stolen attacks, incorrect password update phase, and failure to successfully complete mutual authentication. Subsequently, Islam et al. [26] proposed an improved protocol based on the that proposed by Xu et al. [25]. The protocol was also designed based on ECC. Li et al. [27] designed an authentication scheme based on chaotic mapping; however, Madhusudhan et al. [28] proved that their scheme cannot successfully resist password guessing attacks. Zhang et al. [29] designed a three factor lightweight authentication agreement to address the problem of user anonymity in the e-healthcate system. However, Aghili et al. [30] pointed out that the agreement of Zhang et al. [29] cannot resist denial of service attacks (DOS) and insider attacks, as well as provide user untraceability and desynchronization. Therefore, Aghili et al. [30] proposed an improved scheme, which can provide user anonymity and mutual authentication. Sharma et al. [31] proposed a healthcare service authentication scheme based on cloud Internet of things, but Azrour et al. [32] pointed out that Sharma et al.'s [31] scheme could not resist user impersonatin attacks and offline password guessing attacks. Soni et al. [33] designed an authentication scheme for patient monitoring, but unfortunately, their scheme was proved by Xu et al. [34] that it could not provide perfect forward security. Kaur et al. [35] designed a secure protocol to solve the problem of security authentication in remote surgery. Ali et al. [36] designed a symmetric encryption and decryption scheme for TMIS; however, Yu et al. [37] discovered that this scheme [36] cannot withstand session key exposure attacks, man in the middle attacks (MITM) and impersonation attacks. Masud et al. [38] proposed a lightweight identity authentication scheme based on IoT healthcare. However, this scheme has been proved by Kwon et al. [39] that there are many security problems, such as offline password guessing, user impersonation, insider attacks and cannot ensure user anonymity. We summarize the literature reviewed in Table 1.

Influenced by COVID-19, the demand for remote surgery [40,41] under healthcare environment is gradually increasing. At the same time, the 5G network technology can transmit information with high efficiency and low delay, thereby facilitating remote surgery. The application of a remote surgery is shown in the Fig. 1. Surgeons can operate robotic arms to perform remote surgery for patients, which enables a number patients infected with the virus to receive prompt treatment, reduces the spread of the virus, and provide the stable development of society. Although the development of this technology can bring several benefits, they are highly dependent on the network, and there will be some security problems. For example, if network delay occurs when a surgeon remotely manipulates a robotic arm to operate a patient, the surgeon cannot obtain feedback information in time, which will adversely affect the operation process and severely endanger the patient’s life. In addition, if an illegal surgeon manipulates the robotic arm or an unauthorized robotic arm is utilized, this will also threaten the safety of patients. Therefore, a secure lightweight authentication and key agreement protocol design is required to address these problems.
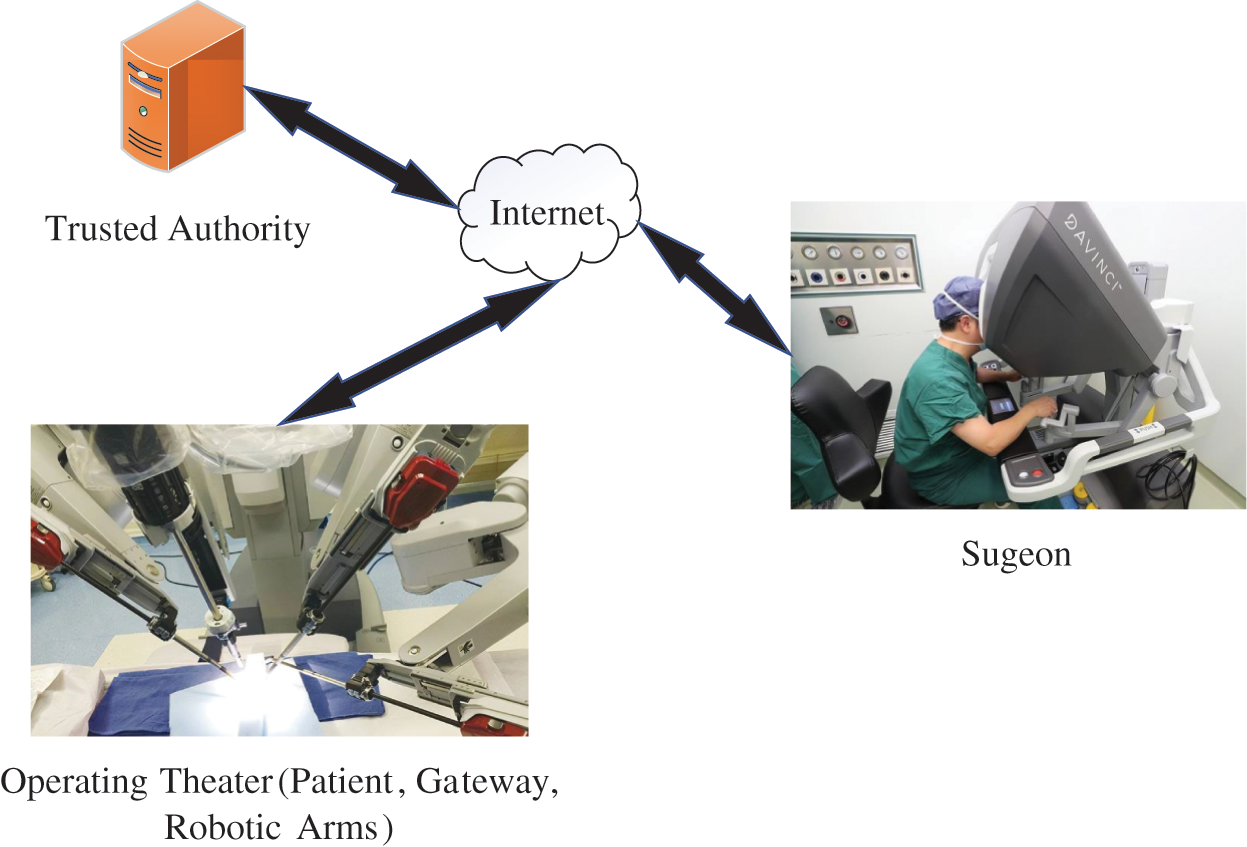
Figure 1: The application of a remote surgery
Recently, Kamil et al. [42] designed a lightweight authentication protocol that primarily solves identity authentication problem in remote surgery. Its remote surgery framework is illustrated in Fig. 2. This framework comprises four entities: a trusted authority (TA), surgeon, gateway, and robotic arm. All medical data during surgery is transmitted through tactile networks. To protect the security and privacy of medical data, the entire operation process needs to be completed under the detection of TA. Before surgery, surgeons and gateways, and the robotic arm must register with TA and obtain a legal identity. After each entity completes its registration, the surgeon, gateway, and robotic arm jointly decide on a session key to transmit data during surgery. They claim that their protocol is secure and efficient. However, we find that their protocol is vulnerable to temporary value disclosure attacks and insider attacks. In this paper, we propose an enhanced protocol suitable for this environment. Our contributions are: (1) We point out that Kamil et al.’s protocol has some security problems. (2) To solve these security problems, we propose an enhanced authentication protocol for remote surgery. Unlike Kamil et al.’s protocol, the registration phase of the robotic arm does not register with the TA via the gateway, because in an operating machine, the gateway and robotic arm are in the same system. We use ProVerif tool and ROR model to evaluate the security of the protocol. In addition, we use informal analysis to conduct a detailed security evaluation of the protocol, and prove that the protocol can resist common attacks, such as MIMT, replay attacks, impersonation attacks, insider attacks, etc. (3) Finally, through security and performance comparison, we find that our protocol is secure and suitable for the remote surgery environment.
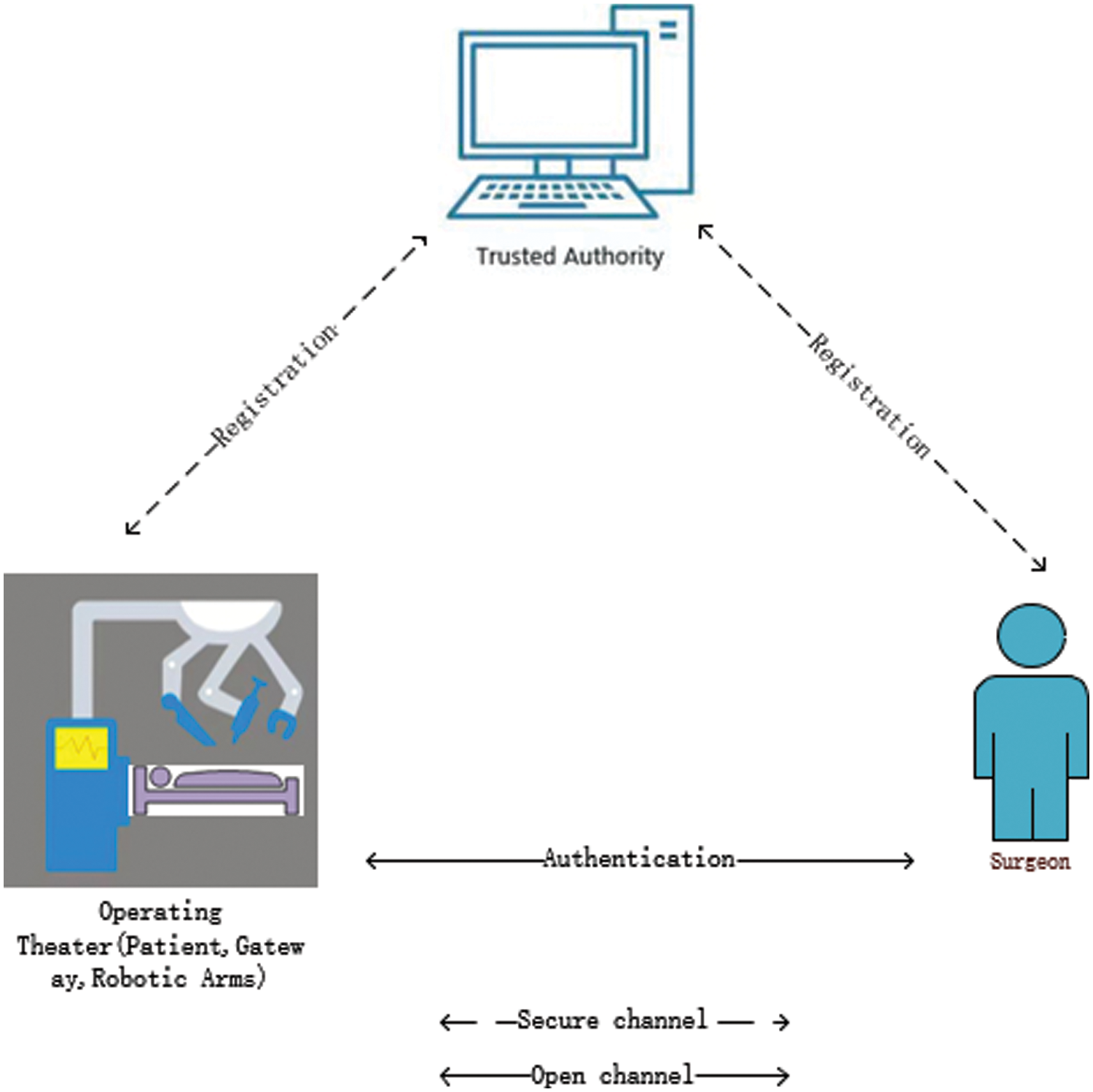
Figure 2: Network model
The remainder of this paper are arranged as follows. In Section 2, we review the protocol proposed by Kamil et al. The cryptanalysis of their protocol is then comprehensively introduced in detail in Section 3. In Section 4, we introduce our proposed protocol. Then, Section 5 presents a few security analyses of our protocol, while the performance comparison is introduced in Section 6. Finally, Section 7 concludes this paper.
2 Review of Kamil el at. Protocol
In this section, we review the protocol presented by Kamil et al. [42]. This protocol comprises seven phases; however, in this paper, we only adopt four phases: surgeon registration phase, gateway and robotic arm registration phase, user login, authentication and key agreement phase.
2.1 Surgeon Registration Phase
Surgeons are required to register with the TA as legitimate users to utilize robotic arms for remote surgeries. Messages at this stage are transmitted on a secure channel. The detailed steps are presented as follows in Table 2:
(1)
(2) After receiving the message sent by
(3) After receiving SC,
2.2 Gateway and Robotic Arm Registration Phase
At this phase, TA selects their respective identities for
(1) TA selects its own identity
2) After receiving the message sent by TA,
3)
2.3 Login and Authentication Phase
1)
2) After receiving the message
3) After receiving message
4) After receiving the message
5) After receiving the message
3 Cryptanalysis of Kamil et al.’s Protocol
In this section, based on the following attacker model [43], we analyze the security of the protocol proposed by Kamil et al. [42], and subsequently deduce that this protocol cannot resist temporary value disclosure attacks, insider attacks.
Attacker Model: Based on D-Y model [44], we define attacker
1)
2)
3)
Insider attacks refers to a malicious person in the system who obtains the information stored in the system by other entities, uses the messages on the public channel, and finally successfully calculates the session key. Suppose a malicious attack
1)
2)
3) After receiving message
4) After
5) After receiving
6) At this point,
1.
2. After
In summary, we logically infer that the protocol proposed by Kamil et al. [42] cannot resist privileged insider attacks.
3.2 Temperory Value Disclosure Attacks
Assuming that attacker
In this section, we introduce the proposed protocol. The protocol comprises four phases: surgeon registration phase, gateway registration phase, robotic arm registration phase, login and authentication phase. Each phase will be comprehensively described in detail next.
The registration phase mainly includes gateway registration, surgeon registration and robtic arm registration, which will be described in detail.
Surgeon Registration Phase: Before operating with a robotic arm, a surgeon must register with the TA as a legal user via a secure channel. Fig. 3 shows the surgeon’s registration process. The specific steps necessary for this registration are as follows:
1) The surgeon
2) After receiving the information sent by
3) After receiving the SC sent by TA, the surgeon stores
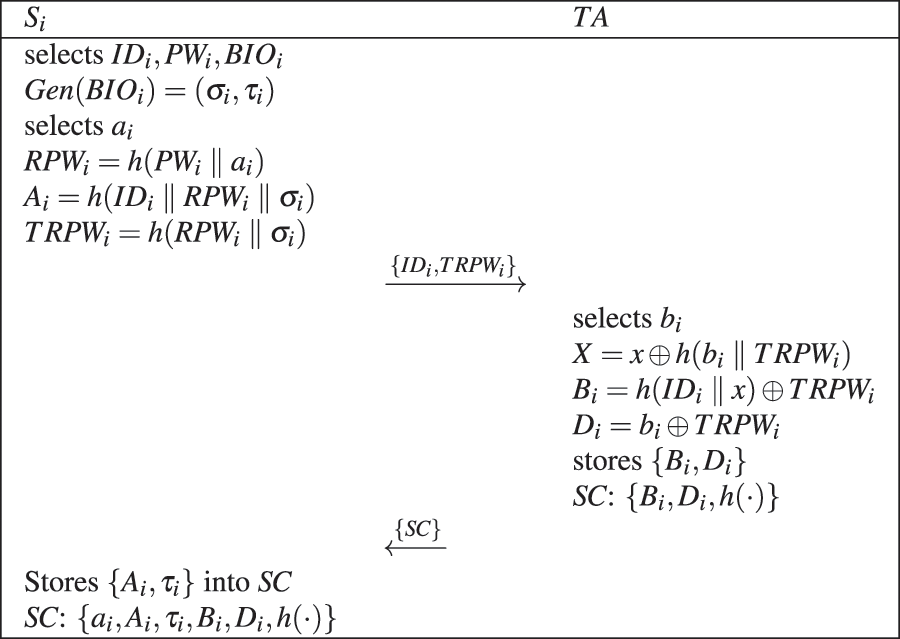
Figure 3: Surgeon registration
Gateway Registration Phase: Before being utilized, the gateway must register with the TA and generate some private data for the authentication phase. Fig. 4 shows gateway’s registration process. The specific steps required are as follows:1. The gateway selects its own
2. After receiving the message sent by the gateway, TA selects a random number
3. Subsequently, the gateway stores
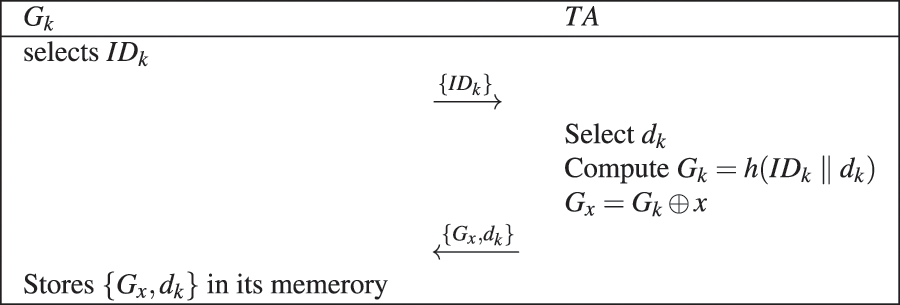
Figure 4: Gateway registration phase
Robotic Arm Registration Phase: Because the robotic arm and gateway are in the same system, the robotic arm is solely required to register with the gateway via a secure channel. Fig. 5 shows robotic arm’s registration process. The specific steps required are comprehensively presented as follows:
1) The robotic arm
2) After receiving a message sent by the robotic arm, gateway selects a random number
3) Finally

Figure 5: Robotic arm registration phase
4.2 Login and Authentication Phase
Before performing long-distance operations, surgeons need to manipulate robotic arms via an access gateway. After
1)
2) After receiving the message
3) After receiving the message
4) After receiving the message
5) When

In this section, we adopt Proverif, ROR model, and informal analysis to validate the security of our proposed protocol
Four entities are adopted in our protocol: TA,
1) ch and sch are used to represent common channel and secure channel, respectively. The registration phase is carried out on the secure channel, while the login and authentication phase is conducted on the public channel. The session key adopts
2)
3)
4)
5) TA’s process is shown in Fig. 7d.
6) Fig. 6d presents the obtained verification results. The final results are “Query not attacker (SKi[]) is true,” “Query not attacker (SKj[]) is true,” “Query not attacker (SKk[]),” “Query inj-event (SurgeonAuthed) ==> inj-event (SurgeonStarted) is true,” “Query inj-event (RMAcGateway) ==> inj-event(GatewayAcSurgeon) is true,” “Query inj-event(GatewayAcRM) ==> inj-event(RMAcGateway) is true,” and “Query inj-event(SurgeonAcGateway) ==> inj-event(GatewayAcRM) is true.” Therefore, our protocol can successfully pass the security verification of Proverif and resist attacks.

Figure 6: Definitions and results

Figure 7: Process
In this section, we perform a security analysis on the proposed protocol in the ROR [19,47] model to demonstrate the protocol’s security.
The proposed protocol contains four entities: a surgeon, gateway, TA, and robotic arm. In the ROR model, we adopt



In the ROR model, if
We played five rounds of the game,
1) Perfect forward security:
2) Temporary information disclosure attack:
For the first event, even if
Because the probabilities of the success and failure of
According to the above formula, we can obtain
Therefore, we can obtain
It is not difficult to infer that our protocol has successfully passed the security verification of ROR model, and that it can resist offline password guessing attacks, smart card stolen attacks, random number disclosure attacks, as well as provide perfect forward security.
5.3 Informal Security Analysis
In this section, we verify that our proposed protocol can resist some common attacks.
Attacker
1) Impersonate Surgeon: An attacker
2) Impersonate gateway: An attacker
3) Impersonate robotic arm: When an attacker
5.3.2 Man-in-the-Middle Attacks
If an attacker
Since no information about
We assume that attacker
6 Security and Performance Comparison
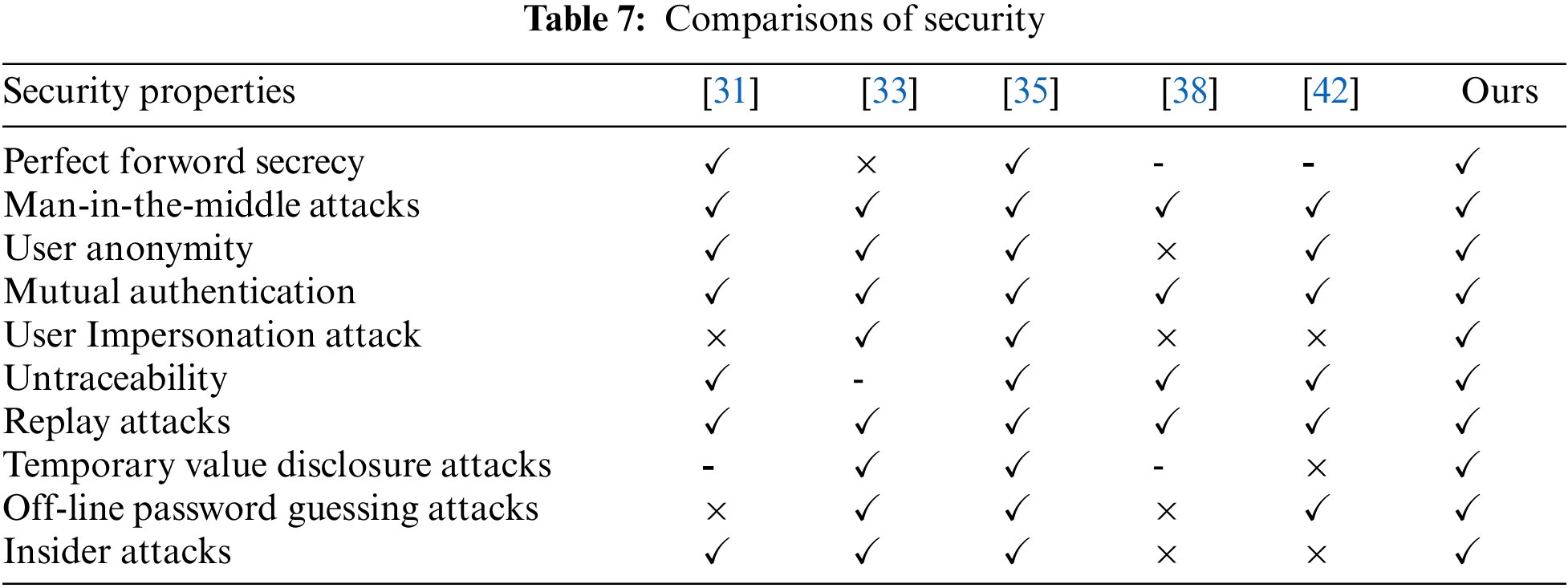
In this section, we compare the security and performance with the protocols of Sharma et al. [31], Soni et al. [33], Kaur et al. [35], Masud et al. [38] and Kamil et al. [42], which are applicable to the healthcare environment. The detailed results of the comparison are comprehensively described in subsections.
In this subsection, we compare the security of these five protocols.
Here, we compare the performance of these five protocols from two aspects: computional cost and communicational cost.
We adopted a computer with Windows10 operating system, Intel (R) core (TM) i5- 8500CPU@ 3.00 GHz 3.00 G processor, and 8 G memory. The development software we use was IntelliJ idea version 2019.3, which is based on the call of Java pairing library, signature library, and symmetric encryption/decryption function. We ran various operations on the computer 50 times, and then use the average value as the reference time for calculating the computional cost. In addition, we approximate the operation time of the fuzzy extractor to the calculation time of point multiplication, and the computational cost of XOR and join operations is negligible. Based on the results in Table 8, we can drive the comparative results of computational cost in Table 9 and Fig. 8 (original). The reason why the computational cost of protocols [33] and [35] is very high is that they both use point multiplication, and protocol a also uses symmetric encryption and decryption, which leads to great computational overhead. The reason why the computational cost of our protocol is higher than that of protocols [31,33] and [42] is that we use a fuzzy extractor, which occupy some computational overhead, and they only use one-way hash functions, resulting in slightly higher computational cost.


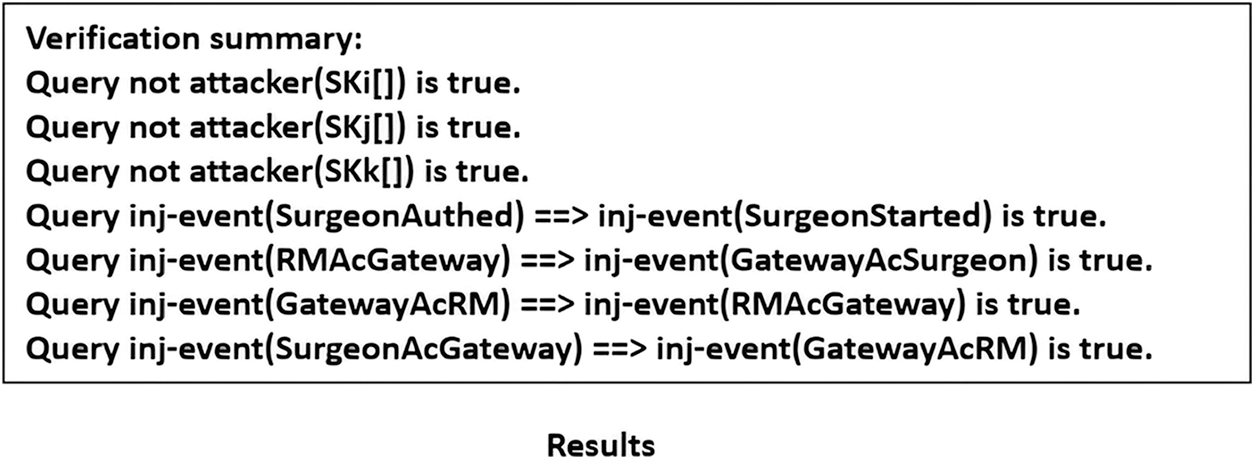
Figure 8: Results
For the communicational cost, we established that the output length of the single hash function H is 256 bits, T represents the timestamp, with a length of 32 bits, ID represents the length of the identity and is 256 bits, the length of encryption operation E is 256 bits, the length of group G is 1024 bits, and s represents the string with a length of 160 bits. According to the above definitions, Table 10 and Fig. 10 comprehensively show the results.
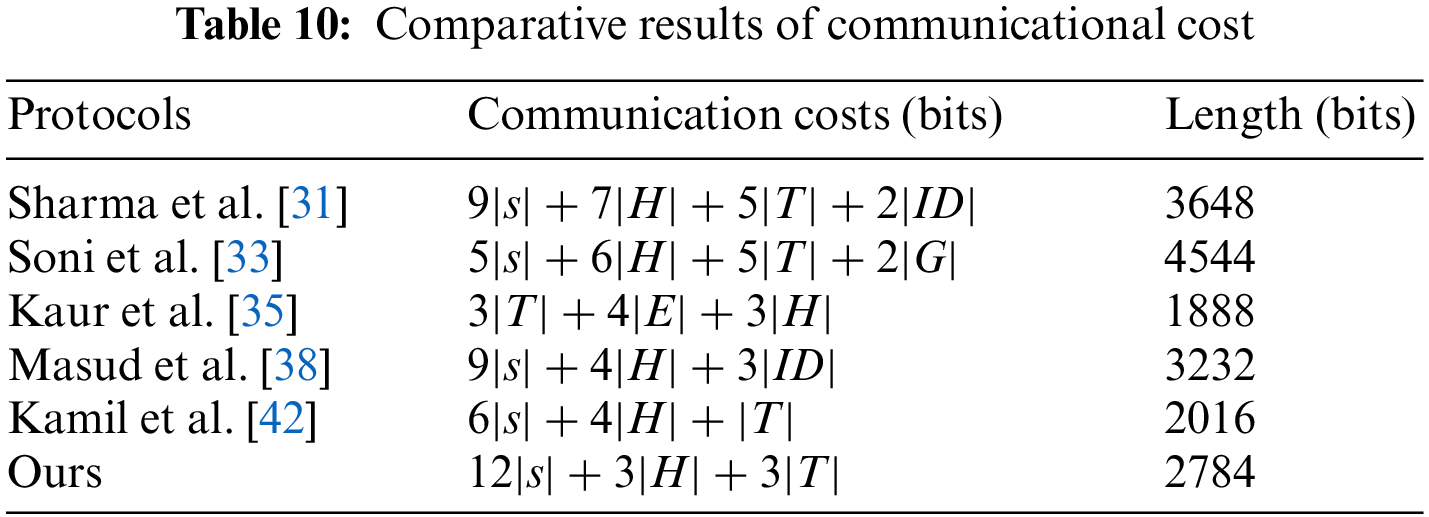
To sum up: Table 7 shows the comparison results of security. Table 9 and Fig. 9 are the comparison results of computational cost. Table 10 and Fig. 10 are the comparison results of communication cost. Although the computing cost of Sharma et al. [31] protocol is lower than ours, its security is not as good as ours, and the communication is also higher than ours; The protocols of Soni et al. [33] is not as good as our protocols in terms of security and performance; Although the protocol of Kaur et al. [35] is more secure and the communication cost is lower than ours, its computing cost is very high; Although the computational cost of Masud et al. [38] protocol is lower than ours, it has security problems and higher communication cost than ours; Although the protocol of Kamil et al. [42] has high performance and is better than ours, its security is worse than ours.
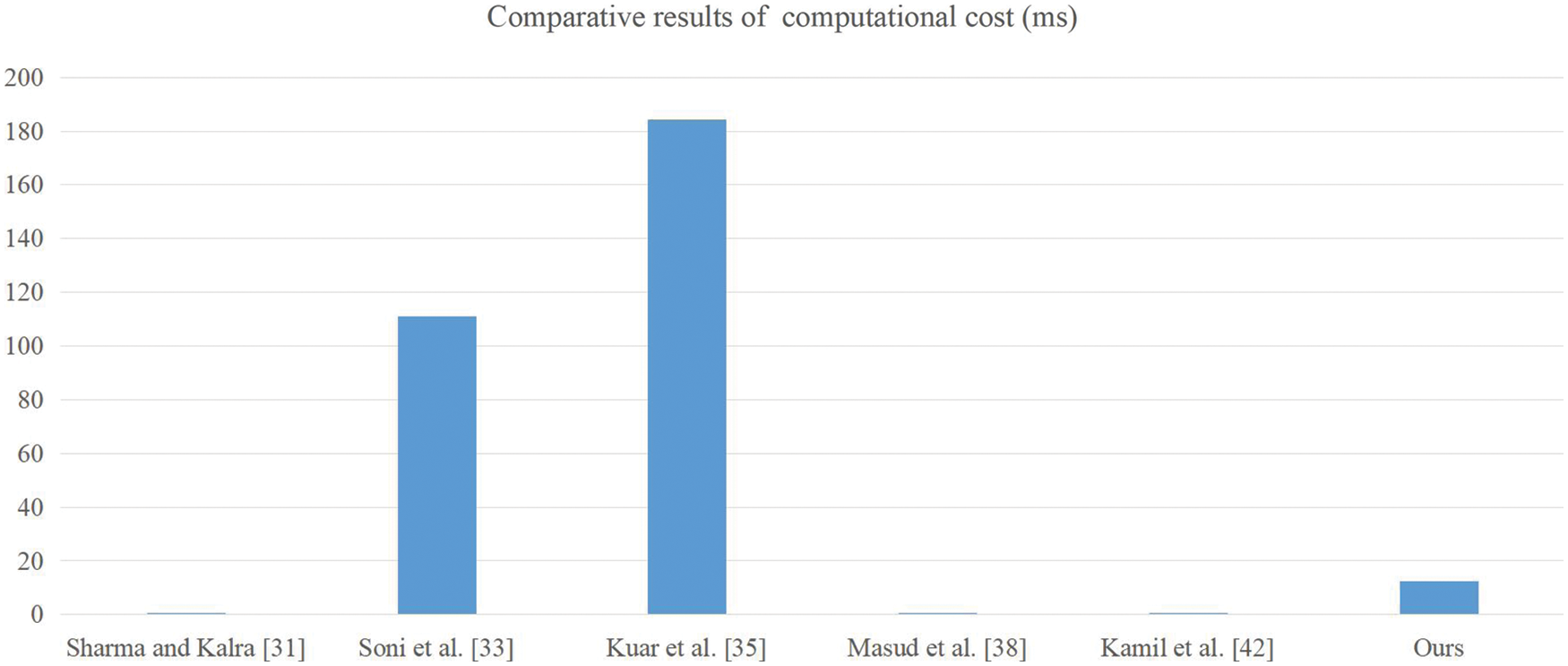
Figure 9: The comparison results of computational cost
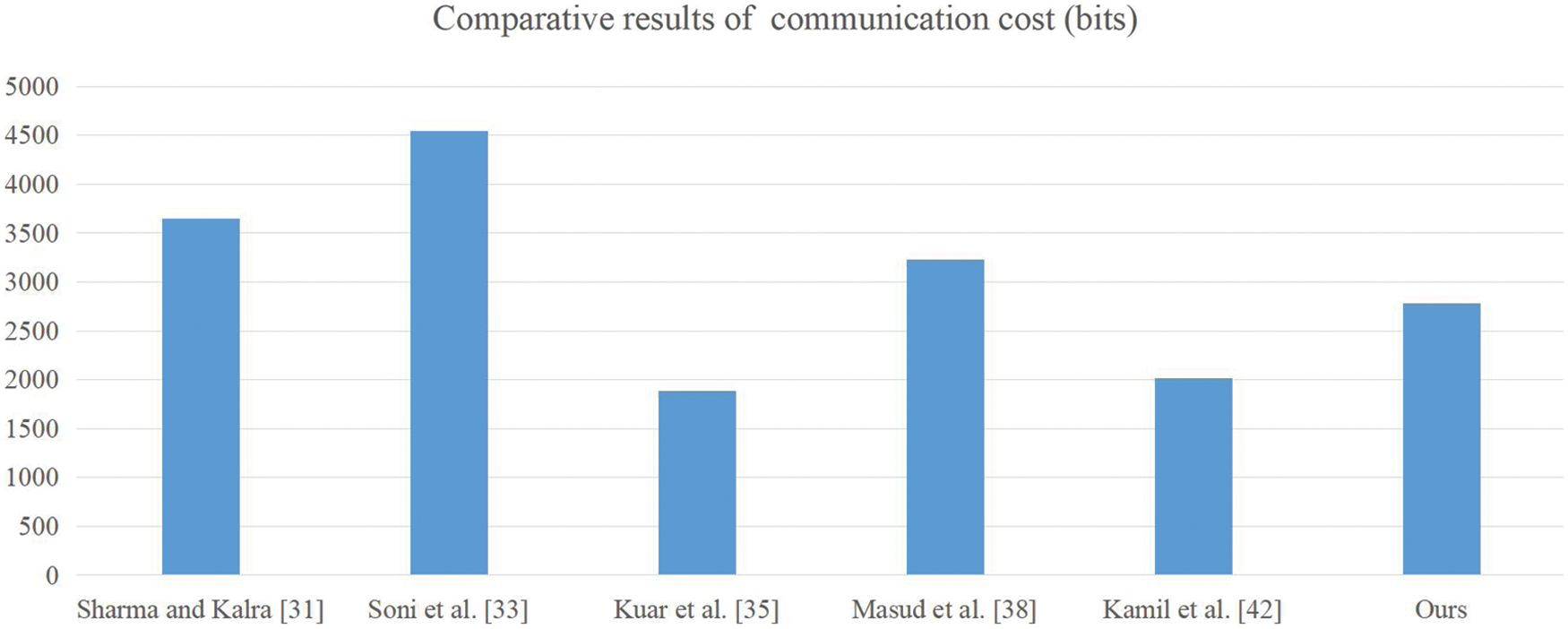
Figure 10: The comparison results of communication cost
In this paper, through the cryptanalysis of the protocol proposed by Kamil et al., we determined that their protocol cannot resist temporary value disclosure attacks and insider attacks. Then, we designed a novel authentication and key agreement protocol for remote surgeries in tactile network environments. We verified the security of our protocol via informal security analysis, and the ROR model and Proverif conducted formal security analysis on our protocol to further validate the security of the protocol. Finally, the performance comparison further indicates that our protocol is more suitable for tactile network environments. Furthermore, we hope that our research results will provide guidance for the development of intelligent medicine.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Xiong, H., Wu, Y., Jin, C., Kumari, S. (2020). Efficient and privacy-preserving authentication protocol for heterogeneous systems in Iot. IEEE Internet of Things Journal, 7(12), 11713–11724. DOI 10.1109/JIoT.6488907. [Google Scholar] [CrossRef]
2. Xiong, H., Zhao, Y., Hou, Y., Huang, X., Jin, C. et al. (2020). Heterogeneous signcryption with equality test for iiot environment. IEEE Internet of Things Journal, 8(21), 16142–16152. DOI 10.1109/JIOT.2020.3008955. [Google Scholar] [CrossRef]
3. Xue, X., Wu, X., Jiang, C., Mao, G., Zhu, H. (2021). Integrating sensor ontologies with global and local alignment extractions. Wireless Communications and Mobile Computing, 2021, 6625184. DOI 10.1155/2021/6625184. [Google Scholar] [CrossRef]
4. Luo, Y., Weimin, Z., Chen, Y. C. (2021). An anonymous authentication and key exchange protocol in smart grid. Journal of Network Intelligence, 6(2), 2414–8105. [Google Scholar]
5. Wu, T. Y., Lee, Y. Q., Chen, C. M., Tian, Y., Al-Nabhan, N. A. (2021). An enhanced pairing-based authentication scheme for smart grid communications. Journal of Ambient Intelligence and Humanized Computing, 1–13. DOI 10.1007/s12652-020-02740-2. [Google Scholar] [CrossRef]
6. Wu, T. Y., Lee, Z., Obaidat, M. S., Kumari, S., Kumar, S. et al. (2020). An authenticated key exchange protocol for multi-server architecture in 5G networks. IEEE Access, 8, 28096–28108. DOI 10.1109/Access.6287639. [Google Scholar] [CrossRef]
7. Wu, J. M. T., Srivastava, G., Jolfaei, A., Fournier-Viger, P., Lin, J. C. W. (2021). Hiding sensitive information in ehealth datasets. Future Generation Computer Systems, 117, 169–180. DOI 10.1016/j.future.2020.11.026. [Google Scholar] [CrossRef]
8. Wu, J. M. T., Tsai, M. H., Xiao, S. H., Liaw, Y. P. (2020). A deep neural network electrocardiogram analysis framework for left ventricular hypertrophy prediction. Journal of Ambient Intelligence and Humanized Computing, 1–17. DOI 10.1007/s12652-020-01826-1. [Google Scholar] [CrossRef]
9. Meng, Z., Pan, J. S., Tseng, K. K. (2019). Pade: An enhanced differential evolution algorithm with novel control parameter adaptation schemes for numerical optimization. Knowledge-Based Systems, 168, 80–99. DOI 10.1016/j.knosys.2019.01.006. [Google Scholar] [CrossRef]
10. Pan, J. S., Liu, N., Chu, S. C., Lai, T. (2021). An efficient surrogate-assisted hybrid optimization algorithm for expensive optimization problems. Information Sciences, 561, 304–325. DOI 10.1016/j.ins.2020.11.056. [Google Scholar] [CrossRef]
11. Wu, J., Xu, M., Liu, F. F., Huang, M., Ma, L. et al. (2021). Solar wireless sensor network routing algorithm based on multi-objective particle swarm optimization. Journal of Information Hiding and Multimedia Signal Processing, 12(1), 1–11. [Google Scholar]
12. Xue, X., Zhang, J. (2021). Matching large-scale biomedical ontologies with central concept based partitioning algorithm and adaptive compact evolutionary algorithm. Applied Soft Computing, 106, 107343. DOI 10.1016/j.asoc.2021.107343. [Google Scholar] [CrossRef]
13. Gritzalis, S., Lambrinoudakis, C., Lekkas, D., Deftereos, S. (2005). Technical guidelines for enhancing privacy and data protection in modern electronic medical environments. IEEE Transactions on Information Technology in Biomedicine, 9(3), 413–423. DOI 10.1109/TITB.2005.847498. [Google Scholar] [CrossRef]
14. Pan, J. S., Sun, X. X., Chu, S. C., Abraham, A., Yan, B. (2021). Digital watermarking with improved SMS applied for QR code. Engineering Applications of Artificial Intelligence, 97, 104049. DOI 10.1016/j.engappai.2020.104049. [Google Scholar] [CrossRef]
15. Zhang, Z., Chen, S., Sun, X., Liang, Y., Zhang, Z. et al. (2021). Trajectory privacy protection based on spatial-time constraints in mobile social networks. Journal of Network Intelligence, 6(3), 485–499. [Google Scholar]
16. Elshafey, M. A., Amein, A. S., Badran, K. S. (2021). Universal image steganography detection using multimodal deep learning framework. Journal of Information Hiding and Multimedia Signal Processing, 12(3), 152–161. [Google Scholar]
17. Chen, C. M., Deng, X., Kumar, S., Kumari, S., Islam, S. (2021). Blockchain-based medical data sharing schedule guaranteeing security of individual entities. Journal of Ambient Intelligence and Humanized Computing, 1–10. DOI 10.1007/s12652-021-03448-7. [Google Scholar] [CrossRef]
18. Shamshad, S., Ayub, M. F., Mahmood, K., Kumari, S., Chaudhry, S. A. et al. (2021). An enhanced scheme for mutual authentication for healthcare services. Digital Communications and Networks, DOI 10.1016/j.dcan.2021.07.002. [Google Scholar] [CrossRef]
19. Wu, T. Y., Wang, T., Lee, Y. Q., Zheng, W., Kumari, S. et al. (2021). Improved authenticated key agreement scheme for fog-driven IOT healthcare system. Security and Communication Networks, 2021, 6658041. DOI 10.1155/2021/6658041. [Google Scholar] [CrossRef]
20. Wu, T. Y., Yang, L., Lee, Z., Chen, C. M., Pan, J. S. et al. (2021). Improved ecc-based three-factor multiserver authentication scheme. Security and Communication Networks, 2021, 6627956. DOI 10.1155/2021/6627956. [Google Scholar] [CrossRef]
21. Wu, Z. Y., Lee, Y. C., Lai, F., Lee, H. C., Chung, Y. (2012). A secure authentication scheme for telecare medicine information systems. Journal of Medical Systems, 36(3), 1529–1535. DOI 10.1007/s10916-010-9614-9. [Google Scholar] [CrossRef]
22. He, D. B., Chen, J. H., Zhang, R. (2012). A more secure authentication scheme for telecare medicine information systems. Journal of Medical Systems, 36(3), 1989–1995. DOI 10.1007/s10916-011-9658-5. [Google Scholar] [CrossRef]
23. Wei, J., Hu, X., Liu, W. (2012). An improved authentication scheme for telecare medicine information systems. Journal of Medical Systems, 36(6), 3597–3604. DOI 10.1007/s10916-012-9835-1. [Google Scholar] [CrossRef]
24. Zhu, Z. (2012). An efficient authentication scheme for telecare medicine information systems. Journal of Medical Systems, 36(6), 3833–3838. DOI 10.1007/s10916-012-9856-9. [Google Scholar] [CrossRef]
25. Xu, X., Jin, Z. P., Zhang, H., Zhu, P. (2014). A dynamic ID-based authentication scheme based on ECC for telecare medicine information systems. Applied Mechanics and Materials, 457, 861–866. DOI 10.4028/AMM.457-458.861. [Google Scholar] [CrossRef]
26. Islam, S. H., Khan, M. K. (2014). Cryptanalysis and improvement of authentication and key agreement protocols for telecare medicine information systems. Journal of Medical Systems, 38(10), 1–16. DOI 10.1007/s10916-014-0135-9. [Google Scholar] [CrossRef]
27. Li, C. T., Lee, C. C., Weng, C. Y., Chen, S. J. (2016). A secure dynamic identity and chaotic maps based user authentication and key agreement scheme for e-healthcare systems. Journal of Medical Systems, 40(11), 1–10. DOI 10.1007/s10916-016-0586-2. [Google Scholar] [CrossRef]
28. Madhusudhan, R., Nayak, C. S. (2019). A robust authentication scheme for telecare medical information systems. Multimedia Tools and Applications, 78(11), 15255–15273. DOI 10.1007/s11042-018-6884-6. [Google Scholar] [CrossRef]
29. Zhang, L., Zhang, Y., Tang, S., Luo, H. (2017). Privacy protection for e-health systems by means of dynamic authentication and three-factor key agreement. IEEE Transactions on Industrial Electronics, 65(3), 2795–2805. DOI 10.1109/TIE.2017.2739683. [Google Scholar] [CrossRef]
30. Aghili, S. F., Mala, H., Shojafar, M., Peris-Lopez, P. (2019). Laco: Lightweight three-factor authentication, access control and ownership transfer scheme for e-health systems in IOT. Future Generation Computer Systems, 96, 410–424. DOI 10.1016/j.future.2019.02.020. [Google Scholar] [CrossRef]
31. Sharma, G., Kalra, S. (2019). A lightweight user authentication scheme for cloud-IOT based healthcare services. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 43(1), 619–636. DOI 10.1007/s40998-018-0146-5. [Google Scholar] [CrossRef]
32. Azrour, M., Mabrouki, J., Chaganti, R. (2021). New efficient and secured authentication protocol for remote healthcare systems in cloud-IOT. Security and Communication Networks, 2021, 5546334. DOI 10.1155/2021/5546334. [Google Scholar] [CrossRef]
33. Soni, P., Pal, A. K., Islam, S. H. (2019). An improved three-factor authentication scheme for patient monitoring using WSN in remote health-care system. Computer Methods and Programs in Biomedicine, 182, 105054. DOI 10.1016/j.cmpb.2019.105054. [Google Scholar] [CrossRef]
34. Xu, G., Wang, F., Zhang, M., Peng, J. (2020). Efficient and provably secure anonymous user authentication scheme for patient monitoring using wireless medical sensor networks. IEEE Access, 8, 47282–47294. DOI 10.1109/Access.6287639. [Google Scholar] [CrossRef]
35. Kaur, K., Garg, S., Kaddoum, G., Guizani, M. (2020). Secure authentication and key agreement protocol for Tactile Internet-based tele-surgery ecosystem. 2020 IEEE International Conference on Communications (ICC), pp. 1–6. Dublin, Ireland. DOI 10.1109/ICC40277.2020.9148835. [Google Scholar] [CrossRef]
36. Ali, Z., Hussain, S., Rehman, R. H. U., Munshi, A., Liaqat, M. et al. (2020). ITSSAKA-MS: An improved three-factor symmetric-key based secure AKA scheme for multi-server environments. IEEE Access, 8, 107993–108003. DOI 10.1109/ACCESS.2020.3000716. [Google Scholar] [CrossRef]
37. Yu, S., Park, Y. (2020). Comments on “ITSSAKA-MS: An improved three-factor symmetric-key based secure AKA scheme for multi-server environments”. IEEE Access, 8, 193375–193379. DOI 10.1109/ACCESS.2020.3032959. [Google Scholar] [CrossRef]
38. Masud, M., Gaba, G. S., Choudhary, K., Hossain, M. S., Alhamid, M. F. et al. (2021). Lightweight and anonymity-preserving user authentication scheme for IOT-based healthcare. IEEE Internet of Things Journal, 9, 2649–2656. DOI 10.1109/JIOT.2021.3080461. [Google Scholar] [CrossRef]
39. Kwon, D., Park, Y., Park, Y. (2021). Provably secure three-factor-based mutual authentication scheme with PUF for wireless medical sensor networks. Sensors, 21(18), 6039. DOI 10.3390/s21186039. [Google Scholar] [CrossRef]
40. Anvari, M., Broderick, T., Stein, H., Chapman, T., Ghodoussi, M. et al. (2005). The impact of latency on surgical precision and task completion during robotic-assisted remote telepresence surgery. Computer Aided Surgery, 10(2), 93–99. DOI 10.3109/10929080500228654. [Google Scholar] [CrossRef]
41. Wazid, M., Das, A. K., Lee, J. H. (2019). User authentication in a tactile internet based remote surgery environment: Security issues, challenges, and future research directions. Pervasive and Mobile Computing, 54, 71–85. DOI 10.1016/j.pmcj.2019.02.004. [Google Scholar] [CrossRef]
42. Kamil, I. A., Ogundoyin, S. O. (2021). A lightweight mutual authentication and key agreement protocol for remote surgery application in tactile internet environment. Computer Communications, 170, 1–18. DOI 10.1016/j.comcom.2021.01.025. [Google Scholar] [CrossRef]
43. Chaudhry, S. A. (2021). Combating identity de-synchronization: An improved lightweight symmetric key based authentication scheme for IOV. Journal of Network Intelligence, 6(4), 656–667. [Google Scholar]
44. Dolev, D., Yao, A. (1983). On the security of public key protocols. IEEE Transactions on Information Theory, 29(2), 198–208. DOI 10.1109/TIT.1983.1056650. [Google Scholar] [CrossRef]
45. Blanchet, B. (2008). A computationally sound mechanized prover for security protocols. IEEE Transactions on Dependable and Secure Computing, 5(4), 193–207. DOI 10.1109/TDSC.2007.1005. [Google Scholar] [CrossRef]
46. Abadi, M., Fournet, C. (2001). Mobile values, new names, and secure communication. ACM Sigplan Notices, 36(3), 104–115. DOI 10.1145/373243.360213. [Google Scholar] [CrossRef]
47. Canetti, R., Goldreich, O., Halevi, S. (2004). The random oracle methodology, revisited. Journal of the ACM, 51(4), 557–594. DOI 10.1145/1008731.1008734. [Google Scholar] [CrossRef]
48. Wang, D., Cheng, H., Wang, P., Huang, X., Jian, G. (2017). Zipf’s law in passwords. IEEE Transactions on Information Forensics and Security, 12(11), 2776–2791. DOI 10.1109/TIFS.2017.2721359. [Google Scholar] [CrossRef]
49. Odelu, V., Das, A. K., Goswami, A. (2015). A secure biometrics-based multi-server authentication protocol using smart cards. IEEE Transactions on Information Forensics and Security, 10(9), 1953–1966. DOI 10.1109/TIFS.2015.2439964. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools