Research on Volt/Var Control of Distribution Networks Based on PPO Algorithm

1  Introduction

In recent years, with the large consumption of traditional energy, energy crisis and environmental pollution have become increasingly serious. At the same time, in order to fit China's energy strategy of “carbon peaking” and “carbon neutralization”, the energy structure dominated by fossil energy is gradually transforming to that dominated by renewable energy, and the new energy industry has developed rapidly [1–5]. The new energy has the advantages of clean, infinite regeneration, small amount of operation and maintenance, but new requirements are put forward for traditional volt/var control (VVC) [6]. For the problem of grid local voltage out of limit caused by the intermittence and fluctuation of photovoltaic output [7], in the traditional VVC, the discrete tap/switch mechanism of on-load tap changers (OLTC) and capacitor banks (CBS) is used to control the voltage [8]. However, with the continuous increase of photovoltaic permeability in the distribution network, the burden of such voltage regulating equipment increases sharply (such as frequent tap switching [9], repeated charging and discharging of energy storage, etc.), which leads to accelerated aging and even damage of the equipment and is unable to deal with the voltage violation caused by high photovoltaic permeability [10]. Because photovoltaic inverter has the advantage of instantaneous response to system voltage changes and can participate in the voltage regulation of distribution network according to the revised IEEE1547 standard [11], photovoltaic inverter is widely used in voltage management under high photovoltaic permeability [12–18].

At the algorithm design level, the early designed photovoltaic inverter participating in the voltage control strategy of distribution network is mainly centralized solution based on optimal power flow (OPF) algorithm [19,20]. However, these methods generally have some problems, such as large amount of calculation, easy to fall into local optimization, heavy dependence on prediction data and difficult to realize on-line control. Considering that photovoltaic inverter has the advantages of flexible regulation of reactive power and deep reinforcement learning model has the ability to process massive and complex data information in real time [21], a real-time voltage regulation method of distribution network based on reinforcement learning is proposed in this paper. The VVC problem is transformed into a Proximal Policy Optimization (PPO) network framework. We take multiple inverters as agents; the action of the agent is determined by the interactive training between the inverter and the environment. This method realizes the voltage management under high photovoltaic permeability. The main contributions of this paper are as follows:

1)   We propose a data-driven real-time voltage control framework, which can quickly deal with the voltage violations caused by high photovoltaic permeability by controlling multiple photovoltaic inverter devices.

2)   We propose a multi-agent deep reinforcement learning (MADRL) algorithm based on photovoltaic inverter. In the off-line training process, the voltage out of limit and the reactive power output of photovoltaic inverter are modeled as penalty terms to ensure the security of power grid.

3)   The load and voltage values of all nodes are integrated into OPENDSS, and the MADRL problem is realized by PPO algorithm. Compared with the traditional method, the voltage regulation efficiency of three-phase distribution system is significantly improved.

2  PPO Algorithm

PPO algorithm is a deep reinforcement learning algorithm based on actor-critic structure. It obtains the optimal policy based on policy gradient. The critic network in PPO algorithm is used to approximate the state value function, and its network parameters are updated by minimizing the estimation deviation of the estimation function. The calculation formula is shown in Eq. (1).

J(ϕ)=rt+∑k=1T−k⁡γk∗rt+k−V(st)(1)

where ϕ is the parameter of critic network and V(st) is the output value of critic network.

In PPO algorithm, actor network is used for approximation strategy, and the network parameters are updated by introducing the concept of importance sampling and continuously optimizing and improving the objective function. The introduction of importance sampling not only improves the utilization of data samples, but also speeds up the convergence speed of the model. The specific method is realized by Eqs. (2)–(8). Assuming that there is a random variable x and the probability density function is p(x), the expected calculation of f(x) is shown in Eq. (2).

Ex∼p[f(x)]=∫⁡f(x)p(x)dx=∫⁡f(x)p(x)q(x)q(x)dx=Ex∼p[f(x)p(x)q(x)](2)

The importance sampling method, i.e., Eq. (2) is applied to PPO algorithm, the objective function of PPO algorithm can be written as Eq. (3) [22].

J(θ)=maxE(st,at)∼πθ′[rθA′(st,at)](3)

A′(st,at)=−V(st)+rt+γrt+1+⋯+γT−t+1rT−1+γT−tV(sT)(4)

rθ=πθ(at|st)πθ′(at|st)(5)

where A′(st,at) is the advantage function sampled according to the strategy and the T-step return value estimation method, which is equivalent to the advantage function in Eq. (2). rθ is the probability ratio of action taken by the new strategy and the old strategy in the current state, which is equivalent to p(x)q(x) that in Eq. (2). The premise of applying Eq. (2) to PPO algorithm is that the gap between strategy probability distribution πθ and πθ′ is within a certain range [23]. Therefore, KL divergence is introduced into PPO algorithm, and the objective function becomes Eq. (6).

J(θ)=E(st,at)∼πθ′[rθA′(st,at)−βKL(πθ,πθ′)](6)

where β represents the penalty for the difference between πθ and πθ′ distribution. Because KL divergence is not easy to calculate, the method of clipping is used to replace KL divergence, which can effectively limit the range of update. The objective function of PPO algorithm including clip function is expressed as Eqs. (7) and (8).

J(θ)=E(st,at)∼πθ′[min(rθA′(st,at),clip(rθ,1−ε,1+ε)A′(st,at))](7)

θ←argmaxθ(J(θ))(8)

3  Proposed VVC Algorithm

According to Markov decision theory and PPO algorithm framework, the distribution network environment is modeled. Taking the reactive power output of each inverter in the distribution network as the regulating variable, after off-line centralized training, the goal of not exceeding the voltage limit of the distribution network under high photovoltaic permeability is finally completed.

3.1 Environmental Modeling

Markov decision process is composed of a five tuple, expressed as (s, a, P, R, R). Power system environment modeling is mainly set from three aspects: state s, action a and reward R. Under the framework of this paper, the main task of the agent is to select the appropriate reactive power output and transmit it to OPENDSS to ensure the convergence of power flow calculation and the node voltage does not exceed the limit.

1)   State:

The state quantity needs to guide the agent to make appropriate actions [24]. The setting of state quantity in this paper is shown in Eqs. (9) and (10), which includes the three-phase voltage of each node in the three-phase distribution network:

S=[U1φ,U2φ,…,Ukφ](9)

φ={a,b,c}(10)

where Ukφ represents the voltage magnitude on phase φ at node k.

2)   Action:

The action quantity needs to guide the agent from the current state to the next state. In this paper, the reactive power output of the inverter is selected as the action, and because the output of the PPO algorithm used in this paper is the probability distribution of the action value, the action value is fixed in a certain range. Therefore, the action value in this paper is expressed as Eqs. (11) and (12).

a=[a1,a2,…,ai](11)

Ai=[amin,amax](12)

where ai represents the reactive output of the three-phase inverter, i.e., aiφ. Ai Represents the action space of the ith agent, where amin and amax represent the upper and lower limits of the action value space. During the training, the value is mapped to the reactive output space of the inverter.

3)   Reward:

The setting of reward value needs to guide the agent to move in the right direction, so as to achieve the target value. In order to achieve the goal of non violation of distribution network voltage under high photovoltaic permeability Eq. (13), the rewards used in constructing PPO algorithm in this paper are shown in Eqs. (14) and (15).

0.95≤|Ukφ|≤1.05(13)

When the node voltage value exceeds the limit after the agent acts, a huge penalty M will be given to the out of limit part, the reward function at the current time is expressed as Eq. (14).

rt=−M∑k⁡∑φ⁡[relu(|Ukφ|−1.05)+relu(0.95−|Ukφ|)](14)

where relu function is a piecewise function, which can change all negative values to 0, while the positive values remain unchanged. Therefore, when the node voltage exceeds the limit, the voltage is moved to the normal range through the reward function Eq. (14) we set.

When the node voltage does not exceed the limit after the agent acts, we set the reward function at the current time as follows [25]:

rt=(Ploss,0t−Plosst)(15)

where Ploss,0t and Plosst respectively refer to the network loss value of the system when the inverter does not take action and after the action. When the inverter acts, the system network loss decreases, the agent will be given a positive reward, otherwise, the agent will be given a corresponding negative reward.

3.2 Model Training Process

The training flow chart of real-time voltage regulation of distribution network based on PPO algorithm is shown in Fig. 1.

Figure 1: Voltage real-time control training framework

Firstly, the network parameters of actor network and critic network are initialized, and the replay buffer capacity and related training parameters are set; Randomly select a group of initial state Eq. (9) from the environment, select the action Eq. (11) of the inverter according to the strategy of the actor network, input state and action into OPENDSS to obtain the state value s′ at the next time, obtain the reward value rt according to Eqs. (14) and (15), and store (st,at,rt,st+1) in the replay buffer. Take l sample values (sl, al, sl+1,rl+1) from the replay buffer, l=1,2,…,L input (sl,sl+1) into the critic network, update the critic network parameters according to Eq. (1), and calculate the advantage function according to the critic network output value and Eq. (4). Input (sl, al) into the actor network, calculate the probability ratio of the old and new strategies to take action al in the state sl according to Eq. (5), and finally calculate the objective function of the actor network through equation Eq. (7), and update its network parameters through Eq. (8), so as to obtain the new strategy.

4  Case Studies and Analysis

4.1 Case Design

In this paper, IEEE 13-bus three phase unbalanced distribution system [26] is used to test whether PPO algorithm can realize voltage management. Four three-phase inverters are placed at nodes 645, 671, 652 and 692. In this case, the load in each node fluctuates randomly by 80%∼120%, and then 1000 groups of training data with random fluctuation are generated through the comprehensive power simulation tool OPENDSS of power distribution network system. The neural network determines the reactive power output of the inverter according to the node voltage value and network loss provided by the training data. The specific implementation process of the algorithm is shown in Table 1.

Specific description of PPO algorithm neural network: In the neural network model designed in this paper, both actor network and critic network adopt fully connected network. Taking actor network as an example, the specific model is shown in Fig. 2. The number of neurons in the input layer is determined by the node voltage in the power system model. In this case, the number of neurons in the input layer is 35, and batch normalization is carried out at the output to enhance the robustness of the model; The number of hidden layers and nodes in actor network and critic network are closely related to the power grid structure. In this case, actor network and critic network adopt the same hidden layer structure, both use two-layer neural networks to construct hidden layers, the number of neurons in each layer is 256, and both use relu function as activation function to enhance the nonlinear mapping ability of the whole neural network; In this case, the number of neurons in the output layer of actor network and critic network is 4 and 1, respectively, and the loss function adopts Adam optimization algorithm.

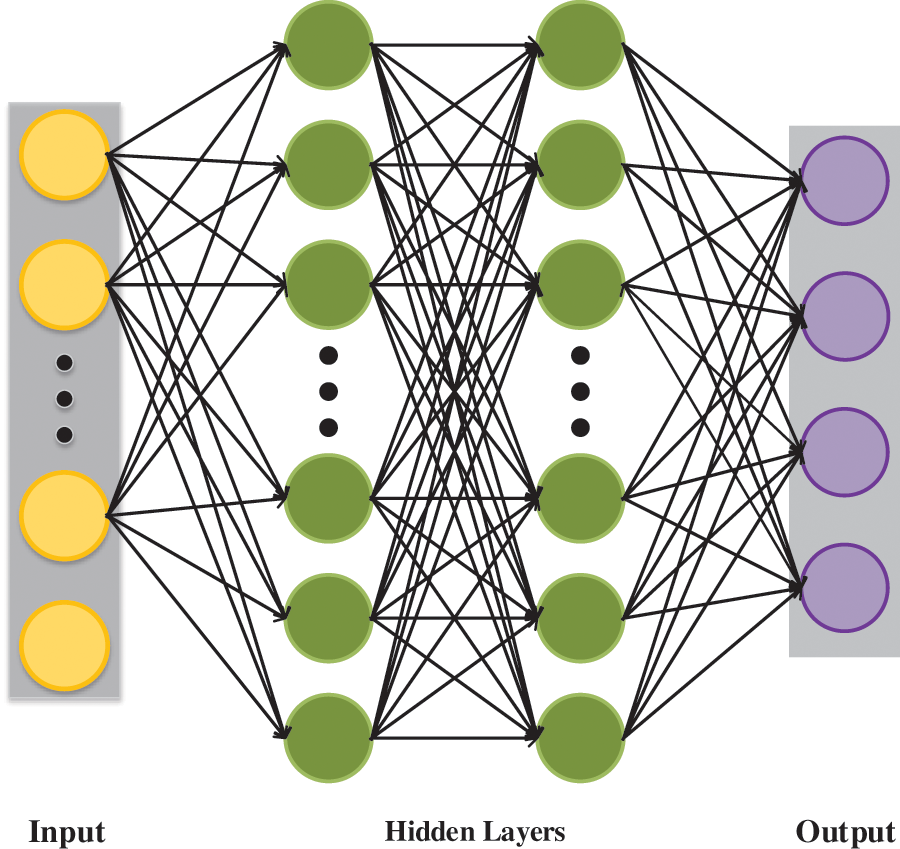
Figure 2: The neural network of actor network

The specific algorithm and model training parameters are shown in Table 2.

4.2 Result Analysis

According to the neural network model and algorithm training process designed in the previous section, the training reward function curve in Fig. 3 and the number of actions taken by the agent in each episode in Fig. 4 are obtained. It can be seen from the reward curve in Fig. 3 that at the beginning, due to the limited training times, the agent could not learn effective action strategies, therefore, the node voltage value after the action of the inverter cannot meet the constraint Eq. (13), and a negative reward will be obtained according to Eqs. (14) and (15); With the continuous training, the agent will gradually move in the correct direction, so it will continue to obtain a positive reward; When the number of training times reaches 8000, the algorithm basically converges, and the action strategy selected by the agent can always obtain a positive reward.

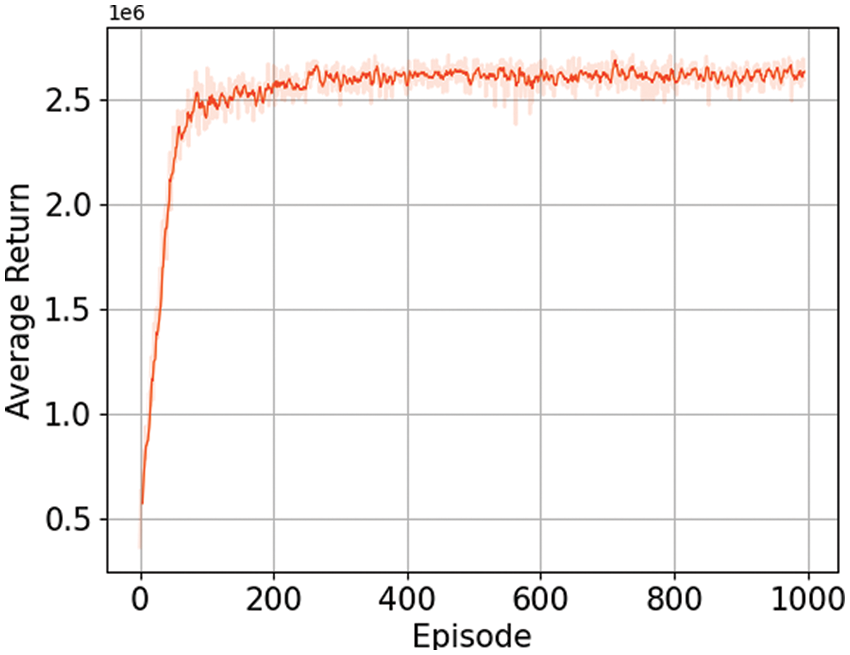
Figure 3: PPO training process in the IEEE 13-bus system

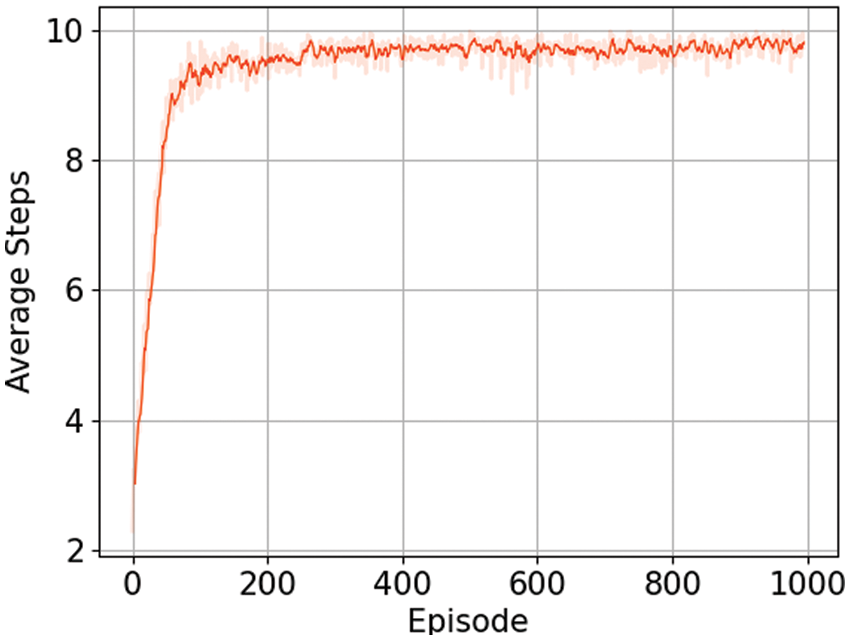
Figure 4: Number of steps taken for 10000 training episode

The algorithm in this paper stipulates that the agent in an episode can act up to 10 times. If the voltage exceeds the limit, the episode will end in advance and proceed to the next episode. By observing Fig. 4, it can be found that with the progress of training, the action times of agents in each episode gradually increase and finally converge to 10 times.

The voltage fluctuation curve of IEEE 13-bus three phase unbalanced system before reactive power regulation is shown in Fig. 5. It can be observed that the voltage fluctuation range is relatively large between 10:00∼15:00, and the voltage value is outside the safe operation limit. The voltage fluctuation curve after reactive power regulation of the system using the VVC method proposed in this paper is shown in Fig. 6. It is obvious that the agent can make the voltage within 0.95∼1.05 after action. Figs. 2–5 comprehensively illustrate that the algorithm designed in this paper can achieve the effect of voltage regulation.

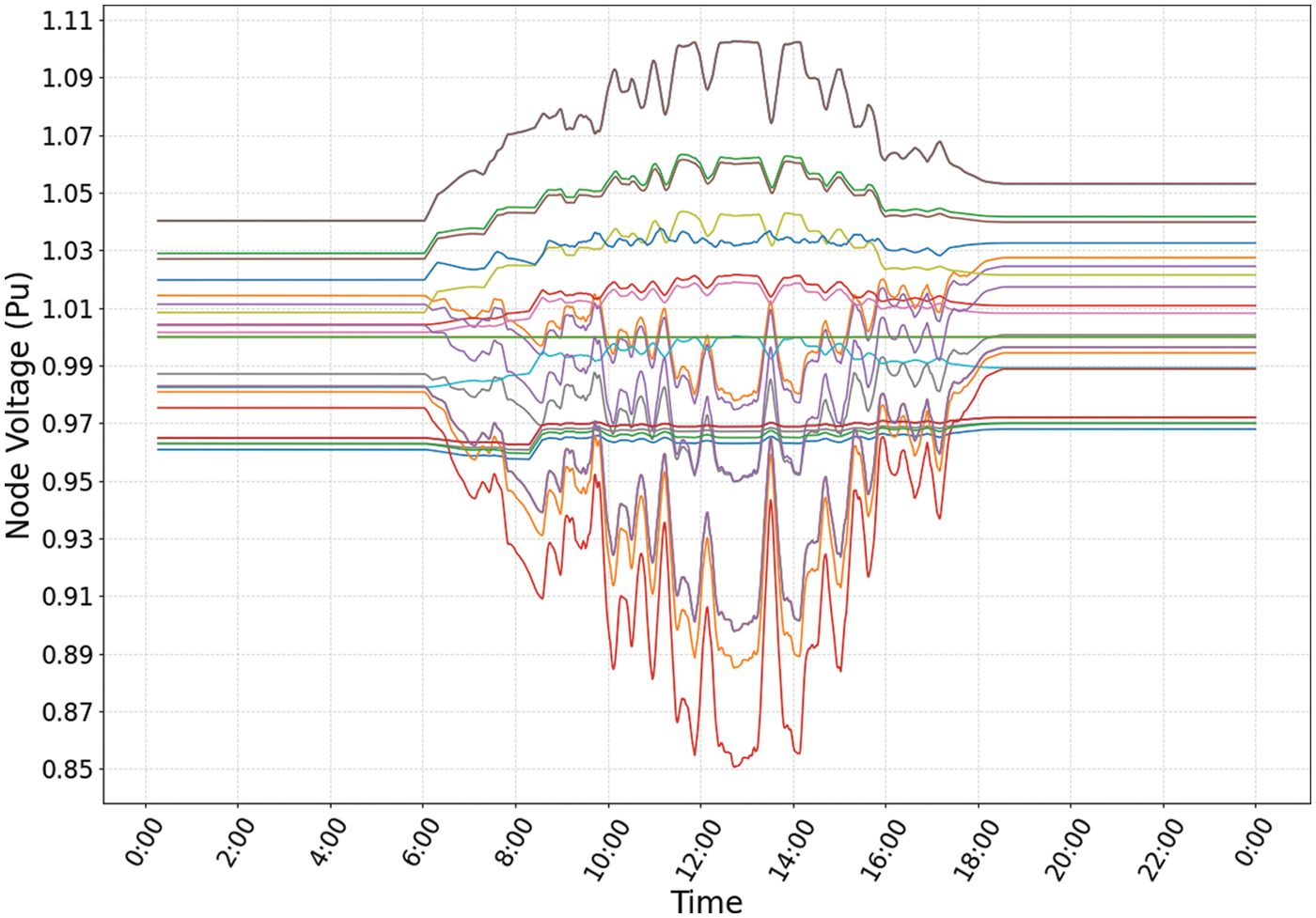
Figure 5: Voltage value before system reactive power regulation

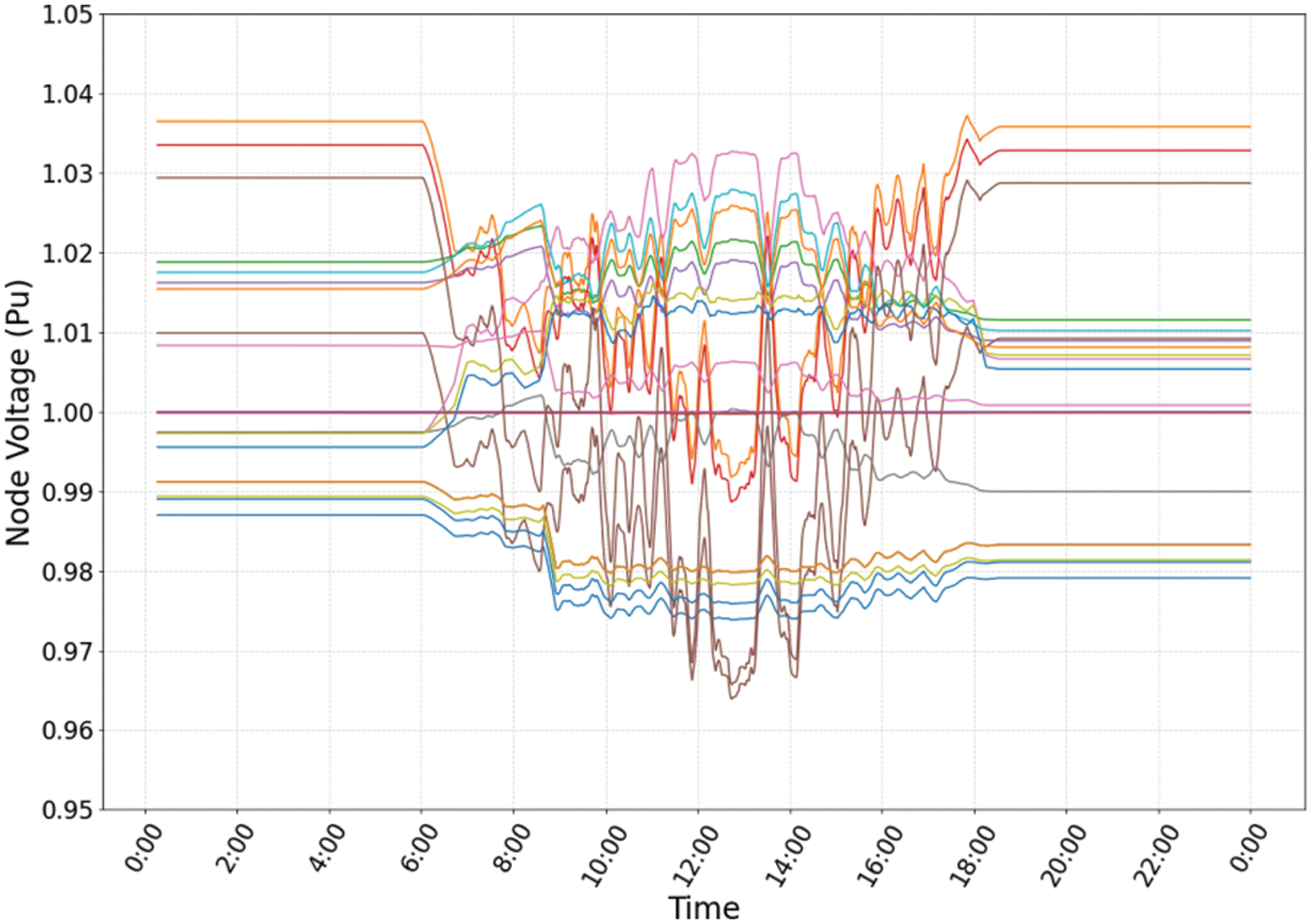
Figure 6: Voltage value after system reactive power regulation

5  Conclusion

In this paper, a voltage regulation method based on PPO is proposed and verified in IEEE 13-bus three-phase unbalanced distribution network. Taking the node load, photovoltaic quantity and inverter in the model as the DRL environment, and through the continuous interaction between the environment and the agent, the model can automatically select the control action, so as to realize the automatic voltage regulation in the distribution network. On the one hand, compared with the traditional voltage regulation using analytical optimization method, PPO algorithm can effectively avoid the inaccurate algorithm performance caused by transforming nonlinear model into linear model, and can quickly adjust the inverter in the face of complex distribution network model, so as to speed up the voltage regulation in distribution network. On the other hand, PPO skillfully removes those parts that make the network parameters change too violently through the clipping operation, so as to realize the screening of data. The filtered data will not produce gradient. Therefore, compared with the strategic gradient algorithm, PPO algorithm has higher stability and data efficiency.

Funding Statement: This work is supported by the Science and Technology Project of State Grid Zhejiang Electric Power Co., Ltd. under Grant B311JY21000A.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Feng, X., Zhang, Y., Kang, L., Wang, L. C., Duan, C. X. et al. (2021). Integrated energy storage system based on triboelectric nanogenerator in electronic devices. Frontiers of Chemical Science and Engineering, 15(2), 238–250. DOI 10.1007/s11705-020-1956-3. [Google Scholar] [CrossRef]

 2.  Liu, C. L., Zhang, Y., Sun, J. R., Cui, Z. H., Wang, K. (2021). Stacked bidirectional LSTM RNN to evaluate the remaining useful life of supercapacitor. International Journal of Energy Research, 46(3), 3034–3043. DOI 10.1002/er.736. [Google Scholar] [CrossRef]

 3.  Feng, X., Li, Q., Wang, K. (2020). Waste plastic triboelectric nanogenerators using recycled plastic bags for power generation. ACS Applied Materials & Interfaces, 13(1), 400–410. DOI 10.1021/acsami.0c16489. [Google Scholar] [CrossRef]

 4.  Wang, K., Liu, C., Sun, J. R., Zhao, K., Wang, L. C. et al. (2021). State of charge estimation of composite energy storage systems with supercapacitors and lithium batteries. Complexity, 2021, 1–15. DOI 10.1155/2021/8816250. [Google Scholar] [CrossRef]

 5.  Cui, Z. H., Wang, L. C., Li, Q., Wang, K. (2021). A comprehensive review on the state of charge estimation for lithium-ion battery based on neural network. International Journal of Energy Research, 2021, 1–18. DOI 10.1002/er.7545. [Google Scholar] [CrossRef]

 6.  Sun, X., Qiu, J. (2021). Two-stage volt/var control in active distribution networks with multi-agent deep reinforcement learning method. IEEE Transactions on Smart Grid, 12(4), 2903–2912. DOI 10.1109/TSG.2021.3052998. [Google Scholar] [CrossRef]

 7.  Hossain, M. I., Yan, R., Saha, T. K. (2016). Investigation of the interaction between step voltage regulators and large-scale photovoltaic systems regarding voltage regulation and unbalance. IET Renewable Power Generation, 10(3), 299–309. DOI 10.1049/iet-rpg.2015.0086. [Google Scholar] [CrossRef]

 8.  Viawan, F. A., Karlsson, D. (2008). Voltage and reactive power control in systems with synchronous machine based distributed generation. IEEE Transactions on Power Delivery, 23(2), 1079–1087. DOI 10.1109/TPWRD.2007.915870. [Google Scholar] [CrossRef]

 9.  Wang, L., Yan, R., Saha, T. K. (2018). Voltage management for large scale PV integration into weak distribution systems. IEEE Transactions on Smart Grid, 9(5), 4128–4139. DOI 10.1109/TSG.5165411. [Google Scholar] [CrossRef]

10. Hu, Z., Wang, X., Chen, H., Taylor, G. A. (2003). Volt/VAr control in distribution systems using a time-interval based approach. IEE Proceedings-Generation, Transmission and Distribution, 150(5), 548–554. DOI 10.1049/ip-gtd:20030562. [Google Scholar] [CrossRef]

11. IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces (2018). In: IEEE Std 1547-2018 (Revision of IEEE Std 1547-2003), pp. 1–138. DOI 10.1109/IEEESTD.2018.8332112. [Google Scholar] [CrossRef]

12. Farivar, M., Neal, R., Clarke, C., Low, S. (2012). Optimal inverter VAR control in distribution systems with high PV penetration. 2012 IEEE Power and Energy Society General Meeting, pp. 1–7. San Diego, CA, USA. [Google Scholar]

13. Dall'Anese, E., Dhople, S. V., Giannakis, G. B. (2014). Optimal dispatch of photovoltaic inverters in residential distribution systems. IEEE Transactions on Sustainable Energy, vol. 5, no. 2, pp. 487–497. IEEE. [Google Scholar]

14. Dall'Anese, E., Giannakis, G. B., Wollenberg, B. F. (2012). Optimization of unbalanced power distribution networks via semidefinite relaxation. 2012 North American Power Symposium (NAPS), pp. 1–6. Champaign, IL, USA. [Google Scholar]

15. Sulc, P., Backhaus, S., Chertkov, M. (2014). Optimal distributed control of reactive power via the alternating direction method of multipliers. IEEE Transactions on Energy Conversion, 29(4), 968–977. DOI 10.1109/TEC.2014.2363196. [Google Scholar] [CrossRef]

16. Demirok, E., González, P. C., Frederiksen, K. H. B., Sera, D., Rodriguez, P. et al. (2011). Local reactive power control methods for overvoltage prevention of distributed solar inverters in low-voltage grids. IEEE Journal of Photovoltaics, 1(2), 174–182. DOI 10.1109/JPHOTOV.2011.2174821. [Google Scholar] [CrossRef]

17. Aghatehrani, R., Golnas, A. (2012). Reactive power control of photovoltaic systems based on the voltage sensitivity analysis. 2012 IEEE Power and Energy Society General Meeting, pp. 1–5. San Diego, CA, USA. [Google Scholar]

18. Jahangiri, P., Aliprantis, D. (2014). Distributed Volt/VAr control by PV inverters. IEEE Transactions on Power Systems, vol. 28, no. 3, pp. 3429–3439. IEEE. [Google Scholar]

19. Yuryevich, J., Wong, K. P. (1999). Evolutionary programming based optimal power flow algorithm. IEEE Transactions on Power Systems, vol. 14, no. 4, pp. 1245–1250. IEEE. [Google Scholar]

20. Liu, C. L., Li, Q., Wang, K. (2021). State-of-charge estimation and remaining useful life prediction of supercapacitors. Renewable and Sustainable Energy Reviews, 150(2), 111408. DOI 10.1016/j.rser.2021.111408. [Google Scholar] [CrossRef]

21. Gan, D., Thomas, R. J., Zimmerman, R. D. (2000). Stability-constrained optimal power flow. IEEE Transactions on Power Systems, 15(2), 535–540. DOI 10.1109/59.867137. [Google Scholar] [CrossRef]

22. Schulman, J., Wolski, F., Dhariwal, P., Radford, A., Klimov, O. (2017). Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347. [Google Scholar]

23. Hua, Y., Wang, N., Zhao, K. (2021). Simultaneous unknown input and state estimation for the linear system with a rank-deficient distribution matrix. Mathematical Problems in Engineering, 2012(12), 1–11. DOI 10.1155/2021/6693690. [Google Scholar] [CrossRef]

24. Lovric, M. (2011). International encyclopedia of statistical science. Berlin: Springer. [Google Scholar]

25. Zhang, Y., Wang, X., Wang, J., Zhang, Y. (2021). Deep reinforcement learning based volt-VAR optimization in smart distribution systems. IEEE Transactions on Smart Grid, 12(1), 361–371. DOI 10.1109/TSG.5165411. [Google Scholar] [CrossRef]

26. IEEE Test Feeder Specifications (2017). http://sites.ieee.org/pes-testfeeders/resources. [Google Scholar]