Open Access

ARTICLE

Static Analysis of Doubly-Curved Shell Structures of Smart Materials and Arbitrary Shape Subjected to General Loads Employing Higher Order Theories and Generalized Differential Quadrature Method

Francesco Tornabene^*, Matteo Viscoti, Rossana Dimitri

Department of Innovation Engineering, School of Engineering, University of Salento, Lecce, 73100, Italy

* Corresponding Author: Francesco Tornabene. Email:

(This article belongs to the Special Issue: Theoretical and Computational Modeling of Advanced Materials and Structures)

Computer Modeling in Engineering & Sciences 2022, 133(3), 719-798. https://doi.org/10.32604/cmes.2022.022210

Received 28 February 2022; Accepted 11 May 2022; Issue published 03 August 2022

Abstract

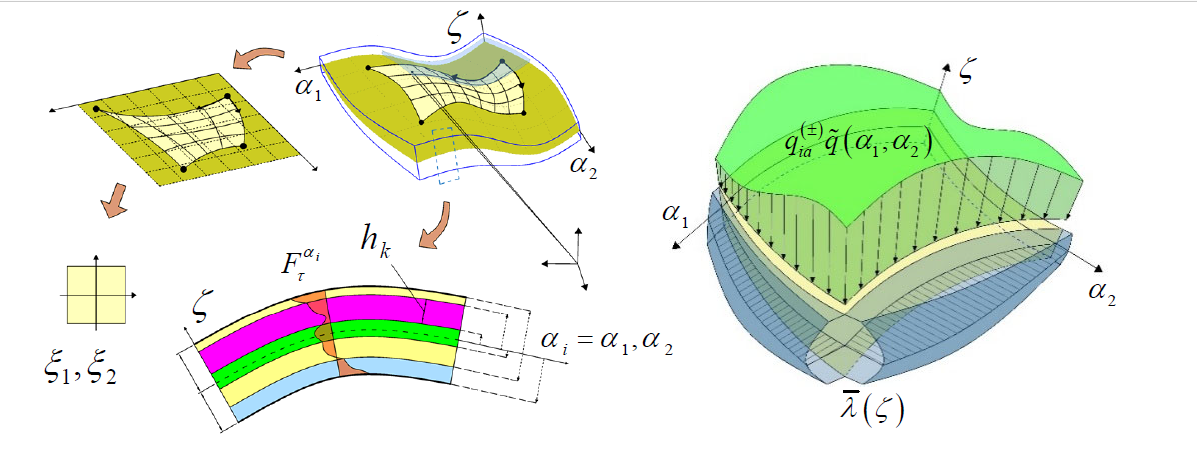
The article proposes an Equivalent Single Layer (ESL) formulation for the linear static analysis of arbitrarily-shaped shell structures subjected to general surface loads and boundary conditions. A parametrization of the physical domain is provided by employing a set of curvilinear principal coordinates. The generalized blending methodology accounts for a distortion of the structure so that disparate geometries can be considered. Each layer of the stacking sequence has an arbitrary orientation and is modelled as a generally anisotropic continuum. In addition, re-entrant auxetic three-dimensional honeycomb cells with soft-core behaviour are considered in the model. The unknown variables are described employing a generalized displacement field and pre-determined through-the-thickness functions assessed in a unified formulation. Then, a weak assessment of the structural problem accounts for shape functions defined with an isogeometric approach starting from the computational grid. A generalized methodology has been proposed to define two-dimensional distributions of static surface loads. In the same way, boundary conditions with three-dimensional features are implemented along the shell edges employing linear springs. The fundamental relations are obtained from the stationary configuration of the total potential energy, and they are numerically tackled by employing the Generalized Differential Quadrature (GDQ) method, accounting for nonuniform computational grids. In the post-processing stage, an equilibrium-based recovery procedure allows the determination of the three-dimensional dispersion of the kinematic and static quantities. Some case studies have been presented, and a successful benchmark of different structural responses has been performed with respect to various refined theories.

---

Graphic Abstract

---

Keywords

---