

 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.019509
ARTICLE
Aczel-Alsina Weighted Aggregation Operators of Simplified Neutrosophic Numbers and Its Application in Multiple Attribute Decision Making
1Rock Mechanics Institute, Ningbo University, Ningbo, 315211, China
2School of Civil and Environmental Engineering, Ningbo University, Ningbo, 315211, China
*Corresponding Author: Rui Yong. Email: yongrui@nbu.edu.cn
Received: 27 September 2021; Accepted: 04 January 2022
Abstract: The simplified neutrosophic number (SNN) can represent uncertain, imprecise, incomplete, and inconsistent information that exists in scientific, technological, and engineering fields. Hence, it is a useful tool for describing truth, falsity, and indeterminacy information in multiple attribute decision-making (MADM) problems. To suit decision makers’ preference selection, the operational flexibility of aggregation operators shows its importance in dealing with the flexible decision-making problems in the SNN environment. To solve this problem, this paper develops the Aczel-Alsina aggregation operators of SNNs for MADM problems in view of the Aczel-Alsina operational flexibility. First, we define the Aczel-Alsina operations of SNNs. Then, the Aczel-Alsina aggregation operators of SNNs are presented based on the defined Aczel-Alsina operations of SNNs. Next, a MADM method is established using the proposed aggregation operators under the SNN environment. Lastly, an illustrative example about slope treatment scheme choices is provided to indicate the practicality and efficiency of the established method. By comparison with the existing relative MADM methods, the results show that the established MADM method can overcome the insufficiency of decision flexibility in the existing MADM methods and demonstrate the metric of flexible decision-making.
Keywords: Simplified neutrosophic number; multiple attribute decision-making; aggregation operators
Multiple attribute decision-making (MADM) is a significant research topic in many fields, such as civil engineering [1], disaster assessment [2], and company investment management [3]. Decision information on complex decision-making problems is generally incomplete, indeterminate, and inconsistent [4]. Due to uncertainty, many challenges have emerged in the decision-making process. Fuzzy decision-making is an important approach in various fuzzy environments. Zadeh introduced fuzzy sets (FS) in 1965 to solve uncertainty problems [5]. Nevertheless, FS is characterized only by its membership function between 0 and 1, rather than a non-membership function [6]. To overcome the weakness of knowledge of non-membership degrees, Atanassov [7] further introduced the intuitionistic fuzzy set (IFS), which is characterized by its membership and non-membership functions. Although all these approaches are useful for describing incomplete information, they cannot handle indeterminate information and inconsistent information in engineering practice. Ashraf et al. [8] proposed the spherical fuzzy set (SFS) which is a generalization of Pythagorean fuzzy set and picture fuzzy set. SFS has proven to be a more effective tool for describing the ambiguities in data than IFS [9]. Smarandache [10] proposed the neutrosophic set (NS) from a philosophical point of view to express indeterminate and inconsistent information. NS contains the truth-membership function, the indeterminacy-membership function, and the falsity-membership function, which are independent of each other. To meet engineering applications, two subclasses of NSs, including single-valued neutrosophic sets (SVNSs) and interval neutrosophic sets (INSs), were proposed [11,12]. Their truth, indeterminacy, and falsity membership functions are restricted within the real unit interval [0,1]. Garg [13] first developed some sine-trigonometric operations laws corresponding to SVNSs to solve the MADM problems. Then, Ashraf et al. [14] proposed some operational laws for SVNSs and developed the MADM method based on single-valued neutrosophic weighted averaging and geometric operators. Garai et al. [15] proposed the ranking approach using the ratio of possibility mean and standard deviation for solving the MADM problem under the SVNS environment. Liu et al. [16] presented an aggregation operator for SVNSs in view of Bonferroni mean, and developed a MADM method under the single-valued neutrosophic environments. Garg et al. [17] developed a method using Frank Choquet Heronian mean operator for handling MADM problems under the linguistic SVNS environment. Ashraf et al. [18] introduced two aggregation operators based on logarithmic operations and used them for decision-making problems under the SVNS environment. In addition, some similarity measures of SVNSs and INSs were presented and utilized in multi-criteria (group) decision making. For example, by the cosine measure between every alternative and the ideal alternative, Fan et al. [19] suggested a decision-making method based on refined-SVNSs and refined-INSs. Ye [3] introduced the concept of simplified neutrosophic sets (SNSs) containing SVNSs and INSs and proposed a MADM method under the SNS environment. To describe the behavior of the decision-maker objectively and subjectively, Garg et al. [20] developed several probabilistic and immediate probability-based averaging and geometric aggregation operators for the collection of SVNSs and INSs. Peng et al. [21] provided a ranking approach based on the outranking relations of SNSs to solve MADM problems. Du et al. [22] suggested two subtraction operational aggregation operators for MADM problems. These important studies have great impacts on improving decision-making problems. However, because of the complexity of current decision-making problems, the MADM methods under the SNS environment need further study.
The aggregation of information is fundamental for obtaining the synthesis of the performance degree of criteria. Various aggregation operators of simplified neutrosophic numbers (SNNs) have been developed by far, such as simplified neutrosophic weighted aggregation operators [3,22,23], single-valued neutrosophic normalized weighted Bonferroni mean operators [24], generalized neutrosophic Hamacher aggregation operators [25]. Among these operators, the weighted arithmetic average operator and the weighted geometric average operator are the most common ones. Ye [3] developed a simplified neutrosophic weighted arithmetic average operator and a simplified neutrosophic weighted geometric average operator for SNNs. However, the sum of any element and the maximum value is not equal to the maximum value by this method. Then, Peng et al. [23] developed two SNN aggregation operators and the comparison method for multi-criteria group decision-making problems. Although these operators provide some inspirations for solving the MADM problems, the flexible decision-making corresponding to favorite priorities of alternatives were not considered comprehensively in the MADM process.
It is widely accepted that the t-norms and their associated t-conorms (e.g., Einstein t-norm and t-conorm, Hamacher t-norm and t-conorm) are crucial operations in fuzzy sets and other fuzzy systems [26]. Aczel et al. [27] presented new operations referred to as Aczel-Alsina t-norm and t-conorm operations, which have the advantage of changeability by adjusting a parameter. Therefore, we can extend the Aczel-Alsina t-norm and t-conorm operations to SNNs and introduce the Aczel-Alsina aggregation operators of SNNs to develop a MADM method that can reflect the flexibility in the decision-making process. This study aims to propose two new aggregation operators under the SNN environment and to develop a MADM approach using these operators for solving the favorite priority of alternatives in MADM problems. An illustrative example of slope treatment scheme selections is presented to investigate the impact of a changeable parameter on decision-making outcomes. The comparative results show the proposed method has its advantage in flexible decision-making corresponding to favorite priorities of alternatives.
This paper is formed by the following parts. The next section introduces the preliminaries of SNNs and two SNN weighted averaging operators. Section 3 proposes the Aczel-Alsina t-norm and t-conorm operations of SNNs. Section 4 develops the SNN Aczel-Alsina weighted averaging (SNNAAWA) and SNN Aczel-Alsina weighted geometric (SNNAAWG) operators and indicates their properties. A MADM approach is developed by the SNNAAWA and SNNAAWG operators in Section 5. In Section 6, an example and the relative comparative analysis are introduced to show the applicability and flexibility of the created MADM approach in the SNN environment. Finally, the conclusions are drawn in Section 7.
Definition 1 [3]. Let S be a space of points (objects), in which a generic element is denoted by s. A SNS K in S is characterized independently by a truth-membership function TK(s), an indeterminacy-membership function IK(s), and a falsity-membership function FK(s), where TK(s), IK(s), FK(s) ∈ [0,1] for each s in S. Then, a SNS (SVNS) K is denoted by
Thus, it is obvious that the sum of TK(s), IK(s), FK(s) satisfies the condition 0 ≤ TK(s) + IK(s) + FK(s) ≤ 3.
Definition 2 [3]. For two SNNs A = <TA(s), IA(s), FA(s)> and B = <TB(s), IB(s), FB(s)>, the relations of them are defined as follows:
(1) A ⊆ B if and only if TA(s) ≤ TB(s), IA(s) ≥ IB(s), FA(s) ≥ FB(s) for any s in S;
(2) A = B if and only if A ⊆ B and B ⊆ A;
(3) AC = {<s, FA(s), 1 – IA(s), TA(s)> |s ∈ S}.
Definition 3 [22]. The operations about any two SNNs A and B are introduced as follows:
(1) λ·A = <1 – (1 – TA(s))λ, IA(s)λ, FA(s)λ>, λ > 0;
(2) Aλ = <TA(s)λ, 1 – (1 – IA(s)) λ, 1 – (1 – FA(s))λ>, λ > 0;
(3)
(4)
Definition 4 [22]. Let Ai = <TAi, IAi, FAi> be a collection of SNNs, where i = 1, 2, … , m, and m is the dimension. The simplified neutrosophic number weighted averaging operator (SNNWA) is defined as follows:
where w = (w1, w2, … , wm) is the weight vector of Ai, and
Then, the aggregated result using the SNNWA operator is represented by
Definition 5 [22]. Let Ai = <TAi, IAi, FAi> be a collection of SNNs, where i = 1, 2, … , m, and m is the dimension. The simplified neutrosophic number weighted geometric operator (SNNWG) is defined as follows:
where w = (w1, w2, … , wm) is the weight vector of Ai, and
Then, the aggregated result using the SNNWG operator is represented by
Definition 6 [22]. For a SNN A, the score function η(A) and accuracy function δ(A) are given as follows:
(1) η(A) = (TA + 1 – IA + 1 – FA)/3;
(2) δ(A) = TA – FA.
Definition 7. For two SNNs A and B, we can sort them according to the following rules:
(1) if η(A) > η(B), it indicates that the superiority of A is over B;
(2) if η(A) = η(B) and δ(A) > δ(B), it indicates that the superiority of A is over B;
(3) if η(A) = η(B) and δ(A) = δ(B), it indicates that the superiority A and B is the same.
3 Aczel-Alsina Weighted Aggregation Operators of SNNs
Aczél-Alsina t-norms and Aczél-Alsina t-conorms are two useful operations, which have obvious advantages of changeability with the activity of parameters [27].
(1) The category
(2) The category
where all n1, n2 ∈ [0,1]; λ is positive constant; TD and SD are drastic t-norm and t-conorm, and they are stated by
Definition 8. Let A = < TA(s), IA(s), FA(s) > and B = < TB(s), IB(s), FB(s) > be any two SNNs, λ ≥ 1, and w > 0. Aczel-Alsina operations are defined as follows:
(1)
(2)
(3)
(4)
Example 1. Let A = < 0.9, 0.3, 0.5 > and B = < 0.6, 0.2, 0.2 > be two SNNs, λ = 3, and w = 0.9. Then, based on the Aczel-Alsina operations defined in Definition 8, we get the following results:
(1)
(2)
(3)
(4)
These operations for the collections of SNNs are based on the concept of Aczél-Alsina t-norms and Aczél-Alsina t-conorms. They are in preparation for developing the weighted averaging and geometric operators that will be discussed in the next section.
4 Two Aczel-Alsina Averaging Aggregation Operators of SNNs
To suit decision makers’ preference selection, it is important to deal with the flexible decision-making problems in the SNN environment. To solve this problem, we developed two Aczel-Alsina averaging aggregation operators of SNNs in this section.
4.1 Aczel-Alsina Weighted Averaging Aggregation Operator
According to the operations in Definition 8, a SNNAAWA operator is proposed here.
Definition 9. Let Ai = <TAi, IAi, FAi> be a collection of SNNs, where i = 1, 2, … , m, and m is the dimension. Then, a SNNAAWA is defined as follows:
where w = (w1, w2, … , wm) is the weight vector of Ai, and
Theorem 1. Set Ai = <TAi, IAi, FAi> (i = 1, 2, …, m) as a collection of SNNs along with the corresponding weight vector w = (w1, w2, … , wm) for wi ∈ [0,1] and
Proof. The proof of Theorem 1 based on the mathematical induction technique is given as follows:
(a) Let i = 2, then
(b) If Eq. (9) holds for i = n, then
(c) Set i = n + 1. Based on Definition 8 and Eq. (8), we have
From the above (a), (b), and (c), we can see that Eq. (9) holds for any i.
When λ = 1, there is
It demonstrates that the SNNWA operator is a special case of the SNNAAWA operator. Compared to the proposed SNNAAWA operator, the SNNWA operator lacks flexibility. Thus, it indicates that the main advantage of the operational flexibility of the proposed operator.
Proposition 1. Let Ai = <TAi, IAi, FAi> (i = 1, 2, … , m) be a group of SNNs. The SNNAAWA operator reflects the following properties from Eq. (6):
(1) Idempotency: If all Ai (i = 1, 2, … , m) are equal, i.e., Ai = A, then SNNAAWA (A1, A2, …, Am) = A.
(2) Boundedness: If the maximum and minimum SNNs are given below:
Thus, Amin ≤ SNNAAWA (A1, A2, …, Am) ≤ Amax can hold.
(3) Monotonicity: Assume
Proof.
(a) Since Ai = <TAi, IAi, FAi> = <TA, IA, FA> = A, we get the following result by Eq. (9):
(b) Since there are inequalities
According to the property Eq. (3) and the score function in Definition 6, we can obtain Amin ≤
(c) Due to
4.2 Aczel-Alsina Weighted Geometric Aggregation Operator
According to the operations in Definition 8, a SNNAAWG operator is proposed here.
Definition 10. Let Ai = <TAi, IAi, FAi> be a collection of SNNs, where i = 1, 2, … , m, and m is the dimension. Then, a SNNAAWG is defined as follows:
where w = (w1, w2, … , wn) is the weight vector of Ai, and
Theorem 2. Set Ai = <TAi, IAi, FAi> (i = 1, 2, …, m) as a group of SNNs along with the corresponding weight vector w = (w1, w2, … , wm) for w ∈ [0,1] and
When λ = 1, we can get
It demonstrates that the SNNWG operator is a special case of the SNNAAWG operator. Compared to the proposed SNNAAWG operator, the SNNWG operator lacks flexibility. Thus, it indicates that the main advantage of the operational flexibility of the proposed operator.
By the similar verification of Theorem 1, Theorem 2 can be easily proved, so it is omitted here.
Similarly, the SNNAAWG operator reflects the following properties from Eq. (11) too.
Proposition 2. Set Ai = <TAi, IAi, FAi> (i = 1, 2, … , m) be a collection of SNNs. The SNNAAWG operator contains the following properties:
(1) Idempotency: If all Ai (i = 1, 2, … , m) are equal, i.e., Ai = A, then SNNAAWG (A1, A2, …, Am) = A.
(2) Boundedness: If the maximum and minimum SNNs are given below:
Thus, Amin ≤ SNNAAWG (A1, A2, …, Am) ≤ Amax can hold.
(3) Monotonicity: Assume
Like the proof process of Proposition 1, Proposition 2 can be easily proved, so we do not repeat it here.
5 MADM Using the SNNAAWA and SNNAAWG Operators
In this section, the SNNAAWA and SNNAAWG operators are used to solve MADM problems with a favorite priority of alternatives under the SNN environment.
Assume that there is a set of n alternatives F = {F1, F2, …, Fn}, and satisfactorily assessed by a set of attributes G = {G1, G2, …, Gm}. Then, the impotence of various attributes Gi (i = 1, 2, …, m) is specified by a weight vector w = (w1, w2, …, wm) for
Let Sji = <TSji, ISji, FSji> for TSji, ISji, FSji ∈ [0,1] be the satisfactory assessment of each attribute for each alternative, where TSji indicates the truth-membership function that the alternative Fj (j = 1, 2, …, n) satisfies Gi. ISji and FSji indicate the indeterminacy membership function and the falsity-membership function, respectively. According to all assessment values, we can yield the decision matrix of SNNs: S = (Sji)n×m.
In this study, the SNNAAWA and SNNAAWG operators are applied to solve the MADM problem, and the procedure for determining the best alternative is provided as the following steps:
Step 1: Utilize the SNNAAWA or SNNAAWG operator to aggregate the SNNs by Eq. (9) or Eq. (11), we get the aggregated SNN KWj (j = 1, 2, …, n) as follows:
or
Step 2: According to the score function in Definition 6, the score values of KWj are obtained.
Step 3: Based on the score values, all alternatives are ranked in a decreasing order, and then the best one is selected concerning the biggest score value.
Step 4: End.
An illustrative example of the slope treatment scheme selections is provided to outline the utilization of the proposed MADM method.
According to the construction arrangement of the town, some excavation works are planned to be carried out in front of a slope. However, the excavation works will significantly influence the stability of the slope and bring threatens to the construction of infrastructure facilities and people's life and property safety. In the preliminary design stage, six exports were invited to give treatment schemes for the slope, and a set of six different treatment schemes F = {F1, F2, F3, F4, F5, F6} were tableted in Table 1. The assessment of these schemes needs to satisfy four attributes: the treatment cost G1, the difficulty of construction G2, the technical risk G3, and the environmental impact G4. The weight vector of the attributes is given by w = (0.35, 0.15, 0.20, 0.30).

The decision-maker needs to evaluate six potential schemes regarding the set of the attributes {G1, G2, G3, G4} under the SNN environment. The evaluation results of different schemes were expressed as the following matrix of SNNs:
Step 1: Utilize the SNNAAWA or SNNAAWG operator to aggregate the SNNs for each scheme by Eq. (9) or Eq. (11). The aggregation results are calculated separately based on the SNNAAWA and SNNAAWG operators. Here, we take the positive constant λ = 1 as an example to show the calculation process.
The aggregated value matrix KW can be obtained by the SNNAAWA operator:
Or the aggregated value matrix KW can be obtained by the SNNAAWG operator:
Step 2: Calculate the score function values.
According to the score function in Definition 6, the score values of KW can be obtained:
or
Step 3: All alternatives were ranked in a decreasing order as follows:
Thus, F1 is the best alternative.
Step 4: Repeat the calculation process by changing the positive constant λ. Then, all decision results are tabulated in Tables 2 and 3.
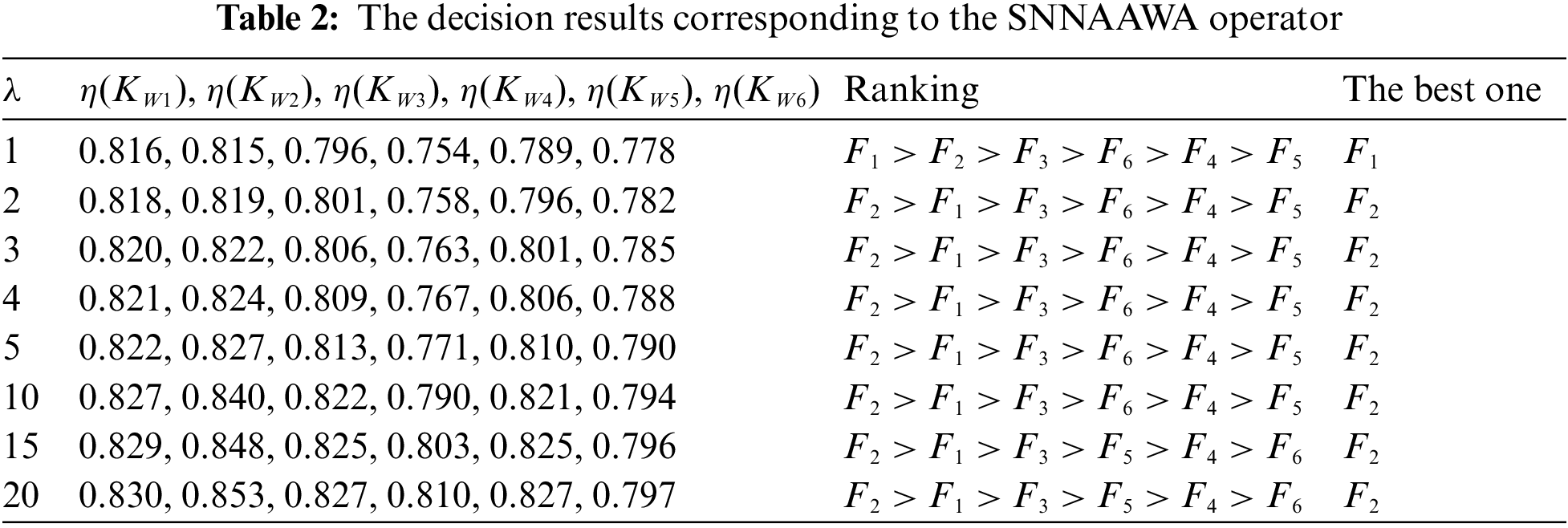
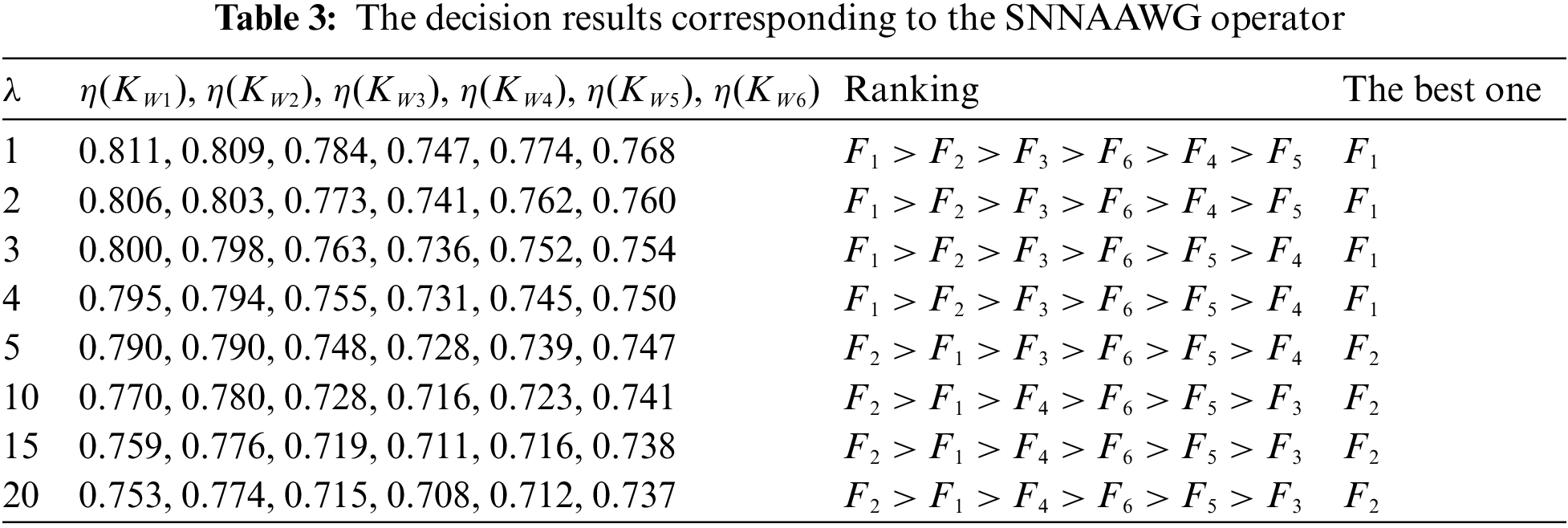
According to the results in Tables 2 and 3, the ranking orders in this MADM example are influenced by different aggregation operators and the values of the positive constant λ. The ranking orders by the SNNAAWA operator show that the best alternative is F1 for λ = 1 or F2 for λ > 1. The ranking orders by the SNNAAWG operator show that the best alternative is F1 for λ = 1, 2, 3, 4 or F2 for λ = 5, 10, 15, 20. Thus, it is obvious that the positive constant λ can affect the priority of all alternatives, which can satisfy the decision-maker’s preferences. Furthermore, the ranking order of the alternatives by the SNNAAWA operator is the same as the ranking result by the SNNAAWG operator for λ = 1, but the ranking orders of the alternatives by the SNNAAWA and SNNAAWG operators are slightly different from each other when λ is greater. Thus, the created new MADM method reflects the flexibility in the decision-making process. From the perspective of flexibility, the SNNAAWG operator has a greater impact on the ranking of alternatives than the SNNAAWA operator. However, to determine the actual aggregation values of the alternatives, various aggregation operators and the positive constant λ could be selected based on the preference of decision makers and the application situations. As motioned in Section 4, the SNNWA and SNNWG operators are the special cases of the SNNAAWA and SNNAAWG operators, respectively. Thus, the results of existing MADM approach using the SNNWA and SNNWG operators are equal to the decision results using the SNNAAWA and SNNAAWG operators for λ = 1. Then, the existing MADM approach using the SNNWA and SNNWG operators lacks the decision flexibility when compared to the proposed MADM method using the SNNAAWA and SNNAAWG operators.
Furthermore, a comparison is made between the proposed MADM method and the existing relative MADM methods using the single-valued neutrosophic sine trigonometric aggregation operators. Garg [13] first introduced the sine-trigonometric operations laws corresponding to SVNSs to solve the MADM problems. Two single-valued neutrosophic weighted operators are proposed based on the defined sine trigonometric operations of SVNNs.
The sine trigonometric weighted averaging aggregation operator is defined as follows [13]:
The sine trigonometric weighted geometric aggregation operator is defined as follows [13]:
Furthermore, in their study, the score function η*(LkW) and accuracy function δ*(LkW) (k = 1, 2) are given as follows [13]:
(1) η*(LkW) = TA – IA – FA;
(2) δ*(LkW) = TA + IA + FA.
The aggregated value matrix can be obtained by the ST-SVNWA operator of Eq. (12):
The aggregated value matrix can be obtained by the ST-SVNWG operator of Eq. (13):
The score values of η*(L1W) can be obtained below:
Then, we have all alternatives ranked in a decreasing order as follows:
The score values of η*(L2W) can be obtained below:
All alternatives are ranked in a decreasing order as follows:
The results show that F1 is the best alternative using the MADM method based on the ST-SVNWA and ST-SVNWG operators. It is consistent with the ranking orders by the SNNAAWA operator for λ = 1 or the SNNAAWG operator for λ = 1, 2, 3, 4. Thus, the existing MADM approaches using the ST-SVNWA and ST-SVNWG operators lack their decision flexibilities when compared to the proposed MADM method by the SNNAAWA and SNNAAWG operators. The preference value is not considered in the existing MADM approaches, while the new MADM method using the SNNAAWA and SNNAAWG operators can indicate the main advantage of flexible decision-making in actual applications by changing the positive constant λ. Therefore, the new MADM method considering decision makers’ preferences is more suitable for real applications and requirements.
To solve the MADM problems under the linguistic SVNS environment, Garg et al. [17] developed a MADM method using Frank Choquet Heronian mean operator. In this study, the SNNAAWA and SNNAAWG operators were proposed under the SNN environment. Compared to the proposed MADM method, the MADM method using Frank Choquet Heronian mean operator can solve decision-making problems which contains the linguistic single-valued neutrosophic numbers. Then, our method can handle decision-making problems with SNNs. In view of the the calculational complexity of aggregation algorithms, however, the SNNAAWA and SNNAAWG operators are relatively simpler than the Frank Choquet Heronian mean operator of linguistic SVNSs [17]. In addition, Garg et al. [20] developed several probabilistic and immediate probability-based averaging and geometric aggregation operators for the collection of SVNSs and INSs. In their research, the concept of probabilistic information was taken to describe the behavior of the decision-maker objectively (in terms of probability) and subjectively (in terms of weights). However, our MADM method does not considered the probabilistic information so as to avoid the probabilistic values yielded from a lot of data.
The aggregation of information plays an important role in decision-making problems. SNN is useful for describing truth, falsity, and indeterminacy information in MADM problems. However, the traditional MADM methods based on existing aggregation operators of SNNs cannot consider the flexible decision-making corresponding to the favorite priorities of alternatives. To suit decision makers’ preference selection, it is required to develop a MADM method that can reflect the flexibility in the decision-making process. For this circumstance, this paper developed the Aczel-Alsina aggregation operators of SNNs for MADM problems in view of the Aczel-Alsina operational flexibility. The SNNAAWA and SNNAAWG operators and their properties were presented according to the Aczel-Alsina operations of SNNs. Then, a new MADM method was established based on the SNNAAWA and SNNAAWG operators under the SNN environment. Finally, a selection problem of slope treatment schemes was utilized to illustrate its application. Based on the comparison with the existing relative MADM methods, the results show that the established MADM method can overcome the insufficiency of decision flexibility in the existing MADM methods. Since logarithmic functions are used in the SNNAAWA and SNNAAWG operators, the power cannot be zero, which shows their limitation. Thus, the proposed operators are necessary complements to existing aggregation operators of SNNs, and the suggested MADM method provides a new way for decision-making problems under the SNN environment.
In the future study, the suggested method in this paper will be applied to other uncertain fields, such as interval-valued neutrosophic numbers, the linguistic SVNS. Besides, this method can be applied to other domains, such as intelligent manufacturing, machine learning, and data mining.
Authors’ Contribution: Jun Ye proposed the Aczel-Alsina weighted aggregation operators; Shigui Du developed the MADM method based on SNNAAWA and SNNAAWG operators; Rui Yong, Aqin Zhu and Yingying Zhang provided the illustrative example and related comparison analysis; we wrote the paper together.
Funding Statement: The study was funded by the National Natural Science Foundation of China (No. 42177117), Zhejiang Provincial Natural Science Foundation (No. LQ16D020001).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Yong, R., Zhu, A., Ye, J. (2019). Multiple attribute decision method using similarity measure of cubic hesitant fuzzy sets. Journal of Intelligent & Fuzzy Systems, 37(1), 1075–1083. DOI 10.3233/JIFS-182555. [Google Scholar] [CrossRef]
2. Fu, J., Ye, J., Cui, W. (2018). An evaluation method of risk grades for prostate cancer using similarity measure of cubic hesitant fuzzy sets. Journal of Biomedical Informatics, 87(8), 131–137. DOI 10.1016/j.jbi.2018.10.003. [Google Scholar] [CrossRef]
3. Ye, J. (2014). A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets. Journal of Intelligent & Fuzzy Systems, 26(5), 2459–2466. DOI 10.3233/IFS-130916. [Google Scholar] [CrossRef]
4. Ye, J. (2019). Hesitant interval neutrosophic linguistic set and its application in multiple attribute decision making. International Journal of Machine Learning and Cybernetics, 10(4), 667–678. DOI 10.1007/s13042-017-0747-8. [Google Scholar] [CrossRef]
5. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. DOI 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
6. Chen, J., Ye, J. (2017). Some single-valued neutrosophic Dombi weighted aggregation operators for multiple attribute decision-making. Symmetry, 9(6), 82. DOI 10.3390/sym9060082. [Google Scholar] [CrossRef]
7. Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]
8. Ashraf, S., Abdullah, S., Mahmood, T. (2018). GRA method based on spherical linguistic fuzzy Choquet integral environment and its application in multi-attribute decision-making problems. Mathematical Sciences, 12(4), 263–275. DOI 10.1007/s40096-018-0266-0. [Google Scholar] [CrossRef]
9. Ashraf, S., Abdullah, S., Mahmood, T. (2020). Spherical fuzzy Dombi aggregation operators and their application in group decision making problems. Journal of Ambient Intelligence and Humanized Computing, 11(7), 2731–2749. DOI 10.1007/s12652-019-01333-y. [Google Scholar] [CrossRef]
10. Smarandache, F. (2001). A unifying field in logics: Neutrosophic logic, neutrosophy, neutrosophic set, probability, and statistics. Multiple-Valued Logic, 95(1), 7–108. DOI 10.1115/1.3426636. [Google Scholar] [CrossRef]
11. Zhang, H. Y., Wang, J. Q., Chen, X. H. (2014). Interval neutrosophic sets and their application in multicriteria decision making problems. The Scientific World Journal, 2014(3), 1–15. DOI 10.1155/2014/645953. [Google Scholar] [CrossRef]
12. Ye, J. (2014). Single valued neutrosophic cross-entropy for multicriteria decision making problems. Applied Mathematical Modelling, 38(3), 1170–1175. DOI 10.1016/j.apm.2013.07.020. [Google Scholar] [CrossRef]
13. Garg, H. (2020). Decision making analysis based on sine trigonometric operational laws for single-valued neutrosophic sets and their applications. Applied and Computational Mathematics, 19(2), 255–276. [Google Scholar]
14. Ashraf, S., Abdullah, S., Zeng, S., Jin, H., Ghani, F. (2020). Fuzzy decision support modeling for hydrogen power plant selection based on single valued neutrosophic sine trigonometric aggregation operators. Symmetry, 12(2), 298. DOI 10.3390/sym12020298. [Google Scholar] [CrossRef]
15. Garai, T., Dalapati, S., Garg, H., Roy, T. K. (2020). Possibility mean, variance and standard deviation of single-valued neutrosophic numbers and its applications to multi-attribute decision-making problems. Soft Computing, 24, 18795–18809. DOI 10.1007/s00500-020-05112-2. [Google Scholar] [CrossRef]
16. Liu, P., Wang, Y. (2014). Multiple attribute decision-making method based on single-valued neutrosophic normalized weighted Bonferroni mean. Neural Computing and Applications, 25(7), 2001–2010. DOI 10.1007/s00521-014-1688-8. [Google Scholar] [CrossRef]
17. Garg, H., Nancy (2019). Multiple criteria decision making based on frank Choquet Heronian mean operator for single-valued neutrosophic sets. Applied and Computational Mathematics, 18(2), 163–188. [Google Scholar]
18. Ashraf, S., Abdullah, S., Smarandache, F. (2019). Logarithmic hybrid aggregation operators based on single valued neutrosophic sets and their applications in decision support systems. Symmetry, 11(3), 364. DOI 10.3390/sym11030364. [Google Scholar] [CrossRef]
19. Fan, C., Ye, J. (2017). The cosine measure of refined-single valued neutrosophic sets and refined-interval neutrosophic sets for multiple attribute decision-making. Journal of Intelligent & Fuzzy Systems, 33(4), 2281–2289. DOI 10.3233/JIFS-17270. [Google Scholar] [CrossRef]
20. Garg, H., Nancy (2020). Multiple attribute decision making based on immediate probabilities aggregation operators for single-valued and interval neutrosophic sets. Journal of Applied Mathematics and Computing, 63(1–2), 619–653. DOI 10.1007/s12190-020-01332-9. [Google Scholar] [CrossRef]
21. Peng, J. J., Wang, J. Q., Zhang, H. Y., Chen, X. H. (2014). An outranking approach for multi-criteria decision-making problems with simplified neutrosophic sets. Applied Soft Computing, 25(3), 336–346. DOI 10.1016/j.asoc.2014.08.070. [Google Scholar] [CrossRef]
22. Du, S., Yong, R., Ye, J. (2020). Subtraction operational aggregation operators of simplified neutrosophic numbers and their multi-attribute decision making approach. Neutrosophic Sets and Systems, 33, 157–168. DOI 10.5281/zenodo.3782881. [Google Scholar] [CrossRef]
23. Peng, J. J., Wang, J. Q., Wang, J., Zhang, H. Y., Chen, X. H. (2016). Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems. International Journal of Systems Science, 47(10), 2342–2358. DOI 10.1080/00207721.2014.994050. [Google Scholar] [CrossRef]
24. Tian, Z. P., Wang, J., Zhang, H. Y., Chen, X. H., Wang, J. Q. (2016). Simplified neutrosophic linguistic normalized weighted Bonferroni mean operator and its application to multi-criteria decision-making problems. Filomat, 30(12), 3339–3360. DOI 10.2298/FIL1612339T. [Google Scholar] [CrossRef]
25. Jamil, M., Abdullah, S., Khan, M. Y., Smarandache, F., Ghani, F. (2019). Application of the bipolar neutrosophic hamacher averaging aggregation operators to group decision making: An illustrative example. Symmetry, 11(5), 698. DOI 10.3390/sym11050698. [Google Scholar] [CrossRef]
26. Liu, P. (2016). The aggregation operators based on Archimedean t-conorm and t-norm for single-valued neutrosophic numbers and their application to decision making. International Journal of Fuzzy Systems, 18(5), 849–863. DOI 10.1007/s40815-016-0195-8. [Google Scholar] [CrossRef]
27. Aczél, J., Alsina, C. (1982). Characterizations of some classes of quasilinear functions with applications to triangular norms and to synthesizing judgements. Aequationes Mathematicae, 25(1), 313–315. DOI 10.1007/BF02189626. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |