Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2022.019765

ARTICLE

Investigation of the Free Vibrations of Radial Functionally Graded Circular Cylindrical Beams Based on Differential Quadrature Method

Xiaojun Huang1,2, Liaojun Zhang1,*, Renyu Ge2, Hanbo Cui2 and Zhedong Xu2

1College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing, 210098, China
2School of Architecture and Civil Engineering, Anhui Polytechnic University, Wuhu, 241000, China
*Corresponding Author: Liaojun Zhang. Email: Ljzhang@hhu.edu.cn
Received: 13 October 2021; Accepted: 16 December 2021

1  Introduction

Functionally graded materials (FGMs) are a new class of advanced composite materials and are extensively employed in many industries such as civil engineering, mechanical engineering, space engineering, etc. So far, research works have generally focused on the free vibrations and buckling of radially graded rectangular cross-section beams. Currently, the free vibration of functionally graded (FG) beams with varying material properties along the direction of one axis have attracted great attention among researchers. Little attention has been paid in recent years to the free vibrations of FG beams with varying material properties along thickness direction. Xiang et al. [1] investigated the free and forced vibrations of beams by varying material elastic modulus along thickness direction under given initial thermal stress. Chakraborty et al. [2] developed a new beam element for the evaluation of the thermoelastic behavior of FG beams taking into account shear deformation. Ching et al. [3] applied meshless local Petrov-Galerkin method to numerically investigate simply supported FGM beams. Sankar et al. [4–6] obtained the elastic solution of FGM beams with shear deformation under transverse or thermal loadings.

As important structural elements, solid or hollow elastic circular cross-section beams are extensively employed in military, mechanical, aviation and civil engineering applications [7] in different forms such as steel ropes of bridges, aircraft landing gears and circular cross-section beams. According to continuum theory, solid or hollow elastic circular cross-section beams could be assumed as circular cross-section beam and bar models with slight error [8–10]. Thus, studying the vibrations of circular cross-section beams is of great theoretical and practical significance. Extensive research has been conducted on circular cylindrical beams and a series of beam theories such as Euler-Bernoulli, Rayleigh and Timoshenko beam theories have been proposed. In the early 1980s, Levinson [11] derived an equation for the calculation of high-order beam theory for bending and free vibrations of rectangular section beams taking into account the influences of inertia term and shear deformation with no need for modified shear coefficient. However, because of the lack of a higher-order theory for FG circular cylindrical beams, few research works have been performed on the mechanical properties of FG beams with circular sections. Loy et al. [12] investigated the free vibrations of FG cylindrical shells. Oh et al. [13] studied the vibration and stability of thin-walls with FG circular cross-sections using a simplified one-dimensional beam model. Law et al. [14] employed wave propagation method to explore the vibrations of cylindrical tubes. Based on nonlocal strain gradient theory, the nonlinear vibrations of beams under different FG distributions were studied by Gao et al. [15–17]. A third-order shear deformation beam model was developed by Ma et al. [18–20] to investigate the dynamic behaviors of straight hollow cylinders with annular cross-section, in which shear stress vanished on the inner and outer surfaces of the pipe.

Although several methods have been developed for the analysis of the free vibrations of FG beams with gradient along axial, radial or thickness directions, they generally suffer from complex computation methods and tedious solving processes. Differential quadrature method (DQM) was firstly introduced by Bellman and Casti in 1971 and presented the advantages of simple formulation, convenient programming, less computation and high precision [21]. Based on the high-order theory of transverse vibrations of circular-section beams. DQM was applied to calculate the free vibration natural frequencies of radial FG circular cylindrical beams at one time and corresponding modal functions could be solved together. According to the basic theory of DQM, the eigenvalue problem of ordinary differential equation for the free vibrations of radial FG circular cylindrical beams was transformed into a set of eigenvalue problems of algebraic equations. Then, the free vibration natural frequencies of radial FG circular cylindrical beams were calculated at one time and corresponding modal functions could be solved together. A circular cylindrical tube was taken as a special case of a bi-layered cylinder where material properties were vanished on the bottom surface. As a special case of an FG beam with circular section characterized by bi-layer material structure, the natural frequencies of thin cylindrical tubes with different boundary conditions can also be calculated by DQM.

2  Theoretical Formulations

A circular cylindrical beam with radial non-homogeneity was considered in this section. For such a structure, a Cartesian coordinate system (x, y, z) was assumed such that x-axis was considered as the neutral axis of cylindrical beam, positive z-axis was directed upward and perpendicular to x-axis, and corresponding elastic displacement components were written as (u,v,w). Meanwhile, polar cylindrical coordinate system (x,r,θ) and corresponding displacement vector (u,ur,uθ) were also employed. When a circular cross-section cylindrical beam is subjected to transverse loads in xoz-plane, distinct u -axial and w -transverse displacements are obvious. When the beam is restricted to transversely move in xoz-plane, the elastic displacement component v along y-direction can be approximately assumed independent from x. In Fig. 1, R is the radius of circular cylindrical beam and q is distributed force applied along a principal axis of beam corresponding to z-direction. It was concluded from this figure that physical quantities in the two coordinate systems had the following geometric relations, as seen the Eq. (1).

y=rcos⁡θ,z=rsin⁡θ,ur=vcos⁡θ+wsin⁡θ(1)

Figure 1: Schematic diagram of cylindrical beams with corresponding coordinates

The relationship between shear strain γxr on circumference and radial displacement ur was stated as Eq. (2a).

γxr=∂ur∂x+∂u∂r(2a)

Substitution of ur in Eq. (1) into Eq. (2a) gave Eq. (2b).

γxr=cosθ∂v∂x+sinθdwdx+cosθ∂u∂z+sinθ∂u∂y=1r(y∂v∂x+zdwdx+y∂u∂z+z∂u∂y)(2b)

When a circular section was exposed to transverse load, axial and transverse displacements were dominated forms. When only cylindrical beam deformation in xoz plane was considered, displacement along y direction was assumed to be constant along the axis, i.e., v=v(y,z). In order to make the shear stress on any circumference boundary zero, let γxr take the following form as Eq. (2c).

y∂u∂z+z(dwdx+∂u∂y)=z(y2+z2−R2)ζ(x)(2c)

where ζ(x) is an undetermined function. To calculate ζ(x), axial displacement was written in the following form as Eq. (2d).

u(x,y,z)=u1(x,z)+zy23ζ(x)(2d)

Substitution of Eq. (2d) into Eq. (2c) gave Eq. (2e).

∂u1∂z=−dwdx+(z2−R2)ζ(x)(2e)

On both sides of the above Eq. (2e), the z integral with respect to the variable resulted in Eq. (2f).

u1=13z3ζ(x)−z[R2ζ(x)+dwdx](2f)

The rotation of cross-section ψ was introduced along centroidal axis as Eq. (2g).

ψ(x)=−R2ζ(x)−dwdx(2g)

Simultaneous Eqs. (2d), (2f) and (2g), elimination function ζ(x), then the expression of the axial displacement is thus derived as follows Eq. (3):

u=zψ−z3+zy23R2(∂w∂x+ψ)(3)

Based on Saint-Venant principle, the stress components of the beam could be neglected; σyy=σzz=τyz=0 [22]. Consequently, τxr=0, and the condition of freedom on circumferential boundary was automatically satisfied from Eq. (4a).

τxr=G(r)(∂ur∂x+∂u∂r)=G(r)zrR2(R2−z2−y2)(∂w∂x+ψ)(4a)

Equations for other stress components σxx, τxy and τxz were demonstrated as Eq. (4b).

{σxx=E(r)∂u∂x=E(r)[z∂ψ∂x−z3+zy23R2(∂2w∂x2+∂ψ∂x)]τxy=G(r)(∂u∂y+∂v∂x)=−2G(r)zy3R2(∂w∂x+ψ)τxz=G(r)(∂u∂z+∂w∂x)=G(r)[∂w∂x+ψ−3z2+y23R2(∂w∂x+ψ)](4b)

Due to the equilibrium of internal forces, bending moment M and shear force Q at any position x of beam could be expressed as Eq. (5).

{M=∫AσxxzdA=E~2∂ψ∂x−E4∂2w∂x2Q=∫AτxzdA=G~0(ψ+∂w∂x)(5)

where

E2=π∫0RE(r)r3drE4=π3R2∫0RE(r)r5dr(6a)

G0=2π∫0RG(r)rdrG2=4π3R2∫0RG(r)r3dr(6b)

E~2=E2−E4G~0=G0−G2(6c)

where E(r) and G(r) are Young's modulus and shear modulus of cylindrical beams depending on r, respectively, when r=0, E(r)  =  Ec and G(r)  =  Gc correspond to material properties in cylindrical beam axis center and r=R, E(r)  =  Es and G(r)  =  Gs correspond to material properties on cylindrical beam surface. Because cylindrical beam was deflected along z-direction, not y-direction, under applied bending moment, only two motion equations were involved for flexural deformation in xoz-plane as Eq. (7).

{∂σxx∂x+∂τxy∂y+∂τxz∂z=ρ(r)∂2u∂t2∂τxz∂x+∂τyz∂y+∂σzz∂z=ρ(r)∂2w∂t2(7)

Substitution of Eq. (4) into Eq. (7) yielded Eq. (8).

{E~2∂2ψ∂x2−E4∂3w∂x3−G~0(∂w∂x+ψ)=ρ~2∂2ψ∂t2−ρ4∂3w∂x∂t2G~0(∂2w∂x2+∂ψ∂x)=ρ0∂2w∂t2−q(8)

where

ρ0=2π∫0Rρ(r)rdrρ2=π∫0Rρ(r)r3drρ4=π3R2∫0Rρ(r)r5dr(9a)

ρ~2=ρ2−ρ4(9b)

where ρ(r) is beam mass density depending on r, when r=0, ρ(r)  =  ρc is material density at cylindrical beam center when r=R, and ρ(r)  =  ρs is material density on circular cross-section beam surface. Introducing auxiliary function F(x) to decouple the formulations presented in Eq. (8) into a single governing equation gave deflection w and rotation ψ as Eqs. (10a) and (10b).

w=F−E~2G~0∂2F∂x2+ρ~2G~0∂2F∂t2(10a)

ψ=ρ4G~0∂3F∂x∂t2−E4G~0∂3F∂x3−∂F∂x(10b)

By substituting Eq. (10) into Eq. (8), the first equation was naturally satisfied and substituting the second equation into Eq. (8) yielded Eq. (11).

E2∂4F(x)∂x4−(ρ2+ρ0E~2G~0)∂4F(x)∂x2∂t2+ρ0∂2F(x)∂t2+ρ0ρ~2G~0∂4F(x)∂t4=q(11)

In order to analyze the free vibrations of radial FG circular cylindrical beams, the introduced auxiliary function F could take the following form Eq. (12).

F=f(x)eiωt(12)

where ω is the free vibrations of circular frequency. Substitute Eq. (12) into Eq. (11) supposing q=0 gave the governing equation of radial FG circular cylindrical beams as Eq. (13).

∂4f(x)∂x4+(ρ2E2+ρ0E~2E2G~0)ω2∂2f(x)∂x2−ρ0E2ω2f(x)+ρ0ρ~2E2G~0ω4f(x)=0(13)

The corresponding boundary conditions of simply-supported (SS), free-free (FF), clamped-clamped (CC) and clamped-free (CF) beams were Eq. (14).

w(0)=w(L)=0M(0)=M(L)=0(14a)

M(0)=Q(0)=0M(L)=Q(L)=0(14b)

w(0)=ψ(0)=0w(L)=ψ(L)=0(14c)

w(0)=ψ(0)=0M(L)=Q(L)=0(14d)

Thus, the solution of the natural frequency of FG cylindrical beams converted to the calculation of Eq. (13) under the boundary condition Eq. (14). For the convenience of programming, ξ=xL was assumed, the governing equation of the free vibrations of circular cross-section beams in Eq. (13) was rewritten into a dimensionless equation as Eq. (15).

f′′′′(ξ)+Ω2a2f′′(ξ)−Ω2a0f(ξ)+Ω4b0f(ξ)=0(15)

where Ω=ωRρc/Gc is dimensionless natural frequency and the parameters a2, a0, b0 were expressed as:

a2=(ρ2E2+ρ0E~2G~0E2)GcL2ρcR2,a0=ρ0E2GcL4ρcR2,b0=ρ~2G~0ρ0E2(GcL2ρcR2)2

To express generality, a CC beam was taken as an example. From Eqs. (10) and (12), the followings could be inferred Eqs. (16) and (17).

Supposingw=0,α1f′′(ξ)−f(ξ)+Ω2α2f(ξ)=0(16)

where α1=E~2G~0L2, α2=GcR2ρcρ~2G~0.

And supposingφ=0α3f′′′(ξ)+f′(ξ)+Ω2α4f′(ξ)=0(17)

where α3=E4G~0L2, α4=GcR2ρcρ4G~0

3  Calculation of the Natural Frequencies of Circular Section Beams by DQM

The vibration modal function f(ξ) of the beams was considered to be differentiable along beam length interval [0, 1] and interval [0, 1] was divided into n discrete elements, assuming ξ0=0 and ξn=1. In this research, non-uniform grid in Eq. (18a) (root of Chebyshev polynomial) was applied to represent node coordinates ξi and equal size uniform grid in Eq. (18b) represented node coordinates ξi:

ξi=12(1−cosiπn),(i=0,1,2,⋯,n)(18a)

ξi=in,(i=0,1,2,⋯,n)(18b)

In the interval [0, 1], the function and its derivatives at each node were represented by a weighted linear sum of the values of discrete n + 1 node functions; the function f(ξ) was described using Lagrange interpolation function as Eq. (19).

f(ξ)=∑j=0nlj(ξ)f(ξj)(19)

where f(ξ) is Lagrange polynomial and is stated as Eq. (20).

lj(ξ)=∏k=0k≠jnξ−ξkξj−ξk(20)

From Eq. (19), the first derivative of function f(ξ) was obtained as Eq. (21).

f′(ξ)=∑j=0nl′j(ξ)f(ξj)(21)

It was divided into n segments along beam length interval [0, 1]. Therefore, Eq. (21) was transformed as Eq. (22).

f′(ξi)=∑j=0nl′j(ξi)f(ξj)(i,j=0,1,⋯,n)(22)

Eq. (22) was reduced to vector form as Eq. (23).

f′=Ann(1)f(23)

where vectors Ann(1), f′, and f were expressed as Eq. (24).

{Ann(1)=(Aij(1))(n+1)×(n+1)f′=(f′(ξ0),f′(ξ1),⋯,f′(ξn))Tf=(f(ξ0),f(ξ1),⋯,f(ξn))T(24)

where Aij(1) is expressed as Eq. (25).

Aij(1)=l′j(ξi)={∏k=0k≠i,jn(ξi−ξk)/∏k=0k≠jN(ξj−ξk) (i≠j)∑k=0k≠in1(ξi−ξk)                       (i=j)(25)

Similarly, from Eq. (23), it could be inferred Eq. (26).

f(r)=Ann(r)f(26)

where f(r)=(f(r)(ξ0),f(r)(ξ1),⋯,f(r)(ξn))T, f(r)=drf/dξr, Aij(r)=drlj(ξ)/dξr, Ann(r)=(Aij(r))(n+1)×(n+1) and Ann(r) is weight coefficient matrix. The relationship between the derivatives of weight coefficient matrix Ann(r) was Eq. (27).

Am(r)=Am(1)Am(r−1)=Am(r−1)Am(1)(r≥2)(27)

The free vibration governing Eq. (15) of circular cross-section beams was rewritten into vector form as Eq. (28).

A(4)f+Ω2a2A(2)f−Ω2a0If+Ω4b0If=0(28)

where I is the identity matrix of order (n+1)×(n+1). Supposing λ=Ω2, Eq. (28) was reduced to the following vector form as Eq. (29).

C1f+λC2f+λ2C3f=0(29)

where C1=A(4), C2=(a2A(2)−a0I), C3=b0I

For general purposes, the boundary conditions of beams were discussed by taking CC beams as example. From Eqs. (16) and (17), boundary conditions were rewritten as the following vector form as Eqs. (30) and (31).

[D1]Il f+λ[D2]Il f=0(30)

where D1=α1A(2)−I,D2=α2I

[D3]Il f+λ[D4]Il f=0(31)

where D3=α3A(3)+A(1),D4=α4A(1)

where Il is the elements of Il -th row with 0 and n, [⋯]Il is a matrix. Substituting Eqs. (30) and (31) into governing Eq. (29), followed by replacing row 0, row 1, row n−1, and row n of the corresponding matrix vector and node substitution method (δ-method) is used to deal with the boundary condition [23]. It was obtained Eq. (32).

C⌢1f+λC⌢2f+λ2C⌢3f=0(32)

Since Eq. (32) contained unknown parameter λ2, it leaded to nonlinear eigenvalue problem. Therefore, a new variable y was introduced as Eq. (33).

y=λf(33)

Eq. (33) could be rewritten into the following vector form Eq. (34).

Iy−λIf=0(34)

where column vector y=(y(ξ0),y(ξ1),⋯,y(ξn))T. From Eqs. (32) and (34), it could be inferred Eq. (35).

[I00C⌢1](yf)−λ[0I−C⌢3−C⌢2](yf)=0(35)

Here, Eq. (35) contained general algebraic characteristic equations including 2(n + 1) unknown vector (Y,f)T with respect to eigenvalue λ. Generalized algebraic eigenvalue problem λ could be solved by QR method. Then, λ=Ω2 was used to obtain the dimensionless natural frequency Ω of radial functionally gradient beams. At the same time, corresponding eigenvector f was solved. Substituting the above equations into Eq. (10) gave the modal curves of deflection w and rotation angle ψ of beams.

4  Numerical Examples and Discussion

4.1 Free Vibrations of Radial FG Cylindrical Beams

To investigate the effects of gradient parameters on the natural frequencies of circular cross-section beams, for simplification, the material properties of circular cylindrical beams were assumed to follow power-law functions as Eq. (36).

{E(r)=Ec+(Es−Ec)(rR)mG(r)=Gc+(Gs−Gc)(rR)mρ(r)=ρc+(ρs−ρc)(rR)m(36)

where m is gradient parameter reflecting volume fraction change effect on material properties. In the following calculations (presented in Tables 1–4), a circular cylindrical beam with the radius to length ratio of R/L=0.1 was applied and n refers to the number of discrete elements along beam length interval (0, 1). Zirconia and aluminum were chosen as outer and the inner surface materials, respectively, and the material properties of which were [24]:

Al : Ec  = 70 GPa,Gc  = 27 GPa, = 2702 kg/m3

ZrO2 : Es  = 200 GPa, Gs  = 77 GPa, ρs  = 5700 kg/m3

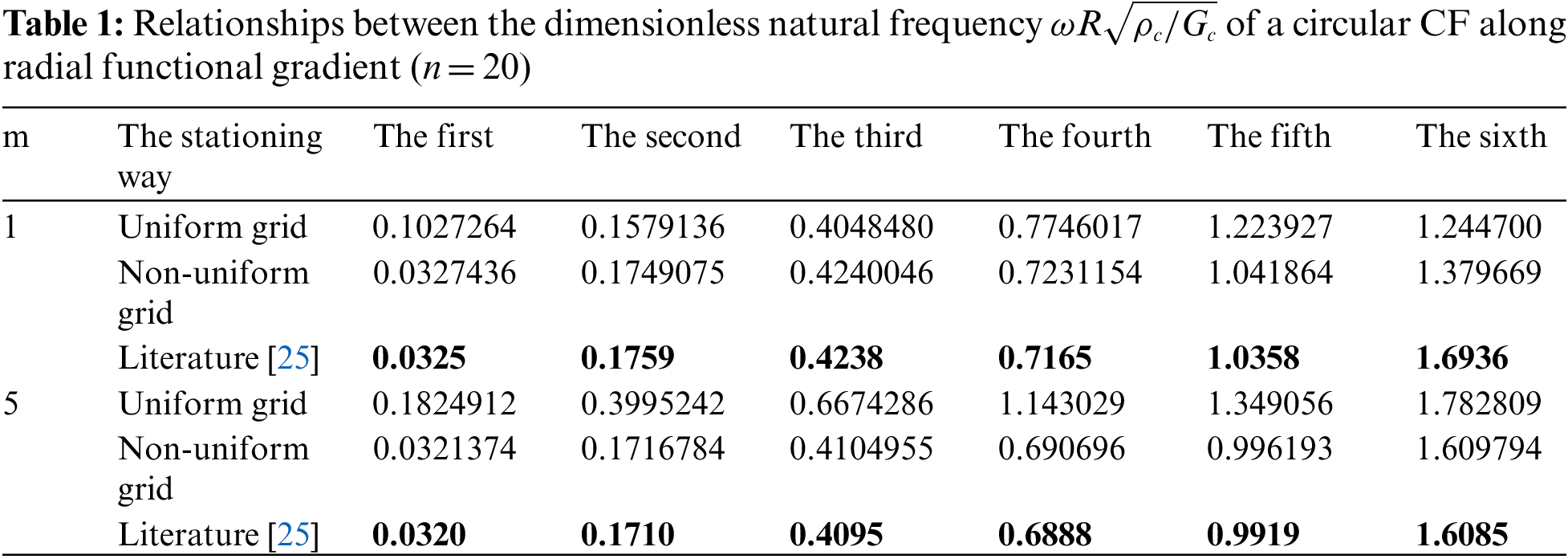
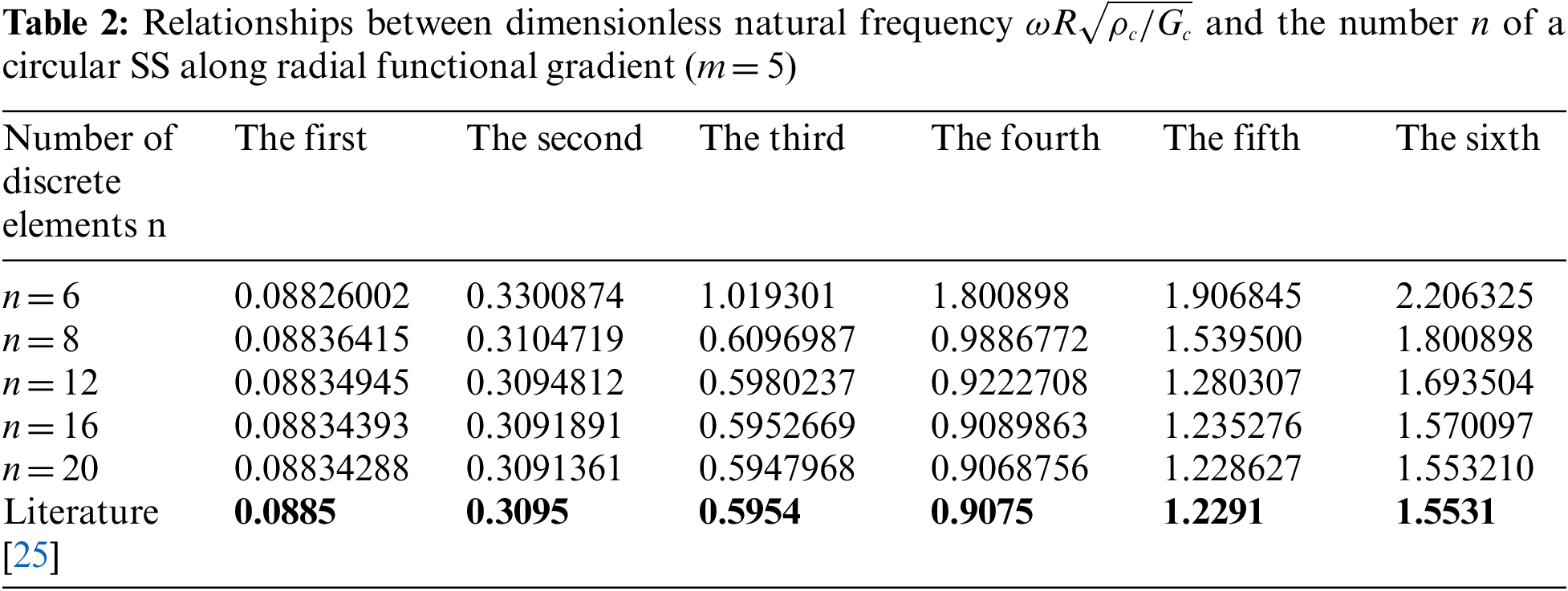
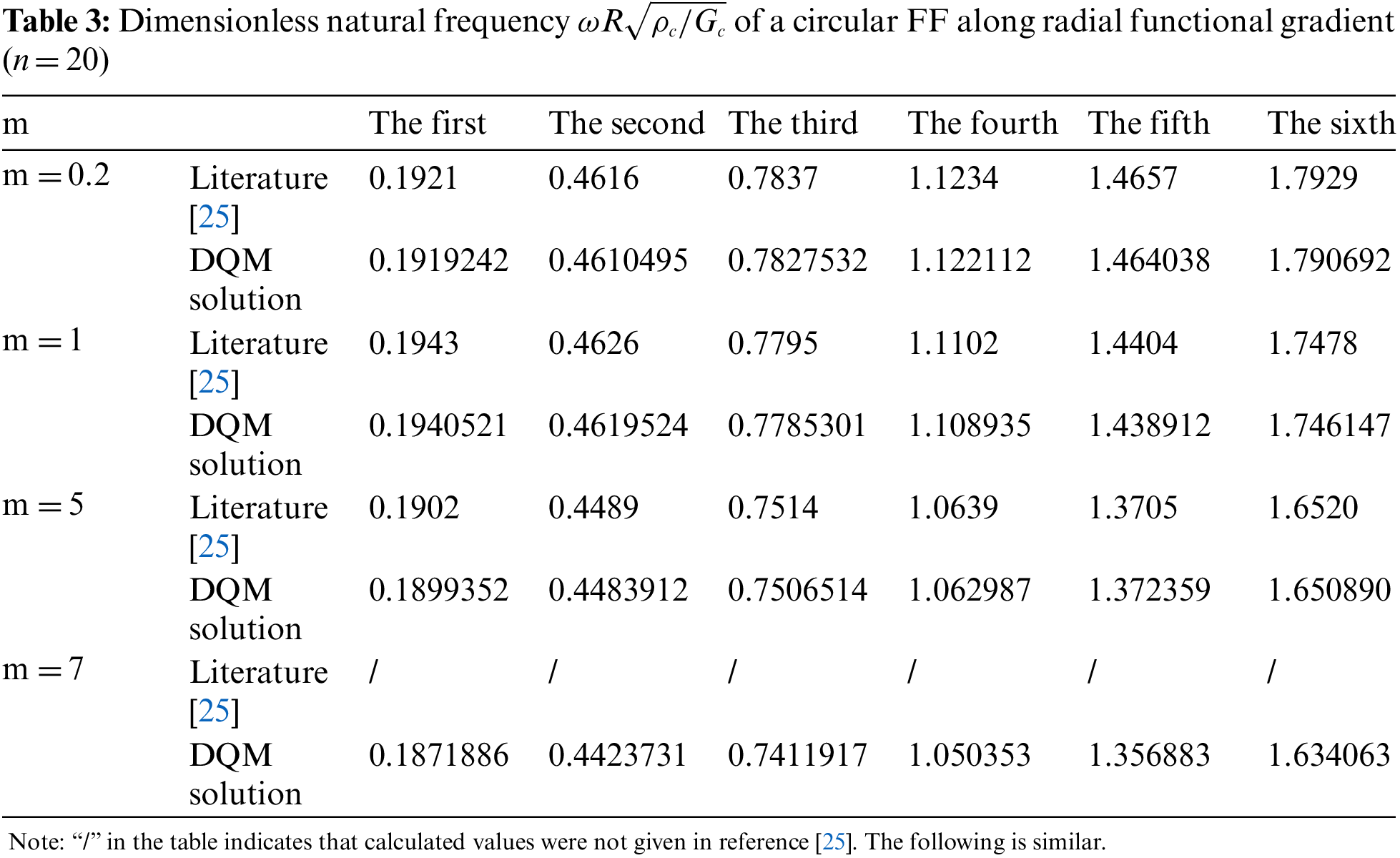
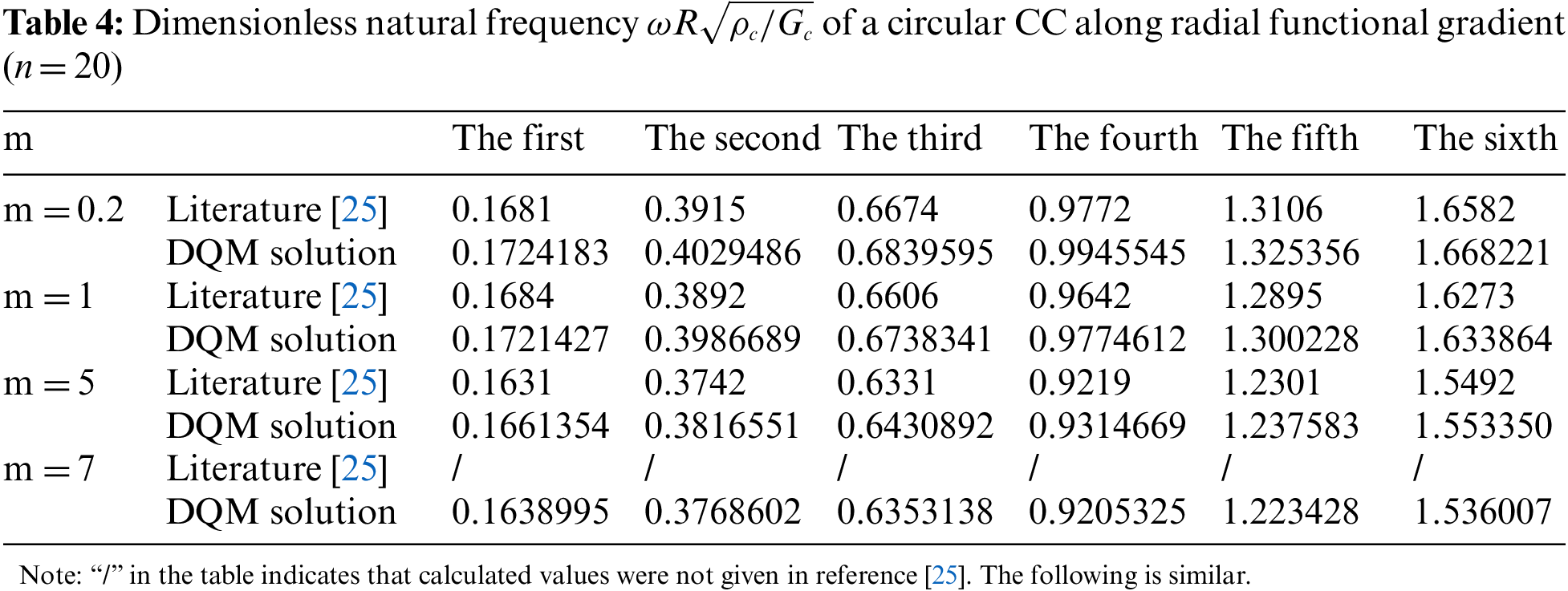
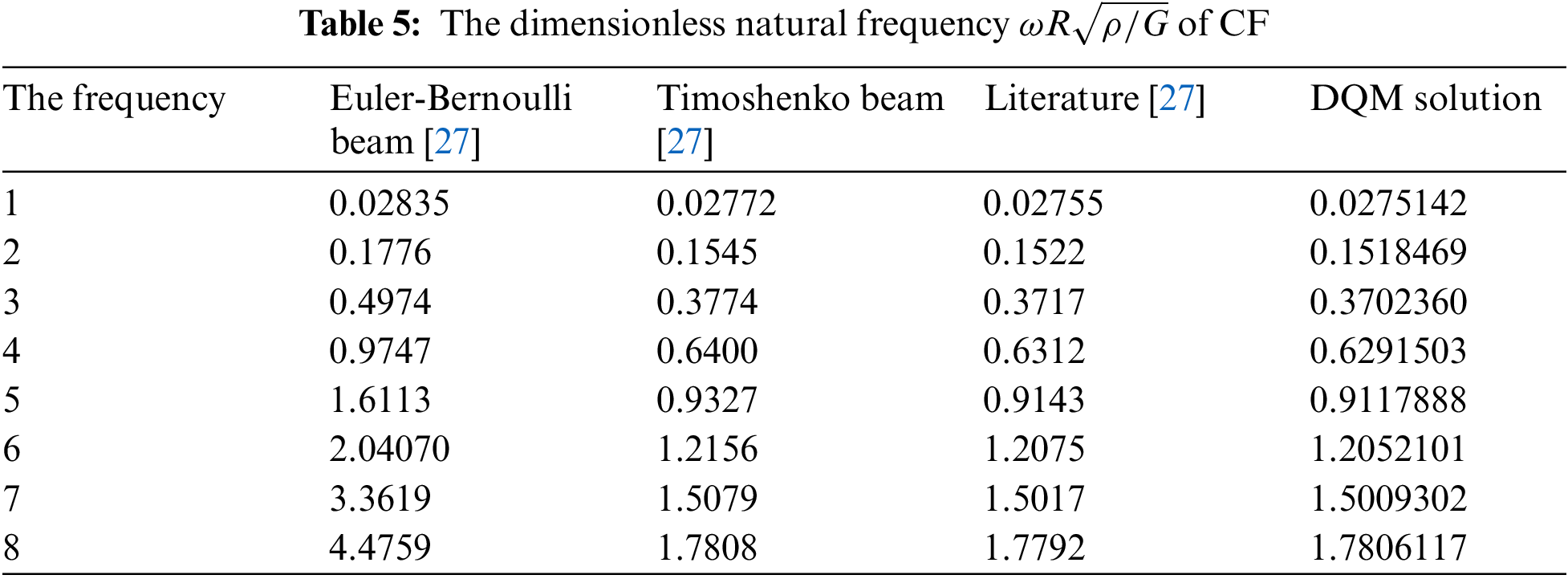
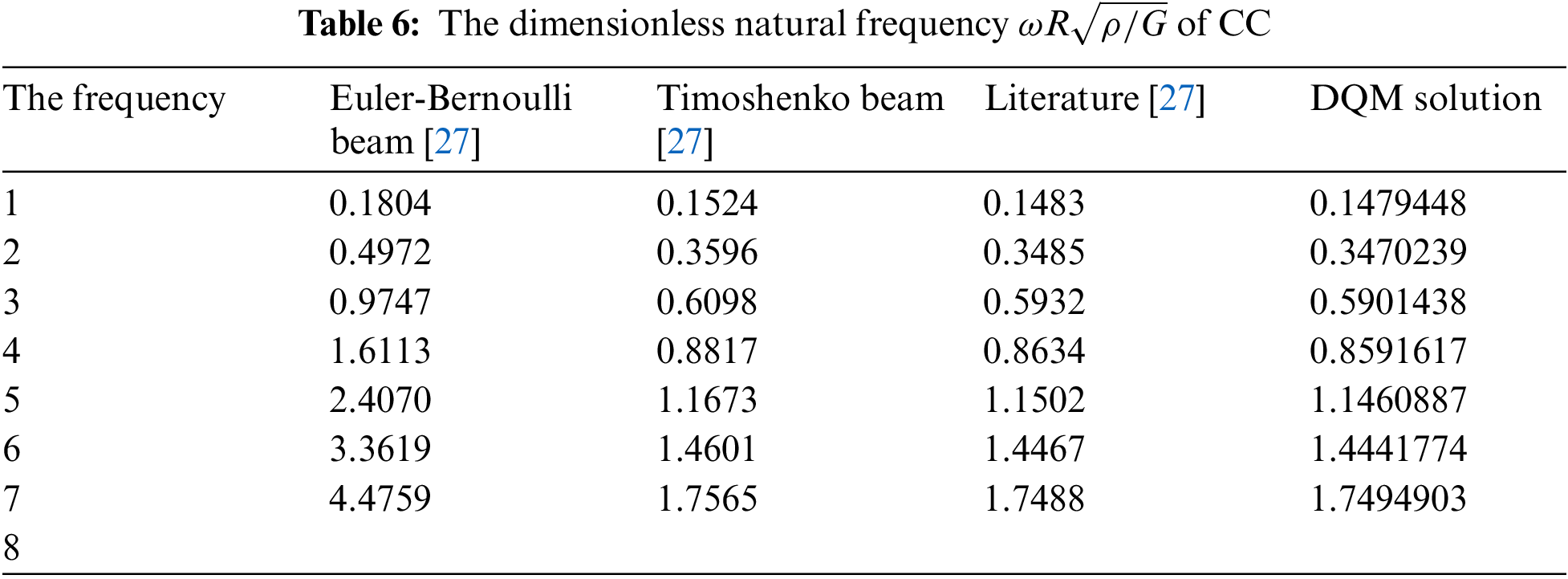
Table 1 summarizes the first six dimensionless natural frequencies of CF in radial FG calculated by DQM (n=20, m=1 and m=5). It was found that the numerical results obtained from non-uniform grid distribution method were identical to those reported in literature [25]; however, large error or even distortions were observed between the numerical results obtained from uniform and equal step size distribution method compared to those reported in literature [25]. The numerical results given in Table 1 show that Eq. (18b) could be used for discrete elements along beam length. The numerical results calculated by DQM were unstable or even distorted, while higher accuracy could be achieved by Eq. (18a). Table 2 summarizes the first six dimensionless natural frequencies of CC in radial functional gradient calculated by DQM (m=5), where Eq. (18a) is applied as the distribution mode of discrete nodes along beam length. As was seen in the table, the numerical results obtained for the first six natural frequencies were close to those reported in reference [25] except for the first and second natural frequencies when n = 6 and 8. Other numerical results obtained for the fourth to sixth natural frequencies had large errors and even distortions. However, the numerical results obtained for the first six natural frequencies were close to those reported in reference [25] through increasing n. In other words, with the increase of the number of discrete elements n, numerical results showed higher accuracy.

Tables 3 and 4 present the first six dimensionless natural frequencies of FF and CC in radial functional gradient calculated by DQM, respectively (n=20, m=0.2, 1, 5 and m=7). As seen from Tables 3 and 4, numerical results obtained from non-uniform grid distribution method showed excellent consistency with those reported in reference [25], which indicated that the high-order theory of transverse vibrations of circular cross-section beams were correct and DQM was effective and accurate for the calculation of the natural frequencies of radial functional gradient circular cross-section beams. The calculation results presented in Tables 3 and 4 also showed that the dimensionless natural frequencies of beams were decreased with the increase of gradient material m. According to Eq. (36), this was because the average stiffness of beams was monotonically decreased with the increase of gradient material m.

Fig. 2 presents the first 15 non-dimensional frequency parameters of five radius-to-length ratios calculated by DQM (n=20, m=3). For smaller values of R/L, i.e., R/L = 0.002 and 0.005, relations between non-dimensional frequency parameter and mode number were almost linear. The relations became non-linear with the increase of radius-to-length ratios.

Figure 2: Non-dimensional frequency parameter Ω of beams under different boundary conditions

In this research, the natural frequencies of the free vibrations of radial FG circular cylindrical beams were calculated using DQM as well as the first and second modal curves of various gradient parameters under different boundary conditions were obtained. Figs. 3 to 6 indicate that the variations of gradient parameters had almost negligible effects on the modal curves of CF and SS, but significant effects on the first and second modal curves of FF and CC. The results were consistent with FG rectangular CF along thickness on effect of material parameters on the modal behavior [26].

Figure 3: Modal diagram of radial FG circular CF (a) First modal diagram (b) Second modal diagram

Figure 4: Modal diagram of radial FG circular SS (a) First modal diagram (b) Second modal diagram

Figure 5: Modal diagram of radial FG circular FF (a) First modal diagram (b) Second modal diagram

Figure 6: Modal diagram of radial FG circular CC (a) First modal diagram (b) Second modal diagram

4.2 Free Vibrations of Isotropic Homogeneous Material Beams

Based on Eq. (36), when m=0, supposing E(r)=Es=E, G(r)=Gs=G, ρ(r)=ρs=ρ, radial FG circular cylindrical beams were simplified to isotropic homogeneous materials beams, where E, G and ρ are, respectively, the elastic modulus, shear elastic modulus and density of the uniform material. Since R/L=0.1 and μ=0.3, based on high-order theory of transverse vibration of circular cross-section beams, the first eight dimensionless natural frequencies ωRρ/G for the circular cross-section beams of isotropic homogeneous materials were calculated by DQM, where n=20 and the distribution mode of discrete elements was non-uniform grid. The obtained results are listed in Tables 5 and 6 and compared to those reported in reference [27]. It was found that numerical results obtained from Euler-Bernoulli beam theory were generally too high because shear deformation was not considered. However, the results showed excellent consistency with those obtained by DQM in literature [27] which were very close to the results obtained from Timoshenko beam theory. It was proved that DQM was feasible and accurate in calculating the natural frequencies of radial functional gradient circular cross-section beams with homogeneous materials. Unlike Euler-Bernoulli and Timoshenko beam theories, a higher-order theoretical beam model was developed which did not require shear correction factor and planar cross-section assumption after deformation.

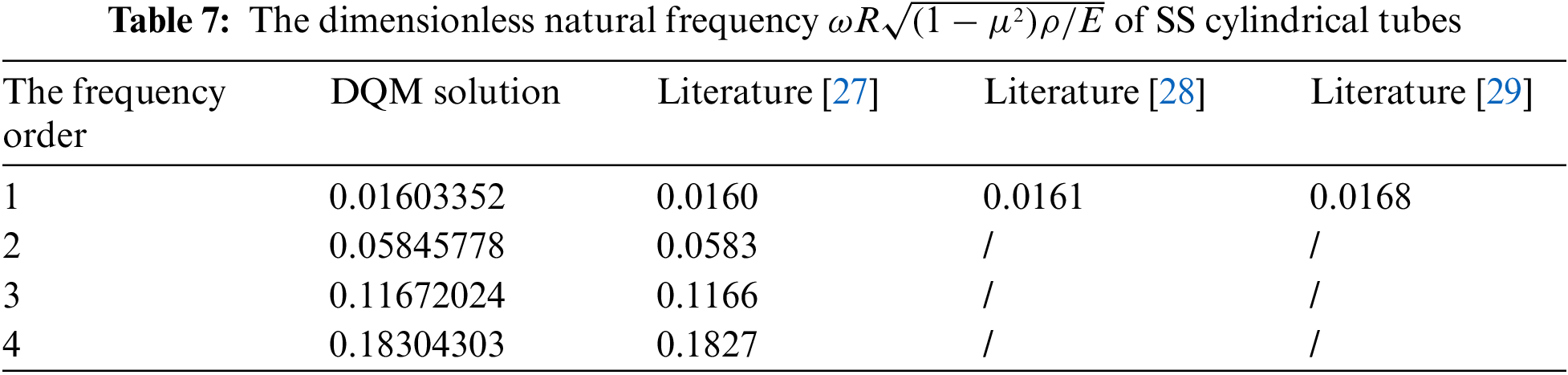
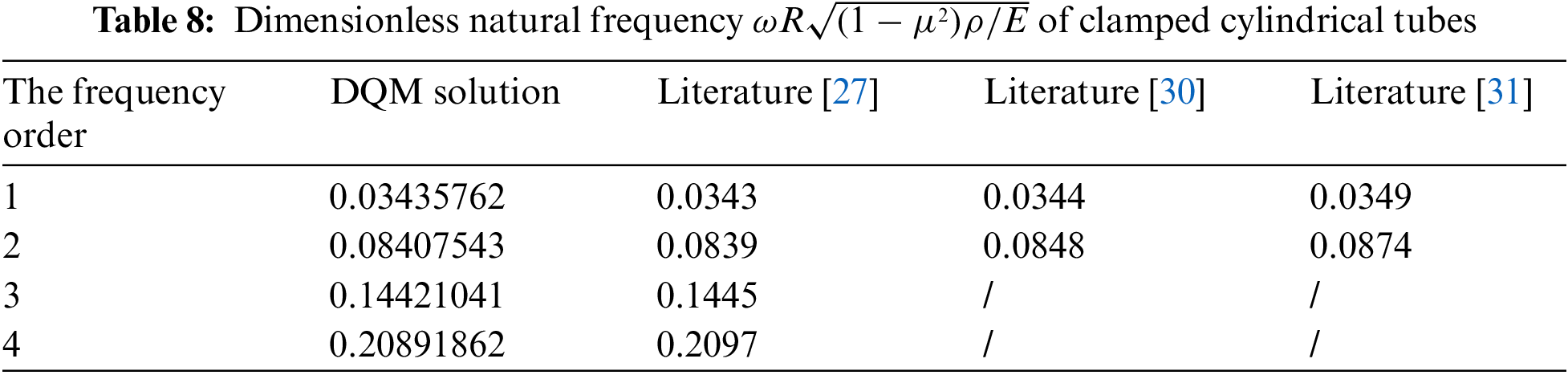
4.3 Free Vibrations of Isotropic Cylindrical Tubes

Isotropic cylindrical tubes could be regarded as special FG materials with bi-layer material structures. The inner of bi-layer had vanishing material properties (i.e., material constant was zero), while the outer of bi-layer was homogeneous. Therefore, the material properties of cylindrical tubes could be rewritten as Eq. (37).

E(r)={E,R−h≤r≤R0,0≤r≤R−h,G(r)={G,R−h≤r≤R0,0≤r≤R−h,ρ(r)={ρ,R−h≤r≤R0,0≤r≤R−h(37)

where h is tube thickness and R is cylindrical tube section radius. Substituting Eq. (37) into Eq. (13) gave the natural frequency governing equation of a FG circular cylindrical tube. R/L=0.05, h/R=0.002, and material Poisson's ratio μ=0.3 were assumed. The distribution mode of discrete elements was non-uniform grid and the number of discrete elements was n=20. The dimensionless natural frequencies ωR(1−μ2)ρ/E of cylindrical tubes under two boundary conditions could be calculated. The results obtained from DQM and those reported in reference [12] are listed in Tables 7 and 8, respectively. As seen from these tables, our results were completely consistent with those in existing literatures, the accuracy of DQM in calculating the natural frequencies of the free vibrations of FG circular cylindrical tubes were validated.

5  Conclusion

In this research, based on the high-order theory of transverse vibration of circular cross-section beams, the calculation equation of natural frequency was converted into a differential equation with natural frequency as eigenvalue. From the above analyses and derivations, the differential equation was transformed into a standard generalized algebraic eigenvalue equation by differential quadrature method theory and the obtained algebraic equations were solved by QR method. Free vibration natural frequencies of a cylindrical beam with circular cross-section was calculated and corresponding modal function curve was achieved. The following main conclusions were drawn:

(1)   In this paper, the natural frequencies of the transverse vibrations of FG circular cross-section beams under different boundary conditions were calculated by DQM. The obtained results were consistent with those reported related literature, which indicated that DQM was highly efficient and precise in calculating the natural frequencies of FG circular cross-section beams.

(2)   Numerical results showed that uniform grid was used for discrete elements along the direction of beam length, the numerical results calculated by DQM were unstable or even distorted, but non-uniform grid was applied to obtain calculation results which were consistent with the results of reported in the existing literatures.

(3)   The circular cylindrical beams of homogeneous materials and cylindrical tubes can be regarded as the special cases of the circular cross-section beams of FGMs. In this paper, based on high-order theory for the transverse vibrations of radial FG circular cylindrical beams, the natural frequencies of circular cross-section beams with homogeneous materials and cylindrical tubes were calculated by DQM. The consistence of numerical results with those reported in existing literature further verified the computational accuracy of DQM.

(4)   The natural frequencies of circular cross-section beams with FG materials and first and second modal curves of different gradient parameters under various boundary conditions could be calculated by DQM. The obtained numerical results showed almost negligible effect on the modals of CF and SS when changing gradient parameters, but these effects were especially obvious for FF and CC.

Acknowledgement: The authors would like to thank the anonymous reviewers for carefully reading the article and this research was financially supported by the National key Research and Development Plan of Ministry of Science and Technology of the People's Republic of China (2017YFC0404903).

Funding Statement: The National key Research and Development Plan of Ministry of Science and Technology of the People's Republic of China (2017YFC0404903).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Xiang, H. J., Yang, J. (2007). Free and forced vibration of a laminated FGM Timoshenko beam of variable thickness under heat conduction. Composites Part B: Engineering, 39(2), 292–303. DOI 10.1016/j.compositesb.2007.01.005. [Google Scholar] [CrossRef]

 2.  Chakraborty, A., Gopalakrishnan, S., Reddy, J. N. (2003). A new beam finite element for the analysis of functionally graded materials. International Journal of Mechanical Sciences, 45(3), 519–539. DOI 10.1016/S0020-7403(03)00058-4. [Google Scholar] [CrossRef]

 3.  Ching, H. K., Yen, S. C. (2005). Meshless local Petrov-Galerkin analysis for 2D functionally graded elastic solids under mechanical and thermal loads. Composites Part B: Engineering, 36(3), 223–240. DOI 10.1016/j.compositesb.2004.09.007. [Google Scholar] [CrossRef]

 4.  Sankar, B. V. (2001). An elasticity solution for functionally graded beams. Composites Science and Technology, 61(5), 689–696. DOI 10.1016/S0266-3538(01)00007-0. [Google Scholar] [CrossRef]

 5.  Elperin, T., Rudin, G. (2002). Thermal stresses in functionally graded materials caused by a laser thermal shock. International Journal of Heat and Mass Transfer, 38(7), 625–630. DOI 10.1007/s002310100252. [Google Scholar] [CrossRef]

 6.  Zhu, H., Sankar, B. V. (2004). Combined Fourier series-Galerkin method for the analysis of functionally graded beams. Journal of Applied Mechanics-Transactions of the Asme, 71(3), 421–424. DOI 10.1115/1.1751184. [Google Scholar] [CrossRef]

 7.  Timoshenko, S. (1974). Vibration problems in engineering, New York: Wiley. [Google Scholar]

 8.  Wong, E. W., Sheehan, P. E., Lieber, C. M. (1997). Nanobeam mechanics: Elasticity, strength, and toughness of nanorods and nanotubes. Science, 277(5334), 1971–975. DOI 10.1126/science.277.5334.1971. [Google Scholar] [CrossRef]

 9.  Sourki, R., Hoseini, S. (2016). Free vibration analysis of size-dependent cracked microbeam based on the modified couple stress theory. Applied Physics A, 122(4), 1–11. DOI 10.1007/s00339-016-9961-6. [Google Scholar] [CrossRef]

10. Huang, Y., Li, X. F. (2010). A new approach for free vibration of axially functionally graded beams with non-uniform cross-section. Journal of Sound & Vibration, 329(11), 2291–2303. DOI 10.1016/j.jsv.2009.12.029. [Google Scholar] [CrossRef]

11. Levinson, M. (1981). A new rectangular beam theory. Journal of Sound & Vibration, 74(1), 81–87. DOI 10.1016/0022-460X(81)90493-4. [Google Scholar] [CrossRef]

12. Loy, C. T., Lam, K. Y., Reddy, J. N. (1999). Vibration of functionally graded cylindrical shells. International Journal of Mechanical Sciences, 41(3), 309–324. DOI 10.1016/S0020-7403(98)00054-X. [Google Scholar] [CrossRef]

13. Oh, S. Y., Librescua, L., Son, O. (2005). Vibration and instability of functionally graded circular cylindrical spinning thin-walled beams. Journal of Sound & Vibration, 285(4), 1071–1091. DOI 10.1016/j.jsv.2004.09.018. [Google Scholar] [CrossRef]

14. Law, K. Y., Lov, C. T. (1995). Effects of boundary conditions on frequencies of a multi-layered cylindrical shell. Journal of Sound & Vibration, 188(3), 363–384. DOI 10.1006/jsvi.1995.0599. [Google Scholar] [CrossRef]

15. Gao, Y., Xiao, W. S., Zhu, H. (2019). Nonlinear vibration analysis of different types of functionally graded beams using nonlocal strain gradient theory and a two-step perturbation method. European Physical Journal Plus, 134(1), 1–24. DOI 10.1140/epjp/i2019-12446-0. [Google Scholar] [CrossRef]

16. Gao, Y., Xiao, W. S., Zhu, H. (2019). Nonlinear vibration of functionally graded nano-tubes using nonlocal strain gradient theory and a two-steps perturbation method. Structural Engineering & Mechanics, 69(2), 205–219. DOI 10.12989/sem.2019.69.2.205. [Google Scholar] [CrossRef]

17. Gao, Y., Xiao, W. S., Zhu, H. (2020). Snap-buckling of functionally graded multilayer graphene platelet-reinforced composite curved nanobeams with geometrical imperfections. European Journal of Mechanics-A/Solids, 82(5), 103993–103993. DOI 10.1016/j.euromechsol.2020.103993. [Google Scholar] [CrossRef]

18. Ma, W. L., Li, X. F., Kang, Y. L. (2020). Third-order shear deformation beam model for flexural waves and free vibration of pipes. The Journal of the Acoustical Society of America, 147(3), 1634–1647. DOI 10.1121/10.0000855. [Google Scholar] [CrossRef]

19. Ma, W. L., Jiang, Z. C., Lee, K. Y., Li, X. F. (2020). A refined beam theory for bending and vibration of functionally graded tube-beams. Composite Structures, 236, 111878–111878. DOI 10.1016/j.compstruct.2020.111878. [Google Scholar] [CrossRef]

20. Ma, W. L., Cheng, C., Chen, X. (2021). Free vibration of radially graded hollow cylinders subject to axial force via a higher-order shear deformation beam theory. Composite Structures, 255(42–43), 112957–112957. DOI 10.1016/j.compstruct.2020.112957. [Google Scholar] [CrossRef]

21. Bellman, R., Casti, J. (1971). Differential quadrature and long-term integration. Journal of Mathematical Analysisand Applications, 34(2), 235–238. DOI 10.1016/0022-247X(71)90110-7. [Google Scholar] [CrossRef]

22. Love, A. E. H. (1944). A treatise of the mathematical theory of elasticity. New York: Dover. [Google Scholar]

23. Zhang, J. L., Zhang, L. J., Ge, R. Y. (2019). Study on natural frequencies of transverse free vibration of functionally graded axis beams by the differential quadrature method. Acta Acustica united with Acustica, 105(6), 1095–1104. DOI 10.3813/AAA.919388. [Google Scholar] [CrossRef]

24. Vel, S. S., Batra, R. C. (2004). Three-dimensional exact solution for the vibration of functionally graded rectangar plates. Journal of Sound & Vibration, 272(3), 703–730. DOI 10.1016/S0022-460X(03)00412-7. [Google Scholar] [CrossRef]

25. Huang, Y., Li, X. F. (2010). Bending and vibration of circular cylindrical beams with arbitrary radial non-homogeneity. International Journal of Mechanical Sciences, 52(4), 595–601. DOI 10.1016/j.ijmecsci.2009.12.008. [Google Scholar] [CrossRef]

26. Sina, S. A., Navazi, H. M., Haddadpour, H. (2009). An analytical method for free vibration analysis of functionally graded beams. Materials & Design, 30(3), 741–747. DOI 10.1016/j.matdes.2008.05.015. [Google Scholar] [CrossRef]

27. Huang, Y., Wu, J. X., Yang, L. E. (2013). Higher-order theory for bending and vibration of beams with circular cross section. Mathematical Problems in Engineering, 80(1), 91–104. DOI 10.1007/s10665-013-9620-2. [Google Scholar] [CrossRef]

28. Soldatos, K. P., Hajigeoriou, V. P. (1990). Three-dimensional solution of the free vibration problem of homogeneous isotropic cylindrical shells and planes. Journal of Sound & Vibration, 137(3), 369–384. DOI 10.1016/0022-460X(90)90805-A. [Google Scholar] [CrossRef]

29. Pradhan, S. C., Loy, C. T., Lam, K. Y., Reddy, J. N. (2000). Vibration characteristics of functionally graded cylindrical shells under various boundary. Applied Acoustics, 61(1), 111–129. DOI 10.1016/S0003-682X(99)00063-8. [Google Scholar] [CrossRef]

30. Blevins Robert, D., Plunkett, R. (1980). Formulas for natural frequency and mode shape. Journal of Applied Mechanics, 47(2), 461–462. DOI 10.1115/1.3153712. [Google Scholar] [CrossRef]

31. Zhang, X. M., Liu, G. B., Law, K. Y. (2001). Vibration analysis of thin cylindrical shells using wave propagation approach. Journal of Sound & Vibration, 293(3), 397–403. DOI 10.1006/jsvi.2000.3139. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.