Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2022.016831

ARTICLE

Performance Evaluation of Electromagnetic Shield Constructed from Open-Cell Metal Foam Based on Sphere Functions

Yuya Hanaoka1,*, Taku Itoh2, Kohei Tateyama3, Susumu Nakata4 and Keiko Watanabe3

1Graduate School of Industrial Technology Nihon University, Narashino, Chiba 275-8575, Japan
2College of Industrial Technology Nihon University, Narashino, Chiba 275-8575, Japan
3College of Science and Engineering Ritsumeican University,, Kusatsu, Shiga 525-8577, Japan
4College of Information Science and Engineering Ritsumeican University, Kusatsu, Shiga 525-8577, Japan
*Corresponding Author: Yuya Hanaoka. Email: ciyu19013@g.nihon-u.ac.jp
Received: 30 March 2021; Accepted: 22 December 2021

1  Introduction

The cell structures of metal foams are divided into two main states: open and closed. Owing to their valuable characteristics (light weight and strong impact absorption), metal foams are expected in many engineering applications such as crash absorbers, train materials, and architectural structures.

This paper focuses on open-cell metal foams. Recently, open-cell metal foams have been assembled into electromagnetic shields [1]. A model of open-cell metal foams has been incorporated as the electromagnetic shield model in electromagnetic wave propagation simulations [2,3]. This model is a simple construction with rectangle holes and constant-width edges. Therefore, it lacks the characteristic structures of real open-cell states, in which the edges have concave-triangular cross-sections and are thickened around the junctions (see Fig. 1). An alternative model [4] has circular holes but does not represent the concave-triangular edges.

Figure 1: Structure of an open-cell metal foam

Another modeling method for open-cell metal foams using implicit functions has been proposed [5]. The implicit functions are appropriately arranged sphere functions. To construct the open-cell model, the sphere functions are combined using constructive solid geometry (CSG). The open-cell model represents the characteristic structures of edges and junctions in real open-cell metals (see Fig. 1). Such a model of the electromagnetic shield will likely outperform the conventional model.

The present study aims to evaluate the performance of an electromagnetic shield constructed in an open-cell model based on [5]. The open-cell-based electromagnetic shield is evaluated in electromagnetic simulations.

2  Open-Cell Structure

Open-cell metal foams are highly porous (see Fig. 1). For this reason, they are typically lightweight, which is advantageous in many applications.

As shown in Fig. 1, open-cell metal foams are assemblages of edges and vertices. Edges (generally called Plateau borders) are conjoined at vertices. The cross-section of a Plateau border is a concave triangle.

3  Modeling of Open Cell Metal Foam

To model open-cell metal foams, we employ the strategy described in [5] as a modeling method of open-cell metal foams. This strategy is briefly described below.

Each shape of the open-cell metal foam is represented by an implicit surface f(x)=0, where x=[x,y,z]T∈R3. The function f(x) has the following properties:

{f(x)<0,(inside of the surface),f(x)>0,(outside of the surface).

In the open cell model of [5], a sphere is represented as

f(x)=(x−a)2+(y−b)2+(z−c)2−r2,(1)

where (a, b, c) and r are the center and radius of the sphere, respectively. An appropriate arrangement of the spheres is shown in Fig. 2a. In this figure, the lines represent implicit surfaces satisfying fi(x)=0. The scalar fields fi(x) can be combined as

Fi+1(x)=min{fi+2(x),Fi(x)},  i=1,2,…,n (2)

where n is the number of spheres. In Fig. 2a, n = 4. Note that, F1(x)=min{f1(x), f2(x)}. Fig. 2b shows the result of applying (2) to Fig. 2a. The model now has edges and junctions. Fig. 3a is the modeling result of an open-cell metal foam [5], and Fig. 3b enlarges the Plateau borders and their junction. As revealed in the figure, the model developed in [5] reasonably replicates the actual shapes of the Plateau borders.

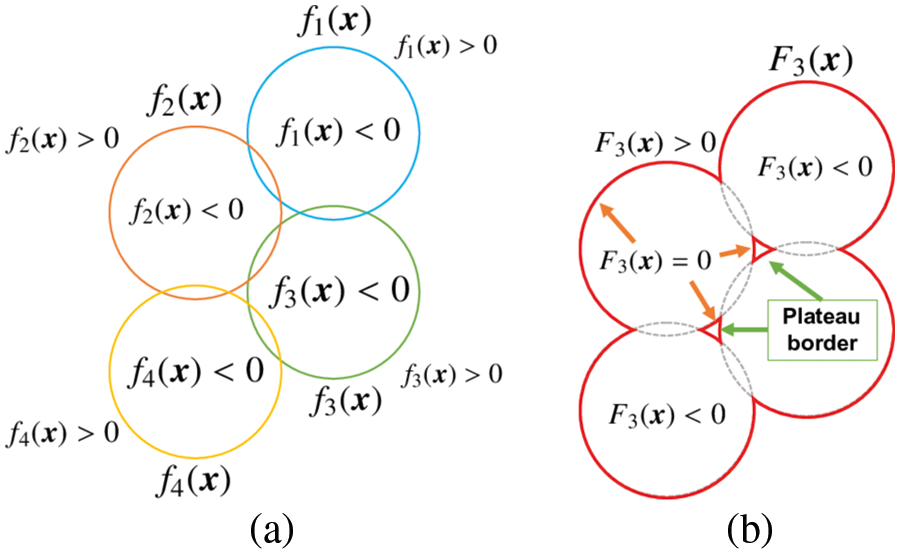
Figure 2: Schematics of (a) arranged spheres and (b) combined spheres after applying (2)

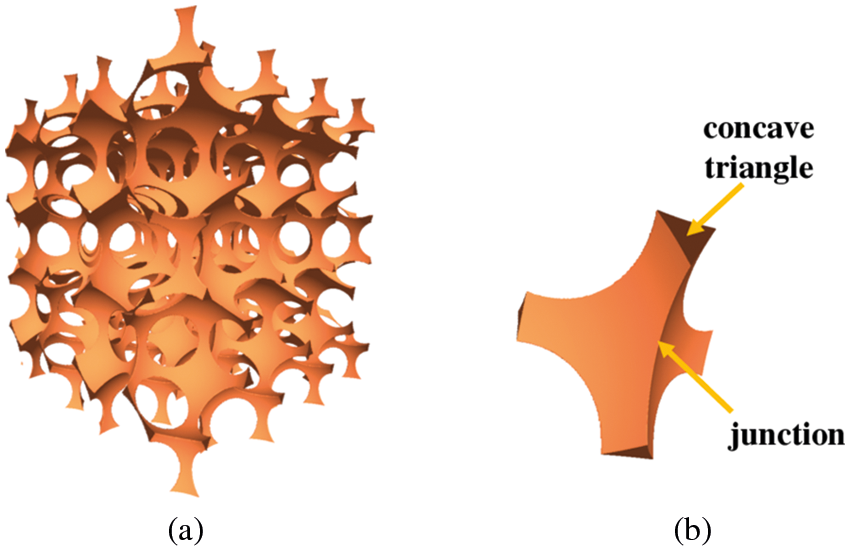
Figure 3: Result of (a) an open-cell metal foam model based on the strategy in [5] and (b) enlarged view around a junction, showing the edge cross-section. The cross-sections of the Plateau borders are shaped like concave triangles

4  Shielding Effectiveness

One application of open-cell metal foams is electromagnetic shielding. The performance of electromagnetic shielding constructed from open-cell metal foams has recently been investigated in numerical simulations [2–4].

To evaluate the shielding effectiveness, we calculate the transmission coefficients between two ports in electromagnetic simulations with and without the metal foam shield generated based on [5]. In addition, we determine the shielding effectiveness SE as follows [3,4]:

SE(dB)=S21−S^21, (3)

where S21 and S^21 denote the transmission coefficients in the absence and presence of the shield model, respectively.

5  Numerical Experiments

In numerical simulations of three-dimensional (3-D) electromagnetic wave propagation, this section investigates the performance of the open-cell metal foam model based on [5]. The model (see Fig. 4 assumes the experimental setup of [3]. Specifically, an electromagnetic shield is inserted between two oppositely-facing horn antennas. The electromagnetic wave is generated from Port 1 of the left antenna in Fig. 4, and the shield model is based on [5]. The horn antennas and shield are surrounded by air, and open boundary conditions are imposed on the system. Fig. 5 illustrates the placements of the antennas and shield in the simulation. The shield is located at 1.5λ from both antennas. The parameters β and λ in Fig. 5 denote the shield thickness and the wavelength used in the simulations, respectively. The waveguide in the horn antenna has a rectangular cross-section, and its parameters A,B,a,b,c,ρe,ρh and ρ (see Fig. 6 and references [6–8] for details) were determined at each target frequency.

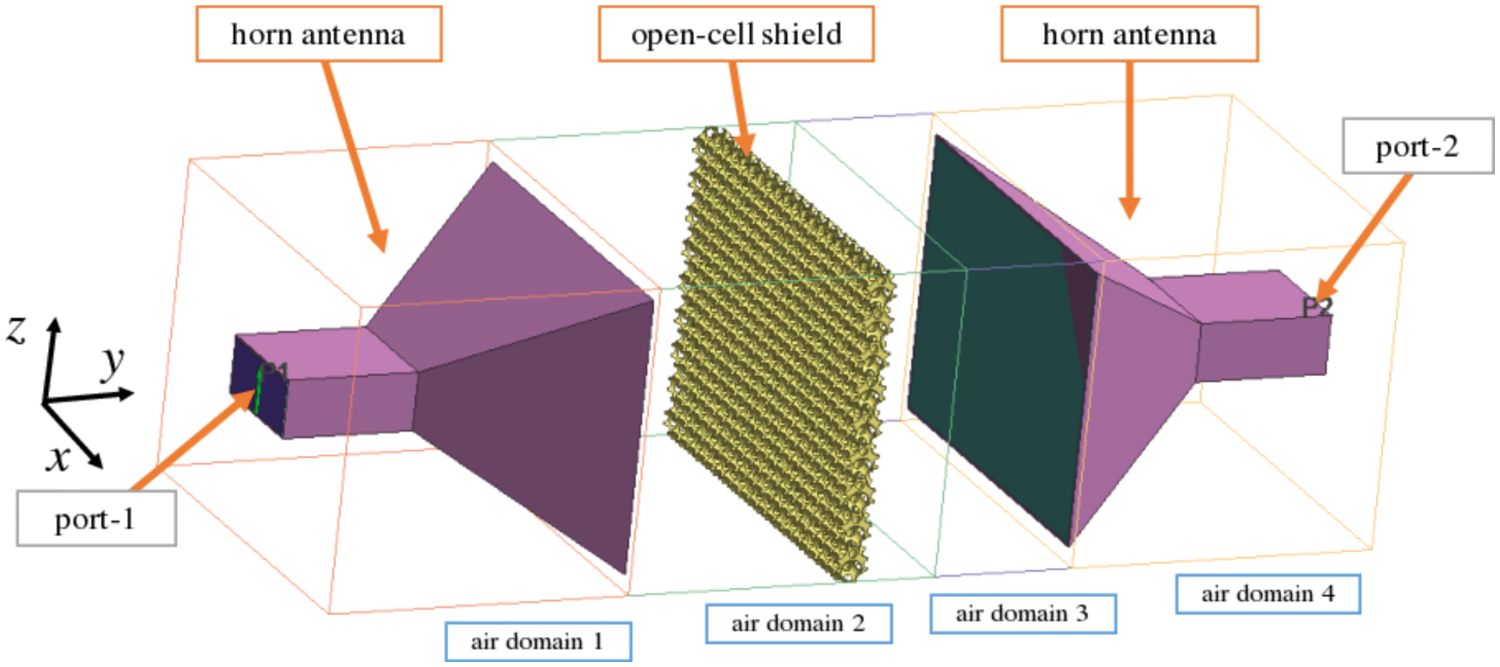
Figure 4: Simulation of electromagnetic shielding by an open-cell metal foam

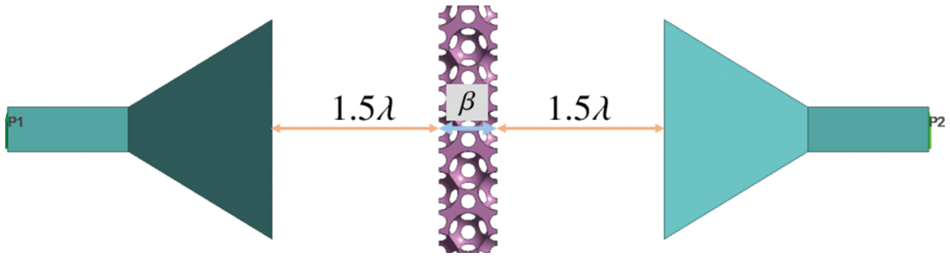
Figure 5: Position of the shield and horn antennas in the model. β and λ denote the shield thickness and the simulation wavelength, respectively

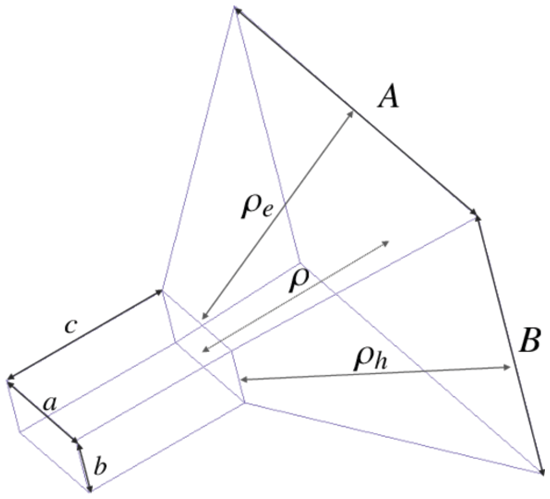
Figure 6: A horn antenna model, showing the geometric parameters

The method in [5] generates a unit model with geometric periodicity in all directions (see Fig. 7a). To construct a shield, we concatenated the unit model as shown in Fig. 7b. The size of the unit model depends on the radius r of the employed spheres. In Fig. 7b, each unit model is represented by a different color to illustrate its placement. Note that the shield is not concatenated in the y-direction; that is, β equals the length of the unit model in the y-direction.

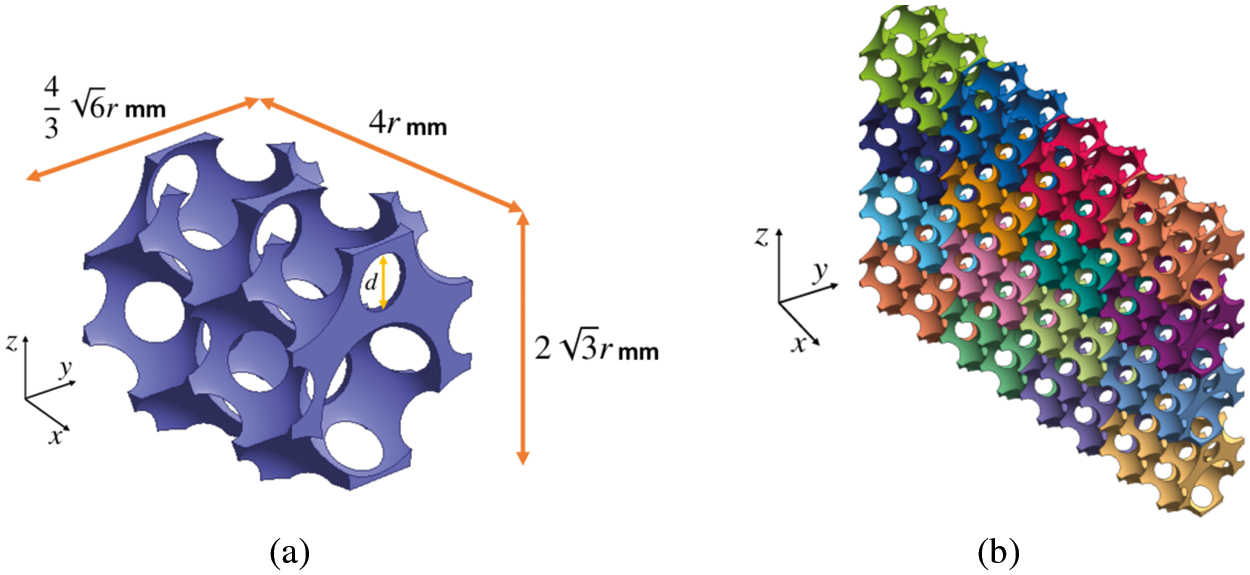
Figure 7: Examples of (a) the unit model based on [5] and (b) a shield model constructed by concatenating the unit model

In the simulations, the air region was divided into four domains (see Fig. 4). To reduce the computational cost of the simulations, the mesh fineness was varied among the domains. The initial mesh resolution of Fig. 4 is shown in Fig. 8. As clarified in this figure, the mesh was finest in air domain 2, which contains the electromagnetic shield, and coarsest in the external parts of air domains 1 and 4. Table 1 shows the initial mesh sizes of air domains 1–4 and the horn antennas. In this table, L denotes the total length in the y-direction of the analysis domain in Fig. 8. Specifically, L=2(c+ρ+1.5λ)+β. The initial mesh sizes in Table 1 were adaptively refined throughout the simulations. Additional simulation configurations are shown in Table 2.

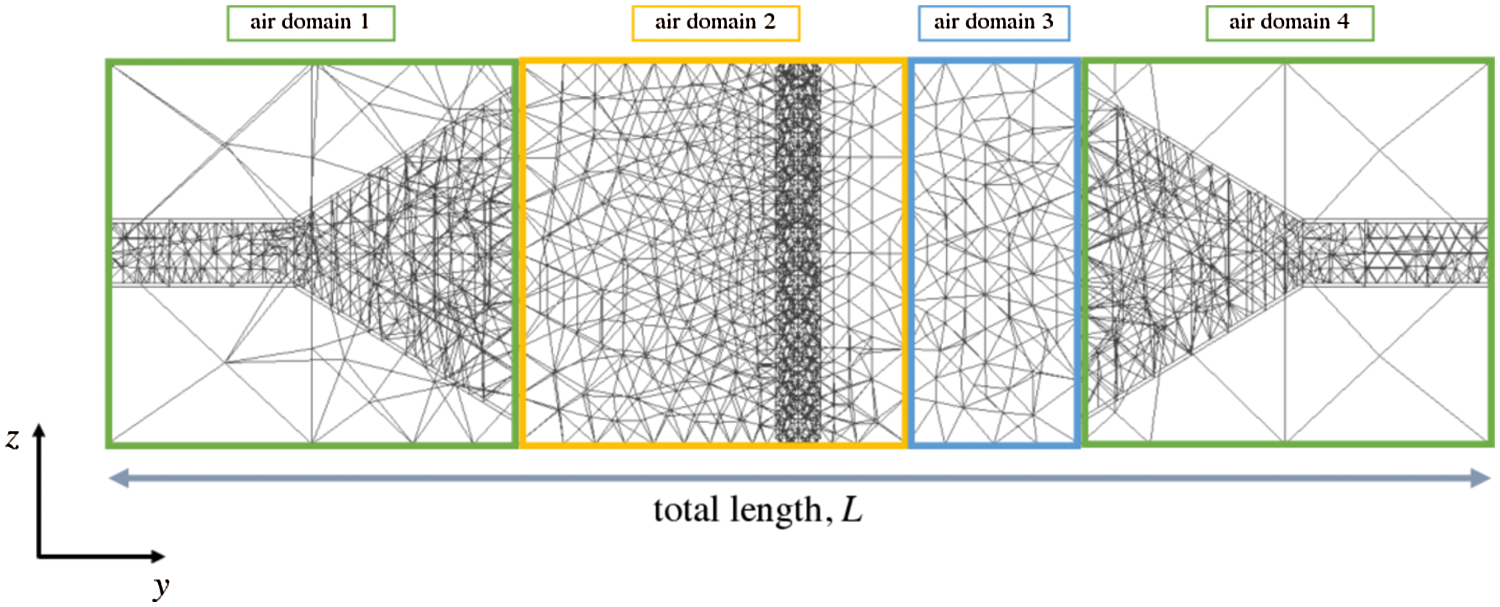
Figure 8: Initial mesh resolution of the model

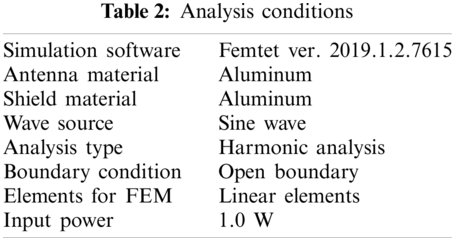
In the simulations, the foam-hole diameter d of the electromagnetic shield constructed from the unit models was varied as 2.5 and 5.0 mm. We additionally set r = 3.0 mm, α=0.25 for d = 2.5 mm, and r = 6.0 mm, α=0.50 mm for d = 5.0 mm. The simulation models were constructed in Femtet simulation software [9], which is based on the finite element method. The performance of the shield was measured in the frequency range 3–13 GHz.

The simulations results are displayed in Fig. 9. We first show the frequency dependence of SE in the 3–13 GHz range. Observe that SE was higher at lower frequencies than at higher frequencies. The maximum SE values in the shields with d = 2.5 and 5.0 mm were 93.558 and 88.354 dB, respectively (both at 3 GHz). The average SE over the 3–13 GHz range was 86.67 dB at d = 2.5 mm and 79.19 dB at d = 5.0 mm. From these results, we conclude that the shield performance can be enhanced by reducing the hole diameter of the metal foam.

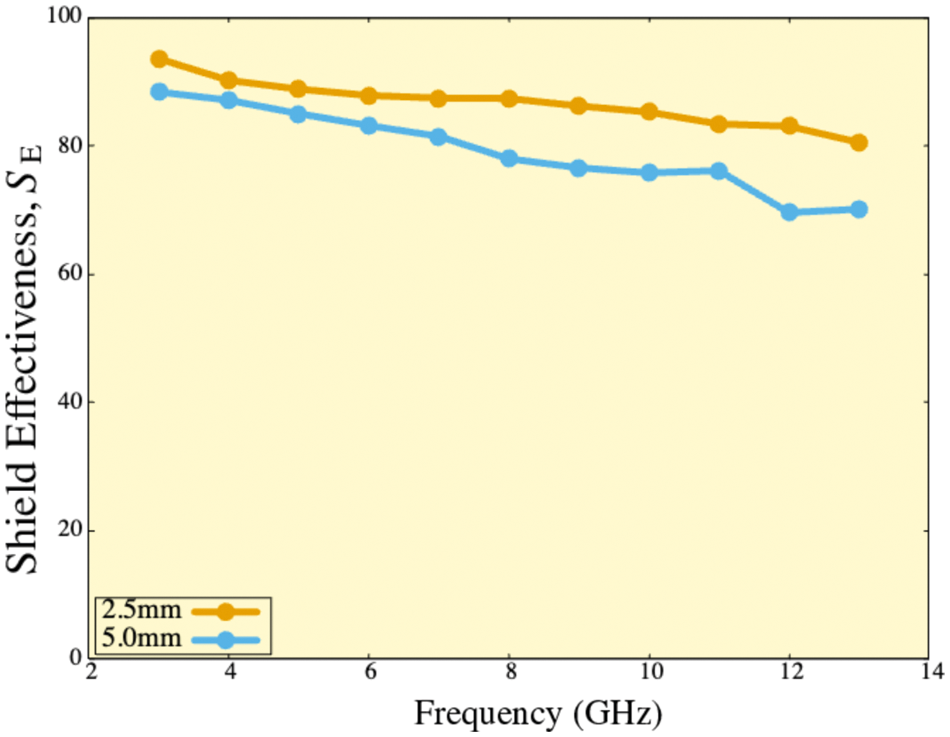
Figure 9: Frequency dependence of the shield effectiveness SE

Figs. 10 and 13 show the results at 8 and 13 GHz in the absence of the shield, respectively. In addition, Figs. 11 and 12 show the results at 8 GHz in the presence of the shields with d = 2.5 and 5.0 mm, respectively. Similarly, Figs. 14 and 15 show the results at 13 GHz in the presence of the shields with d = 2.5 and 5.0 mm, respectively. Panels (a) and (b) of Figs. 10–15 display the arrow plots of electric field E and distributions of |E|, respectively. Note that, in the simulations of Figs. 10 and 13, the total lengths L in the y-direction of the analysis domain were similarly set with those of Figs. 11 and 14, respectively. The results in Figs. 10–15 are presented on the logarithmic scale, and are observed at phase θ=60∘ in the y-z plane (in the middle of the simulation domain of Fig. 4). From Figs. 10–15, we observe that the electromagnetic waves were attenuated by the shield, affirming the effectiveness of the shield constructed by the open-cell model.

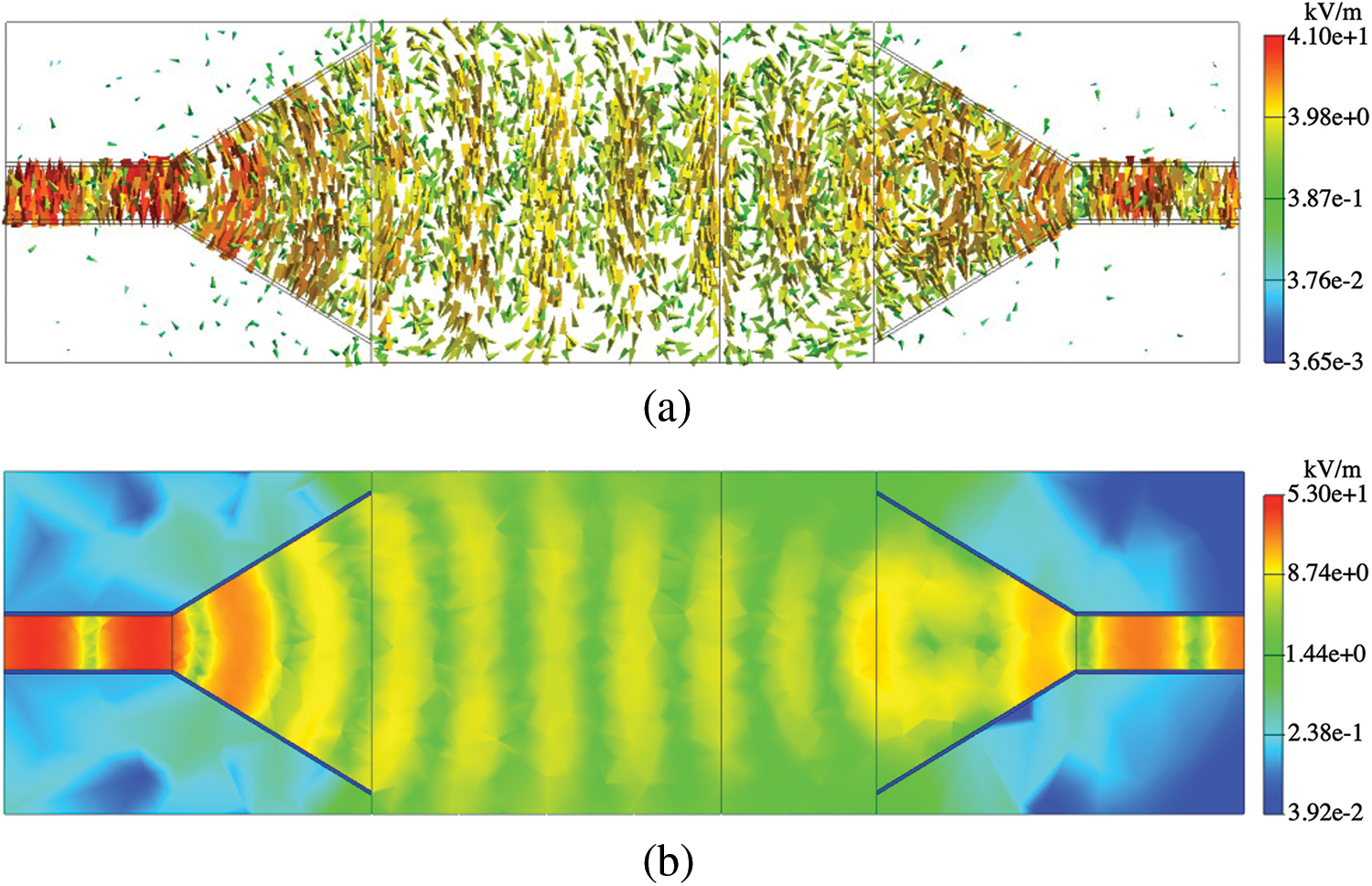
Figure 10: Results of (a) arrow plot of electric field E and (b) distribution of |E| at 8 GHz without the shield in the y-z plane

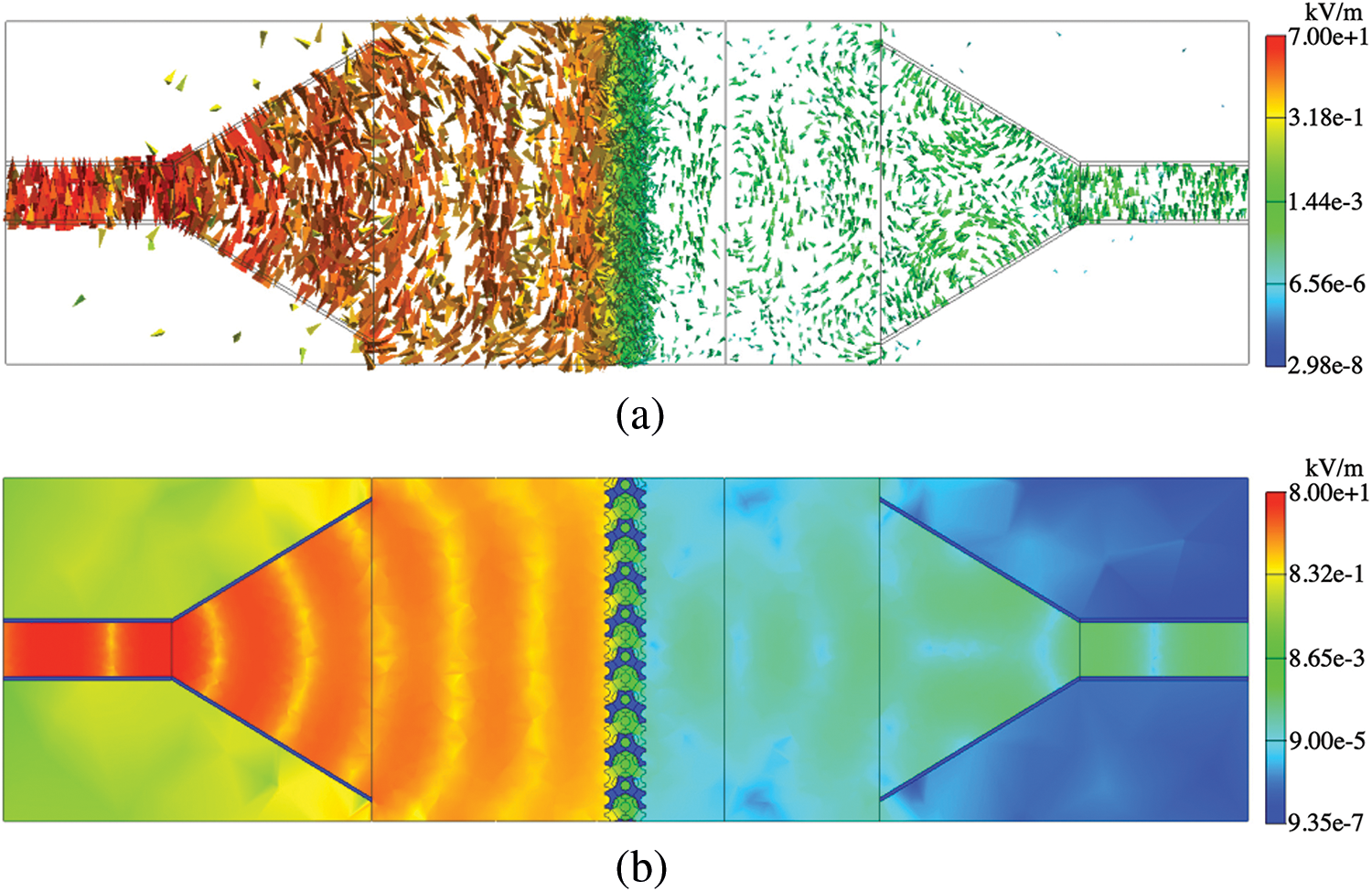
Figure 11: Results of (a) arrow plot of electric field E and (b) distribution of |E| at 8 GHz with the shield of foam diameter d = 2.5 mm in the y-z plane

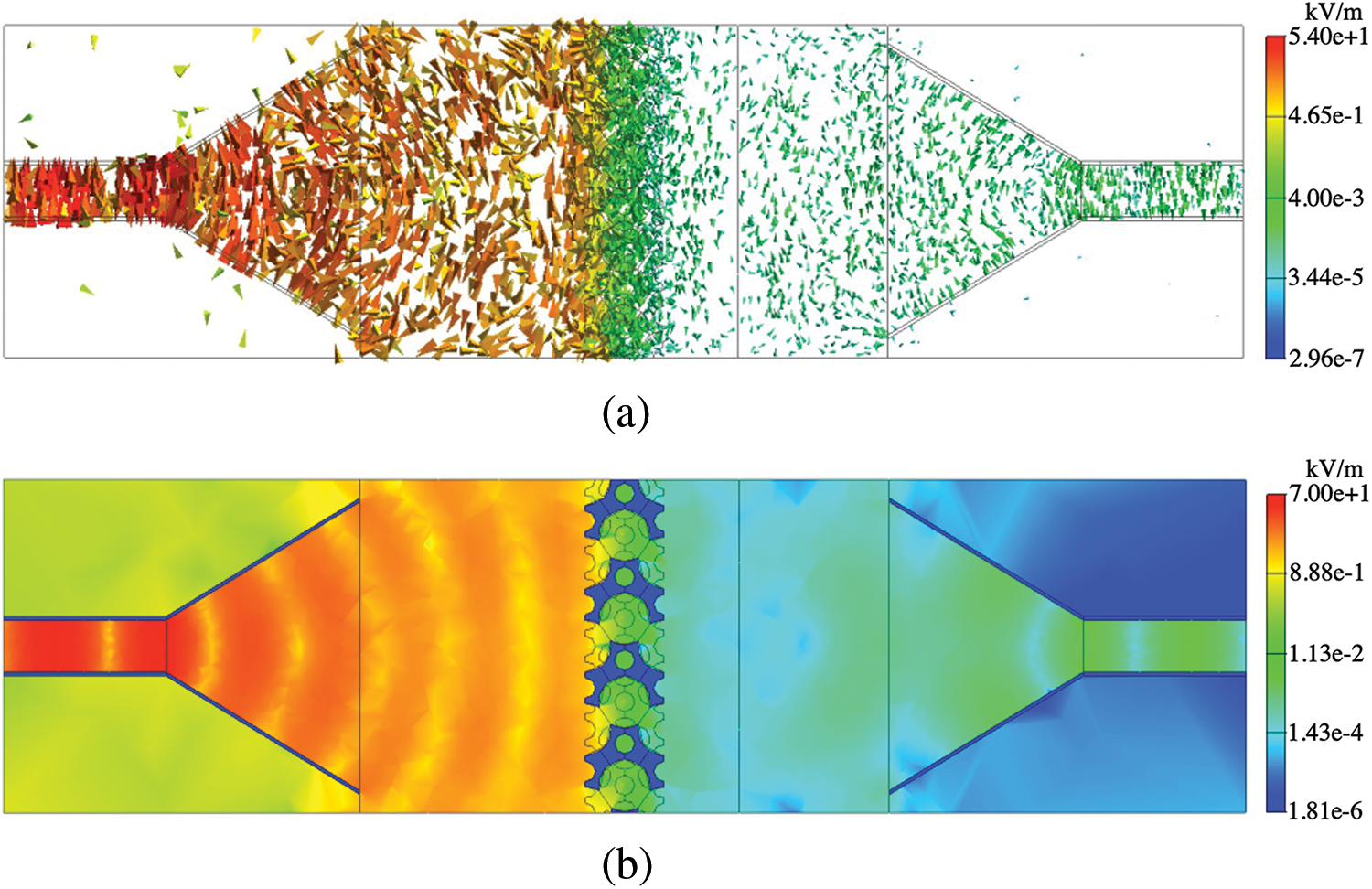
Figure 12: Results of (a) arrow plot of electric field E and (b) distribution of |E| at 8 GHz with the shield of foam diameter d = 5.0 mm in the y-z plane

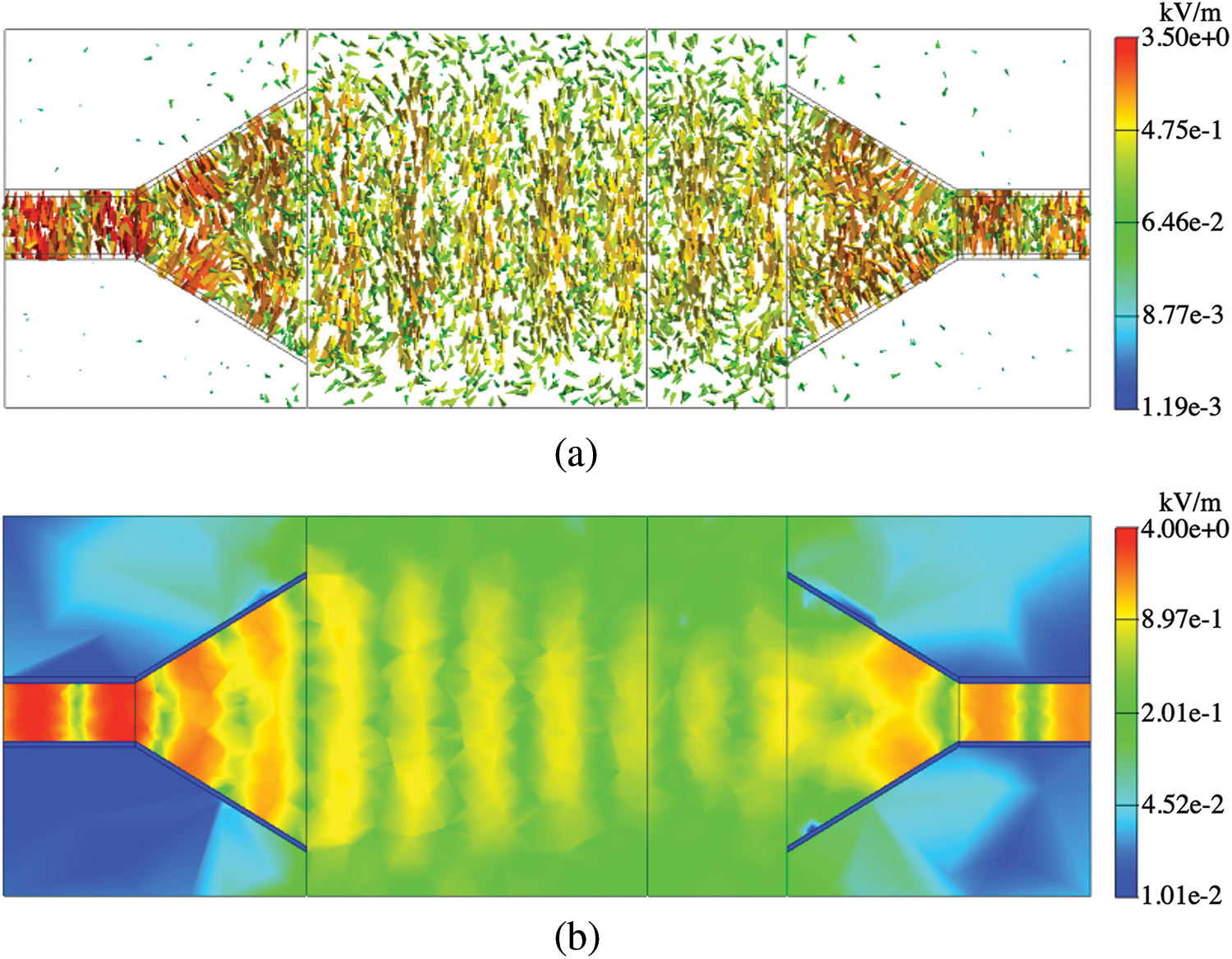
Figure 13: Results of (a) arrow plot of electric field E and (b) distribution of |E| at 13 GHz without the shield in the y-z plane

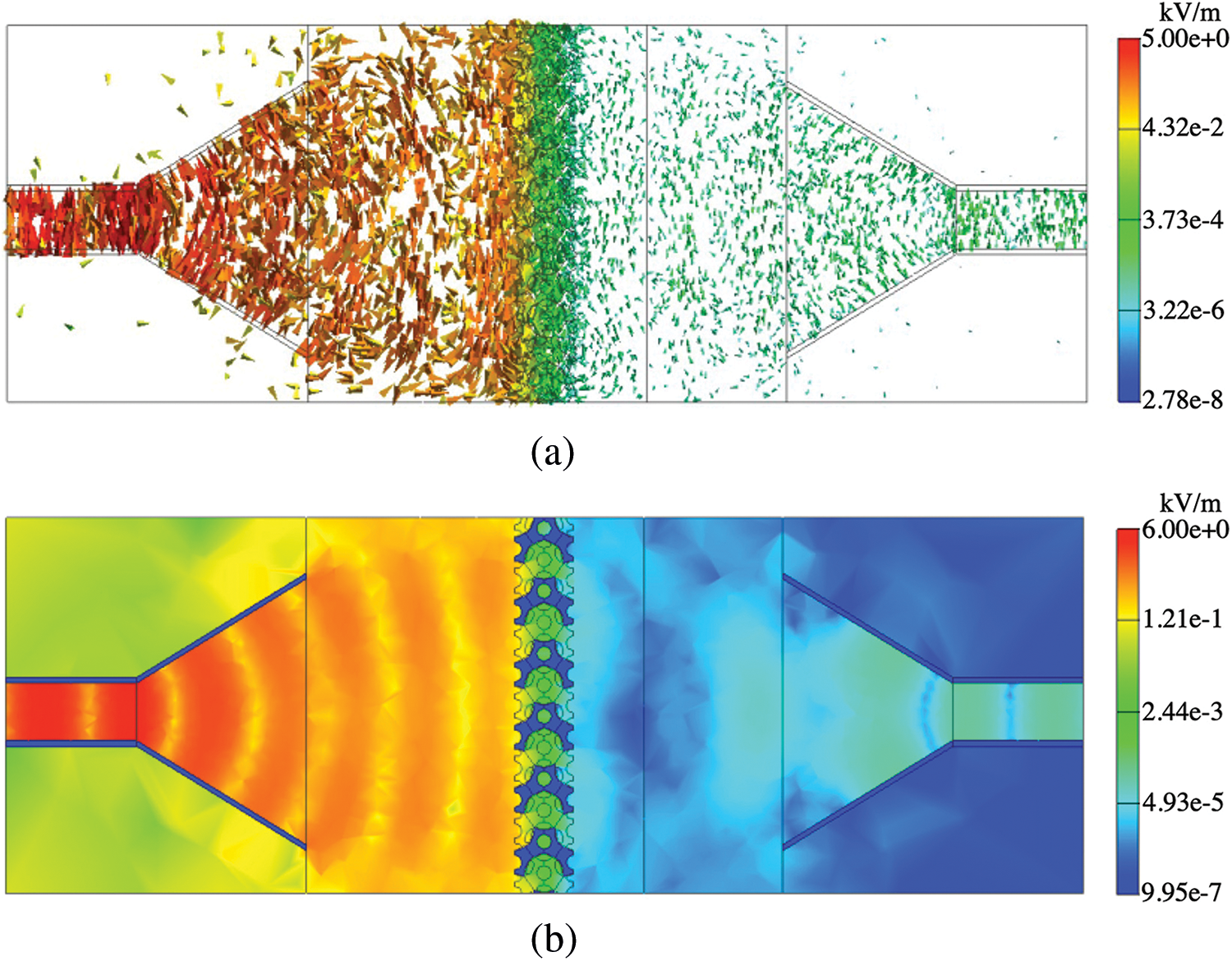
Figure 14: Results of (a) arrow plot of electric field E and (b) distribution of |E| at 13 GHz with the shield of foam diameter d = 2.5 mm in the y-z plane

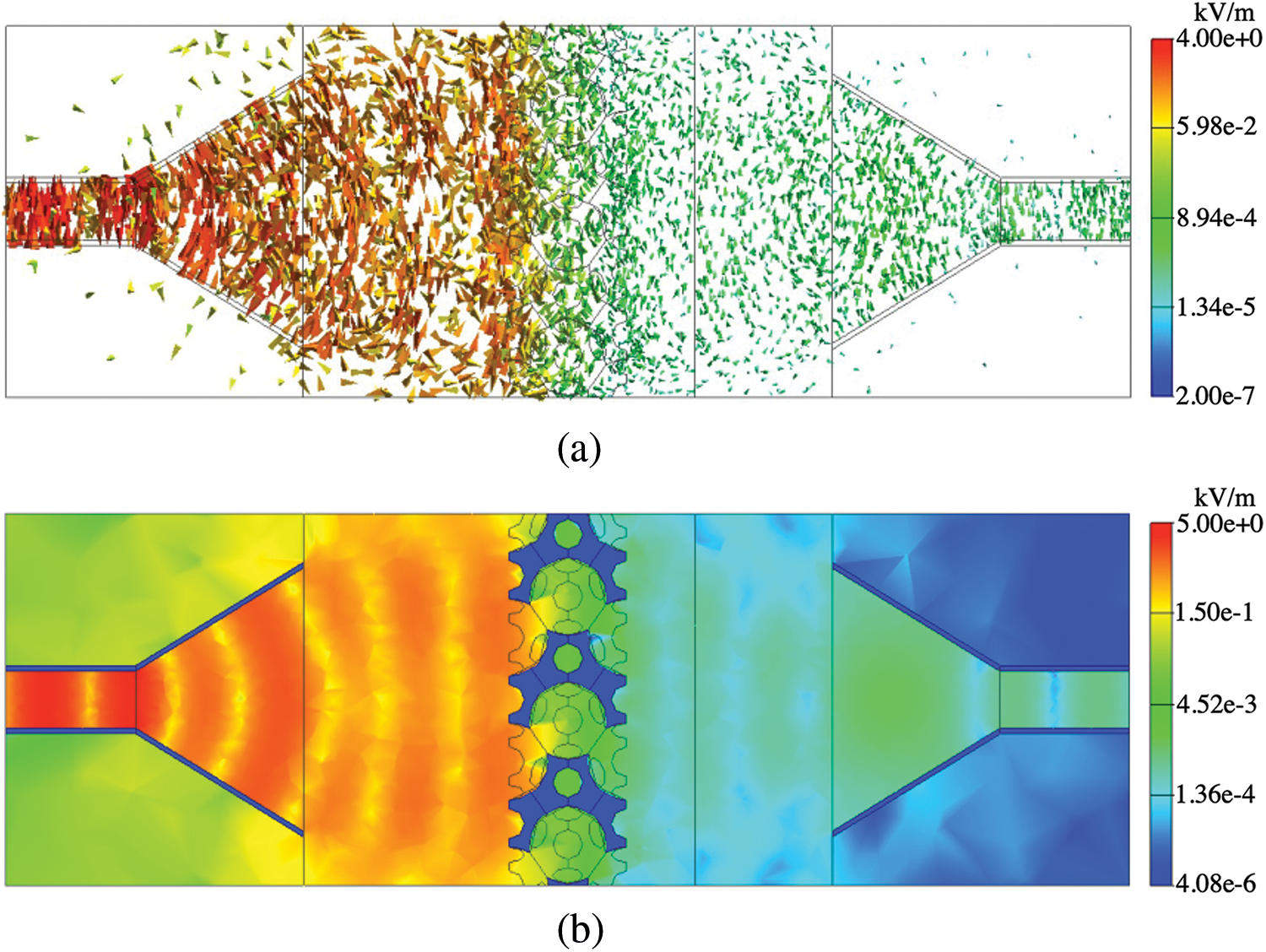
Figure 15: Results of (a) arrow plot of electric field E and (b) distribution of |E| at 13 GHz with the shield of foam diameter d = 5.0 mm in the y-z plane

6  Conclusion

To evaluate the performance of a model constructed from open-cell metal foams [5], we simulated electromagnetic wave propagations between two horn antennas separated by an electromagnetic shield constructed from the model. In the simulations, the hole diameter of the electromagnetic shield was varied as 2.5 and 5.0 mm, and the shield effectiveness was investigated over the frequency range 3–13 GHz. The main conclusions are summarized below:

1.    Shields with holes of both diameters attenuated electromagnetic waves in the 3–13 GHz range.

2.    The effectiveness of the shields with holes of both diameters was enhanced at low frequencies.

3.    The shielding effectiveness was enhanced by reducing the hole diameter of the metal foam.

Overall, we conclude that the shields generated in the open-cell metal foam model can attenuate electromagnetic waves.

In future work, the shield performance will be evaluated over a wider frequency range, and the physical behavior of the open-cell model will be investigated for different shield materials. In addition, other kinds of evaluations such as comparing between the simulation and real experimental results and a structural analysis of the open-cell metal foam model will be performed.

Funding Statement: This work was partially supported by JSPS KAKENHI Grant No. 18K11329.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Kumar, R., Jain, H., Sriam, S., Chaudhary, A., Khare, A. et al. (2020). Lightweight open cell aluminum foam for superior mechanical and electromagnetic interference shielding properties. Materials Chemistry and Physics, 240, 122274. DOI 10.1016/j.matchemphys.2019.122274. [Google Scholar] [CrossRef]

 2.  Losito, O., Barletta, D., Dimiccoli, V. (2010). A Wide-frequency model of metal foam for shielding applications. IEEE Transactions Electromagnetic Compatibility, 52(1), 75–81. DOI 10.1109/TEMC.2009.2035109. [Google Scholar] [CrossRef]

 3.  Wang, L. B., See, K. Y., Ling, Y., Koh, W. J. (2012). Study of metal foams for architectural electromagnetic shielding. Journal of Materials in Civil Engineering, 24(4), 488–493. DOI 10.1061/(ASCE)MT.1943-5533.0000403. [Google Scholar] [CrossRef]

 4.  Rodríguez, F., Meneses, M., Chiné, B. (2019). Computational analysis of metal foams for EMI shielding using Comsol Multiphysics. Comsol Conference, Cambridge. [Google Scholar]

 5.  Hanaoka, Y., Itoh, T., Nakata, S., Watanabe, K. (2020). Sphere-function-based shape modelling of open cell metal foam with plateau borders. Journal of Advanced Simulation in Science and Engineering, 7(1), 89–101. DOI 10.15748/jasse.7.89. [Google Scholar] [CrossRef]

 6.  Balanis, C. A. (2016). Antenna theory: Analysis and design, 4th edition. Hoboken: John Wiley & Sons. [Google Scholar]

 7.  Pasternack Enterprises, Inc. Standard gain horn antennas with waveguide input. https://www.pasternack.com/standard-gain-horn-antennas-with-waveguide-input-category.aspx. [Google Scholar]

 8.  Everything RF. Waveguide sizes (2022). https://www.everythingrf.com/tech-resources/waveguides-sizes. [Google Scholar]

 9.  Murata Software. Femtet (2022). https://www.muratasoftware.com/en/. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.