Interval-Valued Neutrosophic Soft Expert Set from Real Space to Complex Space

Faisal Al-Sharqi; Abd Ahmad; Ashraf Al-Quran

doi:10.32604/cmes.2022.019684

1Department of Mathematical Sciences, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, Bangi, Selangor, 43600, Malaysia
2Department of Mathematics, Faculty of Education for Pure Sciences, University of Anbar, Ramadi, 55431, Iraq
3Preparatory Year Deanship, King Faisal University, Hofuf, Al-Ahsa, 31982, Saudi Arabia
*Corresponding Author: Abd Ghafur Ahmad. Email: ghafur@ukm.edu.my
Received: 08 October 2021; Accepted: 17 December 2021

Abstract: A fuzzy system is a novel computing technique that accesses uncertain information by fuzzy representation. In the decision-making process, fuzzy system and soft computing are effective tools that are tolerant to imprecision, uncertainty, and partial truths. Evolutionary fuzzy systems have been developed with the appearance of interval fuzzy, dual fuzzy, hesitant fuzzy, neutrosophic, plithogenic representations, etc. Moreover, by capturing compound features and convey multi-dimensional data, complex numbers are utilized to generalize fuzzy and neutrosophic fuzzy sets. In this paper, a representation of neutrosophic soft expert systems based on the real and complex numbers in the interval form is proposed. The interval-valued neutrosophic soft expert set (I-VNSES) is defined, and the interval-valued complex neutrosophic soft expert set (I-VCNSES) is formally generalized from the concept of I-VNSES. For both I-VNSES and I-VCNSES, we introduce the relevant basic theoretical operations and study their properties. Based on these new concepts, a generalized algorithm is proposed and applied to handle the imbedded indeterminacy in the two-dimensional interval data. The proposed algorithm is tested on the economic factors that affected the Malaysian economy in 2020 to see which ones are the most influential. Eventually, a comparison of three current approaches is used to back up this study.

Keywords: Interval-valued neutrosophic set; complex neutrosophic set; interval-valued complex neutrosophic set; soft expert set; decision making

Fuzzy sets [1] and its extensions, such as intuitionistic fuzzy sets [2] and neutrosophic sets [3], have provided a wide range of tools that can deal with uncertainty in different types of problems. The neutrosophic set has become increasingly popular in the last two decades as a sophisticated representation of uncertain, incomplete and undetermined data. The neutrosophic set (NS) is characterized by three membership functions which represent truth, falsity, and indeterminacy, and all these three memberships take values in the non-standard interval [0−,1+]. Smarandache [4] and Wang et al. [5] introduced the single-valued neutrosophic set (SVNS) as a result of the fast growth of neutrosophic theory, and this set was later included in various decision-making methods [6–11]. The SVNS is modified from the classical neutrosophic set which membership structure is similar to the original model. Still, all of these membership functions take on values between 0 and 1. In reality, the degree of truth, falsehood, and indeterminacy of a statement might occasionally be expressed by various different interval values rather than being specified precisely in real situations. So, the idea of interval neutrosophic set (INS) was proposed by Wang et al. [12] and gave the set-theoretic operators of INS. Multi-criteria decision-making (MCDM) is one popular branch of decision-making theory and has been extensively studied in numerous researches [13–20]. Decision information is often incomplete, inconsistent, and undetermined, which further complicates the decision-making process. Therefore, the process of integrating the aforementioned uncertainty sets with the MCDM technique has attracted the attention of many researchers. This useful contribution leads to a fruitful output in the relevant research literature [21–26]. On the other hand, in some situations, we need to express some real data of two dimensions, which cannot be expressed by the models mentioned above, which heightens the need for developing several improved hybrid models that can deal effectively with this type of data. Consequently, complex numbers are utilized to generalize fuzzy sets through complex fuzzy set [27] by Ramot et al. Complex fuzzy set is characterized by a unique membership function which consists of two terms called amplitude term and phase term, where the amplitude term handles the uncertainty, and the phase term represents the periodicity. This, in turn, led to the development of many similar models. The most commonly used one which is relevant to this research is the complex neutrosophic set by Ali et al. [28]. A complex neutrosophic set is characterized by three membership functions, each of which consists of amplitude term and phase term. The amplitude terms of the truthiness, falsity and indeterminacy in a complex neutrosophic set are analogous to the membership, non-membership and indeterminate membership functions in a single-valued neutrosophic set. In contrast, the phase terms expressed the periodicity of the information. Thus, complex neutrosophic sets handle the single-valued neutrosophic data, which have the periodic manner. In many real-life applications, it is not easy to find a crisp (exact) neutrosophic membership degree (as in the single-valued neutrosophic set) since we deal with unclear and vague periodic information. To overcome this, Ali et al. proposed an interval complex neutrosophic set (ICNS) [29]. On the other hand, the theory of soft set [30] has been initiated to handle uncertainty but with the construction that differs from other constructions as in the other uncertainty sets. It is a mapping that attaches each parameter from its domain to a subset from the universal set. Since its inception, the soft set has achieved a widespread as a powerful tool that represents complex variables in a systematic way to handle uncertainty. Accordingly, it has been incorporated into other uncertainty sets to improve their efficiency. In addition, Alkhazaleh et al. introduced a more advanced form of a soft set called soft expert set [31] that can incorporate the opinions of many experts in one model, which in turn handle the subjectivity that exists in real-life situations in a more practical manner compared to soft set. Among the significant milestones in the development of soft sets and soft expert sets and their generalizations is introducing the single-valued neutrosophic soft expert set (SVNSES), which combines the advantages of both single-valued neutrosophic set and soft expert. The SVNSES is then improved to the complex neutrosophic soft expert set (CNSES) [32] and complex neutrosophic soft expert relation (CNSER) [33] to solve some complicated real-life problems which contain uncertain, indeterminate, and inconsistent data with two dimensions.

Recently, Al-Sharqi et al. [34] introduced interval-valued complex neutrosophic soft set (I-VCNSS) as a combination of interval complex neutrosophic set and soft set to deal with the problems involved periodicity information and varies with time in interval forms. This model is useful for handling these problems with two-dimensional characterization properties. To make this model more practical for improving new decision-making results, we will improve it into interval-valued complex neutrosophic soft expert sets (I-VCNSES) by extending interval-valued neutrosophic soft expert set from real space to complex space in order to incorporate the advantages of soft expert sets to the interval-valued complex neutrosophic soft sets. The novelty of I-VCNSES appears in its ability to provide a succinct, elegant, and comprehensive representation of two-dimensional neutrosophic information (information presented by the amplitude terms and information presented by the phase terms) as well as the adequate parameterization and the opinions of the experts, all in an interval form. In addition, the economic-related activities such as the effects of certain financial factors on the economy of a country where the period of time of the influence as a second variable and the opinion of many experts play a key role in the final decision. In this paper, we will solve the same types of decision-making problems that have been solved by CNSES and CNSER by using the interval-based membership structure while defining the I-VCNSES. I-VCNSES can describe more information range by virtue of the interval membership values, which more accurately express decision makers’ evaluation information and cause less information distortion.

The main contribution and motivation behind this research can be summarized below:

(1) We extend the concept of I-VNSES that is given in Section 3 to I-VCNSES to incorporate the time frame offered by phase terms, as well as the capacity to express ambiguous, indeterminate, and inconsistent data in two dimensions.

(2) We define some basic operations related to our two notions (I-VNSES and I-VCNSES), namely the complement, union, intersection, AND, and OR. In addition, prove some related properties.

(3) In terms of the application in Section 5, we propose an algorithm to solve decision-making problems in the economic field by converting our model from the complex state (I-VCNSES) to the real state (I-VNSES) and then providing in detail decision steps.

(4) In some real-life problems which the user cannot be solved by soft expert set, fuzzy soft expert set [35], intuitionistic fuzzy soft expert set [36], neutrosophic soft set expert set [37], interval-valued generalized fuzzy soft expert set [38], our first proposed interval neutrosophic soft expert set, etc. To help the user to overcome such problems, an interval-valued complex neutrosophic soft expert set has been introduced.

(5) An interval-valued complex neutrosophic soft expert set(I-VCNSES) can be viewed as follows: soft expert set (SES) ⊆ fuzzy soft expert set (FSES) ⊆ intuitionistic fuzzy soft expert set (IFSES) ⊆ interval-valued generalized fuzzy soft expert set (I-VGFSES) ⊆ neutrosophic soft expert set (NSES)⊆ interval-valued neutrosophic soft expert set(I-VNSES) ⊆ interval-valued complex neutrosophic soft expert set(I-VCNSES). So, it is more effective and useful.

(6) Finally, the main feature in our concept (I-VCNSES) is the presence of the amplitude and phase and their memberships in the form of intervals, and this gives the user more flexibility in the decision-making process.

In this section, we recapitulate the concepts of interval-valued neutrosophic set (I-VNS), complex neutrosophic sets (CNS) and interval-complex neutrosophic set (I-CNS) and give an overview of the operations structures of these concepts that are relevant to the work in this paper.

Definition 2.1. [12] Let U be a space of points (objects) with generic elements in U denoted by u. Then an I-NS AinU is characterized by three membership functions that are a truth TA(u), indeterminacy IA(u), and a falsehood FA(u), such that for each point u in U we have TA(u)=[infTA(u),supTA(u)], IA(u)=[infIA(u), sup IA(u)], FA(u)=[infFA(u), sup FA(u)]⊆[0,1] and 0−≤TA(u)+IA(u)+FA(u)≤3+ for u∈U.

Definition 2.2. [12] Let AandB two I-NSs over a universe U. Then, the fundamental operations of I-VNSs define as follows:

(1) The complement of an I-VNS A is denoted by Ac and is defined as TAc(u)=FA(u), infIAc(u)=1−supIA(u),supIAc(u)=1−infIA(u) and FAc(u)=TA(u) for any u∈U.

infTA(u)≤infTB(u),supTA(u)≤supTB(u), infIA(u)≥infIB(u),supIA(u)≥supIB(u), and infFA(u)≥infFB(u),supFA(u)≥supFB(u) for any u∈U.

(3) The union (intersection) of two INSs AandB is an I-VNS denoted as C = A∪⁡(∩)B and the three membership functions of I-VNSs defined as

Definition 2.3. [28] A complex neutrosophic set S defined on a universe of discourse U is characterized by three memberships that are a truth membership TS(u), indeterminacy membership IS(u), and a falsehood membership FS(u) that assign a complex-valued grade of membership in S to any element u∈U. By definition, all values of TS(u), IS(u) and FS(u) lie within the unit circle in the complex plane and are expressed by TS(u)=tS(u). ejμS(u), IS(u)=iS(u). ejωS(u) and FS(u)=fS(u). ejφS(u) where tS(u), iS(u),fS(u) and μS(u),ωS(u),φS(u) are both real-valued such that tS(u), iS(u),fS(u) belong to the interval [0,1] and μS(u),ωS(u),φS(u) belong to (0,2π] and j=−1.

Definition 2.4. [29] Let U be a space of points (objects) with generic elements in U denoted by u. Then an interval-valued complex neutrosophic set (in short I-VCNS) NinU is defined by three interval membership functions that are a truth interval membership function TN(u), indeterminacy interval membership function IN(u), and a falsehood interval membership function FN(u) as a follows:

where, tNL(u), iNL(u), fNL(u) denote the lower bounds, while tNU(u), tNU(u), tNU(u) denote the upper bounds. Similarly, for the phases interval-valued terms μN(u)=[μNL(u), μNU(u)], ωN(u)=[ωNL(u),ωNU(u)] and φN(u)=[φNL(u),φNU(u)].

Definition 2.5. [29] Let MandN two I-VCNSs over a universe U. Then, the fundamental operations of I-VCNSs define as follows:

Nc={(TNc(u)=tNc(u).ejμNc(u),INc(u)=iNc(u).ejωNc(u),FNc(u)=fNc(u).ejφNc(u)u;u∈U)}.

iNc(u)=(inf iNc(u),supiNc(u)) where infiNc(u)=1−supiN(u) and supiNc(u)=1−infiN(u) with

the phase term ωNc(u)=2π−ωN(u) also fNc(u)=tN(u), while the phase term φNc(u)=2π−φN(u).

(2) The union (intersection) of two I-VCNSs MandN is an I-VCNS denoted as M∪⁡(∩)N and the three membership functions of I-VCNSs defined as

TM∪⁡(∩)N(u)=[inftM∪⁡(∩)N(u),suptM∪⁡(∩)N(u)].ej2πμM∪⁡(∩)N(u)

IM∪⁡(∩)N(u)=[infiM∪⁡(∩)N(u),supiM∪⁡(∩)N(u)].ej2πωM∪⁡(∩)N(u)

FM∪⁡(∩)N(u)=[inffM∪⁡(∩)N(u),supfM∪⁡(∩)N(u)].ej2πφM∪⁡(∩)N(u)

The phase term's union (intersection) is defined in the same way as the amplitude term's union (intersection). The two symbols ∨,∧ indicate operators of max and min operators, respectively.

In this part, we introduce the idea of an interval-valued neutrosophic soft expert set(I-VNSES) as a combination of interval-neutrosophic set(I-NS) and soft expert set (SES). Throughout this paper, U is a universe, E is a parameters set, X is a set of experts and O = {1 = agree, 0 = disagree} is a set of opinions such that Z=E×X×O and A ⊆ Z.

Definition 3.1. A pair (K,A) is an I-VNSES over U, where K is mapping given by K:A→I−VN(U) such that I−VN(U) denotes the power interval-valued neutrosophic set of U.

where the three-interval truth-membership TKα(u), interval indeterminacy-membership IKα(u), and interval falsity membership FKα(u) of (K,A) are as follows:

Example 3.1. Suppose that one of the producing companies wanted to evaluate their products with the help of some experts. Let U={u1,u2,u3} be a set of products, E={e1,e2} a set of decision parameters denote the decision “easy to use” and, “quality”, respectively, and let X={p,q} be a set of experts. Based on the opinions of the experts that the company used, we get the following:

K(e1,p,1)={([0.4,0.6],[0.1,0.7],[0.3,0.5]u1),([0.2,0.4],[0.1,0.1],[0.5,0.9]u2), ([0.5,0.8],[0.2,0.6],[0.2,0.3]u3)}

K(e1,q,1)={([0.7,0.8],[0.1,0.4],[0.3,0.5]u1),([0.4,0.7],[0.2,0.5],[0.3,0.6]u2),([0.1,0.2],[0.6,0.7],[0.8,0.9]u3)}

K(e2,p,1)={([0.1,0.9],[0.2,0.4],[0.1,0.8]u1),([0.1,0.4],[0.3,0.5],[0.6,0.8]u2),([0.4,0.8],[0.1,0.2],[0.2,0.6]u3)}

K(e2,q,1)={([0.2,0.3],[0.7,0.9],[0.7,0.8]u1),([0.3,0.6],[0.5,0.8],[0.4,0.7]u2),([0.8,0.9],[0.3,0.4],[0.1,0.2]u3)}

K(e1,p,0)={([0.5,0.6],[0.8,0.9],[0.4,0.6]u1),([0.5,0.6],[0.8,0.9],[0.4,0.5]u2),([0.2,0.6],[0.1,0.5],[0.5,0.7]u3)}

K(e1,q,0)={([0.5,0.7],[0.2,0.5],[0.3,0.5]u1),([0.5,0.8],[0.3,0.7],[0.2,0.5]u2),([0.6,1],[0.1,0.3],[0,0.3]u3)}

K(e2,p,0)={([0.1,0.8],[0.3,0.4],[0.1,0.8]u1),([0.8,1],[0.2,0.3],[0,0.3]u2),([0.9,0.9],[0.1,0.3],[0.1,0.1]u3)}

K(e2,q,0)={([0.8,0.9],[0.3,0.5],[0.2,0.5]u1),([0.5,0.7],[0.2,0.7],[0.3,0.4]u2),([0.5,0.8],[0.3,0.7],[0.2,0.7]u3)}

The I-VNSES (K,A) is a parameterized family {K(αi),i=1,2,3,…} of all I-VNS of U, and denotes a collection of object approximations.

Definition 3.2. Let (K,A)and(H,B) be two I-VNSESs over U. Then (K,A) is said to be I-VNSE-subset of (H,B) iff

This relationship is indicated by (K,A)⊆(H,B). So, in this case (H,B) is called an I-VNSE-superset of (K,A).

Definition 3.3. Two I-VNSESs (K,A)and(H,B) over U, are said to be equal if (K,A) is an interval-valued neutrosophic soft expert subset of (H,B) and (H,B) is an interval-valued neutrosophic soft expert subset of (K,A) and denoted by (K,A)=(H,B).

Definition 3.4. An I-VNSES (K,A) is knowing to be a null I-VNSES and denoted by (K,A)∅ if for all u∈U the terms of the truth interval membership TK, an indeterminate interval membership IK, and falsehood interval membership FK, are given by tKL(u)=tKU(u) = 0 and iKL(u)=iKU(u)=fKL(u)=fKU(u)=1.

Definition 3.5. An I-VNSES (K,A) said to be an absolute I-VNSES denoted by (K,A)δ if for all u∈U of the truth interval membership TK, an indeterminate interval membership IK, and falsehood interval membership FK are given by tKL(u)=tKU(u) = 1 and iKL(u)=iKL(u)=fKL(u)=fKU(u)=0.

Definition 3.6. An agree I-VNSES (K,A)1 over U is an I-VNSE subset of (K,A), where the opinions of all experts agree are defined as follows:

Definition 3.7. A disagree I-VNSES (K,A)0 over U is an I-VNSE of (K,A), where the opinions of all experts disagree are defined as follows:

Now, we present some fundamental operations on I-VNSESs, namely the complement, union, and intersection of I-VNSESs, alongside deriving their properties and giving some numerical examples.

Definition 3.8. The complement of I-VNSES (K,A) is denoted by (KC,A) and is defined by (K,A) c=(Kc,A) such that:

where, infiKcα(u)=1−supiKα(u) and supiKc(e)(u)=1−infiKα(u), also, fKcα(u) = tKα(u).

K(e1,p,1)={([0.4,0.6],[0.1,0.7],[0.3,0.5]u1),([0.2,0.4],[0.1,0.1],[0.5,0.9]u2),([0.5,0.8],[0.2,0.6],[0.2,0.3]u3)}

Now, by employing the I-VN-complement, we get the complement of the part that is given by

Kc(e1,p,1)={([0.3,0.5],[0.3,0.9],[0.4,0.6]u1),([0.5,0.9],[0.9,0.9],[0.2,0.4]u2),([0.2,0.3],[0.4,0.8],[0.5,0.8]u3)}

(Kc,A)={(α=(e,x,o),[TKαc(u)],[IKαc(u)],[FKαc(u)]):u∈U,α∈A⊆E × X × O} ={α,([tLKcα(u), tUKcα(u)],[iLKcα(u),iUKcα(u)] , [fLKcα(u),fUKcα(u)]:u∈U,α∈A} ={α,([fLKα(u),fUKα(u)],[1−supiLKα(u),1−infiUKα(u)] , [tLKα(u),tUKα(u)]):u∈U,α∈A}.

((K,A)c)c={α,([fLKcα(u),fUKcα(u)],[1−supiLKcα(u)),1−infiUKcα(u))] , [tLKcα(u), tUKcα(u)]):u∈U,α∈A} ={α,([tLKα(u),tUKα(u)],[1−(1−infiLKα(u)),(1−(1−supiUKα(u))],[fLKα(u),fUKα(u)]):u∈U,α∈A} ={α,([tLKα(u),tUKα(u)],[infiLKα(u)),supiUKα(u)], [fLKα(u),fUKα(u)])u∈U,α∈A} =(K,A)

Definition 3.9. The union of two I-VNSESs (K,A) and (G,B) over U is also I-VNSES (H,C), where C=A∪⁡B and ∀c∈C,u∈U.

THc(u)={[inftKc(u),suptKc(u)]ifc∈A−B,[inftGc(u),suptGc(u)]ifc∈B−A,[inftHC(u),suptHC(u)]ifc∈A∩⁡B,

IHc(u)={[infiKc(u),supiKc(u)]ifc∈A−B,[infiGc(u),supiGc(u)]ifc∈B−A,[infiHC(u),supiHC(u)]ifc∈A∩⁡B,

FHc(u)={[inffKc(u),supfKc(u)]ifc∈A−B,[inffGc(u),supfGc(u)]ifc∈B−A,[inffHC(u),supfHC(u)]ifc∈A∩⁡B,

The union (K,A)∪⁡(G,B)=(H,C) and the two symbols ∨,∧ indicate operators of max and min operators, respectively.

Definition 3.10. The intersection of two I-VNSESs (K,A) and (G,B) over U is also I-VNSES (H,C), where C=A∩⁡B and ∀c∈C,u∈U.

THc(u)={[inftKc(u),suptKc(u)]ifc∈A−B,[inftGc(u),suptGc(u)]ifc∈B−A,[inftHC(u),suptHC(u)]ifc∈A∩⁡B,

IHc(u)={[infiKc(u),supiKc(u)]ifc∈A−B,[infiGc(u),supiGc(u)]ifc∈B−A,[infiHC(u),supiHC(u)]ifc∈A∩⁡B,

FHc(u)={[inffKc(u),supfKc(u)]ifc∈A−B,[inffGc(u),supfGc(u)]ifc∈B−A,[inffHC(u),supfHC(u)]ifc∈A∩⁡B,

inftH(c)(u)=∧(inftK(c)(u),inftG(c)(u)),suptH(c)(u)=∧(suptK(c)(u),suptG(c)(u)),

infiH(c)(u)=∨(infiK(c)(u),infiG(c)(u)),supiH(c)(u)=∨(supiK(c)(u),supiG(c)(u)),

inffH(C)(u)=∨(inffK(c)(x),inffG(c)(u)),supiH(C)(u)=∨(supfK(c)(u),supfG(c)(u)).

The intersection (K,A)∩⁡(G,B)=(H,C) and the two symbols ∨,∧ indicate operators of max and min operators, respectively.

Example 3.3. Consider Example 3.1, Let A={(e1,p,1),(e1,q,0),(e2,p,1)} and B={(e1,p,1),(e1,q,0),(e2,p,0)}. Assume that (K,A) and (G,B) are two I-VNSESs over universe U, then

(K,A)={{(e1,p,1),{(⟨[0.4,0.6],[0.1,0.7],[0.3,0.5]⟩u1),(⟨[0.2,0.4],[0.1,0.1],[0.5,0.9]⟩u2),(⟨[0.1,0.7],[0,0.3],[0.3,0.5]⟩u3)}}{(e1,q,0),{(⟨[0.5,0.7],[0.2,0.5],[0.3,0.5]⟩u1),(⟨[0.5,0.8],[0.3,0.7],[0.2,0.5]⟩u2),(⟨[0.6,1],[0.1,0.3],[0,0.3]⟩u3)}}{(e2,p,1),{(⟨[0.1,0.9],[0.2,0.4],[0.1,0.8]⟩u1),(⟨[0.1,0.4],[0.3,0.5],[0.6,0.8]⟩u2),(⟨[0.4,0.8],[0.1,0.2],[0.2,0.6]⟩u3)}}}

(G,B)={{(e1,p,1),{(⟨[0.3,0.5],[0.2,0.4],[0.4,0.7]⟩u1),(⟨[0.5,0.6],[0.1,0.3],[0.3,0.4]⟩u2),(⟨[0.6,0.8],[0.7,0.8],[0.1,0.4]⟩u3)}}{(e1,q,0),{(⟨[0.5,0.6],[0.8,0.9],[0.4,0.6]⟩u1),(⟨[0.5,0.6],[0.8,0.9],[0.4,0.5]⟩u2),(⟨[0.2,0.6],[0.1,0.5],[0.5,0.7]⟩u3)}}{(e2,p,0),{(⟨[0.1,0.8],[0.3,0.4],[0.1,0.8]⟩u1),(⟨[0.8,1],[0.2,0.3],[0,0.3]⟩u2),(⟨[0.9,0.9],[0.1,0.3],[0.1,0.1]⟩u3)}}}

(H,C)={{(e1,p,1),{(⟨[0.4,0.6],[0.1,0.4],[0.3,0.5]⟩u1),(⟨[0.5,0.6],[0.1,0.1],[0.3,0.4]⟩u2),(⟨[0.6,0.8],[0,0.3],[0.1,0.4]⟩u3)}}{(e1,q,0),{(⟨[0.5,0.7],[0.2,0.5],[0.3,0.5]⟩u1),(⟨[0.5,0.8],[0.3,0.7],[0.2,0.5]⟩u2),(⟨[0.6,1],[0.1,0.3],[0,0.3]⟩u3)}}{(e2,p,0),{(⟨[0.5,0.6],[0.8,0.9],[0.4,0.6]⟩u1),(⟨[0.8,1],[0.2,0.3],[0,0.3]⟩u2),(⟨[0.9,0.9],[0.1,0.3],[0.1,0.1]⟩u3)}}{(e2,p,1),{(⟨[0.1,0.9],[0.2,0.4],[0.1,0.8]⟩u1),(⟨[0.1,0.4],[0.3,0.5],[0.6,0.8]⟩u2),(⟨[0.4,0.8],[0.1,0.2],[0.2,0.6]⟩u3)}}}

Proposition 3.2. If (K,A), (G,B) and (H,D) be I-VNSESs over U. Then, we have the following properties:

Proof. (1) By employing Definition 3.9, we will demonstrate that (K,A)∪⁡(G,B) = (G,B)∪⁡(K,A) and we consider the case when c∈A∩⁡B; c=(e,x,o) and the other cases are trivial:

(K,A)∪⁡(G,B)={(c,⟨max{[TKc(u)],[TGc(u)]},min{[IKc(u)],[IGc(u)]},min{[FKc(u)],[FGc(u)]}⟩):u∈U}={(c,⟨max{[TGc(u)],[TKc(u)]},min{[IGc(u)],[IKc(u)]},min{[FGc(u)],[FKc(u)]}⟩):u∈U}=(G,A)∪⁡(K,B)⊟

(3) By using Definition 3.9, we want to prove that ((K,A)∪⁡(G,B))∪⁡(H,D) = (K,A)∪((G,B)∪⁡(H,D)) and we consider the case c∈A∩⁡B; c=(e,x,o) as the other cases are trivial:

(K,A)∪⁡(G,B)={(c,⟨max{[TKc(u)],[TGc(u)]},min{[IKc(u)],[IGc(u)]},min{[FKc(u)],[FGc(u)]}⟩):u∈U}

(K,A)∪⁡(G,B)∪⁡(H,D)={(c,⟨max{max{[TKc(u)],[TGc(u)]},[THc(u)]},min{min{[IKc(u)],[IGc(u)]},[IHc(u)]},(min{min{[FKc(u)],[FGc(u)]},[FHc(u)]}):u∈U}={(c,(max {[TKc(u)]},max{[TGc(u)],[THc(u)]}min {[IKc(u)]},min{[IGc(u)],[IHc(u)]}min {[FKc(u)]},min{[FGc(u),FHc(u)]}):u∈U}=(K,A)∪⁡ ((G,B)∪⁡(H,D)).

In the following, we will introduce the definitions of AND and OR operations on IV-NSESs with a proposition on these two operations.

Definition 3.11. If (K,A) and (G,B) be any two I-VNSESs over a soft universe (U,Z). Then (K,A) and (G,B) denoted by (K,A)∧(G,B) = (H,A×B) where (H,A×B) = H(α,β), such that H(α,β)=K(α)∩G(β), when (α, β)∈A×B, and ∩ represent the intersection of interval-valued neutrosophic set.

Definition 3.12. If (K,A) and (G,B) be any two IV-NSESs over a soft universe (U,Z). Then (K,A) OR (G,B) denoted by (K,A)∨(G,B) = (H,A×B) where (H,A×B) = H(α,β), such that H(α,β)=K(α)∪G(β), when (α, β)∈A×B, and ∪ represent the union of interval-valued neutrosophic set.

Proposition 3.3. If (K,A), (G,B) and (H,D) be I-VNSESs over U. Then, we have the following properties:

Proof. The proof of the above two proposition is similar to the proof of Proposition 3.2 part (3) and (4).

In this part, we establish the idea of I-VCNSES by extending I-VNSES from real space to complex space. We denote U as a universe, E is a set of parameters, X as a set of experts and O = {1 = agree, 0 = disagree} as a set of opinions, such that Z=E×X×O and A⊆Z.

Definition 4.1. A pair (K¯,A) is called an I-VCNSES over U, where K¯ is a mapping given by K¯:A→I−VCN(U), where I-VCN(U) denotes the power interval-valued complex neutrosophic set of U. Thus, the I-VCNSES (K¯,A) can be displayed as:

(K¯,A)={(α=(e,x,o),⟨[TK¯α(u)] ,[IK¯α(u)] , [FK¯α(u)]):u∈U,α∈A⊆E × X × O}=(α, ⟨[tK¯α(u).ej2πωK¯α(u)],[iK¯α(u).ej2πψK¯α(u)],[fK¯α(u).ej2πϕK¯α(u)]⟩):u∈U,α∈A⊆E × X × O.

The amplitude of interval-values terms tK¯α(u),iK¯α(u) and fK¯α(u) can be further divided as tK¯α(u)=[tLK¯α(u),tUK¯α(u)],iK¯α(u)=[iLK¯α(u),iUK¯α(u)] and fK¯α(u)=[fLK¯α(u),fUK¯α(u)],

where, tLK¯α(u),iLK¯α(u),fLK¯α(u) represent the lower bound, while tUK¯α(u),iUK¯α(u),fUK¯α(u) symbolize the upper bound in each interval value respectively. Also, for the phases of interval-values terms: ωK¯α(u)=[ωLK¯α(u),ωUK¯α(u)],ψK¯α(u)=[ψLK¯α(u),ψUK¯α(u)],ϕK¯α(u)=[ϕLK¯α(u),ϕUK¯α(u)].

Example 4.1. Suppose that an electrical appliance sales company develops two types of its products and wants to ask some experts on these products by taking into account the degree of quality and ease of use represented amplitude terms and phase terms, respectively. Suppose U={u1,u2} is a set of electrical appliances, E={e1,e2} is a set of parameters denoting “quality”, “ease of use” respectively and let X={p,q} is a set of experts. In order to obtain the opinion of the two experts, the company distributed a questionnaire to the two experts to make decisions about these two new products, I-VCNSES (K¯,A) will be defined as follows: U={u1,u2}, A={easy to use; quality}={e1,e2}⊆E, and

(K¯,A)={{(e1,p,1),{(⟨[0.4,0.6].ej2π[0.5,0.6],[0.1,0.7].ej2π[0.1,0.3],[0.3,0.5].ej2π[0.8,0.9]⟩u1),(⟨[0.1,0.3].ej2π[0.1,0.3],[0.31,0.7].ej2π[0.6,0.8],[0.4,0.61].ej2π[0.2,0.58]⟩u2)}}{{(e2,p,1),{(⟨[0.2,0.7].ej2π[0.7,0.8],[0.4,0.9].ej2π[0.3,0.5],[0.6,0.8].ej2π[0.5,0.6]⟩u1),(⟨[0.15,0.52].ej2π[0.1,0.3],[0,0.5].ej2π[0.6,0.8],[0.3,0.3].ej2π[0.6,0.7]⟩u2)}}{{(e2,q,1),{(⟨[0.3,0.5].ej2π[0.5,0.6],[0.3,0.9].ej2π[0.1,0.3],[0.4,0.6].ej2π[0.8,0.9]⟩u1),(⟨[0.5,0.9].ej2π[0.3,0.6],[0.9,0.9].ej2π[0.7,0.9],[0.2,0.4].ej2π[0.2,0.5]⟩u2)}}{{(e1,p,0),{(⟨[0.2,0.6].ej2π[0.7,0.8],[0.3,0.4].ej2π[0.6,0.7],[0.3,0.4].ej2π[0.6,0.8]⟩u1),(⟨[0.1,0.3].ej2π[0.2,0.5],[0.3,0.4].ej2π[0.3,0.6],[0.7,0.8].ej2π[0.6,0.9]⟩u2)}}{{ (e1,q,0),{(⟨[0.3,0.8].ej2π[0.3,0.8],[0.2,0.2].ej2π[0.4,0.7],[0.2,0.5].ej2π[0.6,0.8]⟩u1),(⟨[0.4,0.6].ej2π[0.9,1],[0,0.3].ej2π[0.7,0.8],[0,0.4].ej2π[0.4,0.6]⟩u2)}}{{(e2,p,0),{(⟨[0.1,0.6].ej2π[0.3,0.6],[0.4,0.8].ej2π[0.3,0.3],[0.4,0.6].ej2π[0,0.5]⟩u1),(⟨[0.3,0.6].ej2π[0.3,0.6],[0.2,0.6].ej2π[0.5,0.8],[0.5,0.8].ej2π[0.3,0.7]⟩u2)}}{{(e2,q,0),{(⟨[0.5,0.8].ej2π[0.3,0.7],[0.3,0.5].ej2π[0.4,0.7],[0.3,0.6].ej2π[0.1,0.7]⟩u1),(⟨[0.4,0.6].ej2π[0.2,0.6],[0.3,0.4].ej2π[0.5,0.7],[0.4,0.8].ej2π[0.3,0.6]⟩u2)}}}

In the I-VCNSES (K¯,A), the interval amplitude terms and the interval phase terms are between 0 and 1, with an amplitude term near to 0 (1) indicating that the electrical device's quality is low (high) and easy (difficult), and a phase term close to 0 (1) indicating that the device's expire time is short (long).

Based on the Definition 4.1, we introduce two concepts which are the subset and equality of I-VCNSESs.

Definition 4.2. Let (K¯,A)and (H¯,B) be two I-VCNSESs over U. Then (K¯,A) is said to be I-VCNSE-subset of (H¯,B) iff

fUK¯α(u)≥fUH¯β(u) for the amplitude terms and ωLK¯α(u)≤ωLH¯β(u), ψLK¯α(u)≥ψLH¯β(u),ϕLK¯α(u)≥ϕLH¯β(u) and ωUK¯α(u)≤ωUH¯β(u), ψUK¯α(u)≥ψUH¯β(u),ϕUK¯α(u)≥ϕUH¯β(u) for the phase terms for all u∈U.

This relationship is denoted by (K¯,A)⊆(H¯,B) so in this case (H¯,B) is called an I-VCNSE-superset of (K¯,A).

Definition 4.3. Two I-VCNSESs (K¯,A)and (H¯,B) over U are said to be equal if (K¯,A) is an I-VCNSE-subset of (H¯,B) and (H¯,B) is an I-VCNSE-subset of (K¯,A) and denoted by (K¯,A)= (H¯,B).

Definition 4.4. An I-VCNSES (K¯,A) is known to be a null I-VCNSES and denoted by (K¯,A)∅ if for all u∈U and α∈A, then the amplitude and phase terms of the of the three interval membership functions TK¯α(u), IK¯α(u), FK¯α(u) are given by ([0, 0], [1, 1], [1, 1]), respectively.

Definition 4.5. An I-VCNSES (K¯,A) is known to be an absolute I-VCNSES and denoted by (K¯,A)δ if for all u∈U and α∈A, then the amplitude and phase terms of the three interval membership functions TK¯α(u), IK¯α(u), FK¯α(u) are given by ([1, 1], [0, 0], [0, 0]), respectively.

Definition 4.6. An agree I-VCNSES ( K¯,A)1 over U is an I-VCNSE-subset of (K¯,A), where the opinions of all experts agree are written as follows:

Definition 4.7. A disagree I-VCNSES ( K¯,A)0 over U is an I-VCNSE-subset of (K¯,A), where the where the opinions of all experts agree are written as follows:

Next, we provide some fundamental operations on I-VCNSESs, like the complement, union, and intersection of I-VCNSESs, derive essential properties and pertinent laws to this concept as De Morgan's laws, and give some illustrative numerical examples.

Definition 4.8. The complement of an I-VCNSES (K¯,A) is denoted by (K¯C,A) and is defined by (K¯,A) c=(K¯c,A) such that

(K¯,A) c=(K¯c,A)={α=(e,x,o),〈 TK¯αC(u) ,IK¯αC(x) , FK¯αC(x) 〉:u∈U,α∈A⊆E × X × O}={α,〈 tK¯αC(u).ej2πωK¯αC(u) ,iK¯αC(u).ej2πψK¯αC(u),fK¯αC(u).ej2πϕK¯αC(u) 〉:u∈U,α∈A⊆E × X × O}.

where, inf iK¯αC(u)=1−sup iK¯α(u) and supiK¯αC(u)=1− infiK¯α(u) with the phase term ψK¯αC(u)=2π−ψK¯α(u) also fK¯αC(u)=tK¯α(u), while the phase term ϕK¯αC(u)=2π−ϕK¯α(u).

K¯(e1,p,1)={(⟨[0.4,0.6].ej2π[0.5,0.6],[0.1,0.7].ej2π[0.1,0.3],[0.3,0.5].ej2π[0.8,0.9]⟩u1),(⟨[0.2,0.4].ej2π[0.3,0.6],[0.1,0.1].ej2π[0.7,0.9],[0.5,0.9].ej2π[0.2,0.5]⟩u2)}

K¯c(e1,p,1)={(⟨[0.3,0.5].ej2π[0.8,0.9],[0.3,0.9].ej2π[0.7,0.9],[0.4,0.6].ej2π[0.5,0.6]⟩u1),(⟨[0.5,0.9].ej2π[0.2,0.5],[0.9,0.9].ej2π[0.1,0.3],[0.2,0.4].ej2π[0.3,0.6]⟩u2)}

(K¯,A)={(α=(e,x,o),⟨[TK¯α(u)] ,[IK¯α(u)] , [FK¯α(u)]⟩):u∈U,α∈A⊆E × X × O}

(K¯,A) c=(K¯c,A)={(α=(e,x,o),⟨[TK¯αc(u)] , [IK¯αc(u)], [FK¯αc(u)]⟩):u∈U,α∈A⊆E × X × O}={(α,⟨ [tK¯αc(u).ej2πωK¯αc(u)] , [iK¯αc(u).ej2πψK¯αc(u)], [fK¯αc(u).ej2πϕK¯αc(u)]⟩):u∈U,α∈A⊆E × X × O}={(α,⟨[fK¯α(u).ej2π(2π−ωK¯α(u))],[(1−sup iK¯α(u),1− infK¯α(u)).ej2π(2π−ψK¯¯α(u))],[ tK¯α(u).ej2π(2π−ϕK¯α(u))]⟩):u∈U,α∈A⊆E × X × O}.

((K¯,A)c)c={(α,⟨[fK¯αC(u).ej2π(2π−ωK¯αC(u))],[(1−supiK¯αc(u),1−infiK¯αc(u)).ej2π(2π−ψK¯αC(u))],[tK¯αC(u).ej2π(2π−ωK¯αC(u))]⟩):u∈U,α∈A⊆E×X×O}={(α,⟨[tK¯α(u).ej2π(2π−(2π−ωK¯α(u)))],[(1−(1−infiK¯α(u)),1−(1−supiK¯α(u))).ej2π(2π−(2π−ψKÌ¿α(u)))],[fK¯α(u).ej2π(2π−(2π−ωK¯α(u)))]⟩):u∈U,α∈A⊆E×X×O}={(α,⟨[tK¯α(u).ej2πωK¯α(u)],[iK¯α(u).ej2πψKÌ¿(α)(u)],[fK¯α(u).ej2πωK¯α(u)]⟩):u∈U,α∈A⊆E×X×O}=(K¯,A).

Definition 4.9. The union of two I-VCNSESs (K¯,A) and (G¯,B) over U is also I-VCNSES (H¯,C), where C=A∪⁡B and ∀c,u ∈ C ,U, respectively.

TH¯c(u)={[inftKc(u),suptKc(u)].ej2πωK¯c(u) if c∈A−B,[inftGc(u),suptGc(u)].ej2πωG¯c(u) if c∈B−A,[inftHc(u),suptHc(u)].ej2πωH¯c(u) if c∈A∩⁡B,

IH¯c(u)={[infiKc(u),supiKc(u)].ej2πψK¯c(u) if c∈A−B,[infiGc(u),supiGc(u)].ej2πψG¯c(u) if c∈B−A,[infiHc(u),supiHc(u)].ej2πψH¯c(u) if c∈A∩⁡B,

FH¯c(u)={[inffKc(u),supfKc(u)].ej2πΦK¯c(u) if c∈A−B,[inffGc(u),supfGc(u)].ej2πψG¯c(u) if c∈B−A,[inffHc(u),supfHc(u)].ej2πΦH¯c(u) if c∈A∩⁡B,

inftH¯c(u)=∨(inftK¯c(u),inftG¯c(u)),suptH¯c(u)=∨(suptK¯c(u),suptG¯c(u)),

infiH¯c(u)=∧(infiK¯c(u),infiG¯c(u)),supiH¯c(u)=∧(supiK¯c(u),supiG¯c(u)),

inffH¯c(u)=∧(inffK¯c(u),inffG¯c(u)),supfH¯c(u)=∧(supfK¯c(u),supfG¯c(u)),

The phase term's union is defined in the same way as the amplitude term's union (K¯,A)∪(G¯,B)=(H¯,A) and the two symbols ∨,∧ indicate operators of max and min operators, respectively.

Definition 4.10. The intersection of two I-VCNSESs (K¯,A) and (G¯,B) over U is also I-VCNSES (H¯,C), where C=A∩⁡B and ∀c,u ∈ C ,U, respectively.

TH¯c(u)={[inftKc(u),suptKc(u)].ej2πωK¯c(u) if c∈A−B,[inftGc(u),suptGc(u)].ej2πωG¯c(u) if c∈B−A,[inftHc(u),suptHc(u)].ej2πωH¯c(u) if c∈A∩⁡B,

IH¯c(u)={[infiKc(u),supiKc(u)].ej2πψK¯c(u) if c∈A−B,[infiGc(u),supiGc(u)].ej2πψG¯c(u) if c∈B−A,[infiHc(u),supiHc(u)].ej2πψH¯c(u) if c∈A∩⁡B,

FH¯c(u)={[inffKc(u),supfKc(u)].ej2πΦK¯c(u) if c∈A−B,[inffGc(u),supfGc(u)].ej2πψG¯c(u) if c∈B−A,[inffHc(u),supfHc(u)].ej2πΦH¯c(u) if c∈A∩⁡B,

inftH¯c(u)=∧(inftK¯c(u),inftG¯c(u)),suptH¯c(u)=∧(suptK¯c(u),suptG¯c(u)),

infiH¯c(u)=∨(infiK¯c(u),infiG¯c(u)),supiH¯c(u)=∨(supiK¯c(u),supiG¯c(u)),

inffH¯c(u)=∨(inffK¯c(u),inffG¯c(u)),supfH¯c(u)=∨(supfK¯c(u),supfG¯c(u)),

The phase term's intersection is defined in the same way as the amplitude term's intersection (K¯,A)∩(G¯,B)=(H¯,A) and the two symbols ∨,∧ indicate operators of max and min operators, respectively.

Proposition 4.2. If (K¯,A) and (G¯,B) are two I-VCNSESs over U, then the following properties are obtained as a result:

Proof. (1) Suppose that (K¯,A)∪⁡(G¯,B) = (H¯,D), where D=A∪⁡B and ∀α∈D, then by definition 4.9, we get

TH¯α(u)={[inftK¯α(u),suptK¯α(u)].ej2πωK¯α(u) if α∈A−B,[inftG¯α(u),suptG¯α(u)].ej2πωG¯α(u) if α∈B−A,[inftH¯α(u),suptH¯α(u)].ej2πωH¯α(u) if α∈A∩⁡B,

Since (K¯,A)∪⁡(G¯,B) = (H¯,D), then we have ((K¯,A)∪(G¯,B))c=(H¯,D)c = (H¯c,D), ∀α∈D.

TH¯cα(u)={[inffK¯α(u),supfK¯α(u)].ej2π(2π−ωK¯α(u)) if α∈A−B,[inffG¯α(u),supfG¯α(u)].ej2π(2π−ωK¯α(u)) if α∈B−A,[inffH¯α(u),supfH¯α(u)].ej2π(2π−ωH¯α(u)) ifα∈A∩⁡B,

We have, (K¯,A)c = (K¯c,A) and (G¯,B)c = (G¯c,B), then, (K¯,A)c∩(G¯,B)c=(K¯c,A)∩⁡(G¯c,B).

TM¯α(u)={[inftK¯αc(u),suptK¯αc(u)].ej2πωK¯αc(u) if α∈A−B,[inftG¯αc(u),suptG¯αc(u)].ej2πωG¯αc(u) if α∈B−A,[inftM¯αc(u),suptM¯αc(u)].ej2πωM¯αc(u) if α∈A∩⁡B,={[inffK¯α(u),supfK¯α(u)].ej2π(2π−ωK¯α(u)) if α∈A−B,[inffG¯α(u),supfG¯α(u)].ej2π(2π−ωK¯α(u)) if α∈B−A,[inffH¯α(u),supfH¯α(u)].ej2π(2π−ωH¯α(u)) ifα∈A∩⁡B,

Therefore, H¯c and M¯ are the same operators and D=C, which implies T(K¯α∪⁡G¯α)c(u) = T(K¯αc∩⁡G¯αc)(u)∀u∈U.

In the same method, we can get the rest terms. Thus, it follows that ((K¯,A)∪(G¯,B))c = (K¯,A)c∩⁡(G¯,B)c and this completes the proof.

Proposition 4.3. If (K¯,A), (G¯,B) and (H¯,D) be I-VCNSESs over U. Then, we have the following properties:

Proof. The proof of the above four propositions is similar to the proof of proposition 3.2 depending on definitions 4.9, 4.10.

In the following, we will introduce the definitions of AND and OR operations on I-VCNSESs with a proposition on these two operations.

Definition 4.11. If (K¯,A) and (G¯,B) be any two I-VCNSESs over a soft universe (U,Z). Then (K¯,A) AND (G¯,B) denoted by (K¯,A)∧~(G¯,B) = (H¯,A×B), where (H¯,A×B) = H¯(α,β), such that H¯(α,β)=K¯(α)∩G¯(β), when (α, β) ∈ A×B, and ∩ represent the intersection of interval-valued complex neutrosophic set.

Definition 4.12. If (K¯,A) and (G¯,B) be any two I-VCNSESs over a soft universe (U,Z). Then (K¯,A) OR (G¯,B) denoted by (K¯,A)∨~(G¯,B) = (H¯,A×B), where (H¯,A×B) = H¯(a,b), such that H¯(a,b)=K¯(a)∪G¯(a), when (a, b) ∈ A×B, and ∪ represent the union of interval-valued complex neutrosophic set.

Proposition 4.4. If (K¯,A), (G¯,B) and (H¯,D) be I-VCNSESs over U. Then, we have the following properties:

Proof. The proof of the above two proposition is similar to the proof of proposition 4.3 part 3 and 4.

In this part, we will highlight the importance of our model in real life by solving one of the decision-making problems in the economic field.

Example 5.1. In this example, assume that we are interested in knowing the extent to which the Malaysian economy in 2020 is affected by the four economic factors. The four factors are as follows, the plunge in oil prices and commodities commercial, the slowdown in china's economy, the tax (GST) on services and goods that applied this year, and exchange rate variability in this year. Our problem is to order these four destinations in descending order from a maximum influencing the Malaysian economy to a minimum affecting the Malaysian economy in 2020. So let U={u1,u2,u3,u4}, where u1= plunge in oil prices and commodities commercial, u2= slowdown in China's economy, u3= tax (GST) on services and goods, u4= exchange rate variability in this year. And E={e1,e2,e3} be the set of the parameters that represents the main sectors of the Malaysian economy, where e1= industry sector, e2=external trade sector, e3=touris msector. We also assume the set X={p,q} be a set of economic experts which are assigned to analyze those four factors by determining the grade and the full time of the effect of these factors on the aforementioned sectors of the Malaysian-economy as in the following I-VCNSES:

(K,¯A)={(e1,p,1),([0.9,1].ej2π[812,1112],[0.1,0.2].ej2π[112,312],[0,0.1].ej2π[0,0]u1),([0.4,0.5].ej2π[512,612],[0.5,0.6].ej2π[312,412],[0,5,0.7].ej2π[212,412]u2)},{(⟨[0.3,0.4].ej2π[212,312],[0.2,0.3].ej2π[312,512],[0,6,0.7].ej2π[912,1112]⟩u3),(⟨[0.6,0.9].ej2π[712,912],[0.5,0.6].ej2π[512,712],[0,3,0.4].ej2π[0,112]⟩u4)}{(e1,q,1),(⟨[0.5,0.9].ej2π[712,1012],[0.2,0.2].ej2π[112,212],[0.2,0.3].ej2π[0,112]⟩u1),(⟨[0.5,0.7].ej2π[612,712],[0.2,0.4].ej2π[412,512],[0,8,0.9].ej2π[612,812]⟩u2),{(⟨[0.2,0.4].ej2π[112,212],[0.6,0.9].ej2π[612,812],[0,5,0.9].ej2π[812,1012]⟩u3),(⟨[0.6,0.8].ej2π[812,912],[0.3,0.4].ej2π[512,612],[0.2,0.3].ej2π[112,412]⟩u4)}{(e2,p,1),([0.6,0.9].ej2π[712,812],[0.2,0.3].ej2π[312,412],[0,0.2].ej2π[112,212]u1),([0.2,0.4].ej2π[512,712],[0.4,0.5].ej2π[112,312],[0,3,0.4].ej2π[0,112]u2),{([0.1,0.3].ej2π[812,912],[0.4,0.6].ej2π[612,812],[0,7,0.9].ej2π[712,1012]u3),([0.3,0.7].ej2π[712,912],[0.1,0.4].ej2π[512,712],[0.1,0.2].ej2π[412,712]u4)}{(e2,q,1),([0.5,0.7].ej2π[912,1112],[0.1,0.2].ej2π[0,112],[0,0.1].ej2π[212,312]u1),([0.6,0.7].ej2π[412,712],[0.1,0.3].ej2π[112,412],[0.6,0.9].ej2π[212,512]u2),{([0.2,0.4].ej2π[312,812],[0.3,0.5].ej2π[512,612],[0,6,0.8].ej2π[512,712]u3),([0.4,0.5].ej2π[612,812],[0.2,0.5].ej2π[112,312],[0.4,0.8].ej2π[412,612]u4)}{(e3,p,1),([0.6,0.8].ej2π[612,1012],[0,0.1].ej2π[212,312],[0.2,0.4].ej2π[112,212]u1),([0.5,0.7].ej2π[212,412],[0.3,0.4].ej2π[212,412],[0.1,0.2].ej2π[312,612]u2),{([0.3,0.6].ej2π[512,712],[0.2,0.4].ej2π[712,912],[0.5,0.9].ej2π[212,612]u3),([0.3,0.8].ej2π[612,912],[0.2,0.6].ej2π[112,412],[0.3,0.5].ej2π[0,212]u4)}{(e3,q,1),([0.4,0.7].ej2π[312,712],[0.2,0.5].ej2π[412,512],[0.1,0.2].ej2π[212,412]u1),([0.2,0.4].ej2π[312,712],[0.1,0.3].ej2π[612,812],[0.3,0.5].ej2π[412,612]u2),{([0,0.3].ej2π[112,312],[0.4,0.6].ej2π[612,812],[0.5,0.9].ej2π[312,712]u3),([0.2,0.4].ej2π[512,712],[0.3,0.7].ej2π[312,512],[0.3,0.8].ej2π[312,712]u4)}{(e1,p,0),([0.1,0.3].ej2π[112,312],[0.4,0.8].ej2π[712,1112],[0.8,0.9].ej2π[812,1212]u1),([0.4,0.7].ej2π[712,912],[0.3,0.7].ej2π[412,912],[0.2,0.6].ej2π[612,912]u2),{([0.3,0.6].ej2π[512,1012],[0.5,0.8].ej2π[712,912],[0.1,0.3].ej2π[112,412]u3),([0.2,0.3].ej2π[312,412],[0.5,0.8].ej2π[412,612],[0.3,0.9].ej2π[712,1112]u4)}{(e1,q,0),([0.2,0.3].ej2π[212,512],[0.2,0.7].ej2π[712,1012],[0,0.1].ej2π[912,1112]u1),([0.3,0.8].ej2π[412,712],[0.2,0.6].ej2π[512,712],[0.2,0.7].ej2π[212,412]u2),{([0.5,0.8].ej2π[812,1112],[0.1,0.1].ej2π[612,712],[0.6,0.9].ej2π[112,212]u3),([0.6,0.9].ej2π[312,612],[0.3,0.5].ej2π[712,812],[0.1,0.6].ej2π[512,1012]u4)}{(e2,p,0),([0.1,0.3].ej2π[212,412],[0.4,0.8].ej2π[312,812],[0.4,0.7].ej2π[912,1112]u1),([0.3,0.5].ej2π[312,612],[0.2,0.6].ej2π[812,1012],[0.3,0.8].ej2π[712,1212]u2),{([0.1,0.8].ej2π[612,1112],[0.5,0.9].ej2π[512,712],[0.2,0.7].ej2π[212,612]u3),([0.2,0.2].ej2π[512,712],[0.6,0.9].ej2π[712,1012],[0.6,0.8].ej2π[412,1012]u4)}{(e2,q,0),([0.1,0.1].ej2π[112,412],[0.2,0.6].ej2π[812,1212],[0.5,0.5].ej2π[612,912]u1),([0.5,0.8].ej2π[612,812],[0.3,0.6].ej2π[712,1112],[0.5,0.8].ej2π[712,1012]u2),{([0.9,0.9].ej2π[812,1112],[0.2,0.5].ej2π[612,712],[0.2,0.3].ej2π[512,612]u3),([0.2,0.4].ej2π[412,512],[0.4,0.6].ej2π[612,812],[0.5,0.5].ej2π[712,912]u4)}{(e3,p,0),([0,0.5].ej2π[212,412],[0.4,0.9].ej2π[512,1112],[0.1,0.4].ej2π[712,1012]u1),([0.1,0.3].ej2π[112,312],[0.3,0.8].ej2π[612,1112],[0.4,0.8].ej2π[812,1212]u2),{([0.3,0.8].ej2π[712,1012],[0.4,0.7].ej2π[212,512],[0.3,0.6].ej2π[412,912]u3),([0,0.2].ej2π[212,412],[0.3,0.7].ej2π[912,1112],[0.6,0.8].ej2π[612,1012]u4)}{(e3,q,0),(⟨[0.1,0.3].ej2π[312,612],[0.2,0.6].ej2π[512,812],[0,0.3].ej2π[712,1112]⟩u1),(⟨[0.2,0.5].ej2π[312,512],[0.2,0.9].ej2π[312,512],[0.2,0.7].ej2π[612,912]⟩u2),{(⟨[0.4,0.8].ej2π[512,912],[0.1,0.5].ej2π[412,712],[0.6,0.8].ej2π[412,1012]⟩u3),(⟨[0.3,0.7].ej2π[312,912],[0.1,0.4].ej2π[512,712],[0,0.6].ej2π[212,612]⟩u4)}}

In this situation, the amplitude interval terms measurement the impact degree of the above-mentioned factors on the Malaysian economy in 2020, whilst the phase interval terms represent the period of this impact. By this way, the interval-valued complex neutrosophic number

In the approximation K¯(e1,p,1) indicates that the Malaysian economy in 2020 has been greatly affected by the plunge in oil and commodity prices. The lower and upper bounds of the complex interval-valued truth membership function [0.9,1].ej2π[812,1112] shows that expert p strongly supports that the decline in oil and commodity prices has a great impact on the Malaysian economy by amplitude term degree from 0.9 to 1 and this influence extends from 8 to 11 months accordant to the phase term [812,1112]. While the lower and upper bounds of the complex interval-valued indeterminacy membership function [0.1,0.2].ej2π[112,312] reveal that the expert is unable to determine whether there is an effect of a degree between 0.1 and 0.2, and this effect is not clear for a period ranging from 1 to 3 months. For the lower and upper bounds of the complex interval-valued falsity membership function [0,0.1].ej2π[0,0], the expert p assumes that there is no effect of a degree ranging from 0 to 0.1 and that the time in which there is no effect is 0 month. The algorithm given below converts the I-CNSE-values to the INSEV-values using a workable formula. We then convert the INSEVs to normalized SVNSE-values by taking the arithmetic average of TKα(u),IKα(u)andFKα(u), respectively.

Then, we proceed with SVNSE-values to make the final decision using the SVNSE-method [25]. The following steps clarify the proposed algorithm:

The decision is to choose value ui as the solution to the problem. If there is more than one value with the highest ri score, then any one of those values can be chosen as the best solution.

Here, we would like to point out that this method (algorithm) is used with decision-making problems that have information that has a known weight (complete weight information). To implement these steps that were mentioned in the algorithm above, we assume that the weight vector to the amplitude terms is w1=0.6. and the weight vector to the phase terms is w2=0.4.

Now, to convert the I-VCNSES (K¯,A) to the I-VNSES (K,A), and to obtain the weighted aggregation values of TKα(u),IKα(u) andFKα(u),

∀u∈Uand∀α∈A. To clarify this step, we calculate TKα(u),IKα(u)andFKα(u),foru=u1andα=(e1,p,1) as shown below:

TK(α=e1,p,1)(u)=[w1tLK¯(α=e1,p,1)(u)+w2(12π)ρωLK¯(α=e1,p,1)(u),w1tUK¯(α)(u)+w2(12π)ρωUK¯(α=e1,p,1)(u)]=[0.6(0.9)+0.4(12π)2π812,0.6(1)+0.4(12π)2π1112]=[0.8,0.96]

IK(α=e1,p,1)(u)=[w1iLK¯(α=e1,p,1)(u)+w2(12π)βψLK¯(α=e1,p,1)(u),w1iUK¯(α)(u)+w2(12π)βψUK¯(α=e1,p,1)(u)]=[0.6(0.1)+0.4(12π)2π112,0.6(0.2)+0.4(12π)2π312]=[0.09,0.22]

FK(α=e1,p,1)(u)=[w1fLK¯(α=e1,p,1)(u)+w2(12π)γΦLK¯(α=e1,p,1)(u),w1fUK¯(α)(u)+w2(12π)γΦUK¯(α=e1,p,1)(u)]=[0.6(0)+0.4(12π)2π(0),0.6(0.1)+0.4(12π)2π(0)]=[0,0.06]

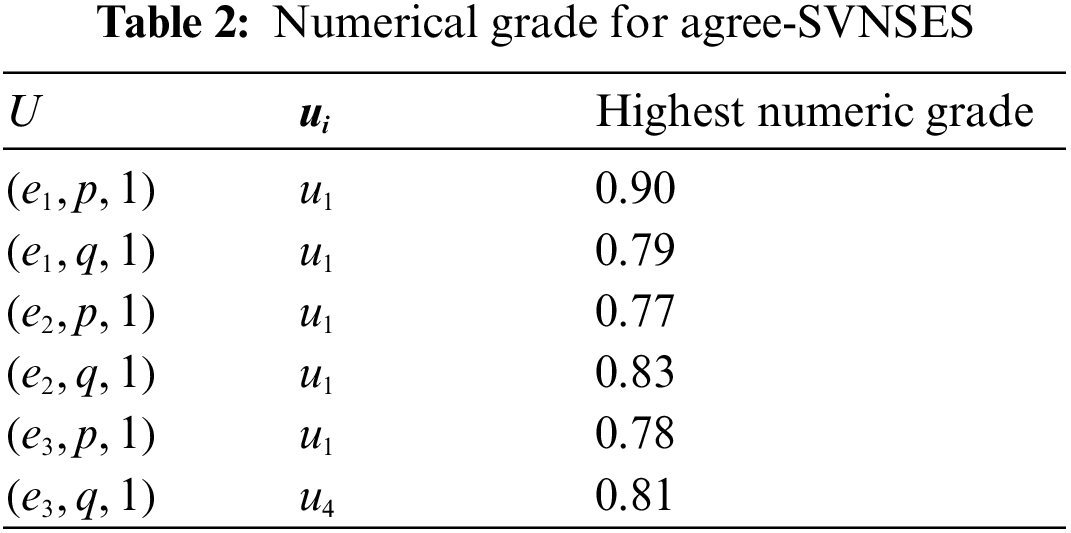
Hence for α=(e1,p,1 ) and u=u1 the I-VNSES (TKα(u), IKα(u), FKα(u)) = ([0.8,0.96], [0.09,0.22], [0,0.06]) Then, we apply Step 3 in the algorithm to get (0.88,0.15,0.03) as these values represent SVNESs. In the same method we calculate the other values. Finally, we get Table 1 which includes the values of MVα(u) in addition to a value of SVNSESs.

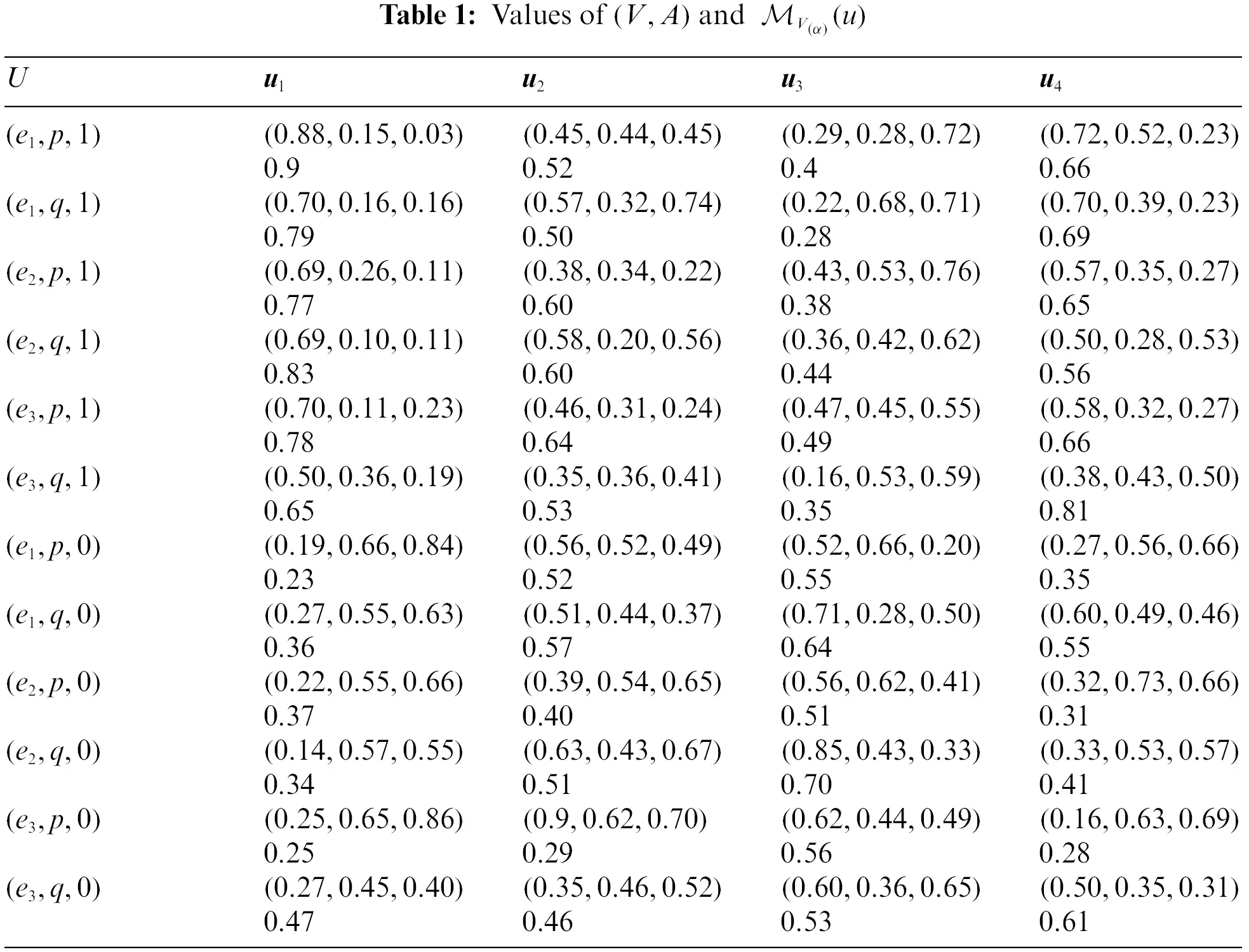
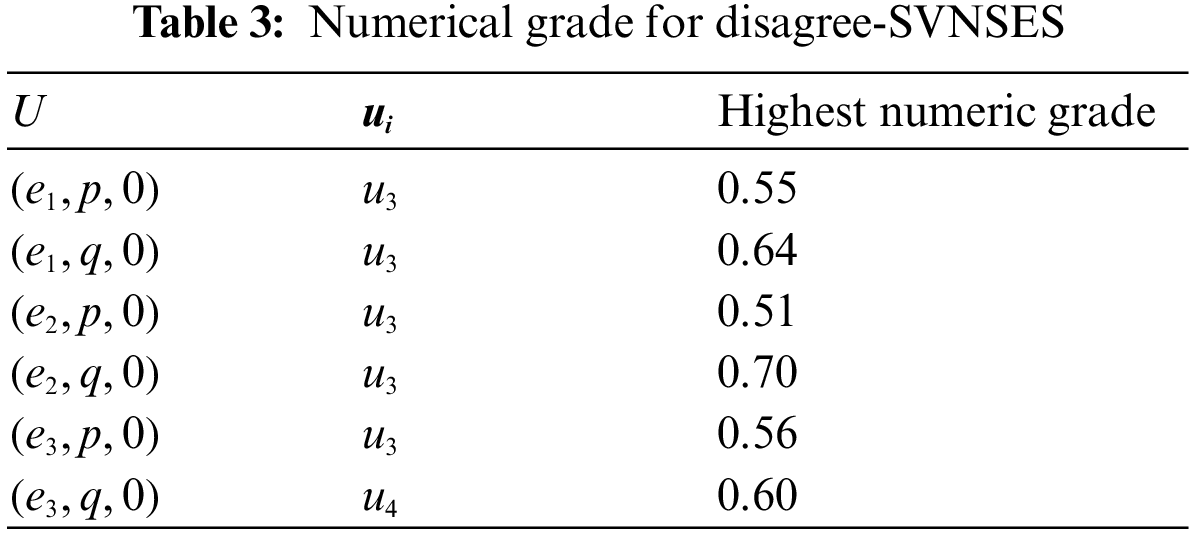
By Tables 2 and 3, we get the highest numerical grade for the elements in the agree-SVNSES and disagree-SVNSES, respectively. The values of Pi,Qi and ri are given in Table 4, where ri=Pi−Qi, represent the final score of each alternative, for all i=1,2,3,4.

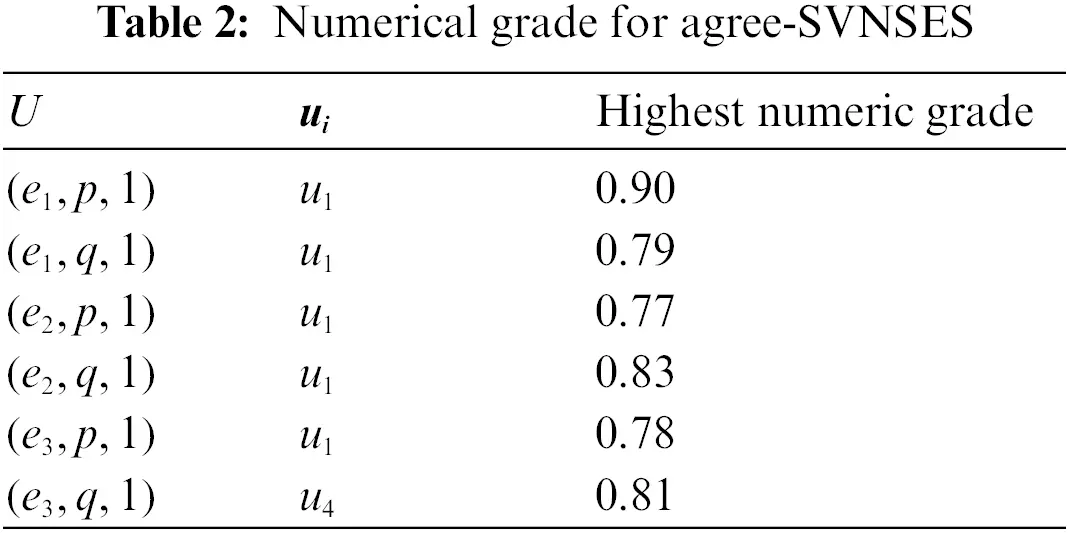
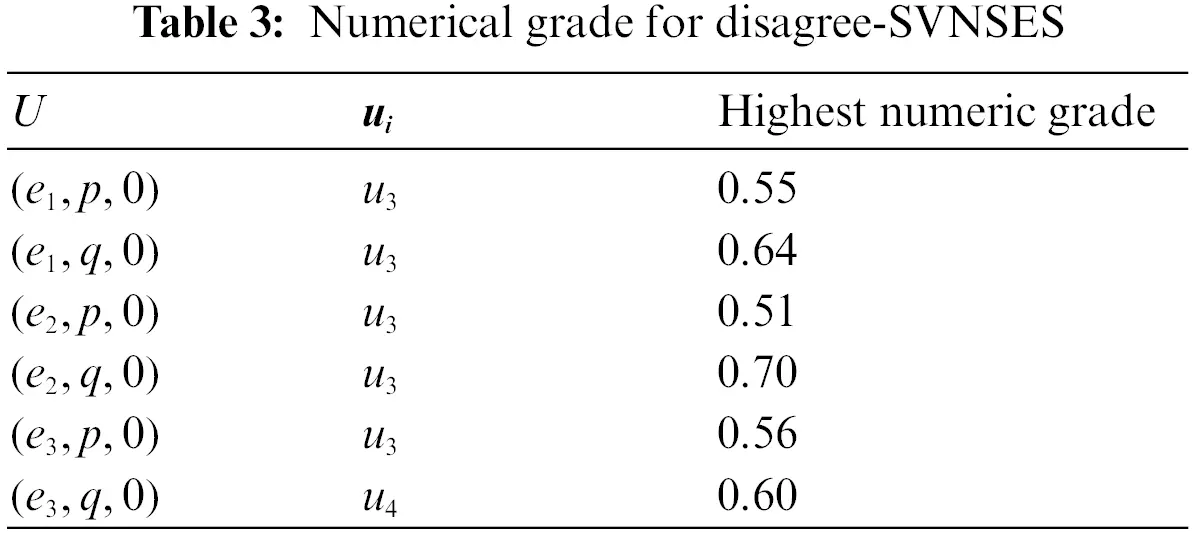
Finally, according to the Step 8 of proposed algorithm, the maximum ri is r1, followed by r4 and r2, where r3 is the minimum ri. Thus, u1 which represents the plunge in oil prices and commodities commercial is the most significant factor influencing Malaysia's economy in 2020, followed by in influence u4 exchange rate variability in this year and u2 the slowdown in china's economy, where u3 which represents the tax (GST) on services and goods that applied this year is the least influential element in the Malaysian economy in 2020.

In this section, we will now compare our second concept (I-VCNSES), which is an expansion of our first concept (I-VNSES) with three existing methods, which is neutrosophic soft set (NSS) [39], single-valued neutrosophic soft expert set (SVNSES) [40], and complex neutrosophic soft expert set (CNSES).

Because neutrosophic soft set lacks the phase term that indicates the time frame, so it is clear that it is unable to solve the decision-making problem given in this work (see Example 5.1), which involves two-dimensional data, i.e., the degree of the influence and the total time of the influence. Another reason is its incapacity to deal with several experts. However, the single-valued neutrosophic soft expert set can deal with more than one expert. But it is not able to deal with problems that involve two-dimensional information (amplitude terms and phase terms) like the problem presented in this work.

The complex neutrosophic soft expert set can overcome the problems which the above two concepts cannot overcome by using neutrosophic expert soft set, by virtue of the phase terms which have the ability to represent the time frame of the interaction between the variables as well as parameterization and the opinions of the experts, all in a single set. In comparison, the main distinguishing feature of our proposed is its ability to describe the grade of three complex memberships in the form of an interval that is a subset of the unit interval. Furthermore, since it is difficult for an expert to express his/her certainty by an exact real number, so it is suitable to choose an interval that expresses the certainty level. Therefore, the I-VCNSESs help in modeling the uncertainty and the consequences of any ignorance, mistakes, and confusion of experts. Therefore, it can be judged that our concept is more important and useful than the above-mentioned concepts.

Our proposed model has certain advantages and limitations. Firstly, our model (I-VCNSES) has the ability to provide a succinct, elegant, and comprehensive representation of two-dimensional interval neutrosophic information (amplitude terms and phase terms) as well as adequate parameterization and opinions of the experts, all in the form of an interval. Secondly, I-VCNSES includes evaluation information missing in the neutrosophic soft model and single-valued neutrosophic soft expert model, such as the time frame which is presented by the phase term. In addition, it has the added advantage of allowing the users to know the opinion of all the experts in an interval model without the necessity for any additional cumbersome operations. Thirdly, the I-VCNSES that is used in our method has the ability to handle the uncertainty information that is captured by the amplitude terms and phase terms of the complex numbers simultaneously. Fourthly, a new practical formula is employed to convert the interval-valued complex neutrosophic soft expert from the complex state to the real state, which gives decision-making with a simple computational process without the need to carry out directed operations on complex numbers. Fifthly, our model represents the information of two-dimensional in interval form, namely information of amplitude term and phase term, thus making our model more appropriate for use in real-life problems like decision-making, medical diagnosis to select the best alternative. Finally, the interval form which characterized our concept gives the user more flexibility in the real decision-making process, where the real decision we get through our concept is characterized as more trustworthy and more acceptable than the other existing concepts in which there is no attention to the interval form. Therefore, these features mentioned above are essential points that distinguish our model from existing models. Our idea, on the other hand, is incapable of handling discontinuous attribute-value sets that correspond to different attributes. Therefore, we recommend for future studies that this gap be overcome by generalizing our concept to an interval-valued complex neutrosophic hypersoft expert set.

A novel mathematical tool is created to highlight the information using time factors and to realize the opinions of all the experts in an interval model. In this article, we established the concept of IV-CNSES by extending our concept of IV-NSES from real space to complex space. The basic operations on both I-VNSES and I-VCNSES, namely subset, complement, union, intersection, AND and OR operations were defined. Subsequently, some basic algebraic properties of these operations were proven. In addition, we showed the importance of this concept in real life through a proposed new algorithm and we applied it to both models to solve a hypothetical decision-making problem related to the economic factors that affected the Malaysian economy in 2020. A comparison of our proposed model with three other existing models indicates the efficiency of our model and also it showed the superiority of our concept over these concepts with flexibility and accuracy in representing two-dimensional interval neutrosophic information. Finally, these flexible new extensions are not applied yet in many fields like computer science, social science, medical science, engineering, etc. So, in future work, we plan to combine this concept with other types of algebraic structures such as group [41,42] and ring [43,44]. We are wishful to provide our work to other MCDM models and applications for modeling vagueness and uncertainty.

Acknowledgement: We are indebted to Universiti Kebangsaan Malaysia for providing financial support and facilities for this research under the Grant TAP-K005825.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. DOI 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]

2. Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]

3. Smarandache, F. (2005). Neutrosophic set–A generalisation of the intuitionistic fuzzy sets. International Journal of Pure and Applied Mathematics, 24, 287–297. [Google Scholar]

4. Smarandache, F. (1999). A unifying field in logics. Neutrosophy: Neutrosophic probability, set and logic, pp. 1–141. Rehoboth, USA: American Research Press. [Google Scholar]

5. Wang, H., Smarandache, F., Zhang, Y., Sunderraman, R. (2010). Single valued neutrosophic sets. Infinite Study. [Google Scholar]

6. Yang, H. L., Guo, Z. L., She, Y., Liao, X. (2016). On single valued neutrosophic relations. Journal of Intelligent & Fuzzy Systems, 30(2), 1045–1056. DOI 10.3233/IFS-151827. [Google Scholar] [CrossRef]

7. Iryna, S., Zhong, Y., Jiang, W., Deng, X., Geng, J. (2020). Single-valued neutrosophic set correlation coefficient and its application in fault diagnosis. Symmetry, 12(8), 1371. DOI 10.3390/sym12081371. [Google Scholar] [CrossRef]

8. Al-Quran, A., Alkhazaleh, S. (2018). Relations between the complex neutrosophic sets with their applications in decision making. Axioms, 7(3), 64. DOI 10.3390/axioms7030064. [Google Scholar] [CrossRef]

9. Şahin, R., Küçük, A. (2015). Subsethood measure for single valued neutrosophic sets. Journal of Intelligent & Fuzzy Systems, 29(2), 525–530. DOI 10.3233/IFS-141304. [Google Scholar] [CrossRef]

10. Wang, J., Zeng, S., Zhang, C. (2020). Single-valued neutrosophic linguistic logarithmic weighted distance measures and their application to supplier selection of fresh aquatic products. Mathematics, 8(3), 439. DOI 10.3390/math8030439. [Google Scholar] [CrossRef]

11. Bera, T., Mahapatra, N. K. (2019). Generalised single valued neutrosophic number and its application to neutrosophic linear programming. Neutrosophic Sets and Systems, 25(1), 85–103. DOI 10.5281/zenodo.2631508. [Google Scholar] [CrossRef]

12. Wang, H., Smarandache, F., Sunderraman, R., Zhang, Y. Q. (2005). Interval neutrosophic sets and logic: theory and applications in computing: Theory and applications in computing, vol. 5. Infinite Study. [Google Scholar]

13. Riaz, M., Hashmi, M. R., Pamucar, D., Chu, Y. M. (2021). Spherical linear diophantine fuzzy sets with modeling uncertainties in MCDM. Computer Modeling in Engineering & Sciences, 126(3), 1125–1164. DOI 10.32604/cmes.2021.013699. [Google Scholar] [CrossRef]

14. Riaz, M., Garg, H., Muhammad, H., Chinram, R. (2021). Multi-criteria decision making based on bipolar picture fuzzy operators and new distance measures. Computer Modeling in Engineering & Sciences, 127(2), 771–800. DOI 10.32604/cmes.2021.014174. [Google Scholar] [CrossRef]

15. Rodzi, Z. M., Ahmad, A. G., Ismail, N. F., Abdullah, N. L. (2021). Z-score functions of hesitant fuzzy sets. Mathematics and Statistics, 9(4), 445–455. DOI 10.13189/ms.2021.090405. [Google Scholar] [CrossRef]

16. Abdel-Basset, M., Gamal, A., Son, L. H., Smarandache, F. (2020). A bipolar neutrosophic multi criteria decision making framework for professional selection. Applied Sciences, 10(4), 1202. DOI 10.3390/app10041202. [Google Scholar] [CrossRef]

17. Zulqarnain, R. M., Xin, X. L., Saeed, M., Smarandache, F., Ahmad, N. (2020). Generalized neutrosophic TOPSIS to solve multi-criteria decision-making problems, vol. 38. Infinite Study. [Google Scholar]

18. Zulqarnain, R. M., Xin, X. L., Saqlain, M., Smarandache, F., Ahamad, M. I. (2021). An integrated model of neutrosophic TOPSIS with application in multi-criteria decision-making problem. Neutrosophic Sets and Systems, 40(1), 15. DOI 10.5281/zenodo.4549340. [Google Scholar] [CrossRef]

19. Rahman, A. U., Saeed, M., Alodhaibi, S. S., Abd, H. (2021). Decision making algorithmic approaches based on parameterization of neutrosophic set under hypersoft set environment with fuzzy, intuitionistic fuzzy and neutrosophic settings. Computer Modeling in Engineering & Sciences, 128(2), 743–777. DOI 10.32604/cmes.2021.016736. [Google Scholar] [CrossRef]

20. Alhazaymeh, K., Al-Qudah, Y., Hassan, N., Nasruddin, A. M. (2020). Cubic vague set and its application in decision making. Entropy, 22(9), 963. DOI 10.3390/e22090963. [Google Scholar] [CrossRef]

21. Xu, D., Peng, L. (2021). An improved method based on TODIM and TOPSIS for multi-attribute decision-making with multi-valued neutrosophic sets. Computer Modeling in Engineering & Sciences, 129(2), 907–926. DOI 10.32604/cmes.2021.016720. [Google Scholar] [CrossRef]

22. Abu Qamar, M., Hassan, N. (2019). An approach toward a Q-neutrosophic soft set and its application in decision making. Symmetry, 11(2), 139. DOI 10.3390/sym11020139. [Google Scholar] [CrossRef]

23. Al-Quran, A., Hassan, N. (2017). Neutrosophic vague soft set and its applications. Malaysian Journal of Mathematical Sciences, 11(2), 141–163. [Google Scholar]

24. Haque, T. S., Chakraborty, A., Mondal, S. P., Alam, S. (2021). New exponential operational law for measuring pollution attributes in mega-cities based on MCGDM problem with trapezoidal neutrosophic data. Journal of Ambient Intelligence and Humanized Computing, 12, 1–18. DOI 10.1007/s12652-021-03223-8. [Google Scholar] [CrossRef]

25. Chakraborty, A., Banik, B., Mondal, S. P., Alam, S. (2020). Arithmetic and geometric operators of pentagonal neutrosophic number and its application in mobile communication service based MCGDM problem. Neutrosophic Sets and Systems, 32, 61–79. DOI 10.5281/zenodo.3723145. [Google Scholar] [CrossRef]

26. Al-Qudah, Y., Hassan, N. (2017). Bipolar fuzzy soft expert set and its application in decision making. International Journal of Applied Decision Sciences, 10(2), 175–191. DOI 10.1504/IJADS.2017.084310. [Google Scholar] [CrossRef]

27. Ramot, D., Milo, R., Friedman, M., Kandel, A. (2002). Complex fuzzy sets. IEEE Transactions on Fuzzy Systems, 10(2), 171–186. DOI 10.1109/91.995119. [Google Scholar] [CrossRef]

28. Ali, M., Smarandache, F. (2017). Complex neutrosophic set. Neural Computing and Applications, 28(7), 1817–1834. DOI 10.1007/s00521-015-2154-y. [Google Scholar] [CrossRef]

29. Ali, M., Dat, L. Q., Son, L. H., Smarandache, F. (2018). Interval complex neutrosophic set: Formulation and applications in decision-making. International Journal of Fuzzy Systems, 20(3), 986–999. DOI 10.1007/s40815-017-0380-4. [Google Scholar] [CrossRef]

30. Molodtsov, D. (1999). Soft set theory-first results. Computers and Mathematics with Applications, 37(4–5), 19–31. DOI 10.1016/S0898-1221(99)00056-5. [Google Scholar] [CrossRef]

31. Alkhazaleh, S., Salleh, A. R. (2011). Soft expert sets. Advances in Decision Sciences, 2011, 757868. DOI 10.1155/2011/757868. [Google Scholar] [CrossRef]

32. Al-Quran, A., Hassan, N. (2018). The complex neutrosophic soft expert set and its application in decision making. Journal of Intelligent & Fuzzy Systems, 34(1), 569–582. DOI 10.3233/JIFS-17806. [Google Scholar] [CrossRef]

33. Al-Quran, A., Hassan, N. (2018). The complex neutrosophic soft expert relation and its multiple attribute decision-making method. Entropy, 20(2), 101. DOI 10.3390/e20020101. [Google Scholar] [CrossRef]

34. Al-Sharqi, F., Al-Quran, A., Ahmad, A. G., Broumi, S. (2021). Interval-valued complex neutrosophic soft set and its applications in decision-making. Neutrosophic Sets and Systems, 40(1), 149–168. DOI 10.5281/zenodo.4568742. [Google Scholar] [CrossRef]

35. Alkhazaleh, S., Salleh, A. R. (2014). Fuzzy soft expert set and its application. Applied Mathematics, 2014, 1349–1368. DOI 10.4236/am.2014.59127. [Google Scholar] [CrossRef]

36. Broumi, S., Smarandache, F. (2015). Intuitionistic fuzzy soft expert sets and its application in decision making. Journal of New Theory, 1(1), 89–105. [Google Scholar]

37. Sahin, M., Alkhazaleh, S., Ulucay, V. (2015). Neutrosophic soft expert sets. Applied Mathematics, 6(1), 116. DOI 10.4236/am.2015.61012. [Google Scholar] [CrossRef]

38. Bin, C. (2019). Interval valued generalised fuzzy soft expert set and its application. The International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery, pp. 991–999. Cham, Springer. [Google Scholar]

39. Jha, S., Kumar, R., Chatterjee, J. M., Khari, M., Yadav, N., Smarandache, F. (2019). Neutrosophic soft set decision making for stock trending analysis. Evolving Systems, 10(4), 621–627. DOI 10.1007/s12530-018-9247-7. [Google Scholar] [CrossRef]

40. Broumi, S., Smarandache, F. (2015). Single valued neutrosophic soft expert sets and their application in decision making. Journal of New Theory, 3(3), 67–88. [Google Scholar]

41. Al-Masarwah, A., Ahmad, A. G. (2019). M-polar (α, β)-fuzzy ideals in BCK/BCI-algebras. Symmetry, 11(1), 44. DOI 10.3390/sym11010044. [Google Scholar] [CrossRef]

42. Abed, M. M., Al-Sharqi, F. G., Mhassin, A. A. (2019). Study fractional ideals over some domains. AIP Conference Proceedings, 2138(1), 030001. DOI 10.1063/1.5121038. [Google Scholar] [CrossRef]

43. Abu Qamar, M., Ahmad, A. G., Hassan, N. (2020). On Q-neutrosophic soft fields. Neutrosophic Sets and Systems, 32(1), 7. DOI 10.5281/zenodo.3723603. [Google Scholar] [CrossRef]

44. Abed, M. M., Al-Sharqi, F., Zail, S. H. (2021). A certain conditions on some rings give PP ring. Journal of Physics: Conference Series, 1818(1), 012068. DOI 10.1088/1742-6596/1818/1/012068. [Google Scholar] [CrossRef]