[BACK]
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.019408
ARTICLE
Aggregation Operators for Interval-Valued Pythagorean Fuzzy Soft Set with Their Application to Solve Multi-Attribute Group Decision Making Problem
Rana Muhammad Zulqarnain1, Imran Siddique2, Aiyared Iampan3 and Dumitru Baleanu4,5,6,*
1Department of Mathematics, University of Management and Technology, Sialkot Campus, Lahore, 54770, Pakistan
2Department of Mathematics, University of Management and Technology, Lahore, 54000, Pakistan
3Department of Mathematics, School of Science, University of Phayao, Mae Ka, Mueang, Phayao, 56000, Thailand
4Department of Mathematics, Cankaya University, Balgat Ankara, 06530, Turkey
5Institute of Space Sciences, Magurele-Bucharest, 077125, Romania
6Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, 40447, Taiwan
*Corresponding Author: Dumitru Baleanu. Email: dumitru.baleanu@gmail.com
Received: 23 September 2021; Accepted: 15 November 2021
Abstract: Interval-valued Pythagorean fuzzy soft set (IVPFSS) is a generalization of the interval-valued intuitionistic fuzzy soft set (IVIFSS) and interval-valued Pythagorean fuzzy set (IVPFS). The IVPFSS handled more uncertainty comparative to IVIFSS; it is the most significant technique for explaining fuzzy information in the decision-making process. In this work, some novel operational laws for IVPFSS have been proposed. Based on presented operational laws, two innovative aggregation operators (AOs) have been developed such as interval-valued Pythagorean fuzzy soft weighted average (IVPFSWA) and interval-valued Pythagorean fuzzy soft weighted geometric (IVPFSWG) operators with their fundamental properties. A multi-attribute group decision-making (MAGDM) approach has been established utilizing our developed operators. A numerical example has been presented to ensure the validity of the proposed MAGDM technique. Finally, comparative studies have been given between the proposed approach and some existing studies. The obtained results through comparative studies show that the proposed technique is more credible and reliable than existing approaches.
Keywords: Interval-valued Pythagorean fuzzy soft set; IVPFSWA operator; IVPFSWG operator; MAGDM
1 Introduction
MAGDM is considered as the most appropriate technique to find the finest alternative from all possible alternatives, following criteria or attributes. Conventionally, it is supposed that all information that accesses the alternative in terms of attributes and their corresponding weights are articulated in the form of crisp numbers. On the other hand, in real-life circumstances, most of the decisions are taken in situations where the objectives and limitations are usually indefinite or ambiguous. To overcome such ambiguities and anxieties, Zadeh offered the notion of the fuzzy set (FS) [1], a prevailing tool to handle the obscurities and uncertainties in decision making (DM). Such a set allocates to all objects a membership value ranging from 0 to 1. Mostly, experts consider membership and a non-membership value in the DM process which cannot be handled by FS. Atanassov [2] introduced the idea of the intuitionistic fuzzy set (IFS) to overcome the aforementioned limitation. In 2011, Wang et al. [3] presented numerous operations on IFS, such as Einstein product, Einstein sum, etc., and constructed some novel AOs. They also discussed some important properties of these operators and utilized their proposed operators to resolve multi-attribute decision making (MADM). Atanassov [4] presented a generalized form of IFS in the light of ordinary interval values, called interval-valued intuitionistic fuzzy set (IVIFS). Garg et al. [5] extended the concept of IFS and presented a novel concept of the cubic intuitionistic fuzzy set (CIFS) which is a successful tool to represent vague data by embedding both IFS and IVIFS directly. They also discussed several desirable properties of CIFS.
The above-mentioned models have been well-recognized by the specialists but the existing IFS is unable to handle the inappropriate and vague data because it is considered to envision the linear inequality between the membership and non-membership grades. For example, if decision-makers choose membership and non-membership values 0.9 and 0.6 respectively, then the above-mentioned IFS theory is unable to deal with it because 0.9 + 0.6 ≥ 1. To resolve the aforesaid limitation, Yager [6] presented the idea of the Pythagorean fuzzy set (PFS) by amending the basic condition κ+δ≤1 to κ2+δ2≤1 and developed some results associated with score function and accuracy function. Rahman et al. [7] developed the Pythagorean fuzzy Einstein weighted geometric operator and presented a MAGDM methodology utilizing their proposed operator. Zang et al. [8] developed some basic operational laws and prolonged the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method to resolve multi-criteria decision-making (MCDM) complications for PFS information. Wei et al. [9] offered the Pythagorean fuzzy power AOs along with basic characteristics, they also established a DM technique to resolve MADM difficulties based on presented operators. Wang et al. [10] offered the interaction operational laws for Pythagorean fuzzy numbers (PFNs) and developed power Bonferroni mean operators. To assess the professional health risk, IIbahar et al. [11] offered the Pythagorean fuzzy proportional risk assessment technique. Zhang [12] proposed a novel DM approach based on similarity measures to resolve multi-criteria group decision making (MCGDM) difficulties for the PFS.
All of the aforementioned techniques have a wide range of applications, but owing to their ineffectiveness, they have several restrictions with the parameterization tool. Presenting a solution to this type of uncertainty and obfuscation Molodtsov [13] established the idea of soft sets (SS) and described some basic operations with their characteristics to handle the above-mentioned confusion and ambiguity. Maji et al. [14] expanded the concept of SS and developed many basic and binary operations for it. Maji et al. [15] developed the fuzzy soft set with some desirable properties by merging two existing notions FS and SS. Maji et al. [16] developed the notion of the intuitionistic fuzzy soft set (IFSS) and some fundamental operations with their necessary properties. Garg et al. [5] presented the cubic IFSS and established some AOs for cubic IFSS. They also planned a DM technique based on their developed operators. Zulqarnain et al. [17] planned the TOPSIS method based on the correlation coefficient for interval-valued IFSS to solve MADM problems. Jiang et al. [18] introduced the notion of the interval-valued intuitionistic fuzzy soft set (IVIFSS) and discussed some of their basic properties. Narayanamoorthy et al. [19] proposed the score function for a normal wiggly hesitant fuzzy set and utilized it to expose the deepest ideas hidden in the thought-level of the decision-makers. Narayanamoorthy et al. [20] introduced the hesitant fuzzy subjective and objective weight integrated method to find weights under hesitant fuzzy information. They also presented a novel ranking methodology for hesitant fuzzy sets. Ramya et al. [21] developed the interval-valued hesitant Pythagorean fuzzy set under the normal wiggly mathematical methodology and used it to solve the MCDM problem. Peng et al. [22] merged two well-known theories PFS and SS and offered the concept of Pythagorean fuzzy soft set (PFSS). Zulqarnain et al. [23] developed the AOs for PFSS with their application for the green supplier chain management. Zulqarnain et al. [24] introduced an advanced form of AOs considering the interaction and construct a DM approach based on their developed interactive AOs. Smarandache [25] prolonged the idea of SS to hypersoft sets (HSS) by substituting the single-parameter function f with a multi-parameter (sub-attribute) function. He privileges that HSS proficiently contracts with inexact data comparative to SS.
MAGDM is a very effective and well-known tool to examine fuzzy data more effectively. Therefore, it is obvious from the published literature that the interval-valued structures are more general and increase more consideration in decision-making difficulties. The choice of vehicle is a key part of real-life and will advise on complications of MAGDM. Lack of thinking about the ambiguity of alternative associations will be the core motivation for some MAGDM concerns about the undesirable consequences. By using a wealth of existing content, it contains previous criticisms and suppressed sensitivities. Many logical and scientific tools/procedures are offended in the literature for choosing the most suitable vehicle. As far as we know, there is currently no work on the AOs of IVPFSS. Therefore, this article proposes some operational laws for interval-valued Pythagorean fuzzy soft numbers (IVPFSN). The presented IVPFSN is well worth observing the inaccurate information that occurs in the complications of daily life. Therefore, the main purpose of this work is to propose new IVPFSWA and IVPFSWG operators based on the established operational laws. An algorithm based on the proposed operators to solve the decision-making problem is proposed. To prove the effectiveness of the proposed decision-making method, we use a numerical example to illustrate it. The main benefit of the proposed operator is that the proposed operator can reduce to IVIFSS and IVFSS operators under some specific conditions of unconfidence. The organization of this paper is given as follows: Section 2 of this paper consists of some basic concepts which help us to develop the structure of the following research. In Section 3, some novel operational laws for IVPFSN have been proposed. Also, in the same section, IVPFSWA and IVPFSWG operators have been introduced based on our developed operators with their basic properties. In Section 4, a MAGDM approach has been constructed based on the proposed AOs. To ensure the practicality of the developed approach a numerical example has been presented for the selection of the best vehicle in Section 5.
2 Preliminaries
This section consists of some basic definitions which will provide a structure to form the following work.
Definition 2.1 [1]
Let U be a collection of objects then a fuzzy set (FS) A over U is defined as
A={(t,κ(t))|t∈U}
where, κA(t):X→[0,1] is a membership grade function.
Definition 2.2 [26]
Let U be a collection of objects then an interval-valued fuzzy set (IVFS) A over U is defined as
A={(t,[κl(t),κu(t)])|t∈U}
where, κl(t), κu(t) ∈ [0,1] and represents the lower and upper bounds of the membership value.
Definition 2.3 [4]
Let U be a collection of objects then an interval-valued intuitionistic fuzzy set (IVIFS) A over U is defined as
A={(t,([κAl(t),κAu(t)],[δAl(t),δAu(t)]))|t∈U}
where, [κAl(t),κAu(t)] and [δAl(x),δAu(x)] are intervals for membership and non-membership grades, respectively, whereas [κAl(t),κAu(t)]and[δAl(t),δAu(t)]⊆[0,1], 0≤κAl(t),κAu(t),δAl(t),δAu(t)≤1, and 0≤κAu(x)+δAu(x)≤1.
Definition 2.4 [27]
Let U be a collection of objects then an interval-valued Pythagorean fuzzy set (IVPFS) A over U is defined as
A={(x,([κAl(t),κAu(t)],[δAl(t),δAu(t)]))|t∈U}
where, [κAl(t),κAu(t)] and [δAl(t),δAu(t)] represents the intervals for membership and non-membership grades, respectively. Furthermore, 0≤(κAu(t))2+(δAu(t))2≤1 and [κAl(t),κAu(t)]⊆[0,1] and [δAl(t),δAu(t)]⊆[0,1].
Definition 2.5 [13]
Let U be a universal set and N={t1,t2,t3,…,tm} be set of attributes then a pair (F,N) is called a soft set (SS) over U where F:N→KU is a mapping and KU is known as a collection of all subsets of universal set U.
Definition 2.6 [19]
Let U be a universal set and N be a set of attributes then a pair (Ω,N) is called an interval-valued intuitionistic fuzzy soft set (IVIFSS) over U. Where Ω:N→IKU is a mapping and IKU is known as a collection of all interval-valued intuitionistic fuzzy subsets of universal set U and A⊂N.
(Ω,A)={t,([κAl(t),κAu(t)],[δAl(t),δAu(t)])|t∈A}
where, [κAl(t),κAu(t)]and[δAl(t),δAu(t)] are intervals for membership grade and non-membership functions respectively with 0≤κAu(t)+δAu(t)≤1.
Definition 2.7
Let U be a universal set and N be set of attributes then a pair ((Ω,N) is called an interval-valued Pythagorean fuzzy soft set (IVPFSS) over U where Ω:N→℘KU is a mapping and ℘KU is known as the collection of all interval-valued Pythagorean fuzzy subsets of universal set U.
(Ω,A)={t,([κAl(t),κAu(t)],[δAl(t),δAu(t)])|t∈A}
where, [κAl(t),κAu(t)],[δAl(t),δAu(t)] are intervals for membership grade and non-membership grade, respectively with 0≤(κAu(t))2+(δAu(t))2≤1 and A⊂N.
Definition 2.8
Let Me=([κl,κu],[δl,δu]) be an interval-valued Pythagorean fuzzy soft number (IVPFSN), then the score function is defined as follows:
S(Me)=(κl)2+(κu)2−(δl)2−(δu)22
Definition 2.9
Let Me=([κl,κu],[δl,δu]) be an IVPFSN, then accuracy function is defined as follows:
S(Me)=(κl)2+(κu)2+(δl)2+(δu)22
3 Aggregation Operators for Interval Valued Pythagorean Fuzzy Soft Sets
In this section, we are going to define operational laws under IVPFSNs. Based on these operational laws, we shall also present interval-valued Pythagorean fuzzy soft weighted average (IVPFSWA) and interval-valued Pythagorean fuzzy soft geometric (IVPFSWG) operators.
3.1 Operational Laws for Interval Valued Pythagorean Fuzzy Soft Numbers
Let Me=([κl,κu],[δl,δu]), Me11=([κ11l,κ11u],[δ11l,δ11u]), and
Me12=([κ12l,κ12u],[δ12l,δ12u]) be three interval-valued Pythagorean fuzzy soft numbers and β be a positive real number, and by algebraic norms, we have
1. Me11⊕Me12=([κ11l2+κ12l2−κ11l2κ12l2,κ11u2+κ12u2−κ11u2κ12u2],[δ11lδ12l,δ11uδ12u])
2. Me11⊗Me12=([κ11lκ12l,κ11uκ12u],[δ11l2+δ12l2−δ11l2δ12l2,δ11u2+δ12u2−δ11u2δ11u2])
3. βMe=([1−(1−κl2)β,1−(1−κu2)β],[δlβ,δuβ])=(1−(1−[κl,κu]2)β,[δlβ,δuβ])
4. Meβ=([κlβ,κuβ],[1−(1−δl2)β,1−(1−δu2)β])=([κlβ,κuβ],1−(1−[δl,δu]2)β)
3.2 Interval Valued Pythagorean Fuzzy Soft Weighted Average Operator
Let Meij=([κijl,κiju],[δijl,δiju]) be a collection of interval-valued Pythagorean fuzzy soft numbers (IVPFSNs), and ωi and νj are the weight vector for experts and parameters, respectively, with given conditions ωi>0,∑i=1nωi=1;νj>0,∑j=1mνj=1. Then, the IVPFSWA operator is defined as IVPFSWA: Ψn⟶Ψ
IVPFSWA(Me11,Me12,…,Menm)=⊕j=1mνj(⊕i=1nωiMeij)
Theorem 3.1
Let Meij=([κijl,κiju],[δijl,δiju]) be a collection of IVPFSNs, where (i=1,2,3…,n and j=1,2,3,…m), and the aggregated value is also an IVPFSN, such as
IVPFSWA(Me11,Me12,…,Menm)
=(1−∏j=1m(∏i=1n(1−[κijl,κiju]2)ωi)νj,∏j=1m(∏i=1n([δijl,δiju])ωi)νj)
where ωi and νj are weight vector for expert’s and attributes respectively with given conditions ωi>0,∑i=1nωi=1;νj>0,∑j=1mνj=1.
Proof. We shall prove the IVPFSWA operator by utilizing the principle of mathematical induction:
For n=1, we get ω1=1. Then, we have
IVPFSWA(Me11,Me12,…,Me1m)=⊕j=1mνjMe1j
IVPFSWA(Me11,Me12,…,Menm)=(1−∏j=1m(1−[κ1jl,κ1ju]2)νj,∏j=1m([δ1jl,δ1ju])νj)
=(1−∏j=1m(∏i=11(1−[κijl,κiju]2)ωi)νj,∏j=1m(∏i=11([δijl,δiju])ωi)νj).
For m=1, we get ν1=1. Then, we have
IVPFSWA(Me11,Me21,…,Men1)=⊕i=1nωiMei1
=(1−∏i=1n(1−[κi1l,κi1u]2)ωi,∏i=1n([δi1l,δ1iu])ωi)
=(1−∏j=11(∏i=1n(1−[κijl,κiju]2)ωi)νj,∏j=11(∏i=1n([δijl,δiju])ωi)νj)
This shows that the above theorem holds for n=1 and m=1. Now, consider the above theorem also holds for m=α1+1,n=α2 and m=α1,n=α2+1, such as
⊕j=1α1+1νj(⊕i=1α2ωiMeij)=(1−∏j=1α1+1(∏i=1α2(1−[κijl,κiju]2)ωi)νj,∏j=1α1+1(∏i=1α2([δijl,δiju])ωi)νj)
⊕j=1α1νj(⊕i=1α2+1ωiMeij)=(1−∏j=1α1(∏i=1α2+1(1−[κijl,κiju]2)ωi)νj,∏j=1α1(∏i=1α2+1([δijl,δiju])ωi)νj)
For m=α1+1 and n=α2+1, we have
⊕j=1α1+1νj(⊕i=1α2+1ωiMeij)=⊕j=1α1+1νj(⊕i=1α2ωiMeij⊕ωα2+1Me(α2+1)j)
=⊕j=1α1+1⊕i=1α2νjωiMeij⊕j=1α1+1νjωα2+1Me(α2+1)j
=(1−∏j=1α1+1(∏i=1α2(1−[κijl,κiju]2)ωi)νj⊕1−∏j=1α1+1((1−[κ(α2+1)jl,κ(α2+1)ju]2)ωα2+1)νj,
∏j=1α1+1(∏i=1α2([δijl,δiju])ωi)νj⊕∏j=1α1+1(([δ(α2+1)jl,δ(α2+1)ju])ω(α2+1))νj)
=(1−∏j=1α1+1(∏i=1α2+1(1−[κijl,κiju]2)ωi)νj,∏j=1α1+1(∏i=1α2+1([δijl,δiju])ωi)νj)
Therefore, it holds for m=α1+1 and n=α2+1. So, we can judge that the above theorem also holds for all values of m and n.
Example 3.1
Let χ={x1,x2,x3} be the set of specialists with weights ωi=(0.38,0.45,0.17)T who wants to choose a bike under some defined set of properties φ={e1=Resale Value,e2=Mileage,e3=Cost of bike} with weights νj=(0.25,0.45,0.3)T. We suppose the rating values of the specialists for each property in the form of IVPFSNs (M,φ)=([κijl,κiju],[δijl,δiju])3×3 is given as
(M,φ)=[([0.3,0.8],[0.4,0.5])([0.4,0.6],[0.3,0.7])([0.5,0.8],[0.5,0.6])([0.1,0.5],[0.2,0.3])([0.3,0.8],[0.5,0.7])([0.2,0.4],[0.2,0.3])([0.2,0.9],[0.2,0.3])([0.5,0.7],[0.2,0.6])([0.2,0.4],[0.2,0.8])]
By using the above theorem, we have
IVPFSWA(Me11,Me12,…,Me33)=(1−∏j=13(∏i=13(1−[κijl,κiju]2)ωi)νj,∏j=13(∏i=13([δijl,δiju])ωi)νj)
=(1−({[0.36,0.91]0.38[0.64,0.84]0.45[0.36,0.75]0.17}0.17{[0.75,0.99]0.38[0.36,0.91]0.45[0.75,0.99]0.17}0.45{[0.19,0.96]0.38[0.51,0.75]0.45[0.84,0.96]0.17}0.3),({[0.4,0.5]0.38[0.3,0.7]0.45[0.5,0.6]0.17}0.25{[0.2,0.7]0.38[0.5,0.7]0.45[0.2,0.3]0.17}0.45{[0.2,0.3]0.38[0.2,0.6]0.45[0.2,0.8]0.17}0.3))
=(1−({[0.6783,0.9648][0.8181,0.9245][0.8406,0.9523]}0.25{[0.8964,0.9962][0.6314,0.9584][0.9523,0.9983]}0.45{[0.5320,0.9846][0.7386,0.8786][0.9708,0.9931]}0.3),({[0.7060,0.7486][0.5817,0.8517][0.8888,0.9168]}0.25{[0.5425,0.8732][0.7320,0.8517][0.7606,0.8149]}0.45{[0.5425,0.6329][0.4847,0.7946][0.7606,0.9628]}0.3))
=(1−([0.4665,0.8494]0.25[0.5390,0.9531]0.45[0.3815,0.8591]0.3),([0.3650,0.5857]0.25[0.3020,0.6060]0.45[0.2000,0.4842]0.3))
=(1−([0.8264,0.9600][0.7572,0.9786][0.7489,0.9555]),([0.7773,0.8748][0.5834,0.7982][0.6170,0.8045]))
=(1−[0.7773,0.8977],[0.2798,0.5617])
=([0.1023,0.2227],[0.2798,0.5617])
=([0.3198,0.4719],[0.2798,0.5617])
3.3 Properties of PFSWA Operator
3.3.1 Idempotency
If Meij=Me=([κijl,κiju],[δijl,δiju])∀i,j, then,
IVPFSWA (Me11,Me12,…,Menm)=Me
Proof: As we know that all Meij=Me=([κijl,κiju],[δijl,δiju]),then, we have
IVPFSWA(Me11,Me12,…,Menm)
=(1−∏j=1m(∏i=1n(1−[κijl,κiju]2)ωi)νj,∏j=1m(∏i=1n([δijl,δiju])ωi)νj)
=(1−((1−[κijl,κiju]2)∑i=1nωi)∑j=1mνj,(([δijl,δiju])∑i=1nωi)∑j=1mνj)
As ∑j=1mνj=1 and ∑i=1nωi=1, then we have
=(1−(1−[κijl,κiju]2),[δijl,δiju])
=([κijl,κiju],[δijl,δiju])
=Me
Hence proved.
3.3.2 Boundedness
Let Meij be a collection of PFSNs where Meij−=(minj mini{[κijl,κiju]},maxj maxi{[δijl,δiju]}) and Meij+=(maxj maxi{[κijl,κiju]},minj mini{[δijl,δiju]}), then
Meij−≤IVPFSWA (Me11,Me12,…,Menm)≤Meij+
Proof. As we know that Meij=⟨[κijl,κiju],[δijl,δiju]⟩ be an IVPFSN, then
minj mini{[κijl,κiju]2}≤[κijl,κiju]2≤maxj maxi{[κijl,κiju]2}
⇒1−maxj maxi{[κijl,κiju]2}≤1−[κijl,κiju]2≤1−minj mini{[κijl,κiju]2}
⇔(1−maxj maxi{[κijl,κiju]2})ωi≤(1−[κijl,κiju]2)ωi≤(1−minj mini{[κijl,κiju]2})ωi
⇔(1−maxj maxi{[κijl,κiju]2})∑i=1nωi≤∏i=1n(1−[κijl,κiju]2)ωi≤(1−minj mini{[κijl,κiju]2})∑i=1nωi
⇔(1−maxj maxi{[κijl,κiju]2})∑j=1nνj≤∏j=1m(∏i=1n(1−[κijl,κiju]2)ωi)νj≤(1−minj mini{[κijl,κiju]2})∑j=1nνj
⇔1−maxj maxi{[κijl,κiju]2}≤∏j=1m(∏i=1n(1−[κijl,κiju]2)ωi)νj≤1−minj mini{[κijl,κiju]2}
⇔minjmini{[κijl,κiju]2}≤1−∏j=1m(∏i=1n(1−[κijl,κiju]2)ωi)νj≤maxj maxi{[κijl,κiju]2}
⇔minj mini{[κijl,κiju]}≤1−∏j=1m(∏i=1n(1−[κijl,κiju]2)ωi)νj≤maxj maxi{[κijl,κiju]} (a)
Similarly, we can prove that
minj mini{[δijl,δiju]}≤∏j=1m(∏i=1n([δijl,δiju])ωi)νj≤maxj maxi{[δijl,δiju]} (b)
Let IVPFSWA (Me11,Me12,…,Menm)=⟨[κσl,κσu],[δσl,δσu]⟩=Mσ, then inequalities (a) and (b) can be transferred into the form: minj mini{[κijl,κiju]}≤Mσ≤maxj maxi{[κijl,κiju]} and minj mini {[δijl,δiju]}≤Mσ≤maxj maxi{[δijl,δiju]}, respectively.
So, by using the score function, we have
S(Mσ)=(κσl)2+(κσu)2−(δσl)2−(δσu)22≤maxj maxi{[κijl,κiju]}−minj mini{[δijl,δiju]}
=S(Meij−)
S(Mσ)=(κσl)2+(κσu)2−(δσl)2−(δσu)22≥minj mini{[κijl,κiju]}−maxj maxi{[δijl,δiju]}=S(Meij+)
Then, by order relation between two IVPFSNs, we have
Meij−≤IVPFSWA (Me11,Me12,…,Menm)≤Meij+
Hence proved.
3.3.3 Shift Invariance
If Me=⟨[κl,κu],[δl,δu]⟩ be an IVPFSN, then
IVPFSWA(Me11⊕Me,Me12⊕Me,…,Menm⊕Me)=IVPFSWA (Me11,Me12,…,Menm)⊕Me
Proof. Consider Me and Meij be two IVPFSNs. Then, by operational laws defined under IVPFSNs defined above, we have
Me⊕Meij=([κl,κu]+[κijl,κiju]2−[κl,κu][κijl,κiju]2,[δl,δu][δijl,δiju]),therefore
IVPFSWA (Me11⊕Me,Me12⊕Me,…,Menm⊕Me)=⊕j=1mνj(⊕i=1nωi(Meij⊕Me))
=(1−∏j=1m(∏i=1n(1−[κijl,κiju]2)ωi(1−[κl,κu]2)ωi)νj,∏j=1m(∏i=1n([δijl,δiju])ωi([δl,δu])ωi)νj)
=(1−(1−[κl,κu]2)∏j=1m(∏i=1n(1−[κijl,κiju]2)ωi)νj,[δl,δu]∏j=1m(∏i=1n([δijl,δiju])ωi)νj)
=((1−∏j=1m(∏i=1n(1−[κijl,κiju]2)ωi)νj,∏j=1m(∏i=1n([δijl,δiju])ωi)νj)⊕([κl,κu],[δl,δu]))
=IVPFSWA (Me11,Me12,…,Menm)⊕Me
Hence proved.
3.3.4 Homogeneity
Prove that IVPFSWA (βMe11,βMe12,…,βMenm)=βIVPFSWA (Me11,Me12,…,Menm) for any positive real number β.
Proof. Let Meij be an IVPFSN and β>0, then by using the operational laws mentioned above, we have
βMeij=(1−(1−[κijl,κiju]2)β,[δijl,δiju]β)
So,
βMe11,βMe12,…,βMenm)
=(1−∏j=1m(∏i=1n(1−[κijl,κiju]2)βωi)νj,∏j=1m(∏i=1n([δijl,δiju])βωi)νj)
=(1−(∏j=1m(∏i=1n(1−[κijl,κiju]2)ωi)νj)β,(∏j=1m(∏i=1n([δijl,δiju])ωi)νj)β)
=β IVPFSWA (Me11,Me12,…,Menm)
which completes the proof.
3.4 Interval Valued Pythagorean Fuzzy Soft Weighted Geometric Operator
Let Meij=⟨[κijl,κiju],[δijl,δiju]⟩ be a collection of interval-valued Pythagorean fuzzy soft numbers (IVPFSNs), and ωi and νj are the weight vector for experts and parameters, respectively, with given conditions ωi>0,∑i=1nωi=1;νj>0,∑j=1mνj=1. Then, the IVPFSWG operator is defined as IVPFSWG: Ψn⟶Ψ
IVPFSWG (Me11,Me12,…,Menm)=⊗j=1m(⊗i=1nMeijωi)νj
Theorem 3.2
Let Meij=⟨[κijl,κiju],[δijl,δiju]⟩ be a collection of interval-valued Pythagorean fuzzy soft numbers (IVPFSNs). Then, the aggregated value obtained by using the IVPFSWG operator is also IVPFSN and
IVPFSWG (Me11,Me12,…,Menm)
=(∏j=1m(∏i=1n([κijl,κiju])ωi)νj,1−∏j=1m(∏i=1n(1−[δijl,δiju]2)ωi)νj)
where ωi and νj are weight vector for expert’s and attributes respectively with given conditions ωi>0,∑i=1nωi=1;νj>0,∑j=1mνj=1.
Proof. We can prove the IVPFSWG operator by using the principle of mathematical induction as follows:
For n=1, we get ω1=1. Then, we have
IVPFSWG(Me11,Me12,…,Me1m)=⊗j=1mMe1jνj
IVPFSWG (Me11,Me12,…,Menm)
=(∏j=1m([κ1jl,κ1ju])νj,1−∏j=1m(1−[δ1jl,δ1ju]2)νj)
=(∏j=1m(∏i=11([κijl,κiju])ωi)νj,1−∏j=1m(∏i=11(1−[δijl,δiju]2)ωi)νj).
For m=1, we get ν1=1. Then, we have
IVPFSWG(Me11,Me21,…,Men1)=⊗i=1n(Mei1)ωi
=(∏i=1n([κi1l,κ1iu])ωi,1−∏i=1n(1−[δi1l,δi1u]2)ωi)
=(∏j=11(∏i=1n([κijl,κiju])ωi)νj,1−∏j=11(∏i=1n(1−[δijl,δiju]2)ωi)νj)
This shows that the above theorem holds for n=1 and m=1. Now, consider the above theorem also holds for m=α1+1,n=α2 and m=α1,n=α2+1, such as
⊗j=1α1+1(⊗i=1α2(Meij)ωi)νj
=(∏j=1α1+1(∏i=1α2([κijl,κiju])ωi,1−∏j=1α1+1(∏i=1α2(1−[δijl,δiju]2)ωi)νj)νj)
⊗j=1α1(⊗i=1α2+1(Meij)ωi)νj
=(∏j=1α1(∏i=1α2+1([κijl,δiju])ωi)νj,1−∏j=1α1(∏i=1α2+1(1−[δijl,δiju]2)ωi)νj)
For m=α1+1 and n=α2+1, we have
⊗j=1α1+1(⊗i=1α2+1(Meij)ωi)νj=⊗j=1α1+1(⊗i=1α2(Meij)ωi⊗(Me(α2+1)j)ωα2+1)νj
=⊗j=1α1+1⊗i=1α2((Meij)ωi)νj⊗j=1α1+1((Me(α2+1)j)ωα2+1)νj
=(∏j=1α1+1(∏i=1α2([κijl,κiju])ωi)νj⊗∏j=1α1+1(([κ(α2+1)jl,κ(α2+1)ju])ω(α2+1))νj,
1−∏j=1α1+1(∏i=1α2(1−[δijl,δiju]2)ωi)νj⊗1−∏j=1α1+1((1−[δ(α2+1)jl,δ(α2+1)ju]2)ωα2+1)νj)
=(∏j=1α1+1(∏i=1α2+1([κijl,κiju])ωi)νj,1−∏j=1α1+1(∏i=1α2+1(1−[δijl,δiju]2)ωi)νj)
It is clarified from the above equation that the theorem holds for m=α1+1 and n=α2+1. So, we can say that the theorem holds for all values of m and n.
Example 3.2
Again, consider Example 3.1 with rating values of the specialists for each property in the form of IVPFSNs (M,φ)=([κijl,κiju],[δijl,δiju])3×3 is given as
(M,φ)=[([0.4,0.5],[0.3,0.8])([0.3,0.7][0.4,0.6])([0.5,0.6],[0.5,0.8])([0.2,0.3],[0.1,0.5])([0.5,0.7],[0.3,0.8])([0.2,0.3],[0.2,0.4])([0.2,0.3],[0.2,0.9])([0.2,0.6],[0.5,0.7])([0.2,0.8],[0.2,0.4])]
By using the above theorem, we have
IVPFSWG(Me11,Me12,…,Me33)
=(∏j=13(∏i=13([κijl,κiju])ωi)νj,1−∏j=13(∏i=13(1−[δijl,δiju]2)ωi)νj)
=(({[0.4,0.5]0.38[0.3,0.7]0.45[0.5,0.6]0.17}0.25{[0.2,0.7]0.38[0.5,0.7]0.45[0.2,0.3]0.17}0.45{[0.2,0.3]0.38[0.2,0.6]0.45[0.2,0.8]0.17}0.3),1−({[0.36,0.91]0.38[0.64,0.84]0.45[0.36,0.75]0.17}0.17{[0.75,0.99]0.38[0.36,0.91]0.45[0.75,0.99]0.17}0.45{[0.19,0.96]0.38[0.51,0.75]0.45[0.84,0.96]0.17}0.3))
=(({[0.7060,0.7486][0.5817,0.8517][0.8888,0.9168]}0.25{[0.5425,0.8732][0.7320,0.8517][0.7606,0.8149]}0.45{[0.5425,0.6329][0.4847,0.7946][0.7606,0.9628]}0.3),1−({[0.6783,0.9648][0.8181,0.9245][0.8406,0.9523]}0.25{[0.8964,0.9962][0.6314,0.9584][0.9523,0.9983]}0.45{[0.5320,0.9846][0.7386,0.8786][0.9708,0.9931]}0.3))
=(([0.3650,0.5857]0.25[0.3020,0.6060]0.45[0.2000,0.4842]0.3),1−([0.4665,0.8494]0.25[0.5390,0.9531]0.45[0.3815,0.8591]0.3))
=(([0.7773,0.8748][0.5834,0.7982][0.6170,0.8045])1−([0.8264,0.9600][0.7572,0.9786][0.7489,0.9555]))
=([0.2798,0.5617],1−[0.7773,0.8977])
=([0.2798,0.5617],[0.1023,0.2227])
=([0.2798,0.5617],[0.3198,0.4719])
3.5 Properties of IVPFSWG
3.5.1 Idempotency
If Meij=Me=([κijl,κiju],[δijl,δiju])∀i,j, then,
IVPFSWG (Me11,Me12,…,Menm)=Me
Proof. As we know that all Meij=Me=([κijl,κiju],[δijl,δiju]), then, we have
IVPFSWG(Me11,Me12,…,Menm)
=(∏j=1m(∏i=1n([κijl,κiju])ωi)νj,1−∏j=1m(∏i=1n(1−[δijl,δiju]2)ωi)νj)
=((([κijl,κiju])∑i=1nωi)∑j=1mνj,1−((1−[δijl,δiju]2)∑i=1nωi)∑j=1mνj)
As ∑j=1mνj=1 and ∑i=1nωi=1, then we have
=([κijl,κiju],1−(1−[δijl,δiju]2))
=([κijl,κiju],[δijl,δiju])
=Me
Hence proved.
3.5.2 Boundedness
Let Meij be a collection of PFSNs where Meij−=(minj mini{[κijl,κiju]},maxj maxi{[δijl,δiju]}) and Meij+=(maxj maxi{[κijl,κiju]},minj mini{[δijl,δiju]}), then
Meij−≤IVPFSWG (Me11,Me12,…,Menm)≤Meij+
Proof. As we know that Meij=([κijl,κiju],[δijl,δiju]) be an IVPFSN, then
minj mini{[δijl,δiju]2}≤[δijl,δiju]2≤maxj maxi{[δijl,δiju]2}
⇒1−maxj maxi{[δijl,δiju]2}≤1−[δijl,δiju]2≤1−minj mini{[δijl,δiju]2}
⇔(1−maxj maxi{[δijl,δiju]2})ωi≤(1−[δijl,δiju]2)ωi≤(1−minj mini{[δijl,δiju]2})ωi
⇔(1−maxj maxi{[δijl,δiju]2})∑i=1nωi≤∏i=1n(1−[δijl,δiju]2)ωi≤(1−minj mini{[δijl,δiju]2})∑i=1nωi
⇔(1−maxj maxi{[δijl,δiju]2})∑j=1nνj≤∏j=1m(∏i=1n(1−[δijl,δiju]2)ωi)νj≤(1−minj mini{[δijl,δiju]2})∑j=1nνj
⇔1−maxj maxi{[δijl,δiju]2}≤∏j=1m(∏i=1n(1−[δijl,δiju]2)ωi)νj≤1−minj mini{[δijl,δiju]2}
⇔minj mini{[δijl,δiju]2}≤1−∏j=1m(∏i=1n(1−[δijl,δiju]2)ωi)νj≤maxj maxi{[δijl,δiju]2}
⇔minj mini{[δijl,δiju]}≤1−∏j=1m(∏i=1n(1−[δijl,δiju]2)ωi)νj≤maxj maxi{[δijl,δiju]} (c)
Similarly, we can prove that
minj mini{[κijl,κiju]}≤∏j=1m(∏i=1n([κijl,κiju])ωi)νj≤maxj maxi{[κijl,κiju]} (d)
Let IVPFSWG (Me11,Me12,…,Menm)=⟨[κσl,κσu],[δσl,δσu]⟩=Mσ, then inequalities (c) and (d) can be transferred into the form:
minj mini{[κijl,κiju]}≤Mσ≤maxj maxi{[κijl,κiju]} and minj mini{[δijl,δiju]}≤Mσ≤maxj maxi{[δijl,δiju]}, respectively.
So, by using the score function, we have
S(Mσ)=(κσl)2+(κσu)2−(δσl)2−(δσu)22≤maxj maxi{[κijl,κiju]}−minj mini{[δijl,δiju]}=S(Meij−)
S(Mσ)=(κσl)2+(κσu)2−(δσl)2−(δσu)22≥minj mini{[κijl,κiju]}−maxj maxi{[δijl,δiju]}=S(Meij+)
Then, by order relation between two IVPFSNs, we have
Meij−≤IVPFSWG (Me11,Me12,…,Menm)≤Meij+
Hence proved.
3.5.3 Shift Invariance
If Me=([κl,κu],[δl,δu]) be an IVPFSN, then
IVPFSWG (Me11⊕Me,Me12⊕Me,…,Menm⊕Me)= IVPFSW(Me11,Me12,…,Menm)⊕Me
Proof. Consider Me and Meij be two IVPFSNs. Then, by operational laws defined under IVPFSNs defined above, we have
Me⊕Meij=([κl,κu]2+[κijl,κiju]2−[κl,κu]2[κijl,κiju]2,[δl,δu][δijl,δiju]), therefore
IVPFSWG (Me11⊕Me,Me12⊕Me,…,Menm⊕Me)
=⊕j=1mνj(⊕i=1nωi(Meij⊕Me))
=(∏j=1m(∏i=1n([κijl,κiju])ωi([κl,κu])ωi)νj,1−∏j=1m(∏i=1n(1−[δijl,δiju]2)ωi(1−[δl,δu]2)ωi)νj)
=([κl,κu]∏j=1m(∏i=1n([κijl,κiju])ωi)νj,1−(1−[δl,δu]2)∏j=1m(∏i=1n(1−[δijl,δiju]2)ωi)νj)
=((∏j=1m(∏i=1n([κijl,κiju])ωi)νj,1−∏j=1m(∏i=1n(1−[δijl,δiju]2)ωi)νj)⊕([κl,κu],[δl,δu]))
=IVPFSWG (Me11,Me12,…,Menm)⊕Me
Hence proved.
3.5.4 Homogeneity
Prove that IVPFSWG (βMe11,βMe12,…,βMenm)=βIVPFSWA (Me11,Me12,…,Menm) for any positive real number β.
Proof: Let Meij be an IVPFSN and β>0, then by using the operational laws mentioned above, we have
βMeij=(1−(1−[κijl,κiju]2)β,[δijl,δiju]β)
So,
IVPFSWG (βMe11,βMe12,…,βMenm)
=(∏j=1m(∏i=1n([κijl,κiju])βωi)νj,1−∏j=1m(∏i=1n(1−[δijl,δiju]2)βωi)νj)
=((∏j=1m(∏i=1n([κijl,κiju])ωi)νj)β,1−(∏j=1m(∏i=1n(1−[δijl,δiju]2)ωi)νj)β)
=βIVPFSWG (Me11,Me12,…,Menm)
which completes the proof.
4 Multi-Attribute Group Decision-Making Approach Based on Proposed Operators
In this section, a decision-making (DM) approach for solving multi-attribute group decision-making (MAGDM) problems based on proposed IVPFSWA and IVPFSWG operators has been developed along with numerical examples.
4.1 Proposed Approach
Let I={I1,I2,I3,…,Is} be the set of s alternatives, X={x1,x2,x3,…xr} be the set of r specialists (decision-makers) and φ={e1,e2,e3,…,em} be the set of m attributes. Let the weighted vector of experts Xi(i=1,2,3,…,r) is ωi=(ω1,ω2,ω3,…,ωn)T such that ωi>0, ∑i=1nωi=1 and the weighted vector of attributes ei(i=1,2,3,…,m) is νj=(ν1,ν2,ν3,…,νn)T such that νj>0,∑j=1nνj=1. A team of specialists provides the decision matrix in the form of IVPFSNs such as Dm×n(Meij)=([κijl,κiju],[δijl,δiju])m×n.
The procedure to apply proposed IVPFSWG and IVPFSWA operators for solving the MAGDM problem is summarized in the following steps:
Step-1: Obtain a decision matrix in the form of PFSNs for alternatives relative to experts.
Dm×n(Meij)=([κijl,κiju],[δijl,δiju])m×n
=[([κ11l,κ11u],[δ11l,δ11u])([κ21l,κ21u],[δ21l,δ21u])([κ12l,κ12u],[δ12l,δ122u])([κ22l,κ22u],[δ22l,δ22u])⋯([κ1nl,κ1nu],[δ1nl,δ1nu])([κ2nl,κ2nu],[δ2nl,δ2nu])⋮⋱⋮([κm1l,κm1u],[δm1l,δm1u])([κm2l,κm2u],[δm2l,δm2u])⋯([κmnl,κmnu],[δmnl,δmnu])], where
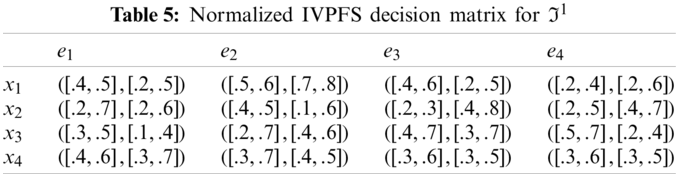
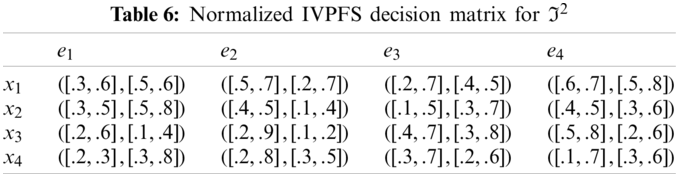
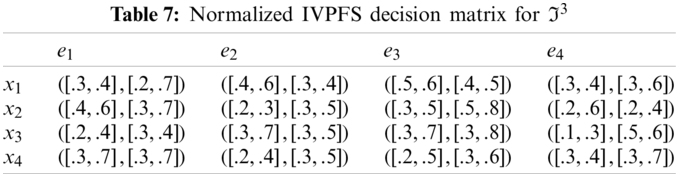
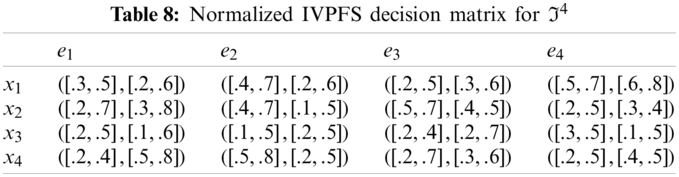
0≤κijl,κiju,δijl,δiju≤1 And 0≤(κiju)2+(δiju)2≤1 ∀i,j are given in Tables 1–4.
Step-2: By using the normalization formula, normalize the decision matrix to convert the rating value of cost type parameters into benefit type parameters.
Meij={Meijc=([κijl,κiju],[δijl,δiju])n×mcost type parameterMeij=([δijl,δiju],[κijl,κiju])n×mbenefit type parameter
Step-3: Use the developed IVPFSWG and IVPFSWA operators to aggregate the IVPFSNs Meij for each alternative I={I1,I2,I3,…,Is} into the decision matrix Mij.
Step-4: Calculate the score values of M for all alternatives.
Step-5: Select the alternative having maximum score value and examine the ranking.
4.2 Numerical Example
Suppose a person wants to buy a car and he has four alternatives such as I1, I2, I3 and I4. There are four considered attributes according to which the person has to take the decision such as e1; price of the car, e2; comfortability, e3; resale value, and,e4; growth rate with the weighted vectorν=(0.3,0.1,0.2,0.4)T. Here e1, e3 are cost type parameters and e2, e4 are benefit type parameters. The person hires a team of four experts Xr(r=1,2,3,4) for decision making with the weighted vector ω=(0.1,0.2,0.4,0.3)T.
4.2.1 By IVPFSWA Operator
Step-1: Obtain Pythagorean fuzzy soft decision matrices (Tables 1–4).




Step-2: Because e1, e3 are cost type parameters, so utilized the normalization formula to obtain normalized Pythagorean fuzzy soft decision matrices are given in the following Tables 5–8.
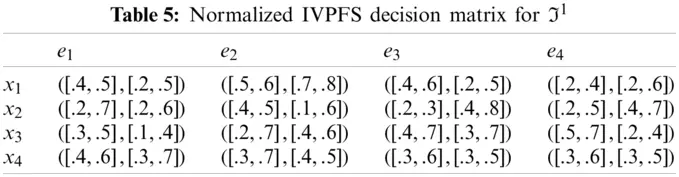
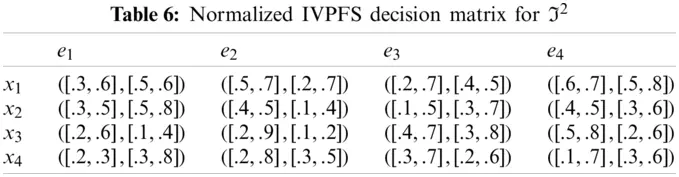
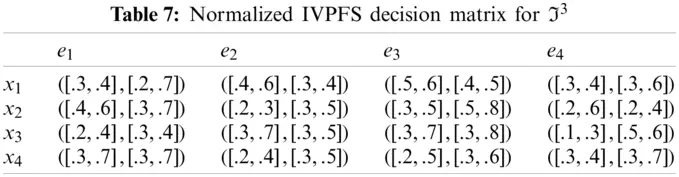
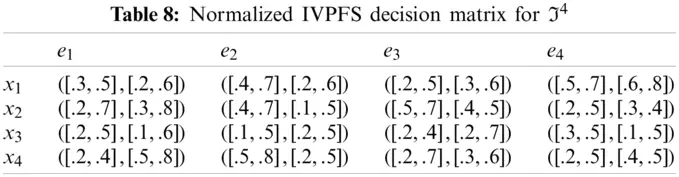
Step-3: Apply the proposed IVPFSWA operator on the acquired data, we will obtain an opinion of the decision-makers.
Θ1=(1−∏j=14(∏i=14(1−[κijl,κiju]2)ωi)νj,∏j=14(∏i=14([δijl,δiju])ωi)νj)
=(1−({[0.75,0.84]0.1[0.64,0.75]0.2[0.64,0.84]0.4[0.84,0.96]0.3}0.3{[0.51,0.96]0.1[0.75,0.84]0.2[0.91,0.96]0.4[0.75,0.96]0.3}0.1{[0.75,0.91]0.1[0.51,0.96]0.2[0.51,0.84]0.4[0.75,0.91]0.3}0.2{[0.64,0.84]0.1[0.51,0.91]0.2[0.64,0.91]0.4[0.64,0.91]0.3}0.4),({[0.2,0.5]0.1[0.7,0.8]0.2[0.2,0.5]0.4[0.2,0.6]0.3}0.3{[0.2,0.6]0.1[0.1,0.6]0.2[0.4,0.8]0.4[0.4,0.7]0.3}0.1{[0.1,0.4]0.1[0.4,0.6]0.2[0.3,0.7]0.4[0.2,0.4]0.3}0.2{[0.3,0.7]0.1[0.4,0.5]0.2[0.3,0.5]0.4[0.3,0.5]0.3}0.4))
=(1−({[0.9716,0.9827][0.9146,0.9441][0.8365,0.9326][0.9490,0.9878]}0.3{[0.9349,0.9949][0.9441,0.9657][0.9629,0.9838][0.9173,0.9876]}0.1{[0.9716,0.9906][0.8740,0.9919][0.7639,0.9326][0.9173,0.9721]}0.2{[0.9564,0.9827][0.8740,0.9813][0.8365,0.9630][0.8747,0.9721]}0.4),({[0.8513,0.9330][0.9311,0.9564][0.5253,0.7579][0.6170,0.8579]}0.3{[0.8513,0.9502][0.6310,0.9029][0.6931,0.9146][0.7597,0.8985]}0.1{[0.7943,0.9124][0.8326,0.9029][0.6178,0.8670][0.6170,0.7597]}0.2{[0.8866,0.9650][0.8326,0.8706][0.6178,0.7578][0.6968,0.8123]}0.4))
=([0.3401,0.5912],[0.2813,0.5574])
Θ2=(1−∏j=14(∏i=14(1−[κijl,κiju]2)ωi)νj,∏j=14(∏i=14([δijl,δiju])ωi)νj)
=(1−({[0.64,0.91]0.1[0.51,0.75]0.2[0.51,0.96]0.4[0.51,0.64]0.3}0.3{[0.75,0.91]0.1[0.75,0.84]0.2[0.75,0.99]0.4[0.75,0.84]0.3}0.1{[0.64,0.96]0.1[0.96,0.99]0.2[0.51,0.84]0.4[0.36,0.75]0.3}0.2{[0.91,0.96]0.1[0.36,0.96]0.2[0.51,0.91]0.4[0.51,0.99]0.3}0.4),({[0.5,0.6]0.1[0.2,0.7]0.2[0.4,0.5]0.4[0.5,0.8]0.3}0.3{[0.5,0.8]0.1[0.1,0.4]0.2[0.3,0.7]0.4[0.3,0.6]0.3}0.1{[0.1,0.4]0.1[0.1,0.2]0.2[0.3,0.8]0.4[0.2,0.6]0.3}0.2{[0.3,0.8]0.1[0.3,0.5]0.2[0.2,0.6]0.4[0.3,0.6]0.3}0.4))
=(1−({[0.9564,0.9906][0.8740,0.9441][0.7639,0.9838][0.8171,0.8747]}0.3{[0.9716,0.9906][0.9441,0.9657][0.8913,0.9960][0.9173,0.9490]}0.1{[0.9564,0.9960][0.9919,0.9980][0.7639,0.9326][0.7360,0.9173]}0.2{[0.9906,0.9959][0.8152,0.9919][0.7639,0.9630][0.8171,0.9970]}0.4),({[0.9330,0.9502][0.7248,0.9311][0.6931,0.7579][0.8123,0.9352]}0.3{[0.9330,0.9779][0.6310,0.8326][0.6178,0.8670][0.6968,0.8579]}0.1{[0.7943,0.9124][0.6310,0.7248][0.6178,0.9146][0.6170,0.8579]}0.2{[0.8866,0.9780][0.7860,0.8706][0.5253,0.8152][0.6968,0.8579]}0.4))
=([0.3470,0.6811],[0.2713,0.5864])
Θ3=(1−∏j=14(∏i=14(1−[κijl,κiju]2)ωi)νj,∏j=14(∏i=14([δijl,δiju])ωi)νj)
=(1−({[0.84,0.91]0.1[0.64,0.84]0.2[0.64,0.75]0.4[0.84,0.91]0.3}0.3{[0.64,0.84]0.1[0.91,0.96]0.2[0.75,0.91]0.4[0.64,0.96]0.3}0.1{[0.84,0.96]0.1[0.51,0.91]0.2[0.51,0.91]0.4[0.91,0.99]0.3}0.2{[0.51,0.91]0.1[0.84,0.96]0.2[0.75,0.96]0.4[0.84,0.91]0.3}0.4),({[0.2,0.7]0.1[0.3,0.4]0.2[0.4,0.5]0.4[0.3,0.6]0.3}0.3{[0.3,0.7]0.1[0.3,0.5]0.2[0.5,0.8]0.4[0.2,0.4]0.3}0.1{[0.3,0.4]0.1[0.3,0.5]0.2[0.3,0.8]0.4[0.5,0.6]0.3}0.2{[0.3,0.7]0.1[0.3,0.5]0.2[0.3,0.6]0.4[0.3,0.7]0.3}0.4))
=(1−({[0.9827,0.9906][0.9146,0.9657][0.8365,0.8913][0.9490,0.9721]}0.3{[0.9564,0.9827][0.9813,0.9919][0.8913,0.9630][0.8747,0.9878]}0.1{[0.9827,0.9959][0.8740,0.9813][0.7639,0.9630][0.9721,0.9970]}0.2{[0.9349,0.9906][0.9657,0.9919][0.8913,0.9838][0.9490,0.9721]}0.4),({[0.8513,0.9649][0.7860,0.8326][0.6931,0.7579][0.6968,0.8579]}0.3{[0.8865,0.9650][0.7860,0.8706][0.7579,0.9146][0.6170,0.7597]}0.1{[0.8866,0.9124][0.7860,0.8326][0.6178,0.9146][0.8123,0.8579]}0.2{[0.8866,0.9650][0.7860,0.8706][0.6178,0.8152][0.6968,0.8985]}0.4))
=([0.3114,0.5751],[0.3190,0.5509])
Θ4=(1−∏j=14(∏i=14(1−[κijl,κiju]2)ωi)νj,∏j=14(∏i=14([δijl,δiju])ωi)νj)
=(1−({[0.75,0.91]0.1[0.51,0.84]0.2[0.75,0.96]0.4[0.51,0.75]0.3}0.3{[0.51,0.96]0.1[0.51,0.84]0.2[0.51,0.75]0.4[0.75,0.96]0.3}0.1{[0.75,0.96]0.1[0.75,0.99]0.2[0.84,0.96]0.4[0.75,0.91]0.3}0.2{[0.84,0.96]0.1[0.36,0.75]0.2[0.51,0.96]0.4[0.75,0.96]0.3}0.4),({[0.2,0.6]0.1[0.2,0.6]0.2[0.3,0.6]0.4[0.6,0.8]0.3}0.3{[0.3,0.8]0.1[0.1,0.5]0.2[0.4,0.5]0.4[0.3,0.4]0.3}0.1{[0.1,0.6]0.1[0.2,0.5]0.2[0.2,0.7]0.4[0.1,0.5]0.3}0.2{[0.5,0.8]0.1[0.2,0.5]0.2[0.3,0.6]0.4[0.4,0.5]0.3}0.4))
=(1−({[0.9716,0.9906][0.8740,0.9657][0.8913,0.9838][0.8171,0.9173]}0.3{[0.9349,0.9959][0.8740,0.9657][0.7639,0.8913][0.9173,0.9878]}0.1{[0.9716,0.9959][0.9441,0.9980][0.9326,0.9838][0.9173,0.9721]}0.2{[0.9827,0.9959][0.8151,0.9441][0.7639,0.9838][0.9173,0.9878]}0.4),({[0.8513,0.9502][0.7248,0.9029][0.6178,0.8151][0.8579,0.9352]}0.3{[0.8866,0.9779][0.6310,0.8706][0.6931,0.7579][0.6968,0.7597]}0.1{[0.7943,0.9502][0.7248,0.8706][0.5253,0.8670][0.5012,0.8122]}0.2{[0.9330,0.9779][0.7248,0.8706][0.6078,0.8152][0.7597,0.8123]}0.4))
=([0.3162,0.7856],[0.2701,0.6137]).
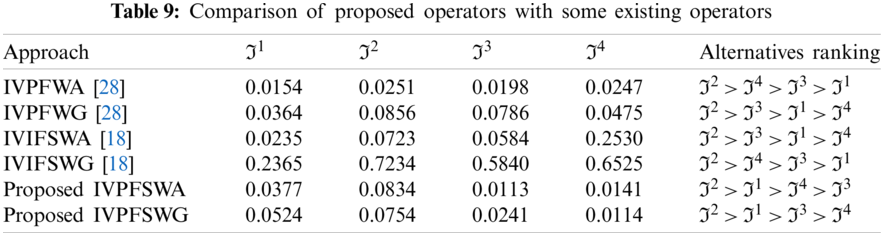
Step-4: Use the score function S=(κl)2+(κu)2−(δl)2−(δu)22 for the interval-valued Pythagorean fuzzy soft set to calculate the score values for all alternatives. S(Θ1)=0.0377, S(Θ2)=0.0834, S(Θ3)=0.0113, and S(Θ4)=0.0141.
Step-5: From the above calculation, we get S(Θ2)>S(Θ1)>S(Θ4)>S(Θ3), which shows that I2 is the best alternative. So, I2>I1>I4>I3.
4.2.2 By IVPFSWG Operator
Step-1: Obtain PFS decision matrices (Tables 1–4).
Step-2: Use the normalization formula to normalize the obtained PFS decision matrices (Tables 5–8).
Step-3: Apply the proposed IVPFSWG operator on the acquired data, we will obtain an opinion of the decision-makers
Θ1=(∏j=14(∏i=14([κijl,κiju])ωi)νj,1−∏j=14(∏i=14(1−[δijl,δiju]2)ωi)νj)
=(,({[0.2,0.5]0.1[0.7,0.8]0.2[0.2,0.5]0.4[0.2,0.6]0.3}0.3{[0.2,0.6]0.1[0.1,0.6]0.2[0.4,0.8]0.4[0.4,0.7]0.3}0.1{[0.1,0.4]0.1[0.4,0.6]0.2[0.3,0.7]0.4[0.2,0.4]0.3}0.2{[0.3,0.7]0.1[0.4,0.5]0.2[0.3,0.5]0.4[0.3,0.5]0.3}0.4),1−({[0.75,0.84]0.1[0.64,0.75]0.2[0.64,0.84]0.4[0.84,0.96]0.3}0.3{[0.51,0.96]0.1[0.75,0.84]0.2[0.91,0.96]0.4[0.75,0.96]0.3}0.1{[0.75,0.91]0.1[0.51,0.96]0.2[0.51,0.84]0.4[0.75,0.91]0.3}0.2{[0.64,0.84]0.1[0.51,0.91]0.2[0.64,0.91]0.4[0.64,0.91]0.3}0.4))
=(({[0.8513,0.9330][0.9311,0.9564][0.5253,0.7579][0.6170,0.8579]}0.3{[0.8513,0.9502][0.6310,0.9029][0.6931,0.9146][0.7597,0.8985]}0.1{[0.7943,0.9124][0.8326,0.9029][0.6178,0.8670][0.6170,0.7597]}0.2{[0.8866,0.9650][0.8326,0.8706][0.0.6178,0.7578][0.6968,0.8123]}0.4),1−({[0.9716,0.9827][0.9146,0.9441][0.8365,0.9326][0.9490,0.9878]}0.3{[0.9349,0.9949][0.9441,0.9657][0.9629,0.9838][0.9173,0.9876]}0.1{[0.9716,0.9906][0.8740,0.9919][0.7639,0.9326][0.9173,0.9721]}0.2{[0.9564,0.9827][0.8740,0.9813][0.8365,0.9630][0.8747,0.9721]}0.4))
=([0.7975,0.8569],[0.6395,0.7586])
Θ2=(∏j=14(∏i=14([κijl,κiju])ωi)νj,1−∏j=14(∏i=14(1−[δijl,δiju]2)ωi)νj)
=(,({[0.2,0.5]0.1[0.7,0.8]0.2[0.2,0.5]0.4[0.2,0.6]0.3}0.3{[0.2,0.6]0.1[0.1,0.6]0.2[0.4,0.8]0.4[0.4,0.7]0.3}0.1{[0.1,0.4]0.1[0.4,0.6]0.2[0.3,0.7]0.4[0.2,0.4]0.3}0.2{[0.3,0.7]0.1[0.4,0.5]0.2[0.3,0.5]0.4[0.3,0.5]0.3}0.4),1−({[0.75,0.84]0.1[0.64,0.75]0.2[0.64,0.84]0.4[0.84,0.96]0.3}0.3{[0.51,0.96]0.1[0.75,0.84]0.2[0.91,0.96]0.4[0.75,0.96]0.3}0.1{[0.75,0.91]0.1[0.51,0.96]0.2[0.51,0.84]0.4[0.75,0.91]0.3}0.2{[0.64,0.84]0.1[0.51,0.91]0.2[0.64,0.91]0.4[0.64,0.91]0.3}0.4))
=(({[0.8513,0.9330][0.9311,0.9564][0.5253,0.7579][0.6170,0.8579]}0.3{[0.8513,0.9502][0.6310,0.9029][0.6931,0.9146][0.7597,0.8985]}0.1{[0.7943,0.9124][0.8326,0.9029][0.6178,0.8670][0.6170,0.7597]}0.2{[0.8866,0.9650][0.8326,0.8706][0.0.6178,0.7578][0.6968,0.8123]}0.4),1−({[0.9716,0.9827][0.9146,0.9441][0.8365,0.9326][0.9490,0.9878]}0.3{[0.9349,0.9949][0.9441,0.9657][0.9629,0.9838][0.9173,0.9876]}0.1{[0.9716,0.9906][0.8740,0.9919][0.7639,0.9326][0.9173,0.9721]}0.2{[0.9564,0.9827][0.8740,0.9813][0.8365,0.9630][0.8747,0.9721]}0.4))
=([0.5643,0.8978],[0.5206,0.7452])
Θ3=(∏j=14(∏i=14([κijl,κiju])ωi)νj,1−∏j=14(∏i=14(1−[δijl,δiju]2)ωi)νj)
=(,({[0.2,0.5]0.1[0.7,0.8]0.2[0.2,0.5]0.4[0.2,0.6]0.3}0.3{[0.2,0.6]0.1[0.1,0.6]0.2[0.4,0.8]0.4[0.4,0.7]0.3}0.1{[0.1,0.4]0.1[0.4,0.6]0.2[0.3,0.7]0.4[0.2,0.4]0.3}0.2{[0.3,0.7]0.1[0.4,0.5]0.2[0.3,0.5]0.4[0.3,0.5]0.3}0.4),1−({[0.75,0.84]0.1[0.64,0.75]0.2[0.64,0.84]0.4[0.84,0.96]0.3}0.3{[0.51,0.96]0.1[0.75,0.84]0.2[0.91,0.96]0.4[0.75,0.96]0.3}0.1{[0.75,0.91]0.1[0.51,0.96]0.2[0.51,0.84]0.4[0.75,0.91]0.3}0.2{[0.64,0.84]0.1[0.51,0.91]0.2[0.64,0.91]0.4[0.64,0.91]0.3}0.4))
=(({[0.8513,0.9330][0.9311,0.9564][0.5253,0.7579][0.6170,0.8579]}0.3{[0.8513,0.9502][0.6310,0.9029][0.6931,0.9146][0.7597,0.8985]}0.1{[0.7943,0.9124][0.8326,0.9029][0.6178,0.8670][0.6170,0.7597]}0.2{[0.8866,0.9650][0.8326,0.8706][0.0.6178,0.7578][0.6968,0.8123]}0.4),1−({[0.9716,0.9827][0.9146,0.9441][0.8365,0.9326][0.9490,0.9878]}0.3{[0.9349,0.9949][0.9441,0.9657][0.9629,0.9838][0.9173,0.9876]}0.1{[0.9716,0.9906][0.8740,0.9919][0.7639,0.9326][0.9173,0.9721]}0.2{[0.9564,0.9827][0.8740,0.9813][0.8365,0.9630][0.8747,0.9721]}0.4))
=([0.6325,0.9658],[0.2365,0.5263])
Θ4=(∏j=14(∏i=14([κijl,κiju])ωi)νj,1−∏j=14(∏i=14(1−[δijl,δiju]2)ωi)νj)
=(,({[0.2,0.5]0.1[0.7,0.8]0.2[0.2,0.5]0.4[0.2,0.6]0.3}0.3{[0.2,0.6]0.1[0.1,0.6]0.2[0.4,0.8]0.4[0.4,0.7]0.3}0.1{[0.1,0.4]0.1[0.4,0.6]0.2[0.3,0.7]0.4[0.2,0.4]0.3}0.2{[0.3,0.7]0.1[0.4,0.5]0.2[0.3,0.5]0.4[0.3,0.5]0.3}0.4),1−({[0.75,0.84]0.1[0.64,0.75]0.2[0.64,0.84]0.4[0.84,0.96]0.3}0.3{[0.51,0.96]0.1[0.75,0.84]0.2[0.91,0.96]0.4[0.75,0.96]0.3}0.1{[0.75,0.91]0.1[0.51,0.96]0.2[0.51,0.84]0.4[0.75,0.91]0.3}0.2{[0.64,0.84]0.1[0.51,0.91]0.2[0.64,0.91]0.4[0.64,0.91]0.3}0.4))
=(({[0.8513,0.9330][0.9311,0.9564][0.5253,0.7579][0.6170,0.8579]}0.3{[0.8513,0.9502][0.6310,0.9029][0.6931,0.9146][0.7597,0.8985]}0.1{[0.7943,0.9124][0.8326,0.9029][0.6178,0.8670][0.6170,0.7597]}0.2{[0.8866,0.9650][0.8326,0.8706][0.0.6178,0.7578][0.6968,0.8123]}0.4),1−({[0.9716,0.9827][0.9146,0.9441][0.8365,0.9326][0.9490,0.9878]}0.3{[0.9349,0.9949][0.9441,0.9657][0.9629,0.9838][0.9173,0.9876]}0.1{[0.9716,0.9906][0.8740,0.9919][0.7639,0.9326][0.9173,0.9721]}0.2{[0.9564,0.9827][0.8740,0.9813][0.8365,0.9630][0.8747,0.9721]}0.4))
=([0.4525,0.5469],[0.1253,0.5263]).
Step-4: Use the score function S=(κl)2+(κu)2−(δl)2−(δu)22 interval-valued for the Pythagorean fuzzy soft set to calculate the score values for all alternatives such as S(Θ1)=0.0524, S(Θ2)=0.0754, S(Θ3)=0.0241, and S(Θ4)=0.0114.
Step-5: From the above calculation, we get the ranking of alternatives S(Θ2)>S(Θ1)>S(Θ3)>S(Θ4), which shows that I2 is the best alternative. So, I2>I1>I3>I4.
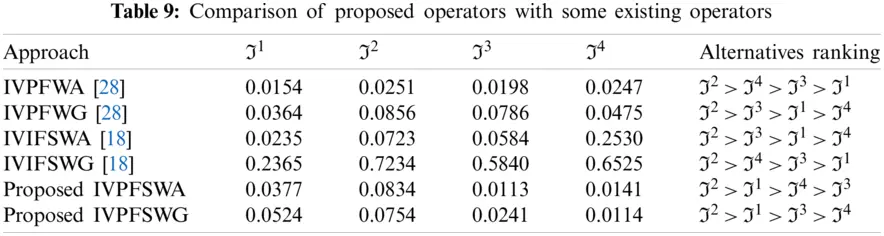
5 Comparative Studies
To highlight the effectiveness of the presented method, a comparison between the proposed model and prevailing methods is proposed in the following section.
5.1 Comparative Analysis with Interval-Valued Pythagorean Fuzzy Weighted Average Operator [28]
Step-1: Obtain an IVPF decision matrices (Tables 1–4).
Step-2: Use normalization formula to normalize the obtained IVPF decision matrices (Tables 5–8).
Step-3: Apply the IVPFWA operator on the acquired data, then we get the opinion of decision-makers.
As we have
IVPFWA(M1,M2,M3,M4,……Mn)=(1−∏i=14(1−[κil,κiu]2)ωi,∏i=14[δil,δiu]ωi)
Θ1=(1−({[0.75,0.84]0.1[0.64,0.75]0.2[0.64,0.84]0.4[0.84,0.96]0.3}{[0.51,0.96]0.1[0.75,0.84]0.2[0.91,0.96]0.4[0.75,0.96]0.3}{[0.75,0.91]0.1[0.51,0.96]0.2[0.51,0.84]0.4[0.75,0.91]0.3}{[0.64,0.84]0.1[0.51,0.91]0.2[0.64,0.91]0.4[0.64,0.91]0.3}),({[0.2,0.5]0.1[0.7,0.8]0.2[0.2,0.5]0.4[0.2,0.6]0.3}{[0.2,0.6]0.1[0.1,0.6]0.2[0.4,0.8]0.4[0.4,0.7]0.3}{[0.1,0.4]0.1[0.4,0.6]0.2[0.3,0.7]0.4[0.2,0.4]0.3}{[0.3,0.7]0.1[0.4,0.5]0.2[0.3,0.5]0.4[0.3,0.5]0.3}))
=(1−({[0.9716,0.9827][0.9146,0.9441][0.8365,0.9326][0.9490,0.9878]}{[0.9349,0.9949][0.9441,0.9657][0.9629,0.9838][0.9173,0.9876]}{[0.9716,0.9906][0.8740,0.9919][0.7639,0.9326][0.9173,0.9721]}{[0.9564,0.9827][0.8740,0.9813][0.8365,0.9630][0.8747,0.9721]}),({[0.8513,0.9330][0.9311,0.9564][0.5253,0.7579][0.6170,0.8579]}{[0.8513,0.9502][0.6310,0.9029][0.6931,0.9146][0.7597,0.8985]}{[0.7943,0.9124][0.8326,0.9029][0.6178,0.8670][0.6170,0.7597]}{[0.8866,0.9650][0.8326,0.8706][0.0.6178,0.7578][0.6968,0.8123]}))
=([0.6071,0.8944],[0.0083,0.1265])
Θ2=(1−({[0.64,0.91]0.1[0.51,0.75]0.2[0.51,0.96]0.4[0.51,0.64]0.3}{[0.75,0.91]0.1[0.75,0.84]0.2[0.75,0.99]0.4[0.75,0.84]0.3}{[0.64,0.96]0.1[0.19,0.96]0.2[0.51,0.96]0.4[0.36,0.75]0.3}{[0.91,0.96]0.1[0.19,0.96]0.2[0.51,0.84]0.4[0.51,0.99]0.3}),({[0.5,0.6]0.1[0.2,0.7]0.2[0.4,0.5]0.4[0.5,0.8]0.3}{[0.5,0.8]0.1[0.1,0.4]0.2[0.3,0.7]0.4[0.3,0.6]0.3}{[0.1,0.4]0.1[0.1,0.2]0.2[0.3,0.8]0.4[0.2,0.6]0.3}{[0.3,0.8]0.1[0.3,0.5]0.2[0.2,0.6]0.4[0.3,0.6]0.3}))
=(1−({[0.9564,0.9906][0.8740,0.9441][0.7639,0.9838][0.8171,0.8747]}{[0.9716,0.9906][0.9441,0.9657][0.8913,0.9960][0.9173,0.9490]}{[0.9564,0.9960][0.7174,0.9918][0.7639,0.9838][0.7360,0.9173]}{[0.9906,0.9959][0.7174,0.9919][0.7639,0.9326][0.8171,0.9970]}),({[0.9930,0.9502][0.7248,0.9311][0.6931,0.7579][0.8123,0.9352]}{[0.9330,0.9780][0.6309,0.8326][0.6178,0.8670][0.6968,0.8579]}{[0.7943,0.9124][0.6310,0.7248][0.6178,0.9146][0.6170,0.8579]}{[0.8866,0.9779][0.7860,0.8706][0.5253,0.8152][0.6968,0.8579]}))
=([0.6357,0.9659],[0.0050,0.1174])
Θ3=(1−({[0.84,0.91]0.1[0.64,0.84]0.2[0.64,0.75]0.4[0.84,0.91]0.3}{[0.64,0.84]0.1[0.91,0.96]0.2[0.75,0.91]0.4[0.91,0.99]0.3}{[0.84,0.96]0.1[0.51,0.91]0.2[0.51,0.91]0.4[0.91,0.99]0.3}{[0.51,0.91]0.1[0.84,0.96]0.2[0.75,0.96]0.4[0.84,0.91]0.3}),({[0.2,0.7]0.1[0.3,0.4]0.2[0.4,0.5]0.4[0.3,0.6]0.3}{[0.3,0.7]0.1[0.3,0.5]0.2[0.5,0.8]0.4[0.2,0.4]0.3}{[0.3,0.4]0.1[0.3,0.5]0.2[0.3,0.8]0.4[0.5,0.6]0.3}{[0.3,0.7]0.1[0.3,0.5]0.2[0.3,0.6]0.4[0.3,0.7]0.3}))
=(1−({[0.9827,0.9906][0.9146,0.9657][0.8365,0.8913][0.9490,0.9721]}{[0.9564,0.9827][0.9813,0.9919][0.8913,0.9630][0.9721,0.9970]}{[0.9827,0.9959][0.8740,0.9813][0.7639,0.9630][0.9721,0.9970]}{[0.9349,0.9906][0.9657,0.9919][0.8913,0.9838][0.9490,0.9721]}),({[0.8513,0.9650][0.7860,0.8326][0.6931,0.7579][0.6968,0.8579]}{[0.8866,0.9650][0.7860,0.8706][0.5759,0.9146][0.6170,0.7597]}{[0.8866,0.9124][0.7860,0.8706][0.6178,0.9146][0.8123,0.8579]}{[0.8866,0.9650][0.7860,0.8706][0.6178,0.8152][0.6968,0.8985]}))
=([0.3652,0.6523],[0.5236,0.6524])
Θ4=(1−({[0.64,0.91]0.1[0.51,0.75]0.2[0.51,0.96]0.4[0.51,0.64]0.3}{[0.75,0.91]0.1[0.75,0.84]0.2[0.75,0.99]0.4[0.75,0.84]0.3}{[0.64,0.96]0.1[0.19,0.96]0.2[0.51,0.96]0.4[0.36,0.75]0.3}{[0.91,0.96]0.1[0.19,0.96]0.2[0.51,0.84]0.4[0.51,0.99]0.3}),({[0.5,0.6]0.1[0.2,0.7]0.2[0.4,0.5]0.4[0.5,0.8]0.3}{[0.5,0.8]0.1[0.1,0.4]0.2[0.3,0.7]0.4[0.3,0.6]0.3}{[0.1,0.4]0.1[0.1,0.2]0.2[0.3,0.8]0.4[0.2,0.6]0.3}{[0.3,0.8]0.1[0.3,0.5]0.2[0.2,0.6]0.4[0.3,0.6]0.3}))
=(1−({[0.9564,0.9906][0.8740,0.9441][0.7639,0.9838][0.8171,0.8747]}{[0.9716,0.9906][0.9441,0.9657][0.8913,0.9960][0.9173,0.9490]}{[0.9564,0.9960][0.7174,0.9918][0.7639,0.9838][0.7360,0.9173]}{[0.9906,0.9959][0.7174,0.9919][0.7639,0.9326][0.8171,0.9970]}),({[0.9930,0.9502][0.7248,0.9311][0.6931,0.7579][0.8123,0.9352]}{[0.9330,0.9780][0.6309,0.8326][0.6178,0.8670][0.6968,0.8579]}{[0.7943,0.9124][0.6310,0.7248][0.6178,0.9146][0.6170,0.8579]}{[0.8866,0.9779][0.7860,0.8706][0.5253,0.8152][0.6968,0.8579]}))
=([0.6357,0.9659],[0.0050,0.1174])
Step-4: Use the score function S=(κl)2+(κu)2−(δl)2−(δu)22 for IVPFS to calculate the score values for all alternatives.
S(Θ1)=(0.4575)2+(0.8569)2−(0.4595)2−(0.7586)22=0.0154
S(Θ2)=(0.6543)2+(0.8978)2−(0.5206)2−(0.7452)22=0.0251
S(Θ3)=(0.6565)2+(0.9548)2−(0.2365)2−(0.3663)22=0.0198
S(Θ4)=(0.4545)2+(0.5459)2−(0.8553)2−(0.2563)22=0.0247
Step-5: Ranking of alternatives S(Θ2)>S(Θ4)>S(Θ3)>S(Θ1). So, I2>I4>I3>I1. Hence, the best alternative is I2.
5.2 Comparison with Interval-Valued Pythagorean Fuzzy Weighted Geometric Operator [28]
Step-1: Obtain an IVPF decision matrices (Tables 1–4).
Step-2: Use normalization formula to normalize the obtained IVPF decision matrices (Tables 5–8).
Step-3: Apply the IVPFWG operator on the acquired data, then we get the opinion of decision-makers.
As we have
IVPFWG(M1,M2,M3,M4,……Mn)=(∏i=14[κil,κiu]ωi,1−∏i=14(1−[δil,δiu]2)ωi)
Θ1=(({[0.2,0.5]0.1[0.7,0.8]0.2[0.2,0.5]0.4[0.2,0.6]0.3}{[0.2,0.6]0.1[0.1,0.6]0.2[0.4,0.8]0.4[0.4,0.7]0.3}{[0.1,0.4]0.1[0.4,0.6]0.2[0.3,0.7]0.4[0.2,0.4]0.3}{[0.3,0.7]0.1[0.4,0.5]0.2[0.3,0.5]0.4[0.3,0.5]0.3}),1−({[0.75,0.84]0.1[0.64,0.75]0.2[0.64,0.84]0.4[0.84,0.96]0.3}{[0.51,0.96]0.1[0.75,0.84]0.2[0.91,0.96]0.4[0.75,0.96]0.3}{[0.75,0.91]0.1[0.51,0.96]0.2[0.51,0.84]0.4[0.75,0.91]0.3}{[0.64,0.84]0.1[0.51,0.91]0.2[0.64,0.91]0.4[0.64,0.91]0.3}))
=(({[0.8513,0.9330][0.9311,0.9564][0.5253,0.7579][0.6170,0.8579]}{[0.8513,0.9502][0.6310,0.9029][0.6931,0.9146][0.7597,0.8985]}{[0.7943,0.9124][0.8326,0.9029][0.6178,0.8670][0.6170,0.7597]}{[0.8866,0.9650][0.8326,0.8706][0.0.6178,0.7578][0.6968,0.8123]}),1−({[0.9716,0.9827][0.9146,0.9441][0.8365,0.9326][0.9490,0.9878]}{[0.9349,0.9949][0.9441,0.9657][0.9629,0.9838][0.9173,0.9876]}{[0.9716,0.9906][0.8740,0.9919][0.7639,0.9326][0.9173,0.9721]}{[0.9564,0.9827][0.8740,0.9813][0.8365,0.9630][0.8747,0.9721]}))
=([0.0083,0.1265],[0.6071,0.8944])
Θ2=(({[0.5,0.6]0.1[0.2,0.7]0.2[0.4,0.5]0.4[0.5,0.8]0.3}{[0.5,0.8]0.1[0.1,0.4]0.2[0.3,0.7]0.4[0.3,0.6]0.3}{[0.1,0.4]0.1[0.1,0.2]0.2[0.3,0.8]0.4[0.2,0.6]0.3}{[0.3,0.8]0.1[0.3,0.5]0.2[0.2,0.6]0.4[0.3,0.6]0.3}),1−({[0.64,0.91]0.1[0.51,0.75]0.2[0.51,0.96]0.4[0.51,0.64]0.3}{[0.75,0.91]0.1[0.75,0.84]0.2[0.75,0.99]0.4[0.75,0.84]0.3}{[0.64,0.96]0.1[0.19,0.96]0.2[0.51,0.96]0.4[0.36,0.75]0.3}{[0.91,0.96]0.1[0.19,0.96]0.2[0.51,0.84]0.4[0.51,0.99]0.3}))
=(({[0.9930,0.9502][0.7248,0.9311][0.6931,0.7579][0.8123,0.9352]}{[0.9330,0.9780][0.6309,0.8326][0.6178,0.8670][0.6968,0.8579]}{[0.7943,0.9124][0.6310,0.7248][0.6178,0.9146][0.6170,0.8579]}{[0.8866,0.9779][0.7860,0.8706][0.5253,0.8152][0.6968,0.8579]}),1−({[0.9564,0.9906][0.8740,0.9441][0.7639,0.9838][0.8171,0.8747]}{[0.9716,0.9906][0.9441,0.9657][0.8913,0.9960][0.9173,0.9490]}{[0.9564,0.9960][0.7174,0.9918][0.7639,0.9838][0.7360,0.9173]}{[0.9906,0.9959][0.7174,0.9919][0.7639,0.9326][0.8171,0.9970]}))
=([0.0050,0.1174],[0.6357,0.9659])
Θ3=(({[0.2,0.7]0.1[0.3,0.4]0.2[0.4,0.5]0.4[0.3,0.6]0.3}{[0.3,0.7]0.1[0.3,0.5]0.2[0.5,0.8]0.4[0.2,0.4]0.3}{[0.3,0.4]0.1[0.3,0.5]0.2[0.3,0.8]0.4[0.5,0.6]0.3}{[0.3,0.7]0.1[0.3,0.5]0.2[0.3,0.6]0.4[0.3,0.7]0.3}),1−({[0.84,0.91]0.1[0.64,0.84]0.2[0.64,0.75]0.4[0.84,0.91]0.3}{[0.64,0.84]0.1[0.91,0.96]0.2[0.75,0.91]0.4[0.91,0.99]0.3}{[0.84,0.96]0.1[0.51,0.91]0.2[0.51,0.91]0.4[0.91,0.99]0.3}{[0.51,0.91]0.1[0.84,0.96]0.2[0.75,0.96]0.4[0.84,0.91]0.3}))
=(({[0.8513,0.9650][0.7860,0.8326][0.6931,0.7579][0.6968,0.8579]}{[0.8866,0.9650][0.7860,0.8706][0.5759,0.9146][0.6170,0.7597]}{[0.8866,0.9124][0.7860,0.8706][0.6178,0.9146][0.8123,0.8579]}{[0.8866,0.9650][0.7860,0.8706][0.6178,0.8152][0.6968,0.8985]}),1−({[0.9827,0.9906][0.9146,0.9657][0.8365,0.8913][0.9490,0.9721]}{[0.9564,0.9827][0.9813,0.9919][0.8913,0.9630][0.9721,0.9970]}{[0.9827,0.9959][0.8740,0.9813][0.7639,0.9630][0.9721,0.9970]}{[0.9349,0.9906][0.9657,0.9919][0.8913,0.9838][0.9490,0.9721]}))
=([0.25650.5265],[0.2336,0.4524])
Θ4=(({[0.5,0.6]0.1[0.2,0.7]0.2[0.4,0.5]0.4[0.5,0.8]0.3}{[0.5,0.8]0.1[0.1,0.4]0.2[0.3,0.7]0.4[0.3,0.6]0.3}{[0.1,0.4]0.1[0.1,0.2]0.2[0.3,0.8]0.4[0.2,0.6]0.3}{[0.3,0.8]0.1[0.3,0.5]0.2[0.2,0.6]0.4[0.3,0.6]0.3}),1−({[0.64,0.91]0.1[0.51,0.75]0.2[0.51,0.96]0.4[0.51,0.64]0.3}{[0.75,0.91]0.1[0.75,0.84]0.2[0.75,0.99]0.4[0.75,0.84]0.3}{[0.64,0.96]0.1[0.19,0.96]0.2[0.51,0.96]0.4[0.36,0.75]0.3}{[0.91,0.96]0.1[0.19,0.96]0.2[0.51,0.84]0.4[0.51,0.99]0.3}))
=(({[0.9930,0.9502][0.7248,0.9311][0.6931,0.7579][0.8123,0.9352]}{[0.9330,0.9780][0.6309,0.8326][0.6178,0.8670][0.6968,0.8579]}{[0.7943,0.9124][0.6310,0.7248][0.6178,0.9146][0.6170,0.8579]}{[0.8866,0.9779][0.7860,0.8706][0.5253,0.8152][0.6968,0.8579]}),1−({[0.9564,0.9906][0.8740,0.9441][0.7639,0.9838][0.8171,0.8747]}{[0.9716,0.9906][0.9441,0.9657][0.8913,0.9960][0.9173,0.9490]}{[0.9564,0.9960][0.7174,0.9918][0.7639,0.9838][0.7360,0.9173]}{[0.9906,0.9959][0.7174,0.9919][0.7639,0.9326][0.8171,0.9970]}))
=([0.6357,0.9659],[0.2564,0.6585]).
Step-4: Use the score function S=(κl)2+(κu)2−(δl)2−(δu)22 for IVPFS to calculate the score values for all alternatives.
S(Θ1)=(0.4575)2+(0.8569)2−(0.4595)2−(0.7586)22=0.030264
S(Θ2)=(0.6543)2+(0.8978)2−(0.5206)2−(0.7452)22=0.0856
S(Θ3)=(0.6565)2+(0.9548)2−(0.2365)2−(0.3663)22=0.0786
S(Θ4)=(0.6357)2+(0.9659)2−(0.2564)2−(0.6585)22=0.0475
Step-5: Ranking of alternatives, S(Θ2)>S(Θ3)>S(Θ4)>S(Θ1). So, I2>I3>I1>I4 . Hence, the best alternative is I2.
Similarly, we can get the outcomes utilizing several other existing operators for comparative studies.
5.3 Comparative Analysis
To verify the effectiveness of the proposed method, we compare the obtained results with some existing methods under the environment of IVPFS and IVIFSS. A summary of all results is given in Table 9. Zulqarnain et al. [17] developed aggregation operators for IVIFSS that are unable to accommodate the decision-makers choices when the sum of upper membership and nonmembership values of the parameters exceeds one. Peng et al. [27] interval-valued Pythagorean fuzzy weighted average operator and Rahman et al. [28] interval-valued Pythagorean fuzzy weighted geometric operator cannot handle the parametrized values of the alternatives. Furthermore, if only one parameter is supposed rather than more than one parameter, the interval-valued Pythagorean fuzzy soft set reduces to the interval-valued Pythagorean fuzzy set. Similarly, if the sum of upper values of membership and nonmembership degree is less or equal to 1. Then, IVPFSS reduced to IVIFSS. Thus, IVPFSS is the most generalized form of interval-valued Pythagorean fuzzy set. Hence, based on the above-mentioned facts, admittedly, the proposed operators in this paper are more powerful, reliable, and successful.
6 Conclusion
In this work, we have introduced two novel aggregation operators such as IVPFSWA and IPFSWG operators. Firstly, we defined operational laws under an interval-valued Pythagorean fuzzy soft environment. Based on these operational laws, we developed the aggregation operators for IVPFSS such as IVPFSWA and IVPFSWG operators with their desirable properties. Furthermore, a DM approach has been established to resolve multi-attribute group decision-making (MAGDM) problems based on presented aggregation operators. To ensure the validity of the established technique, a comprehensive numerical example has been presented. To verify the effectiveness of the proposed method, a comparative analysis with some existing methods is presented. Finally, based on obtained results, it has been concluded that the proposed method in this research is the most feasible and successful method for the MAGDM problem.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zadeh, L. A. (1996). Fuzzy sets. Inforation and Control, 8, 338–353. DOI 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
2. Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20, 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]
3. Wang, W., Liu, X. (2011). Intuitionistic fuzzy geometric aggregation operators based on Einstein operations. International Journal of Intelligent Systems, 26(11), 1049–1075. DOI 10.1002/int.20498. [Google Scholar] [CrossRef]
4. Atanassov, K. T. (1999). Interval-valued intuitionistic fuzzy sets. In: Intuitionistic fuzzy sets, pp. 139–177. Heidelberg: Physica. [Google Scholar]
5. Garg, H., Kaur, G. (2019). Cubic intuitionistic fuzzy sets and their fundamental properties. Journal of Multiple-Valued Logic & Soft Computing, 33, 507–537. [Google Scholar]
6. Yager, R. R. (2013). Pythagorean membership grades in multicriteria decision making. IEEE Transactions on Fuzzy Systems, 22(4), 958–965. DOI 10.1109/TFUZZ.2013.2278989. [Google Scholar] [CrossRef]
7. Rahman, K., Abdullah, S., Ahmed, R., Ullah, M. (2017). Pythagorean fuzzy Einstein weighted geometric aggregation operator and their application to multiple attribute group decision making. Journal of Intelligent & Fuzzy Systems, 33(1), 635–647. DOI 10.3233/JIFS-16797. [Google Scholar] [CrossRef]
8. Zhang, X., Xu, Z. (2014). Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. International Journal of Intelligent Systems, 29(12), 1061–1078. DOI 10.1002/int.21676. [Google Scholar] [CrossRef]
9. Wei, G., Lu, M. (2018). Pythagorean fuzzy power aggregation operators in multiple attribute decision making. International Journal of Intelligent Systems, 33(1), 169–186. DOI 10.1002/int.21946. [Google Scholar] [CrossRef]
10. Wang, L., Li, N. (2020). Pythagorean fuzzy interaction power Bonferroni means aggregation operators in multiple attribute decision making. International Journal of Intelligent Systems, 35(1), 150–183. DOI 10.1002/int.22204. [Google Scholar] [CrossRef]
11. Ilbahar, E., Karaşan, A., Cebi, S., Kahraman, C. (2018). A novel approach to risk assessment for occupational health and safety using Pythagorean fuzzy AHP & fuzzy inference system. Safety Science, 103(9), 124–136. DOI 10.1016/j.ssci.2017.10.025. [Google Scholar] [CrossRef]
12. Zhang, X. (2016). A novel approach based on similarity measure for Pythagorean fuzzy multiple criteria group decision making. International Journal of Intelligent Systems, 31(6), 593–611. DOI 10.1002/int.21796. [Google Scholar] [CrossRef]
13. Molodtsov, D. (1999). Soft set theory—First results. Computers & Mathematics with Applications, 37(4–5), 19–31. DOI 10.1016/S0898-1221(99)00056-5. [Google Scholar] [CrossRef]
14. Maji, P. K., Biswas, R., Roy, A. R. (2003). Soft set theory. Computers & Mathematics with Applications, 45(4–5), 555–562. DOI 10.1016/S0898-1221(03)00016-6. [Google Scholar] [CrossRef]
15. Maji, P. K., Biswas, R., Roy, A. R. (2001). Fuzzy soft sets. Journal of Fuzzy Mathematics, 9, 589–602. [Google Scholar]
16. Maji, P. K., Biswas, R., Roy, A. R. (2001). Intuitionistic fuzzy soft sets. Journal of Fuzzy Mathematics, 9, 677–692. [Google Scholar]
17. Zulqarnain, R. M., Xin, X. L., Saqlain, M., Khan, W. A. (2021). TOPSIS method based on the correlation coefficient of interval-valued intuitionistic fuzzy soft sets and aggregation operators with their application in decision-making. Journal of Mathematics, 2021(10), 1–16. DOI 10.1155/2021/6656858. [Google Scholar] [CrossRef]
18. Jiang, Y., Tang, Y., Chen, Q., Liu, H., Tang, J. (2010). Interval-valued intuitionistic fuzzy soft sets and their properties. Computers & Mathematics with Applications, 60(3), 906–918. DOI 10.1016/j.camwa.2010.05.036. [Google Scholar] [CrossRef]
19. Narayanamoorthy, S., Ramya, L., Kang, D. (2020). Normal wiggly hesitant fuzzy set with multi-criteria decision making problem. AIP Conference Proceedings, 2261(1), 030023. DOI 10.1063/5.0017055. [Google Scholar] [CrossRef]
20. Narayanamoorthy, S., Annapoorani, V., Kang, D., Baleanu, D., Jeon, J. et al. (2020). A novel assessment of bio-medical waste disposal methods using integrating weighting approach and hesitant fuzzy MOOSRA. Journal of Cleaner Production, 275(6), 122587. DOI 10.1016/j.jclepro.2020.122587. [Google Scholar] [CrossRef]
21. Ramya, L., Narayanamoorthy, S., Kalaiselvan, S., Kureethara, J. V., Annapoorani, V. et al. (2021). A congruent approach to normal wiggly interval-valued hesitant Pythagorean fuzzy set for thermal energy storage technique selection applications. International Journal of Fuzzy Systems, 23(6), 1–19. DOI 10.1007/s40815-021-01057-2. [Google Scholar] [CrossRef]
22. Peng, X. D., Yang, Y., Song, J., Jiang, Y. (2015). Pythagorean fuzzy soft set and its application. Computer Engineering, 41(7), 224–229. [Google Scholar]
23. Zulqarnain, R. M., Xin, X. L., Garg, H., Khan, W. A. (2021). Aggregation operators of Pythagorean fuzzy soft sets with their application for green supplier chain management. Journal of Intelligent and Fuzzy Systems, 40(3), 5545–5563. DOI 10.3233/JIFS-202781. [Google Scholar] [CrossRef]
24. Zulqarnain, R. M., Xin, X. L., Garg, H., Ali, R. (2021). Interaction aggregation operators to solve multi criteria decision making problem under Pythagorean fuzzy soft environment. Journal of Intelligent & Fuzzy Systems, 41(1), 1151–1171. DOI 10.3233/JIFS-210098. [Google Scholar] [CrossRef]
25. Smarandache, F. (2018). Extension of soft set to hypersoft set, and then to plithogenic hypersoft set. Neutrosophic Sets and Systems, 22, 168–170. [Google Scholar]
26. Turksen, I. B. (1986). Interval valued fuzzy sets based on normal forms. Fuzzy Sets and Systems, 20(2), 191–210. DOI 10.1016/0165-0114(86)90077-1. [Google Scholar] [CrossRef]
27. Peng, X., Yang, Y. (2016). Fundamental properties of interval-valued Pythagorean fuzzy aggregation operators. International Journal of Intelligent Systems, 31(5), 444–487. DOI 10.1002/int.21790. [Google Scholar] [CrossRef]
28. Rahman, K., Abdullah, S., Shakeel, M., Ali Khan, M. S., Ullah, M. (2017). Interval-valued Pythagorean fuzzy geometric aggregation operators and their application to group decision making problem. Cogent Mathematics, 4(1), 1338638. DOI 10.1080/23311835.2017.1338638. [Google Scholar] [CrossRef]