
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.019280
ARTICLE
Modeling and Experimental Study for Automotive Dry Clutch Sliding Noise
School of Mechanical and Electrical Engineering, Guilin University of Electronic Technology, Guilin, 541004, China
*Corresponding Author: Yubing Gong. Email: gybcome@guet.edu.cn
Received: 14 September 2021; Accepted: 22 November 2021
Abstract: Automotive dry clutches have been found to produce a low frequency sliding noise in many applications, which challenges the ride comfort of vehicles. In order to study this clutch sliding noise, a detailed finite element model including both a pressure plate assembly and a driven plate assembly was developed. Based on this model, a complex eigenvalue analysis is performed in this research. The effect of several major factors on the clutch sliding noise, such as the coefficient of friction, the clamping force, the geometric imperfection of the friction plate, and the thermal deformation of the pressure plate, were investigated numerically. A vehicle road test with clutch sliding noise was conducted for several different conditions. The leading frequencies of the clutch sliding noise in the testing were obtained and compared with the frequencies predicted by the numerical model. The simulation results show the same tendency as the road test. It is found that the clutch sliding noise can be reduced by decreasing the coefficient of friction. With the presence of the surface bumping of the friction plate, the propensity of the clutch sliding noise greatly increases and the corresponding squeal frequencies fall into the range lower than 1 kHz. With the consideration of the thermally introduced deformation of the clutch pressure plate, the possibility of clutch sliding noise is significantly reduced. It is concluded that the model with the incorporation of the thermal deformation of the pressure plate is more effective for the frequency prediction of clutch sliding noise.
Keywords: Dry clutch; complex eigenvalue; clutch sliding noise; influencing factors
As one of the most important parts of an automotive transmission system, the main functions of a clutch include engaging and disengaging the engine torque, preventing the overload of the driveline system, and improving the overall NVH (noise, vibration, and harshness) performance, etc. In practice, some vibroacoustic phenomena are produced for the driveline when a vehicle starts to move and during the slipping step [1–5]. These noises (e.g., eek whoop, scratch, etc.) have become an issue for clutch manufacturers. The mechanisms and the important factors of these automotive clutch sliding noises remain poorly understood.
There are several general mechanisms of friction-induced squeal formation, such as stick-slip, negative friction, velocity slope, sprag-slip, modal coupling, splitting the doublet modes, and the hammering mechanism [6,7]. The analytic method, the numerical analysis method, and the experimental method have been used to study the friction noise, and identify the critical factors and possibility in reducing the effect of the friction noise. The friction surface topography [8], friction surface contact slope angle [9–11], friction coefficient [12], pressure [6,13], contact stiffness [14], temperature [15,16], wear [17,18], and bump of a friction surface [11] have been investigated and found to be related to the friction noise. However, most of this research has been focused on brake squealing, and very few investigations have been conducted on automotive dry clutch sliding noise. Although a methodology intended for brake squealing can be used for dry clutch sliding noise as well, there is a need to investigate the unique characteristics of automotive dry clutch noise, such as the ring-shaped contact area, very high relative rotational speed, and asymmetric boundary conditions.
Pierre Wickramarachi et al. [1] developed an analytical model that included a six degree-of-freedom lumped-parameter system and conducted a complex eigenvalue analysis to study the EEK noise of the automotive dry clutch assembly. During the development of the new noise of the automotive dry clutch assembly, engagement was found. This new noise had never been reported before, and it was similar to the pronunciation of the letters “E-E-K”. Therefore, this harsh noise was defined as the EEK noise (bionic). It was found that the structural stiffness of the pressure plate was a key parameter for the clutch EEK noise with a dominant frequency of approximately 450 to 500 Hz. The simulation result that was obtained seemed to correlate well with empirical observations and experimental observations. Senatore et al. [2,3] presented an original five-degree of freedom mathematical model of an automotive dry clutch mechanism in the engagement phase. From the simulation, the torsional oscillation of the gearbox input shaft with a frequency around 421 Hz in the EEK frequency range was obtained, and this oscillation was unlike that reported in the literature. [1] This excitation of the torsional motion occurred regardless of the rigid wobbling motion of the pressure plate or the bending deformation of transmission shaft. Yasser Aktir et al. [4,5] developed a validated tridimensional finite element (FE) model for an automotive dry automotive clutch for manual transmissions. A high level of gearbox housing acoustic pressure was found at around 580 Hz in the test, and it was predicted well by the numerical model based on the complex eigenvalue approach. The effects of the friction coefficient and the contact pressure between the facing, the pressure plate, and the flywheel on the clutch sliding noise propensity were investigated. It was found that an increase of the friction coefficient and the contact pressure led to the amplification of the clutch instabilities. Ondiz Zarraga et al. [19,20] obtained the high frequency squeal noise of an industrial brake-clutch around 7, 11, and 14 kHz for different pressure and rotation speed conditions. The complex eigenvalue analysis and the transient analysis of this brake-clutch were also carried out. Mean errors of 4% in the squeal frequencies compared with experimental work were obtained. Jakub Šedek et al. [21] used an FE analysis of the strain constraint around the crack tip under cyclic loading and its utilization using the crack growth prediction strip yield model (SYM). The similar simulated crack growth behaviour as the experimental data. The implementation of the variable constraint factor αg into the SYM gave more realistic results than the simulation by the original model, which was non-sensitive to the specimen thickness. Fauziana Lamin et al. [22] proposed a FE simulation of the HPT compression stage with displacement control incremental loading by taking into account an unconstrained HPT configuration to test the plastic behavior of an aluminum alloy during high pressure torsion (HPT) compression loading.
Our current experiments have revealed that the bump area of the friction plate has a significant influence on the propensity of the automotive dry clutch sliding noise. However, this factor of the bump area has never been reported or investigated for the automotive clutch sliding noise. Furthermore, the current solution method to these noise problems is a trial-and-error method, which is both inefficient and expensive.
In this research, a detailed three-dimensional FE model for the Ø260 automotive dry clutch assembly is developed. Based on this FE model, the complex eigenvalue analysis of the dry clutch assembly is conducted in order to explore the unstable frequency of the clutch during the slip phase of the clutch engagement. A corresponding real vehicle road test is performed and the main frequencies of the clutch squeal noise are obtained. The comparison between the simulation and the road test proves the effectiveness of the numerical method. The effect of several important parameters, namely the friction coefficient, the disc bumping of the friction plate and the thermal deformation of the clutch pressure plate on the clutch squeal are investigated.
For the friction noise problem, there are typically two kinds of numerical methods, namely complex eigenvalue analysis (CEA) and dynamic transient analysis. Both methodologies have their advantages and disadvantages. Complex eigenvalue analysis allows all unstable frequencies to be found in one run for one set of operating conditions and is hence very efficient [23]. The disadvantage of the complex eigenvalue analysis method is that only linear models can be used, and there is an overestimation or lack of prediction in the results. Dynamic transient analysis can predict the real unstable frequency in principle, but it requires the consumption of a large amount of computing time [24]. In industrial applications, the complex eigenvalue analysis method is predominantly used due to its efficiency [25]. Therefore, the complex eigenvalue analysis method is adopted in this research.
In general, the one-dimensional equation of motion for a dry friction clutch system can be expressed as [6]:
where [M], [C], and [K] are the matrix of the masses, the damping matrix including the mechanical losses for the internal friction in the materials, and the stiffness matrix of the system, respectively.
where
where
Since the damping matrix
where
The modal damping ratio is given by:
The generalized solution of the initial equation of motion of the friction system relative to the displacements
According to the above equations, the real part
2.2 Finite Element Model of Automotive Dry Clutch
A finite element (FE) model with a simplified geometry of a Ø260 dry clutch assembly is established in this research. In the modeling, the size of the simulation model is 1:1 with the actual model. The inner diameter of the pressure plate is Ø158 mm, the outer diameter is Ø262 mm, the tooth top height 25.5 mm, and the driven plate outer diameter is Ø260 mm. Multi-size control and the hexahedral-dominated meshing method are applied for the meshing of the geometry. In the meshing, the local mesh generation and size control are carried out for each part, with the minimum size of 1mm and the maximum size of 3 mm. The models have 270,568 elements and 850,144 nodes in total. The FE model of the cover assembly is shown in Fig. 1a, and the model of the driven plate assembly is shown in Fig. 1b.
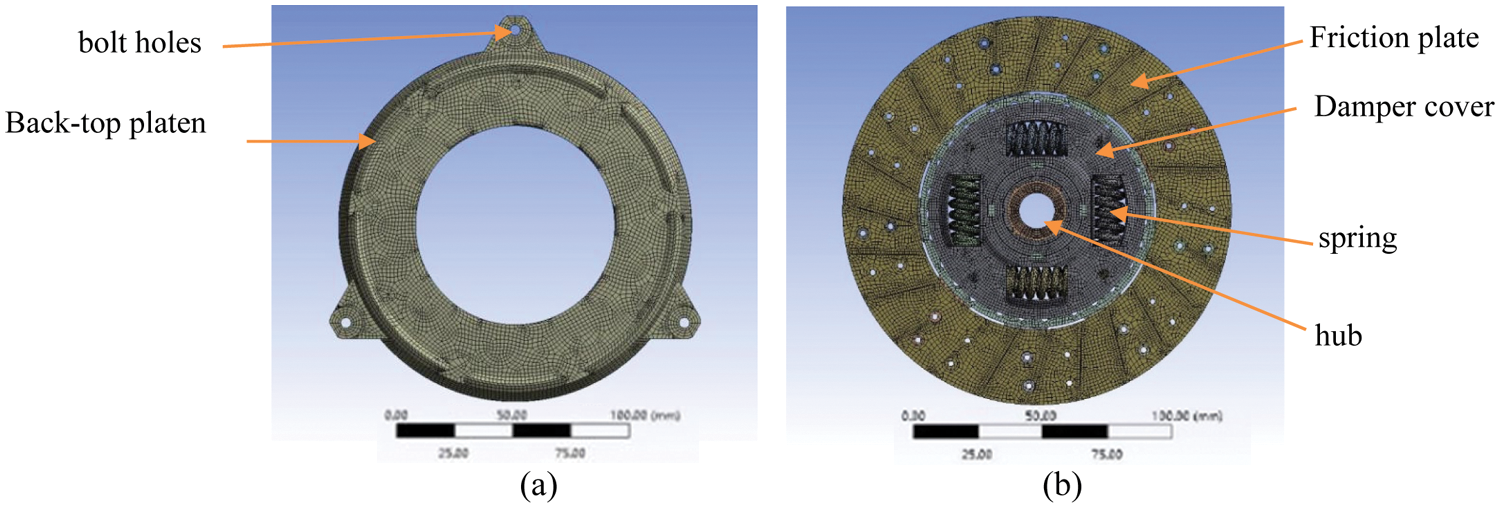
Figure 1: FE mesh model of the pressure plate (a); FE mesh model of the driven plate assembly (b)
All the materials are assumed to be isotropic plastic or isotropic elastic. Specifically, the material model of the pressure plate, the friction disc and the wave cushion spring are isotropic plastic, and the material model of other parts such as the friction plate and springs are isotropic elastic. The material parameters of the pressure plate, the friction plate/lining, the wave cushion spring, and the friction disc are shown in Table 1. HT250 material is used for the pressure plate, 65Mn material for the wave cushion spring, and 08AL material for the friction disc, and structural steel is used for all other parts. In the FE model of the clutch assembly, a contact pair is created between the pressure plate and the driven disc friction plate. The contact type is set frictional contact. The friction contact pair behavior is Asymmetric and the contact algorithm is Augmented Lagrange which updates the contact stiffness at the end of each equilibrium iteration step during the solution. In the contact setting, set the contact surface to close any initial gaps and ignore any initial penetrations. For the other parts of the clutch assembly, the bonded contact pairs are specified, the contact pair behavior is symmetric contact and the contact algorithm is MPC. Commercial ANSYS code is used to execute the numerical model. Displacement constraints of the X-axis and the Y-axis are applied on the three bolt holes of the pressure plate and the spline holes of the driven plate according to the constraints of the bolts and the spline axis in operation, and the displacement constraints of the Z-axis are applied to the end face of the friction plate on the flywheel side. The nominal clamp force of the clutch is assumed to be on the back-top platen of the pressure plate. Unless otherwise specified, in the following discussions, the friction coefficient between the friction plate and the pressure plate is set to 0.4, and the clamp force of the pressure plate of the Ø260 clutch is set to 5,000 N. In the analysis setting, the automatic time stepping is applied to solve the numerical model for improving the convergency.
To investigate the effect of geometric imperfection of the friction surface of the friction plate on the clutch sliding noise, the model shown in Fig. 2 is applied. In this model, the thickness of the friction plate is varied in the circumferential direction and for generality, the sinusoidal variation of the deformation is assumed.

Figure 2: Sketch of thickness variance of the friction plate
3 Sensitivity Analysis and Discussion
Since the sign of the damping ratio of each order mode is always opposite to that of the real part of the eigenvalue according to Eq. (5), the criterion
Five different clutch friction coefficients of 0.1, 0.2, 0.3, 0.4, and 0.5, with the height of the friction plate surface bump fixed to 0.3 mm, are investigated. The results are shown in Fig. 3. With the increase in the coefficient of friction, the real part of the eigenvalue of the unstable mode increases, which indicates that the propensity of the clutch to squeal increases.
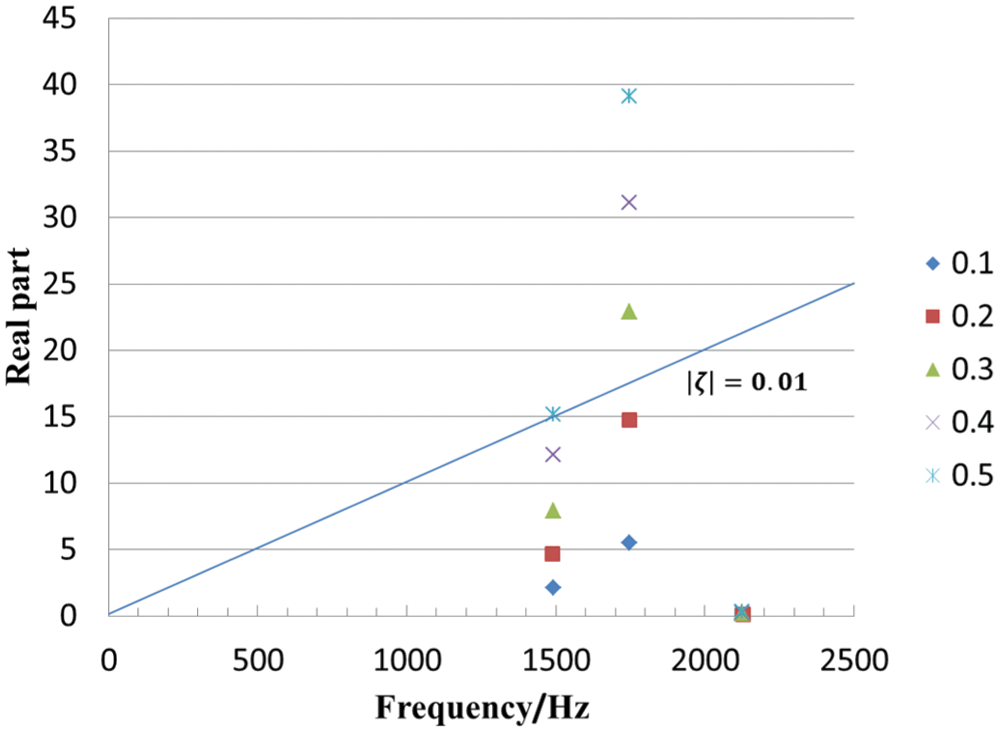
Figure 3: Unstable mode
With the frequency of 1748.8 Hz as an example, the mode coupling phenomenon is shown in Fig. 4. As the coefficient of friction increases, the frequency of the 22nd mode rises whereas the frequency of the 23rd mode decreases. When the friction coefficient becomes 0.1, these two modes are coupled.
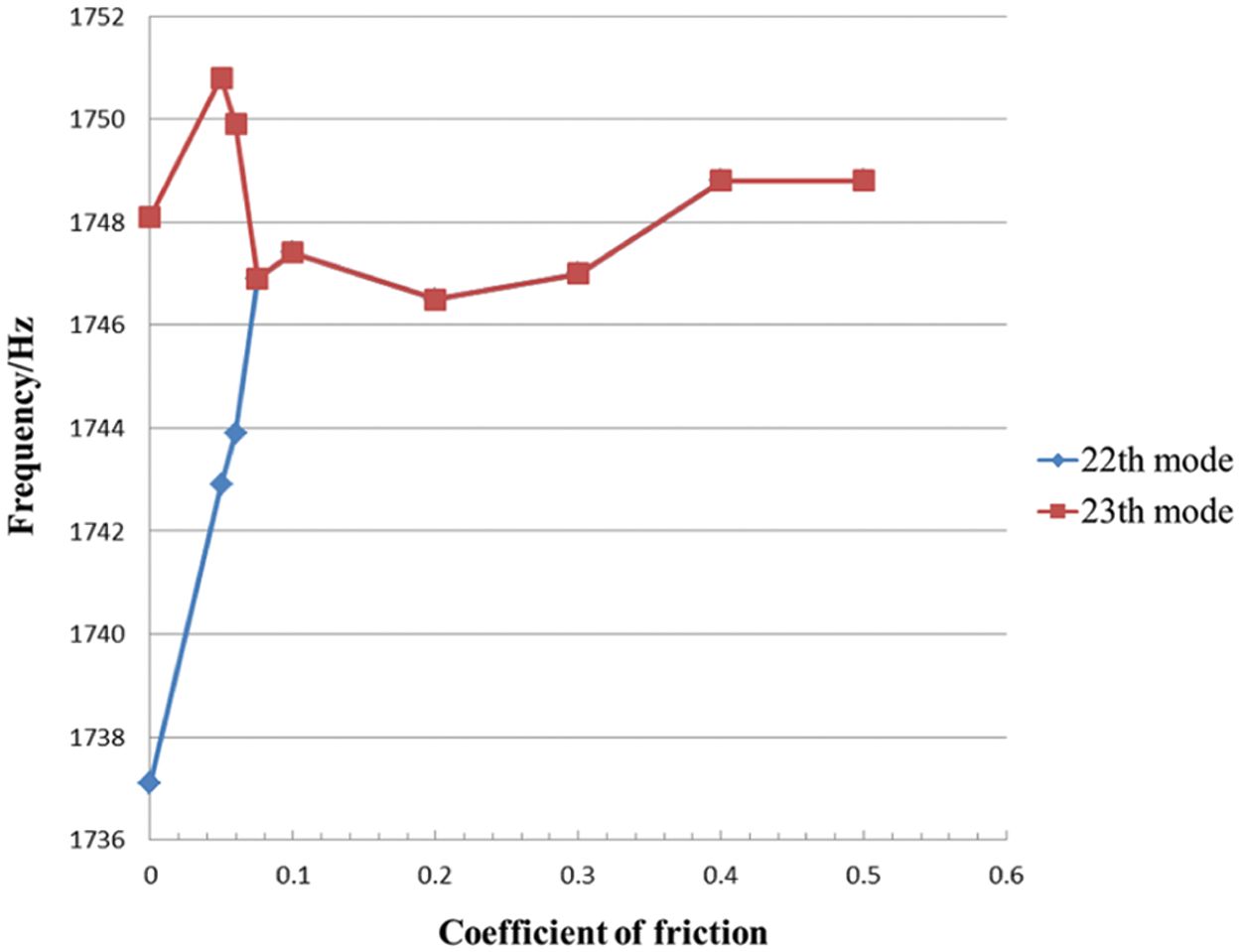
Figure 4: Unstable mode
3.2 Surface Bump of the Friction Plate
The different amounts of the thickness variance of the friction plate in the circumferential direction can be characterized by the height of the surface bump of the friction plate. The effect of the height of the surface bump on the clutch sliding noise is shown in Fig. 5 and Table 2. The real part of the eigenvalue depicted with different symbols varies with the height of the surface bump. It is found that the frequency of the noise decreases as the height of the bump increases from 0 mm to the maximum value of 0.7 mm.
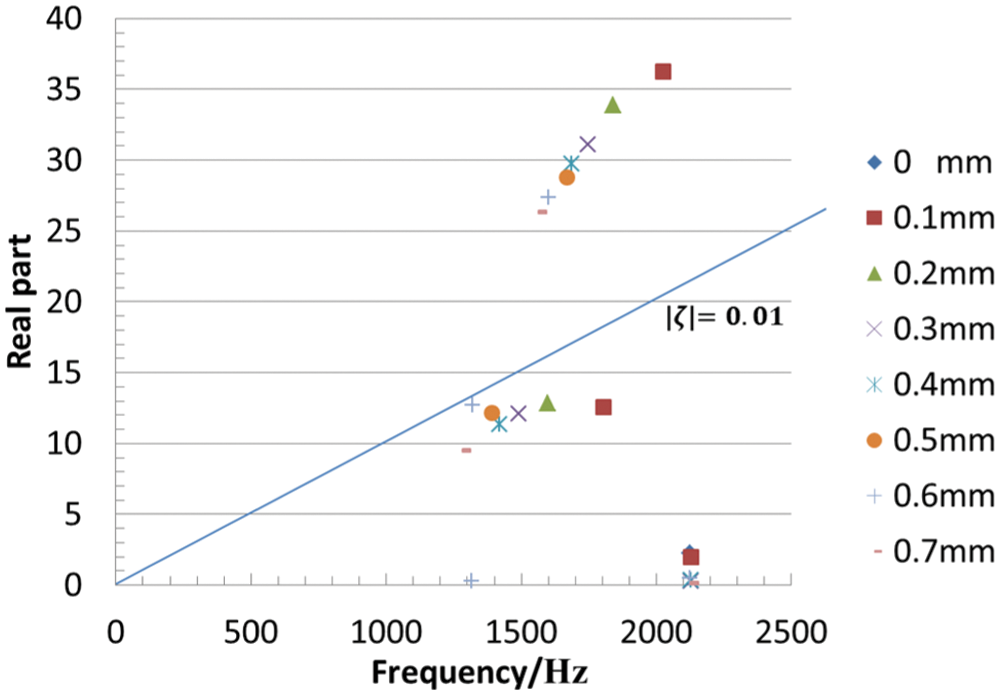
Figure 5: Unstable mode
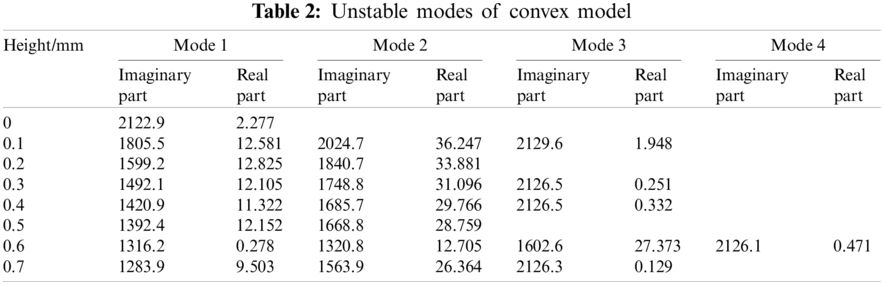
For the case of a surface bump of 0.3 mm, there are three unstable frequencies, namely 1492.1, 1748.8, 2126.5, and the real parts of 1492.1 and 1748.8 Hz are relatively large. The vibration mode of 1492.1 Hz is shown in Fig. 6, in which the mode shape of the clutch pressure plate is circular wobbling, and the mode shape of the friction plate is a tangential swing. The vibration mode of 1748.8 Hz is shown in Fig. 7, in which the bending mode of the pressure plate is coupled with the bending mode of the friction plate.

Figure 6: Vibration mode of the clutch system at the frequency of 1492.1 Hz
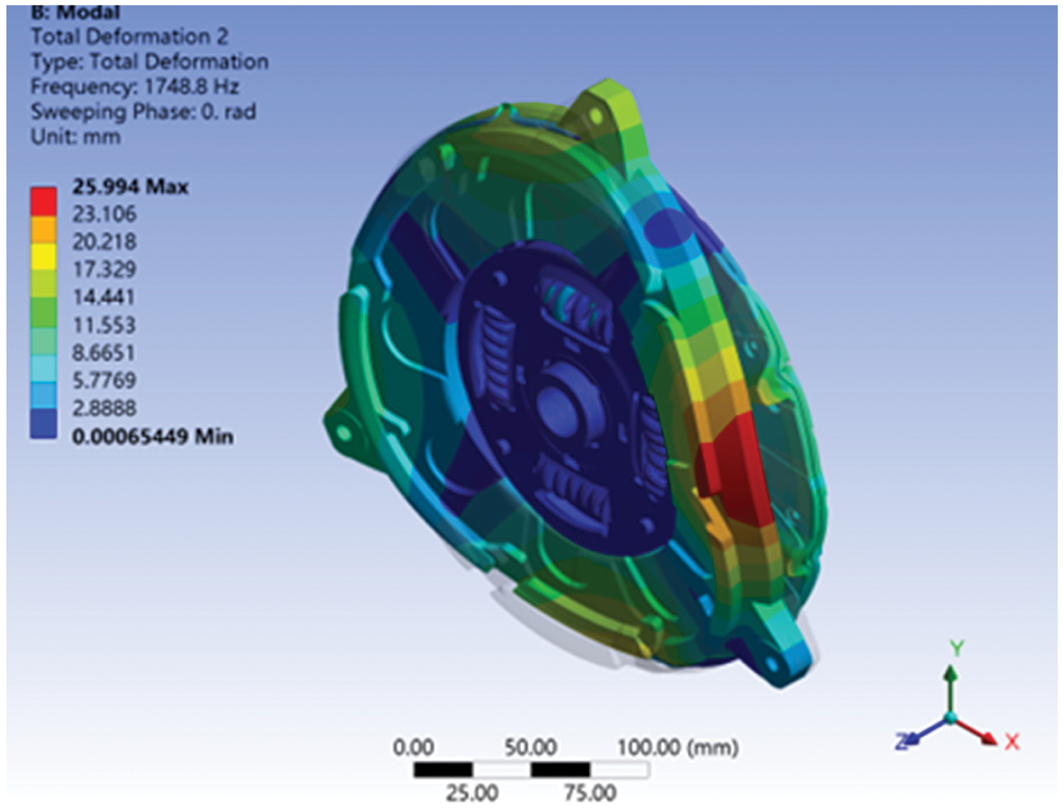
Figure 7: Vibration mode of the clutch system at the frequency of 1748.8 Hz
During the slip phase of the clutch engagement, a large amount of frictional heat is generated and most of the heat is absorbed by the pressure plate. Therefore, the temperature of the pressure plate rises significantly and the corresponding thermal deformation of the pressure plate may exceed the stability limit of the system.
The equivalent heat flux derived from the friction heat is applied onto the friction surface of the pressure plate. The temperature distribution of the pressure plate is shown in Fig. 8 at the end of the slip phase of the engagement. It can be seen from Fig. 8 that the temperature of the friction surface of the pressure plate generally varies with the radius. The maximum temperature of 318°C is located on the outer rim of the pressure plate. Since the three outer bolt hole areas are not involved in the frictional slipping, the temperature at the outer rim near these bolt hole areas is relatively low.
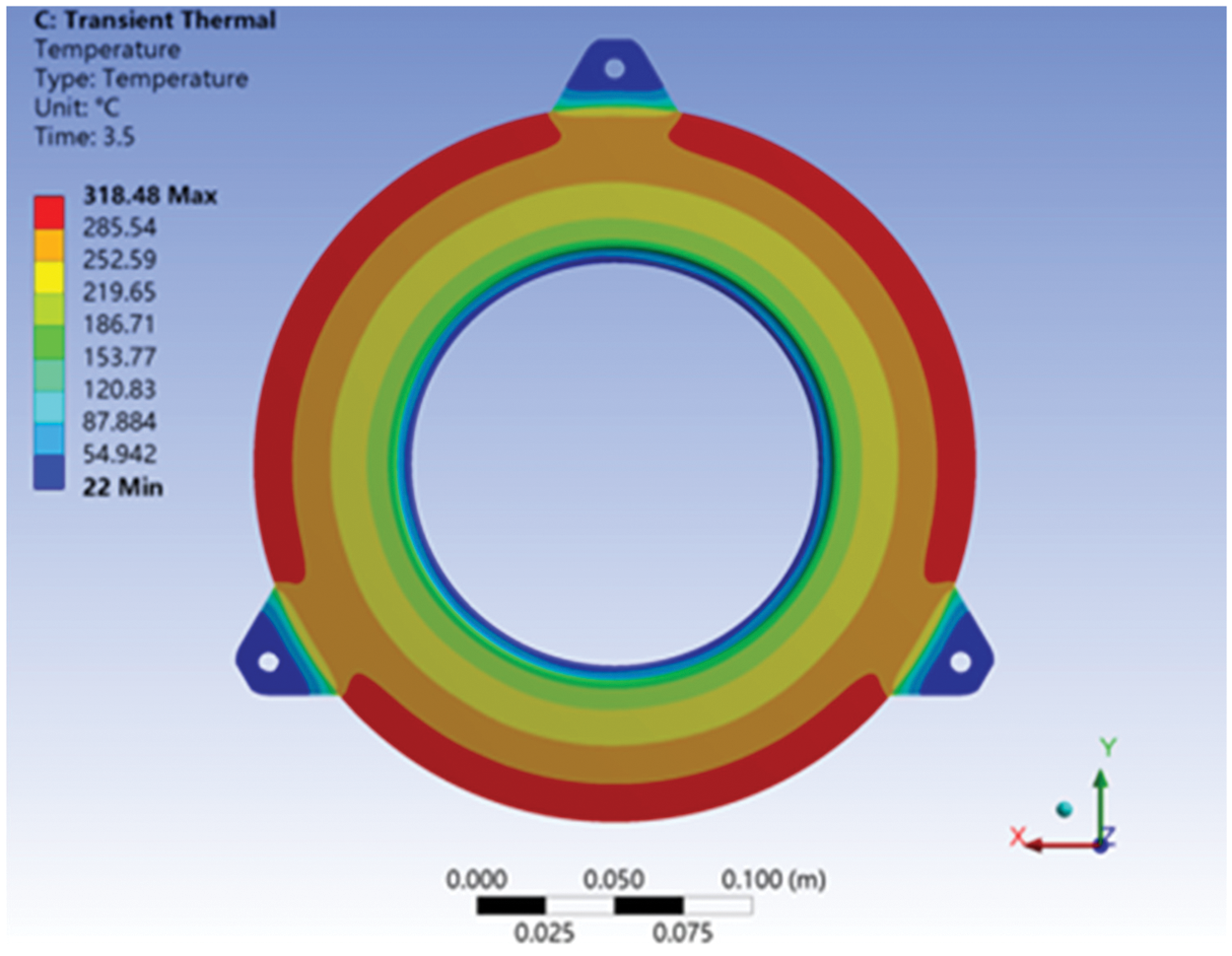
Figure 8: The temperature field of pressure plate
Shown in Figs. 9 and 10 are the contact areas between the pressure plate and the friction plate with and without thermal deformation considered. Without the thermal deformation, the contact area is around the bump area of the friction plate shown in Fig. 10. With the thermal deformation, the actual contact areas only exist on the inner part of the bump area of the friction plate shown in Fig. 9. This change in the contact area leads to the change of the contact stress and eventually influences the system instability.
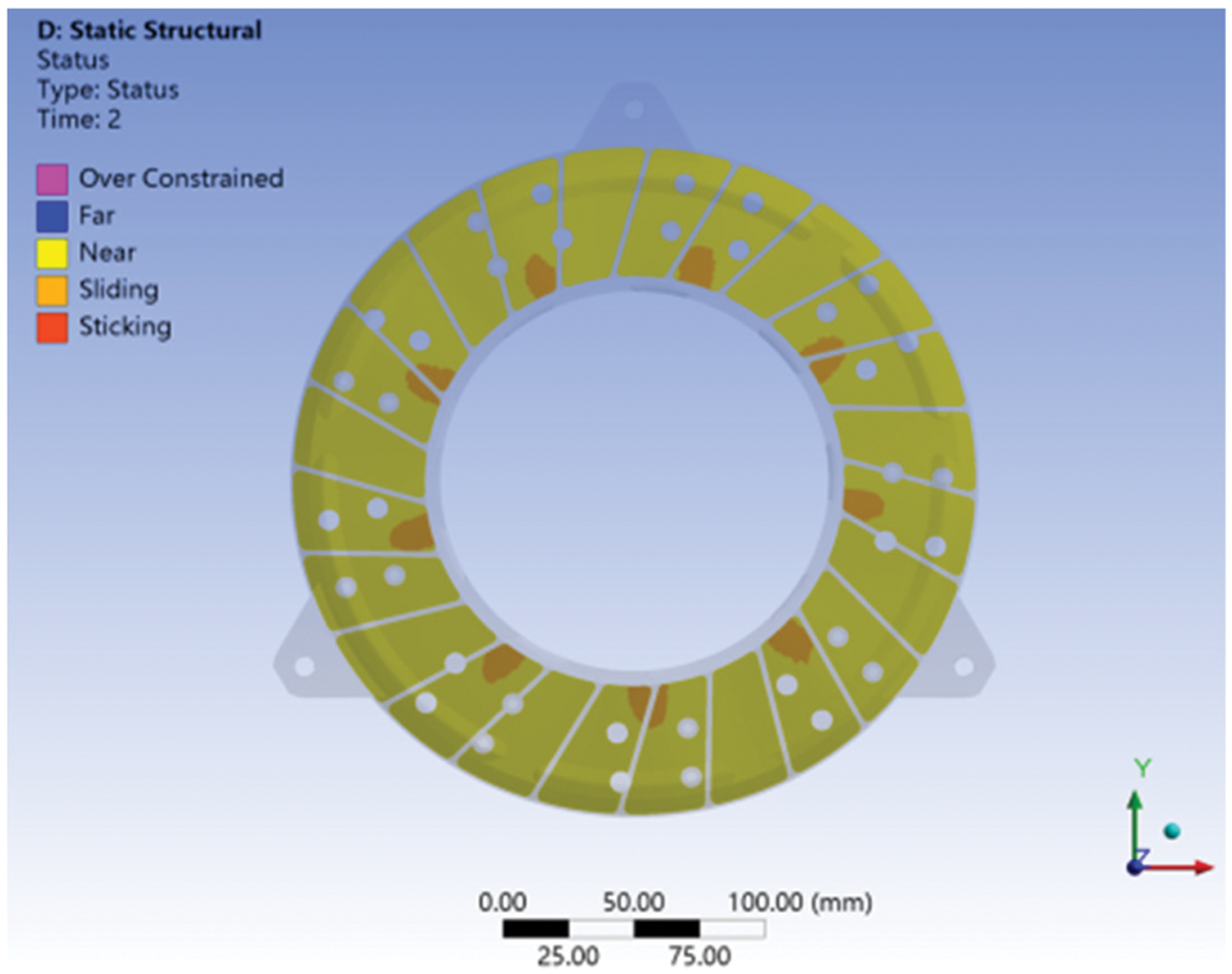
Figure 9: Contact status with thermal deformation
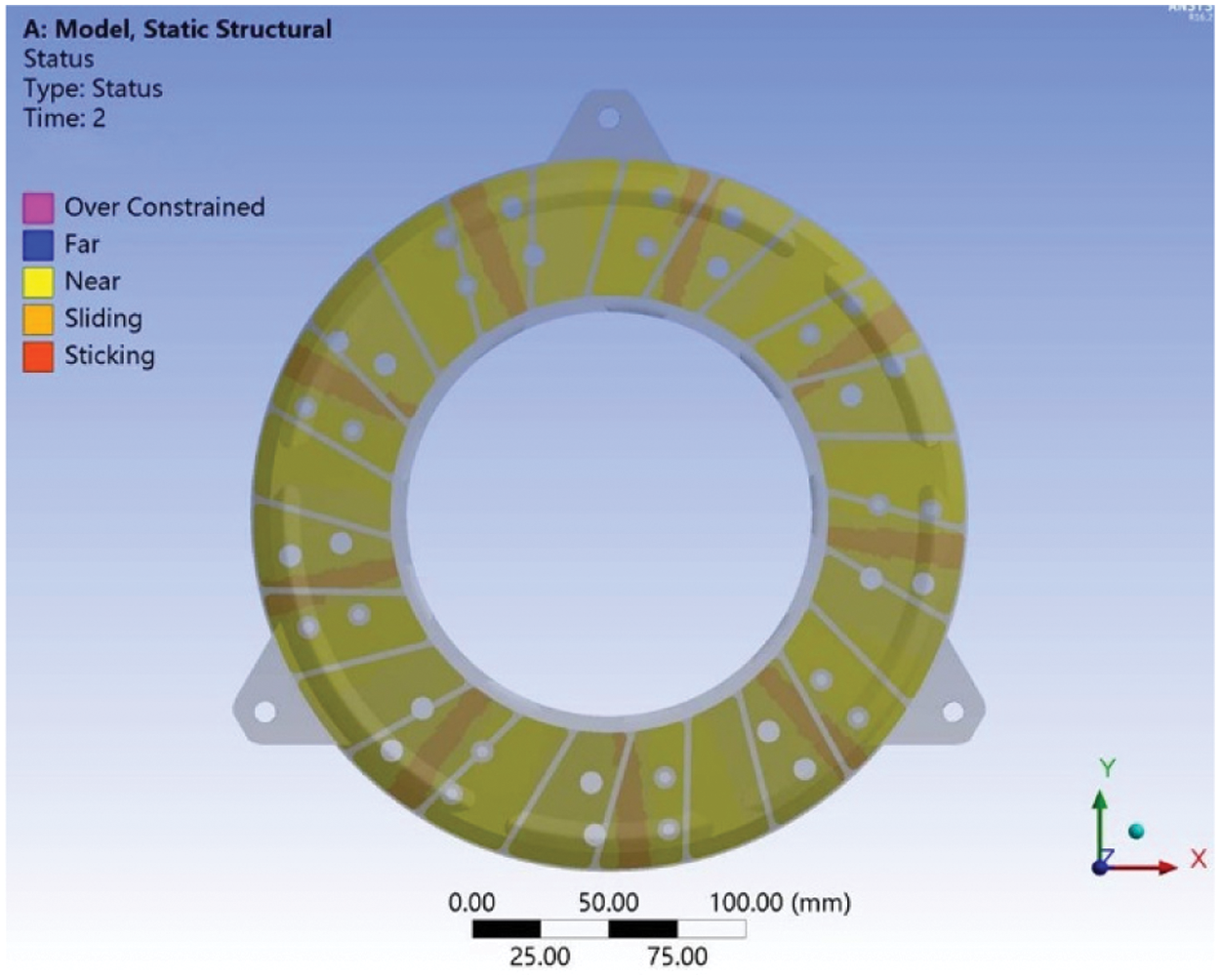
Figure 10: Contact status without thermal deformation
The real part and the frequency of the unstable eigenvalue of the clutch with and without the thermal deformation of the pressure plate are shown in Fig. 11. From Fig. 11, it can be concluded that with the thermal deformation the real part and the frequency of the unstable eigenvalue of the clutch system are significantly reduced. This indicates that the clutch system tends to be more stable when the thermal deformation is considered. This agrees with the experimental data in terms of the tendency of the clutch sliding noise discussed later.
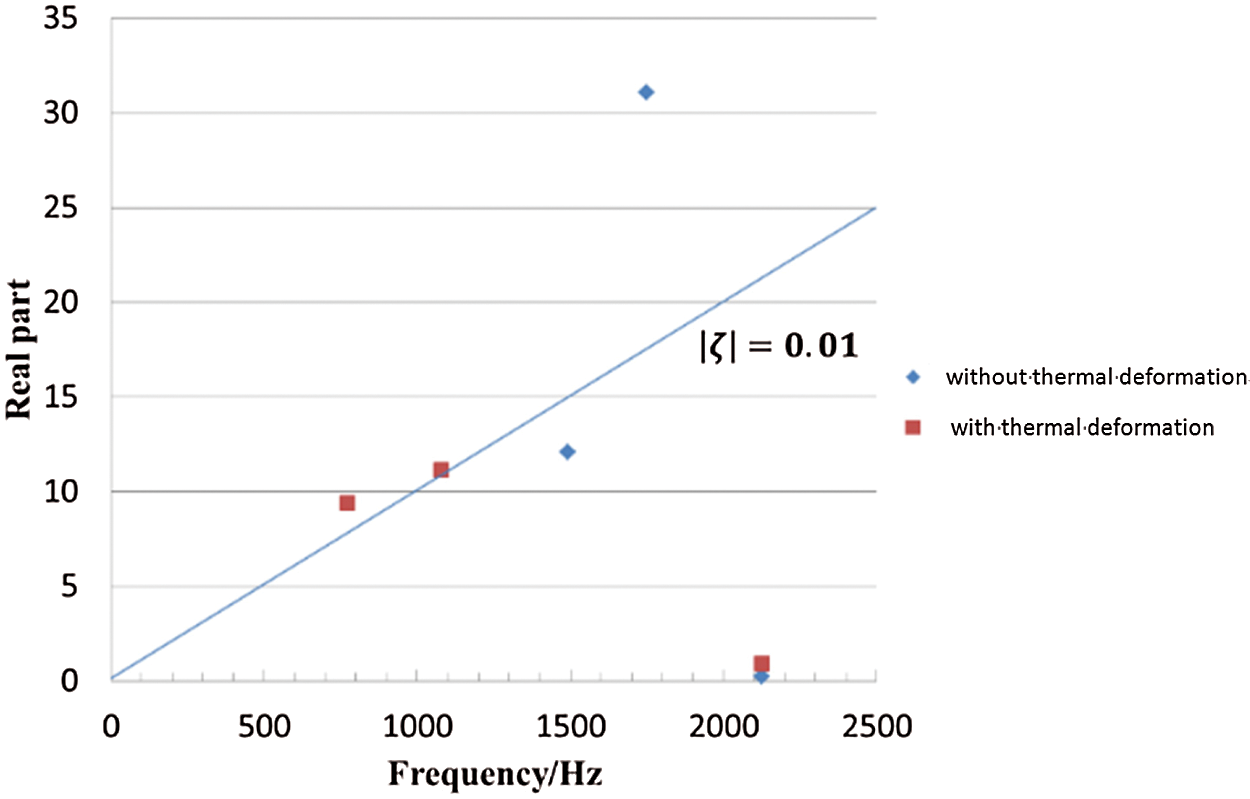
Figure 11: Unstable mode
The test vehicle shown in Fig. 12 is a pickup truck and the vehicle uses a Ø260 clutch assembly. A microphone is installed on the upper part of the driver seat to record the noise. On a slope road with an angle of about 15 degrees, the test vehicle starts to move using the lowest gear. The engine speed is near 1000 RPM~2000 RPM. It is found that there is a clear intermittent squeal when this vehicle is started and accelerated during the slip phase of the clutch engagement. The recorded noise is analyzed with commercial software and three major squeal noise frequencies, namely 494.0, 634.0 and 1172.0 Hz, with the intensity above 100 dB are observed, as shown in Fig. 13.

Figure 12: Test vehicle
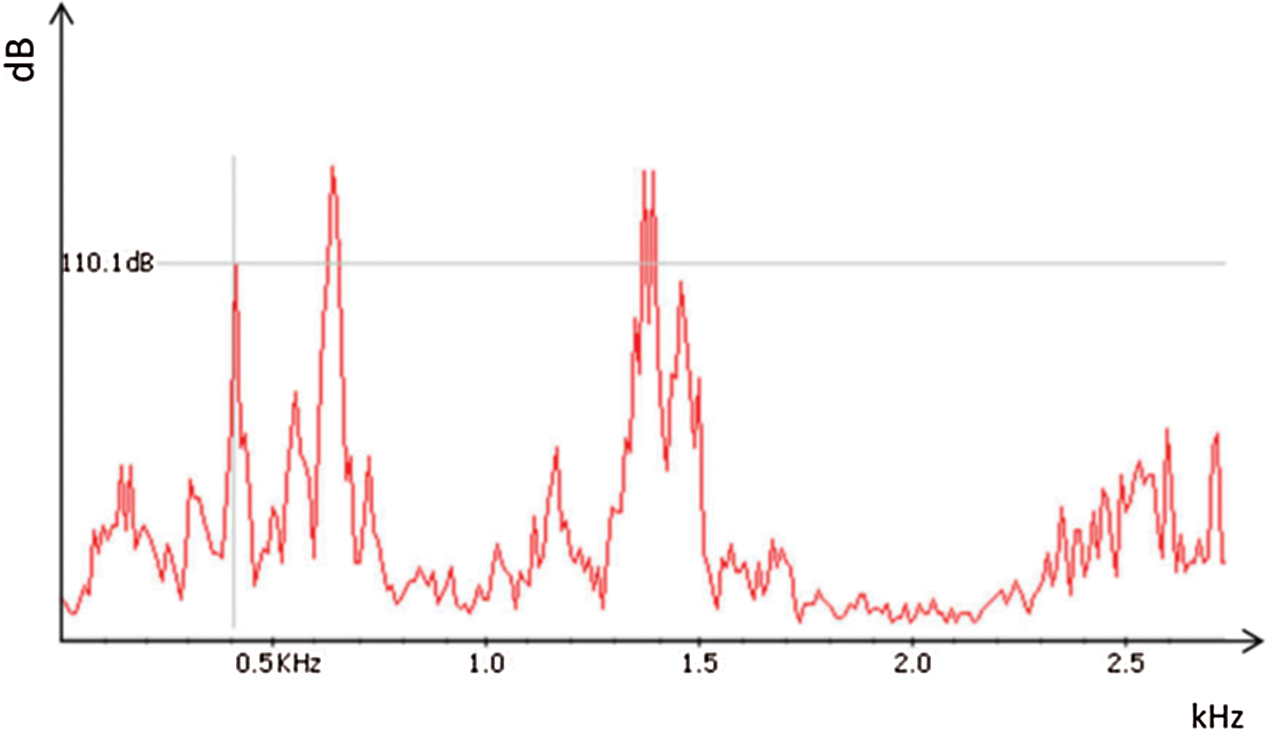
Figure 13: Noise frequency
It is noted that after the vehicle undergoes several continuous start-up operations in the road test conditions mentioned above, normally three times, the sliding noise of the clutch does not occur again. The tested clutch producing the squeal noise was disassembled after the road test. It is found that there is an obvious local contact on the friction plate and that the contact areas are located near the rivet hole as shown in Fig. 14. The correspondingly maximum bump height of the friction plate is about 0.3 mm.

Figure 14: The driven plate assembly of the dry clutch with the sliding noise
Comparing the experiment data with the simulated data, it is found that the complex eigenvalue analysis of the clutch system can essentially predict the low frequency squeal of the clutch, as shown in Table 3. Without consideration of the thermal deformation of the pressure plate, three squeal frequencies, namely 1492.1, 1748.8 and 2121.5 Hz, are predicted. Considering the thermal deformation of the pressure plate, another two squeal frequencies, namely 772.0 and 1079.0 Hz, are predicted. The latter is closer to the test results, which consist of 494.0, 634.0, and 1172.0 Hz. In particular, the practical squeal noise of 1172.0 Hz, with the greatest intensity captured by the simulation with consideration of the thermal deformation with a relative error of 8.6%. This evidence shows that the thermal deformation of the pressure plate should be included in the complex eigenvalue simulation of the clutch sliding noise.

It is noted that the sliding noise of 494.0 Hz measured from the experiment is not effectively predicted by the simulation model. We believe that the uncertainties in the numerical model such as the inaccuracy of the material properties and the overestimation using the complex eigenvalue method may give rise to the errors in the solutions.
To study the factors affecting the sliding noise of dry clutch, a complex eigenvalue analysis is used to model and analyze the factors such as the friction coefficient, the surface bump of the friction plate, and the thermal deformation of the pressure plate. By comparing the sliding noise instability frequency predicted by the simulation with the road test, three conclusions are obtained, as follows. 1) The smaller the friction coefficient is, the more obvious the noise reduction is. 2) The propensity of the clutch to make the sliding noise is greatly affected by the surface bumping of the friction plate. The clutch sliding noise caused by the surface bumping of the friction plate normally occurs at a relatively low-frequency range. 3) The thermally introduced bump-shaped thermal deformation can decrease the possibility of squealing noise.
Acknowledgement: We thank LetPub (www.letpub.com) for its linguistic assistance during the preparation of this manuscript.
Funding Statement: The authors gratefully acknowledge the financial support for this work from the National Natural Science Foundation of China (NSFC) (No. 51965012) and the Key Research and Development Plan of Guangxi Province of China (No. AB18126002).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Wickramarachi, P., Singh, R., Bailey, G. (2005). Analysis of friction-induced vibration leading to ``EEK'' noise in a dry friction clutch. Noise Control Engineering Journal, 53(4), 134–144. DOI 10.3397/1.2839252. [Google Scholar] [CrossRef]
2. Senatore, A., Hochlenert, D., D'Agostino, V., Wagner, U. V. (2013). Driveline dynamics simulation and analysis of the dry clutch friction-induced vibrations in the eek frequency range. ASME 2013 International Mechanical Engineering Congress and Exposition, USA, ASME. DOI 10.1115/IMECE2013-64597. [Google Scholar] [CrossRef]
3. Senatore, A. (2015). Drivetrain vibrations excited by dry clutch in automated manual transmissions. The 19th International Conference on Mechatronics Technology, pp. 1–4. Japan, ICMT. [Google Scholar]
4. Aktir, Y., Brunel, J. F., Dufrenoy, P., Mahe, H. (2014). Modeling squeal noise on dry automotive clutch. International Conference on Noise and Vibration Engineering, pp. 1813–1825. Belgium, Katholieke Univ Leuven. [Google Scholar]
5. Aktir, Y., Brunel, J. F., Dufrenoy, P., Mahe, H. (2016). Three-dimensional finite element model of an automotive clutch for analysis of axial vibrations. Proceedings of the Institution of Mechanical Engineers Part D--Journal of Automobile Engineering, 230(10), 1324–1337. DOI 10.1177/0954407015607377. [Google Scholar] [CrossRef]
6. Kinkaid, N. M., O'Reilly, O. M., Papadopoulos, P. (2003). Automotive disc brake squeal. Journal of Sound and Vibration, 267(1), 105–166. DOI 10.1016/S0022-460X(02)01573-0. [Google Scholar] [CrossRef]
7. Ghazaly, N. M., El-Sharkawy, M., Ahmed, I., Ibrahim, A. (2013). A review of automotive brake squeal mechanisms. Journal of Mechanical Design and Vibration, 1(1), 5–9. DOI 10.12691/jmdv-1-1-2. [Google Scholar] [CrossRef]
8. Wang, X., Mo, J., Ouyang, H., Wang, D., Chen, G. et al. (2016). Squeal noise of friction material with groove-textured surface: An experimental and numerical analysis. Journal of Tribology, 138(2), 147. DOI 10.1115/1.4031399. [Google Scholar] [CrossRef]
9. Vayssière, C., Baillet, L., Linck, V., Berthier, Y. (2005). Influence of contact geometry and third body on squeal initiation: Experimental and numerical studies. World Tribology Congress III, pp. 1363–1364. USA, ASME. DOI10.1115/WTC2005-63839. [Google Scholar] [CrossRef]
10. Zhang, G., Xie, M., Li, J., Qi, G., Pu, X. (2013). Vehicle brake moan noise induced by brake pad taper wear. Journal of Mechanical Engineering, 49(9), 81–86. DOI 10.3901/JME.2013.09.081. [Google Scholar] [CrossRef]
11. Bonnay, K., Magnier, V., Brunel, J. F., Dufrénoy, P., de Saxcé, G. (2015). Influence of geometry imperfections on squeal noise linked to mode lock-in. International Journal of Solids and Structures, 75–76(4), 99–108. DOI 10.1016/j.ijsolstr.2015.08.004. [Google Scholar] [CrossRef]
12. Abubakar, A. R., Abdulamid, M. K., Mohamad, M., Dzakaria, A., AbdGhani, B. (2006). Numerical analysis of disc brake squeal considering temperature dependent friction coefficient. J Mekanikal, 22, 26–38. [Google Scholar]
13. Cantoni, C., Cesarini, R., Mastinu, G., Rocca, G., Sicigliano, R. (2009). Brake comfort–a review. Vehicle System Dynamics, 47(8), 901–947. DOI 10.1080/00423110903100432. [Google Scholar] [CrossRef]
14. Oura, Y., Kurita, Y., Matsumura, Y. (2009). Influence of dynamic stiffness in contact region on disk brake squeal. Journal of Environment and Engineering, 4(2), 234–244. DOI 10.1299/jee.4.234. [Google Scholar] [CrossRef]
15. Ouyang, H., Bakar, A. R. A., Li, L. (2009). A combined analysis of heat conduction, contact pressure and transient vibration of a disk brake. International Journal of Vehicle Design, 51(1–2), 190–206. DOI 10.1504/IJVD.2009.027121. [Google Scholar] [CrossRef]
16. Hassan, M. Z., Brooks, P. C., Barton, D. C. (2009). A predictive tool to evaluate disk brake squeal using a fully coupled thermo-mechanical finite element model. International Journal of Vehicle Design, 51(1–2), 124–142. DOI 10.1504/IJVD.2009.027118. [Google Scholar] [CrossRef]
17. Ostermeyer, G. P., Graf, M. (2013). Influence of wear on thermoelastic instabilities in automotive brakes. Wear, 308(1–2), 113–120. DOI 10.1016/j.wear.2013.09.009. [Google Scholar] [CrossRef]
18. Bakar, A. R. A., Li, L., James, S., Ouyang, H. (2006). Wear simulation and its effect on contact pressure distribution and squeal of a disc brake. Proceedings of the International Conference on Vehicle Braking Technology, pp. 233–242. UK. [Google Scholar]
19. Zarraga, O., Abete, J. M., Ulacia, I., Zabala, B., Uzkudun, O. (2014). On the development of a simple model of a brake-clutch for squeal prediction. EuroBrake 2014 Conference Proceedings, pp. 13–14. France, FISITA. [Google Scholar]
20. Zarraga, O., Ulacia, I., Abete, J. M., Ouyang, H. (2017). Receptance based structural modification in a simple brake-clutch model for squeal noise suppression. Mechanical Systems and Signal Processing, 90(3), 222–233. DOI 10.1016/j.ymssp.2016.12.028. [Google Scholar] [CrossRef]
21. Jakub, Š., Roman, R., Vladislav, O. (2019). FE analysis of strain constraint around the crack tip under cyclic loading. International Journal of Structural Integrity, 11(5), 698–709. DOI 10.1108/IJSI-10-2018-0065. [Google Scholar] [CrossRef]
22. Lamin, F., Ariffin, A. K., Mohamed, I. F. (2019). Finite element analysis of plasticity behaviour of aluminium alloys in high-pressure torsion compressive loading stage. International Journal of Structural Integrity, 10(5), 692–703. DOI 10.1108/IJSI-04-2019-0037. [Google Scholar] [CrossRef]
23. Abubakar, A. R., Ouyang, H. (2006). Complex eigenvalue analysis and dynamic transient analysis in predicting disc brake squeal. International Journal of Vehicle Noise & Vibration, 2(2), 143–155. DOI 10.1504/IJVNV.2006.011051. [Google Scholar] [CrossRef]
24. Nacivet, S., Sinou, J. J. (2017). Modal amplitude stability analysis and its application to brake squeal. Applied Acoustics, 116, 127–138. DOI 10.1016/j.apacoust.2016.09.010. [Google Scholar] [CrossRef]
25. Oberst, S., Lai, J. C. S. (2012). Analysis of disc brake squeal: Progress and challenges. 19th International Congress on Sound and Vibration. pp. 2874–2881. Lithuania, International Institute of Acoustics and Vibration. DOI10.13140/RG.2.1.2185.2568. [Google Scholar] [CrossRef]
26. Hui, L., Shangguan, W., Yu, D. (2017). An imprecise probability approach for squeal instability analysis based on evidence theory. Journal of Sound & Vibration, 387(1), 96–113. DOI 10.1016/j.jsv.2016.10.001. [Google Scholar] [CrossRef]
27. Gräbner, N., Mehrmann, V., Quraishi, S., Schroder, C., Wagner, U. (2016). Numerical methods for parametric model reduction in the simulation of disk brake squeal. ZAMM--Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 96(12), 1388–1405. DOI 10.1002/zamm.201500217. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |