Degenerate <i>s</i>-Extended Complete and Incomplete Lah-Bell Polynomials

Hye Kim; Dae Lee

doi:10.32604/cmes.2022.017616

Processing math: 23%

[BACK]

Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2022.017616

ARTICLE

Degenerate s-Extended Complete and Incomplete Lah-Bell Polynomials

Hye Kyung Kim1,* and Dae Sik Lee2

1Department of Mathematics Education, Daegu Catholic University, Gyeongsan, 38430, Korea
2School of Electronic and Electric Engineering, Daegu University, Gyeongsan, 38453, Korea
*Corresponding Author: Hye Kyung Kim. Email: hkkim@cu.ac.kr
Received: 26 July 2021; Accepted: 26 September 2021

Abstract: Degenerate versions of special polynomials and numbers applied to social problems, physics, and applied mathematics have been studied variously in recent years. Moreover, the (s-)Lah numbers have many other interesting applications in analysis and combinatorics. In this paper, we divide two parts. We first introduce new types of both degenerate incomplete and complete s-Bell polynomials respectively and investigate some properties of them respectively. Second, we introduce the degenerate versions of complete and incomplete Lah-Bell polynomials as multivariate forms for a new type of degenerate s-extended Lah-Bell polynomials and numbers respectively. We investigate relations between these polynomials and degenerate incomplete and complete s-Bell polynomials, and derive explicit formulas for these polynomials.

Keywords: Lah-Bell numbers and polynomials; s-extended Lah-Bell numbers and polynomials; complete s-Bell polynomials; incomplete s-Bell polynomials; s-Stirling numbers of second kind

Mathematics Subject Classification 11F20; 11B68; 11B83

1 Introduction

For nonnegative integers n, k, s such that $n≥k$ , the s-Lah number Ls(n, k) counts the number of partitions of a set with n + s elements into k + s ordered blocks such that s distinguished elements have to be in distinct ordered blocks [1–5]. When s = 0, the Lah numbers appears non-crossing partitions, Dyck paths as well as falling and rising factorials [6]. As multivariate forms for ordinary Bell polynomials and Stirling numbers of the second kind, respectively, both the complete and incomplete Bell polynomials play important role in combinatorics and number theory. Recently, many mathematicians have been studying various degenerate versions of special polynomials and numbers as well as enumerative combinatorics, probability theory, number theory, etc. [7–17]. In [7], as an example considering the psychological burden of baseball hitters, it well expresses the starting point of degenerate special polynomials and numbers being studied by many scholars. Also, both the complete and incomplete Bell polynomials are multivariate forms for Bell polynomials and Stirling numbers of the second kind, respectively. Beginning with Bell [18], these polynomials have been studied by many mathematicians [1,16,19,20]. Recently, Kwon et al. [16] introduced the degenerate incomplete and complete s-Bell polynomials and Kim et al. [20] introduced the incomplete and complete s-extended Lah-Bell polynomials, respectively. With this in mind, we want to study the degenerate versions of complete and incomplete Lah-Bell polynomials as multivariate forms for a new type of degenerate s-extended Lah-Bell polynomials and numbers respectively. In Section 2, we consider new types of degenerate incomplete and complete s-Bell polynomials respectively different from those introduced in [16] for our goal. We study several properties and explicit formulas for them. In Section 3, we define both degenerate incomplete and complete s-extended Lah-Bell polynomials associated with a new type of degenerate s-extended Lah-Bell polynomials respectively, and derive relations between these polynomials and degenerate polynomials in the first part. We also investigate explicit formulas for degenerate complete and incomplete s-extended Lah-Bell polynomials, respectively.

First, we introduce some definitions and properties we needed in this paper.

For a nonnegative integer s, the s-Stirling numbers S(s)2(n, k) of the second kind are given by the generating function

$1k!est(et−1)k=∑n=k∞Sn(s)(n+s,k+s)tnn!,(see [15,16]).$ (1)

When s = 0, S(0)2(n, k) = S2(n, k) are the Stirling numbers of the second kind which are the number of ways to partition a set with n elements into k non-empty subsets.

From (8), it is to see that [15,16] the generating function of the s-Bell polynomials is

$∑n=0∞beln(s)(x)tnn!=ex(et−1)est.$ (2)

When x = 1, $beln(s)(1)=beln(s)=∑k=0nS2(n+s,k+s)$ are called the s-bell numbers.

When s = 0, $beln(0)(x)=beln(x)$ are the ordinary Bell polynomials.

Furthermore, the incomplete s-Bell polynomials.

$Bn+s,k+s(β1,β2,⋯:ν1,ν2,⋯)$ are given by the generating function

$1k!(∑l=1∞βltll!)k(∑i=0∞νi+1tii!)s=∑n=k∞Bn+s,k+s(β1,β2,⋯:ν1,ν2,⋯)tnn!,(see [16]).$ (3)

When s = 0, $Bn+0,k+0(β1,β2,⋯:ν1,ν2,⋯)=Bn,k(β1,β2,⋯,βn−k+1)$ are the incomplete Bell polynomials. From (10), we obtain immediately that [16]

$Bn+s,k+s(s)(β1,β2,⋯:ν1,ν2,⋯)=∑Λ(n,k,s)[n!k1!,k2!⋯(β11!)k1(β22!)k2(β33!)k3⋯]×[s!s0!s1!s2!⋯(ν10!)s0(ν21!)s1(ν32!)s3⋯],$ (4)

where $Λ(n,k,s)$ denotes the set of all nonnegative integers $(ki)i≥1$ and $(si)i≥0$ such that

$∑i≥1ki=k,∑i≥0si=sand∑i≥1i(ki+si)=n.$

The combinatorial meaning of the incomplete s-Bell polynomials is in the reference [18].

The complete s-Bell polynomials $Bn(s)(x1,x2,⋯:y1,y2,⋯)$ are given by the generation function

$exp(∑l=1∞βltll!)(∑i=0∞νi+1tii!)s=∑n=k∞Bn(s)(β1,β2,⋯:ν1,ν2,⋯)tnn!,(see [18]),$ (5)

where exp(t) = et.

When s = 0, $Bn(0)(β1,β2,⋯:ν1,ν2,⋯)=Bn(β1,β2,⋯,βn)$ are the complete Bell polynomials.

Let n, k, s be nonnegative integers with $n≥k$ . It is well known that [2] an explicit formula and the generating function of s-Lah Bell Ls(n, k) are given by, respectively

$Ls(n,k)=n!k!(n+2s−1k+2s−1),$

and

$1k!(t1−t)k(11−t)2s=∑n=k∞Ls(n,k)tnn!.$ (6)

When s = 0, L0(n, k) = L(n, k) are the unsigned Lah-numbers.

Kim et al. [2] introduced the s-extended Lah-Bell polynomials Lbn, s(x) given by the generating function

$ext1−t(11−t)2s=∑n=0∞Lbn,s(x)tnn!.$ (7)

When x = 1, $Lbn,s(1)=Lbn,s=∑k=0nLs(n,k)(n≥0)$ are called the s-extended Lah-Bell numbers. When s = 0, Lbn, 0(x) = Lbn(x) are the Lah-Bell polynomials.

For $λ∈R$ , the degenerate exponential function is defined by

$eλx(t)=(1+λt)xλandeλ(t)=∑n=0∞(1)n,λtnn!,(see [8−11]).$ (8)

where $(x)0,λ=1$ and $(x)n,λ=x(x−λ)(x−2λ)⋯(x−(n−1)λ).$

The degenerate fully Bell polynomials are given by

$eλ(x(eλ(t)−1))=∑n=0∞Beln,λ(x)tnn!,(see [21]).$ (9)

When $λ→0$ , $Beln,λ(x)=beln(x)$ .

In addition, the partially degenerate Bell polynomials are given by

$ex(eλ(t)−1))=∑n=0∞Beln,λ(x)tnn!,(see [12]).$ (10)

When $λ→0$ , $Beln,λ(x)=beln(x)$ .

2 A New Type of Degenerate Complete and Incomplete s-Bell Polynomials

In this section, we introduce new types of degenerate complete s-Bell polynomials and degenerate incomplete s-Bell polynomials different from (9) and (10), respectively. We also give some identities and explicit formulas for these polynomials.

For our goal, we introduce a new type of the degenerate extended s-Bell polynomials defined by

$eλ(x(et−1))eλs(t)=∑n=0∞beln,s,λ(x)tnn!.$ (11)

When x = 1, $beln,s,λ=beln,s,λ(1)$ are called the degenerate extended s-Bell numbers.

When $limλ→0eλ(x(et−1))eλs(t)=exp⁡(x(et−1))exp⁡(t)=∑n=0∞beln,s(x)tnn!$ .

When s = 0, $beln,0,λ(x)=beln,λ(x)$ are the degenerate Bell polynomials.

Theorem 2.1. For $n, s∈N∪0$ , we have

$beln,s,λ(x)=∑m=0n∑k=0m(nm)(1)k,λ(s)n−m,λS2(m,k)xk.$

Proof. From (1), (8) and (11), we observe that

$∑n=0∞beln,s,λ(x)tnn!=eλ(x(et−1))eλs(t)=∑k=0∞(1)k,λxk1k!(et−1)keλs(t)=∑k=0∞(1)k,λxk∑m=k∞S2(m,k)tmm!∑j=0∞(s)j,λtjj!=∑m=0∞∑k=0m(1)k,λxkS2(m,k)tmm!∑j=0∞(s)j,λtjj!=∑n=0∞(∑m=0n∑k=0m(nm)(1)k,λ(s)n−m,λS2(m,k)xk)tnn!.$ (12)

By comparing with the coefficients of both side of (12), we get the desired result.

Theorem 2.2. For $n, s∈N∪0$ , we have

$beln,s,λ(x)=∑k=0∞∑h=0n∑m=0k(nh)(km)mn−h(s)h,λ(1)k,λ(−1)k−mk!xk.$

Proof. From (8) and (11), we observe that

$∑n=0∞beln,s,λ(x)tnn!=eλ(x(et−1))eλs(t)=∑k=0∞(1)k,λxk1k!(et−1)keλs(t)=∑k=0∞(1)k,λxk1k!∑m=0k(km)(−1)k−m∑j=0∞mjtjj!∑h=0∞(s)h,λthh!=∑n=0∞(∑k=0∞∑h=0n∑m=0k(nh)(km)mn−h(s)h,λ(1)k,λ(−1)k−mk!xk)tnn!.$ (13)

By comparing with the coefficients of both side of (13), we get the desired result.

First, we define a new type of the degenerate complete Bell polynomials $Bnλ(β1,β2,⋯,βn)$ associated with the degenerate Bell polynomials $beln,λ(x)$ by

$eλ(∑h=1∞βhthh!)=∑n=0∞Wnλ(β1,β2,⋯,βn)tnn!,$ (14)

and a new type of the degenerate incomplete Bell polynomials $Wn,kλ(β1,β2,⋯,βn−k+1)$ associated with some degenerate Stirling numbers defined by

$1k!(1)k,λ(∑h=1∞βhthh!)k=∑n=k∞Wn,kλ(β1,β2,⋯,βn−k+1)tnn!,(n≥k≥0).$ (15)

Theorem 2.3. For $n≥k≥0$ , we have

$W0λ(β1,β2,⋯,βn)=1Wnλ(β1,β2,⋯,βn)=∑k=1n(1)k,λBn,k(β1,β2,⋯,βn−k+1)if n≥1.$

In particular, we have $Wnλ(x,x,⋯,x)=beln,λ(x).$

Proof. From (3), (4) and (14), we have

$∑n=0∞Wnλ(β1,β2,⋯,βn)tnn!=eλ(∑h=1∞βhthh!)=1+∑k=1∞(1)k,λ1k!(∑h=1∞βhthh!)k=1+∑k=1∞(1)k,λ∑n=k∞Bn,k(β1,β2,⋯,βn−k+1)tnn!=1+∑n=1∞(∑k=1n(1)k,λBn,k(β1,β2,⋯,βn−k+1))tnn!.$ (16)

Therefore, by comparing with coefficients of both sides of (16), we have the desired result.

In particular, from (16), we have

$∑n=0∞Wnλ(x,x,⋯,x)tnn!=eλ(x∑h=1∞thh!)=eλ(x(et−1))=∑n=0∞beln,λ(x)tnn!.$ (17)

Thus, by comparing with coefficients of both sides of (17), we have

$Wnλ(x,x,…,x)=beln,λ(x).$

In next theorem, we obtain a new type of degenerate Stirling numbers of second kind $(1)k,λS2(n,k)$ .

Theorem 2.4. For $n≥k≥0$ , we have

$W0λ(β1,β2,…,βn)=1Wnλ(β1,β2,…,βn)=∑k=1nWn,kλ(β1,β2,⋯,βn−k+1)if n≥1.$

In particular, we get $Wn,kλ(1,1,…,1)=(1)k,λS2(n,k).$

Proof. From (8), (14) and (15), we observe that

$∑n=0∞Wnλ(β1,β2,⋯,βn)tnn!=eλ(∑h=1∞βhthh!)=∑k=0∞1k!(1)k,λ(∑h=1∞βhthh!)k=1+∑k=1∞∑n=k∞Wn,kλ(β1,β2,⋯,βn−k+1)tnn!=1+∑n=1∞∑k=1nWn,kλ(β1,β2,⋯,βn−k+1)tnn!.$ (18)

Therefore, by comparing with coefficients of both sides of (18), we have what we want.

In addition, from (18), we get

$∑n=k∞Wn,kλ(1,1,⋯,1)=(1)k,λ1k!(et−1)k=(1)k,λ∑n=k∞S2(n,k).$

Thus, we have $Wn,kλ(1,1,⋯,1)=(1)k,λS2(n,k).$

Next, for $λ∈R$ , we consider a new type of degenerate incomplete s-Bell polynomials defined by

$Wn+s,k+sλ(β1,β2,⋯:ν1,ν2,⋯)=1k!(∑h=1∞(1)k,λβhthh!)k(∑m=0∞(1)m,λνm+1tmm!)s.$ (19)

From (4) and (19), we have the following explicit formula

For $n≥k≥0$ , we have

$Wn+s,k+sλ(β1,β2,⋯:ν1,ν2,⋯)=∑n=k∞Bn+s,k+s((1)k,λβ1,(1)k,λβ2,⋯:(1)0,λν1,(1)1,λν2,⋯)tnn!=∑Λ(n,k,λ)[n!k1!k2!⋯((1)k,λβ11!)k1((1)k,λβ12!)k2⋯]×[r!s0!s1!⋯((1)0,λν10!)s0((1)1,λν21!)s1⋯],$ (20)

where $Λ(n,k,s)$ denote the set of all nonnegative integers $(ki)i≥1$ and $(si)i≥1$ such that

$∑i≥1ki=k,∑i≥0si=sand∑i≥1i(ki+si)=n$

Naturally, we define a new type of the degenerate complete s-Bell polynomials by

$Wn(s),λ(β1,β2,⋯:ν1,ν2,⋯)=eλ(∑h=1∞βhthh!)(∑m=0∞(1)m,λνm+1tmm!)s,$ (21)

where $λ∈R$ and $n, k∈N$ with $n≥k$ .

We note that

$limλ→∞Wn(s),λ(β1,β2,⋯:ν1,ν2,⋯)=Bn(s)(β1,β2,⋯:ν1,ν2,⋯).$

From (19) and (21), we note that $Wn(s),λ(β1,β2,⋯:ν1,ν2,⋯)=∑k=0nWn+s,k+sλ(β1,β2,⋯:ν1,ν2,⋯).$

Theorem 2.5. For $n, k, s≥0$ with $n≥k$ , we have

$Wn+s,k+sλ(1,1,⋯:1,1,⋯)=(1)k,λS2(n,k)eλs(t).$

Proof. From (1), (8) and (19), we have

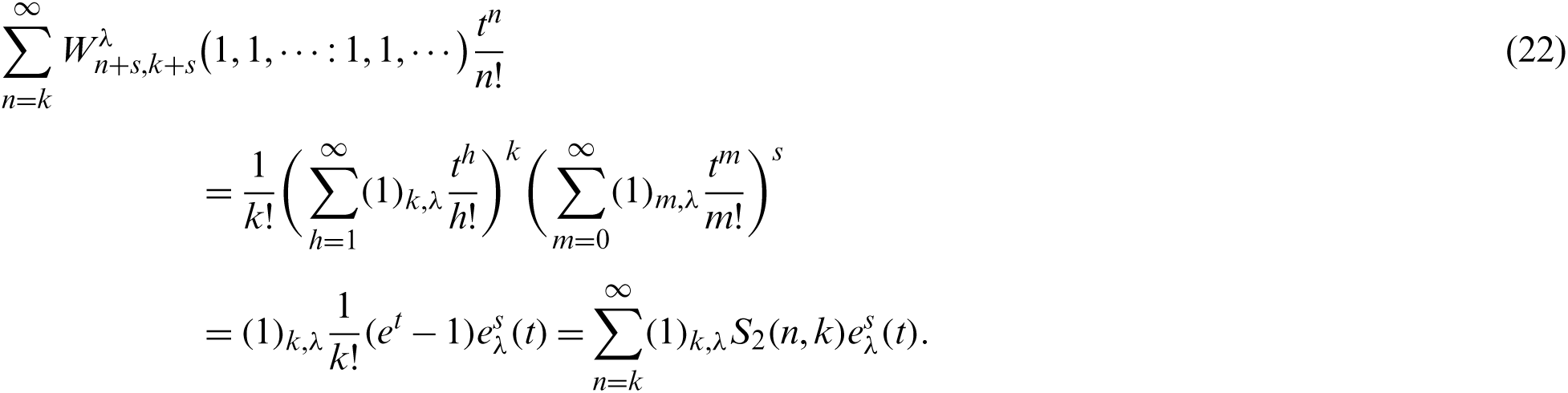
images

Therefore, by comparing with coefficients of both side of (22), we obtain the desired result.

In Theorem 2.5, we obtain a new type of degenerate s-extended Stirling number of second.

Theorem 2.6. For $n≥k≥0$ , we have

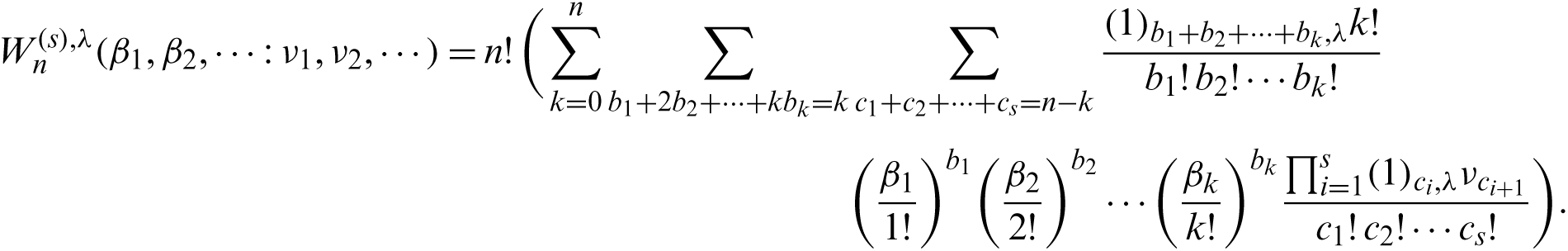
images

Proof. By using (8), we observe that

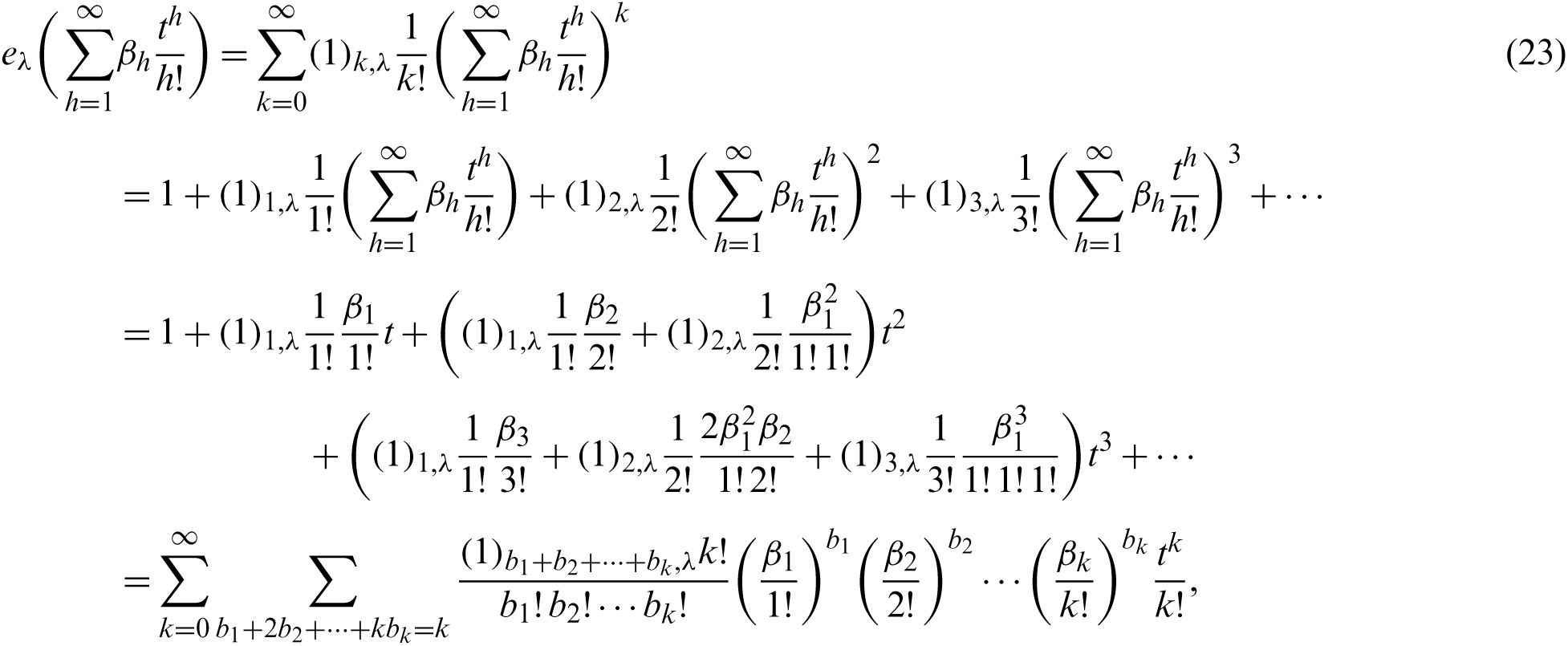
images

and

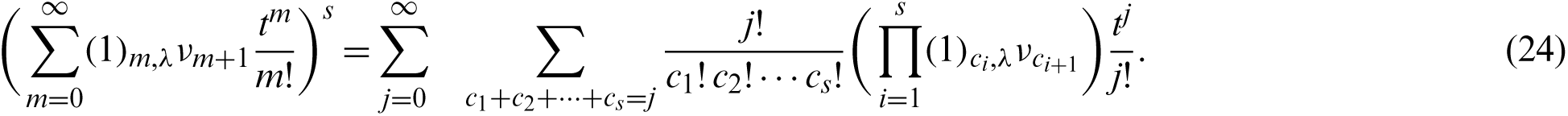
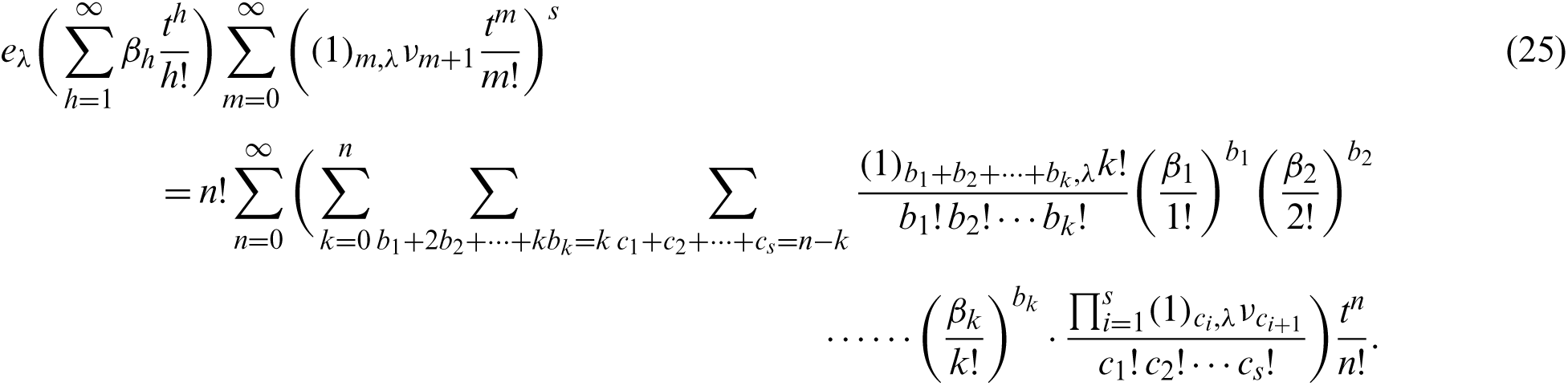
images

From (23) and (24), we get

images

On the other hand, from (21), we have

$eλ(∑h=1∞βhthh!)(∑m=0∞(1)m,λνm+1tmm!)s=∑n=0∞Wn(s),λ(β1,β2,⋯:ν1,ν2,⋯)tnn!.$ (26)

Thus, by comparing with coefficients of (25) and (26), we have what we want.

Next, we consider the extended degenerate complete s-Bell polynomials defined by the generating function

$eλ(z∑h=1∞βhthh!)(∑m=0∞(1)m,λνm+1tmm!)s=∑n=0∞Wn(s),λ(z|β1,β2,⋯:ν1,ν2,⋯)tnn!.$ (27)

Theorem 2.7. For $n≥k≥0$ , we have

$Wn(s),λ(z |β1,β2,⋯:ν1,ν2,⋯)=∑k=0nzkWn+s,k+sλ(β1,β2,⋯:ν1,ν2,⋯).$

When z = 1, we get

$Wn(s),λ(1|β1,β2,⋯:ν1,ν2,⋯)=∑k=0nWn+s,k+s(s),λ(β1,β2,⋯:ν1,ν2,⋯).$

Proof. From (19) and (27), we have

$∑n=0∞Wn(s),λ(z |β1,β2,⋯:ν1,ν2,⋯)tnn!=∑k=0∞zk(1)k,λ1k!(∑h=1∞βhthh!)k(∑m=0∞(1)m,λνm+1tmm!)s=∑k=0∞zk∑n=k∞Wn+s,k+sλ(β1,β2,⋯:ν1,ν2,⋯)tnn!=∑n=0∞(∑k=0nzkWn+s,k+s(s),λ(β1,β2,⋯:ν1,ν2,⋯))tnn!.$ (28)

Thus, by comparing with coefficients of both sides of (28), we have what we want.

Theorem 2.8. For $n, k, s≥0$ with $n≥k$ , we have

$Wn(s),λ(z | 1,1,⋯:1,1,⋯)=beln,s,λ(z).$

Proof. From (27), we observe that

$eλ(z∑l=1∞thl!)(∑m=0∞(1)m,λtmm!)s =∑n=0∞∑k=0nzkWn+s,k+s(s)((1)k,λ,(1)k,λ,⋯:(1)0,λ,(1)1,λ,⋯)tnn!.$ (29)

On the other hand, from (11), we get

$eλ(z ∑l=1∞tll!)(∑m=0∞(1)m,λtmm!)s=eλ(z(et−1))eλs(t)=∑n=0∞beln,s,λ(z)tnn!.$ (30)

Thus, from (29) and (30), we get the desired result.

3 Degenerate $s$ -Extended Complete and Incomplete Lah-Bell Polynomials

In this section, we introduce a new type of the degenerate Lah-Bell polynomials different from Kim-Kim’s in [8] and define both the s-extended complete and incomplete degenerate Lah-Bell polynomials associated with a new type of the degenerate Lah-Bell polynomials. We also demonstrate some interesting properties related to these polynomials and explicit formulas for them.

We consider a new type of the degenerate Lah-Bell polynomials $Lbn,λ(x)$ given by the generating function

$eλ(xt1−t)=∑n=0∞Lbn,λ(x)tnn!.$ (31)

When x = 1, $Lbn,λ(1)=Lbn,λ (n≥0)$ are called the degenerate Lah-Bell numbers (see Figs. 1 and 2).

When $λ→0$ , $Lbn,λ(x)=Lbn(x)$ .

In view of the ordinary Bell polynomials, the degenerate 2s-extended Lah-Bell polynomials are defined by the generating function

$∑n=k∞Lbn,2s,λ(x)=eλx(t1−t)eλ2s(t).$ (32)

When x = 1, $Lbn,2s,λ=Lbn,2s,λ(1)$ are called the degenerate extended 2s-extended Lah-Bell numbers numbers. When s = 0, the degenerate complete s-extended Lah-Bell polynomials are the degenerate Lah-Bell polynomials.

Next, we introduce the degenerate complete Lah-Bell polynomials $LWnλ(x1,x2,⋯,xn)$ defined by the generating function

$eλ(∑h=1∞βhth)=∑n=0∞LWnλ(β1,β2,⋯,βn)tnn!.$ (33)

We note that

$∑n=0∞LWnλ(x,x,⋯,x)tnn!=eλ(x∑h=1∞th)=eλ(xt1−t)=∑n=0∞Lbn,λ(x)tnn!.$ (34)

From (31), we have $LWnλ(x,⋯,x)=Lbn,λ(x)$ and $LWnλ(1,1,⋯,1)=Lbn,λ$ .

From (20) and (34), we get

$∑n=0∞LWnλ(β1,β2,⋯,βn)tnn!=eλ(∑h=1∞h!βhthh!)=∑n=0∞Wnλ(1!β1,2!β2,⋯,n!βn)tnn!.$ (35)

By (14), (15), (35) and Theorem 2.3, we obtain the following theorem.

Theorem 3.1. For $n≥k≥0$ , we have

$LW0λ(β1,β2,⋯,xn)=1 and LWnλ(β1,β2,⋯,βn)=Wnλ(1!β1,2!β2,⋯,n!βn)=∑k=1n(1)k,λBn,k(1!β1,2!β2,⋯,(n−k+1)!βn−k+1).$

Naturally, we can define a new type of the degenerate incomplete Lah-Bell polynomials

$LWn,kλ(β1,β2,⋯,βn−k+1)$ are defined by the generating function

$1k!(1)k,λ(∑h=1∞βhth)k=∑n=k∞LWn,kλ(β1,β2,⋯,βn−k+1)tnn!,(n≥k≥0).$ (36)

Note that when $λ→0$ , $LWn,kλ(1,1,⋯,1)=Lbn$ are the Lah-bell numbers.

From (15) and (36), we observe that

$LWn,kλ(β1,β2,⋯,βn−k+1)=Wn,kλ(1!β1,2!β2,⋯,(n−k+1)!βn−k+1).$ (37)

Theorem 3.2. For $n≥k≥0$ , we have

$LW0λ(β1,β2,⋯,βn)=1,LWnλ(β1,β2,⋯,βn)=∑k=1nLWn,kλ(β1,β2,⋯,βn−k+1)if n≥1.$

Proof.

From (8), (36) and (37), we observe that

$1+∑n=1∞LWnλ(β1,β2,⋯,βn)tnn!=eλ(∑h=1∞βhth)=1+∑k=1∞1k!(1)k,λ(∑h=1∞βhth)k=1+∑k=1∞∑n=k∞LWn,kλ(β1,β2,⋯,βn−k+1)tnn!=1+∑n=1∞(∑k=1nLWn,kλ(β1,β2,⋯,βn−k+1)tnn!).$ (38)

Therefore, by comparing with coefficients of both side of (38), we get the desired identity.

We define the degenerate s-extended incomplete Lah-Bell polynomials

$LWn+2s,k+2sλ(β1,β2,⋯:ν1,ν2,⋯)$ by the generating function

$1k!(1)k,λ(∑h=1∞βhth)k(∑m=0∞(1)m,λνm+1tm)2s=∑n=k∞LWn+2s,k+2sλ(β1,β2,⋯:ν1,ν2,⋯)tnn!.$ (39)

When s = 0, the degenerate incomplete s-extended Lah-Bell polynomials are the degenerate incomplete Lah-Bell polynomials.

From (19) and Theorem 2.5, we get easily the following explicit formula.

Theorem 3.3. For $n≥k≥0$ , we have

$LWn+2s,k+2sλ(β1,β2,⋯:ν1,ν2,⋯)=Wn+2s,k+2sλ(1!β1,2!β2,⋯:0!ν1,1!ν2,⋯)=∑Λ(n,k,2r)[n!k1!,k2!⋯β1k1β2k2⋯][(2s)!s0!s1!⋯ν1s0ν2s1⋯],$

where $Λ(n,k,2s)$ denote the set of all nonnegative integers ${ki}i≥1$ and ${si}i≥0$ such that

$∑i≥1ki=k,∑i≥0si=2sand∑i≥1i(ki+si)=n.$

We also define the degenerate s-extended complete Lah-Bell polynomials

$LWn(2s),λ(z|β1,β2,⋯:ν1,ν2,⋯)$ by the generating function

$eλ(z∑h=1∞βhth)(∑m=0∞(1)m,λνm+1tm)2s=∑n=0∞LWn(2s),λ(z|β1,β2,⋯:ν1,ν2,⋯)tnn!.$ (40)

Theorem 3.4. For $n≥k≥0$ , we have

$LWn+2s,k+2sλ(x,x,x,⋯:10!11!12!⋯)=Lbn,2s,λ(x).$

When x = 1, we have

$LWn+2s,k+2sλ(1,1,1,⋯:10!11!12!⋯)=Lbn,2s,λ.$

Proof. From (32) and (39), we have

$∑n=k∞LWn+2s,k+2sλ(x,x,x,⋯:10!11!12!⋯)tnn!=1k!(1)k,λ(∑h=1∞th)k(xk∑m=0∞(1)m,λtmm!)2s=eλx(t1−t)eλ2s(t)=∑n=k∞Lbn,2s,λ(x).$ (41)

Therefore, by comparing with coefficients of both side of (41), we get the desired result.

From (19), (39) and (40), we note that

$LWn(2s),λ(z|β1,β2,⋯:ν1,ν2,⋯)=∑k=0nzkLWn+2s,k+2sλ(β1,β2,⋯:ν1,ν2,⋯)=∑k=0nzkWn+2s,k+2sλ(1!β1,2!β2,⋯:0!ν1,1!ν2,⋯),$

for $n≥k≥0$ .

Theorem 3.5. For $n≥k≥0$ and $s≥0$ , we have

$LWn(s),λ(β1,β2,⋯:ν1,ν2,⋯)=n!(∑k=0n ∑b1+2b2+⋯+kbk=k∑c1+c2+⋯+c2s=n−k(1)b1+b2+⋯+bk,λ(β1)b1(β2)b2⋯(βk)bkb1!b2!⋯bk!∏i=12s(1)ci,λνci+1).$

Proof. From (17), we have

$eλ(∑h=1∞βhth)=∑k=0∞(1)k,λ1k!(∑h=1∞βhth)k=1+(1)1,λ11!(∑h=1∞βhth)+(1)2,λ12!(∑h=1∞βhth)2+(1)3,λ13!(∑h=1∞βhth)3+⋯=1+((1)1,λ11!β1)t+((1)1,λ11!β2+(1)2,λ12!β12)t2+((1)1,λ11!β3+(1)2,λ12!2β1β2+(1)3,λ13!β13)t3+⋯=∑k=0∞ ∑b1+2b2+⋯+kbk=k(1)b1+b2+⋯+bk,λb1!b2!⋯bk!(β1)b1(β2)b2⋯(βk)bktk,$ (42)

and

$(∑m=0∞(1)m,λνm+1tm)2s=∑j=0∞∑c1+c2+⋯+c2s=j(∏i=12s(1)ci,λνci+1)tj.$ (43)

By (42) and (43), we have

$∑n=0∞LWn(2s),λ(1 |β1,β2,⋯:ν1,ν2,⋯)tnn!=eλ(∑h=1∞βhth)(∑m=0∞(1)m,λνm+1tm)2s=n!∑n=0∞(∑k=0n ∑b1+2b2+⋯+kbk=k∑c1+c2+⋯+c2s=n−k(1)b1+b2+⋯+bk,λ(β1)b1(β2)b2⋯(βk)bkb1!b2!⋯bk!∏i=12s(1)ci,λνci+1)tnn!.$ (44)

Therefore, by comparing with coefficients of both side of (44), we get the desired result.

Remark. We recall the degenerate Lah-Bell numbers $Lbn,λ$ as follows (31):

$eλ(t1−t)=∑n=0∞Lbn,λtnn!.$

In the following figures (x-axis = t, y-axis $=eλ(t1−t))$ in which the simulation program uses Fortran language, We can see the change $Lbn,λ$ depending on $λ$ .

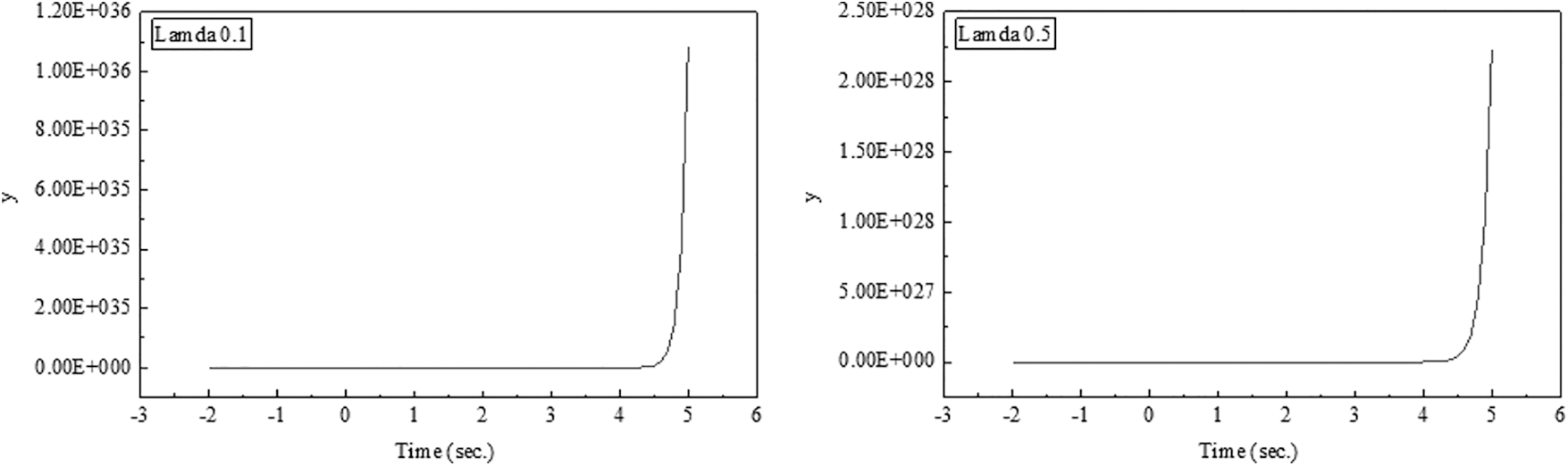
images

Figure 1: Degenerate Lah-Bell numbers when $λ$ = 0.1 and $λ$ = 0.5, respectively

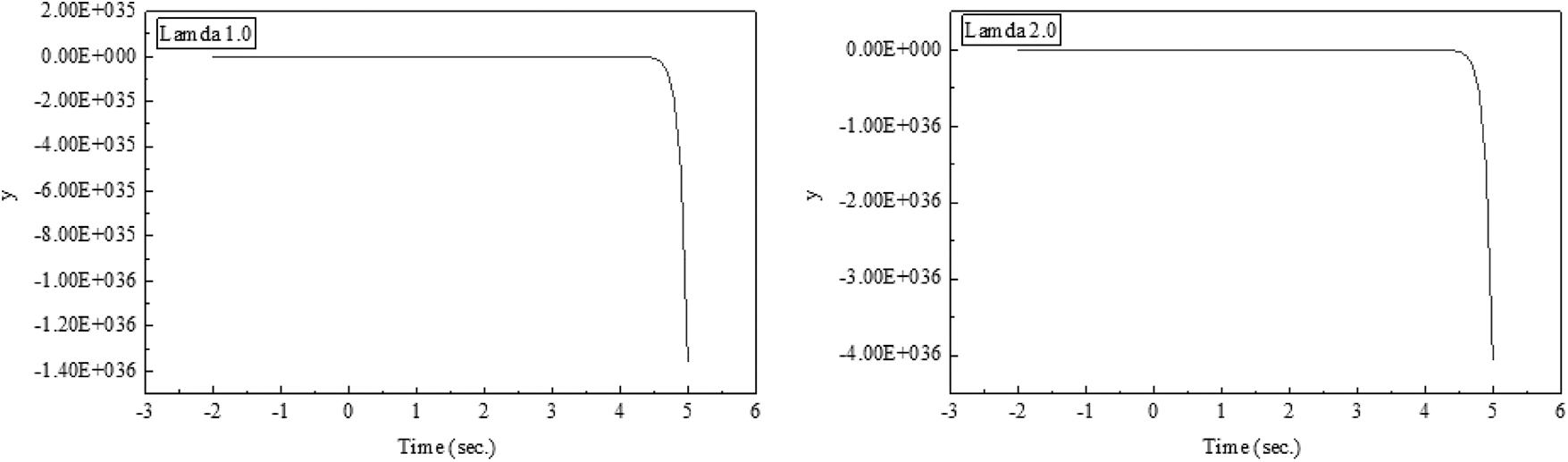
images

Figure 2: Degenerate Lah-Bell numbers when $λ$ = 1.0 and $λ$ = 2.0, respectively

4 Conclusion

In this paper, we introduced both the degenerate s-extended incomplete and complete Lah-Bell polynomials associated with a new type of degenerate s-extended Lah-Bell polynomials. We demonstrated some combinatorial identities between these polynomials and polynomials introduced in Section 2, and explicit formulas for them respectively. In addition, we obtained new types of the degenerate Stirling numbers and s-extended Stirling numbers of the second kind in Theorem 2.4 and 2.5, respectively.

Special polynomials have been applied not only in mathematics and physics, but also in various fields of application [1,3,6,9,17,18,22–27]. In recent years, one of our research areas has been to explore some special numbers and polynomials and their degenerate versions, and to discover their arithmetical and combinatorial properties and some of their applications. We intend to study various degenerate polynomial and numbers using several means such as function generation, combinatorial methods, umbral calculus, differential equations, and probability theory.

Acknowledgement: The authors would like to thank the referees for the detailed and valuable comments that helped improve the original manuscript in its present form. Also, the authors thank Jangjeon Institute for Mathematical Science for the support of this research.

Ethics Approval and Consent to Participate: The authors declare that there is no ethical problem in the production of this paper.

Consent for Publication: The authors want to publish this paper in this journal.

Funding Statement: This work was supported by the Basic Science Research Program, the National Research Foundation of Korea (NRF-2021R1F1A1050151).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Comtet, L. (1974). Advanced combinatorics: The art of finite and infinite expansions. Springer Science and Business Media, D. Reidel Publishing Company. [Google Scholar]

2. Kim, T., Kim, D. S. (2021). r-extended Lah-Bell numbers and polynomials associated with r-Lah numbers. Proceedings of the Jangjeon Mathematical Society, 24(1), 507–514. [Google Scholar]

3. Ma, Y., Kim, D. S., Kim, T., Kim, H., Lee, H. (2020). Some identities of Lah-bell polynomials. Advances in Difference Equations, 2020(510), 1–10. DOI 10.1186/s13662-020-02966-6. [Google Scholar] [CrossRef]

4. Nyul, G., Racz, G. (2015). The r-lah numbers. Discrete Mathematics, 338, 1660–1666. DOI 10.1016/j.disc.2014.03.029. [Google Scholar] [CrossRef]

5. Nyul, G., Racz, G. (2020). Sums of r-Lah numbers and r-Lah polynomials. Ars Mathematica Contemporanea, 18(2), 211–222. DOI 10.26493/1855-3974.1793.c4d. [Google Scholar] [CrossRef]

6. Martinjak, I. Šrekovski R. (2018). Lah numbers and Lindstrom¡s lemma, Comptes Rendus de l’Academie des Sciences–Series I, 356, 5–7. [Google Scholar]

7. Carlitz, L. (1979). Degenerate stirling, Bernoulli and Eulerian numbers. Utilitas Mathematica, 15, 51–88. DOI 10.12691/tjant-3-4-3. [Google Scholar] [CrossRef]

8. Dolgy, D. V., Kim, D. S., Kim, T., Kwon, J., (2020). On fully degenerate bell numbers and polynomials. Filomat, 34(2), 507–514. DOI 10.2298/FIL2002507D. [Google Scholar] [CrossRef]

9. Kim, D. S., Kim, T. (2019). Degenerate bernstein polynomials. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas, 113, 2913–2920. [Google Scholar]

10. Kim, H. K., Lee, D. S. (2020). Note on extended Lah-Bell polynomials and degenerate extended Lah-Bell polynomials. Advanced Studies in Contemporary Mathematics, 30(4), 1–10. DOI 10.17777/ascm2020.30.4.547. [Google Scholar] [CrossRef]

11. Kim, T. (2017). A note on degenerate stirling polynomials of the second kind. Proceedings of the Jangjeon Mathematical Society, 20(3), 319–331. DOI 10.17777/pjms2017.20.3.319. [Google Scholar] [CrossRef]

12. Kim, T., Kim, D. S., Dolgy, D. V. (2017). On partially degenerate bell numbers and polynomials. Proceedings of the Jangjeon Mathematical Society, 20(3), 337–345. DOI 10.17777/pjms2017.20.3.337. [Google Scholar] [CrossRef]

13. Kim, T., Kim, D. S., Kim, H. Y., Kwon, J. (2019). Degenerate stirling polynomials of the second kind and some applications. Symmetry, 11(8), DOI 10.3390/sym11081046. [Google Scholar] [CrossRef]

14. Kim, T., Kim, D. S., Kim, H. Y., Kwon, J. (2020). Some identities of degenerate bell polynomials, Mathematics. 8(1), 40. DOI 10.3390/math8010040. [Google Scholar] [CrossRef]

15. Kim, T., Yao, Y., Kim, D. S., Jang, G. W. (2018). Degenerate r-Stirling numbers and r-Bell polynomials. Russian Journal of Mathematical Physics, 25(1), 44–58. DOI 10.1134/S1061920818010041. [Google Scholar] [CrossRef]

16. Kwon, J., Kim, T., Kim, D. S., Kim, H. Y. (2020). Some identities for degenerate complete and incomplete r-Bell polynomials. Journal of Inequalities and Applications, 2020(23), 1–9. DOI 10.1186/s13660-020-2298-x. [Google Scholar] [CrossRef]

17. Kim, T., Kim, D. S., (2021). Degenerate zero-truncated poisson random variables. Russian Journal of Mathematical Physics, 28(1), 66–72. DOI 10.1134/S1061920821010076. [Google Scholar] [CrossRef]

18. Bell, E. T. (1934). Exponenential polynomials. Annals of Mathematics, 35, 258–277. [Google Scholar]

19. Kim, T., Kim, D. S., Jang, G. W. (2019). On central complete and incomplete Bell polynomials I. Symmetry, 11(2), 288. DOI 10.3390/sym11020288. [Google Scholar] [CrossRef]

20. Kim, T., Kim, D. S., Jang, L. C., Lee, H., Kim, H. Y. (2021). Complete and incomplete bell polynomials associated with Lah-bell numbers and polynomials. Advances in Difference Equations, 2021(101), 1–12. DOI 10.1186/s13662-021-03258-3. [Google Scholar] [CrossRef]

21. Kim, D. S., Kim, T. (2020). Lah-bell numbers and polynomials. Proceedings of the Jangjeon Mathematical Society, 23(4), 577–586. DOI 10.17777/pjms2020.23.4.577. [Google Scholar] [CrossRef]

22. Bibi, S., Abbas, M., Misro, M. Y., Hu, G. (2019). A novel approach of hybrid trigonometric bezier curve to the modeling of symmetric revolutionary curves and symmetric rotation surfaces. IEEE Access, 7, 165779–165792. DOI 10.1109/ACCESS.2019.2953496. [Google Scholar] [CrossRef]

23. Bibi, S., Abbas, M., Miura, K. T., Misro, M. Y. (2020). Geometric modeling of novel generalized hybrid trigonometric bezier-like curve with shape parameters and its applications. Mathematics, 8(6), 967. DOI 10.3390/math8060967. [Google Scholar] [CrossRef]

24. Maqsood, S., Abbas, M., Hu, G., Ramli, A. L. A., Miura, K. T. (2020). A novel generalization of trigonometric bezier curve and surface with shape parameters and its applications. Mathematical Problems in Engineering. DOI 10.1155/2020/4036434. [Google Scholar] [CrossRef]

25. Maqsood, S., Abbas, M., Miura, K. T., Majeed, A., Iqbal, A. (2020). Geometric modeling and applications of generalized blended trigonometric bezier curves with shape parameters. Advances in Difference Equations, 2020(550), 1–18. DOI 10.1186/s13662-020-03001-4. [Google Scholar] [CrossRef]

26. Simsek, Y. (2012). On q-deformed stirling numbers. International Journal of Computer Mathematics, 15(2), 70–80. [Google Scholar]

27. Usman, M., Abbas, M., Miura, K. T. (2020). Some engineering applications of new trigonometric cubic bezier-like curves to free-form complex curve modeling. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 14(4), 10. DOI 10.1299/jamdsm.2020jamdsm0048. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.