Study on the Mechanical Properties of Ni-Ti-Cu Shape Memory Alloy Considering Different Cu Contents

Bingfei Liu; Yangjie Hao

doi:10.32604/cmes.2022.019226

1Transportation Science and Engineering College, Civil Aviation University of China, Tianjin, 300300, China
2Aeronautical Engineering College, Civil Aviation University of China, Tianjin, 300300, China
*Corresponding Author: Bingfei Liu. Email: bfliu@cauc.edu.cn
Received: 10 September 2021; Accepted: 12 November 2021

Abstract: By adding copper to increase the performance, the Ni-Ti-Cu Shape Memory Alloy (SMA), has been widely used in the field of engineering in recent years. A thermodynamic constitutive model for Ni-Ti-Cu SMA considering different copper contents is established in this work. Numerical results for two different copper contents, as examples, are compared with the experimental results to verify the accuracy of the theoretical work. Based on the verified constitutive model, the effects of different copper content on the mechanical properties of Ni-Ti-Cu SMA and the tensile and compressive asymmetric properties of Ni-Ti-Cu SMA are finally discussed, respectively.

Keywords: Shape memory alloy; copper contents; constitutive model; tension and compression asymmetric

Shape memory alloy (SMA), as a type of functional material, has been developed since 1963, due to its superior properties and broad application prospects, which have attracted wide attention from experts and scholars. At present, there are three categories of the SMA that have been put into application [1], the Ni based, the Copper based and the stainless steel based. The Ni-based SMA, especially the NiTi SMA shows excellent properties such as Shape Memory Effect and superelastic [2,3], damping characteristics [4,5], corrosion resistance [6–8] and biocompatibility [9,10]. Based on these characteristics, Ni-based SMA has been widely used in aerospace, machinery, chemical, electronics and medical fields [11–13].

In the past few years, the published work on Ni-based SMA has been mainly focused on the fatigue behaviors, the superelasticity, the corrosion resistance, and mechanical behavior under tension and compression conditions. The results show that by changing the contents of various elements in the alloy or adding a small amount of the rare elements, the performance of such alloy can be improved [14–16]. The research of adding copper to improve the performance of Ni-based SMA through experimental methods has attracted more and more attention from scholars in recent years. Hakan et al. have studied the effect of Cu addition on microstructure and mechanical properties of Ni-based SMA [17]. Musa et al. have studied the effect of Cu addition on porous NiTi SMAs produced by self-propagating high-temperature synthesis [18]. Shelyakov et al. have studied the formation of structure of Ti-Ni-Cu alloys with high copper contents planar flow casting [19]. Chernysheva et al. have studied the effect of local atomic and crystal structure of rapidly quenched Ti-Ni-Cu shape memory alloys with high copper contents [20]. However, most of the above work focused on experimental testing and mechanical performance characterization, and there is little research on its theoretical work.

As for the researches on the Ni-Ti-Cu SMA, the experimental work was published by Li et al. [21]. For different copper contents, the material parameters including the Young’s modulus, the coefficient of thermal expansion and the critical transformation temperatures for the Ni-Ti-Cu SMA are all given. By combining such experimental results and the published constitutive model of the NiTi SMA, a thermodynamic constitutive model for Ni-Ti-Cu SMA considering the effect of the copper contents is established in this work. The numerical results for Ni-Ti-Cu SMA considering the effects of different copper contents and tension-compression asymmetry are discussed, respectively.

Similar to the existing constitutive model for NiTi SMA in the literature [22], the constitutive relation of Ni-Ti-Cu SMA can also be expressed as

where σ and ε are the stress and strain of the Ni-Ti-Cu SMA, respectively, εt is the transformation strain, T is the current temperature, and T0 is the temperature in the reference state. The subscript ℧ indicates that parameter of Ni-Ti-Cu SMA. S℧ and α℧ are the elastic stiffness tensor and the coefficient of thermal expansion tensor of the Ni-Ti-Cu SMA, which can be described as

where S℧A and S℧M are the elastic compliance tensors of the austenite phase and the martensite phase of the Ni-Ti-Cu SMA, respectively. α℧A and α℧M are the coefficient of thermal expansion tensors for the austenite phase and the martensite phase of the Ni-Ti-Cu SMA, respectively. ξ is the martensite volume fraction, according to the existing literature [23], which can be expressed as

ξ=12{cos⁡[a℧M(T−M℧f)−a℧MC℧M(σeff:Λ+12(S℧M−S℧A):σeff+(T−T0)(α℧M−α℧A):σeff)]+1},ξ˙>0 (4)

ξ=12{cos⁡[a℧A(T−A℧s)−a℧AC℧A(σeff:Λ+12(S℧M−S℧A):σeff+(T−T0)(α℧M−α℧A):σeff)]+1},ξ˙<0 (5)

where σeff=3J2, σeff is the average effective stress and J2 is the second deviatoric stress invariant. C℧A and C℧M are the stress influence coefficient of austenite and martensite phase of the Ni-Ti-Cu SMA. M℧s, M℧f, A℧s and A℧f are the critical phase transition temperatures for the Ni-Ti-Cu SMA. The two material constants a℧A and a℧M are described as a℧A=π/(M℧s+M℧f), a℧M=π/(A℧f−A℧s). α℧M and α℧A are the coefficients of thermal expansion for austenite and martensite, respectively.

where Λ is the transformation tensor. H℧ is the maximum transformation strain, σeff′=σeff−13tr(σeff), σ¯eff=(3σeff′:σeff′/2)1/2, ε¯t=(2εt:εt/3)1/2, σeff is the effective stress, σeff′ is the second deviatoric stress, σ¯eff is the average effective stress, ε¯t is the effective strain, εt is the transformation strain [24], and can be expressed as

The experimental data of the material parameters for Ni-Ti-Cu SMA considering the influence of copper contents has been reported by Li et al. [21]. The results show that the parameters for the Ni-Ti-Cu SMA are all approximately proportional to the corresponding parameters for the Ni-Ti SMA. In order to establish the variation relation between Ni-Ti-Cu SMA material parameters and Ni-Ti SMA material parameters with the increase of copper contents, a correction function is provided. It can be obtained by

where the subscript i indicates eight material parameters, namely S, α, C, H, Mf, Ms, As and Af. Dcui are the material parameters of Ni-Ti-Cu SMA. ki are the influence parameters of copper contents on Ni-Ti-Cu SMA material, Di are the material parameters of Ni-Ti SMA.

Then, when these material parameters are given, the stress-strain relationship for Ni-Ti-Cu SMA considering different copper contents can be obtained by Eqs. (1), (4), (5), (7) and (8).

It has been reported in several published literatures that the macroscopic transformation strain of SMA is only related to the second deviatoric stress invariant, which can effectively capture the thermodynamics behaviors of the SMA. However, in order to further simulate the overall mechanical behavior of SMA, it is also necessary to model the tension-compression asymmetry. Therefore, in order to consider the tension and compression asymmetry, the J2−J3 theory is used to calculate the effective stress, which can be described as [25]

where J2=12σeff′:σeff′=:12‖σeff′‖2 is the second deviatoric stress invariant, and J3=Det(σmeff′) is the third deviatoric stress invariant. η℧ and ν℧ are the material parameters of Ni-Ti-Cu SMA, which is similar to the Ni-Ti SMA, can be presented as [25]

η℧=(σMc℧+σMt℧)2σMc℧,ν℧=27(σMc℧−σMt℧)2(σMc℧+σMt℧) (10)

where σMc℧ and σMt℧ are the threshold transformation stress of the Ni-Ti-Cu SMA under uniaxial compression and uniaxial tension, respectively.

The effective stress σmeff considering the tensile compressive asymmetry can be obtained by substituting Eq. (9) into Eq.(8). Then, the effective stress σmeff, can be presented as

σmeff=(σMc℧+σMt℧)2σMc℧(32‖σeff′‖2+27(σMc℧−σMt℧)2(σMc℧+σMt℧)(12‖σeff′‖23Det(σmeff′))) (11)

Then, when these material parameters are given, the stress-strain relationship for Ni-Ti-Cu SMA under consideration of tensile-compression asymmetry can be obtained by Eqs. (1), (4), (5), (7) and (11).

In order to consider the effects of the copper contents, parametric equations for the effect of copper content on material parameters (e.g., Young’s modulus, critical phase transition temperature, maximum phase transition strain, stress effect coefficient) are introduced into the published constitutive model of the shape memory alloys to obtain the correction model for Ni-Ti-Cu SMA with different copper contents. As for the maximum phase transition strain, the cumulative effect of different cycles should be considered.

The material parameters of Ni-Ti-Cu SMA considering the influence of copper contents can be obtained by substituting the material parameters of Li et al. [21] obtained through experiments into Eq. (8), which can be shown in Table 1.

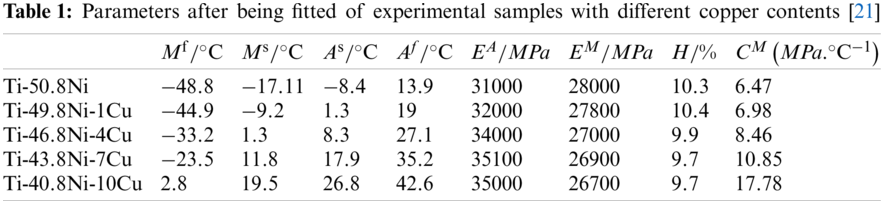
The initial temperature of the material cannot be obtained from Li et al. [21], so assume that T=T0. Substituting the material parameters shown in Table 1 into Eqs. (4), (5), when ξρ=0 or ξρ=1, respectively, the four curves of the critical temperature and the stress of the Ni-Ti-Cu SMA considering different copper contents are obtained, and the results are shown in Fig. 1.

As seen from Fig. 1, for (a)~(f) under no-stress, Mf, Ms, As and Af increase gradually with the increase of copper contents. Fig. 1d describes the predicted critical stress vs. temperature curve for Ti-45.8Ni-5Cu SMA. The critical temperatures of Ti-45.8Ni-5Cu SMA obtained by critical temperature correction function Dcui(i=5∼8) are: Mf=−29.1∘C, Ms=5.4∘C, As=10.9∘C, and Af=29.8∘C.

Figure 1: The relationship between the critical stress and temperature of Ni-based SMA with different copper contents (a) Ti-50.8Ni, (b) Ti-49.8Ni-1Cu, (c) Ti-46.8Ni-4Cu, (d) Ti-45.8Ni-5Cu, (e) Ti-43.8Ni-7Cu, (f) Ti-40.8Ni-10Cu

Then, the accuracy of the Ni-Ti-Cu SMA constitutive model considering the copper contents in the second part need to be verified to ensure that the mechanical properties of Ni-Ti-Cu SMA are further studied under the correct constitutive. And the theoretical models of Ti-50.8Ni SMA and Ti-40.8Ni-10Cu SMA are selected for comparison with experiments. Based on the experiment results, assume that T=T0=25∘C. When ξρ=0 and ξρ=1, substituting the material parameters of Ti-50.8Ni SMA and Ti-40.8Ni-10Cu SMA in Table 1 into Eqs. (4), (5), the critical stress of Ti-50.8Ni SMA and Ti-40.8Ni-10Cu SMA can be obtained. The results can be shown in Table 2.

According to the theoretical derivation in Part 2, the martenite volume fraction can be calculated by Eqs. (4)–(6), and the transformation strain can be calculated by Eqs. (6), (7), then the stress stain relationship for the material can be obtained by Eqs. (1)–(3) with the corresponding material parameters in Table 1 and critical phase transformation stress in Table 2. The model in this work can be used to simulate such behaviors of the SMA materials considering the different Cu contents. In order to verify the correctness of the model, as examples, the theoretical results for the cases with Ti-50.8Ni, and Ti-40.8Ni-10Cu are modeled and compared with the experimental results in Fig. 2. For the case of Ti-50.8Ni SMA, because the current temperature is higher than the Af, the material exhibits pseudo elasticity, and as for the case of Ti-40.8Ni-10Cu, due to the current temperature is lower than the As, there is no reverse phase transition happening.

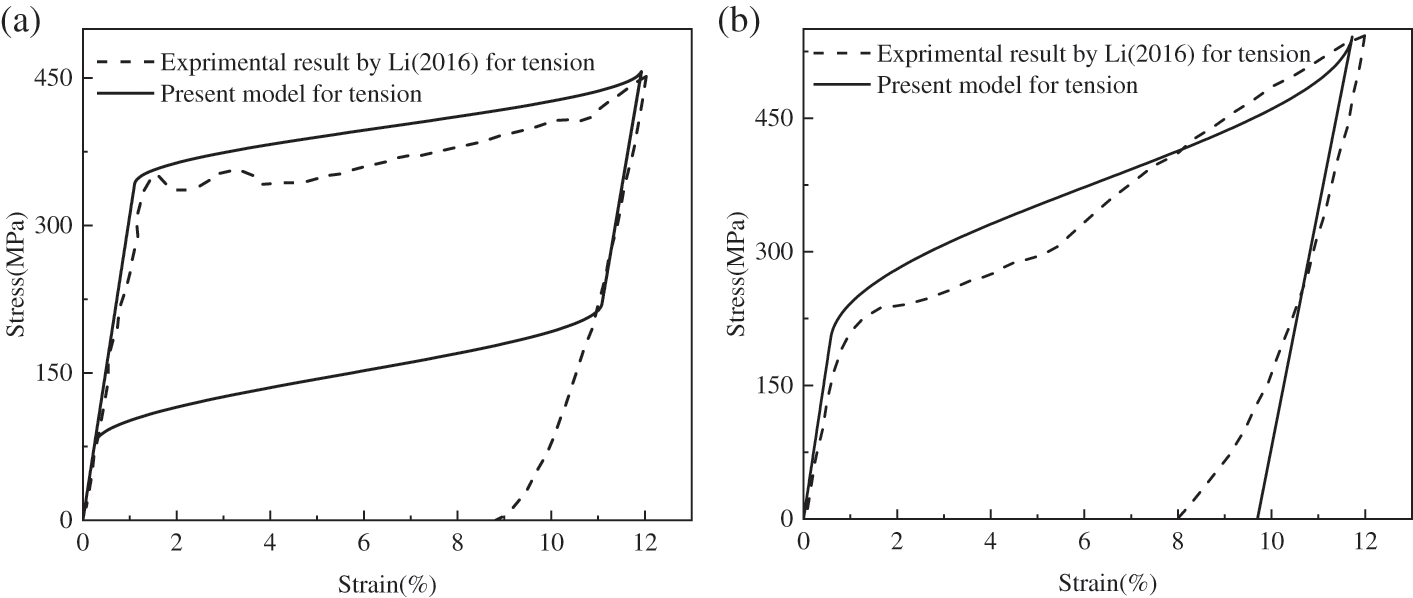
Figure 2: Comparison of theory and experiment under uniaxial tension (a) Ti-50.8Ni, (b) Ti-40.8Ni-10Cu

As shown in Fig. 2, the dotted curve represents the experimental data for the uniaxial compression case published by Li et al. [21]. The solid line is the result of the simulation under uniaxial tension. As shown in the Fig. 2, there are still some differences between the predicted curves and the experimental results. Two main reasons can be analyzed for the preliminary. First, it may be part of the plastic deformation during the phase transition, which is not studied in this work. Secondly, the selected experimental data is obtained by Li through the cyclic loading-unloading process. According to the existing references, the accumulated residual strain during the cycle is relatively large, which conveys that as the number of cycles increases, the residual strain increases rapidly at the beginning and the residual strain tends to be saturated after reaching a certain number of cycles. This cumulative increase in residual strain can be attributed to the dislocation slip of retained martensite and austenite during the cyclic deformation process [26,27].

Based on the verified constitutive model, the effect of different copper contents on mechanical properties of Ni-Ti-Cu SMA, and for different copper contents, the properties of Ni-Ti-Cu SMA considering tension and compression asymmetry will be discussed then, respectively.

For the shape memory effect of SMA, both external load and temperature play a vital role. At a constant temperature, a tensile stress σ is applied to the SMA material. According to the existing literature [23], when σ<σs(σs is the starting stress of martensitic transformation), the martensitic transformation has not yet started and material deforms elastically. When σf<σ<σs(σf is the martensitic transformation completion stress), the SMA material is in the martensitic transformation process. When σ>σf, the martensite transformation is completed and elastic deformation starts.

Then keeping the temperature constant and unloading SMA material. According to Fig. 1, in the temperature range of σs′<0(σs′is the beginning stress of the reverse phase transition), the unloading process is a completely elastic process with no reverse phase transformation.

After completely unloading, keep σ=0 unchanged, and the material is not restricted by the outside environment, then heat the material (T0→T,T>T0). When T0<As, the reverse phase transformation has not yet started, and the material is elastically deformed. When As<T0<Af, the material is in the reverse phase transition process. When Af<T0, reverse phase transition is completed.

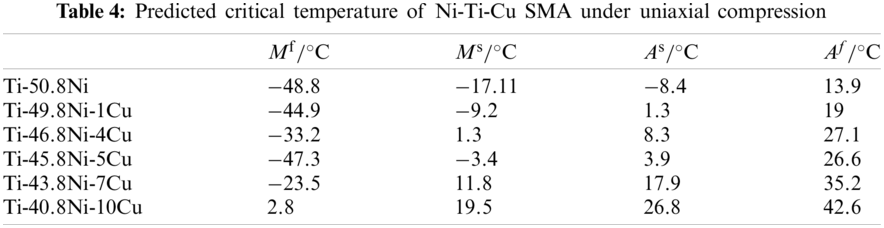
With the increase of copper contents, the stress-strain relation of Ni-Ti-Cu SMA at different initial temperatures are further studied to obtain the influence of copper contents on the stress and strain of Ni-Ti-Cu SMA. According to the curves of the critical stress and temperature of Ni-Ti-Cu SMA shown in Fig. 1, the initial temperature that satisfies the above three temperature ranges (T0<As, As<T0<Af, Af<T0) is selected respectively. Substituting the selected temperatures and the parameters shown in Table 1 into Eqs. (1), (4), (5) and (7), the stress-strain curves at different initial temperatures can be obtained, as shown in Fig. 3.

Fig. 3 shows the stress-strain relation of Ni-Ti-Cu alloys with different contents at different initial temperatures. It can be seen that different copper contents and different initial temperatures have different effects on the mechanical properties of Ni-Ti-Cu alloys. When the copper contents are constant, Ni-Ti-Cu alloys have different mechanical properties at different initial temperatures. When the initial temperature is between Ms and As, the deformation cannot be recovered after unloading. When the initial temperature of the SMA material is in the range of As to Af during loading and unloading, part of the inelastic deformation after unloading can be restored by itself without heating, but there are still some inelastic deformations that cannot be restored. When the initial temperature of the SMA material during loading and unloading is higher than Af, all deformation after being completely unloaded can be fully recovered without heating, which shows the complete superelasticity of the SMA material. Fig. 3d shows the predicted stress-strain relation of Ni-45.8Ti-5Cu alloy at different initial temperatures.

In order to further study the effect of copper contents on the mechanical properties of Ni-Ti-Cu SMA at the same initial temperature, the initial temperature of 25°C and 45°C are selected as the examples, then the stress-strain relation of the Ni-Ti-Cu SMA with different copper contents are given by Fig. 4.

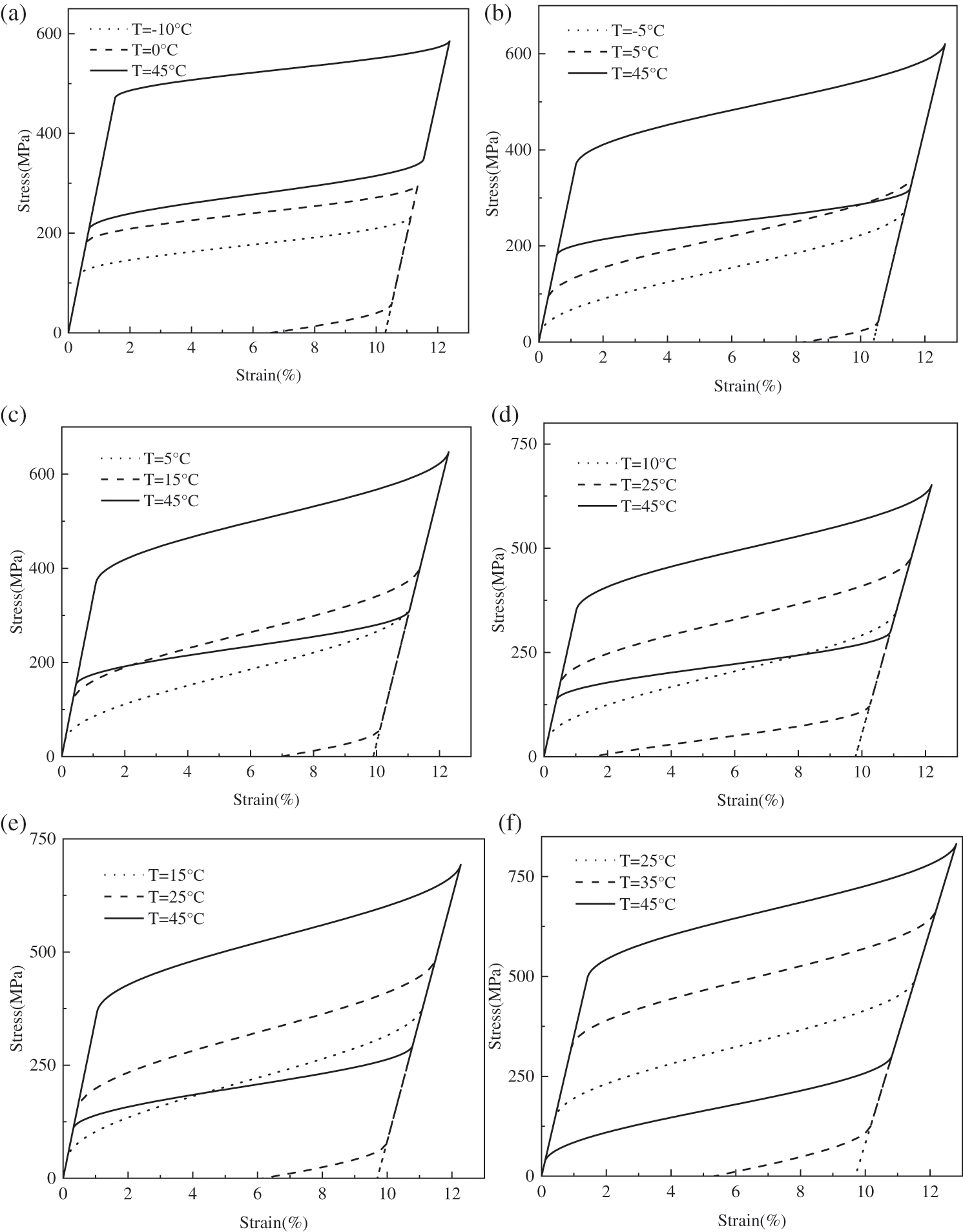
Figure 3: Stress-strain relationship of Ni-Ti-Cu alloys containing at different initial temperatures (a) Ti-50.8Ni, (b) Ti-49.8Ni-1Cu, (c) Ti-46.8Ni-4Cu, (d) Ti-45.8Ni-5Cu, (e) Ti-43.8Ni-7Cu, (f) Ti-40.8Ni-10Cu

As shown in Fig. 4, at the same initial temperatures 25°C or 45°C, the copper contents have an effect on the mechanical properties of Ni-Ti-Cu SMA. Under the initial temperature of 25°C, when the copper contents are less than 1%, Ni-Ti-Cu alloy is completely superelastic. When the copper contents are greater than 4% and less than 10%, Ni-Ti-Cu SMA is partially superelastic. When the copper contents are greater than 10%, the Ni-Ti-Cu SMA does not undergo reorientation. As shown in Fig. 4b, when the initial temperature of the Ni-Ti-Cu SMA is 45°C, all Ni-Ti-Cu SMA with different copper contents can be fully recovered without heating after being completely unloading, showing the complete superelasticity of the material.

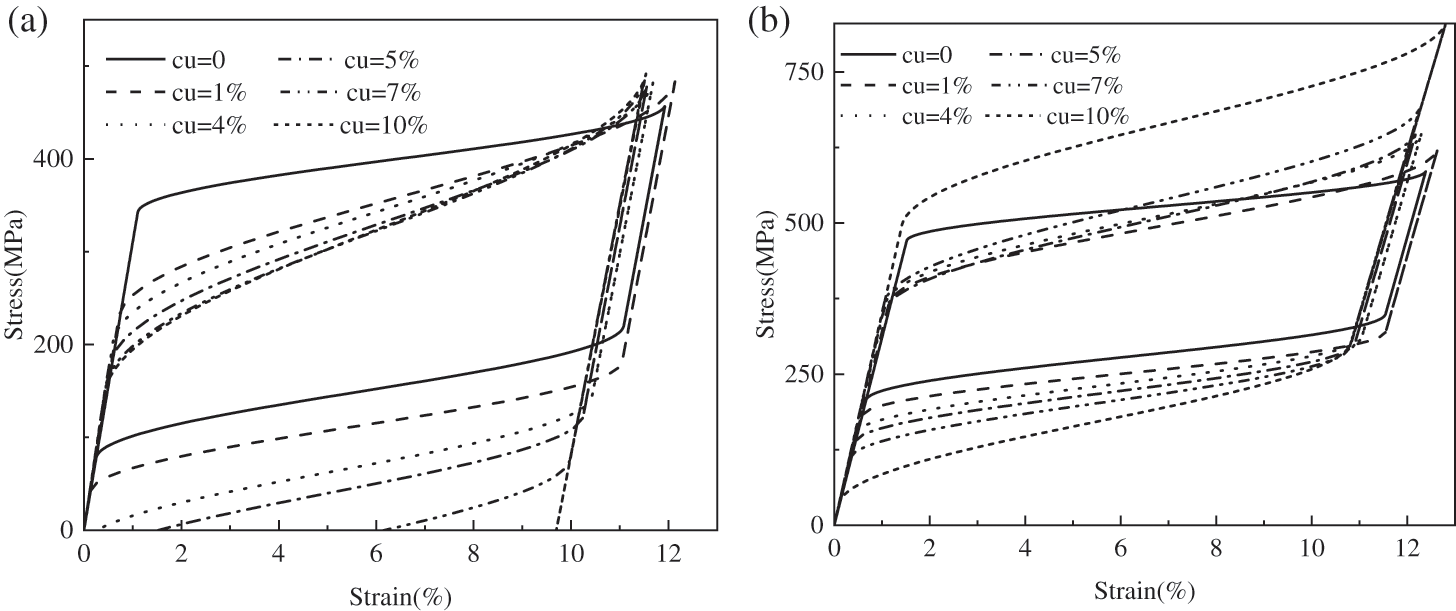
Figure 4: Stress-strain curve at the same initial temperatures 25°C (a) and 45°C (b)

The developed theory of Part 2 will be applied in modeling the constitutive response of the SMA considering the tensile-compressive asymmetry. SMA under uniaxial load is usually studied, so it is difficult to analyze its phase distribution under different loads. In this work, the case of uniaxial loads is analyzed. At isothermal conditions, the uniaxial load is ∑ij=[00∑33000]T. For SMA, we assumed that the isotropic Poisson’s ratio: νA=νM=ν.

In order to obtain the parameters η℧ and ν℧, the critical stresses of the Ni-Ti-Cu SMA under uniaxial tension and uniaxial compression are required. Therefore, through the same calculation as the data in Table 2, the critical stress of Ni-Ti-Cu SMA during uniaxial tension can be obtained. Then, the all material parameters are shown in Table 3.

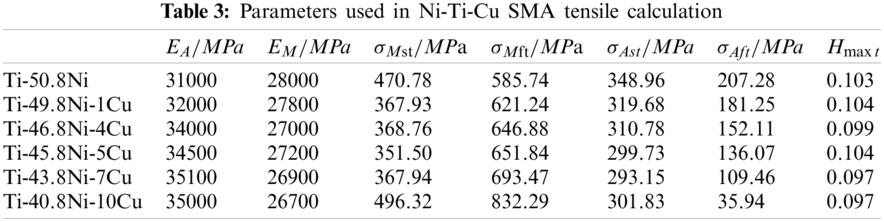
From Table 3, the material parameters required for uniaxial tension can be obtained. In combination with the experimental data, it is assumed that the critical stress and maximum phase transformation strain corresponding to the Ni-Ti-Cu SMA during uniaxial compression should meet the conditions [28]: σc=1.2σt,Hc=0.5Ht.

According to the above assumptions, the critical stress and maximum phase transformation strain can be obtained separately by calculation. It is assumed that T=T0 = 25°C, and under uniaxial tension and uniaxial compression, the elastic modulus E and stress influence coefficient CM of the material itself remain unchanged. Substituting the material parameters mentioned above into Eqs. (4), (5) and (11), when ξρ=0 and ξρ=1, respectively, the critical temperatures under uniaxial compression can be calculated, which are shown in Table 4.

Substituting the material parameters corresponding to uniaxial tension and uniaxial compression into the constitutive model of the second part, the stress-strain relation of the Ni-Ti-Cu SMA considering the asymmetry of tension and compression can be obtained. The numerical results of the stress-strain response for the SMA under uniaxial tension and uniaxial compression are displayed in Fig. 5.

As shown in Fig. 5, the solid line represents the result under uniaxial compression, and the dashed line represents the result under uniaxial tension. It can be found that with the increase of copper contents, the critical stress of Ni-Ti-Cu SMA gradually decreases. And as the increase of copper contents, the maximum transformation strain of Ni-Ti-Cu SMA first decreases and then increases. The predicted mechanical properties of Ni-45.8Ti-5Cu SMA are shown in Fig. 5d.

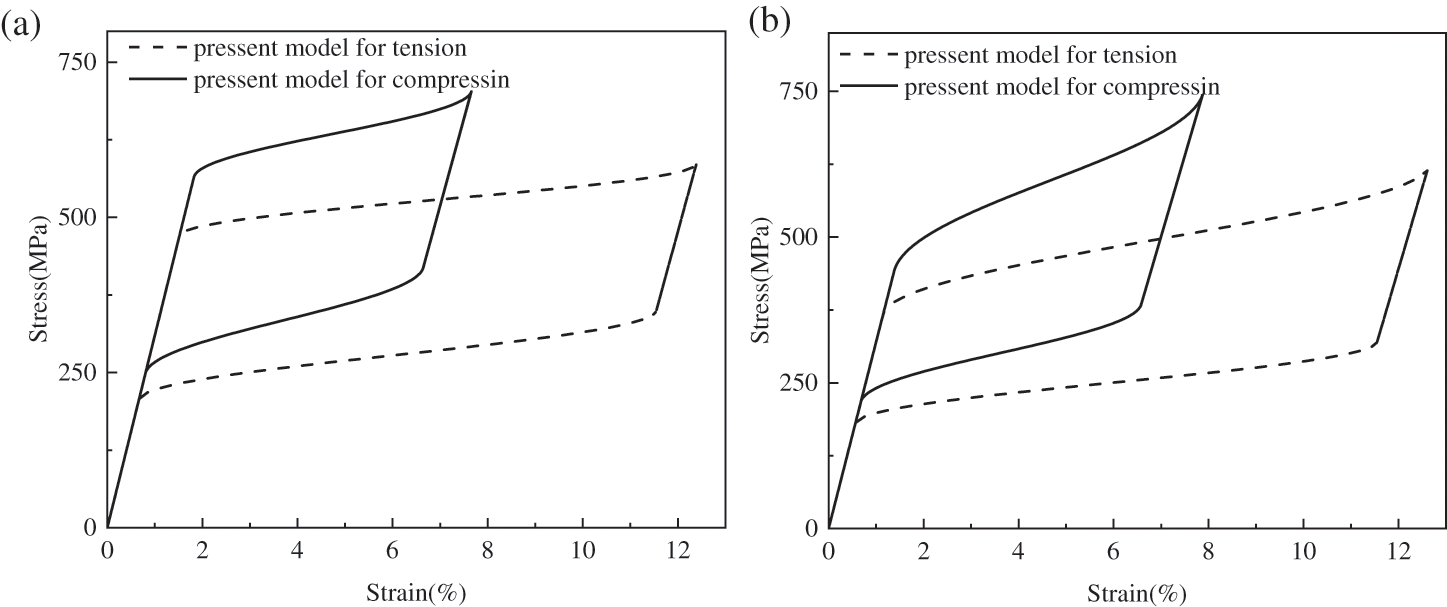
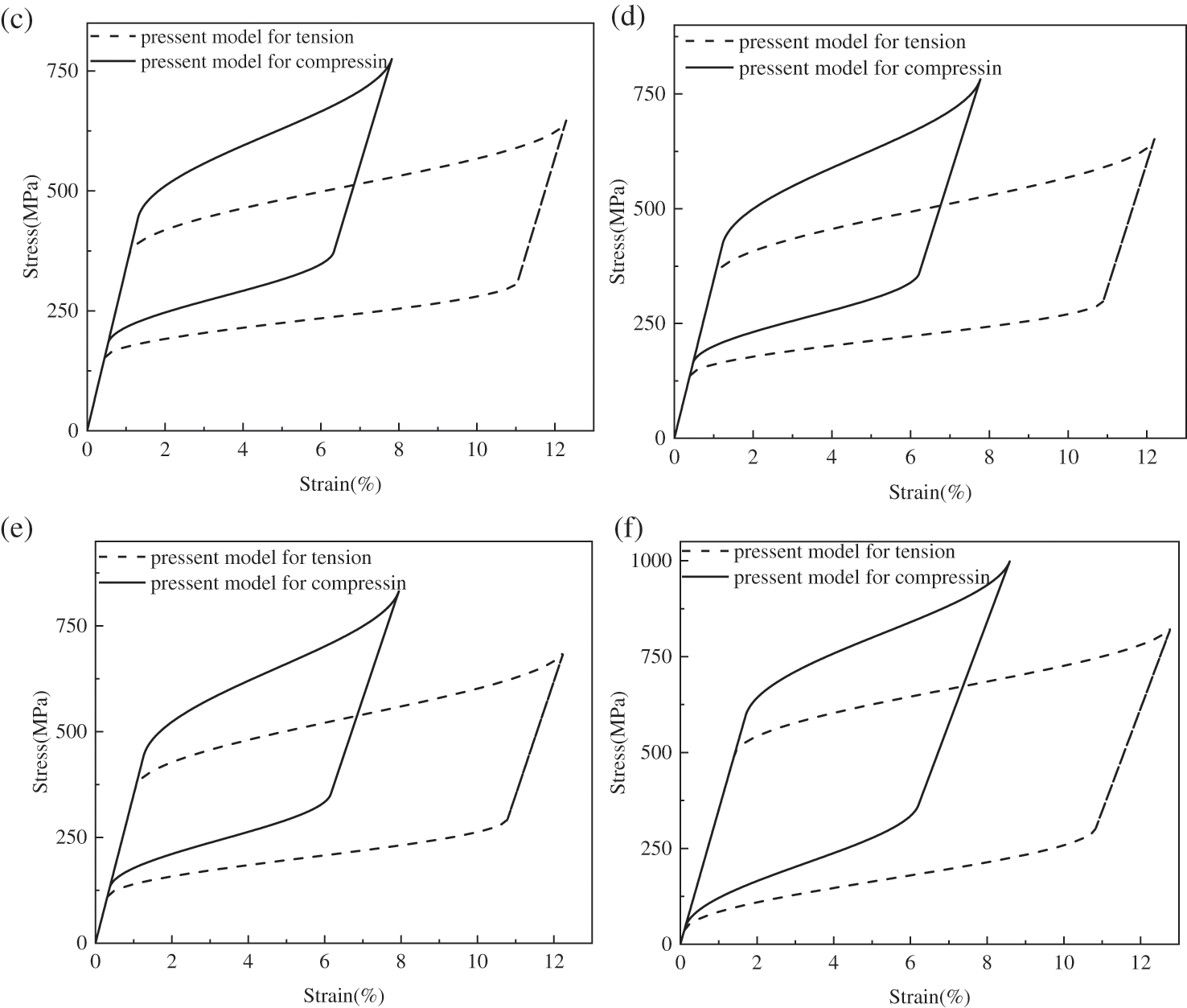
Figure 5: Comparison of stress-strain curves of copper-based SMA specimen under uniaxial tension and uniaxial compression. (a) Ti-50.8Ni, (b) Ti-49.8Ni-1Cu, (c) Ti-46.8Ni-1Cu, (d) Ti-45.8Ni-5Cu, (e) Ti-43.8Ni-7Cu, (f) Ti-40.8Ni-10Cu

In this work, the constitutive model of Ni-Ti-Cu SMA considering the different copper contents is established. The main conclusions are as follows:

1. Different copper contents and different initial temperature have influence on the mechanical properties of Ni-Ti-Cu SMA. When the copper contents are greater than 10%, the Ni-Ti-Cu SMA does not undergo reorientation. When the initial temperature is 45°C, the deformation can be restored due to the superelasticity without heating.

2. At initial temperatures of 25°C and 45°C, the maximum stress in the Ni-Ti-Cu SMA increases gradually with the increase of copper content. And the maximum phase strain decreases slightly with the increase of copper content and the maximum phase strain of Ni-Ti-Cu SMA with different copper contents is basically stable at about 0.1. At the same time, the hysteresis curve range of Ni-Ti-Cu SMA gradually increases with the increase of copper content.

Funding Statement: The authors acknowledge the financial support by National Natural Science Foundation of China (No. 11502284), Key Deployment Projects of the Chinese Academy of Sciences (KFZD-SW-435), the Fundamental Research Funds for the Central Universities of China (3122020077).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Chiu, W., Ishigaki, T., Nohira, N., Umise, A., Hosoda, H. (2021). Effect of Cr additions on the phase constituent, mechanical properties, and shape memory effect of near-eutectoid Ti-4Au towards the biomaterial applications. Journal of Alloys and Compounds,867(6),159037. DOI 10.1016/j.jallcom.2021.159037. [Google Scholar] [CrossRef]

2. Villa, F., Villa, E., Nespoli, A., Passaretti, F. (2021). Internal friction parameter in shape memory alloys: Correlation between thermomechanical conditions and damping properties in NiTi and NiTiCu at different temperatures. Journal of Materials Engineering and Performance,30(5),2605–2616. DOI 10.1007/s11665-021-05609-3. [Google Scholar] [CrossRef]

3. Li, Jia, Wang, P., Meng, Z., He, K. S. (2019). Effect of fe addition on microstructure and mechanical properties of as-cast Ti49Ni51 alloy. Materials,12(19),3114. DOI 10.3390/ma12193114. [Google Scholar] [CrossRef]

4. Viet, N. V., Zaki, W., Umer, R. (2018). Analytical model of functionally graded material/shape memory alloy composite cantilever beam under bending. Composite Structures,203(10),764–776. DOI 10.1016/j.compstruct.2018.07.041. [Google Scholar] [CrossRef]

5. Humbeeck, J. V. (2003). Damping capacity of thermoelastic martensite in shape memory alloys. Journal of Alloys Compounds,355(1–2),58–64. DOI 10.1016/S0925-8388(03)00268-8. [Google Scholar] [CrossRef]

6. Yasenchuk, Y., Marchenko, E., Baigonakova, G., Gunther, S., Kang, J. H. (2020). Study on tensile, bending, fatigue, and in-vivo behavior of porous SHS-TiNi alloy used as a bone substitute. Biomedical Materials,16(2),21001. DOI 10.1088/1748-605X/aba327. [Google Scholar] [CrossRef]

7. Marandi, L., Sen, I. (2021). In-vitro mechanical behavior and high cycle fatigue characteristics of NiTi-based shape memory alloy wire. International Journal of Fatigue,148,106226. DOI 10.1016/j.ijfatigue.2021.106226. [Google Scholar] [CrossRef]

8. Baigonakova, G., Marchenko, E., Chekalkin, T., Kang, J. H., Obrosov, A. (2020). Influence of silver addition on structure, martensite transformations and mechanical properties of TiNi-Ag alloy wires for biomedical application. Materials,13(4721),4721. DOI 10.3390/ma13214721. [Google Scholar] [CrossRef]

9. Sun, Y., Rong, Y., Zhao, Y., Zhao, Y., Chu, P. K. (2020). Electrochemical stability, corrosion behavior, and biological properties of Ni-Ti-O nanoporous layers anodically on NiTi alloy. Corrosion Science,179,109104. DOI 10.1016/j.corsci.2020.109104. [Google Scholar] [CrossRef]

10. Chang, S. H., Huang, J. J. (2012). Biodegradability and anticoagulant properties of chitosan and sulfonated chitosan films coated on TiNi alloys. Surface and Coatings Technology,206(23),4959–4963. DOI 10.1016/j.surfcoat.2012.05.121. [Google Scholar] [CrossRef]

11. Wei, X., Zhu, W., Ban, A., Zhu, D., Dong, H. (2021). Effects of co addition on microstructure and cavitation erosion resistance of plasma sprayed TiNi based coating. Surface and Coatings Technology,409,126838. DOI 10.1016/j.surfcoat.2021.126838. [Google Scholar] [CrossRef]

12. Vieira, B. D. S., Canado, R. H., Freitas, K. M. S., Valarelli, F. P., Oliveira, R. C. G. D. (2019). Effect of clinical use and sterilization process on the transition temperature range of thermally NiTi alloys. The Open Dentistry Journal,13(1),261–266. DOI 10.2174/1874210601913010261. [Google Scholar] [CrossRef]

13. Pieczyska, E. A., Kowalczyk-Gajewska, K., Maj, M., Staszczak, M., Tobushi, H. (2014). Thermomechanical investigation of TiNi shape memory alloy and pu shape memory polymer subjected to cyclic loading. Procedia Engineering,74,287–292. DOI 10.1016/j.proeng.2014.06.264. [Google Scholar] [CrossRef]

14. Zheng, Y. F., Zhang, B. B., Wang, B. L., Wang, Y. B., Li, L.et al. (2011). Introduction of antibacterial function into biomedical TiNi shape memory alloy by the addition of element Ag. Acta Biomaterialia,7(6),2758–2767. DOI 10.1016/j.actbio.2011.02.010. [Google Scholar] [CrossRef]

15. J. W.Wen, A. L.Liu, Y. D.Wang, Y. B., Zhou (2016). Effect of rare earth element yttrium on the isothermal oxidation behavior of aluminide coatings on Ti-Ni shape memory alloys. Rare Metal Materials and Engineering,45(6),1413–1418. DOI 10.1016/S1875-5372(16)30123-0. [Google Scholar] [CrossRef]

16. Li, J., Yi, X., Sun, K., Sun, B., Gao, W.et al. (2018). The effect of Zr on the transformation behaviors, microstructure and the mechanical properties of Ti-Ni-Cu shape memory alloys. Journal of Alloys & Compounds,747,348–353. DOI 10.1016/j.jallcom.2018.03.053. [Google Scholar] [CrossRef]

17. Gökmeşe, H., Tanış, N. A., Bostan, B. (2018). Effect of Cu addition on microstructure and mechanical properties of NiTi based shape memory alloy. International Advanced Researches and Engineering Journal,2(1),20–26. [Google Scholar]

18. Kilic, M., Yenigun, B., Bati, S., Balalan, Z., Kirik, I. (2019). Effect of Cu addition on porous NiTi smas produced by self-propagating high-temperature synthesis. Materials Testing,61(12),1140–1144. DOI 10.3139/120.111439. [Google Scholar] [CrossRef]

19. Shelyakov, A. V., Sevryukov, O. N., Sitnikov, N. N., Borodako, K. A., Khabibullina, I. A. (2020). Formation of structure of TiNiCu alloys with high copper content upon producing by planar flow casting. Journal of Physics Conference Series,1686(1),12056. DOI 10.1088/1742-6596/1686/1/012056. [Google Scholar] [CrossRef]

20. Chernysheva, O., Shelyakov, A., Sitnikov, N., Veligzhanin, A., Sundeev, R. (2021). Local atomic and crystal structure of rapidly quenched tinicu shape memory alloys with high copper content. Materials Letters,285(35),129104. DOI 10.1016/j.matlet.2020.129104. [Google Scholar] [CrossRef]

21. Li, H. F., Qiu, K. J., Zhou, F. Y., Li, L., Zheng, Y. F. (2016). Design and development of novel antibacterial Ti-Ni-Cu shape memory alloys for biomedical application. Scientific Reports,6(1),37475. DOI 10.1038/srep37475. [Google Scholar] [CrossRef]

22. Qidwai, M. A., Lagoudas, D. C. (2000). On thermomechanics and transformation surfaces of polycrystalline NiTi shape memory alloy material. International Journal of Plasticity,16(10–11),1309–1343. DOI 10.1016/S0749-6419(00)00012-7. [Google Scholar] [CrossRef]

23. Wang, Q. (2019). Theoretical research on crack monitoring and self-repairing of SMA intelligent concrete (in Chinese). DOI 10.27627/d.cnki.gzmhy.2019.000402. [Google Scholar] [CrossRef]

24. Boyd, J. G., Lagoudas, D. C. (1996). A thermodynamical constitutive model for shape memory materials. Part I. The monolithic shape memory alloy. International Journal of Plasticity,12(6),805–842. DOI 10.1016/S0749-6419(96)00030-7. [Google Scholar] [CrossRef]

25. Gillet, Y., Patoor, E., Berveiller, M. (1998). Calculation of pseudoelastic elements using a non-symmetrical thermomechanical transformation criterion and associated rule. Journal of Intelligent Material Systems & Structures,9(5),366–378. DOI 10.1177/1045389X9800900505. [Google Scholar] [CrossRef]

26. Yu, C., Kang, G., Kan, Q., Zhu, Y. (2015). Rate-dependent cyclic deformation of super-elastic NiTi shape memory alloy: Thermo-mechanical coupled and physical mechanism-based constitutive model. International Journal of Plasticity,72,60–90. DOI 10.1016/j.ijplas.2015.05.011. [Google Scholar] [CrossRef]

27. Kockar, B., Karaman, I., Kim, J. I., Chumlyakov, Y. I. (2008). Thermomechanical cyclic response of an ultrafine-grained NiTi shape memory alloy. Acta Materialia,56(14),3630–3646. DOI 10.1016/j.actamat.2008.04.001. [Google Scholar] [CrossRef]

28. Zhu, Y., Dui, G. (2010). A macro-constitutive model of polycrystalline NiTi smas including tensile-compressive asymmetry and torsion pseudoelastic behaviors. International Journal of Engineering Science,48(12),2099–2106. DOI 10.1016/j.ijengsci.2010.04.002. [Google Scholar] [CrossRef]