
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.018872
ARTICLE
Detecting and Repairing Data-Flow Errors in WFD-net Systems
1School of Electronics and Information Engineering, Tongji University, Shanghai, 201804, China
2School of Information Science and Technology, Zhejiang Sci-Tech University, Hangzhou, 310018, China
3School of Computer Engineering, Bengbu University, Bengbu, 233030, China
*Corresponding Author: Dongming Xiang. Email: flysky_xdm@163.com
Received: 22 August 2021; Accepted: 03 December 2021
Abstract: Workflow system has become a standard solution for managing a complex business process. How to guarantee its correctness is a key requirement. Many methods only focus on the control-flow verification, while they neglect the modeling and checking of data-flows. Although some studies are presented to repair the data-flow errors, they do not consider the effect of delete operations or weak circulation relations on the repairing results. What's more, repairing some data-flow errors may bring in new errors. In order to solve these problems, we use workflow net with data (WFD-net) systems to model and analyze a workflow system. Based on weak behavioral relations and order relations in a WFD-net system, we formalize four kinds of data-flow errors. After then, we reveal the relations between these errors and organize them into a hierarchy. Furthermore, we propose some new methods to repair data-flow errors in a WFD-net system based on system requirements and repair strategies. Finally, a case study of campus-card recharging shows the applicability of our methods, and a group of experiments show their advantages and effectiveness.
Keywords: Data-flow errors; WFD-net; weak behavioral relations; system requirements
| Nomenclature | |
| Set of Positive Integers | |
| RD | Redundant Data |
| MD | Missing Data |
| LD | Lost Data |
| IND | Inconsistent Data |
A business process is considered as “the specific ordering of work activities across time and place, with a beginning, an end, and clearly identified input and output” [1]. As an information technology of process automation, workflow systems have become a standard solution for managing complex business process models, such as loan approval management [2], supply chain management [3], and knowledge management [4]. In other words, workflow systems can be used to automate, manage, and optimize different kinds of business processes. In general, the design of a workflow system needs to describe control-/data-flows, and then detect their errors [5]. A successful workflow system depends on error-free modeling and analyzing methods. Therefore, it is necessary to keep the correctness of control-/data-flows in a workflow system. Control-flows mainly focus on the partial orders of business activities, while data-flows mainly involve data operations (e.g., read, write, and delete) and guard functions [6–8].
There are many modeling methods that can be used to describe workflow systems, such as Business Process Modeling Notation (BPMN) [9], Business Process Execution Language (BPEL) [10], Event-Driven Process Chains (EPCs) [11], UML Activity Diagrams [11], and Workflow Net with Data (WFD-net) [12]. Compared with these methods, WFD-nets are much suitable to describe and analyze control-/data-flows due to their data labeling functions and guards.
In order to guarantee the correctness of workflow systems, some methods are developed to detect and repair errors. Unfortunately, most of them only focus on the verifications of control-flows while ignoring the checking of data-flows. In fact, data-flows play an important role in workflow design. This is because routing constraints in a workflow are usually based on data operations and guard functions. Moreover, data-flow errors (e.g., redundant data, missing data, lost data, and inconsistent data) may arise even if control-flows are correct [5,13]. Once a workflow model suffers from missing data, it may need high costs to repair unexpected process interruptions. To repair data-flow errors in workflow systems, many studies are done. Awad et al. [9] presented a method to repair missing data in BPMN. After then, Song et al. [10] provided some methods to preserve data-flow correctness in BPEL. Later on, Sharma et al. [14] presented a method to repair data-flow errors in workflows. However, these methods do not consider data-flow errors caused by delete operations, and their workflow models are usually simple (e.g., no loop structures). In order to remove a kind of data-flow error, they may bring in another one. Therefore, they need multiple attempts to repair these errors. What's worse, they may get an incorrect workflow model.
In this paper, we use WFD-net systems to analyze the correctness of control-/data-flows in workflow systems. It is assumed that our control-flows in WFD-net systems are sound (i.e., no deadlocks [9,15,16] or livelocks [17–19]), without taking data operations into consideration [12,20,21]. The aim of this paper is to detect and repair four kinds of data-flow errors (i.e., redundant data, missing data, lost data, and inconsistent data) in WFD-net systems.
The contributions of this paper are given as follows:
1) Based on weak behavioral relations (i.e., weak sequence relation, weak exclusiveness relation, weak circulation relation, and weak concurrency relation) and order relation, we formalize four kinds of data-flow errors in WFD-net systems.
2) We reveal the relations between different kinds of data-flow errors, and further organize them into a hierarchy, which can contribute to correctly repairing data-flow errors without repeated work.
3) We present some methods to repair data-flow errors in WFD-net systems according to several system requirements and repair strategies.
The rest of this paper is organized as follows. In Section 2, we present some related work about data-flow errors. Then, we introduce workflow system modeling and a motivation example in Section 3. In Section 4, we formalize data-flow errors in WFD-net systems, and provide some new methods to repair them. In Section 5, a case study of campus-card recharging is conducted. In Section 6, we do a group of experiments to show the effectiveness of our methods. Finally, conclusion and future work are given in Section 7.
2.1 Detecting Methods for Data-Flow Errors
There have been many methods to detect data-flow errors. Sun et al. [2] provided three basic types of data-flow errors in UML activity diagram, namely missing data, conflicting data, and redundant data. Sundari et al. [22] presented a graph traversal algorithm called GT to detect data-flow errors in workflows. It systematically traversed every workflow route to detect errors like redundant data, missing data, and lost data. Based on the work provided in [2], Sun et al. [23] analyzed the dependencies among different transitions based on the input and output data of activities in a workflow model. Meda et al. [24] provided missing data, inconsistent data, lost data, and redundant data. They also presented a graph traversal algorithm to detect the data-flow errors in unstructured and nested workflows. Sidorova et al. [25] defined the may/must-soundness of a WFD-net system. Haddar et al. [26] provided a data-centric method to manage business processes. Dolean et al. [27] presented a survey of researches on modeling data-flows of business processes, and pointed out that the control-flows cannot be executed without data operations. Kabbaj et al. [5] pointed out that the role of data in a workflow is very important because routing constraints are closely related to data elements. Therefore, a workflow easily leads to an interruption once it contains data-flow errors. In order to solve this problem, they provided a method to detect redundant data, missing data, and lost data (or conflict data). Xiang et al. [6] proposed Petri Net with Data Operations (PN-DO), such as read, write, and delete operations. They formalized redundant data, missing data, lost data, and inconsistent data. Dramski [28] presented missing data in event logs and gave some ways to make some data recovery. Trcka et al. [29,30] put forward six kinds of data-flow errors in WFD-nets, namely missing data, strongly redundant data, weakly redundant data, strongly lost data, weakly lost data, and inconsistent data. von Stackelberg et al. [31] proposed a method to detect strongly redundant data, weakly redundant data, missing data, strongly lost data, weakly lost data, and inconsistent data in BPMN 2.0. Song et al. [32] utilized supervised learning algorithms to predict data-flow errors in an unseen BPEL process. Moreover, they provided an empirical study on data-flow errors in BPEL processes. Mülle et al. [33] considered that the correctness of data-flows in BPMN 2.0 is a challenge. As for the above studies, they did not consider the relations between different kinds of data-flow errors.
2.2 Repairing Methods for Data-Flow Errors
There are many studies on repairing data-flow errors. Awad et al. [9] presented a method to repair missing data. Song et al. [10] provided preserve data-flow correctness in process adaptation. They proposed three criteria to make the process free of missing data, redundant data, and lost data. Technically, they assumed that each activity has 0/1 output. Later on, Sharma et al. [14] presented methods to repair redundant data, missing data, lost data, and inconsistent data in workflows. After then, Jovanovikj et al. [34] provided methods to compare and merge two different models with different data operations. The methods are activity inserted, activity deletion, data object creation, data object to read, data object updated, and data object deletion. These methods can contribute to providing possible ways for the designer to repair data-flow errors in a WFD-net system. As mentioned above, these studies did not consider data-flow errors caused by delete operations, and their workflow models are usually without loop structures. What's more, repairing some kinds of data-flow errors may bring in new data-flow errors. In order to solve these problems, we propose some new methods to repair different kinds of data-flow errors according to several system requirements in this paper.
A Petri net is a 3-tuple
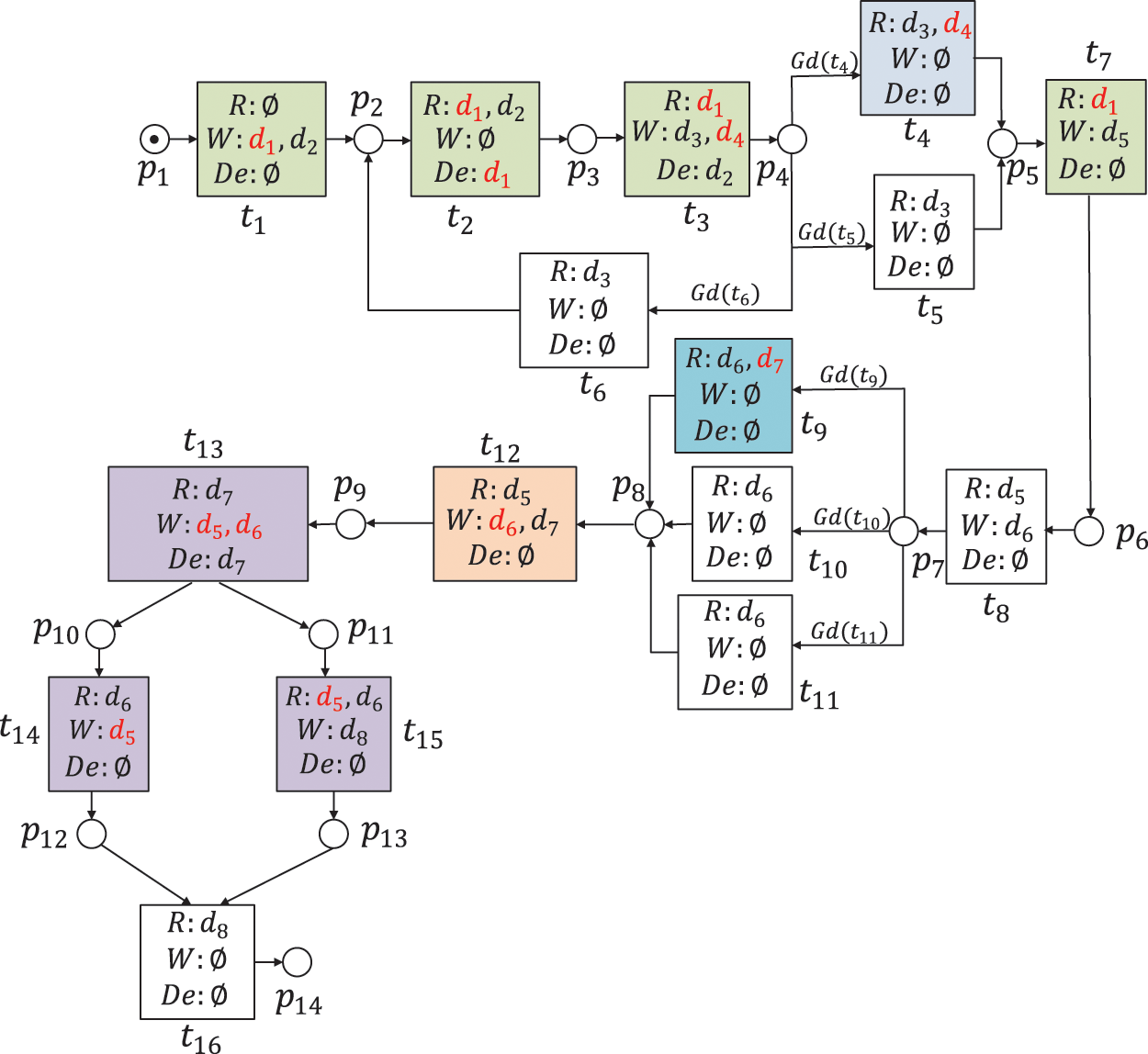
Figure 1: A WFD-net system of campus-card recharging
We model the control-flows of a workflow system as a dedicated class of Petri nets, thereby modeling activities by transitions, conditions by places, and cases as tokens. A typical workflow has a well-defined starting point, and a well-defined ending point imposes syntactic restrictions on Petri nets that result in the following definition of a workflow net (WF-net).
Definition 1 (WF-net [40,41]) A Petri net
(1) There is only one source place
(2)
A WF-net is used as a basic description of control-flows in a workflow process. A WF-net system
Definition 2 (WFD-net [29,30]) A Petri net
(1)
(2) D is a set of data items;
(3)
(4)
(5)
(6)
(7)
A WFD-net system
This part introduces a campus-card recharging process as a motivation example. As shown in Fig. 1, there are 14 places, 16 transitions, 8 data items, 34 data operations (including 19 read operations, 12 write operations, and 3 delete operations), and 6 guard functions. Table 1 illustrates the transitions and data items.
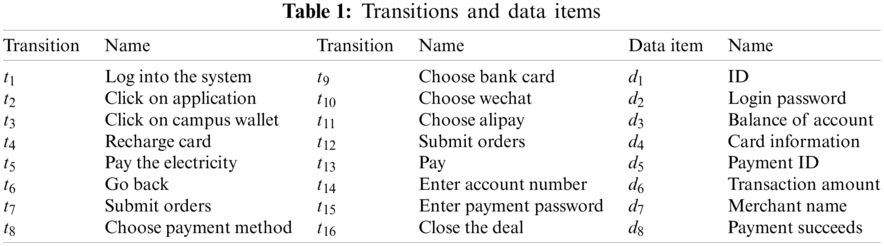
Fig. 1 describes a WFD-net system as follows. Firstly, users log into the system, and produce two data items, i.e., ID and Login Password. Then, they click on the application and campus wallet. After these operations, there are three transitions in weak exclusiveness relations. If the balance of the account is high, users can recharge the campus smart cart. If the balance of the account is middle, they can pay the electricity. Otherwise, they go back to the application. Then, they need to submit orders. After submitting orders, users can choose payment methods, e.g., bank card, Wechat, or Alipay. If the payment amount is high, they can choose bank cards. If the payment amount is middle, they can choose Wechat. Otherwise, they only choose Alipay. After then, they submit and pay for orders. Users need to input account numbers and payment passwords. Finally, they close this deal.
There are some data-flow errors in Fig. 1. For example, the data item
Although some methods are used to repair these errors, e.g., Criteria 1−3 [10] and CorrDF [14], they have some limitations. The method of Criteria 1−3 can repair data-flow errors with transition pairs in weak sequence relations. Each transition reads/writes 0/1 data item. The method of CorrDF can repair data-flow errors caused by incorrect read and write operations in process models with transition pairs in weak sequence relations, weak exclusiveness relations, and weak concurrency relations (Section 4). Unfortunately, they cannot repair data-flow errors caused by delete operations, and their workflow models are usually simple (e.g., no loop structures). What's more, repairing one error may bring in some new kinds of errors. For the example of Fig. 4h, when we repair the error of missing data, we may bring in some redundant data. Therefore, we need to reveal the scope of different kinds of data-flow errors, and present new methods to check and repair data-flow errors according to the real system requirements.
4 Data-flow Errors Checking and Repairing Methods
In this section, we first define enabled conditions of WFD-net systems, and their weak behavioral relations. Then, we present some methods to check and repair data-flow errors.
4.1 Firing Transitions and Weak Behavioral Relations
Definition 3 (Enabled Conditions) Given a WFD-net system
(1) t is control-enabled at M such that
(2) t is data-enabled at M such that each data item read by t must be defined and its guards are evaluated to true, which is denoted by
The firing of an enabled transition t (i.e., control-enabled [42] and data-enabled) at a marking M does not only affect the values of data items and guard functions but also yields a new marking
A new marking
Notice that if a transition
Due to the fact that the modeling of a workflow system is process-oriented in reality, we need to analyze its weak order relation [43].
Definition 4 (Weak Order Relation [43]) Let
In this paper, the set of all weak firing subsequences is denoted by
Based on the weak order relation, we define weak behavioral relations as follows.
Definition 5 (Weak Behavioral Relations) Given a WFD-net system
(1)
(2)
(3)
(4)
Generally speaking,
Definition 6 (Concurrency Relation) Given a WFD-net system
(1)
(2) The guard functions related to
For the example of Fig. 2a, we can find that
Figure 2: Two WFD-net systems. (a) The behavioral relation of
Definition 7 (Distance of Transitions in Weak Circulation Relation) Given a WFD-net system
Based on the definitions of weak behavioral relations, concurrency relation, and distance of transitions in weak circulation relation, we further formalize the order relation of transition pairs in a WFD-net system.
Definition 8 (Order Relation) Given a WFD-net system
(1)
(2)
(3)
For the example of Fig. 2b, we have
4.2 Four Kinds of Data-Flow Errors
Based on order relation, we formalize redundant data, missing data, lost data, and inconsistent data. Before we define these errors, we use
Definition 9 (Redundant Data, RD) Given a WFD-net system
Notice that if there exist
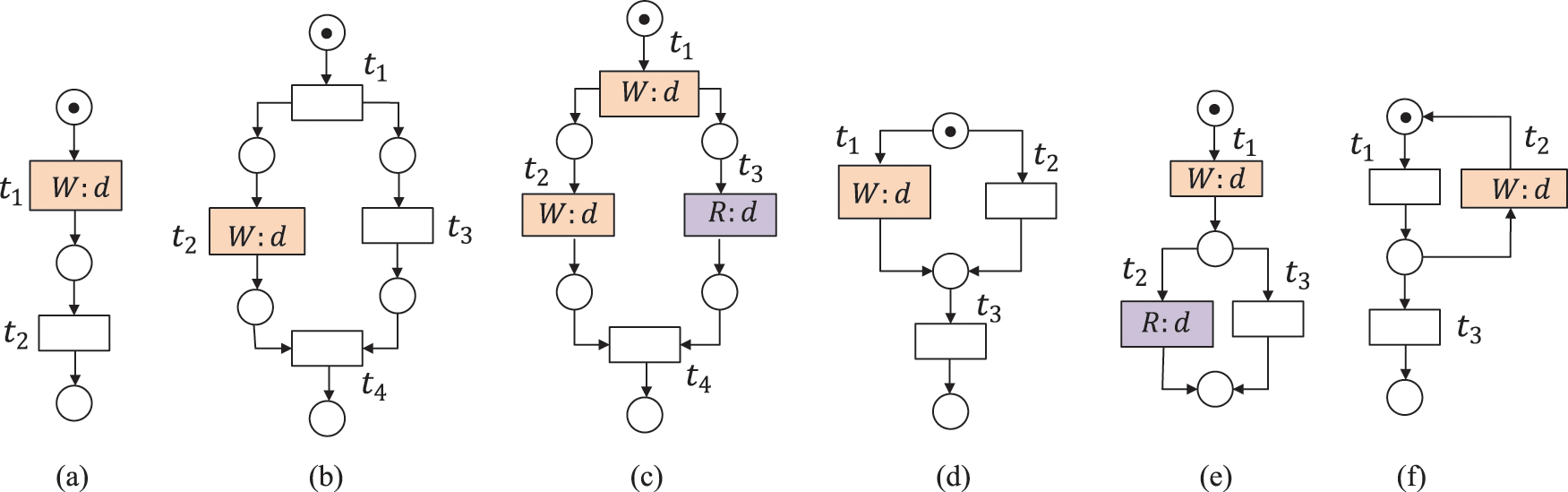
Figure 3: The data item d is redundant, where
A data item d is strongly redundant data (SRD) if the written values of d in all possible execution paths are never read before it is deleted, or the workflow process is completed. A data item d is weakly redundant data (WRD) if there exist some execution paths in which it is written but never read afterward, i.e., before it is deleted, or the workflow process is completed [30]. SRD and WRD belong to redundant data (RD). As shown in Fig. 3, the data item d is redundant, where (a)--(c) suffer from strongly redundant data, and (d)--(f) suffer from weakly redundant data.
Definition 10 (Missing Data, MD) Given a WFD-net system
(1)
(2)
Notice that if there exist
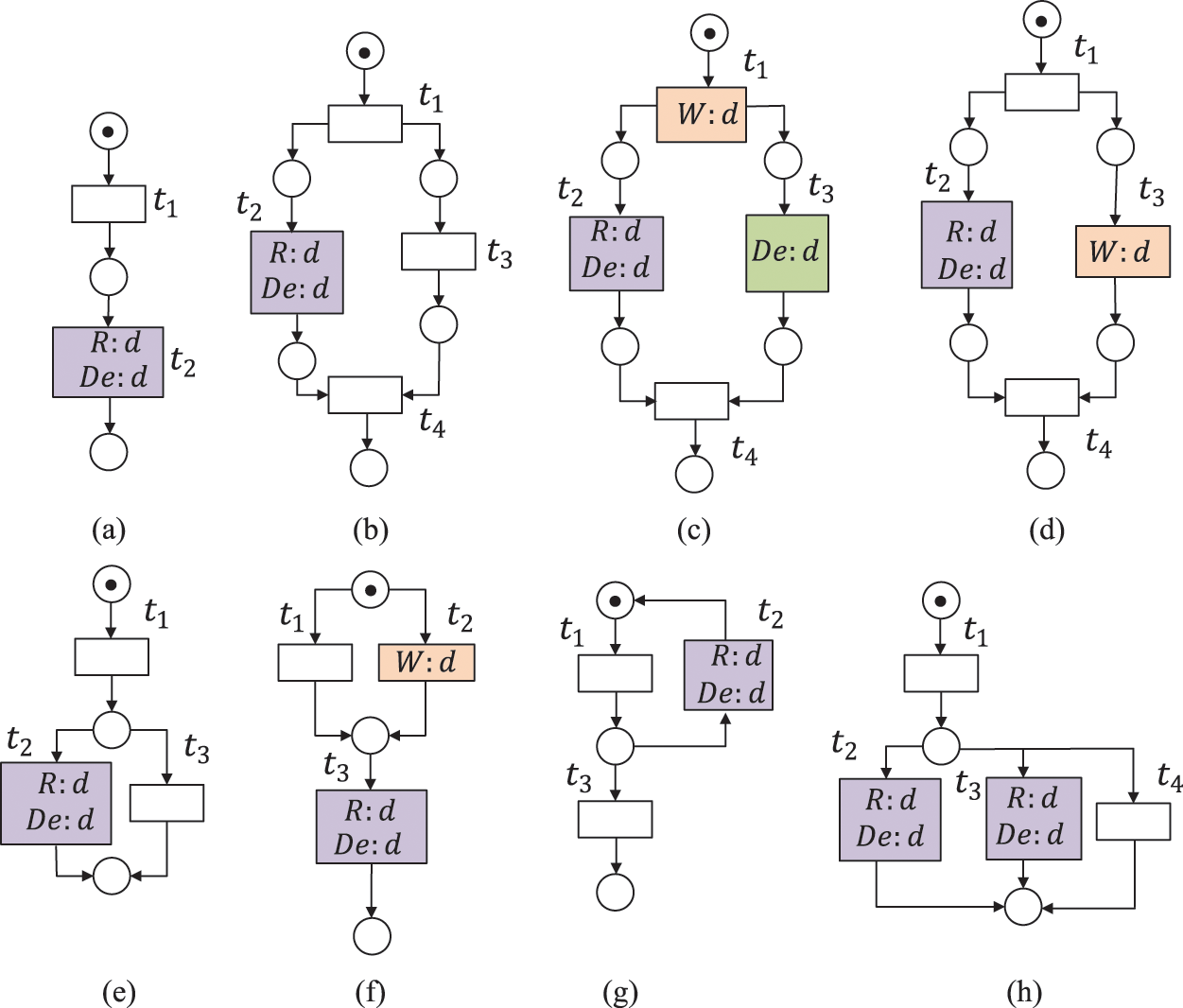
Figure 4: The data item d is missing, where
A data item d is strongly missing data (SMD) if the read or deleted values of d in all possible execution paths are never written before. A data item d is weakly missing data (WMD) if there exist some execution paths where it is read or deleted but never written before [30]. SMD and WMD belong to the missing data (MD). It is a terminal error for the execution of workflow systems [24]. For example, the data item d is strongly missing in Figs. 4a–4c, and it is weakly missing in Figs. 4d–4h.
Definition 11 (Lost Data, LD) Given a WFD-net system
(1)
(2)
which is denoted by
A data item d is strongly lost data (SLD) if the written values of d in all possible execution paths are overwritten without being read or deleted first. A data item
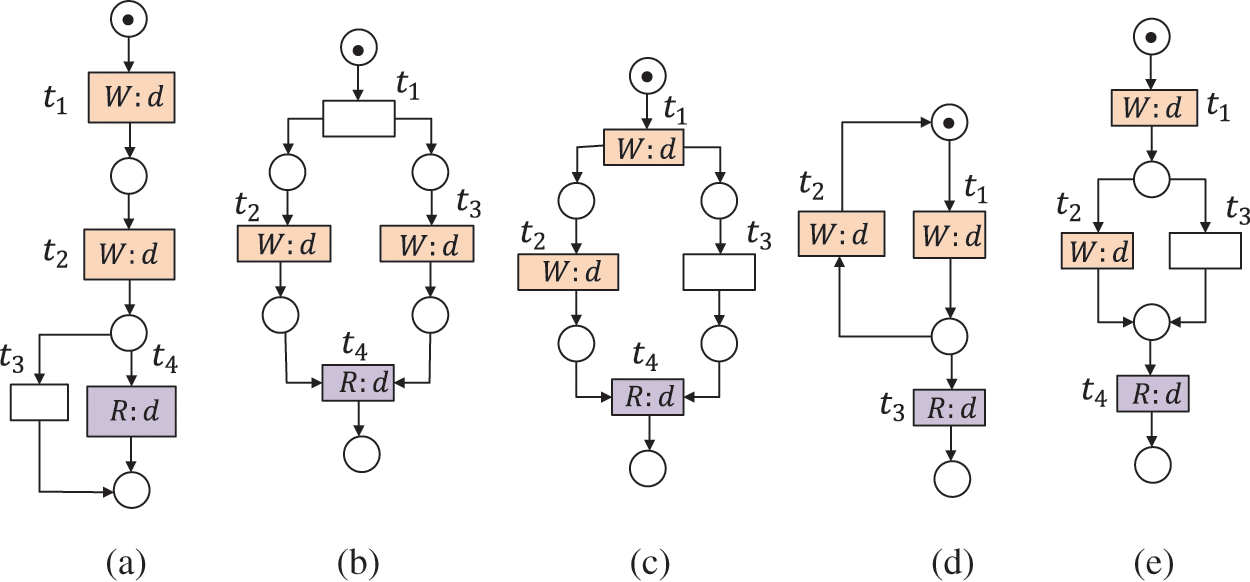
Figure 5: The data item d is lost, where
Definition 12 (Inconsistent Data, IND) Given a WFD-net system
In Fig. 6, the data item d is inconsistent when

Figure 6: The data item d is inconsistent, where
A data item written by one transition may belong to several kinds of data-flow errors. The errors of inconsistent data sometimes lead to redundant, missing, or lost data. Lost data causes redundant data. In order to distinguish their relations, we reveal their scopes, as shown in Fig. 7a.
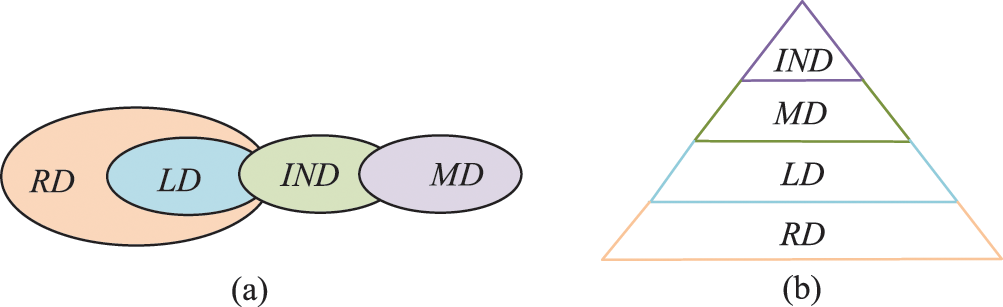
Figure 7: Four kinds of data-flow errors, i.e., redundant data (RD), missing data (MD), lost data (LD), and inconsistent data (IND). (a) The scopes of data-flow errors; (b) The hierarchy of these errors
According to the scopes of data-flow errors, we propose Algorithm 1 to detect them. This algorithm is an iterative procedure, and it consists of seven conditions. It can be used as a road map for implementing data-flow errors detection in a WFD-net system [2].

4.3 Repairing Data-flow Errors
In order to guarantee the correctness of WFD-net systems, we should provide effective methods to repair different kinds of data-flow errors. However, it is unnecessary to delete the read operation in an original WFD-net system because some transitions can fire only through reading these data items [10]. More importantly, we should not change the value we need to repair all kinds of data-flow errors. When a data item in a WFD-net system only consists of a read, write, or delete operation, we need to add a write operation, remove a write operation, or remove a delete operation. How to place these read, write, and delete operations means configuring the data-flow reasonably. In detail, we need to consider the positions of a data item. If the read and write operations are in inappropriate positions, there may appear new data-flow errors. Therefore, we give the following repair strategies according to the real system requirements to repair different kinds of data-flow errors.
System requirements:
(1) Take the value of data items into consideration;
(2) Avoid bringing in any new data-flow errors as far as possible;
(3) Do not lead to any control-flow errors, e.g., deadlock and livelock;
(4) Do not remove the read operation in an original WFD-net system;
(5) Do not bring in more data operations in order to repair the weakly redundant;
(6) Do not repair some kinds of weakly lost data so as to satisfy the non-determinacy of some read operations afterward;
(7) Avoid some data-flow errors caused by the delete operation; and
(8) Make sure that there is no inconsistent data by taking the locking mechanism.
Repair strategies:
(1) Change the firing sequence of transitions;
(2) Combine several transitions into one transition;
(3) Remove redundant write operations;
(4) Remove some undesirable delete operations;
(5) Divide one transition into several transitions; and
(6) Create new transitions with write operations.
As we know, inconsistent data often exists in concurrent programs. We can adopt the locking mechanism [18] to block the executions of multiple threads, e.g., a thread runs in a concurrent program without intervening in other threads. That is, the data item read/deleted by a thread only comes from the main thread or itself. Therefore, we do not provide related algorithms to repair this kind of error in this paper. After then, we propose Algorithms 2–4 to repair missing data, lost data, and redundant data, respectively. In the following algorithms, when we add or remove a transition, we need to add or remove its related places and arcs.
4.3.1 Repairing Missing Data (MD)
In order to repair missing data, we need to add a write operation, or remove a delete operation. It is unnecessary to remove read operations in an actual net as some transitions can fire only through reading these data items. Therefore, we propose Algorithm 2 to repair this kind of error. Its basic solutions are to introduce a transition that can write a required data item d at some point where the error occurs (i.e., Steps (1)--(12) and Steps (23)--(28) in Algorithm 2). Meanwhile, we remove some undesirable d in a delete operation (i.e., Steps (1)--(28) in Algorithm 2), and put the existing d just before all the branches where the error occurs (i.e., Steps (18)--(22) and (27)--(36) in Algorithm 2). After Steps (1)--(12), the missing data in Figs. 4a, 4b, 4d, 4e, 4g and 4h can be repaired. As for the errors in Fig. 4c (resp. Fig. 4f), we can take Steps (18)--(22) (resp. Steps (34)--(36)) to repair them. Fig. 8 shows the repairing results of missing data in Fig. 4.

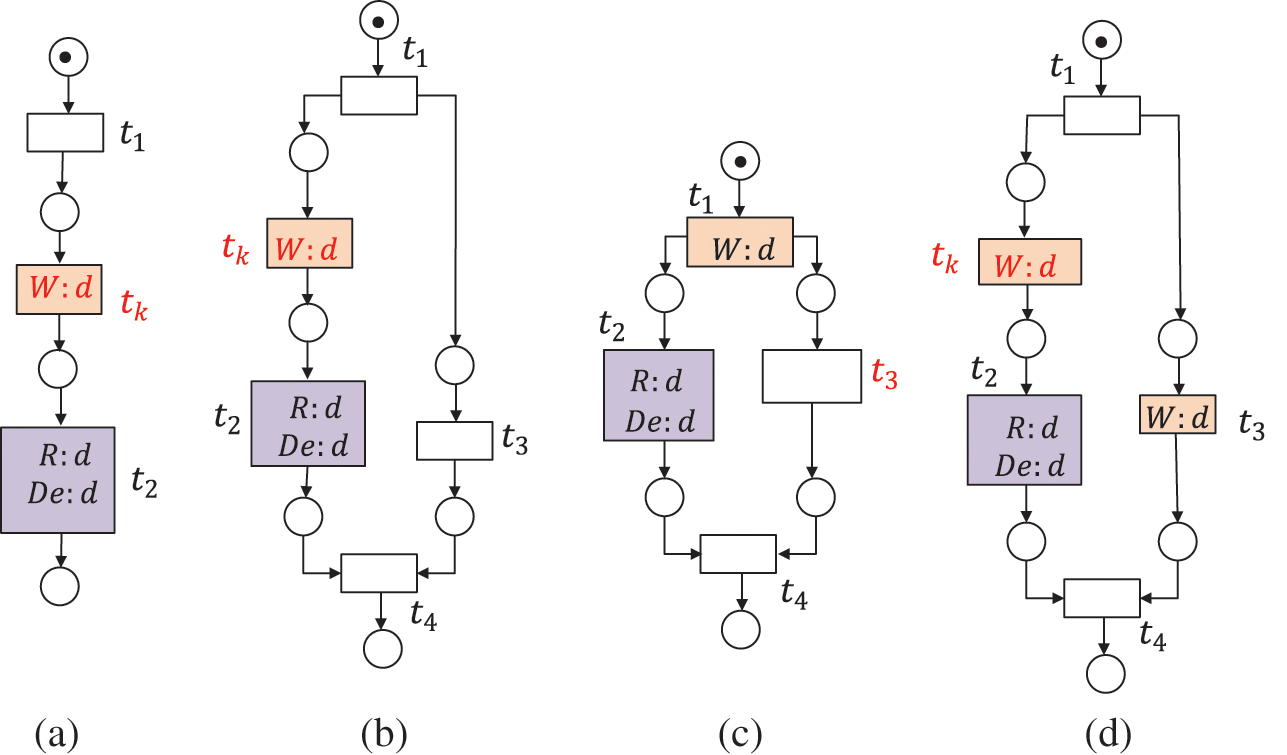
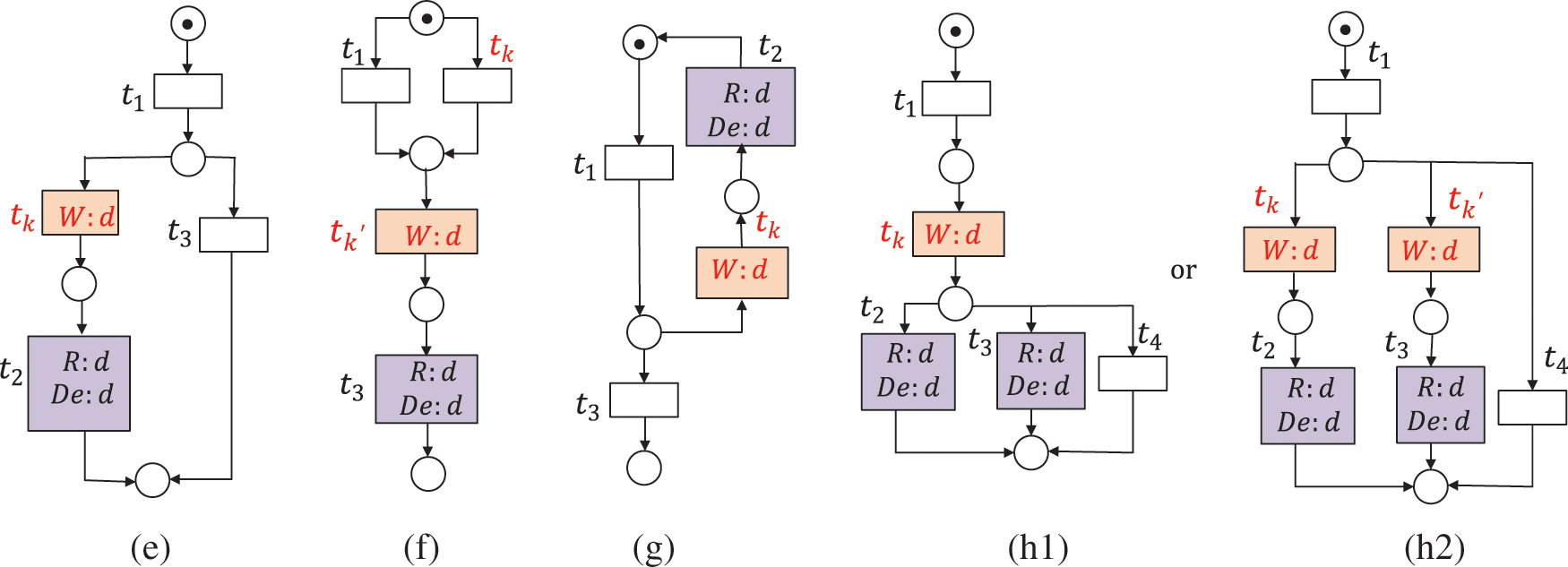
Figure 8: The repairing results of Figs. 4a–4g are shown in (a)--(g), and the repairing result of Fig. 4h is shown in (h1) if
4.3.2 Repairing Unnecessary Lost Data (LD)
In order to repair lost data, we need to remove a write operation [10]. However, some kinds of lost data should not be repaired, especially when the type of a data item d is a variable.
If a data item is lost, it must be redundant, but not vice versa. Therefore, we propose Algorithm 3 to repair lost data before repairing redundant data. Figs. 5a–5e illustrates the cases of lost data. Its basic solutions are to remove the unnecessary data item in a write operation (i.e., Steps (1)--(4), (7)--(8), (11)--(15), and (18)--(19) in Algorithm 3) or not repair (i.e., Steps (5)--(6) and (16)--(17) in Algorithm 3). If a data item d satisfies


Figure 9: The repairing results of Figs. 5a–5d, are shown in (a)--(d), and the repairing result of Fig. 5e is shown in (e1) if
4.3.3 Repairing Unnecessary Redundant Data (RD)
If a data item d is redundant, it may reduce the efficiency of programs. In order to repair this error, we need to remove a write operation [10]. However, some kinds of weakly redundant may make programs consume less memory and time. That is to say, the existence of some weakly redundant may be more convenient, and a moderate amount of weakly redundant are required, as shown in Figs. 10a–10b. Notice that we should not change the value we need when we repair this kind of error, as shown in Fig. 10c. Therefore, the following three kinds of weakly redundant should not be repaired, as shown in Fig. 10.
(1) A data item d is weakly redundant, but it is also read by more than one branch. We use
(2) The write operation of d is not in a weak circulation relation while the read operation is in a weak circulation relation. For the example of Fig. 10b, we use
(3) The data item d satisfies
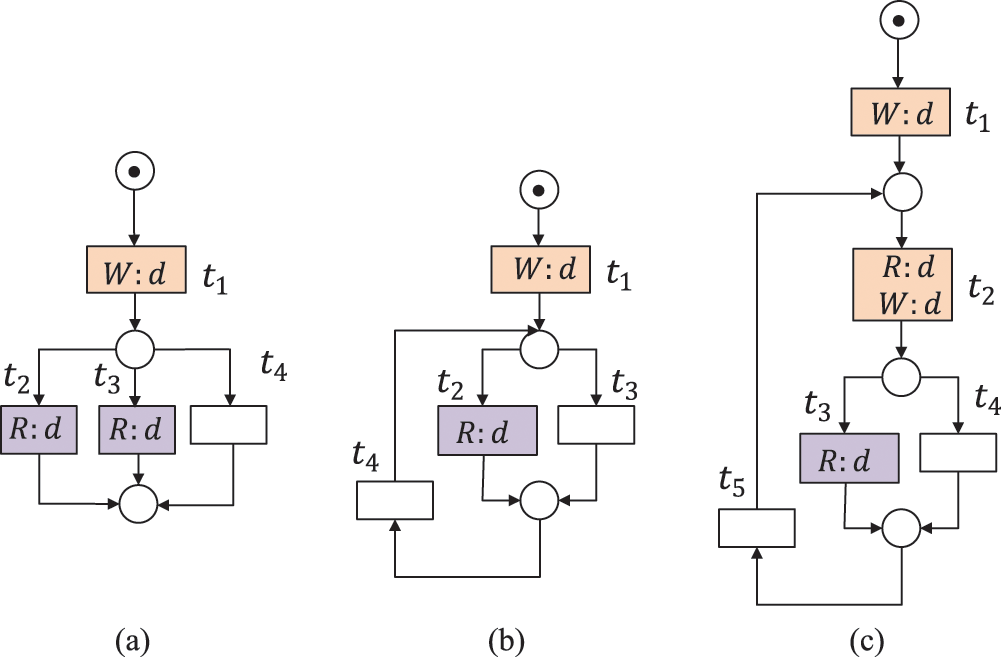
Figure 10: Three kinds of weakly redundant shouldn't be repaired. (a)
Figs. 3a–3f illustrates the cases of redundant data. We propose Algorithm 4 to repair this kind of data-flow error. Its basic solutions are to remove some undesirable data item d in a write operation and delete operation (i.e., Steps (1)--(5) in Algorithm 4). Meanwhile, we divide the transition that produces d into some branches, the transition with d in a write operation just before the transition read it (i.e., Steps (6)--(9) in Algorithm 4), or not repair (i.e., Steps (10)--(11) in Algorithm 4). After Steps (1)--(5), the redundant data in Figs. 3a–3d and 3f can be repaired. As for the errors in Fig. 3e, we can take Steps (6)--(9) to repair them. Fig. 11 shows the repairing results of redundant data in Fig. 3.

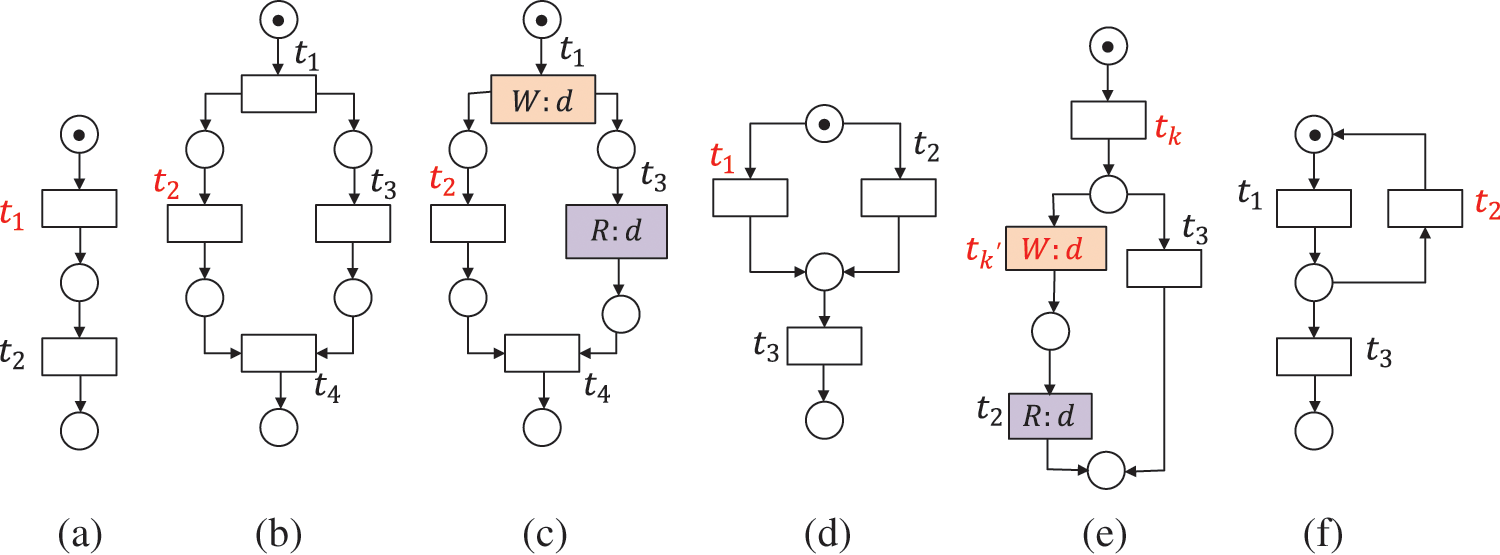
Figure 11: The repairing results of Figs. 3(a)–(f) are shown in (a)--(f)
As we know, the error of inconsistent data exists in weak concurrency relations, and can be avoided by taking a locking mechanism. It needs to be repaired firstly. The errors of redundant data, missing data, and lost data may exist in weak concurrency relations, weak sequence relations, weak exclusiveness relations, and weak circulation relations. For the example of Fig. 4h, we have
This paper aims to detect and repair data-flow errors, and guarantees the correctness of a WFD-net system. For the example of Fig. 1, we can find that the data item
Based on Definitions 9–12, we analyze the data-flow errors in Fig. 1. By taking Algorithms 2–4, we repair these errors, and their results are shown in Fig. 12.
(1) Data items
(2) Due to the fact that
(3) Since
(4) Given
(5) Considering
(6) Given
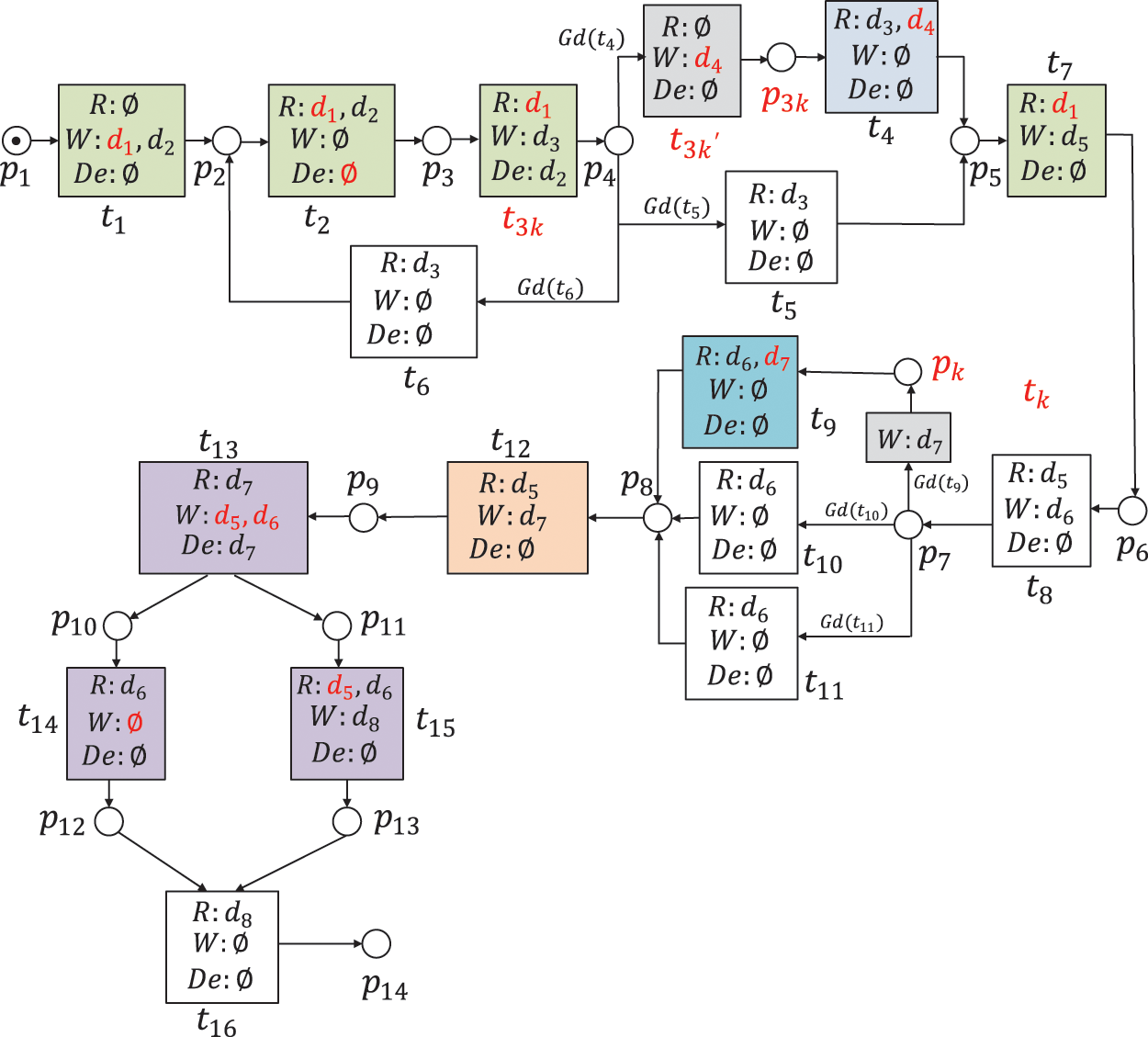
Figure 12: A repaired WFD-net system of Fig. 1
After taking these methods, a repaired WFD-net system is shown in Fig. 12. It is a new WFD-net system without any control-flow or data-flow errors.
In this subsection, we compare our methods with some state-of-the-art methods in terms of repairing functions for data-flow errors (Fig. 13). The method of Criterias 1–3 [10] can repair data-flow errors caused by transition pairs only in weak sequence relations, and its transitions read/write at most one data item. The method of CorrDF [14] can repair data-flow errors caused by transition pairs in weak sequence relations, weak exclusiveness relations, or weak concurrency relations. Unfortunately, these methods cannot repair data-flow errors in weak circulation relations and errors caused by delete operations. By comparison, our methods overcome these deficiencies, as shown in Fig. 13.

Figure 13: A comparison with some state-of-the-art methods (e.g., Criterias 1–3 [10] and CorrDF [14]) in terms of repairing functions for data-flow errors. In this figure,
In reality, a simple pseudo-code easily suffers from different kinds of data-flow errors. In this part, some experimental cases are given to show the advantages of our methods. Their detailed procedures are proceeding as follows. Firstly, we use a WFD-net system to model the real pseudo-code. Secondly, we check the data-flow errors based on Algorithm 1. After that, we use Algorithms 2–4 to repair these data-flow errors in a WFD-net system. Finally, we can obtain the repaired WFD-net system. According to the repaired WFD-net system, we can further repair the errors in the pseudo-code.
6.2.1 Repairing Missing Data (MD)
In the first experiment, we use a WFD-net system to model a simple pseudo-code with missing data, as shown in Figs. 14a and 15a. Due to the fact that the data item a read by

Figure 14: (a) Pseudo-code with missing data (MD) and (b) after being repaired

Figure 15: (a) and (b) are the WFD-net systems of Figs. 14a and 14b
6.2.2 Repairing Unnecessary Lost Data (LD)
In the second experiment, we use a WFD-net system to model a simple pseudo-code with unnecessary lost data, as shown in Figs. 16a and 17a. Due to the fact that the data item a is overwritten without being read or deleted first. Therefore, we have
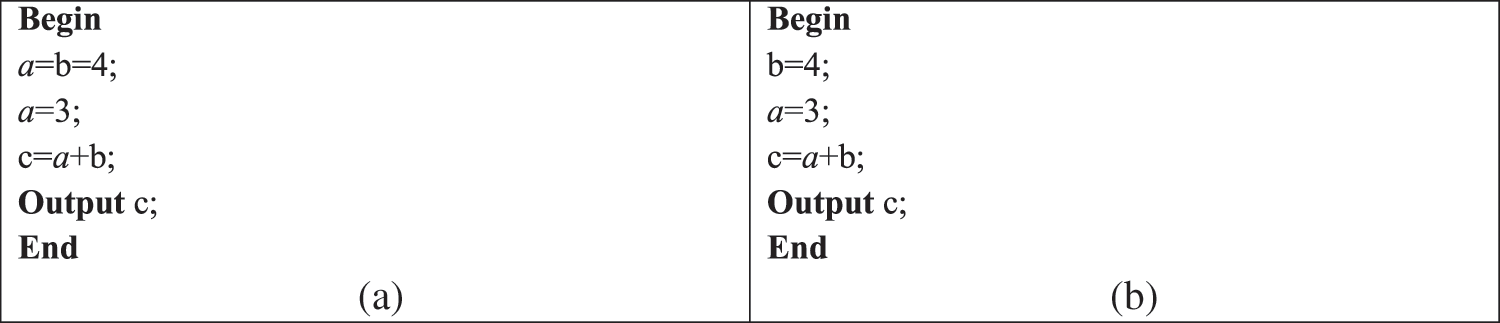
Figure 16: (a) Pseudo-code with Lost data (LD) and (b) after being repaired

Figure 17: (a) and (b) are the WFD-net systems of Figs. 16a and 16b
6.2.3 Repairing Unnecessary Redundant Data (RD)
In the third experiment, we use a WFD-net system to model a simple pseudo-code with redundant data, as shown in Figs. 18a and 19a. Due to the fact that the data item

Figure 18: (a) Pseudo-code with redundant data (RD) and (b) after being repaired

Figure 19: (a) and (b) are the WFD-net systems of Figs. 18a and 18b
6.2.4 Repairing Results of Existing Examples
In the following experiment, we consider examples from the existing references. We present the advantages of our methods in repairing four kinds of data-flow errors. Fig. 20 is the result of our experiment. It shows the numbers of data items on read/write/delete operations, the numbers of guards and transitions, and the numbers of data-flow errors before and after repairing. We can find that after taking our Algorithms 2–4, most of the data-flow errors can be repaired. However, as shown in Algorithm 4, some kinds of redundant data should not be repaired, e.g., redundant data item e shown in Fig. 1 in [30]. Therefore, our methods are more effective.

Figure 20: Our experiment result in terms of the numbers of data items on read/write/delete operations, the numbers of guards and transitions, and the numbers of data-flow errors before and after repairing
WFD-net is a formal functional method to describe the control-/data-flows of workflow systems. It extends WF-net systems with three kinds of data operations (i.e., read, write, and delete operations) and guard functions. A good modeling method and efficient detecting and repairing technique are crucial for the correctness of workflow systems. Based on weak behavioral relations (i.e., weak sequence relation, weak exclusiveness relation, weak circulation relation, and weak concurrency relation) and order relation, we formalize four kinds of data-flow errors (e.g., redundant data, missing data, lost data, and inconsistent data) in a WFD-net system. Then, we reveal the relations between these data-flow errors, and organize them into a hierarchy, which is conducive to correctly repairing data-flow errors without repeated work. Furthermore, some algorithms are developed to detect and repair data-flow errors in WFD-net systems according to system requirements and repair strategies. Compared with the existing methods, our methods can repair data-flow errors in weak circulation relations and errors caused by delete operations. What's more, our methods can avoid bringing in new unnecessary errors when repairing some kinds of data-flow errors.
In the future, we plan to do the following studies:
(1) We analyze the behavioral consistency of WFD-net systems, and study what kind of data-flow error affects the behavioral consistency degree;
(2) We develop a tool to repair some unnecessary data-flow errors automatically based on system requirements; and
(3) We intend to consider the process mining with timestamps in the workflow processes, and use the unfolding-based technique [7] to detect and repair their data-flow errors.
Funding Statement: This work was supported in part by the Shanghai Science and Technology Innovation Action Plan (Grant No. 19511101300), in part by the Key Laboratory of EMBEDded System and Service Computing (Ministry of Education) (Grant Nos. ESSCKF201902 and ESSCKF202102), and in part by the National Nature Science Foundation of China (Grant Nos. 62172299 and 62032019).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Davenport, T. H. (1993). Process innovation: Reengineering work through information technology. Boston, MA, USA: Harvard Business School Press. [Google Scholar]
2. Sun, S. X., Zhao, J. L., Nunamaker, J. F. (2006). Formulating the data-flow perspective for business process management. Information Systems Research, 17(4), 374–391. DOI 10.1287/isre.1060.0105. [Google Scholar] [CrossRef]
3. Stohr, E., Zhao, J. L. (2001). Workflow automation: Overview and research issues. Information Systems Frontiers, 3(3), 281–296. DOI 10.1023/A:1011457324641. [Google Scholar] [CrossRef]
4. Sarnikar, S., Zhao, J. L., Kumar, A. (2004). Organizational knowledge distribution: An experimental evaluation. Americas Conference on Information Systems, pp. 2305–2341. New York. [Google Scholar]
5. Kabbaj, M. I., Abdelkader, B., Bakkoury, Z., Rharbi, A. (2015). Towards an active help on detecting data-flow errors in business process models. International Journal of Computer Science and Applications, 12(1), 16–25. [Google Scholar]
6. Xiang, D. M., Liu, G. J., Yan, C. G., Jiang, C. J. (2018). Detecting data-flow errors based on petri nets with data operations. IEEE/CAA Journal of Automatica Sinica, 5(1), 251–260. DOI 10.1109/JAS.2017.7510766. [Google Scholar] [CrossRef]
7. Xiang, D. M., Liu, G. J. (2020). Checking data-flow errors based on the Guard-driven reachability graph of WFD-net. Computing and Informatics, 39, 193–212. DOI 10.31577/cai_2020_1-2_193. [Google Scholar] [CrossRef]
8. Xiang, D. M., Liu, G. J., Yan, C. G., Jiang, C. J. (2021). A Guard-driven analysis approach of workflow net with data. IEEE Transactions on Services Computing, 14(6), 1650–1661. DOI 10.1109/TSC.2019.2899086. [Google Scholar] [CrossRef]
9. Awad, A., Decker, G., Lohmann, N. (2009). Diagnosing and repairing data anomalies in process models. International Conference on Business Process Management. Business Process Management Workshops, pp. 5–16. Germany. [Google Scholar]
10. Song, W., Ma, X. X., Cheung, S. C., Hu, H., Lü, J. (2010). Preserving data-flow correctness in process adaptation. IEEE International Conference on Services Computing, pp. 9–16. Miami, USA. [Google Scholar]
11. Weidlich, M., Polyvyany, A., Mendling, J., Weske, M. (2011). Causal behavioral profiles-efficient computation, applications, and evaluation. Fundamental Informaticae, 113(3–4), 399–435. DOI 10.3233/FI-2011-614. [Google Scholar] [CrossRef]
12. Koehler, J., Hauser, R., Kuster, J. M. (2008). The role of visual modeling and model transformations in business-driven development. Electronic Notes Theory Computer Science, 211, 5–15. DOI 10.1016/j.entcs.2008.04.025. [Google Scholar] [CrossRef]
13. Sadiq, S., Orlowska, M., Sadiq, W., Foulger, C. (2003). Data flow and validation in workflow modeling. Conferences in Research and Practice in Information Technology, pp. 207–214. Dunedin, New Zealand. [Google Scholar]
14. Sharma, D., Pinjala, S., Sen, A. K. (2014). Correction of data-flow errors in workflows. 25th Australasian Conference on Information Systems, pp. 1–10. Auckland, New Zealand. [Google Scholar]
15. Best, E., Wimmel, H. (2013). Structure theory of Petri nets. In: Transactions on Petri nets and other models of concurrency VII, vol. 7480, pp. 162–224. DOI 10.1007/978-3-642-38143-0_5. [Google Scholar] [CrossRef]
16. Wang, S. G., Gan, M. D., Zhou, M. C., You, D. (2015). A reduced reachability tree for a class of unbounded petri nets. IEEE/CAA Journal of Automatica Sinica, 2(4), 345–352. DOI 10.1109/JAS.2015.7296528. [Google Scholar] [CrossRef]
17. Fang, X. W., Jiang, C. J., Yin, Z. X., Fan, X. Q. (2011). The trustworthiness analyzing of interacting business process based on the induction information. Computer Science and Information Systems, 8(3), 843–867. DOI 10.2298/CSIS100411031F. [Google Scholar] [CrossRef]
18. Clempner, J. (2014). Verifying soundness of business processes: A decision process Petri nets approach. Expert Systems with Applications, 41, 5030–5040. DOI 10.1016/j.eswa.2014.03.005. [Google Scholar] [CrossRef]
19. Lourenco, J. M., Fiedor, J., Krena, B., Vojnar, T. (2018). Discovering concurrency errors. In: Lecture on runtime verification, vol. 10457, pp. 34–60. Germany: Springer. [Google Scholar]
20. Henkel, M., Zdravkovic, J., Johannesson, P. (2004). Service-based processes: Design for business and technology, pp. 21–29. USA: ACM Digital Library. [Google Scholar]
21. Andersson, B., Bergholtz, M., Edirisuriya, A., Ilayperuma, T., Johannesson, P. (2005). A declarative foundation of process models. Lecture Notes in Computer Science, 3520, 233–247. DOI 10.1007/11431855_17. [Google Scholar] [CrossRef]
22. Sundari, M. H., Sen, A. K., Bagchi, A. (2007). Detecting data-flow errors in workflows: A systematic graph traversal approach. 17th Workshop on Information Technology and Systems, pp. 1–6. Montreal. [Google Scholar]
23. Sun, S. H., Zhao, J. L. (2008). Developing a workflow design framework based on data-flow analysis. Proceedings of the 41st Hawaii International Conference on System Sciences, pp. 7–10. Waikoloa. [Google Scholar]
24. Meda, H. S., Sen, A. K., Bagchi, A. (2010). On detecting data-flow errors in workflows. ACM Journal of Data and Information Quality, 2(1), 1–31. DOI 10.1145/1805286.1805290. [Google Scholar] [CrossRef]
25. Sidorova, N., Stahl, C., Trcka, N. (2011). Soundness verification for conceptual workflow nets with data: Early detection of errors with the most precision possible. Information Systems, 36, 1026–1043. DOI 10.1016/j.is.2011.04.004. [Google Scholar] [CrossRef]
26. Haddar, N., Tmar, M., Gargouri, F. (2016). A Data-centric approach to manage business processes. Computing, 98, 375–406. DOI 10.1007/s00607-015-0440-2. [Google Scholar] [CrossRef]
27. Dolean, C. C., Petrusel, R. (2012). Data-flow modeling: A survey of issues and approaches. Informatica Economica, 16(4), 117–130. [Google Scholar]
28. Dramski, M. (2017). Missing data problem in the event logs of transport processes. International Conference on Transport Systems Telematics, pp. 110–120. Katowice. [Google Scholar]
29. Trcka, N., van der Aalst, W. M. P., Sidorova, N. (2008). Analyzing control-flow and data-flow in workflow processes in a unified way. Computer Science Reports, 1–23. DOI 10.1.1.501.519. [Google Scholar]
30. Trcka, N., van der Aalst, W. M. P., Sidorova, N. (2009). Data-flow anti-patterns: Discovering data-flow errors in workflows. International Conference on Advanced Information Systems Engineering, vol. 5565, pp. 425–439. Amsterdam, Netherlands. [Google Scholar]
31. von Stackelberg, S., Putze, S., Mvlle, J., Bohm, K. (2014). Detecting data-flow errors in BPMN 2.0. Open Journal of Information Systems, 1(2), 1–19. [Google Scholar]
32. Song, W., Zhang, C., Jacobsen, H. (2018). An empirical study on data flow bugs in business processes. IEEE Transactions on Cloud Computing, 9(1), 1–14. DOI 10.1109/TCC.2018.2844247. [Google Scholar] [CrossRef]
33. Mülle, J., Tex, C., Bohm, K. (2019). A practical data-flow verification scheme for business processes. Information Systems, 81, 136–151. DOI 10.1016/j.is.2018.12.002. [Google Scholar] [CrossRef]
34. Jovanovikj, I., Yigitbas, E., Gerth, C., Sauer, S., Engels, G. (2019). Detection and resolution of data-flow differences in business process models. CAiSE Forumn 2019, vol. 350, pp. 145–157. Germany: Springer. [Google Scholar]
35. Wang, M. M., Liu, G. J., Zhao, P. H., Yan, C. G., Jiang, C. J. (2018). Behavior consistency computation for workflow nets with unknown correspondence. IEEE/CAA Journal of Automatica Sinica, 5(1), 281–291. DOI 10.1109/JAS.2017.7510775. [Google Scholar] [CrossRef]
36. Qi, L., Zhou, M. C., Luan, W. J. (2018). A two-level traffic light control strategy for preventing incident-based urban traffic congestion. IEEE Transactions on Intelligent Transportation Systems, 19(1), 13–24. DOI 10.1109/TITS.2016.2625324. [Google Scholar] [CrossRef]
37. Song, W., Chang, Z., Jacobsen, H., Zhang, P. W. (2021). Discovering structural errors from business process event logs. IEEE Transactions on Knowledge and Data Engineering (Early Access), 1–14. DOI 10.1109/TKDE.2021.3052927. [Google Scholar] [CrossRef]
38. Wang, S. G., Gan, M. D., Zhou, M. C. (2015). Macro liveness graph and liveness of w-independent unbounded nets. Science in China Series F: Information Sciences, 58(3), 1–10. DOI 10.1007/s11432-014-5239-9. [Google Scholar] [CrossRef]
39. Song, W., Jacobsen, H., Chen, F. F. (2019). Scientific workflow protocol discovery from public event logs in clouds. IEEE Transactions on Knowledge and Data Engineering, 32(12), 2453–2466. DOI 10.1109/TKDE.2019.2922183. [Google Scholar] [CrossRef]
40. Liu, C., Zeng, Q. T., Cheng, L., Duan, H., Zhou, M. C., et al. (2021). Privacy-preserving behavioral correctness verification of cross-organizational workflow with task synchronization patterns. IEEE Transactions on Automation Science and Engineering, 18(3), 1037–1048. DOI 10.1109/TASE.2020.2993376. [Google Scholar] [CrossRef]
41. Zhao, F., Xiang, D. M., Liu, G. J., Jiang, C. J. (2021). A new method for measuring the behavioral consistency degree of WF-net systems. IEEE Transactions on Computational Social Systems (Early Access), 1–14. DOI 10.1109/TCSS.2021.3099475. [Google Scholar] [CrossRef]
42. Guang, M. J., Yan, C. G., Wang, J. L., Qi, H. D., Jiang, C. J. (2021). Benchmark datasets for stochastic petri net learning. International Joint Conference on Neural Networks, pp. 1–8. Shenzhen, China. DOI 10.1109/IJCNN52387.2021.9533785. [Google Scholar] [CrossRef]
43. Weidlich, M., Mendling, J., Weske, M. (2011). Efficient consistency measurement based on behavioral profiles of process models. IEEE Transactions on Software Engineering, 37(3), 410–429. DOI 10.1109/TSE.2010.96. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |