New Hybrid EWMA Charts for Efficient Process Dispersion Monitoring with Application in Automobile Industry

Xuechen Liu; Majid Khan; Zahid Rasheed; Syed Anwar; Muhammad Arslan

doi:10.32604/cmes.2022.019199

Xuechen Liu1, Majid Khan2, Zahid Rasheed3, Syed Masroor Anwar4,* and Muhammad Arslan5

1Faculty of Economics, Taiyuan Normal University, Taiyuan, 030619, China
2Department of Mathematics and Statistics, Riphah International University, Islamabad, 44000, Pakistan
3Department of Mathematics, Women University of Azad Jammu and Kashmir, Bagh, 12500, Pakistan
4Department of Statistics, University of Azad Jammu and Kashmir, Muzaffarabad, 13100, Pakistan
5School of Statistics, Shanxi University of Finance and Economics, Taiyuan, 030619, China
*Corresponding Author: Syed Masroor Anwar. Email: masroorstatistics@gmail.com
Received: 08 September 2021; Accepted: 09 November 2021

Abstract: The EWMA charts are the well-known memory-type charts used for monitoring the small-to-intermediate shifts in the process parameters (location and/or dispersion). The hybrid EWMA (HEWMA) charts are enhanced version of the EWMA charts, which effectively monitor the process parameters. This paper aims to develop two new upper-sided HEWMA charts for monitoring shifts in process variance, i.e., HEWMA1 and HEWMA2 charts. The design structures of the proposed HEWMA1 and HEWMA2 charts are based on the concept of integrating the features of two EWMA charts. The HEWMA1 and HEWMA2 charts plotting statistics are developed using one EWMA statistic as input for the other EWMA statistic. A Monte Carlo simulations method is used as a computational technique to determine the numerical results for the performance characteristics, such as average run length (ARL), median run length, and standard deviation run length (SDRL) for assessing the performance of the proposed HEWMA1 and HEWMA2 charts. In addition, to evaluate the overall performance of the proposed HEWMA1 and HEWMA2 charts, other numerical measures consisting of the extra quadratic loss (EQL), relative average run length (RARL), and performance comparison index (PCI) are also computed. The proposed HEWMA1 and HEWMA2 charts are compared to some existing charts, such as CH, CEWMA, HEWMA, AEWMA HHW1, HHW2, AIB-EWMA-I, and AIB-EWMA-II charts, on the basis aforementioned numerical measures. The comparison reveals that the proposed HEWMA1 and HEWMA2 charts achieve better detection ability against the existing charts. In the end, a real-life data application is also provided to enhance the implementation of the proposed HEWMA1 and HEWMA2 charts practically.

Keywords: Average run length; extra quadratic loss; memory-type charts; Monte Carlo simulations; smoothing parameter

Control charts are the essential tools of the statistical process monitoring (SPM) toolkit, used to detect the shifts in manufacturing and production processes parameter(s). The control charts are generally classified into memory-type and memoryless-type charts [1]. The memoryless-type charts are used only for current information of the process, while the memory-type charts are based on both current and previous information of the process. The basic memoryless-type charts are the Shewhart charts, like the Shewhart X¯, R, and S2 charts, etc. [2]. The Shewhart charts are simple and easy to apply; however, they are only efficient for the cases where large shifts occur in the process parameter(s). On the contrary, the memory-type charts, such as the exponentially weighted moving average (EWMA) and cumulative sum (CUSUM) charts are sensitive in monitoring small-to-intermediate shifts in the process parameter(s).

Roberts [3] was the first to introduce the classical EWMA chart for monitoring the mean level of the process. Later, Hunter et al. [4–7] further investigated the various EWMA-type charts in order to facilitate the application of the classical EWMA chart in mean process monitoring. Recent studies have shown that EWMA-type charts are the most useful tools for researchers. For example, Haq [8], Abbas et al. [9], Ali et al. [10], Tang et al. [11], Haq [12], Rasheed et al. [13], Rasheed et al. [14], etc., are the few recent references in this regard.

In general, most manufacturing and production processes have a shift in the mean level; however, the process variance (or standard deviation) may be shifted from the target in many practical situations. Domangue et al. [15] suggested that monitoring an increase in process variance is more important for the processes. Although the EWMA-types charts are primarily used in mean process monitoring; however, few works address the variance monitoring via these charts. For example, Crowder et al. [16] used the logarithmic transformation to the sample variance S2 in order to develop the EWMA chart (also known as the CH chart) for monitoring the process standard deviation. Similarly, Shu et al. [17] suggested the EWMA chart, denoted as the NEWMA chart, efficiently monitors process variance compared to the CH chart. Correspondingly, Huwang et al. [18] developed the EWMA-type charts for detecting shifts in the process variance and demonstrated that their control charts outperform the CH and NEWMA charts. Equally, Castagliola [19] used the three parameters logarithmic transformation of S2 and proposed the bilateral EWMA chart to monitor the process variance shifts. Besides, Chang et al. [20] designed the optimal EWMA chart in order to monitor the process variance shifts. In addition, Razmy [21] offered the EWMA chart the monitors the standardized process variance. Furthermore, Haq [22] proposed two auxiliary information-based charts, symbolized by AIBEWMA1 and AIBEWMA2 charts, that monitor the process variance efficiently. Also, Ali et al. [23] suggested the generally weighted moving average (GWMA) and hybrid EWMA (HEWMA) chart to monitor process variance changes. Both GWMA and HEWMA perform better than classical memory charts. Other studies based on the EWMA-type charts for tracking the process variance are provided by Saghir et al. [24], Zaman et al. [25], Riaz et al. [26] and Chatterjee et al. [27], etc.

The use of hybrid charts enhances the efficiency of traditional charts. For example, Haq [8] and Haq [28] proposed the HEWMA chart to monitor the mean level of the process. Later on, numerous authors used the HEWMA charts in different process monitoring schemes. The HEWMA charts are more efficient than the classical EWMA and CUSUM charts in terms of small to moderate shifts monitoring. For example, Aslam et al. [29] introduced the HEWMA chart to monitor the mean level of the process under repetitive sampling. Similarly, Aslam et al. [30] monitored the COM-Poisson process by designing the HEWMA chart. Equally, Aslam et al. [31] developed the mixed chart, named the HEWMA-CUSUM chart, for the Weibull process monitoring. Correspondingly, Noor-ul-Amin et al. [32] recommended the HEWMA chart for Phase-II mean monitoring, based on the auxiliary information. Besides, Aslam et al. [33] suggested the HEWMA-p chart to monitor the variance of the non-normal process. Also, Noor et al. [34] constructed the Bayesian HEWMA chart, using two loss functions, to monitor the mean level of the normal process. The other studies about the HEWMA chart are offered by Asif et al. [35], Noor-Ul-Amin et al. [36], etc.

The majority of manufacturing and service processes are affected by the gradual increase in process variance. The increase in the process variance indicates a deterioration in the process performance. This study's first and most important goal is to propose efficient charts with effective shifts detection ability in monitoring an increase in the process variances. So, motivated by Crowder et al. [16], Castagliola [19], and Haq [8], this study proposes two new HEWMA charts to monitor the increasing shifts in the process variance. The proposed charts are known as HEWMA1 and HEWMA2 charts. The design structure of the HEWMA1 chart uses the CH statistic as the input for the HEWMA1 statistic. In the same lines, the CEWMA statistic is considered an input to the HEWMA2 statistic to formulate the HEWMA2 chart. The Monte Carlo simulations are employed to compute the numerical results associated with average run length (ARL), standard deviation run length (SDRL), extra quadratic loss (EQL), relative average run length (RARL), and performance comparison index (PCI) for the proposed HEWMA1 and HEWMA2 charts. Based on these measures, the proposed HEWMA1 and HEWMA2 charts are compared to the existing CH, CEWMA, HEWMA, AEWMA, HHW1, HHW2, AIBEWMA1, and AIBEWMA2 charts. The comparison shows that the proposed HEWMA1 and HEWMA2 charts have better detection ability to detect the shift in the process variance. Finally, two applications of the proposed HEWMA1 and HEWMA2 charts are provided, one with simulated data and the other with real-life data, to aid in the comparison of the proposed charts.

The remainder of the article is set out in the following way: Section 2 presents the existing methods. Likewise, Section 3 lays out the methodologies and formulation of the proposed HEWMA1 and HEWMA2 charts. In addition, the performance evaluation measures and simulation study are included in Section 4. Furthermore, Section 5 consists of the comparison and performance analysis of the proposed HEWMA1 and HEWMA2 charts against some existing charts. Section 6 offers a real-life data application to enhance the performance of the proposed HEWMA1 and HEWMA2 charts. The last section addresses the concluding remarks.

This section defines the process variable in Subsection 2.1. Similarly, Subsection 2.2 explains the details about the transformations to the sample variance. In addition, Subsections 2.3 to 2.6 provide the design and formulation of the CH, CEWMA, HHW2, and HEWMA charts for monitoring process variance, respectively.

Assuming, at the time t=1,2,…, there are X1t,X2t,…,Xit,…,Xnt; i.e., n independent identically normal random variables with mean and variance μt and σt2, i.e., Xit∼N(μt,σt2) for i=1,2,…,n. As the only concern is to detect the increasing changes in σt2, so the mean level of the process is assumed to be IC, i.e., μt=μ. Suppose the underlying process variance remains IC for a particular time, i.e., σt2=σ02 for t<t0, then the process goes in OOC state, i.e., σt2≠σ02 for t≥t0. Let δt denotes the size of shifts in σt2 then it can be defined as a ratio IC process standard deviation to OOC process standard deviation, i.e., δt=σtσ0. So, δt=1 whenever the underlying process is IC, and δt≠1 in the case of the OOC process. If X¯t=1n∑i=1nXit be the sample mean and St2=1n−1∑i=1n(Xit−X¯t)2 denotes the sample variance of the tth subgroup, respectively, then for IC process St2 follows a chi-square distribution with n−1 degrees of freedom, i.e., St2∼σ02n−1χ(n−1)2.

In order to implement the EWMA-type charts, the assumption of normality is required for the plotting statistic of the charts. However, because the sample variance St2 has a chi-square distribution, so it is not an acceptable statistic for the design structure of the EWMA-type charts. In order to cope with this issue, a few transformations are available in the literature, given as follows.

where the ratio St2/σ02 is follows the gamma distribution with parameter (n−1)/2 and 2δt2/(n−1). According to Lawless [37], Wt is a log-gamma random variable and it has a approximate normal distribution, i.e., Wt⋍N(μW,σW2), where μW=ln⁡(δt2)−1n−1−13(n−1)2+215(n−1)4 and σW2=2n−1+2(n−1)2+43(n−1)3+1615(n−1)5.

Castagliola [19] recommended the three-parameter logarithmic transformation of St2 into a new variable, given as

where aT, bT and cT are the three constants of the transformation, defined as; aT=AT−2BTln⁡(σ), bT=BT, cT=CTσ, respectively. The values of AT, BT, CT, μT and σT2 based on the sample size n(n=3,4,5,10,15) are given by Castagliola [19]. The statistic Tt, in this case, is approximately normally distributed with μT and variance σT2, i.e., Tt∼N(μT,σT2).

In order to detect the shifts in the process variance, Quesenberry [38] suggested another transformation defined as

where χt2=(n−1)St2σ02, is chi-square variable with ν=n−1 degrees of freedom, i.e., χt2∼χ(ν)2. The F(⋅;ν) is the distribution function (DF) of the chi-square variable, while Φ−1(⋅) denotes the inverse DF of the standard normal variable. In this case, the statistic Mt follows a standard normal distribution, i.e., Mt∼N(0,1).

Crowder et al. [16] introduced the CH chart, which monitored the process variance shifts. Let {Qt} for t≥1 be the sequence of IID random variable, defined on the sequence {Wt}, where Wt is defined by Eq. (1), then using the recurrence relationship, the CH plotting statistic Qt can be given as

where λ1 is known as the smoothing parameter. The CH statistic mean and variance are, respectively, given as

In the case of large t, the variance of Qt is reduced to; Var(Qt)=λ11−λ1σW2. In order to detect the gradual rise in the process variance, let Qt+ be the charting statistic for the CH chart is given by

The initial value of and Qt+ is set on 0, i.e., Q0+=0. The upper control limit for the CH chart is denoted by UCL(CH)+ and can be defined by

where LCH+ is the CH chart width coefficients and can be computed so that IC ARL\;(ARL0) is approximately equal to the desired value. The CH chart detects the upward shifts in the process whenever Qt+≥UCL(CH)+.

Castagliola [19] proposed the EWMA chart (also known as S2-EWMA chart) to monitor the shifts in the process variance. Hereafter the S2-EWMA chart is labeled as the CEWMA chart. The CEWMA chart used the three parameters logarithmic transformation to S2 to obtain the approximate normality for the plotting statistic. Let {Zt} be the CEWMA sequence, based on another sequence {Tt} for t≥1, where Tt is defined by Eq. (2), then the charting statistic of the CEWMA chart is given by

The Z0 values for various n can be taken from [19]. The Z0 values are close to 0, so one can replace them with 0. Here, the plotting statistic Zt is an approximate normal distributed variable having mean μT and variance λ12−λ1[1−(1−λ1)2t]σT2, i.e., Zt∼N(μT,λ12−λ1[1−(1−λ1)2t]σT2). However, for a large value of t, the factor [1−(1−λ1)2t] tends to 1, and in this case Zt∼N(μT,λ12−λ1σT2). If UCL(CEWMA)+ denotes the upper control limit for the CEWMA chart, then it can be defined as

where LCEWMA+ is called the width coefficient of the CEWMA chart. The CEWMA chart detects OOC signals with increasing shift whenever Zt≥UCL(CEWMA)+.

Huwang et al. [18] proposed the EWMA chart to monitor the process variance, denoted as the HHW2 chart. Let {Rt}, for t≥1 be the HHW2 sequence that based on the IID sequence of random variable {Mt}, where Mt is defined in Eq. (3), then the HHW2 statistic based on the sequence {Rt} is defined as

The initial value of and Rt is set on 0, i.e., R0=0. The plotting statistic Rt has a normal distribution with mean zero, and variance λ12−λ1{1−(1−λ1)2t}, i.e., Rt∼N(0,λ12−λ1[1−(1−λ1)2t]). The time-dependent control limits, UCLt(HHW2) for the HHW2 chart can be defined as

In case of large t values, the upper control limit for of the HHW2 chart is denoted as UCL(HHW2)+ and can be given as

The LHHW2+ is the HHW2 chart width coefficients. The HHW2 chart detects OOC signals whenever Rt fall above the control limits specified in Eq. (12).

Ali et al. [23] followed the idea of [8] and designed the HEWMA chart for process variance. Let the IID {Ht} for t≥1 is known as the HEWMA sequence, which is based on the {Rt}, then the statistic Ht for the HEWMA chart is given as

where Rt is defined by Eq. (10) and λ2 is also a smoothing constant, such that λ2≠λ1. The initial values of Ht are set to 0, i.e., H0=0. The mean E(Ht)=0, and the variance of Ht is given as

Var(Ht)=(λ1λ2λ1−λ2)[∑k=12(1−λk)2{1−(1−λk)2t}1−(1−λk)2−2(1−λ1)(1−λ2){1−(1−λ1)t(1−λ2)t}1−(1−λ1)(1−λ2)]. (14)

The control limit UCLt(HEWMA) for the HEWMA chart, based on Eq. (14) is defined by

UCLt(HEWMA)+=LHEWMA+×(λ1λ2λ1−λ2)[∑k=12(1−λk)2{1−(1−λk)2t}1−(1−λk)2−2(1−λ1)(1−λ2){1−(1−λ1)t(1−λ2)t}1−(1−λ1)(1−λ2)].(15)

When t gets larger, the control limits defined by Eq. (15) is reduced to UCL(HEWMA)+ and given as

UCL(HEWMA)+=LHEWMA+(λ1λ2λ1−λ2)[∑k=12(1−λk)21−(1−λk)2−2(1−λ1)(1−λ2)1−(1−λ1)(1−λ2)]. (16)

where LHEWMA+ is the width coefficient for the HEWMA chart. The HEWMA chart triggers OOC signals whenever Ht≥UCL(HEWMA)+.

Haq [8] suggested the HEWMA chart to monitor the process mean. Similarly, Ali et al. [23] presented the HEWMA chart's design structure for tracking the process variance. Following Haq [8], the HEWMA1 and HEWMA2 charts can be developed using Transformations I and II, respectively. These charts detect increasing shifts in process variance. The methodologies and construction of the HEWMA1 and HEWMA2 charts are, respectively, presented in Subsections 3.1 and 3.2.

The design structure for the HEWMA1 chart can be constructed using the CH statistic as input for the HEWMA1 statistic. Let defined the sequence of IID random variable, say {Ut} for t≥1, based on the CH sequence {Qt} then the HEWMA1 statistic Ut can be defined by the relation given as

where Qt is the CH statistic defined by Eq. (4). The starting value of Ut is equal to 0, i.e., U0=0. The mean of Ut is E(Ut)=0 and its variance, for the case of very large t, is defined as

Var(Ut)=(λ1λ2λ1−λ2)[∑k=12(1−λk)21−(1−λk)2−2(1−λ1)(1−λ2)1−(1−λ1)(1−λ2)]σW2. (18)

In order to monitor the increasing shift in the process, the HEWMA1 statistic is defined as

The initial value of Ut+ is set on 0, i.e., U0+=0. The control limit for upper sided HEWMA1 is given as

UCL(HEWMA1)+=LHEWMA1+(λ1λ2λ1−λ2)[∑k=12(1−λk)21−(1−λk)2−2(1−λ1)(1−λ2)1−(1−λ1)(1−λ2)]σW. (20)

where LHEWMA1+ is the width coefficient for the HEWMA1 chart. The HEWMA1 chart detects OOC signals whenever Ut+≥UCL(HEWMA1)+. Similarly, for monitoring the gradual decrease in the variance, the HEWMA1 statistic is given by

The initial value of Ut− is denoted by U0− set on 0, i.e., U0−=0. The control limit for lower sided HEWMA1 is given as

LCL(HEWMA1)−=LHEWMA1−(λ1λ2λ1−λ2)[∑k=12(1−λk)21−(1−λk)2−2(1−λ1)(1−λ2)1−(1−λ1)(1−λ2)]σW. (22)

The lower-sided HEWMA1 chart detects OOC signals whenever Ut−≤LCL(HEWMA1)−. The control limits defined in Eqs. (20) and (22) are called the HEWMA1 upper and lower control limits, respectively. However, the HEWMA1 two-sided control limits are given as

UCL(HEWMA1)=LHEWMA1(λ1λ2λ1−λ2)[∑k=12(1−λk)21−(1−λk)2−2(1−λ1)(1−λ2)1−(1−λ1)(1−λ2)]σWLCL(HEWMA1)=−LHEWMA1(λ1λ2λ1−λ2)[∑k=12(1−λk)21−(1−λk)2−2(1−λ1)(1−λ2)1−(1−λ1)(1−λ2)]σW}. (23)

The two-sided HEWMA1 chart detects OOC signals whenever Ut≥UCL(HEWMA1) or Ut≤LCL(HEWMA1).

In order to formulate the design of the HEWMA2 chart, the charting statistic of the CEWMA chart can be used as an input for the HEWMA2 statistic. Let {Vt} for t≥1 be the HEWMA2 sequence, then the HEWMA2 chart statistic is Vt, and it can be defined by

where Zt is the HHW2 plotting statistic defined by Eq. (7). The starting values of Vt is equal to Z0 defined by Eq. (8). The expected value for the statistic Vt is E(Vt)=μT and its variance is given as

Var(Vt)=(λ1λ2λ1−λ2)×[∑k=12(1−λk)2{1−(1−λk)2t}1−(1−λk)2−2(1−λ1)(1−λ2){1−(1−λ1)t(1−λ2)t}1−(1−λ1)(1−λ2)]σT2. (25)

UCLt(HEWMA2)=μT+L(HEWMA2)×(λ1λ2λ1−λ2)[∑k=12(1−λk)2{1−(1−λk)2t}1−(1−λk)2−2(1−λ1)(1−λ2){1−(1−λ1)t(1−λ2)t}1−(1−λ1)(1−λ2)]σTLCLt(HEWMA2)=μT−L(HEWMA2)×(λ1λ2λ1−λ2)[∑k=12(1−λk)2{1−(1−λk)2t}1−(1−λk)2−2(1−λ1)(1−λ2){1−(1−λ1)t(1−λ2)t}1−(1−λ1)(1−λ2)]σT}. (26)

The control limits defined in Eq. (26) are known as the two-sided time-dependent control limits; however, in the case of large t values, the two-sided fixed HEWMA2 control limits are defined as

UCL(HEWMA2)=μT+L(HEWMA2)(λ1λ2λ1−λ2)[∑k=12(1−λk)21−(1−λk)2−2(1−λ1)(1−λ2)1−(1−λ1)(1−λ2)]σTLCL(HEWMA2)=μT−L(HEWMA2)(λ1λ2λ1−λ2)[∑k=12(1−λk)21−(1−λk)2−2(1−λ1)(1−λ2)1−(1−λ1)(1−λ2)]σT}. (27)

In this case, The HEWMA2 chart triggers OOC signals whenever Vt≥UCL(HEWMA2) or Vt≤LCL(HEWMA2). The control limits specified in Eq. (27) are the two-sided control limits; however, the HEWMA2 upper control limit is defined as

UCL(HEWMA2)+=μT+LHEWMA2+(λ1λ2λ1−λ2)[∑k=12(1−λk)21−(1−λk)2−2(1−λ1)(1−λ2)1−(1−λ1)(1−λ2)]σT. (28)

The LHAEWMA2+ is known as the chart constants. The HEWMA2 chart detects OOC signals with increasing shift whenever Vt≥UCL(HAEWMA2)+.

This section defines the performance evaluation measures, such as average run length in Subsection 4.1 and overall performance measures in Subsection 4.2. Similarly, the simulation study for the proposed HEWMA1 and HEWMA2 charts is designed in Subsection 4.3. Likewise, Subsection 4.4 provides the choices design parameters for the proposed HEWMA1 and HEWMA2 charts.

The most popular and commonly used performance evaluation measures are the ARL and SDRL measures. The ARL can be defined as the average number of sample points until a chart indicates the OOC signal [2]. The ARL is further categorized as IC ARL (ARL0), and OOC ARL (ARL1). When a process is working in an IC state, the ARL0 should be as large enough to prevent the frequent false alarms, while the ARL1 should be smaller so that the shift is detected quickly [39]. A chart with smaller ARL1 is preferred over the competing charts at a prespecified ARL0 [40].

The ARL and SDRL measures evaluate the performance of the charts on a single specified shift. However, sometimes the researcher may want to investigate the charts performances for the entire range of shifts, i.e., δmin<δ<δmax. For this purpose, the other performance measures, such as extra quadratic loss (EQL), relative average run length (RARL), and performance comparison index (PCI), are used. The details on the EQL, RARL, and PCI measures are provided in the following subsections.

The EQL can be considered as a weighted average of ARL defined over the range of shifts δmin to δmax, using δ2 as a weight. Symbolically, the EQL can be defined as

where ARL(δ) is the ARL at specific shift δ and δmin and δmax are the minimum and maximum shift values, respectively. A chart with a low EQL value is considered to have a better overall detection ability [41].

Like the EQL measure, the RARL also evaluates the overall performance of the charts. The RARL mathematically can be defined as

where ARLbenchmark(δ) is the ARL value for benchmark chart at shift δ. A chart with a smaller ARL at specific δ is known as a benchmark chart. The RARL value for the benchmark chart is always equal to 1. The benchmark chart is considered superior to the competing chart if RARL>1 [42].

The PCI also assesses the overall performance of the best chart. Ou et al. [43] defined the PCI as a ratio of EQL of the best chart to the EQL of the benchmark chart. Mathematically, it can be given by the expression given as

The PCI value for the benchmark chart is equal to be 1, and for the rest of the charts, PCI>1 [44].

The random sample of size n, i.e., X1t,X2t,…,Xit,…,Xnt for t>1, is generated from a normal distribution under different parameter settings. Domangue et al. [15] suggested that monitoring a gradual rise (process deterioration) in the process variance is more important; therefore, an upward shift is considered in the process variance. The shift is reflected in the process standard deviation, i.e., σ=δσ0, where δ= 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9 and 2.0. The Monte Carlo simulation approach is utilized as a computational methodology for the numerical results by designing an algorithm in the statistical package R. At each shift size δ, the simulations are performed with 20,000 replicates. The simulation algorithm for the HEWMA1 and HEWMA2 charts include the following steps:

i) Specify sample size n, smoothing parameters (λ1,λ2) and parameters of the process distribution, i.e., for IC process N(μ0,σ02) and for OOC process N(μ0,(δσ0)2), where δ=σσ0.

ii) Generate random observations X1t,X2t,…,Xnt for t=1,2,… from N(μ0,σ02).

iv) Using Wt from Tt, compute the EWMA statistics, Qt and Zt in Eqs. (4) and (7), respectively.

v) Using Qt and Zt, compute the HEWMA1 statistic Ut+ and HEWMA2 statistic Vt in Eqs. (19) and (24), respectively.

vi) Selected LHEWMA1+ and LHEWMA2+ for desired ARL0 and compute UCL(HEWMA1)+ and UCL(HEWMA2)+ in Eqs. (20) and (28), respectively.

vii) Plot the statistic Ut+ against the UCL(HEWMA1)+ and the statistic Vt against the UCL(HEWMA2)+. If Ut+≥UCL(HEWMA1)+ and Vt≥UCL(HEWMA2)+ then record sequence order called the run length for the HEWMA1 and HEWMA2 charts, respectively.

viii) Repeat Steps (ii)–(vii) m=105 times and record run lengths and hence compute the approximate ARL by ARL=∑j=1mRLjm and approximate SDRL by SDRL=∑j=1m(RLj−ARL)2m−1.

ix) For ARL1 values generate random observations Xit,X2t,…,Xnt for t=1,2,…from N(μ0,(δσ0)2) and repeat the Steps (iii)–(viii).

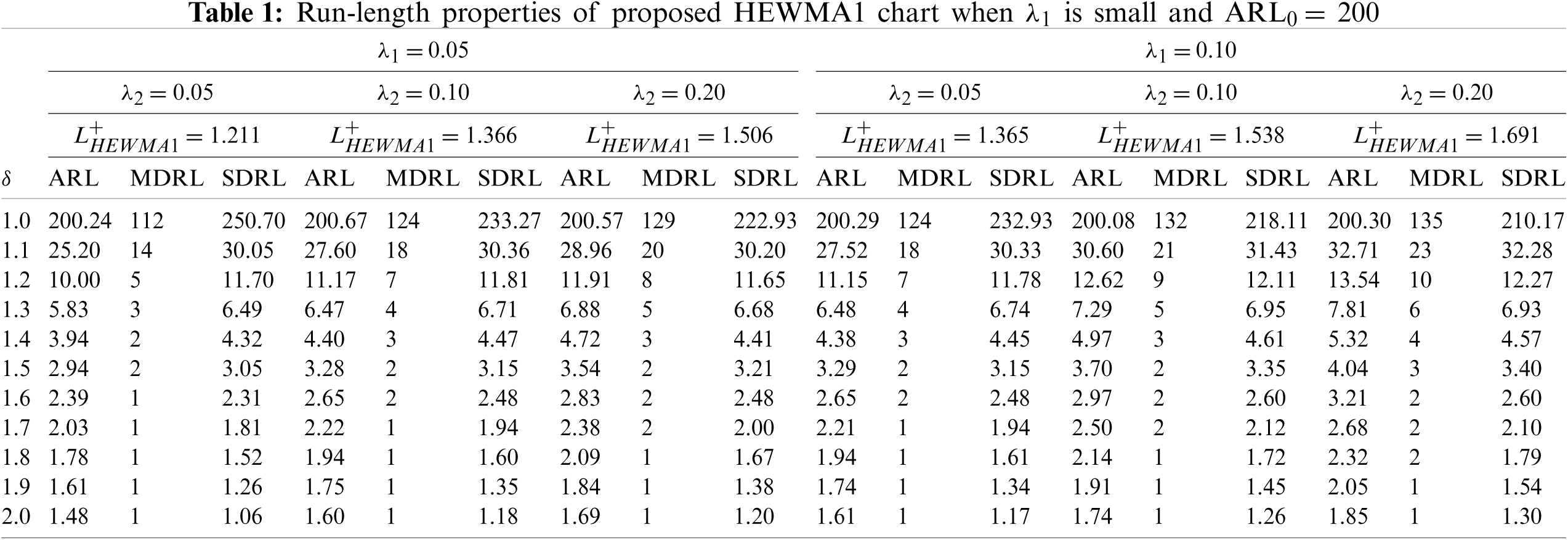
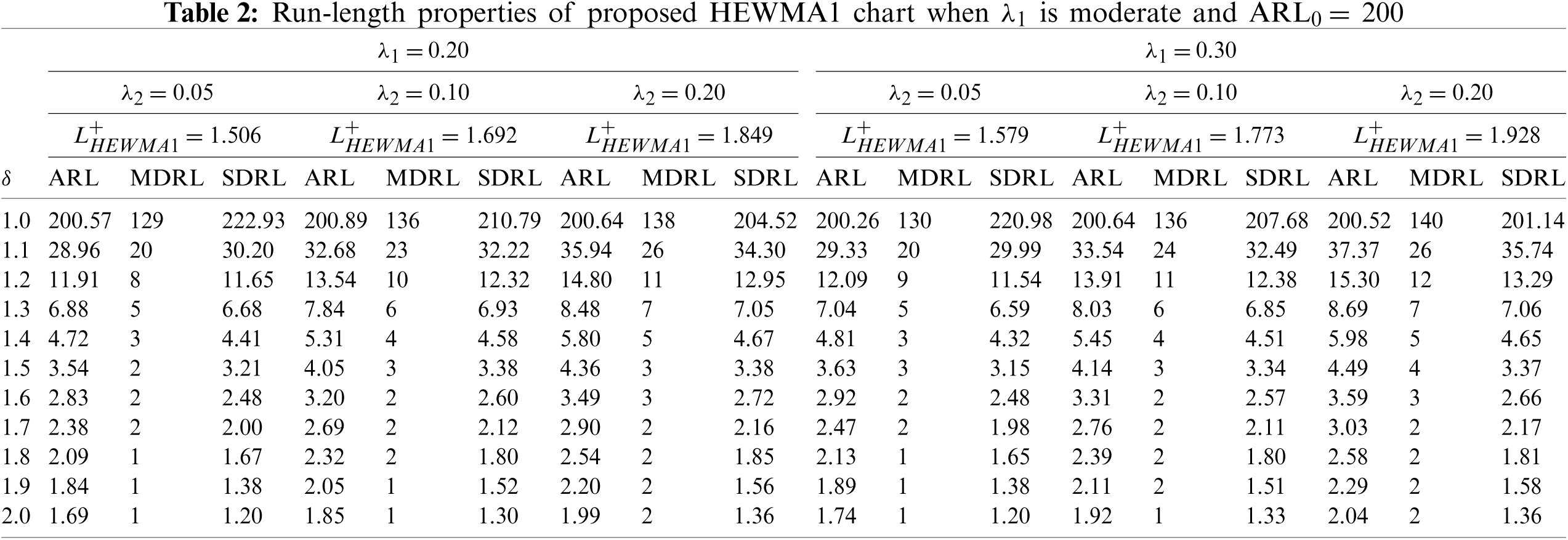
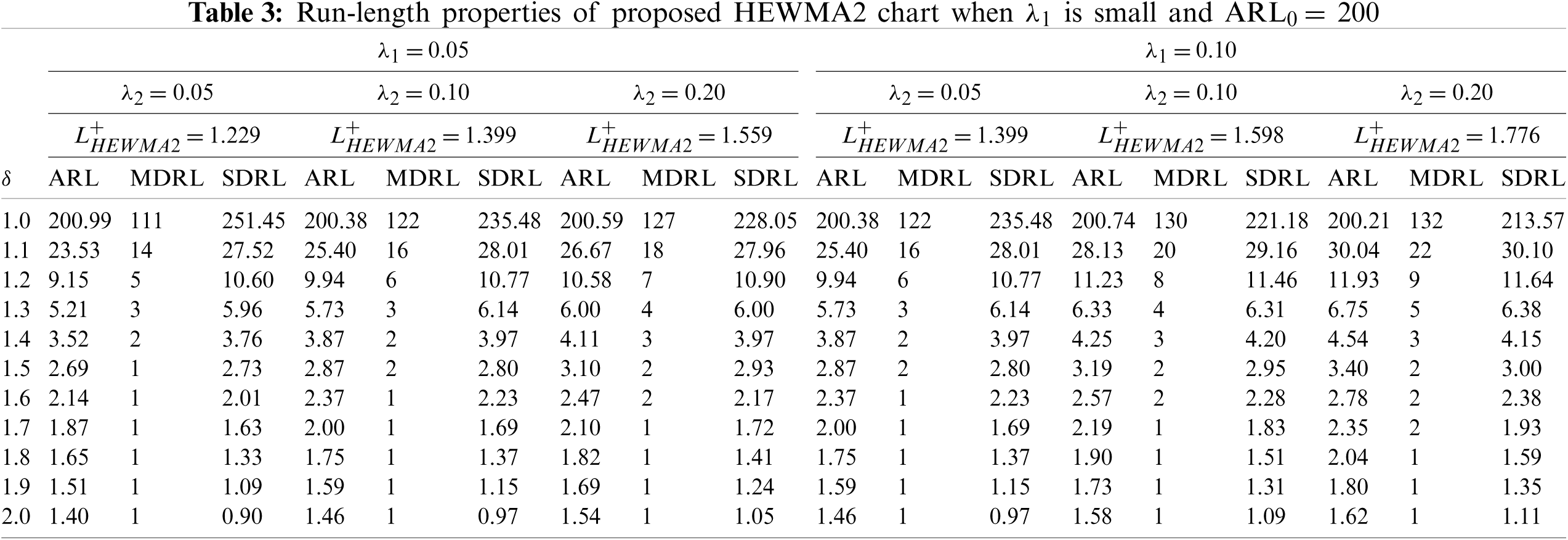
The design parameters for the proposed HEWMA1 and HEWMA2 charts are the smoothing constants λ1, λ2 and the chart width coefficient Lproposed, which have a certain effect on the chart performance. Therefore, the different settings of the design parameters are used in computing ARL, MDRL and SDRL measures. The various combination of smoothing parameters are chosen as (λ1= 0.05, λ2=0.050001,0.1, 0.20), (λ1= 0.1, λ2=0.05,0.100001, 0.20), (λ1= 0.2, λ2=0.05,0.1, 0.200001), (λ1= 0.3, λ2=0.05,0.1, 0.2) to determine the values of LHEWMA1+and LHEWMA2+, so that ARL0=200. The numerical results regarding the proposed HEWMA1 and HEWMA2 charts are displayed in Tables 1–4.

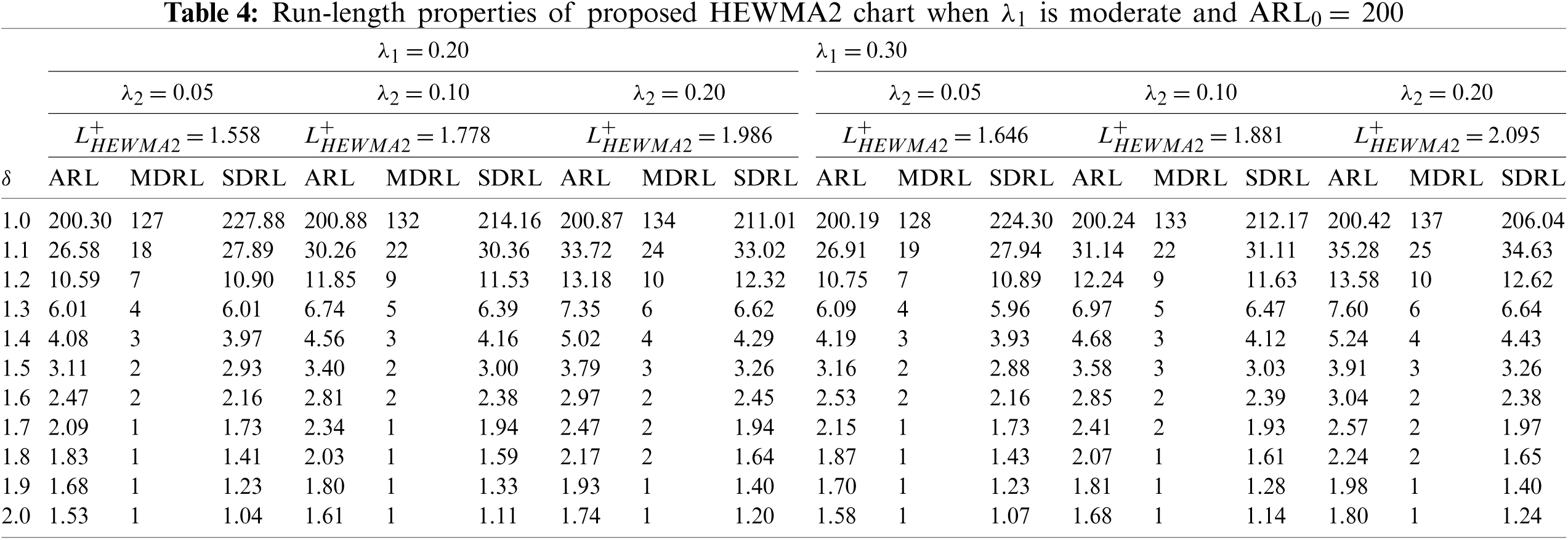
This section addresses the detailed comparative study of the proposed charts to the existing charts. The ARL values in Tables 1–4 reveal that the HEWMA2 chart outperforms the HEWMA1 chart; therefore, the HEWMA2 chart is recommended to compare with the existing charts for better detection performance. Thus the HEWMA2 charts is compared against the existing CH [16], CEWMA [19], HEWMA [23], AEWMA [45], AIBEWMA1, and AIBEWMA2 [22] charts. Table 5 presents the ARL values for comparison, while Table 6 contains the overall performance values. The following Subsections offer further details about the comparisons.

The proposed HEWMA2 chart achieves better performance against the CH chart. For example, at ARL0=200, with λ1=0.1, 0.2, λ2=0.05 and δ=1.1, the proposed HEWMA2 charts provide the ARL1 values 25.40 and 26.91, respectively, whereas the CH chart produces the ARL1= 44.26, 46.63, respectively (see Table 5 & Fig. 1). Similarly, the proposed HEWMA2 chart indicates improved overall performance against the CH chart. As for λ1=0.1 and λ2=0.05 the EQL, PCI, and RARL values of the proposed HEWMA2 charts are 19.5141, 1.0000, and 1.0000, which are less than the EQL, PCI, and RARL values of the CH chart; 27.7505, 1.4221, and 1.8851 (see Table 6).

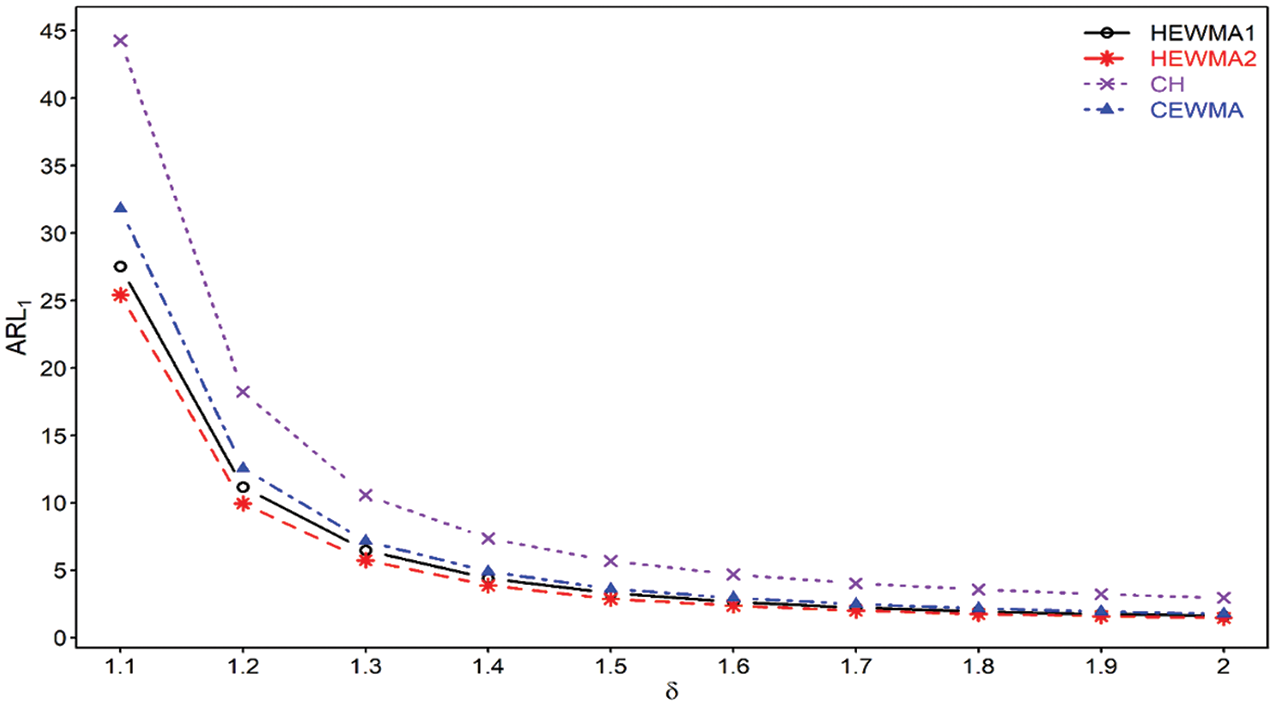
Figure 1: Comparison of proposed HEWMA1 and HEWMA2 charts with CH and CEWMA charts at (λ1,λ2)=0.1 and ARL0=200

The proposed HEWMA2 chart shows lower ARL1 values when it is compared to the CEWMA chart. For instance, assuming ARL0=200, with λ1=0.1, 0.2, λ2=0.05 and δ=1.1 the proposed HEWMA2 chart has ARL1 values of 25.40 and 26.91, respectively, whereas the CEWMA chart owns the ARL1 values of 31.80 and 37.80 (see Table 5 & Fig. 1). Similarly, in terms of overall performance (see Table 6), the proposed HEWMA2 charts attained smaller the EQL, PCI, and RARL values, i.e., 20.1797, 1.0000, and 1.0000 against the CEWMA chart the EQL, PCI, and RARL values, i.e., 23.5747, 1.1682, and 1.2818, respectively, when λ1= 0.2, and λ2=0.05.

The proposed HEWMA2 chart achieves superior performance over the HEWMA chart. For instance, at ARL0=200, λ1=0.1, λ2=0.05 and δ=1.2,1.3,1.4,1.5 the proposed HEWMA2 chart gives the ARL1 values 9.94, 5.73, 3.87, 2.87, whereas the HEWMA chart yields the ARL1= 10.11, 5.75, 3.92, 2.96 (see Table 5 & Fig. 2). Similarly, the proposed HEWMA2 chart indicates improved overall performance against the HEWMA chart. For example, the proposed charts deliver the EQL, PCI, and RARL values as 19.5141, 1.0000, 1.0000, respectively; however, the HEWMA chart provides the EQL, PCI, and RARL values as 20.6981, 1.0607, and 1.1126, respectively (see Table 6).

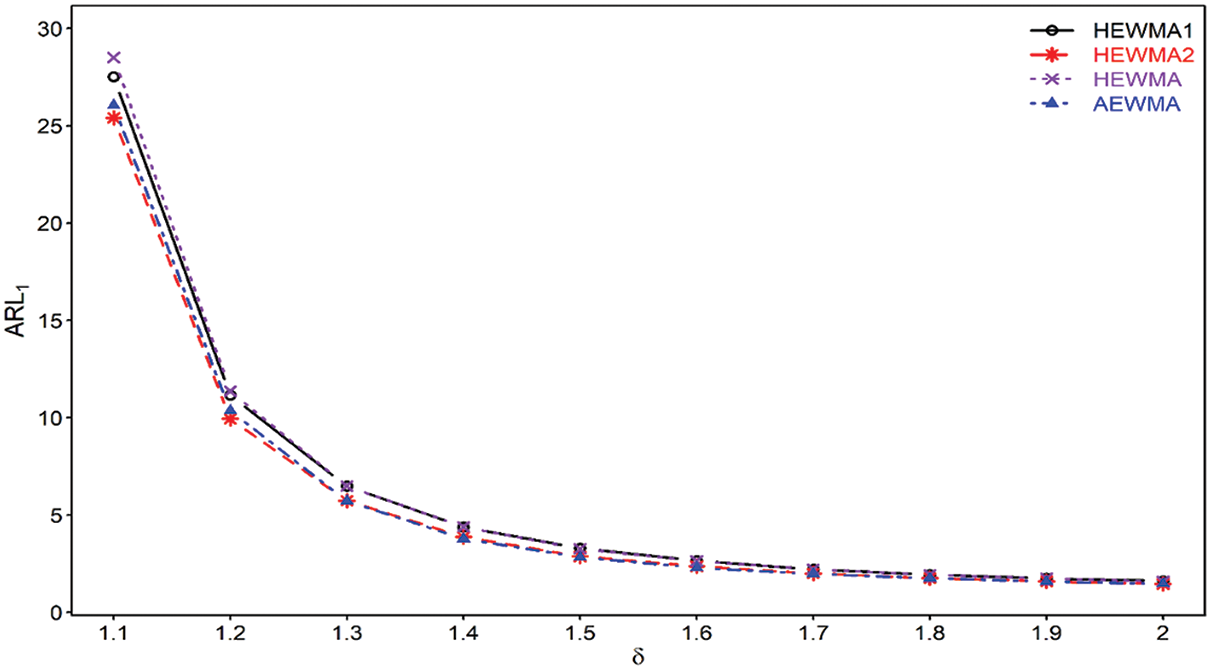
Figure 2: Comparison of proposed HEWMA1 and HEWMA2 charts with HEWMA and AEWMA charts at (λ1,λ2)=0.1 and ARL0=200

Haq [45] developed the adaptive EWMA (AEWMA) chart for monitoring the process variance. The proposed HEWMA2 chart is compared to the AEWMA chart at ARL0=200, and the results indicate that the proposed HEWMA1 and HEWMA2 chart has better detection ability against the AEWMA chart for the small shift, i.e., 1<δ≤1.2. For instance, with ARL0=200, λ1=0.1, λ2=0.05 and δ=1.1,1.2, the proposed HEWMA-2 charts deliver the ARL1 values as 25.40, 9.94, while the AEWMA chart has the ARL1 values equal to 26.04, 10.35 (see Table 5 & Fig. 2). Likewise, when λ1=0.2 and λ2=0.05, the overall performance of the proposed HEWMA2 chart is superior to the AEWMA chart as the proposed chart has a smaller EQL=20.1797 than the AEWMA chart EQL=20.3854 (see Table 6).

Haq [22] proposed the AIBEWMA1 and AIBEWMA2 charts for monitoring the process variance. The comparison of the HEWMA2 chart against the AIBEWMA1 and AIBEWMA2 charts demonstrates that the proposed HEWMA2 chart is more efficient than the AIBEWMA1 and AIBEWMA2 charts. For example, with chart properties, i.e., ARL0=200, λ1=0.1, λ2=0.05, ρ=0.5 and δ=1.1 the ARL1 values for the proposed HEWMA2 charts is observed as 25.40, while the ARL1 values for the AIBEWMA1 and AIBEWMA2 charts are reported as 30.11 and 30.79 (see Table 5 & Fig. 3). Likewise, the proposed charts' EQL, PCI, and RARL values also show the edge in the overall detection ability of the HEWMA2 chart over the AIBEWMA1 and AIBEWMA2 charts. As the EQL, PCI, and RARL values for the proposed HEWMA2 charts are 19.5141, 1.0000, and 1.0000, respectively, where EQL, PCI, and RARL values for the AIBEWMA1 and AIBEWMA2 charts are 20.8605, 1.0690 and 1.1185, and 21.4587, 1.0996 and 1.1919, respectively (see Table 6).

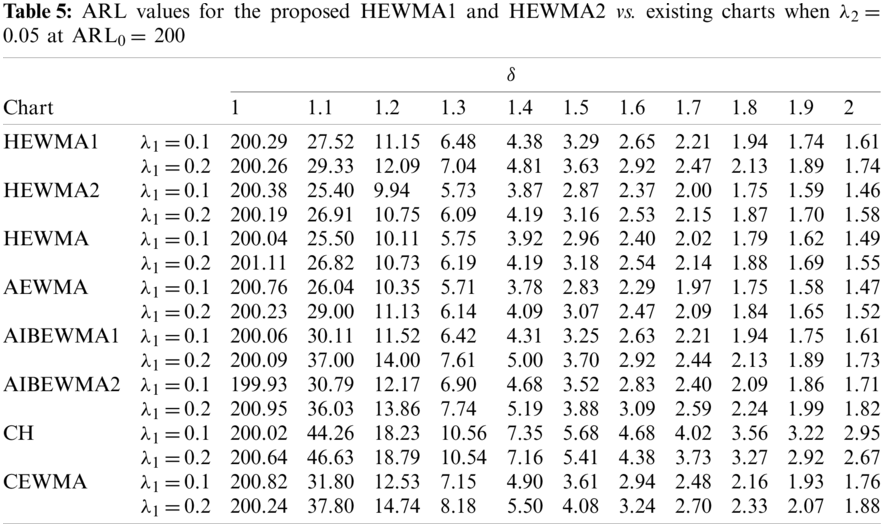
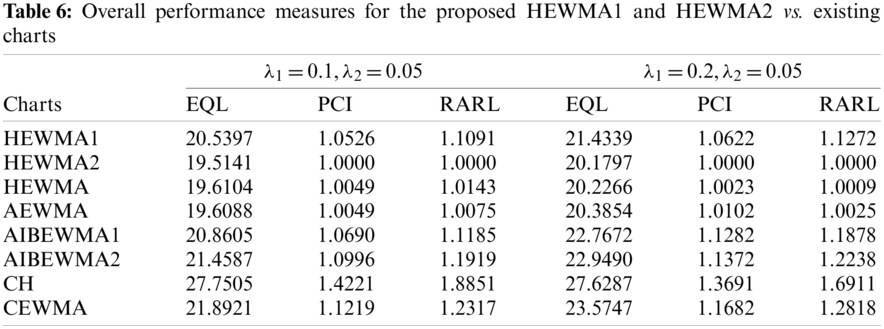
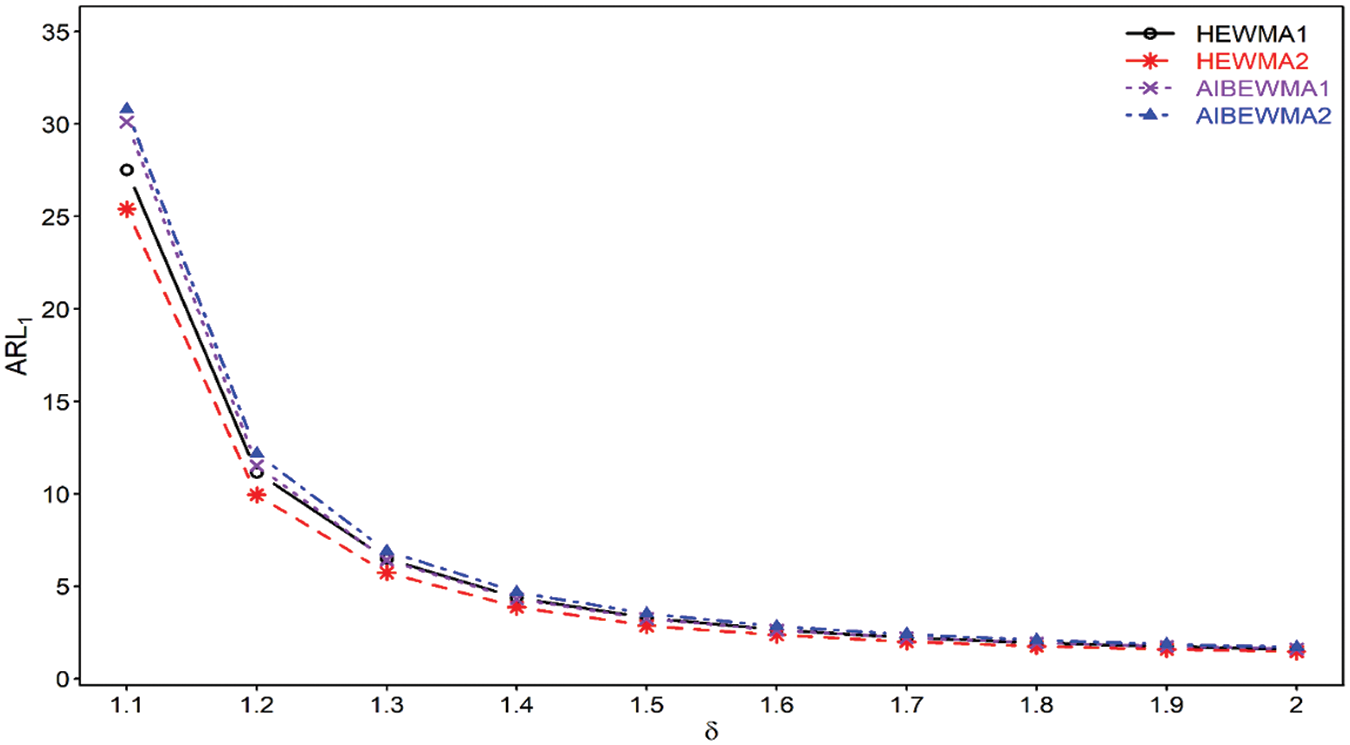
Figure 3: Comparison of proposed HEWMA1 and HEWMA2 charts with AIBEWMA1 and AIBEWMA2 charts at (λ1,λ2)=0.1 and ARL0=200

A few important points related to the HEWMA1 and HEWMA2 charts can be listed as:

i) The HEWMA statistics undoubtedly boost the efficiency of the proposed HEWMA1 and HEWMA2 charts.

ii) The proposed HEWMA2 chart has better detection performance than the proposed HEWMA1 chart (see Tables 1–4).

iii) At different parametric settings, the ARL1 values for the proposed HEWMA1 and HEWMA2 charts are less than the ARL1 values of the CH, CEWMA, HEWMA, AEWMA, AIBEWMA1, and AIBEWMA2 charts (see Section 5).

iv) The overall performance reveals the dominance of HEWMA1 and HEWMA2 charts over the CH, CEWMA, HEWMA, AEWMA, AIBEWMA1, and AIBEWMA2 charts (see Section 5).

v) The proposed HEWMA1 and HEWMA2 charts have better ARL1 performance for smaller λ1 and λ2 (see Tables 1–4).

vi) The control limit coefficient L for the suggested HEWMA1 and HEWMA2 charts increases as λ1 and λ2 increases.

This subsection explains the application of the proposed HEWMA1 and HEWMA2 charts to real-life data. For this purpose, the real-life data are considered, representing the inside diameter of the cylinder bores in an engine block. These real-life data are used by [46,47] in their studies. The data comprise 30 samples, each size n=5 given in Table 7. In order to implement the proposed HEWMA1 and HEWMA2 control along with CH and CEWMA charts, following [23,48], an upward shift of size δ=1.25 is introduced artificially after sample number 16 [49,50]. At ARL0=200, the smoothing parameter values λ1=0.1, λ2=0.05 are used, which provides the width of the the HEWMA1, and HEWMA2, CH and CEWMA charts, respectively, given as LHEWMA1+= 1.365, LHEWMA2+=1.399, LCH+= 1.303 and LCEWMA+=2.198. Using the aforementioned parameters, the charting statistics for the HEWMA1, and HEWMA2, CH and CEWMA charts and their corresponding upper control limits are computed. The charting statistics for HEWMA1, and HEWMA2, CH and CEWMA charts are given in Table 7, while their corresponding upper control limits are given as 0.1528, 0.1314, 0.2547, and 0.4876, respectively. Figs. 4–7 display the charting statistics of the CH, CEWMA, HEWMA1, and HEWMA2 charts against sample number. The results show that the proposed HEWMA1 chart outperforms the CH chart as the proposed HEWMA1 chart trigger the first OOC point after sample number 25, while the CH chart detects OOC point after sample number 28. Overall, the proposed HEWMA1 chart declares 7 OOC points, while the CH chart detects 2 OOC signals. Similarly, the HEWMA2 chart gains better detection ability relative to the CEWMA chart, as as the proposed HEWMA2 chart identifies the first OOC signal at sample number 26, while the CH chart diagnoses OOC signal at sample number 29. This indicates that the proposed HEWMA1 is more efficient than the CH chart, and the HEWMA2 chart achieves better detection ability than the CHWMA chart.

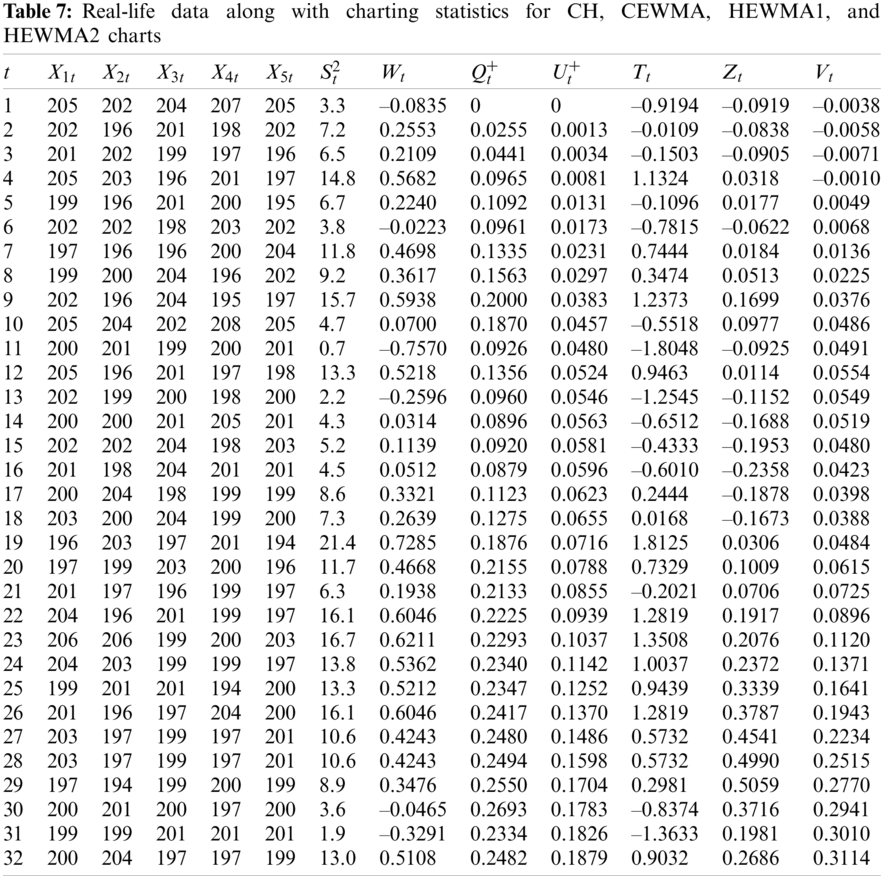
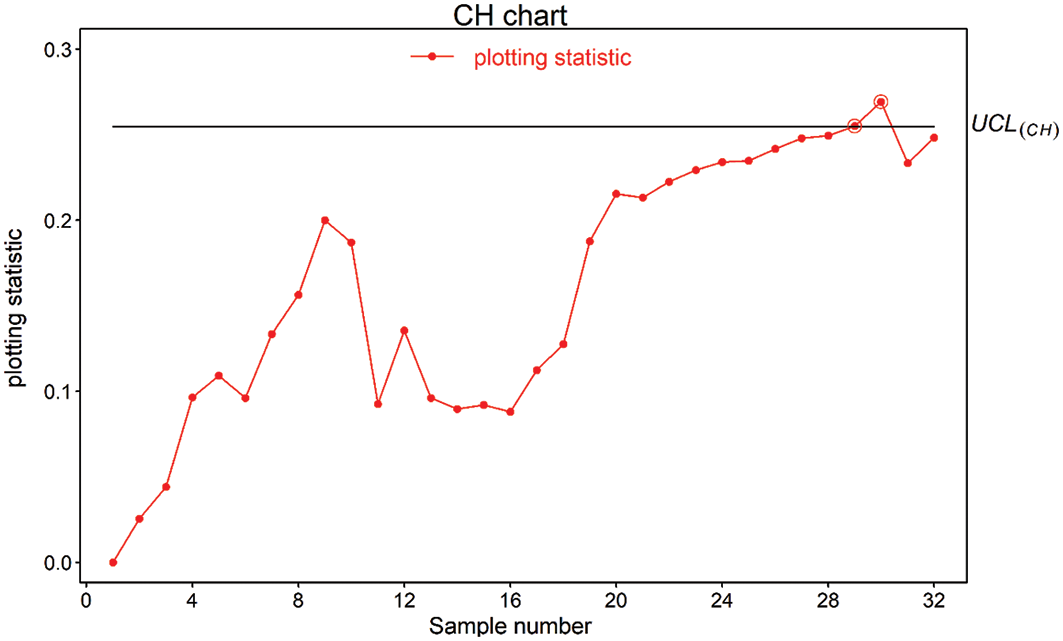
Figure 4: Real-life application of CH chart using (λ1,λ2)=(0.1,0.05) and ARL0=200

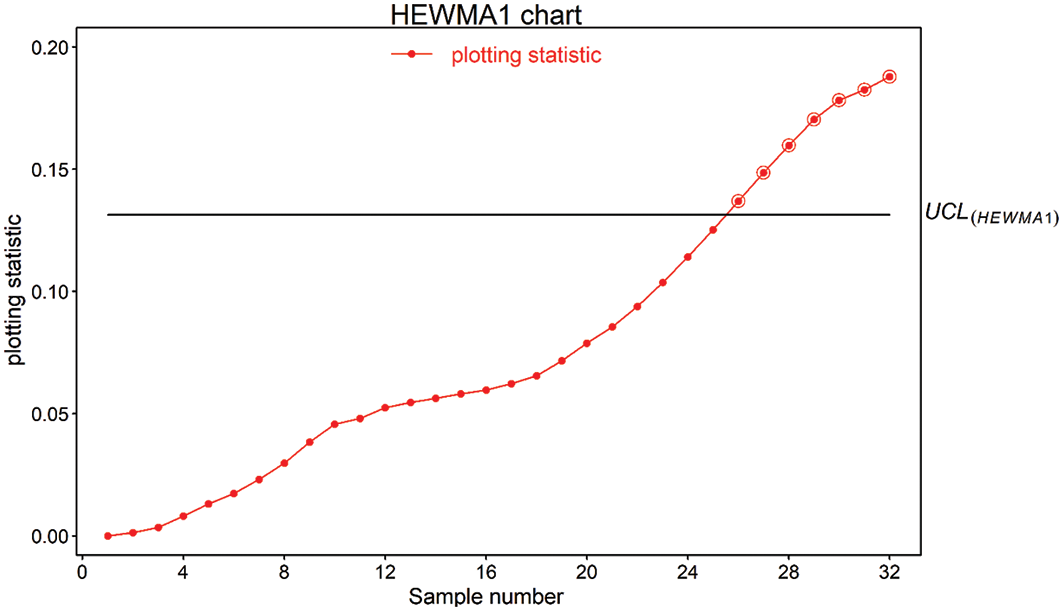
Figure 5: Real-life application of proposed HEWMA1 chart using (λ1,λ2)=(0.1,0.05) and ARL0=200

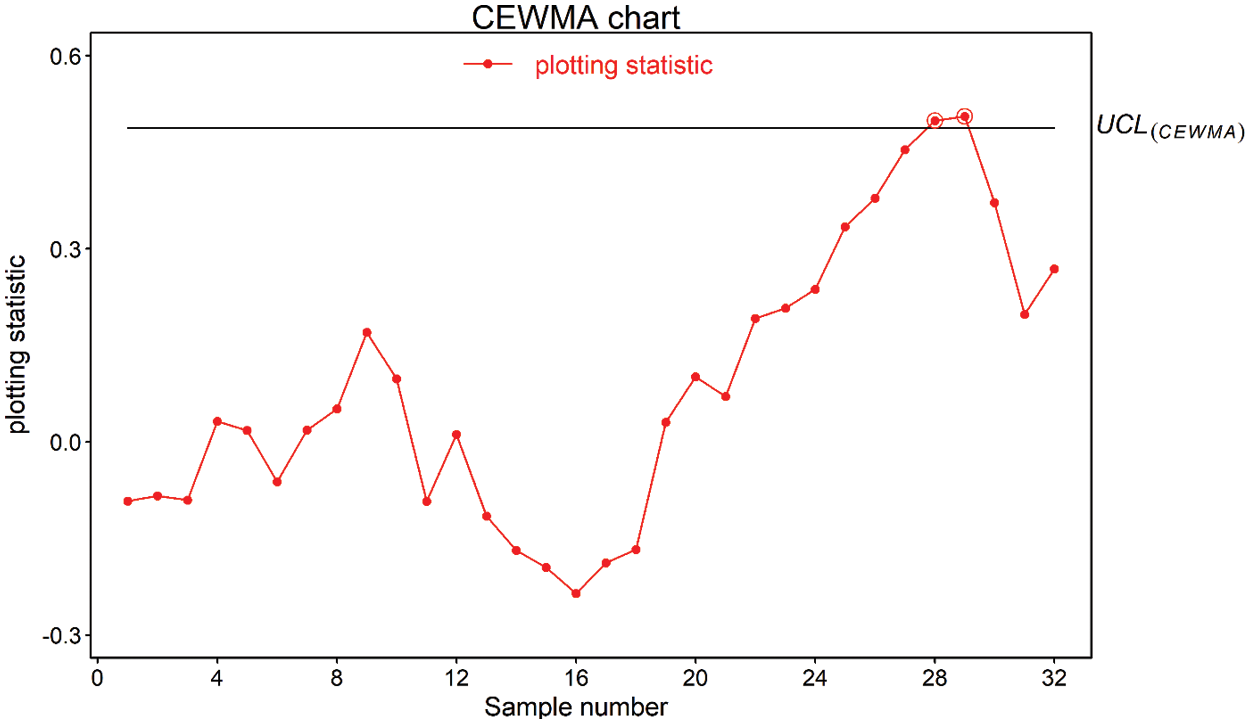
Figure 6: Real-life application of CEWMA chart using (λ1,λ2)=(0.1,0.05) and ARL0=200

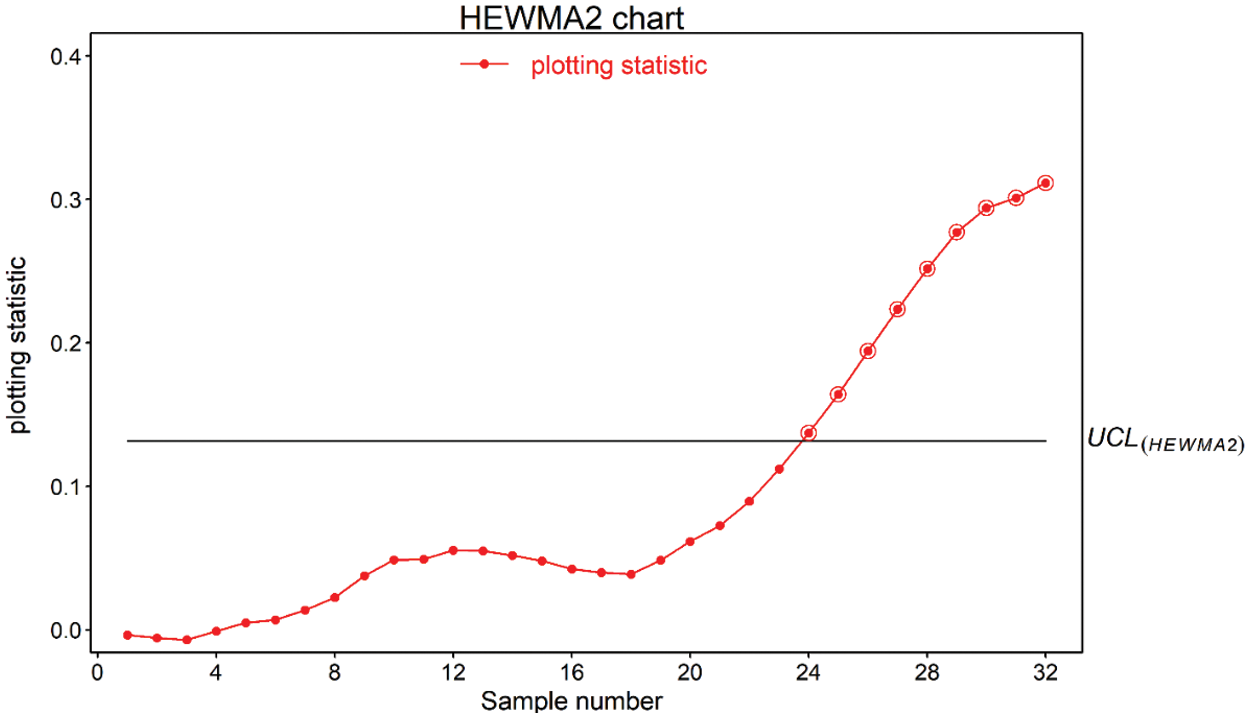
Figure 7: Real-life application of proposed HEWMA2 chart using (λ1,λ2)=(0.1,0.05) and ARL0=200

This paper proposes two new hybrid EWMA charts to monitor the shifts in the process variance. The proposed charts are called HEWMA1 and HEWMA2 charts. The HEWMA1 chart is designed using the CH statistic as the input for the HEWMA1 statistic, while in the same lines, CEWMA statistic is used as the input for the HEWMA2 statistic to construct the proposed HEWMA2 chart. In order to evaluate the performance of the proposed HEWMA1 and HEWMA2 charts, the extensive Monte Carlo simulation approach is used to approximate the run length properties, including the average run length and standard deviation run length. Similarly, to assess the overall performances of the proposed HEWMA1 and HEWMA2 charts, the extra quadratic loss, relative average run length, and performance comparison index are computed. The proposed HEWMA1 and HEWMA2 charts are compared to existing CH, CEWMA, HEWMA, AEWMA, HHW1, HHW2, AIBEWMA1, and AIBEWMA2 charts, and the comparison indicates that the proposed HEWMA1 and HEWMA2 charts outperform the existing charts. In the end, real-life data are analyzed to enhance the efficiency of the proposed HEWMA1 and HEWMA2 charts.

Funding Statement: 2019 Shanxi Province Soft Science Research Program Project ``Research on Sustainable Development Capacity and Classification Construction of Shanxi Development Zone'' (Project No. 2019041005-2).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Ajadi, J. O., Riaz, M., Al-Ghamdi, K. (2016). On increasing the sensitivity of mixed EWMA-CUSUM control charts for location parameter. Journal of Applied Statistics, 43(7), 1262–1278. DOI 10.1080/02664763.2015.1094453. [Google Scholar] [CrossRef]

2. Montgomery, D. C. (2012). Introduction to statistical quality control. New York: John Willey & Sons. [Google Scholar]

3. Roberts, S. (1959). Control chart tests based on geometric moving averages. Technometrics, 1(3), 239–250. DOI 10.1080/00401706.1959.10489860. [Google Scholar] [CrossRef]

4. Hunter, J. S. (1986). The exponentially weighted moving average. Journal of Quality Technology, 18(4), 203–210. DOI 10.1080/00224065.1986.11979014. [Google Scholar] [CrossRef]

5. Crowder, S. V. (1987). A simple method for studying run-length distributions of exponentially weighted moving average charts. Technometrics, 29(4), 401–407. DOI 10.2307/1269450. [Google Scholar] [CrossRef]

6. Crowder, S. V. (1989). Design of exponentially weighted moving average schemes. Journal of Quality Technology, 21(3), 155–162. DOI 10.1080/00224065.1989.11979164. [Google Scholar] [CrossRef]

7. Lucas, J. M., Saccucci, M. S. (1990). Exponentially weighted moving average control schemes—Properties and enhancements. Technometrics, 32(1), 1–12. DOI 10.1080/00401706.1990.10484583. [Google Scholar] [CrossRef]

8. Haq, A. (2013). A new hybrid exponentially weighted moving average control chart for monitoring process mean. Quality and Reliability Engineering International, 29(7), 1015–1025. DOI 10.1002/qre.1453. [Google Scholar] [CrossRef]

9. Abbas, N., Riaz, M., Does, R. J. (2014). Memory-type control charts for monitoring the process dispersion. Quality and Reliability Engineering International, 30(5), 623–632. DOI 10.1002/qre.1514. [Google Scholar] [CrossRef]

10. Ali, R., Haq, A. (2018). A mixed GWMA-CUSUM control chart for monitoring the process mean. Communications in Statistics—Theory and Methods, 47(15), 3779–3801. DOI 10.1080/03610926.2017.1361994. [Google Scholar] [CrossRef]

11. Tang, A., Sun, J., Hu, X., Castagliola, P. (2019). A new nonparametric adaptive EWMA control chart with exact run length properties. Computers & Industrial Engineering, 130(3), 404–419. DOI 10.1016/j.cie.2019.02.045. [Google Scholar] [CrossRef]

12. Haq, A. (2019). A new nonparametric synthetic EWMA control chart for monitoring process mean. Communications in Statistics—Simulation and Computation, 48(6), 1665–1676. DOI 10.1080/03610918.2017.1422750. [Google Scholar] [CrossRef]

13. Rasheed, Z., Zhang, H., Anwar, S. M., Zaman, B. (2021). Homogeneously mixed memory charts with application in the substrate production process. Mathematical Problems in Engineering, 2021, 1–15. DOI 10.1155/2021/2582210. [Google Scholar] [CrossRef]

14. Rasheed, Z., Zhang, H., Arslan, M., Zaman, B., Anwar, S. M. et al. (2021). An efficient robust nonparametric triple EWMA Wilcoxon signed-rank control chart for process location. Mathematical Problems in Engineering, 2021(4), 1–28. DOI 10.1155/2021/2570198. [Google Scholar] [CrossRef]

15. Domangue, R., Patch, S. C. (1991). Some omnibus exponentially weighted moving average statistical process monitoring schemes. Technometrics, 33(3), 299–313. DOI 10.1080/00401706.1991.10484836. [Google Scholar] [CrossRef]

16. Crowder, S. V., Hamilton, M. D. (1992). An EWMA for monitoring a process standard deviation. Journal of Quality Technology, 24(1), 12–21. DOI 10.1080/00224065.1992.11979369. [Google Scholar] [CrossRef]

17. Shu, L., Jiang, W. (2008). A new EWMA chart for monitoring process dispersion. Journal of Quality Technology, 40(3), 319–331. DOI 10.1080/00224065.2008.11917737. [Google Scholar] [CrossRef]

18. Huwang, L., Huang, C. J., Wang, Y. H. T. (2010). New EWMA control charts for monitoring process dispersion. Computational Statistics & Data Analysis, 54(10), 2328–2342. DOI 10.1016/j.csda.2010.03.011. [Google Scholar] [CrossRef]

19. Castagliola, P. (2005). A new S2-EWMA control chart for monitoring the process variance. Quality and Reliability Engineering International, 21(8), 781–794. DOI 10.1002/(ISSN)1099-1638. [Google Scholar] [CrossRef]

20. Chang, T. C., Gan, F. F. (1994). Optimal designs of one-sided EWMA charts for monitoring a process variance. Journal of Statistical Computation and Simulation, 49(1--2), 33–48. DOI 10.1080/00949659408811559. [Google Scholar] [CrossRef]

21. Razmy, A. M., Peiris, T. S. G. (2015). Design of exponentially weighted moving average chart for monitoring standardized process variance. International Journal of Engineering & Technology, 13(5), 74–78. [Google Scholar]

22. Haq, A. (2017). New EWMA control charts for monitoring process dispersion using auxiliary information. Quality and Reliability Engineering International, 33(8), 2597–2614. DOI 10.1002/qre.2220. [Google Scholar] [CrossRef]

23. Ali, R., Haq, A. (2017). New memory-type dispersion control charts. Quality and Reliability Engineering International, 33(8), 2131–2149. DOI 10.1002/qre.2174. [Google Scholar] [CrossRef]

24. Saghir, A., Aslam, M., Faraz, A., Ahmad, L., Heuchenne, C. (2020). Monitoring process variation using modified EWMA. Quality and Reliability Engineering International, 36(1), 328–339. DOI 10.1002/qre.2576. [Google Scholar] [CrossRef]

25. Zaman, B., Lee, M. H., Riaz, M., Abujiya, M. R. (2019). An adaptive approach to EWMA dispersion chart using Huber and Tukey functions. Quality and Reliability Engineering International, 35(6), 1542–1581. DOI 10.1002/qre.2460. [Google Scholar] [CrossRef]

26. Riaz, M., Abbasi, S. A., Abid, M., Hamzat, A. K. (2020). A new HWMA dispersion control chart with an application to wind farm data. Mathematics, 8(12), 2136. DOI 10.3390/math8122136. [Google Scholar] [CrossRef]

27. Chatterjee, K., Koukouvinos, C., Lappa, A. (2020). A new S2-TEWMA control chart for monitoring process dispersion. Quality and Reliability Engineering International, 37(4), 1334–1354. DOI 10.1002/qre.2798. [Google Scholar] [CrossRef]

28. Haq, A. (2016). A new hybrid exponentially weighted moving average control chart for monitoring process mean: Discussion. Quality and Reliability Engineering International, 33(7), 1629–1631. DOI 10.1002/qre.2092. [Google Scholar] [CrossRef]

29. Aslam, M., Azam, M., Khan, N., Jun, C. H. (2015). A control chart for an exponential distribution using multiple dependent state sampling. Quality & Quantity, 49(2), 455–462. DOI 10.1007/s11135-014-0002-2. [Google Scholar] [CrossRef]

30. Aslam, M., Khan, N., Jun, C. (2016). A hybrid exponentially weighted moving average chart for COM-Poisson distribution. Transactions of the Institute of Measurement and Control, 40(2), 456–461. DOI 10.1177/0142331216659920. [Google Scholar] [CrossRef]

31. Aslam, M., Azam, M., Jun, C. H. (2018). A HEWMA-CUSUM control chart for the Weibull distribution. Communications in Statistics—Theory and Methods, 47(24), 5973–5985. DOI 10.1080/03610926.2017.1404100. [Google Scholar] [CrossRef]

32. Noor-ul-Amin, M., Khan, S., Sanaullah, A. (2019). HEWMA control chart using auxiliary information. Iranian Journal of Science and Technology, Transactions A: Science, 43(3), 891–903. DOI 10.1007/s40995-018-0585-x. [Google Scholar] [CrossRef]

33. Aslam, M., Rao, G. S., AL-Marshadi, A. H., Jun, C. H. (2019). A nonparametric HEWMA-p control chart for variance in monitoring processes. Symmetry, 11(3), 356. DOI 10.3390/sym11030356. [Google Scholar] [CrossRef]

34. Noor, S., Noor-ul-Amin, M., Mohsin, M., Ahmed, A. (2020). Hybrid exponentially weighted moving average control chart using Bayesian approach. Communications in Statistics—Theory and Methods. DOI 10.1080/03610926.2020.1805765. [Google Scholar] [CrossRef]

35. Asif, F., Khan, S., Noor-ul-Amin, M. (2020). Hybrid exponentially weighted moving average control chart with measurement error. Iranian Journal of Science and Technology, Transactions A: Science, 44(3), 801–811. DOI 10.1007/s40995-020-00879-3. [Google Scholar] [CrossRef]

36. Noor-Ul-Amin, M., Shabbir, N., Khan, N., Riaz, A. (2020). Hybrid exponentially weighted moving average control chart for mean using different ranked set sampling schemes. Kuwait Journal of Science, 47(4), 19–28. [Google Scholar]

37. Lawless, J. F. (2003). Statistical models and methods for lifetime data. New Jersey: John Wiley and Sons. [Google Scholar]

38. Quesenberry, C. P. (1995). On properties of Q charts for variables. Journal of Quality Technology, 27(3), 184–203. DOI 10.1080/00224065.1995.11979592. [Google Scholar] [CrossRef]

39. Awais, M., Haq, A. (2018). A new cumulative sum control chart for monitoring the process mean using varied L ranked set sampling. Journal of Industrial and Production Engineering, 35(2), 74–90. DOI 10.1080/21681015.2017.1417787. [Google Scholar] [CrossRef]

40. Aslam, M., Anwar, S. M. (2020). An improved Bayesian Modified-EWMA location chart and its applications in mechanical and sport industry. PLoS One, 15(2), e0229422. DOI 10.1371/journal.pone.0229422. [Google Scholar] [CrossRef]

41. Zafar, R. F., Abbas, N., Riaz, M., Hussain, Z. (2014). Progressive variance control charts for monitoring process dispersion. Communications in Statistics-Theory and Methods, 43(23), 4893–4907. DOI 10.1080/03610926.2012.717668. [Google Scholar] [CrossRef]

42. Anwar, S. M., Aslam, M., Riaz, M., Zaman, B. (2020). On mixed memory control charts based on auxiliary information for efficient process monitoring. Quality and Reliability Engineering International, 36(6), 1949–1968. DOI 10.1002/qre.2667. [Google Scholar] [CrossRef]

43. Ou, Y., Wu, Z., Tsung, F. (2012). A comparison study of effectiveness and robustness of control charts for monitoring process mean. International Journal of Production Economics, 135(1), 479–490. DOI 10.1016/j.ijpe.2011.08.026. [Google Scholar] [CrossRef]

44. Anwar, S. M., Aslam, M., Ahmad, S., Riaz, M. (2019). A modified-mxEWMA location chart for the improved process monitoring using auxiliary information and its application in wood industry. Quality Technology & Quantitative Management, 17, 561–579. [Google Scholar]

45. Haq, A. (2018). A new adaptive EWMA control chart for monitoring the process dispersion. Quality and Reliability Engineering International, 34(5), 846–857. DOI 10.1002/qre.2294. [Google Scholar] [CrossRef]

46. Zaman, B., Lee, M. H., Riaz, M., Abujiya, M. R. (2017). An adaptive EWMA scheme-based CUSUM accumulation error for efficient monitoring of process location. Quality and Reliability Engineering International, 33(8), 2463–2482. DOI 10.1002/qre.2203. [Google Scholar] [CrossRef]

47. Zaman, B. (2021). Efficient adaptive CUSUM control charts based on generalized likelihood ratio test to monitor process dispersion shift. Quality and Reliability Engineering International, 37(8), 3192–3220. DOI 10.1002/qre.2903. [Google Scholar] [CrossRef]

48. Abbas, N., Riaz, M., Does, R. J. M. M. (2013). CS-EWMA chart for monitoring process dispersion. Quality and Reliability Engineering International, 29(5), 653–663. DOI 10.1002/qre.1414. [Google Scholar] [CrossRef]

49. Anwar, S. M., Aslam, M., Zaman, B., Riaz, M. (2021). Mixed memory control chart based on auxiliary information for simultaneously monitoring of process parameters: An application in glass field. Computers & Industrial Engineering, 156(3), 107284. DOI 10.1016/j.cie.2021.107284. [Google Scholar] [CrossRef]

50. Anwar, S. M., Aslam, M., Zaman, B., Riaz, M. (2022). An enhanced double homogeneously weighted moving average control chart to monitor process location with application in automobile field. Quality and Reliability Engineering International, 38, pp. 174–194. DOI 10.1002/qre.2966. [Google Scholar] [CrossRef]