

 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.017842
ARTICLE
Design and Mechanical Characterization of an S-Based TPMS Hollow Isotropic Cellular Structure
1College of Mechanical and Power Engineering, China Three Gorges University, Yichang, 443002, China
2Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance, Yichang, 443002, China
*Corresponding Author: Yixian Du. Email: dyx@ctgu.edu.cn
Received: 10 June 2021; Accepted: 19 November 2021
Abstract: Cellular structures are regarded as excellent candidates for lightweight-design, load-bearing, and energy-absorbing applications. In this paper, a novel S-based TPMS hollow isotropic cellular structure is proposed with both superior load-bearing and energy-absorbing performances. The hollow cellular structure is designed with Boolean operation based on the Fischer-Koch (S) implicit triply periodic minimal surfaces (TPMS) with different level parameters. The anisotropy and effective elasticity properties of cellular structures are evaluated with the numerical homogenization method. The finite element method is further conducted to analyze the static mechanical performance of hollow cellular structure considering the size effect. The compression experiments are finally carried out to reveal the compression properties and energy-absorption characteristics. Numerical results of the Zener ratio proved that the S-based hollow cellular structure tends to be isotropic, even better than the sheet-based Gyroid TPMS. Compared with the solid counterpart, the S-based hollow cellular structure has a higher elastic modulus, better load-bearing and energy absorption characteristics.
Keywords: Hollow cellular structure; triply periodic minimal surfaces; isotropic property; energy absorption; load-bearing
Cellular structures are an assembly of prismatic or polyhedral cells with solid edges [1,2]. They originate from biological tissues, such as butterfly wings, stems of plants, bony structures, etc. Inspired by natural materials, various artificial cellular structures are designed, such as hexagon honeycomb structure [3,4], foam material, triply periodic minimal surfaces (TPMS) [5–7]. As novel lightweight metamaterials, cellular structures are characterized of high specific strength, high specific stiffness, and excellent energy-absorption capacity. As a result, they have a brilliant application future in the fields of vehicles, ships, aerospace, etc. Cellular structures have been applied widely mainly for two reasons. Firstly, the breakthrough in advanced manufacturing technologies, such as additive manufacturing [8,9], welding forming [10], enables the fabrication of cellular structures even with complex geometry features. Secondly, the development of design methods including the topology optimization driven design [11] and implicit or explicit parametric modeling [12,13], have enriched the configurations of cellular structures with extraordinary mechanical properties.
However, the load-bearing and energy-absorption application scenarios faced by cellular structures are more challenging and complex. For example, the direction and strength of the impact are highly uncertain in the anti-impact field, which makes a higher demand for functional characteristics, such as pressure resistance, energy-absorption capacity, and isotropic properties. Therefore, cellular structures should maintain their shape as much as possible under the smaller impact load, and absorb more energy under a larger impact load. In the anti-impact field, cellular structures are generally designed with generative topology [14,15] and functionally graded distribution [16] to improve the pressure resistance and energy-absorption ability. As the mechanical performances highly rely on the topological configuration of cellular structures, the topology optimization method is combined with the homogenization theory to design cellular structures with negative Poisson's ratio [17,18] and functional graded cellular structures [19]. It has been proved that cellular structures with negative Poisson's ratio and graded distribution possess excellent buffer and energy-absorption properties under the impact [20]. Compared with the topology optimization method, parametrized modeling method are more convenient to realize the spatial graded distribution of cellular structures. TPMS is the parametric surface cellular structures with zero mean curvature [21,22]. The linear or nonlinear functions can be introduced into the implicit mathematical function of the TPMS to generate graded cellular structures [16]. Also, functionally graded cellular structures have been proved to have both load-bearing and energy-absorption capacity [20].
Apart from the impact resistance and energy absorption characteristics, the isotropic property is also a critical factor in anti-impact protection. Isotropic cellular structures have uniform mechanical responses when subjected to external loads in any direction. It can effectively ensure the safety of protected objects under the impact with highly uncertain directions and strength. In order to obtain isotropic cellular structures, the isotropic constraints can be imposed in the topology optimization model [23,24]. Nevertheless, it is challenging to solve the model in this design method. By contrast, the design process of the hybrid design method is simpler and more efficient. In the hybrid design, the different components are combined to form novel truss-lattice [25], plate-lattice [26,27] and hybrid TPMS [28] with the isotropic property. However, the hybrid design proposed in the literature focuses on improving the isotropic stiffness. Thus, how to enable the isotropic cellular structure with both load-bearing and energy-absorption characteristics is becoming a great challenge.
The hollow design is one of the hybrid design methods. During the process of hollow design, hollow cellular structures [29] are obtained with a thin-wall feature by removing internal materials of solid counterparts. In engineering applications, the compression and energy-absorption characteristics of hollow cellular structures are the most common application scenarios. For instance, under a relative density of 0.3%–5.8%, the compression strength of the pyramid hollow cellular structure can reach 3 to 5 times over the solid cellular structure [30]. For the out-of-plane compressive strength, hollow cellular structures exceed twice their solid counterpart with an equal relative density [31]. Additionally, hollow cellular structures, with a larger specific surface area and internal compressive space, can absorb more energy under impact load [10,16]. The improved performance of hollow cellular structures highly depends on their configuration. The aperture ratio of hollow cellular structures determines their configurations. Hollow cellular structures can obtain isotropic property by adjusting the ratio [32]. However, the hollow design method only suits truss cellular structures composed of hollow tubes. The general cellular structures are difficult to obtain isotropy by the hollow design.
In this paper, we proposed an isotropic hollow cellular structure with both load-bearing and energy absorption properties. The macroscopic effective elasticity and isotropic characteristics are evaluated with the numerical homogenization method [33,34]. Finite element analysis (FEA) is conducted to analyze the load-bearing capacity. Mechanical compression experiments are also carried out to reveal its compression and energy absorption characteristics.
2 Design of the Hollow Cellular Structure
The hollow cellular structure is designed based on the Fischer-Koch (S) based TPMS with complex inner connectivity and spiral outer profile. The S-based TPMS representative volume element is firstly generated with a three-dimensional implicit level set function [5] F (x, y, z), which is defined in Eq. (1). The level parameter t is introduced into Eq. (1) so that the S-based TPMS can be adjusted with varying relative densities.
where x, y, z is the physical coordinate in the high-dimensional space, Ls is the unit cell size. The level parameter t is limited to −18.1 ≤ t ≤ 10.1, which corresponds to the relative density from 1 to 0.
According to the definition of the level set function, the solid, boundary and void area of TPMS are defined by the following function:
where Ω is the surface entity, ∂Ω is the surface boundary, D is the space containing the solid area and surface boundary. The S-based solid cellular structure generated from the 4D level set function is shown in Fig. 1.
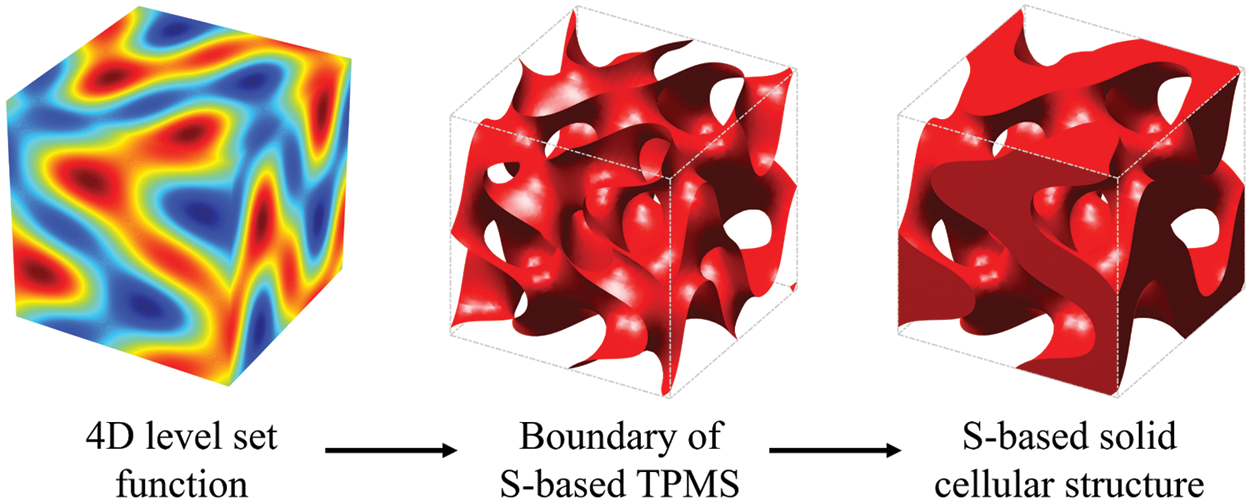
Figure 1: The implicit modeling of the S-based solid cellular structure
In Fig. 2, in order to generate the S-based hollow cellular structure, two S-based solid cellular structures are firstly designed with different level parameters. The subtraction Boolean operation [12] is then performed on the two cellular structures to obtain the S-based hollow cellular structure. The subtraction Boolean operation of the S-based hollow cellular structure is mathematically defined as Eq. (3). The designed hollow cellular structures are graphically shown in Figs. 2a and 2b.
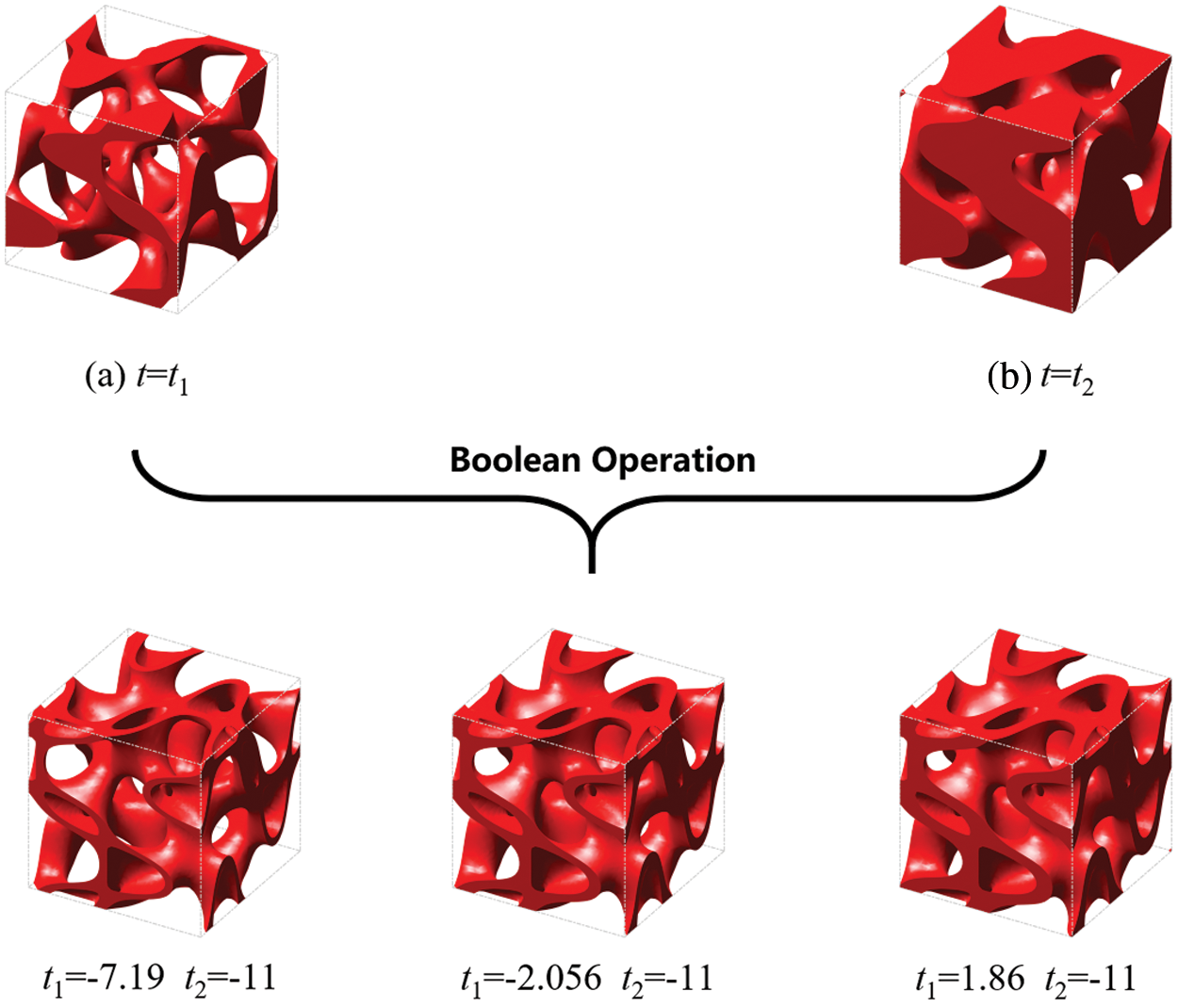
Figure 2: The process of the Boolean operation: (a) t1 = 1.93; (b) t2 = −6.02
The relative density of the S-based hollow cellular structure can be controlled by changing the value t1 and t2. In this paper, the level set function of the S-based hollow cellular structure is defined within a 50 × 50 × 50 discretized mesh. During the Boolean operation, the thin wall of the S-based hollow cellular structure will be penetrated when the relative density is less than 0.2. Closed cavities will be generated in the S-based hollow cellular structure when the relative density is larger than 0.7. As a result, the relative density of the hollow cellular structure is set between 0.2 and 0.7. Correspondingly, the value t2 is fixed to −11 to make the upper limit. The value t1 is adjusted from 7.19 to 2.678 to reach the relative density between 0.2 and 0.7. Fig. 3 shows the relationship between level parameter and the relative density. It is clear that the relative density is almost linear with the level parameter.
The hollow cellular structure designed by the Boolean operation is actually a unit cell. An array of the hollow cellular structure can be obtained by periodically distributing in orthogonal directions. In this work, two periodic S-based solid/hollow cellulars, with a 4 × 4 × 4 array, are designed in Figs. 4a and 4b. The design space is a 40 mm × 40 mm × 40 mm cube, and the size of the unit cell is 10 mm × 10 mm × 10 mm. Due to the geometric complexity of the TPMS, the wall thickness of the S-based hollow cellular structure is non-uniform. The wall thickness, therefore, is not regarded as a parameter to characterize hollow cellular structures. Instead, the relative density and porosity are measurable. According to the level set definition, the average relative density of the unit cell is 0.3. The porosity of the unit cell is 0.7 correspondingly. These periodic cellulars will be used for further FEA, additive manufacturing, and compression experiments.
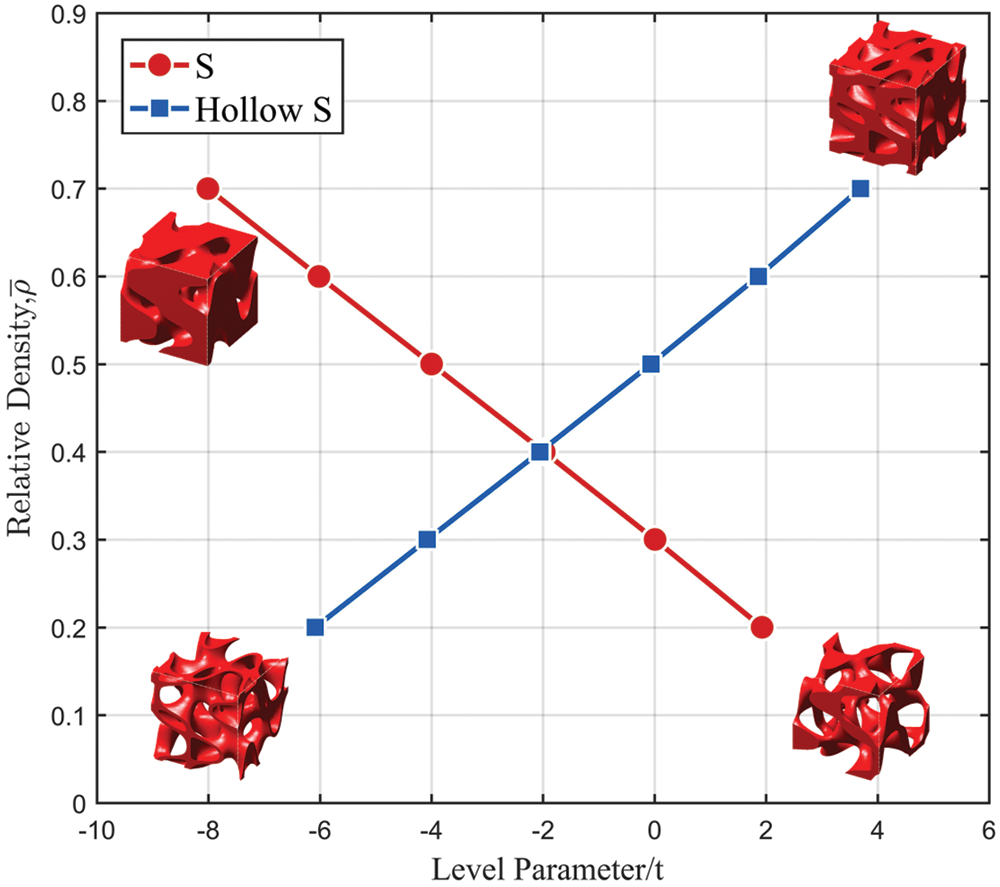
Figure 3: The relative density vs. parameter t
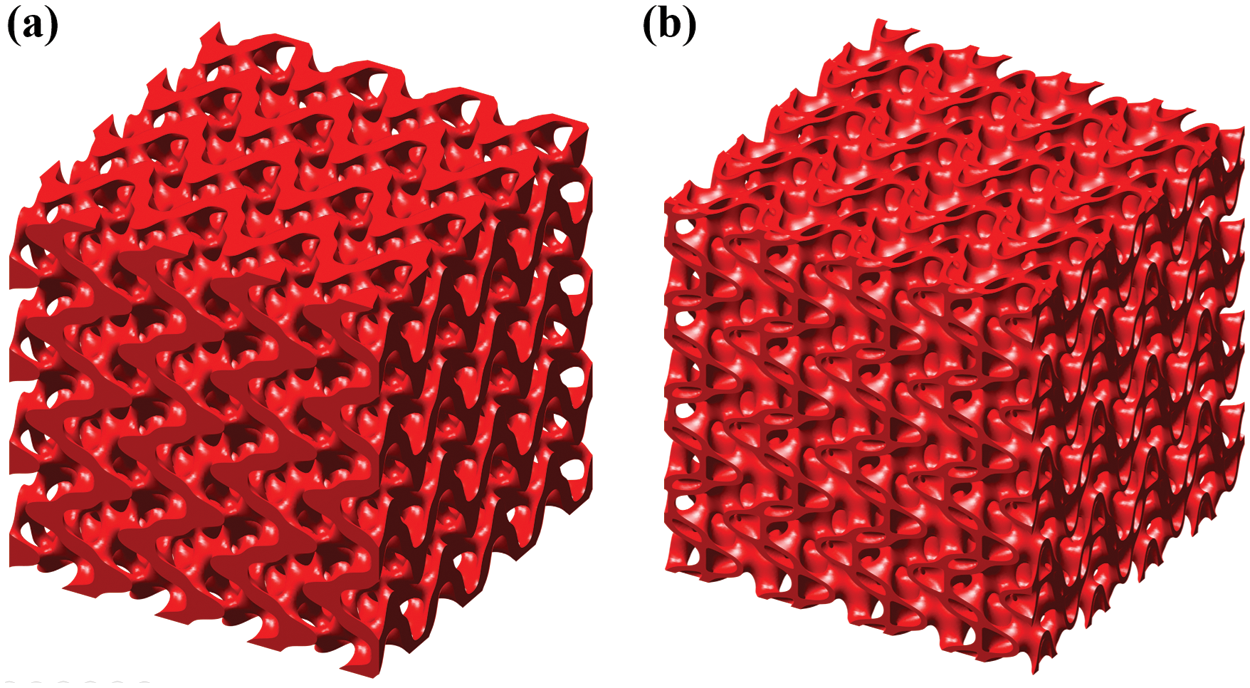
Figure 4: Cellular model: (a) S-based solid; (b) S-based hollow
3 The Numerical Homogenization Method for Cellular Structures
The numerical homogenization method is applied to evaluate the macroscopic effective elasticity tensor of the microscopic cellular structures. The calculated effective elastic tensor can reveal the cellular elasticity characteristics, e.g., bulk modulus, shear modulus and isotropy. Moreover, the homogenized results can also be used to verify the accuracy of the FEA.
The homogenized effective elasticity tensor CH of the S-based cellular structures can be written in a matrix form in terms of elemental mutual energy:
where |V| is the unit cell volume. Ve is the volume of element e. I is a 6 by 6 identity matrix. Be is the element strain-displacement matrix.
The homogenization equilibrium equation is established to calculate the displacement field
The global stiffness matrix K is defined as:
The load vector f corresponds to macroscopic volumetric straining is defined as:
where the strain ɛ composed of six straining tensor, which are
According to the calculation results, the S-based structures belong to the cubic symmetric system. The macroscopic effective tensor is a six-order symmetric matrix with three independent entries. Therefore, C 11 = C 22 = C 33, C 12 = C 13 = C 23, C 44 = C 55 = C 66, and the other components are zero in the effective elasticity tensor. The simplified effective elasticity tensor can be written as follows:
According to Eqs. (9)–(12), the (axial) Young's modulus EH, (axial) bulk modulus KH, (axial) shear modulus GH, and the Zener ratio [35] AH can be calculated using the components of the effective elasticity tensor. Moreover, we can use the Zener ratio to evaluate the isotropy of cellular structures, if the value is close to unity, it means the cellular structure is isotropic.
To be more comparable, Young's modulus EH, bulk modulus KH, and shear modulus GH of S-based TPMS based cellular structures are normalized by Young's modulus Eb, bulk modulus Kb, and shear modulus Gbof the constituent material, regardless of bulk materials, the equations are as follows:
The upper Hashin-Shtrikman (HS) bound [36] of the effective bulk modulus and shear modulus can be defined as:
The upper HS bound Young's modulus EHSU can be calculated by Eqs. (16) and (17):
4 The Effective Characteristics of Cellular Structures
The anisotropy of cellular structures highly relies on the spatial configurations of the unit cell. Although the S-based TPMS is not symmetric in geometry, the results of the homogenization show that it belongs to the form of the cubic crystal system. To visually demonstrate the anisotropy of the S-based hollow and solid cellular structures, Young's modulus surfaces are plotted in 3D space as shown in Fig. 5. When the Zener ratio is unity, Young's modulus surface is a sphere. In that case, the Young's modulus of cellular structures is the same in any directions, which means the cellular structure is isotropic. Fig. 5 shows that the S-based hollow cellular structures have similar Young's modulus in spatial directions. The Young's modulus surfaces of the S-based hollow cellular are more spherical than the S-based solid counterpart.
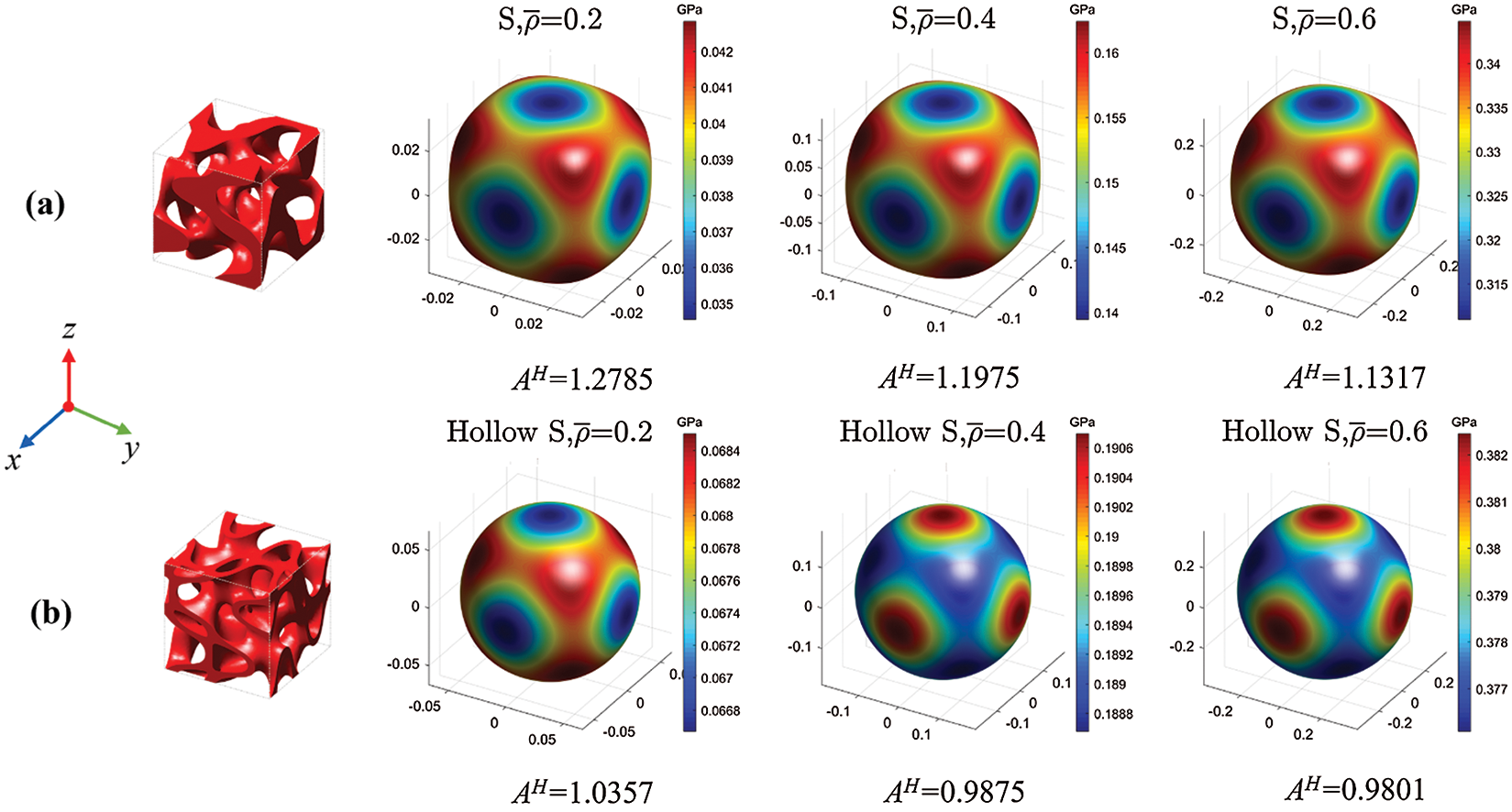
Figure 5: The Young's modulus surface: (a) S-based solid; (b) S-based hollow
From the perspective of Zener ratio, Fig. 6 shows that the S-based hollow cellular structures exhibit better isotropy than the solid counterpart. The Zener ratio of the S-based hollow cellular structure is very close to unity in the whole range of relative densities. On the contrary, the Zener ratio of the S-based solid cellular structure is obviously far beyond the unity. Additionally, it has been reported that the sheet-Gyroid cellular structure is the very few isotropic TPMS found in literature [16]. Compared with the sheet-Gyroid cellular structure, the Zener ratio of the S-based hollow cellular structure is closer to unity.
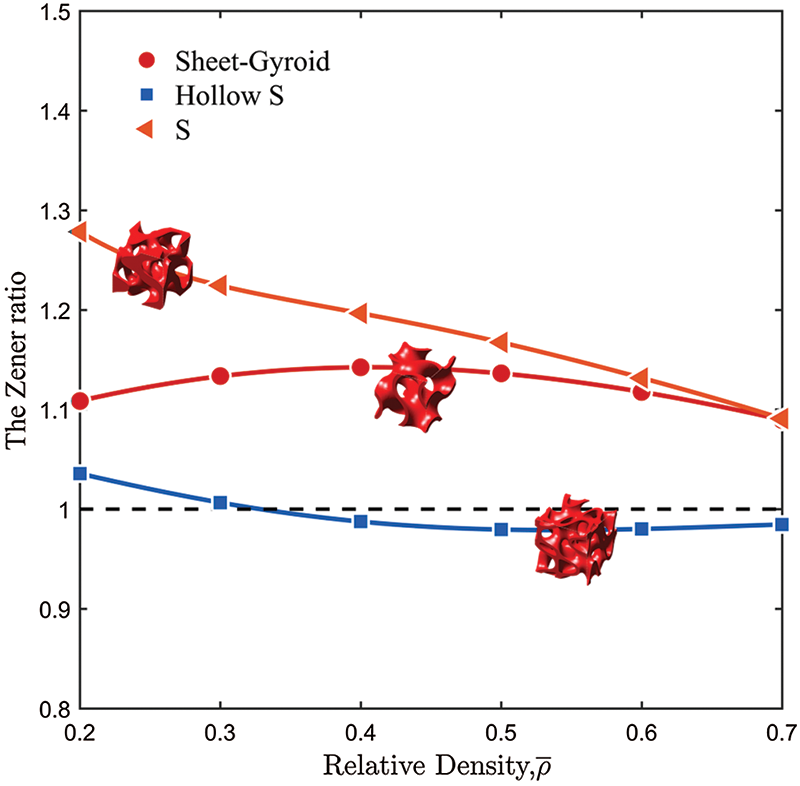
Figure 6: Comparison of the Zener ratio
5 The Static Mechanical Properties of Cellular Structures
The numerical homogenization is conducted to reveal the static mechanical properties of the proposed S-based hollow cellular structure. Fig. 7 demonstrates the dependence of the normalized modulus on the relative density. The upper HS bounds of Young's modulus, bulk modulus, and shear modulus are plotted for comparison. As shown in Fig. 7, the S-based hollow cellular structures exhibit larger Young's modulus, bulk modulus, and shear modulus than the S-based solid counterparts under all relative densities. The results calculated by static FEA and the numerical homogenization method are approximately the same level, which verifies the accuracy of the mechanical characterization for the cellular structures.
The FEA is further performed to reveal the S-based hollow cellular structure in linear elasticity with a specified scale. Specifically, the static structural module of the commercial finite element software is used to solve the linear equilibrium equation to obtain the displacement field of cellular structures. The solution environment of the software is a Windows 10 Professional workstation with a 2.40 GHz CPU and 98 GB RAM. The implicit models of the cellular structures are firstly exported as STL models which are the geometry inputs of the FEA software. The 4-node tetrahedral element is then used to discretize these models. Nylon PA2200 is taken as the material for the geometries. Material properties are specified as follows: Compressive Young's modulus ES = 741 MPa, tensile Young's modulus Et = 1600 MPa, compressive yield strength σS = 54 MPa, tensile yield strength σt = 44 MPa [37]. According to the typical experimental boundary conditions of cellular structures [38,39], the fixed support is applied on the bottom plane. The load is applied on the top plane. The boundary conditions of cellular structures are shown in Fig. 8. F is the applied load, H, L, and W are the height, length and width of cellular structures, respectively. The applied load is 1000 N and increased by 1000 N each time. Ten groups of simulations are conducted for the S-based hollow/solid cellular structures.
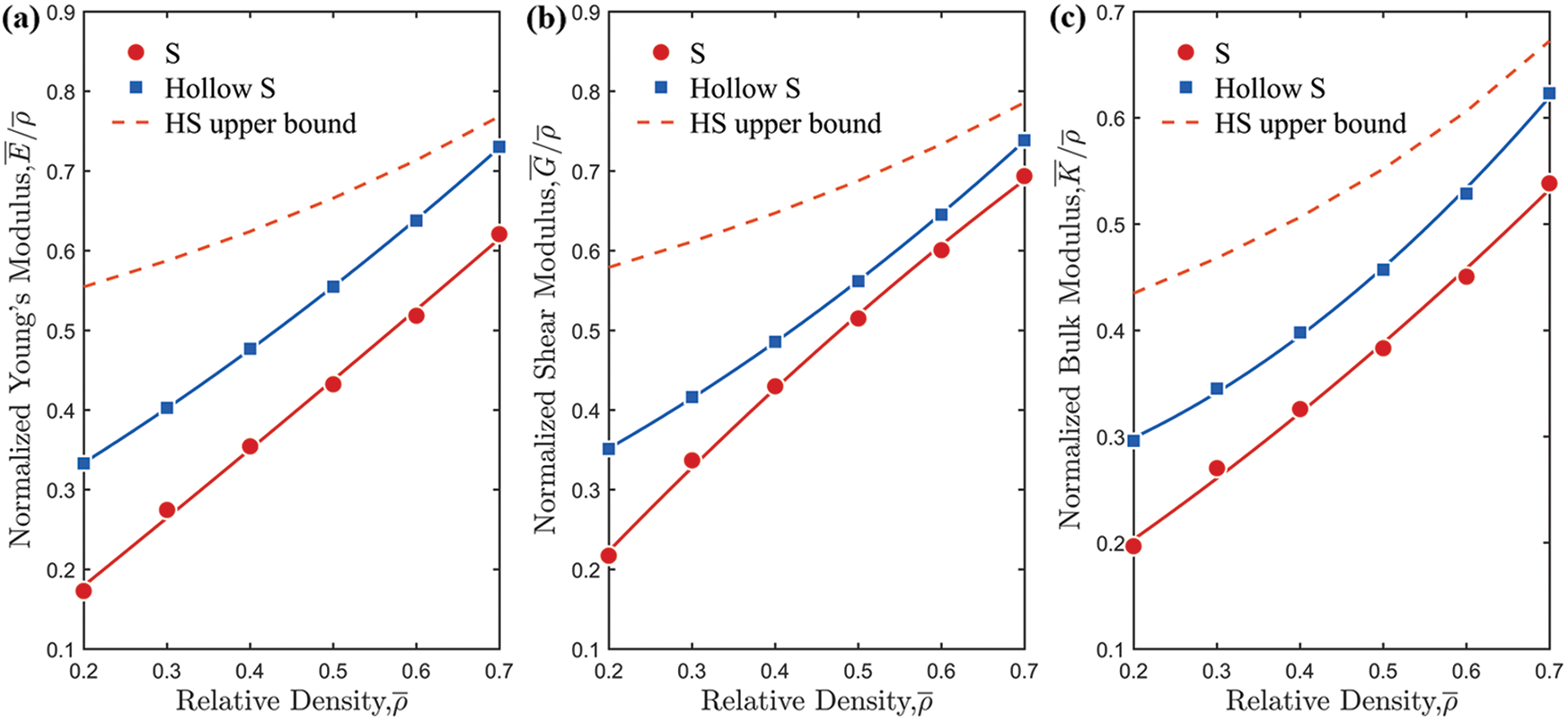
Figure 7: Comparison of the effective elastic modulus: (a) The effective Young's modulus; (b) The effective shear modulus; (c) The effective bulk modulus
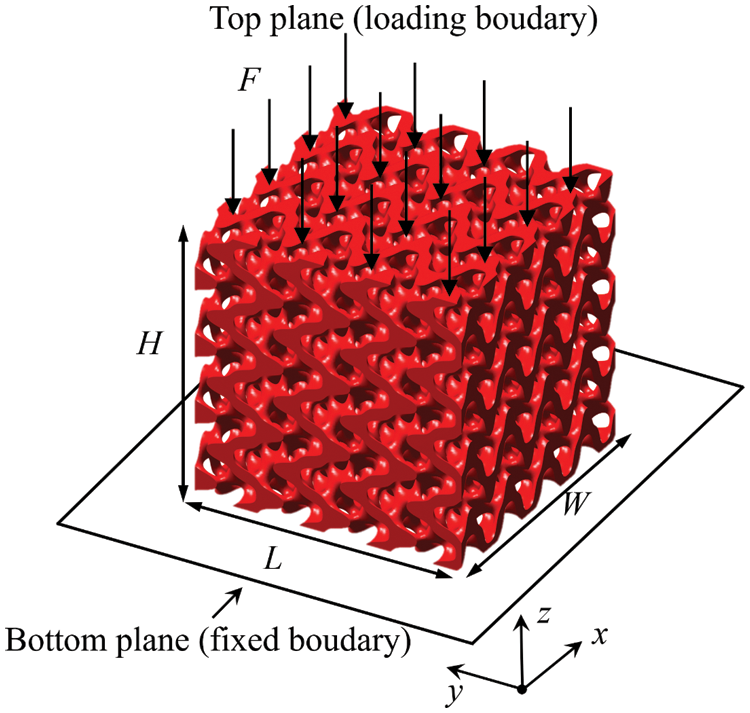
Figure 8: The boundary conditions
The total deformation of the S-based solid and hollow cellular structures is shown in Fig. 9. Under the same static load, the strain of the S-based hollow cellular structure is much smaller than the S-based solid cellular structure. Besides, as plotted in Fig. 10, the strain difference between the two cellular structures increases as the load increased, which means that S-based hollow structures are stiffer than the S-based solid counterpart.
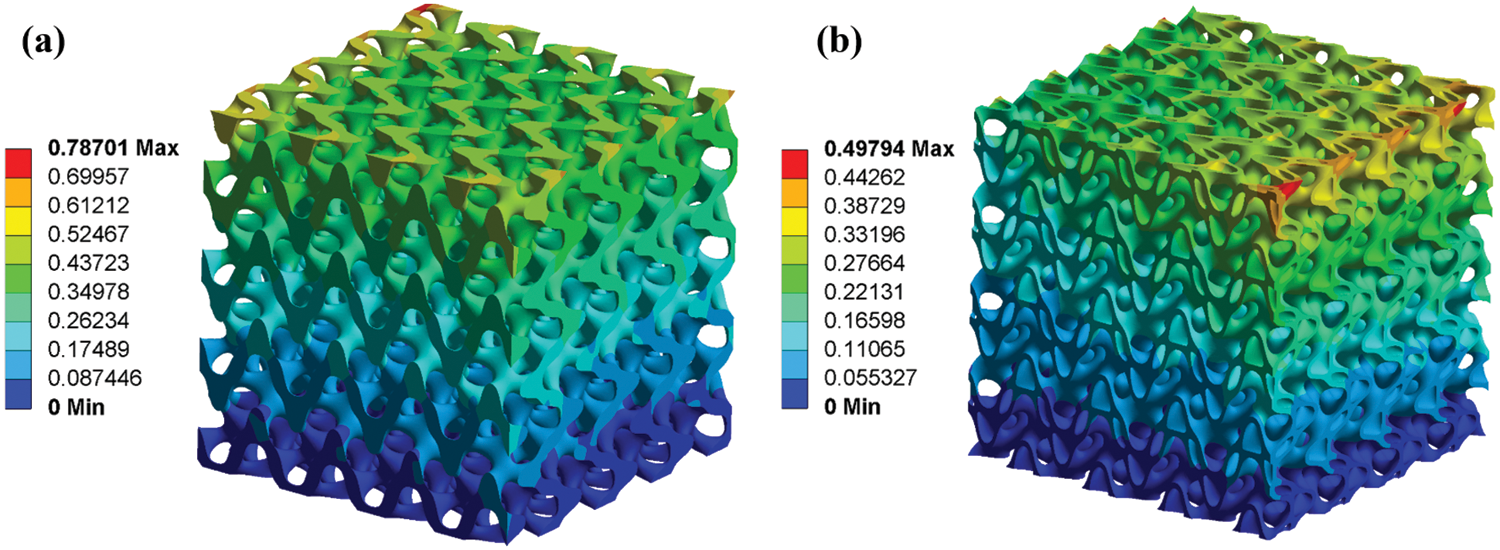
Figure 9: The total deformation: (a) S-based solid; (b) S-based hollow
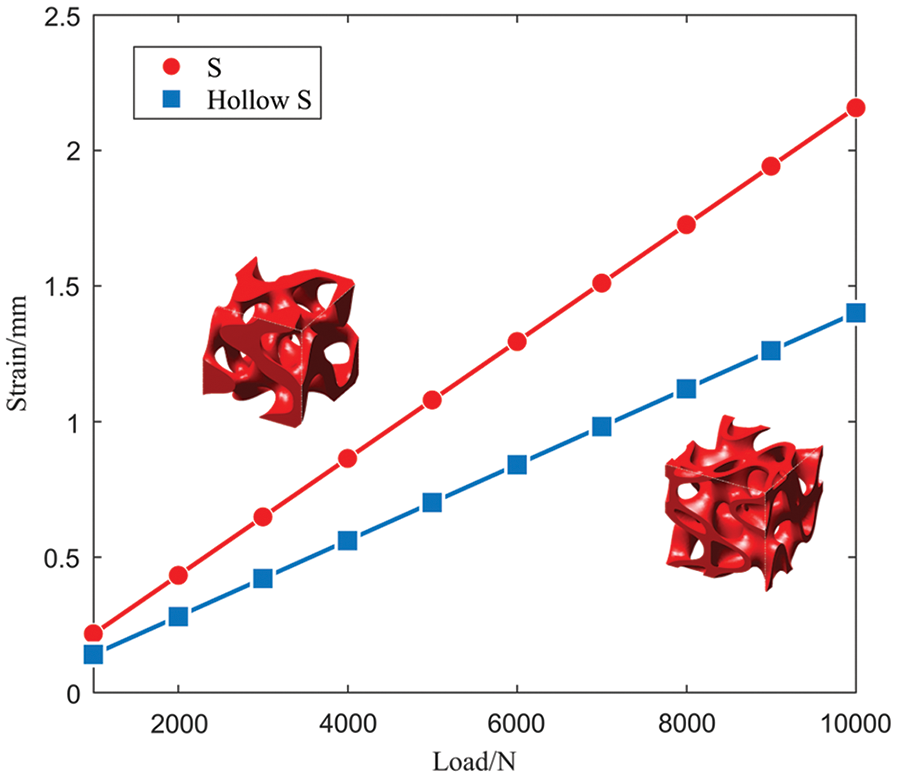
Figure 10: The strain-load curve
In order to verify the accuracy of the FEA, the Young's modulus of the two cellular structures is calculated by Eq. (19):
where, E is the Young's modulus, A is the average traverse area of cellular structures, d is the Y-directional average strain on the top surface of cellular structures.
The Y-directional deformation of the S-based solid and hollow cellular structures is shown in Fig. 11. The S-based hollow cellular structure has a much smaller strain with the same applied load. The comparison results of static FEA and the numerical homogenization method are listed in Fig. 12. The results calculated by FEA and the numerical homogenization method are consistent approximately, which verifies the accurate evaluation of the static mechanical properties of cellular structures.
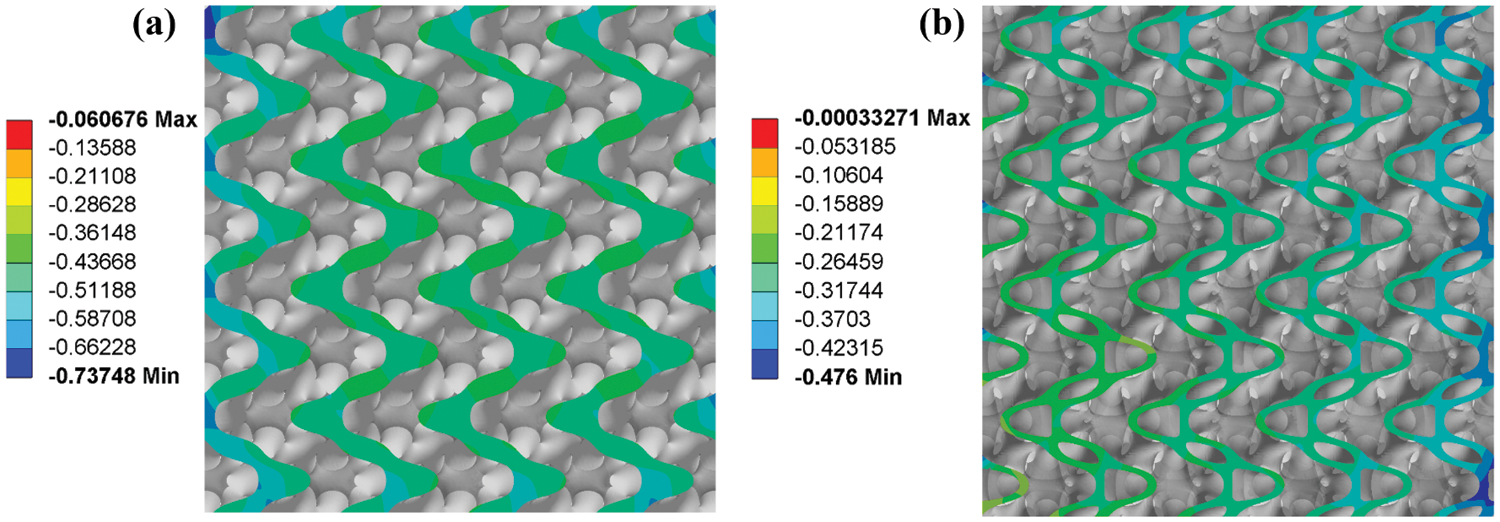
Figure 11: Y-directional deformation: (a) S-based solid; (b) S-based hollow
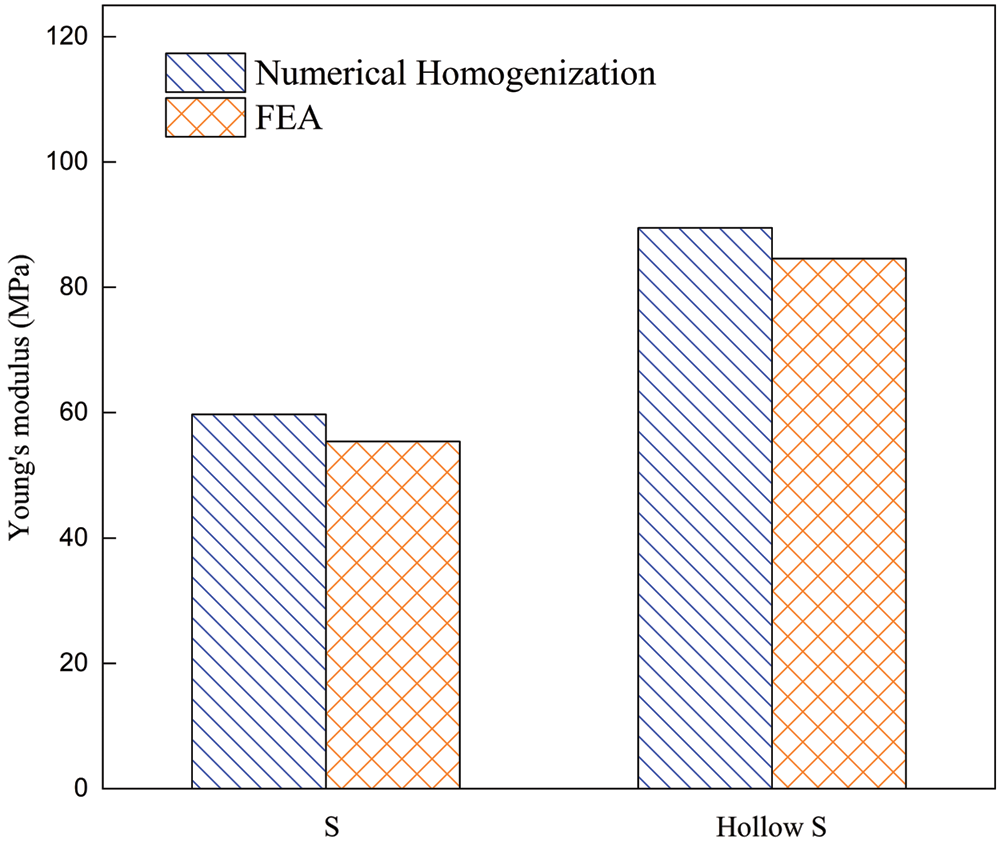
Figure 12: The results of the FEA and the numerical homogenization
6.1 Preparation of the Compression Experiments
To experimentally characterize the mechanical performance of the hollow cellular structure, both of the solid and hollow cellular structures are fabricated by Selective Laser Sintering (SLS) additive manufacturing (AM) technology [40,41] using an industrial 3D printer EOS-P760. It should be noted that there are no supports needed during the manufacturing process with Nylon PA2200 by SLS, which can avoid the impact of supporting defects on the evaluation of mechanical properties. To avoid manufacturing errors in the experimental results, all the experimental specimens are fabricated with the same printing parameters, e.g., 0.1 mm layer thickness, 32 mm/h printing speed, 173°C bed temperature, and 100% density of infill inside the model. The additive manufactured specimens are shown in Fig. 13.
After the AM of the cellular specimens, mechanical compression experiments are performed to reveal the mechanical behaviors of solid and hollow cellular structures. All specimens, at room temperature, are subjected to compressions with a 100 kN microcomputer-controlled electronic universal testing machine. The crosshead loading rate is set to 5 mm/min following the ASTM D695-15 standard [42]. Moreover, a video camera is applied to record the compression deformation process. The printing direction remains consistent with the in-plane direction of the structure to preclude the influence of the manufacturing errors on the experiment results.
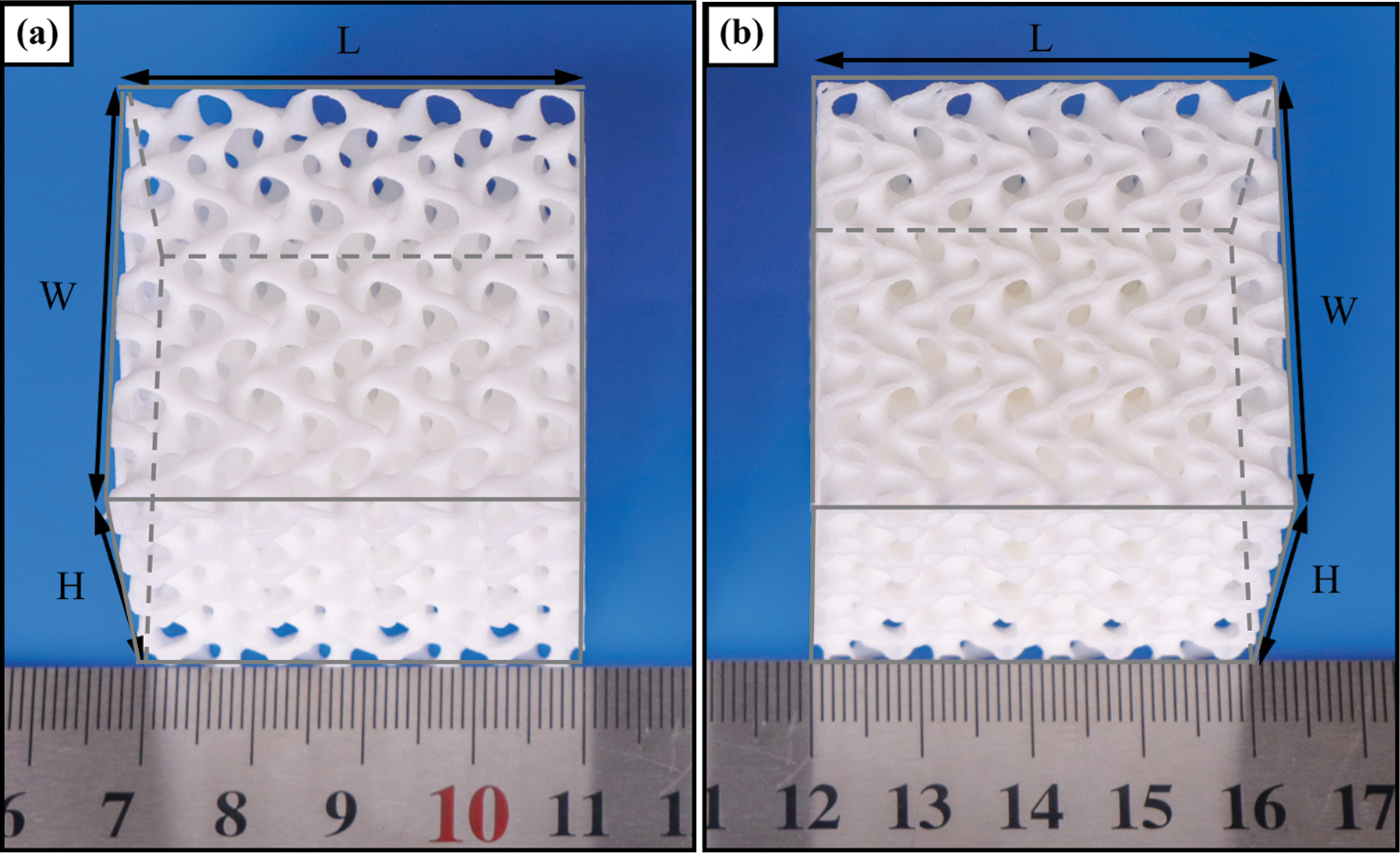
Figure 13: 3D printed specimens: (a) S-based solid; (b) S-based hollow
6.2 Analysis of the Compression Experiments
Fig. 14 shows the compression deformation process of the cellular structures. The process can be divided into five stages based on the movement of the crosshead, e.g., 0%, 15%, 30%, 45%, and 60% of the total compression distance. Both of the S-based solid and hollow cellular structures have the same progressive collapse. Each layer is simultaneously compressed and deformed throughout the process before being densified.

Figure 14: The compression process: (a) S-based solid; (b) S-based hollow
The stress-strain curves of the compression experiments are plotted in Fig. 15. Both of the S-based solid and hollow cellular structures exhibit linear elastic behavior at the low strain stage. In the linear stage, larger maximum stress is observed in the S-based hollow cellular structure than the solid counterpart under the same strain. The S-based hollow cellular structure thus has a higher Young's modulus. The reason is that the S-based solid cellular structure belongs to the cellular type of the rod-like structure, and is prone to crush rapidly under the compression load. The S-based hollow cellular structure, with a characteristic of more continuous surface, tends to gradually collapse when subjected to a compression load. The linearity terminates at the beginning of the plastic collapse. The cellular structures then enter the plastic plateau, which extends up to the densification strain. In this stage, plastic deformation occurs in the cellular structures. According to the experiment results in Fig. 15, the plastic collapse strength of the S-based hollow cellular structure is around 90% larger than the S-based solid cellular structure. As a result, the S-based hollow cellular structure has a higher plastic collapse strength than the S-based solid cellular structure. Following the plastic plateau is densification. The stress of the cellular structures increases sharply in this stage, the S-based hollow cellular structure has a slightly lower densification strain. The cellular structures are compressed completely.
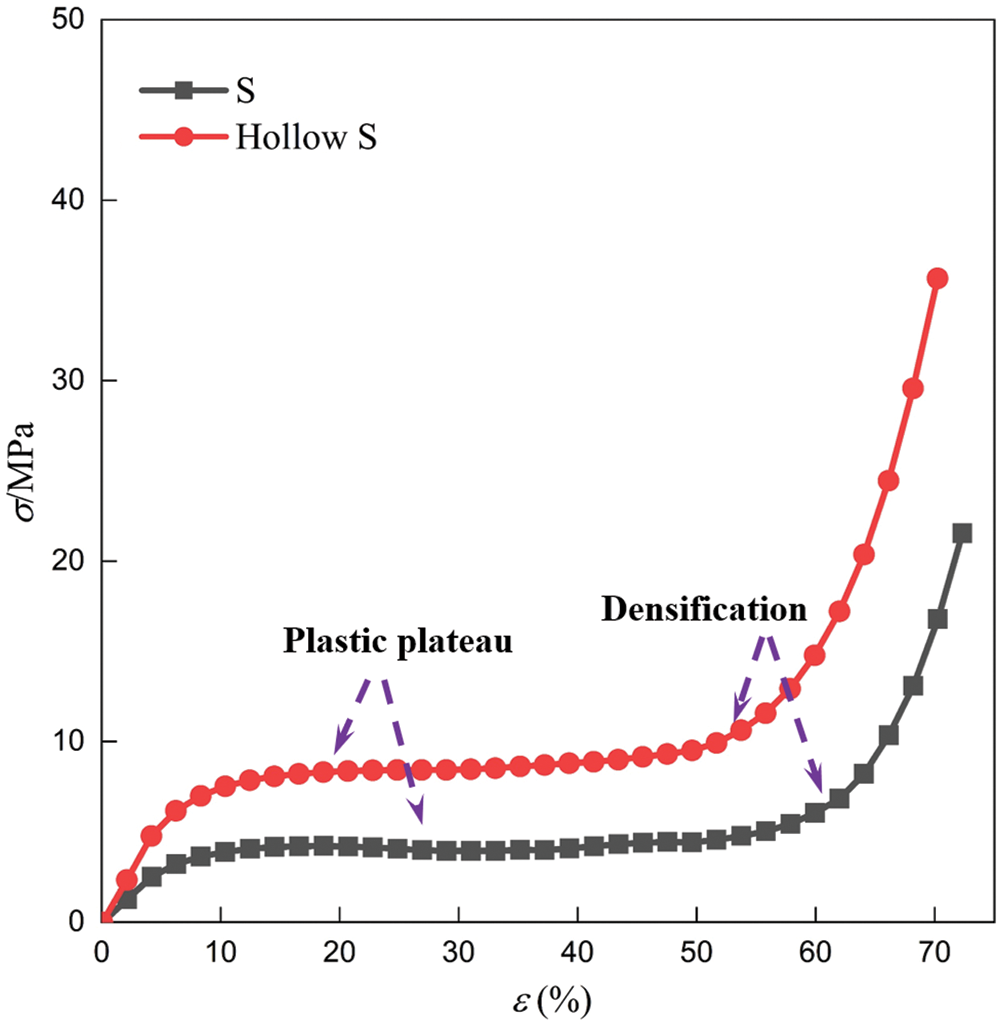
Figure 15: The stress-strain curve
The energy absorption capacity of cellular structures can be quantified by the integral value of the stress in the strain range when it reaches the densifying strain. The integral value is the summation of energy absorbed per unit volume for cellular structures, which is defined in Eq. (20). As shown in Fig. 16, the integral value of the S-based hollow/solid cellular structures increases linearly before densification, which is also crucial for the protected objectives. Moreover, the integral value of the S-based hollow cellular structure is higher than the S-based solid cellular structure within the same strain. The total integral value of the S-based hollow cellular structure is almost 1.67 times that of the S-based solid cellular structure at the range of densification. As a result, compared with the S-based solid cellular structure, the S-based hollow cellular structure has better energy absorption performance.
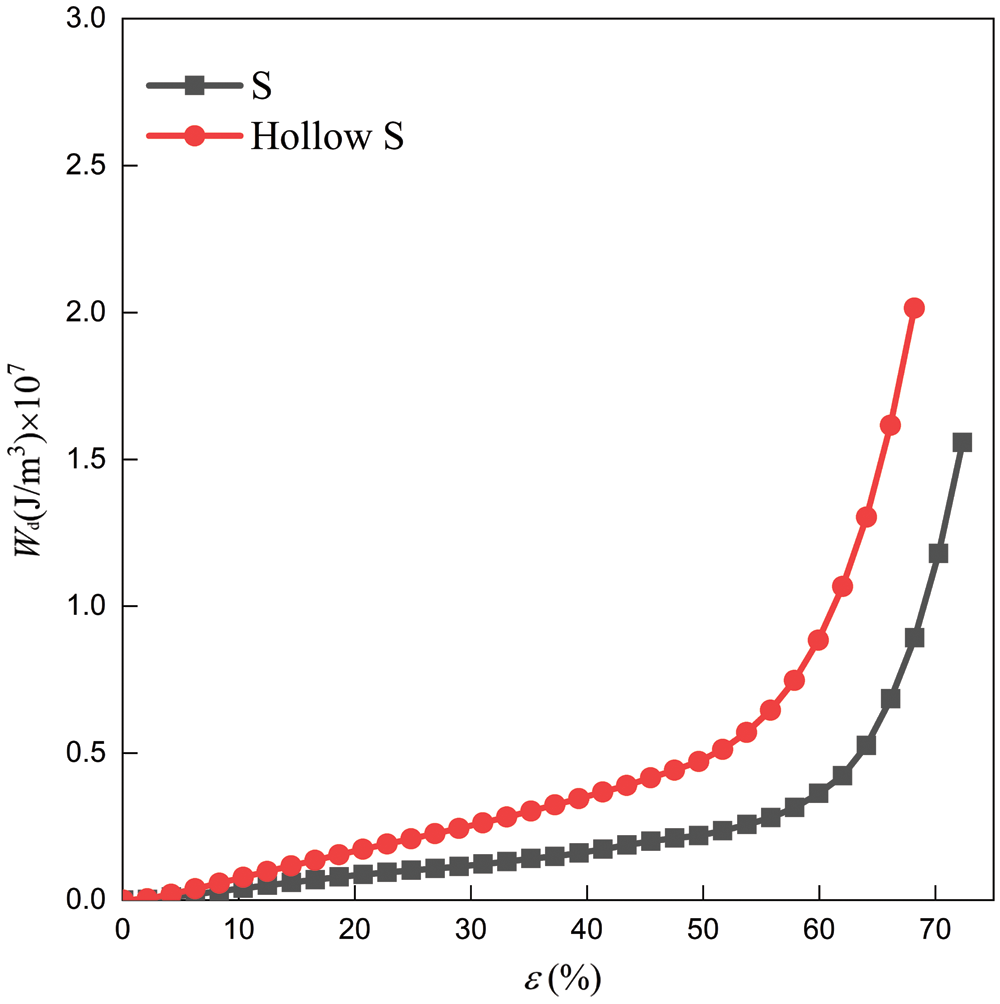
Figure 16: Energy absorbed per unit volume for the S-based solid/hollow cellular structures
To better reveal the various regions of the energy absorbing and help a designer choose select a cellular structure that minimizes the stress while the required energy is absorbed, the energy absorbed per unit volume Wd and stress σ are normalized by Young's modulus of the constituent material as plotted in Fig. 17. The curves in Fig. 17 can be divided into three regions, e.g., Region I, Region II, and Region III. Region I correspond to the elastic deformation of the S-based solid/hollow cellular structures. In this region, the energy absorption of the cellular structures increases linearly, but a small amount of the total energy is absorbed. In Region II, cellular structures enter the plastic plateau, and the absorbed energy increases sharply with very little increase in stress. The cellular structures enter the densified stage in Region III. There are a significant turning point and a subsequent rapid increment in stress.
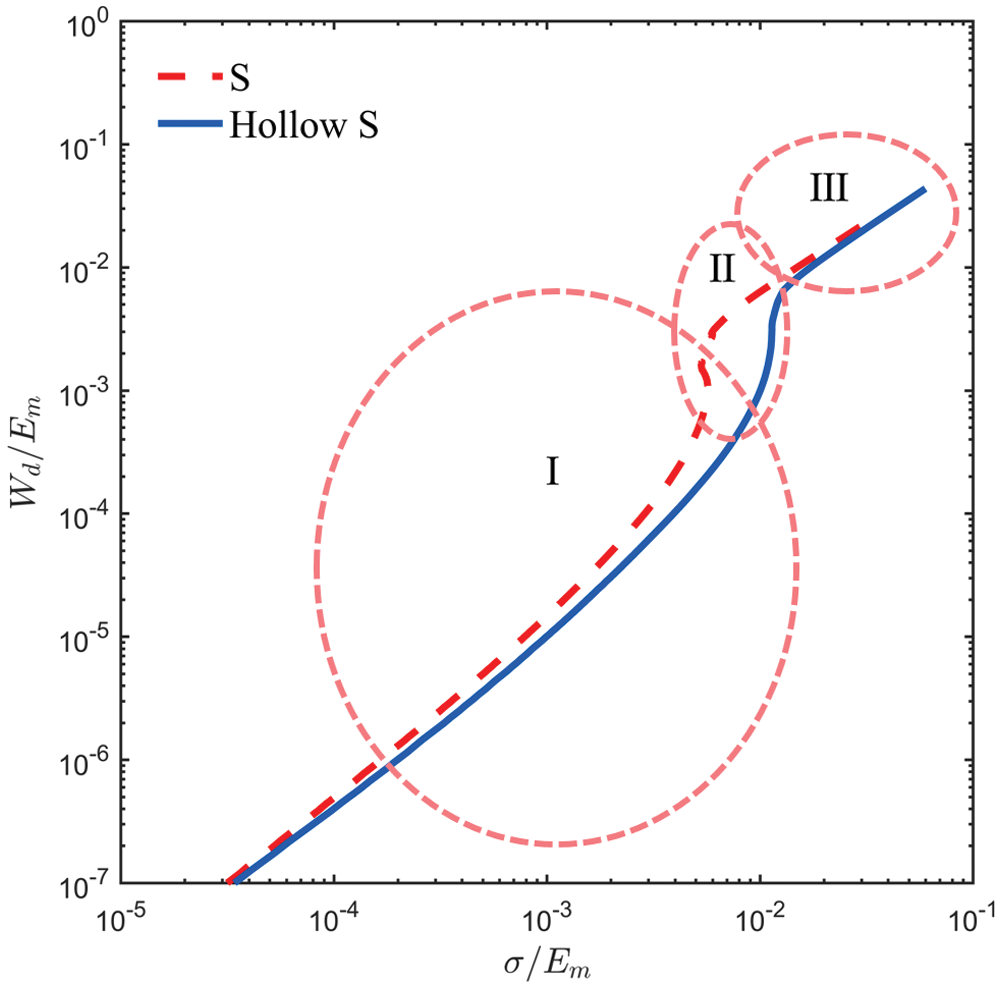
Figure 17: Normalized energy-stress curve
This paper proposes an S-based hollow cellular structure with isotropy characteristic. Numerical homogenization results show that the S-based hollow cellular structure has superior isotropy than the proposed sheet-Gyroid cellular structure. The relative density of the S-based hollow cellular structure has limited influence on the isotropy characteristic. Numerical computations and compression experiments reveal that the S-based hollow cellular structure has higher Young's modulus, shear modulus, bulk modulus, plastic strength, and energy absorption capacity than its solid counterpart. This kind of S-based hollow structure is expected to be a candidate for mechanical metamaterials with superior mechanical responses.
Acknowledgement: The authors are sincerely grateful to the anonymous referees and the editor for their time and effort in providing constructive, and valuable comments and suggestions that have led to a substantial improvement in the paper.
Funding Statement: This research was funded by the National Natural Science Foundation of China (NSFC, Project No. 51775308); National Natural Science Foundation of Hubei (No. 2021CFB236). Youth Talent Project of Hubei Provincial Department of Education (No. Q20201205); Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance Open Foundation (No. 2020KJX04). The authors would like to thank for these financial supports.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Ashby, M. F., Shercliff, H., Cebon, D. (2018). Materials: Engineering, science, processing and design. Oxford, UK: Butterworth-Heinemann. [Google Scholar]
2. Gibson, L., Ashby, M. (1997). Cellular solids: Structure and properties. UK: Cambridge University Press. [Google Scholar]
3. Wang, Z. (2019). Recent advances in novel metallic honeycomb structure. Composites Part B: Engineering, 166, 731–741. DOI 10.1016/j.compositesb.2019.02.011. [Google Scholar] [CrossRef]
4. Zhang, Q. C., Yang, X. H., Li, P., Huang, G. Y., Feng, S. S. et al. (2015). Bioinspired engineering of honeycomb structure–using nature to inspire human innovation. Progress in Materials Science, 74, 332–400. DOI 10.1016/j.pmatsci.2015.05.001. [Google Scholar] [CrossRef]
5. Li, D. W., Dai, N., Tang, Y. L., Dong, G. Y., Zhao, Y. Y. F. (2019). Design and optimization of graded cellular structures with triply periodic level surface-based topological shapes. Journal of Mechanical Design, 141(7), 071402. DOI 10.1115/1.4042617. [Google Scholar] [CrossRef]
6. Maskery, I., Aremu, A. O., Parry, L., Wildman, R. D., Tuck, C. J. et al. (2018). Effective design and simulation of surface-based lattice structures featuring relative densityand cell type grading. Materials & Design, 155, 220–232. DOI 10.1016/j.matdes.2018.05.058. [Google Scholar] [CrossRef]
7. Yan, C., Hao, L., Hussein, A., Young, P. (2015). Ti–6Al–4V triply periodic minimal surface structures for bone implants fabricated via selective laser melting. Journal of the Mechanical Behavior of Biomedical Materials, 51, 61–73. DOI 10.1016/j.jmbbm.2015.06.024. [Google Scholar] [CrossRef]
8. Yánez, A., Herrera, A., Martel, O., Monopoli, D., Afonso, H. (2016). Compressive behaviour of gyroid lattice structures for human cancellous bone implant applications. Materials Science and Engineering: C, 68, 445–448. DOI 10.1016/j.msec.2016.06.016. [Google Scholar] [CrossRef]
9. Yu, S., Sun, J., Bai, J. (2019). Investigation of functionally graded TPMS structures fabricated by additive manufacturing. Materials & Design, 182, 108021. DOI 10.1016/j.matdes.2019.108021. [Google Scholar] [CrossRef]
10. Queheillalt, D. T., Wadley, H. N. (2005). Pyramidal lattice truss structures with hollow trusses. Materials Science and Engineering: A, 397(1–2), 132–137. DOI 10.1016/j.msea.2005.02.048. [Google Scholar] [CrossRef]
11. Bendsoe, M. P., Sigmund, O. (2013). Topology optimization: Theory, methods, and applications. Berlin, Germany: Springer Science & Business Media. [Google Scholar]
12. Osher, S., Fedkiw, R. (2006). Level set methods and dynamic implicit surfaces. NewYork, USA: Springer Science & Business Media. [Google Scholar]
13. Wang, X., Wang, C., Zhou, X., Zhang, M. K., Zhang, P. Y. et al. (2020). Innovative design and additive manufacturing of regenerative cooling thermal protection system based on the triply periodic minimal surface porous structure. Computer Modeling in Engineering & Sciences, 123(2), 495–508. DOI 10.32604/cmes.2020.09778. [Google Scholar] [CrossRef]
14. Vogiatzis, P., Chen, S., Wang, X., Li, T. T., Wang, L. F. et al. (2017). Topology optimization of multi-material negative Poisson's ratio metamaterials using a reconciled level set method. Computer-Aided Design, 83, 15–32. DOI 10.1016/j.cad.2016.09.009. [Google Scholar] [CrossRef]
15. Zhou, G., Ma, Z. D., Li, G. Y., Cheng, A. G., Duan, L. B. et al. (2016). Design optimization of a novel NPR crash box based on multi-objective genetic algorithm. Structural and Multidisciplinary Optimization, 54(3), 673–684. DOI 10.1007/s00158-016-1452-z. [Google Scholar] [CrossRef]
16. Li, D. W., Liao, W. H., Dai, N., Xie, Y. M. (2019). Comparison of mechanical properties and energy absorption of sheet-based and strut-based gyroid cellular structures with graded densities. Materials, 12(13), 2183. DOI 10.3390/ma12132183. [Google Scholar] [CrossRef]
17. Zhang, W. H., Wang, F. W., Dai, G. M., Sun, S. P. (2007). Topology optimal design of material microstructures using strain energy-based method. Chinese Journal of Aeronautics, 20(4), 320–326. DOI 10.1016/S1000-9361(07)60050-8. [Google Scholar] [CrossRef]
18. Vineyard, E., Gao, X. L. (2021). Topology and shape optimization of 2-D and 3-D micro-architectured thermoelastic metamaterials using a parametric level set method. Computer Modeling in Engineering & Sciences, 127(3), 819–854. DOI 10.32604/cmes.2021.015688. [Google Scholar] [CrossRef]
19. Ye, M. L., Gao, L., Li, H. (2020). A design framework for gradually stiffer mechanical metamaterial induced by negative Poisson's ratio property. Materials & Design, 192, 108751. DOI 10.1016/j.matdes.2020.108751. [Google Scholar] [CrossRef]
20. Du, Y. X., Yin, P., Tian, Q. H., Zhou, X. M. (2020). Multi-objective topology optimisation design of lattice structures with negative Poisson's ratio considering energy absorption and load-bearing characteristics. International Journal of Materials and Product Technology, 61(2–4), 90–110. DOI 10.1504/ijmpt.2020.10035506. [Google Scholar] [CrossRef]
21. Schoen, A. H. (1970). Infinite periodic minimal surfaces without self-intersections. Cambridge: National Aeronautics and Space Administration. [Google Scholar]
22. Schwarz, H. A. (1972). Gesammelte mathematische abhandlungen. Berlin, Germany: Springer. [Google Scholar]
23. Xia, L., Breitkopf, P. (2015). Design of materials using topology optimization and energy-based homogenization approach in Matlab. Structural and Multidisciplinary Optimization, 52(6), 1229–1241. DOI 10.1007/s00158-015-1294-0. [Google Scholar] [CrossRef]
24. Wang, Y., Sigmund, O. (2020). Quasiperiodic mechanical metamaterials with extreme isotropic stiffness. Extreme Mechanics Letters, 34, 100596. DOI 10.1016/j.eml.2019.100596. [Google Scholar] [CrossRef]
25. Gurtner, G., Durand, M. (2014). Stiffest elastic networks. Proceedings of the Royal Society A, Mathematical, Physical and Engineering Sciences, 470(2164), 20130611. DOI 10.1098/rspa.2013.0611. [Google Scholar] [CrossRef]
26. Berger, J. B., Wadley, H. N. G., McMeeking, R. M. (2017). Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness. Nature, 543(7646), 533–537. DOI 10.1038/nature21075. [Google Scholar] [CrossRef]
27. Tancogne-Dejean, T., Diamantopoulou, M., Gorji, M. B., Bonatti, C., Mohr, D. (2018). 3D plate-lattices, an emerging class of low-density metamaterial exhibiting optimal isotropic stiffness. Advanced Materials, 30(45), 1803334. DOI 10.1002/adma.201803334. [Google Scholar] [CrossRef]
28. Chen, Z. Y., Xie, Y. M., Wu, X., Wang, Z., Li, Q. (2019). On hybrid cellular materials based on triply periodic minimal surfaces with extreme mechanical properties. Materials & Design, 183, 108109. DOI 10.1016/j.matdes.2019.108109. [Google Scholar] [CrossRef]
29. Surjadi, J. U., Feng, X. B., Fan, R., Lin, W., Li, X. C. et al. (2021). Hollow medium-entropy alloy nanolattices with ultrahigh energy absorption and resilience. NPG Asia Materials, 13(1), 1–7. DOI 10.1038/s41427-021-00306-y. [Google Scholar] [CrossRef]
30. Pingle, S. M., Fleck, N. A., Deshpande, V. S., Wadley, H. N. G. (2011). Collapse mechanism maps for a hollow pyramidal lattice. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 467(2128), 985–1011. DOI 10.1098/rspa.2010.0329. [Google Scholar] [CrossRef]
31. Queheillalt, D. T., Wadley, H. N. G. (2005). Cellular metal lattices with hollow trusses. Acta Materialia, 53(2), 303–313. DOI 10.1016/j.actamat.2004.09.024. [Google Scholar] [CrossRef]
32. Tancogne-Dejean, T., Mohr, D. (2018). Elastically-isotropic elementary cubic lattices composed of tailored hollow beams. Extreme Mechanics Letters, 22, 13–18. DOI 10.1016/j.eml.2018.04.005. [Google Scholar] [CrossRef]
33. Andreassen, E., Andreasen, C. S. (2014). How to determine composite material properties using numerical homogenization. Computational Materials Science, 83, 488–495. DOI 10.1016/j.commatsci.2013.09.006. [Google Scholar] [CrossRef]
34. Tan, P., Tong, L. Y., Steven, G. P., Ishikawa, T. (2000). Behavior of 3D orthogonal woven CFRP composites. Part I. Experimental investigation. Composites Part A: Applied Science and Manufacturing, 31(3), 259–271. DOI 10.1016/S1359-835X(99)00070-6. [Google Scholar] [CrossRef]
35. Zener, C. M., Siegel, S. (1958). Anelasticity of metals. Nuovo Cimento (1955–19657, 544–568. DOI 10.1007/BF02751494. [Google Scholar] [CrossRef]
36. Hashin, Z., Shtrikman, S. (1963). A variational approach to the theory of the elastic behaviour of multiphase materials. Journal of the Mechanics and Physics of Solids, 11(2), 127–140. DOI 10.1016/0022-5096(63)90060-7. [Google Scholar] [CrossRef]
37. Ngim, D. B., Liu, J. S., Soar, R. C. (2009). Design optimization of consolidated granular-solid polymer prismatic beam using metamorphic development. International Journal of Solids and Structures, 46(3–4), 726–740. DOI 10.1016/j.ijsolstr.2008.09.031. [Google Scholar] [CrossRef]
38. Wang, Z. G., Wang, X. X., Gao, T., Shi, C. (2021). Mechanical behavior and deformation mechanism of triply periodic minimal surface sheet under compressive loading. Mechanics of Advanced Materials and Structures, 28(19), 2057–2069. DOI 10.1080/15376494.2020.1829756. [Google Scholar] [CrossRef]
39. Wang, Z. G., Wang, X. X., Liu, K., Zhang, J., Lu, Z. J. (2021). Crashworthiness index of honeycomb sandwich structures under low-speed oblique impact. International Journal of Mechanical Sciences, 208, 106683. DOI 10.1016/j.ijmecsci.2021.106683. [Google Scholar] [CrossRef]
40. Stoia, D. I., Marsavina, L. (2019). Effect of aluminum particles on the fracture toughness of polyamide-based parts obtained by selective laser sintering (SLS). Procedia Structural Integrity, 18, 163–169. DOI 10.1016/j.prostr.2019.08.150. [Google Scholar] [CrossRef]
41. Yan, C. Z., Hao, L., Hussein, A., Bubb, S. L., Young, P. et al. (2014). Evaluation of light-weight AlSi10Mg periodic cellular lattice structures fabricated via direct metal laser sintering. Journal of Materials Processing Technology, 214(4), 856–864. DOI 10.1016/j.jmatprotec.2013.12.004. [Google Scholar] [CrossRef]
42. Standard A. D695, (2015). Standard test method for compressive properties of rigid plastics. West Conshohocken, PA, USA: ASTM International. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |