Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2022.017756

ARTICLE

Investigation on the Mechanical Properties of Polycrystalline Mg Using Molecular Dynamics Simulation

Xiaoxia Liu1,2,*

1School of Science, Ningxia Medical University, Yinchuan, 750021, China
2State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, Dalian University of Technology, Dalian, 116024, China
*Corresponding Author: Xiaoxia Liu. Email: ningdalxx@sina.com
Received: 03 June 2021; Accepted: 20 August 2021

1  Introduction

Magnesium (Mg) and its composites have a wide range of applications in automobiles, aerospace, and electronic communications due to their excellent performance, such as light weight, high specific stiffness, and strength [1,2]. In order to satisfy the special requirements of composites in different fields, it is necessary to study and discuss the mechanical performance of polycrystalline Mg (polyMg) under complex conditions.

The grain size of nanocrystalline materials is usually less than 100 nm, which has different properties compared with traditional materials. It has been pointed out that the size effect may change the deformation mechanism of nanomaterials [3]. At present, several deformation mechanisms of nanomaterials have been proposed, such as the existence of the void phase, a large number of trigeminal boundaries, the reduction of dislocation movement, the slip, and rotation of grain boundaries [4,5]. However, although many experimental results have already been received, there is still a lack of clear and intuitive understanding of the elastoplastic deformation of nanocrystalline materials [6]. Due to the difficulty of repeating and controlling the key parameters of experimental conditions, computer simulations are popular to predict and analyze the properties of materials nowadays.

Molecular dynamics (MD) simulation can not only obtain the trajectory of atoms, but also observe the details of microscopic deformation related to the atoms that cannot be obtained experimentally, so it has been widely used in the study of mechanical properties of materials. Liu et al. [7] used the MD method to study the effect of grain size and shape on tensile mechanical properties of polycrystalline Cu (polyCu). Their calculated results showed that the grain size could be divided into three regions according to the change of flow stress, and the deformation mechanisms in these three regions are different. The effect of grain shape on flow stress is difficult to observe, and has no effect on the plastic deformation mechanism, but has a great influence on elastic modulus. Zhang et al. [8] studied the effect of strain rate on the plastic deformation of polyCu. The results showed that the stress-dominated deformation mechanism at grain boundaries is insensitive to strain rate, while stacking faults impede the movement of some dislocations, which leads to an increase in strain rate sensitivity. Chen et al. [9] investigated the effect of strain rate on the mechanical properties of polyCu. The simulated results showed that the mechanical properties of polyCu were sensitive to high strain rates (1 × 109 s−1∼5 × 1010 s−1), but the properties did not change much at low strain rates (5 × 107 s−1∼1 × 109 s−1). In addition, MD simulations are also widely used in the calculations of polycrystalline graphene reinforced Al matrix composites [10] and other materials [11,12].

Due to the complexity of the HCP structure, little research has been done on polyMg and its composites. Saitoh et al. [13] established grain boundary (GB) models of Mg crystal to study the deformation mechanism under uniaxial tension by the MD method. The results showed that there are significant differences in the deformation mechanisms of GBs from different angles. The high-angle GBs can be used as the nucleation point to emit dislocation, but the edge dislocations appear in Mg crystals with low-angle GBs. Hasan et al. [14] employed the MD method to study the uniaxial tensile deformation of polyMg with different grain sizes. Two distinct deformation mechanisms are obtained from the deformation namo-mechanics. Dislocation-dominated tensile deformation can be observed in samples with large grain sizes, while grain boundary-based mechanisms can be observed in smaller grain-sized samples. The results showed that the number of dislocations in the polyMg samples reduces drastically with the decrease of grain size.

In this paper, the three-dimensional structure of polyMg is studied systematically and comprehensively. The influence of the grain size, temperature and strain rate on the mechanical properties of polyMg are investigated using the MD method. The results are analyzed and discussed on the basis of atomic structure and the stress-strain curve. The obtained results are expected to provide theoretical guidance for the research of polyMg.

2  Calculated Models and Methods

The voronoi [15] method is used to build polyMg samples with different grain sizes. The model has a size of 40.4 nm along with three directions and contains about 2.85 million atoms. The average grain sizes of the samples are 16, 13, 10, 8 and 5 nm, and the corresponding grain numbers are 16, 27, 64, 125 and 512, respectively. Fig. 1 shows the relaxed polyMg models with average grain sizes of 16 and 8 nm.

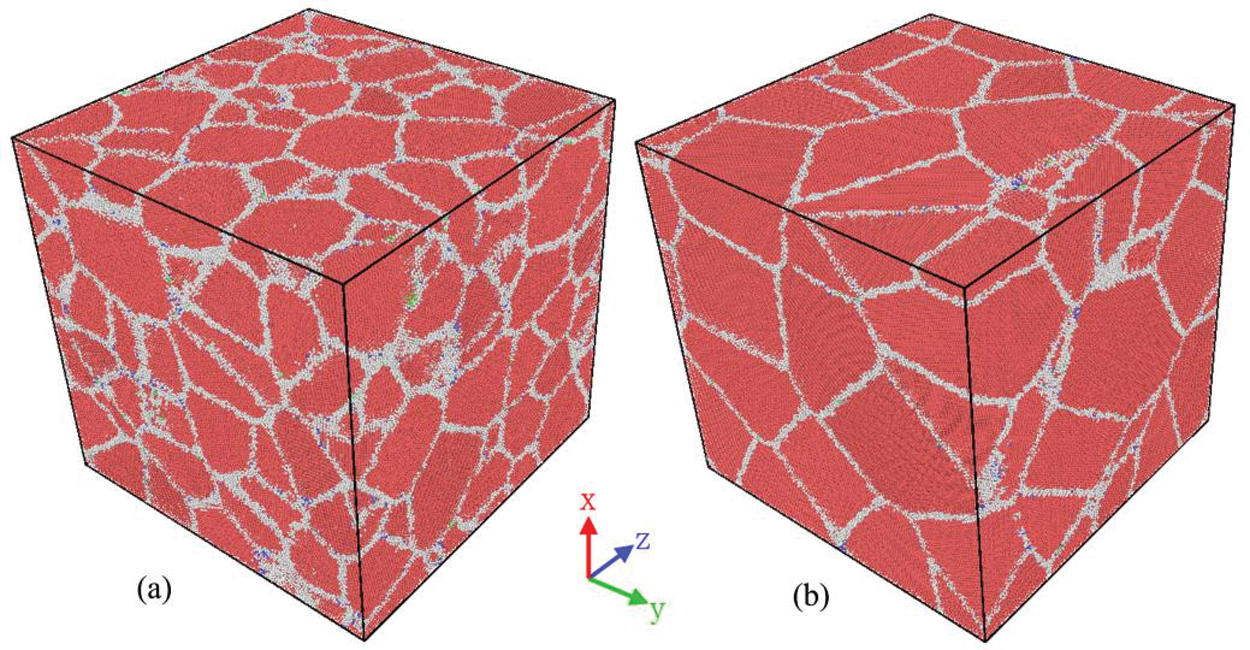
Figure 1: The model of polyMg after relaxation of different grain sizes: (a) 8 nm; (b) 16 nm

Periodic boundary conditions are adopted in all three directions. The conjugate gradient (cg) method is first used to minimize the energy of the model, and then the initial stress of the system is eliminated by relaxing 30 ps under the NPT ensemble. The strain rate of 1 × 109 s−1 is applied along the z-axis, and the other two directions are controlled by zero pressure. During the simulation process, the system temperature is controlled by the Nose-Hoover thermal bath method, and the pressure is controlled by the Parrinello Rahman barostat method. The classical Newtonian equations of motion are integrated by the Velocity Verlet algorithm with a time step of 1 fs.

The atomic stresses in LAMMPS are calculated by the virtual stress theory [16] as follows:

σ=1V∑i[−miu˙i⊗u˙i+12∑j≠irij⊗fij](1)

where V is the volume of the calculated area, mi, ri, and ui are the mass, position and displacement of atom i, u˙i=du/dt indicates the atomic velocity, rij = ri − rj represents the distance from atom i to j, and fij represents the force exerted by atom j on i.

The potential function has a great influence on the accuracy of MD simulations. In this paper, EAM potential function [17] is used to describe the interaction between Mg atoms. The total energy of atom i can be expressed as:

Ei=Fα(∑j≠iραβ(rij))+12∑j≠iϕαβ(rij)(2)

where the first term denotes the insertion energy, and F is a function of the electron density ρ of atom i; ϕαβ represents the interaction potential energy between the atom pairs, α and β are the element types. And j is the adjacent atom of the i, the number of which is determined by the cutoff radius of the potential, and rij is the distance between i and j. The relevant parameters can refer to the literature of Sun et al. [18] and the parameters can accurately describe the properties of atoms.

3  Results and Discussion

3.1 Deformation Mechanism

To study the deformation mechanism of polyMg, the change of atomic structure under tensile loading was analyzed. Fig. 2 shows the cross-sections of polyMg with different average grain sizes (8 and 16 nm) during the tensile process.

Figure 2: The atomic structure of polyMg under different strains (red: HCP, green: FCC, blue: BCC, gray: Other) (a) Grain size =  8 nm; (b) Grain size =  16 nm

As can be seen from Figs. 2a and 2b, when the strain is 0, there are a small number of defect atoms in the grains of all models, while the defect atoms are basically distributed at the grain boundaries during the elastic process. The proportion of grain boundary atoms is 24.3% for small-sized grains (the average grain size of 8 nm), which is significantly higher than that of grain boundary atoms (12.6%) for large-sized grains (average grain size of 16 nm). When the tensile strain of polyMg reaches 0.06, the grain boundary atomic structure of small-sized grains becomes chaotic and disordered, which indicates that violent movement occurs at the grain boundaries. The dislocations of large-sized grains nucleate at the grain boundaries and then propagate to the interior of the grains. During the tensile process, some atoms inside the grains are transformed from HCP to BCC or other structures.

As the strain is about 0.12, some small cracks begin to occur at the grain boundaries of the small-sized grains, and the deformation at the boundaries of the trigeminal grains further becomes larger. Dislocations are emitted to the inside of the grains from grain boundaries, and the atomic structure is converted from HCP to FCC and BCC structures. After the migration of the dislocation along the slip direction, the large grains split into two small grains. The dislocations of large-sized grains are generated from the boundary of grain and then slip within the grain. The movement can leave some stacking faults inside the grains. Some dislocations penetrate through the entire grain to form new grains, and some cracks occur at the grain boundaries.

When the strain is 0.2, it can be seen that there are more dislocations produced inside the grains of both samples, and the cracks at the grain boundaries are further expanded. The grain boundaries of the small grains are seriously deformed. The number of dislocations inside the grains is obviously more than that of the large grains, so the plasticity of the material is good. For larger-sized grains, it can be seen that the number of cracks increases, and the extent of the crack expansion further increases.

Therefore, the deformation mechanisms of polyMg are as follows: the plastic deformation for large average grain size is mainly carried out by dislocation slip and stacking faults inside the grains, while the plastic deformation is primarily the movement and slippage of the grain boundary for small grain size. However, the differences between the deformation mechanisms are not absolutely transformed. The movement and deformation of grain boundary can also be observed in larger-sized grains, while dislocations and stacking faults also exist in smaller grain-sized grains.

3.2 Size Effect

Fig. 3a shows the uniaxial tensile stress-strain curves of polyMg models with different average grain sizes. It can be seen that the stress firstly increases rapidly and reaches to the maximum value at strain 0.03∼0.05, which means that the material begins to enter the plastic deformation stage. Then the stress decreases significantly at the initial stage of plasticity, and gradually tends to decrease slowly when the grain size is greater than or equal to 10 nm. The downward trend of tensile stress in the plastic stage is always relatively gentle if the grain size is less than 10 nm.

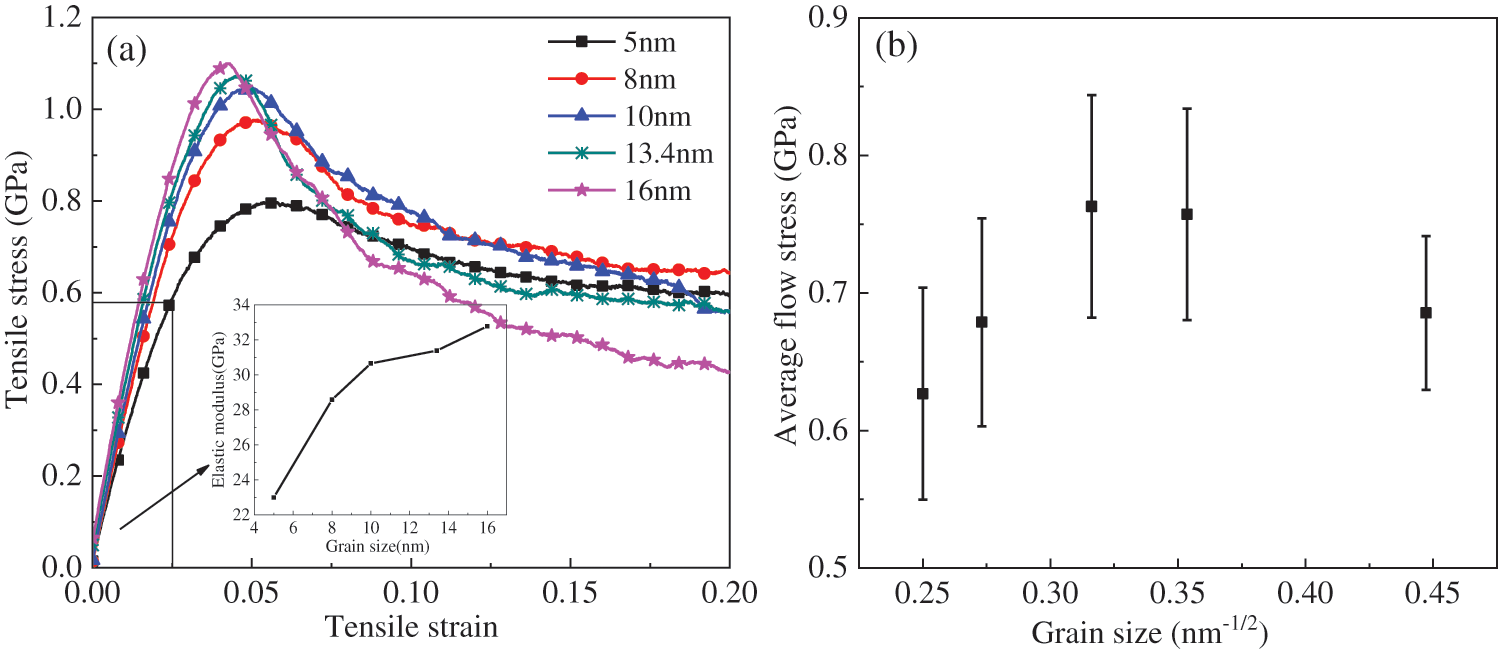
Figure 3: (a) Tensile stress-strain curves of polyMg under uniaxial tension; (b) The relationship between flow stress and grain size

The elastic modulus of polyMg can be obtained by calculating the slope of the linear elastic stage (strain between 0 and 0.025) of the stress-strain curves. From the relationship between the elastic modulus and the grain size shown in the black box in Fig. 3a, it can be seen that the elastic modulus of polyMg decreases with the decrease of grain size. For example, the elastic modulus is 24.42 GPa when the grain size is 5 nm and 34.43 GPa when the grain size is 16 nm. The reason can be concluded that the grain size is smaller, the atomic proportion and degree of grain boundary atoms are higher. According to the higher atomic energy of the grain boundary, a large number of defect atoms will also lead to the decrease of the elastic modulus of the materials. At the same time, the atoms at the grain boundary are arranged disorderly, and the equilibrium distance is greater than the distance between the atoms in the crystal. Therefore, the grain size decreases, the atoms at the grain boundary and the average distance increase. As a result, the strength of the crystal decreases, which also leads to the decrease of the elastic modulus of polyMg.

The flow stress is expressed by the average stress between the strain at 0.06 and 0.16. Fig. 3b shows the relationship between flow stress and the reciprocal square root of grain size. The calculated results show that the grain size of polyMg has a significant effect on the flow stress. As can be seen from the figure that when the grain size is greater than 10 nm, the flow stress decreases with the increase of the grain size, which shows the Hall-Petch effect, and when the grain size is less than 10 nm, the flow stress decreases as the grain size decreases, showing the inverse Hall-Petch effect. Most polycrystalline metals exhibit this kind of inverse Hall-Petch property when the grain size is less than 10 nm [4].

3.3 Temperature Effect

In order to study the effect of temperatures on the tensile mechanical properties of polyMg, the tensile mechanical behaviors of polyMg under different temperatures (200, 300, 400 and 500 K) were investigated. Fig. 4a shows the overall stress-strain curves of the model with an average grain size of 10 nm. The mechanical properties of polyMg are very sensitive to temperature. The maximum tensile stress and elastic modulus decreased with the increase of temperature.

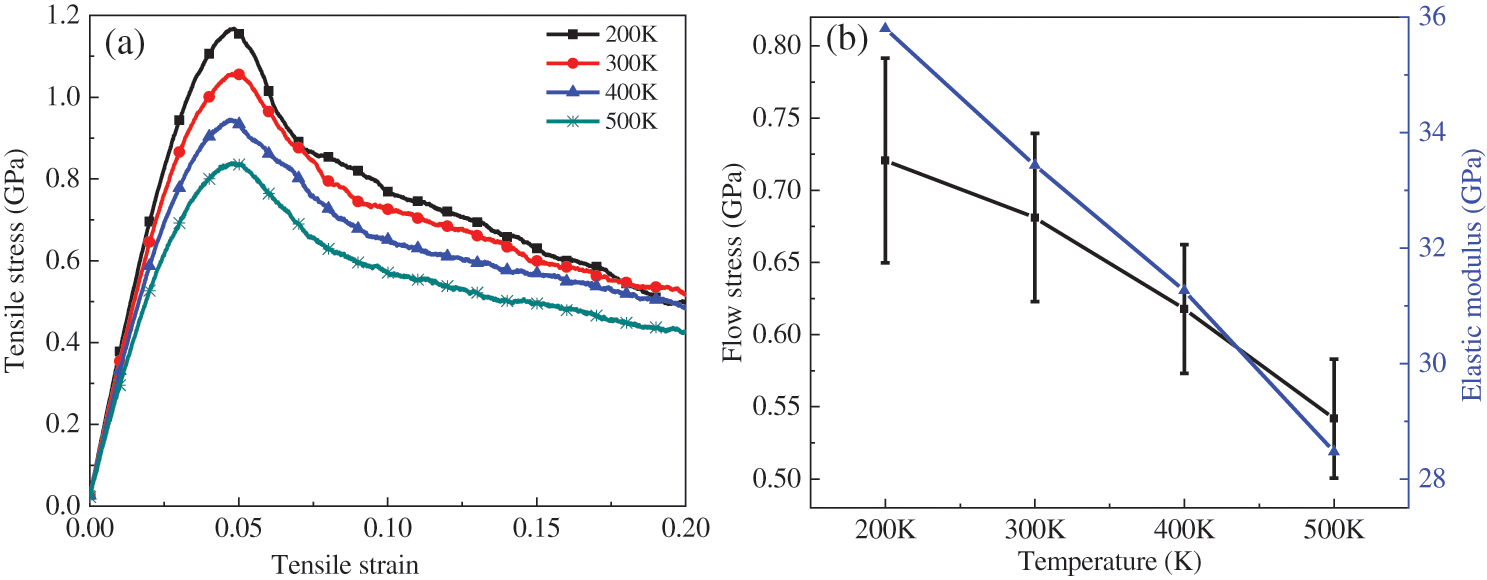
Figure 4: (a) The mechanical properties of polyMg under different temperatures; (b) The relationship between flow stress, elastic modulus, and temperature

The thermal motion of the atoms becomes more active, and the amplitude of the oscillation at the equilibrium position is greater as the temperature rises, so the mutual attraction between the atoms is relatively weaker. When an external loading is applied to the material, the atoms are more easily to break away from their equilibrium position. Therefore, the tensile strength and ultimate tensile strain of the material will decrease, and the mechanical properties will decrease with the increase of temperature.

Fig. 4b shows the relationship between elastic modulus and flow stress at different temperatures. The elastic modulus and flow stress of polyMg decreases linearly with the increase of temperature. When the temperature increases from 200 to 500 K, the elastic modulus decreases from 35.8 to 28.47 GPa, and the value reduces by 20.47%. The equation between the elastic modulus and the temperatures can be obtained by fitting the curve, as shown below:

E=−0.024⋅T+40.7(3)

In addition to thermal vibration, temperature also affects the kinetic energy of the material. As the kinetic energy increases, more defects will be appear in the structure due to the atomic movement, and plastic deformation will be easily reached. Furthermore, due to the structural change at high temperatures, the ability of polyMg to resist plastic deformation will be weakened. These factors will also reduce the flow stress of the material. The temperature has a softening effect on most metals, indicating that the higher the temperature, the more easily the metals reach the yield stage.

3.4 Strain Rate Effect

To investigate the effect of strain rate on the mechanical properties of polyMg, the uniaxial tensile calculations of polyMg are conducted under different strain rates (1 × 109∼2 × 1010 s−1) at 300 K. The stress-strain curves are shown in Fig. 5a. The stress curves rise linearly until the strain reaches 0.025. After the elastic liner stage, the stress gradually increases to a maximum value until the strain reaches 0.05∼0.07. When the strain rate is equal to or less than 8 × 109 s−1, the flow stress has a little change after the strain is greater than 0.1. The stress-strain curves are not consistent with others if the strain rate is equal to or more than 1 × 1010 s−1. For example, the elastic modulus and the maximum tensile stress values are much larger than the other values corresponding to other strain rates.

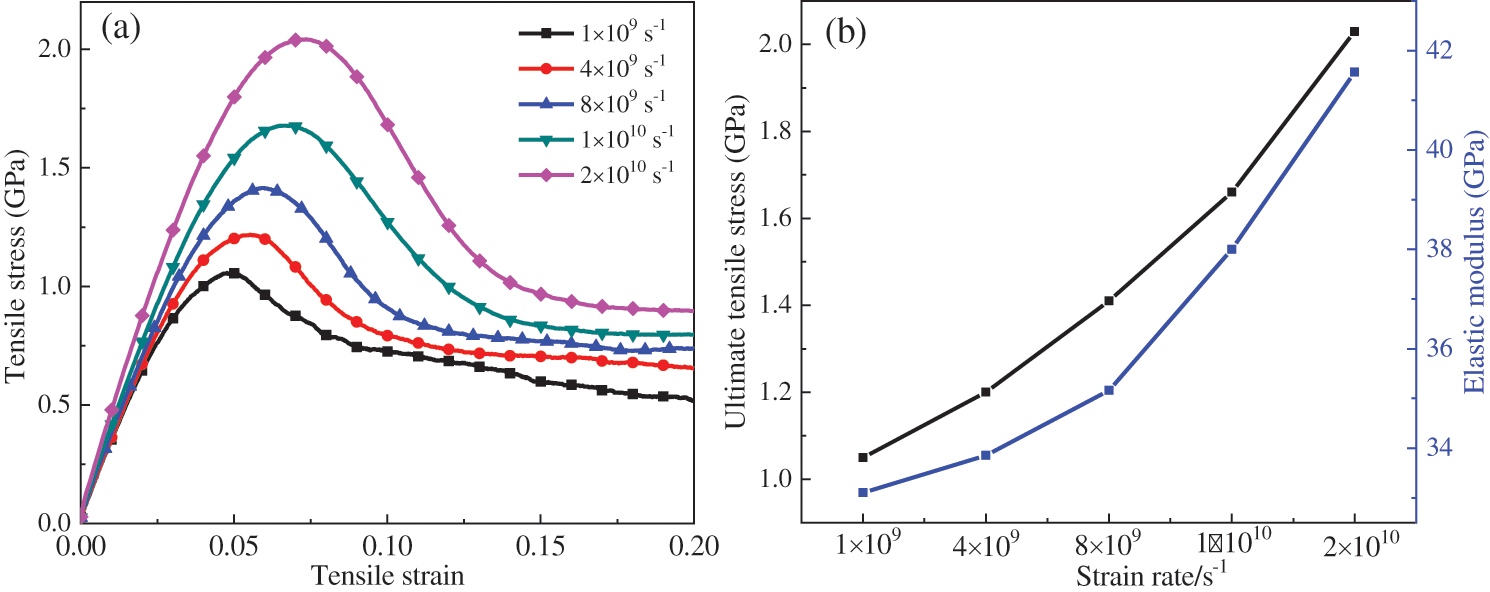
Figure 5: (a) The tensile curves at different strain rates; (b) The relationship between ultimate tensile stress, elastic modulus and strain rate

Fig. 5b shows the relationship between the ultimate tensile stress and elastic modulus for strain rates. It can be obtained that the values increase as the strain rate increases, which means that there is a strain rate hardening effect. The elastic modulus mainly depends on the bonding energy between atoms.

The dynamic loading effect of the entire process increases with the increase of strain rate, and the time for the entire system to uniformly dissipate the work done by the external load decreases, so the energy cannot be evenly distributed, resulting in the energy difference of individual atoms. The difference in the time and opportunity for each atom to reach or even exceed its bonding energy threshold is small if the applied strain rate value is small, resulting in an insignificant difference between elastic modulus and ultimate strain. The difference for each atom to reach or exceed its bonding energy threshold increases when the strain rate increases to a certain value, resulting in a larger difference between the elastic modulus and the ultimate strain.

The plastic strain occurs in the linear elastic phase at high strain rates. This plastic strain mainly occurs at the grain boundary because there is no dislocation movement inside the grain. At the same time, it can be seen that there is a significant bump in the stress-strain curves at a high strain rate. This is mainly because there is less enough time to generate dislocations at the beginning of plastic strain at high strain rates.

4  Conclusion

In this paper, the mechanical properties of polyMg under uniaxial tension are calculated by the MD simulation method, and the influences of different factors on the material properties are analyzed. The main conclusions are obtained as follows:

1)   The elastic modulus and maximum tensile stress of polyMg decrease with the decrease of grain size. When the grain size is greater than 10 nm, the flow stress decreases with the increase of grain size, showing the Hall-Petch effect. The flow stress decreases as the grain size decreases when the grain size is less than 10 nm, which shows the inverse Hall-Petch effect.

2)   The mechanical properties of polyMg decrease with the increase of temperature. When the temperature is 200 K, the elastic modulus is 35.8 GPa, and it rises to 28.47 GPa when the temperature is 500 K. The main reason is that the thermal motion of atoms becomes more intense as the temperature rises. When there is an external loading, the atoms are more likely to leave their equilibrium positions and become unstable, which reduces the performance of the material.

3)   The influence of strain rate on the mechanical properties of polyMg depends on different values. The calculated values of ultimate tensile stress and elastic modulus show that there is a strain rate hardening effect, and the increasing trend of different zones is inconsistent.

Acknowledgement: Thanks to Juan Ma for helping us to carefully revise the grammar and expressions of the full text. The author thanks TopEdit (https://www.topeditsci.com) for its linguistic assistance during the preparation of this manuscript.

Funding Statement: The author received no specific funding for this study.

Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.

References

 1.  Jain, J., Cizek, P., Poole, W. J., Barnett, M. R. (2013). Precipitate characteristics and their effect on the prismatic-slip-dominated deformation behaviour of an Mg–6 Zn alloy. Acta Materialia, 61, 4091–4102. DOI 10.1016/j.actamat.2013.03.033. [Google Scholar] [CrossRef]

 2.  Vahid, A., Hodgson, P., Li, Y. (2017). New porous Mg composites for bone implants. Journal of Alloys and Compounds, 724, 176–186. DOI 10.1016/j.jallcom.2017.07.004. [Google Scholar] [CrossRef]

 3.  Koch, C. C., Malow, T. R. (1999). The ductility problem in nanocrystalline materials. Materials Science Forum, 312–314, 565–574. DOI 10.4028/www.scientific.net/JMNM.2-6.565. [Google Scholar] [CrossRef]

 4.  Meyers, M. A., Mishra, A., Benson, D. J. (2006). Mechanical properties of nanocrystalline materials. Progress in Materials Science, 51(4), 427–556. DOI 10.1016/j.pmatsci.2005.08.003. [Google Scholar] [CrossRef]

 5.  Liu, J., Fan, X., Zheng, W., Singh, D. J., Shi, Y. (2020). Nanocrystalline gold with small size: Inverse Hall–Petch between mixed regime and super-soft regime. Philosophical Magazine, 100(18), 2335–2351. DOI 10.1080/14786435.2020.1765039. [Google Scholar] [CrossRef]

 6.  Mohammadzadeh, R. (2019). Analysis of plastic strain-enhanced diffusivity in nanocrystalline iron by atomistic simulation. Journal of Applied Physics, 125(13), 1–9. DOI 10.1063/1.5085659. [Google Scholar] [CrossRef]

 7.  Liu, B., Zhou, K., Zhong, K., Yao, Y. (2014). Effects of grain size and shape on mechanical properties of nanocrystalline copper investigated by molecular dynamics. Materials Science & Engineering A, 615, 92–97. DOI 10.1016/j.msea.2014.07.066. [Google Scholar] [CrossRef]

 8.  Zhang, T., Zhou, K., Chen, Z. Q. (2015). Strain rate effect on plastic deformation of nanocrystalline copper investigated by molecular dynamics. Materials Science and Engineering: A, 648(11), 23–30. DOI 10.1016/j.msea.2015.09.035. [Google Scholar] [CrossRef]

 9.  Chen, P., Zhang, Z., Liu, C., An, T., Qin, F. (2019). Temperature and grain size dependences of mechanical properties of nanocrystalline copper by molecular dynamics simulation. Modelling and Simulation in Materials Science and Engineering, 27(6), 1–16. DOI 10.1088/1361-651X/ab2621. [Google Scholar] [CrossRef]

10. Han, R. Q., Song, H. Y., Wang, J. Y., Li, Y. L. (2021). Strengthening mechanism of Al matrix composites reinforced by nickel-coated graphene: Insights from molecular dynamics simulation. Physica B: Condensed Matter, 601, 412620. DOI 10.1016/j.physb.2020.412620. [Google Scholar] [CrossRef]

11. Ridaa, A., Micoulautb, M., Rouhauda, E., Makke, A. (2019). Understanding the strain rate sensitivity of nanocrystalline copper using molecular dynamics simulations. Computational Materials Science, 172, 109294. DOI 10.1016/j.commatsci.2019.109294. [Google Scholar] [CrossRef]

12. Rojas-Nunez, J., Valencia, F., Gonzalez, R., Bringa, E. M., Allende, S. et al. (2019). Mechanical performance of lightweight polycrystalline Ni nanotubes. Computational Materials Science, 168, 81–86. DOI 10.1016/j.commatsci.2019.05.062. [Google Scholar] [CrossRef]

13. Saitoh, K. I., Kuramitsu, K., Sato, T., Takuma, M., Takahashi, Y. (2018). Molecular dynamics study on deformation mechanism of grain boundaries in magnesium crystal: Based on coincidence site lattice theory. Journal of Materials, 2018, 1–10. DOI 10.1155/2018/4153464. [Google Scholar] [CrossRef]

14. Hasan, M. S., Lee, R., Xu, W. (2020). Deformation nanomechanics and dislocation quantification at the atomic scale in nanocrystalline magnesium. Journal of Magnesium and Alloys, 2020(8), 1296–1303. DOI 10.1016/j.jma.2020.08.014. [Google Scholar] [CrossRef]

15. Chang, L., Zhou, C. Y., Li, J., He, X. H. (2018). Investigation on tensile properties of nanocrystalline titanium with ultra-small grain size. Computational Materials Science, 142, 135–144. DOI 10.1016/j.commatsci.2017.10.017. [Google Scholar] [CrossRef]

16. Chen, W., Fish, J. (2006). A mathematical homogenization perspective of virial stress. International Journal for Numerical Methods in Engineering, 67(2), 189–207. DOI 10.1002/nme.1622. [Google Scholar] [CrossRef]

17. Finnis, M. W., Sinclair, J. E. (1984). A simple empirical N-body potential for transition metals. Philosophical Magazine A, 50(1), 45–55. DOI 10.1080/01418618408244210. [Google Scholar] [CrossRef]

18. Sun, D. Y., Mendelev, M. I., Becker, C. A., Kudin, K., Haxhimali, T. et al. (2006). Crystal-melt interfacial free energies in hcp metals: A molecular dynamics study of Mg. Physics Review B, 73, 1–12. DOI 10.1103/PhysRevB.73.024116. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.