
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.017998
ARTICLE
Dombi-Normalized Weighted Bonferroni Mean Operators with Novel Multiple-Valued Complex Neutrosophic Uncertain Linguistic Sets and Their Application in Decision Making
1Department of Mathematics and Statistics, International Islamic University, Islamabad, 44000, Pakistan
2Department of Information Technology, Faculty of Science and Technology, Suan Sunandha Rajabhat University, Bangkok, 10300, Thailand
3Division of Computational Science, Faculty of Science, Prince of Songkla University, Hat Yai, Songkhla, 90110, Thailand
*Corresponding Author: Dulyawit Prangchumpol. Email: Dulyawit.pr@ssru.ac.th
Received: 22 June 2021; Accepted: 24 September 2021
Abstract: Although fuzzy set concepts have evolved, neutrosophic sets are attracting more attention due to the greater power of the structure of neutrosophic sets. The ability to account for components that are true, false or neither true nor false is useful in the resolution of real-life problems. However, simultaneous variations render neutrosophic sets unsuitable in specific circumstances. To enable the management of these sorts of issues, we combine the principle of multi-valued neutrosophic uncertain linguistic sets and complex fuzzy sets to develop the principle of multi-valued complex neutrosophic uncertain linguistic sets. Multi-valued complex neutrosophic uncertain linguistic sets can contain grades of truth, abstinence, and falsity, and uncertain linguistic terms, which are expressed as complex numbers whose real and imaginary parts are limited to the unit interval. Some important Dombi laws are elaborated along with Bonferroni mean operators, which offer a flexible general structure with modifiable factors. Bonferroni means aggregation operators perform a significant role in conveying the magnitude level of options and characteristics. To determine relationships among any number of attributes, we develop multi-valued complex neutrosophic uncertain linguistic Dombi-normalized weighted Bonferroni mean operators and discuss their important properties with some special cases. By using these laws, we can deploy the multi-attribute decision-making (MADM) technique using the novel principle of multi-valued complex neutrosophic uncertain linguistic sets. To determine the power and flexibility of the elaborated approach, we resolve some numerical examples based on the proposed operator. Finally, the work is validated with the help of comparative analysis, a discussion of its advantages, and geometric expressions of the elaborated theories.
Keywords: Multi-valued complex neutrosophic uncertain linguistic sets; Dombi normalized weighted Bonferroni mean operators; multi-attribute decision-making methods
MADM is widely applied to real-world problems, but due to the complicated and inconsistent information acquired, the use of crisp sets in these contexts often has limitations. To resolve the problems which occur in certain issues, Zadeh [1] elaborated the principle of the fuzzy set (FS). FSs are more powerful and effective than crisp sets and can contain the truth grade (TG) belonging to the unit interval. But in certain situations, the FS can fail. FSs do not work effectively when an element can either belong or not belong to the set. To deal with these situations, the intuitionistic FS (IFS) was elaborated by Atanassov [2]. IFS extends the FS to include the falsity grade (FG). The main advantage of the IFS is that the sum of both values belongs to the unit interval. IFS has modified FS to enable the management of inconsistent and awkward information in real-world problems. The powerful structure of IFS has been utilized by various scholars. Liu etal. [3] examined a viable weighted-based hybrid approach using interval-valued IFSs; Garg etal. [4] presented a similarity measure using right-angled triangles based on IFSs; Ejegwa etal. [5] initiated a statistical correlation algorithm using IFSs; Xue etal. [6] elaborated measure-based belief functions using IFSs; Aydin etal. [7] explored interval-valued intuitionistic parameterized interval-valued intuitionistic fuzzy soft sets; Szmidt etal. [8] proposed certain measures based on IFSs, and Ghosh etal. [9] elaborated a fixed charge solid transportation problem based on IFSs.
In several scenarios, the conception of IFS has been neglected if an intellectual faces data in the form of yes, abstinence, or no, then the use of IFSs is not effective. To deal with these situations, Smarandache elaborated the neutrosophic set (NS) [10] by extending the IFS to include the abstinence grade (AG). The main advantage of the NS is that sum of triplet values can belong to the unit interval
FS has typically failed when applied to information in the form of two-dimensions in a single set. To briefly explain two-dimensional information with the help of an example, let us assume an individual who needs to buy a vehicle and the crucial factors are the model and year of manufacture. Since the vehicle model changes with the year of manufacture, the decision-making procedure frequently changes. These issues cannot be demonstrated precisely with conventional speculations. Ramot etal. [21] elaborated the principle of complex FS (CFS) to resolve these types of problems. CFS is powerful and more effective than FS and covers the TG whose real and unreal parts belong to the unit interval. But in certain situations, the CFS can fail. CFS is not effective when a decision-maker faces a choice in the form of yes or no. To deal with these situations, Alkouri etal. [22] elaborated the principle of complex IFS (CIFS) by extending CFS to include the FG. The main advantage of CIFS is that the sum of the real part (also for the unreal part) of both values belongs to the unit interval. CIFS has enabled CFS to handle inconsistent and difficult information. Various scholars have utilized the powerful structure of CIFS. Rani etal. [23] initiated distance measures using CIFSs; Kumar etal. [24] developed complex intuitionistic soft sets; Garg etal. [25] elaborated information measures based on CIFSs; Ngan etal. [26] proposed quaternion numbers using CIFSs; Garg etal. [27] elaborated a correlation coefficient by using CIFSs; Rani etal. [28] explored power aggregation operators based on CIFSs; Quek etal. [29] initiated the algebraic structure of complex intuitionistic fuzzy soft sets, and Garg etal. [30] initiated Heronian mean operators using complex intuitionistic uncertain linguistic sets.
Yet, in certain situations, the principle of CIFS can fail. CIFS is not effective when responses can take the form of yes, abstinence, and no. To deal with these situations, Ali et al. elaborated the principle of complex NS (CNS) [31] by extending CIFS to include the AG. The main advantage of the CNS is that some of the real part (also unreal part) of triplet values belong to the interval unit
Nevertheless, in real-world problems, it is not unusual for decision-makers to express their thoughts as quantifiable interpretations. When a consultant assesses a client’s opinion, he may consider it suitable to employ linguistic phrases such as “very good”, “good”, or “medium”, to express an estimation. To manage these problems, Zadeh [39,40] probed the principle of the linguistic variable (LV) to illustrate the inclinations of decision-makers. Furthermore, the principle of 2-tuple LV was created by Herrera et al. [41]. Xu [42] initiated aggregation operators for uncertain linguistic sets (ULSs). Peng etal. [43] initiated power aggregation operators for multi-valued neutrosophic sets (MVNSs); Liu etal. [44] developed the PROMERHEE method using probability MVNSs; Peng etal. [45] explored MVNSs and their applications in decision-making techniques; Liu etal. [46] proposed an extension of the ARAS method using probability MVNSs; Ye etal. [47] initiated a correlation coefficient regarding MVNSs, and Yang etal. [48] developed the Dombi normal weighted Bonferroni mean operator for MVNULSs.
From current accomplishments, we know that operators dependent on Dombi operations have been proposed and applied to combine intuitionistic components, complex intuitionistic components, single-valued neutrosophic components, interval neutrosophic components, and neutrosophic cubic components. They have not been applied to complex MVNSs and MVCNULSs. There has been no exploration of the use of Dombi normalized weighted Bonferroni mean (DNWBM) operators on novel MVCNULNs data. Collection administrators perform numerical tasks like normal, total, count, max, min, and total, on the numeric property of the components in a set. Archimedean Bonferroni mean administrators are the summed-up types of basic collection administrators inferred to adapt to abnormal and convoluted data in genuine issues. Accumulation administrators are numerical capacities that are utilized to consolidate data. That is, they are utilized to consolidate N information (for instance, N mathematical qualities) in a solitary datum. The math mean and the weighted mean are the most notable collection administrators. The middle and the mode can likewise be collection administrators. The primary distinction between the number-crunching means and the weighted mean is that the last option grants us to weight vector various information as per their pertinence. There exist various conglomeration administrators that are applied relying upon the suppositions in the (information types) and the kind of data that we can consolidate in the model. For instance, fluffy integrals license us to allocate pertinence to sets of data sources and not exclusively to individual sources just like the case for the weighted mean. Math and mathematical accumulation administrators are extraordinary sorts of Archimedean Bonferroni mean administrators.
It is important to expand DNWBM dependent on Dombi activities to MVCNULNs. In general, a DNWBM operator has the following qualities. Initially, it has greater flexibility with general boundaries. Then, it can consider both the relationship and the weight of many contentions. Based on the above analysis, the main advantages of the initiated MVCNULSs are discussed below:
(1) If we choose the value of TG, AG, and FG in the form of singleton sets in the initiated MVCNULSs, then the MVCNULSs are changed for complex neutrosophic uncertain linguistic sets.
(2) If we choose the value of TG, AG, and FG in the form of singleton sets and if the value of an uncertain linguistic set is zero in the initiated MVCNULSs, then the MVCNULSs are changed for complex neutrosophic sets.
(3) If we choose the value of the uncertain linguistic set is zero in the initiated MVCNULSs, then the MVCNULSs are changed for multi-valued complex neutrosophic sets.
(4) If we choose the value of AG in the form of zero in the initiated MVCNULSs, then the MVCNULSs are changed for multi-valued complex intuitionistic uncertain linguistic sets.
(5) If the value of AG and FG is zero in the initiated MVCNULSs, then the MVCNULSs are changed for multi-valued complex fuzzy uncertain linguistic sets.
The graphical expressions of the initiated works in this study are presented Fig. 1.
Figure 1: Expressions of the presented approaches
MVCNULSs are more suitable for dealing with quantitative or subjective data in addressing MADM and MAGDM issues. Considering these benefits, the objectives of the paper are the following:
(1) To develop the principle of MVCNULS and their important Dombi laws are also elaborated.
(2) To determine the relationship among any number of attributes, we develop the multi-valued complex neutrosophic uncertain linguistic Dombi normalized weighted Bonferroni mean (MVCNULDNWBM) operator and illustrate its important properties with some specific cases.
(3) To utilize a MADM technique using the novel principle of MVCNULS. To determine the power and flexibility of the elaborated approaches, we resolve some numerical examples using the proposed operator.
(4) The priority of the elaborated work is to determine the advantages and geometric expression of the elaborated theories with the help of comparative analysis.
This study proceeds as follows: In Section 2, we briefly recall some prevailing ideas such as MVNSs and their algebraic laws. The principle and laws of ULSs are also revised with Dombi t-norm (DTN) and Dombi t-conorm (DTCN). The notion of the NWBM operator is also discussed. In Section 3, we combine the principle of MVNULSs and CFSs to develop the principle of MVCNULSs. In Section 4, some important Dombi laws are elaborated. We present the multi-valued complex neutrosophic uncertain linguistic Dombi-normalized weighted Bonferroni mean (MVCNULDNWBM) operator and discuss important properties using specific cases. In Section 5, we utilize the MADM technique with the novel principle of MVCNULS. To determine the strength and flexibility of the elaborated approach, we resolve some numerical examples using the proposed operator. Finally, the work is validated with the help of comparative analysis, advantages, and geometric expression of the elaborated theories. The conclusions drawn are presented in Section 6.
Certain extensions of the FS have been proposed and utilized in the context of aggregation operators, measures, and methods to easily determine the reliability and consistency of the prevailing ideas. The theory of the MVNS is an important and useful principle for the management of awkward and inconclusive information. We will briefly recall some prevailing ideas such as MVNSs and their algebraic laws. The principle of ULSs and their laws are also revised with Dombi t-norm (DTN) and Dombi t-conorm (DTCN). The notion of the NWBM operator is also discussed at the end of this section. In the overall study, the universal set is specified by
Definition 1: [43] A MVNS
where
Moreover, by using any MVNN
To determine relationships among any number of attributes, we define the ordered relations which are stated below:
1. When
2. When
3. When
1. When
2. When
3. When
Definition 2: [42] For a ULS
Numerous scholars have utilized different sorts of t-norm and t-conorm, but the DTN and DTVN offer a flexible arrangement with modifiable factors. On the other hand, DTN and DTVN also perform a significant role in conveying the magnitude level of options and characteristics. Further, the DTN and DTVN are illustrated in the shape of (12) and (13), such that
Definition 3: [48] For any two-real numbers g and h with
Definition 4: [48] Let
where
3 Multi-Valued Complex Neutrosophic Uncertain Linguistic Sets
The principle of FSs has been modified, but the principle of NSs has received more attention due to its powerful structure that includes the TG, AG, and FG which fulfill a need in real-world problems but fail in the face of variations at specific times. Consequently, to manage these issues, we combine the principle of MVNULSs and CFSs to develop the MVCNULS. The MVCNULS contains the TG, AG, FG, and uncertain linguistic terms in the form of complex numbers whose real and unreal parts are limited to the unit interval.
Definition 5: A MVCNULS
where
For any two MVCNULNs
Moreover, by using any MVCNULN
where
1. When
2. When
3. When
1. When
2. When
3. When
4 Dombi Normalized Weighted Bonferroni Mean Operators Based on MVCNULSs
When aggregating any two MVCNULNs, the BM operators are more flexible than other operators. Different operators have been utilized in the environment of fuzzy sets and their generalizations. The goal of this study is to elaborate some important Dombi laws. Additionally, BM operators offer a flexible arrangement with modifiable factors because of Bonferroni’s general structure. On the other hand, BM aggregation operators perform a significant role in conveying the magnitude level of options and characteristics. To determine the relationship among any number of attributes, we present the MVCNULDNWBM operator and discuss its important properties in some special cases.
Definition 6: For any two MVCNULNs
Theorem 1: For any two MVCNULNs
1.
2.
3.
4.
5.
6.
Proof: Straightforward.
Definition 7: For any family of MVCNULNs
where
Theorem 2: For any family of MVCNULNs
where
real part of truth grade
Proof: See the Appendix section.
By choosing the value of weight vectors
Property 1: For any family of MVCNULNs
Proof: See the Appendix section.
Property 2: For any family of MVCNULNs
Proof: See the Appendix section.
Based on the ideas proposed above, we will develop the multi-attribute decision-making technique to determine the reliability and consistency of the elaborated operators.
5 MADM Method Based on Proposed MVCNULSs
Aggregation operators, measures, and methods have been used in the environments of IFSs, PFSs, IVIFSs, IVPFSs, CIFSs, CIVIFSs, NSs, CNSs, and applied in the MADM technique to determine the consistency and strength of current works. But to date, no one has proposed the application of any kind of operator to MVCNULSs in a MADM-based model. The goal of this manuscript is to utilize DNWBM operators based on MVCNULSs to determine the strength of the elaborated work. For this, we chose a group of alternatives
Step 1: Develop the decision matrix, whose every item is in the form of MVCNULNs.
Step 2: Use the MVCNULDNWBM operator to aggregate the entries of the decision matrix.
Step 3: By using the score function, we find the Score values of the aggregated values of Step2.
Step 4: Rank all alternatives and examine the best one.
As shown above, we illustrate certain numerical examples to determine the consistency and validity of the elaborated operators.
Example 1: With the rapid advance of financial globalization, and the developing climate of competition, the rivalry between ventures has become a contest between supply chains. The variety of items entering the market is expanding, and the life cycles of new items are becoming shorter. The instability of the market and other elements drives the search for viable inventory networks, and partnerships with different ventures are essential to improve focus and resist external risks. The critical measure to accomplish this objective is provider choice. Hence, the provider choice issue has acquired a great deal of importance, whether in respect of inventory network or the executive’s decision. To delineate our proposed technique in this article, we use MVCNULNs to give a mathematical guide to choosing green providers in a green inventory network. For this, we choose a family of five possible green suppliers in green supplier chain management
To resolve the above problem, we choose a family of four weight vectors, 0.3, 0.2, 0.3, 0.2. Then, by using the above family of n alternatives and m attributes, we develop an algorithm whose steps are as follows:
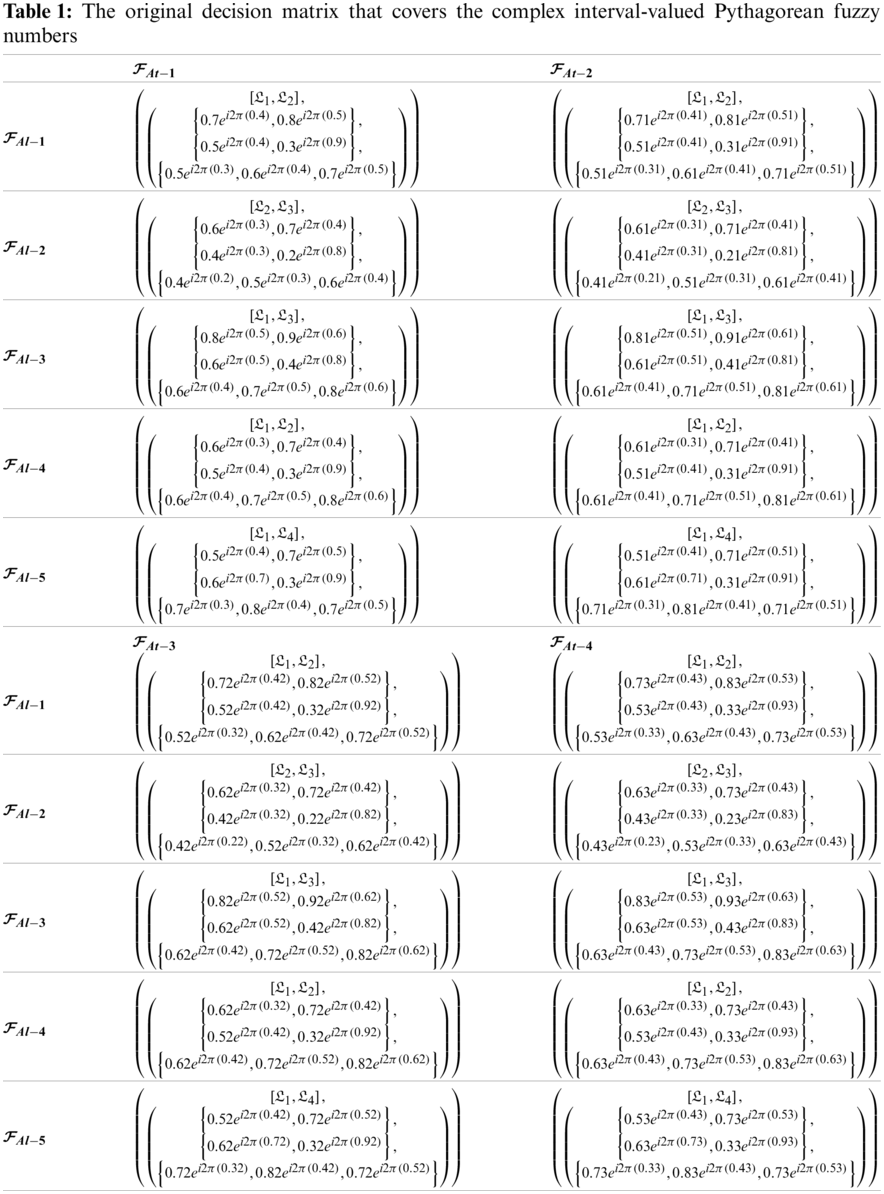
Step 1: We develop the decision matrix, whose every item is expressed in the form of MVCNULNs in Table 1.
Step 2: The MVCNULDNWBM operators used to aggregate the entries of the decision matrix are discussed below:
Step 3: By using the score function, we find the Score values of the aggregated values of Step 2, which are shown below:
Step 4: By using the above Score values, we rank all alternatives and examine the best one such that
or,
Therefore, from the above analysis,
As shown above, by using different values of the parameters
The graphical expression of the information in Table 2 is presented in Fig. 2.
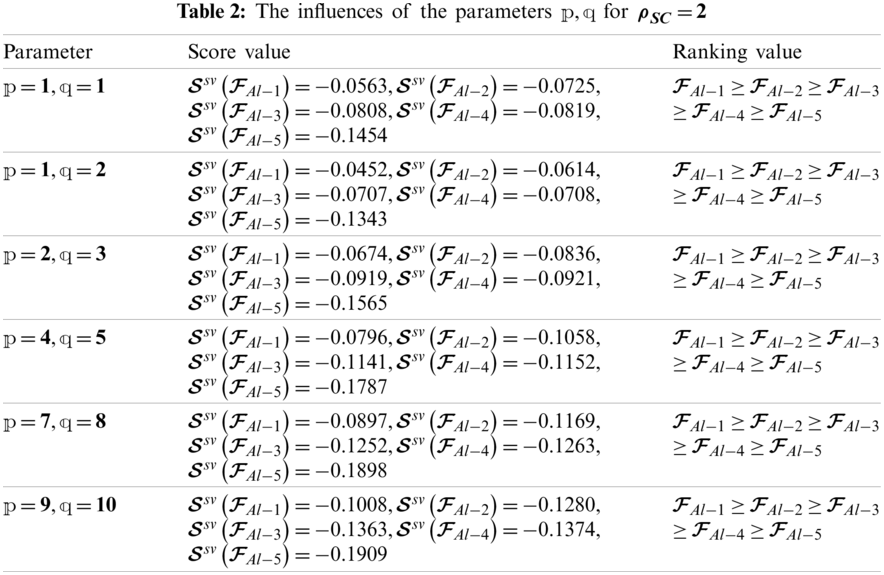
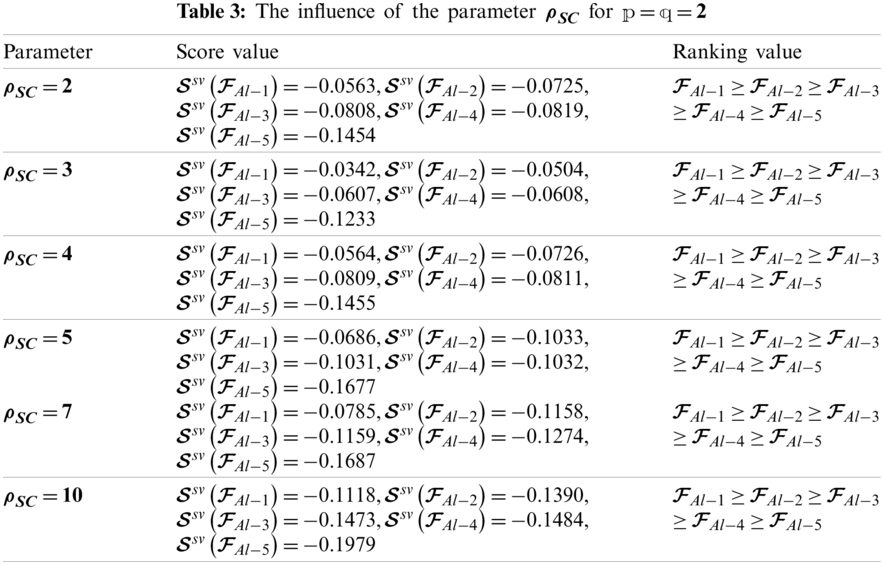
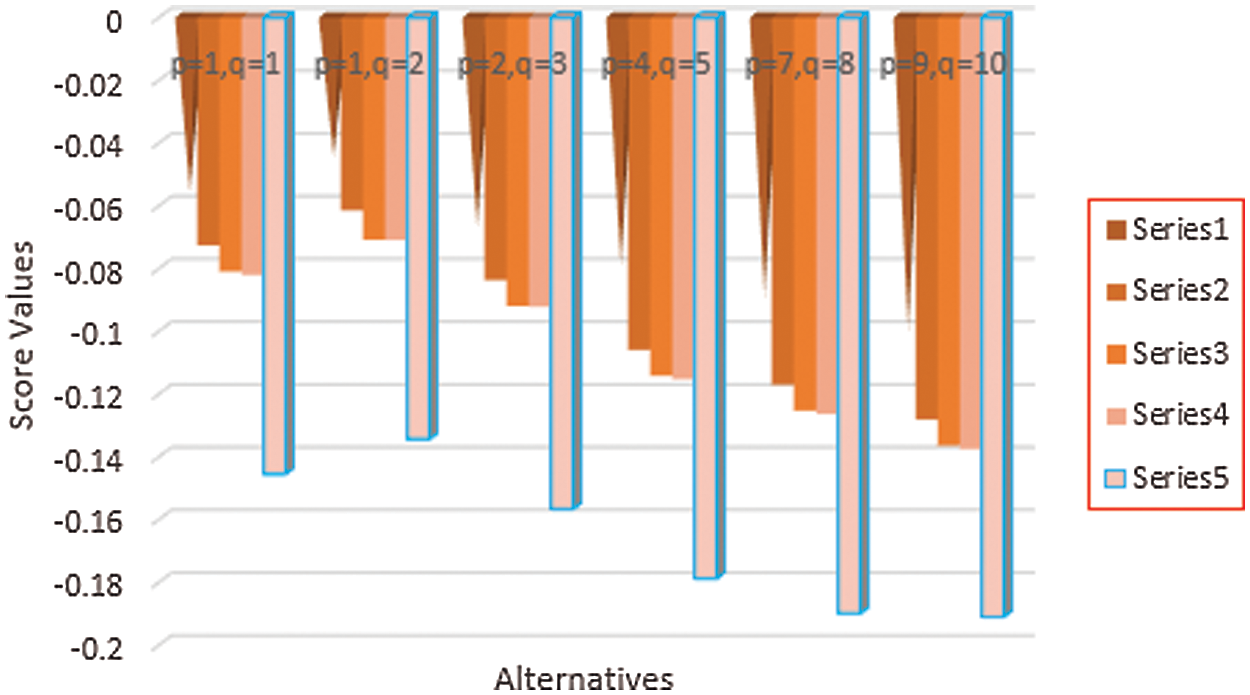
Figure 2: Geometrical expressions of the information in Table 2
Similarly, as shown above, by using the same value of parameters
By using the prevailing works in [43,48,49], the sensitive works are diagnosed below:
1. Power AOs for MVNS was invented by Peng etal. [43], which includes the mixture of power AOs with MVNSs. But a lot of deficiencies exists in [43] under MVNS, because the work in [43] is the particular part of invented works under MVCNULSs. For proposed work is not difficult to handle the data in Peng etal. [43], but the converse is very problematic.
2. DNWBM for MVNULS was invented by Yang etal. [48], which includes the mixture of BM operators with MVNULS s. But a lot of deficiencies exists in [48] under MVNULS, because the work in [48] is the particular part of invented works under MVCNULSs. For proposed work is not difficult to handle the data in Yang etal. [48], but the converse is very problematic.
3. Liu etal. [49] stated the BM operators for MVNSs, which discuss the MVNSs and BM works. But a lot of deficiencies exists in [49] under MVNS, because the work in [49] is the particular part of invented works under MVNLSs. For proposed work is not difficult to handle the data in Liu etal. [49], but the converse is very problematic.
A graphical expression of the information in Table 3 is presented in Fig. 3.
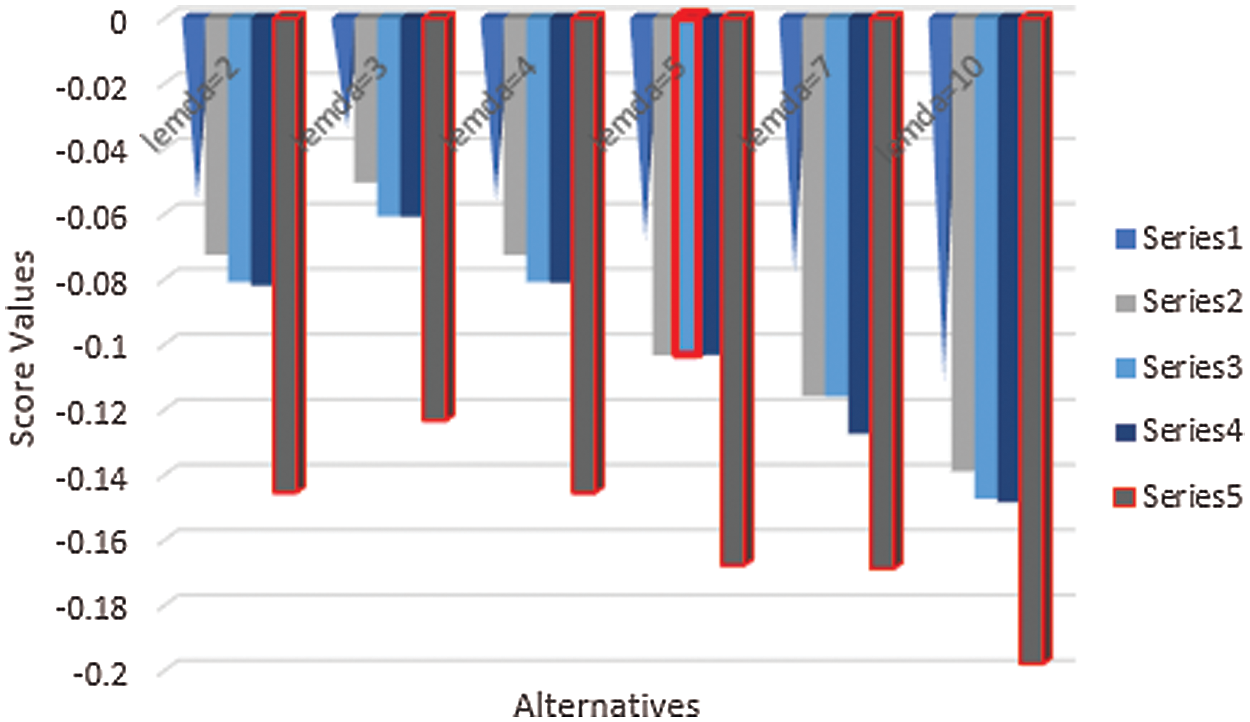
Figure 3: Graphical expressions of the information in Table 3
Hence, our considerations works are beneficial for utilizing in the region of medical areas and decision analysis.
In this study, we developed the principle of multi-valued neutrosophic uncertain linguistic sets and their important Dombi laws were also elaborated by using the investigated multi-valued neutrosophic uncertain linguistic sets. Further, we developed a multi-valued complex neutrosophic uncertain linguistic Dombi-normalized weighted Bonferroni mean operator and discussed important properties of the operator with some specific cases. By using these laws, we deployed the multiple attribute decision making technique under the novel principle of multi-valued neutrosophic uncertain linguistic sets. To determine the strength and flexibility of the elaborated approaches, we resolved some numerical examples based on the proposed operator. Finally, the elaborated work was validated with the help of comparative analysis, a demonstration of its advantages, and geometric expressions.
In the future, we will try to modify the prevailing principle of complex q-rung orthopair fuzzy sets [50], Complex spherical fuzzy sets [51], T-spherical fuzzy sets [52], bipolar soft sets [53], and others [54–57], to generalize and expand the value of this work.
Acknowledgement: Thanks to the co-authors for their help in the research process, for providing language assistance, writing assistance and proofreading for this article.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. DOI http://dx.doi.org/10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
2. Atanassov, K. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]
3. Liu, S., Yu, W., Chan, F. T., Niu, B. (2021). A variable weight-based hybrid approach for multi-attribute group decision making under interval-valued intuitionistic fuzzy sets. International Journal of Intelligent Systems, 36(2), 1015–1052. DOI 10.1002/int.22329. [Google Scholar] [CrossRef]
4. Garg, H., Rani, D. (2021). Novel similarity measure based on the transformed right-angled triangles between intuitionistic fuzzy sets and its applications. Cognitive Computation, 13(2), 447–465. DOI 10.1007/s12559-020-09809-2. [Google Scholar] [CrossRef]
5. Ejegwa, P. A., Onyeke, I. C. (2021). Intuitionistic fuzzy statistical correlation algorithm with applications to multicriteria-based decision-making processes. International Journal of Intelligent Systems, 36(3), 1386–1407. DOI 10.1002/int.22347. [Google Scholar] [CrossRef]
6. Xue, Y., Deng, Y., Garg, H. (2021). Uncertain database retrieval with measure-Based belief function attribute values under intuitionistic fuzzy set. Information Sciences, 546(8), 436–447. DOI 10.1016/j.ins.2020.08.096. [Google Scholar] [CrossRef]
7. Aydın, T., Enginoğlu, S. (2021). Interval-valued intuitionistic fuzzy parameterized interval-valued intuitionistic fuzzy soft sets and their application in decision-making. Journal of Ambient Intelligence and Humanized Computing, 12(1), 1541–1558. DOI 10.1007/s12652-020-02227-0. [Google Scholar] [CrossRef]
8. Szmidt, E., Kacprzyk, J., Bujnowski, P. (2014). How to measure the amount of knowledge conveyed by Atanassov’s intuitionistic fuzzy sets. Information Sciences, 257(3), 276–285. DOI 10.1016/j.ins.2012.12.046. [Google Scholar] [CrossRef]
9. Ghosh, S., Roy, S. K., Ebrahimnejad, A., Verdegay, J. L. (2021). Multi-objective fully intuitionistic fuzzy fixed-charge solid transportation problem. Complex & Intelligent Systems, 7(2), 1009–1023. DOI 10.1007/s40747-020-00251-3. [Google Scholar] [CrossRef]
10. Smarandache, F. (1998). Neutrosophy: Neutrosophic probability, set, and logic: Analytic synthesis & synthetic analysis. American Research Press. [Google Scholar]
11. Zavadskas, E. K., Bausys, R., Lescauskiene, I., Usovaite, A. (2021). MULTIMOORA under interval-valued neutrosophic sets as the basis for the quantitative heuristic evaluation methodology HEBIN. Mathematics, 9(1), 66. DOI 10.3390/math9010066. [Google Scholar] [CrossRef]
12. Tan, R. P. (2021). Decision-making method based on new entropy and refined single-valued neutrosophic sets and its application in typhoon disaster assessment. Applied Intelligence, 51(1), 283–307. DOI 10.1007/s10489-020-01706-3. [Google Scholar] [CrossRef]
13. Ye, J. (2021). Entropy measures of simplified neutrosophic sets and their decision-making approach with positive and negative arguments. Journal of Management Analytics, 8(2), 252–266. DOI 10.1080/23270012.2021.1885513. [Google Scholar] [CrossRef]
14. Abdullah, L., Ong, Z., Mohd Mahali, S. (2021). Single-valued neutrosophic DEMATEL for segregating types of criteria: A case of subcontractors’ selection. Journal of Mathematics, 2021(4), 1–12. DOI 10.1155/2021/6636029. [Google Scholar] [CrossRef]
15. Tufail, Z., Shahid, A. R., Raza, B., Akram, T., Janjua, U. I. (2021). Extraction of a region of interest from brain MRI by converting images into a neutrosophic domain using the modified S-function. Journal of Medical Imaging, 8(1), 014003. DOI 10.1117/1.JMI.8.1.014003. [Google Scholar] [CrossRef]
16. Du, S., Ye, J., Yong, R., Zhang, F. (2021). Some aggregation operators of neutrosophic Z-numbers and their multicriteria decision making method. Complex & Intelligent Systems, 7(1), 429–438. DOI 10.1007/s40747-020-00204-w. [Google Scholar] [CrossRef]
17. Wang, L., Bao, Y. L. (2021). A note on New aggregation operators of single-valued neutrosophic hesitant fuzzy set and their application in multi-attribute decision making. Pattern Analysis and Applications, 24(2), 801–803. DOI 10.1007/s10044-020-00928-y. [Google Scholar] [CrossRef]
18. Wei, G., Wu, J., Guo, Y., Wang, J., Wei, C. (2021). An extended COPRAS model for multiple attribute group decision making based on a single-valued neutrosophic 2-tuple linguistic environment. Technological and Economic Development of Economy, 27(2), 353–368. DOI 10.3846/tede.2021.14057. [Google Scholar] [CrossRef]
19. Jana, C., Pal, M. (2021). Multi-criteria decision making process based on some single-valued neutrosophic Dombi power aggregation operators. Soft Computing, 33(6), 4055. DOI 10.1007/s00500-020-05509-z. [Google Scholar] [CrossRef]
20. Zhao, M., Wei, G., Wu, J., Guo, Y., Wei, C. (2021). TODIM method for multiple attribute group decision making based on cumulative prospect theory with 2-tuple linguistic neutrosophic sets. International Journal of Intelligent Systems, 36(3), 1199–1222. DOI 10.1002/int.22338. [Google Scholar] [CrossRef]
21. Ramot, D., Milo, R., Friedman, M., Kandel, A. (2002). Complex fuzzy sets. IEEE Transactions on Fuzzy Systems, 10(2), 171–186. DOI 10.1109/91.995119. [Google Scholar] [CrossRef]
22. Alkouri, A., Salleh, A. R. (2012). Complex intuitionistic fuzzy sets. AIP Conference Proceedings, 1482(1), pp. 464–470, Puertollano, Spain: American Institute of Physics. [Google Scholar]
23. Rani, D., Garg, H. (2017). Distance measures between the complex intuitionistic fuzzy sets and their applications to the decision-making process. International Journal for Uncertainty Quantification, 7(5), 423–439. DOI 10.1615/Int.J.UncertaintyQuantification.2017020356. [Google Scholar] [CrossRef]
24. Kumar, T., Bajaj, R. K. (2014). On complex intuitionistic fuzzy soft sets with distance measures and entropies. Journal of Mathematics, 2014(3), 1–12. DOI 10.1155/2014/972198. [Google Scholar] [CrossRef]
25. Garg, H., Rani, D. (2019). Some results on information measures for complex intuitionistic fuzzy sets. International Journal of Intelligent Systems, 34(10), 2319–2363. DOI 10.1002/int.22127. [Google Scholar] [CrossRef]
26. Ngan, R. T., Ali, M., Tamir, D. E., Rishe, N. D., Kandel, A. (2020). Representing complex intuitionistic fuzzy sets by quaternion numbers and applications to decision making. Applied Soft Computing, 87(4), 105961. DOI 10.1016/j.asoc.2019.105961. [Google Scholar] [CrossRef]
27. Garg, H., Rani, D. (2019). A robust correlation coefficient measure of complex intuitionistic fuzzy sets and their applications in decision-making. Applied Intelligence, 49(2), 496–512. DOI 10.1007/s10489-018-1290-3. [Google Scholar] [CrossRef]
28. Rani, D., Garg, H. (2018). Complex intuitionistic fuzzy power aggregation operators and their applications in multicriteria decision-making. Expert Systems, 35(6), e12325. DOI 10.1111/exsy.12325. [Google Scholar] [CrossRef]
29. Quek, S. G., Selvachandran, G., Davvaz, B., Pal, M. (2019). The algebraic structures of complex intuitionistic fuzzy soft sets are associated with groups and subgroups. Scientia Iranica, 26(3), 1898–1912. [Google Scholar]
30. Garg, H., Ali, Z., Gwak, J., Mahmood, T., Aljahdali, S. (2021). Some complex intuitionistic uncertain linguistic heronian mean operators and their application in multiattribute group decision making. Journal of Mathematics, 2021(6), 1–31. DOI 10.1155/2021/9986704. [Google Scholar] [CrossRef]
31. Ali, M., Smarandache, F. (2017). Complex neutrosophic set. Neural Computing and Applications, 28(7), 1817–1834. DOI 10.1007/s00521-015-2154-y. [Google Scholar] [CrossRef]
32. Broumi, S., Bakali, A., Talea, M., Smarandache, F., Singh, P. K. et al. (2019). Bipolar complex neutrosophic sets and their application in decision-making problems. In: Fuzzy multi-criteria decision-making using neutrosophic sets, pp. 677–710. Cham: Springer. [Google Scholar]
33. Dat, L. Q., Thong, N. T., Ali, M., Smarandache, F., Abdel-Basset, M. et al. (2019). Linguistic approaches to interval complex neutrosophic sets in decision making. IEEE Access, 7, 38902–38917. DOI 10.1109/ACCESS.2019.2902841. [Google Scholar] [CrossRef]
34. Singh, P. K. (2018). Complex neutrosophic concept lattice and its applications to air quality analysis. Chaos, Solitons & Fractals, 109(7), 206–213. DOI 10.1016/j.chaos.2018.02.034. [Google Scholar] [CrossRef]
35. Quek, S. G., Broumi, S., Selvachandran, G., Bakali, A., Talea, M. et al. (2018). Some results on the graph theory for complex neutrosophic sets. Symmetry, 10(6), 190. DOI 10.3390/sym10060190. [Google Scholar] [CrossRef]
36. Manna, S., Basu, T. M., Mondal, S. K. (2020). A soft set based VIKOR approach for some decision-making problems under complex neutrosophic environment. Engineering Applications of Artificial Intelligence, 89(7), 103432. DOI 10.1016/j.engappai.2019.103432. [Google Scholar] [CrossRef]
37. Li, D. F., Mahmood, T., Ali, Z., Dong, Y. (2020). Decision making based on interval-valued complex single-valued neutrosophic hesitant fuzzy generalized hybrid weighted averaging operators. Journal of Intelligent & Fuzzy Systems, 38(4), 4359–4401. DOI 10.3233/JIFS-191005. [Google Scholar] [CrossRef]
38. Ali, Z., Mahmood, T. (2020). Complex neutrosophic generalised dice similarity measures and their application to decision making. CAAI Transactions on Intelligence Technology, 5(2), 78–87. DOI 10.1049/trit.2019.0084. [Google Scholar] [CrossRef]
39. Zadeh, L. A. (1975). The concept of a linguistic variable and its application to approximate reasoning–-I. Information Sciences, 8(3), 199–249. DOI 10.1016/0020-0255(75)90036-5. [Google Scholar] [CrossRef]
40. Zadeh, L. A. (1975). The concept of a linguistic variable and its application to approximate reasoning–-II. Information Sciences, 8(4), 301–357. DOI 10.1016/0020-0255(75)90046-8. [Google Scholar] [CrossRef]
41. Herrera, F., Martínez, L. (2000). A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Transactions on Fuzzy Systems, 8(6), 746–752. DOI 10.1109/91.890332. [Google Scholar] [CrossRef]
42. Xu, Z. (2004). Uncertain linguistic aggregation operators based approach to multiple attribute group decision making under uncertain linguistic environment. Information Sciences, 168(1–4), 171–184. DOI 10.1016/j.ins.2004.02.003. [Google Scholar] [CrossRef]
43. Peng, J. J., Wang, J. Q., Wu, X. H., Wang, J., Chen, X. H. (2015). Multi-valued neutrosophic sets and power aggregation operators with their applications in multi-criteria group decision-making problems. International Journal of Computational Intelligence Systems, 8(2), 345–363. DOI 10.1080/18756891.2015.1001957. [Google Scholar] [CrossRef]
44. Liu, P., Cheng, S., Zhang, Y. (2019). An extended multi-criteria group decision-making PROMETHEE method based on probability multi-valued neutrosophic sets. International Journal of Fuzzy Systems, 21(2), 388–406. DOI 10.1007/s40815-018-0572-6. [Google Scholar] [CrossRef]
45. Peng, J. J., Wang, J. Q. (2015). Multi-valued neutrosophic sets and their application in multi-criteria decision-making problems. Neutrosophic Sets and Systems, 10(1), 3–17. [Google Scholar]
46. Liu, P., Cheng, S. (2019). An extension of ARAS methodology for multi-criteria group decision-making problems within probability multi-valued neutrosophic sets. International Journal of Fuzzy Systems, 21(8), 2472–2489. DOI 10.1007/s40815-019-00737-4. [Google Scholar] [CrossRef]
47. Ye, J., Song, J., Du, S. (2020). Correlation coefficients of consistency neutrosophic sets regarding neutrosophic multi-valued sets and their multi-attribute decision-making method. International Journal of Fuzzy Systems, 8(1), 338. DOI 10.1007/s40815-020-00983-x. [Google Scholar] [CrossRef]
48. Yang, L., Li, B. (2020). Multiple-valued neutrosophic uncertain linguistic sets with Dombi normalized weighted Bonferroni mean operator and their applications in multiple attribute decision-making problems. IEEE Access, 8, 5906–5927. DOI 10.1109/ACCESS.2019.2963459. [Google Scholar] [CrossRef]
49. Liu, P., Zhang, L., Liu, X., Wang, P. (2016). Multi-valued neutrosophic number Bonferroni mean operators with their applications in multiple attribute group decision making. International Journal of Information Technology & Decision Making, 15(5), 1181–1210. DOI 10.1142/S0219622016500346. [Google Scholar] [CrossRef]
50. Ali, Z., Mahmood, T. (2020). Maclaurin symmetric mean operators and their applications in the environment of complex q-rung orthopair fuzzy sets. Computational and Applied Mathematics, 39(3), 36. DOI 10.1007/s40314-020-01145-3. [Google Scholar] [CrossRef]
51. Ali, Z., Mahmood, T., Yang, M. S. (2020). TOPSIS method based on complex spherical fuzzy sets with bonferroni mean operators. Mathematics, 8(10), 1739. DOI 10.3390/math8101739. [Google Scholar] [CrossRef]
52. Mahmood, T., Ullah, K., Khan, Q., Jan, N. (2019). An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Computing and Applications, 31(11), 7041–7053. DOI 10.1007/s00521-018-3521-2. [Google Scholar] [CrossRef]
53. Mahmood, T. (2020). A novel approach towards bipolar soft sets and their applications. Journal of Mathematics, 2020(5), 1–11. DOI 10.1155/2020/4690808. [Google Scholar] [CrossRef]
54. Garg, H. (2018). Linguistic Pythagorean fuzzy sets and its applications in the multiattribute decision-making process. International Journal of Intelligent Systems, 33(6), 1234–1263. DOI 10.1002/int.21979. [Google Scholar] [CrossRef]
55. Garg, H. (2016). A novel correlation coefficient between Pythagorean fuzzy sets and their applications to decision-making processes. International Journal of Intelligent Systems, 31(12), 1234–1252. DOI 10.1002/int.21827. [Google Scholar] [CrossRef]
56. Riaz, M., Hashmi, M. R. (2019). Linear Diophantine fuzzy set and its applications towards multi-attribute decision-making problems. Journal of Intelligent & Fuzzy Systems, 37(4), 5417–5439. DOI 10.3233/JIFS-190550. [Google Scholar] [CrossRef]
57. Riaz, M., Hashmi, M. R., Kalsoom, H., Pamucar, D., Chu, Y. M. (2020). Linear Diophantine fuzzy soft, rough sets for the selection of sustainable material handling equipment. Symmetry, 12(8), 1215. DOI 10.3390/sym12081215. [Google Scholar] [CrossRef]
Proof of Theorem 2: We proved that the Eq. (27), such that if,
If,
where
then
The result is proved.
Proof of Property 1: By using the idea of the MVCNULDNWBM operator, we have
Proof of Property 2: Based on Eq. (28), we have
and
and it is clear that
Then, we obtained the result, such that
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |