
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.016836
ARTICLE
On ev and ve-Degree Based Topological Indices of Silicon Carbides
1Department of Data Science, Daejin University, Kyunggi, 11159, Korea
2Department of Mathematics, King Abdulaziz University, Jeddah, 21589, Saudi Arabia
3Department of Mathematics, COMSATS University Islamabad, Vehari, 61110, Pakistan
4Department of Mathematics, Division of Science & Technology, University of Education, Lahore, Pakistan
5Research Institute for Natural Sciences, Hanyang University, Seoul, 04763, Korea
*Corresponding Author: Muhammad Imran Qureshi. Email: imranqureshi@cuivehari.edu.pk
Received: 31 March 2021; Accepted: 13 August 2021
Abstract: In quantitative structure-property relationship (QSPR) and quantitative structure-activity relationship (QSAR) studies, computation of topological indices is a vital tool to predict biochemical and physio-chemical properties of chemical structures. Numerous topological indices have been inaugurated to describe different topological features. The ev and ve-degree are recently introduced novelties, having stronger prediction ability. In this article, we derive formulae of the ev-degree and ve-degree based topological indices for chemical structure of Si2C3 − I[a,b].
Keywords: Topological indices; silicon carbide; ev-degree; ve-degree
Researchers have found applications of graph theory and topological models in various scientific research fields during last decades. Theoretical physics, toxicology, computer sciences, pharmacology, pharmaceutical chemistry, engineering and architecture are diverse areas utilizing graph theory and models to make numerous improvements in existing scientific literature [1–4]. Consequently, the collaboration of chemistry and graph theory leads towards foundation of extensive research work. Topological indices (TIs) are result of this alliance, which are numeric parameters used to describe characteristics of molecular graphs of chemical compounds and help in quantitative structure-property relationship (QSPR) and quantitative structure-activity relationship (QSAR), see [5–7].
TIs assist in the course of investigation and prediction of the physio-chemical and biochemical properties, i.e., dipole moment, charge density, stability, melting and boiling points, inter-molecular forces and bond lengths, without laboratory experiments, which reduces consumption of time and cost [1,8–12]. Randíc index, Zagreb index, atom-bond connectivity index, geometric index, harmonic index, etc. [13–19] are some well-known TIs. Recently, Chellali et al. [20] introduced two new degree novel approaches in graph theory, known as ev-degree and ve-degree. Mathematical concepts related to ve-degree and ev-degree are also discussed by Horoldagva et al. [21]. Randíc and Zagreb indices are calculated in [22–24] using ev-degree and ve-degree concepts and found that predicting power of ve-degree Zagreb index is stronger than that of classic Zagreb index.
Silicon, the second most abundant element on earth, has unique physical and chemical properties due to its semi-conductance and nontoxic nature. Silicon carbides has diverse industrial applications because of thermal and chemical stability, high erosion resistance, high melting point, non oxidizing behavior [25–27]. These characteristics and low cost production techniques give superiority to silicon carbides over other semi conductors. Different metal components used in digital gadgets are replaced by silicon carbides due to its power saving property [28,29]. These are widely used in wind turbines, electrical vehicles, solar cells along with different high radiation and temperature tolerant applications.
The main objective of the article is to derive formulae to calculate the ev-degree and ve-degree based TIs for Si2C3 − I[a,b] and study the behavior of the obtained results through mathematical tools.
Let G(V,E) be a graph with V vertex set and E edge set. The degree of a vertex ν is the number of edges incident to ν. Two vertices in a graph are said to be adjacent if these are connected with each other by an edge. Open neighborhood of a vertex ν, denoted by N(ν) is the set of vertices adjacent to ν and if we include ν itself, then set is called closed neighborhood of ν, denoted by N[ν]. The ev-degree of an edge e = νμ is the number of vertices in union of closed neighborhood sets of ν and μ, denoted by dev(e) and number of edges incident to different vertices in closed neighborhood of ν is ve-degree of a vertex ν, denoted by dve(ν). Some recent results on the ev-degree and ve-degree based topological indices can be seen in [30]. The definitions of ev-degree and ve-degree based versions of some topological indices are the following:
The first ve-degree based Zagreb alpha index is as follows:
The first ve-degree based Zagreb beta index is defined as:
The second ve-degree based Zagreb index is given by the formula:
The ve-degree based Randíc index is as follows:
The ev-degree based Randíc index is defined as:
The ve-degree based atom-bond connectivity index is given by the formula:
The ve-degree based geometric-arithmetic index is as follows:
The ve-degree based harmonic index is defined as:
The ve-degree based sum-connectivity index is given by the formula:
We compute these indices by using the vertex partition strategy, the edge partition techniques, expository strategies, sum of degrees of neighboring techniques, degree checking and combinatorial techniques. We use Matlab and Maple for some calculations and verification purpose.
3 The ev and ve Degree Based Indices
Consider the two dimensional molecular structure of Si2C3 − I[a, b] as shown in Fig. 1 having b rows and a number of unit cells in each row. Before proceeding further, we include the following tables which will be used to achieve our results. In Table 1, the total number of vertices and edges are given for our molecular structure having b rows and a number of unit cells in each row. The Table 2 gives the partition of vertex set on the basis of degree of vertices.

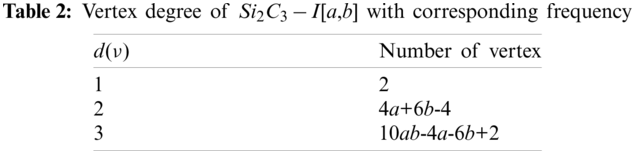
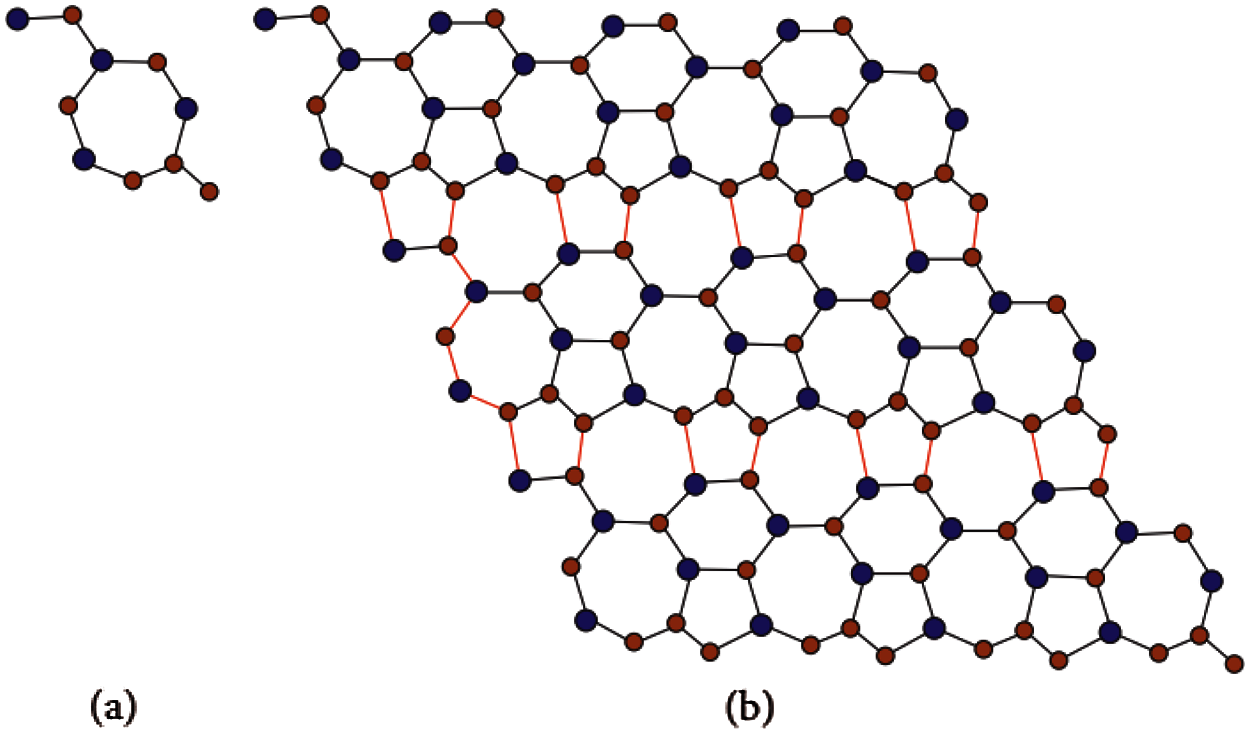
Figure 1: The unit cell and Si2C3 − I [3,4], respectively
• The ev-degree based Zagreb index
To compute the ev-degree based Zagreb index of Si2C3 − I[a, b], we use ev-degree based edges frequency given in Table 3:

• The first ve-degree based Zagreb Alpha index
To compute the first ve-degree based zagreb alpha index of Si2C3 − I[a, b], we use ve-degrees given in Table 4 of vertices partition:

• The first ve-degree based Zagreb Beta index
To compute first ve-degree based Zagreb beta index of Si2C3 − I[a, b], we use ve-degrees of end vertices of each edge given in Table 5:
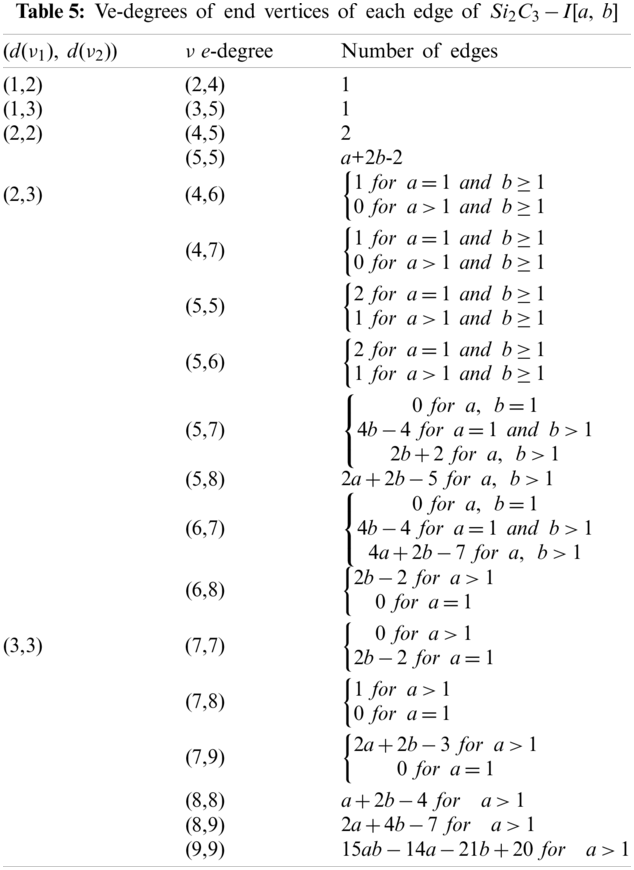
• The second ve-degree based Zagreb index
To compute the second ve-degree based Zagreb index of Si2C3 − I[a, b], we use ve-degrees of end vertices of each edge given in Table 5:
• The ve-degree based Randíc index
To compute the ve-degree based Randíc index of Si2C3 − I[a, b], we use ve-degrees of end vertices of each edge with corresponding frequency as given in Table 5:
• The ev-degree based Randíc index
To compute the ev-degree based Randíc index of Si2C3 − I[a, b], we use ev-degree based edge partition with corresponding frequency given in Table 6:

• The ve-degree based atom-bond connectivity index
To compute the ve-degree based atom-bond connectivity index of Si2C3 − I[a, b], we use ve-degrees of end vertices of each edge with corresponding frequency as given in Table 5:
• The ve-degree based geometric-arithmetic index
To compute the ve-degree based geometric-arithmetic index of Si2C3 − I[a, b], we use ve-degrees of end vertices of each edge with corresponding frequency as given in Table 5:
• The ve-degree based harmonic index
To compute the ve-degree based harmonic index of Si2C3 − I[a, b], we use ve-degrees of end vertices of each edge with corresponding frequency as given in Table 5:
• The ve-degree based sum-connectivity index
To compute the ve-degree based sum-connectivity index of Si2C3 − I[a, b], we use ve-degrees of end vertices of each edge with corresponding frequency as given in Table 5:
In this section, we present the graphical analysis of the computed topological indices for Si2C3 − I[a,b], see Figs. 2–6 which indicate that, numerical values of these descriptors increase with the increment of a and b in the given molecular structure.
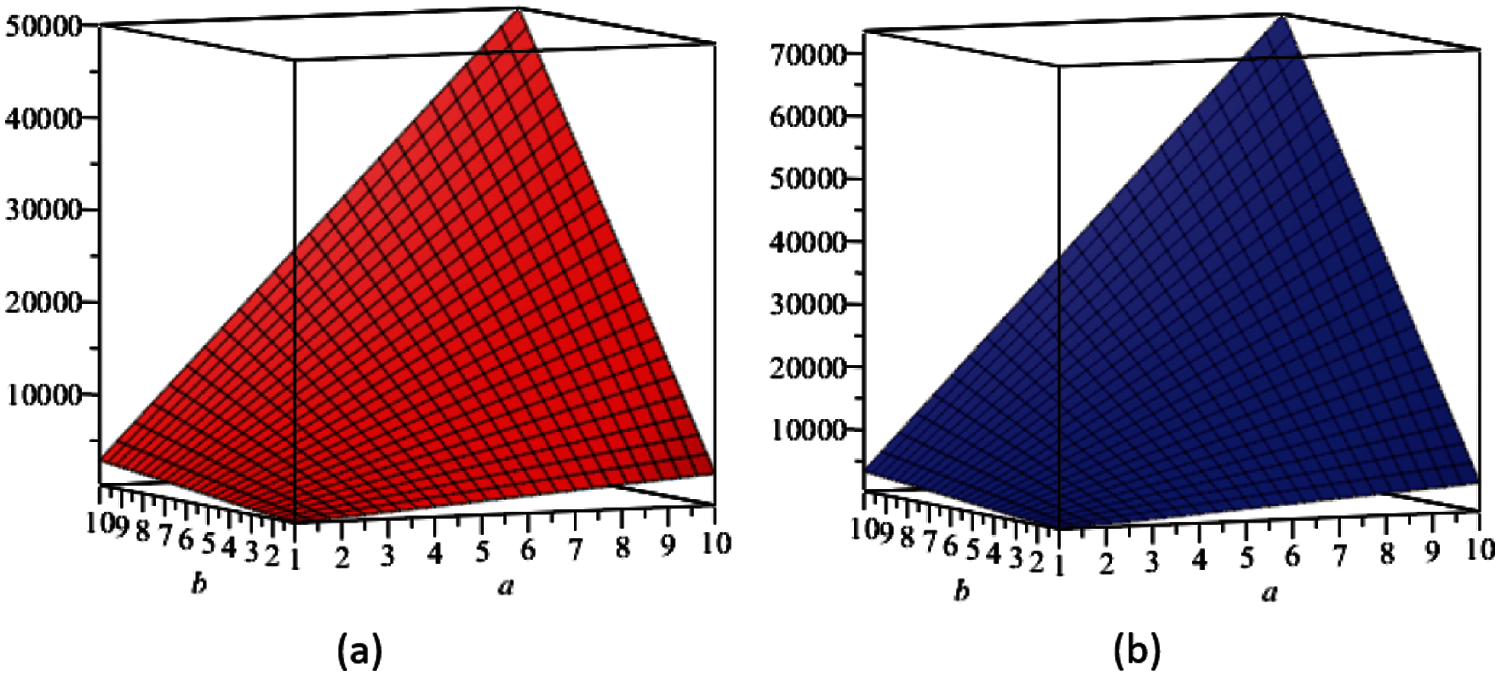
Figure 2: (a) The ev-degree based Zagreb index, (b) The first ve-degree based Zagreb α index
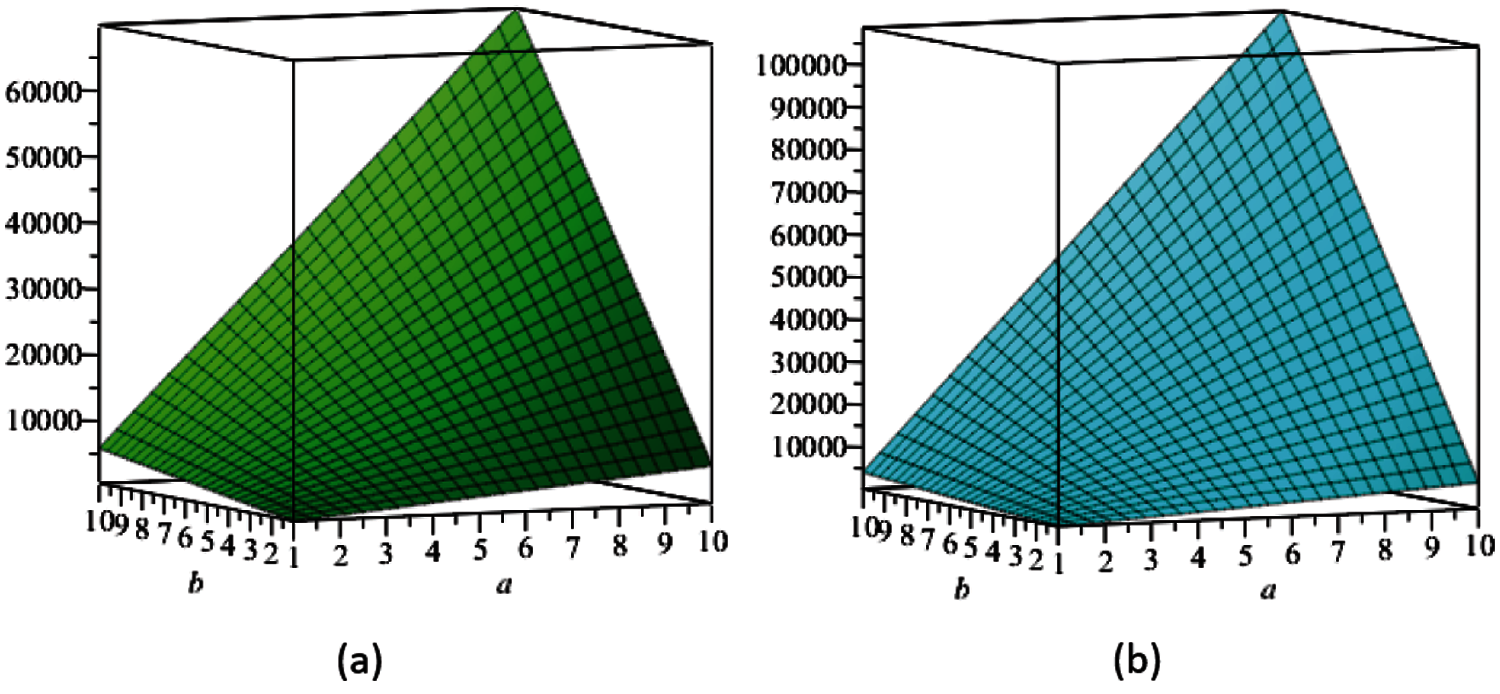
Figure 3: (a) The first ve-degree based Zagreb β index, (b) The second ve-degree based Zagreb index
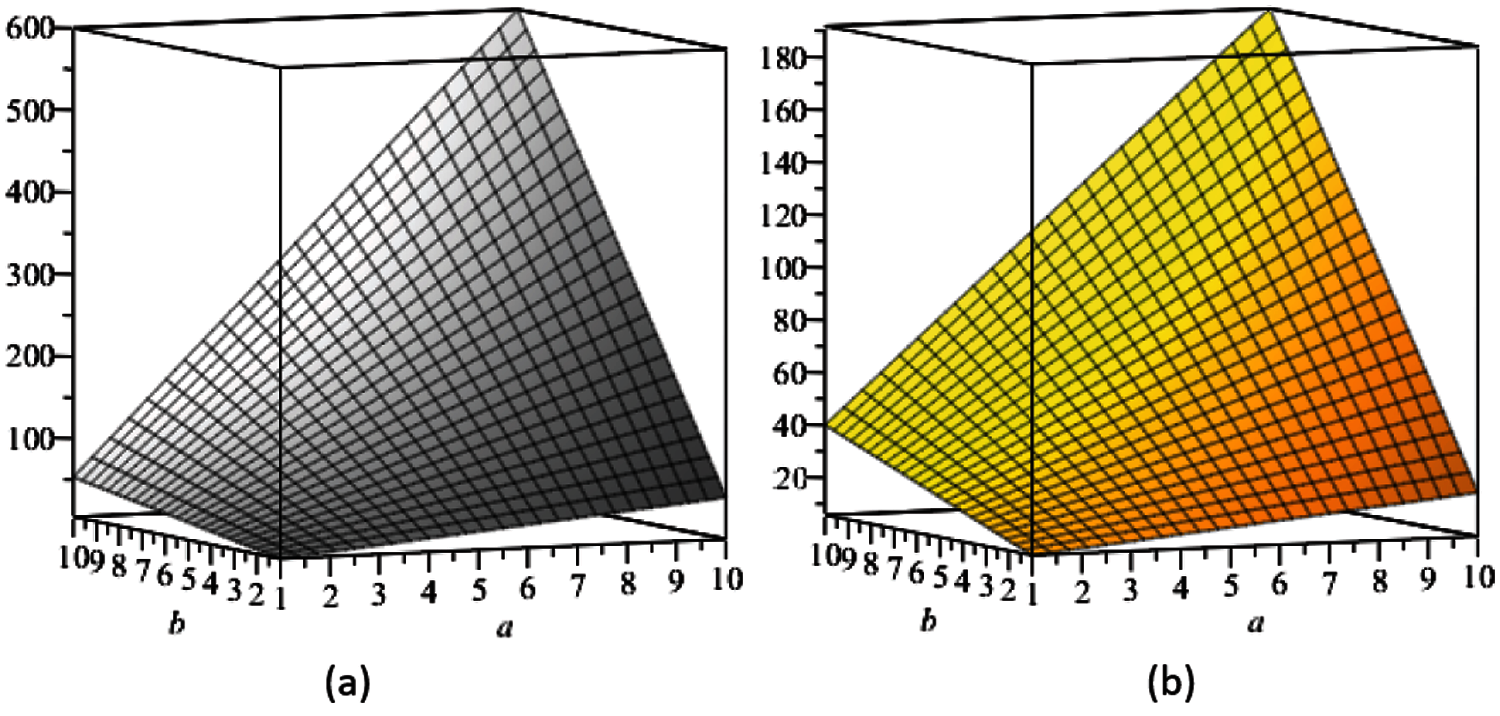
Figure 4: (a) The ev-degree based Randíc index, (b) The ve-degree based Randíc index
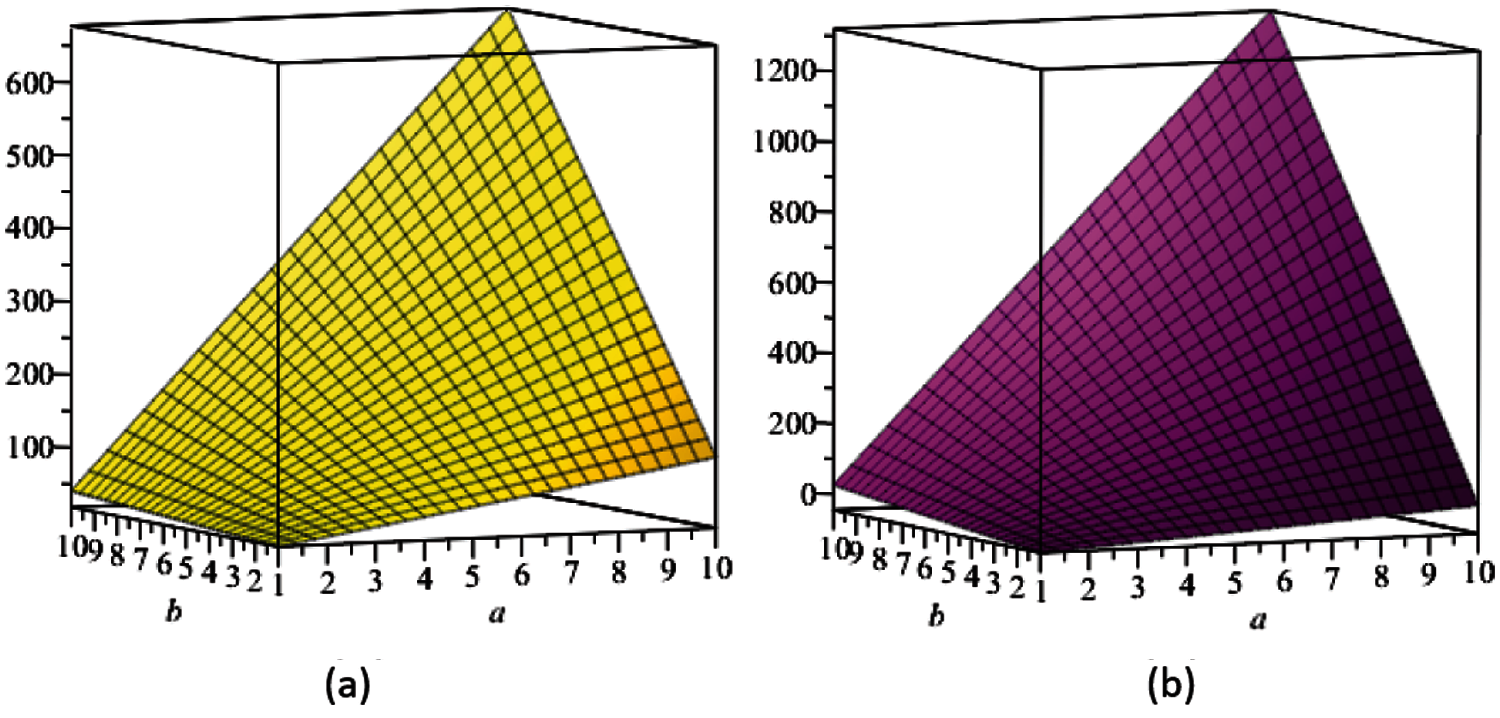
Figure 5: (a) The ve-degree based atomic-connectivity index, (b) The ve-degree based geometric-arithmetic index
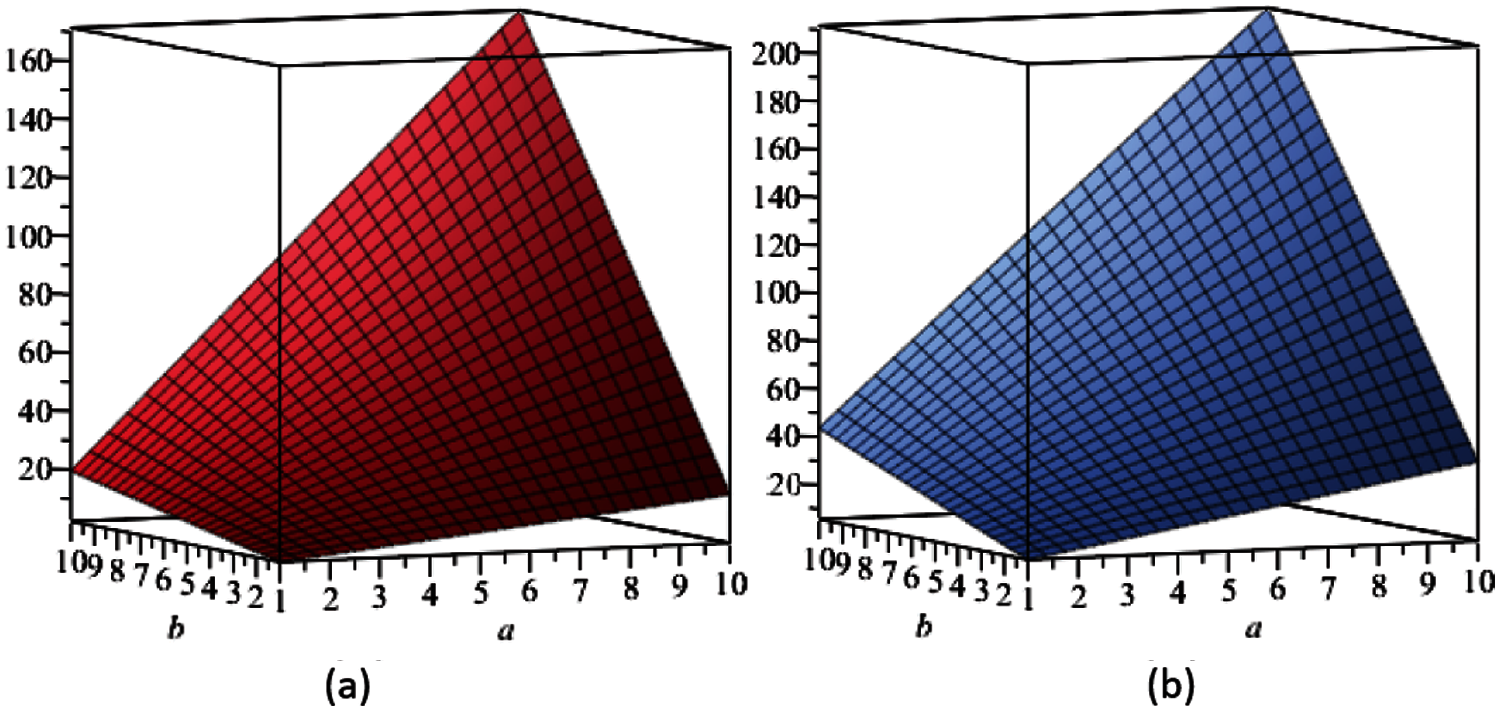
Figure 6: (a) The ve-degree based harmonic index, (b) The ve-degree based sum-connectivity index
In this article, we have provided results related to the ve-degree Zagreb alpha index, first ve-degree Zagreb beta index, second ve-degree Zagreb index, ve-degree Randíc index, ev-degree Randíc index, ve-degree atom-bond connectivity index, ve-degree geometric-arithmetic index, ve-degree harmonic index and ve-degree sum-connectivity index for the two dimensional molecular structure of Si2C3 − I[a,b]. Secondly, we have presented the graphical analysis of the obtained results. At the end, under some assumptions, the comparison among the values of the computed indices has been shown through graphs, see Fig. 7.
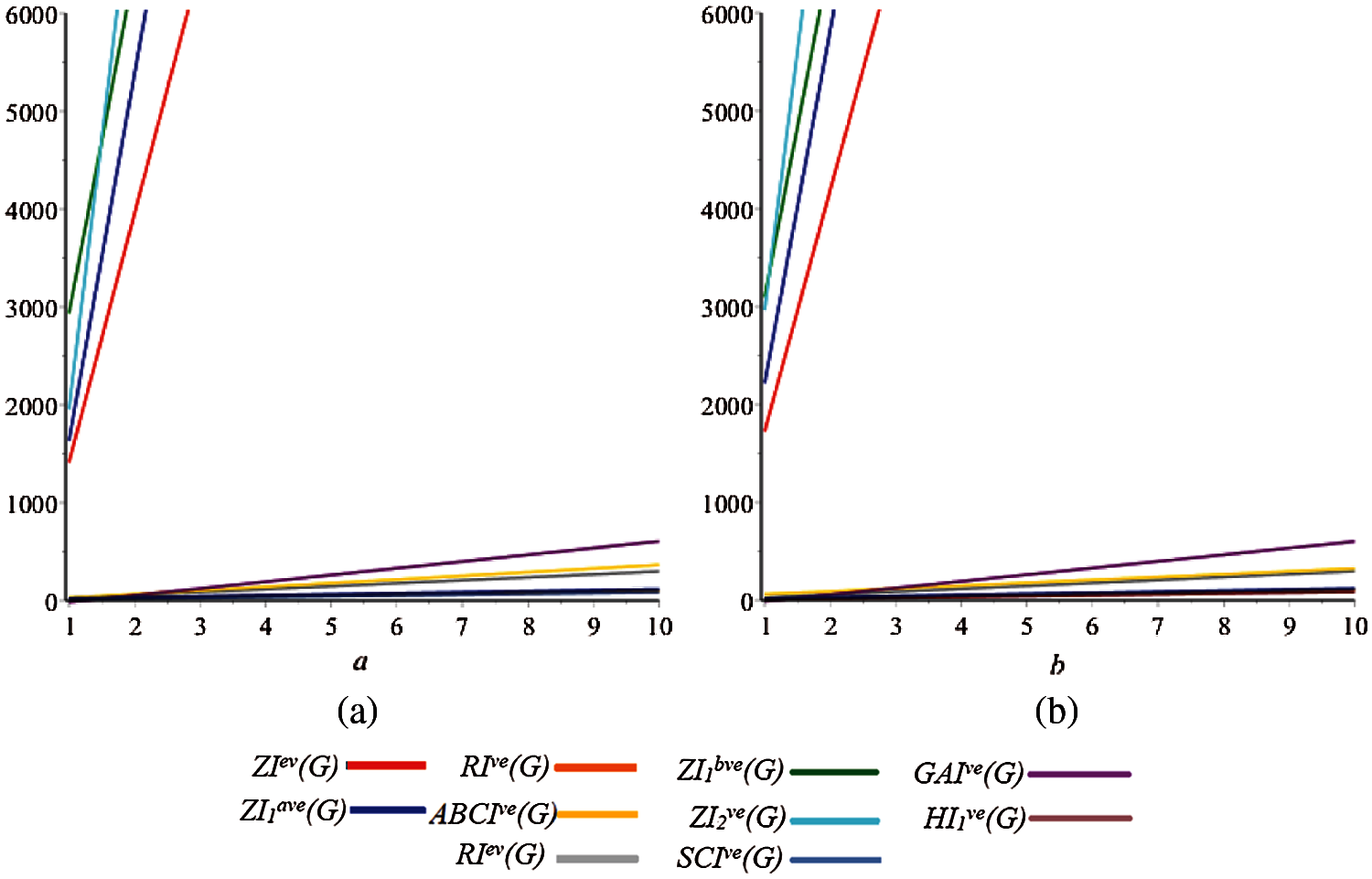
Figure 7: Comparison of indices by keeping one parameter fixed
The Fig. 7 shows that, generally, there are two types of the trends in the out put of the formulae of these indices. The values of the some indices increase rapidly, whereas other values does not show rapid increase. Due to strong prediction ability of ev-degree and ve-degree based topological indices, our results and analysis have potential to play vital role in study of Silicon carbides.
Acknowledgement: All the authors are thankful to their respective institutes.
Funding Statement: This work has no external funding.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Gao, W., Wang, W., Farahani, M. (2016). Topological indices study of molecular structure in anticancer drugs. Journal of Chemistry, 2016(10), 1–8. DOI 10.1155/2016/3216327. [Google Scholar] [CrossRef]
2. Ye, A., Qureshi, M., Fahad, A., Aslam, A., Jamil, M. et al. (2019). Zagreb connection number index of nanotubes and regular hexagonal lattice. Open Chemistry, 17(1), 75–80. DOI 10.1515/chem-2019-0007. [Google Scholar] [CrossRef]
3. Zheng, J., Iqbal, Z., Fahad, A., Zafar, A., Aslam, A. et al. (2019). Some eccentricity-based topological indices and polynomials of poly(ethyleneamidoamine)(PETAA) dendrimers. Processes, 7(7), 433. DOI 10.3390/pr7070433. [Google Scholar] [CrossRef]
4. Zuo, X., Liu, J., Iqbal, H., Ali, K., Rizvi, S. (2020). Topological indices of certain transformed chemical structures. Journal of Chemistry, 2020(8), 1–7. DOI 10.1155/2020/3045646. [Google Scholar] [CrossRef]
5. Estrada, E. (1995). Edge adjacency relationships and a novel topological index related to molecular volume. Journal for Chemical Information and Computer Scientists, 35(1), 31–33. DOI 10.1021/ci00023a004. [Google Scholar] [CrossRef]
6. Taherpour, A., Shafiei, F. (2005). The structural relationship between randic indices, adjacency matrixes, distance matrixes and maximum wave length of linear simple conjugated polyene compounds. Journal of Molecular Structure: THEOCHEM, 726(1–3), 183–188. DOI 10.1016/j.theochem.2005.03.053. [Google Scholar] [CrossRef]
7. Yao, X., Fan, B., Doucet, J., Panaye, A., Liu, M. et al. (2003). Quantitative structure property relationship models for the prediction of liquid heat capacity. QSAR & Combinatorial Science, 2(1), 29–48. DOI 10.1002/(ISSN)1611-0218. [Google Scholar] [CrossRef]
8. Katritzky, A., Jain, R., Lomaka, A., Petrukhin, R., Maran, U. et al. (2001). Perspective on the relationship between melting points and chemical structure. Crystal Growth & Design, 1(4), 261–265. DOI 10.1021/cg010009s. [Google Scholar] [CrossRef]
9. Wiener, H. (1947). Structural determination of paraffin boiling points. Journal of the American Chemical Society, 69(1), 17–20. DOI 10.1021/ja01193a005. [Google Scholar] [CrossRef]
10. Cash, G. (1995). Correlation of physicochemical properties of alkylphenols with their graph-theoretical ɛ parameter. Chemosphere, 31(10), 4307–4315. DOI 10.1016/0045-6535(95)00295-J. [Google Scholar] [CrossRef]
11. Estrada, E., Ivanciuc, O., Gutman, I., Gutierrez, A., Rodriguez, L. (1998). Extended Wiener indices: A new set of descriptors for quantitative structure-property studies. New Journal of Chemistry, 22(8), 819–822. DOI 10.1039/a709255e. [Google Scholar] [CrossRef]
12. Gutman, I., Trinajstic, N. (1972). Graph theory and molecular orbitals: Total φ-electron energy of alternant hydrocarbons. Chemical Physics Letters, 17(4), 535–538. DOI 10.1016/0009-2614(72)85099-1. [Google Scholar] [CrossRef]
13. Binyamin, M., Aslam, A., Ahmad, S., Gao, W. (2019). Calculating topological indices of certain OTIS interconnection networks. Open Chemistry, 17(1), 220–228. DOI 10.1515/chem-2019-0029. [Google Scholar] [CrossRef]
14. Aslam, A., Jamil, M., Gao, W., Nazeer, W. (2018). Topological aspects of some dendrimer structures. Nanotechnology Reviews, 7(2), 123–129. DOI 10.1515/ntrev-2017-0184. [Google Scholar] [CrossRef]
15. Liu, J., Javaid, M., Awais, H. (2019). Computing zagreb indices of the subdivision-related generalized operations of graphs. IEEE Access, 7, 105479–105488. DOI 10.1109/ACCESS.2019.2932002. [Google Scholar] [CrossRef]
16. Liu, J., Javed, S., Javaid, M., Shabbir, K. (2019). Computing first general zagreb index of operations on graphs. IEEE Access, 7, 47494–47502. DOI 10.1109/ACCESS.2019.2909822. [Google Scholar] [CrossRef]
17. Bashir, Y., Aslam, A., Kamran, M., Qureshi, M., Janagir, A. et al. (2017). On forgotten topological indices of some dendrimers structure. Molecules, 22(6), 867. DOI 10.3390/molecules22060867. [Google Scholar] [CrossRef]
18. Munir, M., Nazeer, W., Kang, S., Qureshi, M. I., Nizami, A. et al. (2017). Some invariants of jahangir graphs. Symmetry, 9(1), 17. DOI 10.3390/sym9010017. [Google Scholar] [CrossRef]
19. Fahad, A., Qureshi, M., Noureen, S., Iqbal, Z., Zafar, A. et al. (2021). Topological descriptors of poly propyl ether imine (petim) dendrimers. Biointerface Research Applied Chemistry, 11(3), 10968–10978. [Google Scholar]
20. Chellali, M., Haynes, T., Hedetniemi, S., Lewis, T. (2017). On ve-degrees and ev-degrees in graphs. Discrete Mathematics, 340(2), 31–38. DOI 10.1016/j.disc.2016.07.008. [Google Scholar] [CrossRef]
21. Horoldagva, B., Das, K., Selenge, T. (2019). On ve-degree and ev-degree of graphs. Discrete Optimization, 31(1), 1–7. DOI 10.1016/j.disopt.2018.07.002. [Google Scholar] [CrossRef]
22. Ediz, S. (2017). A new tool for QSPR researches: Ev-degree randic index. Celal Bayar University Journal of Science, 13(3), 615–618. DOI 10.18466/cbayarfbe.339313. [Google Scholar] [CrossRef]
23. Sahin, B., Ediz, S. (2018). On ev-degree and ve-degree topological indices. Iranian Journal of Mathematical Chemistry, 9(4), 263–277. [Google Scholar]
24. Ediz, S. (2018). On ve-degree molecular topological properties of silicate and oxygen networks. International Journal of Computing Science and Mathematics, 9(1), 1–12. DOI 10.1504/IJCSM.2018.090730. [Google Scholar] [CrossRef]
25. Singh, S., Buchanan, R. (2007). SiC-C fiber electrode for biological sensing. Materials Science and Engineering: C, 27(3), 551–557. DOI 10.1016/j.msec.2006.05.053. [Google Scholar] [CrossRef]
26. Norlin, A., Pan, J., Leygraf, C. (2002). Investigation of interfacial capacitance of Pt, Ti and TiN coated electrodes by electrochemical impedance spectroscopy. Biomolecular Engineering, 19(2–6), 67–71. DOI 10.1016/S1389-0344(02)00013-8. [Google Scholar] [CrossRef]
27. Kang, H., Moon, J., Bahng, W., Lee, S., Kim, H. et al. (2017). Oxygen- and photoresist-related interface states of 4H-SiC Schottky diode observed by deep-level transient spectroscopy. Journal of Applied Physics, 122(9), 094504. DOI 10.1063/1.4989912. [Google Scholar] [CrossRef]
28. Shao, Z., Amjadi, J., Sheikholeslami, S., Valinavaz, M. (2019). On the total double roman domination. IEEE Access, 7, 52035–52041. DOI 10.1109/ACCESS.2019.2911659. [Google Scholar] [CrossRef]
29. Zhang, X., Raza, A., Fahad, A., Jamil, M., Chaudhry, M. et al. (2020). On face index of silicon carbides. Discrete Dynamics in Nature and Society, 2020, 1–8. DOI 10.1155/2020/6048438. [Google Scholar] [CrossRef]
30. Ibrahim, M., Zahra, N., Siddiqui, M. K. (2021). On ve-degree and ev-degree based topological indices for the series of benzenoid graphs. Polycyclic Aromatic Compounds, 1–10 (in Press). DOI 10.1080/10406638.2021.1926294. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |