[BACK]
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.017397
ARTICLE
Decision-Making Problems under the Environment of m-Polar Diophantine Neutrosophic N-Soft Set
Shouzhen Zeng1,2, Shahbaz Ali3,*, Muhammad Khalid Mahmood4, Florentin Smarandache5 and Daud Ahmad4
1School of Business, Ningbo University, Ningbo, 315211, China
2College of Statistics and Mathematics, Zhejiang Gongshang University, Hangzhou, 310018, China
3Department of Mathematics, Khawaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan
4Department of Mathematics, University of the Punjab, Lahore, 54590, Pakistan
5Department of Mathematics and Science, University of New Mexico, Gallup, NM 87301, USA
*Corresponding Author: Shahbaz Ali. Email: shahbaz.ali@kfueit.edu.pk
Received: 08 May 2021; Accepted: 15 July 2021
Abstract: Fuzzy models are present everywhere from natural to artificial structures, embodying the dynamic processes in physical, biological, and social systems. As real-life problems are often uncertain on account of inconsistent and indeterminate information, it seems very demanding for an expert to solve those problems using a fuzzy model. In this regard, we develop a hybrid new model m-polar Diophantine neutrosophic N-soft set which is based on neutrosophic set and soft set. Additionally, we define several different sorts of compliments on the proposed set. A proposed set is a generalized form of fuzzy, soft, Pythagorean fuzzy, Pythagorean fuzzy soft, and Pythagorean fuzzy N-soft sets. In this manner, m-polar Diophantine neutrosophic N-soft set is more proficient, a versatile model to oversee vulnerabilities as it likewise survives the downsides of existing models which are to be summed up. Furthermore, we give the application of the proposed set in multi-attribute decision-making problems by defining a new choice-value function.
Keywords: Neutrosophic set; soft set; N-soft set; m-polar diophantine neutrosophic N-soft set; decision making
1 Introduction
The idea of a set and set theory are incredible assets in arithmetic. Shockingly, a non-condition basic set theory for example that the component can either have a place in a set or not, is frequently not appropriate in genuine a daily existence where numerous unclear terms as “enormous benefit,” “high pressing factor,” “moderate temperature,” “dependable instruments,” “safe conditions,” and so forth are broadly utilized. Tragically, such loose depictions cannot be sufficiently taken care of by ordinary mathematical tools.
In fuzzy theory, a recently characterized model by and large beats the downsides of recently characterized models. Because of uncertainty and weaknesses issues in numerous days by day life issues, routine math is not continuously accessible. To manage such issues, different methods such as the theory of possibility, rough set assumption, and fuzzy set theory has been considered as elective models and to keep away from weaknesses too. Inopportunely, the greater part of the options such as science have their own disadvantages and downsides. For example, a large portion of the words like expert, amazing, best, significant is most certainly not quantifiable and uncertain. The rules for words like superb, best, famous, and so forth, hesitate from individual to person.
To deal with such sort of equivocal and unsure data, Zadeh [1] investigated the idea of fuzzy set which is mapping from a universal set X to [0, 1]. Atanassov [2] proposed the fortuitous of intuitionistic fuzzy sets as an expansion of fuzzy sets by presenting the idea of membership and non-membership grades. Molodtsov [3] began the thought of soft set as a mathematical model to oversee vulnerabilities. The chance of soft set has another objective for the researchers due to them utilizes in a wide range of exuberant issues.
Ali et al. [4] presented some new operations on soft set theory. They introduced the ideas of expanded and restricted union and intersections in detail. In [5–7], Yager introduced and investigated several relations on Pythagorean fuzzy set. Peng et al. [8] discussed certain results on Pythagorean fuzzy sets and also defined the Pythagorean fuzzy number in. Peng et al. [9] set up some Pythagorean fuzzy data measures and their applications. Peng et al. [10] proposed some new approaches to manage single-regarded neutrosophic MADM reliant on MABAC, TOPSIS, and new closeness measure with score function. In [11–21], many decision-making problems and algebraic structures are discussed over different fuzzy environments.
Smarandache’s introduced neutrosophic set and then proposed many operation on it 22–24. Neutrosophic set (NS) based on three parameters namely, membership, indeterminacy, and non-membership. Wang et al. [25] propsed the concept of single valued neutrosophic sets. Deli et al. [26] introduced the idea of bipolar neutrosophic set and their applications in multi-criteria decision making problems in. Fatimah et al. [22] introduced the notion of an N-soft set which is an extension of a soft set. Many problems related to decision-making are discussed by using different kind of environments in [27–30].
There are many problems regarding decision-making that need to improveby investigating a new set or model. In this regard, we develop a proposed setthat provides a more batter approximation than existing sets. The proposed work is arranged as follows. In Section 2, some preliminary concepts are given to understand the proposed work. In Section 3, we define the notion of m-polar Diophantine neutrosophic N-soft set and then define some operations on it. In Section 4 , we discuss different types of compliments on the proposed set. We give the comparison table and application in multi-attribute decision-making problems in Section 5 .
2 Preliminaries
In this section, we give some preliminary concepts related to previous existing sets.
Definition 2.1. [1] A fuzzy set is a mapping μ from universal set X to [0, 1] such that, μ:X→[0,1]. The fuzzy set can be written in the form of
FX={(x,μF(x)):x∈X}.
Definition 2.2. [2] An intuitionistic fuzzy set on universal set X is defined as
IX={(x,μI(x),νI(x)):x∈I},
where μI:X→[0,1] and νI:X→[0,1] are the membership and non-membership functions, respectively.
Definition 2.3. [31] The m-polar fuzzy set on a universal set M is a mapping μ:M→[0,1]m and m(X) is the collection of all m-polar fuzzy set on M.
Definition 2.4. [3] The soft set is defined by the set valued mapping φ:I→2T, where I denotes the set of parameters and 2T is the power set of T. The soft set can be written as,
φI=(φ,I)={(t,φ(t)):t∈I,φ(t)∈2T}.
Definition 2.5. [32,33] A fuzzy soft set is defined as
ΓS={(t,γS(t)):t∈T,γS∈F(L)},
where γS:T→F(L) and F(L) is the collection of all fuzzy sets on L and T is the set of parameters with S⊆T.
Definition 2.6. [34] Let X be the crisp set. Intuitionistic fuzzy soft set (IFSS) is interpreted by multi-valued mapping ψ:B→IFX, where IFX represents the collection of all IF-subsets defined over crisp set X (where B⊆X). Thus the IFSS can be expressed as
℧B={(e,ψB(e)):e∈X,ψB∈IFX}.
Definition 2.7. [5] Let X be the crisp set. A Pythagorean fuzzy set (PFS) can be expressed as
P={<ρ,μP(ρ),νP(ρ)>:0≤μP2(ρ)+νP2(ρ)≤1,ρ∈X},
where μP:X→[0,1] and νP:X→[0,1] with the condition that 0≤μP2(ρ)+νP2(ρ)≤1, is known as the degrees of membership and non-membership of ρ ∈ X to the set P.
Definition 2.8. [35] The score function and accuracy function of Pythagorean fuzzy number α = (μα, να) over X is defined as, S(γ)=μγ2−νγ2 and Q(γ)=μγ2+νγ2, with S −1 ≤ γ ≤ 1 and 0 ≤ Q(γ) ≤ 1.
Definition 2.9. [36] The ranking function of Pythagorean fuzzy number γ = (μγ, νγ) over X is defined as
R(γ)=12+rγ(12−2θγπ),
where rγ=μγ2+νγ2 is called commitment strength and θγ is the angle between rγ and μγ. The direction of commitment dγ is dγ=1−2θγπ, where μγ = rγcosθγ, νγ = rγsinθγ.
Definition 2.10. [37] Let X be a non-empty universal set, S be the set of attributes, and Y⊆S. Let D = {0, 1, 2,…, N − 1} be set of grading. The triple (Fp, Y, N) is said to be a Pythagorean fuzzy N-soft set on X, if Fp is a mapping Fp:Y→2X×D×PFN, in which F:Y→2X×D, and P:Y→PFN, where PFN is Pythagorean fuzzy number. That is μ:Y→[0,1] and ν:Y→[0,1] such that
0≤μy2(x)+νy2(x)≤1, ∀y∈Y,∀x∈X.
Hence,
(Fp,Y,N)=((x,dy),(μy(x),νy(x))),dy∈D.
Definition 2.11. [38] A neutrosophic fuzzy set (NS), S over the universal set X is defined as
S={(ψ,μS(ψ),λS(ψ),νS(ψ))},
where mappings μS, λS, νS stand for degree of truth, degree of indeterminacy, degree of falsity.
μS,λS,νS∈[0,1], with 0⩽μS+λS+νS⩽3.
3 m-Polar Diophantine Neutrosophic N-Soft Set
Definition 3.1 Let L = {0, 1, 2,…, N − 1} be the set of grades where N ∈ {2, 3, 4, …}. If X is a non-emty set and E is the family of attributes. Let A be a non-empty subset of E. A m-poler Diophantine neutrosophic N-soft (MPDNNS) set on X is denoted as (℧, A, m, N) or ℧A(m,N), where ℧:A→P(PFX×L) is a mapping (where PFX is the aggregate of all Diophantine neutrosophic subsets over X). That is
(℧,A,m,N)={(e,{⟨ρ,le(ρ)⟩(μ1(ρ),μ2(ρ),…,μm(ρ);λ1(ρ),λ2(ρ),…,λm(ρ);ν1(ρ),ν2(ρ),…,νm(ρ)})
|e∈A,ρ∈X,le(ρ)∈L},
where μe:X→[0,1]m, νe:X→[0,1]m, and λe:X→[0,1]m are mappings along with the property,
0≤∑i=1mμim(ρ)+∑i=1mνim(ρ)+∑i=1mλim(ρ)≤3m.
In particular, μi(ρ) represents the truth-membership, νi(ρ) denotes degree of falsity-membership, λi(ρ) is the degree of indeterminacy and le(ρ) denotes the grading value of the element ρ ∈ X corresponding to the attribute e∈ A to the set (℧, A, m, N). If we write aij = μei(ρj), bij=νei(ρj), dij = λei (ρj), and cij=lej(ρj) where i runs from 1 to m and j runs from 1 to n then the MPDNNS set ℧A(m,N) may be represented in tabular form as
℧A(m,N)e1e2⋯emρ1⟨c11,(a11,a21,⋯,am1;⟨c12,(a11,a21,⋯,am1;⟨c1m,(a11,a21,⋯,am1;d11,d21,⋯,dm1;d11,d21,⋯,dm1;⋯d11,d21,⋯,dm1;b11,b21,⋯,bm1)⟩b11,b21,⋯,bm1)⟩⋯b11,b21,⋯,bm1)⟩ρ2⟨c21,(a12,a22,⋯,am2;⟨c22,(a12,a22,⋯,am2;⟨c2m,(a12,a22,⋯,am2;d12,d22,⋯,dm2;b12,b22,⋯,bm2;⋯b12,b22,⋯,bm2;b12,b22,⋯,bm2)⟩b12,b22,⋯,bm2)⟩⋯b12,b22,⋯,bm2)⟩⋮⋮⋮⋱⋮ρn⟨cn1,(a1n,a2n,⋯,amn;⟨cn2,(a1n,a2n,⋯,amn;⟨cnm,(a1n,a2n,⋯,amn;d1n,d2n,⋯,dmn;d1n,d2n,⋯,dmm;⋯d1n,d2n,⋯,dmn;b1n,b2n,⋯,bmn)⟩b1n,b2n,⋯,bmm)⟩⋯b1n,b2n,⋯,bmn)⟩
and in matrix form as
(℧,A,m,N)=[⟨cij,(aij,dij,bij)⟩]n×m
=(⟨c11,(a11,a21,⋯,am1;⟨c12,(a11,a21,⋯,am1;⟨c1m,(a11,a21,⋯,am1;d11,d21,⋯,dm1;d11,d21,⋯,dm1;⋯d11,d21,⋯,dm1;b11,b21,⋯,bm1)⟩b11,b21,⋯,bm1)⟩⋯b11,b21,⋯,bm1)⟩⟨c21,(a12,a22,⋯,am2;⟨c22,(a12,a22,⋯,am2;⟨c2m,(a12,a22,⋯,am2;d12,d22,⋯,dm2;d12,d22,⋯,dm2:⋯d12,d22,⋯,dm2;b12,b22,⋯,bm2)⟩b12,b22,⋯,bm2)⟩⋯b12,b22,⋯,bm2)⟩⋮⋮⋱⋮⟨cn1,(a1n,a2n,⋯,amn;⟨cn2,(a1n,a2n,⋯,amn;⟨cnm,(a1n,a2n,⋯,amn;d1n,d2n,⋯,dmn;d1n,d2n,⋯,dmm;⋯d1n,d2n,⋯,dmn;b1n,b2n,⋯,bmn)⟩b1n,b2n,⋯,bmm)⟩⋯b1n,b2n,⋯,bmn)⟩)
This matrix is called m-Polar Diophantine neutrosophic N-Soft matrix or shortly MPDNNS matrix.
Note: We use the expression xn + yn = zn in Definition 3.1, which is similar to Diophantine equation. Thats why we call m-polar Diophantine neutrosophic N-soft set instead of m-polar neutrosophic N-soft set.
Definition 3.2. An MPDNNS set ℧A(m,N) over X is known as null MPDNNS set, symbolized as ℧ϕ;(m,0) and defined as
℧ϕ(m,0)={(e,{⟨ρ,lϕ(ρ)⟩(μϕ1(ρ),μϕ2(ρ),⋯,μϕm(ρ);λϕ1(ρ),λϕ2(ρ),⋯,λϕm(ρ);νϕ1(ρ),νϕ2(ρ),⋯,νϕm(ρ)})|e∈A,ρ∈X,lϕ(ρ)∈L},
where, μϕi(ρ) = 0, λϕi(ρ) = 1, νϕi(ρ) = 1, 1 ≤ i ≤ m, and lϕ(ρ) = 0.
Definition 3.3. An MPDNNS set ℧A(m,N) over X is known as absolute MPDNNS set, symbolized as ℧E(m,N−1) and defined as
℧E(m,N−1)={(e,{⟨ρ,lE(ρ)⟩(μE1(ρ),μE2(ρ),⋯,μEm(ρ);νE1(ρ)),νE2(ρ),⋯,νEm(ρ)}):e∈A,ρ∈X,lE(ρ)∈L},
where μEi(ρ) = 1, λEi(ρ) = 0, νEi(ρ) = 0, 1 ≤ i ≤ m, and lϕ(ρ) = N − 1.
Example 3.1. Let X = {ρ1, ρ2, ρ3, ρ4, ρ5, ρ6, ρ7}, E = {e1, e2, e3} and L = {0, 1, 2,…, 5}. Suppose that A = {e1, e3}. Then
℧A(3,6)={(e1,{⟨ρ1,3,(.3,.4,.5;.5,.4,.3;.1,.6,.4)⟩,⟨ρ4,4,(.4,.3,.1;.4,.4,.2;.3,.4,.5)⟩,
⟨ρ7,5,(.6,.2,.55;.3,.1,.2;.4,.3,.5)⟩}),(e3,{⟨ρ2,2,(.2,.1,.7;.6,.6,.5;.8,.4,.6)⟩,
⟨ρ3,1,(.5,.6,.7;.7,.5,.4;.4,.3,.1)⟩,⟨ρ5,2,(.4,.6,.2;.7,.3,.5;.7,.5,.3)⟩})}
is a 3PDN6S set over X. The tabular representation of ℧A(3,6) is
℧A(3,6)e1e2e3ρ1⟨3,(.3,.4,.5;.5,.4,.3;.1,.6,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩ρ2⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨2,(.2,.1,.7;.6,.6,.5;.8,.4,.6)⟩ρ3⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨1,(.5,.6,.7;.7,.5,.4;.4,.3,.1)⟩ρ4⟨4,(.4,.3,.1;.4,.4,.2;.3,.4,0.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩ρ5⟨0,(0,0,0;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨2,(.4,.6,.2;.7,.3,.5;.7,.5,.3)⟩ρ6⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩ρ7⟨5,(.6,.2,.55;.3,.1,.2;.4,.3,0.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩
The corresponding 3PDN6S matrix is (℧, A, 3, 6) = [aij, dij, bij]7×3
=(⟨3,(.3,.4,.5;.5,.4,.3;.1,.6,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨2,(.2,.1,.7;.6,.6,.5;.8,.4,.6)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨1,(.5,.6,.7;.7,.5,.4;.4,.3,.1)⟩⟨4,(.4,.3,.1;.4,.4,.2;.3,.4,0.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨2,(.4,.6,.2;.7,.3,.5;.7,.5,.3)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨5,(.6,.2,.55;.3,.1,.2;.4,.3,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩)
Definition 3.4. Let ℧A(m,N1) and ℧B(m,N2) be MPDNNS sets over X. Then ℧A(m,N1) is MPDNNS subset of ℧B(m,N2), i.e., ℧A(m,N1) ⊆˜ ℧B(m,N2), if
• A⊆B,
• N1 ≤ N2,
• μi,A(ρ) ≤ μi,B(ρ), 1 ≤ i ≤ m,
• λi,A(ρ) ≥ λi,B(ρ), 1 ≤ i ≤ m,
• νi,A(ρ) ≥ νi,B(ρ), 1 ≤ i ≤ m, and
• lA(ρ) ≤ lB(ρ).
It is worth mentioning that ℧A(m,N1) ⊆˜ ℧B(m,N2) it is not necessary each element of ℧A(m,N1) is also in ℧B(m,N2).
Definition 3.5. Let ℧A(m,N1) and ℧B(m,N2) be MPDNNS sets over X. Then ℧A(m,N1) is MPDNNS equal of ℧B(m,N2) i.e., ℧A(m,N1) =˜ ℧B(m,N2), if
• A = B,
• N1 = N2,
• μi,A(ρ) = μi,B(ρ), 1 ≤ i ≤ m,
• λi,A(ρ) = λi,B(ρ), 1 ≤ i ≤ m,
• νi,A(ρ) = νi,B(ρ), 1 ≤ i ≤ m, and
• lA(ρ) = lB(ρ).
Proposition 3.1. If ℧A(m,N) is any MPDNNS set over X, then
(i) ℧ϕ(m,0) ⊆˜ ℧A(m,N),
(ii) ℧A(m,N) ⊆˜ ℧E(m,N−1).
Proof.
(i) The truth-membership, degree of indeterminacy and degree of falsity always fall in [0, 1] according to Definition 3.1 of MPDNNS set. So, 0 ≤ μi,A(ρ), νi,A(ρ) ≤ 1, λi,A(ρ)≤1, and grading value 0≤lA(ρ), ∀ ρ ∈ X and 1 ≤ i ≤ m.
Thus, it follows from Definitions 3.4 and 3.2 of null MPDNNS set ℧ϕ(m,0). Hence, ℧ϕ(m,0) ⊆˜ ℧A(m,N).
(ii) Clearly, μi,A(ρ) ≤ 1, νi,A(ρ) ≥ 0 and νi,A(ρ) ≥ 0 and grading value lA(ρ) ≤ N − 1 for all ρ ∈ X and 1≤i≤m. Thus, it follows from Definitions 3.4 and 3.3 of absolute MPDNNS set. Hence, ℧A(m,N) ⊆˜ ℧E(m,N−1).
Proposition 3.2. If ℧A(m,N), ℧B(m,N) and ℧C(m,N) are MPDNNS sets over X, then
(i) ℧A(m,N) ⊆˜ ℧A(m,N).
(ii) ℧A(m,N) ⊆˜ ℧B(m,N) and ℧B(m,N) ⊆˜ ℧C(m,N)⇒ ℧A(m,N) ⊆˜ ℧C(m,N).
Definition 3.6. Let ℧A(m,N1) and ℧B(m,N2) be MPDNNS sets over X. Then their extended union is defined as ℧C(m,N)∗=℧A(m,N1)∪E˜℧B(m,N2),
℧C(m,N)∗={(e,{⟨ρ,lC(ρ)⟩(μ1,C(ρ),μ2,C(ρ),⋯,μm,C(ρ);λ1,C(ρ),λ2,C(ρ)⋯,λm,C(ρ);ν1,C(ρ),ν2,C(ρ)⋯,νm,C(ρ)})|e∈C,ρ∈X,lC(ρ)∈L}
where,
• C = A ∪ B,
• (m, N)∗ = (m, max{N1, N2}),
• μC(ρ) = max{μi,A(ρ), μi,B(ρ)}, 1 ≤ i ≤ m,
• λC(ρ) = min{λi,A(ρ), λi,B(ρ)} 1 ≤ i ≤ m,
• νC(ρ) = min{νi,A(ρ), νi,B(ρ)} 1 ≤ i ≤ m, and
• lC(ρ) = max{lA(ρ), lB(ρ)} ∀ e ∈ C.
Definition 3.7. Let ℧A(m,N1) and ℧B(m,N2) be MPDNNS sets over X. Then their restricted union is defined as ℧D(m,N)⋄=℧A(m,N1)∪R˜℧B(m,N2),
℧D(m,N)⋄={(e,{⟨ρ,lD(ρ)⟩(μ1,D(ρ),μ2,D(ρ),⋯,μm,D(ρ);λ1,D(ρ),λ2,D(ρ)⋯,λm,D(ρ);ν1,D(ρ),ν2,D(ρ)⋯,νm,D(ρ)})|e∈D,ρ∈X,lD(ρ)∈L}
where,
• D = A ∩ B,
• (m,N)⋄ = (m, max{N1, N2}),
• μD(ρ) = max{μi,A(ρ), μi,B(ρ)}, 1 ≤ i ≤ m,
• λD(ρ) = min{λi,A(ρ), λi,B(ρ)} 1 ≤ i ≤ m,
• νD(ρ) = min{νi,A(ρ), νi,B(ρ)} 1 ≤ i ≤ m, and
• lD(ρ) = max{lA(ρ), lB(ρ)} ∀ e ∈ D.
Example 3.2. Let X = {ρi: i = 1, 2,…, 8}, E = {ei: i = 1, 2, 3} and L = {0, 1, 2,…, 12}. Assume that A={e1,e3}⊆E and B={e2,e3}⊆E. Then
℧A(3,13)={(e1,{⟨ρ2,11,(.1,.9,.7;.5,.3.2;.4,.6,.8)⟩,⟨ρ5,9,(.2,.1,.2;.3,.4,.5;.6,.7,.8)⟩,
⟨ρ7,8,(.3,.4,.5;.6,.7,.6;.5,.4,.3)⟩}),(e3,{⟨ρ3,3,(.4,.3,.4;.5,.6,.8;.7,.6,.5)⟩,
⟨ρ4,6,(.5,.4,.5;.6,.7,.7;.6,.4,.2)⟩,⟨ρ6,5,(.6,.5,.6;.7,.8,.9;.8,.7,.6)⟩})}
is a 3PDN13S set over X. The corresponding ℧A(3,13) matrix is
℧A(3,13)=[⟨ci,(aij;dij;bij)⟩]8×3
=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨11,(.1,.9,.7;.5,.3,0.2;.4,.6,.8)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨3,(.4,.3,.4;.5,.6,.8;.7,.6,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨6,(.5,.4,.5;.6,.7,.7;.6,.4,.2)⟩⟨9,(.2,.1,.2;.3,.4.5;.6,.7,.8)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨5,(.6,.5,.6;.7,.8.9;.8,.7,.6)⟩⟨8,(.3,.4,.5;.6,.7,.6;.5,.4,.3)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (1)
℧B(3,10)={(e2,{⟨ρ1,9,(.7,.6,.4,:.2,.1,.4;.3,.5,.7)⟩,⟨ρ4,6,(.8,.6,.5;.6,.4,.7;.5.8,.9)⟩,
⟨ρ8,8,(.1,.3,.4;.8,.7,.4;.7,.3,.1)⟩}),(e3,{⟨ρ2,1,(.2,.1,.3;.6,.7,.9;.7,.3,.6)⟩,
⟨ρ5,5,(.1,.2,.4;.8,.7,.1;.8,.3,.7)⟩,⟨ρ7,3,(.2,.3,.6;.9,.8,.7;.8,.7,.5)⟩})}
is a 3PDF10S set over X. The corresponding ℧B(3,10) matrix is
℧B(3,10)=[⟨ci,(aij;bij)⟩]8×3
℧B(3,10)=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨9,(.7,.6,.4,:.2,.1,.4;.3,.5,.7)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨1,(.2,.1,.3;.6,.7,.9;.7,.3,.6)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨6,(.8,.6,.5;.6,.4,.7;.5,.8,.9)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨5,(.1,.2,.4;.8,.7,.1;.8,.3,.7)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨3,(.2,.3,.6;.9,.8,.7;.8,.7,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨8,(.1,.3,.4;.8,.7,.4;.7,.3,.1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (2)
Extended union of ℧A(3,13) and ℧B(3,10) is given below in Eq. (3):
℧C(3,13)=℧A(3,13)∪E˜℧B(3,10) where C={e1,e2,e3}
=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨9,(.7,.6,.4,:.2,.1,.4;.3,.5,.7)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨11,(.1,.9,.7;.5,.3,.2;.4,.6,.8)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨1,(.2,.1,.3;.6,.7,.9;.7,.3,.6)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨3,(.4,.3,.4;.5,.6,.8;.7,.6,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨6,(.8,.6,.5;.6,.4,.7;.5.8,.9)⟩⟨6,(.5,.4,.5;.6,.7,.7;.6,.4,.2)⟩⟨9,(.2,.1,.2;.3,.4.5;.6,.7,.8)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨5,(.1,.2,.4;8,.7,.1;.8,.3,.7)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨5,(.6,.5,.6;.7,.8.9;.8,.7,.6)⟩⟨8,(.3,.4,.5;.6,.7,.6;.5,.4,.3)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨3,(.2,.3,.6;.9,.8,.7;.8,.7,.5⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨8,(.1,.3,.4;.8,.7,.4;.7,.3,.1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (3)
Restricted union of ℧A(3,13) and ℧B(3,10) is given below in Eq. (4):
℧D(3,13)=℧A(3,13)∪R˜℧B(3,10) where D={e3}
=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨1,(.2,.1,.3;.6,.7,.9;.7,.3,.6)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨3,(.4,.3,.4;.5,.6,.8;.7,.6,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨6,(.5,.4,.5;.6,.7,.7;.6,.4,.2)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨5,(.1,.2,.4;8,.7,.1;.8,.3,.7)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨5,(.6,.5,.6;.7,.8.9;.8,.7,.6)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨3,(.2,.3,.6;.9,.8,.7;.8,.7,.5⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (4)
Definition 3.8. Let ℧A(m,N1) and ℧B(m,N2) be MPDFNS set over X. Then their extended intersection is defined as
℧C(m,N)∗=℧A(m,N1)∩E˜℧B(m,N2),
℧C(m,N)*={ (e,{ 〈ρ,lC(ρ)〉(μ1,C(ρ),μ2,C(ρ),⋯,μm,C(ρ);ν1,C(ρ),ν2,C(ρ)⋯,νm,C(ρ) }): e∈C,ρ∈X,lC(ρ)∈L}
where,
• C = A∪ B,
• (m, N)∗ = (m, min{N1, N2}),
• μC(ρ) = min{μi,A(ρ), μi,B(ρ)}, 1 ≤ i ≤ m,
• νC(ρ) = max{νi,A(ρ), νi,B(ρ)} 1 ≤ i ≤ m, and
• lC(ρ) = min{lA(ρ), lB(ρ)} ∀ e ∈ C.
Definition 3.9. Let ℧A(m,N1) and ℧B(m,N2) be MPDFNS set over X. Then their restricted intersetion is defined as
℧D(m,N)⋄=℧A(m,N1)∪R˜℧B(m,N2),
℧D(m,N)⋄={(e,{⟨ρ,lD(ρ)⟩(μ1,D(ρ),μ2,D(ρ),⋯,μm,D(ρ);ν1,D(ρ),ν2,D(ρ)⋯,νm,D(ρ)}):e∈D,ρ∈X,lD(ρ)∈L}
where,
• D = A ∩ B,
• (m,N)⋄ = (m, min{N1, N2}),
• μD(ρ) = min{μi,A(ρ), μi,B(ρ)}, 1 ≤ i ≤ m,
• νD(ρ) = max{νi,A(ρ), νi,B(ρ)} 1 ≤ i ≤ m, and
• lD(ρ) = min{lA(ρ), lB(ρ)} ∀ e ∈ D.
Example 3.3. Consider ℧A(3,13) and ℧B(3,10) as given in Example 3.2 by Eqs. (1) and (2), respectively. Extended intersection of ℧A13 and ℧B10 is given below in Eq. (5):
℧C(3,10)=℧A(3,13)∩E˜℧B(3,10) where C={e1,e2,e3}
℧C(3,10)=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (5)
Restricted intersection of ℧A(3,13) and ℧B(3,10) is given below Eq. (6):
℧D(3,10)=℧A(3,13)∩R˜℧B(3,10) where D={e3}
℧D(3,10)=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (6)
Proposition 3.3. If ℧A(m,N1), ℧B(m,N2), ℧C(m,N3) are MPDNFNS set over X, then
(i) ℧A(m,N1)∩E˜℧A(m,N1)=℧A(m,N1).
(ii) ℧A(m,N1)∪E˜℧A(m,N1)=℧A(m,N1).
(iii) ℧A(m,N1)∩E˜℧B(m,N2)=℧B(m,N2)∩E˜℧A(m,N1).
(iv) ℧A(m,N1)∪E˜℧B(m,N2)=℧B(m,N2)∪E˜℧A(m,N1).
(v) ℧A(m,N1)∩E˜(℧B(m,N2)∩E˜℧C(m,N3))=(℧A(m,N1)∩E˜℧B(m,N2))∩˜℧C(m,N3).
(vi) ℧A(m,N1)∪E˜(℧B(m,N2)∪E˜℧C)=(℧A(m,N1)∪E˜℧B(m,N2))∪E˜℧C(m,N3).
(vii) ℧A(m,N1)∩R˜℧A(m,N1)=℧A(m,N1).
(viii) ℧A(m,N1)∪R˜℧A(m,N1)=℧A(m,N1).
(ix) ℧A(m,N1)∩R˜℧B(m,N2)=℧B(m,N2)∩R˜℧A(m,N1).
(x) ℧A(m,N1)∪R˜℧B(m,N2)=℧B(m,N2)∪R˜℧A(m,N1).
(xi) ℧A(m,N1)∩R˜(℧B(m,N2)∩R˜℧C(m,N3))=(℧A(m,N1)∩R˜℧B(m,N2))∩˜℧C(m,N3).
(xii) ℧A(m,N1)∪R˜(℧B(m,N2)∪R˜℧C)=(℧A(m,N1)∪R˜℧B(m,N2))∪R˜℧C(m,N3).
Proof. The proof is obvious from Definitions 3.4, 3.5, 3.6, 3.7, 3.8 and 3.9.
Proposition 3.4. If ℧A(m,N1) and ℧B(m,N2) are MPDNFNS sets over X, then
(i) (℧A(m,N1)∩E˜℧B(m,N2)) ⊆˜ ℧A(m,N1) ⊆˜ (℧A(m,N1)∪E˜℧B(m,N2)).
(ii) (℧A(m,N1)∩E˜℧B(m,N2)) ⊆˜ ℧B(m,N2) ⊆˜ (℧A(m,N1)∪E˜℧B(m,N2)).
(iii) (℧A(m,N1)∩R˜℧B(m,N2)) ⊆˜ ℧A(m,N1) ⊆˜ ℧A(m,N1)∪E˜℧B(m,N2)).
(iv) (℧A(m,N1)∩R˜℧B(m,N2)) ⊆˜ ℧B(m,N2) ⊆˜ (℧A(m,N1)∪E˜℧B(m,N2)).
Proof. Proof of this proposition is obvious from Definitions 3.4, 3.6, 3.8 and 3.9.
4 Complements of m-Polar Neutrosophic Diophantine N-Soft Set
Definition 4.1. Let ℧A(m,N) be MPDNNS sets over X. Then their weak complement is represented as (℧A(m,N))wc and defined by
(℧A(m,N))wc={(e,{⟨ρ,lAwc(ρ)⟩(μ1,Awc(ρ),μ2,Awc(ρ),⋯,μm,Awc(ρ);λ1,Awc(ρ),λ2,Awc(ρ),⋯,λm,Awc(ρ);ν1,Awc(ρ),ν2,Awc(ρ)⋯,νm,Awc(ρ))})|e∈A,ρ∈X,lAwc(ρ)∈L}
where,
• μi,Awc(ρ) = νi,A(ρ), 1 ≤ i≤ m,
• λi,Awc(ρ) = 1 − λi,A(ρ), 1 ≤ i ≤ m,
• νi,Awc(ρ) = μi,A(ρ), 1 ≤ i ≤ m, and
• lAwc(ρ) ∩ lA(ρ) = ∅, ∀ e ∈ A.
Example 4.1. Consider ℧A(3,13) and ℧B(3,10) as given in Example 3.2 by Eqs. (1) and (2), respectively. Weak complement of ℧A(3,13) and ℧B(3,10) are given below in Eqs. (7) and (8):
℧A(3,13)wc=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨10,(.4,.6,.8;.5,.7,0.8;.1,.9,.7)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨5,(.7,.6,.5;.5,.4,.2;.4,.3,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨8,(.6,.4,.2;.4,.3,.3;.5,.4,.5)⟩⟨8,(.6,.7,.8;.7,.6,.5;.2,.1,.2)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨7,(.8,.7,.6;.3,.2.1;.6,.5,.6)⟩⟨6,(.5,.4,.3;.4,.3,.4;.3,.4,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (7)
℧B(3,13)wc=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨8,(.3,.5,.7;.8,.9,.6;.7,.6,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨7,(.7,.3,.6;.4,.3,.1;.2,.1,.3)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨4,(.5,.8,.9;.4,.6,.3;.8,.6,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨6,(.8,.3,.7;.2,.3,.9;.1,.2,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨2,(.8,.7,.5;.1,.2,.3;.2,.3,.6)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨6,(.7,.3,.1;.8,.7,.4;.1,.3,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (8)
Remark 4.1 Again taking week complement of (℧A(3,13))wc and (℧B(3,10))wc which given above in Eqs. (7), (8), respectively. There compliments are given below in Eqs. (9) and (10), respectively.
((℧A(3,13)wc)wc)=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨6,(.1,.9,.7;.5,.3,0.2;.4,.6,.8)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨4,(.4,.3,.4;.5,.6,.8;.7,.6,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨5,(.5,.4,.5;.6,.7,.7;.6,.4,.2)⟩⟨7,(.2,.1,.2;.3,.4.5;.6,.7,.8)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨7,(.6,.5,.6;.7,.8.9;.8,.7,.6)⟩⟨7,(.3,.4,.5;.6,.7,.6;.5,.4,.3)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (9)
((℧A(3,10)wc)wc)=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨4,(.7,.6,.4,:.2,.1,.4;.3,.5,.7)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨3,(.2,.1,.3;.6,.7,.9;.7,.3,.6)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨7,(.8,.6,.5;.6,.4,.7;.5,.8,.9)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨6,(.1,.2,.4;.8,.7,.1;.8,.3,.7)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨5,(.2,.3,.6;.9,.8,.7;.8,.7,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨9,(.1,.3,.4;.8,.7,.4;.7,.3,.1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (10)
Hence from Eqs. (1), (2), (9) and (10). We conclude that ((℧A(3,13))wc)wc ≠ ℧A(3,13) and ((℧B(3,10))wc)wc ≠ ℧B(3,10).
Since null 3PDN10S set is
℧∅(3,0)=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (11)
Since absolute 3PDN10S set is
℧E(3,10)=(⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩⟨9,(1,1,1;0,0,0;0,0,0)⟩) (12)
Weak complement of ℧∅(3,0) and ℧E(3,10) are given below in Eqs. (13) and (14), respectively.
(℧Φ(3,0))wc=(⟨7,(1,1,1;0,0,0;0,0,0)⟩⟨6,(1,1,1;0,0,0;0,0,0)⟩⟨4,(1,1,1;0,0,0;0,0,0)⟩⟨1,(1,1,1;0,0,0;0,0,0)⟩⟨8,(1,1,1;0,0,0;0,0,0)⟩⟨7,(1,1,1;0,0,0;0,0,0)⟩⟨6,(1,1,1;0,0,0;0,0,0)⟩⟨7,(1,1,1;0,0,0;0,0,0)⟩⟨3,(1,1,1;0,0,0;0,0,0)⟩⟨5,(1,1,1;0,0,0;0,0,0)⟩⟨2,(1,1,1;0,0,0;0,0,0)⟩⟨4,(1,1,1;0,0,0;0,0,0)⟩⟨7,(1,1,1;0,0,0;0,0,0)⟩⟨8,(1,1,1;0,0,0;0,0,0)⟩⟨6,(1,1,1;0,0,0;0,0,0)⟩⟨8,(1,1,1;0,0,0;0,0,0)⟩⟨7,(1,1,1;0,0,0;0,0,0)⟩⟨2,(1,1,1;0,0,0;0,0,0)⟩⟨1,(1,1,1;0,0,0;0,0,0)⟩⟨6,(1,1,1;0,0,0;0,0,0)⟩⟨5,(1,1,1;0,0,0;0,0,0)⟩) (13)
(℧E(3,10))wc=(⟨9,(0,0,0;1,1,1;1,1,1)⟩⟨5,(0,0,0;1,1,1;1,1,1)⟩⟨5,(0,0,0;1,1,1;1,1,1)⟩⟨1,(0,0,0;1,1,1;1,1,1)⟩⟨3,(0,0,0;1,1,1;1,1,1)⟩⟨9,(0,0,0;1,1,1;1,1,1)⟩⟨8,(0,0,0;1,1,1;1,1,1)⟩⟨9,(0,0,0;1,1,1;1,1,1)⟩⟨6,(0,0,0;1,1,1;1,1,1)⟩⟨2,(0,0,0;1,1,1;1,1,1)⟩⟨5,(0,0,0;1,1,1;1,1,1)⟩⟨5,(0,0,0;1,1,1;1,1,1)⟩⟨7,(0,0,0;1,1,1;1,1,1)⟩⟨4,(0,0,0;1,1,1;1,1,1)⟩⟨7,(0,0,0;1,1,1;1,1,1)⟩⟨4,(0,0,0;1,1,1;1,1,1)⟩⟨6,(0,0,0;1,1,1;1,1,1)⟩⟨5,(0,0,0;1,1,1;1,1,1)⟩⟨1,(0,0,0;1,1,1;1,1,1)⟩⟨8,(0,0,0;1,1,1;1,1,1)⟩⟨9,(0,0,0;1,1,1;1,1,1)⟩) (14)
From Eqs. (11)–(14), we have (℧∅(3,0))wc≠℧E(3,10) and (℧E(3,10))wc≠℧∅(3,0). Hence, we have following result.
Remark 4.2 Let ℧A(m,N) be MPDNNS sets, ℧∅(m,0) be null MPDNNS and ℧E(m,N−1) absolute MPDNNS over X, then following results that hold in crisp set theory but not hold in MPDNNS set theory
(i) (℧∅(m,0))wc ≠ ℧E(m,N−1).
(ii) (℧E(m,N−1))wc ≠ ℧∅(m,0).
(iii) ((℧A(m,N))wc)wc ≠ ℧A(m,N).
Definition 4.2. Let ℧A(m,N) be MPDNNS set over X. Then their top weak complement is represented as (℧A(m,N))twc and defined by
(℧A(m,N))twc={(e,{⟨ρ,lAtwc(ρ)⟩(μ1,Atwc(ρ),μ2,Atwc(ρ),⋯,μm,Atwc(ρ);λ1,Atwc(ρ),λ2,Atwc(ρ),⋯,λm,Atwc(ρ);ν1,Atwc(ρ),ν2,Atwc(ρ)⋯,νm,Atwc(ρ)})
|e∈A,ρ∈X,lAtwc(ρ)∈L}
where,
• μi,Atwc(ρ) = νi,A(ρ), 1 ≤ i ≤ m,
• λi,Atwc(ρ) = 1 − λi,A(ρ), 1 ≤ i ≤ m,
• νi,Atwc(ρ) = μi,A(ρ), 1 ≤ i ≤ m, and
• lAtwc(ρ)={N−1,if lA(ρ)<N−1,0,if lA(ρ)=N−1,∀e∈A.
The top weak complement of ℧A(3,13) and ℧B(3,10) as given in Example 3.2 by Eqs. (1) and (2) are given below in Eqs. (15) and (16), respectively.
(℧A(3,13))twc=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.4,.6,.8;.5,.7,0.8;.1,.9,.7)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.7,.6,.5;.5,.4,.2;.4,.3,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.6,.4,.2;.4,.3,.3;.5,.4,.5)⟩⟨12,(.6,.7,.8;.7,.6.5;.2,.1,.2)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.8,.7,.6;.3,.2.1;.6,.5,.6)⟩⟨12,(.5,.4,.3;.4,.3,.4;.3,.4,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (15)
(℧B(3,10))twc=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.3,.5,.7;.8,.9,.6;.7,.6,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.7,.3,.6;.4,.3,.1;.2,.1,.3)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.5,.8,.9;.4,.6,.3;.8,.6,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.8,.3,.7;.2,.3,.9;.1,.2,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.8,.7,.5;.1,.2,.3;.2,.3,.6)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.7,.3,.1;.8,.7,.4;.1,.3,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (16)
Proposition 4.1 Let ℧A(m,N) be MPDNNS set, ℧∅(m,0) be null MPDNNS and ℧E(m,N−1) absolute MPDNNS over X, then
(i) (℧∅(m,0))twc = ℧E(m,N−1).
(ii) (℧E(m,N−1))twc = ℧∅(m,0).
Remark 4.3. Again taking top weak complement of (℧A(3,13))twc given in Eq. (15) we have Eq. (17)
((℧A(3,13))twc)twc=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.1,.9,.7;.5,.3,0.2;.4,.6,.8)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.4,.3,.4;.5,.6,.8;.7,.6,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.5,.4,.5;.6,.7,.7;.6,.4,.2)⟩⟨0,(.2,.1,.2;.3,.4.5;.6,.7,.8)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.6,.5,.6;.7,.8.9;.8,.7,.6)⟩⟨0,(.3,.4,.5;.6,.7,.6;.5,.4,.3)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (17)
Hence from Eqs. (1) and (17) we conclude that ((℧A(3,13))twc)twc≠℧A(3,13). Hence we have the following result:
Remark 4.4. Let ℧A(m,N) be MPDNNS set, over X, then ((℧A(m,N))twc)twc ≠ ℧A(m,N).
Definition 4.3. Let ℧A(m,N) be MPDNNS set over X. Then their bottom weak complement is represented as (℧A(m,N))bwc and defined by
(℧A(m,N))bwc={(e,{⟨ρ,lAbwc(ρ)⟩(μ1,Abwc(ρ),μ2,Abwc(ρ),⋯,μm,Abwc(ρ);λ1,Abwc(ρ),λ2,Abwc(ρ),⋯,λm,Abwc(ρ);ν1,Abwc(ρ),ν2,Abwc(ρ)⋯,νm,Abwc(ρ))})
|e∈A,ρ∈X,lAbwc(ρ)∈L}
where,
• μi,Abwc(ρ) = νi,A(ρ), 1 ≤ i ≤ m,
• λi,Abwc(ρ) = 1 − λi,A(ρ), 1 ≤ i ≤ m,
• νi,Abwc(ρ) = μi,A(ρ), 1 ≤ i ≤ m, and
• lAbwc(ρ)={N−1,if lA(ρ)=0,0,iflA(ρ)>0,∀e∈A.
Example 4.2. Consider ℧A(3,13) and ℧B(3,10) as given in Example 3.2 by Eqs. (1) and (2), respectively. Bottom weak complement of ℧A(3,13) and ℧B(3,10) are given below in Eqs. (18) and (19):
(℧A(3,13))bwc=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.4,.6,.8;.5,.7,0.8;.1,.9,.7)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.7,.6,.5;.5,.4,.2;.4,.3,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.6,.4,.2;.4,.3,.3;.5,.4,.5)⟩⟨0,(.6,.7,.8;.7,.6.5;.2,.1,.2)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.8,.7,.6;.3,.2.1;.6,.5,.6)⟩⟨0,(.5,.4,.3;.4,.3,.4;.3,.4,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (18)
(℧B(3,13))bwc=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.3,.5,.7;.8,.9,.6;.7,.6,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.7,.3,.6;.4,.3,.1;.2,.1,.3)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.5,.8,.9;.4,.6,.3;.8,.6,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.8,.3,.7;.2,.3,.9;.1,.2,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.8,.7,.5;.1,.2,.3;.2,.3,.6)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(.7,.3,.1;.8,.7,.4;.1,.3,.4)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (19)
Proposition 4.2. Let ℧A(m,N) be MPDNNS set, ℧∅(m,0) be null MPDNNS and ℧E(m,N−1) absolute MPDNNS over X, then
(i) (℧∅(m,0))bwc = ℧E(m,N:amp:minus;1).
(ii) (℧E(m,N−1))bwc = ℧∅(m,0).
Remark 4.5. Again taking bottom weak complement of (℧A(3,13))bwc as given above in Eq. (18) we have Eq. (20) given below:
((℧A(3,13))bwc)bwc=(⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.1,.9,.7;.5,.3,0.2;.4,.6,.8)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.4,.3,.4;.5,.6,.8;.7,.6,.5)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.5,.4,.5;.6,.7,.7;.6,.4,.2)⟩⟨12,(.2,.1,.2;.3,.4.5;.6,.7,.8)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨12,(.6,.5,.6;.7,.8.9;.8,.7,.6)⟩⟨12,(.3,.4,.5;.6,.7,.6;.5,.4,.3)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩⟨0,(0,0,0;1,1,1;1,1,1)⟩) (20)
Hence from Eqs. (1) and (20) we conclude that ((℧A(3,13))bwc)bwc≠℧A(3,13).
5 Relationships with Existing Models and Application in Multi-Attribute Group Decision-Making
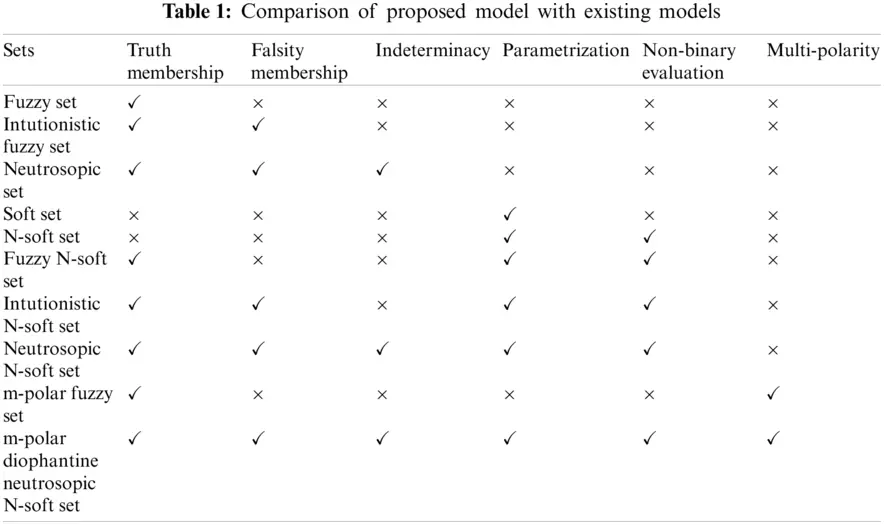
The comparison with existing sets is shown in Table 1.
The following proposed algorithm for the choice values of MPDNNSs:
An Algorithm for the Choice Values of MPDNNSs
1: S = {ρ1, ρ2,…, ρm} is the universal set.
2: T = {e1, e2,…, en} set of attributes.
3: Input MPDFNSs ψA(m,n) with N = {0, 1, 2,…, N − 1}.
4: Calculate Mim=(∑j=1mdαij,∑j=1mRaij). Here,
daij=1−2θaπ,Raij=12+ra(12−2θaπ),
ra=(μ12+μ22+⋯+μm2+λ12+λ22+⋯+λm2+ν12+ν22+⋯+νm2)1/2,
θa=Tan−1(<(λ1,λ2,⋯,λm),(ν1,ν2,⋯,νm)>||(μ1,μ2,⋯,μm)||),
where, <(λ1, λ2,…, λm), (ν1, ν2,…, νm)> = λ1ν1 + λ2ν2 + …, λmνm.
5: Calculate Mtm=max{Mim} with i = 1, 2,…, n.
6: Mtm=max{Mim} can be chosen for any alternative.
Example 5.1. We assume that there are five candidates which appear in the interview and their interviews will be completed in three days. There are three judges which are observed to each candidate separately. The following data are elaborated in Table 2, of each candidate ci, i = 1, 2, 3, 4, 5 which are observed by from judges ji, i = 1, 2, 3.

In Table 3, we find the choice values of all candidates by using proposed algorithm.
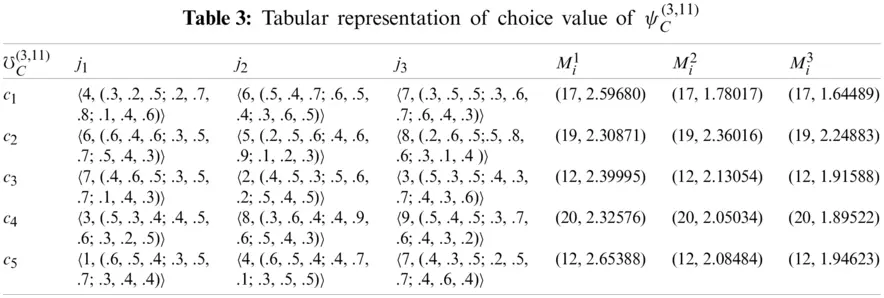
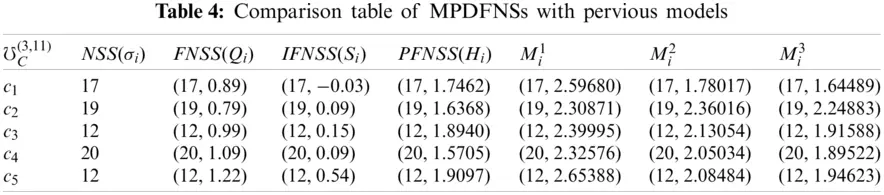
From Table 4, the candidates c5, c2, c2 are leading with respect to days first, second, and third, respectively.
The working of proposed algorithm is shown in Fig. 1.
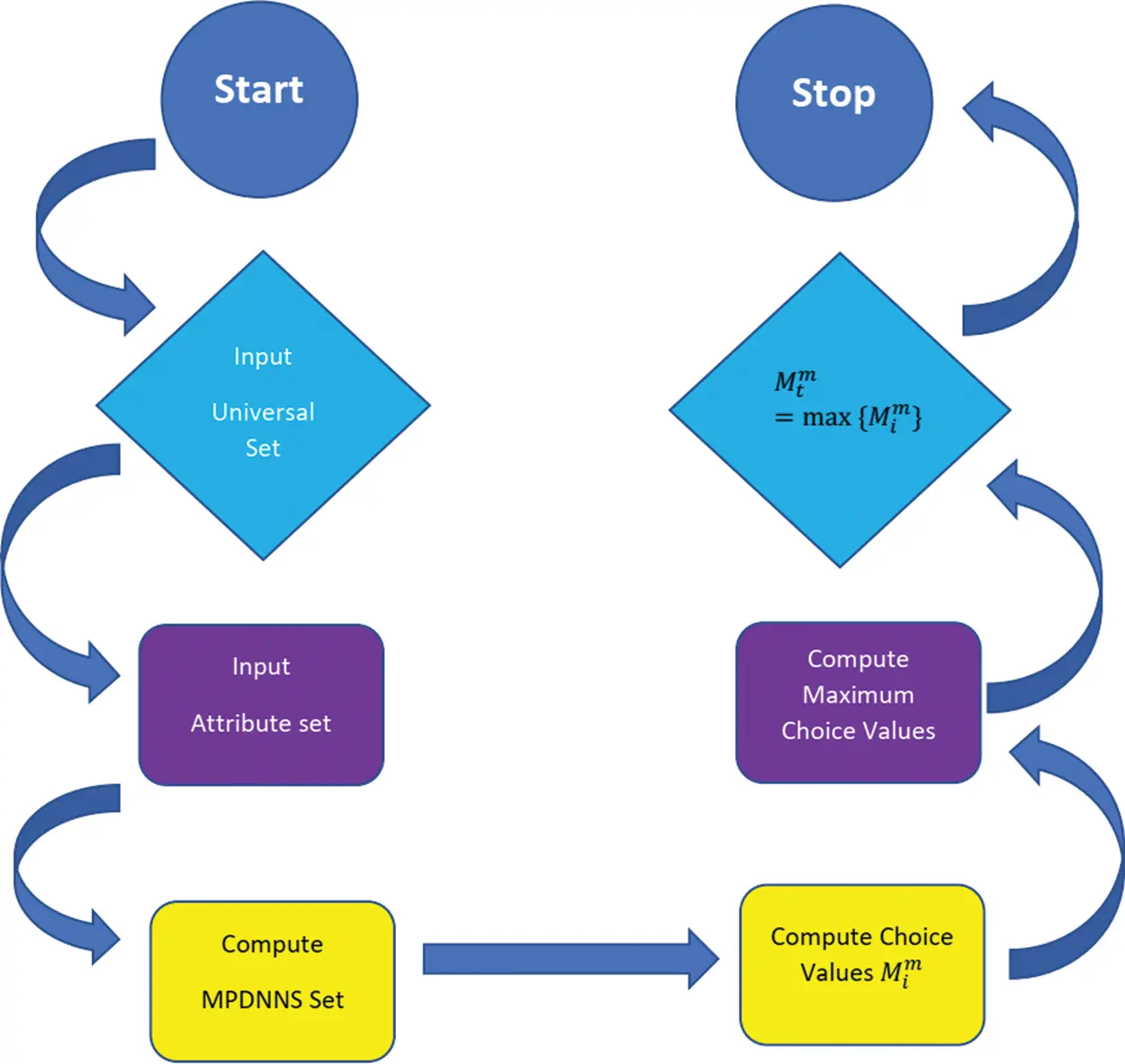
Figure 1: Flow chart of proposed algorithm
5.1 Relationships with Existing Sets
In this subsection, we establish the relationship with existing sets.
Definition 5.1. Let n be a threshold lies between 0 and N for the level, the PFNSS and PFSS over X associated with ℧A(m,N) and n, symbolized by ℧A(n,m,N), defined by, for all a ∈ A,
℧a(n,m,N)={⟨x,(μ(a),ν(a))⟩,if m=1,(x,da)(μ(a),ν(a)),if (x,da)∈F(a),andda≥n,(0,0.5),if da/N≥0.5,(0,1),if da/N<0.5.
Definition 5.2. Let k be a threshold with k ∈ [−1, 1] for the score function, the N-soft over X associated with ℧A(m,N) and k, symbolized by ℧A(k,m,N), defined by, for all a ∈ A,
℧a(k,m,N)={(x,da),if (x,da)∈F(a), and Sa(x)≥k,m=1,1,if Sa(x)>0,m=1,0,if Sa(x)≤0,m=1.
Definition 5.3. Let n be a threshold lies between 0 and N and threshold k with k ∈ [− 1, 1] for the score function, the soft over X associated with ψA(m,N) and (n, k), symbolized by ℧A((n,k),m,N), defined by, for all a ∈ A,
℧A((n,k),1,N)={x∈X|Sa℧(n,1,N)(x)>k,}
For soft set associated with ψA(3,6) and threshold (n, k) = (3, 0.3) is ℧A((3,0.3),1,6) = { }.
From Example 3.1, we have the following outcome which are elaborate in Table 5.

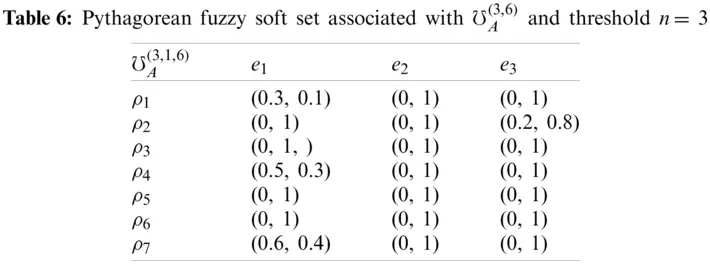
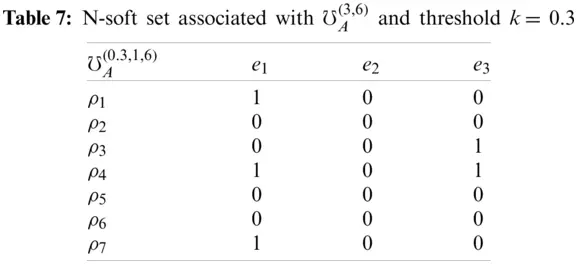
In Tables 6 and 7, we deduce Pythagorean fuzzy soft set and N-soft set from MPDFNSs.
6 Conclusion
In this paper, we investigate a new set namely the m-polar Diophantine neutrosophic N-soft set which is based on neutrosophic set and soft set. We are discussed different types of compliments on the proposed set and elaborate these compliments with examples. The purposed set is a generalized form of fuzzy, soft, Pythagorean fuzzy, Pythagorean fuzzy soft, and Pythagorean fuzzy N-soft sets. Moreover, as an application, we proposed an algorithm for multi-attribute decision-making problems by defining the new score function. In future work, one can discuss algebraic structures and topological properties on m-polar Diophantine neutrosophic N-soft set. Moreover, ones can develop the concept of m-polar Diophantine neutrosophic N-soft graph and then discuss their properties.
Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.
Funding Statement:This work is supported by the Social Sciences Planning Projects of Zhejiang (21QNYC11ZD), Major Humanities and Social Sciences Research Projects in Zhejiang Universities (2018QN058), Fundamental Research Funds for the Provincial Universities of Zhejiang (SJWZ2020002) and Longyuan Construction Financial Research Project of Ningbo University (LYYB2002).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zadeh, L. A. (1965). Information and control. Fuzzy Sets, 8(3), 338–353. DOI 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
2. Atanassov, K. T. (1986). Intuitionistic fuzzy set. Fuzzy Sets and Systems, 20(1), 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]
3. Molodtsov, D. (1999). Soft set theory-first results. Computers and Mathematics with Applications, 37(4–5), 19–31. DOI 10.1016/S0898-1221(99)00056-5. [Google Scholar] [CrossRef]
4. Ali, M. I., Feng, F., Liu, X., Min, W. K., Shabir, M. (2009). On some new operations in soft set theory. Computers and Mathematics with Applications, 57(9), 1547–1553. DOI 10.1016/j.camwa.2008.11.009. [Google Scholar] [CrossRef]
5. Yager, R. R. (2013). Pythagorean fuzzy subsets. Joint IFSA World Congress and NAFIPS Annual Meeting, pp. 57–61. IEEE. DOI 10.1109/IFSA-NAFIPS.2013.6608375. [Google Scholar] [CrossRef]
6. Yager, R. R., Abbasov, A. M. (2013). Pythagorean membership grades, complex numbers, and decision making. International Journal of Intelligent Systems, 28(5), 436–452. DOI 10.1002/int.21584. [Google Scholar] [CrossRef]
7. Yager, R. R. (2013). Pythagorean membership grades in multicriteria decision making. IEEE Transactions on Fuzzy Systems, 22(4), 958–965. DOI 10.1109/TFUZZ.2013.2278989. [Google Scholar] [CrossRef]
8. Peng, X., Yuan, H., Yang, Y. (2017). Pythagorean fuzzy information measures and their applications. International Journal of Intelligent Systems, 32(10), 991–1029. DOI 10.1002/int.21880. [Google Scholar] [CrossRef]
9. Peng, X. D., Yang, Y., Song, J., Jiang, Y. (2015). Pythagorean fuzzy soft set and its application. Computer Engineering, 41(7), 224–229. DOI 10.3969/j.issn.1000-3428.2015.07.043. [Google Scholar] [CrossRef]
10. Peng, X., Dai, J. (2018). Approaches to single-valued neutrosophic MADM based on MABAC, TOPSIS and new similarity measure with score function. Neural Computing and Applications, 29(10), 939–954. DOI 10.1007/s00521-016-2607-y. [Google Scholar] [CrossRef]
11. Zeng, S., Shoaib, M., Ali, S., Smarandache, F., Rashmanlou, H. et al. (2021). Certain properties of single-valued neutrosophic graph with application in food and agriculture organization. International Journal of Computational Intelligence Systems, 14(1), 1516–1540. DOI 10.2991/ijcis.d.210413.001. [Google Scholar] [CrossRef]
12. Gulfam, M., Mahmood, M. K., Smarandache, F., Ali, S. (2021). New Dombi aggregation operators on bipolar neutrosophic set with application in multi-attribute decision-making problems. Journal of Intelligent & Fuzzy Systems, 1–18 (Preprint). [Google Scholar]
13. Hameed, M. S., Mukhtar, S., Khan, H. N., Ali, S., Mateen, M. H. et al. (2021). Pythagorean fuzzy N-Soft groups. International Journal of Electrical and Computer Engineering, 21(2), 1030–1038. [Google Scholar]
14. Liu, J. B., Ali, S., Mahmood, M. K., Mateen, M. H. (2020). On m-polar Diophantine fuzzy N-soft set with applications. Combinatorial Chemistry & High Throughput Screening, 23, 1–18. DOI 10.2174/1386207323666201230092354. [Google Scholar] [CrossRef]
15. Zeng, S., Shoaib, M., Ali, S., Abbas, Q., Nadeem, M. S. (2020). Complex vague graphs and their application in decision-making problems. IEEE Access, 8, 174094–174104. DOI 10.1109/ACCESS.2020.3025974. [Google Scholar] [CrossRef]
16. Mahmood, M. K., Zeng, S., Gulfam, M., Ali, S., Jin, Y. (2020). Bipolar neutrosophic dombi aggregation operators with application in multi-attribute decision making problems. IEEE Access, 8, 156600–156614. DOI 10.1109/ACCESS.2020.3019485. [Google Scholar] [CrossRef]
17. Akram, M., Amjad, U., Davvaz, B. (2021). Decision-making analysis based on bipolar fuzzy N-soft information. Computational and Applied Mathematics, 40(6), 1–39. DOI 10.1007/s40314-021-01570-y. [Google Scholar] [CrossRef]
18. Akram, M., Luqman, A., Kahraman, C. (2021). Hesitant Pythagorean fuzzy ELECTRE-II method for multi-criteria decision-making problems. Applied Soft Computing, 108(3), 107479. DOI 10.1016/j.asoc.2021.107479. [Google Scholar] [CrossRef]
19. Adeel, A., Akram, M., Cagman, N. (2021). Decision-making analysis based on hesitant fuzzy N-Soft ELECTRE-I approach. Soft Computing (Preprint). [Google Scholar]
20. Akram, M., Kahraman, C., Zahid, K. (2021). Extension of TOPSIS model to the decision-making under complex spherical fuzzy information. Soft Computing, 25, 1–25. DOI 10.1016/j.knosys.2021.106793. [Google Scholar] [CrossRef]
21. Akram, M., Alsulami, S., Zahid, K. (2021). A hybrid method for complex pythagorean fuzzy decision making. Mathematical Problems in Engineering, 2021(6), 1–23. DOI 10.1155/2021/9915432. [Google Scholar] [CrossRef]
22. Fatimah, F., Rosadi, D., Hakim, R. F., Alcantud, J. C. R. (2018). N-soft sets and their decision making algorithms. Soft Computing, 22(12), 3829–3842. DOI 10.1007/s00500-017-2838-6. [Google Scholar] [CrossRef]
23. Alcantud, J. C. R., Laruelle, A. (2014). Dis-approval voting: A characterization. Social Choice and Welfare, 43(1), 1–10. DOI 10.1007/s00355-013-0766-7. [Google Scholar] [CrossRef]
24. Ma, X., Liu, Q., Zhan, J. (2017). A survey of decision making methods based on certain hybrid soft set models. Artificial Intelligence Review, 47(4), 507–530. DOI 10.1007/s10462-016-9490-x. [Google Scholar] [CrossRef]
25. Wang, H., Smarandache, F., Zhang, Y., Sunderraman, R. (2010). Single valued neutrosophic sets. Infinite Study. [Google Scholar]
26. Deli, I., Ali, M., Smarandache, F. (2015). Bipolar neutrosophic sets and their application based on multi-criteria decision making problems. International Conference on Advanced Mechatronic Systems, pp. 249–254. Beijing, China, IEEE.DOI 10.1109/ICAMechS.2015.7287068. [Google Scholar] [CrossRef]
27. Zeng, S. Z., Hu, Y. J., Balezentis, T., Streimikiene, D. (2020). A multi-criteria sustainable supplier selection framework based on neutrosophic fuzzy data and entropy weighting. Sustainable Development, 28(5), 1431–1440. DOI 10.1002/sd.2096. [Google Scholar] [CrossRef]
28. Zeng, S., Hu, Y., Xie, X. (2021). Q-rung orthopair fuzzy weighted induced logarithmic distance measures and their application in multiple attribute decision making. Engineering Applications of Artificial Intelligence, 100(7), 104167. DOI 10.1016/j.engappai.2021.104167. [Google Scholar] [CrossRef]
29. Wang, J., Zeng, S., Zhang, C. (2020). Single-valued neutrosophic linguistic logarithmic weighted distance measures and their application to supplier selection of fresh aquatic products. Mathematics, 8(3), 439. DOI 10.3390/math8030439. [Google Scholar] [CrossRef]
30. Zhang, C., Su, W., Zeng, S., Balezentis, T., Herrera-Viedma, E. (2021). A two-stage subgroup decision-making method for processing large-scale information. Expert Systems with Applications, 171(3), 114586. DOI 10.1016/j.eswa.2021.114586. [Google Scholar] [CrossRef]
31. Zhang, H. D., Shu, L. (2016). Dual hesitant fuzzy soft set and its properties. Fuzzy systems & operations research and management, pp. 171–182. Cham: Springer. [Google Scholar]
32. Cagman, N., Enginoglu, S., Citak, F. (2011). Fuzzy soft set theory and its applications. Iranian Journal of Fuzzy Systems, 8(3), 137–147. DOI 10.22111/IJFS.2011.292. [Google Scholar] [CrossRef]
33. Maji, P. K., Biswas, R. K., Roy, A. (2001). Fuzzy soft sets. Journal of Fuzzy Mathematics, 9(3), 589–602. [Google Scholar]
34. Maji, P. K., Biswas, R., Roy, A. R. (2001). Intuitionistic fuzzy soft sets. Journal of Fuzzy Mathematics, 9(3), 677–692. [Google Scholar]
35. Wei, G., Wei, Y. (2018). Similarity measures of Pythagorean fuzzy sets based on the cosine function and their applications. International Journal of Intelligent Systems, 33(3), 634–652. DOI 10.1002/int.21965. [Google Scholar] [CrossRef]
36. Wan, S. P., Jin, Z., Dong, J. Y. (2018). Pythagorean fuzzy mathematical programming method for multi-attribute group decision making with Pythagorean fuzzy truth degrees. Knowledge and Information Systems, 55(2), 437–466. DOI 10.1007/s10115-017-1085-6. [Google Scholar] [CrossRef]
37. Zhang, H., Jia-Hua, D., Yan, C. (2020). Multi-attribute group decision-making methods based on Pythagorean fuzzy N-soft sets. IEEE Access, 8, 62298–62309. DOI 10.1109/ACCESS.2020.2984583. [Google Scholar] [CrossRef]
38. Smarandache, F. (1999). A unifying field in logics. Neutrosophy: Neutrosophic probability, set and logic, pp. 1–141. American Research Press. [Google Scholar]












