Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2022.017032

ARTICLE

New Concepts on Quadripartitioned Bipolar Single Valued Neutrosophic Graph

S. Satham Hussain1, G. Muhiuddin2,*, N. Durga3 and D. Al-Kadi4

1PG and Research Department of Mathematics, Jamal Mohamed College (Autonomus), Tiruchirappalli, 620020, India
2Department of Mathematics, University of Tabuk, Tabuk, 71491, Saudi Arabia
3Division of Mathematics, School of Advanced Sciences, Vellore Institute of Technology-Chennai Campus, Chennai, 600127, India
4Department of Mathematics and Statistic, College of Science, Taif University, Taif, 21944, Saudi Arabia
*Corresponding Author: G. Muhiuddin. Email: chishtygm@gmail.com
Received: 27 April 2021; Accepted: 14 July 2021

1  Introduction

Bipolar fuzzy sets are more useful, beneficial, and applicable in real-world situations. It deals with incomplete information since they do not take into account indeterminate or contradictory data, which can be found in a variety of systems [1,2], including belief systems and decision-support systems [3,4]. As reality vanishes in a black hole due to Hawking radiation or specific/anti-particular emission, the bipolar domain is the most important condition that persists. In a bipolar fuzzy set, an element with a membership degree of 0 is insignificant to the subsequent property, an element with a membership degree of (0,1] is somewhat satisfied by the property, and an element with a membership degree of [−1,0] is quite satisfied by the implied counter-property. On the other hand, to interpret the degree of true and false membership functions, some restrictions allow only to hold incomplete data, but the handling of indeterminate information remains. Can we see an instance, suppose there are ten patients to check a pandemic during testing. In that time, three patients are having positive, five will have negative, and two are undecided or yet to come. By employing the neutrosophic concepts, it can be expressed as x(0.3,0.2,0.5). For the clear understanding, one can characterize the climate as cold as truth, moderate as indeterminacy and hot as false using a neutrosophic set. Hence the neutrosophic field arises to hold the indeterminacy data as well. It generalizes the aforementioned sets from the philosophical viewpoint. The single-valued neutrosophic set is the generalization of intuitionistic fuzzy sets and is used expediently to deal with real-world problems, especially in decision support [5]. The computation of belief in that element (truth), they disbelieve in that element (falsehood) and the indeterminacy part of that element with the sum of these three components are strictly less than 1 and it is proposed by Smarandache [6] and references therein.

In the case of neutrosophic sets, indeterminacy function is considered as an individual term and each element x is characterized by a truth-membership function TA(x), an indeterminacy membership function IA(x) and a falsity-membership function FA(x), each of that from the non-standard unit interval [0−,1+]. Despite the neutrosophic indeterminacy is independent of the truth and falsity-membership values, but it is more general than the hesitation margin of intuitionistic fuzzy sets. It is not sure whether the indeterminacy values relevant to a particular element correspond to hesitant values about its belonging or not belonging to it. In another way, if a person identifies an indeterminacy membership IA(x) with a specific event x, it becomes difficult to understand whether the person’s degree of uncertainty regarding the event’s occurrence is IA(x) or whether the person’s degree of uncertainty regarding the event’s non-occurrence is IA(x). As a result, some authors prefer to model the indeterminacy’s behaviour in the same way they similar to truth-membership, others may prefer to model it, in the same way, they similar to falsity-membership. Wang et al. [5] initiated the concept of a single-valued neutrosophic set and provide its various properties. It has been widely applied in various fields, such as information fusion in which data are combined from different sensors [7], control theory [8], image processing [9], medical diagnosis [10], decision making [11,12], and graph theory [13–20], etc.

When the indeterminacy portion of the neutrosophic set is divided into two parts, we get four components: ‘Contradiction’ (both true and false) and ‘Unknown’ (neither true nor false), that is T,C,U and F which defines a new set called ‘quadripartitioned single valued neutrosophic set’, introduced by Chatterjee et al. [21]. This study is completely based on “Belnap’s four valued logic” [22] and Smarandache’s “Four Numerical valued neutrosophic logic” [23]. By employing the concept of Quadripartitioned Single Valued Neutrosophic Set (QSVNS), this paper presents the quadripartitioned single-valued neutrosophic graphs. Operations on single-valued neutrosophic graphs are studied in [24]. Further, the operations on neutrosophic vague graphs are discussed in [16]. Authors in [25] studied the bipolar quadripartitioned single-valued neutrosophic sets. In [3,26], the authors extensively studied about the concept of bipolar neutrosophic graphs. Moreover, in [27], bipolar single valued neutrosophic graphs are investigated with its related properties. Motivated by the above-mentioned works, to the best of the authors’ knowledge, there is no work reported on the concepts of bipolar quadripartioned single-valued neutrosophic graphs with the application. More concepts related to this study have been studied in [28–31]. The major contributions in this work are explained as follows:

1. The notions of Quadripartitioned Bipolar Single Valued Neutrosophic Graphs (QBSVNGs) are introduced. This manuscript makes the first attempt in the literature about the concept in neutrosophic graphs.

2. In addition, the complete and strong QBSVNG are defined. The operations like a Cartesian product, cross product, lexicographic product, strong product and the composition of QBSVNGs with their properties are discussed.

3. The proposed work will generalise the existing works in the literature [3,24,25,32].

The paper is organized as follows: The basic needed definitions are given in Preliminaries Section 2 . The QBSVNGs are introduced and the operations are explained in Section 3 .

2  Preliminaries

Definition 2.1 [6] Let X be a space of points (objects), with generic elements in X denoted by x. A single valued neutrosophic set A in X is characterised by truth-membership function TA(x), indeterminacy-membership function IA(x) and falsity-membership-function FA(x).

For each point x in X, TA(x),IA(x),FA(x)∈[0,1]. Also

A={x,TA(x),IA(x),FA(x)} and 0≤TA(x)+IA(x)+FA(x)≤3.

Definition 2.2 [6] A Neutrosophic set A is contained in another neutrosophic set B, (i.e) A⊆B if ∀ x∈X, TA(x)≤TB(x),IA(x)≥IB(x) and FA(x)≥FB(x).

Definition 2.3 [24] A neutrosophic graph is defined as a pair G∗=(V,E) where

(i) V={v1,v2,…,vn} such that TA:V→[0,1], IA:V→[0,1] and FA:V→[0,1] denote the degrees of truth-membership function, indeterminacy function and falsity-membership function, respectively and

0≤TA(v)+IA(v)+FA(v)≤3,∀ v∈V.

(ii) E⊆V×V where TB:E→[0,1], IB:E→[0,1] and FB:E→[0,1] are such that

TB(uv)≤min{TA(u),TA(v)},

IB(uv)≤min{IA(u),IA(v)},

FB(uv)≤max{FA(u),FA(v)},

and 0≤TB(uv)+IB(uv)+FB(uv)≤3,∀ uv∈E.

For more details about the following definitions and results, see the article [21].

Definition 2.4 Let X be a non-empty set. A quadripartitioned neutrosopohic set (QSVNS) A over X characterizes each elements x in X by a truth membership function TA, a contradiction membership function CA, an ignorance membership function UA and a false membership function FA such that for each x∈X,TA,CA,UA,FA∈[0,1] and 0≤TA(x)+CA(x)+UA(x)+FA(x)≤4.

Remark 2.5 A QSVNS A can be decomposed to yield two SVNS, say, At and Ab where the respective membership functions and these sets are defined as

TAt(x)=TA(x)=TAb(x)

IAt(x)=CA(x),IAb(x)=UA(x)

FAt(x)=FA(x)=FAb(x),∀x∈X.

In this respect, we stated that while performing set-theoretic operations over these SVNS, the behaviour of IAt is treated similar to that of TAt while the behaviour of IAb is modelled in a way similar to that of FAb.

Definition 2.6 A QSVNS is said to be an absolute QSVNS, deoted by A, if and only if its membership values are respectivley defined as TA(x)=1, CA(x)=1 , UA(x)=0 and FA(x)=0.

Definition 2.7 Consider two QSVNS A and B over X.A is said to be contained in B, denoted by A⊆B if, and only, if TA(x)≤TB(x), CA(x)≤CB(x), UA(x)≥UB(x) and FA(x)≥FB(x).

Definition 2.8 The complement of a QSVNS A, is denoted by Ac and is defined as

Ac=∑i=1n⟨FA(xi),UA(xi),CA(xi),TA(xi)⟩,∀ xi∈X.

i.e., TAc(xi)=FA(xi),CAc(xi)=UA(xi), UAc(xi)=CA(xi),FAc(xi)=TA(xi),∀ xi∈X.

Definition 2.9 The union of two QSVNS A and B is denoted by A∪B and is defined as

A∪B=∑i=1n⟨TA(xi)∨TB(xi),CA(xi)∨CB(xi)

UA(xi)∧UB(xi),FA(xi)∧FB(xi)⟩/X.

Definition 2.10 The intersection of two QSVNS A and B is denoted by A∩B and is defined as

A∩B=∑i=1n⟨TA(xi)∧TB(xi),CA(xi)∧CB(xi)

UA(xi)∨UB(xi),FA(xi)∨FB(xi)⟩/X.

Definition 2.11 A quadripartitioned single valued bipolar neutrosophic set (QSVBNS) A is X defined as an object of the form:

A=⟨x,(T)AP(x),(C)AP(x),(U)AP(x),(F)AP(x),(T)AN(x),(C)AN(x),(U)AN(x),(F)AN(x):x∈X⟩,

where (T)AP,(C)AP,(U)AP,(F)AP:X→[0,1] and (T)AN,(C)AP,(U)AN,(F)AN:X→[−1,0]. The positive membership degrees (T)AP(x),(C)AP(x),(U)AP(x),(F)AP(x) denote respectively the truth-membership, a contradiction-membership, an ignorance membership degrees and falsity membership of x∈X corresponding to a QSVBNS A. The negative membership degrees (T)AN(x),(C)AN(x),(U)AN(x),(F)AN(x) denote respectively the truth-membership, a contradiction membership, an ignorance membership and falsity membership of x∈X to some explicit counter-property corresponding to a QSVBNS A.

Definition 2.12 Let A and B be two QSVBNS over X. Then A is said to be included in B, denoted by A⊆B, if for each x∈X,

(T)AP(x)≤(T)BP(x),(C)AP(x)≤(C)BP(x), (U)AP(x)≥(T)BP(x),(F)AP(x)≥(F)BP(x), and (T)AN(x)≥(T)BN(x),(C)AN(x)≥(C)BN(x), (U)AN(x)≤(U)BN(x),(F)AN(x)≤(F)BN(x).

Definition 2.13 Two QSVBNS A and B are said to be equal if for each x∈X,

(T)AP(x)=(T)BP(x),(C)AP(x)=(C)BP(x), (U)AP(x)=(U)BP(x),(F)AP(x)=(F)BP(x), and (T)AN(x)=(T)BN(x),(C)AN(x)=(C)BN(x), (U)AN(x)=(U)BN(x),(F)AN(x)=(F)BN(x).

3  Quadripartitioned Bipolar Single Valued Neutrosophic Graphs

In this section, the QBSVNGs are introduced, and its operations like Cartesian product, cross product, lexicographic product, strong product and composition are developed.

Definition 3.1 A QBSVNG of a crisp graph G=(V,E) is defined to be a pair G=(R,S) with R=(RP,RN) and S=(SP,SN), where

(i) the functions (TR)P:V→[0,1], (CR)P:V→[0,1], (UR)P:V→[0,1], (FR)P:V→[0,1] and (TR)N:V→[−1,0], (CR)N:V→[−1,0], (UR)N:V→[−1,0], (FR)N:V→[−1,0] represent the degree of truth membership, contradiction membership, ignorance membership and false membership of the element t∈V, respectively, there is no restriction on the sum 0≤(TR)P(t)+(CR)P(t)+(UR)P(t)+(FR)P(t)≤4, −4≤(TR)N(t)+(CR)N(t)+(UR)N(t)+(FR)N(t)≤0 for all t∈V.

(ii) the functions (TS)P:E⊆V×V→[0,1],(CS)P:E⊆V×V→[0,1],(US)P:E⊆V×V→[0,1],(FS)P:E⊆V×V→[0,1] and (TS)N:E⊆V×V→[−1,0],(CS)N:E⊆V×V→[−1,0],(US)N:E⊆V×V→[−1,0],(FS)N:E⊆V×V→[−1,0] are defined as

(TS)P(ts)≤min{(TR)P(t),(TR)P(s)}

(CS)P(ts)≤min{(CR)P(t),(CR)P(s)}

(US)P(ts)≤max{(UR)P(t),(UR)P(s)}

(FS)P(ts)≤max{(FR)P(t),(FR)P(s)},∀ ts∈E,

(TS)N(ts)≥max{(TR)N(t),(TR)N(s)}

(CS)N(ts)≥max{(CR)N(t),(CR)N(s)}

(US)N(ts)≥min{(UR)N(t),(UR)N(s)}

(FS)N(ts)≥min{(FR)N(t),(FR)N(s)},∀ ts∈E.

There is no restriction on the sum of 0≤(TS)P(ts)+(CS)P(ts)+(US)P(ts)+(FS)P(ts)≤4,

−4≤(TS)N(ts)+(CS)N(ts)+(US)N(ts)+(FS)N(ts)≤0 for all t∈V, for all ts∈E. Here R is the QBSVN vertex set of G and S is the QBSVN edge set of G.

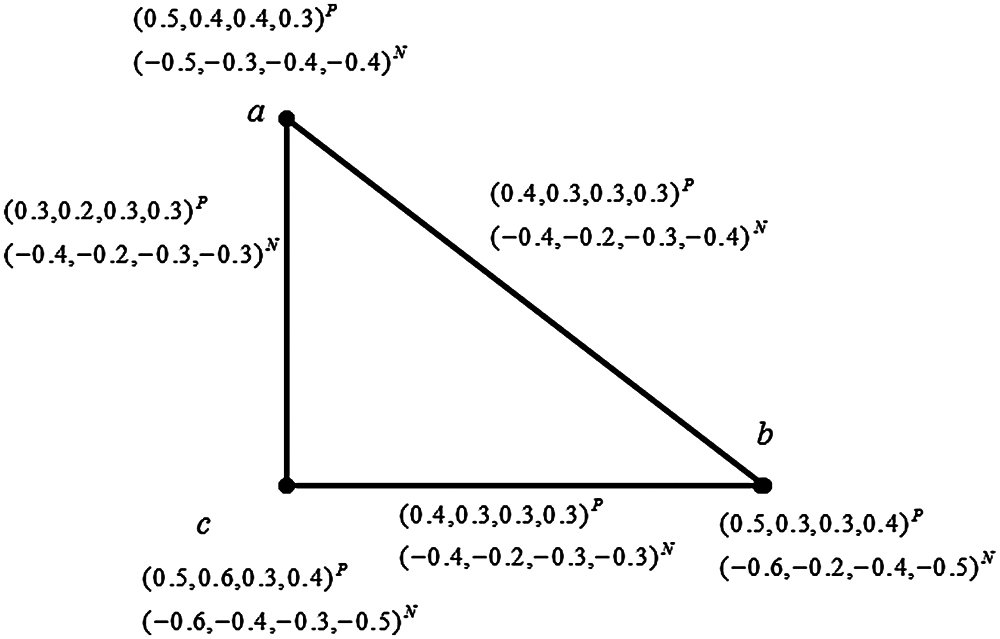
Example 3.1 Consider a crisp graph G=(V,E) such that V={a,b,c} and E={ab,bc,ca} the corresponding QBSVNG G=(R,S) is shown in Fig. 1.

Figure 1: Quadripartitioned bipolar single valued neutrosophic graph

Definition 3.2 A QBSVNG G=(R,S) is called complete if the following conditions are satisfied

(TS)P(ts)=min{(TR)P(t),(TR)P(s)}

(CS)P(ts)=min{(CR)P(t),(CR)P(s)}

(US)P(ts)=max{(UR)P(t),(UR)P(s)}

(FS)P(ts)=max{(FR)P(t),(FR)P(s)},∀ t,s∈V and

(TS)N(ts)=max{(TR)N(t),(TR)N(s)}

(CS)N(ts)=max{(CR)N(t),(CR)N(s)}

(US)N(ts)=min{(UR)N(t),(UR)N(s)}

(FS)N(ts)=min{(FR)N(t),(FR)N(s)},∀ t,s∈V.

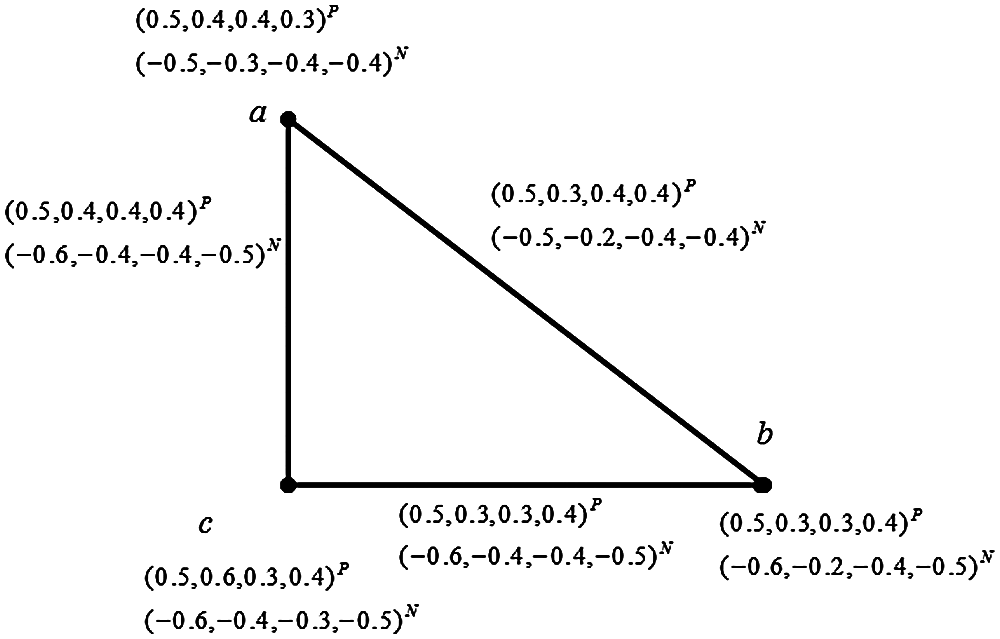
Example 3.2 Consider a crisp graph G=(V,E) such that V={a,b,c} and E={ab,bc,ca} the corresponding QBSVNG G=(R,S) is shown in Fig. 2.

Figure 2: Complete bipolar quadripatitioned single valued neutrosophic graph

Definition 3.3 A QBSVNG G=(R,S) is called strong if the following conditions are satisfied:

(TS)P(ts)=min{(TR)P(t),(TR)P(s)}

(CS)P(ts)=min{(CR)P(t),(CR)P(s)}

(US)P(ts)=max{(UR)P(t),(UR)P(s)}

(FS)P(ts)=max{(FR)P(t),(FR)P(s)},∀ ts∈E and

(TS)N(ts)=max{(TR)N(t),(TR)N(s)}

(CS)N(ts)=max{(CR)N(t),(CR)N(s)}

(US)N(ts)=min{(UR)N(t),(UR)N(s)}

(FS)N(ts)=min{(FR)N(t),(FR)N(s)},∀ ts∈E.

Definition 3.4 The Cartesian product of two QBSVNGs, G1 and G2 is denoted by the pair G1×G2=(R1×R2,S1×S2) and defined as

(i) (T)(R1×R2)P(kl)=(T)R1P(k)∧(T)R2P(l)

(C)(R1×R2)P(kl)=(C)R1P(k)∧(C)R2P(l)

(U)(R1×R2)P(kl)=(U)R1P(k)∨(U)R2P(l)

(F)(R1×R2)P(kl)=(F)R1P(k)∨(F)R2P(l)

(T)(R1×R2)N(kl)=(T)R1N(k)∨(T)R2N(l)

(C)(R1×R2)N(kl)=(C)R1N(k)∨(C)R2N(l)

(U)(R1×R2)N(kl)=(U)R1N(k)∧(U)R2N(l)

(F)(R1×R2)N(kl)=(F)R1N(k)∧(F)R2N(l)

for all (k,l)∈R1×R2.

The membership value of the edges in G1×G2 can be calculated as

(ii) (T)(S1×S2)P(kl1)(kl2)=(T)R1P(k)∧(T)S2P(l1l2)

(C)(S1×S2)P(kl1)(kl2)=(C)R1P(k)∧(C)S2P(l1l2)

(U)(S1×S2)P(kl1)(kl2)=(U)R1P(k)∨(U)S2P(l1l2)

(F)(S1×S2)P(kl1)(kl2)=(F)R1P(k)∨(F)S2P(l1l2)

(T)(S1×S2)N(kl1)(kl2)=(T)R1N(k)∨(T)S2N(l1l2)

(C)(S1×S2)N(kl1)(kl2)=(C)R1N(k)∨(C)S2N(l1l2)

(U)(S1×S2)N(kl1)(kl2)=(U)R1N(k)∧(U)S2N(l1l2)

(F)(S1×S2)N(kl1)(kl2)=(F)R1N(k)∧(F)S2N(l1l2)

for all k∈R1,l1l2∈S2.

(iii) (T)(S1×S2)P(k1l)(k2l)=(T)R2P(l)∧(T)S1P(k1k2)

(C)(S1×S2)P(k1l)(k2l)=(C)R2P(l)∧(C)S1P(k1k2)

(U)(S1×S2)P(k1l)(k2l)=(U)R2P(l)∨(U)S1P(k1k2)

(F)(S1×S2)P(k1l)(k2l)=(F)R2P(l)∨(F)S1P(k1k2)

(T)(S1×S2)N(k1l)(k2l)=(T)R2N(l)∨(T)S1N(k1k2)

(C)(S1×S2)N(k1l)(k2l)=(C)R2N(l)∨(C)S1N(k1k2)

(U)(S1×S2)N(k1l)(k2l)=(U)R2N(l)∧(U)S1N(k1k2)

(F)(S1×S2)N(k1l)(k2l)=(F)R2N(l)∧(F)S1N(k1k2)

for all l∈R2,k1k2∈S1.

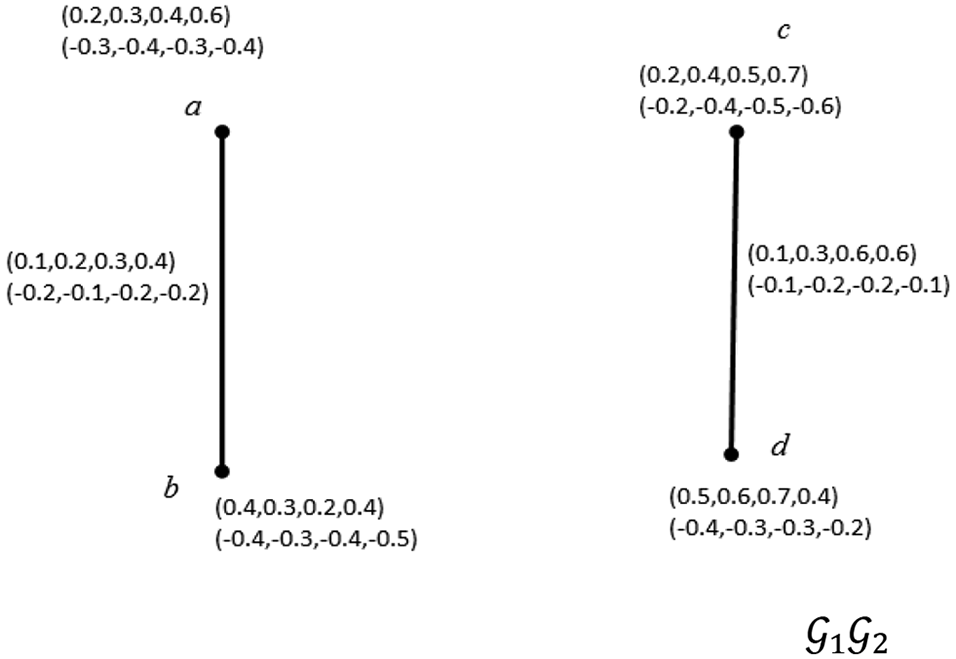
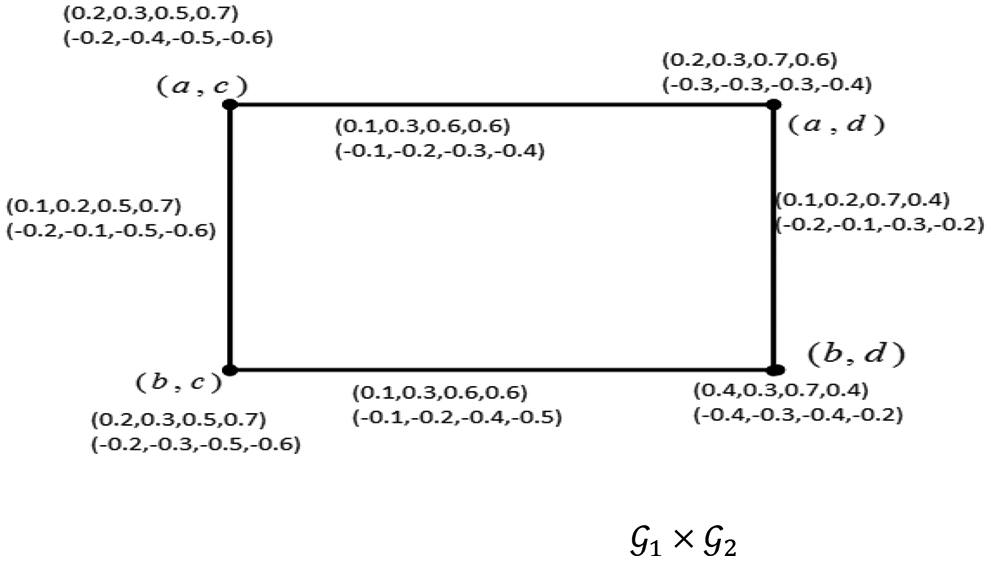
Example 3.3 Consider two QBSVNG G1 and G2 as shown in Fig. 3. Then Cartesian product of G1×G2 is shown in Fig. 4.

Figure 3: G1 and G1 Two bipolar quadripatitioned single valued neutrosophic graph

Figure 4: Cartesian product of quadripatitioned single valued neutrosophic graph

Proposition 3.5 The Cartesian product G1×G2=(R1×R2,S1×S2) of two QBSVNGs G1 and G2 is also the QBSVNG of G1×G2.

Proof. We consider two cases.

Case 1: for k∈R1,l1l2∈S2,

(T)(S1×S2)P((kl1)(kl2))=(T)R1P(k)∧(T)S2P(l1l2)

≤(T)R1P(k)∧[(T)R2P(l1)∧(T)R2P(l2)]

=[(T)R1P(k)∧(T)R2P(l1)]∧[(T)R1P(k)∧(T)R2P(l2)]

=(T)(R1×R2)P(k,l1)∧(T)(R1×R2)P(k,l2)

(C)(S1×S2)P((kl1)(kl2))=(C)R1P(k)∧(C)S2P(l1l2)

≤(C)R1P(k)∧[(C)R2P(l1)∧(C)R2P(l2)]