
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.016838
ARTICLE
Ripple+: An Improved Scheme of Ripple Consensus Protocol in Deployability, Liveness and Timing Assumption
1School of Cyberspace Science, Harbin Institute of Technology, Harbin, 150001, China
2Peng Cheng Laboratory, Shenzhen, 518055, China
3Beijing Jingning Data Technology Co., Ltd., Beijing, 100007, China
*Corresponding Author: Chuanwang Ma. Email: machuanwang@stu.hit.edu.cn
Received: 31 March 2021; Accepted: 13 July 2021
Abstract: Ripple acts as a real-time settlement and payment system to connect banks and payment providers. As the consensus support of the Ripple network to ensure network consistency, Ripple consensus protocol has been widely concerned in recent years. Compared with those Byzantine fault tolerant protocols, Ripple has a significant difference that the system can reach an agreement under decentralized trust model. However, Ripple has many problems both in theory and practice, which are mentioned in the previous researches. This paper presents Ripple+, an improved scheme of Ripple consensus protocol, which improves Ripple from three aspects: (1) Ripple+ employs a specific trust model and a corresponding guideline for Unique Node List selection, which makes it easy to deploy in practice to meet the safety and liveness condition; (2) the primary and view change mechanism are joined to solve the problem discussed by the previous research that Ripple may lose liveness in some extreme scenarios; (3) we remove the strong synchrony clock and timeout during consensus periods to make it suitable for weak synchrony assumption. We implemented a prototype of Ripple+ and conducted experiments to show that Ripple+ can achieve the throughput of tens of thousands of transactions per second with no more than half a minute latency, and the view change mechanism hardly incurs additional cost.
Keywords: Ripple; consensus; decentralized trust; byzantine fault tolerant protocol
As one of the most famous blockchain projects, Ripple plays the role of the bridge among different currencies. It is an Internet transaction protocol which allows people to pay in any currency. Its XRP token was ranked seventh in market capitalization in March 2021. The Ripple network adopts the Ripple consensus protocol as its underlying consensus support to prevent double-spending and ensure the consistency of the network. Unlike proof-of-series consensus adopted in other digital cryptocurrency (such as PoW in Bitcoin [1]), the Ripple consensus protocol is a Byzantine fault tolerant (BFT) protocol with decentralized trust property, which means that each node in the network chooses a subset (i.e., Unique Node List or UNL in the Ripple) of all nodes and reaches an agreement only based on the proposals from its UNL regardless of other proposals. Compared with other BFT protocols with centralized trust (e.g., PBFT [2]), the Ripple consensus protocol is more flexible to apply in a diversifying trusted network. The UNL design ensures that the Ripple consensus protocol can be proved to be secure when each pair of nodes has sufficient UNL overlap [3,4].
However, the safety and the liveness of the Ripple consensus protocol is still controversial, because it's more complicated to reach an agreement in decentralized trust model with Byzantine faults. As described in the original whitepaper [5], assuming that a node requires a minimum percentage of 80% of its UNL (i.e., a quorum) agreeing on a transaction to reach an agreement, two nodes cannot validate conflicting ledgers if their UNL overlap exceeds 20% maximum size of their respective UNLs. The subsequent researches [3,4] show that 20% UNL overlap is not enough. A more accurate UNL overlap is 60% of the average size of two UNLs for safety, while this increases to 90% in the case of extreme network degradation. The conclusion is proved to be correct, while we consider that it is hard to satisfy in reality, especially in a permissionless blockchain with no guideline for UNL selection. Although the recommended trust model in the current Ripple network allows all nodes to trust a single UNL consisting of five nodes [4], we consider that it is not flexible and scalable enough. We design a specific trust model and a corresponding guideline for UNL selection to solve it, and our guideline is proved to satisfy the UNL overlap in [4].
The liveness of the Ripple consensus protocol is another controversial point, which was first analyzed in [4]. However, in the later research [6], the author describes an extreme scenario that the system will get stuck even if only one Byzantine node sends contradictory transactions to different nodes, while we think it is possible in reality. Thus, the liveness cannot be ensured in the Ripple consensus protocol. We refer to the view change mechanism in [2,7] to ensure that the system will not get stuck when similar scenarios appear.
Another disadvantage of the Ripple consensus protocol is that it relies on the synchrony timing assumption. It needs a global heartbeat timer to proceed and enter the next phase during consensus, which is shown in their open source code. This contrasts with other BFT protocols, like weak synchrony assumption in PBFT [2] and asynchrony assumption in HoneyBadgerBFT [8]. It is unrealistic that all nodes have a synchronous clock and the messages can be delivered within a timeout because of the randomness of the network delay. We consider it as an aspect to be improved.
This paper proposes Ripple+, an improved scheme of the Ripple consensus protocol in three aspects:
• Deployability: Ripple+ employs a core set, just like the single agreed-upon UNL in [4], in which core nodes trust each other and select the core set as its UNL. The core set size is uncertain and should be pre-configured. The core set reflects the state of the current network, and the nodes in it are relatively reliable, while Byzantine faults may still occur following the assumption in Ripple that there are at most 20% Byzantine nodes in the UNL. Other nodes in the system that do not belong to the core set are called leaf nodes, which choose a subset of the core set and itself as its UNL. Leaf nodes can join and exit the network freely without affecting the consensus. We solve the problem that Ripple is hard to deploy in reality to meet the safety condition in this way. The minimum core set size and the minimum number of the core nodes trusted by the leaf nodes are given in Section 5 for safety. Although the deployment of the Ripple project in reality has similar ideas with us to ensure the UNL overlap for safety, we consider that Ripple+ is more flexible and scalable than Ripple for leaf nodes have the right to choose which core nodes to trust to a certain extent instead of the whole core set.
Our trust model, in addition to solving the problem of deployability, is also reasonable. Node diversity is common in reality. Similar to other permissionless blockchain projects, in which some super nodes take more responsibilities for the blockchain network, these nodes may have higher power in the role of reality, or they may have more computing power and bandwidth in the network. Thus, they are more suitable to be the core node of the network to take on more tasks in terms of power, resources and reliability. For example, among the banks that access current Ripple to realize a high-performance global payments business, a few strong banks should be selected as the core nodes and others play the role of the leaf nodes.
• Liveness: Amores-Sesar et al. [6] has proved that the core set itself may lose liveness when only one Byzantine node gossips contradictory input transactions in the open phase. To deal with this issue, Ripple+ selects one core node as the primary at any time. The primary is responsible for receiving the transactions from the clients in the open phase, wrapping and gossiping them, while other nodes are not allowed to gossip transactions in the open phase. When there are some valid transactions that still have not been committed to the ledger after a period of time, a timeout will be triggered and the view change will be carried out. The primary will be changed to the node in the next position of the core set. Due to the assumption that there are at most 20% Byzantine nodes in the UNL, the system can recover after a certain duration.
• Timing Assumption: The synchrony assumption in the original Ripple consensus protocol makes it hard to apply in the realistic Internet environment. The synchronous clocks or timeouts are used mainly in the open phase and the establish phase in Ripple. While in Ripple+, the primary wraps all transactions from the clients and gossips them in the open phase, thus there is no need to wait for a certain period before entering the next phase and the nodes start the establish phase once they receive the message from the primary. In the establish phase, we change the conditions of moving into the next iteration round. Specifically, when the node receives messages from over 80% of nodes in its UNL, it calculates the next round proposal based on the messages received from the previous rounds and enters the next round.
We implemented a prototype of Ripple+ with Go language and conducted simulation experiments on a single server to evaluate its performance, in terms of latency, throughput and cost of view change mechanism. On the basis of the experimental results, Ripple+ can achieve a peak throughput of over 10,000 tx/s with about two seconds latency when the core set size is set to 10. While the peak throughput decreases to 2,500 tx/s and the latency increases to 5 s when the core set size increases to 20. As the core set size continues to grow, the latency increases rapidly. Compared with 20 core set size, the latency is approximately six times that of the original when the core set size is doubled. In addition, the cost of view change is only about one hundredth of the consensus latency, which implies that the view change mechanism will not affect the efficiency of Ripple+ seriously. The above experimental results indicate that Ripple+ is suitable to be the consensus support of permissionless blockchain in terms of both latency and throughput.
2.1 Consensus with Decentralized Trust
Researches on the Byzantine fault tolerant (BFT) protocol have been going on for nearly 40 years since Lamport et al. [9,10] pioneer works. In 1999, Castro et al. proposed the famous PBFT [2], the first BFT protocol with
For specific consensus protocol under the decentralized trust model other than Ripple, Stellar [13] is another well-known one, which allows nodes to select their quorum slices and generate quorums according to all nodes’ slices. The system can reach an agreement based on these quorums if the quorum intersection is satisfied. Cobalt [14] can be regarded as an evolution of Ripple. It relies on a novel atomic broadcast algorithm to reach an agreement in an asynchrony network, and can reduce the UNL overlap from 90% to 60% for safety.
2.2 The Ripple Consensus Protocol
The Ripple consensus protocol runs in a permissionless blockchain. Each node in the Ripple network maintains the same ledger and connects with each other via the gossip network. A set of clients update the ledger by submitting transactions to the gossip network. Decentralized trust is a distinctive feature of Ripple. For a node Ni, the network can be divided into two parts, trusted or non-trusted. All Ni's trusted nodes form its UNL. The UNL represents a subset of the network which Ni considers will not collude to defraud, even though there still exist a few Byzantine nodes in the UNL. Ripple assumes a quorum of the UNL which specifies the minimum number of nodes that Ni needs to hear from to make a decision. Ripple sets the quorum threshold to 80% of its UNL size, and at most 20% of its UNL may be Byzantine nodes. Ni can reach an agreement with its UNL by message passing in the gossip network, as long as Ni is assumed to have a reliable channel with any correct node in its UNL. Furthermore, the Ripple network is guaranteed to be secure by limiting the choice of the UNL selection.
Roughly speaking, the protocol consists of three phases:
(1) Open phase: The clients submit transactions to all nodes via the gossip network, then all nodes get the submission and update their candidate set. The open phase ends after a certain period.
(2) Establish phase: The nodes attempt to agree on a set of transactions based on the prior ledger at a regular interval. Each node proposes the transactions in the candidate set as well as their current ledger state as their initial proposal. The nodes only consider the messages received from their UNL that update based on the identical ledger. All nodes propose to each other iteratively in several synchronous rounds, and the transactions whose support rate reaches the threshold in this round will be proposed in the next round, until a quorum of the UNL has the same proposals with its own. In the current Ripple implementation, the threshold goes
(3) Accepted phase: The nodes validate the last closed ledger by gossiping the last closed ledger state via a validation message. Once a node finds that there is a quorum of its UNL with an identical last closed ledger state, the ledger will become a fully validated ledger.
Before starting the establish phase, the nodes will perform the preferred branch algorithm in advance to ensure that there are enough correct nodes working on the identical ledger, otherwise the system may get stuck. The nodes maintain the ledger states of all nodes in its UNL, and update the states according to the validation messages. The nodes construct an ancestor tree according to the ledger sequence and the dependency relationship, and calculate the support count of each ledger in the tree (i.e., the number of the ledgers in the same branch with it, including itself). Then, starting from the root L, the nodes select the child M with the highest support count, and judge whether the support count of M is still the highest when all ledgers with the sequence less than M select any other child. If so, the algorithm recursively calls with M as the root. Otherwise, L is the preferred ledger. In addition, if the output preferred ledger is the ancestor of the node's current ledger, the node treats its current ledger as the preferred ledger.
In [5], the safety was first analyzed that the UNL overlap of any pair of nodes should exceed 20% maximum size of their respective UNLs assuming a quorum of 80%. While a later research [3] states that the UNL overlap should increase to 40% for safety. In [4], the correct condition is given that the UNL overlap should be over 60% of the average size of two UNLs. This paper also points out that this number will increase to 90% in the case of extreme network degradation. In [6], the author describes a simple scenario, in which Ripple violates the safety as a Byzantine node in the UNL overlap sends inconsistent messages. However, we have proved that the scenario does not meet the safety condition in [4], which is shown in Appendix B.
The liveness of the Ripple consensus protocol is analyzed in [4] based on a single agreed-upon UNL X (i.e., the core set in this paper), in which the UNL of each node in X is X itself. The author assumes that X cannot lose liveness and proves that how other nodes in the network can keep liveness. However, in [6], the author describes an extreme scenario that the single agreed-upon UNL X itself gets stuck when a Byzantine node in X sends contradictory transactions to different nodes in the open phase and no other input transactions are sent. Then, no transaction gets over 50% support rate in the first round in the establish phase, thus the consensus will get stuck. We consider that it is not likely in reality, but we have to face it.
Some other related researches elaborate and improve Ripple in different aspects. Mauri et al. [15] gives proof from the view that the quorum size is unknown. It shows that the safety and liveness tolerances, the quorum size and the UNL overlap are strictly correlated, thus Ripple can adjust these parameters dynamically to cater to specific application scenarios. Christodoulou et al. [16] gets a similar result through the experimental observation of Ripple, that the centralization degree of the network can be relaxed (i.e., reduce the UNL overlap) to make it more efficient when there are few Byzantine nodes. Mundhra et al. [17] improves Ripple from information propagation mechanism to obtain efficient information propagation by adding Trustee Node List (TNL), and makes corresponding improvements to the Ripple consensus protocol.
Most of our assumptions are based on Ripple. Specifically, Ripple+ runs in an open system with Byzantine faults. Each node in the network maintains a UNL, which is a set of nodes that it trusts. The node makes decisions only depending on the proposals of its UNL. The network contains a relatively reliable set of nodes, which we call the core set, and the nodes in the core set are called core nodes. All core nodes trust each other and select the core set itself as its UNL. The core set is the basis to ensure safety and liveness. One of the core nodes is chosen to be the primary at any time, which is responsible for receiving the transactions submitted by the clients and gossiping them to all nodes. The primary will be changed to the node in the next position in the core set when a timeout occurs. It can help us to ensure liveness even if the scenario described in [6] happens. The nodes that do not belong to the core set are called leaf nodes, which choose itself and a subset of the core set as its UNL. The leaf nodes can join and exit the network freely. We follow the Ripple's quorum assumption that a quorum is set to 80% of its UNL size and at most 20% nodes of its UNL are Byzantine nodes.
Two kinds of ledgers are maintained by all nodes in the system. The last closed ledger is the most recent ledger that records the latest ratified transactions by a consensus period, while the fully validated ledger is the validation result of the updated last closed ledger. The fully validated ledger represents the state of the current work. In normal cases, two correct nodes will commit the same totally ordered transactions to the ledgers with an identical ledger state, thus generating the identical new ledger. The ledger may be forked due to possible faults and network delays. When it occurs, the node will check and switch to the preferred ledger.
We assume that all core nodes and their addresses are public to the whole network, which means that each pair of correct core nodes is connected by a reliable authenticated point-to-point channel to ensure that the messages can be delivered correctly. Therefore, we use “broadcast” when the messages are propagated only in the core set (this only occurs in the view change mechanism in Ripple+). By contrast, the leaf nodes are unknown to the whole network, thus the core nodes communicate with the leaf nodes via a gossip network. We use “gossip” in this case to differ from “broadcast” in the following paper. The leaf node can join the gossip network by informing several core nodes of its address.
Compared with the strong synchronous clocks in Ripple, Ripple+ only relies on the weak synchrony assumption, which implies that the delay bound is time varying, but does not grow faster than a polynomial function of time indefinitely. We consider it as a timing assumption which is more suitable for the real Internet environment. However, the timeout is adopted in Ripple+ when view change is carried out, as we cannot violate the FLP impossibility [18]. View change is not frequent in Ripple+, and it incurs little extra cost according to our experiments, thus it is acceptable.
As shown in Fig. 1, the system contains several core nodes and leaf nodes. The arrows in Fig. 1 represent the trust relationship, which points from the node to the node it trusts. One of the core nodes is the primary (The blue node in Fig. 1). Each node should pre-configure its UNL, initial view number, the secret keys as well as the neighbors in the gossip network. Then, it initializes the last closed ledger and the fully validated ledger before starting consensus. A new node can join in the network by adding its address to other nodes’ neighbor list and selecting its own UNL.
A consensus period begins when the clients submit the transactions and ends when the transactions are committed to the fully validated ledger. In normal cases, a consensus period composes of four phases:
(1) Submit phase: The clients submit their transactions to the primary, which then receives, checks, wraps and sends these transactions via the gossip network to start a new consensus period.
(2) Open phase: When a node receives the transactions from the primary, it generates its initial proposal and gossips it to start iterations.
(3) Establish phase: The transactions are proposed iteratively among all nodes in several rounds, until there is a transaction set that a quorum of the UNL agrees on. Then the transaction set will be committed to the last closed ledger, and a validation message of the updated last closed ledger state will be gossiped.
(4) Accepted phase: When there is a quorum of the UNL that agrees on the identical last closed ledger, the update will be applied to the fully validated ledger.
When a timeout occurs, which means that there are some valid transactions that have not been committed for a period of time, a view change will be carried out and the primary will be changed to the node in the next position in the core set. Assuming that at most 20% of the core nodes are Byzantine nodes, the scenario in [6] will not happen and the liveness can be guaranteed.
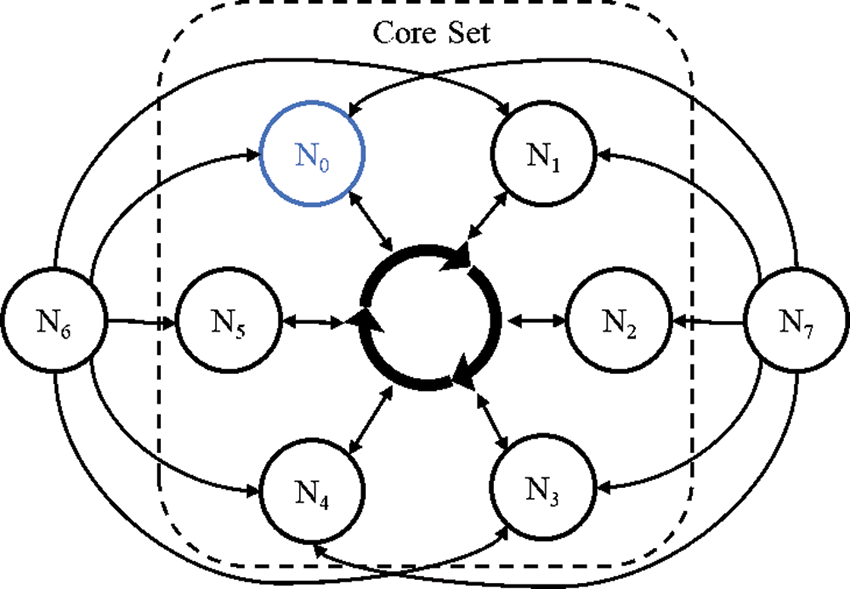
Figure 1: An example of the trust model. The system contains a core set of {N0, N1, N2, N3, N4, N5}. The leaf node N6's UNL is {N0, N1, N3, N4, N5, N6} and the leaf node N7's UNL is {N0, N1, N2, N3, N4, N7}
In this section, we elaborate each phase of Ripple+ in normal cases, the pseudocode is presented in Appendix A.
In the original Ripple, the clients send transactions to all nodes via the gossip network to let as many nodes as possible receive these transactions. The clients do not know exactly who will propose for the transactions they submit, and the nodes do not know exactly how many transactions are submitted. The nodes enter the next phase only after a duration, which is related to the duration of the previous consensus period. Ripple+ introduces a primary to receive the clients’ submissions and determine when to enter the next phase. The primary is chosen from the core set in turn according to the current view number, and its identity is public to all clients and nodes for verification. In the submit phase, the clients only submit their transactions to the primary. The submissions will be forwarded to the primary if other nodes receive them. When the primary considers that it has received enough transactions, it wraps the transactions into a batch and sends them via the gossip network.
When the node receives a gossip message including a list of transactions from the primary, it will start a new consensus period. Firstly, the node initializes its state, including the round number and the proposals of its UNL maintained by its own. Then it checks whether it works on the preferred ledger according to the recent validation messages of the nodes in UNL stored locally. If not, it will switch to it. After that, it generates its initial proposal based on the transactions received from the primary as well as its current last closed ledger state, then gossips it.
The establish phase can be divided into several rounds. In each round, the node receives the proposals from its UNL continuously and maintains their proposal states. When the node has received proposals from a quorum of its UNL in this round, it counts votes for all transactions based on the latest proposal of all nodes in the UNL. The transactions whose support rate exceeds the threshold in this round will be proposed in the next round. This differs from the original Ripple that the latter carries out a vote count only after a predetermined time interval, which means that the process in this phase is synchronous. After the node gossips the new proposal, it will check whether it has reached an agreement with the nodes in its UNL. If there is a quorum of UNL who proposes the identical transaction list with the node and they all state that they are working on an identical ledger, then the node considers that the agreement has been reached and it will commit these transactions to the last closed ledger. After updating the ledger, the node will gossip a validation message containing the state of the updated last closed ledger and enter the accepted phase.
The node maintains the validation states of all nodes in its UNL locally based on the latest validation messages it receives. When a ledger is supported by a quorum of the UNL, the fully validated ledger will be updated to this ledger. Note that even if there is not an agreed-upon ledger, the consensus will not get stuck. The reason is that the accepted phase is parallel to other phases. When the preferred ledger check is carried out in the open phase of the next consensus period, all correct nodes will switch to the same branch based on the validation states maintained locally and reach an agreement in the next consensus period.
As described above, we introduce the primary to avoid the possible scenarios occurred in [6] that the system may lose liveness. However, the primary failure will cause the system to face additional issues. For example, the primary may behave negatively, that is, it intentionally wraps few transactions into a batch in the submit phase to reduce throughput. The primary may also wrap transactions selectively to block a single transaction from being committed, which is considered to lose “fairness” in [19]. We deal with these cases by the view change mechanism.
View change is led by the core set, while the new view will apply to the whole network. We set a timer at each core node and catch timeout exception to determine when to start a view change with the help of the clients. Under normal conditions, only the primary can receive requests from clients. When other core nodes receive a message from a client containing some valid transactions which have not been committed, it starts a timer and forwards the message to the primary. The core node stops the timer when these valid transactions are committed, but restarts it when other valid transactions are received from the clients. If the timer expires, view change will be executed.
The process of the view change is shown in Fig. 2, and the pseudocode is presented in Appendix A. When a core node catches a timeout exception, it stops receiving messages in the open phase and the establish phase, then broadcasts a ViewChange message in the core set containing its last closed ledger state as well as all transactions found but have not been committed. When a core node receives ViewChange messages from over 20% of core nodes and it has never broadcasted a ViewChange message, it also stops receiving messages and broadcasts a ViewChange message.
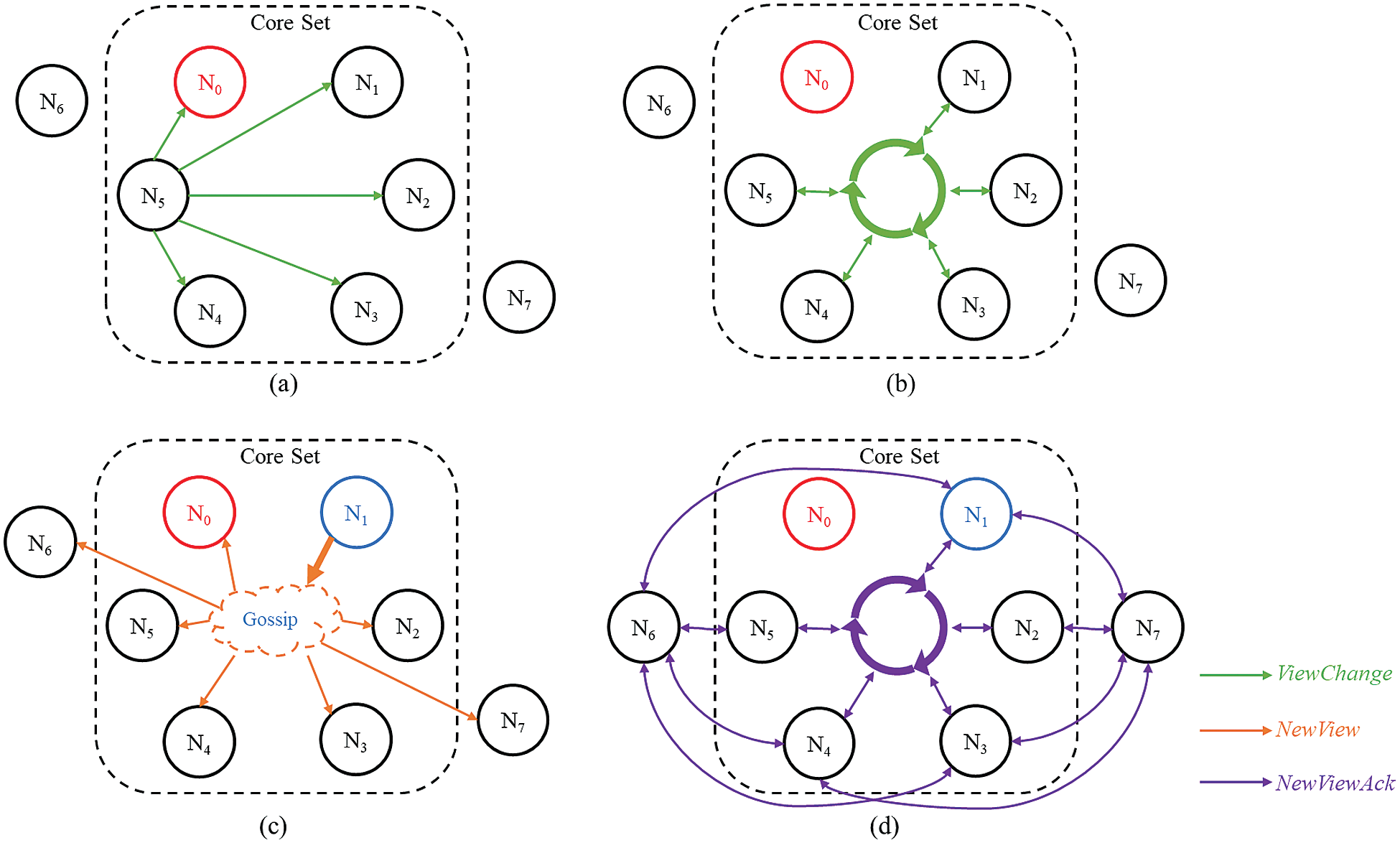
Figure 2: An example of the view change mechanism: (a) N5 detects timeout firstly; (b) All core nodes detect timeout; (c) N1 starts a new view; (d) All nodes change the view
When the core node in the next position of the core set receives the ViewChange messages with the identical view number from a quorum of the core set, it gossips a NewView message to the whole network. A NewView message contains three parts: (1) A ledger state which is the preferred ledger of all ledgers in the ViewChange messages; (2) all transactions found in the ViewChange messages but have not been committed to the preferred ledger; (3) all ViewChange messages with signature it has collected. When a node receives a NewView message, it verifies the message by signature, then adds all transactions in the message to its candidate set, and switches its last closed ledger to the preferred ledger. After that, the node gossips a NewViewAck message. When the node receives NewViewAck messages with the identical view number from a quorum of its UNL, the view change finishes and the node gets ready to enter a new consensus period.
Assuming that the system contains x core nodes, any leaf node chooses a out of x as well as itself as its UNL, and the number of the leaf nodes is uncertain. The quorum size is set to 80% of the UNL, and Byzantine nodes account for at most 20% of the UNL for any node. We will analyze how Ripple+ can ensure safety and liveness under our assumptions. Our proof is mostly based on the conclusion of [4].
According to Proposition 4 in [4], the system can ensure safety if and only if
for any two nodes Ni and Nj. The variables
Any pair of leaf nodes Ni and Nj has a UNL overlap as all leaf nodes choose a out of x core nodes from the core set, and the size of overlap has a minimum value, i.e.,
Apparently,
An additional restriction is
for we need to choose a trusted nodes from x core nodes. Thus, we can obtain the range of a and x based on Eqs. (1)–(6):
In [4], a significantly degraded network in which a node may drop out of the network during a consensus period is also considered. This may cause the inconsistency of the network. The author provides the condition in the Theorem 8 that the protocol can ensure safety in this case:
Again, the range of a and x can be obtained in this case according to the similar analysis above:
In [4], the author proves the liveness of the leaf node based on a single agreed-upon set (i.e., the core set in Ripple+) under the assumption that the core set itself will not get stuck, while it turns out that the assumption is not always true in the later research [6]. Ripple+ has solved this problem by introducing the primary and the view change mechanism. Specifically, when a Byzantine core node sends inconsistent transactions in the open phase, leading to no transaction being committed for a duration, a timeout will be triggered. Then the view change is carried out, and the primary will be changed to the node in the next position of the core set. Under the assumption that there are at most 20% Byzantine nodes in the core set, a correct core node will become the primary after
According to Lemma 10 in [4], the leaf node cannot get stuck when the number of the core nodes it chooses as a part of its UNL is no less than a quorum of its UNL. Thus, the liveness of the leaf node can be ensured in Ripple+ when
6 Implementation and Evaluation
We implemented a prototype of Ripple+ with Go and simulated several nodes on a single server, in which each node runs in an isolated goroutine. The nodes communicate with each other in HTTP POST manner and the communication delay is negligible. We use SHA256 as hash algorithm and ECDSA as digital signature algorithm for message authentication. Public/private key pairs are generated for each node in advance. All global parameters, such as the member of the core set, the quorum size and the threshold of each round, are pre-configured. In addition, we also simulate clients to submit transactions to the primary repeatedly, which then wraps the transactions into a batch and gossips it to all nodes to start a new consensus period. The batch size and the core set size are controlled to analyze the performance of Ripple+ under different conditions.
We take the ledger state of the core set to represent the whole network state. A consensus period finishes when a quorum of the core set updates their fully validated ledgers, while leaf nodes are omitted in our experiments as the messages from the leaf nodes will be ignored by all core nodes in our trust model. In our experiment, the number of the Byzantine nodes does not exceed 20% of each node's UNL size.
We analyze the performance of Ripple+ both in the ideal case and in the common case. Ideally, all nodes will take all the transactions received from the primary as the initial proposal in the establish phase, thus only one iteration is required to reach an agreement on the condition that the primary does not send inconsistent messages in the open phase. While in the common case, the initial proposal may only contain a subset of all transactions received from the primary in the open phase, causing the nodes to have different initial proposals. Thus, the establish phase will last several rounds. This is similar to the original Ripple, because multiple clients submit transactions via the gossip network and each node is not guaranteed to receive all transactions. We will compare the performance of Ripple+ in both cases.
Two metrics are employed to analyze the performance of Ripple+: (1) latency, the time interval between the time the client submits transactions and when the fully validated ledgers are updated by a quorum of the core set. In our experiments, we also measure the latency of the establish phase and the validate phase respectively for further analysis. The submit phase and the open phase are omitted because the latency of these two phases is negligible in total latency; (2) throughput, the number of the transactions committed to the fully validated ledger per unit of time. We control the core set size and the batch size to obtain the maximum throughput of the corresponding conditions.
We set the batch size to 100, then measured the average latency of a single consensus period. Fig. 3 shows the relationship between the average latency and the core set size. A discovery is that the latency increases exponentially with the core set size due to all-to-all communications among all core nodes. Another predictable discovery is that the latency in the ideal case has an advantage compared with the common case because the latter requires more rounds to reach an agreement in the establish phase. It can be found from the figure that the latency in the common case is approximately twice than that in the ideal case under the same conditions.
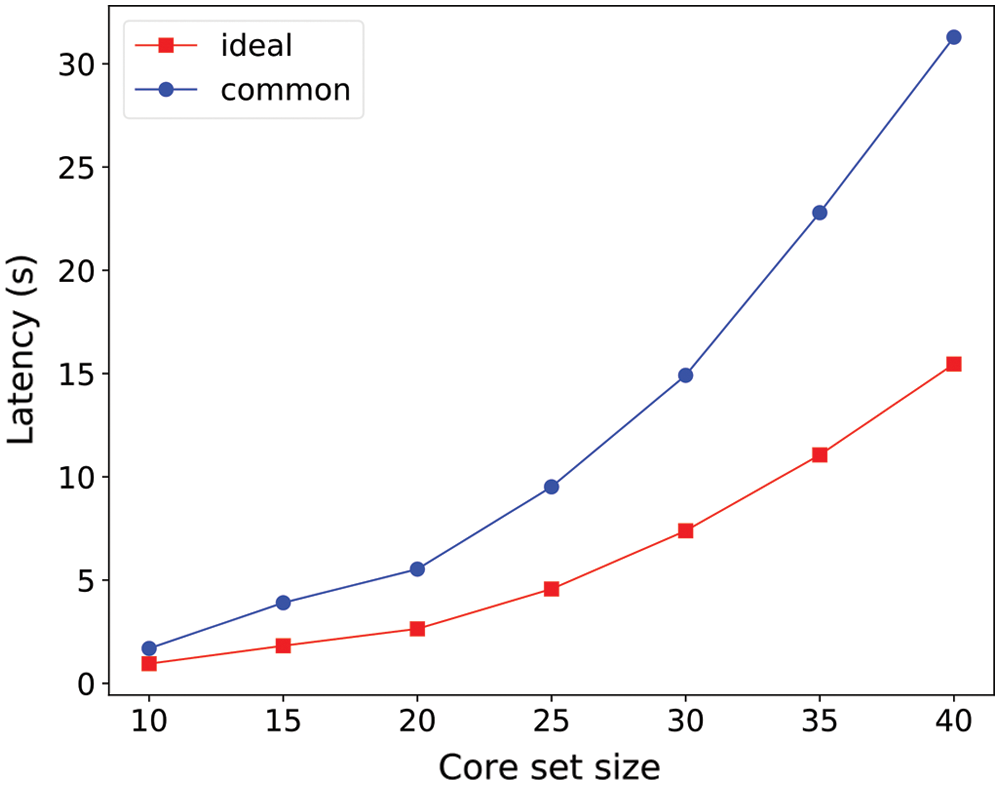
Figure 3: Latency under different core set sizes
The average latency of the establish phase and the validate phase per consensus period are further analyzed in Fig. 4. From the figure, we can see that the establish phase takes up most consensus period, and the latency of this phase increases more obviously compared with the validate phase with the growth of the core set size. Moreover, the latency of the establish phase in the ideal case is much greater than that in the common case, while it takes almost the same time in these two cases in the validate phase.
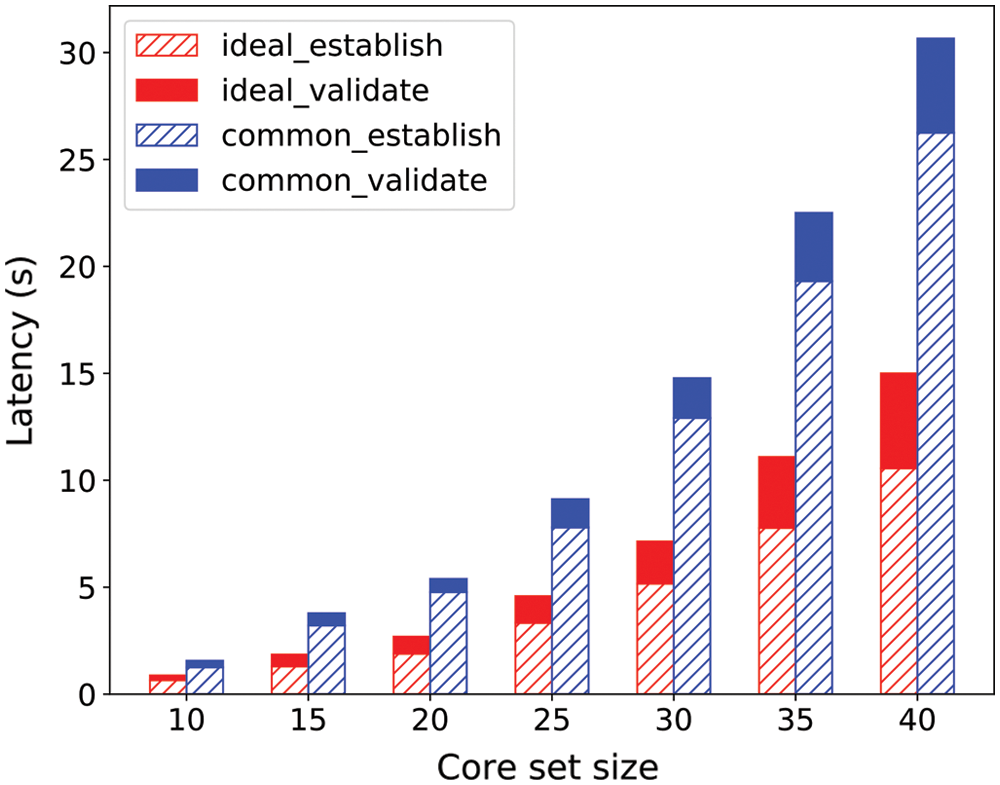
Figure 4: Latency comparison between the establish phase and the validate phase
Fig. 5 shows the throughput under different batch sizes and core set sizes. We can see that the throughput increases rapidly with the batch size when the batch size is small. As the batch size increases, the throughput growth gradually slows down, and finally reaches a peak. The protocol which runs in the ideal cases has a higher throughput than that in the common cases due to fewer iterations in the establish phase. In addition, the throughput is greatly affected by the core set size. Specifically, the throughput approaches to 13,000 tx/s in the ideal case and 11,000 tx/s in the common case when there are 10 core nodes, while only approaches to 3,100 tx/s in the ideal case and 2,500 tx/s in the common case at 20 core set size.
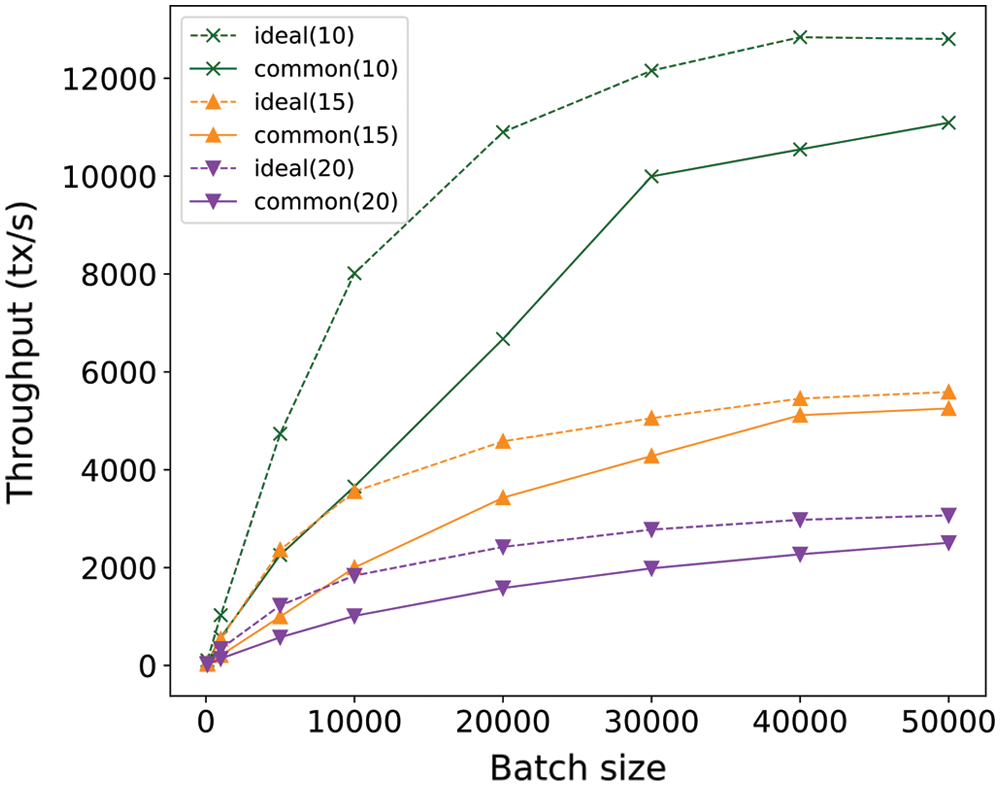
Figure 5: Throughput under different batch sizes and core set sizes
The cost of view change under different core set sizes is shown in Fig. 6, in which the maximum, minimum and average costs are marked after repeated measurements. Similar to the consensus latency, the cost of view change increases exponentially with the core set size. However, the consensus latency is hundreds of times of the cost of view change under the same core set size, which means that the view change mechanism incurs little extra cost to the protocol. In addition, the cost of view change is relatively stable under repeated measurements. Thus, we consider that the view change mechanism improves the liveness of Ripple effectively.
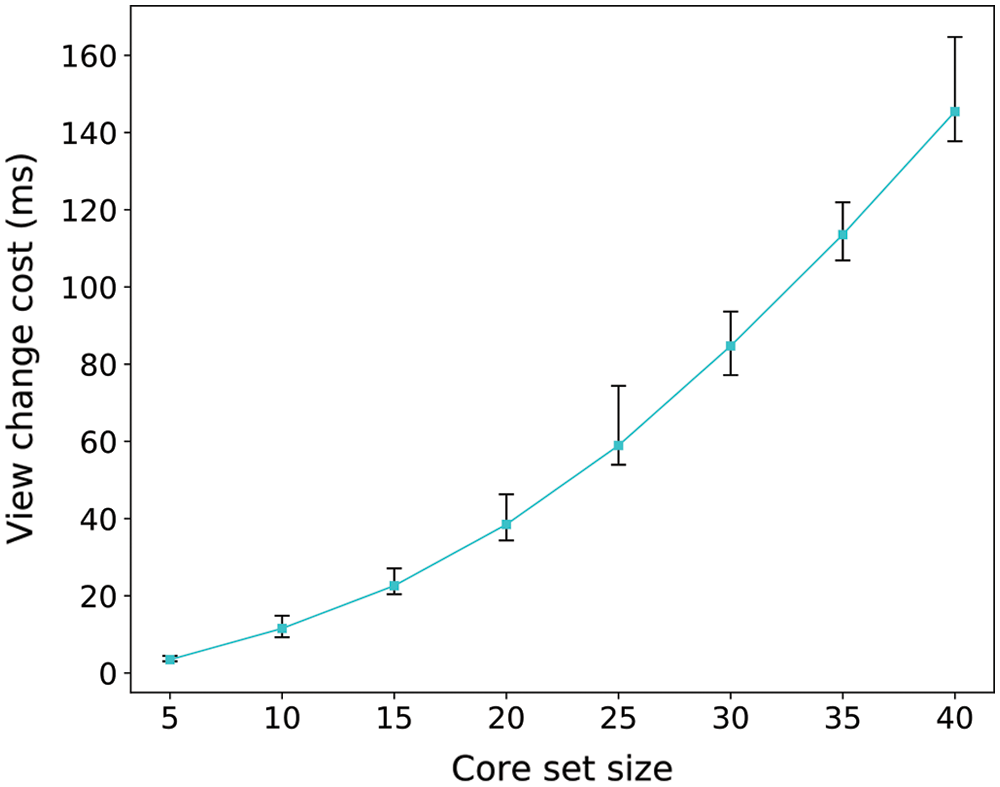
Figure 6: View change latency in different core set sizes
We present Ripple+, improving Ripple from deployability, liveness and timing assumption. It makes Ripple+ easy to deploy that Ripple+ introduces the core set and the guidelines for specifying the UNL choice. It has been proved that our guidelines meet the safety condition. Ripple+ evades the scenario that the system may get stuck by introducing a primary and view change mechanism. The method has been proved to be effective both theoretically and experimentally. In addition, the synchronous clocks and the timeouts are removed in the open phase and the establish phase to make Ripple+ fit for a weak synchrony network. Our experimental results show that Ripple+ is suitable to be consensus support of permissionless blockchain, in terms of both latency and throughput.
Acknowledgement: The authors would like to thank the undergraduate student Junye Zheng from the School of Cyberspace Science and Technology of Harbin Institute of Technology, who provided the experimental data.
Funding Statement: The work is supported by the National Key Research and Development Program (Grant No. 2018YFB1800702), Peng Cheng Laboratory (Grant No. PCL2021A02).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Nakamoto, S. (2008). Bitcoin: A peer-to-peer electronic cash system. Decentralized Business Review, 1–9. [Google Scholar]
2. Castro, M., Liskov, B. (1999). Practical Byzantine fault tolerance. Proceedings of the Third Symposium on Operating Systems Design and Implementation, pp. 173–186. USA: USENIX Association. [Google Scholar]
3. Armknecht, F., Karame, G. O., Mandal, A., Youssef, F., Zenner, E. (2015). Ripple: Overview and outlook. International Conference on Trust and Trustworthy Computing, pp. 163–180. Switzerland: Springer, Cham. DOI 10.1007/978-3-319-22846-4_10. [Google Scholar] [CrossRef]
4. Chase, B., MacBrough, E. (2018). Analysis of the XRP ledger consensus protocol. arXiv preprint arXiv: 1802.07242. [Google Scholar]
5. Schwartz, D., Youngs, N., Britto, A. (2014). The ripple protocol consensus algorithm. Ripple Labs Inc. White Paper, 5(8), 151. [Google Scholar]
6. Amores-Sesar, I., Cachin, C., Mićić, J. (2020). Security analysis of ripple consensus. arXiv preprint arXiv: 2011.14816. [Google Scholar]
7. Liskov, B., Cowling, J. (2012). Viewstamped replication revisited. CSAIL Technical Reports. http://hdl.handle.net/1721.1/71763. [Google Scholar]
8. Miller, A., Xia, Y., Croman, K., Shi, E., Song, D. (2016). The honey badger of BFT protocols. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, pp. 31–42. Vienna, Austria: Association for Computing Machinery. DOI 10.1145/2976749.2978399. [Google Scholar] [CrossRef]
9. Pease, M., Shostak, R., Lamport, L. (1980). Reaching agreement in the presence of faults. Journal of the ACM, 27(2), 228–234. DOI 10.1145/322186.322188. [Google Scholar] [CrossRef]
10. Lamport, L., Shostak, R., Pease, M. (2019). The Byzantine generals problem. Concurrency: The works of leslie lamport, pp. 203–226. USA: Association for Computing Machinery. DOI 10.1145/3335772.3335936. [Google Scholar] [CrossRef]
11. Cachin, C. (2021). Asymmetric distributed trust. International Conference on Distributed Computing and Networking, pp. 3. USA: Association for Computing Machinery. DOI 10.1145/3427796.3433933. [Google Scholar] [CrossRef]
12. Bracciali, A., Grossi, D., de Haan, R. (2021). Decentralization in open quorum systems: Limitative results for ripple and stellar. 2nd International Conference on Blockchain Economics, Security and Protocols, no. 5, pp. 1–20. Germany: Schloss Dagstuhl-Leibniz Center for Informatics. [Google Scholar]
13. Mazieres, D. (2015). The stellar consensus protocol: A federated model for internet-level consensus. Stellar Development Foundation, 32, 1–45. [Google Scholar]
14. MacBrough, E. (2018). Cobalt: BFT governance in open networks. arXiv preprint arXiv: 1802.07240. [Google Scholar]
15. Mauri, L., Cimato, S., Damiani, E. (2020). A formal approach for the analysis of the XRP ledger consensus protocol. 6th International Conference on Information Systems Security and Privacy, pp. 52–63. Valletta, Malta. DOI 10.5220/0008954200520063. [Google Scholar] [CrossRef]
16. Christodoulou, K., Iosif, E., Inglezakis, A., Themistocleous, M. (2020). Consensus crash testing: Exploring ripple's decentralization degree in adversarial environments. Future Internet, 12(3), 53. Basel, Switzerland: Molecular Diversity Preservation. DOI 10.3390/fi12030053. [Google Scholar] [CrossRef]
17. Mundhra, M., Rebeiro, C. (2020). SISSLE in consensus-based ripple: Some improvements in speed, security and last mile connectivity. arXiv preprint arXiv: 2008.01742. [Google Scholar]
18. Fischer, M. J., Lynch, N. A., Paterson, M. S. (1985). Impossibility of distributed consensus with one faulty process. Journal of the ACM, 32(2), 374–382. DOI 10.1145/3149.214121. [Google Scholar] [CrossRef]
19. Cachin, C., Kursawe, K., Petzold, F., Shoup, V. (2001). Secure and efficient asynchronous broadcast protocols. Annual International Cryptology Conference, pp. 524–541. Germany. DOI 10.1007/3-540-44647-8_31. [Google Scholar] [CrossRef]
Appendix A. Pseudocode
In this appendix, we provide pseudocode for both normal cases and view change in Ripple+ described in Section 4. The concept of the variables and the functions are defined as follows:
• UNLi, the unique node list of Ni.
• Statei, the state of Ni, possible value is open, establish, viewchange, newview.
• Viewi, the current view number of Ni.
• CandidateSeti, the transactions that Ni finds but has not committed to the ledger yet.
• LCLi, the last closed ledger maintained by Ni.
• FVLi, the fully validated ledger maintained by Ni.
• Ri, the current round number of Ni during a consensus period.
• Propsi, the proposals received from the UNLi maintained by Ni during a consensus period.
• Valsi, the validate states of all nodes in the UNLi maintained by Ni.
• ViewChangesi, the view change messages received from the UNLi maintained by Ni during a view change period.
• NewViewAcksi, the new view messages received from the UNLi maintained by Ni during a view change period.
• PreferredLedger(), get preferred ledger based on Valsi.
• HasVoted(), judge whether a quorum of the UNLi has voted in the current round.
• TxSupport(), calculate the proposal of next round based on Propsi and threshold.
• CheckConsensus(), check whether a quorum of the UNLi has the same proposal based on Propsi.
• ApplyTxs(), apply transactions to the ledger.
• LedgerSupport(), check whether a quorum of the UNLi has the same ledger state based on Valsi.
• GetPrimary(), get the primary corresponding to the view number.


Appendix B. A Contradiction Proof of Safety Violation Described in [6]
In [6], the author describes a generalized attack scenario with
Under the assumption that the Byzantine nodes are no more than 20% of the total nodes of the UNL, we have the following condition in this scenario:
Thus, we can obtain the range of n and f based on Eqs. (13) and (14):
Now we discuss the range of their UNL overlap
We can discover from Eq. (17) that
Again, given the range of n shown in Eq. (16), we can get the exact range of
However, the conclusion in [4] is that the UNL overlap must be over 60% for safety, which is contradictory to Eq. (19). Thus, the scenario described in [6] does not satisfy the safety condition given in [4].
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |