Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2022.016437

ARTICLE

Sustainable Investment Forecasting of Power Grids Based on the Deep Restricted Boltzmann Machine Optimized by the Lion Algorithm

Qian Wang1, Xiaolong Yang2,*, Di Pu3 and Yingying Fan4

1School of Economics and Management, Jilin Institute of Chemical Technology, Jilin, 132022, China
2School of Economics and Management, Northeast Electric Power University, Jilin, 132012, China
3Digital Grid Research Institute, China Southern Power Grid, Guangzhou, 510000, China
4School of Art, Hebei GEO University, Shijiazhuang, 050031, China
*Corresponding Author: Xiaolong Yang. Email: yangxiaolong@neepu.edu.cn
Received: 06 March 2021; Accepted: 26 July 2021

1  Introduction

With the concept of sustainable development and green economy becoming important themes of current development in various fields, the focus on accelerating the transformation of economic development models has highlighted resource-saving and environment-friendly attributes of society. With the exponential growth of electricity consumption and the expansion of the scale of investment, the critical factors affecting investment in power grids have become increasingly diversified. Investment in power grid enterprises is no longer only affected by traditional factors but is also affected by emerging factors brought by the advancement of power grids. For example, the income model of power grid investment is greatly affected by power system reform [1,2], and the integration and sharing of 5G station construction and basic grid resources also provides new directions for power grid investment. In order to reasonably control costs and optimize resource allocation, power grid enterprises should comprehensively consider the above factors, optimize grid investment plans, and conduct supervision [3]. Therefore, research on investment prediction of power grid enterprises is conducive to the sustainable development of power grids.

For power grid investment forecasting, domestic and foreign scholars have put forward different ideas and solutions. At present, statistical prediction models and artificial intelligence prediction models are widely used in the field of power grid investment prediction. Traditional statistical prediction methods mainly include principal component analysis, regression algorithms, Kalman filter, and clustering. These methods have simple principles, but have longer periods, slower speeds, and larger errors. The intelligent algorithms proposed on the basis of traditional prediction methods include co-integration theory, particle swarm optimization theory, fuzzy analysis, back propagation neural network (BPNN), and support vector machines (SVM). These algorithms are intelligent and personalized, so they are widely used in power grid investment forecasting.

In terms of traditional statistical forecasting models, regression analysis is widely used. For example, Chen [4] comprehensively considered the multi-dimensional constraints, established the investment scale prediction model by using the regression analysis method, and verified its good auxiliary effect on investment planning through empirical analysis. In the artificial intelligence prediction models, BPNN [5] and support vector machines [6] are proven to be highly effective methods. Among them, neural networks have high computing power and fitting efficiency because of their large number of neurons and multiple hidden layers, and they also have a significant effect on the regression and classification of related variables and analysis of function fitting. Some scholars have used BPNN to analyze and predict this. However, due to the principle of gradient descent, the BPNN algorithm is prone to the problem of gradient vanishing and easily falls into the local optimal solution. In order to solve this problem, many scholars use principal component analysis or multiple regression models in combination with the BPNN to form new combined algorithms or use genetic algorithms to improve it. In reference [7], principal component analysis is used to analyze the relevant factors of power engineering investment, and particle swarm optimization is used to optimize the BPNN to establish an innovative prediction model. Liu et al. [8] combined grey prediction, a multiple regression model, and a BPNN in an optimized combination model using an improved genetic algorithm; they proposed a combination prediction model that can combine the model and the original data well. It is proven that the combined model has a shorter convergence time and search efficiency. Although the BPNN's prediction performance has been greatly improved and can obtain more accurate prediction results, it is not suitable for the prediction of few sample data. Therefore, SVM is favored by many scholars because of its strong robustness and good prediction accuracy, which is suitable for few sample data. Dai et al. [9] used the grey correlation analysis method to screen the influencing factors and optimized the Grey Wolf algorithm through differential evolution and SVM. The results demonstrate that the model has a strong generalization ability and a good prediction effect. In order to make up for the shortcomings of the single BPNN or SVM model, some scholars have combined different models to predict the amount of power grid investment. Xu et al. [10] combined SVM, BPNN, and multiple regression models based on the analysis of the indicator system to form a power grid portfolio model. The particle swarm algorithm was used to optimize the investment portfolio model to achieve more accurate investment forecasts.

In addition to the above algorithm, some scholars have used other methods to analyze power grid investment. Liu et al. [11] put forward a calculation model of power grid demand and investment capacity by analyzing the influence of the change in transmission and distribution price on power grid investment decisions. Li et al. [12] mainly used the correlation coefficient method and grey prediction model to realize power grid investment predictions and confirmed the practicability and innovation of the method through data analysis. From the perspective of renewable energy power generation, Wagner [13] analyzed the site selection of wind power investors under different support plans and its impact on grid investment and found that the additional costs brought by site selection had a great impact on grid investment. As a shallow learning algorithm, the above models have limited processing capabilities for complex function problems, and these algorithms are based on prior knowledge and cannot fully reflect the characteristics of the information. A restricted Boltzmann machine (RBM) can abstract the combination of low-level features into high-level features so as to better reflect data features.

In the field of forecasting, RBM plays an important role. For example, Shi et al. [14] combined a depth confidence network and RBM to extract data features. Wan et al. [15] used RBM to build a deep belief network (DBN) model and proposed a deep regression feature learning (DFL) wind speed prediction method. Phan et al. [16] proposed an SRBM model to predict healthy social networks. Internal and external social influences and environmental events form a three-layer training model. This model proves that it is more effective than traditional methods.

However, the generalization ability of RBM is low, and its fixed training rate is not conducive to the network jumping out of the minimum point. Some experts have begun to use various algorithms to optimize it. Cho et al. [17] used Gaussian–Bernoulli to limit the RBM and scientifically optimize the parameters of the RBM. However, Gaussian–Bernoulli had problems such as local convergence and slow convergence. Liu et al. [18] used a genetic algorithm to optimize the RBM, which effectively improved the RBM feature extraction performance. However, genetic algorithms may converge to the local optimum when the fitness function was not properly selected and cannot reach the global optimum. Du et al. [19] weighted the fusion of a clustering algorithm with Time-RBM. Although this effectively improved the prediction accuracy, the clustering algorithm had high computational complexity, and the result depended on the selection of certain empirical parameters. In contrast, as a biomimetic algorithm based on the social behavior of lions, the Lion algorithm has strong robustness and the ability to search for better solutions. It is easy to implement in parallel and has a fast convergence speed. At the same time, the deep restricted Boltzmann machine (DRBM) algorithm can overcome the shortcomings of the RBM and improve the processing capacity of complex data.

Combined with the advantages and improvements of previous methods, this paper proposes a new power grid investment forecasting model based on the DRBM optimized by the Lion algorithm (LA). Considering the characteristics of power grid investment prediction, transmission and distribution price reform (TDPR) and 5G station construction are integrated into the influencing factors for comprehensive consideration. We analyzed the influence factors of power grid investment using a fuzzy threshold method and constructed a power grid investment prediction model using a deep restricted Boltzmann machine optimized by the Lion algorithm (LA-DRBM). The model improved the global search ability and enhanced the abstraction ability of high-dimensional complex data through layer-by-layer feature transformation. Then, a regression model, BPNN, SVM, RBM model, and LA-RBM model were selected for comparative analysis. The empirical study illustrates that the prediction accuracy and generalization performance of the model have been effectively improved.

The rest of the paper is arranged as follows: Section 2 introduces the basic theories of the deep restricted Boltzmann machine and the Lion algorithm; Section 3 carries out the analysis of the influencing factors of the power grid enterprise's investment based on a fuzzy threshold method; Section 4 uses the established model for empirical analysis; and Section 5 presents the conclusions.

2  Basic Theories

2.1 Deep Restricted Boltzmann Machine

2.1.1 Restricted Boltzmann Machine

RBM is a non-feedback random neural network model with two layers. One layer is the visual layer for inputting observation data, and the other layer is the hidden layer for feature extraction [20,21]. In this network, different layers are fully connected, and there is no communication between the same floor. Assuming that the RBM has visible layer neurons and hidden layer neurons, the value of the neuron of the visible layer and the value of the neuron of the hidden layer neuron are denoted, respectively. The structure and principle of the RBM is demonstrated in Fig. 1.

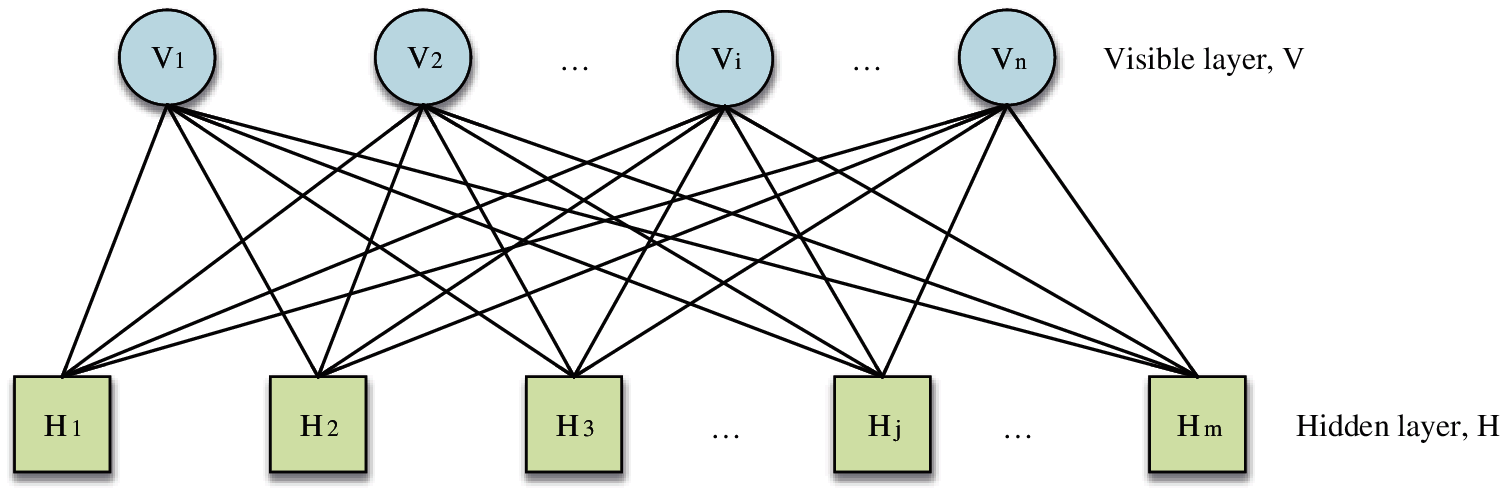
Figure 1: The structure and principle of the RBM model

The RBM is a typical model based on energy function. For a given state (V,H), the energy function of the joint configuration of visible layer variables and hidden layer variables can be expressed as:

E(V,H|℘)=−∑ijnmViHjαij−∑inβiVi−∑jmγjHj.(1)

where αij denotes the weight between the ith node in the visible layer and the jth node in the hidden layer, βi denotes the bias value of the ith node in the visible layer, and γj denotes the bias value of the jth node in the hidden layer. Additionally, ℘={αij,βi,γj} is a set of parameters that need to be adjusted for the model.

On the basis of the energy function of formula (1), the joint probability distribution function under a given state (V,H) can be obtained as:

P(V,H|℘)=e−E(V,H|℘)z(℘)z(℘)=∑V,He−E(V,H|℘)(2)

where z(℘) represents the normalization factor to ensure that the function is standardized.

Under the assumption that the hidden layer unit and the visible layer unit are binary variables, which means ∀i,j,ki∈{0,1},uj∈{0,1}, 1 means that the neuron node is in the activated state, and 0 means that the neuron node is in the inhibited state. Considering that there is no communication in the same layer and full connection between the layers in the RBM, the activation probability of the jth node of the hidden layer under the known condition of the visible layer can be calculated as:

P(Hj=1|V)=φ(αjTV+βj)=11+e−∑i=1m(αijVi+βj)(3)

where φ is the sigmoid function (activation function), which is expressed as:

φ(x)=sigmoid(x)=11+ex(4)

As the RBM structure is symmetrical, the activation probability of the ith node in the visible layer is:

P(Vi=1|H)=φ(αiTH+γi)=11+e−∑i=1n(αijHj+γi)(5)

During training of the RBM model, it is necessary to adjust the parameter ℘={αij,βi,γj} of the model by fitting a given training sample. The given training sample set is T={V1,V2,V3,…,Vn1} (n1represents the number of training samples), where Vi={V1i,V2i,…,Vn2i} (i=1,2,…,n2,n2 represents the number of visible layer nodes, meaning the dimension of the input data).

The objective of optimizing parameters in the RBM is to maximize the likelihood function L℘,T, as follows:

L℘,T=∏i=1n1P(Vi|℘)(6)

Through the logarithmic processing of function L℘,T, that is, the logarithmic processing of the training target, the following results are obtained:

ln⁡L℘,T=ln⁡∏i=1n1P(Vi|℘)ln=∑i=1n1ln⁡P(Vi|℘)(7)

Considering the complexity of likelihood function calculation, this paper uses the reconstruction error instead of the likelihood function for the evaluation function of the RBM. The reconstruction error takes the training sample as the initial state and calculates the difference with the original data after several block Gibbs samples. In the training process of the RBM, the reconstruction error of the jth iteration is calculated as follows:

Errorj=∑m=1n2∑k=1n1Vmk(8)

where m represents the number of visible layer nodes, and k represents the number of training samples.

When the error condition is met, the output result of the hidden layer is the output result of the system.

2.1.2 Deep Restricted Boltzmann Machine

Considering that the RBM, as a single-layer structure, has insufficient ability to extract and process information, this paper takes the RBM as the basic network structure, constructs a multi-layer network structure, and forms a DRBM model [22]. The DRBM model effectively trains the entire network layer by extracting the output of the previous layer of the network as the training data input of the next layer, and its structure is shown in Fig. 2.

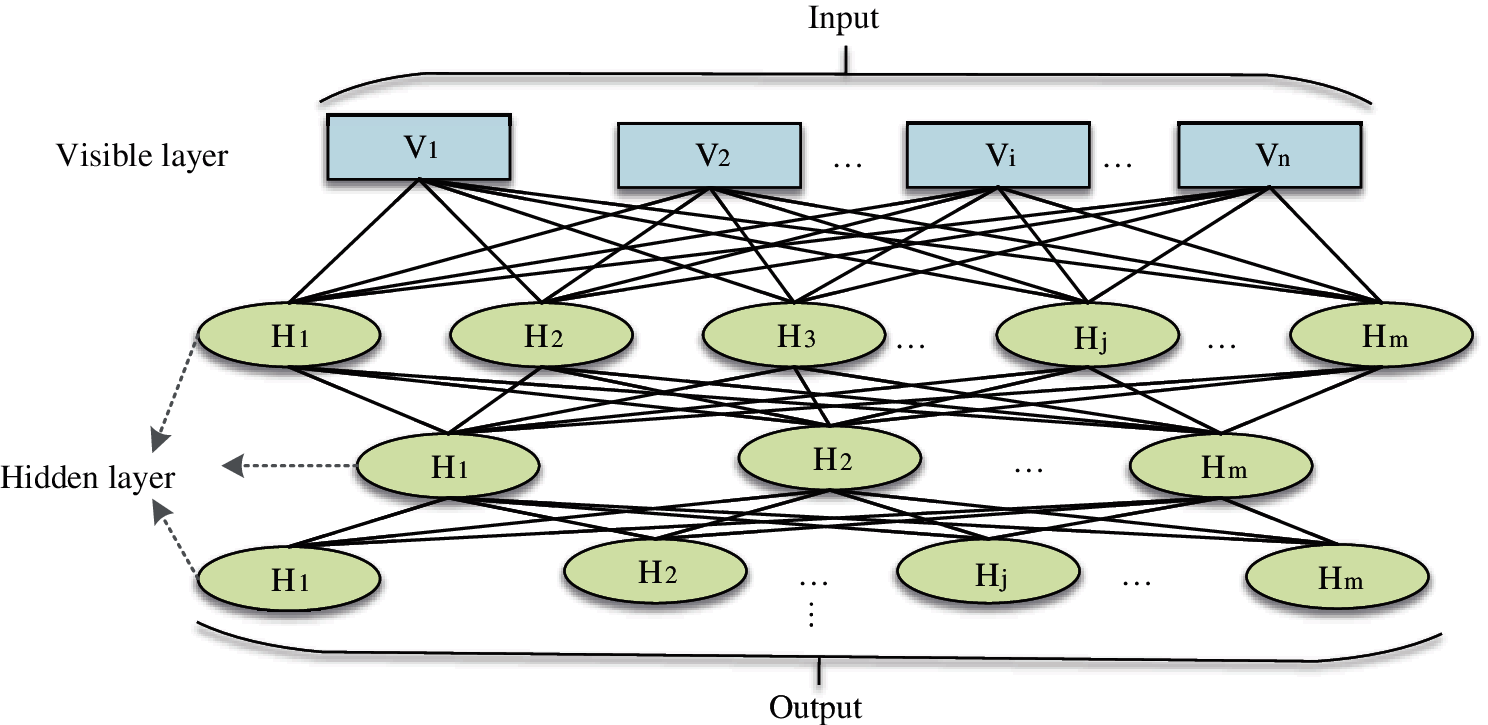
Figure 2: The structure of the DRBM model

Compared with the RBM, the DRBM can extract more abstract space vectors from high-dimensional complex input data through layer-by-layer feature transformation. In addition, the DRBM can train a large number of unlabeled sample data to reduce the impact of error or redundant information on the output results so as to increase the accuracy of the prediction results.

The training set is substituted into the DRBM model for training, and the network output result is the prediction result.

2.2 Lion Algorithm

At the beginning of the 21st century, Rajakumar proposed the Lion algorithm [23]. As a heuristic algorithm based on the group behavior of lions, the algorithm constantly updates the location information of lions by imitating the natural behaviors of lions such as mating, mutation, and territorial defense to reach the goal of seeking the optimal solution. The Lion algorithm performs well in dealing with complex optimization problems [23,24].

The algorithm can be divided into four parts according to the behavior characteristics of the lion group: initial population, mating and mutation, territorial defense, and territorial takeover. Firstly, a random individual is selected as the starting point, and each lion is taken as a solution vector to search according to the target. Then, in these feasible solutions, an iterative operation is carried out. When the termination condition is reached, the optimal solution is obtained. Therefore, the fitness function of the model needs to be determined. Taking this as the basis of the search iteration, suppose the fitness function is:

minf(x1,x2,…,xn),(n≥1)(9)

Considering that the optimization problem of RBM parameters is a complex multi-variable optimization problem, integer coding is selected as the encoding method, which can effectively improve the execution efficiency of the algorithm and simplify the calculation difficulty of the algorithm.

(1)   Initialize the pride

We first set the population size and set the number of lions as 2n (the number of the female lions and the male lions is equal). The male lion sample set is denoted as Xm and Xm=[x1m,x2m,x3m,…,xdm], the female lion sample set is denoted as Xfand Xf=[x1f,x2f,x3f,…,xdf], and d represents the length of the solution vector.

(2)   The pride

Mating is an effective way to generate new individuals. Therefore, mating in the algorithm can make existing solution vectors generate new feasible solution vectors. The process includes steps such as crossover, mutation, clustering, and elimination of weak individuals.

In the algorithm, the crossover based on double probability is introduced; that is, two different probabilities are used for crossover to produce offspring. After Xf and Xm cross, the progeny Xcub was generated, and Xcub=[x1cub,x2cub,x3cub,…,xdcub]. When xim and xjf cross with double probability, four cubs x1∼4cub may be generated.

In the algorithm, mutation is used to generate a new cub by a random mutation with probability p; that is, x1∼4cub becomes x5∼8cub. During the mating process, after the crossover and mutation are completed, eight types of offspring will be formed.

In order to group and cluster, the k-means method can be used for gender grouping of the existing eight species of offspring, which are divided into male cubs (xm_cub) and female cubs (xf_cub).

Finally, in order to update the cub group and maintain its stability, the health status of the two groups of the cubs was compared, and the weak individuals of the excessive group were eliminated so that the number of the two groups of cubs was maintained in balance. Additionally, after the population is updated, the age of the cub is initialized to 0.

(3)   Territorial defense

Territorial defense is a unique behavior of lions. In order to protect the group and demonstrate loyalty, male lions defend against attacks of nomad lions. The defense process is shown in Fig. 3.

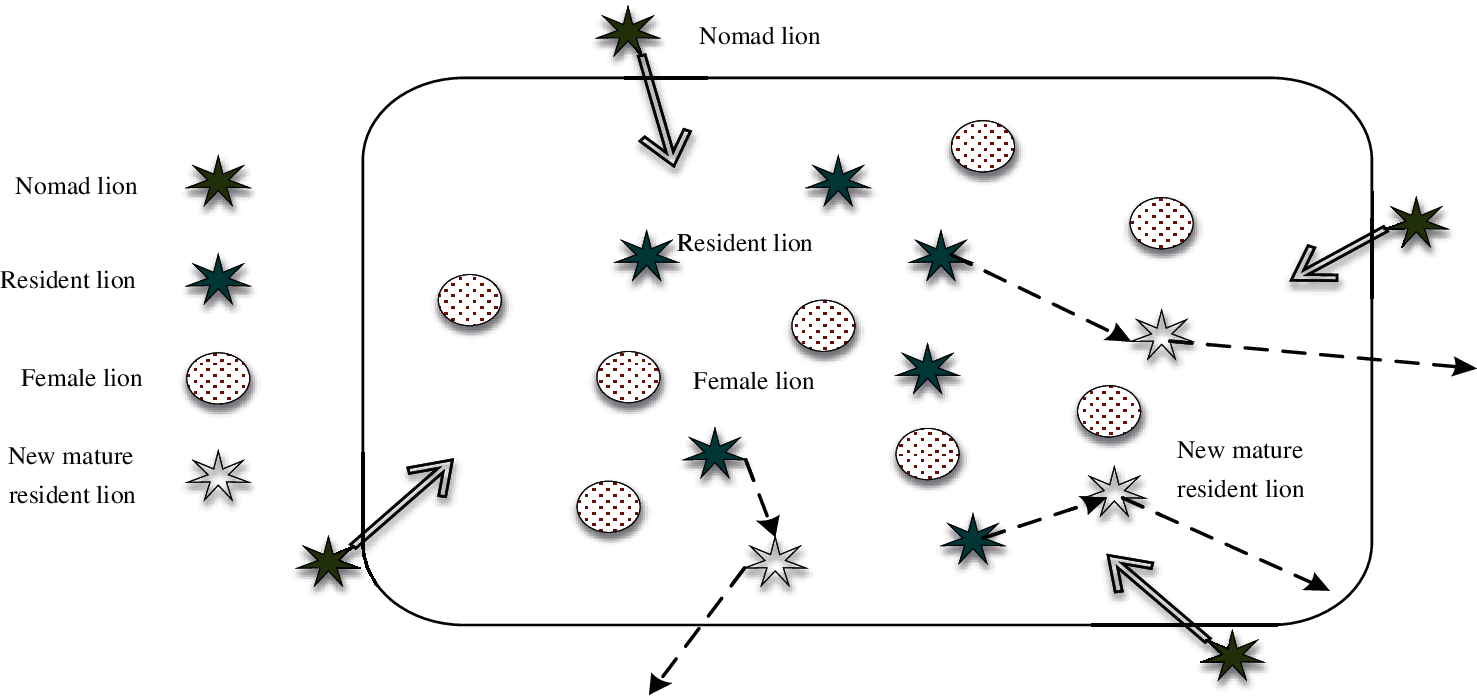
Figure 3: Lion group defense diagram

Firstly, initialize the nomad lions Xnomad and Xnomad=[x1nomad,x2nomad,x3nomad,…,xdnomad] (the method is similar to the initialization of territorial lions). Then, new feasible solutions are generated. The process of territorial attack is also the process of comparing the target value. If f(Xnomad)<f(Xm), a further comparison will be performed. If f(Xnomad)<f(Xpride), this means that xnomad as a new feasible solution is superior to the original feasible solution, then xnomad will replace the original solution. Meanwhile, the male lions and cubs will be eliminated, and the lions of the new territories continue to mate to produce offspring. Otherwise, the original lions continue to reproduce, and the cubs’ age increases by one year until the cubs reach adulthood.

If f(x) is the objective function, and f(Xpride) is the objective function value of the entire population, the calculation formula is as follows:

f(Xpride)={f(Xm)+f(Xf)+agematagecub+1∑k=1||Xm_cub||f(Xkm_cub)+f(Xkf_cub)||Xm_cub||}2(1+||Xm_cub||(10)

where f(Xm) and f(Xf) represent the value of the male lion group and the value of the female lion group; f(Xkm_cub) and f(Xkf_cub) represent the value of the male cub and the value of the female cub, respectively; ||Xm_cub|| denotes the number of male cubs in the population; and agemat represents the age suitable for mating.

(4)   Territorial takeover

The cubs begin to take over the territory when they ware mature, and they are compared as lions with the original lions. The optimal solution (Xbestm and Xbestf) of male and female lions is chosen for mating. Xpridem is composed of Xm and Xm_cub, and Xpridefis composed of Xf and Xf_cub. When choosing Xbestm and Xbestf, the following criteria can be followed:

f(Xbestm)<f(Xpridem),Xbestm≠Xpridem(11)

f(Xbestf)<f(Xpridef),Xbestf≠Xpridef(12)

Let t denote the breeding number of Xbestf, and tstrenth denote the maximum breeding number of female lions (usually set to 5). When the lions begin to mate, t is also initialized to 0 as the lions are initialized, and t increases once every time the lions mate. In the process of territorial takeover, if the original lioness is eliminated, t is initialized to 0. If the original lioness is replaced, t is accumulated on the original basis until the breeding maximum is reached.

Let GEN denote the number of iterations, and GENmax denote the maximum number of iterations. After the above steps are completed, GEN is increased by one, and Step 2 is returned until the termination condition, which is GEN≥GENmax. After the iteration is completed, select the best lion from the population as the final optimal solution.

2.3 Deep Restricted Boltzmann Machine Optimized by Lion Algorithm

The DRBM is a multi-layer structure composed of the traditional RBM. The DRBM has similar problems as the RBM, in that it will become extremely slow due to pathological problems. Therefore, we applied the Lion algorithm to optimize the parameters of the DRBM.

The steps of optimizing the DRBM model by the Lion algorithm are as follows:

(1)   Initialize the DRBM model parameters. For the DRBM, the model parameter is ℘={αij,βi,γj}, αij denotes the weight between the ith node in the visible layer and the jth node in the hidden layer, βi denotes the bias value of the ith node in the visible layer, and γj denotes the bias value of the jth node in the hidden layer.

(2)   Use the training vectors to train the DRBM model and calculate the evaluation function of the model.

(3)   Randomly set the initial population of the Lion algorithm, take the objective function of the DRBM model as the fitness function of the Lion algorithm, and use the Lion algorithm to continuously optimize the model parameters.

The optimization of the DRBM model through the Lion algorithm can speed up the training efficiency of the model and improve the learning ability of the model. The analysis process of the LA-DRBM model is shown in Fig. 4.

Figure 4: LA-DRBM model

3  Analysis of Influencing Factors of the Power Grid Enterprise's Investment Based on Fuzzy Threshold Method

3.1 Fuzzy Threshold Method

As an effective evaluation method of influencing factors, the fuzzy threshold method can judge the critical influencing factors by comparing the calculated fuzzy recognition value with the actual set threshold [25]. This method is suitable for complex and fuzzy evaluation criteria and can combine experience with objective facts to make the evaluation results more accurate. Suppose the factor set of the evaluated object is S and S={s1,s2,⋯,sn}, where n represents the number of influencing factors. The steps of analysis are as follows:

(1)   Determine the evaluation level. Each influencing factor must be evaluated according to certain standards. The evaluation levels are as follows:

V={v1,v2,⋯,vm}(13)

where m represents the number of evaluation levels.

(2)   Establish a fuzzy relationship matrix. Assuming that there are N experts in total, all the experts evaluate each influencing factor according to the grad, and the kth expert evaluates the ith factor si(i=1,2,⋯,n). The evaluation results are shown in Table 1.

xij(k) represents the membership degree of the jth comment vj obtained by the ith factor si in the opinion of the kth expert. Based on all the experts’ opinions, if the score is given according to the tenth system, the overall membership degree tij of the jth comment vj obtained by the ith factor si is calculated as follows:

tij=∑k=1Nxij(k)10N(14)

Therefore, the fuzzy relationship matrix T is calculated as:

T=[t11t12⋯t1mt21t22⋯t1m⋮⋮⋱⋮tn1tn2⋯tnm],0≤tij≤1(15)

where tij represents the overall membership degree of the jth comment vjobtained by the ith factor si.

(3)   Determine the evaluation grade weight vector, and the vector is as follows:

W=(w1,w2,⋯wm)T(16)

where wi≥0,∑wi=1.

It is determined that the weight settings have a great impact on the comprehensive evaluation results.

(4)   Calculate the evaluation result. Multiply the evaluation grade weight vector W and the fuzzy relationship matrix T to obtain the fuzzy comprehensive evaluation result vector B=(b1,b2,⋯,bn)T.

B=T∙W=[t11t12⋯t1mt21t22⋯t1m⋮⋮⋱⋮tn1tn2⋯tnm]∙(w1w2⋯wm)T(17)

(5)   Based on experience, set thresholds and screen critical influencing factors.

3.2 Analysis of Critical Influencing Factors

There are many factors influencing power grid investment, which are closely related to the income of power grid companies, investment benefits, and customer needs [26–28]. At the same time, with the advancement of 5G base station construction and TDPR, power grid investment is also affected by these two factors. Therefore, TDPR and 5G station construction should be considered as two influencing factors in the investment forecast of power grid enterprise. According to the analysis, it can be concluded that the influencing factors of the power grid enterprise's investment mainly include total assets s1, total electricity consumption s2, power supply population s3, load s4, line loss rate s5, ratio of grid assets to income s6, ratio of profits to cost s7, increased load per unit of grid investment s8, return on equity s9, power supply reliability s10, growth rate of electricity sales s11, power generation of renewable energy s12, standard coal saving s13, maximum load of the whole society s14, carbon dioxide emission reduction s15, influence factors of TDPR s16, 5G station construction s17, and so on [29–34].

The fuzzy threshold method is used to analyze the critical influencing factors of power grid investment, and the evaluation level V = {Extremely important, very important, generally important, not very important, not important} is set, and the corresponding weight vector is determined as W = {0.3, 0.25, 0.2, 0.15, 0.1}. Then, the fuzzy relationship matrix is obtained by the expert scoring and calculating the overall membership degree and multiplying it with the weight vector W to obtain the fuzzy comprehensive evaluation result, as shown in Table 2.

According to the results of the comprehensive calculation and the actual situation, the threshold value is set to 5, and the influencing factors with a fuzzy comprehensive evaluation result greater than 5 are the critical influencing factors of power grid investment. It is concluded that the critical influencing factors include total assets s1, total electricity consumption s2, ratio of grid assets to income s6, increased load per unit of grid investment s8, power supply reliability s10, standard coal saving s13, influence factors of TDPR s16, and 5G station construction s17, as shown in Fig. 5.

Figure 5: The critical influencing factors of power grid investment

In the analysis of the influence factors of TDPR and 5G station construction, the two influencing factors are taken into account by introducing correction factors. The correction coefficient of TDPR is λ1, and the correction coefficient of 5G station construction is λ2.

4  Empirical Analysis

According to the analysis of the fuzzy threshold method, the critical influencing factors of power grid investment are total assets s1, total electricity consumption s2, ratio of grid assets to income s6, increased load per unit of grid investment s8, power supply reliability s10, standard coal saving s13, influence factors of TDPR s16, and 5G station construction s17. We took a provincial power grid company (Z power grid company) in the southeast region of China as the research object, and selected data from 2010 to 2020 as samples for analysis. The input vector of the prediction model was {s1, s2, s6, s8, s10, s13}, and the output vector was the investment amount yi. Then, we used the correction factor to correct the forecast result to obtain the final forecast result. The calculation formula is:

y^i=λ1∗λ2∗yi(18)

where y^i is the forecasting value, λ1 is the correction coefficient of TDPR, λ2 is the correction coefficient of 5G station construction, and yi is the initial forecasting value.

In order to reduce the influence of dimensions and units on the prediction results, the extreme value method is used to normalize the original data. The calculation formula is as follows:

xi′={xi−xminxmax−xmin},i=1,2,3,…,n(19)

where xi′ denotes the normalized data, xi represents the original data, and xmax and xmin represent the maximum value and the minimum value of the original data, respectively.

We can use the data of Z grid company from 2010 to 2019 as training set to train the model and use the trained model to predict the company's investment in 2020.

First, set the Lion algorithm parameters, as shown in Table 3.

Then, the lion algorithm is used to iteratively optimize the parameters of the DRBM. At the same time, based on experience, set the correction coefficient λ1 = 1.1, λ2 = 1.2. After training, the comparison result between the actual value and the training prediction value obtained from 2010 to 2019 is shown in Fig. 6. The training time and forecast time of the models are shown in Table 4.

Figure 6: The training results of the LA-DRBM model

According to the graphic analysis, the forecasting value of the sample largely coincides with the actual value, and the fitting effect is excellent.

Calculate the relative error rate (RER) and non-linear function goodness of fit (R2) between the actual value and the forecasting value of the training sample. The calculation formula of the RER and R2 is:

c=y^i−yiyi(20)

R2=1−∑i=1n(y^i−yi)2∑i=1nyi2(21)

where y^i is the forecasting value, and yi is the actual value. The smaller the RER is, the more accurate the prediction result is. The larger the R2 is, the more accurate the prediction result is.

The RER of the training result is shown in Fig. 7.

Figure 7: The RER of the training result of the LA-DRBM model

The analysis result shows that the RERs of the training results are between −0.02 and 0.015, which are small, indicating that the training effect of the model is excellent. Therefore, it can be considered that the model is an effective method to predict the investment amount of power grids.

Finally, we can use the optimized model to forecast the investment of Z grid companies in 2020.

The prediction effect of this model is compared with the prediction effect of the BPNN, SVM, RBM, and regression model. The comparison results are shown in Table 5 and Fig. 8.

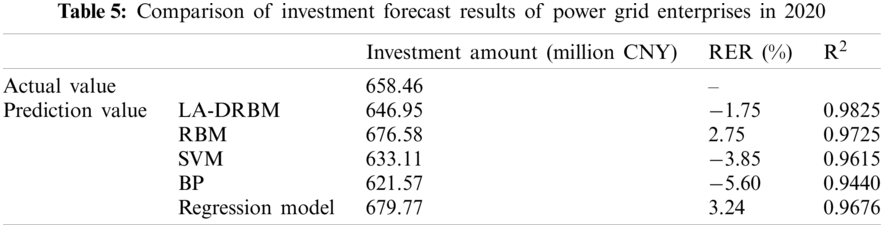
Figure 8: Comparison of RER of the prediction results of each model

According to the analysis results, the RERs for Z grid enterprise's investment forecast in 2020 of the LA-DRBM model, the RBM model, the SVM model, the BP model, and the regression model are −1.75%, 2.75%, −3.85%, −5.60%, and 3.24%, respectively. Among them, the RER of the LA-DRBM model is the smallest. From the analysis of the results, the LA-DRBM model can achieve a good prediction effect and high prediction accuracy in forecasting power grid investment.

5  Conclusions

In order to respond to the requirement of sustainable development of power grid investment and improve the accuracy of power grid investment prediction, a new power grid investment prediction model based on the LA-RBM (deep restricted Boltzmann machine optimized by the Lion algorithm) model is proposed according to the characteristics of power grid planning and the trend of power grid investment. In this paper, the main findings and conclusions are as follows:

(1)   Firstly, the fuzzy threshold method was used to analyze the influencing factors of a power grid enterprise's investment. After analysis, 8 critical influencing factors were screened out of 17 influencing factors, including total assets s1, total electricity consumption s2, ratio of grid assets to include s6, increased load per unit of grid investment s8, power supply reliability s10, standard cost saving s13, influence factors of TDPR s16, and 5G station construction s17. These factors were used as input variables to train the model.

(2)   Then, considering the problem of the insufficient solution speed of the DRBM model, the Lion algorithm was used to optimize the parameters of the DRBM model. The optimized parameter set of the DRBM model was ℘={αij,βi,γj}, where αij denotes the weight between the ith node in the visible layer and the jth node in the hidden layer, βi denotes the bias value of the ith node in the visible layer, and γj denotes the bias value of the jth node in the hidden layer. Through iterative training, a new model (LA-DRBM) suitable for power grid investment prediction was obtained.

(3)   Finally, the LA-RBM power grid investment forecast model was compared with the RBM, SVM, and BPNN. According to the analysis results, the RERs for Z grid enterprise's investment forecast in 2020 of the LA-DRBM model, the RBM model, the SVM model, and the BP model were 3.22%, 7.92%, 9.01%, and 10.77%, respectively. Among them, the RER of the LA-DRBM model was the smallest. From the analysis of the results, the LA-DRBM model can achieve a good prediction effect and high prediction accuracy in forecasting power grid investment.

Therefore, the experimental results fully prove that the LA-DRBM power grid investment forecast model has strong generalization ability and robustness; the prediction accuracy is better than other models; and it can achieve good prediction results. This model provides new ideas and references for power grid investment forecasting.

The innovations of the paper are as follows:

(1)   The LA-DRBM model can abstract the combination of low-level features into high-level features so as to adequately reflect the data characteristics and improve the computational efficiency of the model.

(2)   The LA-DRBM model uses the Lion algorithm to optimize the deep restricted Boltzmann machine, which improves the forecasting accuracy of the model.

(3)   The article introduces the TDPR and 5G station construction as influencing factors, which were used in an innovative index system of influencing factors.

(4)   The model can combine the advantages of a single model and overcome the shortcomings of a single model. The combined model is thus an effective prediction method for power grid investment and has a strong generalization ability and good robustness.

Author Contributions: Conceptualization, Q.W. and X.Y.; formal analysis, D.P.; investigation, Q.W.; resources, Q.W.; data curation, Y.F.; writing—original draft preparation, Q.W. and D.P.; writing—review and editing, X.Y. All authors have read and agreed to the published version of the manuscript.

Funding Statement: This research was funded by the National Key Research and Development Program of China (Grant No. 2020YFB1707804), the 2018 Key Projects of Philosophy and Social Sciences Research (Grant No. 18JZD032), and Natural Science Foundation of Hebei Province (Grant No. G2020403008).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.