
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2021.016720
ARTICLE
An Improved Method Based on TODIM and TOPSIS for Multi-Attribute Decision-Making with Multi-Valued Neutrosophic Sets
School of Science, Southwest Petroleum University, Chengdu, 610500, China
*Corresponding Author: Lijuan Peng. Email: 18428330541@163.com
Received: 19 March 2021; Accepted: 03 June 2021
Abstract: Due to the complexity of decision-making problems and the subjectivity of decision-makers in practical application, it is necessary to adopt different forms of information expression according to the actual situation of specific decision-making problems and choose the best method to solve them. Multi-valued neutrosophic set, as an extension of neutrosophic set, can more effectively and accurately describe incomplete, uncertain or inconsistent information. TODIM and TOPSIS methods are two commonly used multi-attribute decision-making methods, each of which has its advantages and disadvantages. This paper proposes a new method based on TODIM and TOPSIS to solve multi-attribute decision-making problems under multi-valued neutrosophic environment. After introducing the related theory of multi-valued neutrosophic set and the traditional TODIM and TOPSIS methods, the new method based on a combination of TODIM and TOPSIS methods is described. And then, two illustrative examples proved the feasibility and validity of the proposed method. Finally, the result has been compared with some existing methods under the same examples and the proposed method's superiority has been proved. This paper studies this kind of decision-making problem from algorithm idea, algorithm steps and decision-making influencing factors.
Keywords: Multi-valued neutrosophic set; TODIM; TOPSIS; multi-attribute decision-making
Multi-attribute decision-making (MADM) problem refers to how to rank alternatives and select the optimal one when the decision-making problem contains multiple attributes. As an important part of modern decision-making science, it has made significant progress and wide application since the early 1960s. Its methodology and theory have been applied to many fields, such as investment decision-making [1,2], project evaluation [3], personnel management [4], supplier selection [5–8], medical equipment selection [9,10], and urban sustainability assessment [11], etc.
A complete MADM process mainly consists of two core parts: representation of decision information and integration of decision information. The representation of decision information refers to using correct language to express decision information correctly. Due to the complexity of the objective problems and the vagueness of the subjective thinking of decision makers in practical applications, it is difficult for decision makers to give accurate evaluation values for MADM problems with inaccurate, uncertain or incomplete information. In this case, fuzzy language is considered to be the best tool to express fuzzy information. Therefore, there emerge a lot of sets to describe uncertain decision information. Such as fuzzy set, soft set, neutrosophic set (NS) [12], pathogenic hypersoft set [13], and their variants, etc. As a generalization of the intuitionistic fuzzy set, neutrosophic set [12] is used to describe uncertain, discontinuous and incomplete information. The main idea of NS is to describe every value statement in three-dimensional neutrosophic space, where each dimension of the space represents respectively the truth-membership (T), the indeterminacy-membership (I) and the falsity-membership (F) of the statement under consideration, and T, I, F are standard or non-standard real subsets of
The second core part of MADM is integrating decision information and the ranking or selection of alternatives. At present, commonly used decision-making methods mainly contain TODIM (TOmada de Decisao Iterativa Multicriterio) [17], TOPSIS (The Order Performance technique based on Similarity to Ideal Solution) [18], VIKOR (VIsekriterijumska optimization I KOmpromisno Resenje) [19], EDAS (Evaluation Based on Distance from Average Solution) [20], PROMETHEE (Preference Ranking Organization METhod for Enrichment Evaluations) [21], MULTIMOORA (MULTIple Multi-Objective Optimization by Ratio Analysis) [22], and their variants, etc. Among them, TODIM method considers the psychological behavior of decision makers, which is closer to the actual situation. Besides, TOPSIS method is also an excellent MADM method for its simple and efficient calculation. Therefore, this paper mainly discusses the TODIM and TOPSIS methods.
As a most used MADM method, TODIM method takes psychological behavior of decision makers into consideration which is more in line with actual decision-making situations. Therefore, it has been developed rapidly and widely used since it was proposed by Gomes et al. [17]. Fan et al. [23] solved the hybrid MADM problem by TODIM method, with the attribute values given in forms of crisp numbers, interval numbers and fuzzy numbers; Ömür et al. [24] combined the TODIM method and linguistic term set (LTS) for solving the supplier selection problem; Liu et al. [25] extended the TODIM method to multi-attribute group decision-making (MAGDM) with intuitionistic uncertain linguistic information; Wang et al. [26] used the TODIM method to solve the hybrid MADM problems with four different forms: crisp number, interval number, triangular fuzzy number and trapezoidal fuzzy number; Wang et al. [16] proposed the TODIM method with MVNS; Jiang et al. [27] proposed a TODIM method for MADM problem with incomplete evaluations in the form of crisp numbers; Qin et al. [5] used the TODIM method with type-2 fuzzy sets for green supplier selection and performed the comparative analysis with the TOPSIS method; Ji et al. [28] defined a projection-based TODIM method under multi-valued neutrosophic environments and applied it in personnel selection; Based on an improved TODIM method, Wang et al. [29] solved a MADM problem with interval grey number; Wang et al. [30] proposed the probability multi-valued linguistic neutrosophic set and used the TODIM method for solving the multi-criteria group decision-making (MCGDM) problems; Xu et al. [31] and Xu et al. [32] discussed the MADM problem with TODIM method under the single-valued neutrosophic and interval neutrosophic environment; Mao et al. [33] used TODIM for enterprise performance evaluation of strategic emerging industries under probabilistic linguistic term environment; In order to deal with linguistic hesitant fuzzy information in multi-criteria decision-making (MCDM) problems, Zhou et al. [34] applied TOPSIS, VIKOR, and TODIM methods; Considering the behavior of decision makers, Chen et al. [35] used the TODIM method to deal with uncertain linguistic MAGDM and compared this method with TOPSIS method.
TOPSIS method is also a popular MADM method for its efficient and straightforward calculation. Rıdvan et al. [36] extended the TOPSIS method to MCDM problem with single valued neutrosophic information; Ye [37] developed an extended TOPSIS method for a MAGDM problem based on the single-valued neutrosophic linguistic set (SVNLS); Tian et al. [38] combined INS and TOPSIS to establish two optimisation models for MCDM; Liu et al. [39] proposed a TOPSIS method for MAGDM with INN based on cloud model; Biswas et al. [40] proposed a TOPSIS method for MAGDM under single-valued neutrosophic environment; Liang et al. [1] presented an extended TOPSIS method combined with LNN in metallic mining projects investment; Liang et al. [4] introduced a linguistic neutrosophic MCGDM TOPSIS method to university human resource management; Chen et al. [6] handled a green supplier selection with TOPSIS method based on the OWA distance of the SVNLS; Liu et al. [41] proposed a neutrosophic hesitant fuzzy linguistic term set and combined the TOPSIS method to solve MCDM problem; Huang et al. [2] used the TOPSIS method to solve the investment problem under intuitionistic fuzzy environment; Giri et al. [42] used the TOPSIS method for solving the MADM in the form of interval trapezoidal neutrosophic number; Chai et al. [43] handled a MADM problem based on SVNS and TOPSIS method; Tan et al. [44] proposed a method based on intuitionistic (hesitant) fuzzy set (IHFS) and TOPSIS; Abdel-Basset et al. [9,10] combined bipolar neutrosophic numbers and TOPSIS for estimating the intelligent medical devices selection, and further proposed a novel TOPSIS method with type-2 neutrosophic numbers for developing supplier selection; Nguyen et al. [45] developed a new TOPSIS method based on the proposed intuitionistic (hesitant) fuzzy set theory; Pei et al. [46] introduced a fuzzy linguistic multiset TOPSIS method and applied it in linguistic decision-making problems; Elhassouny et al. [47] simplified the TOPSIS method and combined it with SVNS for decision-making.
Based on different methodologies, each MADM method has its advantages, disadvantages and scope of application. For this, with the increasing number of decision-making methods, more and more researchers begin to consider combining the existing methods to propose some improved methods. Some studies of combining TODIM or TOPSIS with other methods are proposed. Ji et al. [48] proposed a QUALIFLEX method with a TODIM-based concordance index for treatment selection; Yang et al. [49,50] obtained the weight by DEMATEL and then ranked the alternatives by TOPSIS method; Abdel-Basset et al. [7] built a framework of supplier selection problems, which employed ANP to calculate weights of selected criteria and used TOPSIS to rank alternatives; Tian et al. [3] combined the DEMATEL method and TODIM method to handle the market segment evaluation and selection under single-valued neutrosophic environment; Bai et al. [8] presented a method based on grey theory and TOPSIS for sustainable supplier selection; With the LTS, Liu et al. [51] presented a novel integrated FMEA model based on cloud model theory and TOPSIS method; Tang et al. [11] determined the positive/negative ideal solution (P/NIS) of urban sustainability through TOPSIS method, and then ranked alternatives by grey relational analysis.
Based on the above analysis, this paper proposes a method by combining the TODIM and TOPSIS methods under the MVNS, considering the bounded rationality of decision makers. The main motivations behind this paper are as follows:
(1) TODIM method fully considers the decision makers’ risk aversion attitude on the basis of prospect theory, and can reflect the decision makers’ risk preference by adjusting the parameters, which is more in line with the actual decision-making requirements. However, any two alternatives need to be compared in TODIM method and also lead to high computational complexity. It is meaningful to find an improvement method that not only reflects the bounded rationality of decision makers, but also overcome its computational complexity.
(2) TOPSIS method sorts the alternatives according to their closeness to the ideal solution (PIS and NIS) rather than making a pairwise comparison of any two alternatives thereby reduces the number of comparisons between alternatives and makes the calculation simple. But it only considers the closeness between each alternatives and the PIS (NIS), and does not taking the decision makers’ risk aversion attitude into account. Therefore, finding an improvement method based on TOPSIS method to reflect the bounded rationality of decision makers is significant.
(3) MVNS is a good tool to describe the incomplete, indeterminate and inconsistent information accurately. Therefore it is necessary to propose a hybrid method under MVNS environment that not only has concise calculation process and scientific results but considers the decision makers’ risk attitude.
In summary, inspired from these two methods, this paper proposed a new method based on TOPSIS and TODIM methods under MVNS environment. This hybrid method not only has concise calculation like TOPSIS method but also takes the decision makers’ aversion attitude into account, which makes it has good scientificity, accuracy and maneuverability.
The reminder of this paper unfolds as Tab. 1.

For a better understanding the content of this paper, this section introduces some basic concepts of NSs and MVNSs and their related definitions.
Definition 1. [12] Let X be a space of points (objects), with a generic element in X denoted by
So,
Definition 2. [12] The complement of a NS A is denoted by
Definition 3. [12] A NS A is contained in the other NS B,
2.2 Multi-Valued Neutrosophic Sets (MVNSs)
Definition 4. [16] Let X be a space of points (objects), a MVNS A in X is characterized by
where
(1)
(2)
(3)
Especially,
(1) if
(2) if
(3) if
(4) if
For convenience, suppose that
Definition 5. [16] The complement of a MVNS A is denoted by
Example 1: Let
Definition 6. [16] Let A be a MVNS, so the expectation of
where
Example 2: Let
Definition 7. [16] Let
Example 3: Let
Definition 8. [16] Let
Example 4: Let
3.1 The Traditional TODIM Method
The traditional TODIM method is a MADM method proposed by Gomes et al. [17] on the basis of the foreground theory in 1991. The main idea of this method is to establish the relative superiority function of one alternative over other alternatives based on the value function of the foreground theory. According to the obtained superiority, the ranking of alternatives is determined. The traditional TODIM method can only be used to deal with the fact that the attribute value is real. The main steps of TODIM method with MVNS in [16] are as follows:
Suppose that there are m alternatives
Step 1: Standardize the decision information. That is, normalizing
Step 2: Figure out
Step 3: Figure out the dominance degree of
Step 4: Work out the overall dominance of
Step 5: Ranking all alternatives according to the value of
It can be seen that TODIM method fully considers the decision makers’ risk aversion attitude on the basis of prospect theory, and can reflect the decision makers’ risk preference by adjusting the parameters, thereby resulting in a more accurate decision-making process. However, decision-making information needs to be standardized firstly. Besides, any two alternatives also need to be compared in TODIM method in the case of more decision-making data, which leads to high computational complexity and large amount of calculation (such as distance and expectation values).
3.2 The Traditional TOPSIS Method
TOPSIS is a MADM method based on geometric thinking, which ranks candidate alternatives relatively far from ideal solutions and negative ideal solutions. On the basis of the TOPSIS method with IHFS in paper [44], we transformed it into a multi-valued neutrosophic environment and proposed a TOPSIS method with MVNS. The following shows the complete steps.
Let alternatives are
Step 1: Get the decision matric and the corresponding weight.
Step 2: Figure out the weighted normalization matrix.
Step 3: Determine the positive ideal solution (PIS)
and if
where
Step 4: Calculate the distance between
Step 5: Figure out the relative approximation coefficients of each alternative according to
Step 6: Ranking the alternative according to the value of
TOPSIS method puts forward PIS (NIS) as reference point and only needs to compare each alternative with the ideal solution, which reduces the number of comparisons between alternatives when facing more decision-making data. So the calculation of TOPSIS method is simpler than TODIM method. However, from the formula of relative approximation coefficients, it can be seen that this method only uses distance measure to judge the quality of alternatives, and does not take the decision makers’ risk aversion attitude into account, which lacks subjectivity.
4 The Proposed Method Based on TODIM and TOPSIS
When faced with a large amount of decision-making data, to consider the risk attitude of decision makers and simplify the calculation process, a hybrid MADM method based on TOPSIS and TODIM is proposed in this section.
Suppose in a MADM problem, there are
Step 1. Obtain the decision matrix
Step 2. Determine the PIS
and if
where
Step 3. Calculate the distance between
Step 4. Figure out
Step 5. According to the concept of value function and behavioral economics in prospect theory, if the PIS is taken as a reference point, then the alternatives will lose relative to the PIS; on the contrary, if the NIS is taken as a reference point, the alternatives will benefit. So the cost function is
The parameter
Step 6. Figure out the overall value
It is obvious that the proposed method does not need to standardize the overall decision-making data according to attribute classification and it does not need to calculate the distance between any two alternatives and the expectation value of each alternative. In this sense, the proposed method is simpler than TODIM method in calculation. Besides, the proposed method is also based on TODIM method, taking the bounded rationality of decision makers into account, thus making up for the shortcoming of TOPSIS method. Therefore, facing to large number of alternatives, the proposed method can reduce the computational complexity and load more than TODIM or TOPSIS, which lead to a more simple decision-making process and a more reasonable result.
In this section, two illustrate examples of the personnel selection problem and teaching evaluation problem adapted from Wang et al. [16] and Ye [52] are mentioned to demonstrate the validity and feasibility of the proposed methodology.
5.1 Case 1: Company Personnel Selection
Personnel selection is an important part of modern human resource management and also an important part of the company's operation. It is directly related to the company's output quality and efficiency. Good talents are the guarantee of good products. In the personnel selection process, the interviewer needs to evaluate candidates based on their performance in various aspects, which can be regarded as an MADM process. Thinking about the ambiguity and complexity of people's thinking and language, MVMS can be used to express the evaluation information of the interviewer.
Suppose that a food company wants to hire a product manager. After preliminary screening of dozens of resumes, there are four candidates in the talent market that meet the recruitment requirements, which are denoted by
Step 1. Obtain the decision matrix
The original decision matrix is obtained as shown in Tab. 2.

Step 2. Determine the PIS
According to the attributes characteristics,

Step 3. Calculate the distance
According to Eq. (4), the distance
Step 4. Figure out
According to Eq. (7), the relative weights of
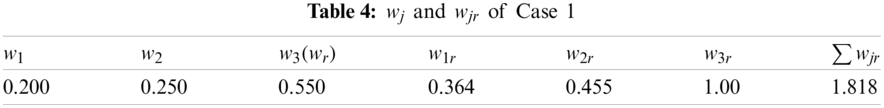
Step 5. Calculate the dominance degree matrices.
Let the parameter
Step 6. Figure out the overall value
Finally, the overall dominances are shown in Tab. 5. It is obvious that

5.2 Case 2: University Teaching Evaluation
Teaching evaluation is an important means for education administrative departments to supervise the teaching quality of colleges and universities. The purpose is to improve the quality of education and teaching. It is not only an important part of the teaching process but the basis of effective teaching and successful teaching. Specifically, according to certain teaching goals and standards, such as teaching completion, teaching concepts, teaching quality, etc., it systematically detects teachers’ teaching and evaluates its value, advantages and disadvantages, in order to improve. This can also be regarded as a MADM problem. Due to the complexity of the reality, its attribute values are often not directly represented by crisp set. In this condition, MVNS has become a good tool for expressing attribute values.
Assume that an education administration department in a certain place wants to evaluate the teaching of four local universities which are denoted by
Step 1. Obtain the decision matrix
The original decision matrix is obtained as shown in Tab. 6.

Step 2. Determine the PIS
According to the description,

Step 3. Calculate the distance
Then, the distance
Step 4. Figure out
Next, according to Eq. (7), the relative weights of

Step 5. Calculate the dominance degree matrices.
Assume the parameter
Step 6. Figure out the overall value
Finally, the overall dominances are shown in Tab. 9. The final result explains that

Since the proposed method is based on TODIM method, the parameter
As mentioned in Section 4, parameter
Case 1: Let parameter
Case 2: Tab. 11 shows the results of case 2 when parameter


In summary, when the parameter
In order to verify the effectiveness, feasibility and superiority of the proposed methodology, we compared the results of the two cases applied in Section 5 with some existing methods. Details are as follows:
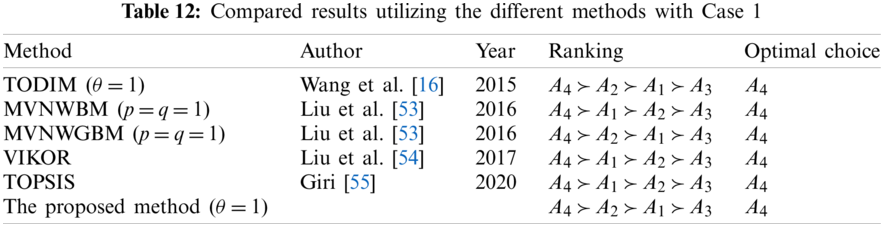
Case 1: In recent years, there have been several MADM methods to solve the MVNS environment such as TODIM method proposed by Wang et al. [16], whose are also the proposer of MVNS, MVNWBM operator and MVNWGBM operator [53], etc. Besides, MVNS was also called single-valued neutrosophic hesitant fuzzy set (SVNHFS) by Ye [52]. There are also some methods to solve single-valued neutrosophic hesitant fuzzy set MADM problem. So we compared the results of Case 1 with five existing methods. To be specific, the comparative study was based on the same illustrative example in which the weights of attributes are
As shown in Tab. 12, it can be seen that, the ranking result of the proposed method when
Case 2: There are many approaches to deal with MCDM in SVNHFS environment, such as the approaches based on Weight operators [52], Hamming distance [56], Correlation coefficient [57], Choquet aggregation Operators [58], and so on. They can also be used in MVNS environment. Therefore, as in Case 1, these approaches are used to deal with Case 2 and compared with the proposed method. For the convenience of comparison, the weights are all set
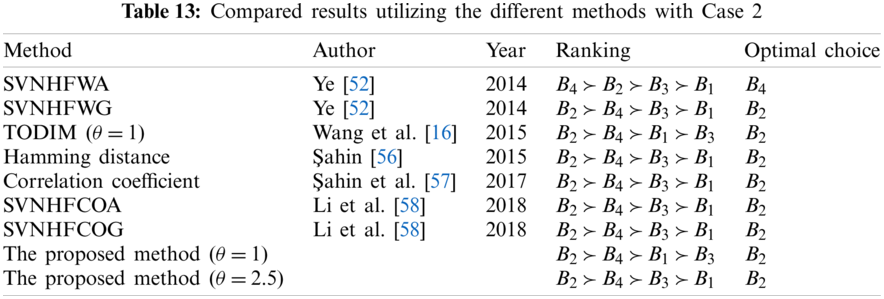
From Tab. 13, we can see that the final results of the several methods are slightly different. The ranking obtained by SVNHFWA operator is different from others, and the optimal choice is
In summary, among the above methods, only the proposed method and TODIM method take the decision makers bounded rationality into account, which can make the result more accurate. But when the alternatives or attributes increase, the calculation amount of the proposed method is much smaller than that of the traditional TODIM method. In this sense, the proposed method is superior to the TODIM method. Thus, the advantages of the proposed method are as follows:
(1) Based on the TODIM method, it considers the bounded rationality of decision makers and reflect the risk preference of decision makers by adjusting the loss attenuation coefficient
(2) The proposed method does not need to standardize the original matrix according to different attributes, which simplifies the calculation process to a certain extent.
(3) The proposed method uses PIS and NIS in the TOPSIS method as reference points, and uses the distance between the alternatives and the reference point to replace the pairwise comparison between alternatives, which makes the calculation simple. When faced with a large amount of decision-making data, the proposed method can use relatively simple calculations to obtain more reasonable result.
As a subset of neutrosophic set, MVNS is an excellent tool to describe uncertainty, incomplete and imprecise information. The elements in the truth-membership, the indeterminacy-membership and the falsity-membership in MVNS are extended to finite sets of discrete values, which enriched the expression of fuzzy information on the basis of fuzzy languages such as SVNS and INS. Therefore, based on the traditional TODIM and TOPSIS methods and the related research achievements of MVNS, this paper proposed a new method to handle the MCDM problems under MVNS environment. First, the traditional TODIM and TOPSIS methods are reviewed. And then, the specific steps of the hybrid method are introduced. In the new method, the distance between the alternatives and the ideal solutions is calculated by standardized Hamming distance of MVNS. Subsequently, the proposed method is used to solve two MADM problems about company personnel selection and university teaching evaluation under MVNS environment. These two cases all illustrate the feasibility and applicability of the proposed method. Moreover, by adjusting the loss attenuation coefficient
There are several directions for future research. Firstly, in addition to personnel selection and teaching evaluation, the proposed method should be used in more fields, such as venture capital selection, medical diagnoses, supplier selection, and so on. In addition, the proposed method assumes that the weight of the attribute is given by the decision maker, and does not discuss the situation with unknown attribute weight. Therefore, in the future, we will devote ourselves to improving the method to cover this deficiency and applying it to natural and complex decision-making processes.
Acknowledgement: Thanks to the co-authors for their help in the research process, for providing language assistance, writing assistance and proofreading for this article.
Funding Statement: This research was funded by the Humanities and Social Sciences Foundation of Ministry of Education of the Peoples Republic of China (17YJA630115). The recipient of the founding is DX.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Liang, W., Zhao, G., Wu, H. (2017). Evaluating investment risks of metallic mines using an extended TOPSIS method with linguistic neutrosophic numbers. Symmetry, 9, 149–167. DOI 10.3390/sym9080149. [Google Scholar] [CrossRef]
2. Huang, Y., Jiang, W. (2018). Extension of TOPSIS method and its application in investment. Arabian Journal for Science and Engineering, 43, 693–705. DOI 10.1007/s13369-017-2736-3. [Google Scholar] [CrossRef]
3. Tian, Z., Wang, J., Zhang, H. (2018). Hybrid single-valued neutrosophic MCGDM with QFD for market segment evaluation and selection. Journal of Intelligent and Fuzzy Systems, 34, 177–187. DOI 10.3233/JIFS-171055. [Google Scholar] [CrossRef]
4. Liang, R., Jiang, Z., Wang, J. (2018). A linguistic neutrosophic multi-criteria group decision-making method to university human resource management. Symmetry, 10, 364–389. DOI 10.3390/sym10090364. [Google Scholar] [CrossRef]
5. Qin, J., Liu, X., Pedrycz, W. (2016). An extended TODIM multi-criteria group decision making method for green supplier selection in interval type-2 fuzzy environment. European Journal of Operational Research, 258, 626–638. DOI 10.1016/j.ejor.2016.09.059. [Google Scholar] [CrossRef]
6. Chen, J., Zeng, S., Zhang, C. (2018). An OWA distance-based, single-valued neutrosophic linguistic TOPSIS approach for green supplier evaluation and selection in Low-carbon supply chains. International Journal of Environmental Research and Public Health, 15, 1439–1454. DOI 10.3390/ijerph15071439. [Google Scholar] [CrossRef]
7. Abdel-Basset, M., Mohamed, M., Smarandache, F. (2018). A hybrid neutrosophic group ANPTOPSIS framework for supplier selection problems. Symmetry, 10, 226–248. DOI 10.3390/sym10060226. [Google Scholar] [CrossRef]
8. Bai, C., Sarkis, J. (2018). Integrating sustainability into supplier selection: A grey-based TOPSIS analysis. Technological and Economic Development of Economy, 24, 2202–2224. DOI 10.3846/tede.2018.5582. [Google Scholar] [CrossRef]
9. Abdel-Basset, M., Manogaran, G., Gamal, A., Smarandache, F. (2019a). A group decision making framework based on neutrosophic TOPSIS approach for smart medical device selection. Journal of Medical Systems, 43, 38. DOI 10.1007/s10916-019-1156-1. [Google Scholar] [CrossRef]
10. Abdel-Basset, M., Saleh, M., Gamal, A., Smarandache, F. (2019b). An approach of TOPSIS technique for developing supplier selection with group decision making under type-2 neutrosophic number. Applied Soft Computing Journal, 77, 438–452. DOI 10.1016/j.asoc.2019.01.035. [Google Scholar] [CrossRef]
11. Tang, J., Zhu, H., Liu, Z., Jia, F., Zheng, X. (2019). Urban sustainability evaluation under the modified TOPSIS based on grey relational analysis. International Journal of Environmental Research and Public Health, 16, 256–277. DOI 10.3390/ijerph16020256. [Google Scholar] [CrossRef]
12. Smarandache, F. (1998). Neutrosophy. Neutrosophic probability, set, and logic, ProQuest information and learning. USA: Ann Arbor. [Google Scholar]
13. Gayen, S., Smarandache, F., Jha, S., Singh, M. K., Broumi, S. et al. (2020). Introduction to plithogenic hypersoft subgroup. Neutrosophic Sets and Systems, 33, 208–233. DOI 10.5281/zenodo.3782897. [Google Scholar] [CrossRef]
14. Wang, H., Smarandache, F., Zhang, Y., Sunderraman, R. (2010). Single valued neutrosophic sets. Multispace Multistructure, 4, 410–413. [Google Scholar]
15. Wang, H., Smarandache, F., Zhang, Y., Sunderraman, R. (2005). Interval neutrosophic sets and logic: Theory and applications in computing. Infinite Study, Hexis. [Google Scholar]
16. Wang, J., Li, X. (2015). TODIM method with multi-valued neutrosophic sets. Control and Decision, 30, 1139–1142. DOI 10.13195/j.kzyjc.2014.0467. [Google Scholar] [CrossRef]
17. Gomes, L., Lima, M. (1991). TODIM: Basic and application to multicriteria ranking of projects with environmental impacts. Foundations of Computing and Decision Sciences, 16, 113–127. [Google Scholar]
18. Hwang, C. L., Yoon, K. (1994). Multiple attribute decision making: Methods and applications. New York, NY: Springer. [Google Scholar]
19. Opricovic, S. (1998). Multicriteria optimization of civil engineering systes. Faculty of Civil Engineering, Belgrade. [Google Scholar]
20. Keshavarz Ghorabaee, M., Zavadskas, E. K., Olfat, L., Turskis, Z. (2015). Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica, 26, 435–451. DOI 10.15388/Informatica.2015.57. [Google Scholar] [CrossRef]
21. Brans, J. P., Vincke, P. H. (1985). Note---A preference ranking organisation method. Management Science, 31(6), 647–656. DOI 10.1287/mnsc.31.6.647. [Google Scholar] [CrossRef]
22. Brauers, W., Zavadskas, E. K. (2010). Project management by multimoora as an instrument for transition economies. Ukio Technologinis Ir Ekonominis Vystymas, 16, 5–24. DOI 10.3846/tede.2010.01. [Google Scholar] [CrossRef]
23. Fan, Z., Zhang, X., Chen, F., Liu, Y. (2013). Extended TODIM method for hybrid multiple attribute decision making problems. Knowledge-Based Systems, 42, 40–48. DOI 10.1016/j.knosys.2012.12.014. [Google Scholar] [CrossRef]
24. Ömür, T., Gökhan, A. (2015). A fuzzy TODIM approach for the supplier selection problem. International Journal of Computational Intelligence Systems, 8, 317–329. DOI 10.1080/18756891.2015.1001954. [Google Scholar] [CrossRef]
25. Liu, P., Teng, F. (2015). An extended TODIM method for multiple attribute group decision making based on intuitionistic uncertain linguistic variables. Journal of Intelligent and Fuzzy Systems, 29, 701–711. DOI 10.3233/IFS-141441. [Google Scholar] [CrossRef]
26. Wang, F., Li, H. (2015). Novel method for hybrid multiple attribute decision making based on TODIM method. Journal of Systems Engineering and Electronics, 26, 1023–1031. DOI 10.1109/JSEE.2015.00111. [Google Scholar] [CrossRef]
27. Jiang, Y., Liang, X., Zhang, Y. (2015). Method of TODIM decision making for incomplete evaluations. Operations Research and Management Science, 24, 116–121. [Google Scholar]
28. Ji, P., Zhang, H., Wang, J. (2016). A projection-based TODIM method under multi-valued neutrosophic environments and its application in personnel selection. Neural Computing and Applications, 29, 221–234. DOI 10.1007/s00521-016-2436-z. [Google Scholar] [CrossRef]
29. Wang, X., Dang, Y. (2016). Multiple attribute decision-making model with interval grey number based on improved TODIM method. Control and Decision, 31, 261–266. DOI 10.13195/j.kzyjc.2014.1419. [Google Scholar] [CrossRef]
30. Wang, N., Zhang, H. (2017). Probability multivalued linguistic neutrosophic sets for multi-criteria group decision-making. International Journal for Uncertainty Quantication, 7, 207–228. DOI 10.1615/Int.J.UncertaintyQuantification.2017019632. [Google Scholar] [CrossRef]
31. Xu, D., Wei, C., Wei, G. (2017). TODIM method for single-valued neutrosophic multiple attribute decision making. Information, 8, 125–143. DOI 10.3390/info8040125. [Google Scholar] [CrossRef]
32. Xu, D., Hong, Y., Qiao, H. (2018). Multiple attribute decision making based on neutrosophic sets in venture capital. Engineering Letters, 26, 441–446. [Google Scholar]
33. Mao, X., Shang, N., Zhnag, R., Wu, M. (2018). TODIM method based on probabilistic linguistic term sets and Its application in enterprise performance evaluation of strategic emerging industries. Operations Research and Fuzziology, 8, 151–160. DOI 10.12677/ORF.2018.84019. [Google Scholar] [CrossRef]
34. Zhou, H., Wang, J., Zhang, H. (2018). Multi-criteria decision-making approaches based on distance measures for linguistic hesitant fuzzy sets. Journal of the Operational Research Society, 69, 661–675. DOI 10.1080/01605682.2017.1400780. [Google Scholar] [CrossRef]
35. Chen, Y., Yue, X., Liu, Y., Zhang, Z., Sun, D. (2019). Probabilistic uncertain linguistic decision-making for considering the behavior of decision makers. Mathematics in Practice and Theory, 49, 152–161. [Google Scholar]
36. Rıdvan, Ş., Muhammed, Y. (2014). A multi-criteria neutrosophic group decision making metod based TOPSIS for supplier selection. Computer Science, 197, 231–235. DOI 10.5281/zenodo.23068. [Google Scholar] [CrossRef]
37. Ye, J. (2015). An extended TOPSIS method for multiple attribute group decision making based on single valued neutrosophic linguistic numbers. Journal of Intelligent and Fuzzy Systems, 28, 247–255. DOI 10.3233/IFS-141295. [Google Scholar] [CrossRef]
38. Tian, Z., Zhang, H., Wang, J., Wang, J., Chen, X. (2016). Multi-criteria decision-making method based on a cross-entropy with interval neutrosophic sets. International Journal of Systems Science, 47, 3598–3608. DOI 10.1080/00207721.2015.1102359. [Google Scholar] [CrossRef]
39. Liu, P., Liu, X., Xu, L. (2016). The TOPSIS method for multiple attribute group decision making with interval neutrosophic number based on cloud model. Review of Economy and Management, 3, 73–78. DOI 10.13962/j.cnki.37-1486/f.2016.03.008. [Google Scholar] [CrossRef]
40. Biswas, P., Pramanik, S., Giri, B. (2016). TOPSIS method for multi-attribute group decision making under single-valued neutrosophic environment. Neural Computing and Applications, 27, 727–737. DOI 10.1007/s00521-015-1891-2. [Google Scholar] [CrossRef]
41. Liu, D., Chen, X., Peng, D. (2018). Cosine distance measure between neutrosophic hesitant fuzzy linguistic sets and its application in multiple criteria decision making. Symmetry, 10, 602–620. DOI 10.3390/sym10110602. [Google Scholar] [CrossRef]
42. Giri, B., Molla, M., Biswas, P. (2018). TOPSIS method for MADM based on interval trapezoidal neutrosophic number. Neutrosophic Sets and Systems, 22, 151–167. [Google Scholar]
43. Chai, Q., Li, P., Di, R., Zhang, Y. (2018). TOPSIS method for single-valued neutrosophic sets. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 32, 262–265. [Google Scholar]
44. Tan, C., Zhi, S. (2018). TOPSIS method with intuitionistic hesitant fuzzy sets. Operations Research and Management Science, 27, 66–73. [Google Scholar]
45. Nguyen, T., Luu, Q., Le, H., Nguyen, D., Alid, M. et al. (2019). Dynamic interval valued neutrosophic set: Modeling decision making in dynamic environments. Computers in Industry, 108, 45–52. DOI 10.1016/j.compind.2019.02.009. [Google Scholar] [CrossRef]
46. Pei, Z., Liu, J., Hao, F., Zhou, B. (2019). FLM-Topsis: The fuzzy linguistic multiset TOPSIS method and its application in linguistic decision makings. Information Fusion, 45, 266–281. DOI 10.1016/j.inffus.2018.01.013. [Google Scholar] [CrossRef]
47. Elhassouny, A., Smarandache, F. (2019). Neutrosophic modifications of simplified TOPSIS for imperfect information (NS-TOPSIS). Neutrosophic Sets and Systems, 24, 100–113. [Google Scholar]
48. Ji, P., Zhang, H., Wang, J. (2017). Fuzzy decision-making framework for treatment selection based on the combined QUALIFLEX-TODIM method. International Journal of Systems Science, 48, 3072–3086. DOI 10.1080/00207721.2017.1365968. [Google Scholar] [CrossRef]
49. Yang, W., Pang, Y. (2018a). New multiple attribute decision making method based on DEMATEL and TOPSIS for multi-valued interval neutrosophic sets. Symmetry, 10, 115–131. DOI 10.3390/sym10040115. [Google Scholar] [CrossRef]
50. Yang, W., Pang, Y. (2018b). New multi-valued neutrosophic multiple attribute decision making method based on DEMATEL and TOPSIS. Fuzzy Systems and Mathematics, 32, 136–143. DOI 10.3390/sym10040115. [Google Scholar] [CrossRef]
51. Liu, H. C., Wang, L. E., Li, Z., Hu, Y. P. (2019). Improving risk evaluation in FMEA with cloud model and hierarchical TOPSIS method. IEEE Transactions on Fuzzy Systems, 27, 84–95. DOI 10.1109/TFUZZ.2018.2861719. [Google Scholar] [CrossRef]
52. Ye, J. (2014). Multiple-attribute decision-making method under a single-valued neutrosophic hesitant fuzzy environment. Journal of Intelligent Systems, 24, 23–36. DOI 10.1515/jisys-2014-0001. [Google Scholar] [CrossRef]
53. Liu, P., Zhang, L., Liu, X., Wang, P. (2016). Multi-valued neutrosophic number Bonferroni mean operators with their applications in multiple attribute group decision making. International Journal of Information Technology & Decision Making, 15, 1–30. DOI 10.1142/S0219622016500346. [Google Scholar] [CrossRef]
54. Liu, P., Zhang, L. (2017). An extended multiple criteria decision making method based on neutrosophic hesitant fuzzy information. Journal of Intelligent & Fuzzy Systems, 32, 4403–4413. DOI 10.3233/JIFS-16136. [Google Scholar] [CrossRef]
55. Giri, B. C., Molla, M. U., Biswas, P. (2020). TOPSIS method for neutrosophic hesitant fuzzy multi-attribute decision making. Informatica, 31, 35–63. DOI 10.15388/20-INFOR392. [Google Scholar] [CrossRef]
56. Şahin, R. (2015). Distance and similarity measures for multiple attribute decision making with single-valued neutrosophic hesitant fuzzy information. New Trends in Neutrosophic Theory and Applications, 35–54. [Google Scholar]
57. Şahin, R., Liu, P. D. (2017). Correlation coefficient of single-valued neutrosophic hesitant fuzzy sets and its applications in decision making. Neural Computing & Applications, 28, 1–9. DOI 10.1007/s00521-015-2163-x. [Google Scholar] [CrossRef]
58. Li, X., Zhang, X. (2018). Single-valued neutrosophic hesitant fuzzy choquet aggregation operators for multi-attribute decision making. Symmetry, 10, 50. DOI 10.3390/sym10020050. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |