Uncertainty Analysis of Seepage-Induced Consolidation in a Fractured Porous Medium

Guo, Lingai; Fahs, Marwan; Hoteit, Hussein; Gao, Rui; Shao, Qian

doi:10.32604/cmes.2021.016619

1School of Civil Engineering, Wuhan University, Wuhan, 430072, China
2Institut Terre et Environnement de Strasbourg, Université de Strasbourg, CNRS, ENGEES, UMR 7063, Strasbourg, France
3Physical Science and Engineering Division, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia
*Corresponding Authors: Rui Gao. Email: gaorui@whu.edu.cn; Qian Shao. Email: qian.shao@whu.edu.cn
Received: 12 March 2021; Accepted: 23 June 2021

Abstract: Numerical modeling of seepage-induced consolidation process usually encounters significant uncertainty in the properties of geotechnical materials. Assessing the effect of uncertain parameters on the performance variability of the seepage consolidation model is of critical importance to the simulation and tests of this process. To this end, the uncertainty and sensitivity analyses are performed on a seepage consolidation model in a fractured porous medium using the Bayesian sparse polynomial chaos expansion (SPCE) method. Five uncertain parameters including Young’s modulus, Poisson’s ratio, and the permeability of the porous matrix, the permeability within the fracture, and Biot’s constant are studied. Bayesian SPCE models for displacement, flow velocity magnitude, and fluid pressure at several reference points are constructed to represent the input-output relationship of the numerical model. Based on these SPCE models, the total and first-order Sobol’ indices are computed to quantify the contribution of each uncertain input parameter to the uncertainty of model responses. The results show that at different locations of the porous domain, the uncertain parameters show different effects on the output quantities. At the beginning of the seepage consolidation process, the hydraulic parameters make major contributions to the uncertainty of the model responses. As the process progresses, the effect of hydraulic parameters decreases and is gradually surpassed by the mechanical parameters. This work demonstrates the feasibility to apply Bayesian SPCE approach to the uncertainty and sensitivity analyses of seepage-induced consolidation problems and provides guidelines to the numerical modelling and experimental testing of such problems.

Keywords: Fractured porous media; sensitivity analysis; polynomial chaos expansions; poroelasticity

Seepage in porous media is a common phenomenon in civil engineering that provides both advantages and disadvantages. On one hand, land subsidence resulting from the seepage process is a critical problem that may induce foundation deformation and differential settlement, and can even damage the surface buildings [1–3]. On the other hand, soil consolidation induced by seepage can improve the compressive strength and bearing capacity of the building foundation [4–6]. During the compaction of a saturated porous medium, the seepage of fluid and the consolidation of solid happen simultaneously until the pore pressure dissipates and the effective stress of porous matrix balances with the external load. In this process, the fluid-solid interaction plays an important role and makes the problem difficult to be analyzed. Moreover, the existence of fractures and weak intercalations, which brings about the change of local flow distribution and deformation in the porous medium, makes the problem even more complex [7,8].

For decades, the seepage-induced consolidation of porous media has been extensively studied [9–13]. The one-dimensional consolidation theory was firstly established by Terzaghi [14], which has been widely applied to the modeling and simulation of land subsidence. Then Biot [15] proposed the generalized three-dimensional consolidation theory based on Terzaghi’s work, and extended the theory to anisotropic and nonlinear porous materials [16,17]. Biot’s constant αB was introduced as a new physical constant to capture the influence of fluid pressure on the solid deformation. Other than saturated porous media, a one-dimensional consolidation theory for unsaturated soil was presented by Fredlund et al. [18]. The expression of αB was given in a different manner by Zienkiewicz [19], and the basic formulation describing both static and dynamic behaviors of porous media was obtained. With the development of numerical techniques and computational methods, numerical modeling has been extensively used to study the seepage consolidation process and to predict the fluid flow and deformation in porous media during this process [20–22]. In the simulation, the fluid is usually assumed to flow through the porous skeleton according to Darcy’s law. The solid deformation is modeled using the mechanical equilibrium equation with consideration of poroelasticity, which counts for the effect of fluid flow on solid deformation within a porous medium. Meanwhile, the influence of solid deformation on the fluid flow is taken into account by including the porosity change in governing equations. This fluid-solid interaction during seepage consolidation process can be simulated accurately by solving these governing equations using appropriate numerical methods in the premise that all the model parameters are predetermined by experiments, which is a difficult task in real geotechnical applications as the material properties are typically heterogeneous and anisotropic. Therefore, the numerical simulation of seepage-induced consolidation in porous media exhibits significant uncertainty resulting from the uncertain physical parameters [23,24].

Sensitivity analysis (SA) is a method that measures how the uncertainty of the model solution can be apportioned to the uncertainty of model parameters, and determines the most influential parameters [25]. To understand the impact of uncertain parameters on the fluid flow and solid deformation in porous media, SA has been increasingly applied to geotechnical models. Morris’ method was used by Jin et al. [24] and Chen et al. [26] to perform SA on the numerical model based on the Boit’s consolidation theory and the nonlinear rheological theory to study the influence of model parameters on land subsidence and ground fissures. Guo et al. [27] developed a three-dimensional hydraulic-thermal model of the Guide Basin, and assessed the uncertainty of the model output that originates from 9 uncertain physical parameters in this model. The Monte Carlo method was used by Li et al. [28] to perform uncertainty and sensitivity analyses so as to analyze the stability of the Bian Jia Gou tailings pond under flooding conditions. Soueid et al. [29] established a stochastic numerical framework for inverting self-potential data based on the Markov chains Monte Carlo method to localize seeps in dams and characterize their permeability and Darcy velocity. Recently, Liu et al. [30] performed a SA on the numerical model of layered periodic foundations based on the Gauss–Lobatto integration, and showed better convergence of this method than the Monte Carlo-based methods. Although some studies have been found in the literature to apply SA to geotechnical models, to date, there are only few SA studies regarding the seepage consolidation process in fractured porous media [23,31].

The most commonly used techniques to perform SA on mathematical models include the Morris’ method, Monte Carlo-based methods, sparse polynomial chaos expansion-based methods. Polynomial chaos expansion has been demonstrated to be efficient and robust for the analyses of uncertainty and sensitivity on the computer models in engineering. In this work, we use a new algorithm proposed by Shao et al. [32] to perform SA and assess uncertainty on the seepage consolidation model in fractured porous media. This algorithm constructs sparse polynomial chaos expansion (SPCE), representing the input-output relation based on the Bayesian model averaging. This approach has been proven to be efficient and accurate in several engineering applications [33–36]. Once constructing the SPCE of the original numerical model, the Variance-based Sobol’ indices, which measure the impact of input uncertain parameters on the model output, are easy to be calculated analytically from SPCE. This approach not only quantitatively assesses the impact of each uncertain input parameter, but also captures its interaction with other parameters on the model output. The same physical model, as shown in literature [20], is adopted to simulate the seepage consolidation in fractured porous media, where the mechanical and hydraulic properties of the porous material are assumed isotropic. The physical parameters characterizing the porous medium such as the permeability, Young’s modulus, Poisson’s ratio, and Biot’s constant are considered as uncertain input parameters. The fluid pressure, velocity, and deformation of the porous matrix are the model responses of interest. Through this study, the critical parameters that have significant influence on the fluid flow and solid deformation are determined and their effects are quantified by Sobol’ indices. The results are expected to identify the dominant parameters on the seepage consolidation process in fractured porous media, and to provide a guideline to the modeling and experiments in geotechnical engineering applications.

This paper is organized as follows. Section 2 describes the problem formulation of the seepage consolidation in fractured porous media. Section 3 briefly introduces the SPCE approach and Sobol’ indices. Section 4 discusses the SA results for the seepage consolidation model in a fractured porous medium. Finally, conclusions are given in Section 5.

The system under consideration is a two-dimensional domain shown in Fig. 1, which is a typical example and widely used to study the seepage consolidation [20,37,38]. In this domain, a quadrangle enclosure of W = 10 m and H = 16 m is filled by a saturated heterogeneous porous medium. A fracture of L = 8 m locates in the center of the domain with an inclination of θ = 45° and the fracture thickness is 0.05 m. The domain is assumed to be sealed on the right, left, and bottom boundaries, while the top boundary is allowed to drain freely. A uniformly distributed mechanical load of 10 kN/m2 is applied to the top of the domain and kept constant throughout the seepage consolidation process. The bottom boundary of the domain is fixed, that is, no displacement is allowed on this boundary. On the left and right boundaries, the horizontal displacement is prescribed to be 0, and the fracture is assumed traction free. The plane strain condition is considered for the solid mechanics. The properties of the fluid and the porous medium are assumed to be constant during the consolidation process.

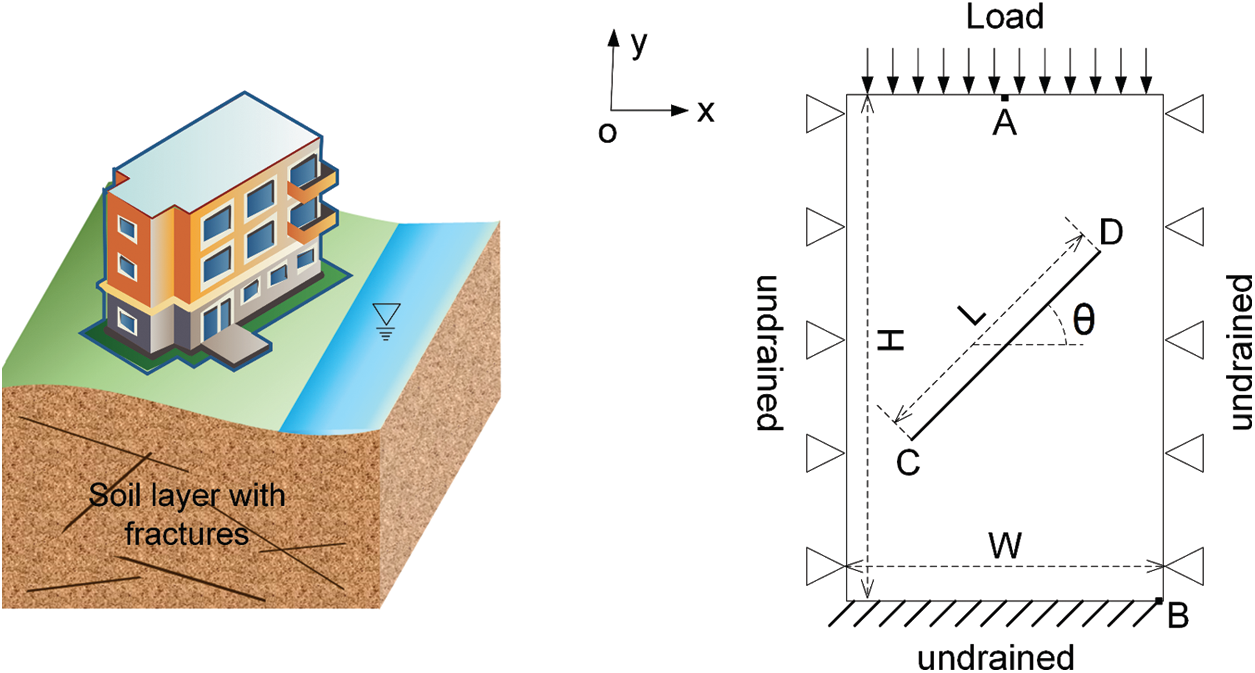
Figure 1: Schematic diagram of the seepage consolidation model in a fractured porous medium under a mechanical load

Darcy’s law and the continuity equation are used to describe the fluid flow in the fractured porous media:

where, k is the permeability of the porous medium, p is the fluid pressure, q is the Darcy’s velocity, ρ is the fluid density, Qs is the source or sink term, and ϕ is the porosity of the medium. In the deformable porous media, the porosity ϕ is a function of the fluid pressure and the deformation of porous matrix [39]:

where αB is Biot’s poroelasticity constant, ϕ0 is the initial porosity of the undeformed porous media, u is the displacement vector, and Sp=(1−αB)(αB−ϕ0)Kd with Kd=E3(1−2ν) representing the effective bulk modulus of the porous media. Herein E and ν denote effective Young’s modulus and Poisson’s ratio of the porous matrix, respectively. Substituting Eq. (3) into Eq. (2) and eliminating ρ, the continuity equation takes the form as follows:

where, εv=∇⋅u is the volumetric strain determined by the displacement vector, and Sρ=ϕχf with χf=1ρ∂ρ∂p representing the fluid compressibility. Combining Darcy’s law, Eq. (4) can be written as:

To calculate the deformation and stress of the porous matrix during the seepage consolidation, the quasi-static mechanical equilibrium equation is used:

where, f is the body force, and σ(u,pm) is the total stress tensor depending on the displacement vector u and the pore pressure pm arising from the fluid flow in porous media. The constitutive relation between the elastic stress and strain in porous media is described by the Biot’s poroelasticity theory:

where, D is the stiffness tensor defined by effective Young’s modulus and Poisson’s ratio of the porous media, ε=(∇u+∇Tu)/2 is the strain tensor related to the displacement tensor, and αB is Biot’s poroelasticity constant defined by αB=(KS−KT)/KS, with KT and KS representing the bulk modulus of soil sample and solid grains, respectively [19,40].

Eqs. (5) and (6) are to be solved simultaneously over the domain, and the fully coupled solution of displacement and pressure are calculated in the numerical model at each time step. The model parameters to be studied, i.e., Young’s modulus (E), Poisson’s ratio (v), the permeability of the porous matrix (k1), the permeability within the fracture (k2), and Biot’s constant (αB), are effective properties of the porous matrix and the fracture. Notably, although the porous media is deformable, we do not consider the effect of porosity variation on the effective properties of the porous media.

Sensitivity analysis is an efficient approach to quantify the contribution of the uncertain input parameters to the variability of the output results. The Bayesian SPCE approach proposed by Shao et al. [32] is employed to perform SA on the seepage consolidation in the fractured porous media. To this end, a polynomial chaos expansion representing the input-output relation of the physics-based model is constructed as follows:

where, x=(x1,x2,…,xn) is the vector of normalized input parameters, which are assumed independent on each other and uniformly distributed over the n-dimensional unit hypercube Kn, the scalar y is the model output of interest, ψb(x) is a multidimensional polynomial given by the tensor product of univariate standardized shifted-Legendre polynomials, ab’s are the polynomial chaos coefficients to be determined, b=b1…bn(bi∈N,1≤i≤n) is a n-dimensional index, and bi represents the degree of the univariate polynomial ψbi(xi). To make the problem computationally tractable, a truncation is performed to retain a finite number of polynomial terms:

where, d is the truncation order of the polynomial chaos expansion and Ad,n is the subset of Nn such that Ad,n={b∈Nn:|b|=∑i=1nbi≤d}.

To compute the polynomial chaos coefficients in Eq. (9), the regression-based methods are usually adopted [41]. However, when a large number of terms exist in the polynomial chaos expansion, the regression-based methods encounter computational problems such as overfitting and curse of dimensionality. To avoid such problems, a sparse representation of the polynomial chaos expansion model is constructed based on the Bayesian model averaging:

where, A is the subset of Ad,n and if the condition card(A)≪card(Ad,n) is satisfied, the polynomial chaos expansion is considered as sparse. The sparsity of the polynomial chaos representation is realized by retaining only the terms that make significant contributions to the model response of interest. The Kashyap information criterion, which considers the compromise between the model simplicity and fitting goodness, is deployed to conduct the quantitative selection of the SPCEs.

Once we obtain the SPCE model which represents the input-output relation of the physical model, the variance-based Sobol’ indices of each input parameter can be easily derived. The total variance of the output variable is calculated from the polynomial chaos coefficients ab as follows:

The sth-order partial variance of the output due to the cooperation of the uncertain input parameters {xi1,…,xis} can be estimated by:

The sth-order Sobol’ indices are defined by the ratio of partial variance to the total variance taking the form of Si1…is=Vi1…is/V. Specifically, the first-order and total order Sobol’ indices are respectively given by:

where, the first-order Sobol’ indices Si evaluate the variance of model response due to xi alone and the total order Sobol’ indices SiT summarize the overall contribution of the input variable xi by taking into account its marginal and interactive effects. Noting that all Sobol’ indices are ranging from 0 to 1. If the Sobol’ index of an input parameter is approaching 0, it indicates that this parameter has negligible influence on the uncertainty of model output. Otherwise, if the Sobol’ index of an input parameter is close to 1, this parameter is deemed having an important contribution to the output uncertainty. Besides, the marginal effect of the input parameter xi is calculated by:

where ∫Kn−1dx∼i computes the integral of a function over all variables except xi.

To evaluate the influence of uncertain parameters on the seepage-induced consolidation process in a fractured porous medium, a numerical model is developed using COMSOL Multiphysics and verified by comparing the solution against the results in the literature. The problem shown in Fig. 1 is modelled using the poroelasticity multiphysics module, which couples the fluid flow and solid mechanics in porous media. The fracture is considered as an extremely narrow zone with weak mechanical properties (e.g., very small Young’s modulus comparing to the porous matrix) and a large value of permeability. A mesh containing 4608 triangular elements and 2863 nodes is used to discretize the pressure and displacement fields simultaneously. The parameters adopted are listed in Tab. 1, which are the same as in Lamb et al. [20] for the purpose of comparison and verification. A time-dependent study is performed, and the simulated displacement and pressure fields from 1 day to 100 days in the fractured porous domain are shown in Fig. 2. To verify these results, the vertical displacement and pressure values at the reference points A and B (see Fig. 1), respectively, are extracted at different time steps during the seepage consolidation process. The evolution of the vertical displacement at point A and the pressure at point B in 100 days are plotted and compared with the results in Lamb et al. [20], and good agreements are found in Fig. 2. Notably, the vertical displacement at point A is negative in our study, while it is positive in Lamb et al. [20], as different coordinate systems are used. Hence, the absolute values of vertical displacement are compared in Fig. 2b.

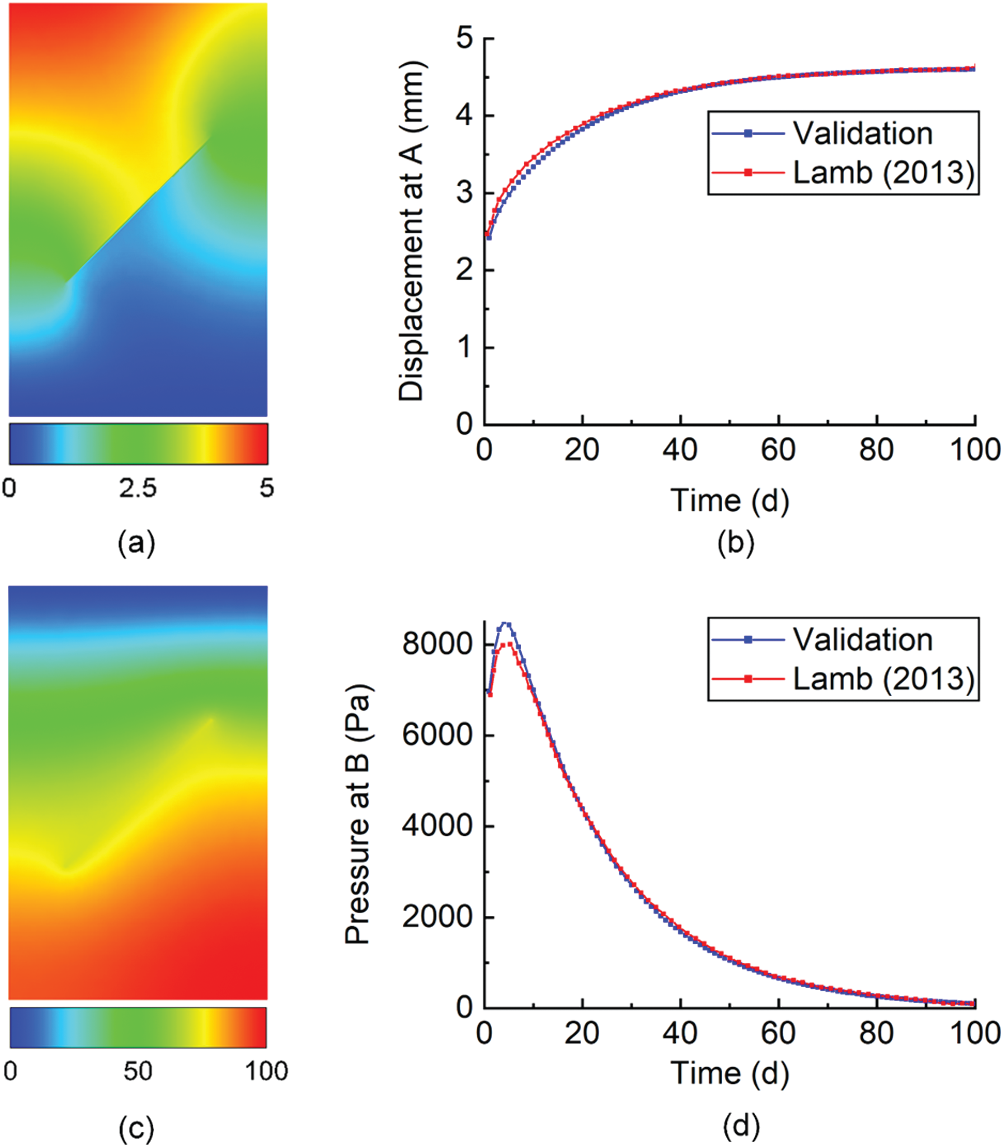
Figure 2: Verification of the seepage consolidation model. (a) Displacement field after 100 days (mm) (b) Surface displacement change during 100 days (c) Pressure field after 100 days (Pa) (d) Pressure change during 100 days

Subsequently, this verified numerical model is used to generate sample data for the uncertainty analysis of seepage-induced consolidation in a fractured porous medium. To this end, 5 uncertain input parameters are analyzed, including Young’s modulus (E), Poisson’s ratio (v), the permeability of the porous matrix (k1), the permeability within the fracture (k2), and Biot’s constant (αB). These parameters are assumed to be statistically independent with each other and varying within the uncertain ranges as listed in the Tab. 2. To evaluate the effect of these uncertain parameters, several quantities of interest are analyzed using the aforementioned numerical model. The flow velocity magnitude, the pressure, and the vertical displacement within the domain are considered to characterize the fluid flow and deformation of the porous media during the seepage consolidation. Noting that in some cases, the seepage consolidation progresses very slowly, and it can be time-consuming to obtain a steady-state solution using the numerical model. Thus, the seepage consolidation in a duration of 100 days is of special interest in this study.

In order to perform uncertainty and sensitivity analyses on the seepage consolidation model, the Bayesian approach is used to build SPCE models that describe the relationship between the input parameters and the output responses of the numerical model. For this purpose, several output quantities are assessed to capture the characteristics of the model performance, including the vertical displacement (uA) and the flow velocity magnitude (QA) at point A and the pressure (PB) at point B (Fig. 1). These quantities are typical for the characterization of the seepage consolidation in the considered porous domain. In this problem, the seepage and consolidation are induced by a mechanical load applied on the top surface, which is free to flow, and thus, the vertical displacement and flow velocity on the top surface (point A) is of interest. The pressure at point A is a constant equal to 0 during the consolidation process, but the pressure at the bottom boundary (point B) changes significantly, which is thereby selected as the model response of interest.

The flow chart of performing uncertainty and sensitivity analyses on the seepage consolidation model using the Bayesian SPCE approach is shown in Fig. 3. To train the Bayesian SPCE models, we first randomly generate 210 data for each input parameter (i.e., E, v, k1, k2, and αB) that is uniformly distributed in the uncertain range (Tab. 2), and thus we obtain a dataset containing 210 × 5 values for input parameters. This input dataset is then used to model the seepage consolidation process in COMSOL Multiphysics, from which the output metrics including the vertical displacement, the magnitude of flow velocity, and the pressure at reference points at 100 days for each calculation are exported (Fig. 3). As a result, a dataset containing 210 × 3 output metrics is obtained corresponding to the 210 × 5 uncertain input parameters. This combined dataset (including the input parameters and output metrics) of sample size 210 × 8 is then randomly split into two datasets, i.e., a training dataset of sample size 29 × 8 and a validation dataset of the same sample size. Using the training dataset, three SPCE models representing the relationship between the output metrics and the input parameters are constructed respectively in the Bayesian framework, e.g., uA≅MAu(E,ν,k1,k2,αB), QA≅MAQ(E,ν,k1,k2,αB), and PB≅MAP(E,ν,k1,k2,αB). The validation dataset is deployed to check the validity and robustness of the constructed Bayesian SPCE models.

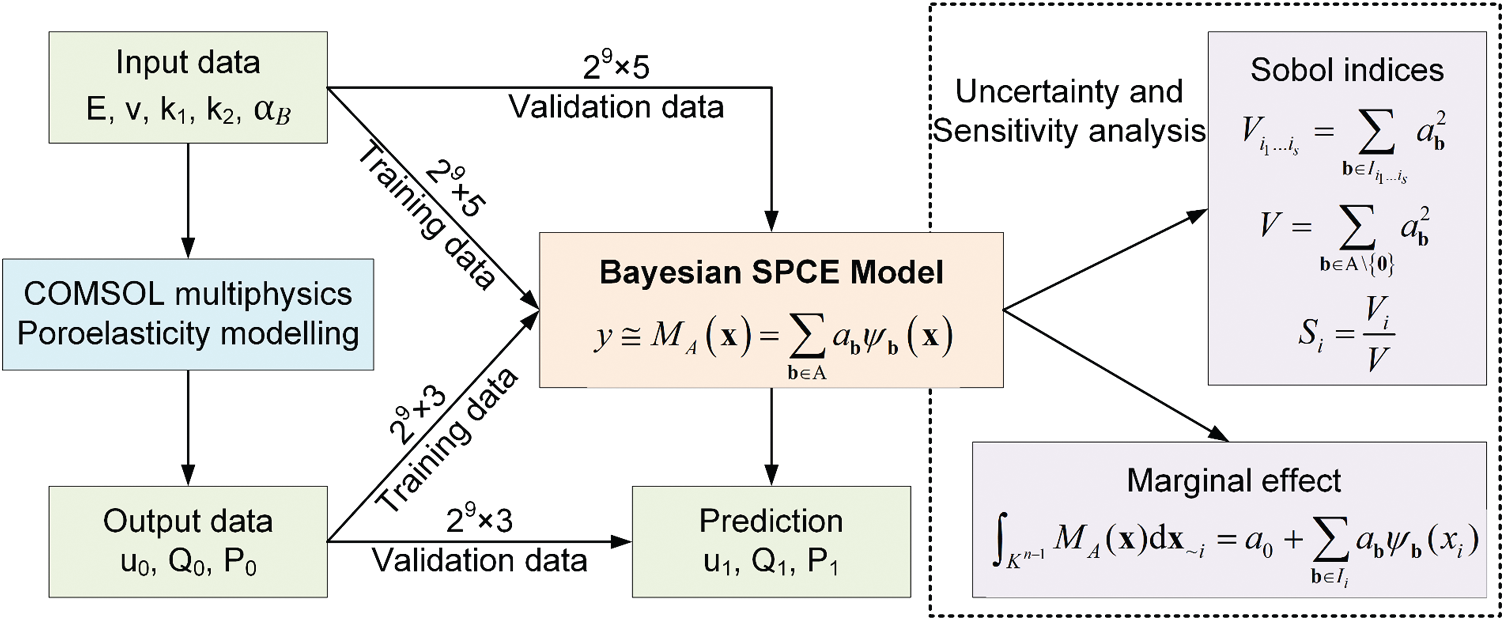
Figure 3: The flow chart of performing uncertainty and sensitivity analyses on the seepage consolidation model using Bayesian SPCE approach

Fig. 4 shows the comparison between the Bayesian SPCE-predicted output quantities and the numerically calculated data from both the training and validation datasets. The calculated vertical displacement and the magnitude of flow velocity at point A varies from less than −30 to −5 mm and from 0 to 6.0 × 10−10 m/s, respectively, due to the uncertainty of input parameters. Similarly, the calculated pressure at point B exhibits a large uncertainty and increases from 0 to approximately 1.0 × 104 Pa with the variation of input parameters. For the displacement, velocity, and pressure, excellent agreements are found between the numerically calculated results and the Bayesian SPCE-predicted results on both training and validation datasets. Specifically, the coefficients of determination (R2), which measure the ability of a statistical model to fit or explain the observed data, on the training datasets of displacement, velocity, and pressure are larger than 0.99. The values of R2 on the validation datasets (>0.98) are slightly smaller than those on the training datasets (Fig. 4). For the three output metrics, the Bayesian SPCE model performs the best on the displacement of point A, exhibiting R2 values of 0.9999 and 0.9998 for training and validation datasets, respectively. The comparative performances of the constructed Bayesian SPCE models on both the training and validation datasets show their good ability to well reproduce the numerical model responses and indicate their sufficient accuracy to calculate reliable sensitivity indices for assessing the effect of each uncertain input parameter.

Figure 4: Comparison of model outputs between the Bayesian SPCE-predicted values and model-calculated data at 100 days, including the training dataset and the validation dataset: (a) the vertical displacement at point A, (b) the magnitude of flow velocity at point A, and (c) the pressure at point B

Based on the above constructed Bayesian SPCE models, the total and first-order Sobol’ indices of each uncertain input parameter are calculated using Eqs. (11)–(14) and plotted in Fig. 5. These Sobol’ indices measure how much the uncertainty of each input parameter contributes to the uncertainty in the vertical displacement and flow velocity at point A and the pressure at point B after 100 days’ consolidation. It is observed that for each output metric, the influences of the input parameters are different. For instance, the uncertainty of the vertical displacement at point A is mainly attributed to the uncertainty in the Young’s modulus of the porous matrix, while that of the pressure at point B is dominated by the uncertainty in the permeability of the porous matrix. More detailed discussions for each output metric are as follows.

Figure 5: The total and first-order Sobol’ indices of the uncertain input parameters on the vertical displacement and flow velocity magnitude at point A and the pressure at point B after 100 days. (a) Vertical displacement (b) Flow velocity magnitude (c) Pressure

The variation of the displacement at point A arises mainly from the uncertainty in Young’s modulus of the porous matrix, where the total and first-order Sobol’ indices of E are larger than 0.85 (Fig. 5a). The Poisson’s ratio and the permeability of the porous matrix show slight influences on the vertical displacement at point A after 100 days, with Sobol’ indices smaller than 0.1. The effects of the permeability within the fracture and Biot’s constant are negligible. Notably, the values of total and first-order Sobol’ indices for each parameter have little difference, indicating that the interaction effect between different input parameters is not significant. Furthermore, the marginal effect describing the individual influence of each uncertain input parameter on the vertical displacement at point A is presented (Fig. 6). Note that the Sobol’ indices of the permeability within the fracture (k2) are 0, resulting in no marginal effect of k2. The absolute values of the vertical displacement at point A decreases monotonously with the increase of v, E, and αB, and increases with the increase of k1 (Fig. 6). The increase of Poisson’s ratio means that the compressibility of the porous medium becomes smaller, leading to smaller displacements under a compressive load. The increase of Young’s modulus means that the porous medium is more resistant to deformation under a certain mechanical load, which yields a smaller absolute value of the vertical displacement. The increase of permeability in the porous matrix means that the fluid is easier to be discharged out of the domain, resulting in a decrease of pore pressure within the porous media, which in turn makes the domain easier to deform. Typically, the permeability only shows effect on the settlement rate, but has no impact on the final deformation of porous media when the seepage consolidation process reaches steady state. Therefore, the influence of permeability observed on displacement in Fig. 6 is due to that we consider the vertical displacement after 100 days and the steady state may not be achieved yet.

Figure 6: Marginal effect of each uncertain input parameter on the vertical displacement of point A at 100 days. (a) Effect of Poisson’s ratio (b) Effect of Young’s modulus (c) Effect of matrix permeability (d) Effect of Biot’s constant

Furthermore, the uncertainty of the vertical displacement in the entire domain is analyzed using the Bayesian SPCE approach. To this end, the vertical displacement after 100 days on each node of the domain is considered as an output metric and exported from the COMSOL Multiphysics. For each output metric, a Bayesian SPCE model is trained, eventually resulting in 2863 Bayesian SPCE models, and based on which the Sobol’ indices are calculated. Figs. 7a– 7c show respectively the spatial distribution of the mean, variance, and standard deviation of the vertical displacement resulting from the uncertain input parameters. The mean values of the vertical displacement range between −14 and 0 mm in the porous domain. Due to the fracture, a discontinuity is observed in the displacement-related distributions, and the absolute values of the vertical displacement above the fracture are significantly larger than that below the fracture. Also, the discrepancy of the vertical displacement from the mean value caused by the uncertain input parameters primarily happens in the upper part above the fracture. Figs. 7d–7h show the spatial maps of sensitivity of the vertical displacement to each uncertain input parameter, i.e., Poisson’s ratio, Young’s modulus, the permeability of the porous matrix, the permeability within the fracture, and Biot’s constant, where the total order Sobol’ indices involving the individual effect of each uncertain input parameter and its interaction effects with the other parameters are shown. The influence of input parameters on the vertical displacement depends on the location lying in the domain. For instance, Poisson’s ratio shows negligible influence on the vertical displacement above the fracture (total order Sobol’ indices of approximately 0), while has significant effect on that below the fracture (Fig. 7d). Notably, Young’s modulus makes the major contribution to the uncertainty of the vertical displacement in the zone lying above the fracture, where the mean value and the standard deviation of the displacement are relatively large (Figs. 7a–7c and 7e). In the zone lying below the fracture, although the complementary effect of Poisson’s ratio, Young’s modulus, the permeability of the porous matrix, and Biot’s constant on the uncertainty of vertical displacement seems noticeable, the mean, variance, and standard deviation values of the vertical displacement are almost zero. Therefore, the effect of all considered parameters on the vertical displacement below the fracture is negligible. The permeability within the fracture shows little influence on the vertical displacement distribution in the entire porous domain.

Figure 7: Spatial distribution of the (a) mean, (b) variance, and (c) standard deviation of the vertical displacement and spatial distribution of the total Sobol’ indices of (d) the Poisson’s ratio v, (e) the Young’s modulus E, (f) the permeability in porous matrix k1, (g) the permeability within fracture k2, and (h) the Biot’s constant αB on the vertical displacement at 100 days

Unlike the vertical displacement, the uncertain input parameters show comparable Sobol’ indices on the velocity magnitude of fluid flow at point A (Fig. 5b). Young’s modulus and Poisson’s ratio are the most important parameters that contribute to the uncertainty in the flow velocity magnitude at point A, exhibiting Sobol’ indices values of approximately 0.59 and 0.27, respectively. The permeability of the porous matrix and Biot’s constant also show considerable effects on the variation of the flow velocity. Notably, the total order Sobol’ indices of Poisson’s ratio, Young’s modulus, and permeability of porous matrix are significantly larger than the corresponding first-order Sobol’ indices, indicating that the coupling effects among them are important to the uncertainty of the flow velocity magnitude. Specifically, although the first-order sensitivity index of the permeability k1 is small, the total Sobol’ index shows a non-negligible effect of k1 on the flow velocity, which majorly originates from the coupling effect between k1 and other parameters. The marginal effects shown in Fig. 8 illustrate the univariate influence caused by each uncertain input parameter on the flow velocity magnitude at point A. Poisson’s ratio and Young’s modulus of the porous matrix show negative influences on the flow velocity magnitude (Figs. 8a and 8b). As aforementioned, the increase of the Poisson’s ratio and Young’s modulus means smaller compressibility and stronger resistance to deformation of the porous medium, respectively, both yielding a smaller deformation of the domain, which then leads to a decrease of the fluid pressure and the flow velocity magnitude. In contrast to v and E, Biot’s constant shows an almost linearly positive effect on the flow velocity magnitude (Fig. 8d). A turn point is observed in the marginal effect of k1 (Fig. 8c). When the permeability of porous matrix is small, i.e., k1 < 3 × 10−16 m2, the velocity magnitude increases with the increase of k1, while after the turn point (k1 > 3 × 10−16 m2), the velocity magnitude declines gradually with the increase of k1.

Figure 8: Marginal effect of each uncertain input parameter on the flow velocity magnitude of point A at 100 days. (a) Effect of Poisson’s ratio (b) Effect of Young’s modulus (c) Effect of matrix permeability (d) Effect of Biot’s constant

Furthermore, to analyze uncertainty in the flow velocity at the transient state during the seepage consolidation process, the total order Sobol’ indices of the uncertain input parameters for each time step during the 100 days are calculated. The flow velocity magnitude at three reference points are selected as shown in Fig. 1, including the central point of top boundary (point A) and the left and right tips of the fracture (points C and D). The evolution of the Sobol’ indices for the flow velocity at the reference points A, C, and D is shown in Fig. 9. At the beginning of the consolidation process, the permeability of the porous matrix k1 makes the dominant contribution to the uncertainty of the flow velocity at the reference points. As the seepage consolidation progresses, the influence of permeability k1 is gradually surpassed by that of Young’s modulus and Poisson’s ratio. At the reference point A, which is away from the fracture, the flow velocity is not affected by the permeability within the fracture k2. Contrarily, at reference points C and D, the permeability within the fracture shows significant effect on the flow velocity, especially at the beginning of the process. As shown in Figs. 9b and 9c, during the first 20 days, the permeability of the porous matrix and the fracture jointly make the major contribution to the uncertainty in flow velocities near the fracture. In general, the hydraulic properties (k1 and k2) have dominant effects on the fluid flow at the beginning, and the mechanical properties (E and v) show more significant effects in the long run. Additionally, the properties within the fracture show local effect on the fluid flow near the fracture, but have little influence on the overall performance of the domain.

Figure 9: The evolution of total order Sobol’ indices for flow velocity magnitude at the reference points A, C, and D in the transient regime. (a) STi for velocity at A (b) STi for velocity at C (c) STi for velocity at D

The variation of the fluid pressure at point B arises mainly from the uncertainty in the permeability of the porous matrix, which exhibits the total and first-order Sobol’ indices of approximately 0.7 (Fig. 5c). Young’s modulus and Poisson’s ratio show moderate influence on the fluid pressure at point B, while the effect of the Biot’s constant is slight. The differences between the values of total and first-order Sobol’ indices for v, E, and k1 indicate that the interaction effect exists between these input parameters. The marginal effect of Poisson’s ratio, Young’s modulus, and Biot’s constant on the fluid pressure at point B shows a similar tendency as that on fluid velocity at point A (Figs. 8 and 10). As aforementioned, the increase of the Poisson’s ratio and Young’s modulus results in a smaller deformation of the porous domain under a certain mechanical load, which in turn leads to a lower fluid pressure at point B. The permeability of the porous matrix shows a positive marginal effect on the fluid pressure within a narrow range when k1 < 5 × 10−17 m2. As the permeability increases, the pressure at point B first encounters a sharp falling and then followed by a slow declination.

Figure 10: Marginal effect of each uncertain input parameter on the pressure of point B at 100 days. (a) Effect of Poisson’s ratio (b) Effect of Young’s modulus (c) Effect of matrix permeability (d) Effect of Biot’s constant

The seepage-induced consolidation process in a fractured porous medium is modeled numerically, and the uncertainty of the model is analyzed using the Bayesian SPCE approach. To perform the uncertainty and sensitivity analyses, Bayesian SPCE models are constructed to reproduce the relationship between the input parameters (i.e., Young’s modulus, Poisson’s ratio, the permeability of the porous matrix, the permeability within the fracture, and Biot’s constant) and the output metrics (including the vertical displacement, the flow velocity magnitude, and the fluid pressure at reference points). The comparative performances of the constructed SPCE models on the training and validation datasets demonstrate their sufficient accuracy in calculating the Sobol’ indices for uncertain parameters. The uncertainties in the model output metrics are quantitatively attributed to the five uncertain input parameters by the Sobol’ indices. As a result, the following conclusions are drawn:

(1) For the settlement in the seepage consolidation process, Young’s modulus of the porous matrix E makes the major contribution to the uncertainty in the settlement near the drainage outlet. While in the region below the fracture, the settlement is extremely small (almost zero), and thus, the effect of these parameters is negligible.

(2) For the flow velocity magnitude, the hydraulic properties (k1 and k2) have dominant effects at the beginning of the seepage consolidation process, and the mechanical properties (E and v) show more significant effects in the long run. The properties within the fracture show only local effect on the fluid flow near the fracture, but have little influence on the overall performance of the domain.

(3) For the fluid pressure, both hydraulic and mechanical properties have important contributions to the uncertainty in model responses, in which the permeability of the porous matrix shows a major effect on the pressure at the bottom boundary.

This work shows feasibility and effectiveness of the Bayesian SPCE approach for performing uncertainty and sensitivity analyses on the seepage consolidation problem. The influences of uncertain input parameters on the model performance are presented and discussed, which provides guidelines to the numerical modelling and experimental testing of such problems. In this work the fracture topology is assumed to be certain. More realistic analysis would include the effect of uncertain fracture topology on model outputs, which would require an efficient numerical model as the automatic mesh updating is needed to change the fracture topology. This would be an interesting topic for further studies.

Acknowledgement: This work was supported by the National Natural Science Foundation of China (11702199).

Funding Statement: National Natural Science Foundation of China (11702199), Qian Shao. National Natural Science Foundation of China (URL: https://nsfc.gov.cn).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Xu, Y. S., Shen, S. L., Cai, Z. Y., Zhou, G. Y. (2008). The state of land subsidence and prediction approaches due to groundwater withdrawal in China. Natural Hazards, 45(1), 123–135. DOI 10.1007/s11069-007-9168-4. [Google Scholar] [CrossRef]

2. Luo, Z. J., Zeng, F. (2011). Finite element numerical simulation of land subsidence and groundwater exploitation based on visco-elastic-plastic Biot’s consolidation theory. Journal of Hydrodynamics, 23(5), 615–624. DOI 10.1016/S1001-6058(10)60157-6. [Google Scholar] [CrossRef]

3. Logan, G. A., Jones, A. T., Kennard, J. M., Ryan, G. J., Rollet, N. (2010). Australian offshore natural hydrocarbon seepage studies, a review and re-evaluation. Marine and Petroleum Geology, 27(1), 26–45. DOI 10.1016/j.marpetgeo.2009.07.002. [Google Scholar] [CrossRef]

4. Zhang, Y., Chan, D., Wang, Y. (2012). Consolidation of composite foundation improved by geosynthetic-en-cased stone columns. Geotextiles and Geomembranes, 32(4), 10–17. DOI 10.1016/j.geotexmem.2011.10.006. [Google Scholar] [CrossRef]

5. Gourvenec, S., Randolph, M. F. (2010). Consolidation beneath circular skirted foundations. International Journal of Geomechanics, 10(1), 22–29. DOI 10.1061/(ASCE)1532-3641(2010)10:1(22). [Google Scholar] [CrossRef]

6. Abusharar, S. W., Zheng, J. J., Chen, B. G. (2009). Finite element modeling of the consolidation behavior of multi-column supported road embankment. Computers and Geotechnics, 36(4), 676–685. DOI 10.1016/j.compgeo.2008.09.006. [Google Scholar] [CrossRef]

7. Kraaijeveld, F., Huyghe, J. M., Remmers, J. J. C., de Borst, R. (2013). Two-dimensional mode I crack propagation in saturated ionized porous media using partition of unity finite elements. Journal of Applied Mechanics, 80(2), 1–12. DOI 10.1115/1.4007904. [Google Scholar] [CrossRef]

8. Mei, Y., Kuznetsov, S., Goenezen, S. (2016). Reduced boundary sensitivity and improved contrast of the regularized inverse problem solution in elasticity. Journal of Applied Mechanics, 83(3), 1–10. DOI 10.1115/1.4031937. [Google Scholar] [CrossRef]

9. Sridharan, A., Prakash, K. (1999). Simplified seepage consolidation test for soft sediments. Geotechnical Testing Journal, 3, 235–244. DOI 10.1520/GTJ11114J. [Google Scholar] [CrossRef]

10. Robinson, R. G., Tan, T. S., Lee, F. H. (2003). A comparative study of suction-induced seepage consolidation vs. centrifuge consolidation. Geotechnical Testing Journal, 26(1), 92–101. DOI 10.1520/GTJ11109J. [Google Scholar] [CrossRef]

11. Berilgen, S. A., Berilgen, M. M., Ozaydin, I. K. (2006). Compression and permeability relationships in high water content clays. Applied Clay Science, 31(3), 249–261. DOI 10.1016/j.clay.2005.08.002. [Google Scholar] [CrossRef]

12. Roesyanto, Iskandar, R., Silalahi, S. A., Fadliansyah (2018). Soil settlement analysis in soft soil by using preloading system and prefabricated vertical draining runway of Kualanamu Airport. IOP Conference Series: Materials Science and Engineerin, vol. 309, pp. 12024. Sumatera Utara, Indonesia. [Google Scholar]

13. Huang, M. H., Zhao, M. H. (2020). A general analytical solution for one dimensional consolidation of unsaturated soil incorporating impeded drainage boundaries. Computers and Geotechnics, 128(3), 103801. DOI 10.1016/j.compgeo.2020.103801. [Google Scholar] [CrossRef]

14. Terzaghi, K. (1943). Theoretical soil mechanics: Theory of consolidation, pp. 265–296. DOI 10.1002/9780470172766. [Google Scholar] [CrossRef]

15. Biot, M. A. (1941). General theory of three-dimensional consolidation. Journal of Applied Physics, 12(2), 155–164. DOI 10.1063/1.1712886. [Google Scholar] [CrossRef]

16. Biot, M. A. (1955). Theory of elasticity and consolidation for a porous anisotropic solid. Journal of Applied Physics, 26(2), 182–185. DOI 10.1063/1.1721956. [Google Scholar] [CrossRef]

17. Biot, M. A. (1956). General solutions of the equation of elasticity and consolidation for a porous material. Journal of Applied Mechanics, 78, 91–96. DOI 10.1115/1.4011213. [Google Scholar] [CrossRef]

18. Fredlund, D. G., Hasan, J. U. (1979). One-dimensional consolidation theory: Unsaturated soils. Canadian Geotechnical Journal, 16(3), 521–532. DOI 10.1139/t79-058. [Google Scholar] [CrossRef]

19. Zienkiewicz, O. C. (1982). Basic formulation of static and dynamic behaviours of soil and other porous media. Applied Mathematics and Mechanics, 3(4), 457–469. DOI 10.1007/BF01908222. [Google Scholar] [CrossRef]

20. Lamb, A. R., Gorman, G. J., Elsworth, D. (2013). A fracture mapping and extended finite element scheme for coupled deformation and fluid flow in fractured porous media. International Journal for Numerical and Analytical Methods in Geomechanics, 37(17), 2916–2936. DOI 10.1002/nag.2168. [Google Scholar] [CrossRef]

21. Ma, H., Song, Y., Bu, C., Yang, Y. (2019). Symmetrized splitting operator method for dynamic consolidation problem of saturated porous semi-infinite foundation. Soil Dynamics and Earthquake Engineering, 126(11), 105803. DOI 10.1016/j.soildyn.2019.105803. [Google Scholar] [CrossRef]

22. Ochmański, M., Spacagna, R. L., Modoni, G. (2020). 3D numerical simulation of consolidation induced in soft ground by EPB technology and lining defects. Computers and Geotechnics, 128(3), 103830. DOI 10.1016/j.compgeo.2020.103830. [Google Scholar] [CrossRef]

23. Houmadi, Y., Ahmed, A., Soubra, A. H. (2012). Probabilistic analysis of a one-dimensional soil consolidation problem. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 6(1), 36–49. DOI 10.1080/17499518.2011.590090. [Google Scholar] [CrossRef]

24. Jin, W. Z., Luo, Z. J., Wu, X. H. (2016). Sensitivity analysis of related parameters in simulation of land subsidence and ground fissures caused by groundwater exploitation. Bulletin of Engineering Geology and the Environment, 75(3), 1143–1156. DOI 10.1007/s10064-016-0897-z. [Google Scholar] [CrossRef]

25. McRae, G. J., Tilden, J. W., Seinfeld, J. H. (1982). Global sensitivity analysis-a computational implementation of the Fourier amplitude sensitivity test (FAST). Computers and Chemical Engineering, 6(1), 15–25. DOI 10.1016/0098-1354(82)80003-3. [Google Scholar] [CrossRef]

26. Chen, Z., Luo, Z. (2017). Sensitivity analysis of parameters on Biot’s consolidation full coupled model. Journal of Nanchang University (Engineering & Technology), 39(4), 354–361. DOI 10.3969/j.issn.1006-0456.2017.04.009. [Google Scholar] [CrossRef]

27. Guo, L. L., Zhang, Y. B., Wang, Z. C., Zeng, J., Zhang, Y. J. et al. (2020). Parameter sensitivity analysis and optimization strategy research of enhanced geothermal system: A case study in guide Basin, Northwestern China. Renewable Energy, 153(113980), 813–831. DOI 10.1016/j.renene.2020.02.058. [Google Scholar] [CrossRef]

28. Li, T., Liu, G., Wang, C., Wang, X., Li, Y. (2020). The probability and sensitivity analysis of slope stability under seepage based on reliability theory. Geotechnical and Geological Engineering, 38(4), 3469–3479. DOI 10.1007/s10706-020-01226-4. [Google Scholar] [CrossRef]

29. Soueid Ahmed, A., Revil, A., Bolève, A., Steck, B., Vergniault, C. et al. (2020). Determination of the permeability of seepage flow paths in dams from self-potential measurements. Engineering Geology, 268(1), 105514. DOI 10.1016/j.enggeo.2020.105514. [Google Scholar] [CrossRef]

30. Liu, X., Ren, Y., Song, X., Witarto, W. (2020). A global sensitivity analysis method based on the Gauss–Lobatto integration and its application in layered periodic foundations with initial stress. Composite Structures, 244, 112297. DOI 10.1016/j.compstruct.2020.112297. [Google Scholar] [CrossRef]

31. Li, X., Zhang, H. (2010). Monte Carlo analysis of probability of one-dimensional consolidation in saturated clay soil ground. International Conference on Computer and Information Application, pp. 335–338. Tianjin, China. [Google Scholar]

32. Shao, Q., Younes, A., Fahs, M., Mara, T. A. (2017). Bayesian sparse polynomial chaos expansion for global sensitivity analysis. Computer Methods in Applied Mechanics and Engineering, 318(11), 474–496. DOI 10.1016/j.cma.2017.01.033. [Google Scholar] [CrossRef]

33. Rajabi, M. M., Fahs, M., Panjehfouladgaran, A., Ataie-Ashtiani, B., Simmons, C. T. et al. (2020). Uncertainty quantification and global sensitivity analysis of double-diffusive natural convection in a porous enclosure. International Journal of Heat and Mass Transfer, 162(6), 120291. DOI 10.1016/j.ijheatmasstransfer.2020.120291. [Google Scholar] [CrossRef]

34. Shao, Q., Gao, E., Mara, T., Hu, H., Liu, T. et al. (2020). Global sensitivity analysis of solid oxide fuel cells with Bayesian sparse polynomial chaos expansions. Applied Energy, 260(5), 114318. DOI 10.1016/j.apenergy.2019.114318. [Google Scholar] [CrossRef]

35. Koohbor, B., Fahs, M., Ataie-Ashtiani, B., Belfort, B., Simmons, C. T. et al. (2019). Uncertainty analysis for seawater intrusion in fractured coastal aquifers: Effects of fracture location, aperture, density and hydrodynamic parameters. Journal of Hydrology, 571(SP479), 159–177. DOI 10.1016/j.jhydrol.2019.01.052. [Google Scholar] [CrossRef]

36. Shao, Q., Liu, J., Huang, Q., Yang, J., Hu, H. et al. (2019). A data-driven analysis on bridging techniques for heterogeneous materials and structures. Mechanics of Advanced Materials and Structures, 28(1), 1–15. DOI 10.1080/15376494.2018.1546415. [Google Scholar] [CrossRef]

37. Liu, F., Zhao, L. Q., Liu, P. L., Luo, Z. F., Li, N. Y. et al. (2015). An extended finite element model for fluid flow in fractured porous media. Mathematical Problems in Engineering, 2015(1), 604212–604210. DOI 10.1155/2015/604212. [Google Scholar] [CrossRef]

38. Sheng, M., Li, G., Shah, S., Lamb, A. R., Bordas, S. P. A. (2015). Enriched finite elements for branching cracks in deformable porous media. Engineering Analysis with Boundary Elements, 50, 435–446. DOI 10.1016/j.enganabound.2014.09.010. [Google Scholar] [CrossRef]

39. Palomino Monteagudo, J. E., Rodriguez, A. A., Florez, H. (2011). Simulation of flow in discrete deformable fractured porous media. Society of Petroleum Engineers, 1, 21–23. DOI 10.2118/141267-MS. [Google Scholar] [CrossRef]

40. Biot, M. A., Willis, D. G. (1957). The elastic coefficients of the theory of consolidation. Theoretical Soil Mechanics, 24, 594–601. DOI 10.1115/1.4011606. [Google Scholar] [CrossRef]

41. Sudret, B. (2008). Global sensitivity analysis using polynomial chaos expansions. Reliability Engineering and System Safety, 93(7), 964–979. DOI 10.1016/j.ress.2007.04.002. [Google Scholar] [CrossRef]