[BACK]
images Computer Modeling in Engineering & Sciences images

DOI: 10.32604/cmes.2021.016611

ARTICLE

Numerical Solutions of a Novel Designed Prevention Class in the HIV Nonlinear Model

Zulqurnain Sabir1, Muhammad Umar1, Muhammad Asif Zahoor Raja2,* and Dumitru Baleanu3,4

1Department of Mathematics and Statistics, Hazara University, Mansehra, 21120, Pakistan
2Future Technology Research Center, National Yunlin University of Science and Technology, Yunlin, 64002, Taiwan
3Department of Mathematics, Cankaya University, Ankara, 06790, Turkey
4Institute of Space Science, Magurele, Bucharest, 77125, Romania
*Corresponding Author: Muhammad Asif Zahoor Raja. Email: rajamaz@yuntech.edu.tw
Received: 11 March 2021; Accepted: 10 May 2021

Abstract: The presented research aims to design a new prevention class (P) in the HIV nonlinear system, i.e., the HIPV model. Then numerical treatment of the newly formulated HIPV model is portrayed handled by using the strength of stochastic procedure based numerical computing schemes exploiting the artificial neural networks (ANNs) modeling legacy together with the optimization competence of the hybrid of global and local search schemes via genetic algorithms (GAs) and active-set approach (ASA), i.e., GA-ASA. The optimization performances through GA-ASA are accessed by presenting an error-based fitness function designed for all the classes of the HIPV model and its corresponding initial conditions represented with nonlinear systems of ODEs. To check the exactness of the proposed stochastic scheme, the comparison of the obtained results and Adams numerical results is performed. For the convergence measures, the learning curves are presented based on the different contact rate values. Moreover, the statistical performances through different operators indicate the stability and reliability of the proposed stochastic scheme to solve the novel designed HIPV model.

Keywords: Prevention class; HIV; supervised neural networks; infection model; artificial neural networks; convergence curves; active-set algorithm; adams results; genetic algorithms

1  Introduction

Humankind is facing many deathly infection viruses for many years. HIV is one infectious virus that exists almost in each continent of the world with a low or high rate. Most viruses do not have proper treatment and vaccinations like coronavirus, dengue virus, and HIV [1–3]. Humanity can survive such diseases by taking some prevention or precautionary measures. The present study introduces a prevention class (P) in the HIV nonlinear mathematical system, i.e., the HIPV model. This prevention class describes the mathematical form based on four parameters, i.e., injection drug, safety measures, avoid from pregnancy and contact rate. The introductory HIPV nonlinear mathematical model takes the form as:

{H′(τ)=q−kV(τ)H(τ)+r(1−H(τ)+I(τ)Hmax()01)I′(τ)=−βI(τ)+kH(τ)V(τ),I0=i2,P′(τ)=aP(τ)+bP(τ)−cI(τ)+δI(τ)P0=i3,V′(τ)=nβI(τ)−γV(τ),V0=i4,(1)

where H(τ), I(τ), P(τ) and V(τ) indicate the T-cells concentration, individuals infected from this virus, prevention measures and particles free from virus, respectively. Furthermore, Tmax shows the maximum T-cells concentration, r represents the T-cells growth rate concentration, a indicates the injection drug, b shows the safety measures, c is used to avoid from pregnancy, δ describes the contact rate, q is the source of uninfected T-cells, n shows the virus particles made by infected T-cell and k indicates the virus rate. Many researchers using various schemes have investigated the HIV nonlinear systems. Few of them are Khan et al. [4] explored the fractional order HIV model involving the Liouville–Caputo and Atangana–Baleanu–Caputo derivatives. Wang et al. [5] calculated the travelling wave solutions for a nonlocal dispersal HIV infection dynamical model. Jiang et al. [6] discussed the dynamics of stochastic HIV-1 infection model with logistic growth. Arshad et al. [7] presented the effects of the HIV infection on CD4+ T-cell population based on a fractional-order model. Naik et al. [8] presented the global dynamics of a fractional order model for the transmission of HIV epidemic with optimal control. Elaiw et al. [9] checked the stability of delayed HIV dynamics models with two latent reservoirs and immune impairment. Lin et al. [10] presented the threshold dynamics of an HIV-1 virus model with both virus-to-cell and cell-to-cell transmissions, intracellular delay, and humoral immunity. Zhang et al. [11] discussed the stabilization and sustained release of HIV inhibitors by encapsulation in silk fibroin disks. Beside these, many renewed relevant studies are reported recently for HIV dynamics, see in [12–17] and references cited therein.

All these citations related to HIV model have their individual novelty, merits and advantages. But no one has designed the prevention class in the nonlinear HIV model. The aim of this current work is to design the HIPV model and investigate numerically by using the artificial neural networks together with the competence of the hybrid of global and local search schemes called genetic algorithm (GA) and active-set approach (ASA), i.e., GA-ASA. The stochastic schemes have been applied to explore many linear/nonlinear, singular/non-singular and biological, delayed, fractional, prediction and pantograph differential models. Few well-known applications related to these applications are Thomas-Fermi singular system [18], singular models using Gudermannian kernel functions [19], mathematical model for random matrix theory [20], nonlinear model based on prey-predator [21], Bouc–Wen hysteresis ODEs model for piezostage actuator [22], mosquito dispersal model [23], nonlinear Van-der Pol Mathieu's oscillatory models [24], functional singular system [25], squeezing flow with heat transfer model [26], delay differential model [27], nonlinear electric circuit models [28], singular three-point differential system [29], financial market forecasting model [30], transmission model in human head [31], nonlinear dusty plasma systems [32] and multi- singular fractional systems [33]. The workflow diagram of the HIPV model is presented in Fig. 1.

images

Figure 1: Workflow diagram of the HIPV nonlinear mathematical model

Some novel prominent features of the current work are described as:

•   The design of prevention class in the HIV nonlinear mathematical system is presented using the injection drug, safety measures, avoid from pregnancy and contact rate.

•   The designed HIPV nonlinear system is effectively solved by using the ANN along with the optimization of GA-ASA combinations.

•   For the convergence of HIPV system, the learning curves through GA and GA-ASAS are presented using different values of the contact rate.

•   The consistent overlapped outcomes through GA-ASA and the Adams numerical routines validate the exactness of the designed scheme.

•   The endorsement of the presentation is trained for different statistical valuations to get the numerical solutions of HIPV system.

•   The advantages of the designed scheme are simply performed for the nonlinear HIPV system, easy to understand, operated efficiently, constancy and inclusive applicability are the other significant influences.

The remaining parts of current research are described as: Section 2 designates the methodology and statistical presentations. Section 3 shows the result simulations. Section 4 indicates the final declarations and future research reports.

2  Proposed Structure

The designed structure of ANNs by using the optimization of GA-ASA is presented in two steps for solving the nonlinear mathematical HIPV model, given as:

•   For the ANNs parameters, the design of fitness function is presented.

•   Essential settings are provided to optimize the fitness function using the hybrid combination of GA-ASA.

2.1 Structure of ANNs

The mathematical formulations to solve each class of the nonlinear Human Immunodeficiency Prevention Virus (HIPV) are obtainable in this section. The proposed solutions of the nonlinear HIPV model are respectively represented as H^, I^, P^ and V^, given as:

[H^(τ),I^(τ),P^(τ),V^(τ)]=[∑k=1m⁡cH,kg(wH,kτ+aH,k),∑k=1m⁡cI,kg(wI,kτ+aI,k),∑k=1m⁡cP,kg(wP,kτ+aP,k),∑k=1m⁡cV,kg(wV,kτ+aV,k)](2)

[H^′(τ),I^′(τ),P^′(τ),V^′(τ)]=[∑k=1m⁡cH,kg′(wH,kτ+aH,k),∑k=1m⁡cI,kg′(wI,kτ+aI,k),∑k=1m⁡cP,kg′(wP,kτ+aP,k),∑k=1m⁡cV,kg′(wV,kτ+aV,k)]

In the above system, W represents the unknown weight vector as:

W=[WH,WI,WP,WV], for WH=[cH,ωH,aH], WI=[cI,ωI,aI], WP=[cP,ωP,aP] and WV=[cV,ωV,aV], where

cH=[cH,1,cH,2,…,cH,m],cI=[cI,1,cI,2,…,cI,m],cP=[cP,1,cP,2,…,cP,m],cV=[cV,1,cV,2,…,cV,m],wH=[wH,1,wH,2,…,wH,m],wI=[wI,1,wI,2,…,wI,m],wP=[wP,1,wP,2,…,wP,m],wV=[wV,1,wV,2,…,wV,m],aH=[aH,1,aH,2,…,aH,m],aI=[aI,1,aI,2,…,aI,m],aP=[aP,1,aP,2,…,aP,m],aV=[aV,1,aV,2,…,aV,m].

The log-sigmoid g(τ)=(1+exp⁡(−τ))−1 is used as an activation function in the above system, given as:

[H^(τ),I^(τ),P^(τ),V^(τ)]=[∑k=1mcH,k1+e−(wH,kτ+aH,k),∑k=1mcI,k1+e−(wI,kτ+aI,k),∑k=1mcP,k1+e−(wP,kτ+aP,k),∑k=1mcV,k1+e−(wV,kτ+aV,k),][H^(τ),I^(τ),P^(τ),V^(τ)]=[∑k=1mwH,kcH,ke−(wH,kτ+aH,k)1+e−(wH,kτ+aH,k),∑k=1mwI,kcI,ke−(wI,kτ+aI,k)1+e−(wI,kτ+aI,k),∑k=1mwp,kcP,ke−(wP,kτ+aP,k)1+e−(wP,kτ+aP,k),∑k=1mwV,kcV,ke−(wV,kτ+aV,k)1+e−(wV,kτ+aV,k),](3)

The optimization of an error based ‘fitness function’ is performed using the GA-ASA procedures is given as:

e=e1+e2+e3+e4+e5,(4)

e1=1N∑k=1N∑⁡[H^k′−q+kV^kH^k−rH^k+r(H^k+I^kHmax()^k^k)[]2](5)

e2=1N∑k=1N⁡[I^k′+βI^k−kV^kH^k]2,(6)

e3=1N∑k=1N⁡[P^k′−aP^k−bP^k+cI^k−δI^k]2,(7)

e4=1N∑k=1N⁡[V^k′−nβI^k+γV^k]2,(8)

e5=14[(H^0−i1)2+(I^0−i2)2+(P^0−i3)2++(V^0−i4)2],(9)

where H^k=H(τk),I^k=I(τk),P^k=P(τk),V^k=V(τk),τk=kh and hN=1. The values e1, e2, e3 and e4 represent the fitness functions related to system (1), while, e5 represents the initial conditions of the HIPV nonlinear system (1).

2.2 Optimization Performances: GA-ASA

In this section, the optimal performance through GA-ASA for solving the mathematical HIPV nonlinear model is presented. The designed ANNs structure through GA-ASA for solving the nonlinear mathematical HIPV model is shown in Fig. 2.

images

Figure 2: Designed arrangements of the current approach to solve the HIPV nonlinear mathematical model

GA is a global search optimization procedure, which is implemented to solve the stiff, complicated and nonlinear systems. In this study, GA is implemented as an optimization procedure to solve the HIPV model. To find the best solutions of the network, GA works through the selection operator, crossover process, reproduction practice and mutation procedure. Recently, GA has been applied in extensive optimization practices like as, system of hospitalization expenditure [34], higher order nonlinear singular systems [35], feature group in cancer microarray virus [36], singular functional based boundary value models [37], nonlinear Troesch's system [38], vehicle system routine [39], active noise control systems [40,41], monorail vehicle system dynamics [42] and economic load dispatch problem [43].

ASA is known as a quick and rapid local search optimization scheme, which is broadly executed to solve both types of models based on constrained/unconstrained systems. ASA is implemented in numerous optimizations networks based complex models. In recent few years, ASA is implemented to execute the real-time optimal control [44], multi-rigid-body dynamic contact problems [45], a class of nonlinear problems with monotone operators [46], predictive control for a ball and beam system [47] and large scale optimization of cardiac defibrillation [48]. For the slowness of the global search method, the hybridization procedure is applied via GA-ASA and comprehensive pseudocode of the ANN using GA-ASA combination is shown in Tab. 1.

images

2.3 Performance Measures

The statistical operator performances based on the “variance account for (VAF),” “mean absolute deviation (MAD),” “Theil's inequality coefficient (TIC)” and “semi interquartile range (S.I.R)” along with the Global performances of these operators are mathematically presented to solve the HIVP nonlinear model in this section.

{[VAFH,VAFI,VAFP,VAFV]=[(1−var(Hr−H^r)var(Hr))×100,(1−var(Ir−I^r)var(Ir))×100,(1−var(Pr−P^r)var(P)r)×100,(1−var(Vr−V^r)var(Vr))×100][E-VAFH,E-VAFI,E-VAFP,E-VAFV]=[|100−VAFH,100−VAFI,100−VAFP,100−VAFV|](10)

[MADH,MADI,MADP,MADV]=[∑r=1n⁡|Hr−H^r|,∑r=1n⁡|Ir−I^r|,∑r=1n⁡|Pr−P^r|,∑r=1n⁡|Vr−V^r|](11)

[TICH,TICI,TICP,TICV]=[1n∑r=1n⁡(Hr−H^r)2(1n∑r=1n⁡Hr2+1n∑r=1n⁡H^r2),1n∑r=1n⁡(Ir−I^r)2(1n∑r=1n⁡Ir2+1n∑r=1n⁡I^r2)1n∑r=1n⁡(Pr−P^r)2(1n∑r=1n⁡Pr2+1n∑r=1n⁡P^r2),1n∑r=1n⁡(Vr−V^r)2(1n∑r=1n⁡Vr2+1n∑r=1n⁡V^r2)](12)

{S.I Range=0.5×(q3−q1),q1=1st quartile q3=3rd quartile,(13)

In the above network, r shows the grid point, while H^,I^,P^ and V^ represent the approximate solutions.

3  Simulations and Results

In this section, the details solution for solving the HIPV nonlinear model are provided. For the convergence measures of the prevention class, six different cases have been presented based on the contact rate. Moreover, the obtained results have been compared with the Adams numerical results to authenticate the correctness of the HIPV nonlinear model. The statistical performances are also provided by taking different measures to check the consistency and reliability of the proposed scheme. The updated mathematical form of the nonlinear HIPV system with suitable parameters is given as:

{H′(τ)=0.1−0.0027V(τ)H(τ)+3(1−H(τ)+I(τ)Hmax()0)I′(τ)=−0.3I(τ)+0.0027H(τ)V(τ),I0=0.1,P′(τ)=−0.00001P(τ)+0.1P(τ)−0.0001I(τ)+0.1I(τ)P0=i3,V′(τ)=3I(τ)−2.4V(τ),V0=i4(14)

The formulation of the fitness function using the above system becomes as:

e=1N∑i=1N∑([H^r′−0.1+0.0027V^rH^r−3(1−H^r+I^rHmax()^r^r)[]2[I^r′+0.3I^r−0.0027V^rH^r]2]+[P^r′+0.00001P^r−0.1P^r+0.0001I^r−0.1I^r]2+[V^r′−3I^r+2.4V^r]2)+14[(H^0)2+(I^0−0.1)2+(P^0)2+(V^0)2].(15)

The optimization of the above fitness function is performed to solve the HIPV nonlinear system using the hybrid combination of GA-ASA for 100 executions by taking 120 variables. The best weight vectors show the proposed solutions of the HIPV nonlinear mathematical model presented as:

H^(τ)=−1.84601+e−(1.4151τ−0.4679)−0.00011+e−(−10.13τ+0.7461)−3.23481+e−( −1.362τ+0.9250)−0.98031+e−( −0.155τ+2.8074)            −0.38161+e−( −0.473τ+0.0295)−0.57471+e−( 1.2265τ−0.8254)+9.21271+e−( 4.4776τ−6.4223)−0.32021+e−( 2.0001τ−0.9602)          +4.38651+e−( −4.876τ−6.5474)+0.05441+e−(1.0053τ−1.0499),(16)

I^(τ)=−0.37471+e−(−0.187τ+0.9055)+0.66001+e−(0.2312τ−0.2922)+0.64751+e−( −0.346τ+0.1366)+0.34491+e−( −0.389τ−1.2008)          −0.00341+e−( 0.3385τ+1.7020)−0.42431+e−( −0.190τ+0.5338)−0.39161+e−( 0.2793τ−1.4906)+0.00391+e−( −1.591τ−1.5890)          −0.01001+e−( 2.0616τ+1.7314)+0.01931+e−( −0.176τ−0.0933),(17)

P^(τ)=0.82781+e−(0.2509τ−0.0931)+0.22471+e−(−0.159τ−1.1961)−1.60781+e−( 1.0943τ+0.1828)−0.34411+e−( −0.148τ+0.4059)          −0.07331+e−( −0.3225τ−0.7296)−1.61581+e−( 0.2680τ−0.939)+1.37991+e−( 1.1403τ+0.1218)+0.03541+e−( −1.190τ+0.5803)          −0.21751+e−( −0.6083τ−1.4061)+0.87431+e−( 0.3117τ−0.157),(18)

V^(τ)=−0.000021+e−(14.918τ+0.2385)−0.24991+e−(−0.026τ−0.1360)−0.19651+e−( −0.149τ−0.2649)+1.28221+e−( −0.203τ+0.0967)          −0.84451+e−( −0.100τ−1.2035)−0.42621+e−( −2.375τ−1.3635)+0.19121+e−( −0.024τ−0.3418)−2.24401+e−( −3.639τ−3.8513)          −0.23461+e−( −0.388τ+1.8755)−0.02531+e−( −0.234τ−0.8591).(19)

The fitness function shown in Eq. (4) is applied for the optimization of the hybrid computing arrangements of GA-ASA for solving the nonlinear HIPV model. The convergence or learning curves, restructured generations of the fitness functions are plotted in Figs. 3–8 by taking different values of the contact rate (δ) based on the nonlinear HIPV mathematical model. One may observed that in the start the optimization performance of fitness function using GA is fast but after few generations its convergence competency reduced. Then the hybridization process of GA with the local search ASA is implemented that shows more proficiency in order to solve the nonlinear HIPV system. Hence, the reliability and steadfast convergence are obtained to solve the nonlinear HIPV system using the GA-ASA. One may accomplish that the accuracy through convergence is obtained using the stochastic GA-ASA process for solving the nonlinear HIPV mathematical model.

images

Figure 3: Convergence curves using the optimization process for solving the nonlinear HIPV system by taking contact rate δ=0.1 (a) Convergence curve based on GA (b) Convergence curve based on GA-ASA

images

Figure 4: Convergence curves using the optimization process for solving the nonlinear HIPV system by taking contact rate δ=0.2 (a) Convergence curve based on GA (b) Convergence curve based on GA-ASA

images

Figure 5: Convergence curves using the optimization process for solving the nonlinear HIPV system by taking contact rate δ=0.3 (a) Convergence curve based on GA (b) Convergence curve based on GA-ASA

images

Figure 6: Convergence curves using the optimization process for solving the nonlinear HIPV system by taking contact rate δ=0.4 (a) Convergence curve based on GA (b) Convergence curve based on GA-ASA

images

Figure 7: Convergence curves using the optimization process for solving the nonlinear HIPV system by taking contact rate δ=0.5 (a) Convergence curve based on GA (b) Convergence curve based on GA-ASA

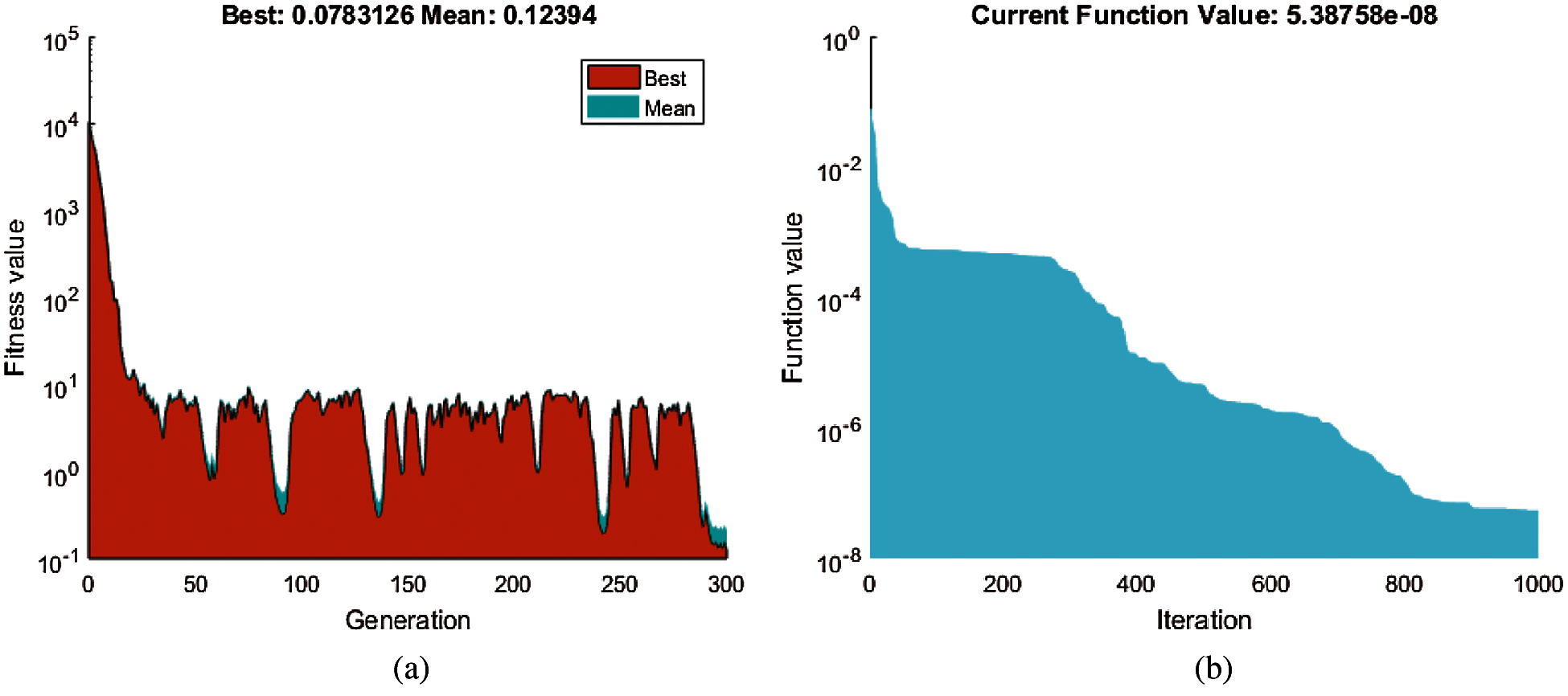
images

Figure 8: Convergence curves using the optimization process for solving the nonlinear HIPV system by taking contact rate δ=0.6 (a) Convergence curve based on GA (b) Convergence curve based on GA-ASA

imagesimages

Figure 9: Best set of weight vectors along with the comparison of best, mean and reference solutions to solve the HIPV nonlinear mathematical system (a) Best weights for H(τ) (b) Best weights for I(τ) (c) Best weights for P(τ) (d) Best weights for V(τ) (e) Results for class H(τ) (f) Results for class I(τ) (g) Results for class P(τ) (h) Results for class V(τ)

The proposed numerical solutions are obtained using the above systems (16–19) for 0 to 1 input with the step size of 0.1 of the HIPV nonlinear mathematical model along with the best weights drawn in the Figs. 9a–9d. While the second half of Figs. 9e–9h presents the comparison of the best and mean results with the Adam reference results to solve the HIPV nonlinear model. The overlapping of the results shows the confidence and perfection of the designed scheme. Fig. 10 shows the absolute error (AE) plots for each class of the HIPV nonlinear model. The best and mean AE values are plotted for each category of the HIPV model. One may observe that the best AE values of the categories H(τ), I(τ), P(τ) and V(τ) lie around 10–06–10–08, 10−08−10−10, 10−06−10−07 and 10−05−10−07, respectively. While, the mean values of AE for each category of the HIPV model lie around 10−02−10−04, 10−05−10−06, 10−05−10−06 and 10−04−10−05, respectively. Fig. 11 represents the performance operators based on E-VAF, MAD and TIC values to solve the HIPV nonlinear model. One may see that the best performance of the H(τ) class using the operators E-VAF, MAD and TIC lie around 10−10−10−11, 10−06−10−07 and 10−10−10−11, respectively. The best performances of I(τ) for these statistical operators lie around 10−11−10−12, 10−07−10−08 and 10−11−10−12, respectively. While, the best performances of P(τ) and V(τ) based on these performances lie around 10−08−10−09, 10−06−10−07 and 10−10−10−11, respectively. On the behalf of these performances, one can accomplish that the proposed scheme is precise.

images

Figure 10: AE values for each category of the HIPV nonlinear model (a) AE for class H(τ) (b) AE for I(τ) class (c) AE for P(τ) class (d) AE for V(τ) class

images

Figure 11: Performance operators based on E-VAF, MAD and TIC values to solve the HIPV nonlinear model

The graphical representations along with histograms and boxplots using the statistical actions to authenticate the convergence measures are given in Figs. 12–14 for solving the HIPV model. Fig 12 shows the TIC values for 100 trials to solve the HIPV nonlinear model and almost 95% runs achieved very good accuracy level that are in between 10−10−10−10. The MAD performances are plotted in Fig. 13 and almost 95% runs achieved accuracy level in between 10−04−10−06. Likewise, the E-VAF performance are plotted in Fig. 14 and one can observe that almost 95% runs achieved an accuracy level in between 10−06−10−08. These best presentations of the runs using the ANN along with GA-ASA are found to be satisfactory for the E-VAF, TIC and MAD operators.

images

Figure 12: Convergence plots for the TIC values along with histogram/Boxplots to solve the HIPV nonlinear model

images

Figure 13: Convergence plots for the MAD values along with histogram/Boxplots to solve the HIPV nonlinear model

images

Figure 14: Convergence plots for the E-VAF values along with histogram/Boxplots to solve the HIPV nonlinear model

images

images

The statistical presentations taking different gages like Minimum (Min), S.I Range, standard deviation (ST. D), Maximum (Max), Mean and Median (Med) are used to check the validation of the HIPV nonlinear model given in Tabs. 2–5. In these tables, the Min and Max gages respectively indicate the best and worst performances for hundred executions. For H(τ) class, the performances based on “Min,” “Max,” “Med,” “Mean,” “S.I Range” and “ST.D” lie around 10−06−10−08, 10−01−10−02, 10−04−10−06, 10−02−10−05, 10−04−10−06 and 10−02−10−05, respectively. For I(τ) class, the performances based on “Min,” “Max,” “Med,” “Mean,” “S.I Range” and “ST.D” lie around 10−08−10−10, 10−04−10−05, 10−06−10−07, 10−02−10−05, 10−05−10−06 and 10−05−10−06, respectively. Similarly, for P(τ) class, the performances based on “Min,” “Max,” “Med,” “Mean,” “S.I Range” and “ST.D” lie around 10−07−10−10, 10−05−10−06, 10−06−10−07, 10−03−10−05, 10−06−10−07 and 10−05−10−06, respectively. Moreover, for V(τ) class, the performances based on “Min,” “Max,” “Med,” “Mean,” “S.I Range” and “ST.D” lie around 10−07−10−09, 10−04−10−05, 10−05−10−06, 10−05−10−06, 10−05−10−07 and 10−05−10−06, respectively. These small values performances designate the worth and value of the designed scheme to solve the HIPV nonlinear model. One may find through these accomplished actions that the proposed approach is precise, accurate and stable.

images

images

The performance of the global “G-MAD,” “G-EVAF” and “G-TIC” operatives for hundred executions based on the proposed scheme are shown in Tab. 6 to solve the HIPV nonlinear model. These Min global “G-MAD,” “G-TIC” and “G-EVAF” performances are found around 10−05−10−06, 10−09−10−10 and 10−06−10−08, while the global S.I Range performances are found around 10−05−10−06, 10−09−10−10 and 10−06−10−08 for the HIPV nonlinear model. These close ideal values of the global performances indicate the precision, accurateness and correctness of the proposed scheme.

images

4  Conclusions

The presented work is related to introducing a new prevention class in the nonlinear HIV system named HIPV model. HIV is a virus with no treatment, so prevention is one of the best options to control or spread this type of dangerous virus. The introduced prevention class uses the four subclasses named injection drug, safety measures, avoid from pregnancy and contact rate. This designed HIPV nonlinear model is solved using the ANNs and optimization is performed using the hybrid procedure of GA-ASA. For the convergence of the HIPV model, six different contact rate values have been analyzed through the process of GA-ASA. The reliable accuracy through convergence is obtained using the stochastic GA-ASA process for solving the nonlinear HIPV mathematical model. For the correctness of the designed HIPV model and the proposed stochastic scheme, the proposed results through the GA-ASA optimization process overlapped with the Adams numerical solutions. An activation log-sigmoid function is applied along with 120 variables. For the precision and accuracy of the proposed numerical approach, the statistical based performances of TIC, MAD and E-VAF for 100 executions using 120 variables have been provided. For the TIC, MAD and E-VAF convergence, most of the runs have achieved a very high accuracy level for solving each class of the nonlinear HIPV model. Moreover, the valuations through statistics based Min, ST.D, Mean, S.I range, Max, Median further validate the value of the designed ANN along with the GA-ASA. The global presentations with high ranks of these statistical operators have also been performed for solving the nonlinear HIPV system.

In the future, the designed ANN along with GA-ASA is proficient to solve the prediction model [49,50], fluidics nonlinear systems [51–54], biological nonlinear systems for Hepatitis-B virus [55], transmissibility of measles [56] and novel COVID-19 dynamics [57–58].

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Umar, M., Sabir, Z., Raja, M. A. Z., Shoaib, M., Gupta, M. et al. (2020). A stochastic intelligent computing with neuro-evolution heuristics for nonlinear SITR system of novel COVID-19 dynamics. Symmetry, 12(10), 1628. DOI 10.3390/sym12101628. [Google Scholar] [CrossRef]

 2.  Umar, M., Sabir, Z., Raja, M. A. Z., Sánchez, Y. G. (2020). A stochastic numerical computing heuristic of SIR nonlinear model based on dengue fever. Results in Physics, 19, 103585. DOI 10.1016/j.rinp.2020.103585. [Google Scholar] [CrossRef]

 3.  Umar, M., Sabir, Z., Amin, F., Guirao, J. L., Raja, M. A. Z. (2020). Stochastic numerical technique for solving HIV infection model of CD4+ T cells. The European Physical Journal Plus, 135(6), 403. DOI 10.1140/epjp/s13360-020-00417-5. [Google Scholar] [CrossRef]

 4.  Khan, A., Gómez-Aguilar, J. F., Khan, T. S., Khan, H. (2019). Stability analysis and numerical solutions of fractional order HIV/AIDS model. Chaos, Solitons & Fractals, 122, 119–128. DOI 10.1016/j.chaos.2019.03.022. [Google Scholar] [CrossRef]

 5.  Wang, W., Ma, W. (2018). Travelling wave solutions for a nonlocal dispersal HIV infection dynamical model. Journal of Mathematical Analysis and Applications, 457(1), 868–889. DOI 10.1016/j.jmaa.2017.08.024. [Google Scholar] [CrossRef]

 6.  Jiang, D., Liu, Q., Shi, N., Hayat, T., Alsaedi, A. et al. (2017). Dynamics of a stochastic HIV-1 infection model with logistic growth. Physica A: Statistical Mechanics and its Applications, 469, 706–717. DOI 10.1016/j.physa.2016.11.078. [Google Scholar] [CrossRef]

 7.  Arshad, S., Baleanu, D., Bu, W., Tang, Y. (2017). Effects of HIV infection on CD4+ T-cell population based on a fractional-order model. Advances in Difference Equations, 2017(1), 92. DOI 10.1186/s13662-017-1143-0. [Google Scholar] [CrossRef]

 8.  Naik, P. A., Zu, J., Owolabi, K. M. (2020). Global dynamics of a fractional order model for the transmission of HIV epidemic with optimal control. Chaos, Solitons & Fractals, 138, 109826. DOI 10.1016/j.chaos.2020.109826. [Google Scholar] [CrossRef]

 9.  Elaiw, A. M., Raezah, A. A., Azoz, S. A. (2018). Stability of delayed HIV dynamics models with two latent reservoirs and immune impairment. Advances in Difference Equations, 2018(1), 414. DOI 10.1186/s13662-018-1869-3. [Google Scholar] [CrossRef]

10. Lin, J., Xu, R., Tian, X. (2017). Threshold dynamics of an HIV-1 virus model with both virus-to-cell and cell-to-cell transmissions, intracellular delay, and humoral immunity. Applied Mathematics and Computation, 315, 516–530. DOI 10.1016/j.amc.2017.08.004. [Google Scholar] [CrossRef]

11. Zhang, L., Herrera, C., Coburn, J., Olejniczak, N., Ziprin, P. et al. (2017). Stabilization and sustained release of HIV inhibitors by encapsulation in silk fibroin disks. ACS Biomaterials Science & Engineering, 3(8), 1654–1665. DOI 10.1021/acsbiomaterials.7b00167. [Google Scholar] [CrossRef]

12. Naik, P. A., Zu, J., Owolabi, K. M. (2020). Modeling the mechanics of viral kinetics under immune control during primary infection of HIV-1 with treatment in fractional order. Physica A: Statistical Mechanics and its Applications, 545, 123816. DOI 10.1016/j.physa.2019.123816. [Google Scholar] [CrossRef]

13. Naik, P. A., Zu, J., Ghoreishi, M. (2020). Stability analysis and approximate solution of sir epidemic model with crowley-martin type functional response and holling type-II treatment rate by using homotopy analysis method. Journal of Applied Analysis & Computation, 10(4), 1482–1515. DOI 10.11948/20190239. [Google Scholar] [CrossRef]

14. Naik, P. A., Owolabi, K. M., Yavuz, M., Zu, J. (2020). Chaotic dynamics of a fractional order HIV-1 model involving AIDS-related cancer cell. Chaos, Solitons & Fractals, 140, 110272. DOI 10.1016/j.chaos.2020.110272. [Google Scholar] [CrossRef]

15. Umar, M., Sabir, Z., Raja, M. A. Z., Aguilar, J. G., Amin, F. et al. (2021). Neuro-swarm intelligent computing paradigm for nonlinear HIV infection model with CD4+ T-cells. Mathematics and Computers in Simulation, 188, 241–253 DOI 10.1016/j.matcom.2021.04.008. [Google Scholar] [CrossRef]

16. Culshaw, R. V., Ruan, S., (2000). A delay-differential equation model of HIV infection of CD4+ T-cells. Mathematical Biosciences, 165(1), 27–39. DOI 10.1016/S0025-5564(00)00006-7. [Google Scholar] [CrossRef]

17. Boukhouima, A., Lotfi, E. M., Mahrouf, M., Rosa, S., Torres, D. F. et al. (2021). Stability analysis and optimal control of a fractional HIV-aIDS epidemic model with memory and general incidence rate. The European Physical Journal Plus, 136(1), 1–20. DOI 10.1140/epjp/s13360-020-01013-3. [Google Scholar] [CrossRef]

18. Sabir, Z., Manzar, M. A., Raja, M. A. Z., Sheraz, M., Wazwaz, A. M. (2018). Neuro-heuristics for nonlinear singular thomas-Fermi systems. Applied Soft Computing, 65, 152–169. DOI 10.1016/j.asoc.2018.01.009. [Google Scholar] [CrossRef]

19. Sabir, Z., Raja, M. A. Z., Arbi, A., Altamirano, G. C., Cao, J. (2021). Neuro-swarms intelligent computing using gudermannian kernel for solving a class of second order lane-emden singular nonlinear model. AIMS Mathematics, 6(3), 2468–2485. DOI 10.3934/math.2021150. [Google Scholar] [CrossRef]

20. Raja, M. A. Z., Shah, Z., Manzar, M. A., Ahmad, I., Awais, M. et al. (2018). A new stochastic computing paradigm for nonlinear painlevé II systems in applications of random matrix theory. The European Physical Journal Plus, 133(7), 1–21. DOI 10.1140/epjp/i2018-12080-4. [Google Scholar] [CrossRef]

21. Umar, M., Sabir, Z., Raja, M. A. Z. (2019). Intelligent computing for numerical treatment of nonlinear prey-predator models. Applied Soft Computing, 80, 506–524. DOI 10.1016/j.asoc.2019.04.022. [Google Scholar] [CrossRef]

22. Naz, S., Raja, M. A. Z., Mehmood, A., Zameer, A., Shoaib, M. (2021). Neuro-intelligent networks for bouc–Wen hysteresis model for piezostage actuator. The European Physical Journal Plus, 136(4), 1–20. DOI 10.1140/epjp/s13360-021-01382-3. [Google Scholar] [CrossRef]

23. Umar, M., Raja, M. A. Z., Sabir, Z., Alwabli, A. S., Shoaib, M. (2020). A stochastic computational intelligent solver for numerical treatment of mosquito dispersal model in a heterogeneous environment. The European Physical Journal Plus, 135(7), 1–23. DOI 10.1140/epjp/s13360-020-00557-8. [Google Scholar] [CrossRef]

24. Jadoon, I., Raja, M. A. Z., Junaid, M., Ahmed, A., ur Rehman, A. et al. (2021). Design of evolutionary optimized finite difference based numerical computing for dust density model of nonlinear van-der Pol mathieu's oscillatory systems. Mathematics and Computers in Simulation, 181, 444–470. DOI 10.1016/j.matcom.2020.10.004. [Google Scholar] [CrossRef]

25. Sabir, Z., Raja, M. A. Z., Umar, M., Shoaib, M. (2020). Neuro-swarm intelligent computing to solve the second-order singular functional differential model. The European Physical Journal Plus, 135(6), 474. DOI 10.1140/epjp/s13360-020-00440-6. [Google Scholar] [CrossRef]

26. Almalki, M. M., Alaidarous, E. S., Maturi, D., Raja, M. A. Z., Shoaib, M. (2020). A levenberg–Marquardt backpropagation neural network for the numerical treatment of squeezing flow with heat transfer model. IEEE Access, 8, 227340–227348. DOI 10.1109/Access.6287639. [Google Scholar] [CrossRef]

27. Guirao, J. L., Sabir, Z., Saeed, T. (2020). Design and numerical solutions of a novel third-order nonlinear emden–Fowler delay differential model. Mathematical Problems in Engineering, 2020. DOI 10.1155/2020/7359242. [Google Scholar] [CrossRef]

28. Mehmood, A., Zameer, A., Ling, S. H., ur Rehman, A., Raja, M. A. Z., (2020). Integrated computational intelligent paradigm for nonlinear electric circuit models using neural networks, genetic algorithms and sequential quadratic programming. Neural Computing and Applications, 32(14), 10337–10357. DOI 10.1007/s00521-019-04573-3. [Google Scholar] [CrossRef]

29. Sabir, Z., Baleanu, D., Shoaib, M., Raja, M. A. Z. (2021). Design of stochastic numerical solver for the solution of singular three-point second-order boundary value problems. Neural Computing and Applications, 33(7), 2427–2443. DOI 10.1007/s00521-020-05143-8. [Google Scholar] [CrossRef]

30. Bukhari, A. H., Raja, M. A. Z., Sulaiman, M., Islam, S., Shoaib, M. et al. (2020). Fractional neuro-sequential ARFIMA-lSTM for financial market forecasting. IEEE Access, 8, 71326–71338. DOI 10.1109/Access.6287639. [Google Scholar] [CrossRef]

31. Raja, M. A. Z., Umar, M., Sabir, Z., Khan, J. A., Baleanu, D. (2018). A new stochastic computing paradigm for the dynamics of nonlinear singular heat conduction model of the human head. The European Physical Journal Plus, 133(9), 364. DOI 10.1140/epjp/i2018-12153-4. [Google Scholar] [CrossRef]

32. Bukhari, A. H., Sulaiman, M., Raja, M. A. Z., Islam, S., Shoaib, M. et al. (2020). Design of a hybrid NAR-rBFs neural network for nonlinear dusty plasma system. Alexandria Engineering Journal, 59(5), 3325–3345. DOI 10.1016/j.aej.2020.04.051. [Google Scholar] [CrossRef]

33. Sabir, Z., Raja, M. A. Z., Shoaib, M., Aguilar, J. G. (2020). FMNEICS: Fractional meyer neuro-evolution-based intelligent computing solver for doubly singular multi-fractional order lane–Emden system. Computational and Applied Mathematics, 39(4), 1–18. DOI 10.1007/s40314-020-01350-0. [Google Scholar] [CrossRef]

34. Zhou, T., Lu, H., Wang, W., Yong, X. (2019). GA-SVM based feature selection and parameter optimization in hospitalization expense modeling. Applied Soft Computing, 75, 323–332. DOI 10.1016/j.asoc.2018.11.001. [Google Scholar] [CrossRef]

35. Sabir, Z., Raja, M. A. Z., Guirao, J. L., Shoaib, M. (2020). Integrated intelligent computing with neuro-swarming solver for multi-singular fourth-order nonlinear Emden–Fowler equation. Computational and Applied Mathematics, 39(4), 1–18. DOI 10.1007/s40314-020-01330-4. [Google Scholar] [CrossRef]

36. Sayed, S., Nassef, M., Badr, A., Farag, I. (2019). A nested genetic algorithm for feature selection in high-dimensional cancer microarray datasets. Expert Systems with Applications, 121, 233–243. DOI 10.1016/j.eswa.2018.12.022. [Google Scholar] [CrossRef]

37. Sabir, Z., Wahab, H. A., Umar, M., Erdoğan, F. (2019). Stochastic numerical approach for solving second order nonlinear singular functional differential equation. Applied Mathematics and Computation, 363, 124605. DOI 10.1016/j.amc.2019.124605. [Google Scholar] [CrossRef]

38. Majeed, K., Masood, Z., Samar, R., Raja, M. A. Z. (2017). A genetic algorithm optimized morlet wavelet artificial neural network to study the dynamics of nonlinear troesch's system. Applied Soft Computing, 56, 420–435. DOI 10.1016/j.asoc.2017.03.028. [Google Scholar] [CrossRef]

39. Mohammed, M. A., Ghani, M. K. A., Hamed, R. I., Mostafa, S. A., Ahmad, M. S. et al. (2017). Solving vehicle routing problem by using improved genetic algorithm for optimal solution. Journal of Computational Science, 21, 255–262. DOI 10.1016/j.jocs.2017.04.003. [Google Scholar] [CrossRef]

40. Khan, W. U., He, Y., Raja, M. A. Z., Chaudhary, N. I., Khan, Z. A. et al. (2021). Flower pollination heuristics for nonlinear active noise control systems. Computers, Materials & Continua, 67(1), 815–834. DOI 10.32604/cmc.2021.014674. [Google Scholar] [CrossRef]

41. Raja, M. A. Z., Aslam, M. S., Chaudhary, N. I., Nawaz, M., Shah, S. M. (2019). Design of hybrid nature-inspired heuristics with application to active noise control systems. Neural Computing and Applications, 31(7), 2563–2591. DOI 10.1007/s00521-017-3214-2. [Google Scholar] [CrossRef]

42. Jiang, Y., Wu, P., Zeng, J., Zhang, Y., Zhang, Y. et al. (2020). Multi-parameter and multi-objective optimisation of articulated monorail vehicle system dynamics using genetic algorithm. Vehicle System Dynamics, 58(1), 74–91. DOI 10.1080/00423114.2019.1566557. [Google Scholar] [CrossRef]

43. Raja, M. A. Z., Ahmed, U., Zameer, A., Kiani, A. K., Chaudhary, N. I. (2019). Bio-inspired heuristics hybrid with sequential quadratic programming and interior-point methods for reliable treatment of economic load dispatch problem. Neural Computing and Applications, 31(1), 447–475. DOI 10.1007/s00521-017-3019-3. [Google Scholar] [CrossRef]

44. Koehler, S., Danielson, C., Borrelli, F. (2017). A primal-dual active-set method for distributed model predictive control. Optimal Control Applications and Methods, 38(3), 399–419. DOI 10.1002/oca.2262. [Google Scholar] [CrossRef]

45. Barboteu, M., Dumont, S. (2018). A primal-dual active set method for solving multi-rigid-body dynamic contact problems. Mathematics and Mechanics of Solids, 23(3), 489–503. DOI 10.1177/1081286517733505. [Google Scholar] [CrossRef]

46. He, X., Yang, P. (2019). The primal-dual active Set method for a class of nonlinear problems with-monotone operators. Mathematical Problems in Engineering, 2019. DOI 10.1155/2019/2912301. [Google Scholar] [CrossRef]

47. Nak, H., Akkaya, Ş, Yumuk, E. (2017). Active set method based model predictive control for a ball and beam system. 10th International Conference on Electrical and Electronics Engineering, pp. 871–875. Bursa, Turkey, IEEE. [Google Scholar]

48. Chamakuri, N., Kunisch, K. (2017). Primal-dual active set strategy for large scale optimization of cardiac defibrillation. Applied Mathematics and Computation, 292, 178–193. DOI 10.1016/j.amc.2016.07.035. [Google Scholar] [CrossRef]

49. Sabir, Z., Raja, M. A. Z., Wahab, H. A., Shoaib, M., Aguilar, J. G., (2020). Integrated neuro-evolution heuristic with sequential quadratic programming for second-order prediction differential models. Numerical Methods for Partial Differential Equations. DOI 10.1002/num.22692. [Google Scholar] [CrossRef]

50. Sabir, Z., Guirao, J. L., Saeed, T., Erdoğan, F. (2020). Design of a novel second-order prediction differential model solved by using adams and explicit runge–Kutta numerical methods. Mathematical Problems in Engineering, 2020. DOI 10.1155/2020/9704968. [Google Scholar] [CrossRef]

51. Umar, M., Sabir, Z., Imran, A., Wahab, A. H., Shoaib, M. et al. (2020). The 3-D flow of casson nanofluid over a stretched sheet with chemical reactions, velocity slip, thermal radiation and brownian motion. Thermal Science, 24 (5), 2929–2939. DOI 10.2298/TSCI190625339U. [Google Scholar] [CrossRef]

52. Umar, M., Akhtar, R., Sabir, Z., Wahab, H. A., Zhu, Z. et al. (2019). Numerical treatment for the three-dimensional eyring-powell fluid flow over a stretching sheet with velocity slip and activation energy. Advances in Mathematical Physics, 2019. DOI 10.1155/2019/9860471. [Google Scholar] [CrossRef]

53. Sajid, T., Tanveer, S., Sabir, Z., Guirao, J. L. G., (2020). Impact of activation energy and temperature-dependent heat source/sink on Maxwell–sutterby fluid. Mathematical Problems in Engineering, 2020. DOI 10.1155/2020/5251804. [Google Scholar] [CrossRef]

54. Sabir, Z., Ayub, A., Guirao, J. L., Bhatti, S., Shah, S. Z. H. (2020). The effects of activation energy and thermophoretic diffusion of nanoparticles on steady micropolar fluid along with brownian motion. Advances in Materials Science and Engineering, 2020. DOI 10.1155/2020/2010568. [Google Scholar] [CrossRef]

55. Shaikh, T. S., Fayyaz, N., Ahmed, N., Shahid, N., Rafiq, M. et al. (2021). Numerical study for epidemic model of hepatitis-b virus. The European Physical Journal Plus, 136(4), 1–22. DOI 10.1140/epjp/s13360-021-01248-8. [Google Scholar] [CrossRef]

56. Farooqi, A., Ahmad, R., Alotaibi, H., Nofal, T. A., Farooqi, R. et al. (2021). A comparative epidemiological stability analysis of predictor corrector type non-standard finite difference scheme for the transmissibility of measles. Results in Physics, 21, 103756. DOI 10.1016/j.rinp.2020.103756. [Google Scholar] [CrossRef]

57. Sanchez, Y. G., Sabir, Z., Guirao, J. L. (2020). Design of a nonlinear SITR fractal model based on the dynamics of a novel coronavirus (COVID). Fractals, 28, 2040026. DOI 10.1142/S0218348X20400265. [Google Scholar] [CrossRef]

58. Umar, M., Sabir, Z., Raja, M. A. Z., Amin, F., Saeed, T. et al. (2021). Integrated neuro-swarm heuristic with interior-point for nonlinear SITR model for dynamics of novel COVID-19. Alexandria Engineering Journal, 60(3), 2811–2824. DOI 10.1016/j.aej.2021.01.043. [Google Scholar] [CrossRef]

images This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.