Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2021.016775

ARTICLE

Monte Carlo Simulation of Fractures Using Isogeometric Boundary Element Methods Based on POD-RBF

Haojie Lian1, Zhongwang Wang2,3,*, Haowen Hu3, Shengze Li4, Xuan Peng5 and Leilei Chen2,3

1Key Laboratory of In-Situ Property-Improving Mining of Ministry of Education, Taiyuan University of Technology, Taiyuan, 030024, China
2School of Architecture and Civil Engineering, Huanghuai University, Zhumadian, 463003, China
3College of Architecture and Civil Engineering, Xinyang Normal University, Xinyang, 464000, China
4Artificial Intelligence Research Center, National Innovation Institute of Defense Technology, Beijing, 100071, China
5Department of Mechanical Engineering, Suzhou University of Science and Technology, Suzhou, 215009, China
*Corresponding Author: Zhongwang Wang. Email: wangzw9620@163.com
Received: 25 March 2021; Accepted: 22 April 2021

1  Introduction

Uncertainties are ubiquitous in engineering applications that may arise from different sources such as inherent material randomness, geometric dimensions, manufacturing errors, and dynamic loading. Because deterministic analysis fails to characterize randomness field, stochastic analysis techniques have been extensively studied to strengthen the credibility of computational prediction of uncertainty problems [1]. There are three main variants of stochastic analysis: perturbation based techniques [2], stochastic spectral approaches [3,4], and Monte Carlo simulation (MCs) [5–7]. Among them, the MCs is regarded as the most versatile and simplest approach, and often used as the reference solution to verify the results of Perturbation method and Spectral method, but the exhaustive sampling in MCs leads to a heavy computational burden arising from both solving physical problems and constructing analysis-suitable geometric models that must be addressed carefully.

Combining Proper Orthogonal Decomposition (POD) and Radial Basis Functions (RBF) [8–11] is an effective technique of model order reduction [12–14]. The POD represents the solution field with the special ordered orthogonal functions in a low-dimensional subspace, which is constructed based on a discrete number of system responses obtained from the evaluation of the full order models (FOM) [15]. POD reduces the degrees of freedom by capturing the dominant components of high-dimensional processes because it offers the optimal basis in the sense that the approximation error is minimal in L2 norm. On the other hand, the RBF builds a surrogate model through interpolating the data in the reduced space, whereby it admits continuous approximation of system responses for any arbitrary combination of input parameters [16] and thus does not need to solve partial differential equation for each sample.

The pre-processing time of MCs in constructing geometric models can be reduced with isogeometric analysis (IGA) [17]. The key idea of IGA is employing spline functions used to construct geometric models in Computer Aided Design (CAD), for example Non-Uniform Rational B-splines (NURBS), T-splines [18], PHT-splines [19,20], and subdivision surfaces [21], as the basis functions to discretize physical fields. Compared to traditional Lagrange polynomial based methods, the main advantage of IGA lies in its ability of integrating numerical analysis and CAD. IGA enables one to perform numerical analysis directly from CAD models without meshing, which is particularly beneficial to uncertainty qualification since it requires fast generation of a large number of models. IGA also offers the benefits of geometric exactness, flexible refinement scheme and high order continuity that are amenable to numerical analysis.

Fracture mechanics is crucial in structural integrity assessment and damage tolerance analyses, but simulation of fracture behaviors poses significant challenges to Finite Element Methods (FEM) for the following reasons: (1) the mesh in proximity to cracks should be several orders of magnitude finer than that used for stress analysis; (2) a remeshing procedure is inevitable when cracks extend; (3) stress singularity or high stress gradients need to be captured. The extended finite element method (XFEM) incorporates enrichment functions to solution space and thus allows for crack propagation in a fixed mesh, but it still relies on a fine and good-quality mesh and necessitates special techniques to represent crack surfaces like Level Set Method. In comparison, Boundary Element Method (BEM) [22–26] has proven a useful tool for fracture simulation. Since BEM only discretizes the boundary of the domain, it not only reduces the degrees of freedom and facilities mesh generation, but more importantly, extends the crack by simply adding new elements at the front of cracks. In addition, as a semi-analytical method, BEM evaluates stress more accurately which is critical in extracting stress intensity factors. Furthermore, isogeometric analysis within the context of boundary element method (IGABEM) inherits the advantage of IGA in integration of CAD and numerical analysis and that of BEM in dimension reduction. IGA with BEM is also natural because both of them are boundary-represented. Since its inception, IGABEM has been successfully applied to potential [27–31], linear elasticity [32–36], acoustics [37–44], electromagnetics [45], structural optimization [40,46–49], etc., Peng et al. [50,51] applied IGABEM to two dimensional and three dimensional linear elasticity fracture mechanics, and demonstrates the accuracy and efficiency of IGABEM in this area.

This paper presents a novel procedure for solving uncertainty problems of fracture mechanics. In this method, the IGABEM is employed for fracture analysis, and MCs for addressing multiple random parameters. The computational cost is reduced by combination of POD and RBF. The remaining of this paper is structured as follows. Section 2 introduces the fundamentals of MCs in stochastic analysis. Section 3 illustrates how to apply POD and RBF to MCs. Section 4 formulates IGABEM in linear elasticity fracture mechanics. Several numerical examples are given in Section 5 to test the reliability, accuracy and efficiency of the proposed method, followed by conclusions in Section 6.

2  Stochastic Analysis with Monte Carlo Simulation

Monte Carlo simulation (MCs) directly characterizes uncertainties by calculating expectations and variances from a large number of samples. For a random variable X associated with the probability density function p(x), the two probabilistic moments are defined as

E[X]=∫-∞+∞xp(x)dxD[X]=∫-∞+∞(x-E[X])2p(x)dx(1)

where E[X] is the expectation of the random variable X, and D(X) represents its variance, whose square root is the standard deviation.

According to the law of large numbers, the average of the results obtained from a number of samples should converge to the expectation as more sampling points are selected, which is the theoretical basis of MCs. Suppose g(X) is an arbitrary function of the random variable X. The expectation and variance of g(X) can be approximated by

E[g(X)]≈1N∑i=1Ng(xi) (2)

D[g(X)]≈1N-1[∑i=1N(g(xi)-E[g(x)])]2 (3)

where N is the sample size, and the order of convergence rate is O(N−1/2).

MCs in structural analysis can be conducted in the following steps [15]: (1) Identify the random variables that are the source of the uncertainties in the system. (2) Determine the probability density functions of the random variables. (3) Use a random number generator to produce a set of samples which are adopted as the input parameters. (4) Employ a numerical method in deterministic analysis to evaluate the solution for each sample. (5) Based on the outputs of numerical analysis for all of the samples, we calculate the expectation and variance of the system using Eqs. (2) and (3) [52]. From the above, it can be seen that MCs is easy to implement because the existing numerical simulation codes can be directly used without modification. In addition, MCs is versatile and is suitable for complex uncertainty problems. However, Step 3 of MCs is very time consuming because the numerical simulation needs to be conducted as many times as the number of sampling points. The large sample size can enhance the accuracy but may lead to higher computational cost.

3  Proper Orthogonal Decomposition (POD) and Radial Basis Functions (RBF)

As mentioned above, MCs is prohibitively expensive because it needs to solve the physical problems at many samples. This procedure can be accelerated by the reduced-order moeling based on POD and RBF. Let α be an input random variable that has an influence on the structural responses. At the first step, we solve the FOM for a series of samples αi of the random variable. The system responses λ(αi) corresponding to the i-th sample point is called snapshots, which can be collected to form the following snapshot matrix Λ:

Λ=[λ(α1),λ(α2),…,λ(αm)]=[λ11λ12…λ1mλ21λ22…λ2m⋮⋮⋱⋮λn1λn2…λnm](4)

where Λ∈Rn×m, n indicates the number of responses for any input variable, and m the number of samples. λi,j is the i-th response of the structure for the j-th sample. Decomposing the matrix Λ through Singular Value Decomposition (SVD), we arrive at

Λ=UΣVT=∑j=1rujσjvjT(5)

where r= min(m,n). U∈Rn×n and V∈Rm×m are orthogonal matrices whose entries are denoted by uij and vij, respectively. uj and vj are the eigenvectors of ΛΛT and ΛTΛ, respectively. The two eigenvectors are also called the left and right singular matrices of matrix Λ, respectively. Σ∈Rn×m is a diagonal matrix in which the diagonal elements σj (also called singular values) are arranged in descending order.

By defining φj=uj and aj(αi)=σjvij, Eq. (5) can be rewritten as

λ(αi)=∑j=1rφjaj(αi)(6)

where φj is defined as the orthogonal basis, and aj(αi) is the corresponding amplitude. Using Eq. (6), the system responses at the selected samples can be expressed by a linear combination of φj and aj(αi), which constitutes a reduced-order model (ROM) with less degrees of freedom than the FOM.

Eq. (6) only approximates a discrete number of system responses that are already computed using the FOM. To achieve a continuous approximation of system responses for any arbitrary input parameters, the radial basis functions (RBF) are used to interpolate the amplitudes in the reduced subspace

a(α)≈â(α)=∑i=1Nηiϕi(α)(7)

where N is the number of samples, ϕi is the i-th RBF and ηi the corresponding coefficient. ϕ(α) takes the form of Gaussian kernel function

ϕi(α)=e-(1/γi2)∥α-αi∥(8)

in which the symbol ∥⋅∥ represents the Euclidean norm, and the coefficient γi determines the width of the basis functions.

By letting a(αj)=â(αj), the values of the coefficient η can be determined by solving Eq. (7). Substituting Eq. (7) into Eq. (6) gives rise to

λ(α)=∑j=1rφjâj(α)(9)

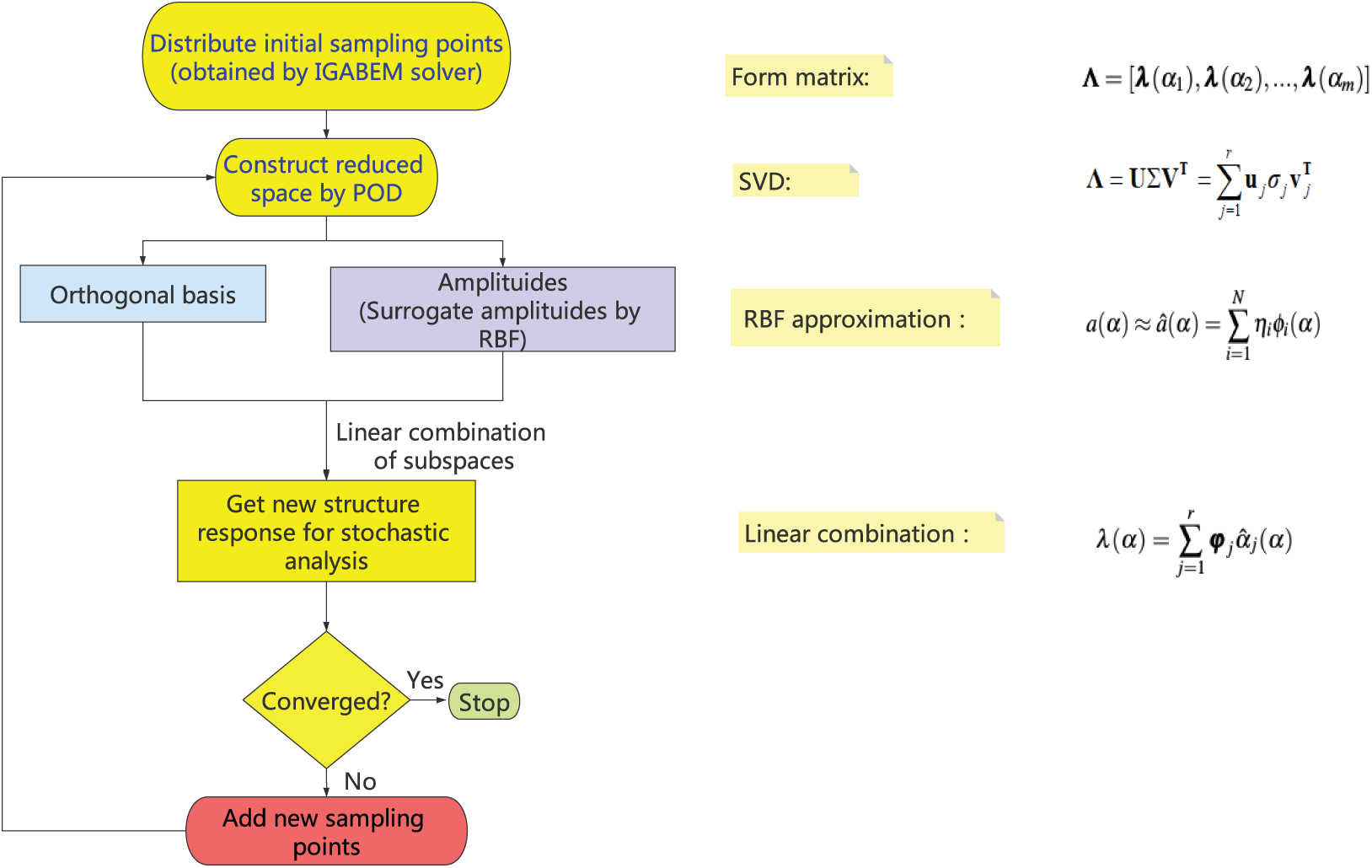
Figure 1: Th flow chart

Hence, the system response for any sample of the stochastic variable can be obtained straightforwardly by Eq. (9) without needing to solve the partial differential equations repeatedly. The algorithm mentioned above is illustrated in the Fig. 1. The POD-RBF enable us to conduct MCs without needing to perform FOM simulation for all of the sample points. However, the FOM is still essential for getting snapshots which is solved by IGABEM in our work as detailed in the following section. Therefore, the number of the samples or snapshots should be selected carefully to strike a balance between the accuracy and efficiency. In the future, we will introduce error estimation technique to improve the performance of our method. In addition, it is highlighted that in order to further enhance the computational efficiency, the number of basis functions in Eqs. (5) and (9) can be decreased by selecting the basis functions corresponding to the elements with larger values in Σ.

4  Fracture Modeling with IGABEM

4.1 Boundary Integral Equations in Fracture Mechanics

Consider an arbitrary domain Ω enclosed by boundary Γ, where the portion of boundary Γū is prescribed displacement boundary condition, Γt̄ is imposed traction boundary condition, and Γc is a traction free crack with the upper surface Γc+ and the lower surface Γc- (Fig. 2).

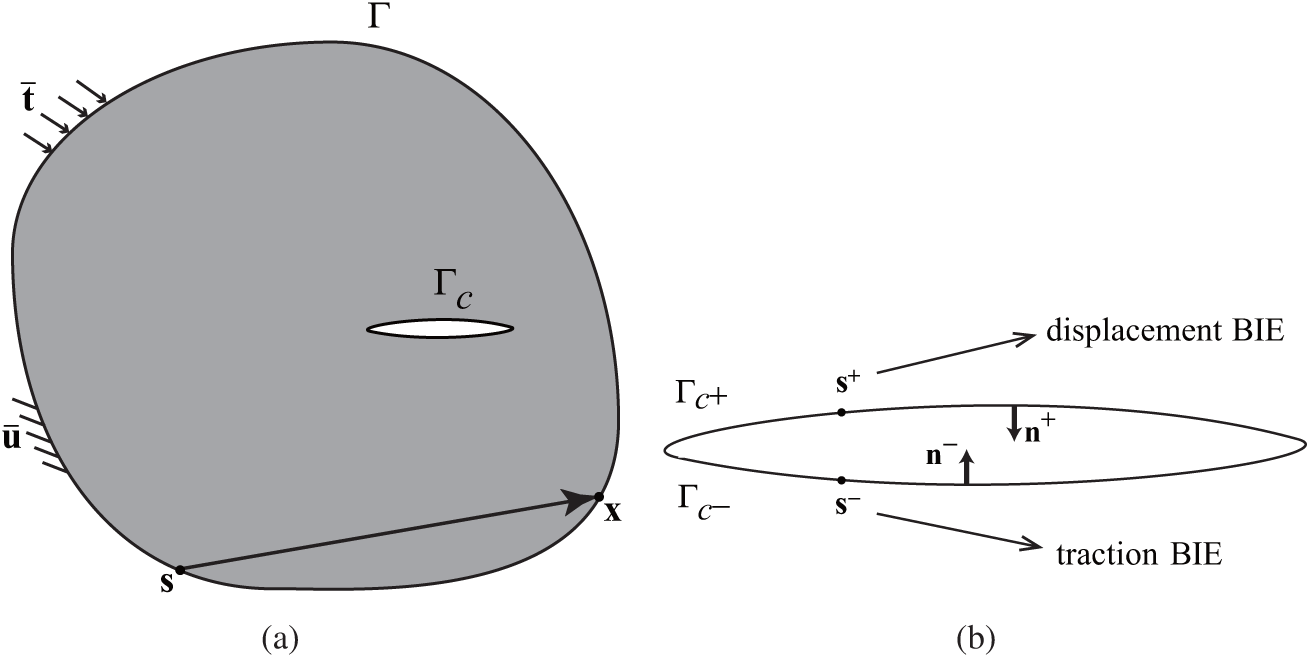
Figure 2: A crack model (a) a cracked elastic body; (b) crack surfaces

Because the crack upper surfaces and lower surfaces are geometrically overlapping, the source points on the two surfaces will coincide and thus the boundary integral equations (BIE) corresponding to them are identical to each other, which leads to the degradation of the system matrix. An effective approach—dual boundary element method (DBEM) [53] can overcome this difficulty by using the traction BIE on one of the crack surface (Γc+), and the displacement BIE on the other crack surface (Γc-) and the rest of the boundary (Γ) (Fig. 2b) [53], i.e.,

cij(s)uj(s)=∫Γ[Uij*(s,x)tj(x)-Tij*(s,x)uj(x)]dΓ(x),for s∈Γc-cij(s)tj(s)=∫Γ[Dijk*(s,x)tj(x)-Sijk*(s,x)uj(x)]dΓ(x),for s∈Γc+(10)

where s and x are the source point and the field point, respectively. Uij* and Tij* are the fundamental solutions of displacement boundary integral equations, and D*ijk and S*ijk are fundamental solutions of traction boundary integral equations (Appendix A). cij(s) denotes the jump term and equals 0.5 δij for smooth boundaries.

4.2 IGABEM for Fracture Mechanics

As a powerful geometric modeling technique, NURBS is the industrial standard of CAD and also central to isogeometric analysis. Given a knot vector Ξ=[ξ0,ξ1,…,ξm], which is a non-decreasing set of coordinates in parametric space, a B-spline basis function is defined as follows:

Ni,0={1,if ξi≤ξ<ξi+10,otherwise (11)

Ni,p(ξ)=ξ-ξiξi+p-ξiNi,p-1(ξ)+ξi+p+1-ξξi+p+1-ξi+1Ni+1,p-1(ξ) (12)

where n denotes the order of basis functions and ξ the parametric coordinate. As an extension of B-splines, NURBS basis function is written as

Ri,p(ξ)=Ni,p(ξ)wi∑k=1nNk,p(ξ)wk(13)

where Ri,p(ξ) is the NURBS basis function and wi the weight. A NURBS curve can be constructed by linear combination of NURBS basis functions and the associated coefficients

x(ξ)=∑i=1nRi,p(ξ)Pi(14)

where x stands for the Cartesian coordinate of a point and ξ is its parametric coordinate. Pi represents the Cartesian coordinates of control points in the physical space.

In IGABEM, NURBS are used not only for building geometries but also discretizing the boundary integral equations. Hence, the displacement and traction around the boundary can be expressed piecewisely as a linear combination of the NURBS basis function and the nodal parameters,

uj(ξ)=∑l=1p+1Rl,p(ξ)djltj(ξ)=∑l=1p+1Rl,p(ξ)qjl(15)

where djl and qjl are the coefficients for discretizing the displacements and the tractions, respectively. It is noteworthy that they are not the nodal displacements or tractions because the NURBS basis functions lack the Kronecker-delta property.

By substituting Eq. (15) into the boundary integral equation (10), we can get the following discretization formulation of Eq. (10)

cij(s)∑I=1p+1NIē(ξ^′)djIē=∑e=1Ne∑I=1p+1[∫-11Uij*(x(ξ^),s)NIe(ξ^)J(ξ^)dξ^]qjIe-∑e=1Ne∑I=1p+1[∫-11Tij*(x(ξ^),s)NIe(ξ^)J(ξ^)dξ^]djIe(16)

cij(s)∑I=1p+1NIē(ξ^′)tjIē=∑e=1Ne∑I=1p+1[∫-11Dijk*(x(ξ^),s)NIe(ξ^)J(ξ^)dξ^]qjIe-∑e=1Ne∑I=1p+1[∫-11Sijk*(x(ξ^),s)NIe(ξ^)J(ξ^)dξ^]djIe(17)

where ē represents the ē-th NURBS element, and ξ^′ is the local coordinate of the collocation point. In order to perform Gaussian quadrature, we map all the variables from physical space to local coordinate space ξ^∈(-1,1), and the Jacobian transformation matrix J(ξ^) is calculated as follows:

J(ξ^)=dΓdξ^=dΓdξdξdξ^(18)

The boundary element method involves weakly singular, strongly singular and hyper singular integrals, which have to be addressed carefully. For this purpose, the subtraction of singularity technique is used, whose implementation details can be seen in [50]. After solving the governing linear equations of IGABEM, we can obtain the displacement and traction field around the boundary. Then, we are able to evaluate the stress intensity factors (SIFs) with M integral [54] and predict the crack propagation direction with maximum hoop stress criterion [55]. See Appendix B for details.

5  Numerical Examples

In the following examples, the input random variables are supposed to follow the Gaussian distribution with the expectation being 0.5 and the standard deviation being 0.033. The sampling method for Gaussian distribution function used in this paper is to select sample points in the interval [E-3D,E+3D]. It is noted that only the problems with a single random input variable are considered in the present paper.The application of the method for the problems with multidimensional random input variables will be investigated in the future.

5.1 Inclined Center Crack Problem

A plate model with an inclined center crack under remote biaxial tension is considered in this section, as shown in Fig. 3. The crack inclination angle is β∈[0,π/2], edge length L = 1, and crack length 2a = 0.02. The load σ0 is applied in the X2-direction and λσ0 is applied in the X1-direction, in which λ is the load ratio that varies from 0 to 1 and σ0=1. The Young’s modulus is E = 1 and Poisson’s ratio υ=0.3. The M integral method is used for evaluating SIFs in this example. The analytical solution of the SIFs for the inclined center crack problem is available, as follows [56]:

K1=σπa(cos2β+λsin2β)K2=σπa(1-λ)cosβsinβ(19)

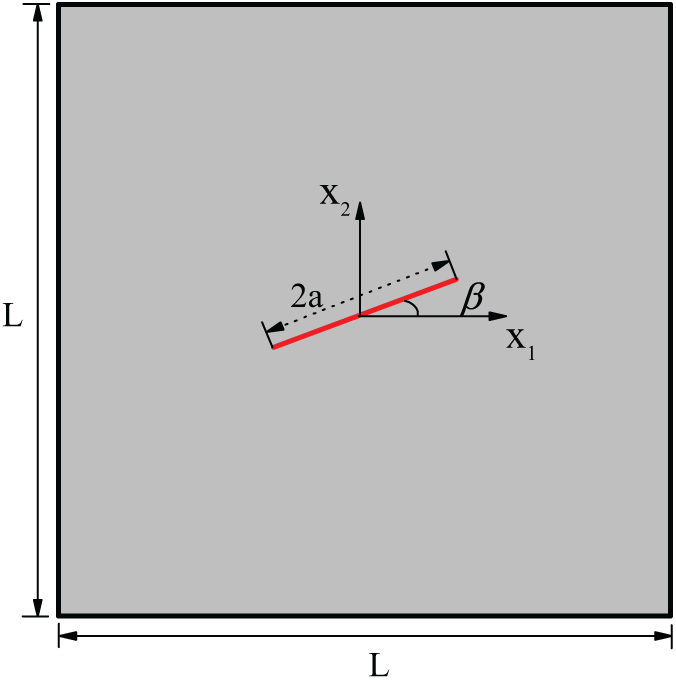
Figure 3: Structural model for an inclined center crack problem

The number of NURBS elements on the initial crack surface is set as 3, and the total DOFs is 86. We fix the crack angle β to be π/4, and set the load ratio λ as the input parameter. The response vector consists of 48 nodal displacements in X2-direction and two SIFs (K1 and K2). Before MCs is carried out we firstly test the accuracy of ROM in evaluating SIFs. We select 21 sample points of λ that are evenly distributed in the interval [0,1] to get the reduced bases of POD and interpolate the system responses with RBF. It is found that the values of K1 and K2 computed by the numerical solution with ROM have a good agreement with the analytical solutions, as shown in Fig. 4.

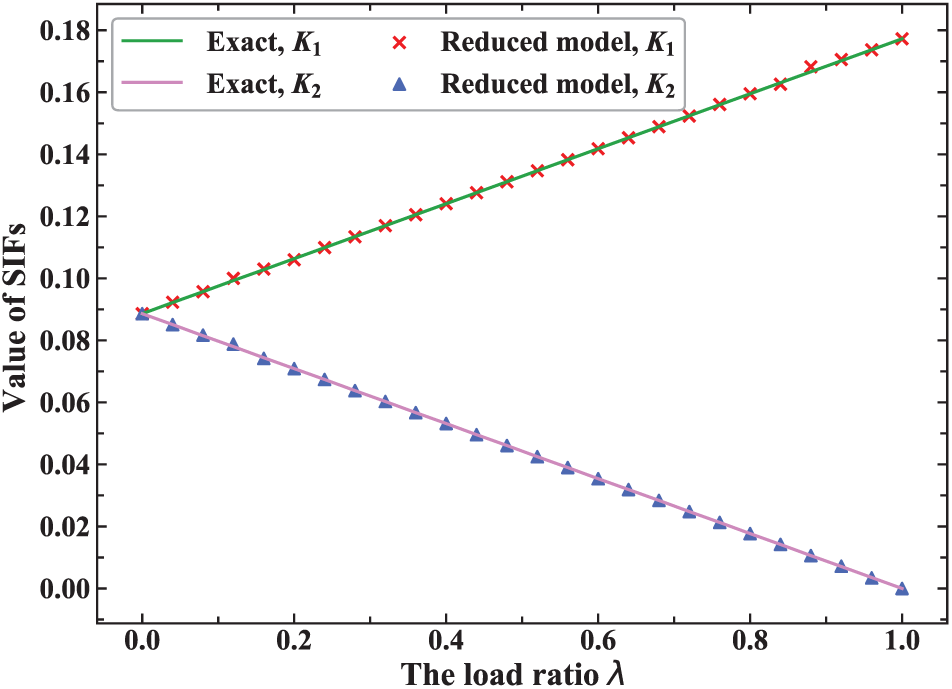
Figure 4: The variation of SIFs with the load ratio λ

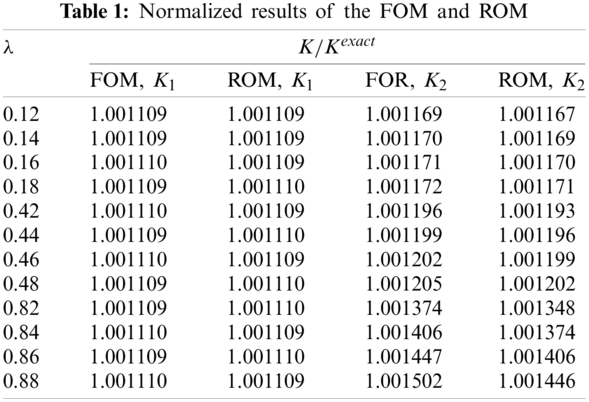
Tab. 1 lists the normalized values of SIFs (the values divided by the exact solution) calculated by the FOM with IGABEM and that by the ROM with POD-RBF. The normalized value of K1 changes slightly with the increase of λ, while the normalized value of K2 increases steadily. Generally, both the results of the FOM and ROM are in good agreement with the analytical solutions. It is worth noting that the width γ of Gaussian kernel function has an important influence on the accuracy of RBF interpolation. According to the literature [57], the parameter γ can be determined via γ=N-1m, where N represents the number of samples and m represents the dimension of the random variable.

To investigate the influence of the sample size on the accuracy of ROM, we construct a vector, 0.02,0.04,…,1, for different values of λ. From the vector, 20, 40, 60 and 80 samples are selected to form the reduced space, respectively, and the remaining points of the vector are used as the prediction points whose SIFs are computed with the ROM based on POD-RBF. We introduce R-squared method to quantify the accuracy of numerical results, as follows:

R2=1-∑i=1n(yi-ŷi)2∑i=1n(yi-ȳi)2(20)

where n is the total number of the predication points, the subscript i the i-th prediction point, yi the numerical value of the SIF, ŷi the analytical solution of the SIF, and ȳi the average of the analytical solutions of the SIFs over these prediction points. The value of evaluation coefficient R2 is between 0 and 1, which indicates the deviation of numerical solutions and the exact solutions. The closer its value is to 1, the higher the accuracy of the numerical result is. As shown in Tab. 2, the evaluation coefficient R2 gradually increases with the sample number. When the sample number is 80, the evaluation coefficient R2 is 1.000, suggesting that the result of ROM is consistent with the analytical solution. It is also noted that R2 = 0.859 when the sample size is 20, so a good accuracy can still be reached with moderate sample size.

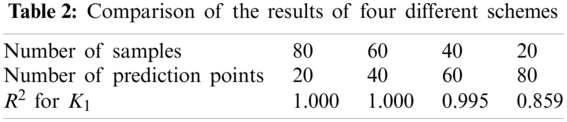
Next, we conduct MCs to evaluate the expectation and standard deviation of stress intensity factors. The following three different schemes are adopted for comparison.

1.    Stochastic fracture analysis with MCs using FOM is conducted based on 51 samples of λ that are evenly distributed between 0 and 1. Correspondingly the system equations need to be solved with IGABEM 51 times.

2.    We build the ROM with 10, 20, 30, and 40 samples, respectively, and then perform MCs using the 51 samples. In this case, the dimension of the matrix Σ in Eq. (5) is selected as min(m,n).

3.    Similar to Case 2, the MCs is performed with the ROM that is established with 10, 20, 30 and 40 samples, respectively. However, we will further decrease the number of the reduced bases of the ROM by truncating the Σ matrix by 10-0.22σmax.

As can be seen from Figs. 5 and 6, when the number of samples for reduced-order modeling is small, the results of Cases 2 and 3 have large deviation from that of Case 1. However, with the increase of samples, the solutions of Cases 2 and 3 approach that of Case 1 rapidly. With 30 samples, the solutions of Cases 2 agree with Case 1 well, which demonstrates that the combination of POD and RBF can evaluate the expectation and standard deviation in stochastic analysis accurately. In addition, because the number of reduced bases in Case 3 is decreased, a larger error occurs compared to Case 2 although the computational time is further accelerated. Therefore, it is very important to select an appropriate order for the ROM based on POD-RBF to strike a balance between its accuracy and efficiency.

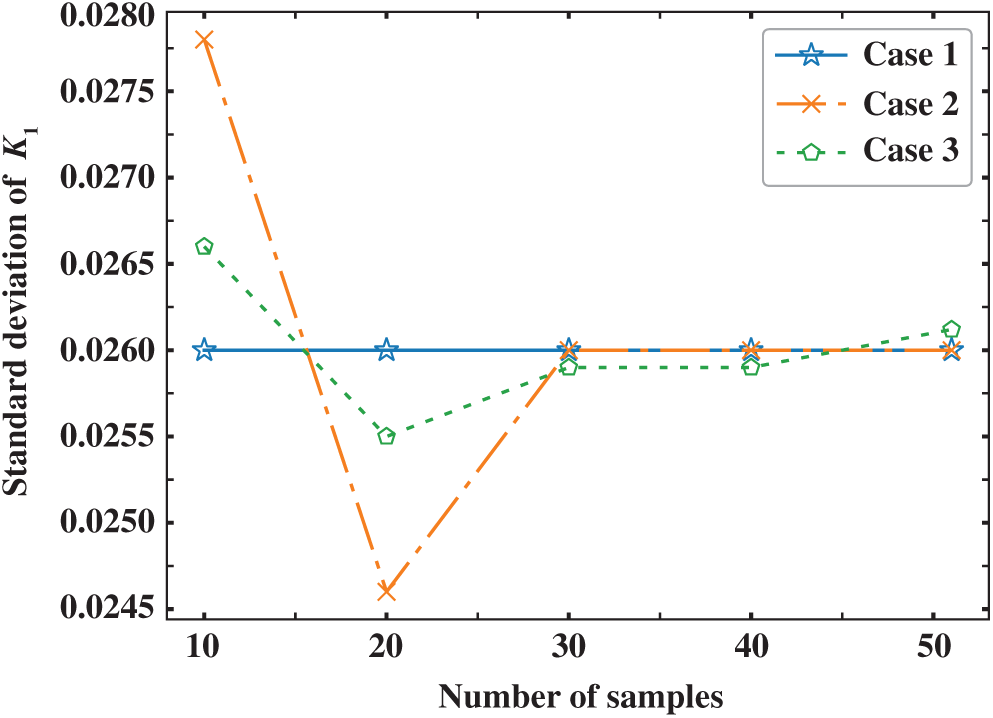
Figure 5: Standard deviation of K1

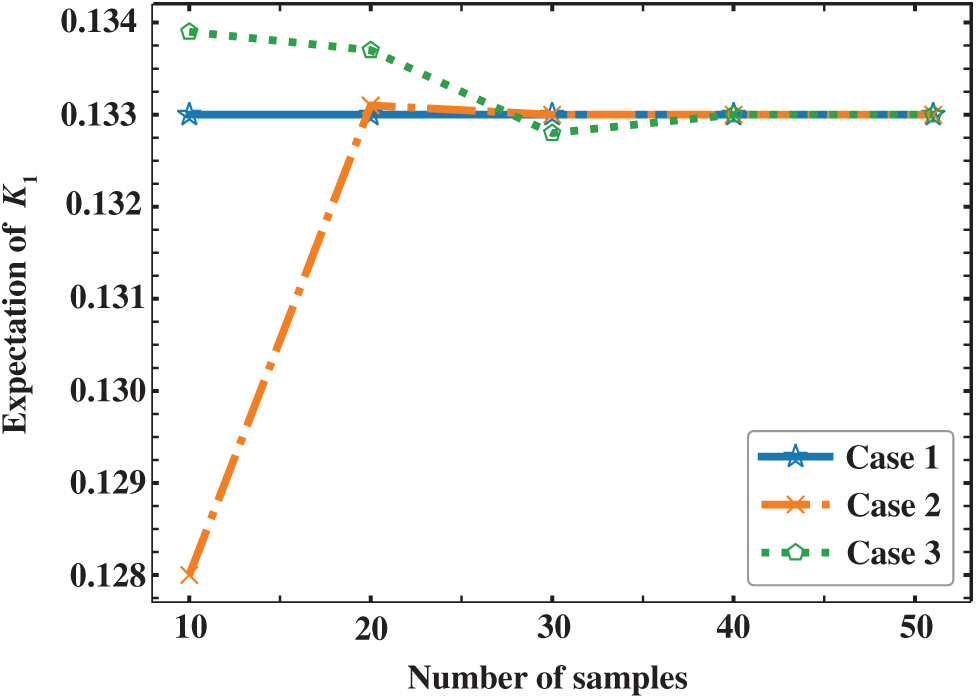
Figure 6: Expectation of K1

Now we fix the load ratio λ at 0.5, and study the influence of the crack inclination angle β on the fracture analysis results. 50 samples of the input parameter β∈(0,π2) are used for Monte Carlo simulation, in which 25 samples are used for ROM. The SIFs in terms of different input variables are evaluated by POD-RBF and FOM, respectively (Fig. 7). Tab. 3 lists the values of the expectation and standard deviation of SIFs computed by MCs with FOM and ROM, respectively. It can be found from this table that the results of ROM and the FOM have good agreement to each other, which verifies the correctness and effectiveness of the algorithm.

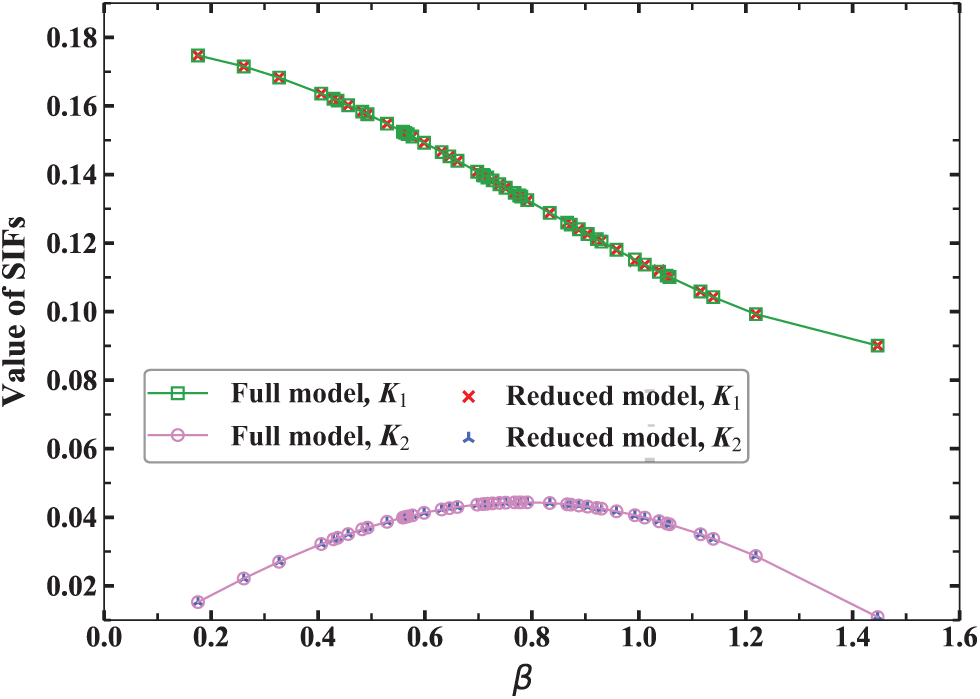
Figure 7: The value of SIFs obtained by using FOM and ROM

5.2 Cracks at Rivet Holes

In this section, we further test the performance of this algorithm using an example of a plate with two rivet holes, as shown in Fig. 8. The Young’s modulus is E = 1000 and Poisson’s ratio υ=0.3. The load is σy=1 and σx=0. The crack inclination angle θ=π/4, initial crack length a = 0.1, and the number of NURBS elements on the crack surface is 3.

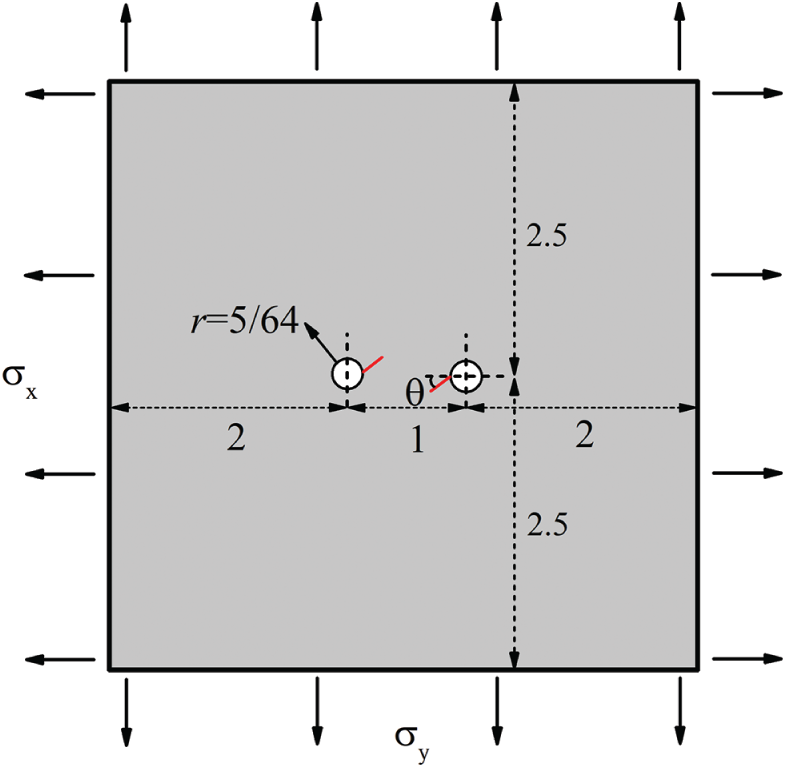
Figure 8: A plate with initial cracks emanating from the holes [58]

Suppose the radius r∈(0.041,0.286) of the right circular hole is a random variable and follows a Gaussian distribution. Based on the FOM simulation with IGABEM, Fig. 9 shows that the K1 of the right crack increases significantly with r. We select 20 samples to construct ROM, and conduct MCs with 40 sampling points. Tab. 4 shows the expectation, standard deviation and calculation time of MCs with FOM and ROM. It can be seen that the ROM leads to the results that are consistent with the FOM, and meanwhile reduces computational time.

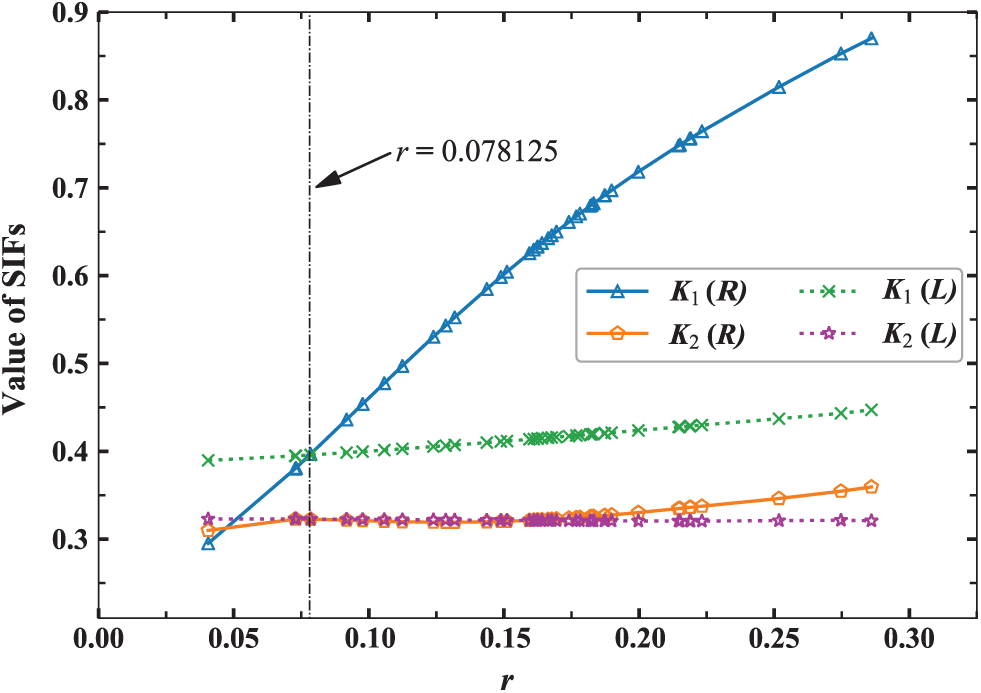
Figure 9: The value of SIFs for two crack surface with the input parameter

Now we consider the influence of material parameter on displacement of cracks. The elastic modulus E∈(500,1500) is set as the input variable, which follows Gaussian distribution. 51 samples are used for MCs, and 25 samples are used to construct the ROM based on POD and RBF. We choose the displacements of four collocation points on the crack surface as the response functions, whose coordinates are (2.91598244, 2.49410744), (2.85147368, 2.42959868), (2.08401756, 2.50589256), and (2.14852632, 2.57040132), respectively. Tab. 5 shows the expectation, relative standard deviation (RSD) of the displacement in y direction and calculation time corresponding to reduced-order and full-order MCs, respectively. It can be found from Tab. 5 that the stochastic analysis results of ROM are consistent with that of FOM.

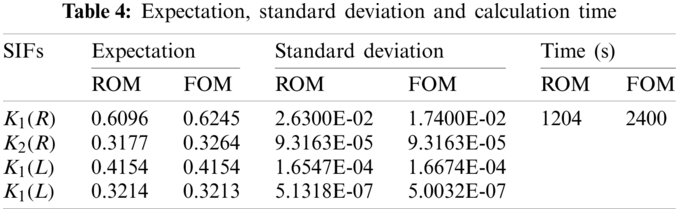
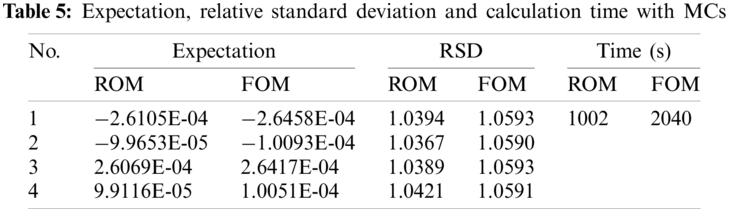
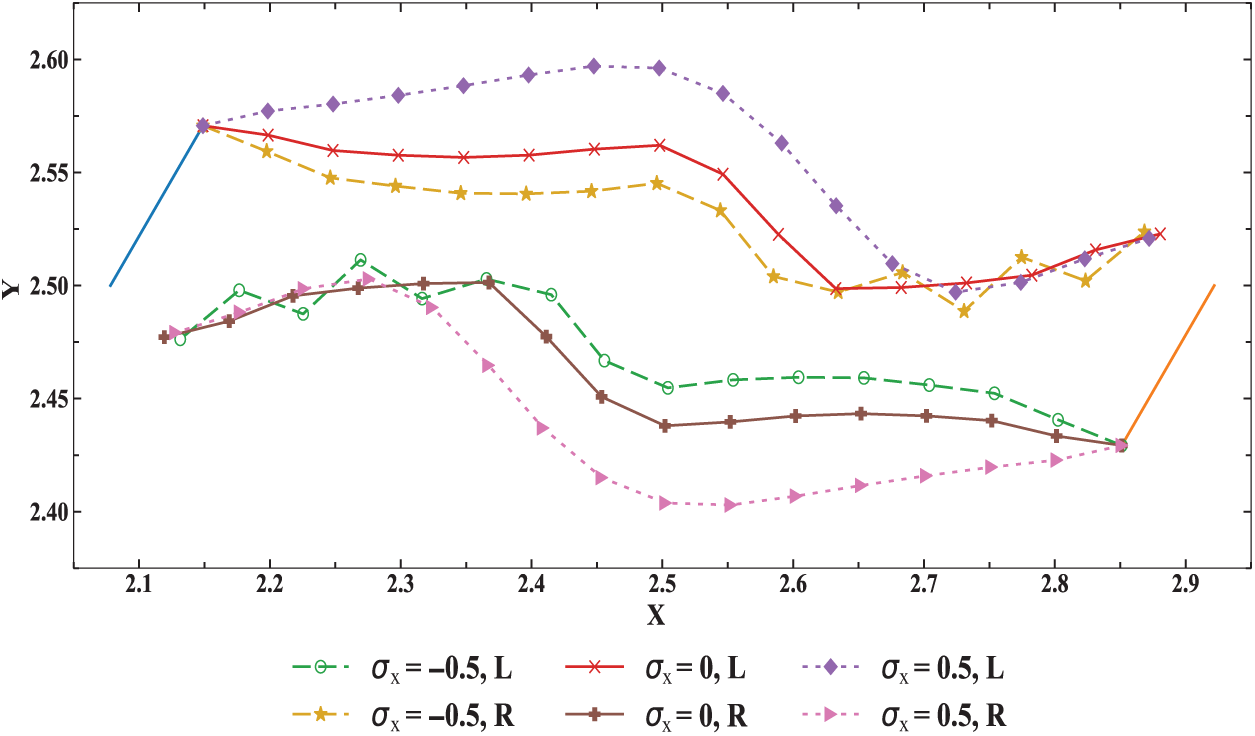
Figure 10: Crack propagation path under different loads

We also study how the crack propagation path is influenced by the input parameter of σx. The crack propagation distance is fixed at 0.05 for each iteration step. A total of 16 steps are solved here. The path of crack propagation for σx=-0.5,0,0.5 is depicted in Fig. 10. Supposing the input parameter σx follows Gaussian distribution, we calculate the expectation and standard deviation of crack propagation path, which are represented by the coordinates of a series of crack tip positions. 10 samples are employed for reduced-order modeling and and 20 samples for MCs. It can be seen from Tab. 6 that the expectation and standard deviation of the crack extension path obtained from the ROM and that from the FOM have good consistency. It demonstrates the correctness and effectiveness of the stochastic analysis method proposed in this work.

6  Conclusion

The paper presents a novel framework for Monte Carlo simulation of multi-dimensional uncertainties of two-dimensional linear fracture mechanics. We use the NURBS to build the geometric model and discretize boundary integral equations. The IGABEM eliminates the repeatedly meshing procedure in uncertainty quantification, and retains the geometric exactness. The combination of POD and RBF accelerates the stochastic analysis and maintains good accuracy at low frequencies. In this work, the POD-RBF is used to approximate the structural response of a single random input variable. The method can also be extended to the problems with multidimensional random input variables, which will be investigated in the future. In addition, the present method will be applied to three dimensional problems and multi-physics coupling problems.

Funding Statement: The authors thank the financial support of National Natural Science Foundation of China (NSFC) under Grant (Nos. 51904202, 11902212, 11901578).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Stefanou, G. (2009). The stochastic finite element method: Past, present and future. Computer Methods in Applied Mechanics and Engineering, 198(9), 1031–1051. DOI 10.1016/j.cma.2008.11.007. [Google Scholar] [CrossRef]

 2.  Marcin, K. (2007). Generalized perturbation-based stochastic finite element method in elastostatics. Computers and Structures, 85(10), 586–594. DOI 10.1016/j.compstruc.2006.08.077. [Google Scholar] [CrossRef]

 3.  Ghanem, R., Spanos, P. (1991). Stochastic finite elements: A spectral approach. Berlin, Germany: Springer-Verlag. [Google Scholar]

 4.  Chen, N., Soares, C. (2008). Spectral stochastic finite element analysis for laminated composite plates. Computer Methods in Applied Mechanics and Engineering, 197(51–52), 4830–4839. DOI 10.1016/j.cma.2008.07.003. [Google Scholar] [CrossRef]

 5.  Hurtado, J., Barbat, A. (1998). Monte carlo techniques in computational stochastic mechanics. Archives of Computational Methods in Engineering, 5(1), 3–30. DOI 10.1007/BF02736747. [Google Scholar] [CrossRef]

 6.  Spanos, P., Zeldin, B. (1998). Monte carlo treatment of random fields: A broad perspective. Applied Mechanics Reviews, 51(3), 219–237. DOI 10.1115/1.3098999. [Google Scholar] [CrossRef]

 7.  Feng, Y., Li, C., Owen, D. (2010). A directed monte carlo solution of linear stochastic algebraic system of equations. Finite Elements in Analysis and Design, 46(6), 462–473. DOI 10.1016/j.finel.2010.01.004. [Google Scholar] [CrossRef]

 8.  Broomhead, D., Lowe, D. (1998). Radial basis functions, multi-variable functional interpolation and adaptive networks. Royal signals and radar establishment. The Annals of Statistics, 26(3), 801–849. [Google Scholar]

 9.  Buljak, V., Maier, G. (2011). Proper orthogonal decomposition and radial basis functions in material characterization based on instrumented indentation. Engineering Structures, 33(2), 492–501. DOI 10.1016/j.engstruct.2010.11.006. [Google Scholar] [CrossRef]

10. Buljak, V. (2012). Proper orthogonal decomposition and radial basis functions for fast simulations. Inverse analyses with model reduction, pp. 85–139. Berlin, Germany: Springer. [Google Scholar]

11. Rogers, C., Kassab, A., Divo, E., Ostrowski, Z., Bialecki, R. (2012). An inverse pod-RBF network approach to parameter estimation in mechanics. Inverse Problems in Science and Engineering, 20(5), 749–767. DOI 10.1080/17415977.2012.693080. [Google Scholar] [CrossRef]

12. Pinnau, R. (2008). Model reduction via proper orthogonal decomposition. Berlin Heidelberg: Springer. [Google Scholar]

13. Chinesta, F., Ladeveze, P., Cueto, E. (2011). A short review on model order reduction based on proper generalized decomposition. Archives of Computational Methods in Engineering, 18(4), 395–404. DOI 10.1007/s11831-011-9064-7. [Google Scholar] [CrossRef]

14. Kerfriden, P., Goury, O., Rabczuk, T., Bordas, S. (2013). A partitioned model order reduction approach to rationalise computational expenses in nonlinear fracture mechanics. Computer Methods in Applied Mechanics and Engineering, 256(5), 169–188. DOI 10.1016/j.cma.2012.12.004. [Google Scholar] [CrossRef]

15. Ding, C., Deokar, R., Cui, X., Li, G., Cai, Y. et al. (2019). Proper orthogonal decomposition and monte carlo based isogeometric stochastic method for material, geometric and force multi-dimensional uncertainties. Computational Mechanics, 63(3), 521–533. DOI 10.1007/s00466-018-1607-4. [Google Scholar] [CrossRef]

16. Li, S., Trevelyan, J., Wu, Z., Lian, H., Wang, D. et al. (2019). An adaptive SVD-Krylov reduced order model for surrogate based structural shape optimization through isogeometric boundary element method. Computer Methods in Applied Mechanics and Engineering, 349(1), 312– 338. DOI 10.1016/j.cma.2019.02.023. [Google Scholar] [CrossRef]

17. Hughes, T., Cottrell, J., Bazilevs, Y. (2005). Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 194(39–41), 4135–4195. DOI 10.1016/j.cma.2004.10.008. [Google Scholar] [CrossRef]

18. Bazilevs, Y., Michler, C., Calo, V., Hughes, T. (2010). Isogeometric variational multiscale modeling of wall-bounded turbulent flows with weakly enforced boundary conditions on unstretched meshes. Computer Methods in Applied Mechanics and Engineering, 199(13–16), 780–790. DOI 10.1016/j.cma.2008.11.020. [Google Scholar] [CrossRef]

19. Nguyen-Thanh, N., Kiendl, J., Nguyen-Xuan, H., Wüchner, R., Bletzinger, K. et al. (2011). Rotation free isogeometric thin shell analysis using PHT-splines. Computer Methods in Applied Mechanics and Engineering, 200(47–48), 3410–3424. DOI 10.1016/j.cma.2011.08.014. [Google Scholar] [CrossRef]

20. Wang, P., Xu, J., Deng, J., Chen, F. (2011). Adaptive isogeometric analysis using rational PHT-splines. Computer-Aided Design, 43(11), 1438–1448. DOI 10.1016/j.cad.2011.08.026. [Google Scholar] [CrossRef]

21. Cirak, F., Scott, M., Antonsson, E., Ortiz, M., Schröder, P. (2002). Integrated modeling, finite-element analysis, and engineering design for thin-shell structures using subdivision. Computer-Aided Design, 34(2), 137–148. DOI 10.1016/S0010-4485(01)00061-6. [Google Scholar] [CrossRef]

22. Banerjee, P., Cathie, D. (1980). A direct formulation and numerical implementation of the boundary element method for two-dimensional problems of elasto-plasticity. International Journal of Mechanical Sciences, 22(4), 233–245. DOI 10.1016/0020-7403(80)90038-7. [Google Scholar] [CrossRef]

23. Cruse, T. (1996). Bie fracture mechanics analysis: 25 years of developments. Computational Mechanics, 18(1), 1–11. DOI 10.1007/BF00384172. [Google Scholar] [CrossRef]

24. Seybert, A., Soenarko, B., Rizzo, F., Shippy, D. (1985). An advanced computational method for radiation and scattering of acoustic waves in three dimensions. The Journal of the Acoustical Society of America, 77(2), 362–368. DOI 10.1121/1.391908. [Google Scholar] [CrossRef]

25. Liu, Y. (2015). Analysis of shell-like structures by the boundary element method based on 3-D elasticity: Formulation and verification. International Journal for Numerical Methods in Engineering, 41(3), 541–558. DOI 10.1002/(SICI)1097-0207(19980215)41:3¡541::AID-NME298¿3.0.CO;2-K. [Google Scholar] [CrossRef]

26. Gu, Y., Gao, H., Chen, W., Zhang, C. (2016). A general algorithm for evaluating nearly singular integrals in anisotropic three-dimensional boundary element analysis. Computer Methods in Applied Mechanics and Engineering, 308(15), 483–498. DOI 10.1016/j.cma.2016.05.032. [Google Scholar] [CrossRef]

27. Gu, J., Zhang, J., Li, G. (2012). Isogeometric analysis in BIE for 3-D potential problem. Engineering Analysis with Boundary Elements, 36(5), 858–865. DOI 10.1016/j.enganabound.2011.09.018. [Google Scholar] [CrossRef]

28. Campos, L., Albuquerque, E., Wrobel, L. (2017). An ACA accelerated isogeometric boundary element analysis of potential problems with non-uniform boundary conditions. Engineering Analysis with Boundary Elements, 80(39), 108–115. DOI 10.1016/j.enganabound.2017.04.004. [Google Scholar] [CrossRef]

29. Gong, Y., Dong, C., Qin, X. (2017). An isogeometric boundary element method for three dimensional potential problems. Journal of Computational and Applied Mathematics, 313, 454–468. DOI 10.1016/j.cam.2016.10.003. [Google Scholar] [CrossRef]

30. Gong, Y., Dong, C., Bai, Y. (2017). Evaluation of nearly singular integrals in isogeometric boundary element method. Engineering Analysis with Boundary Elements, 75(3), 21–35. DOI 10.1016/j.enganabound.2016.11.005. [Google Scholar] [CrossRef]

31. Takahashi, T., Matsumoto, T. (2012). An application of fast multipole method to isogeometric boundary element method for laplace equation in two dimensions. Engineering Analysis with Boundary Elements, 36(12), 1766–1775. DOI 10.1016/j.enganabound.2012.06.004. [Google Scholar] [CrossRef]

32. Simpson, R., Bordas, S., Lian, H., Trevelyan, J. (2013). An isogeometric boundary element method for elastostatic analysis: 2D implementation aspects. Computers & Structures, 118(3), 2–12. DOI 10.1016/j.compstruc.2012.12.021. [Google Scholar] [CrossRef]

33. Scott, M., Simpson, R., Evans, J., Lipton, S., Bordas, S. et al. (2013). Isogeometric boundary element analysis using unstructured T-splines. Computer Methods in Applied Mechanics and Engineering, 254(21–26), 197–221. DOI 10.1016/j.cma.2012.11.001. [Google Scholar] [CrossRef]

34. Gu, J., Zhang, J., Chen, L., Cai, Z. (2015). An isogeometric BEM using PB-spline for 3-D linear elasticity problem. Engineering Analysis with Boundary Elements, 56(11), 154–161. DOI 10.1016/j.enganabound.2015.02.013. [Google Scholar] [CrossRef]

35. Han, Z., Cheng, C., Hu, Z., Niu, Z. (2018). The semi-analytical evaluation for nearly singular integrals in isogeometric elasticity boundary element method. Engineering Analysis with Boundary Elements, 95(39), 286–296. DOI 10.1016/j.enganabound.2018.07.016. [Google Scholar] [CrossRef]

36. Wang, Y., Benson, D. (2015). Multi-patch nonsingular isogeometric boundary element analysis in 3D. Computer Methods in Applied Mechanics and Engineering, 293(41), 71–91. DOI 10.1016/j.cma.2015.03.016. [Google Scholar] [CrossRef]

37. Simpson, R., Scott, M., Taus, M., Thomas, D., Lian, H. (2014). Acoustic isogeometric boundary element analysis. Computer Methods in Applied Mechanics and Engineering, 269(139), 265–290. DOI 10.1016/j.cma.2013.10.026. [Google Scholar] [CrossRef]

38. Keuchel, S., Hagelstein, N., Zaleski, O., von Estorff, O. (2017). Evaluation of hypersingular and nearly singular integrals in the isogeometric boundary element method for acoustics. Computer Methods in Applied Mechanics and Engineering, 325(10), 488–504. DOI 10.1016/j.cma.2017.07.025. [Google Scholar] [CrossRef]

39. Chen, L., Marburg, S., Zhao, W., Liu, C., Chen, H. (2019). Implementation of isogeometric fast multipole boundary element methods for 2D half-space acoustic scattering problems with absorbing boundary condition. Journal of Theoretical and Computational Acoustics, 27(2), 1850024. DOI 10.1142/S259172851850024X. [Google Scholar] [CrossRef]

40. Chen, L., Lian, H., Liu, Z., Chen, H., Atroshchenko, E. et al. (2019). Structural shape optimization of three dimensional acoustic problems with isogeometric boundary element methods. Computer Methods in Applied Mechanics and Engineering, 355(2), 926–951. DOI 10.1016/j.cma.2019.06.012. [Google Scholar] [CrossRef]

41. Chen, L., Liu, C., Zhao, W., Liu, L. (2018). An isogeometric approach of two dimensional acoustic design sensitivity analysis and topology optimization analysis for absorbing material distribution. Computer Methods in Applied Mechanics and Engineering, 336(39), 507–532. DOI 10.1016/j.cma.2018.03.025. [Google Scholar] [CrossRef]

42. Liu, C., Chen, L., Zhao, W., Chen, H. (2017). Shape optimization of sound barrier using an isogeometric fast multipole boundary element method in two dimensions. Engineering Analysis with Boundary Elements, 85, 142–157. DOI 10.1016/j.enganabound.2017.09.009. [Google Scholar] [CrossRef]

43. Chen, L., Zhang, Y., Lian, H., Atroshchenko, E., Bordas, S. (2020). Seamless integration of computer-aided geometric modeling and acoustic simulation: Isogeometric boundary element methods based on Catmull–Clark subdivision surfaces. Advances in Engineering Software, 149(2), 102879. DOI 10.1016/j.advengsoft.2020.102879. [Google Scholar] [CrossRef]

44. Chen, L., Lu, C., Zhao, W., Chen, H., Zheng, C. J. (2020). Subdivision surfaces-boundary element accelerated by fast multipole for the structural acoustic problem. Journal of Theoretical and Computational Acoustics, 28(2), 2050011. DOI 10.1142/S2591728520500115. [Google Scholar] [CrossRef]

45. Simpson, R., Liu, Z., Vazquez, R., Evans, J. (2018). An isogeometric boundary element method for electromagnetic scattering with compatible B-spline discretizations. Journal of Computational Physics, 362(39), 264–289. DOI 10.1016/j.jcp.2018.01.025. [Google Scholar] [CrossRef]

46. Li, K., Qian, X. (2011). Isogeometric analysis and shape optimization via boundary integral. Computer-Aided Design, 43(11), 1427–1437. DOI 10.1016/j.cad.2011.08.031. [Google Scholar] [CrossRef]

47. Lian, H., Kerfriden, P., Bordas, S. (2016). Implementation of regularized isogeometric boundary element methods for gradient-based shape optimization in two-dimensional linear elasticity. International Journal for Numerical Methods in Engineering, 106(12), 972–1017. DOI 10.1002/nme.5149. [Google Scholar] [CrossRef]

48. Lian, H., Kerfriden, P., Bordas, S. (2017). Shape optimization directly from CAD: An isogeometric boundary element approach using T-splines. Computer Methods in Applied Mechanics and Engineering, 317(4), 1–41. DOI 10.1016/j.cma.2016.11.012. [Google Scholar] [CrossRef]

49. Chen, L., Lu, C., Lian, H., Liu, Z., Zhao, W. et al. (2020). Acoustic topology optimization of sound absorbing materials directly from subdivision surfaces with isogeometric boundary element methods. Computer Methods in Applied Mechanics and Engineering, 362(3–5), 112806. DOI 10.1016/j.cma.2019.112806. [Google Scholar] [CrossRef]

50. Peng, X., Atroshchenko, E., Kerfriden, P., Bordas, S. (2017). Linear elastic fracture simulation directly from CAD: 2D nurbs-based implementation and role of tip enrichment. International Journal of Fracture, 204(1), 55–78. DOI 10.1007/s10704-016-0153-3. [Google Scholar] [CrossRef]

51. Peng, X., Atroshchenko, E., Kerfriden, P., Bordas, S. (2017). Isogeometric boundary element methods for three dimensional static fracture and fatigue crack growth. Computer Methods in Applied Mechanics and Engineering, 316(23–24), 151–185. DOI 10.1016/j.cma.2016.05.038. [Google Scholar] [CrossRef]

52. Doucet, A., Freitas, N., Gordon, N. (2001). Sequential monte carlo methods in practice. New York, NY: Springer. [Google Scholar]

53. Hong, H., Chen, J. (1988). Derivations of integral equations of elasticity. Journal of Engineering Mechanics, 114(6), 1028–1044. DOI 10.1061/(ASCE)0733-9399(1988)114:6(1028). [Google Scholar] [CrossRef]

54. Yau, J., Wang, S., Corten, H. (1980). A mixed-mode crack analysis of isotropic solids using conservation laws of elasticity. Journal of Applied Mechanics, 47(2), 335–341. DOI 10.1115/1.3153665. [Google Scholar] [CrossRef]

55. Erdogan, F., Sih, G. (1963). On the crack extension in plates under plane loading and transverse shear. Journal of Basic Engineering, 85(4), 519–525. DOI 10.1115/1.3656897. [Google Scholar] [CrossRef]

56. Smith, D., Ayatollahi, M., Pavier, M. (2001). The role of T-stress in brittle fracture for linear elastic materials under mixed-mode loading. Fatigue & Fracture of Engineering Materials & Structures, 24(2), 137–150. DOI 10.1046/j.1460-2695.2001.00377.x. [Google Scholar] [CrossRef]

57. Wang, D., Wu, Z., Fei, Y., Zhang, W. (2014). Structural design employing a sequential approximation optimization approach. Computers and Structures, 134(4598), 75–87. DOI 10.1016/j.compstruc.2013.12.004. [Google Scholar] [CrossRef]

58. Moës, N., Dolbow, J., Belytschko, T. (1999). A finite element method for crack growth without remeshing. International Journal for Numerical Methods in Engineering, 46(1), 131–150. DOI 10.1002/(SICI)1097-0207(19990910)46:1¡131::AID-NME726¿3.0.CO;2-J. [Google Scholar] [CrossRef]

Appendix A: Fundamental Solution

The fundamental solutions of displacement integral equation Uij* and Tij* are

Uij*=18π(1-υ)μ[(3-4υ)δij ln(1r)+r,ir,j] (A.1)

Tij*=-28π(1-υ)r[A(nir,j-njr,i)+nmr,m(Aδij+2r,ir,j)] (A.2)

The fundamental solutions of traction integral equation D*ijk and S*ijk are

Dijk*=14π(1-υ)1r[(1-2ν)(δkir,j+δkjr,i-δijr,k)+2r,ir,jr,k]nk(s)(A.3)

Sijk*=μ2π(1-υ)1r2{2r,mn,m[(1-2ν)δijr,k+υ(δikr,j+δjkr,i)-4r,ir,jr,k]+2υ(nir,jr,k+njr,ir,k)+(1-2ν)(2nkr,ir,j+njδik+niδjk)-(1-4υ)nkδij}nk(s)(A.4)

Appendix B: Evaluation of Stress Intensity Factors

The M integral based on the J integral is an effective method to extract SIFs. The Jk integral is defined as follows:

Jk:= limΓε→0∫Γε(Wδjk-σijui,k)njdΓ= limΓε→0∫ΓεPkjnjdΓ(B.1)

where Pkj is the Eshelby tensor, strain energy density W=1/2σijεij. The center point of polar coordinate system is located at the crack tip. The limited integral boundary Γε is an open circle with a center at the crack tip, as shown in Fig. A.1.

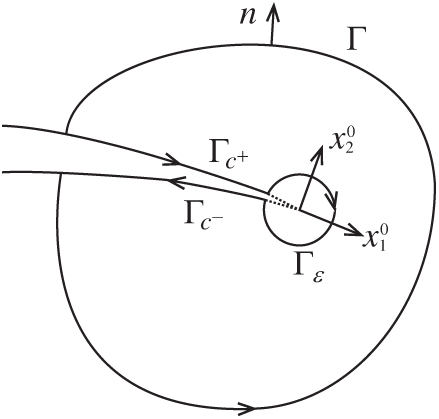
Figure A.1: J integral

Now, consider two independent equilibrium states of an elastically deformable object, the actual state (superscript ‘1’) and the auxiliary state (superscript ‘2’). Superimpose these two equilibrium states into one equilibrium state. It is assumed that the crack surface is flat in a sufficiently small radius of the contour circle. The conservation law can be reduced to the path-independent J integral along an arbitrary path Γε enclosing the crack tip located at the origin of the coordinates. Thus, the J integral of the superposition state can be expressed as

J(1+2)=∫Γε[12(σij(1)+σij(2))(εij(1)+εij(2))δ1j-(σij(1)+σij(2))∂(ui(1)+ui(2))∂x1]njdΓ(B.2)

Rearranging Eq. (B.2) into the following formulas:

J(1+2)=J(1)+J(2)+M(1,2)(B.3)

where

M(1,2)=∫Γε[W(1,2)δ1j-σij(1)∂ui(2)∂x1-σij(2)∂ui(1)∂x1]njdΓ(B.4)

with W(1, 2) being the mutual potential energy density of the elastic body.

The J integral under two states can be expressed as a function associated with K, as follows:

J(1+2)=J(1)+J(2)+2α(K1(1)K1(2)+K2(1)K2(2))(B.5)

where α=(1-υ2)E for plane strain problem, otherwise α=1E for plane stress problem.

Upon substitution of Eq. (B.3) into (B.5), we can obtain new expression of the M integral, as follows:

M(1,2)=2α(K1(1)K1(2)+K2(1)K2(2))(B.6)

The M integral shown in Eqs. (B.4) and (B.6) only involves interaction terms, which can be directly used to solve the mixed mode crack problem of linear elastic solids.

After SIFs are calculated, the direction of crack propagation can be determined by the maximum hoop stress criterion, the discriminant equation is as follows:

θc=2arctan[-2(K2/K1)1+1+8(K2/K1)2](B.7)

where θc is the direction of crack propagation, in which the hoop stress is maximum. It can be seen that the accuracy of crack propagation simulation is mainly determined by K2/K1.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.